Sparse Binary Relation Representations for Genome Graph Annotation

Abstract

High-throughput DNA sequencing data are accumulating in public repositories, and efficient approaches for storing and indexing such data are in high demand. In recent research, several graph data structures have been proposed to represent large sets of sequencing data and to allow for efficient querying of sequences. In particular, the concept of labeled de Bruijn graphs has been explored by several groups. Although there has been good progress toward representing the sequence graph in small space, methods for storing a set of labels on top of such graphs are still not sufficiently explored. It is also currently not clear how characteristics of the input data, such as the sparsity and correlations of labels, can help to inform the choice of method to compress the graph labeling. In this study, we present a new compression approach, Multi-binary relation wavelet tree (BRWT), which is adaptive to different kinds of input data. We show an up to 29% improvement in compression performance over the basic BRWT method, and up to a 68% improvement over the current state-of-the-art for de Bruijn graph label compression. To put our results into perspective, we present a systematic analysis of five different state-of-the-art annotation compression schemes, evaluate key metrics on both artificial and real-world data, and discuss how different data characteristics influence the compression performance. We show that the improvements of our new method can be robustly reproduced for different representative real-world data sets.

1. Introduction

Over the past decade, there has been an exponential growth in the global capacity for generating DNA sequencing data (Stephens et al., 2015). Various sequencing efforts have started to amass data from populations of humans (UK10K Project, 2015) and other organisms (Weigel and Mott, 2009; Zhang 2015). For these well-studied organisms, already assembled reference sequences are the common starting point for comparative and functional analyses. Unfortunately, a large proportion of DNA sequencing data, in particular data originating from nonmodel organisms or collected in metagenomics studies, are lacking a genome reference. Whereas general guidelines exist for the former case (Church et al., 2011), genome assembly for metagenomics is much less well defined. Its vastness and the currently lacking standards for indexing such data make an integrated analysis daunting even for field experts.

To make this host of data efficiently searchable, it is necessary to employ a search index. However, when building an index on the sequence data alone, only presence or absence of a query can be tested. To support relating queries to information such as source genomes, haplotypes, or functional annotations, additional labels must be associated with the index. To facilitate this, approaches for storing additional data on an indexed graph have been suggested, such as the graph positional Burrows–Wheeler transform (Novak and Paten, 2016) for storing haplotype information as genome graphs or succinct representations of labeled de Bruijn graphs (Iqbal et al., 2012; Almodaresi et al., 2017; Muggli et al., 2017) for the representation of sets of sequences. In this context, dynamic representations of such data have also recently received attention (Mustafa et al., 2018; Pandey et al., 2018).

The problem of efficiently representing these types of relations is also addressed in other fields. Commonly referred to as compressed binary relations, a growing body of theoretical work addresses such approaches (Barbay et al., 2013). Successful applications of similar techniques include the efficient representation of large web graphs (Brisaboa et al., 2009) and Resource Description Framework (RDF) data sets (Álvarez-García et al., 2011). We provide a more detailed description of some of these approaches in Section 2.

In this study, we present a new method for compressing abstract binary relations. Providing as background a comprehensive benchmark of existing compression schemes, we show that our approach has superior performance on both artificial and real-world data sets.

Our article has the following structure: after introducing our notation, we begin by defining the abstract graph, and the associated annotation structures that we wish to compress (Section 2.1). We then provide descriptions of our proposed compression technique and competing methods (Section 2.2). Finally, we compare the compression performance of these methods on different types of graph annotations (Section 3) and close with a brief discussion of our results and an outlook on future study (Section 4).

2. Methods

After introducing our notation, we give an overview of all methods implemented for this study and provide a description of our methodological contributions.

2.1. Preliminaries

We operate in the following setting: we are given a k-dimensional de Bruijn graph over a set of given input sequences S. The node set V shall be defined as the set of all consecutive subsequences of length k (k-mers) of sequences in S

$$V=\left\{s_{i:i+k-1}|s\in S,i=1,\dots ,|s|-k+1\right\},$$ (1)

where s_i:j denotes the subsequence of s from position i up to and including position j, and |s| is the length of s. A directed edge exists from node u to node v, if u_2:k = v_1:k − 1.

To represent relations between sources of the input sequences S and the nodes V, we now define the concept of a labeled de Bruijn graph and proceed by discussing the more general problem of representing a graph labeling.

Each node $v\in V$ that we refer to as an object is assigned a finite set of labels $\ell \left(v\right)\subset L$. We represent this graph labeling as a binary relation $ℛ\subset V\times L$. A trivial representation of $ℛ$ taking $\left|V\right|\cdot \left|L\right|$ bits of space is a binary matrix $A\in {\left\{0,1\right\}}^{\left|V\right|\times \left|L\right|}$. We use Aⁱ and A_j to denote its rows and columns, respectively.

In the following sections, we discuss various methods described in the recent literature and present our improvements in efficiently representing $ℛ$. In addition to minimal space, we also require that the following set of operations can be carried out efficiently on the compressed representation of $ℛ$:

• query_labels $\left(v\right)=\left\{l\in L|\left(v,l\right)\in ℛ\right\}$. Given an object $v\in V$ (a k-mer in the underlying de Bruijn graph), return the set of labels $\ell \left(v\right)$ assigned to it.

• query_objects $\left(l\right)=\left\{v\in V|\left(v,l\right)\in ℛ\right\}$. Given a label $l\in L$ (e.g., a genome or sample ID), return the set of objects assigned to that label.

• query_relation $\left(v,l\right)$. Given an object $v\in V$ and a label $l\in L$, check whether $\left(v,l\right)$ is in the relation $ℛ$, $queryrelation\left(v,l\right)=1_{\left\{\left(v,l\right)\in ℛ\right\}}$.

2.2. Binary relation representation schemes

For compressing the binary relation $ℛ$, we consider the following representations suggested in the recent literature. As an abstraction, we use the representation of $ℛ$ as a binary matrix $A\in {\left\{0,1\right\}}^{\left|V\right|\times \left|L\right|}$ (referred to as the binary relation matrix) to illustrate the individual methods.

2.2.1. Column-major sparse matrix representation

As a simple baseline technique, we compress the positions of the nonzero indices in each column independently using Elias–Fano encoding (Okanohara and Sadakane, 2007). Although this method does not take into account similarity between columns for compression, this feature allows for a trivial parallel construction implementation in which each column is computed in a separate process. For our experiments, this serves as the initial representation of the binary matrix, which is then queried during the construction of all other matrix representations.

2.2.2. Flat row-major representation

As a second baseline method, this representation concatenates all rows of A into a joint vector that is subsequently compressed using Elias–Fano encoding. This approach, for instance, is used by VARI (Muggli et al., 2017) and its extensions (Alipanahi et al., 2018).

2.2.3. Rainbowfish

The current state-of-the-art for genome graph labeling is a row-major representation of the binary relation matrix A in which an optimal coding is constructed for the set of rows in A (Almodaresi et al., 2017). More precisely, let $A^{i_1},\dots ,A^{i_r}\in {\left\{0,1\right\}}^{\left|L\right|}$ denote the unique rows of A, sorted by their number of occurrences in A in nonincreasing order, where $r\le \left|V\right|$. To encode A, we start by forming a matrix $A\prime \in {\left\{0,1\right\}}^{r\times \left|L\right|}$ of sorted unique rows, $A{\prime }_j^t=A_j^{i_t}$. Then we compress $A\prime$ with the flat row-major representation using an RRR vector (named after the initials of the three original authors Raman et al. (2002) as the underlying storage technique and construct a coding vector $(i\left(v\right)-1)v\in V$, where $i\left(v\right)$ maps each node $v\in V$ to the index of the row in $A\prime$ corresponding to the labeling of v. The coding vector is represented in a variable-length packed binary coding with a delimiter vector (Almodaresi et al., 2017) compressed into an RRR vector (Raman et al., 2002).

2.2.4. Binary relation compressed with wavelet trees

This method involves a translation of the $\left|ℛ\right|$ nonzero elements of A into a string, which is then represented using a conventional wavelet tree (Barbay et al., 2013). Given the binary relation matrix, its set bits are iterated in row-major order and their respective column indices are stored contiguously in a string over the alphabet $\left\{1,\dots ,\left|L\right|\right\}$ represented with a wavelet tree that enables efficient queries. The number of set bits in each row of A is stored in a delimiter vector using unary coding and compressed into an RRR vector.

2.2.5. Hierarchical compressed column-major representation (BRWT)

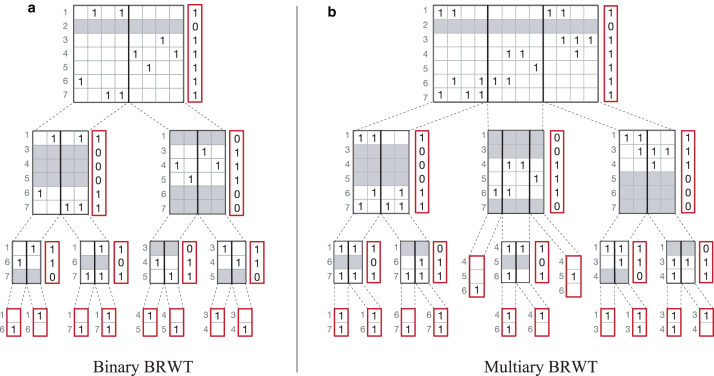
Described as binary relation wavelet trees in the original literature (Barbay et al., 2013), in contrast to binary relation compressed with wavelet trees (BinRel-WT), this representation directly acts on binary matrices without translation into a sequence. First, an index vector I with elements $I_i={\vee }_j{A}_j^i$ is computed by merging all matrix columns through bitwise OR operations on the rows and stored to represent the root of the tree. Then, the rows composed entirely of 0's are discarded from A and two equal-sized submatrices $A\prime$ and $A\prime \prime$ (which may contain rows composed entirely of 0's) of the binary relation matrix A are constructed by splitting A and are passed to the left and right children of the root. The compression proceeds recursively. Construction terminates when a node is assigned a single column, which is stored as its index column (Fig. 1a). For reconstruction of the matrix elements, it is sufficient to only store the index vectors associated with each node of the BRWT.

FIG. 1.

Schematic of hierarchical compressed column-major representations. (a) BRWT for the binary case. Gray rows correspond to all-zero rows, also indicated through the vector to the right of each matrix. Each child encodes only nonzero rows of the submatrix passed to it by its respective parent. Numbers to the left of each matrix are the respective row-indices in the initial matrix. (b) Multi-BRWT in the multiary case. Notation is as in the binary case. Stored vectors are shown in red. BRWT, binary relation wavelet tree.

In the next section, we consider the problem of topology optimization during BRWT construction and propose Multi-BRWT, an extension of BRWT that allows its nodes to have arbitrary number of children as well as to arbitrarily distribute the columns of a parent node to its children. Afterward, we propose a two-step approach for Multi-BRWT construction along with two specific algorithms as its implementation for improving the compression performance of Multi-BRWT.

2.3. Multiary, topology-optimized BRWTs

Our first extension to the BRWT scheme is the introduction of an n-ary tree topology, Multi-BRWT (Split n), allowing for matrices to be vertically split into more than two submatrices (Fig. 1b). The construction and querying for Multi-BRWT (Split n) is analogous to the case of binary BRWT. In computational experiments on artificial and real-world data, we show that in most cases, Multi-BRWT (Split n) with arity >2 provides a higher compression ratio than the simple binary BRWT scheme (Section 3). Note that Multi-BRWT (Split n) with the maximum allowed arity $n=\left|L\right|$ is equivalent to the baseline column-major sparse matrix representation as it keeps all columns of the input binary relation matrix unchanged except for the case when the input matrix has all-zero rows.

To proceed with our second extension, let us consider binary relations with far fewer labels than objects, $\left|L\right|\ll \left|V\right|$, a condition that is commonly met in annotated genome graphs from biological data. In these contexts, the number of k-mers is usually in the billions and the number of labels is on the order of thousands (Section 3.2).

Our second extension consists in introducing arbitrary assignments of columns from the matrices encoded in the nodes of the Multi-BRWT to their children. These assignments are represented by dictionaries stored in the Multi-BRWT nodes, but the $\left|L\right|\ll \left|V\right|$ constraint makes the space overhead from storing these negligible compared with the space needed to encode the index vectors. Thus, we exclude the problem of representing these assignments from further consideration and leave that as a small technical detail.

We now focus on the problem of constructing a Multi-BRWT structure that satisfies certain local optimality conditions with respect to compression ratio.

2.3.1. Problem setting

Let us set this problem formally. Given a binary matrix A, let $\tau$ be the set of all Multi-BRWTs representing A (i.e., the set of all rooted trees with $\left|L\right|$ labeled leaves). Let $Size\left(I\right)$ denote the size of a compressed binary vector I in bits. For instance, if I is of length n with m set bits, $Size\left(I\right)=n$ for an uncompressed bit vector, and $Size\left(I\right)\approx \lceil {log}_2\left(\right.\begin{array}{c}n\\ m\\ \end{array}\left)\right.\rceil$ for RRR vectors (Raman et al., 2002). We then neglect the space required for dictionaries defining the column assignments and we define the size of the Multi-BRWT $T\in \tau$ as the space required to store all its index vectors including the vectors in leaves:

$$Size\left(T\right):={\sum }_{i\in N}Size\left(I_i\right),$$ (2)

where N is the set of all nodes of the Multi-BRWT T and I_i corresponds to the index vector stored in node i. Thus, we wish to find an optimal Multi-BRWT by minimizing the storage space,

$$T^{\ast }={arg\; min}_{T\in \tau }Size\left(T\right).$$ (3)

We refer to this as the Multi-BRWT problem.

2.3.2. Optimized Multi-BRWT construction

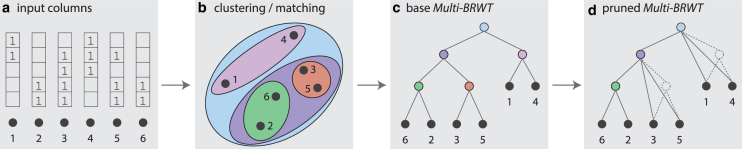
By analogy to the NoSQL table compaction problem (Ghosh et al., 2015), it can be shown that Multi-BRWT constrained on the space of binary trees with the uncompressed bit vector representation as the underlying structure for storing the index vectors is NP-hard. Thus, we propose a two-step approach for finding a good Multi-BRWT structure (Fig. 2). First, we build a binary Multi-BRWT by hierarchical clustering of the index vectors according to their similarity, the number of shared set bits. Then, we optimize the arity of the chosen Multi-BRWT by selecting a node subset $N\prime$, which includes the root and leaves of the base Multi-BRWT, $\left\{r,v_1,\dots ,v_{\left|L\right|}\right\}\subset N\prime \subset N$. To keep the resulting Multi-BRWT valid (allowing for reconstruction of the initial matrix A), we reassign all nodes in $N\prime$ to their nearest common ancestors remaining in $N\prime$.

FIG. 2.

Schematic describing the construction of Multi-BRWT. (a) The columns of the input binary matrix depicted as numbered black dots are considered independently. (b, c) Columns are hierarchically pair-matched based on number of shared entries, forming the base Multi-BRWT topology. (d) Pruning internal nodes of Multi-BRWT to optimize the tree structure for a smaller representation size.

As a specific implementation of the proposed two-step construction approach, we consider two heuristic greedy optimization procedures. In the first step, we perform greedy matching of the index vectors starting from the columns of the input binary relation matrix, and repeat recursively for the aggregated parent index vectors until we merge all into a single index vector placed in the root. In the second step of the construction approach, we consider another greedy algorithm for optimizing the size of the Multi-BRWT by removing some of its internal nodes and thereby increasing the arity of the tree.

2.3.3. Greedy pairwise matching for finding a base Multi-BRWT approximation

To find an initial approximate solution to the Multi-BRWT problem (base Multi-BRWT), we propose a greedy algorithm in which an initial greedy pairwise matching (GPM) step is performed on the columns of the input binary relation matrix A to optimize their initial order before construction (Fig. 2a–c). Given the input columns $A_1,\dots ,A_{\left|L\right|}$ and their corresponding object queries $o_i=queryobjects\left(i\right)$, we first compute cardinalities of their pairwise intersections $s_{ij}=|o_i\cap o_j|$. Then, we sort all the computed similarities $\left\{s_{ij}\right\}$ in nonincreasing order and match pairs of columns greedily. Afterward, we compute the aggregated index columns by merging the matched columns through bitwise-OR operations to form the index vectors and repeat this algorithm recursively.

2.3.4. Efficient pairwise distance estimation

The proposed greedy approximation method takes as input a matrix of pairwise column similarities $\left\{s_{ij}\right\}$. For m input columns of length n, computing each entry of this matrix costs $O\left(n\right)$, and thus, the time complexity of computing the full similarity matrix is $O\left(n{m}^2\right)$, which is a considerable overhead for data sets with a typical size of $m\sim 10^3$ and $n\sim 10^9$. To make the estimation of the pairwise similarities cheaper, we approximate these on a submatrix composed of rows sampled randomly from matrix A. Moreover, we prove the following lemma to show that using just $O\left(ln\left(m\right)∕{\epsilon }^2\right)$ random rows is sufficient for approximating the pairwise similarities with a small relative error $\epsilon$ with high probability, if each column has a sufficiently large number of set bits.

Lemma 1 (Subsampling lemma). Suppose we are given subsets of a universe set, $o_1,\dots ,o_m\subset \left\{1,\dots ,n\right\}$, with the minimum cardinality $d={min}_{i=1}^m\left|o_i\right|$, $d>0$. We sample the elements of $\left\{1,\dots ,n\right\}$ independently with the same probability p to form a sampled set of objects $S\subset \left\{1,\dots ,n\right\}$ and define subsampled sets as ${õ}_i=o_i\cap S$. Consider the union cardinalities $u_{ij}=|o_i\cup o_j|$ with their approximators ${û}_{ij}=\frac{1}{p}|{õ}_i\cup {õ}_j|$. For all $0<\epsilon <1$, $0<\delta <1$, and

$$p\ge min\left\{\right.\frac{3ln\left(\frac{m^2+m}{\delta }\right)}{d{\epsilon }^2},1\left\}\right.,$$

we claim

$$Pr\left(\right.{\bigcap }_{i,j=1}^m\left\{|{û}_{ij}-u_{ij}|<\epsilon u_{ij}\right\}\left)\right.\ge 1-\delta .$$

See Section 2 in the Supplementary Data for proof.

According to Lemma 1, with the subsampling technique we can approximate the union cardinalities up to an $\epsilon$-fraction with high probability. Thus, for instance, for estimating the number of set bits in the bitwise OR of each pair of $m=3000$ columns in a matrix with $n=10^9$ rows, where each column has at least $d=6\cdot 10^6$ set bits, with imprecision factor $\epsilon =0.1$ and target probability $1-\delta =0.98$, it is sufficient to subsample just $pn=3nln\left(\right.\frac{m^2+m}{\delta }\left)\right.∕d{\epsilon }^2<10^6$ rows of the matrix. Similar bounds can be obtained for sufficiently large intersection cardinalities, estimated in the proposed GPM algorithm.

2.3.5. Refining Multi-BRWT by pruning

Starting the procedure in the leaves' parents and applying it to each node except for the root recursively, we estimate the cost of removing each current node by the following formula:

$$CostRem\left(v\right)={\sum }_{c\in Children\left(v\right)}Size\left(I\prime \left(c\right)\right)-\left[Size\left(I\left(v\right)\right)+{\sum }_{c\in Children\left(v\right)}Size\left(I\left(c\right)\right)\right],$$ (4)

where $I\left(v\right)$ denotes the index vector stored in the node v and $I\prime \left(c\right)$ denotes the updated index vector that would be stored in the node c if its parent v was removed and the node c was reassigned to its grandparent. Now we simplify the formula for estimating the cost of removing a node in Multi-BRWT by introducing an assumption that the size of bit vector I of length n with m set bits is fully defined by these two parameters, that is, $Size\left(I\right)=Size\left(n,m\right)$. Now, it is easy to see that after reassigning the node c with the index vector $I\left(c\right)$ of length n_c with m_c set bits to the parent of its parent v with index vector $I\left(v\right)$ of length n_v with m_v set bits, the node c updates and replaces its index vector $I\left(c\right)$ with a vector $I\prime \left(c\right)$ of length n_v with m_c set bits. This provides us with the following simplified formula for estimating the cost of removing a node from the Multi-BRWT

$$CostRem\left(v\right)={\sum }_{c\in Children\left(v\right)}Size\left(n_v,m_c\right)-\left[Size\left(n_v,m_v\right)+{\sum }_{c\in Children\left(v\right)}Size\left(n_c,m_c\right)\right].$$ (5)

Equation (5) can be efficiently computed without rebuilding the current structure of the Multi-BRWT. As a result, a decision about removing node v from the Multi-BRWT is made if the cost $CostRem\left(v\right)$ is negative, leading thereby to a decrease of the Multi-BRWT in size. In our practical implementation we use the following formula for approximating the size required for storing an RRR bit vector (Navarro and Providel, 2012) with block size t: $Size\left(n,m\right)=\lceil {log}_2\left(\right.\begin{array}{c}n\\ m\\ \end{array}\left)\right.\rceil +n\lceil {log}_2\left(t+1\right)∕t\rceil .$

2.4. Implementation details

We implement the underlying de Bruijn graph as a hash table storing k-mers packed into 64 bit integers with 64 bit indexes assigned to the k-mers, or as a complete de Bruijn graph represented by a mapping of k-mers to $4^k$ row indexes of the binary relation matrix.

In the column-major representation, the columns of the binary relation matrix are stored using bit vectors represented with Elias-Fano encoding (sd-vector) implemented in sdsl-lite (Gog et al., 2014). The same data structure is used for storing the single long vector in the row flat representation.

BinRel-WT (sdsl) compressor uses the implementation of wavelet tree from the sdsl-lite library, using an RRR vector to store its underlying bit vector. The delimiter vector uses the RRR vector implementation from sdsl-lite.

The BinRel-WT compressor uses the binary relation implementation from Ramírez (2016). This implementation stores the underlying bit vector of the wavelet tree in uncompressed form.

Our BRWT is implemented as a tree in memory, compressing the index vectors as RRR vectors. To avoid multiple passes through the matrix rows, we construct the BRWT using a bottom-up approach. Given a fixed clustering of the matrix columns, the leaves of the BRWT are constructed first, followed by their parents constructed for the index vectors propagated from the children nodes. To speed up the greedy matching algorithm, we sample randomly $10^6$ rows in each experiment and use those to approximate the number of bits shared in the input columns and the index vectors during the Multi-BRWT construction. When optimizing the tree arity (as described in Section 2.3), we use the formula $Size\left(n,m\right)=\lceil {log}_2\left(\right.\begin{array}{c}n\\ m\\ \end{array}\left)\right.\rceil +n\lceil {log}_2\left(t+1\right)∕t\rceil$ as an estimate for the size of bit vector I of length n with m set bits, which is provided by the authors of sdsl-lite for the implementation of RRR vectors (Gog et al., 2014). We use a block size of $t=63$.

All SD vectors are constructed with default template parameters, whereas all RRR vectors are constructed with a block size of 63.

2.4.1. Code availability

All methods implemented and evaluated in this article are available at (https://github.com/ratschlab/genome_graph_annotation).

2.5. Data

2.5.1. Simulated data

To profile our compressors, we generated several different series of synthetic binary matrices of varying densities (see Section 1 in the Supplementary Data for a more detailed description). In total we generated three different kinds of series: (i) random matrices with uniformly distributed set bits, (ii) initially generated random matrix rows duplicated and permuted randomly, and (iii) initially generated random matrix columns duplicated and permuted randomly. The motivation behind these series is as follows: the best performing state-of-the-art compressors exploit redundancy between rows of the binary relation matrix (Pandey et al., 2018). However, the usual structure of annotated de Bruijn graphs often implies a correlation structure on the columns not necessarily leading to redundant rows, for instance when the sequences of many similar or closely related samples are inserted. Although for a small (and sufficiently highly correlated) number of columns this correlation translates into rows and increases the number of redundant ones, for larger label sets this is usually not the case. Thus, approaches exploiting correlation structure on the columns might fare better. To test this hypothesis, we generated three different kinds of synthetic data, reflecting uncorrelated rows/columns, redundant rows, and redundant columns for series (i), (ii), and (iii), respectively. Please note that approach (ii) is the most favorable for the state-of-the-art, as row redundancy rather than high correlation is simulated.

2.5.2. Real-world data

For evaluating all approaches in a real-world setting, we have chosen two data sets well known in the community and representative of typical applications.

2.5.3. Kingsford human RNA-Seq

This data set consists of 2652 Human RNA-Seq experiments originally drawn from Solomon and Kingsford (2018) and subsequently used in Pandey et al. (2018) for comparison.

2.5.4. NCBI RefSeq

This data set consists of all 79,448 reference sequences from Release 88 of the NCBI RefSeq database (O'Leary et al., 2016). Each sequence has been annotated with its associated family rank taxonomic ID from the NCBI Taxonomy (Agarwala et al., 2017). This results in a total of 3173 unique labels for the sequences.

3. Results and Discussion

3.1. Experiments on artificial data

Based on the artificial data set described in Section 2.5, we evaluated how the compression performance changes depending on the characteristics of the input binary relation matrix A of a simple structure.

3.1.1. Dependency of compression ratio on matrix structure

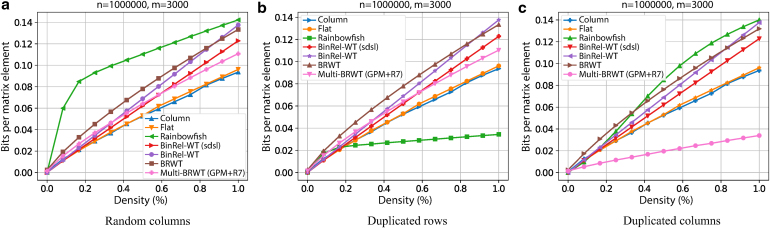
One of the key characteristics of the binary relation matrix A is its density, the number of set bits divided by the total number of entries in A. For reference, the labels for a sequencing-based de Bruijn graphs typically exhibit very low densities, commonly $<0.5\%$. Especially in this low-density region, we find that the properties of the binary relation matrix have a strong effect on the compression ratio of individual methods. A second determinant of performance is whether any assumptions are made on the properties of the data.

On sparse fully random data, the baseline compressors fare very well (Fig. 3a), as no assumptions can be made about relationships. Notably, Rainbowfish, which exploits redundancy among the rows, generates considerable overhead for very low densities. In the field of BRWT methods, the Multi-BRWT is closest to the best performing choices. In the setting of redundant rows (data set ii); (Fig. 3b), as expected, Rainbowfish shows the strongest performance, clearly exploiting the row redundancy. Again, among the BRWT methods, the Multi-BRWT performs best.

FIG. 3.

Size of the representation of $A\in {\left\{0,1\right\}}^{{10}^6\times 3\cdot {10}^3}$ with densities $d<0.01$ using different approaches: (a) uniformly random bits, (b) uniformly random rows with multiplicity 5, and (c) uniformly random columns with multiplicity 5. We expect approach (c) to be best reflecting the real-world data of a de Bruijn graph built on related sequences. BinRel-WT, binary relation compressed with wavelet trees; GPM, greedy pairwise matching.

Finally, in the setting that comes closest to a typical task of labeling de Bruijn graphs derived from sequencing data (Fig. 3c), the Multi-BRWT approach shows superior performance. Exploiting shared patterns in columns of the matrix, Multi-BRWT achieves a fivefold improvement in compression ratio compared with Rainbowfish and more than twofold compared with the closest competitor. Notably, the baseline binary BRWT has no advantage over the other baseline methods. Furthermore, we observe that this performance gain increases with the total number of columns in the matrix (Supplementary Figs. S1 and S2).

3.2. Experiments on real-world data

To compare the compression performance of the considered methods under a variety of conditions, we have constructed two test data sets that exhibit different matrix sparsity characteristics.

3.2.1. Kingsford human RNAseq (2652 read sets)

We filtered the 2652 raw sequencing read sets with the KMC (Kokot et al., 2017) tool to extract frequent unique canonical k-mers (defined as the lexicographical minimum of the k-mer and its reverse complement) from each ($k=20$). We used the same k value and thresholds for the k-mer frequency level as Pandey et al. (2018). Using the k-mers extracted, we constructed a de Bruijn graph with 3,693,178,415 nodes and annotated these with their source read sets, which resulted in 2586 labels (66 filtered read sets were empty) and a binary relation (annotation) matrix of density $\sim 0.19\%$. As a baseline for comparison, we used the straightforward column-compressed annotation, which required a total of 36.56 Gigabytes of space. We used this as a starting point to convert the annotation into the other formats.

The results are summarized in Table 1 and Supplementary Table 1 (for RRR vectors of block size 127). As expected, the simple row-based and BinRel-WT representations require >30 Gb in total. The current state-of-the-art method, Rainbowfish, reduces this by 23% to 23.16 Gb, exploiting the redundancy of rows in the input matrix. The basic BRWT benefits from the patterns shared by columns and drastically improves on Rainbowfish, showing a 39% lower size. We further reduce this size through our generalized approach using Multi-BRWT. Although some increase in arity reduces size compared with the binary case, a higher arity does not necessarily translate into lower space, as certain submatrices do not benefit from being grouped. The smallest fixed-arity representation is Multi-BRWT (Split 5), requiring 13 Gb of storage space and 222 minutes of compute time to construct with four threads (375 minutes of total user time measured with the g-time utility).

Table 1.

The Measured Size of the Compressed Binary Relation Matrix for Different Representations, in Gigabytes

Methods	Kingsford	RefSeq
Column	36.56	80.18
Flat	41.21	121.60
Rainbowfish	23.16	136.65
BinRel-WT	49.57	N/A
BinRel-WT (sdsl)	31.44	150.59
BRWT	14.05	57.24
Multi-BRWT (Split 3)	13.20	53.95
Multi-BRWT (Split 5)	13.01	53.09
Multi-BRWT (Split 7)	13.27	53.54
Multi-BRWT (Split 10)	13.54	54.77
Multi-BRWT (Split 13)	14.10	56.25
Multi-BRWT (GPM)	10.60	50.13
Multi-BRWT (GPM + Relax 3)	10.16	47.20
Multi-BRWT (GPM + Relax 5)	9.94	44.22
Multi-BRWT (GPM + Relax 7)	9.94	44.03
Multi-BRWT (GPM + Relax 10)	9.95	43.73
Multi-BRWT (GPM + Relax 20)	9.95	43.62

Multi-BRWT (Split n) denotes the n-ary BRWT. Multi-BRWT (GPM) denotes the binary BRWT optimized with the GPM. Multi-BRWT (GPM + Relax t) denotes the Multi-BRWT (GPM) with internal nodes pruned to reduce the representation size, where each node has at most t children. The construction times can be found in the Supplementary Data.

BinRel-WT, binary relation compressed with wavelet trees; BRWT, binary relation wavelet tree; GPM, greedy pairwise matching.

Bold values are max in each block.

We improved the compression performance of a binary BRWT through the GPM procedure described in Section 2.3. This strategy further decreases the size by another 18% to 10.6 Gb. Finally, optimizing the tree topology using the GPM procedure and selectively removing internal nodes (reassigning children to their grandparents) while maintaining a constraint on each node's maximum number of children leads to the smallest space achieved in our experiments. By applying this technique, we decrease the required space to 9.94 Gb (Multi-BRWT [GPM + Relax 5], with at most five children for each node). This is a 29% improvement over the basic BRWT representation and a 57% improvement over Rainbowfish. The Multi-BRWT (GPM + Relax 5) representation took 187 and 141 minutes of the compute time with 30 threads (858 and 252 minutes of total user time) for the first and the second stages of the construction algorithm, respectively. (See Supplementary Table 2 for an overview of all construction times.)

3.2.2. RefSeq reference genomes

Compression of the complete RefSeq genome annotation (release 88) resulted in a de Bruijn graph of dimension $k=15$ containing $n=1,073,741,824$ nodes, leading to a binary relation matrix of n rows and $m=3173$ columns with density $\sim 3.8\%$, which is relatively high for a genome graph annotation and can be explained by the small k-mer size used.

This is a substantially larger data set with less dependency between labels (columns). With the Multi-BRWT (GPM + Relax 20) representation, we were able to achieve a compressed storage size of only 43.6 Gb (Table 1). Conversion from the column-compressed representation to Multi-BRWT (GPM + Relax 20) took 625 and 733 minutes of the compute time with 30 threads (32 and 37 hours of total user time) for the first and the second Multi-BRWT construction stages, respectively, which is quite reasonable for a real-world setting.

Also here, the basic BRWT method improves drastically over the column compressed baseline (29%), and the Multi-BRWT approach considerably surpasses the basic BRWT method (24% reduction in size). One can see that the state-of-the-art method Rainbowfish performs very poorly on the RefSeq data set, which can be explained by the high density of the annotation matrix.

The construction of the BinRel-WT representation exceeded our available memory (2 Tb).

All experiments were performed on a Intel(R) Xeon(R) CPU E7-8867 v3 (2.50 GHz) processor from ETH's shared high-performance compute systems.

3.2.3. Supplementary results

Compression ratios for methods with underlying RRR vector block size of 127 can be found in the Supplementary Data.

4. Conclusion

We have presented a series of compressed representation methods for binary relations, building upon and improving on the existing literature. By generalizing BRWTs to multiary trees with improved partitioning schemes and adaptive arity to reduce data representation overhead, we have improved on state-of-the-art compression techniques for both simulated and real-world biological data sets.

We have shown that the structure of the input data has a strong influence on the compression performance and methods such as Rainbowfish benefit from presence of redundancy in rows or their correlations (when multiple objects carry a similar set of labels). It is noteworthy that in a real-world setting, where more and more labels are added to the set, the number of redundant rows decreases (ultimately leading to a set of mostly independent rows) and these methods work less well. Interestingly, it is especially this setting that regularly occurs in the labeling of genome graphs, where an underlying set of (related) sequences is assigned a growing set of different labels.

We have presented a method that copes very well with an increasing number of related columns as well as with the increasing density of the compressed binary matrix, and we showed that this results in considerable performance gains on both synthetic and typical real-world data. Our method, Multi-BRWT, led to a 24%–29% reduction in size compared with the basic BRWT scheme on real-world data, and to a 57%–68% reduction compared with the closest state-of-the-art method for compressing graph annotations, Rainbowfish.

A natural extension of this study will involve the utilization of dynamic vectors in the underlying storage of BRWTs to allow for their use in dynamic database contexts. Of particular interest are the ability to rearrange columns and use of dynamic compressed structures to avoid expensive decompression and recompression steps when performing updates.

Another interesting direction is the development of hybrid BRWT schemes that take the shape of Multi-BRWT but assign multiple columns to the leaves of the tree, using arbitrary schemes for compressing these. This would take advantage of both column and row structure in the binary relation matrix. These approaches are also beneficial for tackling the problem of achieving similar time complexities for both object and label queries on the compressed representation of the binary relations.

Overall, we conclude that, despite the advancements in compression over the recent years, there is still much room and many degrees of freedom in compressor design for further improvement.

Author Disclosure Statement

Gunnar Ratsch is a member of the advisory board of Computomics GmbH. All other authors declare they have no competing financial interests.

Funding Information

We thank the members of the biomedical informatics group for fruitful discussions and critical questions, and Torsten Hoefler and Mario Stanke for constructive feedback on the graph setup. Harun Mustafa and Mikhail Karasikov are funded by the Swiss National Science Foundation Grant No. 407540_167331 “Scalable Genome Graph Data Structures for Metagenomics and Genome Annotation” as part of Swiss National Research Programme (NRP) 75 “Big Data.”

Supplementary Material

Supplementary Data

Supplementary Table S1

Supplementary Table S2

Supplementary Figure S1

Supplementary Figure S2