Review of methods for space–time disease surveillance

Abstract

A review of some methods for analysis of space–time disease surveillance data is presented. Increasingly, surveillance systems are capturing spatial and temporal data on disease and health outcomes in a variety of public health contexts. A vast and growing suite of methods exists for detection of outbreaks and trends in surveillance data and the selection of appropriate methods in a given surveillance context is not always clear. While most reviews of methods focus on algorithm performance, in practice, a variety of factors determine what methods are appropriate for surveillance. In this review, we focus on the role of contextual factors such as scale, scope, surveillance objective, disease characteristics, and technical issues in relation to commonly used approaches to surveillance. Methods are classified as testing-based or model-based approaches. Reviewing methods in the context of factors other than algorithm performance highlights important aspects of implementing and selecting appropriate disease surveillance methods.

1. Introduction

Early detection of unusual health events can enable coordinated response and control activities such as travel restrictions, movement bans on animals, and distribution of prophylactics to susceptible members of the population. Our experience with Severe Acute Respiratory Syndrome (SARS), which emerged in southern China in late 2002 and spread to over 30 countries in 8 months, indicates the importance of early detection (Banos and Lacasa, 2007). Disease surveillance is the principal tool used by the public health community to understand and manage the spread of diseases, and is defined by the World Health Organization as the ongoing systematic collection, collation, analysis and interpretation of data and dissemination of information in order for action to be taken (World Health Organization, 2007). Surveillance systems serve a variety of public health functions (e.g., outbreak detection, control planning) by integrating data representing human and/or animal health with statistical methods (Diggle, 2003), visualization tools (Moore et al., 2008), and increasingly, linkage with other geographic datasets within a GIS (Odiit et al., 2006).

Surveillance systems can be designed to meet a number of public health objectives and each system has different requirements in terms of data, methodology and implementation. Outbreak detection is the intended function of many surveillance systems. In syndromic surveillance systems, early-warning signals are provided by analysis of pre-diagnostic data that may be indicative of people’s care-seeking behaviour during the early stages of an outbreak. In contrast, systems designed to monitor food and water-borne (e.g., cholera) pathogens are designed for case detection, where one case may trigger a response from public health workers. Similarly, where eradication of a disease in an area is a public health objective, surveillance may be designed primarily for case detection. Alternatively, where a target disease is endemic to an area, perhaps with seasonal variation in incidence, such as rabies, monitoring space–time trends may be the primary surveillance objective (Childs et al., 2000).

Surveillance systems differ with respect to a number of qualities which we term contextual factors. For evaluation of surveillance systems, this is well known, as the evaluative framework set out by the Centre for Disease Control and Prevention (CDC) encompasses assessment of simplicity, flexibility, data quality, acceptability, sensitivity, predictive value positive, representativeness, timeliness, and stability (Buehler et al., 2004). Selection of appropriate methods for space–time disease surveillance should consider system-specific factors indicative of the context under which they will be used (Table 1 ). These factors are summarized in Table 1, and are the axes along which we will review methods for space–time disease surveillance.

Table 1.

Contextual factors for evaluation of methods for space–time disease surveillance.

Factor	Description
Scale	The spatial and temporal extent of the system (e.g., local/regional/national/international)
Scope	The intended target of the system (e.g., single disease/multiple disease, single host/multiple host, known pathogens/unknown pathogens)
Function	The objective(s) of the systems (outbreak detection, outbreak characterization, outbreak control, case detection, situational awareness (Mandl et al., 2004, Buehler et al., 2004), bio-security and preparedness (Fearnley, 2008))
Disease characteristics	Is the pathogen infectious? Is this a chronic disease? How does it spread? What is known about the epidemiology of the pathogen?
Technical	The level of technological sophistication in the design of the system and its users (data type and quality, algorithm performance, computing infrastructure and/or reliability, user expertise)

There has been rapid expansion in the development of automated disease surveillance systems. Following the 2001 bioterrorism attacks in the United States, there was expanded interest and funding for the development of electronic surveillance networks capable of detecting a bioterrorist attack. Many of these were designed to monitor data that precede diagnoses of a disease (i.e., syndromic surveillance). By May 2003 there were an estimated 100 syndromic surveillance systems in development throughout the US (Buehler et al., 2003). Due to the noisy nature of syndromic data, these systems rely heavily on advanced statistical methods for anomaly detection. As data being monitored in syndromic systems precede diagnoses they contain a signal that is further removed from the pathogen than traditional disease surveillance, so in addition to having potential for early warning, there is also greater risk of false alarms (i.e., mistakenly signaling an outbreak) (Stoto et al., 2004).

One example is a national surveillance system called BioSense developed by the CDC in the United States. BioSense is designed to support early detection and situational awareness for bioterrorism attacks and other events of public health concern (Bradley et al., 2005). Data sources used in BioSense include Veterinary Affairs and Department of Defense facilities, private hospitals, national laboratories, and state surveillance and healthcare systems. The broad mandate and national scope of the system necessitated the use of general statistical methods insensitive to widely varying types, quality, consistency and volume of data. Two methods used in BioSense are a generalized linear mixed-model which estimates counts of syndrome cases based on location, day of the week and effects due to seasonal variation and holidays. Counts are estimated weekly for each syndrome-location combination. A second temporal surveillance approach computed for each syndrome under surveillance is a cumulative sum of counts where events are flagged as unusual if the observed count is two standard deviations above the moving average. The selection of surveillance methods in BioSense considered factors associated with heterogeneity of data sources and data volume among others.

Another example is provided by a state-level disease surveillance system developed for Massachusetts called the Automated Epidemiological Geotemporal Integrated Surveillance (AEGIS) system, where both time-series modelling and spatial and space–time scan statistics are used (Reis et al., 2007). The modular design of the system allowed for ‘plug-in’ capacity so that functionality already implemented in other software (i.e., SaTScan) could be leveraged. In AEGIS, daily visit data from 12 emergency department facilities are collected and analyzed. The reduced data volume and greater standardization enable more advanced space–time methods to be used as well as tighter integration with the system’s communication and alerting functions (Reis et al., 2007).

Decisions on method selection and utilization are based on a variety of factors, yet most reviews of statistical methods for surveillance data compare and describe algorithms from a purely statistical or computational perspective (e.g., Buckeridge et al., 2005, Sonesson and Bock, 2003, Yan et al., 2006). The selection of statistical approaches to surveillance for implementation as part of a national surveillance system is greatly impacted by design constraints due to scalability, data quality and data volume whereas the use of surveillance data for a standalone analysis by a local public health worker may be more impacted by software availability, learning curve, and interpretability. Selection of appropriate statistical methods is key to enabling a surveillance system to meet its objectives.

A frequently cited concern of surveillance systems is how to evaluate whether they are meeting their objectives (Reingold, 2003, Sosin and DeThomasis, 2004). A framework for evaluation developed by the CDC considers outbreak detection a function of timeliness, validity, and data quality (Buehler et al., 2004). The degree to which these factors contribute to system effectiveness may vary for different surveillance systems, especially where objectives and system experiences differ. For example, newly developed systems in developing countries may place a greater emphasis on evaluating data quality and representativeness, as little is known about the features of the data streams at early stages of implementation (Lescano et al., 2008). Algorithm performance is usually measured by sensitivity, specificity and timeliness. Sensitivity is the probability of an alarm given an outbreak, and specificity is the probability of no alarm when there is no outbreak. Timeliness is measured in number of time units to detection, and has been a focus of systems developed for early outbreak detection (Wagner et al., 2001). The importance of each of these measures of performance need to be evaluated in light of the system’s contextual factors outlined in Table 1.

Our goal in this review of approaches to space–time disease surveillance is to synthesize major surveillance methods in a way that will focus on the feasibility of implementation and highlight contrasts between different methods. First, we aim to place methods in the context of some key aspects of practical implementation. Second, we aim to highlight how methods of space–time disease surveillance relate to different surveillance contexts. Disease surveillance serves a number of public health functions under varying scenarios and methods need to be tailored and suited to particular contexts. Finally, we provide guidance to public health practitioners in understanding methods of space–time disease surveillance. We limit our focus to methods that use data encoded with both spatial and temporal information.

This paper is organized as follows. The next section describes space–time disease surveillance. Following, is a description of different statistical approaches to space–time disease surveillance with respect to the contextual factors outlined in Table 1. We conclude with a summary and brief discussion of our review.

2. Space–time disease surveillance methods

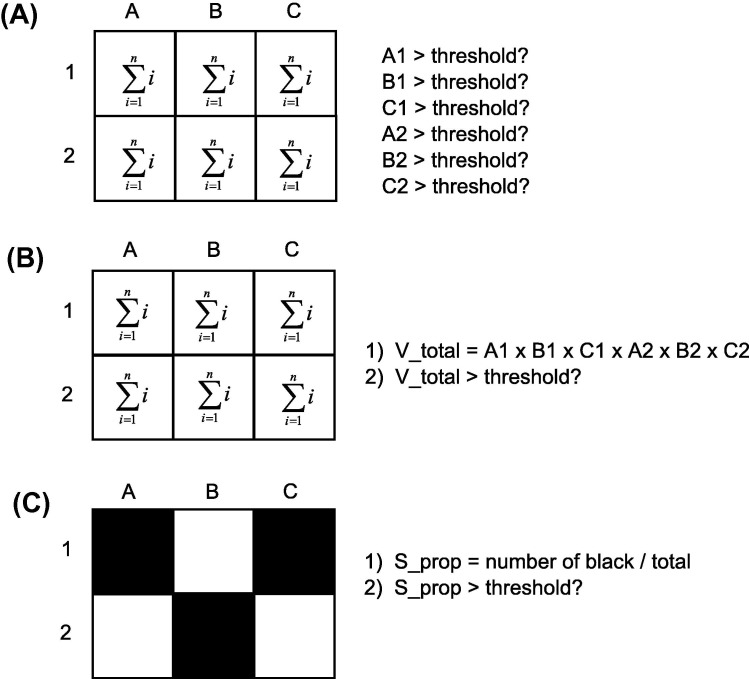
Methods for space–time disease surveillance can address a surveillance objective in a variety of ways. Most methods assume a study area made up of smaller, non-overlapping sub-regions where cases of disease are being monitored. The variable under surveillance is the count of the number of cases. In retrospective analysis, the data are fixed and methods are used to determine whether an outbreak occurred during the study period, or characterize the spatial-temporal trends in disease over the course of the study period (Marshall, 1991). In the prospective scenario, the objective is to determine whether any single sub-region or collection of sub-regions is undergoing an outbreak (currently), and analysis occurs in an automated, sequential fashion as data accumulate over time. Prospective methods require special consideration as data do not form a fixed sample from which to make inferences about (Sonesson and Bock, 2003). Parallel surveillance methodologies compute a test statistic separately for each sub-region and signal an alarm if any of sub-regions are significantly anomalous (Fig. 1 A). While in vector accumulation methods, test statistics in a parallel surveillance setting are combined to form one general alarm statistic (Fig. 1B). Conversely, a scalar accumulation approach computes one statistic over all sub-regions for each time period (Frisen and Sonesson, 2005) (Fig. 1C). For example, Rogerson (1997) used the Tango (1995) statistic to monitor changes in spatial point patterns.

Fig. 1.

Methods for prospective surveillance. (A) Parallel surveillance where a test statistic is computed separated for each region under surveillance and each assessed individually. (B) Vector accumulation where test statistics in a parallel setting are combined to form one alarm statistic which is evaluated. (C) Scalar accumulation where on statistic is computed over all regions under surveillance and evaluated.

2.1. Statistical tests

Statistical tests in space–time disease surveillance generally seek to determine whether disease incidence in a spatially and temporally defined subset is unusual compared to the incidence in the study region as a whole. Thus, this class of methods is designed to detect clusters of disease in space and time, and suit surveillance systems designed for outbreak detection. Most spatial cluster detection methods such as the Geographical Analysis Machine (Openshaw et al., 1987), density estimation (Bithell, 1990, Lawson and Williams, 1993), Turnbull’s method (Turnbull et al., 1990), the Besag and Newell (1991) test, spatial autocorrelation methods such as the Gi∗ (Getis and Ord, 1992), and LISAs (Anselin, 1995), and the spatial scan statistic (Kulldorff and Nagarwalla, 1995) are types of statistical tests. The development of methods for space–time cluster detection naturally evolved from these purely spatial methods. We can stratify methods in the statistical test class into three types: tests for space–time interaction, cumulative sum methods, and scan statistics.

2.1.1. Tests for space–time interaction

Space–time interaction of disease indicates that the cases cluster such that nearby cases in space occur at about the same time. The form of the null hypotheses is usually conditioned on population, and can factor in risk covariates such as age, occupation, and ethnicity. Detecting the presence of space–time interaction can be a step towards determining a possible infectious etiology for new or poorly understood diseases (Aldstadt, 2007). Additionally, non-infectious diseases exhibiting space–time interaction may suggest the presence of an additional causative agent, such as a point source of contamination and/or pollution or an underlying environmental variable. These methods require fixed samples of space–time data representing cases of disease.

All tests for space–time interaction consider the number of cases of disease that are related in space–time, and compare this to an expectation under a null hypothesis of no interaction (Kulldorff and Hjalmars, 1999). The Knox test (1964) uses a simple test statistic which is the number of case pairs close both in space and in time. This count is compared to the null expectation conditional on the number of pairs close only in space, and the number of pairs close only in time; i.e., the times of occurrence of the cases are independent of case location. A major shortcoming of the Knox (1964) method is that the definition of “closeness” is arbitrary. Mantel’s (1967) test addresses this by summing across all possible space–time pairs, while Diggle et al. (1995) identify clustering at discrete distance bands in the space–time K function. For infectious diseases, it is likely that near space–time pairs are of greater importance, so Mantel suggests a reciprocal transformation such that distant pairs are weighted less than near pairs. The Mantel test can in fact be used to test for association between any two distance matrices, and is often used by ecologists to test for interaction between space and another distance variable such as genetic similarity (Legendre and Fortin, 1989).

The reciprocal transformation used in the Mantel statistics assumes a distance decay effect. While this may be appropriate for infectious diseases, for non-infectious diseases or diseases about which little is known, this assumed functional form of disease clustering may be inappropriate. A different approach is taken by Jacquez (1996) where relations in space and time are defined by a nearest neighbour relation rather than distance. Here, the test statistic is defined by the number of case pairs that are k nearest neighbours in both space and time. When space–time interaction is present, the test statistic is large. Another method for testing an infectious etiology hypothesis given by Pike and Smith (1974), assesses clustering of cases relative to another control disease, though selection of appropriate controls can be difficult.

The scale of the disease surveillance context can impact the selection of space–time interaction tests because these tests are sensitive to changes in the underlying population at risk (population shift bias). Therefore, large temporal scales will be more likely to exhibit changes in population structure and introduce population shift bias. An unbiased version of the Knox test given by Kulldorff and Hjalmars (1999) accounts for this by adjusting the statistic by the space–time interaction inherent in the background population. Changes in background population over time can be incorporated into all space–time interaction tests using a significance test based on permutations conditioned on population changes. However, this obviously requires data on the population over time which may not always be easy to obtain.

Space–time interaction tests are univariate and therefore only suitable for testing cases of a single disease. Consideration of multiple host diseases is possible, though there is no mechanism to test for interaction or relationships between different host species. Another major consideration is the function of the surveillance system or analytic objective. Interaction tests can only report the presence or absence of space–time interaction. They give no information about the spatial and temporal trends in cases, nor consider naturally occurring background heterogeneity. A final point is that these tests use case data, and therefore require geo-coded singular event data, making these methods unsuitable when disease data are aggregated to administrative units.

2.1.2. Cumulative sum (CUSUM) methods

Cumulative sum methods for space–time surveillance developed out of traditional statistical surveillance applications such as quality control monitoring of industrial manufacturing processes. In CUSUM analysis, the objective is to detect a change in an underlying process. In application to disease surveillance, the data are in the form of case counts for sub-regions of a larger study area. A running sum of deviations is recalculated at each time period. For a given sub-region, a count y_t of cases at time t is monitored as follows

$$S_t=\max (0\text{,}{S}_{t-1}+y_t-k)$$ (1)

where S_t is the cumulative sum alarm statistic, k is a parameter which represents the expected count, so that observed counts in exceedence of k are accumulated. At each time period, an alarm is signalled if S_t is greater than a threshold parameter h. If a CUSUM is run long enough, false alarms will occur as exceedences are incrementally accumulated. The false-positive rate is controlled by the expected time it takes for a false alarm to be signalled, termed the in-control average run length, denoted ARL₀. The ARL₀ is directly related to the threshold value for h, which can be difficult to specify in practice. High values of h yield long ARL₀ and vice versa. In practice, approximations are used to estimate a value for h for a chosen ARL₀ (Siegmund, 1985), though this remains a key issue in CUSUM methods.

The basic univariate CUSUM in (1) can be extended to incorporate the spatial aspect of surveillance data. In this sense, CUSUM is a temporal statistical framework around which a space–time statistical test can be built. In an initial spatial extension, Rogerson (1997) coupled the (global) Tango statistic (1995) for spatial clustering in a CUSUM framework. For a point pattern of cases of disease, compute the spatial statistic, and use this value of the statistic to condition the expected value at the next time period. Observed and expected values are used to derive a z-score which is then monitored as a CUSUM (Rogerson, 2005a). One scalar approach taken by Rogerson (2005b) is to monitor only the most unexpected value, or peak, of each time period as a Gumbel variate (Gumbel distribution is used as a statistical distribution for extreme values). An additional approach is to compute a univariate CUSUM in a parallel surveillance framework (Woodall and Ncube, 1985). Here the threshold parameter h must be adjusted to account for the multiple tests occurring across the study area. Yet this approach takes no account of spatial relationships between sub-regions (i.e., spatial autocorrelation).

CUSUM surveillance of multiple sub-regions can be considered a multivariate problem where a vector of differences between the observed and expected counts for each sub-region is accumulated. Spatial relationships between sub-regions can be incorporated by explicitly modelling the variance–covariance matrix. Rogerson and Yamada (2004) demonstrate this approach by monitoring a scalar variable representing the multivariate distance of the accumulated differences between observed and expected over all sub-regions. This is modelled as

$$\mathit{MC}{1}_t=\max (0\text{,}||S_t||-{\mathit{kn}}_t)$$ (2)

where ||S_t|| = $\sqrt{S_t^t{\sum }^{-1}{S}_t}$, and $\sum$ is a variance–covariance matrix capturing spatial dependence, and S_t is a 2 ×  p vector of differences between observed and expected cases of disease in time t for each p sub-region (Rogerson and Yamada, 2004).

CUSUM methods are attractive for prospective disease surveillance because they offer a temporal statistical framework within which spatial statistics can be integrated. They therefore overcome one of the limitations of traditional spatial analysis applied to surveillance in that repeated testing over time (and space) can be corrected for. A full description of the inferential properties of the CUSUM framework is given by Rogerson (2005a). These methods are therefore most appropriate for long temporal scales, especially when historical data are used to estimate the baseline. Multivariate CUSUM given by Rogerson and Yamada (2004) is for a singular disease over multiple sub-regions, but could be used to monitor multiple diseases over multiple sub-regions. This may be most applicable in a syndromic surveillance application. The simplicity of univariate CUSUM makes training and technical expertise less of a factor than the multivariate case. Multivariate CUSUM is also more difficult to interpret and specification of the threshold parameter requires simulation experimentation or a large temporal extent from which to establish a baseline.

2.1.3. Scan statistics

Scan statistics developed originally for temporal clustering by Naus (1965) test whether cases of disease in a temporally defined subset exceed the expectation given a null hypothesis of no outbreak. The length of the temporal window is varied systematically in order to detect outbreaks of different lengths. This approach was first extended to spatial cluster detection in the Geographical Analysis Machine (Openshaw et al., 1987). The spatial approach looks for clusters by scanning over a map of cases of disease using circular search areas of varying radii. Kulldorff and Nagarwalla (1995) refined spatial scanning with the development of the spatial scan statistic which adjusts for the multiple testing of many circular search areas. The spatial scan statistic overcomes the multiple-testing problem (common to many local spatial analysis methods) by taking the most likely cluster defined by maximizing the likelihood that the cases within the search area are part of a cluster compared to the rest of the study area. Significance testing for this one cluster is then assessed via Monte Carlo randomization. Secondary clusters can be assessed in the same way and ranked by p-value.

In Kulldorff (2001), the spatial scan statistic is extended to space–time, such that cylindrical search areas are used where the spatial search area is defined by cylinder radius, and the temporal search area is defined by cylinder height. In prospective analysis, candidate cylinders are limited to those that start at any time during the study period and end at the current time period (i.e., alive clusters). Significance is determined through randomization and comparing random permutations to the likelihood ratio maximizing cylinder in the observed data. An additional consideration to take account of multiple hypothesis testing over time (correlated sequential tests) is given by including previously tested cylinders (which may be currently ‘dead’) in the randomization procedure (Kulldorff, 2001).

The space–time scan statistic (Kulldorff, 2001) approaches the surveillance problem in a novel way and aptly handles some key shortcomings of other local methods (multiple testing, locating clusters, pre-specifying cluster size). However, a limitation is that the expectation is conditional on an accurate representation of the underlying population at risk, data which may be hard to obtain. In long term space–time surveillance scenarios, accurate population estimates between decennial censuses are rare or must be interpolated. In syndromic applications, where cases are affected by unknown variations in care-seeking behaviours, the raw population numbers may not accurately reflect the at-risk population. In Kulldorff et al. (2005), the expected value for each unit under surveillance is estimated from historical case data rather than population data. Generating the expected value from the history of the process under surveillance is most suitable for real-time prospective surveillance contexts where the current state of the process is of interest. This extension allows the application of the space–time scan statistic in a wider range of surveillance applications.

A remaining limitation of the cylindrical space–time scan statistic is the use of circular search area over the map. The power of the scan statistics that use circular-based search areas decline as clusters become more irregular in shape, for example, for cases clustered along a river valley or where disease transmission is linked to the road network. The spatial scan statistic has been extended to detect irregularly-shaped clusters in Patil and Taillie (2004) and Tango and Takahashi (2005). Extensions of these approaches to space–time are active areas of research. A space–time version of the Tango and Takahashi (2005) method uses spatial adjacency of areal units added incrementally up to K nearest neighbour units which are connected through time to form 3-dimensional prism search areas (Takahashi et al., 2008). A similar approach is given by Costa et al. (2007). However, these methods are very computationally intensive.

Scan statistics are one of the most widely used statistical methods for outbreak detection in surveillance systems. Space–time scan statistics are able to detect and locate clusters of disease, and can condition expected counts for individual sub-regions on population data or on previous case data, making these methods suitable for implementation where data volume is large. The scope of scan statistics, like most statistical tests, is limited to monitoring case data, either case event point data or counts by sub-region. Scan statistics are best served to detect and locate discrete localized outbreaks. Secondary clusters can be identified by ranking candidate clusters by their likelihood ratio. Yet region-wide outbreaks cannot be detected with scan-statistics because of the assumed form of a cluster as a compact geographical region where cases are greater than expected. Novel space–time methods that search for raised incidence via graph-based connectivity may model spatial relationships of disease processes more accurately than circular search areas. However, the computational burden and complexity of these approaches limits their use to expert analysts and researchers. At the root of the problem is a conceptual discrepancy between the definition of a disease outbreak (which disease surveillance systems are often interested in detecting) and a disease cluster (defined by spatial proximity) which is common to all statistical testing methods for space–time surveillance (Lawson, 2005).

2.2. Model-based approaches

Model-based approaches to surveillance developed recently as the need emerged to include other variables into the specification of our expectation of disease incidence. For example, we often expect disease prevalence to vary with age, gender, and workplace of the population under surveillance. Statistical models allow for these influences to adjust the disease risk through space and time. A second impetus for the development of statistical models for disease surveillance is that a large part of epidemiology concerned with estimating relationships between environmental variables and disease risk (i.e., ecological analysis) provided a methodological basis from which to draw. Modelling for space–time disease surveillance is relatively recent, and this is a very active area of statistical surveillance research. Again we stratify statistical models into three broad classes: generalized linear mixed models, Bayesian models, and models of specific space–time processes.

2.2.1. Generalized linear mixed models

Generalized linear mixed models (GLMM) offer a regression-based framework to model disease counts or rates using any of the exponential family of statistical distributions. This allows flexibility in the expected distribution of the response variable, as well as flexibility in the relationship between the response and the covariate variables (the link function). One application of this approach to prospective disease surveillance for detection of bioterrorist attacks is given by Kleinman et al. (2004). Here, the number of cases of lower respiratory infection syndromes in small geographic areas act as a proxy for possible anthrax inhalation. A GLMM approach is used to combine fixed effects for covariate variables (i.e., season, day of the week) with a random effect that accounts for varying baseline risks in different geographic areas. In Kleinman et al. (2004), the logit link function is used in a binomial logistic model to estimate the expected number of cases y_it in area i for time t. This is a function of the probability of an individual being a case in area i at time t and the number of people n_it in area i at time t.

$$E(y_{\mathit{it}}|b_i)=n_{\mathit{it}}{p}_{\mathit{it}}$$ (3)

This expectation is conditional on a location specific random effect b_i and is then converted to a z-score and evaluated to determine if it is unusual (i.e., an emerging cluster). This approach was extended to a model using Poisson random effects in Kleinman (2005). The use of GLMM in prospective surveillance has also been suggested for use in west nile virus surveillance due to the ease with which covariates can be included and flexibility in model specification (Johnson, 2008).

The GLMM approach has attractive advantages as a flexible modelling tool. Particularly, relaxation of distributional assumptions, flexibility in link functions, and the ability to model spatial relationships (at multiple spatial scales) as random effects make GLMM useful for prospective space–time disease surveillance. The scale and scope of the surveillance context does not limit a model-based approach, and models may be even more useful when data abnormalities such as time lags occur (as estimates can be based on covariates alone). One feature of GLMM that are important for many disease surveillance contexts are the ease with which spatial hierarchies can be incorporated. Ecological relationships that are structured hierarchically that impact disease emergence (e.g., climate, vegetation, vector life-cycle development) can be represented and accounted for. Further, human drivers of disease emergence (e.g., land-use policies, travel patterns, demographics) are often organized hierarchically through administrative units. In social sciences GLMMs are often used (i.e., multi-level models) that incorporate these ‘contextual effects’ on an outcome variable. A further advantage of GLMMs is their ability to incorporate spatial variation in the underlying population at risk by conditioning the expected value on the random effect component (b_i in Eq. (3)). Where fewer people are present, the expected value is adjusted toward the mean. This can somewhat account for the small-numbers problem of SMRs in epidemiology, reducing the likelihood of estimating extremely low expected values in rural areas.

2.2.2. Bayesian models

Bayesian models have been used extensively in disease mapping studies (Best et al., 2005, Lawson, 2009). Analysis of disease in a Bayesian framework centers around inference on unknown area-specific relative risks. Inference on this unknown risk distribution is based on the observed data y and a prior distribution. These are combined via a likelihood function to create a distribution for model parameters which can be sampled for prediction. Bayesian models have been applied for retrospective space–time surveillance (e.g., MacNab, 2003) and are now being developed for prospective space–time disease surveillance.

The basic Bayesian model can incorporate space and time dependencies. In Abellan et al. (2008) a model is described where the counts of disease are taken to be binomial distributed, and the next level of the model is composed of a decomposition of the unknown risks into model parameters for general risk, spatial effects, temporal effects, and space–time interaction. Estimation requires specifying prior distributions for each of the model components and sampling the posterior distribution via Monte Carlo markov chain (MCMC) methods. Here, the authors describe space–time Bayesian models for explanation of overall patterns of disease, speculating on their use in disease surveillance contexts. Rodeiro and Lawson (2006a) offer a similar model based on a Poisson distributed disease count. Specifically, the counts y_i are Poisson with mean a function of the expected number of cases e_ij in location i at time j and the area-specific relative risk rr_ij.

$$\log ({\mathit{rr}}_{\mathit{ij}})=u_i+v_i+t_j+{\gamma }_{\mathit{ij}}$$ (4)

Similar to Abellan et al. (2008), the log (rr_ij) are decomposed into spatial effects u_i, uncorrelated heterogeneity v_i, temporal trend t_j, and space–time interaction ${\gamma }_{\mathit{ij}}\text{.}$ Again, these components need prior distributions specified. For the spatial correlation term, a conditional autoregressive model (CAR) is suggested for modelling spatial autocorrelation. Residuals are then extracted from model predictions for incoming data and can be used to assess how well the data fits the existing model. As discussed in Rodeiro and Lawson (2006a), monitoring residuals in this way makes the detection of specific types of disease process change feasible by adjusting how residuals are evaluated. While adding to the complexity of the analysis, this may be of great use in a surveillance application.

Alternative proposals such as Bayesian cluster models with “a priori” cluster component for spatiotemporal disease counts was developed by Yan and Clayton (2006). More recently, Bayesian and empirical Bayes semi-parametric spatiotemporal models with temporal spline smoothing were developed for the analysis of univariate spatiotemporal small area disease and health outcome rates (MacNab, 2007a, MacNab and Gustafson, 2007, Ugarte et al., 2009) and multivariate spatiotemporal disease and health outcome rates (MacNab, 2007b). Tzala and Best (2008) also proposed Bayesian hierarchical latent factor models for the modelling of multivariate spatiotemporal cancer rates. These spatiotemporal models, with related Bayesian and empirical Bayes methods of inference, may also be considered for disease surveillance applications.

The statistical methodology for applying Bayesian models to surveillance in space–time is still being developed, and as such these approaches are suited primarily to researchers. Bayesian models are attractive because they allow expert and local knowledge of disease processes to be incorporated via the specification of prior distributions on model parameters. However, this can also be a drawback, as a subjective element is introduced to the model. It is generally recommended that sensitivity analysis be conducted on a variety of candidate priors for model parameters (e.g., MacNab and Gustafson, 2007, MacNab, 2007a). These technical aspects of model-fitting require advanced statistical training. A further complexity of Bayesian models is estimation. MCMC methods are required for generating the posterior distributions for these types of models and are computationally very demanding (although see Rodeiro and Lawson, 2006b). This might negate the use of these approaches in surveillance contexts that require daily refitting of models (i.e., fine temporal resolution), however, monthly or annual model refitting may be possible. As with GLMMs, Bayesian models lend themselves to modelling hierarchical spatial relationships, and this can be important for both ecological and human-mediated drivers of disease emergence.

2.2.3. Models of specific space–time processes

Some modelling approaches to surveillance have been designed to model specific types of spatial processes, generally represented as a realization from a statistical distribution. While all models require some distributional assumptions, those considered here purport to associate specific statistical processes with disease processes in the context of surveillance. In Held et al. (2005), a model is based on a Poisson branching process whereby outcomes are dependent on both model parameters describing a particular property (e.g., periodicity) and past observed data. Spatial and space–time effects can also be included as an ordinary multivariate extension. A useful aspect of this formulation for disease surveillance is the separation of the disease process at time t into two parts: an endemic part v and an epidemic part with conditional rate $\lambda y_{t-1}$

$${\mu }_t=v+\lambda y_{t-1}$$ (5)

The endemic component can also be adjusted for seasonality, day of the week effects and other temporal trends. Extended to the multivariate case, the model becomes

$${\mu }_t=n_{\mathit{it}}v+\lambda y_{i\text{,}t-1}$$ (6)

where the endemic rate adjusted by the number of people in area i at time t, and area-specific previous model estimates for the epidemic part. Spatial dependence can be incorporated by adding a spatial effects term that accounts for correlated estimates in $\lambda y_{i\text{,}t-1}$ via a weights matrix. However, this type of model yields separate parameters for each geographical unit.

A point process methodology for prospective disease surveillance is presented in Diggle et al. (2005). Point data representing cases are modelled with separate terms for spatial variation, temporal variation, and residual space–time variation. The method is local, in the sense that recent cases are used for prediction, producing continuously varying risk surfaces. However, there are also global model parameters which estimate the background variation in space and time estimated from historical data. Outbreaks are defined when variation in the residual space–time process exceeds a threshold value c. Different values for the threshold parameter are evaluated and exceedence probabilities are mapped. Model parameters are fixed allowing the model to be run daily on new data. However, as noted in Diggle et al. (2005), this may fail to capture unknown temporal trends, and periodic refitting may be required.

A different approach is given by Järpe (1999), which instead of decomposing the process into separate components, monitors a single parameter of spatial relationships in a surveillance setting. This is similar in spirit to Rogerson’s work (Rogerson, 1997) monitoring point patterns with spatial statistics, though here a specific underlying process is assumed: the Ising model. The Ising model represents a binary-state two dimensional lattice (sites coded 0 or 1). There are two parameters for the Ising model; one governs the overall intensity (probability of a site being a 1), and another the spatial interaction (probability of nearby sites being alike). In Järpe (1999), the intensity parameter is assumed equal and unchanging, and the surveillance is performed on the interaction parameter under different lattice sizes and types of change. The interaction parameter is essentially a global measure of spatial autocorrelation. This can then be monitored using temporal surveillance statistics such as CUSUM. Since the properties of the underlying model are known, Järpe is able to detect very small changes in spatial autocorrelation which could indicate the shift of a disease from endemic to epidemic. While significant spatial autocorrelation is often present at both endemic and epidemic states, changes in clustering can reveal threshold dynamics of the process in a surveillance setting. This is a common feature of forest insect epidemics (Peltonen et al., 2002). Further, the effect of the lattice size can easily be estimated, and as lattice size is increased, sensitivity to changes in the interaction parameter increases as well.

While most methods discussed thus far have been developed with the analysis of aggregated counts of disease in mind, analysis of sites on a lattice may have applicability in certain disease surveillance contexts. For example, square lattices are used for remotely sensed image processing, and surveillance of the presence or absence of a disease in these sampling units using an Ising model-based approach could incorporate remotely sensed environmental covariates (e.g., normalized differential wetness index) as is commonly done for zoonotic disease risk mapping and forecasting (Kitron et al., 1996, Rogers et al., 1996, Wilson, 2002). However, it is unclear how covariates are included in the Ising model. This highlights an important point with model-based approaches to prospective surveillance: the main advantage of models is to incorporate extra information and to estimate smooth relative risks, yet as models grow in complexity they become more difficult to re-fit. This has implications for how suitable models are in different surveillance contexts. Where the temporal scale is large, expected counts can be based on observed data rather than using census or other data sources. This is particularly important where diseases follow seasonal trends. With limited temporal data available, estimating model parameters may make be impacted by regular variation in disease occurrence. For surveillance systems monitoring many small areas (i.e., large spatial scale), the Held et al. (2005) model would be of limited value as separate parameters need to be estimated for every sampling unit. Broad scale patterns over large areas might better captured by the point process approach of Diggle et al. (2005). Although here, case event data with fine spatial resolution is required.

For all modelling approaches, complex decisions are required such as what covariates to include, how often to re-fit the model, how to test incoming data for fit against the existing model which require advanced statistical knowledge. This limits the applicability of modelling approaches to advanced analysts and researchers except for use in a black-box sense by analysts and public health practitioners. Surveillance models can be tailored to detect specific types of disease process changes, such as a region-wide increase, or small changes in spatial autocorrelation suggesting a shift from endemic to epidemic states. However, models also required additional tests to determine if incoming data differ from the expected (i.e., modelled) pattern of cases. Thus, in practice surveillance models are best utilized to estimate a realistic relative risk, and can then be combined with statistical tests such as CUSUM (Järpe, 1999) and scan statistics (Kleinman et al., 2005).

2.3. Emerging research areas

Research into space–time disease surveillance methods has increased dramatically over the last two decades. Many new methods are designed for specific surveillance systems, or are in experimental/developmental stages and not used in practical surveillance. Here, we report on some newly developed approaches for public health surveillance to alert readers to the most recent developments in these emerging research areas.

While test and model-based approaches to surveillance build on classical statistical methods, many recent space–time disease surveillance methods have been developed specifically to take advantage of advanced computing power and data sources. These approaches include networks (Reis et al., 2007, Wong and Moore, 2006) simulation-based methods such as agent-based models (Eubank et al., 2004) and bootstrap models (Kim and O’Kelly, 2008), and hidden markov models (Madigan, 2005, Sun and Cai, 2009, Watkins et al., 2009).

Other new methods are designed to address limitations of existing surveillance methods. One problem for most methods of surveillance, is the specification of the null hypothesis, or expected disease prevalence. While expected rates are generally conditional on population data, spatial heterogeneity in the background rates are rarely accounted for. That is, complete spatial randomness (CSR) is the underlying null model. Goovaerts and Jacquez (2004) have used geostatistical approaches, estimating spatial dependence of background rates via the semivariogram, to develop more realistic null models for disease cluster detection. The geostatistical framework has the advantage of estimating spatial dependence from the data, rather than defining it a priori via a spatial weights matrix as is common in disease mapping models.

Another problem common to most surveillance methods is that maps of disease represent either home address (case events) or small areas (tract counts). Unusual clusters on the map imply heightened risk is associated with those locations. However, movement of animals and people decouples the location of diagnosis from disease risk by modifying exposure histories. Methods that account for mobility may be an important area for future surveillance, especially in the context of real-time, prospective outbreak detection. The relationship between case, location, and exposure is further complicated by disease latency periods, which gives rise to space–time lags in diagnoses (Schaerstrom, 1999). This may be most important in the context of retrospective cluster analysis and investigation of possible environmental risk factors. Statistical tests have been developed to account for exposure history and mobility for case-control data (Jacquez and Meliker, 2009) and case-only data (Jacquez et al., 2007). Kernel-based approaches to risk estimation that incorporate duration at each location have been utilized for amyotrophic lateral sclerosis (Sabel et al., 2003). The general approach is to model and analyze the space–time path of individuals in the sense of Hägerstrand (1967). As personal location data continues to become ubiquitous due to new technology such as GPS-enabled cell phones, surveillance methods that account for individual space–time histories may see more application in public health surveillance.

3. Summary

The development of space–time disease surveillance systems holds great potential for improving public health via early warning and monitoring of health. The selection of which method(s) to implement in a given context is dependent on a variety of factors (Table 2 ). This review has demonstrated that there is no best method for all systems. There are many aspects to consider when thinking about methods for space–time disease surveillance. Many of the methods described in this review are active areas of research and new methods are constantly being developed. As more data sources become available, this trend is expected to continue, and the methods described here provide a snapshot of options available to public health analysts and researchers. A brief outline of some of the factors reviewed and how they relate to surveillance methods is given below.

Table 2.

Summary of contextual factors on methods of space–time disease surveillance.

Class	Type	Scale	Scope	Function	Characteristics	Technical
Test	CUSUM	Temporal statistical framework useful for long time periods of sequential surveillance	Univariate CUSUM useful for single diseases while multivariate CUSUM useful when multiple diseases or syndromes are under surveillance	Primarily for outbreak detection	Multivariate CUSUM is not sensitive to outbreak type (one extreme vs. many subtle rises) whereas the univariate is	Difficulty in specification and understanding of the threshold parameter
Test	Interaction	Population shift bias increases with spatial and temporal scale	Cannot analyze interactions and relationships in multiple host diseases	Can only detect presence of interaction. Limited utility for outbreak detection. Best used as screening method	Interaction tests cannot capture interactions and flows between units under surveillance (spatial autocorrelation)	Require geo-coded event data of cases of disease. Ease of understanding and interpretation. Subjectivity in specification of critical distances in space and time
Test	Scan	Space–time scan statistics are able to detect and locate clusters. Using the permutation-based approach can make use of temporal history of data. Appropriate mostly where there is a large volume of data in space and time	Scan statistics are designed to monitor one data stream, and therefore in and of themselves are not suitable for multiple disease. Can be combined with models as in Kleinman et al. (2005)	Monitoring p-values of primary and secondary clusters can be useful for assessing trends over time, although primary function is for discrete localized outbreak detection	Cylindrical search areas assume compact cluster form. Extensions using graph-based connectivity for search areas are computationally very demanding. Spatial relationships not defined by proximity may be more important for disease spatial processes	Can be used with point event data or count data. Ease of understanding and interpretation of results of analysis
Model	GLMM	Increase in utility as the size of the surveillance database grows. Temporal trends can be incorporated as model parameters. Frequent refitting of complex models can be difficult	Models can be formulated for risks, incidence and counts of diseases. Very flexible in how dependent variable is structured	Monitoring space–time trends in disease incidence, however, all modelling approaches need to be coupled with a statistical test to determine unexpected events (i.e., outbreaks)	Can incorporate hierarchical effects of covariates easily including spatial effects	The most accessible of modelling approaches but requires knowledge of statistical distributions. Limited mostly to researchers and statistical analysts. Flexible choice of statistical distributions compared to OLS modelling
Model	Bayesian	Same as above	Same as above	Same as above	Same as above	Priors need to be specified for model parameters. Advanced statistical knowledge required. Fitting complex space–time Bayesian models requires MCMC methods. Not suitable if need to be re-fit often
Model	Processes	Can be used with data of any scale as testing is against a specified process	Multiple hosts and pathogens can be accounted for though may be difficult to parameterize	Generally high sensitivity to detecting different types of change such as periodic outbreaks or gradual shifts away from the process. Needs to be coupled with a statistical test	Characteristics of disease (e.g., transmission, serial interval) can determine choice of process. Can also be used as exploratory tool	Models in this class vary greatly. Technical factors will be specific to individual process models selected

The spatial scale of the surveillance context is an important factor for selecting appropriate methods. Spatial effects (i.e., clustering) are likely only of interest when cases/counts collected over a relatively large, heterogeneous area are being analyzed. Over smaller more homogeneous areas, where spatial effects are negligible, temporal surveillance is optimal. When space–time surveillance is warranted, choice of which surveillance approach to use may be impacted by how spatial effects can be incorporated. Where spatial scale is small, one would likely focus on either process models or statistical tests which use an underlying distribution for the null hypothesis (i.e., Poisson model). The temporal scale of surveillance is also important. Large temporal scales can use either testing or modelling methods, and most suit methods where baselines are estimated from previous cases, such as with the space–time permutation scan statistic. Short temporal scales are not appropriate for models when diseases have complex day of the week effects or seasonal variation in incidence. Scale will also affect the computational burden placed on the system. Many approaches reviewed here, particularly statistical tests such as scan statistics, use approximate randomization to generate a distribution of a test statistic under the null hypothesis. Methods that utilize randomization procedures, while powerful, impose constraints when applied with large spatial–temporal datasets.

Most methods are designed for a single disease and all methods are suitable for single host diseases, but finer detail in case distribution may be important for multiple host zoonotic diseases. Stratification into separate diseases by host type will result in a loss of information as associations between host types will be lost. As zoonotic diseases make up the majority of emerging infectious diseases (Greger, 2007), multiple host surveillance methods are required. Multivariate tests such as multivariate CUSUM can be used to monitor multiple signals. Modelling approaches can also be used by creating a generalized risk index as the variable under surveillance. Multivariate extensions to existing methods can be used to monitor associations between two diseases, for example, human and animal strains of the same pathogen.

The objective of surveillance is one of the main drivers of method selection. All statistical tests are commonly used for outbreak detection. In general, modelling approaches are better suited to monitoring space–time trends. For what has been termed situational awareness, multiple signals are usually monitored. This is often the case in large syndromic applications such as BioSense and ESSENCE. These contexts are best suited to a modelling approach, as often heterogeneity needs to be modelled with covariates.

Consideration of technical expertise is required for practical disease surveillance. Broadly speaking, greater statistical expertise is required for model-based methods than testing (understanding model assumptions, parameterizing models, preparing covariate data, and interpreting output), while testing concepts are generally easier to grasp. However, for epidemiologists already familiar with generalized linear mixed models, some model approaches that incorporated space and time may be quickly attainable, such as that of Kleinman et al. (2004). Yet for analysts from a health geography or spatial analysis background, testing methods might be more familiar. In any case, the use of space–time surveillance methods in public health will only increase in the future, and it is important that training and education keep pace with the changing methods available for surveillance data analysis.