Causal role of motor preparation during error-driven learning

Summary

Current theories suggest that an error-driven learning process updates trial-by-trial to facilitate motor adaptation. How this process interacts with motor cortical preparatory activity—which current models suggest plays a critical role in movement initiation—remains unknown. Here, we evaluated the role of motor preparation during visuomotor adaptation. We found preparation time was inversely correlated to variance of errors on current trials, and mean error on subsequent trials. We also found causal evidence that intracortical microstimulation during motor preparation was sufficient to disrupt learning. Surprisingly, stimulation did not affect current trials, but instead disrupted the update computation of a learning process, thereby affecting subsequent trials. This is consistent with a Bayesian estimation framework, where the motor system reduces its learning rate, by virtue of lowering error sensitivity, when faced with uncertainty. This interaction between motor preparation and the error-driven learning system may facilitate new probes into mechanisms underlying trial-by-trial adaptation.

eTOC

Vyas et al. use microstimulation to establish a causal relationship between motor cortical preparatory activity and learning. Disrupting preparatory activity affects subsequent, but not stimulated trials. Preparatory activity plays a critical role in trial-by-trial update computations of a learning process.

Introduction

Current theories suggest that when an error is experienced during motor execution, sensory feedback carrying this signal is sent to a trial-by-trial learning process (Figure 1). This learning process is also thought to include as input an efference copy of the original outgoing motor command as well as sensory feedback during the movement epochs (Shadmehr et al., 2010; Wolpert et al., 1995). The learning process performs computations by comparing the efference copy with sensory feedback in order to generate an update that improves the behavior on the subsequent attempt (Figure 1, “update arrow”). The precise nature of the update computation and where in the brain such an error-driven process resides is still an active area of investigation (McNamee and Wolpert, 2019). The overall learning process comprises multiple distinct components, at least one of which is slow and error-driven, i.e., overcoming errors happens gradually on a trial-by-trial basis using efference copies and sensory feedback (Golub et al., 2015; Krakauer and Shadmehr, 2006; Krakauer et al., 2019; Shadmehr and Mussa-Ivaldi, 1994; Tanaka et al., 2009). Other components act on faster timescales, with varying sensitivities to error and retention characteristics (Smith et al., 2006).

Figure 1: Framework for trial-by-trial motor learning.

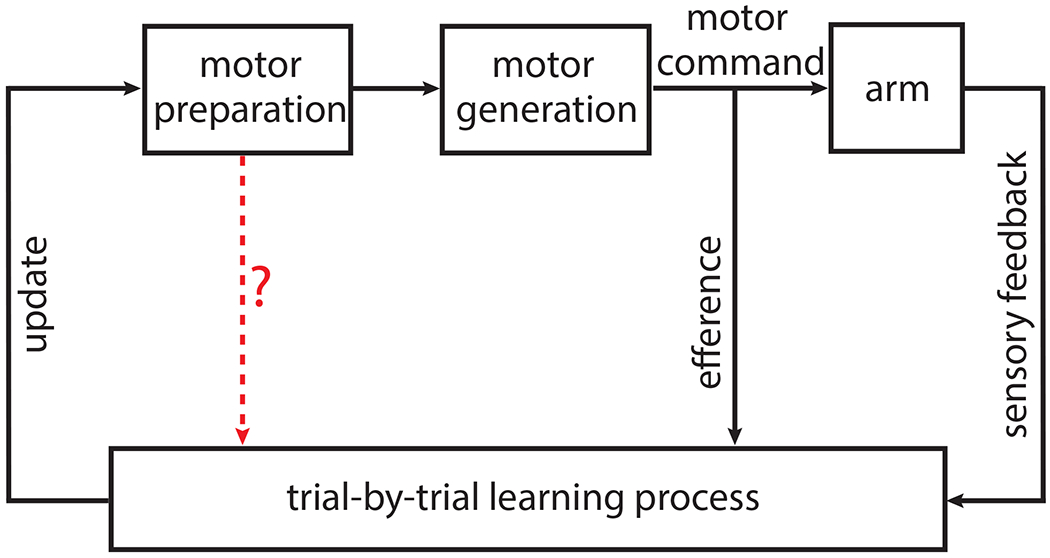
Conceptual block diagram for error-driven motor learning. Beginning with motor preparation at the top left, the loop represents the progression of one trial during motor adaptation into an update that will affect subsequent trials. Motor efference signals and sensory feedback contribute to error-driven learning. The red arrow represents the key hypothesis being tested in this study: does there exist an interaction between neural activity during motor preparation and a trial-by-trial learning process, and if so, what is the nature of this interaction? This is consistent with standard formulations of control theory; the brain (here, motor preparation and motor generation) is viewed as a “controller,” whose function is to generate commands that drive a “plant” (here, the arm). During learning, sensory feedback and efference copies are analyzed by a “state estimator” (here, the learning process), which performs internal state updates to facilitate feedback control (McNamee and Wolpert, 2019).

For reaching movements, the overall trial-by-trial learning process ultimately causes systematic changes to neural activity in motor cortex, driving changes in behavior that overcomes the errors. Current models of motor cortical function propose that movement-period activity evolves according to the laws of a neural dynamical system, whose initial state is set during motor preparation (Afshar et al., 2011; Ames et al., 2014; Churchland et al., 2006a, 2012, 2010b; Elsayed et al., 2016; Kaufman et al., 2014; Lara et al., 2018; Michaels et al., 2016). While many prior studies have explored the link between preparatory neural activity and movement production in motor cortex (Even-Chen et al., 2019; Riehle and Requin, 1993; Tanji and Evarts, 1976; Wise, 1985), there is little evidence for its role, if any, during motor learning (Kawai et al., 2015).

Recent reports have identified that a correlate of error-driven learning can be readout on single trials from the motor cortical neural state during preparation (Stavisky et al., 2017; Vyas et al., 2018). That is, learning induces systematic changes in neural activity during motor preparation that correlate with improvements in behavior. While this demonstrates that the error-driven learning process influences neural activity during preparation, it remains unknown whether preparatory activity directly contributes back to the error-driven learning process. Recently, Sheahan and colleagues demonstrated that preparing for different movement sequences allows human participants to adapt successfully in contexts that would otherwise interfere (Sheahan et al., 2016). These findings suggest that neural activity specifically during motor preparation (and not execution) is sufficient to separate motor memories and prevent interference. While these behavioral findings do not implicate a particular brain region, previous studies have shown that preparatory activity in motor cortex reflects precise details of the upcoming movement; these details have the potential to inform a learning process (Even-Chen et al., 2019; Pandarinath et al., 2018; Shenoy et al., 2013). This raises the tantalizing possibility that preparatory activity could directly provide trial-by-trial information to the update computation of the learning process to facilitate motor adaptation (hypothesis schematized in Figure 1 via red arrow).

In this study, our experiments and analyses reveal an intriguing relationship between motor preparation and the update computation of a trial-by-trial learning process. Concretely, we show that (1) preparation time is inversely correlated with the learning, (2) intracortical microstimulation causes no statistically significant deficit on the current trial, but instead disrupts learning on the subsequent trial, and (3) deficits to learning are consistent with a Bayesian estimation framework, whereby the learning process reduces sensitivity to error on stimulated trials. To our knowledge, these results constitute the first causal evidence for the role of motor preparation during learning and provide a new lens through which to investigate the computations underlying trial-by-trial adaptation.

Results

Two Rhesus monkeys (P and V) were trained to move the handle of a passive manipulandum to drive a computer cursor from the center of a screen to one of seven radially arranged targets (Figure 2A, top). Each session was broken into three blocks: baseline, adaptation, and washout (Figure 2A, bottom). During the adaptation block, a visuomotor rotation (VMR) was applied (±45°), where animals had to move their arm in the opposite direction to the VMR angle (i.e., “anti-VMR” direction) in order to drive the cursor directly to the target. Both animals adapted to the VMR at a similar rate as previously reported and exhibited after-effects during post-adaptation washout (Figure 2B–C).

Figure 2: Task design and behavior.

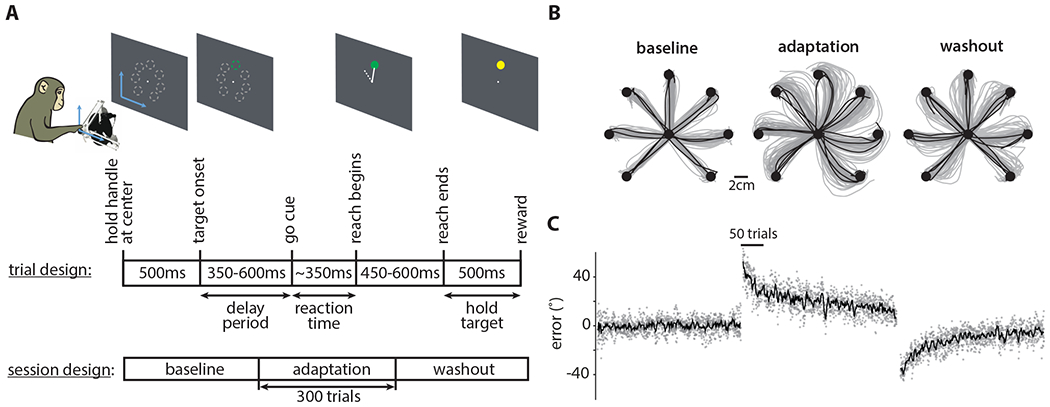
A. Monkeys performed 2D cursor movements using a passive manipulandum. Reaches were made to one of seven targets arranged radially 8cm from the center of the screen. When a VMR was applied, the cursor’s movements were offset by the corresponding angle. (Top) Each trial had an instructed delay period uniformly sampled from 350-600ms (for the data presented in (B) and (C)) that preceded the go-cue. (Bottom) Each session had baseline, adaptation, and washout blocks consisting of 300 trials each.

B. Representative arm movement trajectories from Monkey V for the baseline, adaptation, and washout blocks from one session. Gray and black correspond to the first 90% and the last 10% of the trials in each block respectively.

C. Plotted is the error angle during baseline, adaptation, and washout as a function of trial number for five sessions from Monkey V. Gray dots correspond to individual trials, and the black line corresponds to the median. The error was computed as the angle between the cursor’s position (measured at the halfway point to the target) and the vector pointing from the workspace center to the target.

Longer preparation times yield greater learning

We began by replicating previous findings that more preparation time, i.e., a longer delay period, yields faster reaction times (Churchland et al., 2006b) (Figure 3A; Monkey P: Normal Z = 12.82, p < 1e-30; Monkey V: Normal Z = 12.79. p < 1e-30); previous studies have shown similar relationships with other movement parameters, e.g., accuracy (Marinovic et al., 2017). We hypothesized an analogous relationship may hold between preparation time and the degree of compensation. Contrary to this prediction, we found no statistically significant relationship between mean kinematic error and preparation time (Figure 3B; Monkey P: n = 52, t = −0.02, p = 0.9; Monkey V: n = 55, t = 1.61, p = 0.11). Previous studies have explored the role of task-related variability in learning, where increased variability drives early learning (Wu et al., 2014). Here, we found that the variance of the error distribution was inversely correlated with preparation time (Figure 3C; Monkey P: n = 48, t = −2.75, p < 0.01; Monkey V: n = 53, t = −2.69, p < 0.01). Previous studies have also suggested that the trial-by-trial learning process has access to a history of observed errors, i.e., the brain recognizes errors it has previously experienced (Herzfeld et al., 2014) and prior experience of errors (and not successful actions) is necessary and sufficient for learning retention or savings (Leow et al., 2016). We hypothesized that more preparation time could facilitate learning, i.e., decrease in kinematic error on the subsequent trial. Consistent with this prediction, we found that errors were inversely correlated with preparation time on the previous trial (Figure 3D; Monkey P: n = 50; t = −2.79, p < 0.01; Monkey V: n = 55, t = −2.4, p < 0.05). This suggests that more preparation time on a given trial facilitates a better update to some learning process, which manifests as decreased error on the subsequent trial. These results dovetail with previous human behavioral findings that explore the role of preparation time and learning. Haith and colleagues found that savings was not observed if after preparing a particular reach the target was switched at the go-cue, thereby allowing little preparation time for the movement (Haith et al., 2015). Fernandez-Ruiz and colleagues found that reaction times were positively correlated with error reduction rate, and if reaction times were constrained, subjects showed slower error reduction rates (Fernandez-Ruiz et al., 2011).

Figure 3: Longer preparation times yield greater learning.

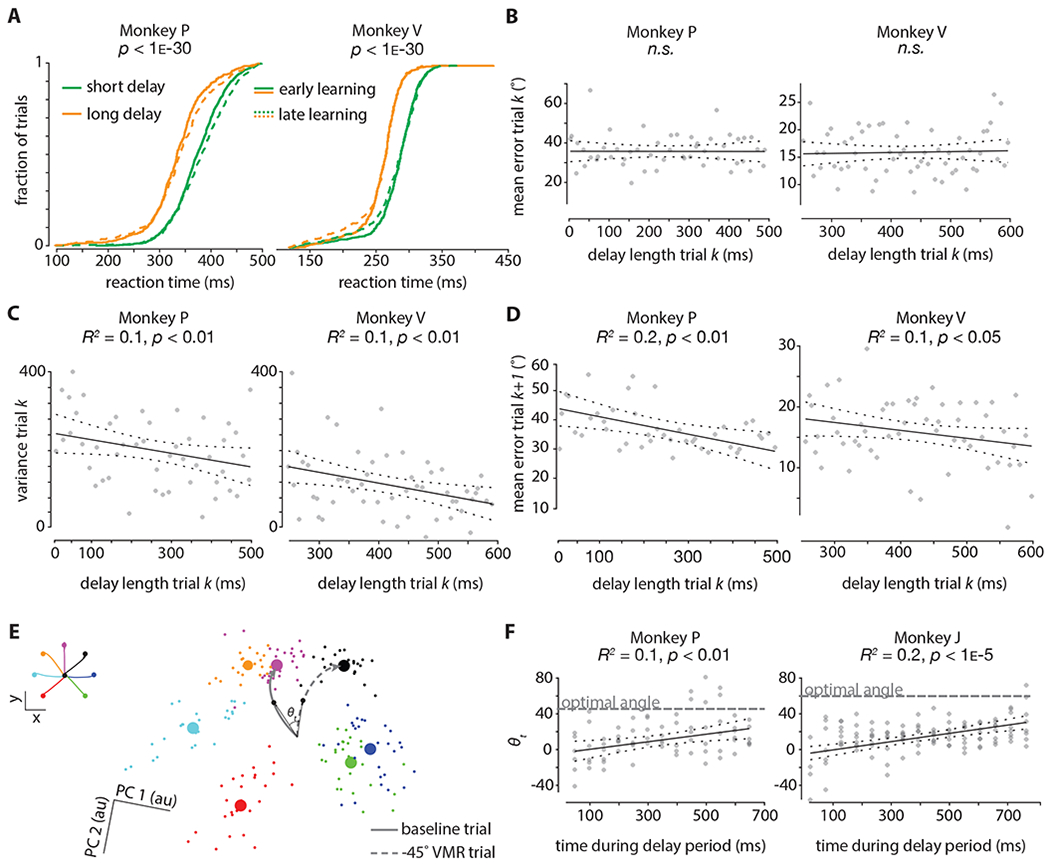
A. Cumulative reaction time distributions (pooled across all sessions). Green denotes short delay periods (0-300ms), and orange denotes long delay periods (300-600ms). Dotted lines denote the first 150 trials during adaptation, and solid lines denote the last 150 trials during adaptation. The p-values were obtained from the Wilcoxon rank-sum test and compare trials with short delay periods and trials with long delay periods.

B. Correlation between the length of the delay period on trial k and the mean error on that same trial k. Data were binned in 50ms bins. The p-values are for the F-test on the model, which tests whether the fit is significantly better than a model with only a constant term. The plotted data (same for (C) and (D)) is pooled across five sessions; the first 25 trials (i.e., ‘early learning’) are considered from each session. The delay length for Monkey P was drawn randomly on every trial from a uniform distribution from 0ms-500ms; for Monkey V this was between 250ms-600ms.

C. Correlation between the length of the delay period on trial k and the variance in the distribution of errors (in 50ms bins) on that same trial k. The p-values are for the F-test on the model, which tests whether the fit is significantly better than a model with only a constant term. Delay period distribution was the same as in (B).

D. Correlation between the length of the delay period on trial k and the mean error (in 50ms bins) on the next trial k+1. The p-values are for the F-test on the model, which tests whether the fit is significantly better than a model with only a constant term. Delay period distribution was the same as in (B).

E. Delay period neural activity from a representative session projected into a 2D subspace found using Principal Components Analysis on 200ms of trial-averaged neural activity from a baseline block. Small dots are two-trial-averages projected into the subspace; large circles are cluster centroids. Colors correspond to the seven reach directions shown in the inset (top left). Gray lines correspond to hypothetical baseline and −45° VMR trial neural trajectories during the delay period; angle (θ_t) is computed between the trajectories for each time point t at a 10ms resolution.

F. The angle between neural trajectories during the delay period (θ_t) is computed at a 50ms resolution between baseline and −45° (−60° for Monkey J) VMR trajectories; each trajectory is a 5-trial average. The gray ‘optimal angle’ line corresponds to the ‘anti-VMR’ angle, i.e., 45° and 60° for Monkeys P and J respectively. Plotted is the correlation between the time during the delay period and the angle (θ_t) between trajectories. The p-values are for the F-test on the model, which tests whether the fit is significantly better than a model with only a constant term. The delay length for Monkey P was drawn randomly on every trial from a uniform distribution from 0ms-650ms; for Monkey J this was between 0ms-750ms. Data is pooled across sessions such that a population of at least 50 tuned neural units (channels on the Utah electrode arrays for Monkey J; channels on the V-probe for Monkey P) during early learning (first 25 trials) are analyzed. Note that data is shown for Monkey J, and not Monkey V, in this panel (see methods for details).

Previously, we showed that a readout of the error-driven learning process is reflected in dorsal premotor cortex (PMd) as the neural population preparatory state; this state rotates systematically in concert with the behavior during VMR learning, and results in an “anti-VMR” neural pattern post-adaptation (Vyas et al., 2018). Similar systematic changes in preparatory activity are observed when subjects adapt to changes in visuomotor gain; here instead of a rotation, a constant scale factor is applied to the speed of the cursor being controlled (Stavisky et al., 2017). We also previously showed that generating preparatory states closer to the optimal state is correlated with behavioral improvements, e.g., faster reaction times (Afshar et al., 2011). Here, we wanted to build on these findings by investigating how the dynamics of the preparatory state evolve during the delay period on single trials. We found that the state continued to move along a direction approaching the optimal “anti-VMR” pattern (Figure 3E–F; Monkey P: n = 90, F-statistic vs constant model = 7.21, p < 0.01; Monkey J: n = 75, F-statistic vs constant model = 15.17, p < 1e-5). This analysis, while consistent with our previous studies, further reveals that the neural population dynamics of the circuit during the delay period facilitate within-trial refinement of the neural state towards an advantageous position in state space for performing the task.

The additional preparation time presumably does not result in further updates by the learning process as no error signal is present. Instead, our results suggest the motor system may utilize this period to yield a low noise estimate of the currently learned internal state of the learning process. That is, the black “update” arrow in Figure 1 is likely noisy, which can seemingly be overcome, at least partially, with more preparation time. This is consistent with previous findings that the onset of the target stabilizes the preparatory state, potentially towards a pattern that incorporates the currently learned internal state (Churchland et al., 2010a). This is likely advantageous as a more stable estimate could explain reduced variability in errors associated with the executed movement (Figure 3C) and increased learning (Figure 3D). We note, however, that given the timescale of 100s of milliseconds, other computations may occur during this time, in addition to resolving the potentially noisy interaction between the learning process and motor preparation. Perhaps additional time allows for the explicit system to contribute to learning, which could involve more time-consuming processes. Taken together, these results suggest that refinement of preparatory activity is correlated with updates of a learning process and trial-by-trial adaptation.

ICMS during motor preparation is sufficient to disrupt learning

Next, we evaluated if a causal relationship exists between preparatory activity and visuomotor learning. We performed sub-threshold intracortical microstimulation (ICMS) in PMd (at sites demonstrating strong preparatory tuning) near the end of the delay period (labeled as “go cue ICMS” in Figure 4A and Figure S1) (Churchland and Shenoy, 2007; Mazurek and Schieber, 2017). ICMS was performed 50 times during adaptation (Figure 4B). For comparison, for the same number of sessions, no ICMS was performed. We found that learning across ICMS trials progressed more slowly than across non-ICMS trials (Figure 4C, left; df = 470, t = 4.09, p < 1e-5, effect size = 4.07). This relationship also held when ICMS was performed during the washout, instead of during adaptation (Figure 4C, right; df = 310, t = −2.61, p < 0.01, effect size = 3.66). These results demonstrate a causal relationship between motor preparation and learning.

Figure 4: ICMS during motor preparation is sufficient to disrupt learning.

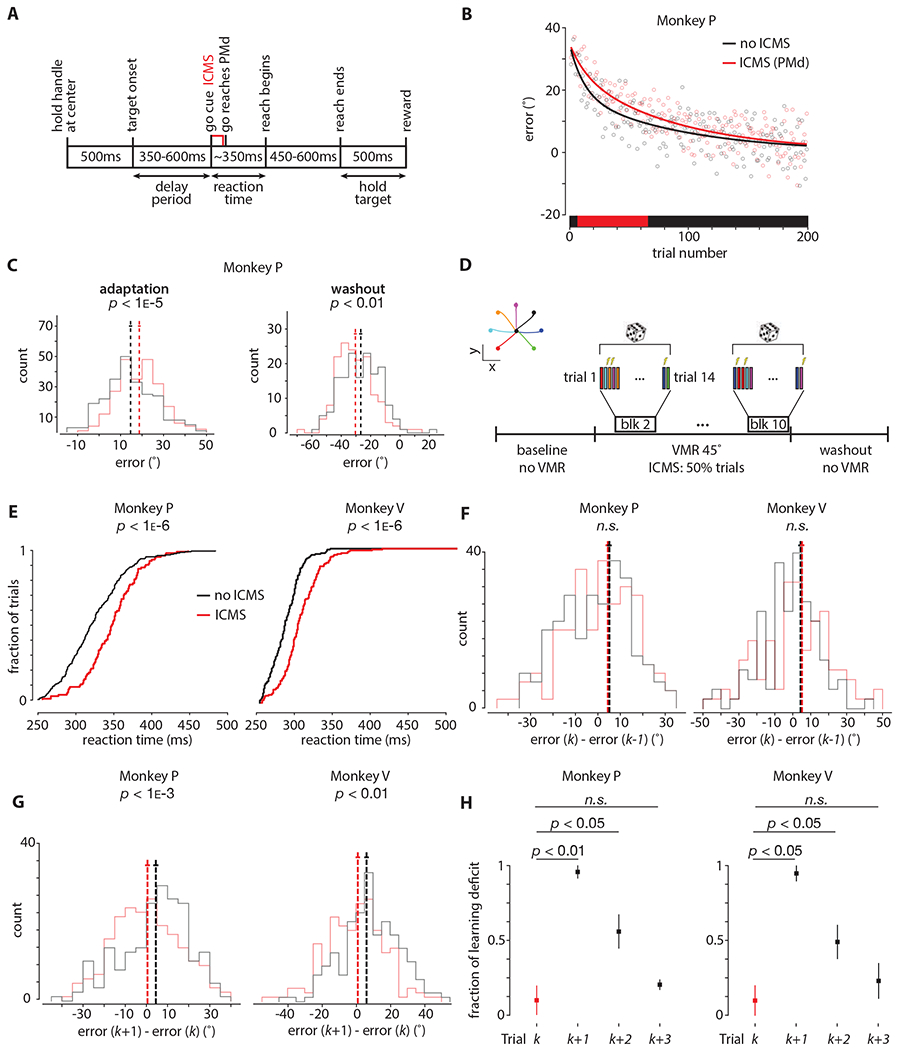
A. Timing diagram. Intracortical microstimulation (ICMS) was delivered near the end of the delay period (i.e., ‘go-cue’) for 60ms (333Hz; 150μs cathodal and anodal pulses, separated by 200μs) in PMd and M1. See Figure S1 for relevant ICMS controls.

B. ICMS (red) and non-ICMS (black) are performed on separate sessions. For ICMS sessions, electrical stimulation is performed on trials 8-57 (for a total of 50 trials), denoted by the red box on the horizontal axis. The first block (7 trials; one for each reach condition) is used to assess effects of savings; the session is excluded if savings is present. The solid lines denote exponential decay fits to data across all sessions. Data is shown for four ICMS and four non-ICMS sessions from Monkey P.

C. (Left) Same data as (B) presented in histogram form. Vertical dashed lines show means of distributions, and horizontal solid lines mean ± s.e.m. (Right) Similar to (B) except ICMS is performed during the washout, instead of during adaptation. The p-values were obtained from two-tailed Student’s t-tests.

D. Task design. ICMS was interleaved with non-ICMS trials during 45° VMR adaptation for exactly 50% of the trials. Reach conditions (inset, top left) were balanced such that each condition received ICMS and non-ICMS within each block. A total of 10 blocks were collected during adaptation. The first block was 7 trials (one for each reach condition, and no ICMS), blocks 2-10 were 14 trials each (two for each reach condition; one ICMS and one non-ICMS). The ordering of ICMS and non-ICMS trials was randomized within each block.

E. Cumulative reaction time distributions (pooled across all sessions in PMd) for the ICMS (red) and non-ICMS (black) trials during adaptation. See Figure S2 for ICMS early vs late during learning.

F. Histograms of learning on ICMS and non-ICMS trials. The horizontal axis corresponds to learning, i.e., the error on the current trial k less the error on the previous trial k−1. Trial k−1 is non-ICMS; trial k is ICMS (red histogram) or non-ICMS (black histogram). The p-values were obtained from two-tailed Student’s t-tests.

G. Histograms of learning on trials immediately following ICMS and non-ICMS trials. The horizontal axis corresponds to learning, i.e., the error on the next trial k+1 less the error on the current trial k. Trial k is ICMS (red histogram) or non-ICMS (black histogram); trial k+1 is non-ICMS. Vertical dashed lines show means of distributions, and horizontal solid lines mean ± s.e.m. The p-values were obtained from two-tailed Student’s t-tests. See Figure S3B–D for a more detailed breakdown for this analysis.

H. Time course of normalized learning deficit due to ICMS across four trials; trial k is ICMS (shown as red), trials k+1, k+2, and k+3 are non-ICMS (shown as black). Learning deficit is defined as the difference between the mean learning for ICMS and non-ICMS trials, i.e., it is the same measure as the difference in means in (F) and (G). The distributions are created by performing the same analysis as (F) - (G) on a session-by-session basis, where each session contributes one data point; dots denote the median, and the bars denote the full extent of the data. Trial k is the same data as (F), trial k+1 is the same data as (G), trials k+1 and k+2 repeat the analysis in (G), except isolating pairs of non-ICMS trials that follow ICMS (on trial number k). Data are normalized such that the minimum (across sessions) of trial k is zero, and the maximum (across sessions) of trial k+1 is one. This is done to more easily demonstrate the fraction of the learning deficit (relative to trial k+1) that persists across trials k+2 and k+3. The p-values were obtained from the Wilcoxon rank-sum test using unnormalized data.

This observed learning deficit could be caused by one of at least three different mechanisms. (1) Disrupting preparatory activity could only disrupt the kinematics on the current trial. The underlying learning process would be unaffected, thus future trials without ICMS would be unaffected. (2) Disrupting preparatory activity could disrupt the kinematics, and thus the error signal, which is an input to the learning process. The update machinery of the learning process would be unaffected, however, by virtue of the degraded input, the resulting update would be affected, and thus learning on the next trial would be disrupted. (3) Disrupting preparatory activity might not affect the kinematics nor the error signal on ICMS trials, but instead only affect the update machinery of the learning process. This would manifest as no disruption to the degree of error compensation on ICMS trials but would instead manifest as impaired learning on subsequent trials. In order to disambiguate between these hypotheses, we designed a new experiment where ICMS trials were interleaved with non-ICMS trials during learning (Figure 4D).

We first replicated the previously reported reaction time penalty for stimulated trials (Figure 4E; Monkey P: Normal Z = 6.82, p < 1e-6; Monkey V: Normal Z = 6.59. p < 1e-6) (Churchland and Shenoy, 2007). We then found that ICMS during trials early in learning led to larger reaction time deficits than did ICMS during trials late in learning (Figure S2) (cf. Figure 3A, no statistically significant relationship between preparation time and reaction time for early vs late learning). Intriguingly, apart from these reaction time penalties, we found no further deficits, including no statistically significant difference in the error distribution (Figure 4F; Figure S1). We then examined learning from the ICMS trial to the following trial (which itself was a non-ICMS trial), and found significant deficits compared to trials following no ICMS (Figure 4G and Figure S3; Monkey P: Normal Z = −3.45, p < 0.001, effect size = 3.95; Monkey V: df = 370, t = −3.16, p < 0.01, effect size = 3.87). Collectively, these results demonstrate that ICMS during motor preparation is sufficient to disrupt learning, consistent with hypothesis (3) described above. Next, we evaluated the time constant for which the observed learning deficit persisted by isolating non-ICMS trials that follow an initial ICMS trial. We considered 4-tuples of trials where a single ICMS trial was followed by three non-ICMS trials. We found that the effect of ICMS persisted for approximately three trials (Figure 4H; Monkey P: Normal Z = −2.8871, p < 0.01 between trials k and k+1, and Normal Z = −2.4082, p < 0.05 between trials k and k+2; Monkey V: Normal Z = −2.3001, p < 0.05 between trials k and k+1, and Normal Z = −2.1974, p < 0.05 between trials k and k+2).

Learning deficits from ICMS are dose, time-point, and brain-region dependent

The learning process is hypothesized to make updates on a trial-by-trial basis using the visual error signal to drive adaptation (Inoue et al., 2016). The results here suggest that when ICMS is performed during motor preparation, error reduction on ICMS trials relative to previous trials is statistically indistinguishable from pairs of trials with no ICMS. Therefore, ICMS-driven disruption of learning cannot result from disrupted error signals arising from that movement, as the present trial has indistinguishable kinematics (apart from a reaction time penalty; Figure 4E–F). Instead, these results imply that ICMS affects the update computation of the learning process, as the error reduction on post-ICMS trials relative to ICMS trials is significantly impaired relative to pairs of trials with no ICMS, and that this disruption is not mediated by altering the error signal itself.

These results, however, do not directly implicate preparatory activity. Thus, we reanalyzed the data from stimulating in PMd, separating trials with short delay periods (350-450ms) and trials with long delay periods (500-600ms). We found that stimulating trials with longer delay periods led to a greater deficit in learning, further supporting the interpretation that ICMS slows learning via disruption of preparatory activity (Figure 5A; Monkey P: df = 352, t = −2.3, p < 0.05, effect size = 4.01; Monkey V: df = 378, t = −2.6, p < 0.05, effect size = 3.95).

Figure 5: Learning deficits from ICMS are dose, time-point, and brain-region dependent.

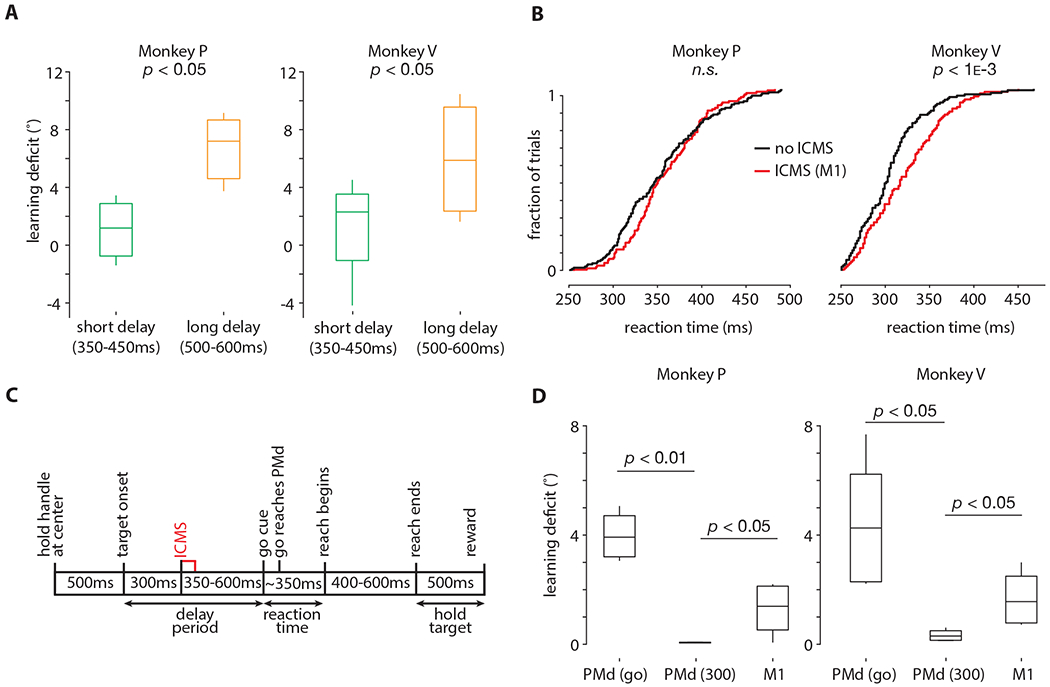
A. Same data as (Figure 4G), except trials with short (350-400ms) and long (500ms-600ms) delay periods are separately analyzed. Horizontal bars denote the median; vertical bars denote the full extent of the data; boxes denote the 25th and 75th percentile of the data. Learning deficit is defined in the same way as reported in Figure 4H. The p-values were obtained from the Wilcoxon rank-sum test.

B. Cumulative reaction time distributions (pooled across all sessions in M1) for the ICMS (red) and non-ICMS (black) trials during adaptation. Same ICMS protocol as Figure 4A. The p-values were obtained from the Wilcoxon rank-sum test.

C. Timing diagram for ‘early’ ICMS. Same ICMS parameters as Figure 4A, except ICMS is delivered 300ms into the delay period, followed by a second variable length delay period of 350-600ms. Thus, animals experience a total delay period of 650-900ms, where ICMS arrives at 300ms.

D. Box plots of learning deficit for the three ICMS conditions, i.e., ICMS in PMd at the go-cue, ICMS in Ml at the go-cue, and ICMS in PMd 300ms into the delay period. Bar plots are computed in the same manner as (A), without separating by preparation time. The data in the box plots are across sessions; each session contributes one data point, i.e., the difference in means as reported in (Figure 4G).

We also performed ICMS near the go-cue in primary motor cortex (M1), where there is significantly less preparatory activity (Figure 5B). As in PMd, we found no statistically significant deficits on stimulated trials, but a disruption to learning, albeit to a smaller degree than ICMS in PMd (Figure 5D, rightmost bar; Monkey P: Normal Z = −2.1, p < 0.05, effect size = 1.6; Monkey V: df = 337, t = −2.3, p < 0.05, effect size = 1.2). This may be due to proportionally less preparatory activity in M1, less involvement of M1 in visuomotor remapping, and/or fewer anatomical connections between M1 and the brain region(s) implementing the learning process.

Next, we performed an additional experiment in PMd where animals were provided a 650-900ms delay period, but we stimulated 300ms into that period (Figure 5C). This experiment was motivated by the hypothesis that the preparatory activity could recover following ICMS if sufficient additional time during the delay period was provided. In this condition, we found no deficits to learning (Figure 5D, middle bar; Monkey P: df = 341, t = −3.11, p < 0.01, effect size = 3.7; Monkey V: df = 341, t = −2.2, p < 0.05, effect size = 3.5). This suggests that the preparatory state may recover in time for the update computation to proceed without disruption. This result also argues that the act of stimulation during motor preparation alone does not disrupt trial-by-trial learning in a temporally non-specific manner.

Taken together, these results suggest that the observed deficit to learning from ICMS are dose-dependent (Figure 5A), brain-region dependent (Figure 5B; 5D, right), and temporally specific (Figure 5C; 5D, middle).

Discussion

In this study we investigated the role of motor preparation during visuomotor learning. Previous studies have explored the role of preparatory neural activity in movement initiation, suppression, higher-level goal setting, and more abstract cognitive planning. Here, we focused our attention instead on uncovering the relationship, if any, between preparatory activity and the process that facilitates trial-by-trial adaptation (Paz et al., 2003; Perich et al., 2018; Sheahan et al., 2016; Stavisky et al., 2017; Vyas et al., 2018). We started by correlating the amount of preparation time with learning. While our results replicated the finding that more preparation time yields faster reaction times (Churchland et al., 2006b), we did not find any statistically significant benefit to magnitude of the error on trials with more time to prepare. We did, however, find that allowing longer preparation times yielded smaller variance on the current trial, and smaller errors on the subsequent trial. How the learning process uses reduction in variability to perform its update, if at all, remains unknown. It may be tempting to link the reduction in variability to the greater learning, but the mechanism that would support this is unclear. Prior work inspired by reinforcement learning suggests that increase in task-relevant variability (or action exploration) can actually enhance learning (Wu et al., 2014). Collectively, these results suggest that distinct aspects of variability may differentially help and hinder learning; further work is needed to understand this multifaceted relationship.

The behavioral findings led us to formulate a hypothesis where motor preparation contributes to the update computation of a trial-by-trial learning process. To test this, we used ICMS during the delay period to disrupt preparatory activity during a subset of interleaved learning trials. We found that ICMS reduced learning on subsequent trials, while not affecting any statistically significant kinematic change on that stimulated trial (Figure S1). This confirms that ICMS disrupted the update computation without disrupting the visual error signals that guide this update. Additionally, by varying the timing of ICMS during motor preparation, we found that ICMS must be performed close to the go-cue in order to observe deficits in learning.

There are several implications of this result. First, this controls for any longer-term effects of stimulation manifesting as deficits on subsequent trials. Second, this suggests that the effects of ICMS are time-point specific, i.e., learning deficits are only present when ICMS is performed close to the go-cue. Updates to the learning process start to occur at movement-onset, as soon as visual errors are computed. The results here suggest that the update is primarily sensitive to the preparatory state at the go-cue (Figure 1, data appear to constrain the timing of the red arrow). One possible mechanism is that a signal occurring near the time of the go-cue triggers an interaction between the preparatory state and the learning process, where it informs the update computation that will occur once the reach is made. A triggering signal that meets these criteria was recently characterized; Kaufman and colleagues identified that the largest response component in motor cortex is condition-invariant, i.e., it reflects timing and not type of movement, and it rapidly changes during the reaction time epoch (Kaufman et al., 2016). The onset of this condition-independent signal (CIS) may transition the neural state from a preparatory “attractor-like” region in state space, to another region where, presumably following an appropriately-timed input, strong rotational dynamics are observed just before movement onset (Churchland et al., 2012; Sussillo et al., 2015) (Vyas, Golub, Sussillo, and Shenoy, 2020). The CIS-mediated hypothesis does not preclude interactions between the preparatory state and the learning process later in the same trial. Instead, it suggests that the learning process is unable to incorporate such future interactions; otherwise learning would not be disrupted on the post-ICMS trial as activity in preparatory dimensions likely recovers well before the end of the ICMS trial. We note, however, that this is speculative; at minimum, the results suggest that a disrupted preparatory state at CIS-onset is sufficient to affect the update machinery in a fashion that cannot be rescued by future, potentially “corrected,” preparatory states.

Alternatively, perhaps the learning process provides the comparison between efference copy and sensory feedback, but some other brain region that relies on motor cortical preparatory activity (which could include premotor cortex), generates the update. This would not require the exact interaction that is being proposed here (Figure 1). More progress towards this possibility, however, requires further research on determining all the brain regions comprising the learning process, and the exact nature of the update computation itself. The key takeaway is that our data constrain the time-window in which ICMS is effective at disrupting the update computation, where the CIS is one candidate signal that arises within that window that could enable an interaction between the learning process and the preparatory neural dimensions.

We evaluated the quantitative effects of ICMS on learning as probed through non-ICMS trials that follow an ICMS trial (Figure 4H), and through a long string of ICMS trials (Figure 4B–C). These empirical findings suggest a learning rate modulation mechanism that may be helpful under normal circumstances. That is, the learning process may actively monitor the reliability of its inputs and adjust its learning rate accordingly to achieve robustness to perturbations. This is analogous to a mechanism proposed by a recent human behavioral study, which suggests that the motor system controls its learning rate through an error sensitivity parameter that is a function of the history of previously experienced errors; sensitivity is lowered when the environment is made more unpredictable (Herzfeld et al., 2014). This is also consistent with ideas from Bayesian estimation; in particular, work by Wei and Kording suggests that the system reduces its learning rate if there is less confidence on a particular trial (Wei and Körding, 2009).

We speculate that perhaps our neural perturbation introduced uncertainty in downstream brain regions that leads to a qualitatively similar result as these previous studies. The learning process likely reduces error sensitivity to combat the uncertainty introduced by the initial ICMS perturbation; if no further stimulation occurs, the learning rate gradually returns to baseline (consistent with Figure 4G). On the other hand, repeated ICMS does not lead to further reductions in error sensitivity, as the errors are not influenced directly by ICMS and presumably no further uncertainty is introduced with additional stimulation (consistent with Figure 4B–C; ICMS disrupts the learning rate initially, but does not continue to further slow learning with repeated stimulation).

Furthermore, motor adaptation is a slow process overall, which suggests the system is designed to make gradual adjustments to control parameters to avoid unstable overcorrections, and consequently may not have evolved to counter large, unexpected perturbations. This interpretation, however, might be specific to visuomotor adaptation, as one rarely encounters large visual distortions in the natural world. On the other hand, fast and slow adaptation processes are general phenomena, and it is possible that some neural machinery is shared between them. One interesting avenue for future work could explore the role of preparatory activity within more complex tasks (e.g., skilled movements) where timescales of learning can be directly manipulated (Krakauer et al., 2017, 2019). Future studies would perhaps also benefit from an improved task design in which the VMR perturbation angle changed randomly from trial-to-trial to prevent adaptation from saturating, thus the result would not ride on top of an asymptotic learning function.

All of our results regarding preparatory activity and its engagement with the learning process do not rest upon any assumptions about the nature of the update or even the brain region where the computation might take place. Our results argue that the update computation engages with neural activity in motor cortex during motor preparation. Prior work suggests that the most promising brain region to look for such error-driven updates is the cerebellum (Donchin et al., 2012); our proposal regarding a desired interaction between preparatory activity and trial-by-trial learning is further supported by recent evidence demonstrating the engagement of the cortico-cerebellar loop during motor preparation (Chabrol et al., 2019; Gao et al., 2018; Wagner et al., 2019). Additionally, other work has demonstrated that when explicit processes are suppressed, increase in cerebellar excitability via non-invasive brain stimulation increases implicit adaptation (Leow et al., 2017a).

It is important to consider alternative explanations for the results here, in which VMR learning still engages the CIS and gain mechanisms, but where disruption to preparatory activity specifically does not produce the deficit to learning. Our results demonstrate that near the time of the go-cue there exists some path by which ICMS disrupts the update of the learning process. However, it is conceivable that this disruption could be unrelated to disrupting preparatory activity and the subsequent interaction between the learning process and the preparatory state. ICMS could be disrupting the update computation via an alternative pathway, rather than through the normal pathway for driving adaptation. Additionally, ICMS could potentially disrupt more than just the preparatory neural dimensions. For example, error signals and the corresponding error-updating neural dimensions play a key role in adaptation, e.g., (Inoue et al., 2016; Williams et al., 2018). Future work in the form of studying error-updating dimensions in motor cortex, e.g., (Even-Chen et al., 2017), and/or recording and modeling activity from other nodes in the motor system, including parietal cortex, basal ganglia, and the cerebellum, could resolve the remaining ambiguities regarding the precise impact of ICMS. Nevertheless, at minimum, our study reveals both a region-specific and a time-specific path from motor cortex to the learning process, which when disrupted causes deficits to learning (Figure 5). This coincides with correlative evidence for increased learning with additional preparation time (Figure 3D).

While VMR adaptation is no doubt partly driven by the trial-by-trial error signal, there are multiple components that underlie the learning process. We have largely focused on the implicit, error-driven component, but there is also an explicit, cognitive component. In studies with human participants, it is possible to at least partly dissociate between these processes (though there still seems to be no consensus regarding the best methods to do so or their relative effectiveness, e.g., (Leow et al., 2017b). In non-human primate animal models, it has yet to be established what the balance of implicit and explicit processes might be. To that end, in this study we cannot attribute which processes the animals engage (though they are at least engaging the implicit process) and which of these processes are disrupted by ICMS. Prior work by Mazzoni and Krakauer suggests that the explicit component is overridden by the motor planning system when there is conflict between the processes (Mazzoni and Krakauer, 2006). Here, we did not see the expected behavioral consequences of such conflict. To that end, it is unlikely that we are preferentially disrupting the explicit process, as that would likely not lead to post-ICMS errors as reported here. It is also unlikely that we specifically disrupted only the implicit process, as ICMS is not a specific enough perturbation, though we have no way to probe this. Further, we cannot distinguish whether ICMS disrupted either the fast or the slow adaptive process as previously described by Smith and colleagues (Smith et al., 2006). Nonetheless, having established a causal relationship between neural activity during motor preparation and the trial-by-trial learning process, future work can begin to overcome the limitations described here by designing experiments that disentangle the contribution of preparation on the various components of learning.

One final lens through which to view our results comes as a direct prediction of the initial condition hypothesis, which proposes that the role of preparatory activity is to initialize peri-movement neural population dynamics (Afshar et al., 2011; Churchland et al., 2010b). If a learning process wants to improve behavior on a trial-by-trial basis, then under the initial condition hypothesis it could shape the movement period dynamics by influencing the initial condition directly. Subsequently, the update computation could be guided by the preparatory state which initialized the reach just made. Thus, one would expect an interaction between preparatory activity and the update computation as a means for the learning process to perform an update that best sets the initial condition for the next trial. This proposal is consistent with that of Sheahan and colleagues for separating interfering motor memories (Sheahan et al., 2016). This may also relate to observational learning, where neural activity during preparation informs a learning process without motor commands or efference copy, e.g., (Vyas et al., 2018). Having found evidence for the link between motor preparation and the trial-by-trial learning process, future studies can perhaps further bridge together the dynamical systems perspective of motor control with the current framework for investigating error-driven learning.

STAR Methods

LEAD CONTACT AND MATERIALS AVAILABILITY

Further information and requests for resources and reagents should be directed to and will be fulfilled by the Lead Contact, Saurabh Vyas (smvyas@stanford.edu).

EXPERIMENTAL MODEL AND SUBJECT DETAILS

All animal protocols were approved by the Stanford University Institutional Animal Care and Use Committee. Recordings were made from motor cortical areas of three male adult monkeys (Macaca mulatta), P (16 kg, 13 years old), V (9 kg, 10 years old) and J (16 kg, 15 years old), while they performed an instructed delay reaching task (Figure 2A). Use of two animals is standard practice in the field. Data from Monkey J was introduced only for the analyses presented in Figure 3F once it was no longer possible to perform further neural recordings from Monkey V.

Monkeys P and V were implanted with a head restraint and a recording chamber (NAN Instruments for Monkey P and Crist Instrument Company for Monkey V) during a sterile surgery. The chambers were located over the left, caudal, dorsal premotor cortex (based on coordinates derived from a Rhesus monkey atlas). Monkey P’s chamber had a 30mm inner diameter, whereas Monkey V’s chamber had a 19mm inner diameter. The chambers were placed flush with the skull, adhered using methyl methacrylate. Within each chamber, a thin layer of methyl methacrylate was deposited above the exposed skull. During the same surgery, a “ground screw” was placed on the posterior part of the implant; the tip of the screw was in contact with the surface of the dura underneath the skull. Prior to recordings and stimulation, small craniotomies (3mm each in diameter; two in PMd and one in M1) were made under anesthesia (ketamine).

Monkey J had two chronic 96-electrode arrays (1mm electrodes, spaced 400μm apart; Blackrock Microsystems), one implanted in the dorsal aspect of the premotor cortex (PMd) and one implanted in the primary motor cortex (M1). The arrays were implanted 7 years prior to these experiments. The location of the arrays was comparable to the PMd and M1 sites from Monkeys P and V.

METHOD DETAILS

Task design.

Monkeys performed a previously reported (Vyas et al., 2018) instructed-delay reaching task by grasping a custom designed handle (Shapeways, Inc.), which included a force/torque sensor (ATI Industrial Automation). The handle and force sensors were attached to a passive manipulandum (Force Dimension Inc.). This device was controlled by custom software (https://github.com/djoshea/haptic-control) and allowed to move freely in the frontoparallel plane. The handle of the device was not visible to the monkeys; instead monkeys were shown a visual cursor on a screen located at eye level coupled to the device’s position with 13-20ms latency. Method details for Monkey J have been previously described (Vyas et al., 2018). All monkeys made reaches to one of seven randomly cued targets arranged 8cm from the center of the screen, equally spaced along a ring; the target in the 270° position was omitted. There was an additional target at the center of the screen. Each trial started with the monkey holding the cursor on the central target for 200ms. Then, during a variable delay period (uniformly sampled; these delays vary from 0ms-900ms if pooled across all experiments but see captions of each Figure for precise delay period distributions), the monkey was informed of the cued target, but had to continue to hold the central target. At the go-cue, the monkey had 2s to acquire the target, which included getting the cursor within a 2x2cm window of the center of the target. The target needed to be held for 200ms, at which point a success tone played, and the monkey received a juice reward. Re-acquisition of the target was allowed as long as the 2s had not elapsed. The monkey failed the trial if he moved the cursor during the delay period (movement greater than 1mm/s) or did not acquire the target within 2s. Failure resulted in no reward, and a failure tone. In addition to the baseline task, monkeys also performed blocks with an active visuomotor rotation (VMR), parametrized by angle θ. Here, the cursor trajectory was rotated by angle θ, and thus in order to move the target in a straight line, monkeys needed to move their arm in the -θ direction. Each session was broken into three blocks: a baseline block (typically 300 trials), a VMR block (typically 300 trials, except for the experiments in Figure 4), and a washout block (typically 300 trials). VMR angles of ±45° (Monkeys P and V), and −60° (Monkey J) are reported in this study.

Electrophysiology.

At the start of each session, a linear electrode array (24 channel V-probe; Plexon, Inc.) was affixed to a micromanipulator (NAN Instruments) and lowered at 5μm/s through a non-penetrating blunt guide tube into motor cortex to a depth of approximately 2mm. Depth was assessed separately on each session; typically the probe was advanced until neural activity was observed on the bottom channel on the probe, then the probe was lowered an additional 1.5-2mm, or until neural activity spanned all 24 channels. The probe was allowed to settle for 60min before any recordings were made. The probe was connected to a head stage, which relayed the signal to a front-end amplifier (Blackrock Microsystems). Broadband signals were recorded on each channel and filtered at the amplifier (0.3Hz one pole high-pass filter, 7.5kHz three pole low-pass filter). The signals were also digitized to 16-bit resolution over ±8.196mV (resolution = 0.25μV) and sampled at 30kHz. Each channel was differentially amplified relative to a common reference within the V-probe. To aid with noise rejection, the probe was shorted to the guide tube, as well as covered from all sides with an electromagnetic shielding mesh fabric, which was also shorted to the guide tube. Offline, units that had a signal-to-noise ratio of at least 1.5 were kept. In PMd, approximately 10-20 units were measured at each session. This procedure was followed for all measurements made in Monkeys P and V. On microstimulation sessions (see the ‘Electrical stimulation’ section below) the same procedure was followed, except single channel tungsten microelectrodes (Frederick Haer Company, Inc.) were used in lieu of V-probes.

In Monkey J voltage signals were band-pass filtered from each channel on the two arrays (range: 250Hz – 7.5KHz). The signals were then processed to detect multi-unit “threshold crossing” spikes. Spikes were detected at each point where the voltage crossed below a threshold of −4.5 times the root-mean-square (RMS) voltage. For the population analysis in Figure 3, no spike sorting or assignment of spikes to individual neurons was performed (Trautmann et al., 2019).

Intracortical microstimulation (ICMS).

For microstimulation, single channel tungsten microelectrodes (250μm shank diameter, less than 1μm tip diameter, 110mm length, 5-7MΩ impedance measured at 1KHz; Frederick Haer Company, Inc.) were used. Prior to performing ICMS, the electrodes were inserted into PMd and M1 (as described in the ‘Electrophysiology’ section) to measure and characterize neural activity; coarse attempts, i.e., playing the neural data through a speaker and listening for changes in spike rate as the monkey performed baseline reaches, were made to verify that the location contained neural activity modulated to arm movements. After finding the first depth that contained neural activity, the probe was lowered an additional 1mm. The stimulation was performed using a S88X Grass electrical stimulator (Astro-Med, Inc.). The task, implemented in Simulink Real-Time Target (The MathWorks, Inc.), sent a TTL pulse to trigger the stimulation. The current flowed through the brain from the electrode to the ground screw. All experiments used biphasic pulses delivered at 333Hz for 60ms (balanced 150μs cathodal then anodal pulses separated by 200μs). The stimulation amplitude varied between 15-120μA, depending on brain region, and was chosen and then set for that particular session. In order to select this amplitude, a “threshold” was found on each session as follows. At the start of the experiment, the monkey sat in a comfortable resting position, with his contralateral (right) arm laying in a visible position. The experimenter attempted to visually confirm a twitch in the wrist and/or forearm as he manually delivered a single 60ms train of ICMS. The “threshold” was defined as the minimum current needed to evoke a brief movement or twitch of the wrist or forearm. The experimenter started at 30μA, incrementing by 30μA if no such movement was observed; if 150μA was reached and no movement was observed, the stimulation electrode was driven an additional 100μm into cortex. Once a threshold was found, the stimulation amplitude was set to be 5-20% below this level, where the precise choice was based on a value that no longer elicited any movements. Across both Monkey P and V, we found higher thresholds on average in PMd than in Ml by a factor of about 2-3X, though thresholds as low as 40μA were observed in PMd.

Preparatory neural state analysis.

In Figure 2E the preparatory neural state is analyzed using a standard application of Principal Components Analysis (PCA). First, all data is arranged into a tensor with dimensions corresponding to neurons, time, and trials. This tensor is then reshaped into a matrix with dimensions corresponding to trial-averaged conditions, seven reach directions in this case, and firing rates of every neuron over time, where time here is selected to be 200ms just preceding the go-cue. PCA is applied to this data matrix, and the top two dimensions (i.e., PCs) are visualized (Figure 3E). Second, on a condition-by-condition basis, 2-trial-averaged neural data is projected into the two PCs (small dots in Figure 3E).

In Figure 3F, the dynamics of the preparatory state during the delay period are considered. A cartoon of the analysis is shown in Figure 3E (gray arrows, solid and dotted). In brief, for each reach condition, 5-trial-averaged neural trajectories are considered; one 5-trial-averaged trajectory from a baseline block (with no VMR), and one 5-trial-averaged trajectory from the VMR block (−45° for Monkey P or −60° for Monkey J). Trials from the VMR block are only considered for “early learning,” i.e., the first 150 trials of learning, and are appropriately matched with the baseline block. These trajectories correspond to trials with a delay period of length at least 650ms (750ms for Monkey J). For each time point (in 50ms bins), the angle between these trajectories is found; the angle is found in the full-dimensional space, i.e., not just in the 2D PC space. Figure 3F plots these angles as a function of time during the delay period. For every 50ms time bin, each point corresponds to the angle between one pair of 5-trial-averaged trajectories; in Figure 3F the points are further averaged across sessions, though this is only for ease of visualization as all the data is used for the regression. The “optimal angle” corresponds to the “anti-VMR” angle, i.e., 45° and 60° for Monkeys P and J respectively. This angle corresponds to the angle at which a reach would produce no error.

Computing error and learning metrics.

In Figure 3 error is computed as an angle between the vector that points in a straight line from the center of the workspace to the cued target and the point on the cursor trajectory as it crosses the halfway point between the center of the workspace and the target. In Figure 4F this error metric is computed between a pair of trials, i.e., the error is computed for the current trial k and the previous trial k−1. Previous work has demonstrated that error during motor adaptation exhibits spatial generalization (Thoroughman and Shadmehr, 2000). Thus, we computed the error in one of two ways: first, we only considered pairs of trials where the target directions were within a 45° spatial window; second, we empirically estimated the magnitude of spatial generalization (from a separate block of VMR trials) and then scaled the error difference by that magnitude, denoted by κ. This is meant to capture the intuition that if a reach is made to a 0° target on trial k, and then a reach is made to a 135° target on trial k+1, one does not expect any learning that happened on trial k to affect learning on trial k+1. As both approaches yielded similar results, the factor κ was used for all analyses as it allowed for all the data to be considered.

In order to estimate κ, we use three sessions where the animals perform the same number of trials as for the primary data, and measure how much learning transfers to the other targets when only adapting to a single (top, 0 degree) target. The other six targets (with no VMR present) are presented randomly during adaptation (which themselves have no VMR active). The resulting error in the opposite direction is a measure of the transfer of learning. We can then define κ as a fraction capturing the amount of adaptation transferred. The exact values of κ that are used in this study (averaged across the three monkeys, though the differences across animals were less than 5%) are: Targets = [−135°, −90°, −45°, 0° (active VMR), 45°, 90°, 135°] Kappa = [0.00±0.00, 0.08±0.00, 0.37±0.13, 1.00, 0.32±0.17, 0.10±0.01, 0.00±0.00]

In Figure 4G the same procedure is followed, except the current trial k and the next trial k+1 are considered. In Figure 5, the learning deficit is defined as the effect size of Figure 4G; concretely, the learning deficit is defined as:

$${\left[\mathrm{error}\right(k+1)-\mathrm{error}(k\left)\right]}_{\mathrm{non-ICMS}}-{\left[\mathrm{error}\right(k+1)-\mathrm{error}(k\left)\right]}_{\mathrm{ICMS}}$$

QUANTIFICATION AND STATISTICAL ANALYSIS

MATLAB (Mathworks, Inc.) was used for all statistical analyses. For all histograms, first a Kolmogorov-Smirnov (KS) test is used to confirm normality, then the significance of the difference in the distributions is determined using a two-tailed Student’s t-test, assuming nonequal variances. If the KS test does not confirm that the data is normally distributed, then a Wilcoxon rank-sum test (or the paired, i.e., signed test) is used as appropriate. For all linear regressions a F-test is used to determine if the fit is significantly better than a model with only a constant term, i.e., the slope of the fitted line is significantly different from zero. Partial correlations are used to rule out influence from other experimental parameters, as appropriate. For all bar plots, a Wilcoxon rank-sum test (or the paired, i.e., signed test) is used. For the reaction time distributions, a KS test followed by a two-tailed Student’s t-test is used. For all tests, p = 0.05 is set as the significance threshold.

DATA AND CODE AVAILABILITY

The data, materials, animal protocols, and analysis details necessary to reproduce the results in this study will be made available by the Lead Contact (Saurabh Vyas, smvyas@stanford.edu) upon reasonable request.

Key Resources Table

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Experimental Models: Organisms/Strains
Rhesus macaques (Mucacca mulatta)	Wisconsin and Yerkes Primate Centers	N/A
Software and Algorithms
MATLAB	The MathWorks, Inc.	https://www.mathworks.com/products/matlab.html
Simulink RealTime	The MathWorks, Inc.	https://www.mathworks.com/products/simulink-real-time.html
Haptic Control	Custom; Chai 3D	https://github.com/djoshea/haptic-control https://www.chai3d.org/
Other
Cerebus system	Blackrock Microsystems	http://blackrockmicro.com/neuroscience-research-products/neural-data-acquisition-systems/cerebus-daq-system/
Utah microelectrode array (96 channel)	Blackrock Microsystems	http://blackrockmicro.com/neuroscience-research-products/low-noise-ephys-electrodes/blackrock-utah-array/
Digital-to-analog card	National Instruments	NI DAQ
Haptic feedback device	Force Dimension Inc.	Model: Delta.3
3D printed handle for haptic device	Shapeways Inc.	N/A
Force/Torque sensor	ATI Industrial Automation	Model: Mini40
Polaris optical tracking system	Northern Digital	https://www.ndigital.com/medical/products/polaris-family/
Recording chamber (Monkey P), microdrive, and associated electronics	NAN Instruments	http://naninstruments.com
Recording chamber (Monkey V)	Crist Instrument Company, Inc.	6-ICO-J0 O degree Screw Style CILUX Chamber
Linear multielectrode array (24 channel)	Plexon, Inc.	PLX-VP-24-15ED-100-SE-100-25(640)-CT-500
Grass S88X electrical stimulator	Astro-Med, Inc.	http://www.neurolabparts.com/stimulators/99-grass-astro-med-stimulators-model-s88x.html
Tungsten single channel microelectrode	Frederick Haer Company, Inc.	Part #: UEWLGCSEEN1E

Highlights.

• Longer motor preparation times yield greater learning

• Motor preparation plays a causal role in visuomotor adaptation

• Motor cortical preparatory state engages with a learning process

• Disrupting preparatory states likely reduces learning by lowering error sensitivity