Highlights
-
•
Spatial model fit is adequate when network contacts are limited to small distances.
-
•
Spatial model fit is poor when network contacts exists over long distances.
-
•
Results for spatial models tested were fairly consistent for all contact networks.
-
•
Results show the importance of collecting high quality network information.
Keywords: Individual-level models, Markov chain Monte Carlo, Epidemic modeling, Contact network, Spatial approximation
Abbreviations: ILM, individual-level model; MCMC, Markov chain Monte Carlo; SARS, severe acute respiratory syndrome; SIR, susceptible-infected-removed
Abstract
Often, when modeling infectious disease spread, the complex network through which the disease propagates is approximated by simplified spatial information. Here, we simulate epidemic spread through various contact networks and fit spatial-based models in a Bayesian framework using Markov chain Monte Carlo methods. These spatial models are individual-level models which account for the spatio-temporal dynamics of infectious disease. The focus here is on choosing a spatial model which best predicts the true probabilities of infection, as well as determining under which conditions such spatial models fail. Spatial models tend to predict infection probability reasonably well when disease spread is propagated through contact networks in which contacts are only within a certain distance of each other. If contacts exist over long distances, the spatial models tend to perform worse when compared to the network model.
1. Introduction
Having the ability to produce accurate mathematical models of infectious disease spread can help provide researchers and government officials with the knowledge needed for making policy decisions directed toward containment of disease spread. Quick and accurate disease models may answer critical questions that can potentially save lives and protect economies. For example, severe acute respiratory syndrome (SARS) in 2003 had a drastic affect on tourism, food and travel, costing China 8.5 and Canada 4.3 billion US dollars (Beutels et al., 2009). Another example is given by Meltzer et al. (1999) who estimated the economic impact of a future influenza pandemic in the United States at 71.3 to 166.5 billion US dollars.
Generally, infectious diseases propagate via complex individual-level interactions, or contacts, between infected and susceptible individuals in the population. Combining all individual contact information into a contact network enables researchers to analyze disease spread through the population. There is a substantial amount of literature on network based epidemiology in diseases such as foot-and-mouth disease and avian influenza, e.g. (Cauchemez et al., 2011, Dubé, 2009, Jewell et al., 2009, Marchbanks et al., 2011, Streftaris and Gibson, 2004, Zhen et al., 2011).
However, network data that we may wish to use to model the spread of various diseases is often difficult to obtain. Collection of such data is expensive and there are issues regarding recall and privacy encroachment. A connection, or a contact between two individuals, is usually deemed to be any contact between individuals by which the disease can spread from an infected individual to a susceptible individual. The connections themselves can be hard to describe, as researchers must quantify the type of relationship or contact needed for infection to transfer (Keeling and Eames, 2005). The networks may be social in nature, spatial proximity based, or demographic (Kolaczyk et al., 2009). For example, a network may be defined by sexual activity between two individuals in the case of a sexually transmitted disease. Alternatively, if trying to model the spread of the Norwalk virus in people, we might use knowledge about which individuals live together in the same house, attend the same schools, or work together, etc. If modeling a livestock disease at the level of individual farms, say, we may want data on the trade networks, supply networks, and even social networks of farmers and farm workers.
Due to the complexity of, and difficulties in obtaining accurate information about, such networks, simplifications are sometimes made in the model being used. For example, we may use a spatial network, rather than a more desirable trade network. Examples of such spatial simplification can be found in a number of models of the UK 2001 foot-and-mouth disease epidemic (Chis Ster and Ferguson, 2007, Chis Ster et al., 2009, Deardon et al., 2010, Keeling et al., 2001). Plant epidemiologists often make such simplifications as their subjects are generally stationary thus allowing infective pressures to decrease exponentially with distance (exponential decay), with a power of distance (geometric decay) or with a nearest neighbor effect (Beutels et al., 2009, Filipe and Maule, 2004). A piecewise function, similar in concept to the nearest neighbor effect only with a given probability of infection from a long distance source, has also been used in modeling wildlife infectious diseases in which a physical barrier (such as a river) reduces mixing within the population (Smith et al., 2005). The simplest assumption to make for any infectious disease model is to assume homogeneous mixing within the population thereby, with no other covariate information, assuming equal infective pressure on all individuals within the population. Bansal et al., 2007 provides insight into the ability of homogeneous-mixing compartmental model’s ability to predict the characteristics of network-based epidemics.
Deardon et al., 2010 define a class of individual-level models (ILMs) that can be used to model the spread of disease when its spread depends on various individual-level risk factors. Spatio-temporal aspects of the infectious disease can easily be incorporated into such ILMs, enabling researchers to incorporate spatial proximity to infectious individuals in the model. Similarly, network information can be included in such models. The statistical process of fitting the model to observed data is one key aspect of analyzing epidemic data. ILMs, and similar models, can be fit to data within a Bayesian statistical framework using Markov chain Monte Carlo (MCMC).
The purpose of this paper is to examine the effect of using spatial information as a proxy to more complex network information when fitting ILMs to epidemic data. Our intention with this paper is to present generic insights into the cost of using a spatial model when the underlying population is connected by a spatially-based network. This is carried out via two simulation studies. These studies involve simulating epidemics, propagated through networks of varying complexity, and comparing the results obtained when both network-based, and spatial-based, ILMs are fit to the simulated data.
The paper is laid out as follows. The general ILM framework and specific ILMs used in the paper will be outlined in Section 2. Epidemic study and model assessment criteria will also be discussed. Section 3 presents the results of the simulation studies via the use of our chosen model assessment criteria. Conclusions that are made from the results as well as a list of possible future work will be given in Section 4.
2. Methodology
2.1. General model framework
The general framework of individual-level models (ILMs) for infectious disease is presented in Deardon et al. (2010). Here, we briefly review this framework in the context of a susceptible-infectious-removed (SIR) compartmental class of models.
In a discrete time SIR model each individual i can be in one of three states at any time point: implies that the individual is susceptible to the disease; implies that the individual is infected and is infectious; implies that the individual is removed from the population and no longer able to be infected or infect other individuals (e.g. by recovering and gaining immunity to the disease or dying). An individual i in one of these states at time t is denoted to be in the set , or , respectively. The epidemic history comprises for where, is the time at which the last infectious individual enters the removed state. Individuals within the epidemic may only move from and . Individuals are defined as discrete points in space and time with the probability of a susceptible individual i becoming infected with the disease at time t equal to
| (1) |
where is a function representing potential risk factors associated with susceptible individual i contracting the disease; is a function representing potential risk factors associated with infectious individual j transmitting the disease; is an infection kernel representing potential risk factors involving both infected and susceptible individuals j and i, respectively; is a function that accounts for some random behavior within the epidemic that cannot be explained by the other terms in the model (e.g. infection of a susceptible individual by an infectious individual from outside the observed population). For the purpose of this paper is set to zero.
We define the epidemic history as . Given the complete epidemic history the likelihood can be computed as:
| (2) |
where, is the observed epidemic data; is a vector of parameters;
is the set of newly infected individuals at time ; and is the set of susceptible individuals at time .
We now introduce the specific forms of the general ILM, given in (1), used in this paper. Here, if the infection kernel , where is the Euclidean distance between individuals i and j, then we refer to the infection kernel as a distance kernel.
2.2. Network ILM
The primary epidemic-driving characteristic of the network ILM is the existence (or not) of an edge in a contact network representing the existence of a link between two individuals through which disease can potentially transfer. The probability that individual i is infected at time t under the network ILM is given by:
| (3) |
where, is an infectivity parameter, and
| (4) |
The contact network remains constant over time and is utilized when allowing the epidemic to spread within the population and fitting the network ILM model.
2.3. Geometric ILM
The geometric ILM is based upon a geometric distance kernel where
characterizes the risk of infection depending on the distance. Here, the probability that individual i is infected at time t is given by:
| (5) |
where, is an infectivity parameter for contracting the disease, is the spatial parameter, and is the Euclidean distance between individuals i and j.
2.4. Exponential ILM
The exponential kernel model is based upon a distance kernel . The probability that individual i is infected at time t is defined by:
| (6) |
where is an infectivity parameter for contracting the disease and is the spatial parameter.
2.5. Constant piecewise model
The constant piecewise model is characterized by a distance kernel that is based on a piecewise constant infectivity dependant on a single change-point. The probability that individual i is infected at time t is given by:
| (7) |
where,
2.6. Homogeneous mixing model
The homogeneous mixing model is the simplest model among all models being tested. Probabilities of infection are based purely on the number of infected individuals in the population at a given time. The probability that individual i is infected at time t is defined by:
| (8) |
where, is a constant transmissibility parameter. Thus, at any given time t each susceptible individual has an equal chance of being infected.
2.7. Epidemic simulation
Here we consider two studies, the purpose of which is to answer the question, how far can the spatial proxy to the true underlying network be relied on to provide reasonable model fit.
2.7.1. Epidemic simulation study one
The epidemic population consists of 625 individuals, positioned on a 25 × 25 grid such that each individual, i, is located spatially at the coordinates for all combinations of . Simulated contact networks produced for this study are based on three parameters, , and radius r. The probability of an undirected connection between two individuals within distance r of each other is equal to , while the probability of a connection for distances greater than r is . A contact network for a given population can be generated for given , and r parameters. A total of 27 combinations of parameter values are used to generate epidemics. The values of the parameters used are: , and . Epidemics are then simulated using the contact network generated and the network model (3) with and an infectious period of two time units for each individual. A simulation with alternative infectivity parameters was also generated with and an infectious period of six time units for each individual. The epidemic begins when one randomly selected individual becomes infectious at . The epidemic proceeds with the probability of infection being calculated for each susceptible individual at each time point t according to the network model (3) with or accordingly. The epidemic runs for . There are 10 epidemics simulated per parameter combination.
2.7.2. Epidemic simulation study two
The population for this study contains the same number of individuals, grid layout and size as study one. However, contact networks used in this study incorporate the existence of super-spreaders in a population in which the underlying probability of contact decays continuously over distance. This underlying probability of an undirected connection between two individuals follows a geometric spatial decay according to
| (9) |
Additionally, super-spreaders are superimposed on the network. These super-spreaders are randomly chosen individuals that are forced to have a relatively large number of connections with other individuals selected completely randomly from within the population.
In this study, the spatial decay parameter, , is either set at “high” or “low” rates of 1.1 and 0.75, respectively. The number of super-spreaders is set at either 10 or 40. The number of random connections for each super-spreader is simulated from a Poisson distribution with a mean of either 20 or 50. Therefore, eight parameter combinations are used to generate contact networks. Epidemics are then simulated in the same procedure and according to the same network model (3) as in study one.
2.8. Choice of contact network
The algorithms for both contact networks were chosen and created to provide broad yet sensible examples of possible networks. The piecewise function for generating contact information within study one is simple with a clear change-point spatial relationship. An example of this system could be seen in developing countries where travel distance is localized. The super-spreader concept of study two increases the randomness and connectivity within the contact network. Lloyd-Smith et al. (2005) postulate that super-spreading is inherent within many epidemics, this concept drove the methodology behind this contact network. In both cases the underlying network generators were chosen with the view that they would generate a wide range of networks, some of which a spatial ILM might be able to model well, and some of which not.
The networks produced under these schemes will also be applicable to a wide range of disease systems, from systems in which spread is very local (eg. soil borne plant pathogens causing root rot), local with longer distance transmission (eg. domestic animal disease spread via animal contact such as porcine reproductive and respiratory syndrome) with or without super-spreaders (eg. markets in the case of a farming system), and very random (less spatial) systems such as influenza in humans.
2.9. Model fitting
Models are fit within a Bayesian framework which uses the likelihood, , to update prior information, , to attain the posterior distribution:
Each of the models described (network ILM, geometric ILM, exponential ILM, constant piecewise and homogeneous mixing models) are fitted to the simulated epidemic via Metropolis-Hastings Markov chain Monte Carlo with uniform random walk proposals for each parameter. All priors used, except for that of the constant piecewise radius parameter, are vague, consisting of independent positive half-normal distributions with a mode of zero and variance of 1000. A uniform distribution with bounds of one and ten was used for the radius parameter of the constant piecewise model. This was done to force the fitting of a piecewise kernel and to not allow or , which essentially results in the homogeneous mixing model (see Section 4). MH-MCMC chains are run for 50,000 iterations with a burn-in period of 5000. Convergence is confirmed through visual inspection. Posterior means values for each model parameter were calculated individually for all
2.10. Assessing model fit
Model fit was evaluated at the individual and population level via several assessment techniques. The first criterion is carried out by a comparison of the one-step ahead probability of infection under the posterior mean of each of the fitted models with that of the true model. This is carried out as follows for a given fitted model. In an otherwise susceptible population, six individuals are randomly infected in an area within the centre of the population, corners of the area being given by coordinates (10,10), (10,18), (18,10), and (18,18). These infectious individuals make up the set . The set contains the remaining 619 individuals not in . The probability of infection at the next time point is then calculated via the network model of (3), with , for the susceptible individuals, . Let be this true probability of infection with
| (10) |
where is the true contact network. Infection probabilities for the susceptible individuals, , are then calculated under the various models using their respective posterior mean estimates (and the true contact network for the network ILM). The posterior mean value used is based only on the individual epidemic replication under consideration. Let be the probability of infection of individual under the fitted model. Given and we define
| (11) |
| (12) |
where, and are the number of individuals in sets and , respectively. Thus, is the proportion of absolute differences between the fitted probabilities of susceptible individuals being infected under the true model and other considered models that exceed the cutoff value of 0.1. The final reported is an average over all ten epidemic replicates. A model which has a smaller is considered to be a better fitting model. This model assessment technique allows for the evaluation of model fit at the individual level and is an effective assessment criterion as it provides an overall measure of predictive power for each model at the individual level.
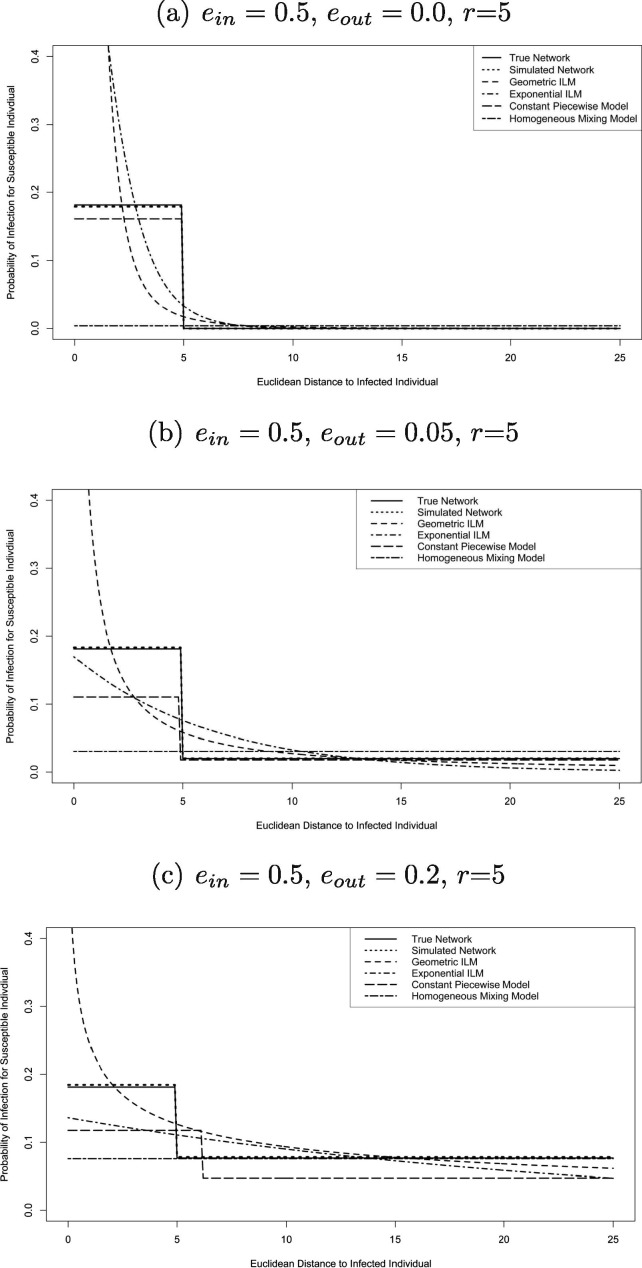
The probability of a susceptible individual i becoming infected by a single infectious individual j plotted against the distance between the individuals under the true model and posterior means of the fitted model for each network parameter combination for study one was also used to determined model fit at the individual level. These plots present how each model’s spatial characteristics change the probability of infection, this can be compared to the true contact network’s model change.
Evaluation of model fit at the population level involved analyzing the posterior predictive distribution of the epidemic timeline. The epidemic timeline is defined as the number of newly infected individuals at each time point. Every posterior predicted epidemic timeline is estimated by drawing a value at random from the respective model parameter’s posterior distribution and allowing the epidemic to spread according to the model and its posterior value(s) within the same population for which the posterior information is based on. This procedure is repeated one hundred times for each epidemic. The resulting plot presents a posterior predictive distribution of the epidemic timeline which can be compared to the true epidemic timeline of the original data. Precision and bias of the epidemic timeline posterior predictive distribution can then be analyzed and assessed for each model at the qualitative level. Quantitate information about the posterior predictive distribution of the epidemic timeline was obtained by calculating the mean predicted squared error, MPSE.
| (13) |
where, is the predicted number of newly infected individuals at time t for a given posterior predictive epidemic timeline i and is the true number of newly infected individuals of the original epidemic. The MPSE, quantifies the variance and bias of each model’s posterior predictive distribution for the epidemic timeline. The MPSEs of the ten replicates for each contact network parameter are then averaged and compared, with lower values indicating better results.
3. Results
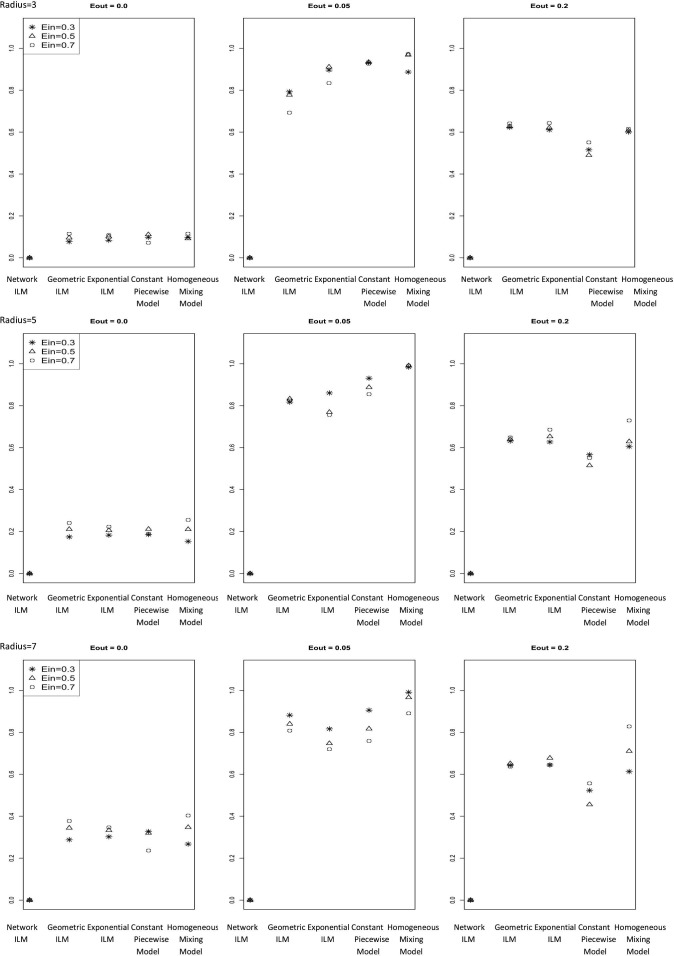
The mean for study one and two with and infectious period equal to two time units are displayed in Fig. 1 and Fig. 2 , respectively.
Fig. 1.
Average proportion of infection probability differences for susceptible individuals that exceed the cut off value of 0.1 (average ) for each combination of and r of study one ( and infectious period = 2)
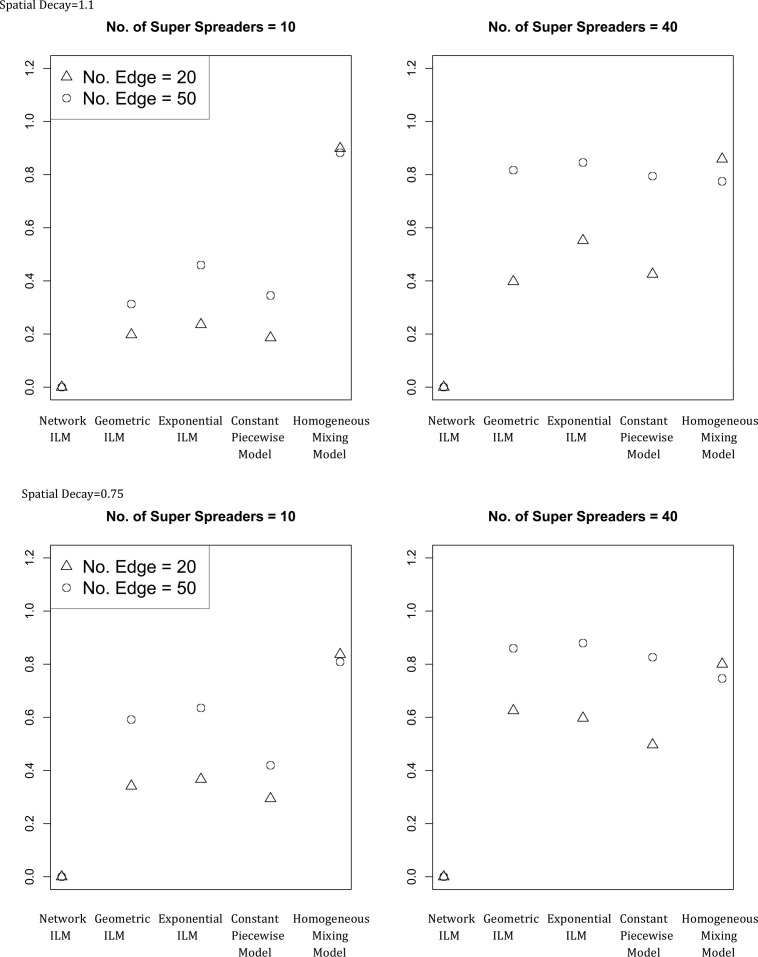
Fig. 2.
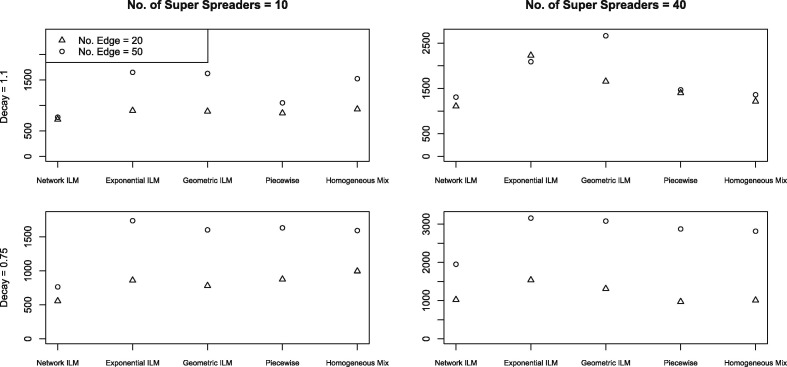
Average proportion of infection probability differences for susceptible individuals that exceed the cut off value of 0.1 (average ) for each combination of and n of study two. ( and infectious period = 2)
The posterior mean values of each parameter are the averages over 10 replicates for each fitted model. They are listed within the Supplementary material along with all remaining MPSE and data tables for study one and two with and infectious period equal to six time units.
3.1. Network ILM results
The network ILM was the model for which the best results were expected since the observed epidemic was simulated using a network ILM. Further, the true underlying contact network over which the observed epidemic was generated was used in the fitted model. For all 27 parameter combinations of study one and all 8 parameter combinations of study two, are zero for the network ILM.
Results of the MPSE for the network ILM were generally favorable compared to the other models tested.
3.2. Epidemic simulation study one – non-network models common results
The non-network models fit were the geometric ILM, exponential ILM, constant piecewise model and the homogeneous mixing model. There seem to be no obvious simple relationships between and either or r. However, with and infectious period equal to six time units there was an apparent increase in with increasing . The network parameter that had by far the greatest effect on was . All non-network models produced the lowest values for parameter combinations involving . The values for all non-network models were substantially higher than the values for the network ILM. Non-network model values ranked on average from lowest to highest were given by constant piecewise model, geometric ILM, exponential ILM, and finally the homogeneous mixing model. Results between the geometric ILM and exponential ILM were often similar.
Plots of the fitted probability of a susceptible individual becoming infected by an infectious individual against the distance between the two individuals for each of the fitted models under the posterior means, along with the true model, for study one can be seen in Fig. 3 for various combinations of the network parameters.
Fig. 3.
The probability of a randomly selected susceptible individual i becoming infected by a single infectious individual j against the distance between the individuals under the true model and posterior means of the fitted model for said network parameter combinations of study one.
Similar to the results, MPSE values were highly related to the value, with the lowest MPSEs from . Model performance for the MPSE depended on the value. In all cases the network ILM had the lowest MPSE values followed by homogeneous mixing model, constant piecewise model, exponential ILM, and geometric ILM for and however, for the homogeneous mixing model performed the poorest.
3.3. Epidemic simulation study two – non-network models common results
Increases in the number of super-spreaders, the number of connections for each super-spreader and the spatial decay rate show a propensity to increase values for all models but the homogeneous mixing model, for which the opposite effect on is seen. The lowest values for the geometric, exponential and constant piecewise models occurred for the parameter combination with the lowest amount of network connection (). The parameter combination with the highest amount of network connectivity () resulted in the lowest for the homogeneous mixing model. Non-network model values ranked on average from lowest to highest were given by constant piecewise model, geometric ILM, exponential ILM, and homogeneous mixing model.
MPSE values were highly correlated to the degree of super-spreading and contacts within the network, as with the results. Model performance evaluated by the MPSE was similar for low super-spreading populations. Generally the network ILM had the lowest MPSE values followed by homogeneous mixing model, constant piecewise model, geometric ILM and exponential ILM.
3.4. Overall comparison of models
3.4.1. Geometric model
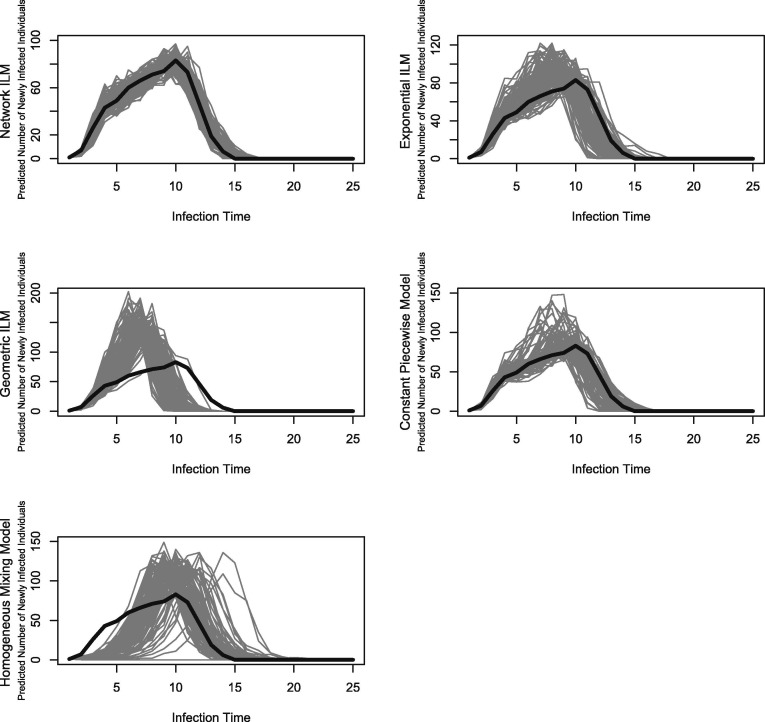
Fig. 3 shows that the geometric ILM predicts the probability of a susceptible individual becoming infected by an infectious individual against distance from the infectious individual for study one fairly well. However, susceptible individuals with small distances from a infectious individual have infection probabilities under the fitted model which are highly inflated; similarly the right tail approaches zero which underestimates the probability of an infection of susceptible individuals that are far from the infectious individual. The geometric ILM’s posterior predictive distribution of the epidemic timeline for is consistent with reference to the original distribution but have the highest variance about the true epidemic timeline. Additionally, a faster spreading epidemic is predicted for the geometric ILM posterior predictive distributions of the epidemic timeline for , an example of which can be seen in Fig. 4 .
Fig. 4.
Posterior predictive distribution of the epidemic timeline for all models tested. Presented for study one with , infectious period equal to two time units, and r = 3. The solid black line describes the true epidemic timeline.
3.4.2. Exponential model
The exponential ILM tended to result in values similar to the geometric ILM, however, the geometric ILM on average was slightly better. Fig. 3 shows that the exponential ILM underestimates the probability of a susceptible individual becoming infected against distance from the infectious individual for study one. The exponential ILM posterior predictive distribution of the epidemic timeline for all is consistent with the original distribution but has high variance about the true epidemic timeline (see Fig. 5, Fig. 6 ).
Fig. 5.
Study one ( and infectious period=2) – mean predicted squared error of each model’s posterior predictive distribution of the epidemic timeline.
Fig. 6.
Study two ( and infectious period=2) – mean predicted squared error of each model’s posterior predictive distribution of the epidemic timeline.
3.4.3. Constant piecewise model
The constant piecewise model produced the best results under the criterion and favorable results using the MPSE criteria. Fig. 3 shows that the constant piecewise model predicts the probability of a susceptible individual becoming infected by a infectious individual against distance between the two individuals well for study one, but did underestimate infection probability for susceptible individuals and improperly estimate the radius. The constant piecewise model posterior predictive distribution of the epidemic timeline for all is consistent with the original distribution. The variance is lowest in the class of spatial models and has only slightly higher variance than the homogeneous mixing model for the cases.
3.4.4. Homogeneous mixing model
The homogeneous mixing model predicts the probability of a susceptible individual becoming infected by an infectious individual using the distance between the two individuals very poorly, for study one. The average results were also poor for both studies one and two. Results at the individual level were poor because the homogeneous mixing model does not take into account the distance factor, as all susceptible individuals have the same infection probability at any given time. This notion is an advantage, however, when contact networks contain a large amount of super-spreaders and/or an increased number of connections per super-spreader. As such, the results for the MPSE were favorable as the overall population, with increased connectivity, can be well modeled by a homogeneous mixing model. The homogeneous mixing model’s posterior predictive distributions of the epidemic timeline for are consistent with reference to the original distribution. The variance is lowest in comparison to all spatial model at these levels. The posterior predictive distribution of the epidemic timeline for is severely inconsistent with the true epidemic occurring earlier than predicted, this can be seen in Fig. 4.
4. Discussion
The purpose of this paper, as stated in Section 1, was to examine the effects of using a spatial kernel based ILM to model disease spread actually propagated through a contact network. This was carried out by simulating epidemics propagated through two types of random networks. The first type specified the probability of an edge existing between two individuals as depending on the distance between two individuals being greater, or less than, some constant. Spatial distance within the second study was also used to determine the probability of an edge between two individuals, but was based on a continuously spatially-decaying probability. The second study added complexity through the inclusion of super-spreaders. Various ILMs were then fit to the resulting data. Model fit at the individual level was assessed by considering the one-step ahead predictive probability of infection based on the posterior mean values of the parameters for the fitted models with that of the true model. At the population-level model fit was assessed my analyzing the posterior predictive distribution of the epidemic timeline through a mean predicted squared error calculation.
We have seen that in situations where there are only contacts between individuals within a relatively short distance of each other (i.e. in study one) or are less likely to have contacts over long distances ( in study two), there is relatively little difference between the performance of each of the spatial models as they all tend to fit reasonably well, in terms of predicting infection probability. However, when contacts occur over longer distances, the spatial models tend to perform poorly. If the probability of a long-distance contact is relatively high (i.e. in study one, or n and/or SS are high in study two), it seems that each of the spatial models performed roughly as poorly as each other, with perhaps a slight preference for the constant piecewise model. Model fit results were not surprising given the mechanics of the simulation. Essentially in the first study, a piecewise function was used for the contact network generation and as such the constant piecewise model would be expected to approximate this aspect well. In the case of the second study, the homogeneous mixing model showed improved results when the super-spreader information overpowered the underlying spatial decay. The super-spreader aspect of the contact network is random and therefore would be best approximated by the homogeneous mixing model.
The homogeneous mixing model is a special case of the constant piecewise model. When the radius parameter () of the piecewise kernel is outside the bounds of the possible infection distances observed (i.e. or ). Preliminary model fit of the constant piecewise model utilized a vague prior of a positive half-normal distributions with a mode of zero and variance of 1000 for . The resulting MCMC chain would often converge to a homogeneous mixing model case. For the purpose of this simulation study we wanted to force the constant piecewise model to be fitted and thus restrict the radius () parameter from extremely low or high values. The use of an informative prior, as described in Section 2.9, applied this restriction. Of course, such MCMC convergence issues are indicative of model uncertainty. In the case of a real data analysis, researchers may want to explore this model uncertainty and could do so using techniques such as reversible jump MCMC to explore the joint parameter and model space (Richardson and Green, 1997).
There are numerous avenues for further work potentially open to us. Only two types of contact network generators have been studied in this paper. It would be interesting to analyze the results of using the various spatial ILMs for different types of more complex networks. For example, contact structure could be a function of several sub-networks. An example of this might be given by considering influenza for human populations in which different networks describe contacts from living in the same household, attending the same school/workplace, visiting the same general practitioners, and so on.
In this paper, we assumed a known and fixed infectious period for each individual. Obviously, it would be more realistic to have a situation where the infectious period, and possibly a latent period, are generated from some distribution. The infectious periods and latent periods for individuals could then be estimated as part of a data-augmented MCMC scheme, along with the distribution of those periods. This was not done here, to avoid the substantial, additional computational burden that would result from such a scheme and to avoid extra uncertainty which could confuse results.
As previously stated, obtaining complete contact network information is exceedingly challenging. Studies into the amount of uncertainty about the network information that could be incorporated into a Bayesian analysis, in which the network itself is treated as an unknown parameter, before conclusions drawn from the model becomes unreliable, would also be of interest.
The intention of this paper was to present generic insights into the cost of using a spatial model when the underlying population is connected by a spatially-based network. We therefore purposefully avoided using a specific application. Of course, when modeling a real life outbreak and specific disease system, the model to be fit will need to be tailored to the data collected, as well as the underlying disease system. We have seen that the performance of the simple spatial disease transmission models can break down easily under various scenarios when the underlying contact structure is more complex. Optimal model fit is achieved when the structure of the model incorporates the characteristics of the disease spread; this includes the contact network. If modeling a wildlife epidemic, steps must be taken to determine how the mixing is occurring. At a spatial level this may mean incorporating aspects describing within herd dynamics, immigration and emigration rates, physical barriers to movement, and peak times of activity. With airborne pathogens spread to plants, models highlighting the spatial decay may indeed be adequate but could be improved upon if windspeed and other weather characteristics were also taken into account. Perhaps the overriding lesson to be drawn from the results shown here is the importance of putting in place a policy of procedures to collect high quality network (and other) data from the system of interest.
Footnotes
Supplementary data associated with this article can be found, in the online version, at http://dx.doi.org/10.1016/j.sste.2013.07.001.
Contributor Information
Nadia Bifolchi, Email: nbifolch@uoguelph.ca.
Rob Deardon, Email: rdeardon@uoguelph.ca.
Zeny Feng, Email: zfeng@uoguelph.ca.
Appendix A. Supplementary data
References
- Bansal S., Grenfell B.T., Meyers L.A. When individual behaviour matters: homogeneous and network models in epidemiology. J R Soc Interface. 2007;4:879–891. doi: 10.1098/rsif.2007.1100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beutels P., Jia N., Zhou Q.Y., Smith R., Cao W., de Vlas S.J. The economic impact of SARS in Beijing, China. Trop Med Int Health. 2009;14(1):85–91. doi: 10.1111/j.1365-3156.2008.02210.x. [DOI] [PubMed] [Google Scholar]
- Cauchemez S., Bhattarai A., Marchbanks T.L., Fagan R.P., Ostroff S., Ferguson N.M., Swerdlow D.D. Role of social networks in shaping disease transmission during a community outbreak of 2009 H1N1 pandemic influenza. Proc Natl Acad Sci USA. 2011;108(7):2825–2830. doi: 10.1073/pnas.1008895108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chis Ster I., Ferguson N.M. Transmission parameters of the 2001 foot and mouth epidemic in Great Britain. PLoS ONE. 2007;2(6):502. doi: 10.1371/journal.pone.0000502. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chis Ster I., Singh B.K., Ferguson N.M. Epidemiological inference for partially observed epidemics: the example of the 2001 foot and mouth epidemic in Great Britain. Epidemics. 2009;1(1):21–34. doi: 10.1016/j.epidem.2008.09.001. [DOI] [PubMed] [Google Scholar]
- Deardon R., Brooks S.P., Grenfell B.T., Keeling M.J., Tildesley M.J., Savill N.J., Shaw D.J., Woolhouse M.E.J. Inference for individual-level models of infectious diseases in large populations. Stat Sin. 2010;20:239–261. [PMC free article] [PubMed] [Google Scholar]
- Dubé C. University of Guelph; Guelph, Ontario: 2009. Network analysis of dairy cattle movements in Ontario to support livestock disease simulation modelling. Thesis. [Google Scholar]
- Filipe J.A.N., Maule M.M. Effects of dispersal mechanisms on spatio-temporal development of epidemics. J Theor Biol. 2004;226:125–141. doi: 10.1016/s0022-5193(03)00278-9. [DOI] [PubMed] [Google Scholar]
- Jewell C., Kypraios T., Christley R., Roberts G. A novel approach to real-time risk prediction for emerging infectious diseases: a case study in avian influenza H5N1. Prev Vet Med. 2009;91(1):19–28. doi: 10.1016/j.prevetmed.2009.05.019. [DOI] [PubMed] [Google Scholar]
- Keeling M.J., Eames K.T.D. Networks and epidemic models. J R Soc Interface. 2005;2:295–307. doi: 10.1098/rsif.2005.0051. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Keeling M.J., Woolhouse M.E., Shaw D.J., Matthews L., Chase-Topping M., Haydon D.T., Cornell S.J., Kappey J., Wilesmith J., Grenfell B.T. Dynamics of the 2001 UK foot and mouth epidemic: stochastic dispersal in a heterogeneous landscape. Science. 2001;294(5543):813–817. doi: 10.1126/science.1065973. [DOI] [PubMed] [Google Scholar]
- Kolaczyk E.D. Statistical analysis of network data. Springer; New York, NY: 2009. (Statistics). [Google Scholar]
- Lloyd-Smith J.O., Schreiber S.J., Kopp P.E., Getz W.M. Superspreading and the effect of individual variation on disease emergence. Nature. 2005;438(7066):355–359. doi: 10.1038/nature04153. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marchbanks T.L., Bhattarai A., Fagan R.P., Ostroff S., Sodha S.V., Moll M.E., Lee B.Y., Chang C.C.H., Ennis B., Britz P. An outbreak of 2009 pandemic influenza A (H1N1) virus infection in an elementary school in Pennsylvania. Clin Infect Dis. 2011;52(Suppl. 1):S154–S160. doi: 10.1093/cid/ciq058. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meltzer M., Cox N., Fukuda K. The economic impact of pandemic influenza in the United States: priorities for intervention. Emerg Infect Dis. 1999;5(5):659–671. doi: 10.3201/eid0505.990507. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Richardson S., Green P.J. On Bayesian analysis of mixtures with an unknown number of components. J R Stat Soc Series B Stat Methodol. 1997;59(4):731–792. [Google Scholar]
- Smith D.L., Waller L.A., Russell C.A., Childs J.E., Real L.A. Assessing the role of long-distance translocation and spatial heterogeneity in the raccoon rabies epidemic in Connecticut. Prev Vet Med. 2005;71(3):225–240. doi: 10.1016/j.prevetmed.2005.07.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Streftaris G., Gibson G.J. Bayesian analysis of experimental epidemics of foot-and-mouth disease. Proc R Soc Lond [Biol] 2004;271(1544):1111–1117. doi: 10.1098/rspb.2004.2715. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhen J., Juping Z., Li-Peng S., Gui-Quan S., Jianli K., Huaiping Z. Modelling and analysis of influenza A (H1N1) on networks. BMC Public Health. 2011;11(Suppl. 1):1–9. doi: 10.1186/1471-2458-11-S1-S9. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.