The utility of LASSO-based models for real time forecasts of endemic infectious diseases: A cross country comparison

Graphical abstract

Highlights

• •A LASSO based forecast model for endemic infectious diseases is proposed.
• •Predictions at 4 weeks achieve desirable accuracy.
• •Models predict outbreaks but may struggle to predict outbreak size.

Abstract

Introduction

Accurate and timely prediction for endemic infectious diseases is vital for public health agencies to plan and carry out any control methods at an early stage of disease outbreaks. Climatic variables has been identified as important predictors in models for infectious disease forecasts. Various approaches have been proposed in the literature to produce accurate and timely predictions and potentially improve public health response.

Methods

We assessed how the machine learning LASSO method may be useful in providing useful forecasts for different pathogens in countries with different climates. Separate LASSO models were constructed for different disease/country/forecast window with different model complexity by including different sets of predictors to assess the importance of different predictors under various conditions.

Results

There was a more apparent cyclicity for both climatic variables and incidence in regions further away from the equator. For most diseases, predictions made beyond 4 weeks ahead were increasingly discrepant from the actual scenario. Prediction models were more accurate in capturing the outbreak but less sensitive to predict the outbreak size. In different situations, climatic variables have different levels of importance in prediction accuracy.

Conclusions

For LASSO models used for prediction, including different sets of predictors has varying effect in different situations. Short term predictions generally perform better than longer term predictions, suggesting public health agencies may need the capacity to respond at short-notice to early warnings.

1. Introduction

Outbreaks such as those caused by the Severe Acute Respiratory Syndrome Coronavirus (SARS CoV), the influenza A(H1N1)pdm09 pandemic of 2009, and more recently the Middle East Respiratory Syndrome Coronavirus (MERS-CoV), Ebola virus and Zika virus have demonstrated the high potential risk of emerging and re-emerging infectious diseases to spread within and between countries [1], [2], [3], [4], [5]. These in turn cause increasing challenges for public health systems, including the increasing burden of infectious disease, and the need to build a surveillance and response system that is able to identify newly emerging disease rapidly, both regionally and internationally which calls for international collaboration, and the need for drug and vaccine research and production [6], [7], [8]. While the response to endemic diseases may be less urgent, the burden caused by pathogens such as influenza or malaria is high [9], [10], [11], and due to their endemicity, many countries have long standing surveillance systems to track outbreaks and guide response, from vector control to hospital bed utilization [12], [13], [14], [15]. Early warning systems aiming to predict epidemics as soon as possible can allow control methods to be carried out rapidly and increase their chance of success [16], [17]. To do so, decision makers need to be able to make accurate forecasts of incidence and to automate this forecasting process based on routinely collected notification data [18]. If accurate forecasts were available in both the near and far future, effective policies could then be targeted to the expected future needs. Existing approaches to real-time forecasting include generalized linear regression, seasonal autoregressive integrated moving average (SARIMA) model or a simpler ARIMA form of it, phenomenological models like the logistic growth model and Richards model, and mechanistic models like the SIR models [19], [20], [21], [22], [23], [24]. Often such approaches involve the challenge of integrating environmental factors including temperature, humidity and rainfall, which may influence pathogen transmission directly or affect the vector activities (for vector borne diseases), especially in temperate regions [25], [26], [27], [28], [29]. For instance, influenza virus is more transmissible in low temperature and low humidity conditions [30], [31], while the primary vector of dengue, the yellow fever mosquito Aedes aegypti, favors higher temperature [32], [33]. The availability of real time data-streams on seasonal variation and climatic variability therefore holds the potential to lead to more accurate prediction algorithms, potentially improving public health response.

Least Absolute Shrinkage and Selection Operator (LASSO) regression is a machine learning method that can find patterns within large datasets while avoiding the problem of over-fitting [34]. Estimation and variable selection are simultaneously carried out using the LASSO method, and as such it is commonly used in studies in fields with large numbers of explanatory variables to reduce the variable space. This algorithm trades off model accuracy with model parsimony by introducing a penalty term into the objective function (which in standard linear regression is the sum of squares of residuals). The penalty term can, for linear regression models, be made equivalent to a constraint on the sum of the absolute parameter coefficients. This constraint imposed by LASSO regression has the effect of shrinking some estimated coefficients towards zero, which may help reduce biases caused by separation in some forms of regression [35], while simultaneously producing some parameter estimates that are exactly 0, so that the covariate associated with this coefficient is not associated with the outcome variable in that model. The optimal balance between model accuracy and complexity is typically obtained through cross-validation: repeatedly partitioning the data into training and validation sets, varying the degree of penalty, optimizing the regression parameters for each penalty value, then selecting the penalty that minimizes out of sample predictive accuracy. Computationally efficient methods to explore the penalty and parameter space exist [36], making it feasible to use LASSO as part of a ‘real-time’ forecasting pipeline for routinely collected health data such as infectious disease notifications. This computational speed allows the forecasting to adapt to changes in the underlying disease dynamics by permitting refitting of the model each time new data are reported, which may be important for diseases in which the severity changes between outbreaks, such as influenza [37]. Forecasts at different time horizons can be obtained through splicing together separate LASSO models, each trained on the data available at the time of the forecast, but tailored to predict at different windows into the future.

The LASSO method has previously been used in dengue outbreak prediction in Singapore, where it is now routinely used to guide vector control policy [38]. The objective of this paper is to apply the LASSO method to infectious disease forecasting and assess more generally in which situations LASSO models will provide useful forecasts. Unlike conventional use of the LASSO method to variable selection, the primary interest of our application of the LASSO-based method on infectious disease data is to make forecast of incidences in the future, rather than to identify the potential risk factors to explain the epidemics of these infectious diseases.

In particular, we assess for diseases with different transmission modalities, in different climatic zones, how accurate short to medium time forecasts can be, and what data streams are necessary for accurate forecasts. We apply the method to four countries from different latitudes—Japan, Taiwan, Thailand and Singapore—to cover temperate, sub-tropical and tropical settings.

2. Methods

2.1. Sources of data

Four representative countries with distinct climates were selected for analysis based on Köppen-Geiger climate classification [39] – Japan with humid continental and subtropical climate; Taiwan with humid subtropical and oceanic climate; Thailand with tropical wet and savannah climate and Singapore with tropical rainforest climate. Four representative infectious diseases were included in the study: two mosquito-borne infections (Dengue and Malaria) and two infections that spread from person to person (Hand Foot and Mouth Disease (HFMD) and Chickenpox). For all four pathogens, a relationship has previously been found between incidence and climatic variables [40], [41], [42] or for there to be a seasonality to incidence [43]. Not all four pathogens were considered for each country: some are not present in each country while others are not captured in routine infectious disease surveillance systems.

The notified numbers of chickenpox, HFMD cases in Japan were collected by the National Institute of Infectious Diseases (NIID) [44]. Both were reported as average cases per week per sentinel reporting, to accommodate varying reporting rates. We extracted weekly data from 2001 to 2012.

Monthly reported cases of chickenpox, dengue, and malaria in Thailand for the period 2003–2013 were obtained from the Bureau of Epidemiology, Department of Disease Control, Ministry of Public Health, Thailand [45]. The number of incident cases were collected from government hospitals, public health offices and health centers by the National Disease Surveillance [46] and were reported online.

Ministry of Health, Singapore, actively monitors and publishes the incidence of dengue and HFMD in Singapore, both being notifiable diseases. Weekly number of incidences for the period 2003 and 2014 were obtained from the Weekly Infectious Diseases Bulletin [47].

Weekly number of dengue cases from 2003 to 2014 were extracted from Taiwan National Infectious Disease Statistics System [48]. Both indigenous and imported cases were included in the count.

Epidemiological week as per US Centers for Disease Control and Prevention was used in our analysis using the EpiWeek package in R [49].

Climatic data for Taiwan, Thailand and Singapore were obtained from the Weather Underground [50] which documented among other variables, historical temperature, humidity, sea level pressure, and visibility. Only temperature (daily highest, average and lowest) and relative humidity (daily highest, average and lowest) were used in our models due to insufficient historical data of other climatic variables. Climatic data for Japan were obtained from the Japan Meteorological Agency [51], which provides and archives various weather information. Weekly mean temperature, relative humidity and rainfall information were used in our model. For all locations, the weather data at the capital (Tokyo, Taipei, Bangkok and Singapore) was used to represent overall national weather.

2.2. Statistical analysis

Wavelet analyses were done to explore periodicity of all endemic diseases and climatic variables in four countries. The wavelet approach was based on a wavelet function which analyses locality in time and frequency [52]. Wavelet transformation ($W_t(s)$) as the convolution of the time series $x_t$ with Morlet function ${\psi }_0(\eta )$ at scale $s$ was conducted:

$$W_t(s)={\displaystyle \sum _{k=0}^{T-1}}{\widehat{x}}_k{\widehat{\psi }}^{\ast }(s{\omega }_k)e^{i{\omega }_{k}n{\delta }_t}$$

where ${\widehat{x}}_k$ is the discrete Fourier transform of $x_t$: ${\widehat{x}}_k=\frac{1}{T}{\sum }_{t=0}^{T-1}{x}_t{e}^{-2\pi \mathit{ikt}/T}$, $k=0\text{,}\dots \text{,}T-1$ the frequency index, and $\widehat{\psi }(s\omega )$ the Fourier transform of Morlet function: $\widehat{\psi }(s\omega )={\pi }^{-\frac{1}{4}}H(\omega )e^{-{(s\omega -{\omega }_0)}^2/2}$, where ${\omega }_0$ refers to the nondimensional frequency and is set to 6 to satisfy the admissibility condition [53].

The wavelet transformation $W_t(s)$ can be divided into amplitude, $|W_t(s)|$, and phase, ${\tan }^{-1}[\mathfrak{I}\left\{W_n\right)\left((s)\right\}/\mathfrak{R}\left\{W_n\right)\left((s)\right\}]$, where $\mathfrak{R}\left\{W_n\right)\left((s)\right\}$ is the real part of the transform and $\mathfrak{I}\left\{W_n\right)\left((s)\right\}$ the imaginary part. The wavelet power spectrum is defined as $|W_t(s){|}^2$ [54].

Least Absolute Shrinkage and Selection Operator (LASSO) regression [34] is used for the prediction models. As incidence data were generally right skewed and with increased stochasticity during epidemics, we controlled for skewness and heteroscedasticity by log-transforming (after adding one to) the observed number of cases for all analyses, or mean number of cases per sentinel for Japan.

We build separate LASSO models for each disease, in each country, and for each forecast window based on similar sets of candidate predictors (adapting the approach used in Ref. [38]). Each candidate predictor appeared several times in each model, at different historical lags. To allow for contagion and typical epidemic duration, we used past incidence of up to a half year (26 weeks for Japan, Taiwan and Singapore; 6 months for Thailand) as autocovariates. We accommodated non-linearities in the relationship between past and future incidence by using the quadratic of past incidence (again, up to one half year in the past) as a potential covariate; the inclusion of additional polynomial terms did not improve the results and hence were omitted. We used climatic variables (minimum, maximum and average temperature, humidity and rainfall) of up to 4 weeks (one month for Thailand). We also used a month indicator that associated each epidemiological week with a single calendar month to represent potential seasonal variation beyond those governed by the climatic data. Wavelet transformations of the covariates and outcomes were not used, to ensure that only data available at the time of the forecast were used to make the forecast.

For each forecast window (from $k=1$ time unit to 6, for Thailand (the data being monthly) or 26, for Japan, Taiwan and Singapore (weekly)), a separate LASSO model was developed which used data available at the time of the forecast only. The selection of the time window was dependent on the resolution of notification data for each disease. Each LASSO model is as follows:

$$y_{t+k}={\alpha }_{t_k}+{\beta }_{t_k}{y}_t+{\beta }_{t_k-1}{y}_{t-1}+\dots +{\beta }_{t_k-25}{y}_{t-25}+{\gamma }_{t_k}{y}_t^2+{\gamma }_{t_k-1}{y}_{t-1}^2+\dots +{\gamma }_{t_k-25}{y}_{t-25}^2+{\delta }_{t_k}{c}_t+\dots +{\delta }_{t_k-3}{c}_{t-3}+{\theta }_{k_1}{\text{Jan}}_{t+k}+{\theta }_{k_2}{\text{Feb}}_{t+k}+\dots +{\theta }_{k_{12}}{\text{Dec}}_{t+k}+{\epsilon }_{t_k}$$

where $y_t$ is the log number of cases at time $t$, $y_t^2$ the square of the log number of cases at time $t$, $c_t$ the climatic variable at time $t$, and ${\text{Jan}}_t$, ${\text{Feb}}_t$, …, ${\text{Dec}}_t$ are indicator variables for the month at time $t$.

This was subject to the constraint

$$\sum _{i=0}^{25}\left|{\beta }_{t_k-i}\right|+\sum _{i=0}^{25}\left|{\gamma }_{t_k-i}\right|+\sum _{i=0}^3\left|{\delta }_{t_k-i}\right|+\sum _{i=1}^{12}\left|{\theta }_{k_i}\right|⩽p.$$

The $p$ and penalty term λ have a one-to-one correspondence in LASSO, which can equivalently be formulated as a constraint to the total absolute size of the parameters, or as a penalty to the log-likelihood determined by their total absolute size. The choice of the optimal $p$ in this study was based on ten-fold cross validation for that dataset (country, disease, forecast length combination). Ten-fold cross validation was carried out by partitioning the total data set into 10 approximately equal-sized subsamples. Each subsample was used in turn as the validation set while the rest were used as the training set, the performance was measured through the mean squared error (of the difference between the forecast and the data) on each validation set and averaged over the ten folds. The constraint (or equivalently, penalty term) that optimized the out of sample performance was then used to refit the model and make projections. In this way, the optimal complexity of the model—from the perspective of out of sample prediction—can be determined via the constraint. We developed both (a) ‘real time’ forecasts, in which both the parameters and the predictions were regenerated based on available data at that time, and (b) one set of ‘retrospective’ forecasts, which used the last of the real time forecasts, to summarize effects of covariates.

Following standard practice, covariates were z-scored prior to estimation and the coefficients rescaled afterwards.

As the models were built separately for each forecast window, the variables selected and their lags and parameter magnitude and sign may differ substantially.

2.3. Sensitivity analysis

Eight models with different combination of predictor types were used for each disease/country/forecast length to assess the importance of including each datastream in the predictive algorithm. Details of the components in each model are shown in Table 1 .

Table 1.

Sets of predictors in different models.

Models	Incidence	Squared incidence	Climatic variables	Monthly effect
1	√	.	.	.
2	√	√	.	.
3	√	.	√	.
4	√	.	.	√
5	√	√	√	.
6	√	√	.	√
7	√	.	√	√
8	√	√	√	√

2.4. Accuracy

To assess prediction accuracy of the models, we made out-of-sample forecasts and compared with data observed. For each time point and each prediction window, a 95% projection interval—which we define here as an interval derived from the best fitting model with random errors overlaid, but excluding parametric uncertainty—was derived and the percentage of such intervals successfully capturing the actual value was calculated.

To assess if the prediction models were able to detect early signs of elevated levels of transmission—which we defined to be time windows (weeks or months) in which the number of cases is more than the 75th percentile of what has been observed in the preceding year—we calculated the fraction of predictions in which the projection correctly classified the data as being above or below that threshold. This was calculated separately for each length of forecast window. An accuracy of 75% is expected for a poorly predictive model. One-sided binomial tests were done to all prediction windows and those that significantly identify the early signs at an accuracy of more than 75% were identified.

Prediction accuracy was measured by the mean absolute percentage error (MAPE), root mean squared error (RMSE), and R-squared, for each forecast window. Relative prediction error as compared to the simplest incidence only model at all forecast windows was calculated to assess model complexity and accuracy. All statistical analysis were performed using R Statistical Software [55].

3. Results

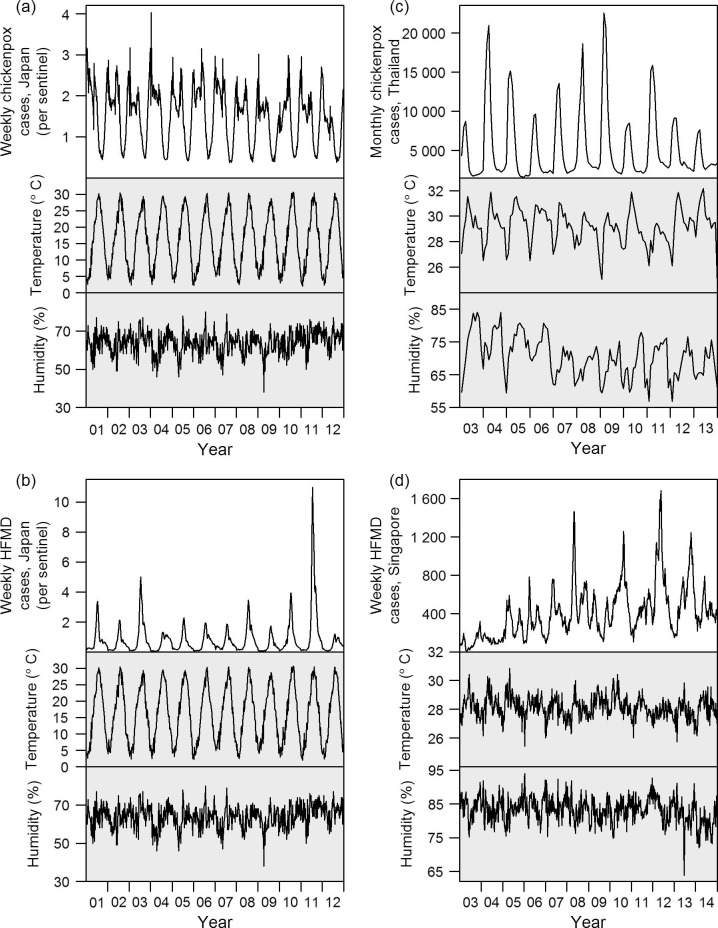
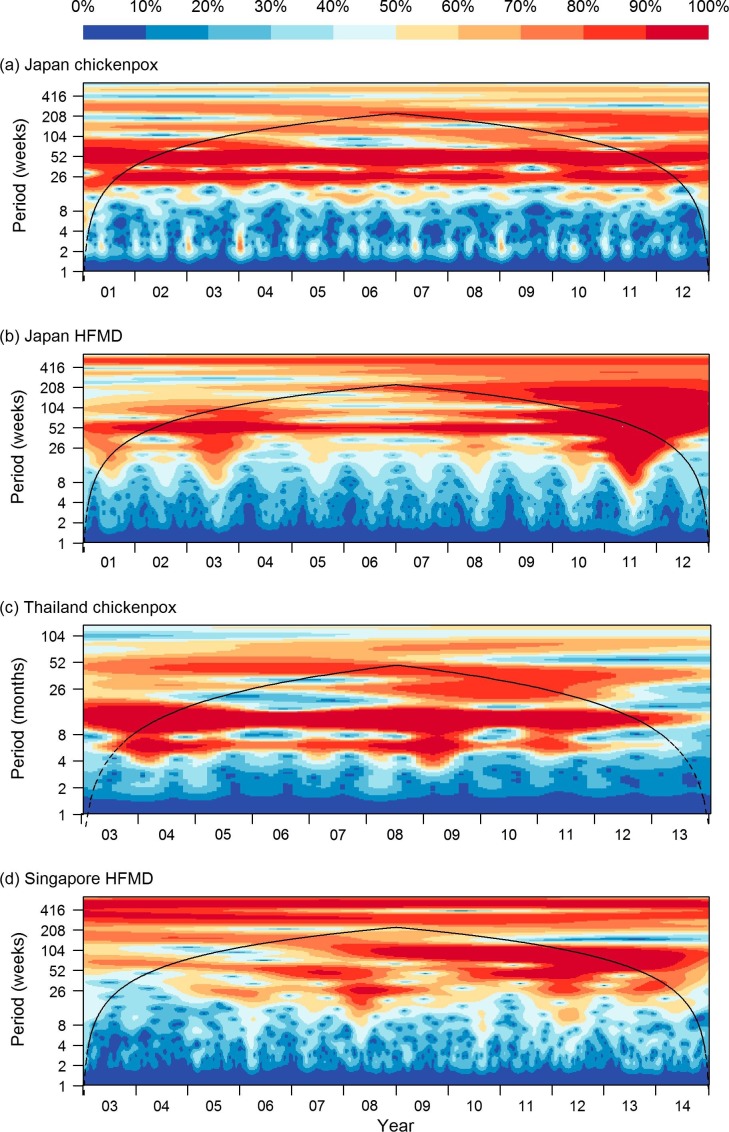
Climatic and incidence patterns of the diseases are presented in Fig. 1 . Four representative diseases were shown in this figure (others are presented in Supplementary Figs. 1–4). At further distances from the equator, temperature and humidity show more obvious annual cycles, and there is concomitantly more cyclicity in disease incidence, as indicated in the power spectra illustrated in Fig. 2 . Power spectra of average temperature and humidity are presented in Supplementary Figs. 5 and 6. Temperature in all countries has a period of one year but the cyclic effect is more marked in temperate and subtropical regions, and less so in equatorial Singapore. Average humidity displays one-year cycle in temperate and subtropical regions, but again not Singapore, although the effect is not as obvious as with average temperature. Although in temperate regions, there is an apparent synchronicity between incidence and climatic factors, in tropical regions like equatorial Singapore, there was little variation in either temperature or humidity, and similarly no observed cycle of disease incidence. In addition, there was no correlation observable between cases and climate, either in incidence itself or the change in incidence (reflecting transmissibility).

Fig. 1.

Incidence and climatic (temperature and humidity) patterns of four representative diseases. (a) Chickenpox in Japan; (b) HFMD in Japan; (c) chickenpox in Thailand; (d) HFMD in Singapore. Year 01 corresponds to the year 2001 of the common era, et cetera.

Fig. 2.

Wavelet power spectrum for (a) chickenpox in Japan; (b) HFMD in Japan; (c) chickenpox in Thailand; (d) HFMD in Singapore. For each panel, the power spectrum values are categorised by decile prior to plotting.

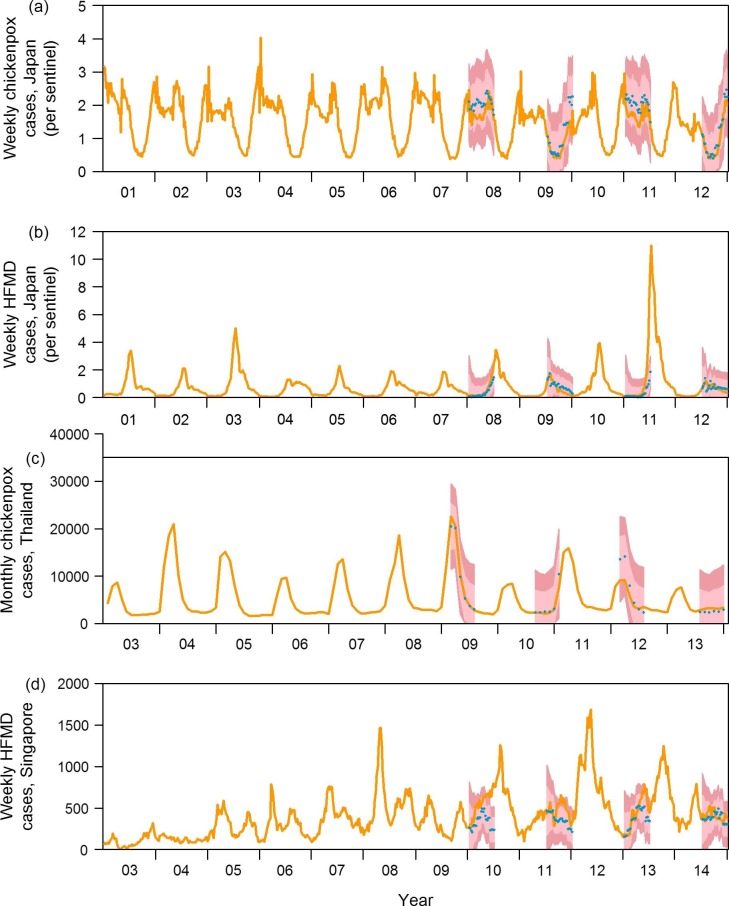
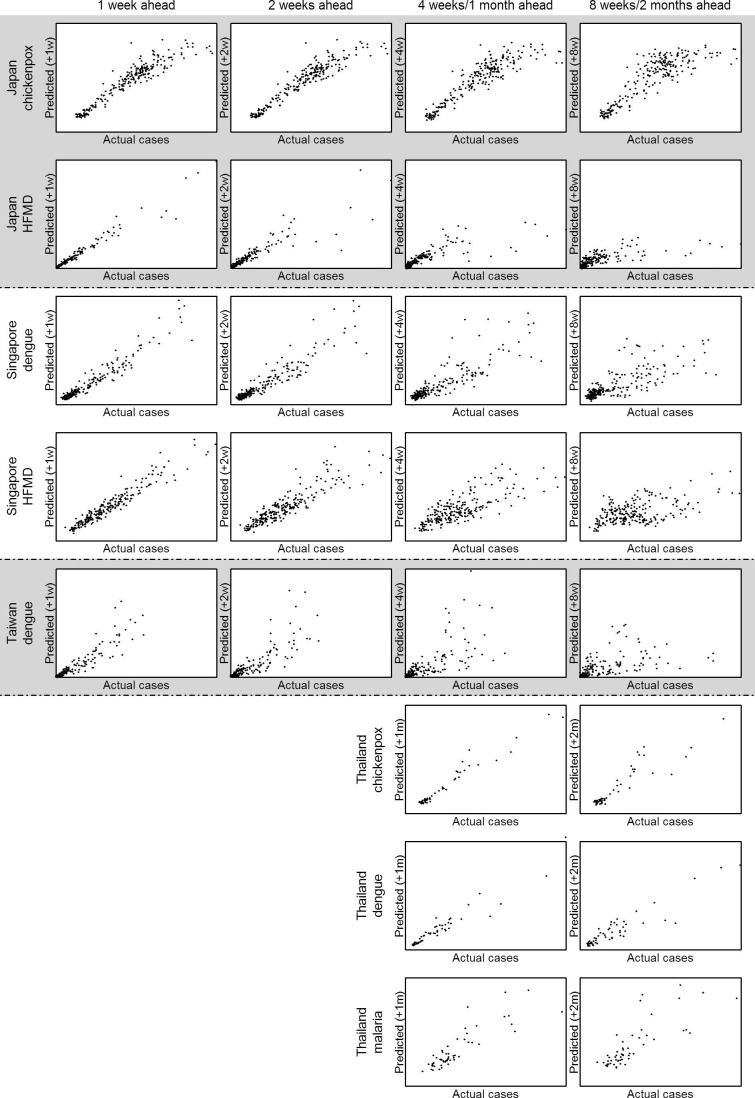
Fig. 3 shows the actual incidences as well as forecasts at four prediction points for the four diseases presented in Fig. 1 (predictions at other time points/diseases are presented in Supplementary Videos 1–8) using the model with all variable sets. At each time point, up to six month ahead predictions are shown in the figure, using data available at the time the prediction was made. The number of variables from each category that were selected by our LASSO models are presented in Supplementary Fig. 7 and the effect size of each climatic variable at different lags for all forecast windows are shown in Supplementary Fig. 8. Generally, the 95% projection interval of the forecast captured the actual scenario more than 80% of the time, indicating slight under-coverage. Coverage rates for the full models are tabulated in Table 2 . MAPE for full models at all prediction windows are shown in Table 3 . RMSE and R-squared values for full models are included in Supplementary Tables 1 and 2. For most diseases, predictions made beyond 4 weeks ahead were increasingly discrepant from the actual scenario.

,

,

,

,

,

,

,

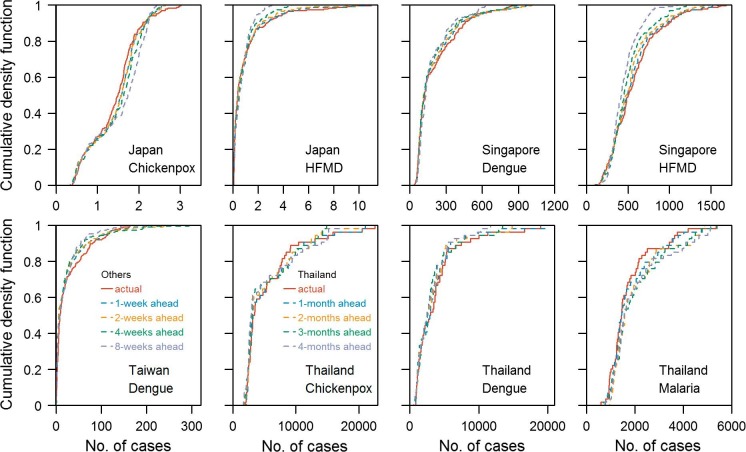
Predicted cases against actual cases at 1 week, 2 weeks, 4 weeks and 8 weeks for all prediction period for all diseases were plotted in Fig. 4 . For all diseases, as the prediction window gets longer, the magnitude of the error grows, especially for the largest sizes of outbreaks where there is likely to be more stochastic variability. Cumulative density functions of the observed time series of all diseases and predicted time series at various forecast windows are shown in Fig. 5 : those derived from predictions are generally close to that from the observed time series. Short term predictions generally performed better than longer term predictions. Table 4 shows the classification accuracy of our prediction models being able to correctly classify one week/month to be an epidemic week/month. A percentage above 75% suggested that the prediction model performed better than a random guess. Models that passed the binomial test of having accuracy significantly higher than 75% were marked with the asterisk. Predictions for HFMD epidemic were generally accurate even at long prediction windows; for most other diseases, prediction within 5 weeks were above 75%. However, for chickenpox in Japan and dengue in Singapore, only predictions within 3 and 4 weeks were significantly above 75% from the Binomial test. This suggests that the approach can predict the timing of periods of elevated transmission at about one month in advance but that the absolute magnitude is hard to predict accurately, given the larger errors at high levels exhibited in Fig. 4.

Fig. 3.

Actual incidence (orange line) and forecasts (blue dots, dark red 95% projection interval, pink 70% projection interval) at four time points for each of the representative diseases. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

Table 2.

Fraction of 95% projection intervals that cover the eventual value for full models for all diseases at all prediction windows.

	Japan		Singapore		Taiwan	Thailand
Prediction Window	Chickenpox	HFMD	Dengue	HFMD	Dengue	Chickenpox	Dengue	Malaria
1	100%	100%	100%	100%	99%
2	100%	98%	100%	100%	98%
3	100%	96%	99%	98%	97%
4	100%	96%	98%	96%	96%	100%	100%	100%
5	100%	95%	98%	94%	94%
6	100%	94%	97%	87%	92%
7	100%	92%	95%	83%	91%
8	100%	91%	93%	77%	89%	100%	98%	96%
9	100%	91%	91%	74%	86%
10	100%	90%	90%	73%	85%
11	100%	90%	88%	71%	82%
12	100%	89%	86%	69%	80%	100%	98%	96%
13	100%	89%	83%	64%	80%
14	100%	89%	84%	63%	81%
15	100%	90%	83%	63%	81%
16	100%	90%	83%	63%	81%	100%	94%	100%
17	100%	91%	89%	65%	80%
18	100%	90%	91%	64%	80%
19	100%	90%	92%	64%	80%
20	99%	90%	91%	64%	80%	100%	93%	98%
21	99%	90%	90%	65%	81%
22	99%	90%	91%	63%	82%
23	99%	90%	90%	63%	82%
24	99%	90%	89%	63%	81%	100%	94%	98%
25	100%	90%	86%	63%	82%
26	100%	90%	82%	63%	81%

Table 3.

Mean Absolute Percentage Error for full models for all diseases at all prediction windows.

	Japan		Singapore		Taiwan	Thailand
Prediction Window	Chickenpox	HFMD	Dengue	HFMD	Dengue	Chickenpox	Dengue	Malaria
1	0.10	0.18	0.17	0.12	0.47
2	0.10	0.31	0.20	0.18	0.57
3	0.13	0.40	0.23	0.23	0.64
4	0.14	0.46	0.26	0.26	0.66	0.09	0.15	0.20
5	0.16	0.51	0.29	0.29	0.67
6	0.18	0.58	0.31	0.31	0.70
7	0.19	0.65	0.33	0.33	0.70
8	0.20	0.69	0.35	0.35	0.74	0.17	0.24	0.29
9	0.22	0.69	0.36	0.38	0.75
10	0.22	0.68	0.36	0.41	0.77
11	0.23	0.75	0.37	0.43	0.80
12	0.23	0.83	0.39	0.45	0.80	0.24	0.25	0.31
13	0.23	0.89	0.38	0.46	0.82
14	0.25	0.89	0.39	0.47	0.80
15	0.25	0.93	0.39	0.48	0.79
16	0.25	0.95	0.40	0.49	0.80	0.28	0.30	0.31
17	0.25	0.92	0.42	0.51	0.80
18	0.25	0.91	0.42	0.51	0.79
19	0.24	0.90	0.42	0.51	0.82
20	0.24	0.92	0.42	0.53	0.82	0.28	0.32	0.30
21	0.24	0.92	0.43	0.53	0.79
22	0.24	0.85	0.45	0.52	0.79
23	0.23	0.69	0.46	0.51	0.78
24	0.23	0.66	0.46	0.50	0.79	0.31	0.33	0.32
25	0.21	0.64	0.47	0.51	0.81
26	0.22	0.60	0.46	0.51	0.81

Fig. 4.

Predicted cases against actual incidence at 1 week, 2 weeks, 4 weeks (1 month), and 8 weeks (2 months) for all prediction period for all diseases.

Fig. 5.

Cumulative density functions (CDF) for observed time series for all diseases and the CDF for predicted time series at various forecast windows.

Table 4.

Percentage of our prediction model correctly classify a predicted future week/month being an epidemic week/month. An epidemic week/month is defined as when the number of cases is more than the 75th percentile of the level in the past year. Percentage above 75% is shown bold. Models that had significantly higher accuracy than 75% are marked with an asterisk.

	Japan		Singapore		Taiwan	Thailand
Prediction Window	Chickenpox	HFMD	Dengue	HFMD	Dengue	Chickenpox	Dengue	Malaria
1	89%*	97%*	90%*	99%*	93%*
2	87%*	97%*	88%*	96%*	93%*
3	86%*	97%*	83%*	95%*	91%*
4	78%	95%*	81%*	94%*	89%*	98%*	98%*	100%*
5	76%	93%*	79%	91%*	89%*
6	75%	91%*	80%	90%*	86%*
7	72%	89%*	75%	87%*	83%*
8	71%	88%*	73%	85%*	80%*	94%*	94%*	100%*
9	68%	88%*	69%	81%*	80%*
10	69%	88%*	71%	80%*	77%
11	70%	88%*	70%	79%	75%
12	69%	88%*	71%	80%*	75%	93%*	96%*	100%*
13	71%	87%*	70%	81%*	74%
14	70%	87%*	68%	81%*	76%
15	69%	87%*	69%	81%*	77%
16	71%	86%*	71%	80%*	76%	91%*	93%*	100%*
17	73%	86%*	70%	80%*	77%
18	72%	88%*	73%	80%*	77%
19	73%	89%*	71%	80%*	76%
20	71%	90%*	71%	80%*	77%	89%*	93%*	100%*
21	71%	90%*	73%	79%	78%
22	70%	89%*	73%	79%	77%
23	68%	89%*	72%	80%*	77%
24	70%	89%*	71%	80%*	77%	87%*	91%*	100%*
25	71%	89%*	71%	78%	77%
26	73%	89%*	71%	81%*	76%

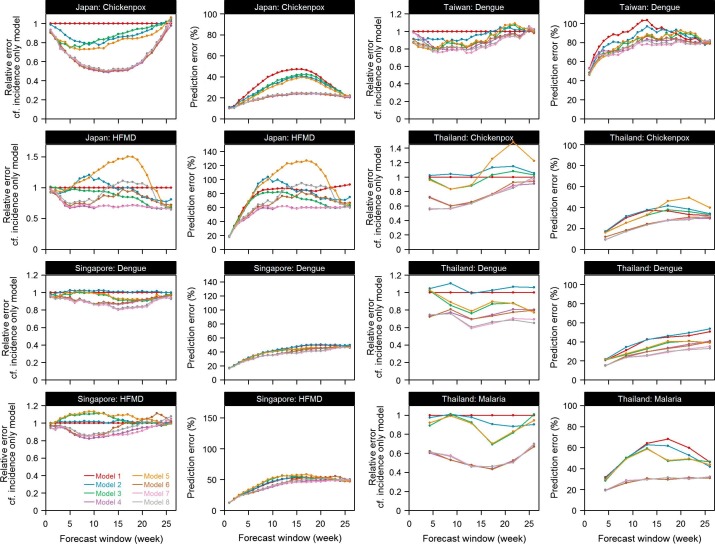
The trade-off between model complexity and efficiency was assessed by constructing models with different groups of variables and comparing the forecasts based on these models (Fig. 6 , an enlarged version is shown in Supplementary Figs. 9 and 10). The prediction errors arising from each model were then compared with the simplest incidence only model. A ratio substantially less than 1 shows prediction accuracy increased by including the set(s) of variables. For some diseases like chickenpox in Thailand, dropping some variables affected prediction accuracy by a large extent, indicating the importance of including monthly effect to achieve greater accuracy in predictions. For other diseases like dengue in Taiwan, dropping the climatic variables had only minimal effect on the accuracy of the predictions, which suggests that the features in those sets are not necessary for routine predictions. Panels in the second and fourth columns in Fig. 6 showed prediction error for all diseases for different prediction windows. Prediction error was quantified by the mean absolute percentage error. In line with our previous observations, as the prediction window gets longer, prediction error increases. More complicated models show less prediction error but the improvements varied by diseases and countries.

Fig. 6.

Relative prediction error for models of different complexity as compared to the simplest incidence only model and absolute prediction error measured by MAPE for all models.

4. Discussion

Applying the LASSO method to data on recent incidence and climate leads to around 20% or lower prediction error for short term predictions, even for an aseasonal, tropical country like Singapore in which the presence of randomness in outbreak occurrence may be strongly felt [56]. Most of the variation in incidence was explained by the autoregressive terms as there was no or minimal improvement in forecast accuracy by including more variables other than autoregressive terms in the prediction model shown in Fig. 6. Long term predictions were not accurate, even when we include multiple climatic variables as candidate features. We believe this reflects the difficulty in using weather data relating to current conditions to predict disease levels in several months—in contrast, most other analyses use climate data from near the time point being forecast [28], [57], which is typically not available in real time. Hence the utility of predictive analytics for infectious disease policy making is mostly for immediate response over the next few weeks rather than months.

This LASSO-based method we proposed for forecast provides an insight into the potential utilization of LASSO regression outside its usual application in the area of variable selection, for real time forecasting. This approach can readily be automated to run on routinely collected case data, but the accuracy of the prediction is very much dependent on the timeliness at which such data become available. This calls for a comprehensive regional and country level infectious diseases surveillance system, whether using clinician/laboratory driven case notification, or mining of electronic medical records. Weather data, in contrast, are widely posted to sources like the Weather Underground which can be mined in real-time. An example of this in practice can be found in Singapore, where the National Environment Agency has a weekly dengue forecast, as described elsewhere [38]. The LASSO model building process involves identifying the model complexity through optimal out of sample predictive performance, and as such it is naturally suited to making forecasts. By fitting separate models at each forecast window, variables whose predictive performance is expressed differently at different lags can be efficiently exploited: this might be particularly beneficial for vector borne diseases in which the effect of weather on transmission is mediated through one or more generations of vectors.

In large countries, and in particular those that span multiple latitudes, we anticipate that the accuracy of the predictions will improve if regional information rather than aggregated country-level data streams are used. The aggregation averages the whole country and thus attenuates regional differences in both climate and incidence. Future work could assess the impact of disaggregation for countries like Japan for which prefectural level data are available.

By using past disease incidence and seasonal terms, LASSO has many of the characteristics of traditional time series models (e.g. the SAR in SARIMA) which have frequently been used for prediction of infectious disease time series [20], [58], [59], [60], [61]. What is less clear is how to incorporate structural information about outbreak data, such as the typical Gaussian incidence curve that is seen in both empirical data [62] and theoretical transmission dynamic models [63], or the known impact of changing herd immunity levels [64]. This may also help predict atypical outbreaks, such as the 2009 influenza pandemic which occurred in the Northern Hemisphere’s summer [65], and for which extrapolating approaches like LASSO may break down.

5. Limitations

There are several limitations to this study. Regression models, including those built using LASSO, may be effective in providing accurate predictions, but differ from traditional epidemic models such as susceptible-infected-removed compartmental models, network models [66] or individual based simulation [67], which seek to describe the transmission dynamics of contagious diseases, and can therefore be used to predict the effect of interventions or novel scenarios. A further limitation is that, for simplicity, only weather information from the capitals were used in the study, but for countries like Japan, Thailand and Taiwan, there are great variation between climatic conditions in the North and the South. Prediction accuracy might improve if incidence and weather information can be collected at a finer resolution.

We suspect that even the accuracy of short term forecasts may be reduced should new epidemiological conditions replace those that the model was trained on. Examples of this would be the emergence of a new strain or variant, such as an influenza pandemic [68], more virulent strain of the virus [69], or a virus moving into a new population [70]. It would also break down in the presence of changing control efforts such as school closure [71] or novel vector control [72]. In such situations, a mechanistic modelling approach [73] may be better able to predict the epidemic dynamics until sufficient training data are available.

6. Conclusion

Regression models using LASSO were built to forecast incidence for four endemic diseases in four countries. For some diseases including one set of variables may improve predictive accuracy substantially while for other diseases, the simpler models give similar results as more complex models. For all diseases, short-term prediction were generally much better than longer term predictions, which suggests that public health agencies may need the capacity to respond at short-notice to early warnings of possible infectious disease outbreaks should models based on this approach be implemented routinely.

Funding

The work was partially supported by the Singapore Population Health Improvement Centre (SPHERIC), National University Health System.

Declarations of interest

None.