A Method of High-Resolution Radiotherapy Delivery Fluences with a Pair of Fields with Orthogonal Collimator Settings: A Study on Ten Head-and-Neck Cancer Patients

Abstract

Context:

Introduction of dual-layer multileaf collimator (MLC) radiotherapy linear accelerators into clinical practice is an important development in advanced external beam radiotherapy. A method of delivering comparable high-resolution fluences with a single-layer MLC is presented.

Aims:

The aims of this study are to present new algorithms and approaches to define high-resolution hypermodulated fluences, obtain orthogonal decomposition of fluences, and deliver them on a linear accelerator with single MLC from two perpendicular collimator settings.

Materials and Methods:

High-resolution fluences were defined using Monte Carlo (MC) calculation. A novel use of a limited-memory, bounded, Broyden–Fletcher–Goldfarb–Shanno algorithm was used to decompose such fluences to ones deliverable with a pair of fields with mutually orthogonal collimator settings. Such a technique, here named cross motion leaf calculator (XMLC), is compared against single sliding window (SSW) technique typically used in intensity-modulated radiation therapy (IMRT). An electronic portal imaging device (EPID) is used, and the results were compared with gamma analysis. Furthermore, MC was used to determine dose distributions for computed tomography images of ten head-and-neck cancer patients.

Results:

Gamma analysis (3%, 3 mm) against ideal fluence is considerably more favorable to XMLC (94% ± 4%) versus SSW (76% ± 5%). Furthermore, the dose–volume histogram (DVH) analysis showed that XMLC enables delivery of fluences superior to that of IMRT and these results in clinically relevant enhancements in DVH results.

Conclusions:

At the time of writing of this study, there were more than 12,000 medical linear accelerators in clinical use, and XMLC can prove itself useful wherever linac is equipped with MLC but cannot delivery latest techniques, such as volumetric modulated arc therapy.

INTRODUCTION

One of the main issues with multileaf collimator (MLC) in radiotherapy is a coarse resolution of radiation fluence perpendicular to the line of leaf motion.[1,2,3] This resolution is limited by the width of the leafs.

To overcome this problem, the most obvious solution was implemented as soon as technical conditions allowed it narrowing the leaf width. Although the resulting 0.5-cm width leafs are standard in a modern photon radiotherapy, this is still tens of times coarser modulation than along the leaf motion.[4] Recently, a solution using dual-layer MLC entered the radiotherapy practice. Initia/Azimutherapy Company offered a commercial dual-layer MLC device that has demonstrated field-shaping capabilities greater than other MLC systems available at the time.[5] Varian Medical Systems introduced Halcyon, a fast-rotating O-ring linear accelerator system with dual-layer MLC, into clinical practice,[5] which clearly demonstrates that such technologies are sound development path of photon radiotherapy.

Nevertheless, medical linear accelerators with single-layer MLC are broadly in use, and a method to increase fluence resolution in direction orthogonal to the leaf motion is of general interest. Hence, different approaches tried to exploit existing technology to increase fluence resolution.[6,7,8,9] These approaches are isocenter shifting, continuous collimator rotation, and orthogonal decomposition of high-resolution fluences to be delivered in single leaf swipe in orthogonal collimator settings.[6,7,8,9] The use of orthogonal collimator field pair to deliver comparable fluences was already done, but the work was a proof-of-concept and was limited to simple geometrical shapes.[9]

In this study, a different method of delivery high-resolution radiotherapy fluences with a pair of fields with orthogonal collimator settings is presented. The method was developed independently and goes all the way to connect planning, fluence processing and decomposition, MLC sequencing, and electronic portal imaging device (EPID) verification. It allows linear accelerators with single MLC device to deliver clinically relevant high-resolution fluences comparable to those of dual-layer MLC linear accelerators without potentially expensive hardware upgrade. Further development is reported, allowing for processing of arbitrary fluence, enhancing orthogonal decomposition, postprocessing, and delivery so that the method can be assessed in clinical context. This algorithm is named cross motion leaf calculator (XMLC) and it is written in Python 3.6. The method was tested in ten head-and-neck cancer patients. The dose differences and gamma analysis of comparisons of ideal fluences and single sliding window (SSW) fields and XMLC are presented.

MATERIALS AND METHODS

Test patient data and ideal fluence definition

Computed tomography (CT) images and structure sets of ten consecutive head-and-neck cancer patients, who completed radiotherapy at the University Clinical Hospital Mostar, serve as test data in the presented work. Each image set consists of 1.25-mm slices acquired in helical mode with GE LightSpeed RT CT scanner. The structure set contains clinical target volume, planning target volume (PTV), and organs at risk (OARs) needed for basic inverse planning. Image preprocessing was done with MatRad, an open-source multimodality radiation treatment planning system written in MatLab.[10,11]

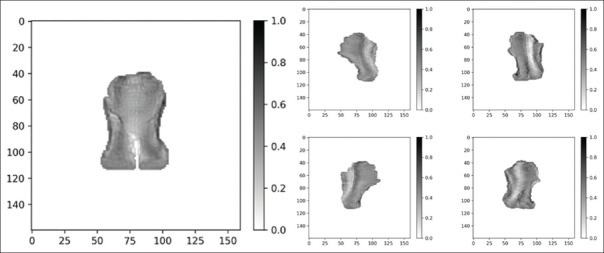
A Voxel Monte Carlo (VMC++) algorithm was used to determine the relation between dose distribution and beamlet intensities.[12] VMC++ is a proven and reliable algorithm that may be used for photon-beam patient dose computations without a clinically significant loss in accuracy.[13] The energy spectrum of all fields was a National Research Council of Canada (NRC) spectrum of a 6 MV Varian Clinac 2100 as distributed with VMC++. The pixel dimension of fluence map was set to be 2.5 mm × 2.5 mm as measured in the isoplane at source-to-imager distance 100 cm. For each patient and for both methods compared in this study, namely SSW and XMLC, the radiation plan parameters were the same five equidistant gantry angles (0, 72°, 144°, 216°, 288° in IEC1217 scale) and the positioning of the isocenter. The collimator orientations were 0° and 90° for XMLC and 0° for SSW (IEC1217 scale). For the purpose of inverse planning optimization, the Interior Point OPTimizer (IPOPT) was used, a free and open-source algorithm used to provide inverse planning capabilities for the MatRad.[14] Several square overdosing and square deviation constraints were placed upon PTV, spinal cord, brainstem, and parotids. Constraint type and weights were set according to the clinical experience but were the same for all the patients. Using the same plan template for different patients would produce suboptimal results in the clinical context, but it was used so the effect of high-resolution fluences on resulting dose distribution could be assessed. Then, inverse planning run produced five ideal fluences for each patient. An example of such fluence set is reproduced in Figure 1.

Figure 1.

A set of five ideal fluences corresponding to 0°, 72°, 144°, 216°, and 288° gantry angles (IEC1217). Resolution of fluences is 2.5 mm × 2.5 mm in the isocenter plane, at source to image distance (SID) =100 cm

Ideal fluence orthogonal decomposition

In this work, high-resolution fluence is delivered with two fields that have mutual orthogonal collimator settings. In each field, the MLC apparatus performs a SSW operation. A decomposition of the ideal fluence was done in order that the sum of two-field output is as close to ideal fluence as possible. It has already been shown before, by applying preprocessing “constant gradient constraint” filter, the ideal fluence can be rearranged with the requirement that the pixel with the lowest intensity receives equal contributions from both components.[9] Then, it is possible to decompose the ideal fluence so that resulting components can be sensibly fed to the leaf sequencer. This, previously presented solution, does not guarantee a solution closest to the ideal fluence in the least-squares sense because existing beamlets with negative intensity were simply clamped to the zero value.[9] While it may seem reasonable from a physical perspective, it considerably contributes to the observed “spikiness” that hampers the efficient delivery. Namely, key factors of efficient delivery for any beam with dynamic leaves are maximal value and maximal complexity of the fluence to be delivered. Complexity is a quantity associated with a dose profile of a single leaf pair and is equal to the sum of all positive changes of intensity calculated in either direction of leaf motion.[15] The number of monitor units (MU) of a SSW field is directly proportional to the maximum value of the fluence to be delivered and also heavily depends on the maximal complexity. Therefore, to achieve an efficient delivery, one needs to account those quantities when performing orthogonal decomposition. We propose a new approach to this issue by reformulating the problem, outlined in Figure 2, as inhomogeneous system oflinear equations:

Figure 2.

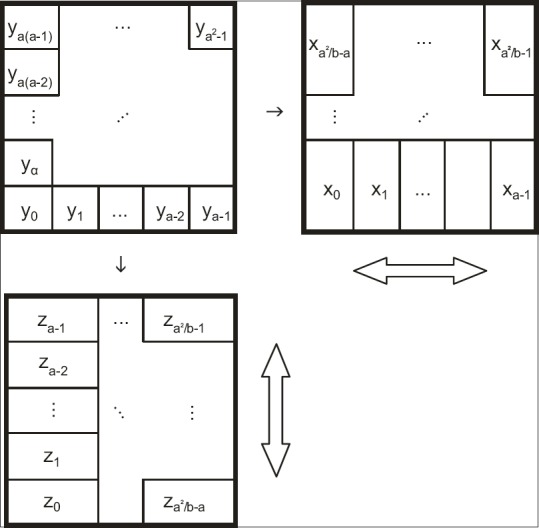
Schematic orthogonal decomposition of an ideal fluence to two fluences deliverable with two fields with mutually orthogonal collimator settings. Hollow arrows indicate direction of leaves motion for the particular orthogonal component

where 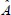is a linear operator constructed to provide an appropriate summation of orthogonal components; 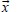contains the beamlet intensities of both orthogonal components (x_p, z_q); and, 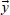contains flattened ideal fluence (y_r). Ideal fluence is parameterized with, the number of fluence pixels along the edge of the largest available field, and, the number of fluence pixels covered by a cross-section of a single leaf. Such formulation is convenient for direct aperture optimization. The decomposition schematics are given in Figure 2.

Since this is an overdetermined and usually inconsistent system of equations, the exact solution does not exist. As a first step to finding approximate solution, a vector 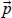is determined by minimizing 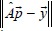. Then, this solution which also may have negative components is applied as an initial input to the limited memory Broyden–Fletcher–Goldfarb–Shanno bounded algorithm (L-BFGS-B) with constraints that variables (beamlet intensities) must be non-negative.[16] Furthermore, since such ill-defined systems may have an entire class of equally good solutions in the least-squares sense, it is possible to include normalized fluence maximums and/or normalized complexities of both orthogonal components into the cost function of L-BFGS-B algorithm.[17] This is done so that the sum of MU of orthogonal components of XMLC be approximately equal to the competing SSW field, which was one of the design goals of this method. This goal was achieved by defining the cost function to include two key measures; the first was root mean square (RMS) difference between ideal fluence and the sum of decomposition components and the second one is the sum of maximums of decomposition components. We introduced into the cost function parameter P ∈ (0,1), which was a measure of the relative contribution to the cost function of sum of fluence maximums with respect to the RMS difference from ideal function. The effects of variation of parameter P were analyzed for all available fields and are presented in Figure 3. Setting parameter P low will have the effect of low noise (low RMS difference), but the components' maximums will be quite large. On the other hand, high parameter P suppresses the maximums but produces more noise (high RMS difference). To determine optimal value of the parameter P, one needs to consider the formula for total number of MU for a field with complexity c and maximum value in the optimal fluence OF_max [15] which is given by

Figure 3.

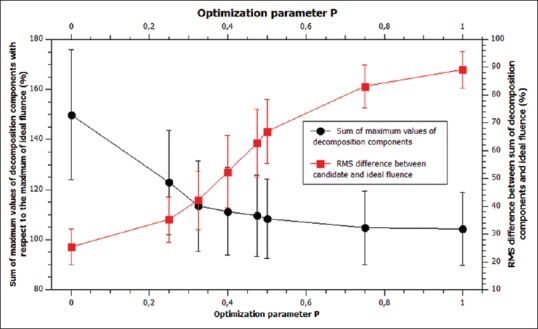
Dependence of the decomposition components fluence maximums and root mean square difference between ideal and candidate fluence with parameter P

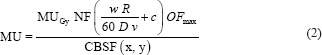
The analysis showed several key insights; first, the complexity of decomposition components depended only slightly on parameter P but presents considerable computational burden when included in the cost function. Throughout the tested range of the parameter P, the complexity of decomposition components was c = 89% ± 9% with respect to SSW field complexity and therefore did not have a negative impact on the total MU count. The difference in MU count may arise from the fact that collimator backscatter factor is not symmetrical in field widths and that the fields are usually rectangular, but typically value within parentheses is dominated by the complexity and not the first term. This procedure gives “target” complexity for postprocessing algorithm that will ensure approximately the same number of MUs for both techniques but with XMLC still delivering higher resolution fluence. On the other hand, fluence maximums of decomposition components changes significantly with P and it was determined that P = 0.325 was optimal relative contribution that achieves design stated goals: total MU number of XMLC is equal or less with respect to SSW, with noise of produced field considerably suppressed – it is much closer to the unclamped least-squares solution than the clamped-filtered one and will suffer the “spikiness” considerably less. To demonstrate this, a comparison of RMS difference over (a) entire 40 cm × 40 cm field and (b) limited only to the high gradient areas of fluence of the clinically relevant case is presented in Table 1.

Table 1.

Comparison of root mean square difference of fluences determined by different techniques with respect to the ideal fluence

RMS difference with respect to ideal fluence	Unclamped LSS (%)	L-BFGS-B algorithm (%)	Clamped LSS (%)
Maximal field (40 cm × 40 cm)	100	105	120
High gradient area	100	108	120

RMS: Root mean square, L-BFGS-B: Limited memory Broyden–Fletcher–Goldfarb–Shanno bounded algorithm (L-BFGS-B), LSS: Least square solution

This shows that the novel approach provides a solution that has no negative intensity beamlets by definition; it is much closer to what a real device can deliver but considerably suppressed noise in resulting summed fluence.

Once F-BFGS-B orthogonal components are defined, further processing is needed to incorporate the fact that the physical device will have MLC radiation leakage and transmission that needs to be accounted for.

Leaf sequencing and delivery of decomposition components

In order to deliver decomposition components, a leaf sequencer as described in Eclipse Algorithms Reference Guide was implemented.[15] This leaf sequencer is a part of XMLC algorithm. It underperforms when compared with Varian's proprietary leaf sequencer Varian leaf motion calculator (VLMC, Varian Medical Systems). This is demonstrated with slightly larger MU factors, but the trade-off between efficiency and clear insight of inner workings of leaf sequencer is found to be more than acceptable. All the key features of the VLMC were reproduced within XMLC. These were: the dosimetric leaf gap, a small, apparent retraction of leafs to adjust for rounded leaf tips; the transmission factor, modeling leaf leakage by averaging the for intra- and interleaf leakage components; the tongue-and-groove effect, which accounts for fluence perturbation along the exposed side of a leaf due to influence of protruded and depressed mechanical fittings; the wide field support allowing to deliver a fluence that has dimension larger than maximal leaf extension; and the dynamic leaf gap, a safety distance margin designed to prevent leaf collision while in motion.

Input for XMLC is a fluence of arbitrary resolution which is then decomposed into two fields with perpendicular collimator settings, taking into account leaf leakage, as described in 2.2. A leaf sequence is produced for each of decomposition components and is saved in Varian's. mlc file format, ready to be fed to MLC controller.[18] One of the key technical limitations when producing leaf sequences is that MLC controller design limits the number of so-called control points to 320 with default value of 166. Control points are particular moments within delivery time when the MLC controller instructs any leaf to change its direction of motion and/or its speed. The required number of control points grows with complexity of the fluence profile. With normal intensity-modulated radiation therapy (IMRT) sequencing, one has option to smooth input fluences until the required number of control points for field delivery falls below upper limit. With orthogonal decomposition and delivery, one cannot afford much smoothing as the “noise” is detailed information needed to adequately sum orthogonal components. At this point, own implementation of leaf sequences shows as an asset as it was possible to carefully preprocess fluence and postprocess leaf sequences, so the information was preserved. The first step was to remove very small fluctuations in the fluence that were not dosimetrically relevant but took up valuable control points. This was done by applying what may be called a running window linear regression filter. Simply, for each fluence profile that shall be delivered with a leaf pair, a filter was applied from either side to identify the sequence of fluence points that do not differ from best-fit line with a small tolerance. All such subsequences were clipped to the regression function, therefore, smoothing the small perturbations, removing the interior points of fluence. Then, this processed fluence was fed in the XMLC leaf sequencer. Resulting leaf sequences suffered from the fact that all leaf pairs, no matter the complexity of the assigned fluence profile was, performed at maximum efficiency in the sense that, at any time, at least one leaf was moving at the maximum speed. While this may sound as a positive property, key problem is that pair movements are independent, and each allocates independent control point sets that often number more than allowed by MLC controller. The solution is that, except for the pair delivering the most complex fluence profile, all other leaf pairs are slowed down, so the change in the leaf motion corresponds in time when the leaf pairs that produce more complex fluence profiles also change motion. While losing nothing in dosimetric sense, this saves the machine from unnecessary wear-and-tear, allows that allotted control points be used more efficiently and that any remaining control points are used to reinforce precision of leaf motions along longer paths.

The aSi-based electronic portal imaging device for dosimetry verification

The EPID used in verification of the ideal fluence delivery was commercially available aSi imaging device (aS500, Varian Medical Systems) mounted on a Clinac DMX linear accelerator fitted with 80-leaf dynamic mode capable Millennium 80 MLC (Varian Medical Systems). EPID has an active area of ~40 cm × 30 cm divided into 512 × 384 pixels with linear density of 0.784 px/mm. EPID dosimetry is clinically commissioned following manufacturer's instructions.[19] The linear accelerator itself is properly commissioned and maintained, observing relevant literature to perform commissioning and quality assurance. For any fluence map, an EPID prediction was made with algorithm as presented in the work of Van Esch et al.[20] where portal dose image per MU is given as

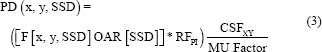
OAR is off-axis ratio that accounts for radial beam profile and is extracted from pencil-beam algorithm commissioned for clinical use, F being the fluence that is delivered, the product of which is convolved with a properly normalized kernel of the form

The predicted image was further corrected with a ratio of collimator scatter factor (CSF) and MU factor. The CSF may be reasonably accurately presented as a ratio of linear accelerator output factor and phantom scatter factor determined from the convolved ideal field fluence. Readers interested in further details should consult the original work.[20]

The outlined workflow allows that arbitrary CT image and structure sets be imported and processed for inverse optimization, extraction of an ideal fluences of arbitrary resolution, and decomposition of fluences in novel ways that circumvent some limitations of previously presented research, safely deliver them on a Varian Clinac linear accelerator, and record the resulting fluences with an EPID device. Although the algorithms in the presented sequence themselves do not limit the resolution of the ideal fluence, there are, of course, physical and computational limits. Due to these limits, we estimated that fluences with resolution below 1 mm × 1 mm critically suffered from small errors in leaf motion performance and collimator rotation precession. Portal predictions for high-resolution fluences were also produced. It should be pointed out that the results of the measurement and computation were proper DICOM image files that could be compared in any compatible software.

Fluence analysis and dose distributions

To compare and analyze fluences, Python packages numpy and PyMedPhys.gamma were used.[21,22,23] Convolved, radially corrected ideal fluences were compared with measured EPID images. The first step was automatching where a small translation was calculated by minimizing RMS of image difference on a grid around origin. This allowed for small positioning corrections, all of which were within warning level set by EPID quality control (QC) procedures. The same correction translation was applied to all images of any patient. Automatched images were then analyzed for dose difference by direct subtraction, and gamma function was also calculated. Gamma analysis library PyMedPhys.gamma is an implementation of algorithm which is validated against other gamma analysis software and gauge images.[24] All comparisons were strictly relative. Parameters of gamma analysis were 3% of maximum of source image, 3 mm distance to agreement, and with 10% source image maximum cutoff.

Dose distribution analysis was performed by utilizing the results of Monte Carlo calculations. For each of ten head-and-neck cancer patients, two distributions were compared: one resulting from summation of orthogonal decomposition components and the other one was SSW fluence as can be delivered with MLC Millennium 80 which was used for beam delivery. Dose–volume histograms (DVH) were created with MatRad software. As noted earlier, using the same rigid plan template for multiple patients would produce suboptimal plans for clinical usage, but in this work, typical clinical tools, such as patient-specific optimization constraints and beam angle optimizers, were excluded on purpose so that fluence quality and resolution have a principal effect on dose distributions. Key Level 2 dose indicators as recommended by ICRU Report No. 83 were determined and presented.[25]

RESULTS

Dose difference and gamma analysis of fluences

To demonstrate achieved precision of the presented method, EPID images of MLC fields produced with (a) a classic approach with a sliding window technique delivered with one field and (b) sliding windows delivered with two fields having orthogonal collimator settings as presented in this study were compared to the EPID prediction of an ideal fluence. Leaf sequencing for both techniques was done with XMLC so any resulting differences were inherent to the techniques, and not due to different leaf sequencers. The presented analysis was performed for all fields of all patient plans, and a typical single field analysis is presented.

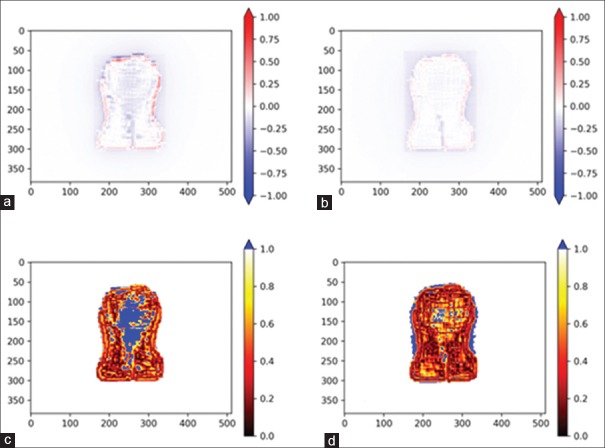
Figure 4 shows dose difference and gamma analyses, between ideal fluence EPID prediction and the best available delivery using SSW and XMLC, as described in this study. Note that all points with gamma >1 are colored solid blue.

Figure 4.

Dose difference (a and b) and gamma analysis (c and d) of images of electronic portal imaging device images of beams created with different techniques (single sliding window [a and c] and cross multileaf collimators [b and d]) with respect to the ideal fluence

Average gamma pass result for SSW is 76% ± 5% versus 94% ± 4% for XMLC.

Comparison of dose distributions using single sliding window and XMLC dose delivery technique for ten head-and-neck cancer patients

Level 2 dose indicators as recommended in ICRU 83 were determined and are summarized in Tables 2 and 3.[25] For each dose indicator, values were averaged across the entire study group, separately for XMLC and SSW. The results of different delivery techniques were tested for statistically significant differences using Kolmogorov–Smirnov test at confidence level P = 0.05. The quantities that are found to be statistically significantly different are printed in bold.

Table 2.

Comparison of dose indicator for target volumes for different techniques for ten head-and-neck cancer patients

Technique	Mean dose (Gy)	D2% (Gy)	D5% (Gy)	D95% (Gy)	D98% (Gy)
SSW	1.974	2.040	2.025	1.890	1.827
XMLC	1.997	2.057	2.037	1.952	1.918
	V1.9Gy (%)	V1.95Gy (%)	V2.05Gy (%)	V2.1Gy (%)	HI2Gy
SSW	93.9	82.3	1.2	0.1	0.107
XMLC	98.4	95.1	3.0	0.4	0.070

SSW: Single sliding window, XMLC: Cross motion leaf calculator

Table 3.

Comparison of dose indicators for serial organs for different techniques for ten head-and-neck cancer patients

Organ (technique)	Mean dose (Gy)	D2% (Gy)	D5% (Gy)
Brainstem (SSW)	11.0	29.7	27.1
Brainstem (XMLC)	10.9	30.0	27.7
Spine (SSW)	25.3	46.9	46.0
Spine (XMLC)	24.1	45.0	44.5

SSW: Single sliding window, XMLC: Cross motion leaf calculator

HI_2Gy is a homogeneity indicator that is defined as, 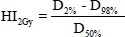with HI_2Gy =0.0 which indicates that the dose distribution is almost homogeneous.

DISCUSSION

The presented method of delivery of high-resolution fluences is a part of contemporary effort of development of external photon radiotherapy. It includes planning, high-resolution fluence processing and decomposition, MLC sequencing, and EPID verification to allow linear accelerators with single MLC device to deliver clinically relevant high-resolution fluences comparable to those of dual-layer MLC linear accelerators without potentially expensive hardware upgrade.

The results of dose difference and gamma analysis of comparison of ideal fluences and single SSW and ideal fluences and XMLC are presented [Figure 4]. The RMS difference between SSW EPID images and ideal fluences is systematically greater in magnitude and statistical significance, than the RMS difference of XMLC EPID images. Similarly, gamma analysis (3%, 3 mm) against ideal fluence is considerably more favorable to XMLC (94% ± 4%) versus SSW (76% ± 5%). SSW result may seem oddly low, but one needs to bear in mind that the reference image is an ideal fluence, not the portal prediction fluence that is usually used, i.e., in plan verification procedures clinical settings where gamma pass percentage is much higher. Reviewing images demonstrate expected key weakness in SSW technique – wherever fluence gradient perpendicular to the leaf motion direction is present, dose difference will be substantial as visualized by parallel cold and hot streaks in Figure 4a. These streaks are the key cause of the presented dose difference, increased gamma analysis failure, and adverse dose distribution effects. On the other hand, such features are considerably less present for XMLC Figure 4b. A fine cold “web” of deviation, 1 cm spaced, as presented in Figure 4b and Figure 4d, is imprinted by interleaf leakage, which is not present in ideal fluence. Furthermore, XMLC fields' fluences are much less robust when dose cutoff is lowered, as the area within jaws-defined field, but out of the high-intensity area is coming into consideration in gamma analysis and the passing percentage falls sharply due to leakage. The gamma analysis in Figure 4c shows the SSW technique struggles with modulations orthogonal to the leaf motion.

Dose distributions analysis through DVHs shows that the coverage of target volumes is considerably better with XMLC fluences than those of SSW. Key target dose indicators [Table 2] are better with statistical significance, as proven with Kolmogorov–Smirnov test for two samples at confidence level P = 0.05. Using the same test, there is no statistical difference between doses of parallel OARs [Table 4] nor serial OARs [Table 3]. This is the consequence of conscious decision when designing optimization parameters where target coverage was given precedence. Key dose and homogeneity indicators show that XMLC has better target coverage at the same level of risk as IMRT.

Table 4.

Comparison of dose indicators for parallel organs for different techniques for ten head-and-neck cancer patients

Organ (technique)	Mean dose (Gy)	D2% (Gy)	V1Gy (%)
Right parotid (SSW)	31.5	57.3	49.8
Right parotid (XMLC)	31.3	59.1	50.1
Left parotid (SSW)	31.3	55.7	49.0
Left parotid (XMLC)	31.2	57.2	48.6

SSW: Single sliding window, XMLC: Cross motion leaf calculator

The key steps of this study are orthogonal decomposition method and leaf sequencing. There are a number of propositions of new decomposition methods besides[9] to be employed with dual-layer MLC.[26,27] The presented method of orthogonal decomposition has two advantages, namely L-BFGS-B algorithm with its flexible cost function enables fast and bounded decomposition. Algorithms that allow negative intensity beamlets suffer RMS deviations after clamping to zero [Table 1]. With L-BFGS-B algorithm, all intensities are a priori nonnegative which allows more precise decomposition with less noise [Table 1]. Another advantage is that the presented method can integrate leaf transmission radiation into map of usable fluence. There are inherent limitations of integrating transmission into useful beam, as such beam is hardened and its fluence is not trivially additive. Maintaining low ratio of transmitted radiation intensity with respect to the intensity of the primary beam will ensure no detrimental effect will occur on dose distributions.[28] Other methods can also be used to suppress transmission, such as jaw tracking capability of smart leaf motion calculator (Varian Medical Systems). Leaf sequencing is at the proof-of-the-concept level and could be further improved by exploiting orthogonal configuration to efficiently correct for interleaf leakage and tongue-and-groove effect. MU efficiency can also be improved by implementing methods as proposed elsewhere.[29,30]

At the time of writing of this study, there were more than 12,000 medical linear accelerators in clinical use,[31] and XMLC can provide better coverage of target volumes or sparing of OARs wherever linac is equipped with MLC but cannot delivery latest techniques, such as volumetric modulated arc therapy.

CONCLUSIONS

A string of robust measuring techniques and algorithms are presented that allow the delivery of high-resolution fluences on a single MLC linear accelerator. Key processes are an orthogonal decomposition of such fluence into two well-defined, achievable fluences that are delivered with two fields with mutually orthogonal collimator settings, using sliding window technique and leaf sequencing that allows MU efficient delivery. The presented work demonstrates that such technique is superior with respect to classic, single field sliding window by means of measuring the output on an EPID device, but it is also shown that it suffers critical setback because of excessive radiation leakage and transmission which are usually associated with hypermodulated plans. Further research continues to mitigate these problems by developing new methods and using available technologies. Furthermore, the presented work may be used to research the dosimetric implications of the introduction of dual-layer linear accelerators into clinical practice.

Financial support and sponsorship

Nil.

Conflicts of interest

There are no conflicts of interest.