Modeling particle dispersion and deposition in indoor environments

Abstract

Particle dispersion and deposition in man-made enclosed environments are closely related to the well-being of occupants. The present study developed a three-dimensional drift-flux model for particle movements in turbulent indoor airflows, and combined it into Eulerian approaches. To account for the process of particle deposition at solid boundaries, a semi-empirical deposition model was adopted in which the size-dependent deposition characteristics were well resolved. After validation against the experimental data in a scaled isothermal chamber and in a full-scale non-isothermal environmental chamber, the drift-flux model was used to investigate the deposition rates and human exposures to particles from two different sources with three typical ventilation systems: mixing ventilation (MV), displacement ventilation (DV), and under-floor air distribution (UFAD). For particles originating from the supply air, a V-shaped curve of the deposition velocity variation as a function of particle size was observed. The minimum deposition appeared at 0.1–$0.5\mathrm{\mu }\mathrm{m}$. For supermicron particles, the ventilation type and air exchange rate had an ignorable effect on the deposition rate. The movements of submicron particles were like tracer gases while the gravitational settling effect should be taken into account for particles larger than $2.5\mathrm{\mu }\mathrm{m}$. The temporal increment of human exposure to a step-up particle release in the supply air was determined, among many factors, by the distance between the occupant and air outlet. The larger the particle size, the lower the human exposure. For particles released from an internal heat source, the concentration stratification of small particles (diameter $<10\mathrm{\mu }\mathrm{m}$) in the vertical direction appeared with DV and UFAD, and it was found the advantageous principle for gaseous pollutants that a relatively less-polluted occupied zone existed in DV and UFAD was also applicable to small particles.

Nomenclature

$a$

air exchange rate

C

particle mass concentration

$C_0$

initial indoor particle concentration

$C_{\mathrm{cell}}$

particle concentration in the first cell normal to the wall

$C_t$

indoor particle concentration at time t

$C_{\mathrm{wall}}$

particle concentration at the walls

D

particle diameter

$D_{\mathrm{p}}$

Brownian diffusivity

J

mass flux of particles to the wall per unit area

k

particle deposition rate

L

distance between adjacent particles

$S_{\mathrm{c}}$

particle source term

St

Stokes number

t

time

$u^{*}$

friction velocity

$\overrightarrow{V}$

vector of air velocity

$\overrightarrow{V_{\mathrm{s}}}$

vector of particle settling velocity

$v_{\mathrm{d}}$

particle deposition velocity

$v_{\mathrm{s}}$

particle settling velocity

$V_{\mathrm{dep}}^{+}$

dimensionless deposition velocity

y

the normal distance between the wall and the first cell center

Greek symbols

${\epsilon }_{\mathrm{p}}$

turbulent diffusivity

${\upsilon }_{\mathrm{g}}$

kinetic air viscosity

${\upsilon }_{\mathrm{t}}$

turbulent viscosity of air

${\mu }_{\mathrm{eff}}$

effective viscosity

$\rho$

the density of the air

${\rho }_{\mathrm{P}}$

the material density of the particles

${\sigma }_{\mathrm{c}}$

non-dimensional number

${\tau }_{\mathrm{C}}$

average time between particle–particle collisions

${\tau }_{\mathrm{r}}$

particle residual time

${\tau }_{\mathrm{V}}$

momentum response time of a particle

1. Introduction

The emergence of severe acute respiratory syndrome (SARS), the unremitting threat of avian influenza, and the possible terrorist attacks via airborne release of aerosolized chemical or biological agents into a building generate more concerns on particles/droplets movement indoors. Several reports have shown that many infectious diseases can be transmitted via the airborne route (Nardell et al., 1986, Mangili and Gendreau, 2005). A recent multi-disciplinary systematic review reveals that there is a strong and sufficient evidence to demonstrate the association between ventilation, airflow pattern in buildings and the spread of infectious diseases (Li et al., 2007). Besides human-generated virus laden bio-aerosols, smoke particles could increase respiratory irritation and aggravation of existing respiratory or cardiovascular disease, an asbestos fiber exposure for prolonged periods increases the risk of lung cancer, and miner aerosols may be carcinogenic or mutagenic (GN, 1999). Generally, the health hazards caused by particulate matter depend on the component, size, shape, density, and chemical reactivity of the particles.

Comprehensive reviews on indoor particles have been given by Nazaroff (2004) and Wallace (1996). Because of the various sources, the indoor particle size range extends from submicron to larger than $100\mathrm{\mu }\mathrm{m}$ in diameters (more than 1000 times difference). This poly-disperse feature, or broad particle size spectrum, makes transport process complicated since the dynamic property is strongly related to particle size. For instance, fine submicron particles with a small relaxation time may follow almost exactly the main airstreams, acting like a tracer gas, while coarse particles with their diameter of $100\mathrm{\mu }\mathrm{m}$ may fall 1 m within 4 s in a still environment. The complex behavior of indoor particulate matter may include dispersion, deposition, re-suspension, coagulation, and even phase change. In order to solve the indoor air quality problems and to control the particle dispersion, understanding of the particle-laden turbulent flow is important. However, our present knowledge on turbulence limits the further exploration of the nature of interaction between turbulence and an individual particle. Therefore, it is so far still difficult to predict the indoor particle concentration when considering all mechanisms.

Mathematically, there are two treatments of indoor particle movements: the Euler–Lagrange method and the Euler–Euler method. The selection between them is based on the “job” (research objective) and the “cost” (required computational resources) (Loth, 2000). Generally, the Lagrangian method may be comparatively memory intensive and computationally inefficient in order to ensure statistically stable results. However, the Lagrangian method is attractive if interests are in the particle dispersion history. Holmberg and Li (1998) have justified the two application requirements of the Euler–Euler method in the modeling of indoor environments. These are that the particle size should be significantly smaller than the Kolmogorov microscale and that there should be enough particles in each computational cell so that the particle phase can be statistically assumed as a continuum. The Kolmogorov microscale is at the magnitude of 1 mm for a normal ventilated room (Etheridge and Sandberg, 1996), which is at least several times of indoor particle sizes. The interaction between particles and airstreams in built environments is considered as one-way coupling for saving computational load (Chen et al., 2006). It means a dilute dispersed phase flow, in which particle movements are determined by the state of the airflow. Both the transfer of momentum and heat from particles to fluids and particle–particle interactions are ignored. For this treatment to be valid, the particulate loading should be low since it has a significant impact on phase interaction. For a typical indoor particle concentration in residential buildings in Hong Kong, the 24 h suspended particulate levels varied from 45.8 to $122.2\mathrm{\mu }\mathrm{g}{\mathrm{m}}^{-3}$, as measured by Chao et al. (1998). It can be estimated that the corresponding $L/D$ is of the order of ${10}^3$ and ${\tau }_V/{\tau }_C$ ${10}^{-2}$. Thus, the one-way coupling in the modeling of indoor environment is feasible (Crowe et al., 1998).

In this paper, one of the simplified Eulerian methods, i.e. a drift-flux model, is used to investigate particle distribution in an enclosed environment. The drift-flux model can easily incorporate the effects of Brownian and turbulent diffusion and gravitational settling effect. The drift-flux models have been practiced before and the particle concentrations are predicted (Murakami et al., 1992, Zhao et al., 2004). The purpose of this work is to improve the wall boundary treatment in the drift-flux model with the help of one deposition model. After validation against two sets of experimental data, the new drift-flux model is applied to compare the transient occupant exposure in a mock-up terrorist attack in a ventilated room with mixing ventilation (MV), displacement ventilation (DV), and under-floor air distribution (UFAD). The dispersion and distribution of particles generated from a heat source, which would represent an office machine, in these three types of air distribution methods are also investigated.

2. Methods

2.1. Drift-flux model

The governing equation of the particle concentration is similar to Navier–Stokes equations, except that it integrates the gravitational settling effect of particles into the convection term:

$$\frac{\mathrm{\partial }(\rho C)}{\mathrm{\partial }t}+\nabla ·(\rho (\stackrel{\Rightarrow }{V}+{\stackrel{\Rightarrow }{V}}_{\mathrm{S}})C)=\nabla ·\left(\frac{{\mu }_{\mathrm{eff}}}{{\sigma }_{\mathrm{C}}}\nabla C\right)+S_{\mathrm{C}}\text{.}$$ (1)

The gravitational settling velocity of particles (${\stackrel{\Rightarrow }{V}}_{\mathrm{S}}$) is calculated by Stokes equation (Hinds, 1999). Here ${\sigma }_{\mathrm{C}}$ is set as 1.0. The term ${\mu }_{\mathrm{eff}}/{\sigma }_{\mathrm{C}}$ can also be written as $D_{\mathrm{p}}+{\epsilon }_{\mathrm{P}}$. Eq. (1) is discretized directly into algebraic equation by the finite volume method, not like the other numerical treatments in which the settling term $\rho {\overline{V}}_{\mathrm{S}}C$ is moved into the source term. The drift-flux model is not a fully-coupled multi-fluid model, and in the progress of CFD calculation the indoor flow field and temperature field are solved firstly using standard $k$–$\epsilon$ model including buoyancy effect plus standard wall function. After the convergence is reached, Eq. (1) is solved solely based on the one-way coupling assumption.

2.2. Particle deposition mechanism

Although the amount of deposited particles is usually much smaller than that of particles exhausted by ventilation, in buildings with low air exchange rate particle deposition may constitute a major removal process (Thatcher et al., 1996). To quantify the deposition in the engineering calculation, some prediction models have been set up (Shimada et al., 1989, Nazaroff and Cass, 1989). The semi-empirical model by Lai and Nazaroff (2000) links the air velocity to the macrodeposition velocity, with no consideration given to the effect of spatial distribution of particles. This model accounts for the effects of Brownian and turbulent diffusion and gravitational settling. With the assumption that the deposition flux is one-dimensional and constant in the concentration boundary layer, and the particle eddy diffusivity equals the fluid turbulent viscosity (${\epsilon }_{\mathrm{p}}={\upsilon }_{\mathrm{t}}$), the dimensionless deposition velocity can be expressed by the following equation:

$$v_{\mathrm{d}}^{+}=\left\{\begin{array}{cc}{\displaystyle \frac{v_{\mathrm{s}}^{+}}{1-\exp (-v_{\mathrm{s}}^{+}I)}}\hfill & \mathrm{upward}\mathrm{surface},\hfill \\ {\displaystyle \frac{v_{\mathrm{s}}^{+}}{\exp (-v_{\mathrm{s}}^{+}I)-1}}\hfill & \mathrm{downdard}\mathrm{surface},\hfill \\ {\displaystyle \frac{u^{*}}{I}}\hfill & \mathrm{vertical}\mathrm{surface},\hfill \end{array}\right)$$ (2)

where $v_{\mathrm{s}}^{+}=v_{\mathrm{s}}/u^{*}$, $v_{\mathrm{d}}^{+}=v_{\mathrm{d}}/u^{*}$, $I=1/v_{\mathrm{d}}^{+}={\int }_{r^{+}}^{30}({\upsilon }_{\mathrm{g}}/({\epsilon }_{\mathrm{p}}+D_{\mathrm{p}}))\mathrm{d}{y}^{+}$, $y^{+}={\mathit{yu}}^{*}/{\upsilon }_{\mathrm{g}}$, $r^{+}=(D/2)(u^{*}/{\nu }_{\mathrm{g}})$. In their derivation, the turbulent viscosity in the boundary layer is evaluated by the DNS results of Kim et al. (1987). This model is practical to use and has a stronger physical foundation compared with previous ones. More recently, Zhao and Wu (2006) have improved the Lai and Nazaroff's model by adding the effect of turbophoresis. The prediction accuracy is enhanced for particles larger than $1\mathrm{\mu }\mathrm{m}$.

2.3. Boundary conditions

Different from dealing with the governing equation of a tracer gas where a zero-flux condition can be assumed at the solid boundary, particle deposition should be taken into account at the walls since a net transport of particles towards walls creates concentration gradients (Fig. 1 ). Zhao et al. (2004) assumed $\mathrm{\partial }C/\mathrm{\partial }n=0$ at walls for particles. In the work by Holmberg and Li (1998), they considered $C_{\mathrm{wall}}$ as $\alpha C_{{\mathrm{cell}}_{,}}$ where $0⩽\alpha ⩽1$. The appropriate value of $\alpha$ was obtained empirically from deposition measurement.

Fig. 1.

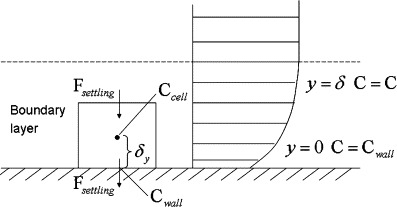
Boundary conditions of the near wall particle concentration field.

In the present work, the Lai and Nazaroff's model, as described by Eq. (2), is used to evaluate deposition velocities (Lai and Nazaroff, 2000). The deposition flux is defined as $J=v_{\mathrm{d}}{C}_{\mathrm{cell}}=(D_{\mathrm{p}}+{\epsilon }_{\mathrm{P}})(\mathrm{d}C/\mathrm{d}y)+\mathrm{i}{v}_{\mathrm{s}}{C}_{\mathrm{cell}}$, where $C_{\mathrm{cell}}$ is the particle concentration in grid cells outside the boundary layer. In the present numerical implementation of the model, a nominal particle concentration $C_{\mathrm{wall}}$ is defined as

$$C_{\mathrm{wall}}=C_{\mathrm{cell}}-C_{\mathrm{cell}}(v_{\mathrm{d}}-\mathrm{i}{v}_{\mathrm{s}})\frac{\delta y}{(D_{\mathrm{p}}+{\epsilon }_{\mathrm{P}})}$$ (3)

by using $(C_{\mathrm{cell}}-C_{\mathrm{wall}})/\delta y$ to substitute $\mathrm{d}C/\mathrm{d}y$, where i is to characterize the wall surface orientation ($\mathrm{i}=0$ for a vertical surface; $\mathrm{i}=1$ for an upward facing horizontal surface; $\mathrm{i}=-1$ for a downward facing horizontal surface). In our simulation using Eq. (3), it is found that usually the particle concentration gradient is highest at downward facing surfaces, and lowest at upward facing surfaces. It is in line with the modeling of aerosol in a chamber by Holmberg and Li (1998). They found that the $\alpha$ values were 0.9, 0.99, and 0.65 for walls, floor, and ceiling, respectively. This approximate zero-gradient of particle concentration at floor means that particle deposition at floor is mainly caused by gravitational settling, not by diffusion. For particles larger than $0.5\mathrm{\mu }\mathrm{m}$, the deposition velocity is nearly the same as the settling velocity and the effect of local airflow condition (denoted by the friction velocity) can be ignored (Lai and Nazaroff, 2000). This phenomenon is also proved by the experimental work (Thatcher and Nazaroff, 1997). They found that, for micron-scale particles, gravitational settling onto upward facing surfaces dominated the overall rate of deposition. It should be noted that, as is common in all turbulence models involving the use of wall functions, the first cell size close to the wall greatly affects the simulation results. Exhibited in the current model, the $C_{\mathrm{wall}}$ value will be grid-dependent, and it is essential that the first normal grid point should be located beyond the buffer layer ($y^{+}>30$). Secondly, the deposition models used by Lai and Nazaroff (2000), as well as by Zhao and Wu (2006) usually under-predict the deposition flux onto the downward facing surfaces, especially for coarse particles. Maybe deposition mechanisms, other than diffusion, gravitational settling, and turbophoresis, also play an important role. Here it demands the further development of enhanced deposition models.

3. Validation

3.1. Isothermal condition

Chen et al. (2006) measured the concentration of mono-dispersed $10\mathrm{\mu }\mathrm{m}$ particle with a material density of $1400\mathrm{kg}{\mathrm{m}}^{-3}$ in a simple model room (Fig. 2 ). Particles were mixed into the supply air with a stable particle flow rate by a solid particle disperser. Using the Eulerian approach introduced above, both the airflow and the particle concentrations are simulated in the present study for the model validation purpose. Since the air is supplied at the ceiling level and exhausted at the floor level, one large eddy and a small recirculation zone at the left lower corner are formed (Fig. 2). Fig. 3 a shows the simulated $10\mathrm{\mu }\mathrm{m}$ particle concentration distribution at the center plane, and the particle concentration is normalized by the inlet concentration. A high gradient in the vertical direction is observed due to the gravitation. Particles deposit onto the floor, causing a relatively low concentration at the lower part of the room. The initial supply velocity of particles ($0.225\mathrm{m}{\mathrm{s}}^{-1}$) and the effect of convection result in a higher concentration in the right half of the room. For comparison purposes, simulated concentration distribution for $1\mathrm{\mu }\mathrm{m}$ particles is presented in Fig. 3b, and very uniform distribution can be observed. The well-mixing assumption is acceptable for $1.0\mathrm{\mu }\mathrm{m}$ particles while it may not be right for $10\mathrm{\mu }\mathrm{m}$ particles. The concentration at the outlet opening is 0.25 for $10\mathrm{\mu }\mathrm{m}$ particles, and 0.96 for $1.0\mathrm{\mu }\mathrm{m}$ particles. Most of the $10\mathrm{\mu }\mathrm{m}$ particles deposits onto the floor. However, for $1.0\mathrm{\mu }\mathrm{m}$ particles, the deposition loss can be ignored. The simulated and measured concentration profiles for the $10\mathrm{\mu }\mathrm{m}$ particles are compared in Fig. 4 .Because the airflow in this experiment was relatively simple and isothermal, a fine agreement is achieved.

Fig. 2.

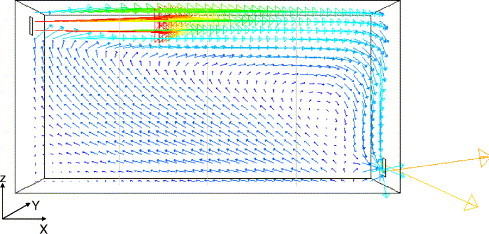
Airflow pattern at the center plane ($Y=0.2\mathrm{m}$) of the model room ($L=0.8\mathrm{m}$, $W=0.4\mathrm{m}$, $H=0.4\mathrm{m}$), the inlet and outlet are $0.04\mathrm{m}\times 0.04\mathrm{m}$, the inlet air velocity is $0.225\mathrm{m}{\mathrm{s}}^{-1}$.

Fig. 3.

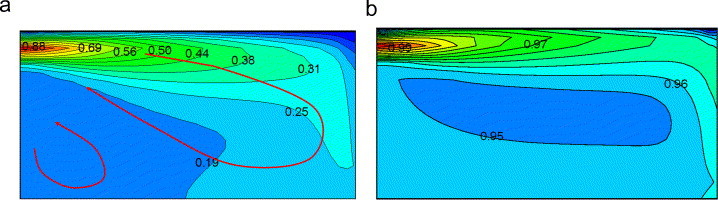
Simulated particle concentration distributions at the center plane ($Y=0.2\mathrm{m}$) (a) $10\mathrm{\mu }\mathrm{m}$ particle concentration and (b) $1.0\mathrm{\mu }\mathrm{m}$ particle concentration.

Fig. 4.

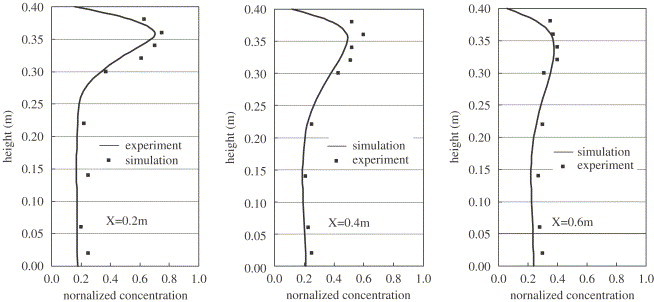
A comparison of simulated and measured $10\mathrm{\mu }\mathrm{m}$ particle concentrations at the center plane.

3.2. Non-isothermal condition

Isothermal experiments in a scaled-chamber may not be suitable and representative for indoor airflow studies, where buoyancy effects and temperature differences exist. Zhang and Chen (2006) carried out an experimental study on indoor particle dispersion in a full-scale environmental chamber with UFAD (Fig. 5 ). Air was supplied to the chamber at a total flow rate of $0.0944{\mathrm{m}}^{-3}{\mathrm{s}}^{-1}$ by two openings located on the floor, and was exhausted at the ceiling. Four heated manikins and six lamps installed on the ceiling were used to simulate heat sources in a normal room. Liquid droplets with a low evaporation rate were introduced by a carrier gas (nitrogen, at a flow rate of $7\times {10}^{-5}{\mathrm{m}}^3{\mathrm{s}}^{-1}$) into the room at a position 0.3 m above the floor ($X=1.5\mathrm{m}$, $Y=2.1\mathrm{m}$, $Z=0.3\mathrm{m}$). The diameter of the mono-disperse spherical particles was $0.7\mathrm{\mu }\mathrm{m}$. Particle concentrations were monitored at the exhaust outlet, and at five height levels (0.4, 0.8, 1.2, 1.6, 1.8 m) of six locations (from P1 to P6 as shown in Fig. 5). These experimental data are used to validate the present simulation results.

Fig. 5.

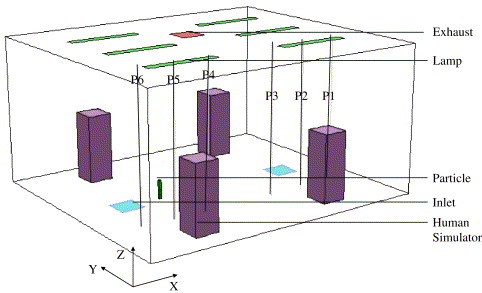
A sketch of the environmental chamber configuration ($X=4.8\mathrm{m}$, $Y=4.2\mathrm{m}$, $Z=2.4\mathrm{m}$).

Temporal evolution of particle concentration at the exhaust is modeled (Fig. 6 ). At the time $t=0\min$, particle emission is initiated at a steady flux. The stable concentration at the exhaust is denoted as 1.0. The numerical prediction is in accord with the experimental data. The time required to reach the stable outlet concentration is obviously dependent on the particle release location. If the particle is generated in a recirculation zone, or so called a dead zone, it can be imagined that it takes a longer time for the particles to be ventilated out of the room. Here the concept of residual life time can be employed. In a pulse emission of n particles, if the portion of the particles that can arrive at the exhaust is $\alpha$ and each particle takes time $t_i$, the particle residual life time can be defined as

$${\tau }_{\mathrm{r}}=\frac{{\sum }_1^{\alpha \times n}{t}_i}{\alpha \times n}\text{.}$$ (4)

We replaced the $0.7\mathrm{\mu }\mathrm{m}$ particles by a tracer gas and other coarse particles (7, 14, and $21\mathrm{\mu }\mathrm{m}$) and simulated the temporal development of the exhaust concentrations for comparison. The time required to arrive at the stable concentration is almost the same. Previous studies in a channel flow (Brandon and Aggarwal, 2001) and in free shear layers (Loth, 1998) have revealed that particle dispersion depends on Stokes number (St) which is the ratio of the particle response time to the characteristic time. Particles with $\mathit{St}<0.1$ behave like fluid particles, whereas those with $\mathit{St}\approx 1.0$ no longer faithfully follow the trajectories of fluid particles but can still respond readily to fluid velocity fluctuations and those with $\mathit{St}>1.0$ diffuse at a much slower rate than that of a scalar field inasmuch as their inertia is too great to be significantly affected by the turbulent dispersion. The experiment by Hishida et al. (1992) confirmed that with $\mathit{St}\sim O(1)$ particle dispersion coefficients became larger than the eddy diffusivity of the fluid phase. However, since the particle turbulent diffusivity is expressed by fluid turbulent viscosity this phenomenon is not evidently captured by the present drift-flux model. In the frame of Lagrangian method, the Stokes number effect on particle dispersion and ${\tau }_{\mathrm{r}}$ can be easily calculated in that each particle trajectory is simulated. These two issues will be included in our next research stage in which dispersion characteristic is investigated by large eddy simulation (LES) plus Lagrangian approach.

Fig. 6.

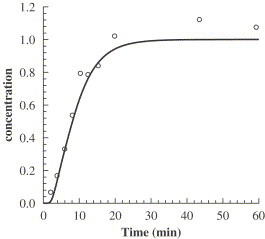
Simulated and measured temporal normalized concentration at the exhaust (circles: experimental data; solid line: simulations).

Fig. 7 further compares the detailed concentration distributions. For location P1, P2, and P3, the numerical data match the measured data. The greatest difference appears at P6. As explained by Zhang and Chen (2006), in the experiment the concentration fluctuation near the source was relatively strong owing to flow fluctuation from the particle generator.

Fig. 7.

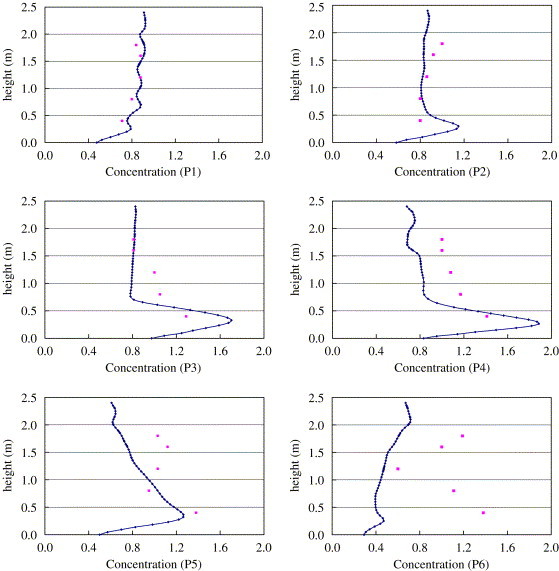
A comparison of simulated and measured particle concentrations.

4. Applications

4.1. Cases description

In this section, using the aforementioned drift-flux model, we aim to compare particle dispersion and deposition characteristics with three typical air distribution systems, namely, the MV, DV, and UFAD, in a hypothetic room with the dimensions of 4.0 m (length) $\times 3.0\mathrm{m}$ (width) $\times 2.7\mathrm{m}$ (height) (Fig. 8 ). With DV, a large wall-mounted diffuser was located at the floor level to supply cool air at a low speed, and an exhaust at the ceiling level. For MV, an inlet diffuser with small opening was set at the upper level, and an outlet at the floor level. For the UFAD, a round swirling diffuser is mounted on the floor, which is simulated by eight small square cells, as shown in Fig. 9 . Each cell has a different airflow direction and is in charge of one-eighth of the total supply rate. The angle between the outlet airflow and the floor is ${30}^{\circ }$. This method is figured out by Kobayashi and Chen (2003) through smoke visualization. A vertical heat source beside the desk was specially designed to create different level of vertical thermal stratification. In the simulations we used a breathing numerical thermal manikin (NTM) (Gao and Niu, 2007) to rigorously simulate the inhaled particle concentrations.

Fig. 8.

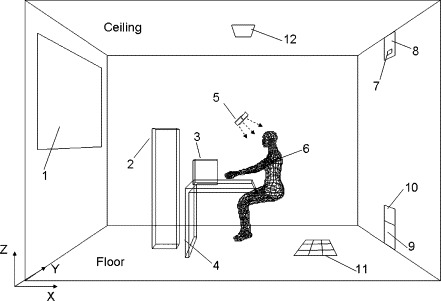
Configuration of the simulated office (room length ($X$) 4 m, width ($Y$) 3 m, height ($Z$) 2.7 m; 1—window; 2—vertical heat source; 3—computer; 4—table; 5—personalized ventilation air terminal device (circular outlet with a diameter of 20 cm, not activated in the present study); 6—human body; 7—mixing ventilation inlet $0.2\mathrm{m}\times 0.05\mathrm{m}$; 8—displacement ventilation outlet $0.4\mathrm{m}\times 0.3\mathrm{m}$; 9—mixing ventilation outlet $0.4\mathrm{m}\times 0.3\mathrm{m}$; 10—displacement ventilation inlet $0.4\mathrm{m}\times 0.5\mathrm{m}$; 11—UFAD inlet $0.21\mathrm{m}\times 0.21\mathrm{m}$; 12—UFAD outlet $0.4\mathrm{m}\times 0.4\mathrm{m}$).

Fig. 9.

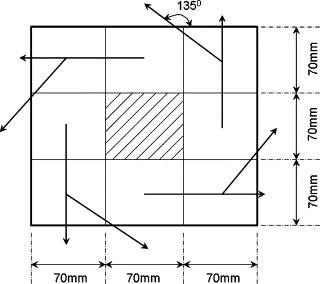
Swirling floor diffuser simulation.

The Navier–Stokes equations are solved with a commercial code (Fluent, 2005) based on a finite-volume method. The numerical methods and boundary conditions are summarized in Table 1 . The simulated results of velocity and temperature distributions have been discussed before (Gao et al., 2007). Here highlighted are the deposition and concentration distributions of particles whose material density is $1000\mathrm{kg}{\mathrm{m}}^{-3}$.

Table 1.

The details of numerical methods

Turbulence model	Standard $k$–$\epsilon$ model
Numerical schemes	Upwind second order difference for the convection term; SIMPLEC algorithm
Window	Uniform heat flux 150 W
Floor, ceiling, walls	Adiabatic wall
Vertical heat source	Uniform heat flux 100 W
Human body	Fixed skin temperatures at $31{}^{\circ }\mathrm{C}$
Computer	Uniform heat flux 120 W
Desk	Adiabatic
MV inlet	Airflow rate $51\mathrm{l}{\mathrm{s}}^{-1}$, turbulence intensity 30%, turbulence length scale 0.005 m, $19{}^{\circ }\mathrm{C}$
DV inlet	Airflow rate $51\mathrm{l}{\mathrm{s}}^{-1}$, turbulence intensity 15%, turbulence length scale 0.03 m, $19{}^{\circ }\mathrm{C}$
UFAD inlet	Airflow rate $51\mathrm{l}{\mathrm{s}}^{-1}$, turbulence intensity 15%, turbulence length scale 0.03 m, $19{}^{\circ }\mathrm{C}$
MV/DV/UFAD outlet	Velocity and temperature: free slip
Nose	Steady inhalation, respiration rate $8.4\mathrm{l}{\min }^{-1}$, turbulence intensity 20%, hydraulic diameter 0.01 m

4.2. Mean deposition velocity and deposition rate coefficient

Particles are released from the surface of the vertical heat source. In the current study the mean deposition velocity is expressed as an area-weighted average of deposition velocities at solid surfaces. The deposition rate coefficient thus can easily be obtained by multiplying the mean deposition velocity by the surface-to-volume ratio. As to the studied room configuration the surface-to-volume ratio is $2.16{\mathrm{m}}^{-1}$. The mean deposition velocities in different air distributions and at various air exchange rates are shown in Figs. 10 and 11 , respectively. The V-shaped deposition curve as a function of particle size is observed. Particles with diameters of 0.1 and $0.5\mathrm{\mu }\mathrm{m}$ have minimum deposition velocities since in this diameter range the total effects of diffusion and settling are minimal. The effect of ventilation condition on deposition velocity is particle size dependent. For particles which are larger than $0.5\mathrm{\mu }\mathrm{m}$, the mean deposition velocity is independent of ventilation types and air exchange rates, i.e. $v_{\mathrm{d}}\approx f({\rho }_{\mathrm{P}},D)$. This result is expectable if we look into the present-used deposition model by Lai and Nazaroff (2000). The reason is that deposition flux onto the floor is 3–4 orders of magnitude higher than the total flux onto the vertical walls and ceiling and that gravitational sedimentation is the only dominant factor. That is, for particles larger than $0.5\mathrm{\mu }\mathrm{m}$, deposition velocity is a function of their physical properties, i.e. density and size, which increases as the particle size increases. However, the situation is entirely different for particles smaller than $0.5\mathrm{\mu }\mathrm{m}$ because gravitational settling is overwhelmed by the turbulent and Brownian diffusion. For 0.01 and $0.1\mathrm{\mu }\mathrm{m}$ particles, the mean deposition velocity is highest in MV and lowest in DV (Fig. 10). In the mixing ventilated room, a higher air exchange rate results in a higher deposition velocity (Fig. 11). Both can be explained by a higher level of indoor air velocities in MV compared to DV and at higher ventilation rates. For these submicron particles, $v_{\mathrm{d}}=f({\rho }_{\mathrm{P}},D,u^{*})$, and a higher friction velocity leads to a higher deposition velocity. This agrees well with the experimental measurements in a chamber (Nomura et al., 1997) and in residential houses (He et al., 2005). They found that the deposition rate coefficient increased with the air exchange rate. Through monitoring the transient particle concentrations and using the following equation

$$\ln \left(\frac{C_t}{C_0}\right)=-(a+k)t$$ (5)

the deposition coefficient $k$ was determined by fitting a line to a plot of the log of $C_t/C_0$ versus time and subtracting a from the slope.

Fig. 10.

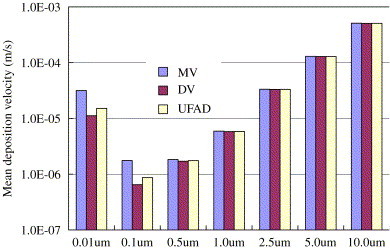
The effect of air distribution methods on the average deposition velocities.

Fig. 11.

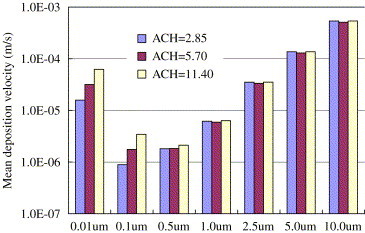
The effect of air change rates on the average of deposition velocities in the mixing ventilated room.

4.3. Human exposure

Human exposures in two scenarios are investigated here. Case A is that in an imagined terrorist attack harmful or toxic airborne agents are released into the room supply air, with a concentration of $1.0\mathrm{\mu }\mathrm{g}{\mathrm{m}}^{-3}$ as a step-up function. Case B is that particles are uniformly generated from the vertical heat source (item 2 in Fig. 8) at a rate of $0.154\mathrm{\mu }\mathrm{g}{\mathrm{s}}^{-1}$. In case A, two issues are of practical meanings: (1) the time evolution of the particle concentration in the occupant's inhaled air after the release into the supply air and (2) the stable inhaled concentration after the steady condition is achieved. In case B, it is of interest whether there is a vertical stratification of concentration in DV and UFAD if particle source and heat source are combined into one, such as with the presence of a copy machine.

4.3.1. Human exposure in Case A

Fig. 12 shows the temporal development of inhaled particle concentrations. The increment of inhaled concentration, as an exponential expression of time is observed. The time required to reach 90% of the final steady concentration is listed in the legend of Fig. 12. For $1.0\mathrm{\mu }\mathrm{m}$ particles, the temporal increment, like a tracer gas, is faster in UFAD, and slowest in MV, with DV in the middle. It takes 17, 19, and 23 min to reach 90% of the ultimate maximum concentration in UFAD, DV, and MV, respectively. It is obvious that these time values are dependent on the location. If the occupant's head is very close to the air supply the inhaled concentration will reach the concentration level in the supply air promptly. In the current study the occupant is seated closer to the air outlets in UFAD and DV than in MV. However, as particle size becomes larger, an interesting phenomenon is found. In MV, the 90% cut-off time is 6.3 min for $20.0\mathrm{\mu }\mathrm{m}$ particles, 13.2 min for $10.0\mathrm{\mu }\mathrm{m}$ particles, which are much less than 23 min for $1.0\mathrm{\mu }\mathrm{m}$ particles. In UFAD, the 90% cut-off time for $10.0\mathrm{\mu }\mathrm{m}$ particles is only slightly less than that for $1.0\mathrm{\mu }\mathrm{m}$ particles, which is 15 min. However, this cut-off time is non-sensitive to particle size in DV. We consider that high air supply velocities in UFAD, and especially in MV, make the particle movements more convection dominant than in DV.

Fig. 12.

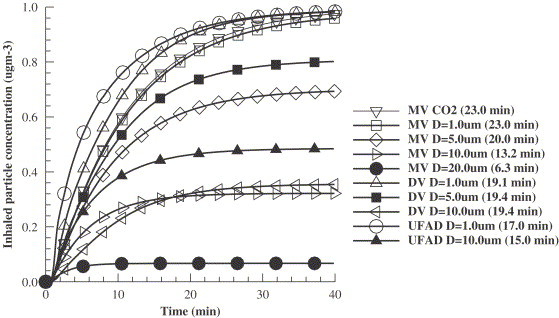
Temporal human exposures (inhaled particle concentration) in the DV, UFAD, and MV cases.

Fig. 13 shows the ultimate stable human exposure. Inhaled concentration of $1.0\mathrm{\mu }\mathrm{m}$ particles equals approximately to the supply concentration, which is $1.0\mathrm{\mu }\mathrm{g}{\mathrm{m}}^{-3}$, irrespective of the ventilation types. For 2.5, 5.0, and $10.0\mathrm{\mu }\mathrm{m}$ particles, the inhaled concentration decreases as particle size increases. For the same size, human exposure is highest in UFAD and lowest in MV.

Fig. 13.

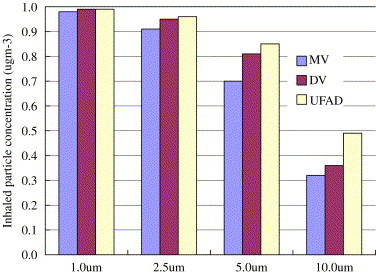
Human exposures in the DV, UFAD, and MV cases (the inlet concentration is $1.0\mathrm{\mu }\mathrm{g}{\mathrm{m}}^{-3}$).

One of the multiple benefits of UFAD is improving room ventilation by delivering fresh air closer to the occupants. However, this benefit may become a disadvantage in a terrorist attack because of the shorter distance between the air outlet and the occupant, causing the fastest and highest exposure to the airborne agents among the three air distribution types. In some modern open-plan office buildings, floor-mounted air diffusers are installed in workstations for conditioning the personal environments of the office workers. Typically, the occupant has control over the air supply rate, direction, and even temperature to accommodate the individual thermal preference. These systems are variously called “task/ambient conditioning”, “localized thermal distribution”, and “personalized ventilation” systems (Bauman and Arens, 1996). Air is supplied from the underfloor plenum formed by installation of a raised access floor. Imaging that the supply air is polluted by airborne biochemical agents, they will quickly reach the breathing zone of the occupant, resulting in a serious attack.

Murakami et al. (1992) proposed an indicator to determine whether the gravitational settling effect can be ignored. The indicator is the ratio of room air time scale, i.e. the reciprocal of air exchange rate, to particle's settling time. Table 2 lists the falling times over 1 m vertical distance and their corresponding air exchange rate if this indicator is set to 1, which means that the particle settling time and the room time scale are comparable. The air exchange rates from 0.71 to 10.81 are reasonable in a naturally ventilated room and an operating room, respectively. Therefore for 2.5, 5.0, and $10.0\mathrm{\mu }\mathrm{m}$ particles, gravitation should be taken into account. These particles are in a transitional size range, below which gravitation can be neglected, and above which gravitation becomes dominant. It is manifested in Fig. 13, where $1.0\mathrm{\mu }\mathrm{m}$ particles behave approximately as a tracer gas, whereas the others not. For particles of $20\mathrm{\mu }\mathrm{m}$, the simulation results indicated that the gravitational force is so strong that the inhaled concentration is less than 6.7% of the room supply concentration, i.e. $0.067\mathrm{\mu }\mathrm{g}{\mathrm{m}}^{-3}$, in all ventilation types.

Table 2.

Droplet falling time as a function of size and the corresponding air exchange rate

Droplet diameter ($\mathrm{\mu }\mathrm{m}$)	Falling time of 1 m (s)	Air exchange rate (${\mathrm{h}}^{-1}$)
1.0	29 070	0.12
2.5	5076	0.71
5.0	1311	2.75
10.0	333	10.81
20.0	84	42.86

The problem of inhalability in modern workplaces and indoor environments has been studied before (Aitken et al., 1999, Hsu and Swift, 1999, Kennedy and Hinds, 2002), which is defined, based on a substantial body of work, as aspiration efficiency or inhalable fraction of the mouth or nose for a breathing, full-size manikin as a function of particle aerodynamic diameter. Aitken et al. (1999) placed a manikin with a head and upper body only in a cuboid chamber ($1\mathrm{m}\times 1\mathrm{m}\times 3\mathrm{m}$) ventilated by an upside-to-downside airflow at a velocity less than $0.1\mathrm{m}{\mathrm{s}}^{-1}$. The oral inhalability of $13\mathrm{\mu }\mathrm{m}$ alumina particles is 83%, 84%, and 92% at a breathing rate of 6, 10, and $20,\mathrm{l}{\min }^{-1}$, respectively. Similarly, Hsu and Swift (1999) found the inhalability of $13\mathrm{\mu }\mathrm{m}$ alumina particles to be $73.8\pm 7.1\%$ under oronasal breathing condition in a calm chamber whose inside dimensions are $0.9\mathrm{m}\times 0.9\mathrm{m}$ and of height of 1.8 m. Some studies have given out empirical equations to predict inhalability as a function of particle aerodynamic diameter (Vincent et al., 1990, Kennedy and Hinds, 2002). There exist some differences between the results since inhalability, which is measured in a uniform concentration field, is also dependent on many other factors, such as the approaching air velocity, body-to-wind orientation, breathing frequency, and respiration tidal volume. For comparison, human exposure to $13\mathrm{\mu }\mathrm{m}$ particles in MV is simulated because a relatively uniform concentration distribution is created in MV. The average particle concentration at the breathing zone is $0.25\mathrm{\mu }\mathrm{g}{\mathrm{m}}^{-3}$ and inhaled concentration is $0.20\mathrm{\mu }\mathrm{g}{\mathrm{m}}^{-3}$, and thus the inhalability is 80%, which falls within the experimental range.

4.3.2. Human exposure in Case B

The particle concentrations and air temperatures at different height levels at one location behind the human body ($X=2.8\mathrm{m}$, $Y=1.5\mathrm{m}$) are illustrated in Fig. 14 . With MV particle concentration is almost uniform except at the points close to the ceiling where there is a clean supply airflow. The larger the particles, the lower the mean indoor concentrations. For particles smaller than $5.0\mathrm{\mu }\mathrm{m}$, human exposure is nearly equal to the outlet concentration. However for larger particles, human exposure is much less than the exhaust concentration due to the aspiration efficiency mentioned above. With DV a vertical concentration stratification is observed. It is shown that the buoyant upward airflows in a displacement ventilated room are able to bring the particles to the upper zone. Because of the heavy gravitational settling effects, this principle cannot be applied to $20\mathrm{\mu }\mathrm{m}$ particles. As a result, human exposure is greatly lower than that with MV for 0.1, 1.0, 2.5, and $5.0\mathrm{\mu }\mathrm{m}$ particles, but larger for 10.0 and $20.0\mathrm{\mu }\mathrm{m}$ particles. As for gaseous pollutants, DV is still preferable to MV for fine particles. It so happened that a portion of 10.0 and $20.0\mathrm{\mu }\mathrm{m}$ particles, which are too heavy to be carried up, are locked in the breathing height, resulting in a higher exposure in DV. With UFAD the vertical stratification for 0.1, 1.0, and $2.5\mathrm{\mu }\mathrm{m}$ particle also appears and human exposure is lower than that with MV, but slightly higher than that with DV. But owing to the weak carry-up effect, particles larger than $5.0\mathrm{\mu }\mathrm{m}$ are unable to be entrained to the upper level.

Fig. 14.

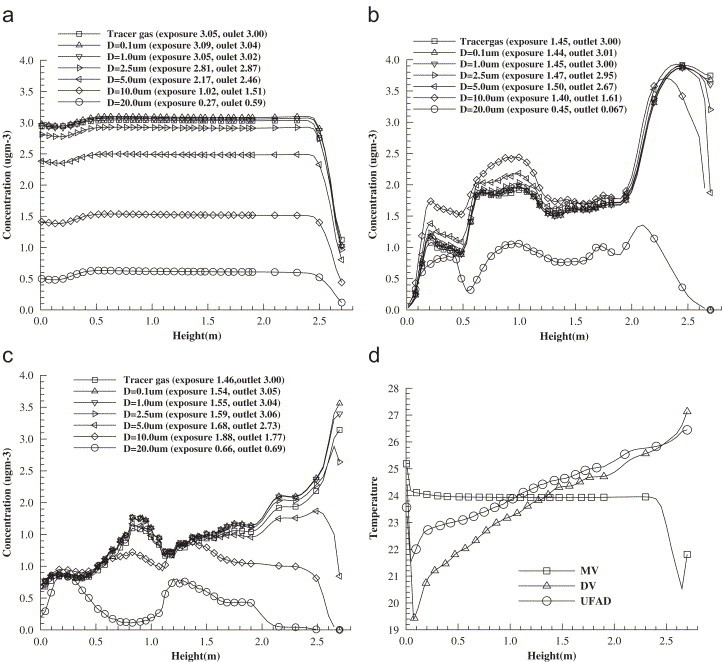
Vertical distribution of particle concentration where the particles are generated from the heat source in the MV room (a), DV room (b), UFAD room (c), and vertical temperature distribution (d).

The distinct particle distributions in these three ventilation methods are a consequence of different indoor airflow patterns. It is easy to understand that in MV a strong jet flow with a high momentum causes a full mixing of indoor air. In comparison to DV where supply air is delivered at low velocities, UFAD systems deliver air through floor diffusers at higher velocities. In order to reduce the local drafts at low levels, floor air outlets are designed to maximize air mixing within the occupied zone, which diminishes the ventilation performance compared to DV systems. This is why the concentration closely above the floor in DV (see Fig. 14b) is almost zero while this is not the case with UFAD. With UFAD systems, the thermal plumes generated from heat sources are a minor, secondary characteristic of the system, with the primary air motion in the occupied zone created by the high velocity floor diffuser (McDonell, 2003). However, DV systems are designed to minimize the mixing of air in the occupied zone, and thermal plumes are the dominant air movement characteristic. Room air is displaced out at a higher portion of the space by a continual supply of fresh air. As shown by Fig. 14(d), a steeper vertical temperature gradient is formed with DV than with UFAD, and the temperatures of air close to the floor is higher with UFAD, since swirling diffuser is characterized by a swirling discharge airflow pattern that is intended to produce high induction and limited throws (Webster et al., 2002). This steeper temperature gradient induces a stronger carry-up effect in DV.

5. Conclusions

In this study a simplified Eulerian method, i.e. a drift-flux model, is developed with an improvement on the solid boundary condition with the help of a semi-empirical deposition model, and implemented into a commercial CFD code through user defined function. The model predicts the spatial distribution of particle concentration very well in the case of the isothermal flow. Since the flow is characterized by fully developed forced convection turbulence, which can be well predicted by the $k$–$\epsilon$ turbulence model, the comparison may well indicate that the accurate simulation of the turbulent flow field is the prerequisite for accurate particle dispersion modeling.

The application of the drift-flux model to compare the mean deposition velocity and human exposures to particles from supply air and indoor sources in MV, DV, and UFAD reveals some interesting features when particle sizes are taken into account. The V-shape of the deposition curve as a function of particle size is observed. For supermicron particles, the ventilation type and air exchange rate have an ignorable effect on deposition rate coefficient. The movements of submicron particles are like tracer gases, whereas the gravitational effect should be taken into account for particles larger than $2.5\mathrm{\mu }\mathrm{m}$. Human exposure to the particulate matters released into the supply air decreases as particle size increase due to the enhancement of deposition, and this exposure is also determined by the relative locations of the occupant and the air outlet. UFAD systems, which are reported to be able to improve ventilation effectiveness, would become the most vulnerable systems in a terrorist attack in the form of releasing biochemical aerosols in ventilation ducts, in terms of the shortest response time the occupants would have. With particle sources located within an internal heat source, desirable vertical concentration stratification appears in DV and UFAD for particles up to $10.0\mathrm{\mu }\mathrm{m}$. The advantageous principle of DV and UFAD that there is a less polluted occupied zone for non-passive gaseous pollutants is also applicable to particles whose diameters are less than a certain value which depends on the strength of the buoyancy force.

Although some meaningful results have been obtained with the present numerical methods, improvement is still needed in several aspects of the models used. For instance, the application of concentrations in the first normal cells makes the deposition flux grid dependent, and the diffusion term in the governing equation of concentration does not address the size-dependent dispersion characteristics of particles.