Abstract
Background
Many researchers have evaluated the performance of outbreak detection algorithms with recommended parameter values. However, the influence of parameter values on algorithm performance is often ignored.
Methods
Based on reported case counts of bacillary dysentery from 2005 to 2007 in Beijing, semi-synthetic datasets containing outbreak signals were simulated to evaluate the performance of five outbreak detection algorithms. Parameters’ values were optimized prior to the evaluation.
Results
Differences in performances were observed as parameter values changed. Of the five algorithms, space–time permutation scan statistics had a specificity of 99.9% and a detection time of less than half a day. The exponential weighted moving average exhibited the shortest detection time of 0.1 day, while the modified C1, C2 and C3 exhibited a detection time of close to one day.
Conclusion
The performance of these algorithms has a correlation to their parameter values, which may affect the performance evaluation.
Keywords: Outbreak detection algorithms, Evaluation, Parameter values, Outbreak simulation
1. Introduction
Following the outbreak of severe acute respiratory syndrome [1] in 2003, there has been a growing recognition of the necessity and urgency of early outbreak detection of infectious diseases. In January 2004, the National Disease Surveillance, Reporting and Management System were launched in China. The system which covers 37 infectious diseases has the potential to provide timely analysis and early detection of outbreaks. However, as the passive surveillance system relies on accumulated case and laboratory reports, which are often delayed and sometimes incomplete, the opportunity to contain the spread of the disease is often missed.
As increasing numbers of early outbreak detection algorithms are now being used in public health surveillance [2], [3], [4], [5], [6], [7], [8], [9], there is a need to evaluate their performance. Due to a lack of complete and real data pertaining from historical outbreaks, the performance of these systems have been previously difficult to evaluate [10]. Adding to these difficulties is the fact that the information obtained from historical outbreaks may be heterogeneous, due to changes in the outbreak surveillance criteria’s over time. In order to compensate for missing or heterogeneous information, semi-synthetic datasets can be created which contain the outbreak signals, using a software tool. By using this tool, the parameters of the outbreak including the desired duration, temporal pattern and the magnitude (based on a predefined criteria), can be specially set.
This approach has been documented in a number of previous studies, which have compared the performance of early outbreak detection algorithms using simulated outbreaks [11], [12], [13], [14], [15], [16], [17], [18]. The simulation enables the performance assessment and provides much-need comparative findings about outbreak detection algorithms. However, there are still limited studies examining how the performance varies with the values of these algorithm parameters. Our study aimed to observe the relationship between the algorithms’ performance and their parameters values. The outcomes of this study may help improve the accuracy and objectivity of the evaluation of these algorithms and provide guidelines for future research and implementation.
2. Methods
2.1. Baseline data
Bacillary dysentery is one of the key epidemic potential diseases in Beijing. It commonly occurs in summer and in regions with high population densities. With economic development and improvements in sanitary conditions in China, the incidence of bacillary dysentery has decreased substantially from 1990 to 2003 [19]. Between 2004 and 2007, data from the National Disease Surveillance Reporting and Management System showed that the average incidence rate of bacillary dysentery was 235.9 cases per 100,000 in Beijing. Whilst there has been a substantial decline in the disease burden, bacillary dysentery continues to be a major public health problem in Beijing.
The observed daily case counts of bacillary dysentery from 2005 to 2007 in Beijing were extracted from the National Disease Surveillance Reporting and Management System [20] for this study. The onset date of illness and area code at the sub-district level was extracted for each reported case. This data was used as the baseline for the outbreak simulation. Data from 2005 to 2006 were used to adjust and optimize the parameter values of the algorithms, while data from 2007 were used to evaluate the algorithms.
2.2. Data simulation
The outbreak criteria was defined on the basis of the bacillary dysentery reporting criteria specified in the National Protocol for Information Reporting and Management of Public Health Emergencies (Trial) [21]. This protocol was issued by the Health Emergency Office of the Ministry of Health (MOH) at the end of 2005. In the protocol, a bacillary dysentery outbreak was defined as the occurrence of 10 or more bacillary dysentery cases in the same school, natural village or community within 1–3 days. Based on this definition, there was only one actual outbreak in the summer of 2007. During this outbreak, 10 children from a middle school were clinically diagnosed as having bacillary dysentery and four were culture positive for Shigella sonnei. The first case became ill on the evening of the 21st of July and was taken to hospital the next day. Two cases were reported on the 22nd of July, a further four on the 23rd of July, and two on the 24th July. As there were insufficient documents collected during the outbreak, a simulated outbreak signal had to be produced.
Before the simulation, the actual outbreak was excluded by replacing actual data with a 7-day moving average for fear of contamination. Our simulation approach used semi-synthetic data, that was, authentic baseline data injected with artificial signals [9]. The AEGIS-Cluster Creation Tool (AEGIS-CCT) was used to generate outbreak signals [22]. First, the duration was fixed at three days and the outbreak magnitude varied from 10 to 20. The outbreak magnitude was fixed at 10 cases and the duration was varied from one to three days.
The temporal progression of these outbreaks included a random, a linear, and an exponential growth spread (12 signals for each temporal progression pattern). A total of 36 different outbreak signals were finally simulated. Considering the spatial distribution and seasonal variability of bacillary dysentery, we randomly selected 30 (10 for each pattern) from a possible 100 sub-districts (townships), where the incidence was higher than the average incidence in Beijing, and then randomly selected one day as the starting date of an outbreak from the high incidence seasons. The remaining six outbreak signals were randomly added to the low incidence seasons and areas. Simulations injected into the baseline data from the selected sub-districts (2005–2006) were used to observe the relationship between the algorithm performance and the parameter value. This data allowed us to select the optimal combination of parameter values. Simulations added to the baseline data from 2007 were used to evaluate the algorithm. In order to reduce sampling errors, means were calculated by repeating the sampling 50 times.
2.3. Evaluation indices
Evaluation indices included sensitivity, specificity and time to detection [14]. An outbreak was considered to be detected when a signal was triggered: (1) within the same period as the start and end date of the particular simulated outbreak; and (2) within the same sub-district as what the simulation was geographically located in. In our study, sensitivity was defined as the number of outbreaks in which ⩾1 day was flagged, divided by the number of simulated outbreaks. Specificity was defined as the number of days that were not flagged divided by the number of non-outbreak days. Time to detection was defined as the interval between the beginning of the simulated outbreak and the first day flagged by the algorithm, divided by the number of simulated outbreaks. Time to detection was zero, if the algorithm flagged a simulated outbreak on the first day. Time to detection was three, if the algorithm did not produce a flag on any of the days during the period of the simulated outbreak. Time to detection is an integrated index that reflects both timeliness and sensitivity of an algorithm.
2.4. Evaluation criteria
We intended to find a simple and practical criterion to evaluate the performance of these algorithms. Generally, the parameter values with the shortest time to detection were considered as preferable. The disparity in specificity between the parameter values was also taken into consideration. Priority was given to the value with the higher specificity, if the time to detection was either equal to or had a difference of less than half a day and the difference between the specificities was >5.0%.
2.5. Outbreak detection algorithms
We compared the performance of five outbreak detection algorithms, the exponential weighted moving average (EWMA), C1-MILD (C1), C2-MEDIUM (C2), C3-ULTRA (C3) and the space–time permutation scan statistic model.
We calculated the EWMA, using a 28-day baseline based on day t − 30 through till day t − 3 within each sub-region [15]. If the observed values were x i ∼ N (μ, σ 2), the weighted daily counts of each sub-district were calculated as:
| (1) |
| (2) |
In the algorithm, λ (0 < λ < 1) was the weighting factor, and k was the control limit coefficient [15], [23]. They are the adjustable parameters. Based on the range in values of k found in previous literature [23], k was set as 0 < k ⩽ 3. The adjustment interval for λ and k was set as 0.1 and 0.5, respectively. The moving standard deviation (S) was used as the estimate of σ; and the moving average (MA) was used as the estimate of μ.
The cumulative sum (CUSUM) algorithm keeps track of the accumulative deviation between the observed and expected values. For CUSUM, the accumulated deviation St was defined as:
| (3) |
S_{0} = 0·kσxt is the allowed shift from the mean to the detected. St is the current CUSUM calculation, and St −1 is the previous CUSUM calculation. We found that there was an aberration when the mean μ 0 shifted to μ 0 + kσx· h was the decision value. In EARS, k was set as 1 and when St > h = 2, an alarm would be trigged [24].
When the denominator σxt equals to zero, 0.2 was taken to replace zero in EARS. However, as both sides of the equation can be multiplied (St = max (0, St −1 + ((Xt − (μ 0 + kσxt))/σxt )) > 2) by σxt, the decision value was changed to hσxt (referred to as H).
BioSense originally implemented the C1, C2 and C3 methods but has since modified the C2 method (referred to as W2). In our study, we did not use the threshold; k or decision values set in EARS, rather we adjusted these values to achieve a preferable efficiency for aberration detection. Additionally, we did not use 0.2 when σxt was 0, rather the actual value. Based on the previous literatures [13], [25], [26], we determined the value range of H and k, as 3σ ⩽ H ⩽ 5σ and 0 < k ⩽ 1.5, respectively. The adjustment interval for k and H was set as 0.1 and 0.5σ, respectively. We modified the three original CUSUM referred to as C1, C2 and C3 to C1′, C2′ and C3′ in the reporting of the results in this study.
The equation is written as
| (4) |
| (5) |
C3′ was the sum of Ct, Ct−1 and Ct−2 derived from C2′. MA 1 was the moving sample average and S 1 was the moving standard deviation of the case count reported from baseline. MA 2 and S 2 were the moving sample average and moving standard deviation of the case count reported during baseline period, with a 2-day lag. The moving standard deviation (S) was used as the estimate of σ; and the moving average (MA) was used as the estimate of μ. The length of the baseline comparison period for all three methods was 7-days in order to account for the day of the week effect [13], [14].
The space–time permutation scan statistic model utilizes thousands to millions of overlapping cylinders to define the scanning window, each of which is a possible candidate for an outbreak. The circular base represents the geographical area of the potential outbreak from zero to some designated maximum value. The height of the cylinder represents the time period of a potential cluster. The probability function for any given window is proportional to [27], [28]:
| (6) |
where Czd was the observed number of cases in subzone z and during day d. C was the total number of observed cases during the whole study phase T for the whole study region. CA was the observed case count scanned in cylinder A. The generalized likelihood ratio (GLR) was calculated as a measure of the evidence that cylinder A contains an outbreak. Among the many cylinders evaluated, the one with the maximum GLR constitutes the space–time cluster of cases that is least likely to be a chance occurrence and, hence, is the primary candidate for a true outbreak. The size and location of the scanning window is under dynamic change [28]. The maximum temporal cluster size was determined by considering the incubation period of the disease studied. For bacillary dysentery, the average incubation period was 1–3 days. Therefore, the maximum temporal cluster size in this study was set as (1d, 3d, 5d and 7d). The maximum spatial cluster size can be determined in virtue of the geographical area or the proportion of the whole population. Since data on the proportion of the population in each sub-district were unavailable, the maximum spatial cluster size in this study was set as (2, 5, 8 and 10 km), referring to the geographical area of each sub-district. The performance was analyzed using P values of 0.05.
2.6. Data analysis
Analyses were undertaken using EXCEL, SPSS software (version 13.0 for Windows; SPSS Inc., Chicago, IL), AEGIS-CCT (available from http://sourceforge.net/projects/chipcluster/), JAVA programming (available from http://java.com/zh_CN/) and SaTScan (available from www.satscan.org). SPSS was used for data processing, descriptive statistics and the chi-square test. The Bonferroni correction was applied for multiple comparisons to control the family wise error rate. The significance level α for an individual test was calculated by dividing the family wise error rate (0.05) by the number of tests [29]. EWMA and the cumulative sum were coded by JAVA programming to find out whether the incidence level was abnormal. SaTScan was used to analyze the clustering of cases in different sub-districts in Beijing based on space–time permutation scan statistics and whether the incidence level was abnormal.
3. Results
3.1. Adjustment and optimization of parameter
The correlation coefficients between the three evaluation indices (sensitivity, specificity and time to detection) and parameter values were calculated. Table 1 showed the correlation coefficients with Pearson’s r and P values. All algorithms showed strong relation between the evaluation indices and the parameter’ values, except space–time permutation scan statistic. Great majority of the correlation was statistically significant, with P values less than 0.05(two-tailed). However, for space–time permutation scan statistic, specificity showed no relation to the spatial cluster size. Only when the maximum temporal cluster size was set as 3d, both sensitivity and time to detection exhibited a significant correlation with the spatial cluster size (P < 0.05).
Table 1.
Correlation between the three evaluation indices (sensitivity, specificity and time to detection) and parameter values for five algorithms with P values#.
| Algorithms | Sensitivity |
Specificity |
Time to detection |
|||
|---|---|---|---|---|---|---|
| Pearson’s r | P value | Pearson’s r | P value | Pearson’s r | P value | |
| λ value for EWMA (k = 1.0) | — | — | 0.526 | 0.118 | −0.897 | 0.000⁎ |
| λ value for EWMA(k = 2.0) | 0.837 | 0.003⁎ | 0.684 | 0.029⁎ | −0.990 | 0.000⁎ |
| λ value for EWMA (k = 3.0) | 0.921 | 0.000⁎ | 0.780 | 0.008⁎ | −0.990 | 0.000⁎ |
| k value for C1′ (H = 3σ) | −0.918 | 0.000⁎ | 0.969 | 0.000⁎ | 0.987 | 0.000⁎ |
| k value for C1′ (H = 4σ) | −0.973 | 0.000⁎ | 0.937 | 0.000⁎ | 0.992 | 0.000⁎ |
| k value for C1′ (H = 5σ) | −0.908 | 0.000⁎ | 0.904 | 0.001⁎ | 0.995 | 0.000⁎ |
| k value for C2′ (H = 3σ) | −0.759 | 0.000⁎ | 0.982 | 0.000⁎ | 0.973 | 0.000⁎ |
| k value for C2′ (H = 4σ) | −0.907 | 0.000⁎ | 0.961 | 0.000⁎ | 0.984 | 0.000⁎ |
| k value for C2′ (H = 5σ) | −0.938 | 0.000⁎ | 0.943 | 0.001⁎ | 0.959 | 0.000⁎ |
| k value for C3′ (H = 3σ) | −0.694 | 0.004⁎ | 0.998 | 0.000⁎ | 0.956 | 0.000⁎ |
| k value for C3′ (H = 4σ) | −0.818 | 0.000⁎ | 0.994 | 0.000⁎ | 0.962 | 0.000⁎ |
| k value for C3′ (H = 5σ) | −0.866 | 0.000⁎ | 0.995 | 0.000⁎ | 0.960 | 0.000⁎ |
| Spatial cluster size for space–time permutation scan statistic (3d) | −0.958 | 0.042⁎ | — | — | 0.962 | 0.038⁎ |
| Spatial cluster size for space–time permutation scan statistic (7d) | −0.835 | 0.165 | — | — | 0.756 | 0.244 |
| Spatial cluster size for space–time permutation scan statistic (10d) | −0.746 | 0.254 | — | — | 0.538 | 0.462 |
Pearson’s r was calculated directly for those variables showing linear relation. While for those variables showing relation of log linear, Pearson’s r was calculated after applying logarithmic transformation.
P value was less than 0.05 (2-tailed).
Fig. 1, Fig. 2, Fig. 3, Fig. 4 describe the average sensitivity, specificity and time to detection of the five algorithms. The top plot of Fig. 1 shows the sensitivity versus λ values for the three control limit coefficients (k). In all of the combinations of λ and k values, the sensitivities were greater than 90%. As λ increased from 0 to 0.9, the sensitivity also increased. The middle plot of Fig. 1 shows the specificity of the three k values. Specificity of the three k values had a similar change trend by λ value, increasing until λ = 0.3, and then declining gradually. The bottom plot of Fig. 1 shows the effect of λ values on detection timeliness of EWMA. Time to detection declined gradually with the increasing λ values. Among these combinations of different λ and k values, λ = 0.9, k = 1.0 showed the shortest detection time, with a specificity of 89.5%. There were only two combination of λ and k values that had a detection time longer than half a day (λ = 0.1, k = 2.0 and λ = 0.1, k = 3.0). Out of the remaining combinations, there were 11 which had specificity greater than 89.5%. Within these 11 combinations, λ = 0.7, k = 3.0 showed the greatest specificity (97.2%). According to the evaluation criteria, we concluded that λ = 0.7, k = 3.0 was the optimal parameter for EWMA.
Fig. 1.
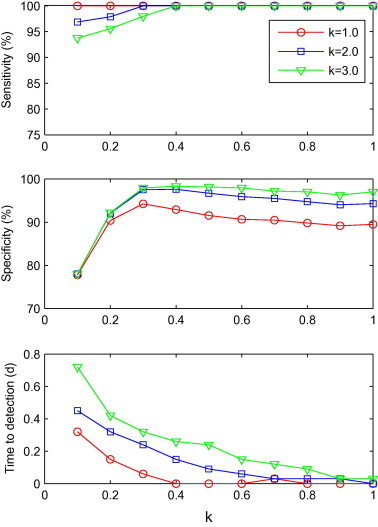
Sensitivity, specificity and time to detection for EWMA with a combination of λ and k (λ = 0.1, 0.2, ..., 1.0; k = 1.0, 2.0 and 3.0), shown from top to bottom.
Fig. 2.
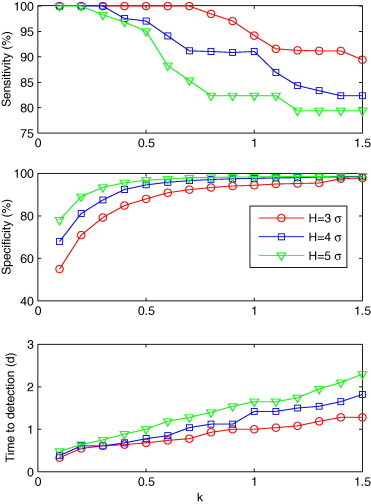
Sensitivity, specificity and time to detection for C1′ with a combination of k and H (k = 0.1, 0.2, ..., 1.5; H = 3σ, 4σ and 5σ), shown from top to bottom.
Fig. 3.
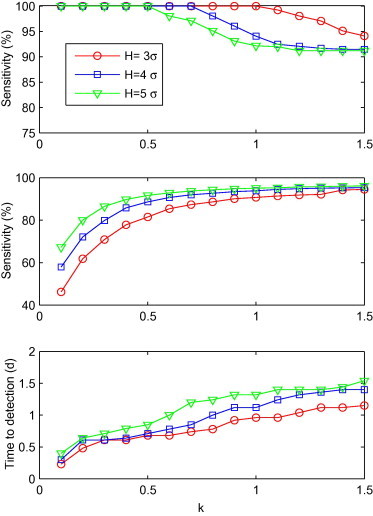
Sensitivity, specificity and time to detection for C2′ with a combination of k and H (k = 0.1, 0.2, ..., 1.5; H = 3σ, 4σ and 5σ), shown from top to bottom.
Fig. 4.
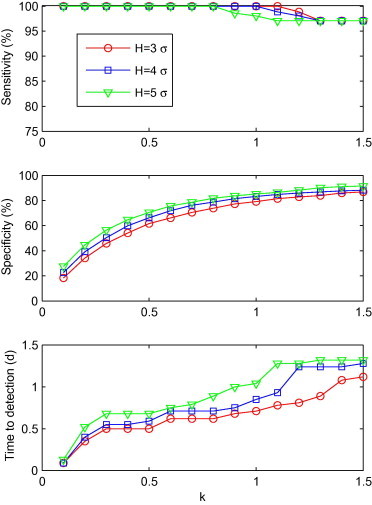
Sensitivity, specificity and time to detection for C3′ with a combination of k and H (k = 0.1, 0.2, ..., 1.5; H = 3σ, 4σ and 5σ), shown from top to bottom.
Fig. 2 shows the influence of different H and k values on sensitivity, time to detection and specificity. The sensitivity was shown to decrease as k increased. As the sensitivity decreased, time to detection increased. Among the combinations of H and k values, (H = 3σ, k = 0.1) had the shortest time to detection of 0.3 day (specificity: 55%). There were 14 combinations with a detection time of half a day longer than (H = 3σ, k = 0.1). All of these 14 combinations had specificities greater than 55%, with the highest one being 95.6%, when H = 5σ, k = 0.4. According to the evaluation criteria, (H = 5σ, k = 0.4) was found to be the optimal combination for C1′.
The relationship between performance and the combination of H and k values for C2′ is shown in Fig. 3 . We found that sensitivity declined as k increased from 0.1 to 1.5. In comparison, specificity and time to detection increased as sensitivity declined. The combination of (H = 3σ, k = 0.1) showed the shortest detection time (0.2d), with a specificity of 46.2%. Similarly, 14 combinations had a detection time which was half a day longer than (H = 3σ, k = 0.1). The specificities for all of these 14 combinations was greater than 46.2%, with the highest one recorded at 88.6%, when H = 4σ, k = 0.5. Accordingly, (H = 4σ, k = 0.5) was thought the optimal combination for C2′.
Fig. 4 shows the influence of sensitivity, time to detection and specificity of H and k values for C3′. The specificity and time to detection had an overall growth of λ value. Sensitivity declined gradually as λ increased. Among the combinations of H and k values, (H = 3σ, k = 0.1) had the shortest time to detection (0.1d), with a specificity of 18.3%. Likewise, there were 14 combinations with a detection time half a day longer than (H = 3σ, k = 0.1). 13 out of these 14 combinations had specificities greater than 18.3%, the highest one being 73.9%, when H = 3σ and k = 0.8. Consequently, (H = 3σ, k = 0.8) was thought as the optimal combination for C3′.
We found that the space–time permutation scan statistics exhibited no real difference in the specificity when the parameter combinations were changed (Table 2 ). When the maximum temporal cluster size was set as 3d and the maximum spatial cluster size of 2 km, the detection time was found to be the shortest. This combination also resulted in the highest specificity and sensitivity. Thus the optimal parameter was taken as 3d (maximum temporal cluster size) and 2 km (maximum spatial cluster size).
Table 2.
Average sensitivity, specificity and time to detection for space–time permutation scan statistics with various combinations of spatial and temporal cluster size.
| Spatial cluster size (km) | Temporal cluster size = 3d |
Temporal cluster size = 7d |
Temporal cluster size = 10d |
||||||
|---|---|---|---|---|---|---|---|---|---|
| Sensitivity (%) | Specificity (%) | Time to detection (d) | Sensitivity (%) | Specificity (%) | Time to detection (d) | Sensitivity (%) | Specificity (%) | Time to detection (d) | |
| 2 | 96.9 | 99.9 | 0.2 | 90.6 | 99.9 | 0.4 | 96.9 | 99.9 | 0.3 |
| 5 | 84.4 | 99.9 | 0.5 | 81.3 | 99.9 | 0.6 | 81.3 | 99.9 | 0.6 |
| 8 | 84.4 | 99.9 | 0.5 | 84.4 | 99.9 | 0.5 | 87.5 | 99.9 | 0.4 |
| 10 | 81.3 | 99.9 | 0.6 | 81.3 | 99.9 | 0.6 | 84.4 | 99.9 | 0.5 |
3.2. Evaluation of the algorithms
Five commonly used algorithms were evaluated by comparing the performance with their optimized parameters values. The performance of these algorithms is shown in Table 3 with P values. According to Bonferroni’s procedure, the significance level α for an individual test was calculated by dividing the family wise error rate (0.05) by four. This was found to be 0.0125. Of the algorithms evaluated, space–time permutation scan statistics had a higher average specificity than any other algorithms (P < 0.001), followed by EWMA (95.2%), while C3′ showed the lowest specificity (73.7%). EWMA had the shortest time to detection (0.1d), while C1′ showed the longest time to detection of one day. Space–time permutation scan statistics had a relatively longer time to detection compared to EWMA (0.2d), but this difference was not statistically significant (P = 0.081 > 0.0125). According to the evaluation criteria and statistical test, we could conclude that space–time permutation scan statistics was the optimal algorithm, followed by EWMA. Space–time permutation scan statistics had a specificity of 99.9%, which meant that only one false alarm occurred per 1000 days, whereas EWMA was evaluated to trigger one false alarm for every 21 days.
Table 3.
Specificity and time to detection for five algorithms based on the optimize combinations of parameter value.
| Algorithms | Specificity (%) |
Time to detection (d) |
||
|---|---|---|---|---|
| Mean | Test lower CI | Mean | Test lower CI | |
| EWMA (0.7, 3.0) | 95.2 | <0.001 | 0.1 | >0.0125 |
| C1′ (0.4, 5σ) | 95.7 | <0.001 | 1.0 | <0.001 |
| C2′ (0.5, 4σ) | 89.2 | <0.001 | 0.8 | <0.001 |
| C3′ (0.8, 3σ) | 73.7 | <0.001 | 0.7 | <0.001 |
| Space–time permutation scan statistic (3d, 2 km) ⁎ | 99.9 | — | 0.2 | — |
Space–time permutation scan served as control group. According to Bonferroni’s procedure, the family wise error rate was 0.05, divided by the number of test. The significance level α for an individual test was 0.05/4, being 0.0125.
4. Discussion
The burden of bacillary dysentery has long been thought to be great in many developing countries [30]. Detecting outbreaks in their early stages may prevent secondary infections, and subsequently an epidemic from occurring. The benefits of this extend not only to the individual, but also to the community in terms of morbidity prevented and costs saved.
From the case study in 2007, the outbreak was detected when the accumulated number of cases reached the threshold (10 cases in 3 days within the same geographic area). The problem with this method of detection is that the optimal opportunity to curb an outbreak is often missed. In the event of a pandemic influenza or another emerging inflection, missing this opportunity may have national or global implications.
We observed that the effects of the same algorithm varied significantly with different parameter values. For example, the time to detection and specificity were 73.9% and 0.6d for C3′ (H = 3σ, k = 0.8) versus 61.8% and 0.6d for C2′ (H = 3σ, k = 0.2). If the performance of C3′ and C2′ were compared with these values, C3′ (H = 3σ, k = 0.8) seemed to be better than C2′ (H = 3σ, k = 0.2) according to the evaluation criteria, which might lead to the conclusion that C3′ was more effective than C2′. In fact, C2′ (H = 4σ and k = 0.4) had a detection time of 0.6d and a specificity of 85.8%, 11.9% higher than 73.9% (C3′, H = 3σ, k = 0.8). In this case, C2′ (H = 4σ and k = 0.4) were better than C3′ (H = 3σ and k = 0.8). The difference in performance of the two algorithms is largely caused by the difference between parameters’ values. Therefore, parameter values should be optimized prior to the performance evaluation of algorithms.
A wide range of outbreak detection algorithms are available including: temporal, spatial and spatial–temporal [31]. In this study, we used both the temporal and spatial information of the reported cases. The temporal information refers to the onset date of the illness, and spatial information refers to the sub-district where the case currently resides at. CUSUM and EWMA are commonly used to analyze the temporal data, as they can be adjusted to identify a meaningful change from the expected range of data values. We calculated the daily case counts reported for each sub-district, and then judged whether the change from the expected value was significant within each sub-district. So in our study, CUSUM and EWMA can also give us both the temporal and spatial information of the signal.
Our study focused on the correlation between algorithm parameter values and their performance. By calculating the correlation coefficient and comparing the performance of different algorithms with various values, we observed a strong correlation between them. The differences in the parameter values may have resulted from a difference in the performances among these algorithms. Consequently, we recommend that before evaluating the effectiveness of an outbreak detection algorithm, parameter values should be optimized to remove the noise which has resulted from the potential influence of parameter value for a given disease.
In our study we found that space–time permutation scan statistics and the EWMA outperformed other algorithms both in terms of timeliness and accuracy for detecting bacillary dysentery outbreaks. EWMA applies weighting factors which decrease exponentially. The choice of weighting factor λ is the key for successful outbreak detection. With proper λ value, EWMA control procedure can be adjusted to be sensitive to a small or gradual drift in the process. We feel that adjusting λ value should be an imperative step before applying EWMA into practice. Space–time permutation scan statistics consider both the temporal and spatial factors. The scanning window is under dynamic change to avoid selection bias. However, space–time scan statistics do not consider population movements. In addition, space–time scan statistics can only identify clusters in simple regular shapes. If the cluster does not conform to a regular shape, the algorithm may have a poor performance. Therefore, when space–time permutation scan statistics are used to detect the outbreaks, it is imperative to understand the cluster shape. Only in the right shape, can space–time permutation scan statistics demonstrate a high detection efficacy. Aside from these limitations, the use of space–time permutation scan statistics allowed the early outbreak detection for bacillary dysentery.
Previously, Hutwagner et al. [14] compared the time to detection with simulation based on influenza like illness and pneumonia data. In her study, C1, C2 and C3 were found to have an increasing time to detection. In comparison, we found a decline in the detection time for our modified C1, C2 and C3. These differences in the time to detection calculations may explain the differences between the two studies. In our study, when the algorithms failed to detect the simulated outbreak, time to detection was set as the largest value (3 days). As we know, C1, C2 and C3 have increasing sensitivities. Obviously, as the sensitivity increased from C1 to C3, the number of missed outbreaks decreased and consequently the time to detection declined accordingly. An integrated time to detection might be recommended, in order to address this limitation [14].
Theoretically, the optimal parameter value can maximize the algorithm’s ability to detect aberration in disease incidence and minimize the probability of producing a false alarm. The balance between the accuracy and timeliness is still a matter of debate. In our study, we set simple and practical evaluation criteria’s. Considering the time to detection integrating effect of sensitivity, we simplified the three evaluation indices to two, time to detection and specificity. The former reflected both the timeliness and sensitivity, and the latter reflected the accuracy of outbreak detection. We made timeliness the priority over accuracy due to bacillary dysentery’s short incubation period and the fact that it can be both food-borne and water-borne. When deciding which index should be given the priority, practitioners should take the length of incubation, the mode of transmission and the current situation (climatic, social, demographic, economic factors, etc.) into consideration.
The variation in patterns of the evaluation indices with the change of parameter values observed in our study was found to be consistent with previous related studies [9], [12], [14], [15], [32], [33]. For example, Hutwagner et al. [14] observed that C1, C2 and C3 had increasing sensitivity, but a decreasing specificity as the sensitivity increased. In our study, we also observed this change in sensitivity and specificity in our modified C1′, C2′ and C3′. In our study we observed a growth in sensitivity and specificity as weighing values increased from 0 to 0.3. It seemed that the range of weighting values from 0.4 to 0.9 enabled a better performance. This recommendation was also made by Jackson et al. [15], who suggested weighing values of 0.4 and 0.9 for EWMA.
There are several factors which may limit the generalization of our findings. To apply these five algorithms, information on the specific setting (workplaces, schools etc.) is often required. This information is usually not available in the current National Disease Surveillance Reporting and Management System in China. Consequently, the sensitivity of the five algorithms may be less when a bacillary dysentery outbreak occurs in a school, as the cases may be scattered in different sub-districts. It is therefore important to collect extra information on workplaces, schools and other units. Due to a lack of actual outbreaks, we injected simulated outbreaks into the baseline so we could undertake a performance assessment on these outbreak detection algorithms. We changed the size, magnitude, temporal progressive pattern, season and spatial distribution of bacillary dysentery, in order to have a variety of outbreak conditions to test. As these are approximations, it is difficult to evaluate how close our simulations came to the actual outbreak. Consequently, further research is needed in predicting the actual performance of these algorithms.
Acknowledgments
Funded by: Beijing Natural Science Foundation (7082047), Program for Excellent Talents in Beijing of China (0302600112) and National High Technology Research and Development Program of China (2008AA02Z416).
Dr. Xiaoli Wang is a public health doctor from the Institute for Infectious Diseases of Beijing Center for Disease Prevention and Control and Capital Medical University School of Public Health and Family Medicine.
References
- 1.Seto W.H., Tsang D., Yung R.W., Ching T.Y., Ng T.K., Ho M. Advisors of Expert SgoHA, Yung RWH, Peiris JSM. Effectiveness of precautions against droplets and contact in prevention of nosocomial transmission of severe acute respiratory syndrome (SARS) Lancet. 2003;361:1519–1520. doi: 10.1016/S0140-6736(03)13168-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Kleinman K.P., Abrams A.M., Kulldorff M., Platt R. A model-adjusted space–time scan statistic with an application to syndromic surveillance. Epidemiol Infect. 2005;133:409–419. doi: 10.1017/s0950268804003528. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Hutwagner L., Thompson W., Seeman G.M., Treadwell T. The bioterrorism preparedness and response Early Aberration Reporting System (EARS) J Urban Health. 2003;80:i89–i96. doi: 10.1007/PL00022319. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Yih W.K., Caldwell B., Harmon R., Kleinman K., Lazarus R., Nelson A. National bioterrorism syndromic surveillance demonstration program. MMWR Morb Mortal Wkly Rep. 2004;53(Suppl.):43–49. [PubMed] [Google Scholar]
- 5.Yih K.W., Abrams A., Danila R., Green K., Kleinman K., Kulldorff M. Ambulatory-care diagnoses as potential indicators of outbreaks of gastrointestinal illness – Minnesota. MMWR Morb Mortal Wkly Rep. 2005;54(Suppl.):157–162. [PubMed] [Google Scholar]
- 6.Wong W.K., Moore A., Cooper G., Wagner M. WSARE: what’s strange about recent events? J Urban Health. 2003;80:i66–i75. doi: 10.1007/PL00022317. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Reis B.Y., Mandl K.D. Time series modeling for syndromic surveillance. BMC Med Inform Decis Mak. 2003;3:2. doi: 10.1186/1472-6947-3-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Lewis M.D., Pavlin J.A., Mansfield J.L., O’Brien S., Boomsma L.G., Elbert Y. Disease outbreak detection system using syndromic data in the greater Washington DC area. Am J Prev Med. 2002;23:180–186. doi: 10.1016/s0749-3797(02)00490-7. [DOI] [PubMed] [Google Scholar]
- 9.Mandl K.D., Reis B., Cassa C. Measuring outbreak-detection performance by using controlled feature set simulations. MMWR Morb Mortal Wkly Rep. 2004;53(Suppl.):130–136. [PubMed] [Google Scholar]
- 10.Siegrist D., Pavlin J. Bio-ALIRT biosurveillance detection algorithm evaluation. MMWR Morb Mortal Wkly Rep. 2004;53(Suppl.):152–158. [PubMed] [Google Scholar]
- 11.Buckeridge D.L., Owens D.K., Switzer P., Frank J., Musen M.A. Evaluating detection of an inhalational anthrax outbreak. Emerg Infect Dis. 2006;12:1942–1949. doi: 10.3201/eid1212.060331. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Buckeridge D.L., Switzer P., Owens D., Siegrist D., Pavlin J., Musen M. An evaluation model for syndromic surveillance: assessing the performance of a temporal algorithm. MMWR Morb Mortal Wkly Rep. 2005;54(Suppl.):109–115. [PubMed] [Google Scholar]
- 13.Fricker R.D., Jr., Hegler B.L., Dunfee D.A. Comparing syndromic surveillance detection methods: EARS’ versus a CUSUM-based methodology. Stat Med. 2008;27:3407–3429. doi: 10.1002/sim.3197. [DOI] [PubMed] [Google Scholar]
- 14.Hutwagner L., Browne T., Seeman G.M., Fleischauer A.T. Comparing aberration detection methods with simulated data. Emerg Infect Dis. 2005;11:314–316. doi: 10.3201/eid1102.040587. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Jackson M.L., Baer A., Painter I., Duchin J. A simulation study comparing aberration detection algorithms for syndromic surveillance. BMC Med Inform Decis Mak. 2007;7:6. doi: 10.1186/1472-6947-7-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Kleinman K.P., Abrams A., Mandl K., Platt R. Simulation for assessing statistical methods of biologic terrorism surveillance. MMWR Morb Mortal Wkly Rep. 2005;54(Suppl.):101–108. [PubMed] [Google Scholar]
- 17.Lumley T., Sebestyen K., Lober W.B., Painter I. An open source environment for the statistical evaluation of outbreak detection methods. AMIA Annu Symp Proc. 2005:1037. [PMC free article] [PubMed] [Google Scholar]
- 18.Watkins R.E., Eagleson S., Hall R.G., Dailey L., Plant A.J. Approaches to the evaluation of outbreak detection methods. BMC Public Health. 2006;6:263. doi: 10.1186/1471-2458-6-263. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Gao T., Liu G.R., Li X.Y., Jia L., Liu Y., YW T. Analysis about epidemic situation of dysentery in near upon fourteen years in Beijing. Chin J Prev Med. 2007;41:54–57. [PubMed] [Google Scholar]
- 20.Ma J.Q., Wang L.P., Qi X.P., Shi X.M., Yang G.H. Conceptual model for automatic early warning information system of infectious diseases based on internet reporting surveillance system. Biomed Environ Sci. 2007;20:208–211. [PubMed] [Google Scholar]
- 21.China MoHotpsro. National Protocol for Information Reporting and Management of Public Health Emergencies (Trial); 2005.
- 22.Cassa C.A., Iancu K., Olson K.L., Mandl K.D. A software tool for creating simulated outbreaks to benchmark surveillance systems. BMC Med Inform Decis Mak. 2005;5:22. doi: 10.1186/1472-6947-5-22. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Linnet K. The exponentially weighted moving average (EWMA) rule compared with traditionally used quality control rules. Clin Chem Lab Med. 2006;44:396–399. doi: 10.1515/CCLM.2006.077. [DOI] [PubMed] [Google Scholar]
- 24.Benneyan J.C. Statistical quality control methods in infection control and hospital epidemiology, part I: introduction and basic theory. Infect Control Hosp Epidemiol. 1998;19:194–214. doi: 10.1086/647795. [DOI] [PubMed] [Google Scholar]
- 25.Carpenter T.E. Evaluation and extension of the cusum technique with an application to Salmonella surveillance. J Vet Diagn Invest. 2002;14:211–218. doi: 10.1177/104063870201400304. [DOI] [PubMed] [Google Scholar]
- 26.Sibanda T., Sibanda N. The CUSUM chart method as a tool for continuous monitoring of clinical outcomes using routinely collected data. BMC Med Res Methodol. 2007;7:46. doi: 10.1186/1471-2288-7-46. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Kulldorff M., Athas W.F., Feurer E.J., Miller B.A., Key C.R. Evaluating cluster alarms: a space–time scan statistic and brain cancer in Los Alamos, New Mexico. Am J Public Health. 1998;88:1377–1380. doi: 10.2105/ajph.88.9.1377. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Kulldorff M., Heffernan R., Hartman J., Assuncao R., Mostashari F. A space–time permutation scan statistic for disease outbreak detection. PLoS Med. 2005;2:e59. doi: 10.1371/journal.pmed.0020059. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Ludbrook J. Multiple comparison procedures updated. Clin Exp Pharmacol Physiol. 1998;25:1032–1037. doi: 10.1111/j.1440-1681.1998.tb02179.x. [DOI] [PubMed] [Google Scholar]
- 30.von Seidlein L., Kim D.R., Ali M., Lee H., Wang X., Thiem V.D., Canhdo G., Chaicumpa W., Agtini M.D., Hossain A., Bhutta Z.A., Mason C., Sethabutr O., Talukder K., Nair G.B., Deen J.L., Kotloff K., Clemens J. A multicentre study of Shigella diarrhoea in six Asian countries: disease burden, clinical manifestations, and microbiology. PLoS Med. 2006;3:e353. doi: 10.1371/journal.pmed.0030353. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Buckeridge D.L., Burkom H., Campbell M., Hogan W.R., Moore A.W. Algorithms for rapid outbreak detection: a research synthesis. J Biomed Inform. 2005;38:99–113. doi: 10.1016/j.jbi.2004.11.007. [DOI] [PubMed] [Google Scholar]
- 32.Hutwagner L.C., Thompson W.W., Seeman G.M., Treadwell T. A simulation model for assessing aberration detection methods used in public health surveillance for systems with limited baselines. Stat Med. 2005;24:543–550. doi: 10.1002/sim.2034. [DOI] [PubMed] [Google Scholar]
- 33.Besculides M., Heffernan R., Mostashari F., Weiss D. Evaluation of school absenteeism data for early outbreak detection, New York City. BMC Public Health. 2005;5:105. doi: 10.1186/1471-2458-5-105. [DOI] [PMC free article] [PubMed] [Google Scholar]


