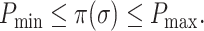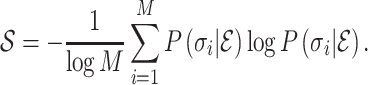Abstract
Spatial spread of infectious diseases among populations via the mobility of humans is highly stochastic and heterogeneous. Accurate forecast/mining of the spread process is often hard to be achieved by using statistical or mechanical models. Here we propose a new reverse problem, which aims to identify the stochastically spatial spread process itself from observable information regarding the arrival history of infectious cases in each subpopulation. We solved the problem by developing an efficient optimization algorithm based on dynamical programming, which comprises three procedures: 1) anatomizing the whole spread process among all subpopulations into disjoint componential patches; 2) inferring the most probable invasion pathways underlying each patch via maximum likelihood estimation; and 3) recovering the whole process by assembling the invasion pathways in each patch iteratively, without burdens in parameter calibrations and computer simulations. Based on the entropy theory, we introduced an identifiability measure to assess the difficulty level that an invasion pathway can be identified. Results on both artificial and empirical metapopulation networks show the robust performance in identifying actual invasion pathways driving pandemic spread.
Keywords: Identifiability, infectious diseases, metapopulation, networks, process identification, spatial spread
I. Introduction
The frequent outbreaks of emerging infectious diseases in recent decades lead to great social, economic, and public health burdens [1]–[3]. This trend is partially due to the urbanization process and, in particular, the establishment of long-distance traffic networks, which facilitate the dissemination of pathogens accompanied with passengers [4], [5]. Real-world examples include the transnational spread of severe acute respiratory syndrome (SARS)-coronavirus in 2003 [6], the global outbreak of A (H1N1) pandemic flu in 2009 [7], [8], avian influenza in Southeast Asia [9], [10], the spark of Ebola infections in western countries in 2014 [11], and recent potential outbreak of middle east respiratory syndrome [12].
During almost the same epoch, the theory of complex networks has been developed as a valuable tool for modeling the structure and dynamics of/on complex systems [13]–[16]. In the study of network epidemiology, networks are often used to describe the epidemic spreading from human to human via contacts, where nodes represent persons and edges represent interpersonal contacts [17]–[22]. To characterize the spatial spread between different geo-locations, simple network models are generalized with metapopulation framework, in which each node represents a population of individuals that reside at the same geo-region (e.g., a city), and the edge describes the traffic route that drives the individual mobility between populations [18], [19]. The networked metapopulation models have been applied to study the real-world cases such as SARS [6], A (H1N1) pandemic flu [23], and Ebola [11], which can capture some key dynamic features including peak times, basic epidemic curves, and epidemic sizes. Quantitative model results can be used to evaluate the effectiveness of control strategies [24]–[28], such as optimizing the vaccine allocation.
The numerical computing of large-scale metapopulation models is time-consuming, because of the requirement of high-level computer power. The model calibrations need high-resolution data for incidence cases, which may not be available or accurate during the early weeks of initial outbreaks [4]. Hence, continuous model training with data collected in real-time is essential in achieving a reliable model prediction [29]. Generally, model results are the ensemble average over numerous simulation realizations, which aims to predict the mean and variance of epidemic curves, while in reality there is no such thing described by the average over different realizations [30]. To extract more meaningful information from epidemic data generated by surveillance systems, recent studies (particularly in engineering fields) start paying attention to reverse problems, such as source detection and network reconstruction, which are briefly summarized here.
A. Related Works
The theory of system identification has been established in engineering fields, usually used to infer system parameters. The use of system identification in epidemiology mainly focuses on inferring epidemic parameters, such as the transmission rate and generation time [31], which relies on constructing dynamical systems of ordinary differential equations. The methodology of system identification is not helpful in solving high-dimensional stochastic many-body systems, such as metapopulation models.
Source detection for rumor spreading on complex networks is becoming a popular topic, attracting extensive discussions in recent years. The target is to figure out the causality that can trigger the explosive dissemination across social networks, such as Facebook, Twitter, and Weibo. For example, using maximum likelihood (ML) estimators, Shah and Zaman [32] proposed the concept of rumor centrality that quantifies the role of nodes in network spreading. Luo et al. [33] designed new estimators to infer infection sources and regions in large networks. Wang et al. [34], [36] and Dong et al. [35] extended the scope by using multiple observations, which largely improves the detection accuracy. Another interesting topic is the network inference, which engages in revealing the topology structure of a network from the hint underlying the dynamics on a network [37]. Some useful algorithms (e.g., NetInf) have been proposed in [38]–[42]. Note that the algorithms for source detection and network inference are not feasible in identifying the spreading processes on metapopulation networks.
Using metapopulation networks models, some heuristic measures have been proposed to understand the spatial spread of infectious diseases, which are most related to this paper. Gautreau et al. [30] developed an approximation for the mean first arrival time between populations that have direct connection, which can be used to construct the shortest path tree (SPT) that characterizes the average transmission pathways among populations. Brockmann and Helbing [4] proposed a measure called “effective distance,” which can also be used to build the SPT. Using a different method based on the ML, Balcan et al. [43] generated the transmission pathways by extracting the minimum spanning tree from extensive Monte Carlo simulation results. Details about these measures will be given in Section IV, which compares the algorithmic performance.
B. Motivation
Current algorithms to inferring pandemic spatial spread generally make use of the topology features of metapopulation networks or extensive epidemic simulations. The resulting outcome is an ensemble average over all possible transmission pathways, which may fail in capturing those indeed transmitting the disease between populations, because of the high-level stochasticity and heterogeneity in the spreading process.
Good news comes from the development of modern sentinel and Internet-based surveillance systems, which becomes increasingly popular in guiding public health control strategies. Such systems can or will provide high-resolution, location-specific data on human and poultry cases [44]. Human mobility data are also available from mass transportation systems or GPS-based mobile Apps [3]. Integrating these data often used in different fields, a natural reverse problem poses itself, which is the central interest of this paper: is it probable to design an efficient algorithm to identify or retrospect the stochastic pandemic spatial spread process among populations by linking epidemic data and models.
C. Our Contributions
Main contributions of this paper are as follows.
-
1)
A novel reverse problem of identifying the stochastic pandemic spatial spread process on metapopulation networks is proposed, which cannot be solved by existing techniques.
-
2)
An efficient algorithm based on dynamical programming is proposed to solve the problem, which comprises three procedures. First, the whole spread process among all populations will be decomposed into disjoint componential patches, which can be categorized into four types of invasion cases (INCs). Then, since two types of INCs contain hidden pathways, an optimization approach based on the ML estimation is developed to infer the most probable invasion pathways underlying each path. Finally, the whole spread process will be recovered by assembling the invasion pathways of each patch chronologically, without burdens in parameter calibrations and computer simulations.
-
3)
An entropy-based measure called identifiability is introduced to depict the difficulty level an INC can be identified. Comparisons on both artificial and empirical networks show that our algorithm outperforms the existing methods in accuracy and robustness.
The remaining sections are organized as follows. Section II provides the preliminary definitions and problem formulation. Section III describes the procedures of our identification algorithm, and introduces the identifiability measure. Section IV performs computer experiments to compare the performance of algorithms. Section V gives the conclusion.
II. Preliminary and Problem Formulation
This section first elucidates the structure of networked metapopulation model, and then provides the preliminary definitions and problem formulation.
A. Networked Metapopulation Model
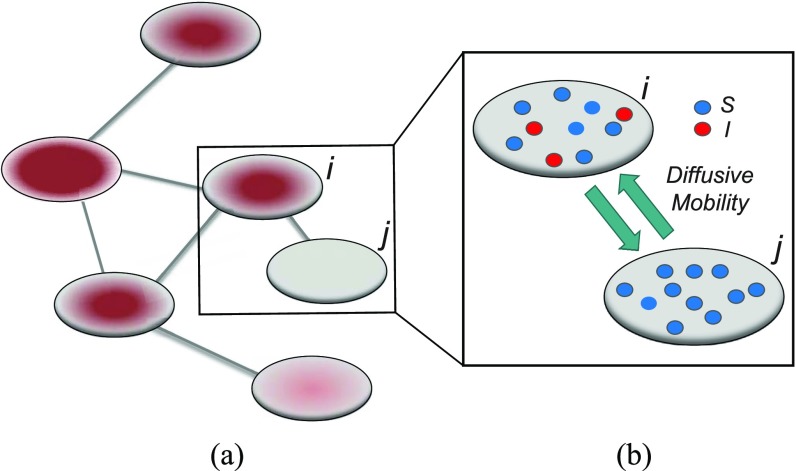
In the networked metapopulation model, individuals are organized into social units such as counties and cities, defined as subpopulations, which are interconnected by traffic networks of transportation routes. The disease prevails in each subpopulation due to interpersonal contacts, and spreads between subpopulations via the mobility of infected persons. Fig. 1 illustrates the model structure.
Fig. 1.

Illustration of a networked metapopulation model, which comprises six subpopulations/patches that are coupled by the mobility of individuals. In each subpopulation, each individual can be in one of two disease statuses (i.e., susceptible and infectious), shown in different colors. Each individual can travel between connected subpopulation. (a) Networked metapopulation. (b) Two subpopulations.
Within each subpopulation, individuals mix homogeneously. This assumption is partially supported by recent empirical findings on intraurban human mobility patterns [19], [45]–[48]. The intrapopulation epidemic dynamics are characterized by compartment models. Considering the wide applications in describing the spread of pathogens, species, rumors, emotion, behavior, crisis, etc. [32], [33], [35], [49], we used the susceptible-infected (SI) model in this paper. Define 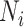 as the population size of each subpopulation
as the population size of each subpopulation 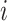 ,
,  the number of infected cases in subpopulation
the number of infected cases in subpopulation 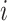 at time
at time 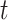 ,
, 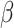 the transmission rate that an infected host infects a susceptible individual shared the same location in unit time. As such, the risk of infection within subpopulation
the transmission rate that an infected host infects a susceptible individual shared the same location in unit time. As such, the risk of infection within subpopulation 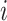 at time
at time 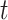 is characterized by
is characterized by 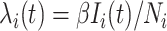 . Per unit time, the number of individuals newly infected in subpopulation
. Per unit time, the number of individuals newly infected in subpopulation 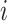 can be calculated from a binomial distribution with probability
can be calculated from a binomial distribution with probability 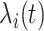 and trails equalling the number of susceptible persons
and trails equalling the number of susceptible persons 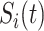 .
.
The mobility of individuals among subpopulations is conceptually described by diffusion dynamics, 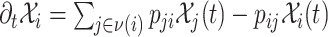 , where
, where 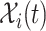 is a placeholder for
is a placeholder for 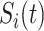 or
or 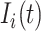 ,
, 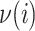 is the set of subpopulations directly connected with subpopulation
is the set of subpopulations directly connected with subpopulation 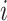 , and
, and 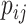 is the per capita mobility rate from subpopulation
is the per capita mobility rate from subpopulation 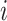 to
to 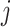 , which equals the ratio between the daily flux of passengers from subpopulation
, which equals the ratio between the daily flux of passengers from subpopulation 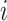 to
to 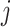 and the population size of departure subpopulation
and the population size of departure subpopulation 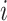 . The ensemble of mobility rates
. The ensemble of mobility rates 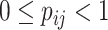 defines a transition matrix
defines a transition matrix 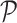 , determined by the topology structure and traffic fluxes of the mobility network. The interpopulation mobility of individuals is simulated with binomial or multinomial process (Appendix A). For more details in modeling rules, refer to [19].
, determined by the topology structure and traffic fluxes of the mobility network. The interpopulation mobility of individuals is simulated with binomial or multinomial process (Appendix A). For more details in modeling rules, refer to [19].
B. Basic Definitions
The epidemic arrival time (EAT) is the first arrival time of infectious hosts traveling to a susceptible subpopulation. At a given EAT, at least an unaffected (susceptible) subpopulation will be contaminated, characterizing the occurrence of invasion events. Herein, S (I) denotes a (an) susceptible (infected) subpopulation.
For an invasion event, organizing newly contaminated subpopulations (remaining unaffected prior to that invasion event) into set 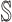 , and infected subpopulations into set
, and infected subpopulations into set 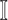 , we define the four types of INC as follows.
, we define the four types of INC as follows.
-
1)
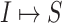 :
: 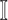 and
and 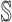 both are composed of a single subpopulation respectively, which represents that a previously unaffected subpopulation is infected by the new arrival of infectious host(s) from its unique neighboring infected subpopulation.
both are composed of a single subpopulation respectively, which represents that a previously unaffected subpopulation is infected by the new arrival of infectious host(s) from its unique neighboring infected subpopulation. -
2)
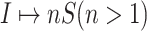 : In this case,
: In this case, 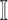 only consists of a single subpopulation, while
only consists of a single subpopulation, while 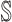 contains
contains 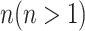 subpopulations. This represents that
subpopulations. This represents that 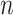 previously unaffected subpopulations are contaminated due to the new arrival of infectious hosts from their common infected subpopulation in
previously unaffected subpopulations are contaminated due to the new arrival of infectious hosts from their common infected subpopulation in 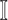 .
. -
3)
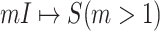 :
: 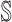 only consists of a single subpopulation, and
only consists of a single subpopulation, and 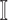 contains
contains 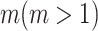 subpopulations. This means that the newly infected subpopulation in
subpopulations. This means that the newly infected subpopulation in 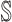 is infected by the arrival of infected host(s) from
is infected by the arrival of infected host(s) from 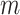 potential upstream subpopulations in
potential upstream subpopulations in 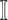 through the invasion edges.
through the invasion edges. -
4)
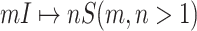 : In this case,
: In this case, 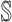 and
and 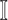 both are composed of no less than two subpopulations, and they constitute a connected subgraph. Each previously unaffected subpopulation in
both are composed of no less than two subpopulations, and they constitute a connected subgraph. Each previously unaffected subpopulation in 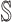 is contaminated due to the simultaneous arrival of infected hosts from
is contaminated due to the simultaneous arrival of infected hosts from 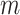 potential source subpopulations in
potential source subpopulations in 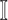 . Each subpopulation in
. Each subpopulation in 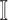 may lead to the contamination of at least one but no more than
may lead to the contamination of at least one but no more than 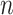 neighboring downstream subpopulations in
neighboring downstream subpopulations in  through the invasion edges. Multiple edges between any pair of subpopulations are forbidden.
through the invasion edges. Multiple edges between any pair of subpopulations are forbidden.
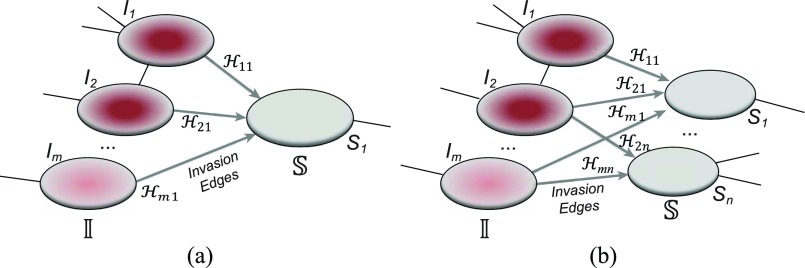
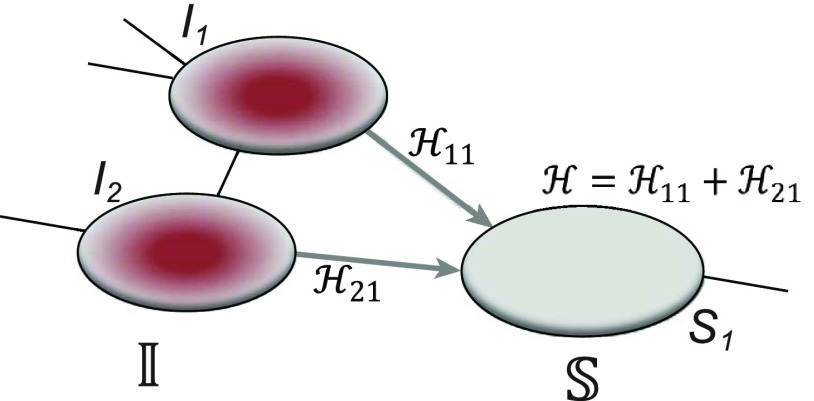
Fig. 2(a) and (b) illustrates the two scenarios of 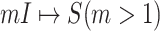 and
and 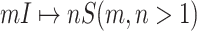 . A decomposition procedure of invasion partition (INP) is used to generate the components of INCs in each invasion event. The heuristic search algorithm to proceed the INP is given in Algorithm 1 if an invasion event occurs.
. A decomposition procedure of invasion partition (INP) is used to generate the components of INCs in each invasion event. The heuristic search algorithm to proceed the INP is given in Algorithm 1 if an invasion event occurs.
Fig. 2.
(a) Example of the 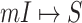 INC, in which
INC, in which 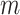 infected subpopulations invade one susceptible subpopulation. The red patches denote the infected subpopulations, while the plain patch is the subpopulation that remains susceptible before time
infected subpopulations invade one susceptible subpopulation. The red patches denote the infected subpopulations, while the plain patch is the subpopulation that remains susceptible before time 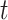 but will be contaminated during that time step due to the arrival of infectious cases from upstream infected subpopulations. (b) Example of the
but will be contaminated during that time step due to the arrival of infectious cases from upstream infected subpopulations. (b) Example of the 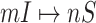 INC, in which
INC, in which 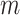 infected subpopulations invade
infected subpopulations invade 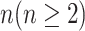 susceptible subpopulations.
susceptible subpopulations.
Algorithm 1 INP
-
1:
for an invasion event, collect all newly infected
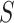 as initially
as initially 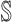 and their previously infected neighbors as
and their previously infected neighbors as 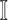 ;
; -
2:
start with an arbitrary element
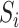 in set
in set 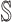 ;
; -
3:
find all neighbors
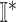 of
of 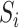 in set
in set 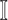 ;
; -
4:
find the new neighbors
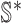 in the
in the 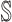 if have;
if have; -
5:
find the new neighbors in the
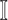 if have;
if have; -
6:
repeat the above two steps until cannot find any new neighbors in
 and
and 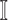 , we get an INC consisting of
, we get an INC consisting of 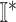 and
and 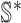 , then update the
, then update the 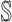 and
and 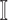 ;
; -
7:
repeat the 2-6 steps to get new INCs until there are no elements in
 .
.
C. Problem Formulation
Suppose that the spread starts at an infected subpopulation. It forms the invasion pathways when this source invades many susceptible subpopulations and the cascading invasion goes on. We record the infected individuals of each subpopulation per unit time. From the data, we should know when a subpopulation is infected and how many infected individuals in this subpopulation, but we may not know which infected subpopulations invade this subpopulation if it has (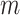 ,
, 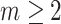 ) infected neighbor subpopulations through the corresponding edge(s) [see Fig. 2(a)] at that time step. The question of interest is how to identify the instantaneous spatial invasion process just according to the surveillance data. Herein, we know the network topology including subpopulation size and travel flows, such as the city populations of airports and travelers by an airline of the real network of American airports network (ANN).
) infected neighbor subpopulations through the corresponding edge(s) [see Fig. 2(a)] at that time step. The question of interest is how to identify the instantaneous spatial invasion process just according to the surveillance data. Herein, we know the network topology including subpopulation size and travel flows, such as the city populations of airports and travelers by an airline of the real network of American airports network (ANN).
Define an invasion pathway which are the directed edges that infected individuals invade to susceptible subpopulations at EAT. To identify it, we proceed the following invasion pathways identification (IPI) algorithm.
-
1)Decompose the whole pathways as four types of INCs by the INP at each EAT; suppose the whole invasion pathways
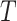 are anatomized into
are anatomized into 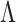 of four INCs. Let
of four INCs. Let 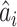 denote the identified invasion pathways based on the surveillance data
denote the identified invasion pathways based on the surveillance data 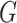 of that INC
of that INC 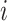 and the given graph
and the given graph 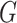 . According to the (stochastic) dynamic programming, we have the following equation to optimally solve this problem:
. According to the (stochastic) dynamic programming, we have the following equation to optimally solve this problem: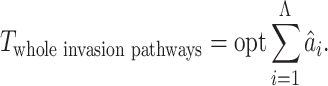
-
2)For each INC, we first judge whether it has a unique set of invasion pathways or more than one potential invasion pathways. When an INC has more than one possible invasion pathway, each set of which is called potential invasion pathway. If it has more than one potential invasion pathway, we estimate the true invasion pathways
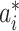 , denoted by
, denoted by 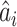 , based on the surveillance data
, based on the surveillance data 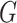 of that INC and the given graph
of that INC and the given graph 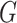 . A potential pathway belonged to that INC is denoted by
. A potential pathway belonged to that INC is denoted by 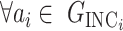 . To make this estimation, we shall compute the likelihood of a potential invasion pathway
. To make this estimation, we shall compute the likelihood of a potential invasion pathway 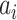 . With respect to this setting, the ML estimator of
. With respect to this setting, the ML estimator of 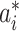 with respect to the networked metapopulation model given by that INC maximizes the correct identification probability. Therefore, we define the ML estimator
with respect to the networked metapopulation model given by that INC maximizes the correct identification probability. Therefore, we define the ML estimator
where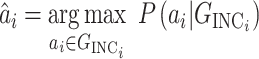
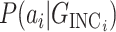 is the likelihood of observing the potential pathway
is the likelihood of observing the potential pathway 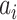 assuming it is the true pathway
assuming it is the true pathway 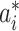 . Thus we would like to evaluate
. Thus we would like to evaluate 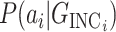 for all
for all 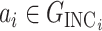 and then choose the maximal one.
and then choose the maximal one.
III. Identification Algorithm to Invasion Pathway
According to our above INP decompose algorithm, it is easy to identify the invasion pathways for the INC scenario 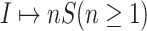 (they have the only invasion pathway from their neighbor infected subpopulation). Thus our invasion pathways’ identification algorithm mainly deals with the other two kinds of INCs
(they have the only invasion pathway from their neighbor infected subpopulation). Thus our invasion pathways’ identification algorithm mainly deals with the other two kinds of INCs 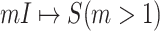 and
and 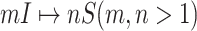 . To make the description clear, we restate the term
. To make the description clear, we restate the term 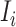 denotes subpopulation
denotes subpopulation 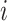 which is infected, and its number of infected individuals of
which is infected, and its number of infected individuals of  at time
at time 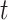 is denoted by
is denoted by 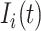 .
.
As time evolves, infected hosts travel among subpopulations, inducing the spatial pandemic dispersal. For each INC, by analyzing the variance of infected hosts in each subpopulation 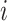 , we define three levels of extent of subpopulations observability to reflect the information held for the inference of relevant invasion pathway.
, we define three levels of extent of subpopulations observability to reflect the information held for the inference of relevant invasion pathway.
-
1)
Observable Subpopulation: Subpopulation
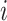 is observable during an INC, given the occurrence of the three most evident (subpopulation’s) status transitions. The first refers to the transition
is observable during an INC, given the occurrence of the three most evident (subpopulation’s) status transitions. The first refers to the transition 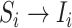 , accounting that the previously unaffected subpopulation
, accounting that the previously unaffected subpopulation 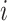 is contaminated during that INC due to the arrival of infected hosts. The second concerns the transition
is contaminated during that INC due to the arrival of infected hosts. The second concerns the transition 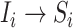 , in which the previously infected subpopulation
, in which the previously infected subpopulation 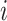 becomes susceptible again during that INC, since the infected hosts do not trigger a local outbreak and leave
becomes susceptible again during that INC, since the infected hosts do not trigger a local outbreak and leave 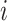 . In the third transition
. In the third transition 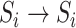 , despite of having infected subpopulations in the neighborhood, subpopulation
, despite of having infected subpopulations in the neighborhood, subpopulation  remains unaffected during that INC due to no arrival of infected hosts. Fig. 3(a) illustrates such observable transitions.
remains unaffected during that INC due to no arrival of infected hosts. Fig. 3(a) illustrates such observable transitions. -
2)
Partially Observable Subpopulation: Subpopulation
 is partially observable during an INC occurring at time
is partially observable during an INC occurring at time 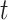 , if its number of infected hosts is decreased, i.e.,
, if its number of infected hosts is decreased, i.e., 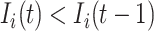 and
and  , which implies that at least
, which implies that at least 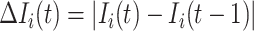 infected hosts leave
infected hosts leave 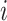 during that INC. It is impossible to distinguish their mobility destinations unless the INC
during that INC. It is impossible to distinguish their mobility destinations unless the INC 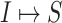 or
or 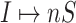 occurs. Fig. 3(b) illustrates the partially observable subpopulation.
occurs. Fig. 3(b) illustrates the partially observable subpopulation. -
3)
Unobservable Subpopulation: Subpopulation
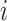 is unobservable during an INC occurring at time
is unobservable during an INC occurring at time  , if its number of infected hosts has not been decreased, i.e.,
, if its number of infected hosts has not been decreased, i.e., 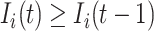 , considering the difficulty in judging whether there present infected hosts leaving subpopulation
, considering the difficulty in judging whether there present infected hosts leaving subpopulation 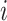 during that INC [see Fig. 3(c) for an illustration].
during that INC [see Fig. 3(c) for an illustration].
Fig. 3.

Illustration of neighbors classification in terms of status transitions: (a) Observable 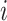 . (b) Partially observable
. (b) Partially observable  . (c) Unobservable
. (c) Unobservable 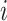 .
.
We further categorize the edges emanated from each infected subpopulation in set 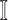 into four types, i.e., invasion edges, observable edges, partially observable edges, and unobservable edges.
into four types, i.e., invasion edges, observable edges, partially observable edges, and unobservable edges.
-
1)
Invasion Edges: In an INC, invasion edges represent each route emanated from subpopulation
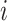 in
in 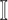 to subpopulation
to subpopulation 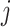 in
in 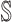 . They are considered as a unique category, because invasion edges contain all invasion pathway (an invasion pathway must be an invasion edge, but an invasion edge may not an invasion pathway). In Fig. 2(a) and (b), the invasion edges are illustrated. The following three types of edges are not belong to the routes between sets
. They are considered as a unique category, because invasion edges contain all invasion pathway (an invasion pathway must be an invasion edge, but an invasion edge may not an invasion pathway). In Fig. 2(a) and (b), the invasion edges are illustrated. The following three types of edges are not belong to the routes between sets 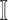 and
and  , but they are the edges emanated from
, but they are the edges emanated from 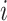 to subpopulation
to subpopulation 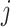 that is not belong to
that is not belong to 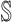 .
. -
2)
Observable Edges: For infected subpopulation
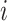 in
in 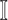 , any edge emanated from
, any edge emanated from 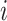 is observable, if it connects
is observable, if it connects 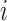 with observable subpopulation
with observable subpopulation 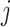 that only experiences the transition
that only experiences the transition 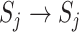 or
or 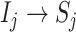 from
from 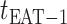 to
to 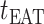 . Here, it is intuitive that in subpopulation
. Here, it is intuitive that in subpopulation 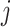 there is no arrival of infected hosts from subpopulation
there is no arrival of infected hosts from subpopulation 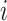 .
. -
3)
Partially Observable Edges: For infected subpopulation
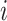 in
in 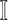 , any edge is partially observable, if it connects
, any edge is partially observable, if it connects 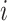 with a partially observable subpopulation.
with a partially observable subpopulation. -
4)
Unobservable Edges: For infected subpopulation
 in
in  , any edge is unobservable, if it connects
, any edge is unobservable, if it connects 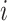 with an unobservable subpopulation.
with an unobservable subpopulation.
The classification of subpopulations and edges are used to compute the corresponding subpopulation’s transferring estimator in Section III of both INCs of 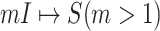 and
and 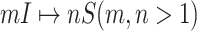 .
.
A. Case of 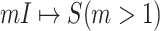
As shown in Fig. 2(a), a typical INC 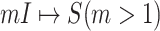 is composed of two sets of subpopulations, i.e., the previously infected subpopulations
is composed of two sets of subpopulations, i.e., the previously infected subpopulations 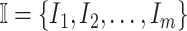 and the previously unaffected subpopulation
and the previously unaffected subpopulation 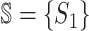 . Suppose that subpopulation
. Suppose that subpopulation 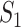 is contaminated at time
is contaminated at time 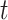 due to the appearance of
due to the appearance of 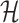 infected hosts (
infected hosts (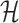 is a positive integer number) that come from the potential sources in
is a positive integer number) that come from the potential sources in 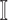 . If the actual number of infected hosts from subpopulation
. If the actual number of infected hosts from subpopulation 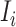 is
is 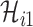 ,
, 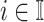 , we have
, we have
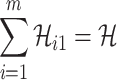 |
with the conditions 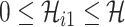 and
and 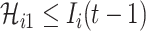 .
.
1). Accurate Identification of Invasion Pathway:
Given a few satisfied prerequisites, (3) can has a unique solution, which implies that the invasion pathways of that INC can be identified accurately. Theorem 1 elucidates this scenario.
Theorem 1 (Accurate Identification of Invasion Pathway):
With the following conditions: 1) among
possible sources illustrated in set
, there are only
partially observable subpopulations
, whose neighboring subpopulations (excluding the invasion destination
) only experience the transition
to
or
to
at that EAT and 2)
, the invasion pathway of an INC
can be identified accurately.
Proof:
According to the definition of observability, in an INC, the number of local infected hosts in an involved partially observable source
will be decreased by [
] due to their departure. If the subpopulations in the neighborhood of
only experience the transition of
to
or
to
from
to
, they are impossible to receive the infected hosts from subpopulation
. Therefore, the newly contaminated subpopulation
is the only destination for those infected travelers departing from the partially observable sources. Since
, the second condition guarantees that (3) only has a unique solution, which corresponds to the accurate identification of invasion pathways of this INC.
2). Potential Invasion Pathway:
If the conditions of Theorem 1 are unsatisfied, (3) has multiple solutions, each solution corresponds to a set of potential invasion pathways that can result in the related INC. Due to the heterogeneity in the traffic flow on each edge and the number of infected hosts within each contaminated source, each set of potential pathways is associated with a unique likelihood, which also identifies the occurrence probability of the corresponding solution of (3). Therefore, the identification of invasion pathway that induce an INC can be transformed to searching the most probable solution of (3).
We define the solution space 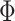 of (3) of the INC
of (3) of the INC 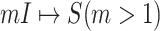 , which subjects to two conditions: 1)
, which subjects to two conditions: 1)  and 2)
and 2)  ,
, 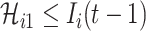 . The second condition is obvious, since the number of infected travelers departing from the source
. The second condition is obvious, since the number of infected travelers departing from the source 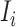 cannot exceed
cannot exceed 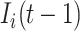 . Let us assume that
. Let us assume that 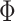 contains
contains  solutions, and a typical solution is formulated as
solutions, and a typical solution is formulated as 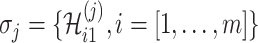 . Obviously, each solution
. Obviously, each solution  corresponds to a potential invasion pathway
corresponds to a potential invasion pathway 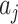 .
.
Through the INC 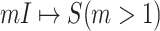 , the observed event
, the observed event 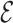 shows that the destination
shows that the destination 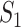 is contaminated due to the arrival of totally
is contaminated due to the arrival of totally 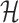 infected hosts from the potential sources
infected hosts from the potential sources 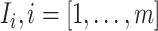 . With this posterior information, we first measure the likelihood of each possible solution
. With this posterior information, we first measure the likelihood of each possible solution 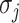 , which corresponds to the reasoning event that for each source
, which corresponds to the reasoning event that for each source 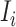 ,
, 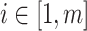 ,
, 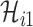 infected hosts are transferred to
infected hosts are transferred to 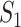 . It is evident that
. It is evident that 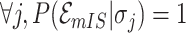 , since
, since 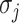 will lead to the occurrence of event
will lead to the occurrence of event 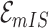 , which corresponds to
, which corresponds to 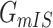 .
.
According to Bayes’ theorem, the likelihood of the solution  is characterized by
is characterized by
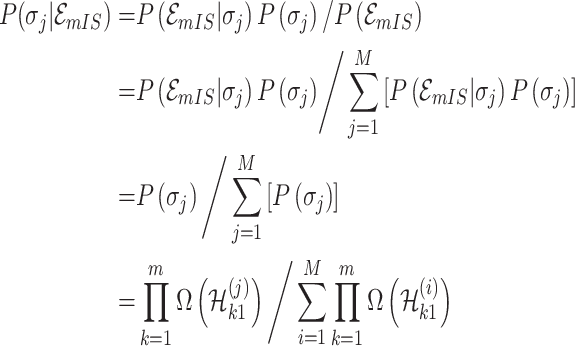 |
where 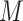 represents the number of potential solution
represents the number of potential solution 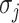 , and the last item
, and the last item 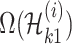 represents the mobility likelihood transferring estimator of infected subpopulation
represents the mobility likelihood transferring estimator of infected subpopulation 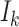 in
in 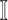 .
.
One linchpin of our algorithm in handling the scenario 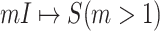 is to estimate the probability of transferring
is to estimate the probability of transferring 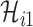 infected hosts from each infected subpopulation
infected hosts from each infected subpopulation 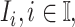 to the destination subpopulation
to the destination subpopulation 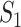 . Based on the independence between the intrasubpopulation epidemic reactions and the intersubpopulation personal diffusion, we introduce a transferring estimator to analyze the individual mobility of each source
. Based on the independence between the intrasubpopulation epidemic reactions and the intersubpopulation personal diffusion, we introduce a transferring estimator to analyze the individual mobility of each source 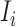 , which is in particular useful if there are partially observable and unobservable edges emanated from the focal infected subpopulation.
, which is in particular useful if there are partially observable and unobservable edges emanated from the focal infected subpopulation.
The specific formalisms of the transferring estimator are defined according to the three types of infected subpopulation 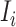 consisted of set
consisted of set 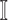 which are unobservable subpopulation, partially observable subpopulation, and observable subpopulation with transition of
which are unobservable subpopulation, partially observable subpopulation, and observable subpopulation with transition of 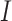 to
to 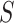 .
.
a). Unobservable subpopulation  :
:
Due to the occurrence of 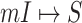 , among all
, among all 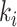 edges emanated from subpopulation
edges emanated from subpopulation 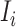 , there is only one invasion edge in that INC, labeled as
, there is only one invasion edge in that INC, labeled as 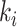 , along which the traveling rate is
, along which the traveling rate is 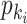 and
and 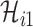 infected hosts are transferred to the destination
infected hosts are transferred to the destination  . Assume that there are
. Assume that there are 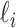 (
(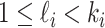 ) unobservable and partially observable edges, labeled as
) unobservable and partially observable edges, labeled as 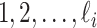 , respectively. Along each unobservable or partially observable edge, the traveling rate is
, respectively. Along each unobservable or partially observable edge, the traveling rate is  ,
, 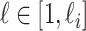 , and
, and 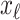 infected hosts leave
infected hosts leave 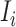 . Accordingly, in total
. Accordingly, in total 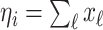 infected hosts leave
infected hosts leave 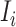 through the unobservable and partially observable edges. There remain
through the unobservable and partially observable edges. There remain 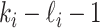 observable edges, labeled as
observable edges, labeled as 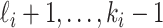 , respectively. Along each observable edge, the traveling rate is
, respectively. Along each observable edge, the traveling rate is 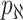 ,
, 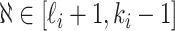 , and
, and 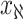 infected hosts leave
infected hosts leave 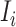 . With probability
. With probability 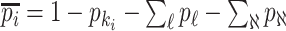 , an infected host keeps staying at source
, an infected host keeps staying at source 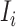 .
.
Since the infected hosts transferred by unobservable and partially observable edges are untraceable, it is unable to reveal the actual invasion pathways resulting in that INC accurately. Fortunately, the message of traveling rates on each edge is available by collecting and analyzing the human mobility transportation networks. Therefore, the mobility multinomial distribution [(31) in Appendix A] can be used to obtain the conditional probability that 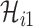 infected hosts are transferred from infected source
infected hosts are transferred from infected source 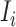 to destination
to destination 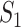 , which is measured by the following transferring estimator:
, which is measured by the following transferring estimator:
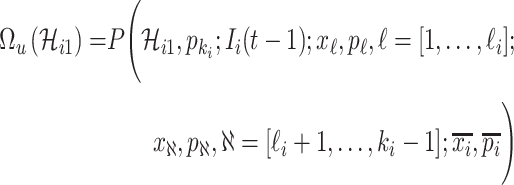 |
where  accounts for the number of infected hosts that do not leave source
accounts for the number of infected hosts that do not leave source 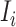 after the INC. Here, the observed number of infected persons in source
after the INC. Here, the observed number of infected persons in source  before the INC, i.e.,
before the INC, i.e., 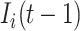 , is used for the estimation, since the probability that a newly infected host also experiencing the mobility process is very low. Considering the conservation of infected hosts, and the implication of observable edges (i.e.,
, is used for the estimation, since the probability that a newly infected host also experiencing the mobility process is very low. Considering the conservation of infected hosts, and the implication of observable edges (i.e.,  ), we have
), we have 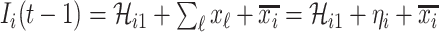 . Taking into account all scenarios that fulfill the condition
. Taking into account all scenarios that fulfill the condition 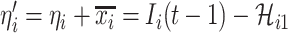 , the transferring estimator is simplified by the marginal distribution of (4), that is
, the transferring estimator is simplified by the marginal distribution of (4), that is
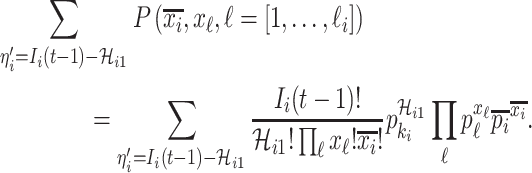 |
With independence, the transferring estimator becomes
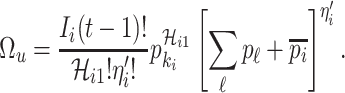 |
b). Observable subpopulation  (
(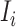 to
to 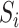 ):
):
If the infected hosts of source 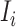 all leave to travel from
all leave to travel from 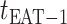 to
to 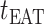 , the subpopulation
, the subpopulation 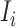 is observable at that INC. In this case, we have additional posterior messages, i.e.,
is observable at that INC. In this case, we have additional posterior messages, i.e.,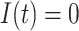 and
and  . Here, the number of infected hosts transferred to
. Here, the number of infected hosts transferred to 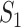 cannot exceed the total number of infected travelers departing from source
cannot exceed the total number of infected travelers departing from source 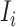 , i.e.,
, i.e., 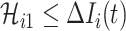 . In this regard, the probability that
. In this regard, the probability that  infected hosts arrive in destination
infected hosts arrive in destination 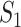 is measured by the following transferring estimator:
is measured by the following transferring estimator:
 |
c). Partially observable subpopulation 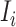 :
:
If source 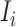 is partially observable, we can develop the inference algorithm with an additional posterior message, which reveals that at least
is partially observable, we can develop the inference algorithm with an additional posterior message, which reveals that at least 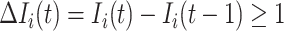 infected hosts leave the focal source
infected hosts leave the focal source 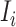 after the occurrence of that INC. In order to measure the conditional probability that
after the occurrence of that INC. In order to measure the conditional probability that 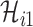 infected hosts are transferred from source
infected hosts are transferred from source 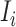 to destination
to destination 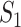 , we inspect all possible scenarios in detail, as follows.
, we inspect all possible scenarios in detail, as follows.
Type 1:
 , i.e., the observed reduction in the number of infected hosts
, i.e., the observed reduction in the number of infected hosts 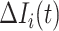 is less than those transferred from
is less than those transferred from 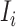 to
to 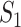 . Here, we consider all cases that are in accordance with this condition.
. Here, we consider all cases that are in accordance with this condition.
If all 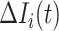 confirmed infected travelers are transferred from
confirmed infected travelers are transferred from 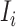 to
to 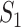 , the transferring estimator can be used to quantify the conditional probability that the remaining
, the transferring estimator can be used to quantify the conditional probability that the remaining 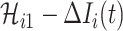 infected hosts concerned also visit
infected hosts concerned also visit 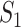 , that is
, that is
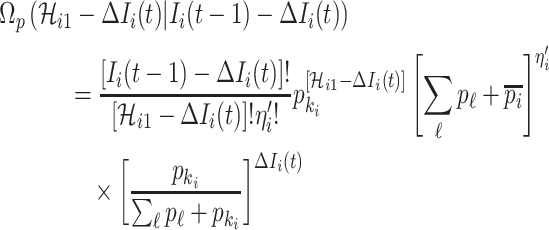 |
where 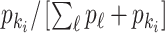 represents the relative traveling rate that any person from source
represents the relative traveling rate that any person from source 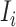 is transferred to
is transferred to 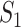 , thus the last item on the right-hand side (RHS) accounts for the probability that
, thus the last item on the right-hand side (RHS) accounts for the probability that 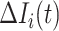 confirmed infected travelers all visit
confirmed infected travelers all visit 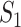 .
.
If only a fraction of 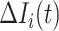 confirmed infected travelers are transferred from
confirmed infected travelers are transferred from 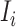 to
to  , the situation is more complicated. Assume that
, the situation is more complicated. Assume that 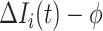 (
(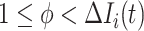 ) confirmed travelers successfully come to
) confirmed travelers successfully come to 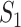 , the corresponding transferring estimator becomes
, the corresponding transferring estimator becomes
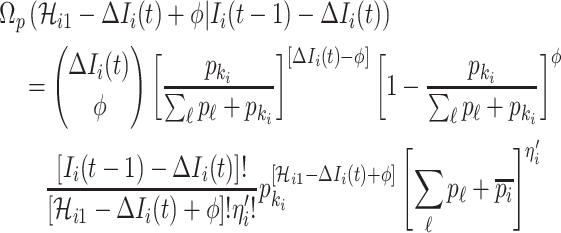 |
where the first item on the RHS accounts for the probability that 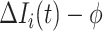 confirmed visitors visit
confirmed visitors visit 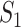 .
.
If all 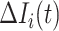 confirmed infected travelers from
confirmed infected travelers from 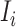 are not transferred to
are not transferred to  , the conditional probability that among the remaining
, the conditional probability that among the remaining 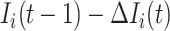 infected hosts,
infected hosts, 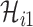 infected travelers are transferred to
infected travelers are transferred to 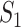 , which is measured by the following transferring estimator:
, which is measured by the following transferring estimator:
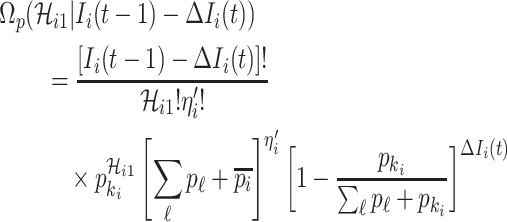 |
where the last item on the RHS accounts for the probability that 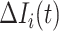 confirmed infected travelers all do not visit
confirmed infected travelers all do not visit 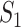 .
.
Taking into account all the above cases, the probability that  infected hosts arrive at destination
infected hosts arrive at destination 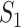 is measured by the following transferring estimator:
is measured by the following transferring estimator:
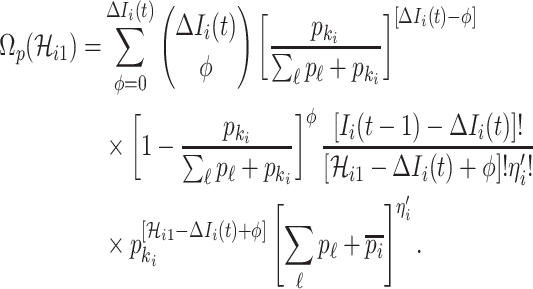 |
Type 2:
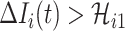 , i.e., the observed reduction in the number of infected hosts
, i.e., the observed reduction in the number of infected hosts 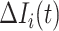 exceeds the number of infected hosts transferred to
exceeds the number of infected hosts transferred to  . Similar to the above analysis, we develop the transferring estimator by considering all possible cases that are in accordance with this condition.
. Similar to the above analysis, we develop the transferring estimator by considering all possible cases that are in accordance with this condition.
If 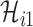 infected hosts transferred to
infected hosts transferred to 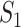 are all from the observable travelers
are all from the observable travelers 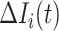 , the transferring estimator becomes
, the transferring estimator becomes
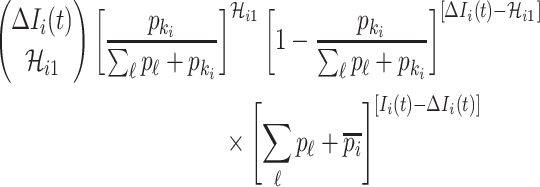 |
where the last item accounts for the constraint that the remaining 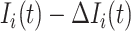 infected hosts will not be transferred to
infected hosts will not be transferred to 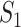 .
.
Similar to type 1, the other two cases are: only a fraction of 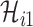 infected hosts transferred to
infected hosts transferred to 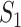 are from the observable travelers
are from the observable travelers 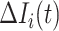 , and
, and 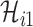 infected hosts transferred to
infected hosts transferred to  are all not from the observable travelers
are all not from the observable travelers 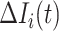 , we can also derive the transferring estimators.
, we can also derive the transferring estimators.
Taking into account all these cases, the probability that 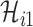 infected hosts move to the destination subpopulation
infected hosts move to the destination subpopulation 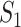 is measured by the following transferring estimator:
is measured by the following transferring estimator:
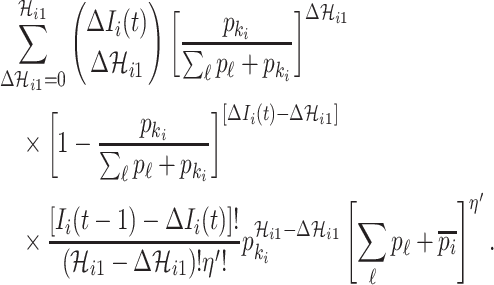 |
Generally, set  consists of the three classes of subpopulations
consists of the three classes of subpopulations 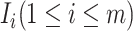 discussed above: unobservable subpopulation, partially observable subpopulation, and observable subpopulation of
discussed above: unobservable subpopulation, partially observable subpopulation, and observable subpopulation of 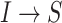 . According to (4), generally each potential pathway
. According to (4), generally each potential pathway 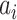 corresponds to a potential solution
corresponds to a potential solution 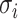 , the most-likely invasion pathway for a
, the most-likely invasion pathway for a 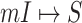 can be identified as
can be identified as
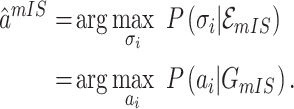 |
B. Case of 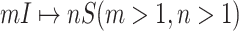
Finally, we consider the case of 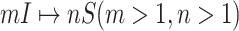 , which is more complicated than
, which is more complicated than  , because some infectious populations in set
, because some infectious populations in set 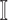 may have more than one invasion edge to the corresponding susceptible subpopulations in set
may have more than one invasion edge to the corresponding susceptible subpopulations in set 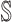 , and the number of elements in set
, and the number of elements in set  are more than one, which obey a joint probability distribution of transferring likelihood. As shown in Fig. 2, an INC
are more than one, which obey a joint probability distribution of transferring likelihood. As shown in Fig. 2, an INC 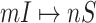 includes set
includes set 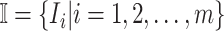 and
and 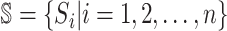 . The first arrival infected individuals invaded each susceptible subpopulation in set
. The first arrival infected individuals invaded each susceptible subpopulation in set 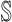 are
are 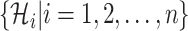 , respectively. Here, denote
, respectively. Here, denote 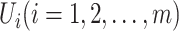 the subset of susceptible neighbor subpopulations in set
the subset of susceptible neighbor subpopulations in set 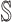 of infected subpopulation
of infected subpopulation 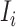 , and
, and 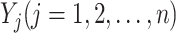 the subset of infected neighbor subpopulations in set
the subset of infected neighbor subpopulations in set 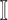 of susceptible subpopulation
of susceptible subpopulation  .
.
We define 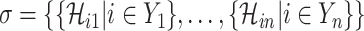 a potential solution for the
a potential solution for the 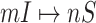 , if subject to two conditions:
, if subject to two conditions:
-
1)
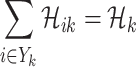
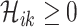 ;
; -
2)
for any
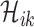 which denotes the number of infected hosts travel to subpopulation
which denotes the number of infected hosts travel to subpopulation 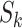 from
from 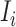 at
at 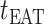 , we have
, we have 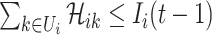 , where
, where 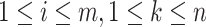 .
.
If a 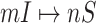 has
has 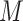 potential solutions, let
potential solutions, let 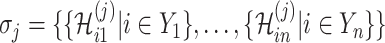 ,
, 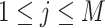 .
.
Similarly, we first discuss the accurately identifiable pathway for a given  , then estimate the most-likely numbers of each
, then estimate the most-likely numbers of each  as accurate as possible by designing our identification algorithm, since one solution of (16) corresponds to one invasion pathway of an INC
as accurate as possible by designing our identification algorithm, since one solution of (16) corresponds to one invasion pathway of an INC 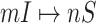 .
.
1). Accurate Identification of Invasion Pathway:
Given a few satisfied prerequisites, for all 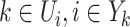 of the equations constituted by (16) can has a unique solution, which implies that the invasion pathway of that INC can be identified accurately. Theorem 2 elucidates this scenario.
of the equations constituted by (16) can has a unique solution, which implies that the invasion pathway of that INC can be identified accurately. Theorem 2 elucidates this scenario.
Theorem 2 (Accurate Identification of Invasion Pathway):
With the following conditions: 1) the number of invasion edges
; 2) the neighbor subpopulations of each subpopulation in set
are with the transition
to
or
to
except their neighbor subpopulations in set
during
to
; and 3)
, the invasion pathway of an INC
can be identified accurately.
Proof:
Since the number of infected individuals in the partially observable subpopulation
reduces at time
, i.e.,
and
, it is inevitable that a few infected carries diffuse away from subpopulation
. Occurring the state transitions of
at time
, subpopulations in the neighborhood of
(excluding the new contaminated subpopulation
) cannot receive infected travelers. Therefore, the only possible destination for those infected travelers is subpopulation
.
The conditions 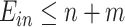 and
and 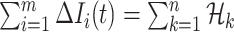 make the equations
make the equations 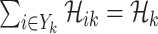 and
and 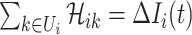 only has the unique solution
only has the unique solution 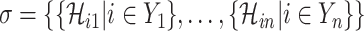 . The reason is that rank
. The reason is that rank 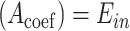 , where
, where 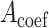 is the coefficient matrix of equations
is the coefficient matrix of equations 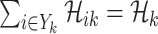 and
and 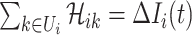 . Thus the invasion pathway of this
. Thus the invasion pathway of this 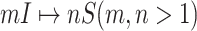 can be identified accurately.
can be identified accurately.
2). Potential Invasion Pathway:
If the conditions of Theorem 2 are unsatisfied, the equations constituted by (16) has multiple solutions, each solution corresponds to a set of potential invasion pathways that can result in the related 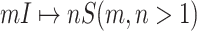 . We derive the transferring likelihood of each potential solution similar to case of
. We derive the transferring likelihood of each potential solution similar to case of 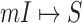 . Therefore, the likelihood of solution
. Therefore, the likelihood of solution 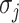 is characterized by
is characterized by
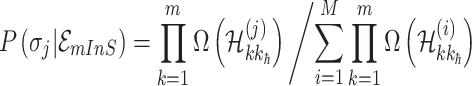 |
where 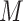 represents the number of solution
represents the number of solution 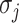 , and the last item
, and the last item 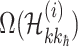 represents the transferring estimator of infected subpopulation
represents the transferring estimator of infected subpopulation 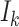 in
in 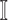 ,
, 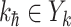 . Note that
. Note that 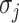 and
and 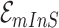 correspond to a potential invasion pathway
correspond to a potential invasion pathway 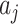 of
of 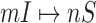 and
and 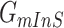 , respectively.
, respectively.
Now we discuss the transferring estimator of subpopulation 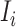 according to its extent of subpopulation observability.
according to its extent of subpopulation observability.
-
1)
Subpopulation
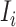 has only one neighbor (invasion edge) in set
has only one neighbor (invasion edge) in set 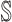 . In this case, the transferring estimator is the same as the depicted one in
. In this case, the transferring estimator is the same as the depicted one in 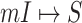 .
. -
2)
Subpopulation
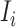 has
has 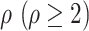 neighbors (invasion edges) in set
neighbors (invasion edges) in set 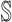 .
.
Suppose there are totally 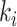 edges emanate from
edges emanate from 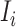 which consist of the following three kinds.
which consist of the following three kinds.
-
1)
There are
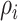 invasion edges (
invasion edges (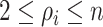 ), labeled
), labeled 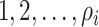 , along which the traveling rates are
, along which the traveling rates are 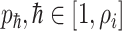 , and
, and 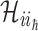 invade the subpopulations in the subset
invade the subpopulations in the subset 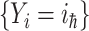 , respectively.
, respectively. -
2)
There are
 unobservable and partially observable edges, labeled
unobservable and partially observable edges, labeled 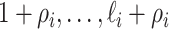 , respectively. Along each unobservable or partially observable edge, the traveling rate is
, respectively. Along each unobservable or partially observable edge, the traveling rate is 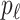 ,
, 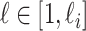 , and
, and  infected hosts leave
infected hosts leave  . Accordingly, in total
. Accordingly, in total  infected hosts leave
infected hosts leave 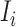 through the unobservable and partially observable edges.
through the unobservable and partially observable edges. -
3)
There remain
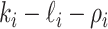 observable edges, labeled as
observable edges, labeled as 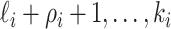 , respectively. Along each observable edge, the traveling rate is
, respectively. Along each observable edge, the traveling rate is 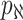 ,
,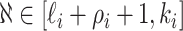 , and
, and 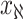 infected hosts leave
infected hosts leave 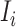 . With probability
. With probability 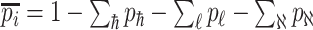 , an infected host keeps staying at the source
, an infected host keeps staying at the source 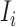 . There are
. There are 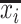 infected hosts staying in subpopulation
infected hosts staying in subpopulation 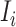 with the probability
with the probability 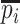 . Because
. Because 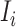 connects the unobservable and partially observable infected subpopulations, we only know the sum
connects the unobservable and partially observable infected subpopulations, we only know the sum 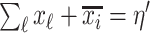 .
.
Now, we employ the following estimators to evaluate the transferring likelihood of the three categories of 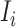 .
.
a). Unobservable subpopulation 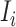 :
:
Because 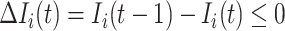 , we do not know whether and how many infected individuals travel to which destinations. Similar to the INC
, we do not know whether and how many infected individuals travel to which destinations. Similar to the INC 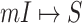 , the transferring likelihood estimator of
, the transferring likelihood estimator of 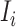 is
is
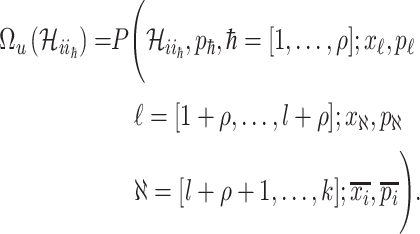 |
By means of the observable edges, the transferring estimator can be simplified as
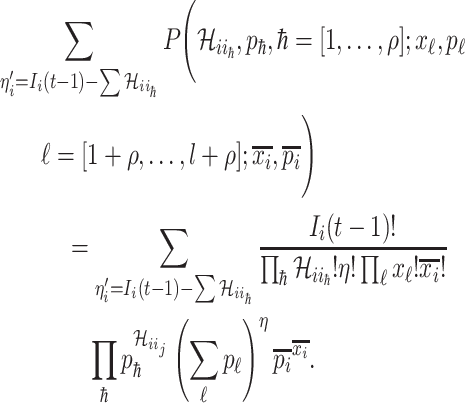 |
Then the transferring estimator becomes by the marginal distribution as
 |
b). Observable subpopulation 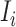 (
(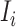 to
to 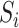 ):
):
For this situation, 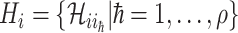 all come from
all come from 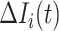 . The transferring likelihood estimator of a
. The transferring likelihood estimator of a 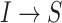 observable subpopulation
observable subpopulation 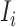 is
is
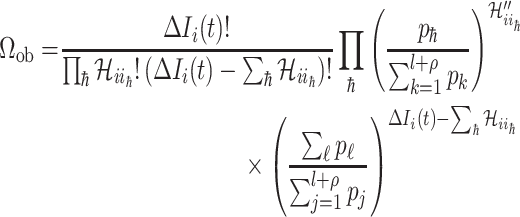 |
where 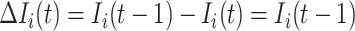 .
.
c). Partially observable subpopulation 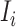 :
:
Due to 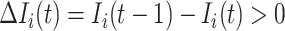 , at least
, at least 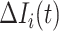 infected hosts leave source
infected hosts leave source 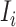 from
from 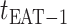 to
to  .
.
We first decompose 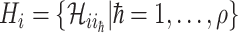 as two subsets:
as two subsets: 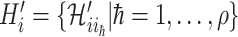 and
and 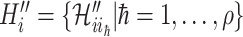 ,
, 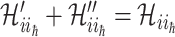 , where
, where 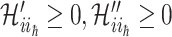 . Denote
. Denote 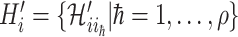 the infected hosts coming from
the infected hosts coming from 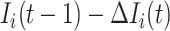 , and
, and 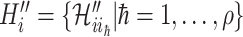 the infected hosts coming from
the infected hosts coming from 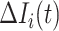 . Then we analyze the transferring estimator on the following two types.
. Then we analyze the transferring estimator on the following two types.
Type 1 ( ): Suppose
): Suppose 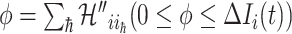 , which represents the number of infected hosts coming from
, which represents the number of infected hosts coming from  . Given a fixed
. Given a fixed 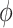 , there may be more than one permutation
, there may be more than one permutation 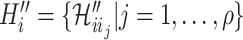 for
for 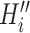 . The transferring likelihood estimator is
. The transferring likelihood estimator is
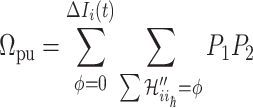 |
where
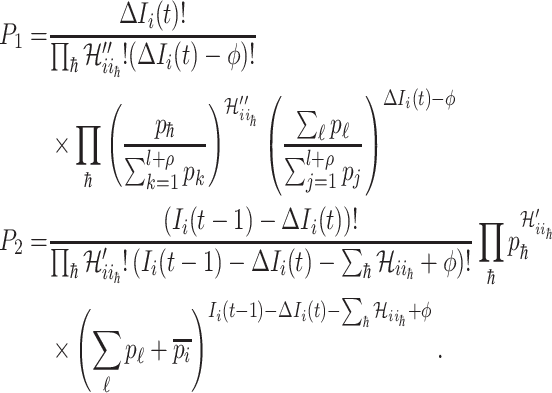 |
Type 2 (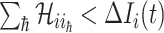 ): Suppose
): Suppose 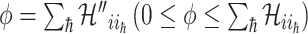 , which represents the number of infectious hosts coming from
, which represents the number of infectious hosts coming from 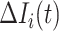 . Given a fixed
. Given a fixed 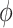 , there may be more than one solution for
, there may be more than one solution for 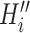 . The transferring likelihood estimator is
. The transferring likelihood estimator is
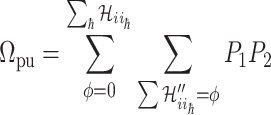 |
where 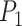 and
and 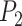 are the same as those in (22).
are the same as those in (22).
According to (17), the most-likely invasion pathways for an INC  can be identified as
can be identified as
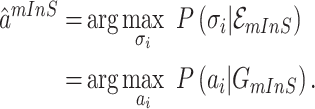 |
Note that if the first arrival infectious individuals 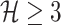 , there may be multiple potential solutions corresponding to one potential pathway. For example, a
, there may be multiple potential solutions corresponding to one potential pathway. For example, a 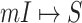 is illustrated in Fig. 4. In this situation, we merge the transferring likelihood of potential solutions of
is illustrated in Fig. 4. In this situation, we merge the transferring likelihood of potential solutions of 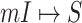 or
or 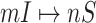 if they belong to the same invasion pathways, then find out the most-likely invasion pathways, which are corresponding to the maximum transferring likelihood.
if they belong to the same invasion pathways, then find out the most-likely invasion pathways, which are corresponding to the maximum transferring likelihood.
Fig. 4.

Example of 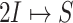 INC. Suppose that three infected cases reach subpopulation
INC. Suppose that three infected cases reach subpopulation 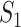 simultaneously, which means
simultaneously, which means 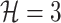 . The three possible permutations are:
. The three possible permutations are: 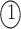
 ;
; 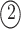
 ,
,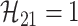 ; and
; and 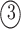
 . The permutations
. The permutations  and
and 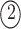 indicate the same pathways, but
indicate the same pathways, but 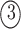 is different.
is different.
According to (1) and (2), the whole invasion pathway 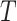 can be reconstructed chronologically by assembling all identified invasion pathway of each INC after identification of four classes of INCs. To depict the IPI algorithm explicitly, the pseudocode for our algorithm is given in Algorithm 2.
can be reconstructed chronologically by assembling all identified invasion pathway of each INC after identification of four classes of INCs. To depict the IPI algorithm explicitly, the pseudocode for our algorithm is given in Algorithm 2.
Algorithm 2 IPI
-
1:
Inputs: the time series of infection data
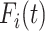 and topology of network
and topology of network 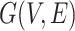 (including diffusion rates
(including diffusion rates  )
) -
2:
Find all invasion events via EAT data
-
3:
for each invasion event
-
4:
Invasion partition to find out the
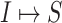 ,
, 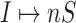 ,
, 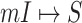 and
and 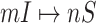 .
. -
5:
for each
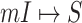 or
or 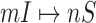
- 6:
-
7:
compute the unique invasion pathway
-
8:
end if
-
9:
if don’t satisfy conditions of Th 1 or Th 2 compute the all
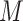 potential solutions
potential solutions 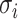
-
10:
compute the
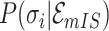 or
or 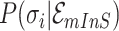
-
11:
merge the
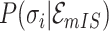 or
or 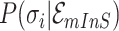 of potential solution
of potential solution 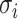 if they belong to same pathway
if they belong to same pathway -
12:
end if
-
13:
end for
-
14:
find the maximal
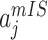 and
and  invasion pathway
invasion pathway -
15:
end for
-
16:
reconstruct the whole invasion pathways (T) by assembling each invasion cases chronologically
C. Analysis of IPI Algorithm
Science IPI algorithm is based on hierarchical-iteration-like decomposition technique, which reduce the temporal-spatial complexity of spreading, it can handle large-scale spatial pandemic. Note that the invasion infected hosts 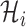 at EAT always are very small (generally ≤ 3). Therefore, the computation cost of our IPI algorithm is small, and we employ the enumeration algorithm to compute each of
at EAT always are very small (generally ≤ 3). Therefore, the computation cost of our IPI algorithm is small, and we employ the enumeration algorithm to compute each of 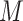 potential permutations. In this section, we only discuss the simplest situation that one pathway only corresponds to one permitted solution in an INC. The situation of one pathway corresponds to multiplex potential solutions can be extended.
potential permutations. In this section, we only discuss the simplest situation that one pathway only corresponds to one permitted solution in an INC. The situation of one pathway corresponds to multiplex potential solutions can be extended.
Denote 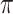 the probability corresponding to the most likely pathways for a given INC. Thus we have
the probability corresponding to the most likely pathways for a given INC. Thus we have
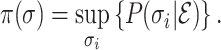 |
Property 1:
Given an INC “
” or “
,”
, there must exist
and
satisfying
Proof:
Suppose that
, where
is the number of potential solutions. Thus
; Because
, let
We have
.
D. Identifiability of Invasion Pathway
Accordingly, our IPI algorithm first decomposes the whole invasion pathways into four classes of INCs. Some INCs are easy to identify, but some are difficult. Therefore, it is important to describe how possible an INC can be wrongly identified. The identification extent of an INC relates with the absolute value of 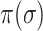 and information given by the probability vector of all potential invasion pathways. We employ the entropy to describe the information of likelihood vector, which contains the all likelihood of
and information given by the probability vector of all potential invasion pathways. We employ the entropy to describe the information of likelihood vector, which contains the all likelihood of 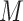 potential solutions/pathways of an INC.
potential solutions/pathways of an INC.
Definition 1 (Entropy of Transferring Likelihoods of
Potential Solutions):
According to Shannon entropy, we define the normalized entropy of transferring likelihood
as
This likelihood entropy
tells the information embedded in the likelihood vector of the potential solutions of a given INC.
The bigger of 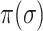 and the smaller of entropy
and the smaller of entropy 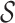 , the easier to identify the epidemic pathways for an INC. Define identifiability of invasion pathways to characterize the feasibility an INC can be identified
, the easier to identify the epidemic pathways for an INC. Define identifiability of invasion pathways to characterize the feasibility an INC can be identified
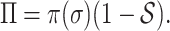 |
Although the likelihood entropies of some INCs are small (less than 0.5), they are still difficult to identify, because their 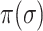 are much less than 0.5. Therefore, identifiability
are much less than 0.5. Therefore, identifiability  describes the practicability of a given
describes the practicability of a given 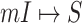 or
or 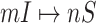 better than only using
better than only using 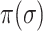 or likelihoods entropy
or likelihoods entropy 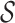 . The identifiability statistically tells us why some INCs are easy to identify, whose
. The identifiability statistically tells us why some INCs are easy to identify, whose  are more than 0.5, and why some INCs are difficult to identify, whose
are more than 0.5, and why some INCs are difficult to identify, whose 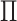 are much less than 0.5.
are much less than 0.5.
Next we show that there exist the upper and lower boundaries of identifiability 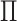 for a given INC.
for a given INC.
Theorem 3:
Given an INC “
” or “
,”
is the identifiability computed by the IPI algorithm. There exist a lower boundary
and an upper boundary
that
where
.
Proof:
, where
. According to Fano’s inequality, the entropy
.
On the other hand, we note that function 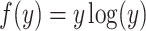 is strictly convex. According to Jensen’s inequality,
is strictly convex. According to Jensen’s inequality, 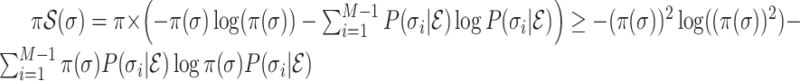 .
. 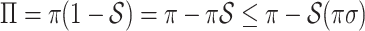 . Therefore,
. Therefore, 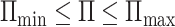 , where
, where 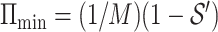 and
and 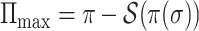 . That completes the proof of Theorem 3.
. That completes the proof of Theorem 3.
IV. Computational Experiments
To verify the performance of our algorithm, we proceed networked metapopulation-based Monte Carlo simulation method to simulate stochastic epidemic process on the AAN and the Barabasi–Albert (BA) networked metapopulation.
The AAN is a highly heterogeneous network. Each node of the AAN represents an airport, the population size of which is the serving area’s population of this airport. The directed traffic flow is the number of passengers through this edge/airline. The data of the AAN we are used to simulate is based on the true demography and traffic statistics [50]. We take the maximal component consisted of 404 nodes (airports/subpopulations) of all American airports as the network size of the ANN. The average degree of the AAN is nearly 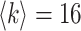 . The total population of the AAN is the
. The total population of the AAN is the 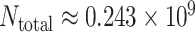 , which covers most of the population of the USA.
, which covers most of the population of the USA.
The BA network obeys heterogeneous degree distribution [51], which holds two properties of growth and preference attachment. For a BA networked metapopulation, each node is a subpopulation containing many individuals. The details of how to generate a BA networked metapopulation including travel rates setting is presented in Appendix B. To test the performance of our algorithm to handle large-scale network, the subpopulations number of the BA networked metapopulation is fixed as 3000. This is nearly equal to the number of the world airports network [52]. We fix 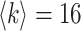 as the average degree of the BA networked metapopulation. The initial population size of each subpopulation is
as the average degree of the BA networked metapopulation. The initial population size of each subpopulation is 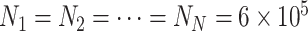 , and the total population is
, and the total population is 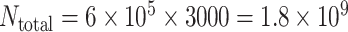 , which covers most of the active travelers of the world.
, which covers most of the active travelers of the world.
A. Networked Metapopulation-Based Monte Carlo Simulation Method to Simulate Stochastic Epidemic Process
At the beginning, we assume only one subpopulation is seeded as infected and others are susceptible. Thus 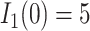 ,
, 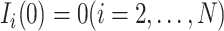 . We record and update each individual’s state (i.e., susceptible or infected) at each time step. At each
. We record and update each individual’s state (i.e., susceptible or infected) at each time step. At each 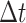 (
(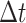 is defined as the unit time from
is defined as the unit time from 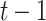 to
to 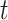 ), the transmission rate
), the transmission rate 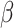 and diffusion rate
and diffusion rate 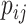 are converted into probabilities. The rules of individuals reaction and diffusion process in
are converted into probabilities. The rules of individuals reaction and diffusion process in 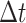 are as follows.
are as follows.
1). Reaction Process:
Individuals which are in the same subpopulation are homogeneously mixing. Each susceptible individual (in subpopulation 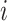 ) becomes infected with probability
) becomes infected with probability 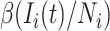 . Therefore, the average number of newly added infected individuals is
. Therefore, the average number of newly added infected individuals is 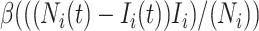 , but the simulation results fluctuate from one realization to another. The reaction process is simulated by binomial distribution.
, but the simulation results fluctuate from one realization to another. The reaction process is simulated by binomial distribution.
2). Diffusion Process:
After reaction, the diffusion process of individuals between different subpopulation posterior to the reaction process is taken into account. Each individual from subpopulation 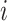 migrates to the neighboring subpopulation
migrates to the neighboring subpopulation 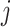 with probability
with probability 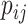 . The average number of new infectious travelers from subpopulation
. The average number of new infectious travelers from subpopulation 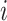 to
to 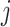 is
is 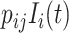 . The diffusion process is simulated by binomial distribution or multinomial distribution.
. The diffusion process is simulated by binomial distribution or multinomial distribution.
B. Numerical Results
We compared our IPI algorithm with three heuristic algorithms that generate the SPT or minimum spanning tree of the metapopulation networks.
-
1)
Average-Arrival-Time (ARR)-Based SPT [30]: The minimum distance path from subpopulation
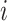 to subpopulation
to subpopulation 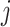 over all possible paths is generated in terms of mean first arrival time. Thus the average-arrival-time-based SPT is constructed by assembling all shortest paths from the seed subpopulation to other subpopulations of the whole network.
over all possible paths is generated in terms of mean first arrival time. Thus the average-arrival-time-based SPT is constructed by assembling all shortest paths from the seed subpopulation to other subpopulations of the whole network. -
2)
Effective (EFF)-Distance-Based Most Probable Paths Tree [4] Methods: From subpopulation
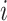 to subpopulation
to subpopulation 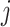 , the effective distance
, the effective distance 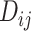 is defined as the minimum of the sum of effective lengths along the arbitrary legs of the path. The set of shortest paths to all subpopulations from seed subpopulation
is defined as the minimum of the sum of effective lengths along the arbitrary legs of the path. The set of shortest paths to all subpopulations from seed subpopulation 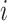 constitutes an SPT.
constitutes an SPT. -
3)
Monte Carlo-Maximum-Likelihood (MCML)-Based Most Likely Epidemic Invasion Tree [43]: To produce a most likely infection tree, they constructed the minimum spanning tree from the seed subpopulation to minimize the distance. Some recent works [53]–[55] uses machine learning or genetic algorithms to infer transmission networks from surveillance data. Because of the distinction in model assumptions and conditions, we do not perform comparison with them.
We consider to access the identification accuracy for the inferred invasion pathways. This accuracy is defined by the ratio between the number of corrected identified invasion pathways by each method and the number of true invasion pathways, respectively. We also compute the accuracy of accumulative INCs of  and
and  . This accuracy is defined by the ratio between the number of corrected identified invasion pathways by each method in this class of INC and the number of true invasion pathways in this classes of INC. Additionally, we investigate the identification accuracy of early stage of a global pandemic spreading, which is important to help understand how to predict and control the prevalence of epidemics.
. This accuracy is defined by the ratio between the number of corrected identified invasion pathways by each method in this class of INC and the number of true invasion pathways in this classes of INC. Additionally, we investigate the identification accuracy of early stage of a global pandemic spreading, which is important to help understand how to predict and control the prevalence of epidemics.
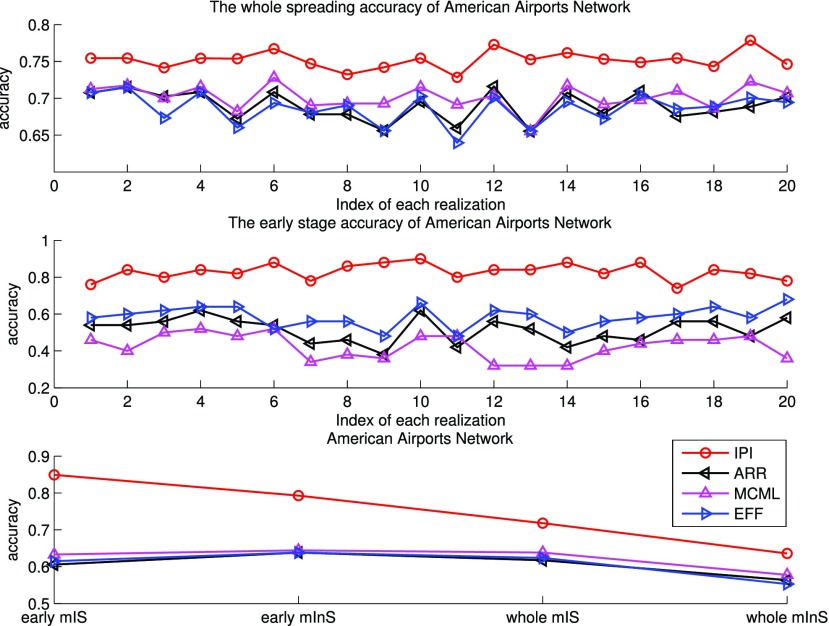
In Fig. 5 (top and middle), we observe the whole identification accuracy and the early-stage identification accuracy. Fig. 5 (bottom) shows the early and whole accumulative identification accuracy of 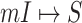 and
and 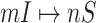 through 20 independent realizations on the AAN for each algorithm, respectively. The simulation results show our algorithm is outperformance, which indicates heterogeneity of structure of the AAN plays an important role.
through 20 independent realizations on the AAN for each algorithm, respectively. The simulation results show our algorithm is outperformance, which indicates heterogeneity of structure of the AAN plays an important role.
Fig. 5.

Top and middle: identified accuracy for the whole and early stage (before appearance of the first 50 infected subpopulations) invasion pathways for 20 independent spreading realizations on the AAN. Bottom: accumulative identified accuracy of INCs ( and
and 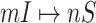 ) for the early stage and the whole invasion pathways on the AAN.
) for the early stage and the whole invasion pathways on the AAN.
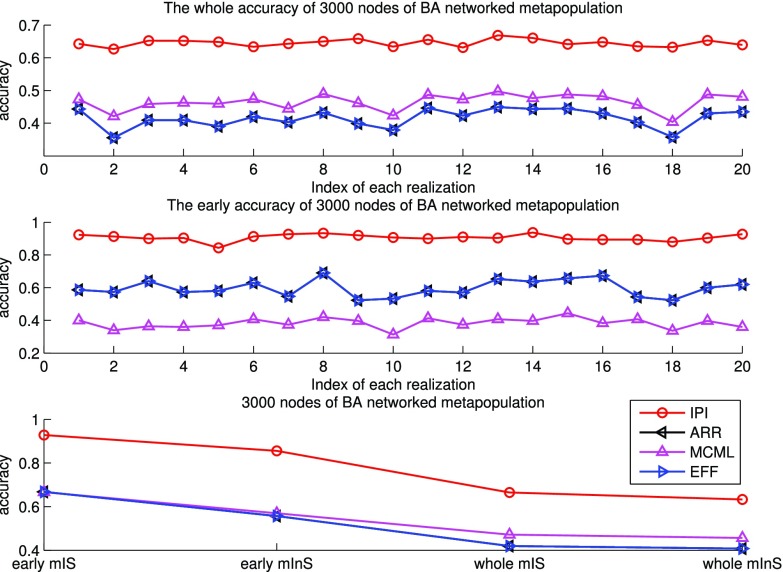
Fig. 6 shows the results of the BA networked metapopulation with 3000 subpopulations, the top of which presents the identification accuracy of whole invasion pathway for each realization of the four algorithms, while Fig. 6 (middle) shows the identification accuracy of early stage invasion pathway for each realization. Fig. 6 (bottom) shows accumulative identified accuracy of 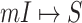 and
and 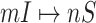 of 20 realizations for four algorithms respectively. The simulation results indicate that our algorithm can handle a large scale networked metapopulation with robust performance. Note that the performance of the ARR for the BA networked metapopulation is the same as that of the EFF, because our parameter
of 20 realizations for four algorithms respectively. The simulation results indicate that our algorithm can handle a large scale networked metapopulation with robust performance. Note that the performance of the ARR for the BA networked metapopulation is the same as that of the EFF, because our parameter 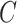 is a constant in the diffusion model (see Appendix B). Fig. 7 shows the comparison of the actual invasion pathways and the most likely identified invasion pathways for a given realization, during the early stage on the AAN.
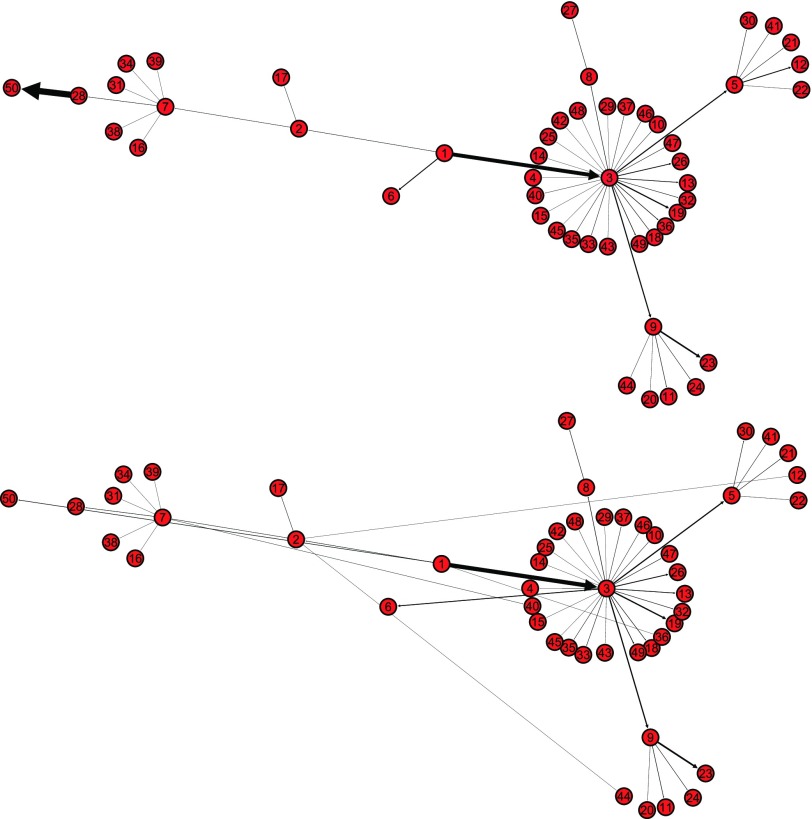
is a constant in the diffusion model (see Appendix B). Fig. 7 shows the comparison of the actual invasion pathways and the most likely identified invasion pathways for a given realization, during the early stage on the AAN.
Fig. 6.
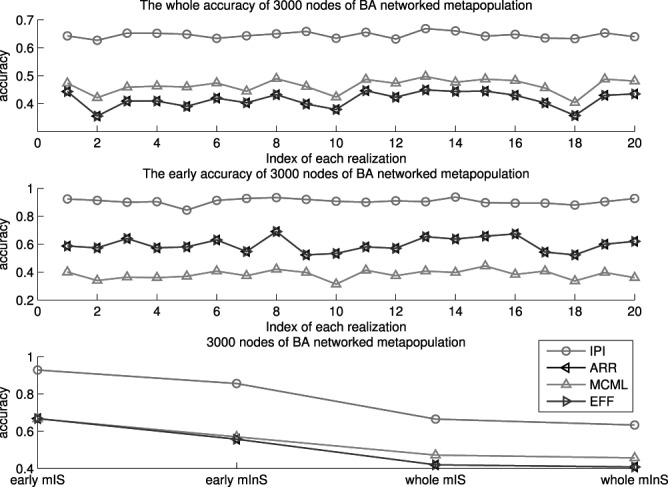
Top and middle: identified accuracy for the whole and early stage invasion pathways for 20 independent spreading realizations on 3000 subpopulations of the BA networked metapopulation. Bottom: accumulative identified accuracy of  and
and  for the early stage (the first 300 infected subpopulations) and the whole invasion pathways on 3000 subpopulations of the BA networked metapopulation.
for the early stage (the first 300 infected subpopulations) and the whole invasion pathways on 3000 subpopulations of the BA networked metapopulation.
Fig. 7.
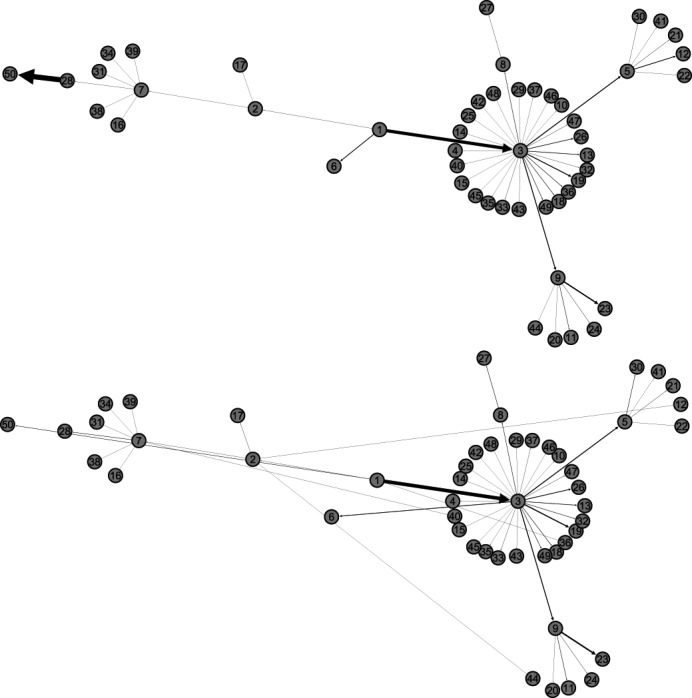
Illustration of the actual invasion pathways and the most likely identified invasion pathways, in a given realization, during the early stage (before the appearance of 50 infected subpopulations) on the AAN. Subpopulation 1 is the seed.
The numerical results suggest that networks with different topologies yield different identification performances, which indicate an identification algorithm should embed in both effects of spreading and topology. Our algorithm takes into account both heterogeneity of epidemics (the number of infected individuals) and network topology (diffusion flows).
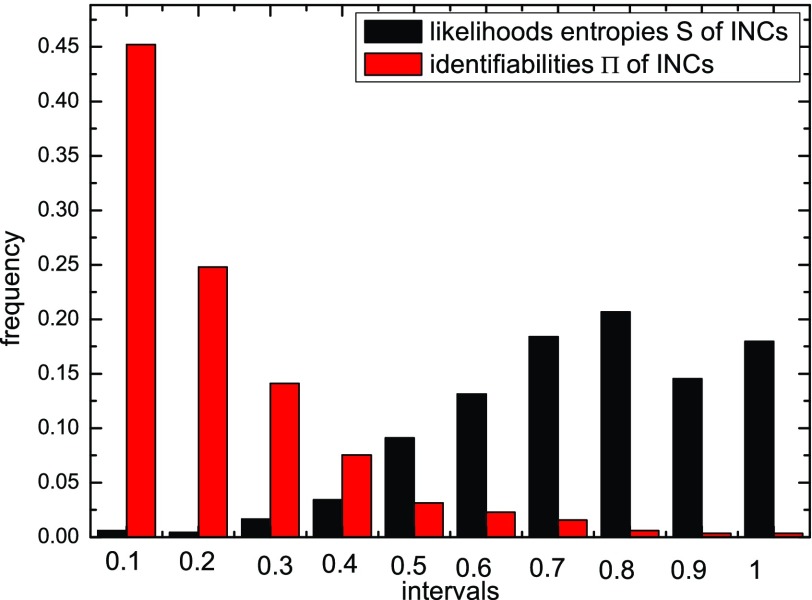
We finally test the identifiability of an INC. Fig. 8 shows the entropy and identifiability of wrongly identified 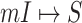 of 20 realizations on the AAN. The smaller the identifiability of an INC is, the easier it is prone to be wrongly identified. The identifiability depicts the wrongly identified
of 20 realizations on the AAN. The smaller the identifiability of an INC is, the easier it is prone to be wrongly identified. The identifiability depicts the wrongly identified 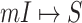 more reasonable than the likelihoods entropy. It indicates that identifiability
more reasonable than the likelihoods entropy. It indicates that identifiability  has a better performance to distinguish whether an INC is difficult to identify or not than using the likelihoods entropy.
has a better performance to distinguish whether an INC is difficult to identify or not than using the likelihoods entropy.
Fig. 8.

Statistics analysis of the likelihoods entropy and identifiability of wrongly identified 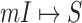 of 20 realizations of epidemic spreading on the AAN.
of 20 realizations of epidemic spreading on the AAN.
V. Conclusion
To conclude, we have proposed an identification framework as the so called IPI algorithm to explore the problem of inferring invasion pathway for a pandemic outbreak. We first anatomize the whole invasion pathway into four classes of INCs at each EAT. Then we identify four classes of INCs, and reconstruct the whole invasion pathway from the source subpopulation of a spreading process. We introduce the concept of identifiability to quantitatively analyze the difficulty level that an INC can be identified. The simulation results on the AAN and large-scale BA networked metapopulation have demonstrated our algorithm held a robust performance to identify the spatial invasion pathway, especially for the early stage of an epidemic. We conjecture the proposed IPI algorithm framework can extend to the problems of virus diffusion in computer network, human to human’s epidemic contact network, and the reaction dynamics may extend to the susceptible-infected-removed or susceptible-infected-susceptible dynamics.
Biographies

Jian-Bo Wang (S’15) received the B.Eng. degree in electronic science and technology from the Hefei University of Technology, Hefei, China, in 2005, and the M.Sc. degree in system theory from the University of Shanghai for Science and Technology, Shanghai, China, in 2010. He is currently pursuing the Ph.D. degree in circuits and systems with the Department of Electronic Engineering, Fudan University, Shanghai.
His current research interests include modeling and analyzing the spatial spread of emerging infectious diseases, statistics, optimization, and network science.
Mr. Wang was a recipient of the Fudan University Excellent Doctoral Research Program (985 Program) in 2013, the Excellent Master Dissertation Award of Shanghai Municipality in 2012, and the Outstanding University Graduates from Shanghai Municipal Government in 2010.

Lin Wang (M’14) received the B.Sc. degree in applied physics from the Department of Physics, Southeast University, Nanjing, China, in 2006, the M.Sc. degree in theoretical physics from the School of Physics, Nankai University, Tianjin, China, in 2009, and the Ph.D. degree in circuits and systems from the Department of Electronic Engineering, Fudan University, Shanghai, China, in 2013.
He is currently a Post-Doctoral Fellow with the WHO Collaborating Centre for Infectious Disease Epidemiology and Control, School of Public Health, Li Ka Shing Faculty of Medicine, University of Hong Kong, Hong Kong. His current research interests include mathematical and statistical epidemiology, infectious diseases modeling, stochastic processes, decision and optimization, self-organizing, and networking systems.
Dr. Wang was a recipient of the Excellent Doctoral Dissertation Award of Shanghai Municipality in 2015, the Outstanding University Graduates from Shanghai Municipal Government in 2013, and the Best Student Paper Award in Seventh Chinese Conference on Complex Networks in 2011. He serves as a Reviewer for about 20 journals and IEEE Transactions.

Xiang Li (M’05–SM’08) received the B.Sc. and Ph.D. degrees in control theory and control engineering from Nankai University, Tianjin, China, in 1997 and 2002, respectively.
He was with the International University of Bremen, Bremen, Germany, and Shanghai Jiao Tong University, Shanghai, China, as a Humboldt Research Fellow in 2005 and 2006 and an Associate Professor from 2004 to 2007. He joined Fudan University, Shanghai, China, as a Professor of Electronic Engineering in 2008. He served as the Head of the Electronic Engineering Department, Fudan University, in 2010–2015. He is the Founding Director of the Research Center of Smart Networks and Systems, School of Information Science and Engineering, Fudan University. He has (co-)authored four research monographs and over 200 peer-refereed publications in journals and conferences. His current research interests include theories and applications of complex network and network science.
Prof. Li was a recipient of the National Science Foundation for Distinguished Young Scholar of China in 2014, the Shanghai Science and Technology Young Talents Award in 2010, the Shanghai Natural Science Award (First Class) in 2008, and the IEEE Guillemin-Cauer Best Transactions Paper Award from the IEEE Circuits and Systems Society in 2005. He serves and served as an Associate Editor for the IEEE Transactions on Circuits and Systems—I: Regular Papers, the IEEE Circuits and Systems Society Newsletter, and Control Engineering Practice, and a Guest Associate Editor of the International Journal of Bifurcations and Chaos.
Appendix A. Mobility Operator
We discuss the individual mobility operator. Due to the presence of stochasticity and independence of individual mobility, the number of successful transform of individuals between or among adjacent subpopulations is quantified by a binomial or a multinomial process, respectively. If the focal subpopulation 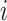 only has one neighboring subpopulation
only has one neighboring subpopulation 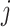 , the number of individuals in a given compartment
, the number of individuals in a given compartment  (
( and
and 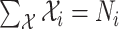 ) transferred from
) transferred from 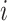 to
to 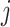 per unit time,
per unit time, 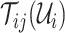 , is generated from a binomial distribution with probability
, is generated from a binomial distribution with probability 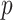 representing the diffusion rate and the number of trials
representing the diffusion rate and the number of trials 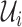 , that is
, that is
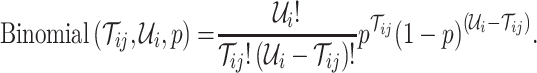 |
If the focal subpopulation  has multiple neighboring subpopulations
has multiple neighboring subpopulations 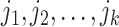 , with
, with 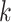 representing
representing 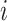 ’s degree, the numbers of individuals in a given compartment
’s degree, the numbers of individuals in a given compartment 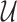 transferred from
transferred from 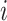 to
to 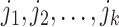 are generated from a multinomial distribution with probabilities
are generated from a multinomial distribution with probabilities 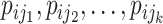 (
(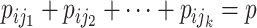 ) representing the diffusion rates on the edges emanated from subpopulation
) representing the diffusion rates on the edges emanated from subpopulation 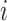 and the number of trails
and the number of trails 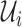 , that is
, that is
 |
where  .
.
Appendix B. Generic Diffusion Model to Generate Barabasi–Albert Metapopulation Network
We develop a general diffusion model to generate a BA metapopulation network in Section V, which characterizes the human mobility pattern on the empirical statistical rules of air transportation networks.
The diffusion rate from subpopulation  to
to  is
is 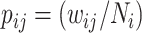 , where
, where 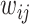 denotes the traffic flow from subpopulation
denotes the traffic flow from subpopulation 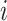 to
to 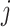 . These empirical statistical rules are verified in the air transportation network [52]:
. These empirical statistical rules are verified in the air transportation network [52]: 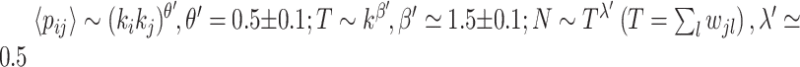 .
.
All the above empirical formulas relate to node’s degree 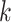 . To generate an artificial transportation network, we introduce a generic diffusion model to determine the diffusion rate
. To generate an artificial transportation network, we introduce a generic diffusion model to determine the diffusion rate
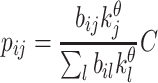 |
where 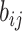 stands for the elements of the adjacency matrix (
stands for the elements of the adjacency matrix (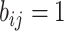 if
if 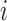 connects to
connects to 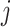 , and
, and 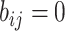 otherwise),
otherwise), 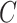 is a constant, and
is a constant, and 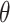 is a variable parameter. We assume that parameter
is a variable parameter. We assume that parameter 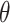 follows the Gaussian distribution
follows the Gaussian distribution 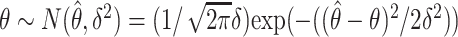 . Based on the empirical rule of
. Based on the empirical rule of  , where
, where 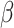 is approximately linear with
is approximately linear with 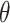 , the least squares estimation is employed to evaluate parameters
, the least squares estimation is employed to evaluate parameters 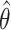 and
and 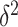 if we set the initial population of each node and constant
if we set the initial population of each node and constant 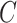 . Then, for a given BA network, we get a BA networked metapopulation in which real statistic information is embedded by using the above method.
. Then, for a given BA network, we get a BA networked metapopulation in which real statistic information is embedded by using the above method.
Funding Statement
This work was supported in part by the National Science Fund for Distinguished Young Scholars of China under Grant 61425019, the National Natural Science Foundation under Grant 61273223, and the “Shu Guang“ project supported by Shanghai Municipal Education Commission and Shanghai Education Development Foundation under Grant 14SG03. The work of J.-B. Wang and L. Wang was in part supported by the Fudan University Excellent Doctoral Research Program (985 Program).
Contributor Information
Jian-Bo Wang, Email: jianbowang11@fudan.edu.cn.
Lin Wang, Email: sph.linwang@hku.hk.
Xiang Li, Email: lix@fudan.edu.cn.
References
- [1].Keeling M. J. and Rohani P., Modeling Infectious Diseases in Humans and Animals. Princeton, NJ, USA: Princeton Univ. Press, 2008. [Google Scholar]
- [2].Heesterbeek H., et al. , “Modeling infectious disease dynamics in the complex landscape of global health,” Science, vol. 347, no. 6227, pp. 1–10, Mar. 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [3].Fitch J. P., “Engineering a global response to infectious diseases,” Proc. IEEE, vol. 103, no. 2, pp. 263–272, Feb. 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [4].Brockmann D. and Helbing D., “The hidden geometry of complex, network-driven contagion phenomena,” Science, vol. 342, no. 6164, pp. 1337–1342, Dec. 2013. [DOI] [PubMed] [Google Scholar]
- [5].McMichael A. J., “Globalization, climate change, and human health,” New England J. Med., vol. 368, no. 14, pp. 1335–1343, Apr. 2013. [DOI] [PubMed] [Google Scholar]
- [6].Mclean A. R., May R. M., Pattison J., and Weiss R. A., Eds., SARS: A Case Study in Emerging Infections. New York, NY, USA: Oxford Univ. Press, 2005. [Google Scholar]
- [7].Fraser C., et al. , “Pandemic potential of a strain of influenza A (H1N1): Early findings,” Science, vol. 324, no. 5934, pp. 1557–1561, Jun. 2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [8].Yang Y., et al. , “The transmissibility and control of pandemic influenza A (H1N1) virus,” Science, vol. 326, no. 5953, pp. 729–733, Oct. 2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [9].Yu H., et al. , “Human infection with avian influenza A H7N9 virus: An assessment of clinical severity,” Lancet, vol. 382, no. 9887, pp. 138–145, Jun. 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [10].Lam T. T.-Y., et al. , “Dissemination, divergence and establishment of H7N9 influenza viruses in China,” Nature, vol. 522, pp. 102–105, Jun. 2015. [DOI] [PubMed] [Google Scholar]
- [11].Gomes M. F. C., et al. , “Assessing the international spreading risk associated with the 2014 West African Ebola outbreak,” PLoS Currents Outbreaks, vol. 6, Sep. 2014. Doi: 10.1371/currents.outbreaks.cd818f63d40e24aef769dda7df9e0da5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [12].Cowling B. J., et al. , “Preliminary epidemiological assessment of MERS-CoV outbreak in South Korea, May to June,” Eurosurveillance, vol. 20, no. 25, pp. 7–13, Jun. 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [13].Wang X. and Chen G., “Complex network: Small-world, scale-free, and beyond,” IEEE Circuits Syst. Mag., vol. 3, no. 1, pp. 6–20, Jan-Mar 2003. [Google Scholar]
- [14].Newman M. E. J., Networks: An Introduction. New York, NY, USA: Oxford Univ. Press, 2010. [Google Scholar]
- [15].Tan C. W., Chiang M., and Srikant R., “Fast algorithms and performance bounds for sum rate maximization in wireless networks,” IEEE/ACM Trans. Netw., vol. 21, no. 3, pp. 706–719, Jun. 2013. [Google Scholar]
- [16].Yang B., Liu J., and Liu D., “Characterizing and extracting multiplex patterns in complex networks,” IEEE Trans. Syst., Man, Cybern. B, Cybern., vol. 42, no. 2, pp. 469–481, Apr. 2012. [DOI] [PubMed] [Google Scholar]
- [17].Fu X., Small M., and Chen G., Propagation Dynamics on Complex Networks: Models, Methods and Stability Analysis. New York, NY, USA: Wiley, 2013. [Google Scholar]
- [18].Pastor-Satorras R., Castellano C., Van Mieghem P., and Vespignani A., “Epidemic processes in complex networks,” Rev. Mod. Phys., vol. 87, no. 3, pp. 925–979, Jul-Sep 2015. [Google Scholar]
- [19].Wang L. and Li X., “Spatial epidemiology of networked metapopulation: An overview,” Chin. Sci. Bull., vol. 59, no. 28, pp. 3511–3522, Jul. 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [20].Chen P.-Y., Cheng S.-M., and Chen K.-C., “Optimal control of epidemic information dissemination over networks,” IEEE Trans. Cybern., vol. 44, no. 12, pp. 2316–2328, Dec. 2014. [DOI] [PubMed] [Google Scholar]
- [21].Griffin C. and Brooks R., “A note on the spread of worms in scale-free networks,” IEEE Trans. Syst., Man, Cybern. B, Cybern., vol. 36, no. 1, pp. 198–202, Feb. 2006. [DOI] [PubMed] [Google Scholar]
- [22].Chen L.-C. and Carley K. M., “The impact of countermeasure propagation on the prevalence of computer viruses,” IEEE Trans. Syst., Man, Cybern. B, Cybern., vol. 34, no. 2, pp. 823–833, Apr. 2004. [DOI] [PubMed] [Google Scholar]
- [23].Balcan D., et al. , “Seasonal transmission potential and activity peaks of the new influenza A(H1N1): A Monte Carlo likelihood analysis based on human mobility,” BMC Med., vol. 7, no. 45, pp. 1–12, Sep. 2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [24].Ferguson N. M., et al. , “Strategies for mitigating an influenza pandemic,” Nature, vol. 442, no. 7101, pp. 448–452, Jul. 2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [25].Colizza V., Barrat A., Barthelemy M., Valleron A. J., and Vespignani A., “Modeling the worldwide spread of pandemic influenza: Baseline case and containment interventions,” PLoS Med., vol. 4, no. 1, pp. 95–110, Jan. 2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [26].Wang L., Zhang Y., Huang T., and Li X., “Estimating the value of containment strategies in delaying the arrival time of an influenza pandemic: A case study of travel restriction and patient isolation,” Phys. Rev. E, vol. 86, no. 3, Sep. 2012, Art. ID 032901. [DOI] [PubMed] [Google Scholar]
- [27].Halloran M. E., et al. , “Modeling targeted layered containment of an influenza pandemic in the United States,” Proc. Nat. Acad. Sci. USA, vol. 105, no. 12, pp. 4639–4644, Mar. 2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [28].Wu J. T., Leung G. M., Lipsitch M., Cooper B. S., and Riley S., “Hedging against antiviral resistance during the next influenza pandemic using small stockpiles of an alternative chemotherapy,” PLoS Med., vol. 6, no. 5, pp. 1–11, May 2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [29].Lofgren E. T., et al. , “Opinion: Mathematical models: A key tool for outbreak response,” Proc. Nat. Acad. Sci. USA, vol. 111, no. 51, pp. 18095–18096, Dec. 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [30].Gautreau A., Barrat A., and Barthélemy M., “Global disease spread: Statistics and estimation of arrival times,” J. Theor. Biol., vol. 251, no. 3, pp. 509–522, Apr. 2008. [DOI] [PubMed] [Google Scholar]
- [31].Miao H., Xia X., Perelson A. S., and Wu H., “On identifiability of nonlinear ODE models and applications in viral dynamics,” SIAM Rev., vol. 53, no. 1, pp. 3–39, Feb. 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [32].Shah D. and Zaman T., “Rumors in a network: Who’s the culprit?” IEEE Trans. Inf. Theory, vol. 57, no. 8, pp. 5163–5181, Aug. 2011. [Google Scholar]
- [33].Luo W., Tay W. P., and Leng M., “Identifying infection sources and regions in large networks,” IEEE Trans. Signal Process., vol. 61, no. 11, pp. 2850–2865, Jun. 2013. [Google Scholar]
- [34].Wang Z., Dong W., Zhang W., and Tan C. W., “Rumor source detection with multiple observations: Fundamental limits and algorithms,” in Proc. ACM SIGMETRICS, Austin, TX, USA, Jun. 2014, pp. 1–13. [Google Scholar]
- [35].Dong W., Zhang W., and Tan C. W., “Rooting out the rumor culprit from suspects,” in Proc. IEEE Int. Symp. Inf. Theory (ISIT), Istanbul, Turkey, Jul. 2013, pp. 2671–2675. [Google Scholar]
- [36].Wang Z., Dong W., Zhang W., and Tan C. W., “Rooting our rumor sources in online social networks: The value of diversity from multiple observations,” IEEE J. Sel. Topics Signal Process., vol. 9, no. 4, pp. 663–677, Jun. 2015. [Google Scholar]
- [37].Han X., Shen Z., Wang W.-X., and Di Z., “Robust reconstruction of complex networks from sparse data,” Phys. Rev. Lett., vol. 114, no. 2, Jan. 2015, Art. ID 028701. [DOI] [PubMed] [Google Scholar]
- [38].Gomez-Rodriguez M., Leskovec J., and Krause A., “Inferring networks of diffusion and influence,” in Proc. 16th ACM SIGKDD Conf. Knowl. Disc. Data Mining (KDD), Washington, DC, USA, Jul. 2010, pp. 1019–1028. [Google Scholar]
- [39].Gomez-Rodriguez M., Leskovec J., and Krause A., “Inferring networks of diffusion and influence,” ACM Trans. Knowl. Disc. Data, vol. 5, no. 4, pp. 1–37, Feb. 2012. [Google Scholar]
- [40].Gomez-Rodriguez M., Balduzzi D., and Schölkopf B., “Uncovering the temporal dynamics of diffusion networks,” in Proc. 28th Int. Conf. Mach. Learn. (ICML), Bellevue, WA, USA, Jul. 2011, pp. 561–568. [Google Scholar]
- [41].Gomez-Rodriguez M., Leskovec J., Balduzzi D., and Schölkopf B., “Uncovering the structure and temporal dynamics of information propagation,” Netw. Sci., vol. 2, no. 1, pp. 26–65, Apr. 2014. [Google Scholar]
- [42].Daneshmand H., Gomez-Rodriguez M., Song L., and Schölkopf B., “Estimating diffusion network structures: Recovery conditions, sample complexity & soft-thresholding algorithm,” in Proc. 31st Int. Conf. Mach. Learn. (ICML), vol. 32 Beijing, China, Jun. 2014, pp. 793–801. [PMC free article] [PubMed] [Google Scholar]
- [43].Balcan D., et al. , “Multiscale mobility networks and the spatial spreading of infectious diseases,” Proc. Nat. Acad. Sci. USA, vol. 106, no. 51, pp. 21484–21489, Dec. 2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [44].Tsui K.-L., Wong Z. S.-Y., Goldsman D., and Edesess M., “Tracking infectious disease spread for global pandemic containment,” IEEE Intell. Syst., vol. 28, no. 6, pp. 60–64, Nov-Dec 2013. [Google Scholar]
- [45].Barthélemy M., “Spatial networks,” Phys. Rep., vol. 499, nos. 1–3, pp. 1–101, Feb. 2010. [Google Scholar]
- [46].Bazzani A., Giorgini B., Rambaldi S., Gallotti R., and Giovannini L., “Statistical laws in urban mobility from microscopic GPS data in the area of Florence,” J. Stat. Mech., vol. 2010, no. 5, May 2010, Art. ID P05001. [Google Scholar]
- [47].Peng C., Jin X., Wong K.-C., Shi M., and Liò P., “Collective human mobility pattern from taxi trips in urban area,” PLoS ONE, vol. 7, no. 4, Apr. 2012, Art. ID e34487. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [48].Liang X., Zhao J., Dong L., and Xu K., “Unraveling the origin of exponential law in intra-urban human mobility,” Sci. Rep., vol. 3, Oct. 2013, Art. ID 2983. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [49].Brooks-Pollock E., Roberts G. O., and Keeling M. J., “A dynamic model of bovine tuberculosis spread and control in Great Britain,” Nature, vol. 511, no. 7508, pp. 228–231, Jul. 2014. [DOI] [PubMed] [Google Scholar]
- [50].Wang L., Li X., Zhang Y.-Q., Zhang Y., and Zhang K., “Evolution of scaling emergence in large-scale spatial epidemic spreading,” PLoS ONE, vol. 6, no. 7, Jul. 2011, Art. ID e21197. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [51].Albert R. and Barabasi A.-L., “Statistical mechanics of complex networks,” Rev. Mod. Phys., vol. 74, no. 1, pp. 47–97, Jan. 2002. [Google Scholar]
- [52].Barrat A., Barthélemy M., Pastor-Satorras R., and Vespignani A., “The architecture of complex weighted networks,” Proc. Nat. Acad. Sci. USA, vol. 101, no. 11, pp. 3747–3752, Mar. 2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [53].Wan X., Liu J., Cheung W.-K., and Tong T., “Inferring epidemic network topology from surveillance data,” PLoS ONE, vol. 9, no. 6, Jun. 2014, Art. ID e100661. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [54].Shi B., Liu J., Zhou X.-N., and Yang G.-J., “Inferring plasmodium vivax transmission networks from tempo-spatial surveillance data,” PLoS Negl. Trop. Dis., vol. 8, no. 2, Feb. 2014, Art. ID e2682. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [55].Yang X., Liu J., Zhou X.-N., and Cheung W.-K., “Inferring disease transmission networks at a metapopulation level,” Health Inf. Sci. Syst., vol. 2, no. 8, Nov. 2014. Art. ID PMC4375841. [DOI] [PMC free article] [PubMed] [Google Scholar]