Abstract
This paper introduces a nonlinear dynamic model to study spatial and temporal dynamics of epidemics of susceptible-infected-removed type. It involves modeling the respective collections of epidemic states and syndromic observations as random finite sets. Each epidemic state consists of the number of infected individuals in an isolated population system and the corresponding partially known parameters of the epidemic model. The infectious disease could spread between population systems with known probabilities based on prior knowledge of ecological and biological features of the environment. The problem is then formulated in the context of Bayesian framework and estimated via a probability hypothesis density filter. Each population system under surveillance is assumed to be homogenous and fixed, with daily reports on the number of infected people available for monitoring and prediction. When model parameters are partially known, results of numerical studies indicate that the proposed approach can help early prediction of the epidemic in terms of peak and duration.
Keywords: Filtering, nonlinear dynamic systems, spatiotemporal phenomena, syndromic surveillance
I. Introduction
An epidemic is a term used in epidemiology that refers to “the appearance of new cases of a particular disease in a given human population, during a given time period, at a rate that substantially exceeds the expected number based on recent experience” [1]. The effects of an epidemic can quickly spread from a region to a country, or even a group of countries [2] ranging from a local cluster of a communicable disease to a global threat, as in the case of the ongoing epidemics of AIDS, tuberculosis, and the recent outbreaks of avian influenza (H5N1), SARS, and H1N1 (swine flu) [3], [4].
In surveillance terms, “syndromic” or “prediagnosis” relates to a specific set of symptoms not requiring laboratory confirmation for diagnosis. While syndromic observations are available much earlier than that of postdiagnosis reports, they are not deterministic and suffer from noisy and incomplete data [5]– [7]. The goal of syndromic surveillance is estimating and predicting any increase in the rate of reported cases, allowing a timelier public health response [8], [9].
Syndromic surveillance algorithms and its applications have recently attracted significant attention by scientific community and the governments [8] and there is a plethora of literature devoted to this topic (more comprehensive reviews are provided in [10]– [12] and references therein).
Generally, the problem is often formulated as prospective evaluation of a single-time series. Unfortunately there is not an extensive body of the literature focusing on analysis of multiple data sources with spatial information [13]. A straightforward approach to incorporate spatial information is to apply a separate single-time series approach within each spatial region. In practice, however, the different time series under study may be influenced by common confounding factors, and so they are likely to be correlated [14]. For example, an infectious agent in one region could spread to neighboring areas through various forms of transition pathways, with similar peak and duration [15].
In this paper, a recursive information fusion algorithm is presented for the prediction of epidemic progress amongst a set of isolated population systems. These population systems could represent a specific geographical area such as a city or a country. The population dynamics within each area is described independently, with additional terms accounting for the probability of spread. The problem is then formulated in the Bayesian context of nonlinear multitarget filtering and estimated using a probability hypothesis density (PHD) filter with particle systems implementation known as particle-PHD or sequential Monte Carlo (SMC) PHD filter in tracking literature. While the Bayesian formulation and the nonlinear filtering implementation have been considered earlier, see [16]– [18], none has considered the case of spatial spread of the disease. This paper introduces a novel multitarget approach to include spatial information of reported cases while providing temporal estimates of epidemic peak and duration. We formulate and solve the optimal Bayes predictor when there are several sources of syndromic data streams (each from a specific area) and the number of outbreaks is unknown. The observation data in this case could be noisy and missed in some short intervals, as typically in the case of syndromic data [6]. Numerical results are provided in this paper as a proof of concept using syndromic data based on a real-world epidemic in Switzerland.
The celebrated susceptible-infected-removed (SIR) model [19]–
[21] is a suitable epidemiological
model for our framework. The epidemic curve in the SIR model is formulated by only two parameters of the population:
contact rate 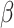 and recovery time
and recovery time 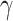 . With values of these parameters at hand, the number of infected people
could be predicted at each time step based on the current population of infected and susceptible.
. With values of these parameters at hand, the number of infected people
could be predicted at each time step based on the current population of infected and susceptible.
Our choice of the SIR model was driven by its widespread adaptation and relevance for the operational context of the problem, which is the short-term prediction for an emerging epidemic that is spreading rapidly. Although the attractive simplicity of the SIR model is a plus, there are some shortcomings involved. A clear downside of this model is the inability to describe any spatial aspects of infectious disease spread [22] , which is addressed in the proposed approach.
II. Motivation
The analysis of infection spread through linked populations systems is of great significance [23] and attracts considerable attention; the Foot and Mouth Disease epidemic of 2001 being an important example [24]. An excellent review of the literature on spatial epidemic models can be found in [5] and [25].
Incorporating spatial information into the epidemic model is motivated by two factors. These factors could contribute to earlier and more accurate modeling during the initial stages of epidemic, and are discussed in this section.
In order to benefit from spatial information, reported data from all geographical areas of interest should be modeled in a holistic approach. This is where single time-series approaches, including single-target filtering, fall short. Spatial information in these methods, if considered at all, is usually handled by running a separate algorithm for each region. Consequently, the spatial autocorrelation is neglected [5].
A. Spatial Patterns of Spread
Spatial patterns and disease spread directions could be observed during the course of an epidemic. In European continent, for example, a west–east direction of influenza spread was observable for several years [26]. The 2003/2004 influenza season in Switzerland is a clear instance of such pattern. The first wave of the epidemic appears in the final weeks of 2003 in Geneva, Switzerland, and then, spreads to nearby cities in the following weeks [15].
Ecological and geographical features could also shape certain patterns of spatial spread. In fox rabies, for example, rivers act as barriers that holds back further spread of the disease [27] .
Once an outbreak is detected, prior knowledge on patterns and directions of spread could contribute to earlier predictions for clean areas, based on their risk of contamination.
B. Behavioral Similarity of Epidemics
Because of the spatial variability of the population (contact rate and recovery time), it is hypothesized that the epidemic curves could vary from place to place and even wave to wave [28]. Therefore, an epidemic in one population system could evolve differently after spreading to another. However, the variability of this kinetic process for the same strain could be usually modeled by a limited range of parameter values [29]. Pandemic influenza cases, for example, are suggested to be latent for two days and infectious for 2.5 days [30].
III. Problem Formulation
A. Modeling Population Dynamics
According to the SIR model, the population of a system can be subdivided into three interacting groups: susceptible,
infectious, and removed individuals [21],
[31]. Let the number of susceptible, infectious, and removed denoted by 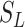 ,
, 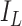 , and
, and 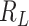 , respectively, so that
, respectively, so that 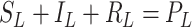 , where
, where 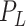 is the total size of
the population system
is the total size of
the population system 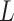 . To represent an epidemic progress in
time as a dynamic model, the following differential equations based on the ‘‘conservation’’
law for the population are derived:
. To represent an epidemic progress in
time as a dynamic model, the following differential equations based on the ‘‘conservation’’
law for the population are derived:
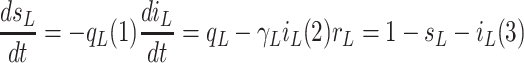 |
where
-
1)
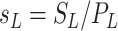 ,
, 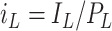 , and
, and 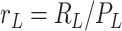 are the normalized compartment sizes;
are the normalized compartment sizes; -
2)
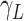 represents the
average infectious period of the disease;
represents the
average infectious period of the disease; -
3)
the term
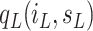 describes
the social interactions between the individuals of population. As in the classical SIR model, we assume
describes
the social interactions between the individuals of population. As in the classical SIR model, we assume
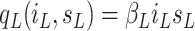 . The contact rate parameter
. The contact rate parameter
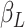 is a product
is a product 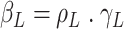 , with
, with 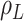 being the basic reproductive number, which represents the average number of new infections produced
by direct contact with a single infected individual that would be expected in a population of entirely susceptible
subjects.
being the basic reproductive number, which represents the average number of new infections produced
by direct contact with a single infected individual that would be expected in a population of entirely susceptible
subjects.
The epidemic model parameters can be assumed to be partially known for every population as interval values, that is
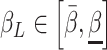 and
and
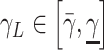 for
each population system of area
for
each population system of area 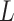 under study.
under study.
B. Measurement Model
For each area 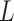 (with an ongoing epidemic) at a specific
time step
(with an ongoing epidemic) at a specific
time step 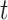 , we assume
, we assume
 |
where 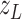 is the observable proportion
(reported cases at time
is the observable proportion
(reported cases at time 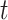 ) of infected population in area
) of infected population in area
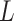 . The noise term
. The noise term 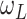 is added to simulate the randomness of real-world syndromic observations (measurements
noise), which is assumed to be uncorrelated to other population systems.
is added to simulate the randomness of real-world syndromic observations (measurements
noise), which is assumed to be uncorrelated to other population systems.
The collection of all measurement for all population systems (observable proportion of infected population) at time
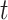 is denoted by
is denoted by
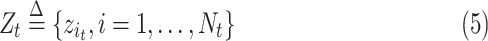 |
where 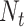 is the total number of measurements
reported at time
is the total number of measurements
reported at time 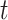 . The aforementioned model allows for
reports on the number of cases to be missed and to include noisy or false reports. The problem is then to estimate the
“true” number of infected areas and normalized number of infected
. The aforementioned model allows for
reports on the number of cases to be missed and to include noisy or false reports. The problem is then to estimate the
“true” number of infected areas and normalized number of infected 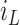 and susceptible
and susceptible 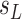 at time
at time
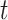 , together with model parameters, for each area using
observations
, together with model parameters, for each area using
observations 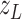 of
(4), collected at time
of
(4), collected at time 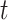 .
.
C. Handling Spatial Information
Modeling spatial population dynamics in humans or animals requires comprehensive ecological and biological knowledge of the pathogenesis of the infectious agent. Accurate reporting of the variables involved (including mobility range, dispersal rates, contact rates, etc.) is paramount for realistic construction of a spatial model [4], [32]. In practice, however, such information is not readily available and can be very expensive to obtain [33] . Moreover, available data primarily reflect politically defined reporting units rather than biologically relevant ecological units [27].
To avoid complications that arise from comprehensive modeling of population dynamics, our model is reduced to the basic assumption of infectious disease spread based on predefined probabilities between each pair of population systems.
IV. Proposed Approach
A. Optimal Bayesian Solution
The model (1)– (3) are given in continuous time. For a recursive algorithm, a discrete-time approximation of this model is required. The state vector for each target area is adopted as
 |
where 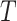 denotes the matrix transpose. It
includes
denotes the matrix transpose. It
includes 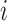 and
and 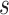 for every infected area and also the imprecisely known parameters
for every infected area and also the imprecisely known parameters 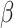 and
and 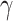 as well as the area
identifier
as well as the area
identifier 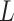 .
.
The state is assumed to follow a Markov process on state space 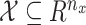 . Let
. Let 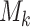 be the
number of ongoing epidemics detected at
be the
number of ongoing epidemics detected at 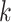 , where
, where
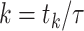 is the discrete time index for small integration
interval
is the discrete time index for small integration
interval 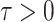 . Suppose that, at time
. Suppose that, at time  , the targets are
, the targets are 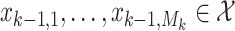 . At the next time step, a subset of these targets may not exist
(finished epidemics), the surviving targets evolve to their new states, and some new targets may appear (due to
disease spread to new areas or spontaneous epidemic emergence). This results in new states
. At the next time step, a subset of these targets may not exist
(finished epidemics), the surviving targets evolve to their new states, and some new targets may appear (due to
disease spread to new areas or spontaneous epidemic emergence). This results in new states 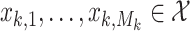 .
.
The state vector in from of (6) includes all the required information for each target (i.e., an ongoing epidemic of SIR type for an isolated population system). Following the discussions provided in Section II, the spread of disease from one area to another, as well as the possibility of new epidemic emergence in areas under study, should also be modeled. The problem is that the state evolution model for each area cannot be processed independently. Moreover, the number of infected areas in this case is unknown and false alarms in the number of reported cases (clutter) are possible.
The random finite set (RFS) [34] approach to multitarget tracking is an emerging and promising approach to address these limitations [35], [36]. In the RFS formulation, the collection of individual targets is treated as a set-valued state, and the collection of individual observations is treated as a set-valued observation, i.e.
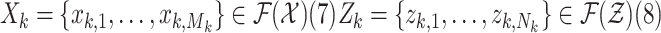 |
where 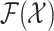 and
and 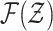 are the respective collections of all finite subsets of
are the respective collections of all finite subsets of
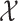 and
and 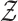 .
.
Set-valued states and set-valued observations modeling approach allows the problem of dynamically estimating
multiple targets in the presence of noisy and incomplete data [34]–
[37]. The problem of spatial monitoring of epidemics is then formulated as multitarget tracking and is posed as
a filtering problem with multitarget state space 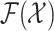 and observation space
and observation space 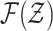 .
.
The RFS that models the multitarget state, is the union of state vectors that survived from previous time step, those which have been spawned by existing targets and those which appear spontaneously, and is given by
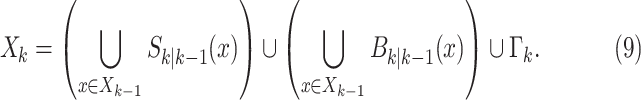 |
In the aforementioned formulation, the first term is the RFS of epidemic states at discrete time index
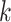 given the previous states
given the previous states 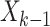 (survived targets).
(survived targets). 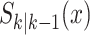 can take on either
can take on either 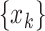 when the
epidemic continues, or
when the
epidemic continues, or 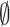 when the epidemic period is
passed. The second term represents the RFS of newly infected areas spawned from the previous epidemics at time step
when the epidemic period is
passed. The second term represents the RFS of newly infected areas spawned from the previous epidemics at time step
 . The last term, RFS
. The last term, RFS 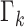 , accounts for spontaneous epidemic emergence in clean areas.
, accounts for spontaneous epidemic emergence in clean areas.
The multitarget measurement at time step 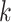 is modeled by the
RFS
is modeled by the
RFS
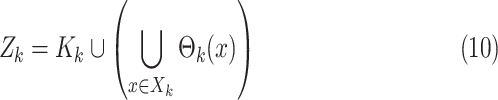 |
where 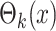 is the RFS of
measurements from multitarget state
is the RFS of
measurements from multitarget state 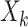 , and
, and 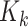 is the RFS of measurements due to false reports (clutter). For a given
target
is the RFS of measurements due to false reports (clutter). For a given
target 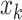 , the term
, the term 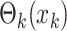 can take on either
can take on either 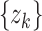 when the target is detected (there is a report available for kth day) with
probability
when the target is detected (there is a report available for kth day) with
probability 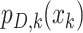 , or
, or 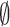 when the target is missed with probability
when the target is missed with probability 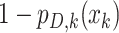 .
.
The formal Bayesian solution is given in the form of the multitarget posterior density 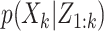 . Based on the posterior density, our aim is to predict the progress of
the epidemic across areas under study at the next time step
. Based on the posterior density, our aim is to predict the progress of
the epidemic across areas under study at the next time step 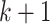 , using the dynamic model equations.
, using the dynamic model equations.
The multitarget Bayes filter propagates the multitarget posterior density 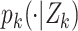 conditioned on the sets of observations up to time
conditioned on the sets of observations up to time 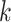 ,
, 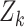 , with the following
recursions.
, with the following
recursions.
Step 1–Prediction:
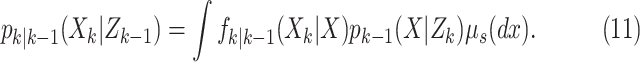 |
Step 2–Update:
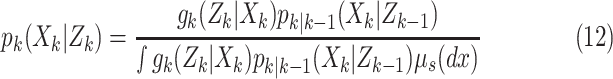 |
where the dynamic model is governed by the multitarget transition density 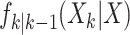 and multitarget likelihood
and multitarget likelihood 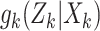 and
and 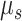 is an
appropriate reference measure on
is an
appropriate reference measure on 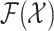 [38]. The randomness in the multitarget evolution and observation described by
(9) and (10) are,
respectively, captured in
[38]. The randomness in the multitarget evolution and observation described by
(9) and (10) are,
respectively, captured in 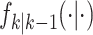 and
and 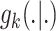 [39]
.
[39]
.
The function 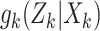 is the joint multitarget
likelihood function of observing the set of measurements,
is the joint multitarget
likelihood function of observing the set of measurements, 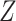 ,
given the set of target states
,
given the set of target states 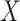 . The parameters for this
density are the set of observations
. The parameters for this
density are the set of observations 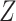 , the unknown set of
targets
, the unknown set of
targets 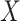 , observation noise, probability of detection
, observation noise, probability of detection
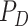 , false alarm
, false alarm 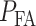 , and clutter models [40].
, and clutter models [40].
The evolution of the epidemic state, by neglecting the process noise for the moment, can be written according to
(1) and (2)
as 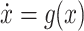 where
where
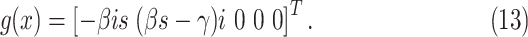 |
For a small integration interval 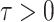 , one could
approximate the state evolution in time using the Euler method:
, one could
approximate the state evolution in time using the Euler method:
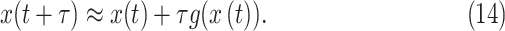 |
The state evolution in discrete time can be expressed as
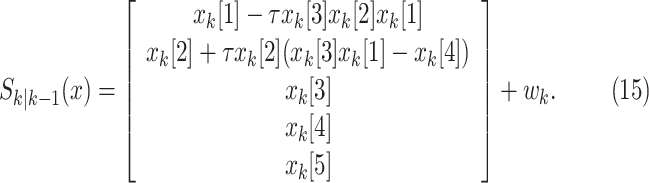 |
In this notation, 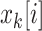 represents the i
th component of vector
represents the i
th component of vector 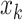 . Process noise
. Process noise  in (14) is assumed to be
zero-mean white Gaussian with a diagonal covariance matrix
in (14) is assumed to be
zero-mean white Gaussian with a diagonal covariance matrix  of size
of size 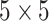 . Its components, except the first two, are
set to zero based on assumption that
. Its components, except the first two, are
set to zero based on assumption that 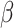 and
and
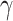 are constant during the epidemic.
are constant during the epidemic.
As mentioned earlier, spatial spread is modeled by a set of predefined probabilities of transition pathways between
areas. In this setting, 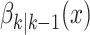 , returns an state
vector of (6) with area identifier selected based on the transition
probability of area
, returns an state
vector of (6) with area identifier selected based on the transition
probability of area 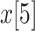 to other areas
to other areas 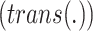 , and is defined by
, and is defined by
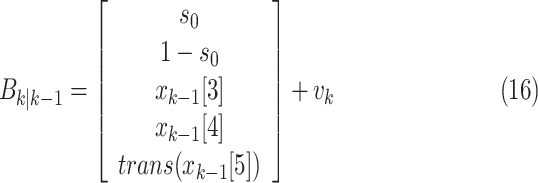 |
where 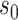 is a small random number representing
the initial population of susceptible and
is a small random number representing
the initial population of susceptible and  is zero-mean
white Gaussian noise with a diagonal covariance matrix
is zero-mean
white Gaussian noise with a diagonal covariance matrix 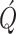 modeling the variation in epidemic parameters in the new population system. The components of matrix
modeling the variation in epidemic parameters in the new population system. The components of matrix
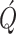 are set to zero except the second and third
components. Subroutine
are set to zero except the second and third
components. Subroutine 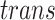 generates a random number
identifying an area under study, such that the area with the highest transition probability with
generates a random number
identifying an area under study, such that the area with the highest transition probability with 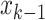 [5] has a higher probability
of selection.
[5] has a higher probability
of selection.
B. Estimation With Particle-PHD Filter
The recursion (11) and
(12) involves multiple integrals on the space 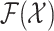 , which are computationally intractable [39]. Therefore, the
multitarget Bayes filter is computationally intractable. The PHD filter [41]
is an approximation that propagates the first-order statistical moment, or PHD, of the RFS of states in time
[35]. Since the PHD filter operates on the single-target state space, it
avoids the combinatorial problem that arises from data association. These outstanding features of the PHD filter are
extremely attractive for practical problems [39]. In our study, the problem
of data association is resolved by including the area identifier (
, which are computationally intractable [39]. Therefore, the
multitarget Bayes filter is computationally intractable. The PHD filter [41]
is an approximation that propagates the first-order statistical moment, or PHD, of the RFS of states in time
[35]. Since the PHD filter operates on the single-target state space, it
avoids the combinatorial problem that arises from data association. These outstanding features of the PHD filter are
extremely attractive for practical problems [39]. In our study, the problem
of data association is resolved by including the area identifier (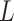 ) in the state vector, because the origin of reported cases of infection is always available.
) in the state vector, because the origin of reported cases of infection is always available.
For a RFS 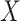 on
on 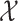 with probability distribution P, its first-order moment is nonnegative
function
with probability distribution P, its first-order moment is nonnegative
function 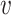 on
on 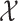 , called the intensity or PHD [35] in tracking literature,
such that for each region
, called the intensity or PHD [35] in tracking literature,
such that for each region 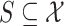
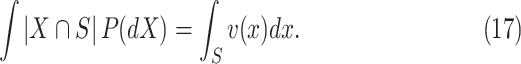 |
Hence, the total mass
 |
gives the expected number of elements of 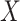 that
are in
that
are in 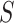 . The local maxima of the intensity
. The local maxima of the intensity 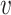 are points in
are points in 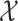 with the highest density of expected number of targets, and therefore, can be used to generate estimates for elements
of
with the highest density of expected number of targets, and therefore, can be used to generate estimates for elements
of 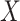 [39].
[39].
Let 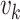 and
and 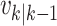 denote the respective intensities associated with the multitarget posterior density
denote the respective intensities associated with the multitarget posterior density
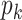 and the multitarget predicted density
and the multitarget predicted density 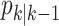 in the recursion (11)
and (12). It can be shown that the posterior intensity can be
propagated in time via the PHD recursion.
in the recursion (11)
and (12). It can be shown that the posterior intensity can be
propagated in time via the PHD recursion.
Step 1– Prediction:
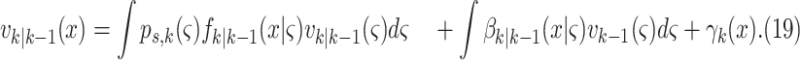 |
Step 2– Update:
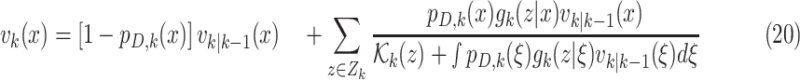 |
where 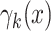 is intensity of the birth
RFS
is intensity of the birth
RFS 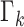 ,
, 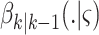 is intensity of the spawn RFS
is intensity of the spawn RFS 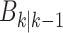 ,
, 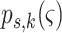 is the
probability of survival with previous state
is the
probability of survival with previous state 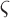 ,
,
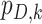 is the proability of detection, and
is the proability of detection, and 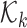 is the intensity of clutter RFS
is the intensity of clutter RFS 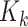 .
.
Since the PHD recursion involves multiple integrals that have no closed-form solutions in general, we develop an approximate solution. Generic sequential Monte Carlo techniques have been proposed to propagate the posterior intensity in time (see [42] and references therein). In this approach, state estimates are extracted from the particles representing the posterior intensity using clustering techniques such as k-means or expectation maximization [43], [44]. The k-means approach was adopted for this study.
The particle-PHD approximates the intensity of the posterior PDF 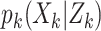 by a weighted random sample. Given a sequence of measurement sets
by a weighted random sample. Given a sequence of measurement sets 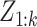 , the approximation at time step
, the approximation at time step 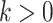 is given as follows.
is given as follows.
In the initialization step, particles are distributed across the state space according to the
prior. The initial intensity function 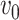 is given by
is given by
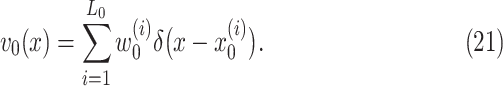 |
Here, 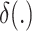 is the Dirac delta function and
is the Dirac delta function and
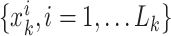 are support points or particles
with associated weights
are support points or particles
with associated weights 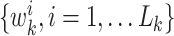 constructing a random measure
constructing a random measure 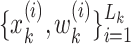 , where
, where 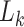 is the particle count for step
is the particle count for step
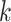 . The weights are selected based on the principle of
importance sampling and are normalized such that
. The weights are selected based on the principle of
importance sampling and are normalized such that 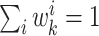 .
.
The particles are propagated in the prediction stage using the dynamic model
(15) and (16).
Particles are also added to allow for new epidemics representing the term 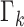 in (9). The predicted intensity function
in (9). The predicted intensity function
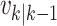 at time step
at time step  is
is
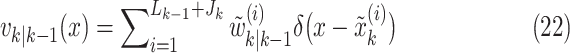 |
where
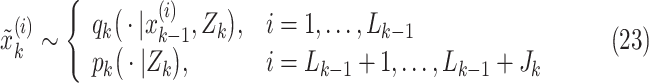 |
and
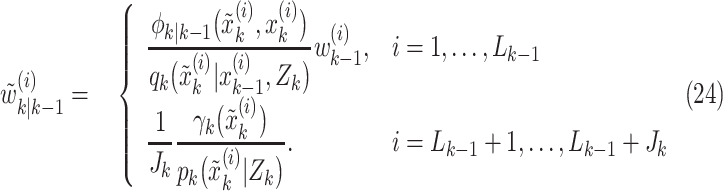 |
In the aforementioned equations 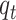 and
and 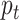 are two important sampling proposal densities by which the samples are
obtained. Here, the
are two important sampling proposal densities by which the samples are
obtained. Here, the 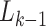 particles are predicted forward
by the kernel
particles are predicted forward
by the kernel 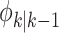 that captures the dynamic
model (14) and (16)
, and an additional
that captures the dynamic
model (14) and (16)
, and an additional 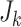 particles are drawn to detect new
and emergent epidemics.
particles are drawn to detect new
and emergent epidemics.
The prediction steps are carried out until a set of measurements of reported cases 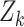 becomes available, at time index
becomes available, at time index 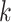 . When the measurements are received, weights are calculated for the particles based on their
likelihoods, which are determined by the statistical distance of the particles to the set of observations (i.e.,
ongoing epidemics). Given that the particle representation of the predicted intensity function is available at time
step
. When the measurements are received, weights are calculated for the particles based on their
likelihoods, which are determined by the statistical distance of the particles to the set of observations (i.e.,
ongoing epidemics). Given that the particle representation of the predicted intensity function is available at time
step 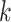 , the updated intensity function
, the updated intensity function
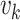 is given by
is given by
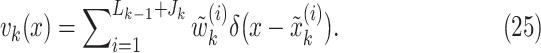 |
In this formulation, 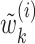 are given by
are given by
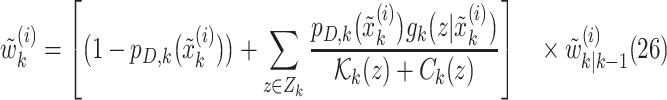 |
where 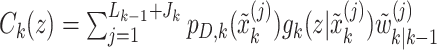 . We, therefore, have a
discrete weighted approximation of the true posterior
. We, therefore, have a
discrete weighted approximation of the true posterior  . The sum of the weights gives the estimated number of ongoing epidemics. For more details on
prediction and update steps see [40] and
[43] and for detailed implementation techniques including resampling step see
[42].
. The sum of the weights gives the estimated number of ongoing epidemics. For more details on
prediction and update steps see [40] and
[43] and for detailed implementation techniques including resampling step see
[42].
V. Numerical Results
A. Simulation Setup
An experimental dataset based on the reported cases in 2003/2004 influenza season in Switzerland (see Section II) is used for prediction of an epidemic. Three cities Geneva, Bern, and Lausanne were chosen for the following experiments.
This choice was driven by two main factors; first there is one dominant influenza strain in the period of interest, and second clear empirical spatial patterns of disease spread could be observed.
In the model, it is assumed that measurements from different cities are available for each day (using interpolation of weekly data) during the course of the epidemic, with the exception of a few days with possible missed reports. For each simulation day, daily counts above a specified threshold are provided to the algorithm. In order to study the algorithm behavior in different scenarios, manual modification to daily numbers and the threshold were performed in some experiments, when needed.
The problem is then to perform estimation at each time step when new measurements are reported until the
“cutoff” day, after which the goal is to predict the epidemic curve (which is the number of infected
population through time). The prediction is performed using the estimated parameters of the SIR model in the state
vector. The predictive performance of the proposed algorithm was compared with the ‘‘true’’
number of reported cases obtained from the dataset, and also with the result of a SIR curve fit obtained using an
exhaustive search. The initial number of particles was set to 6000 consisting of  for the survived and spawned targets and
for the survived and spawned targets and 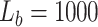 for new targets. The algorithm assumed partial knowledge of model parameters using
for new targets. The algorithm assumed partial knowledge of model parameters using
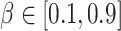 and
and 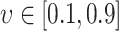 . Disease transition probabilities were also selected based on
real-world data such that transition Geneva to Lausanne and Lausanne to Bern has the highest probabilities assigned.
More precise estimates of these parameters could be obtained from detailed epidemiological studies of an emerging
epidemic. These estimates would then simply be incorporated into models such as the one here.
. Disease transition probabilities were also selected based on
real-world data such that transition Geneva to Lausanne and Lausanne to Bern has the highest probabilities assigned.
More precise estimates of these parameters could be obtained from detailed epidemiological studies of an emerging
epidemic. These estimates would then simply be incorporated into models such as the one here.
The dataset files and implementation sources files in MATLAB are available from https://prlab.um.ac.ir/index.php/resources/.
B. Prediction Performance
In the following set of results, prediction errors for the upcoming observations at each cutoff day during the course of the epidemic are calculated. The results are compared with the SIR fit over the observations using an exhaustive search. Regression and model fitting approaches are common in the biosurveillance literature for comparison and validation [7], [45].
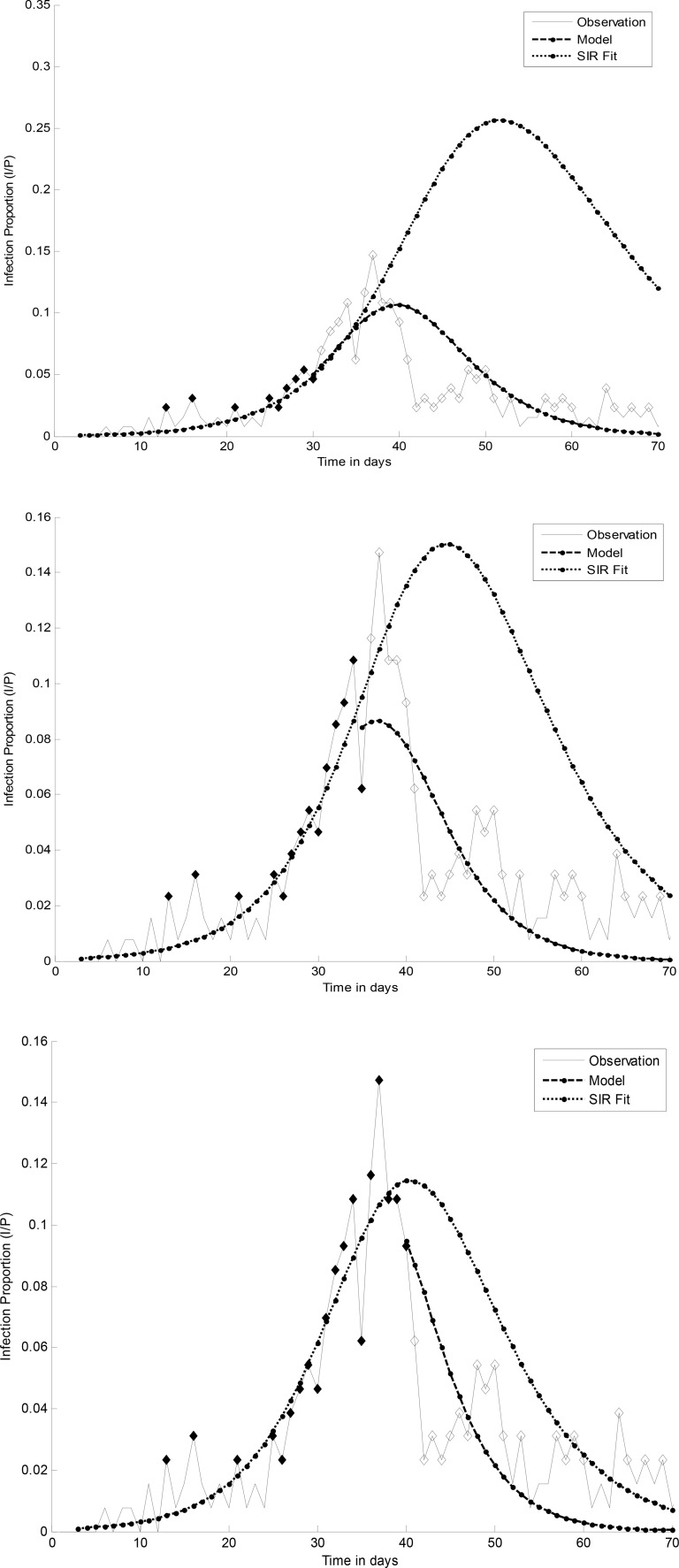
Fig. 1 compares the prediction results of the model and SIR fit for
different cutoff days. This figure serves to demonstrate the prediction robustness of the proposed algorithm by
filtering out noisy data and incorporating prior knowledge into the model. Although the predefined intervals for
parameters 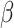 and
and 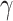 were the same, the fitted SIR curve suffers from imprecise predictions and high
fluctuations, especially during the early days of monitoring.
were the same, the fitted SIR curve suffers from imprecise predictions and high
fluctuations, especially during the early days of monitoring.
Fig. 1.
Prediction results for day 30, 35, and 40 for Lausanne. The bold and thin dashed lines are the predicted curves for model and the SIR fit, respectively.
C. Prior Knowledge in Early Prediction
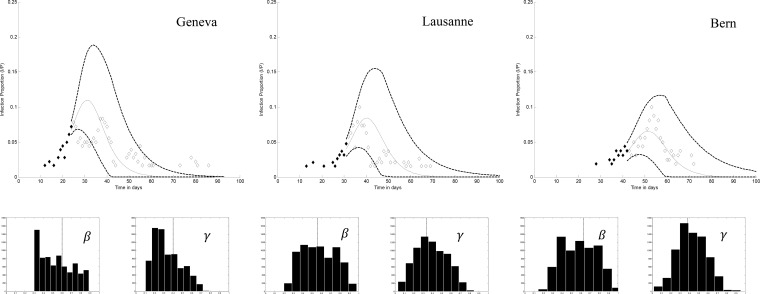
As more observations become available, prior knowledge on partially known model parameters is increased. The possible similarity of epidemic waves (see Section II-B) would then help improve early prediction when a new population is infected.
Fig. 2 displays estimation and prediction results after ten days of monitoring the epidemic waves for selected cities. It is observed that the 95% confidence interval area gets tighter in the second and third wave. A subset of particles for Lausanne and Bern are generated based on current estimates in Geneva and Lausanne, respectively, using (15), which improves convergence for these cities. In the second and third waves, the particles are more concentrated in the vicinity of SIR fit.
Fig. 2.
Estimated epidemic curves and histograms of model parameters 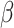 and
and 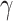 after ten days of monitoring in
selected cities. Predicted curve and 95% confidence intervals are displayed by solid and dashed lines,
respectively. In the histograms, the vertical dashed line is the result of SIR fit over all observations.
after ten days of monitoring in
selected cities. Predicted curve and 95% confidence intervals are displayed by solid and dashed lines,
respectively. In the histograms, the vertical dashed line is the result of SIR fit over all observations.
Studying Fig. 2, one can make the observation that in accordance with
our expectations, the estimation and prediction results are more certain when prior knowledge of parameters
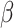 and
and 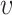 is gathered during the first wave. However, even when the knowledge of these parameters is imprecise,
the reported cases corresponding to what we consider as the ‘‘true’’ number of infected people
(empty diamonds) are always enveloped by predictions after a few days of monitoring.
is gathered during the first wave. However, even when the knowledge of these parameters is imprecise,
the reported cases corresponding to what we consider as the ‘‘true’’ number of infected people
(empty diamonds) are always enveloped by predictions after a few days of monitoring.
D. Disease Transition Probabilities
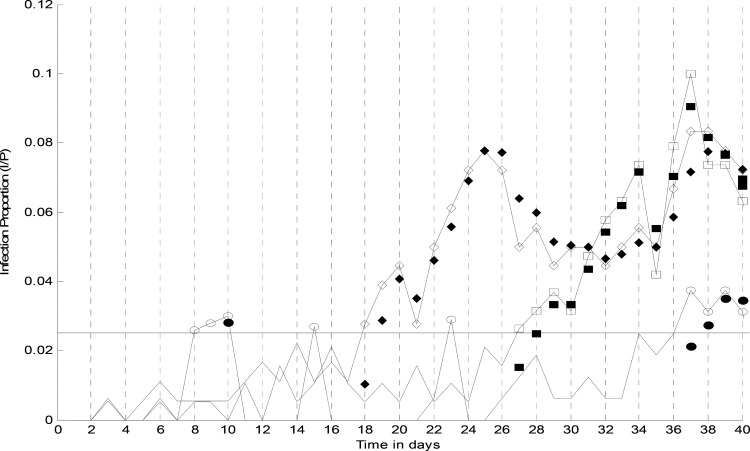
Based on the prior knowledge of west–east direction of epidemic spread [26] , [15], disease transition probabilities were selected such that the first wave of influenza epidemic is more probable to appear in Geneva. The epidemic would spread to Lausanne with high probability and from there to the next city, Bern. The following experiment studies the influence of the predefined disease transition probabilities on the proposed algorithm. In Fig. 3 the “true” observations for the first 40 days of monitoring, together with state estimate of infected population are displayed. The horizontal solid line is the event threshold, determining which observations are fed to the filtering algorithm.
Fig. 3.
Influence of epidemic transition probability in model behavior. Empty circles, diamonds and squares are “true” number of reported cases for Bern, Geneva, and Lausanne, respectively. The filled marks represent model estimated number of reported cases and the horizontal solid line is the threshold. The epidemic is expected to start in Geneva and from there spread to Lausanne and Bern.
Disease transition probabilities dictate the corresponding population system in the randomly generated state vectors. In this case, more state vectors for Geneva are generated.
Since the set of the state vectors representing spontaneous epidemics 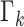 contains more particles for Geneva, on days 8 and 9 the (manually modified) number of
reported cases are not detected as an ongoing epidemic and are ignored as false alarms simply because the summation of
the corresponding particle weights (
contains more particles for Geneva, on days 8 and 9 the (manually modified) number of
reported cases are not detected as an ongoing epidemic and are ignored as false alarms simply because the summation of
the corresponding particle weights (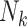 ) is not greater than
1, until the third report on day 10. Comparing with the algorithm behavior on day 18, a single report for Geneva is
estimated as an epidemic and is tracked during the following days.
) is not greater than
1, until the third report on day 10. Comparing with the algorithm behavior on day 18, a single report for Geneva is
estimated as an epidemic and is tracked during the following days.
Once an ongoing epidemic is detected in a city, detection sensitivity is increased for its neighbors as more
particles are generated, representing target birth through spatial spread with 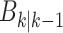 in (16). This is the case of the first
report of Lausanne on day 26 and also the sixth report of Bern on day 36.
in (16). This is the case of the first
report of Lausanne on day 26 and also the sixth report of Bern on day 36.
E. Spatial Information
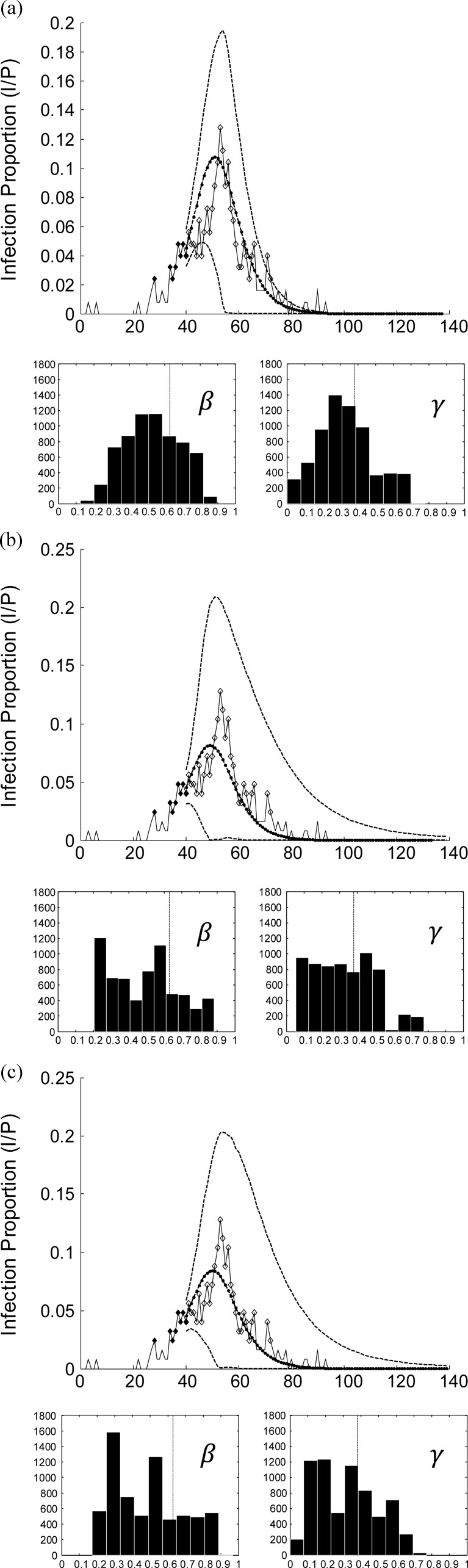
In this section, the effects of spatial information in prediction results are studied. To this end, a comparison of the prediction accuracy and confidence of the proposed algorithm with a version of the algorithm with no spatial information (zero disease transition probability) and also a similar approach based on a single target (no spatial information) particle filter [16], is provided.
With disease transition probabilities defined beforehand, prior knowledge on SIR model parameters in form of range values are acquired during the monitoring phase. This improves the prediction results by providing a set of starting points in the search space of the problem for the newly infected areas.
As depicted in Fig. 4, the confidence interval is tighter and the predicted parameters are more concentrated around the “right” answer in the proposed algorithm as opposed to the other two methods.
Fig. 4.
Prediction results and confidence interval after 40 days of monitoring in city Bern; (a) proposed algorithm, (b) proposed algorithm with no spatial information provided and (c) single target particle filter implementation with no spatial information as in [16]. Marks and symbols as in Fig. 2.
By ignoring disease transition probabilities [see Fig. 4(b)], the prior knowledge on SIR model parameters is lost. It can be observed that the confidence margin in this case is larger and the histogram of predicted parameters display a wide range of possibilities. This is also true for any similar algorithm without this kind of prior knowledge as shown in Fig. 4 (c).
F. Peak Duration and Intensity Prediction
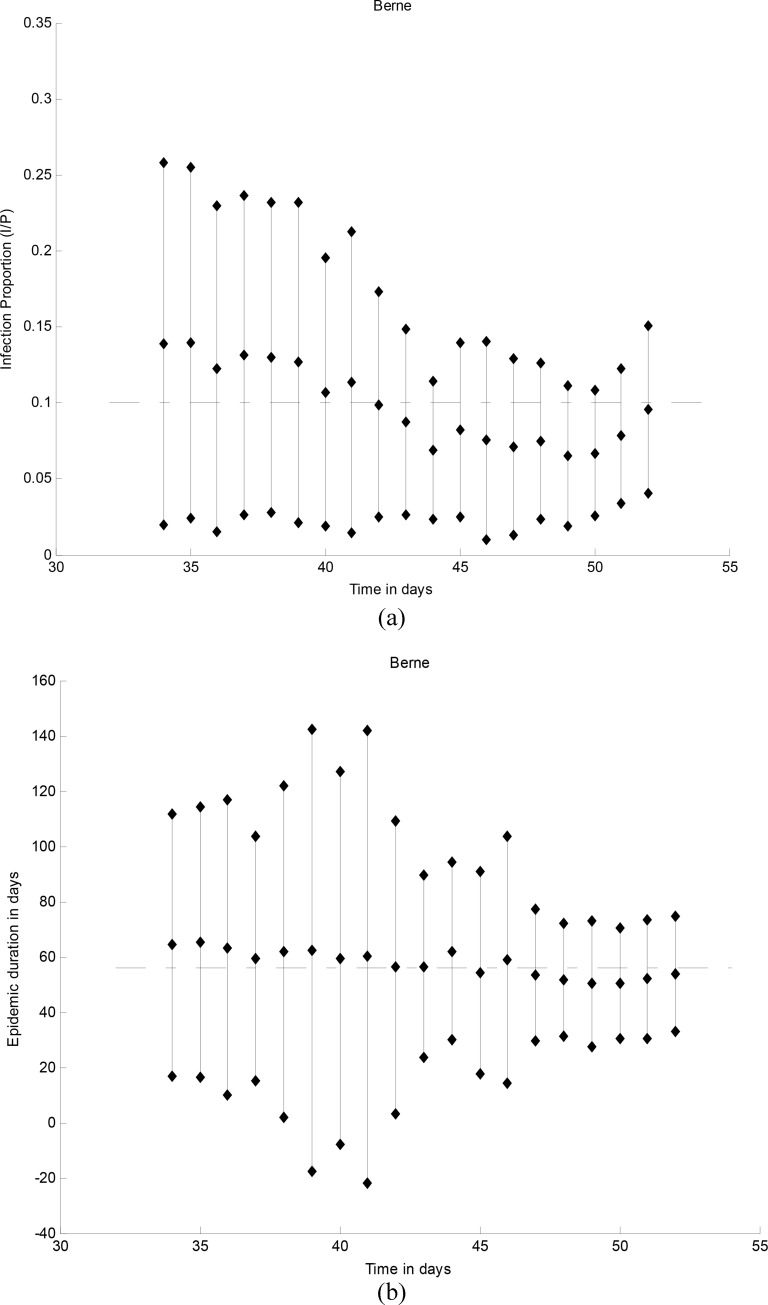
Prediction performance of epidemic duration and peak intensity is studied in the final set of results (see
Fig. 5). For the epidemic in Bern, 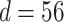 and
and 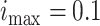 . At each
cutoff day, intensity is computed using the approximate formulae from Theorem 2.1 in
[46] under the assumption that initial susceptible population
. At each
cutoff day, intensity is computed using the approximate formulae from Theorem 2.1 in
[46] under the assumption that initial susceptible population 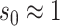 and initial infected population
and initial infected population 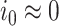 .
.
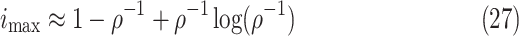 |
where 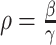 (see
Section III-A). Parameters
(see
Section III-A). Parameters 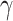 and
and 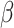 are estimated from the
observations available up to the cutoff day (current estimate of the state vector). The duration of the epidemic is
calculated by measuring the size of an SIR curve simulation using the estimated
are estimated from the
observations available up to the cutoff day (current estimate of the state vector). The duration of the epidemic is
calculated by measuring the size of an SIR curve simulation using the estimated 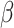 and
and 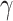 . The results further
show that duration and intensity are reasonably acceptable, even in short periods of observation. The uncertainty in
estimation decreases as more observations become available.
. The results further
show that duration and intensity are reasonably acceptable, even in short periods of observation. The uncertainty in
estimation decreases as more observations become available.
Fig. 5.
(a) Epidemic peak intensity 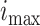 and (b)
duration
and (b)
duration 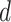 for cutoff days 34–52 in reported cases of
city of Bern together with the confidence intervals. The results are averaged over ten runs of the algorithm.
Parameter values obtained by fitting a SIR curve to data of the epidemic wave are shown with the horizontal line.
for cutoff days 34–52 in reported cases of
city of Bern together with the confidence intervals. The results are averaged over ten runs of the algorithm.
Parameter values obtained by fitting a SIR curve to data of the epidemic wave are shown with the horizontal line.
VI. Conclusion
In this paper, we proposed an algorithm for estimation and prediction of epidemic outbreaks formulated in the context of multitarget nonlinear filtering, based on the set of observations of the number of infected people in loosely coupled population systems. The epidemic progression in time is modeled using the classical compartmental SIR model. While an independent set of SIR parameters is used to model the epidemic dynamics within each area, the proposed framework is capable of modeling spatial information as well. This is carried out by defining a set of transition probabilities between each pair of monitored geographical areas. Prediction and estimation results for newly infected areas also benefit from early convergence by narrowing the range of possible model parameters based on epidemic behavior in neighboring areas. The algorithm, implemented as a particle-PHD filter, provides continuous estimation of the state of all epidemics, including the infected population and the partially known parameters of the SIR model for every population system. Experimental results show that the proposed framework can be useful in providing timely prediction of the epidemic peak and duration when the uncertainty in prior knowledge of model parameters is limited.
The proposed method is rather a conceptual solution for a new biosurveillance and still at its early stages of development. Further research is concerned with practical problems regarding its operational deployment. For instance, there is a potential challenge in selecting more complicated epidemic models and also incorporating population migration patterns (variable population). Our future work would involve a generalization of the proposed framework to include more realistic criterions with regards to known ecological and biological features of animal and human populations.
Biographies

Amin Zamiri was born in Tehran, Iran, in 1985. He received the B.S. degree from the Ferdowsi University of Mashhad, Mashhad, Iran and the M.S. degree in software engineering from Shahid Beheshti University, Tehran, Iran, in 2010.
He is currently a researcher at Ferdowsi University of Mashhad. His research interests include multisource multitarget information fusion, data mining and artificial intelligence.

Hadi Sadoghi Yazdi received the B.S. degree in electrical engineering from Ferdowsi Mashad University of Iran, in 1994, the M.Sc. and the Ph.D. degrees in electrical engineering from Tarbiat Modarres University of Iran, Tehran, in 1996 and 2005, respectively. He works in Department of Computer Engineering as Associate Professor at Ferdowsi University of Mashhad. His research interests include pattern recognition, and optimization in signal processing. He has more than 40 journal publications in the areas of interest.

Sepideh Afkhami Goli received her B.S. degree from Ferdowsi University of Mashhad, Iran and M.S. degree in Information Technology from Sharif University, Tehran, Iran.
She is currently working towards Ph.D. degree at Calgary University, Alberta, Canada, focusing on multisource multitarget information fusion, data mining and artificial intelligence with applications in cooperative intelligent transportation systems.
Contributor Information
Amin Zamiri, Email: amin.zamiri@gmail.com.
Hadi Sadoghi Yazdi, Email: h-sadoghi@um.ac.ir.
Sepideh Afkhami Goli, Email: sepideh.afkhamigoli@ucalgary.ca.
References
- [1].Le Strat Y. and Carrat F. , “Monitoring epidemiologic surveillance data using hidden Markov models,” Stat. Med., vol. 18 , no. 24, pp. 3463–3478, 1999. [DOI] [PubMed] [Google Scholar]
- [2].Jiang X., Wallstrom G. , Cooper G. F., and Wagner M. M., “Bayesian prediction of an epidemic curve,” J. Biomed. Inform., vol. 42, no. 1, pp. 90– 99, Feb. 2009. [DOI] [PubMed] [Google Scholar]
- [3].Liang H. and Xue Y. , “Investigating public health emergency response information system initiatives in China,” Int. J. Med. Inform. , vol. 1, no. 2, p. 9–10, 2004. . [DOI] [PMC free article] [PubMed] [Google Scholar]
- [4].Anderson R. M., Fraser C. , Ghani A. C., Donnelly C., Riley S., Ferguson N. M. , Leung G. M., Lam T. H., and Hedley A. J., “ Epidemiology, transmission dynamics and control of SARS: The 2002–2003 epidemic ,” Philos. Trans. Roy. Soc. Lond. B., Biol. Sci., vol. 359, no. 1447 , pp. 1091–1095, Jul. 2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5].Robertson C., Nelson T. A. , Macnab Y. C., and Lawson A. B., “Review of methods for space-time disease surveillance,” Spat. Spatiotemporal Epidemiol., vol. 1, no. 2–3, pp. 105 –116, Jul. 2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [6].Manitz J., “ Automated detection of infectious disease outbreaks,” Diploma thesis, Ludwig-Maximilians-Universität München, München, Germany, 2010. [Google Scholar]
- [7].Zhou X., Li Q. , Zhu Z., Zhao H., Tang H., and Feng Y., “Monitoring epidemic alert levels by analyzing internet search volume,” IEEE Trans. Biomed. Eng., vol. 60 , no. 2, pp. 446–452, Feb. 2013. . [DOI] [PubMed] [Google Scholar]
- [8].Paterson B. J. and Durrheim D. N., “The remarkable adaptability of syndromic surveillance to meet public health needs,” J. Epidemiol. Global Health, vol. 3, no. 1, pp. 41–47, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [9].Woodall W. H., Marshall J. B. , Joner M. D., and Shannon E., “On the use and evaluation of prospective scan methods for health-related surveillance,” J. Roy. Statist. Soc., Ser. A, vol. 171, pp. 223–237, 2008. [Google Scholar]
- [10].Sonesson C. and Bock D. , “A review and discussion of prospective statistical surveillance in public health,” J. Roy. Statist. Soc., Ser. A , vol. 166, no. 1, pp. 5–21, 2003 . [Google Scholar]
- [11].Straif-Bourgeois S. and Ratard R., “Handbook of Epidemiology,” in Handbook of Epidemiology. New York, NY, USA : Springer-Verlag, 2005, pp. 1328– 1362. [Google Scholar]
- [12].Wagner M., Moore A. , and Aryel R., Handbook of Biosurveillance. New York, NY, USA : Academic, 2006. [Google Scholar]
- [13].Buckeridge D. D. L., Burkom H., Campbell M., Hogan W. R., and Moore A. W., “ Algorithms for rapid outbreak detection: A research synthesis,” J. Biomed. Inform., vol. 38, no. 2, pp. 99–113, 2005. [DOI] [PubMed] [Google Scholar]
- [14].Corberán-Vallet A., “Prospective surveillance of multivariate spatial disease data,” Stat. Methods Med. Res., vol. 21, pp. 457–477, Apr. 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [15].Smieszek T., Balmer M. , Hattendorf J., Axhausen K. W., Zinsstag J., and Scholz R. W., “Reconstructing the 2003/2004 H3N2 influenza epidemic in Switzerland with a spatially explicit, individual-based model ,” BMC Infect. Dis., vol. 11, no. 1, pp. 115 –133, Jan. 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [16].Skvortsov A. and Ristic B. , “Monitoring and prediction of an epidemic outbreak using syndromic observations,” Math. Biosci., vol. 240, no. 1, pp. 12–19, Nov. 2012. [DOI] [PubMed] [Google Scholar]
- [17].Jègat C., Carrat F. , Lajaunie C., and Wackernagel H., “Early detection and assessment of epidemics by particle filtering ,” in geoENV VI—Geostatistics for Environmental Applications, vol. 15, Soares A., Pereira M., and Dimitrakopoulos R., Eds. Dordrecht, Netherlands: Springer, 2008, pp. 23 –35. [Google Scholar]
- [18].Ristic B., “ Predicting the progress and the peak of an epidemic,” in Proc. IEEE Int. Conf. Acoustics, Speech Signal Process., 2009, pp. 513–516 .
- [19].Sazonov I., Kelbert M. , and Gravenor M. B., “The speed of epidemic waves in a one-dimensional lattice of SIR models,” Math. Model. Nat. Phenom., vol. 3, no. 4, pp. 28–47, Dec. 2008. [Google Scholar]
- [20].Daley D. J. and Gani J. , Epidemic Modelling: An Introduction . Cambridge, U.K.: Cambridge Univ. Press, 2001. [Google Scholar]
- [21].Murray J. D., Mathematical Biology, 3rd ed. London, U.K.: Springer-Verlag, 1989. [Google Scholar]
- [22].Keeling M. J. and Danon L. , “Mathematical modelling of infectious diseases,” Brit. Med. Bull., vol. 92, pp. 33 –42, Jan. 2009. [DOI] [PubMed] [Google Scholar]
- [23].Rass L. and Radcliffe J. , “Spatial deterministic epidemics,” Bull. Amer. Math. Soc., vol. 42, no. 4 , pp. 521–527, 2005. [Google Scholar]
- [24].Ferguson N., Donnelly C. , and Anderson R., “Transmission intensity and impact of control policies on the foot and mouth epidemic in Great Britain,” Nature, vol. 413, pp. 542–548, 2001. [DOI] [PubMed] [Google Scholar]
- [25].Mollison D., Epidemic Models: Their Structure and Relation to Data. Cambridge, U.K.: Cambridge Univ. Press, 1995. [Google Scholar]
- [26].Paget J. and Marquet R. , “Influenza activity in Europe during eight seasons (1999–2007): An evaluation of the indicators used to measure activity and an assessment of the timing, length and course of peak activity (spread) across Europe,” BMC Infect. Dis., vol. 30, no. 7, pp. 141–148 , 2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [27].Smith D. L., Lucey B. , Waller L. A., Childs J. E., and Real L. A., “ Predicting the spatial dynamics of rabies epidemics on heterogeneous landscapes,” Proc. Nat. Acad. Sci. USA, vol. 99, no. 6, pp. 3668 –72, Mar. 2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [28].Lee S. S. and Wong N. S. , “Reconstruction of epidemic curves for pandemic influenza A (H1N1) 2009 at city and sub-city levels,” Virol. J. , vol. 7, no. 1, pp. 321–327, Jan. 2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [29].Hall I. M., Gani R. , Hughes H. E., and Leach S., “Real-time epidemic forecasting for pandemic influenza,” Epidemiol. Infect., vol. 135, no. 3, pp. 372– 385, Apr. 2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [30].Flahault A, Letrait S , Blin P., Hazout S., Ménarés J., and Valleron A. J., “ Modelling the 1985 influenza epidemic in France,” Stat. Med., vol. 7 , pp. 1147–1155, 1988. [DOI] [PubMed] [Google Scholar]
- [31].Anderson R. and May R. , “Population biology of infectious diseases: Part I,” Nature, vol. 280, pp. 361 –367, 1979. [DOI] [PubMed] [Google Scholar]
- [32].Deal B., Farello C. , Lancaster M., Kompare T., and Hannon B., “ A dynamic model of the spatial spread of an infectious disease: the case of fox rabies in Illinois ,” Environ. Model. Assessment, vol. 5, pp. 47 –62, 2000. [Google Scholar]
- [33].Plowright W., “ Research on wildlife diseases: Is a reappraisal necessary?” Revue Scientifique et Technique de l'OIE, vol. 7, no. 4, pp. 783 –795, 1988. [DOI] [PubMed] [Google Scholar]
- [34].Mahler R., “ The random set approach to data fusion,” Proc. SPIE, vol. 2234, pp. 287–295, 1994. [Google Scholar]
- [35].Mahler R., “ Multitarget Bayes filtering via first-order multitarget moments,” IEEE Trans. Aerosp. Electron. Syst., vol. 39, no. 4, pp. 1152 –1178, Oct. 2003. [Google Scholar]
- [36].Goodman I., Mahler R. , and Nguyen H., Mathematics of Data Fusion. New York, NY, USA : Springer, 1997. [Google Scholar]
- [37].Mahler R., “ Global integrated data fusion,” presented at the 7th Nat. Symp. Sens. Fusion, Albuquerque, NM, USA, 1994. [Google Scholar]
- [38].Vo B., Singh S. , and Doucet A., “Sequential Monte Carlo methods for multitarget filtering with random finite sets,” IEEE Trans. Aerosp. Electron. Syst., vol. 41 , no. 4, pp. 1224–1245, Oct. 2005 . [Google Scholar]
- [39].Vo B.-N. and Ma W.-K. , “The Gaussian mixture probability hypothesis density filter,” IEEE Trans. Signal Process., vol. 54, no. 11, pp. 4091–4104, Nov. 2006. [Google Scholar]
- [40].Clark D., “ Multiple target tracking with the probability hypothesis density filter,” Ph. D. thesis, Heriot-Watt University, Riccarton, U.K., 2006. [Google Scholar]
- [41].Mahler R. P., “ A theoretical foundation for the Stein–Winter probability hypothesis density (PHD) multi-target tracking approach,” presented at the MSS Nat. Symp. Sensor Data Fusion, San Antonio, TX, USA, 2000. [Google Scholar]
- [42].Stordal A. S., “ Sequential Monte Carlo methods for Bayesian filtering,” Ph.D. thesis, University of Bergen, Bergen, Norway, 2008. [Google Scholar]
- [43].Sidenbladh H., “ Multi-target particle filtering for the probability hypothesis density,” in Proc. 6th Int. Conf. Inform. Fusion, 2003, pp. 800– 806.
- [44].Zajic T. and Mahler R. , “Particle-systems implementation of the PHD multitarget-tracking filter,” Proc. SPIE, vol. 5096, pp. 291–299, 2003. [Google Scholar]
- [45].Vullings R., de Vries B. , and Bergmans J. W. M., “An adaptive Kalman filter for ECG signal enhancement,” IEEE Trans. Biomed. Eng., vol. 58, no. 4 , pp. 1094–1103, Apr. 2011. [DOI] [PubMed] [Google Scholar]
- [46].Hethcote H., “ The mathematics of infectious diseases,” SIAM Rev., vol. 42, no. 4, pp. 599–653, 2000. [Google Scholar]