A simple model for COVID-19

Abstract

An $S{L}_1{L}_2{I}_1{I}_2{A}_1{A}_{2}R$ epidemic model is formulated that describes the spread of an epidemic in a population. The model incorporates an Erlang distribution of times of sojourn in incubating, symptomatically and asymptomatically infectious compartments. Basic properties of the model are explored, with focus on properties important in the context of current COVID-19 pandemic.

1. Introduction

As part the authors’ work on COVID-19, we have relied several times on a specific model derived from an earlier model (Arino, Brauer, van den Driessche, Watmough, & Wu, 2007). This model, like that previous model, is applicable to a variety of emerging and re-emerging pathogens exhibiting an observable latent period as well as symptomatic and asymptomatic infections. The specificity of the present model is the further incorporation of Erlang distributions of the time of sojourn in some of the important compartments in the model. Indeed, most of the work we have carried out so far on COVID-19 has concerned predictions over a short time period, often no more than a month. In this context, incorporating a better description of sojourn times is extremely important. The present model generalises the simple 3-compartment SIR model to age of infection models, providing a reasonable approximation to the details of progression through infection with a minimal number of parameters and the convenience of an ODE model over integral or PDE models.

In this short note, we present this model and explain some of its features in the context of the current COVID-19 pandemic. We also conduct a simple sensitivity analysis in order to highlight the most important parameters in the model.

The main conclusion of the analysis here is that model responses are highly sensitive to the value of the parameter describing the fraction of cases that are asymptomatic, highlighting the need for intensive research to get a better handle on the value of this critical parameter.

2. The model

We use a simple variation on the classic SLIAR epidemic model for susceptible, latently infected, symptomatic and asymptomatic infectious and removed individuals, with numbers denoted respectively S, L, I, A and R (Arino, Brauer, van den Driessche, Watmough, & Wu, 2006). The SLIAR epidemic model has often been used to describe the propagation of diseases caused by virus leading to respiratory illness such as influenza (Jin et al., 2011; Kim, Lee, & Jung, 2017; Li et al., 2020). Contrary to SLIR (or SEIR) models, it allows to consider infection by asymptomatic individuals, which in the case of COVID-19 has been reported to have substantially contributed to disease propagation (Li et al., 2020).

As the time scale of interest is short, the model has no birth or natural death, only death by removal from the infectious compartments I and A. It is therefore an epidemic model, as opposed to an endemic model. Furthermore, because the time horizon for simulations is very short in comparison to reported estimates of incubation period (Backer, Klinkenberg, & Wallinga, 2020; Lauer et al., 2020a) and communicable period (Hu et al., 2020), making a more appropriate description of sojourn times in the incubation, symptomatically infectious and asymptomatically infectious compartments is important. Although not ideal, we use an Erlang distribution, i.e., a Gamma distribution with integer shape parameter. To simplify the problem, we use two compartments for each of the L, I and A states (Arino, 2020). We could use more if need be; the overall set up would vary very little.

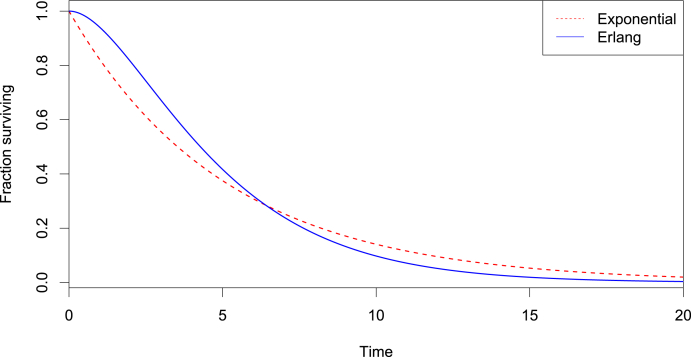
Let us briefly justify this modification in the current context. Consider, for instance, the incubation period, i.e., the time between infection and the onset of symptoms. A wide range of possible durations has been reported. Let us suppose, for instance, that the mean incubation period of COVID-19 is 5.2 days as reported by (Lauer et al., 3AD). Then, comparing the fraction of individuals infected at time 0 and still incubating at time t, we obtain Fig. 1. The Erlang distribution thus allows both a less pronounced early end and a less extended duration of the incubation period. If need be, we could further extend this behaviour by adding more compartments and thus increasing the shape parameter of the Erlang distribution.

Fig. 1.

Comparison of the survival functions of an exponential and an Erlang distributions with mean 5.2 days (and shape 2 in the case of the Erlang distribution).

Note that this does not increase the complexity of the model and, for instance, parameter fitting procedures, since we use the same parameter for all compartments in these “chains”; for instance, the incubation period is described using the single parameter ε; the only difference with the exponential case is that, here, $2/\epsilon$ is the mean sojourn time in the combined $L_1$ and $L_2$ compartments.

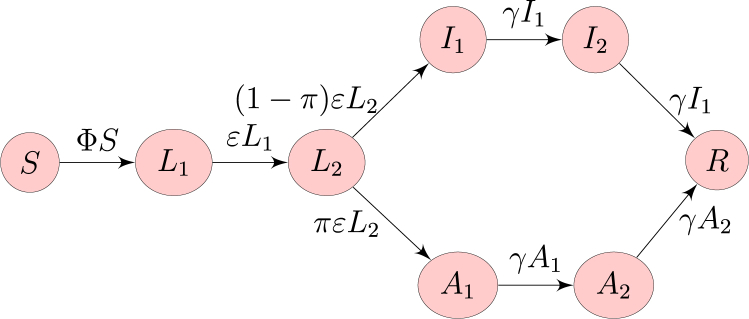
The flow diagram of the model is as shown in Fig. 2.

Fig. 2.

Flow diagram of the $S{L}_1{L}_2{I}_1{I}_2{A}_1{A}_{2}R$ model. Here, $\text{Φ}=f\left(\mathbf{x}\right)\left(I_1+I_2+\xi \left(A_1+A_2\right)+\eta L_2\right)$ is the force of infection.

We suppose that incidence takes the form

$$\Phi S=f\left(\mathbf{x}\right)\left(I_1+I_2+\eta L_2+\xi \left(A_1+A_2\right)\right)S,$$ (1)

where β is the transmission coefficient, η and ξ are the attenuation factors for transmission by incubating and asymptomatic cases, respectively, $\mathbf{x}=\left(S,L_1,L_2,I_1,I_2,A_1,A_2,R\right)$ is the state vector and $f:{\mathrm{ℝ}}_{+}^8\to {\mathrm{ℝ}}_{+}$ is the function describing the nature of the overall incidence function. As in Fig. 2, we can also think of incidence as taking the form $\text{Φ}S$; $\text{Φ}$ in this case is the force of infection. Typical choices for f include $f\left(\mathbf{x}\right)=\beta$, making the incidence mass action, and $f\left(\mathbf{x}\right)=\beta /⟨\mathbf{1},x⟩$, with $\mathbf{1}=\left(1,\dots ,1\right)$, giving proportional incidence.

The system governing the behaviour is then the following:

$$S’=-f\left(\mathbf{x}\right)\left(I_1+I_2+\xi \left(A_1+A_2\right)+\eta L_2\right)S$$ (2a)

$$L_1’=f\left(\mathbf{x}\right)\left(I_1+I_2+\xi \left(A_1+A_2\right)+\eta L_2\right)S-\epsilon L_1$$ (2b)

$$L_2’=\epsilon \left(L_1-L_2\right)$$ (2c)

$$I_1’=\left(1-\pi \right)\epsilon L_2-\gamma I_1$$ (2d)

$$I_2’=\gamma \left(I_1-I_2\right)$$ (2e)

$$A_1’=\pi \epsilon L_2-\gamma A_1$$ (2f)

$$A_2’=\gamma \left(A_1-A_2\right)$$ (2g)

$$R’=\gamma I_2+\gamma A_2.$$ (2h)

Note that it is assumed that there can be transmission during the incubation period, as this was reported (Tong et al., 2020). Thus, the compartment $L_2$ can be interpreted as consisting of pre-symptomatic infectious individuals. A fraction π of individuals is assumed to go into an asymptomatic phase following incubation (and correspondingly, $1-\pi$ develop symptoms). Finally, ε and γ describe the rates at which incubation and infectiousness end, respectively. By properties of Erlang distributions, the average times spent incubating and infectious (symptomatically or asymptomatically) are $2/\epsilon$ and $2/\gamma$ time units, respectively.

3. Some properties of the model

The purpose of this paper is not to conduct a thorough mathematical analysis of (2). We refer to (Arino et al., 2006) for considerations on the behaviour of a version of this model with only one of each disease status compartments. It is useful, though, to summarise some elementary properties of (2).

3.1. Behaviour of the model

An epidemic model such as (2), as compared to endemic models with demographic components, only has one possible long term outcome: a disease-free equilibrium ${\mathbf{E}}_0$ in which the only two potentially positive components are S and R. As is customary with such models, we denote $S_{\infty }={\text{lim}}_{t\to \infty }S\left(t\right)$ and $R_{\infty }={\text{lim}}_{t\to \infty }R\left(t\right)$ the limiting values of S and R. Because of the structure of the model, these limits always exist [3, Theorem 5.1].

As with other simple epidemic models of this type, the main interest is to know whether, following the introduction of infected individuals in the population, the number of infected individuals goes through an exponential growth phase, indicating an epidemic phase, before the disease becomes extinct. This is decided using the basic reproduction number ${\mathcal{R}}_0$. To find its value, we use the method in (Arino et al., 2007), using the notation therein. First, $D=1$ since $S\in {\mathbb{R}}^m$ with $m=1$. The matrix $\text{Π}=\left[p_{ij}\right]$ (to avoid confusion with the fraction π of asymptomatic cases) has entry $p_{ij}$ the fraction of the jth susceptible compartment moving, upon infection, to the ith infected compartment. Therefore, here it is a vector, $\text{Π}={\left(\mathrm{1,0,0,0,0,0}\right)}^T$, since all new infections move to the $L_1$ compartment. The row vector b describes the relative horizontal transmissions. It takes the form $b=\left(0,\eta ,\mathrm{1,1},\xi ,\xi \right)$. The function denoted $\beta \left(x,y,z\right)$ in (Arino et al., 2007) is $f\left(x\right)$ here. Finally, the matrix V describing transitions between and out of infected states takes the form

$$V=\left(\begin{array}{cccccc}\epsilon & 0& 0& 0& 0& 0\\ -\epsilon & \epsilon & 0& 0& 0& 0\\ 0& -(1-\pi )\epsilon & \gamma & 0& 0& 0\\ 0& 0& -\gamma & \gamma & 0& 0\\ 0& -\pi \epsilon & 0& 0& \gamma & 0\\ 0& 0& 0& 0& -\gamma & \gamma \end{array}\right)$$

and has inverse

$$V^{-1}=\left(\begin{array}{cccccc}1/\epsilon & 0& 0& 0& 0& 0\\ 1/\epsilon & 1/\epsilon & 0& 0& 0& 0\\ \left(1-\pi \right)/\gamma & \left(1-\pi \right)/\gamma & 1/\gamma & 0& 0& 0\\ \left(1-\pi \right)/\gamma & \left(1-\pi \right)/\gamma & 1/\gamma & 1/\gamma & 0& 0\\ \pi /\gamma & \pi /\gamma & 0& 0& 1/\gamma & 0\\ \pi /\gamma & \pi /\gamma & 0& 0& 1/\gamma & 1/\gamma \end{array}\right).$$

From (Arino et al., 2007), the basic reproduction number of (2) is then

$${\mathcal{R}}_0=f\left({\mathbf{E}}_0\right)b{V}^{-1}\text{Π}DS\left(0\right),$$

where $S\left(0\right)$ is the susceptible population at the initial time. Note that for this formula to hold, $f\left({\mathbf{E}}_0\right)$ must be defined. In other words, the basic reproduction number takes the form

$${\mathcal{R}}_0^{\left(f\right)}=f\left({\mathbf{E}}_0\right)\left(2\frac{\pi \xi }{\gamma }+2\frac{1-\pi }{\gamma }+\frac{\eta }{\epsilon }\right)S\left(0\right),$$ (3)

where the superscript $\left(f\right)$ is used to show dependence on the nature of f. If $f\left(\mathbf{x}\right)=\beta$, i.e., we use mass action incidence, then

$${\mathcal{R}}_0^{\left(\text{MA}\right)}=\beta \left(2\frac{\pi \xi }{\gamma }+2\frac{1-\pi }{\gamma }+\frac{\eta }{\epsilon }\right)S\left(0\right),$$ (4)

whereas in the case of proportional or frequency-dependent incidence, $f\left({\mathbf{E}}_0\right)=\beta /S\left(0\right)$ and

$${\mathcal{R}}_0^{\left(\text{FD}\right)}=\beta \left(2\frac{\pi \xi }{\gamma }+2\frac{1-\pi }{\gamma }+\frac{\eta }{\epsilon }\right).$$ (5)

Observe that the latter form stems from the fact that at ${\mathbf{E}}_0$, $⟨\mathbf{1},{\mathbf{E}}_0⟩=S_{\infty }+R_{\infty }$ and the latter equals $S\left(0\right)$ since the model clearly preserves the total population.

3.2. Final size relations

One measure of particular importance in the context of COVID-19 and other emerging or re-emerging pathogens is the epidemic final size $S\left(0\right)-S_{\infty }$. The final size is often expressed in terms of the attack rate $\left(S\left(0\right)-S_{\infty }\right)/S\left(0\right)$.

In the case where incidence is mass action, since we have a single susceptible class, the method in (Arino et al., 2007) provides an explicit final size relation,

$$\text{ln}\left(\frac{S\left(0\right)}{S_{\infty }}\right)=\frac{{\mathcal{R}}_0^{\left(\text{MA}\right)}}{S\left(0\right)}\left(S\left(0\right)-S_{\infty }\right)+\beta b{V}^{-1}\mathbf{I}\left(0\right),$$

where $\mathbf{I}\left(0\right)={\left(L_1\left(0\right),L_2\left(0\right),I_1\left(0\right),I_2\left(0\right),A_1\left(0\right),A_2\left(0\right)\right)}^T$ is the initial infected population. This simplifies to

$$\text{ln}\left(\frac{S\left(0\right)}{S_{\infty }}\right)=\frac{{\mathcal{R}}_0^{\left(\text{MA}\right)}}{S\left(0\right)}\left(S\left(0\right)-S_{\infty }+L_1\left(0\right)+L_2\left(0\right)\right)+\frac{\beta }{\gamma }\left(2I_1\left(0\right)+I_2\left(0\right)+2\xi A_1\left(0\right)+\xi A_2\left(0\right)\right).$$ (6)

With other incidence functions, we obtain inequalities of the form

$$\text{ln}\left(\frac{S\left(0\right)}{S_{\infty }}\right)\ge \frac{{\mathcal{R}}_0^{\left(f\right)}}{S\left(0\right)}\left(S\left(0\right)-S_{\infty }\right)+f\left(K\right)b{V}^{-1}\mathbf{I}\left(0\right),$$

where K is the initial total population size. Similarly to (6), this can easily be simplified but is not shown here.

Thus, in the case of mass action incidence, the most used incidence in the case of epidemics, finding the final size of the epidemic (or, equivalently, the epidemic attack rate) requires to solve the simple transcendental equation (6), which is easily done at least numerically.

3.3. Detecting the turning point and the peak

Other measures of particular importance in the context of the study of an epidemic outbreak are the timing of the peak as well as the disease prevalence at the peak. In the discussion that follows, assume incidence is mass action.

In a classic ODE Kermack-McKendrick SIR model, the peak is easily characterised as the point in phase space where $I’=0$. Because of the number of compartments, the peak here can be studied in two parts. Before the peak is actually reached, there is first a point in time at which incidence starts to decrease; this is sometimes called the turning point of the epidemic. In the present model, this point is reached when $L_1’=0$, i.e., with mass action incidence, when

$$S=\frac{\epsilon L_1}{\beta \left(\eta L_2+I_1+I_2+\xi \left(A_1+A_2\right)\right)}=:\mathrm{\Psi }\left(\mathbf{I}\right),$$ (7)

where $\mathbf{I}=\left(L_1,L_2,I_1,I_2,A_1,A_2\right)$. Note that $\mathrm{\Psi }$ is not defined everywhere in phase space; for instance, it is not defined at ${\mathbf{E}}_0$ nor if one considers an $\mathbf{I}$ with sign pattern $(+,\mathrm{0,0,0,0,0})$. However, past initial transients and before $\mathbf{I}$ becomes close to ${\mathbf{E}}_0$, (7) provides a characterisation of the phase the epidemic is currently in. If $S>\mathrm{\Psi }\left(\mathbf{I}\right)$, then the “natural tendency” of the epidemic is to propagate more. When enough susceptible individuals have been “consumed” by the infection, i.e., when $S<\mathrm{\Psi }\left(\mathbf{I}\right)$, the epidemic cannot sustain itself anymore. For perspective, in the context of COVID-19 and using time units of days and mass action incidence, ε is of the order of ${10}^{-1}$ while β is typically several order of magnitude smaller, so the factor $\epsilon /\beta$ in (7) is in the range $[{10}^4,{10}^7]$. Note that because only $I_1$ and $I_2$ are observable, determining whether (7) holds is impossible in the field. On the other hand, this is easily done when considering numerical simulations.

The peak is then the point at which prevalence of the infection in the population is maximum. Here, we focus on the observable peak, i.e., the one that can actually be measured in real life data. Because of that, we consider the peak to happen at the time when the observable part of the epidemic, i.e., the number of infectious individuals $I_1+I_2$, is maximum. Thus, at the peak, $I_1’+I_2’=0$, i.e.,

$$\left(1-\pi \right)\epsilon L_2=\gamma I_2.$$ (8)

Since $\left(1-\pi \right)\epsilon L_2$ is the rate at which new symptomatic infections occur and $\gamma I_2$ is the rate at which symptomatic infections are resolved, either by recovery or death, the occurrence of conditions necessary for the peak to take place can be inferred from the data. So, while (7) is not observable, (8) is.

3.4. Start date of the epidemic in a location

When conducting a numerical investigation of the system properties, finding the date at which to start simulations is important. We describe here the methodology used to do so.

In this work, we do not account for “structural” under-reporting of cases and thus assume that the observable quantity in our model, in terms of infection, is the number of new symptomatic cases. As a consequence, we take, for a given location, the time $t_c$ at which the first c confirmed cases are reported. A location is thus characterised by a pair $\left(t_c,c\right)$.

For illustration, take the situation of cumulative confirmed case counts in China as reported to WHO, which was of 547 cases on January 22, 2020, i.e., (t_c=2020_01_22,c=547). We seek the initial date $t_i$ for China such that, on January 22, 2020, China has this cumulative confirmed case count when solving (2) numerically and with the parameters considered. Given a point u in parameter space, we initiate a simulation with initial time $t_0=0$. We solve (2) numerically, forward in time over the interval $[0,t]$, with $S\left(0\right)$ the population of China, $L_1\left(0\right)=1$ and all other state variables equal to zero. This gives a solution $\mathbf{x}\left(t,t_0=0,u\right)$. Extracting $L_2(t,t_0=0,u)$ from this solution, we compute

$$C\left(t\right)={\int }_{t_0=0}^t\left(1-\pi \right)\epsilon L_2\left(s,t_0,u\right)ds.$$

As $\left(1-\pi \right)\epsilon L_2$ is the rate at which individuals enter the $I_1$ compartment, $C\left(t\right)$ represents the total number of individuals having become infectious at time t, i.e., the cumulative number of symptomatic infections t days after the introduction of the first infectious individual in the population. We then let $t^{\text{∗}}$ be the point when $C\left(t^{\text{∗}}\right)=547$; $t_i$ for China, with the parameters u, is then $t_i=\text{2020\_01\_22}-t^{\text{∗}}$.

Note that a random point in parameter space might lead to a situation where ${\mathcal{R}}_0<1$. This is used in parameter estimation to disqualify such points. Other points that would be disqualified are those such that $t^{\text{∗}}$ is too large. These aspects will be discussed in further work on the topic.

4. Sensitivity analysis

A global sensitivity analysis is carried out to characterise the impact of uncertainty of factors (inputs of the model) on model outputs. The inputs of model and their ranges are listed in Table 1; p inputs associated to the model parameters are considered. The number of observable cases during the course of the epidemic and at the peak, and the timing of the peak are the outputs of interest here. The number of observable cases is the cumulative confirmed case count $\mathrm{C}\left(\mathrm{t}\right)$.

Table 1.

Model parameters. Incubation time and Infectious period give the parameters $\epsilon =2/\left(\text{Incubation time}\right)$ and $\gamma =2/\left(\text{Infectious period}\right)$, respectively.

Parameter	Definition	Range
β	transmission coefficient	$[5\times {10}^{-7},{10}^{-4}]$
η	attenuation of transmission for incubating individuals	$\left[\mathrm{0,0.2}\right]$
ξ	attenuation of transmission for asymptomatic individuals	$\left[\mathrm{0,1}\right]$
π	fraction of asymptomatic cases	$\left[\mathrm{0,1}\right]$
Incubation time	mean duration of incubation	$\left[\mathrm{1,14}\right]$
Infectious period	mean duration of infectious period	$\left[\mathrm{2,14}\right]$

The variance-based analysis is performed using the R package multisensi. For each factor, $m=7$ values are chosen using Latin hypercube sampling with uniform distributions on the range considered for the factor of interest (Table 1). Then, using a complete factorial design approach, $m^p$ scenarios are generated. Simulations are run for these $m^p=7^6=\mathrm{117,649}$ scenarios with the same initial condition $S\left(0\right)=\mathrm{100,000}$, $I_1\left(0\right)=1$ and $L_1\left(0\right)=L_2\left(0\right)=I_2\left(0\right)=R\left(0\right)=0$. Then, sensitivity indices are computed using a classic ANOVA decomposition (Lamboni, Makowski, Simon, Gabrielle, & Monod, 2009; Monod, Naud, & Makowski, 2006).

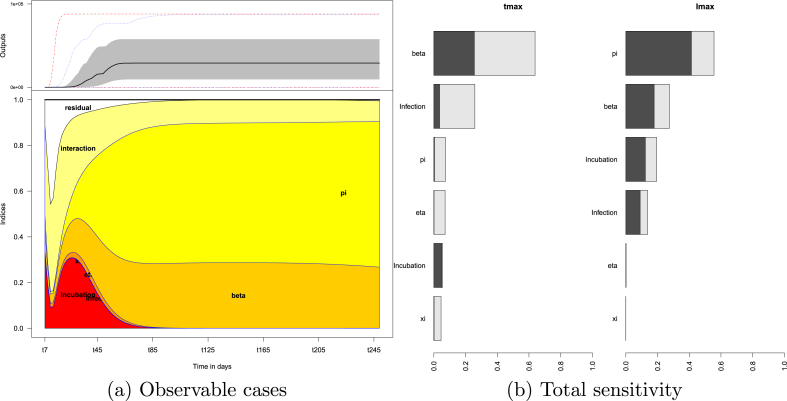
Fig. 3a shows the influence of factors on the number of observable cases over time. The sensitivity indices are computed every 2 days over a period of 250 days. The lower panel of Fig. 3a details, at each time point, contributions (normalised to 1) of model parameters to the total variability of model responses. At a given time $t_j$, the relative lengths of the coloured segments represent the relative contributions of the main effect sensitivity indices to this total variability. Interactions between two factors is denoted “interaction” and those involving three or more factors is denoted “residual”.

Fig. 3.

Sensitivity analysis results: (a) Effects of factors on the number of observable cases as a function of time. The upper panel shows inter-quartile (grey area) and median (bold line) output values over time. The lower panel displays the sensitivity indices over time for the main effects and the first-order interactions (interaction between two factors). Residuals correspond to contribution to the variance from interactions between three or more factors. (b) Effects of factors on the time of the peak $t_{\text{max}}$ and size of the peak $I_{max}$. Bars represent total indices of sensitivity for each factor. The dark grey parts of bars are the main effect sensitivity indices, light grey parts correspond to first-order interactions.

For instance, at $t_{85}$ (after 85 days), the number of observable cases is mostly sensitive to the main effect of π. The main effect of the transmission coefficient β accounts for one-third of the variability. Interactions between factors contribute to about one-tenth of the output variability. In the long-run, this trend persists.

In the early dynamics, the variability is due to the main effects of incubation time and interactions between factors.

Fig. 3b displays the total sensitivity, a measure of influence of each factor; the outputs considered here are the timing of the peak and value of the observable variables at the peak, $t_{\text{max}}$ and $I_{max}$ respectively. In each bar (total sensitivity), the main effect (dark grey) and interaction between the factor of interest and another (light grey) are detailed. The time of the peak $t_{\text{max}}$ is affected by the transmission β and incubation time. The value of the peak $I_{max}$ is mainly influenced by the proportion of asymptomatic π, the duration of incubation and infectiousness and transmission β. The transmission coefficient (β) has the most influence on $t_{\text{max}}$ whereas $I_{max}$ is most impacted by the proportion π of asymptomatic cases. Furthermore, note that for the most influential factors of $t_{\text{max}}$ the first-order interactions contribute the most to their total sensitivity. The timing of peak of observable case numbers results mostly from the interplay between factors.

5. Discussion

The model presented here can be used to consider some of the aspects of spread of a novel or re-emergent pathogen. We have focused here on practical aspects of the use of the model, focusing on the need, in emergency response settings, to provide a fast evaluation of outcomes.

Model (2) consists of 8 differential equations, but its parametrisation involves the same number of parameters as the 5 equations model from which it is derived (Arino et al., 2006). Because a lot is unknown during the early stages of a crisis like the ongoing COVID-19 pandemic, simple models that can be fitted using a minimal number of parameters are extremely useful.

In a time of crisis, it is however also important not to oversell the capabilities of a model. We have been considering many variations on the current model, as part of work conducted in Canada regarding COVID-19. While this base model has proved very helpful in many circumstances, it is unable in particular to provide insights into testing or contact tracing. Other modelling paradigms such as individual-based (IBM) or agent-based (ABM) models are much better suited to answer questions in this area. A continuous-time Markov chain model version of this model has for instance been considered to answer specific questions where a better understanding of the infection chains is required, such as importations of cases into new locations.

Where our model is quite appropriate, on the other hand, is when reasonably sized populations are considered. In this case, it can easily be shown, as had been done in (Arino et al., 2006), that ODE models provide essentially similar results to population-level IBM and ABM.

This highlights another strength of this type of approach: ODE models are quite amenable to extensive sensitivity analyses, bringing forward an important non methodological conclusion of the present work. One of the most influential factor/parameter in the model considered is the proportion of asymptomatic cases. The basic reproduction number ${\mathcal{R}}_0$ (through the transmission parameter β and its interaction with other parameters) determines the time of the peak of observable cases whereas the value of the peak, and thus the impact on the health care system, depends critically on the proportion of cases that are asymptomatic. This highlights the imperious need for more research, both in the field and in modelling, to understand the drivers of asymptomaticity and its prevalence among cases.

Declaration of competing interest

We have no conflict of interest.

Handling Editor: Jianhong Wu