A COVID-19 epidemic model with latency period

Abstract

At the beginning of a COVID-19 infection, there is a period of time known as the exposed or latency period, before an infected person is capable of transmitting the infection to another person. We develop two differential equations models to account for this period. The first is a model that incorporates infected persons in the exposed class, before transmission is possible. The second is a model that incorporates a time delay in infected persons, before transmission is possible. We apply both models to the COVID-19 epidemic in China. We estimate the epidemiological parameters in the models, such as the transmission rate and the basic reproductive number, using data of reported cases. We thus evaluate the role of the exposed or latency period in the dynamics of a COVID-19 epidemic.

1. Introduction

In (New England Journal of Me, 2020) it is reported that transmission of COVID-19 infection may occur from an infectious individual, who is not yet symptomatic. In (Report of theO-China J, 2019) it is reported that COVID-19 infected individuals generally develop symptoms, including mild respiratory symptoms and fever, on an average of 5–6 days after infection (mean 5–6 days, range 1–14 days). In (Yanget al., 2020) it is reported that the median time prior to symptom onset is 3 days, the shortest 1 day, and the longest 24 days. It is evident that these time periods play an important role in understanding COVID-19 transmission dynamics. (see Table 1, Table 2, Table 3)

Table 1.

Parameters and initial conditions of the model SEIRU.

Symbol	Interpretation	Method
$t_0$	Time at which the epidemic started	fitted
$S_0$	Number of susceptible at time $t_0$	fixed
$E_0$	Number of asymptomatic and noninfectious at time $t_0$	fitted
$I_0$	Number of asymptomatic but infectious at time $t_0$	fitted
$U_0$	Number of unreported symptomatic infectious at time $t_0$	fitted
.	Transmission rate	fitted
N	First day of the public interventions	fitted
μ	Intensity of the public interventions	fitted
$1/\alpha$	average duration of the exposed noninfectious period	fitted
$1/\nu$	Average time during which asymptomatic infectious are asymptomatic	fixed
f	Fraction of asymptomatic infectious that become reported symptomatic infectious	fixed
${\nu }_1=f\nu$	Rate at which asymptomatic infectious become reported symptomatic	fitted
${\nu }_2=\left(1-f\right)\nu$	Rate at which asymptomatic infectious become unreported symptomatic	fitted
$1/\eta$	Average time symptomatic infectious have symptoms	fixed

Table 2.

Cumulative daily reported case data from January 19, 2020 to March 18, 2020, reported for mainland China by the National Health Commission of the People's Republic of China and the Chinese CDC (Chinese Center for Disease Control and Prevention, 1180). The data corresponds to cumulative reported cases confirmed by testing.

January
19	20	21	22	23	24	25
198	291	440	571	830	1287	1975
26	27	28	29	30	31
2744	4515	5974	7711	9692	11791
February
1	2	3	4	5	6	7
14380	17205	20438	24324	28018	31161	34546
8	9	10	11	12	13	14
37198	40171	42638	44653	46472	48467	49970
15	16	17	18	19	20	21
51091	$70548-17409$	$72436-17409$	$74185-17409$	$75002-17409$	$75891-17409$	$76288-17409$
22	23	24	25	26	27	28
$76936-17409$	$77150-17409$	$77658-17409$	$78064-17409$	$78497-17409$	$78824-17409$	$79251-17409$
29
$79824-17409$
March
1	2	3	4	5	6	7
$80026-17409$	$80151-17409$	$80270-17409$	$80409-17409$	$80552-17409$	$80651-17409$	$80695-17409$
8	9	10	11	12	13	14
$80735-17409$	$80754-17409$	$80778-17409$	$80793-17409$	$80813-17409$	$80824-17409$	$80844-17409$
15	16	17	18
$80860-17409$	$80881-17409$	$80894-17409$	$80928-17409$

Table 3.

Table of the Median Absolute Deviation of model SEIRU and SEIRUδ.

ODE		DDE
Figure	${\text{MAD}}_{ODE}$	Figure	${\text{MAD}}_{DDE}$
Fig. 4 (a)	1717	Fig. 6 (a)	662
Fig. 4 (b)	1251	Fig. 6 (b)	796
Fig. 4 (c)	1899	Fig. 6 (c)	1095
Fig. 4 (d)	1485	Fig. 6 (d)	1967
Fig. 5 (a)	893	Fig. 7 (a)	178
Fig. 5 (b)	572	Fig. 7 (b)	485
Fig. 5 (c)	754	Fig. 7 (c)	585
Fig. 5 (d)	713	Fig. 7 (d)	852

In this work, we will examine the latency period of COVID-19 infection, that is, the period of time in which newly infected individuals are asymptomatic and noninfectious. We illustrate the latency period in Fig. 1 below:

Fig. 1.

Key time periods of COVID-19 infection. The latent or exposed period before symptoms and transmissibility, the incubation period before symptoms appear, the symptomatic period, and the transmissibility period, which may overlay the asymptomatic period.

In the present article we develop two mathematical models to study the impact of the latency period. One is a ODE (ordinary differential equations) model, with an exposed class of infected individuals, who are not yet infectious. The other is a DDE (delay differential equations) model, with a time delay in newly infected individuals, before they become infectious. The DDE model can be derived from a continuous age of infection model, which can be reduced to a system of DDE. The derivation of such models is described in (Magal & McCluskey, 2013). We refer to (Tang et al., 2020; Yanget al., 2020) for early models with exposure applied to COVID-19.

As mentioned in (Liu, Magal, Seydi, & Webb, 2020), asymptomatic infectious cases are not usually reported to medical authorities, and reported infectious cases are typically only a fraction of the total number of the symptomatic infectious individuals. In this work, we examine the number of asymptomatic infectious cases and unreported infectious cases, as well as the number of reported infectious cases, for the COVID epidemic in mainland China. We note that public measures in China, beginning January 26, strongly attenuated the epidemic. One of our objectives is to understand how these measures, such as isolation, quarantine, and public closings, reduce the final size of the epidemic. We examine how the latency period, tied contact tracing and to a 14-day medical observation or quarantine period for exposed persons, mitigates the final size of the epidemic.

2. Models

2.1. Model with a compartment E of exposed infected individuals not yet infectious

This model has a compartment in the system of ODE that corresponds to exposed or latent infected individuals. We will designate this model as the SEIRU model:

$$\{\begin{array}{ll}S\text{'}\left(t\right)=-\tau \left(t\right)S\left(t\right)[I\left(t\right)+U\left(t\right)],& \\ E\text{'}\left(t\right)=\tau \left(t\right)S\left(t\right)[I\left(t\right)+U\left(t\right)]-\alpha E\left(t\right)& \\ I\text{'}\left(t\right)=\alpha E\left(t\right)-\nu I\left(t\right)& \\ R\text{'}\left(t\right)={\nu }_{1}I\left(t\right)-\eta R\left(t\right)& \\ U\text{'}\left(t\right)={\nu }_{2}I\left(t\right)-\eta U\left(t\right).& \end{array}$$ (2.1)

Here $t\ge t_0$ is time in days, $t_0$ is the beginning date of the epidemic, $S\left(t\right)$ is the number of individuals susceptible to infection at time t, $E\left(t\right)$ is the number of asymptomatic noninfectious individuals at time t, $I\left(t\right)$ is the number of asymptomatic but infectious individuals at time t, $R\left(t\right)$ is the number of reported symptomatic infectious individuals at time t, and $U\left(t\right)$ is the number of unreported symptomatic infectious individuals at time t. This system is supplemented by initial data

$$S\left(t_0\right)=S_0>0,E\left(t_0\right)=E_0>0,I\left(t_0\right)=I_0>0,U\left(t_0\right)=U_0>0,R\left(t_0\right)=R_0=0.$$ (2.2)

The exit flux of the exposed class E is describe by the term $-\alpha E\left(t\right)$. The means that the time of exposure follows an exponential law, and the average value of the exposure time is $1/\alpha$, which can be, for example, 6 h, 12 h, 1 day, 2 days, 3 days, etc …. The model contains an asymptomatic infectious class corresponding to the $I\left(t\right)$-equation. The dynamics of the symptomatic infectious individuals are decomposed into the $R\left(t\right)$-equation, which corresponds to the reported symptomatic infectious individuals (symptomatic infectious with severe symptoms), and the $U\left(t\right)$-equation, which corresponds to the unreported symptomatic infectious individuals (symptomatic infectious with mild symptoms). The flux of individuals leaving the class I is $\nu I\left(t\right)$. We assume that a fraction f are reported and a fraction $1-f$ are unreported. Thus, ${\nu }_1=f\nu \text{ and }{\nu }_2=\left(1-f\right)\nu .$

The time-dependent parameter $\tau \left(t\right)$ is the transmission rate. During the early phase of the epidemic, when the cumulative number of reported cases grows approximately exponential, . is a constant value ${\tau }_0$. After January 23, strong government measures in all of China, such as isolation, quarantine, and public closings, strongly impacted the transmission of new cases. The actual effects of these measures were complex, and we use a time-dependent exponentially decreasing transmission rate $\tau \left(t\right)$ to incorporate these effects after the early exponentially increasing phase. The formula for $\tau \left(t\right)$ during the exponential decreasing phase is derived by a fitting procedure to the data:

$$\{\begin{array}{ll}\tau \left(t\right)={\tau }_0,0\le t\le N,& \\ \tau \left(t\right)={\tau }_0\text{exp}\left(-\mu \times \left(t-N\right)\right),N<t.& \end{array}$$ (2.3)

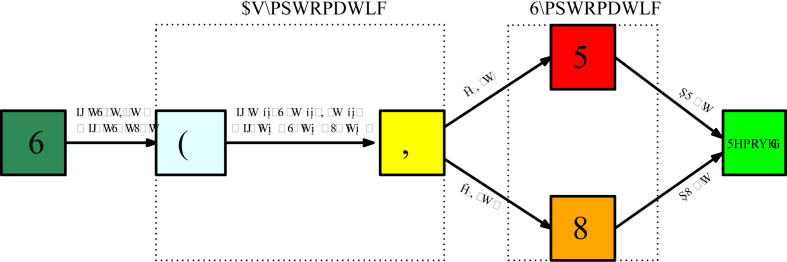
Day N corresponds to the day when the public measures take effect, and μ is the rate at which they take effect. A schematic diagram of the model is given in Fig. 2, and the parameters of the model are listed in Table 2.1 below (see Fig. 3).

Fig. 2.

Flow chart for the model SEIRU.

Fig. 3.

Flow chart for the model SEIRUδ.

2.2. Model with a constant time delay δ in the I class equation

This model has a time delay δ in the $I\left(t\right)$ equation in the system of DDE that contains the latency period. We will designate this model as the SEIRUδ model:

$$\{\begin{array}{ll}S\text{'}\left(t\right)=-\tau \left(t\right)S\left(t\right)[I\left(t\right)+U\left(t\right)],& \\ I\text{'}\left(t\right)=\tau \left(t-\delta \right)S\left(t-\delta \right)[I\left(t-\delta \right)+U\left(t-\delta \right)]-\nu I\left(t\right)& \\ R\text{'}\left(t\right)={\nu }_{1}I\left(t\right)-\eta R\left(t\right)& \\ U\text{'}\left(t\right)={\nu }_{2}I\left(t\right)-\eta U\left(t\right).& \end{array}$$ (2.4)

This system is supplemented by initial data

$$S\left(t_0+\theta \right)=S_0\left(\theta \right)>0,I\left(t_0+\theta \right)=I_0\left(\theta \right)>0,U\left(t_0+\theta \right)=U_0\left(\theta \right)>0,\forall \theta \in [-\delta ,0],\text{ and }R\left(t_0\right)=0.$$ (2.5)

In the model SEIRUδ, the duration of exposure is constant and equal to δ. The exposed class is given by the integral formula

$$E\left(t\right)={\int }_{t-\delta }^t\tau \left(\sigma \right)S\left(\sigma \right)[I\left(\sigma \right)+U\left(\sigma \right)]d\sigma .$$ (2.6)

or alternatively, by using the differential equation

$$E\text{'}\left(t\right)=\tau \left(t\right)S\left(t\right)[I\left(t\right)+U\left(t\right)]-\tau \left(t-\delta \right)S\left(t-\delta \right)[I\left(t-\delta \right)+U\left(t-\delta \right)].$$ (2.7)

$E\left(t\right)$ can be decoupled from the equations in the DDE system SEIRUδ, since it can be obtained from $S\left(t\right)$, $I\left(t\right)$, and $U\left(t\right)$. The parameters and initial conditions of the SEIRUδ model are given in Table 2.1, and a schematic diagram of the model is given in Fig. 2.2.

2.3. Data for the COVID-19 epidemic in China

In our simulations of models SEIRU and SEIRUδ for COVID-19 in mainland China, we will use the following data:

3. Estimation of the parameters and initial conditions

The parameters τ, ν, ${\nu }_1$, ${\nu }_2$, η, α, δ, as well as the starting time $t_0$ and the initial conditions $S\left(t_0\right)$, $E\left(t_0\right)$, $I\left(t_0\right)$, $U\left(t_0\right)$, are uncertain. Our objective is to identify them from specific time data of reported symptomatic infectious cases. To identify the unreported asymptomatic infectious cases, we assume that the cumulative reported symptomatic infectious cases at time t consist of a constant fraction f of the total number of symptomatic infectious cases at time t. In other words, we assume that the removal rate ν of infectious asymptomatic cases $I\left(t\right)$ takes the following form: $\nu ={\nu }_1+{\nu }_2$, where ${\nu }_1=f\nu$ is the removal rate of reported symptomatic infectious individuals, and ${\nu }_2=\left(1-f\right)\nu$ is the removal rate of unreported symptomatic infectious individuals due to all causes. The cumulative number of reported symptomatic infectious cases at time t, denoted by $CR\left(t\right)$, is

$$CR\left(t\right)={\nu }_1\underset{t_0}{\overset{t}{\int }}I\left(s\right)ds.$$ (3.1)

Our method is the following: We assume that $CR\left(t\right)$ has the following form when the epidemic is in the early exponentially growing phase:

$$CR\left(t\right)={\chi }_1\text{exp}\left({\chi }_{2}t\right)-{\chi }_3.$$ (3.2)

We evaluate . using the reported cases data. By using the method in Section 6.1 (Supplementary material), we estimate the starting time $t_0$ for the models from

$$CR\left(t_0\right)=0\iff {\chi }_{1}exp\left({\chi }_2{t}_0\right)-{\chi }_3=0\Rightarrow t_0=\frac{1}{{\chi }_2}\left(\text{ln}\left({\chi }_3\right)-\text{ln}\left({\chi }_1\right)\right).$$

We fix $S_0=1.40005\times {10}^9$, which corresponds to the total population of mainland China. We assume that the variation in $S\left(t\right)$ is small during this exponentially growing phase. We fix $\nu ,\eta ,f,\alpha$. We assume that the transmission rate $\tau \left(t\right)\equiv {\tau }_0$ is constant during this exponentially growing phase. We identify ${\tau }_0$ from ${\chi }_1,{\chi }_2,{\chi }_3$ for each of the models SEIRU and SEIRUδ.

3.1. Parameters and initial conditions for model SEIRU

We fix the fraction $f=0.8$ of symptomatic infectious cases that are reported. Thus, $80\text{\%}$ of infectious cases are reported. We assume $1/\nu$, the average time during which the patients are asymptomatic infectious is 5 days or 7 days. We assume that $1/\eta$, the average time during which a patient is symptomatic infectious, is 7 days. Since f is known, we obtain

$${\nu }_1=f\nu =0.8/5\left(\text{or }0.8/7\right)\text{ and }{\nu }_2=\left(1-f\right)\nu =0.2/5\left(\text{or }0.2/7\right).$$ (3.3)

From Section 6.1 (Supplementary material), we obtain

$$E_0=\frac{{\chi }_2+\nu }{\alpha }{I}_0,U_0=\frac{{\nu }_2}{{\chi }_2+\eta }{I}_0,$$

$${\tau }_0=\frac{\left({\chi }_2+\alpha \right)E_0}{S_0[I_0+U_0]}=\frac{\left({\chi }_2+\nu \right)\left({\chi }_2+\alpha \right)\left({\chi }_2+\eta \right)}{\alpha S_0\left({\chi }_2+\eta +{\nu }_2\right)}.$$ (3.4)

From Section 6.2 (Supplementary material), we obtain basic reproductive number ${\mathcal{R}}_0$ for model SEIRU

$${\mathcal{R}}_0=\frac{\left({\chi }_2+\nu \right)\left({\chi }_2+\alpha \right)\left({\chi }_2+\eta \right)}{\alpha \nu \left({\chi }_2+\eta +{\nu }_2\right)}\left(1+\frac{\left(1-f\right)\nu }{\eta }\right).$$

3.2. Parameters and initial conditions for model SEIRUδ

The values of f, ν, and η are the same as for model SEIRU. From Section 6.3 (Supplementary material), we obtain

$$S\left(t_0+\theta \right)=S_0\left(\theta \right)=S_0,\theta \in [-\delta ,0],$$ (3.5)

$$I\left(t_0+\theta \right)=I_0\left(\theta \right)=\frac{{\chi }_3{\chi }_2}{f\nu }{e}^{{\chi }_2\theta },\theta \in [-\delta ,0],$$ (3.6)

$$U_0\left(t_0+\theta \right)=U_0\left(\theta \right)=\frac{\left(1-f\right)\nu }{\eta +{\chi }_2}{I}_0\left(\theta \right),\theta \in [-\delta ,0]$$ (3.7)

and

$${\tau }_0=\frac{{\chi }_2+\nu }{S_0}\frac{\eta +{\chi }_2}{{\nu }_2+\eta +{\chi }_2}{e}^{{\chi }_2\delta }.$$ (3.8)

From Section 6.4 (Supplementary material), we obtain the basic reproductive number ${\mathcal{R}}_0$ for model SEIRUδ

$${\mathcal{R}}_0=\frac{{\tau }_0{S}_0}{\nu }\left(1+\frac{{\nu }_2}{\eta }\right)=\frac{{\chi }_2+\nu }{\nu }\frac{\eta +{\chi }_2}{{\nu }_2+\eta +{\chi }_2}{e}^{{\chi }_2\delta }\left(1+\frac{\left(1-f\right)\nu }{\eta }\right).$$

4. Comparisons of the models with the data

We use the data from Table 2.3 to numerically simulate models SEIRU and SEIRUδ.

4.1. Comparison of model SEIRU with data

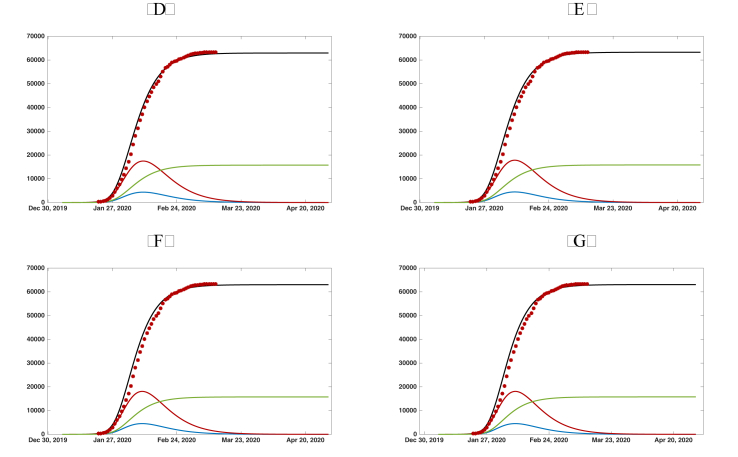
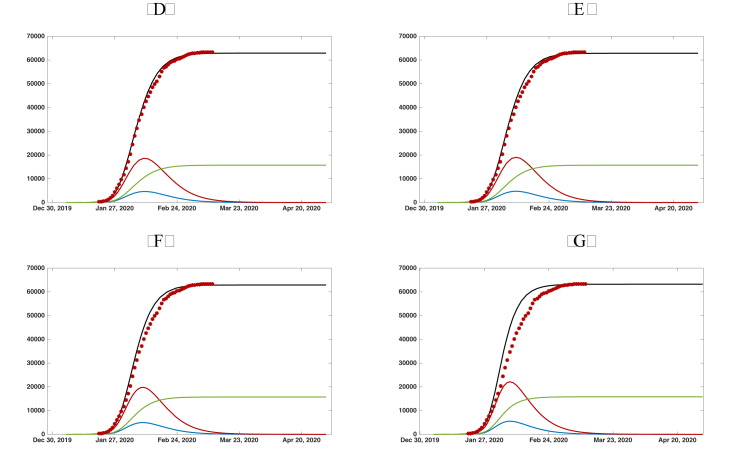
In Fig. 4.1 and , we plot the graphs of $CR\left(t\right)$, $CU\left(t\right)$, $R\left(t\right)$, and $U\left(t\right)$ from the numerical simulation of model SEIRU. We use ${\chi }_1=0.2254$, ${\chi }_2=0.3762$, ${\chi }_3=1$, $f=0.8,\eta =1/7,$ $t_0=3.9607$, and $S_0=1400050000$ in both Fig. 4.1 and . We take $\nu =1/5$ in Fig. 4.1 and $\nu =1/7$ in Fig. 4.1. We take four different values for α: $1/4,1/2,1,3$ in both Fig. 4.1 and Fig. 4. The value of μ is chosen so that the simulations align with the cumulative reported case data. In this way, we are able to predict the future values of the epidemic from early cumulative reported case data. We see from the simulations the following: for Fig. 4.1, with $\nu =1/5$, the simulations are almost the same; for Fig. 4.1, with $\nu =1/7$, the simulations are almost the same.

Fig. 5.

Graphs of the reported cumulated symptomatic infectious individuals $t\to CR\left(t\right)$ (black solid line), unreported cumulated symptomatic infectious individuals $t\to CU\left(t\right)$ (green solid line), $t\to U\left(t\right)$ (blue solid line), and $t\to R\left(t\right)$ (red solid line). The red dots are the data of the reported cumulated confirmed cases for mainland China in Table 2. We use ${\chi }_1=0.2254$, ${\chi }_2=0.3762$, ${\chi }_3=1$, $f=0.8,\eta =1/7,\nu =1/7$, and $S_0=1400050000$. (a) $\mu =0.1539,1/\alpha =6hours$. (b) $\mu =0.169,1/\alpha =12hours$. (c) $\mu =0.198,1/\alpha =1day$. (d) $\mu =0.3,1/\alpha =3days$.

Fig. 6.

Graphs of the reported cumulated symptomatic infectious individuals $t\to CR\left(t\right)$ (black solid line), unreported cumulated symptomatic infectious individuals $t\to CU\left(t\right)$ (green solid line), $t\to U\left(t\right)$ (blue solid line), and $t\to R\left(t\right)$ (red solid line). The red dots are the data of the reported cumulated confirmed cases for mainland China in Table 2. We use ${\chi }_1=0.2254$, ${\chi }_2=0.3762$, ${\chi }_3=1$, $f=0.8,\eta =1/7,\nu =1/5$, $t_0=3.9607$, and $S_0=1400050000$. (a) $\mu =0.1273,\delta =1/4$. (b) $\mu =0.1432,\delta =1/2$. (c) $\mu =0.177,\delta =1$. (d) $\mu =0.373,\delta =3$.

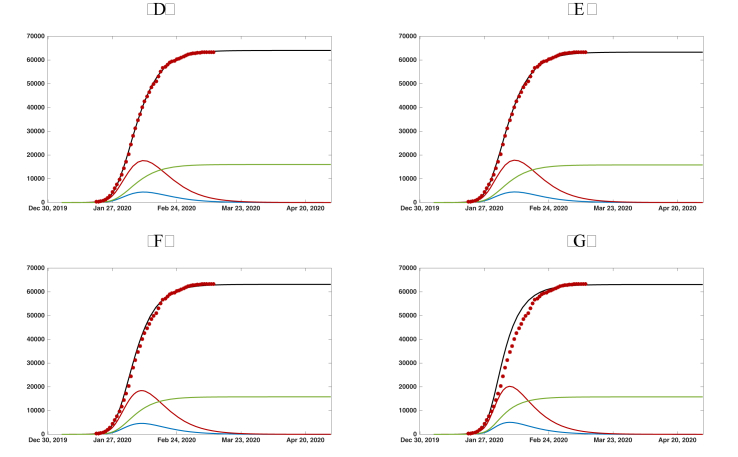
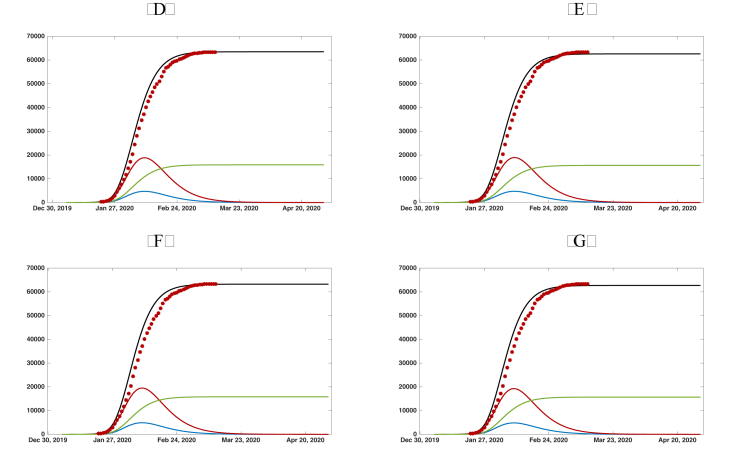
Fig. 7.

Graphs of the reported cumulated symptomatic infectious individuals $t\to CR\left(t\right)$ (black solid line), unreported cumulated symptomatic infectious individuals $t\to CU\left(t\right)$ (green solid line), $t\to U\left(t\right)$ (blue solid line), and $t\to R\left(t\right)$ (red solid line). The red dots are the data of the reported cumulated confirmed cases for mainland China in Table 2. We use ${\chi }_1=0.2254$, ${\chi }_2=0.3762$, ${\chi }_3=1$, $f=0.8,\eta =1/7,\nu =1/7$, $t_0=3.9607$, and $S_0=1400050000$. (a) $\mu =0.1515,\delta =1/4$ day. (b) $\mu =0.17,\delta =1/2$ day. (c) $\mu =0.2093,\delta =1$ day. (d) $\mu =0.454,\delta =3$ days.

Fig. 4.

Graphs of the reported cumulated symptomatic infectious individuals $t\to CR\left(t\right)$ (black solid line), unreported cumulated symptomatic infectious individuals $t\to CU\left(t\right)$ (green solid line), $t\to U\left(t\right)$ (blue solid line), and $t\to R\left(t\right)$ (red solid line). The red dots are the data of the reported cumulated confirmed cases for mainland China in Table 2. We use ${\chi }_1=0.2254$, ${\chi }_2=0.3762$, ${\chi }_3=1$, $f=0.8,\eta =1/7,\nu =1/5$, $t_0=3.9607$, and $S_0=1400050000$. (a) $\mu =0.1276,1/\alpha =6hours$. (b) $\mu =0.142,1/\alpha =12hours$. (c) $\mu =0.166,1/\alpha =1day$. (d) $\mu =0.25,1/\alpha =3days$.

4.2. Comparison of model SEIRUδ with data

In Fig. 4.2 and , we plot the graphs of $CR\left(t\right)$, $CU\left(t\right)$, $R\left(t\right)$, and $U\left(t\right)$ from the numerical simulation of model SEIRUδ. We use ${\chi }_1=0.2254$, ${\chi }_2=0.3762$, ${\chi }_3=1$, $f=0.8,\eta =1/7,$ $t_0=3.9607$, and $S_0=\mathrm{1,400,050,000}$ in both Fig. 4.2 and . We take $\nu =1/5$ in Fig. 4.2 and $\nu =1/7$ in Fig. 4.2. We take four different values for δ: $1/4,1/2,1,3$ in both Fig. 4.2 and Fig. 4. The value of μ is chosen so that the simulations align with the cumulative reported case data. In this way, we are able to predict the future values of the epidemic from early cumulative reported case data. We see from the simulations the following: for Fig. 4.2, with $\nu =1/5$, the simulation for $\delta =1/4$ is almost the same as $\delta =1/2$, the simulations for $\delta =1$ and $\delta =3$ do not agree with the data, and thus, δ cannot be greater than 5 days; for Fig. 4.2, with $\nu =1/7$, the simulations for $\delta =1/4$, $\delta =1/4$, and $\delta =1$ are almost the same and for $\delta =3$, the simulation does not agree with the data, and thus, δ cannot be greater than 7 days.

5. Discussion

We have developed two models SEIRU and SEIRUδ of the COVID-19 epidemic in China that incorporate key features of this epidemic: (1) the importance of implementation of major government public restrictions designed to mitigate the severity of the epidemic; (2) the importance of both reported and unreported cases in interpreting the number of reported cases; and (3) the importance of asymptomatic infectious cases in the disease transmission. The main difference from our previous papers (Liu et al., 2020) and (Liu, Magal, Seydi, & Webb, Webb) is that we consider a latency period in the two models. In model SEIRU, an exposed class E is used to model latency. Newly infected individuals enter the class E, where they are neither symptomatic nor infectious. From this exposed class, noninfectious asymptomatic individuals enter an infectious asymptomatic class I. From I, asymptomatic infectious individuals enter a class R or U where they are symptomatic infectious, and later are reported R or unreported U. In model SEIRUδ a time delay is used to model latency. Newly infected individuals enter the class I after a fixed time delay δ, and then proceed through classes R and U.

In order to compare the models SEIRU and SEIRUδ, we use the Median of Absolute Deviation (MAD) as an indicator:

$$MAD=\text{median}\left(CR-C{R}_{Data}\right),$$ (5.1)

where $C{R}_{Data}$ is the vector of the cumulative number of reported cases from Table 2.3, while $CR$ is the vector of predicted cumulative number of reported cases of the model. The following table summaries the MAD of models SEIRU and SEIRUδ.

From Table 5, it is evident that Fig. 4.1(b) is the best fit for model SEIRU (which corresponds to $1/\alpha =12$hours) and Fig. 4.2(a) is the best fit for model SEIRUδ (which corresponds to $\delta =6$hours) (see Table 4). This mean that for both models, $\nu =1/7$is better than $\nu =1/5$. Furthermore, Table 5 also indicates that model SEIRUδ gives a better prediction than model SEIRU. We also deduce that the best exposure period varies between 6 h for model SEIRUδ and 12 h for model SEIRU. Our finding is consistent with Zou (Zouet al., 2020) where the high viral load observed for COVID-19 was used to explain that the transmission can occur at the early stage of the infection. This gives an explanation for the very short exposure period which give the best fit with data here. This also justifies the fact that in our previous articles (Liu et al., 2020; Liu et al., Webb; Magal & Webb, 2020) we neglected the exposure period.

Table 5.

Predicted turning point and final size of the DDE model SEIRUδ. The turning point for $I\left(t\right)U\left(t\right)$and $R\left(t\right)$is the time t at which these functions reach a maximum.

Figure	Final	Final size	Final size	Turning point	Turning point
	size	Reported	Unreported	of$R\left(t\right),U\left(t\right)$	of$I\left(t\right)$
Fig. 6 (a)	78633	62907	15728	day 39.4	day 33.9
Fig. 6 (b)	78562	62850	15712	day 39.1	day 33.7
Fig. 6 (c)	78590	62872	15718	day 38.6	day 33.4
Fig. 6 (d)	79011	63209	15802	day 37.1	day 32.3
Fig. 7 (a)	80043	64035	16008	day 39.6	day 33.8
Fig. 7 (b)	79139	63312	15827	day 39.3	day 33.5
Fig. 7 (c)	78934	63147	15787	day 38.7	day 33.1
Fig. 7 (d)	78839	63071	15768	day 37.0	day 33.8

Table 4.

Predicted turning point and final size of the ODE model SEIRU. The turning point for $I\left(t\right)U\left(t\right)$. and $R\left(t\right)$is the time t at which these functions reach a maximum.

Figure	Final	Final size	Final size	Turning point	Turning point
	size	Reported	Unreported	of$R\left(t\right),U\left(t\right)$	of$I\left(t\right)$
Fig. 4 (a)	79346	63477	15869	day 39.4	day 33.9
Fig. 4 (b)	78241	62593	15648	day 39.0	day 33.7
Fig. 4 (c)	79036	63229	15807	day 38.9	day 33.6
Fig. 4 (d)	78363	62691	15672	day 38.8	day 33.4
Fig. 5 (a)	78688	62950	15738	day 39.4	day 33.6
Fig. 5 (b)	79097	63278	15819	day 39.2	day 33.5
Fig. 5 (c)	78754	63003	15751	day 38.9	day 33.3
Fig. 5 (d)	78805	63044	15761	day 38.9	day 33.1

We summarize in the following tables the predicted turning point and final size, respectively, for models SEIRU and SEIRUδ.

For our model without latency in (Liu et al., Webb), the turning point of the asymptomatic infectious cases $I\left(t\right)$ is approximately day 35 = February 4. The turning point of the reported cases $R\left(t\right)$ and the unreported cases $U\left(t\right)$ is approximately day 41 = February 10, and the final size of cumulative cases is approximately 79,400 with approximately 63,500 reported, 15,900 unreported. For the ODE model SEIRU, Fig. 4.1 (b) (the best one according to MAD) predicts a turning point of the asymptomatic infectious cases $I\left(t\right)$ at approximately day 34 = February 3. The turning point of the reported cases $R\left(t\right)$ and the unreported cases $U\left(t\right)$ is approximately day 39 = February 8, and the final size of cumulative cases is approximately 63,278 reported, 15,819 unreported. For the DDE model SEIRUδ, Fig. 4.2 (a) (the best one according to MAD) predicts a turning point of the asymptomatic infectious cases $I\left(t\right)$ at approximately day 34 = February 3. The turning point of the reported cases $R\left(t\right)$ and the unreported cases $U\left(t\right)$ is approximately day 40 = February 9, and the final size of cumulative cases is approximately 64,035 reported 16,008 unreported.

Our analysis of the latency period for the COVID-19 epidemic in mainland China is applicable to COVID-19 epidemics in other regions.

6. Supplementary material

The part is devoted to the parameters estimation's of the models by assuming the reported cases data are exponentially growing. We assume that this exponential phase occurs before any public intervention. Therefore we assume that

$$\tau \left(t\right)={\tau }_0$$

for both SEIRU and SEIRUδ models.

6.1. Method to estimate the parameters and initial conditions of SEIRU from the number of reported cases

In the following we fix $f,\nu ,\eta ,\alpha$.

• Step 1Since f, α, η and ν are fixed, we know that

$${\nu }_1=f\nu \text{ and }{\nu }_2=\left(1-f\right)\nu .$$

• Step 2By using equation (3.1) and (3.2) we obtain

$$CR\text{'}\left(t\right)={\nu }_{1}I\left(t\right)\iff {\chi }_1{\chi }_{2}exp\left({\chi }_{2}t\right)={\nu }_{1}I\left(t\right)$$ (6.1)

and

$$\frac{exp\left({\chi }_{2}t\right)}{exp\left({\chi }_2{t}_0\right)}=\frac{I\left(t\right)}{I\left(t_0\right)},$$

and therefore

$$I\left(t\right)=I_{0}exp\left({\chi }_2\left(t-t_0\right)\right).$$ (6.2)

Moreover by using (6.2) at $t=t_0$

$$I_0=\frac{{\chi }_1{\chi }_{2}exp\left({\chi }_2{t}_0\right)}{f\nu }=\frac{{\chi }_3{\chi }_2}{f\nu }.$$ (6.3)

• Step 3In order to evaluated the parameters of the model we replace $S\left(t\right)$ by $S_0=1.40005\times {10}^9$ in the right-hand side of (2.1) (which is equivalent to neglecting the variation of susceptibles due to the epidemic, which is consistent with the fact that $t\to CR\left(t\right)$ grows exponentially). Therefore, it remains to estimate ${\tau }_0$, $E_0,$ and $U_0$ in the following system:

$$\{\begin{array}{l}E\text{'}\left(t\right)={\tau }_0{S}_0[I\left(t\right)+U\left(t\right)]-\alpha E\left(t\right)\\ I\text{'}\left(t\right)=\alpha E\left(t\right)-\nu I\left(t\right)\\ U\text{'}\left(t\right)={\nu }_{2}I\left(t\right)-\eta U\left(t\right).\end{array}$$ (6.4)

By using the second equation we obtain

$$E\left(t\right)=\frac{1}{\alpha }[I\text{'}\left(t\right)+\nu I\left(t\right)],$$

and therefore by using (6.2) we must have

$$I\left(t\right)=I_0\text{exp}\left({\chi }_2\left(t-t_0\right)\right)\text{ and }E\left(t\right)=E_0\text{exp}\left({\chi }_2\left(t-t_0\right)\right).$$

Then, by using the first equation we obtain

$$U\left(t\right)=\frac{1}{{\tau }_0{S}_0}[E\text{'}\left(t\right)+\alpha E\left(t\right)]-I\left(t\right)$$

and then

$$U\left(t\right)=U_0\text{exp}\left({\chi }_2\left(t-t_0\right)\right).$$

By substituting these expressions into (6.4), we obtain

$$\{\begin{array}{c}{\chi }_2{E}_0={\tau }_0{S}_0[I_0+U_0]-\alpha E_0\\ {\chi }_2{I}_0=\alpha E_0-\nu I_0\\ {\chi }_2{U}_0={\nu }_2{I}_0-\eta U_0.\end{array}$$ (6.5)

Remark 6.1

Here we fix ${\tau }_0$ in such a way that the value ${\chi }_2$ becomes the dominant eigenvalue of the linearized equation (6.5), and $\left(E_0,I_0,U_0\right)$ is the positve eigenvector associated to this dominant eigenvalue ${\chi }_2$. Thus, we apply implicitly the Perron-Frobenius theorem. Moreover the exponentially growing solution $\left(E\left(t\right),I\left(t\right),U\left(t\right)\right)$ that we consider (which is starting very close to $\left(\mathrm{0,0,0}\right)$) follows the direction of the positive eigenvector associated with the dominant eigenvalue ${\chi }_2$.

From the second and third equations of (6.5) we obtain

$$E_0=\frac{{\chi }_2+\nu }{\alpha }{I}_0,U_0=\frac{{\nu }_2}{{\chi }_2+\eta }{I}_0,$$

and by substituting these expressions into the first equation of (6.5) we obtain

$${\tau }_0=\frac{\left({\chi }_2+\alpha \right)E_0}{S_0[I_0+U_0]}=\frac{\left({\chi }_2+\nu \right)\left({\chi }_2+\alpha \right)\left({\chi }_2+\eta \right)}{\alpha S_0\left({\chi }_2+\eta +{\nu }_2\right)}.$$ (6.6)

6.2. Computation of the basic reproductive number ${\mathcal{R}}_0$ of model SEIRU

In this section we apply results in Diekmann, Heesterbeek and Metz (Diekmann, Heesterbeek, & Metz, 1990) and Van den Driessche and Watmough (Van den Driessche & Watmough, 2002). The linearized equation of the infectious part of the system is given by

$$\{\begin{array}{ll}E\text{'}\left(t\right)=\tau S_0[I\left(t\right)+U\left(t\right)]-\alpha E\left(t\right)& \\ U\text{'}\left(t\right)={\nu }_{2}I\left(t\right)-\eta U\left(t\right).& \\ I\text{'}\left(t\right)=\alpha E\left(t\right)-\nu I\left(t\right)& \end{array}$$ (6.7)

The corresponding matrix is

$$A=\left[\begin{array}{ccc}-\alpha & \tau S_0& \tau S_0\\ 0& -\eta & {\nu }_2\\ \alpha & 0& -\nu \end{array}\right]$$

and the matrix A can be rewritten as

$$A=V-S$$

where

$$V=\left[\begin{array}{cccc}0& \tau S_0& \tau S_0& \\ 0& 0& {\nu }_2& \\ \alpha & 0& 0& \end{array}\right]\text{ and }S=\left[\begin{array}{cccc}\alpha & 0& 0& \\ 0& \eta & 0& \\ 0& 0& \nu & \end{array}\right].$$

Therefore, the next generation matrix is

$$V{S}^{-1}=\left[\begin{array}{cccc}0& \frac{\tau S_0}{\eta }& \frac{\tau S_0}{\nu }& \\ 0& 0& \frac{{\nu }_2}{\nu }& \\ 1& 0& 0& \end{array}\right]$$

and we obtain that

$${\mathcal{R}}_0=\frac{\tau S_0}{\nu }\left(1+\frac{{\nu }_2}{\eta }\right).$$ (6.8)

By using (6.6) we obtain

$${\mathcal{R}}_0=\frac{\left({\chi }_2+\nu \right)\left({\chi }_2+\alpha \right)\left({\chi }_2+\eta \right)}{\alpha S_0\left({\chi }_2+\eta +{\nu }_2\right)}\frac{S_0}{\nu }\left(1+\frac{{\nu }_2}{\eta }\right)$$

and by using ${\nu }_2=\left(1-f\right)\nu$ we obtain

$${\mathcal{R}}_0=\frac{\left({\chi }_2+\nu \right)\left({\chi }_2+\alpha \right)\left({\chi }_2+\eta \right)}{\alpha \nu \left({\chi }_2+\eta +{\nu }_2\right)}\left(1+\frac{\left(1-f\right)\nu }{\eta }\right).$$ (6.9)

6.3. Method to estimate the parameters of model SEIRUδ from the number of reported cases

• Step 1We have

$${\nu }_1=f\nu \text{ and }{\nu }_2=\left(1-f\right)\nu .$$

• Step 2By using equation (3.2) we obtain

$$CR\text{'}\left(t\right)={\nu }_{1}I\left(t\right)\iff {\chi }_1{\chi }_{2}exp\left({\chi }_{2}t\right)={\nu }_{1}I\left(t\right)$$ (6.10)

and

$$\frac{exp\left({\chi }_{2}t\right)}{exp\left({\chi }_2{t}_0\right)}=\frac{I\left(t\right)}{I\left(t_0\right)},$$

and therefore

$$I\left(t\right)=I\left(t_0\right)exp\left({\chi }_2\left(t-t_0\right)\right).$$ (6.11)

Moreover, by using (6.10) at $t=t_0$,

$$I\left(t_0\right)=\frac{{\chi }_1{\chi }_{2}exp\left({\chi }_2{t}_0\right)}{f\nu }=\frac{{\chi }_3{\chi }_2}{f\nu },U\left(t_0\right)=\frac{{\nu }_2}{{\chi }_2+\eta }{I}_0.$$ (6.12)

• Step 3In order to evaluate the parameters of the model SEIRUδ, we replace $S\left(t\right)$ by $S_0=1.40005\times {10}^9$ in the right-hand side of (2.4) (which is equivalent to neglecting the variation of susceptibles due to the epidemic, and is consistent with the fact that $t\to CR\left(t\right)$ grows exponentially). Therefore, it remains to estimate ${\tau }_0$ and η in the following system:

$$\{\begin{array}{l}I\text{'}\left(t\right)=\tau S_0[I\left(t-\delta \right)+U\left(t-\delta \right)]-\nu I\left(t\right)\\ U\text{'}\left(t\right)={\nu }_{2}I\left(t\right)-\eta U\left(t\right).\end{array}$$ (6.13)

By using the first equation we obtain

$$U\left(t\right)=\frac{1}{\tau S_0}[I\text{'}\left(t\right)+\nu I\left(t\right)]-I\left(t\right),$$

and therefore by using (6.11) we must have

$$I\left(t\right)=I\left(t_0\right)\text{exp}\left({\chi }_2\left(t-t_0\right)\right)\text{ and }U\left(t\right)=U\left(t_0\right)\text{exp}\left({\chi }_2\left(t-t_0\right)\right),$$

so by substituting these expressions into (6.13) we obtain

$$\left\{\begin{array}{l}{\chi }_{2}I\left(t_0\right)=\tau S_0\left[I\right(t_0)+U(0)\\ {\chi }_{2}U\left(t_0\right)={\nu }_{2}I\left(t_0\right)-\eta U\left(t_0\right).\end{array}\right\}$$ (6.14)

Remark 6.2

Here we fix ${\tau }_0$ in such a way that the value ${\chi }_2$ becomes the dominant eigenvalue of the linearized equation (6.14) and $\left(I\left(t_0\right),U\left(t_0\right)\right)$ is the positve eigenvector associated to this dominant eigenvalue ${\chi }_2$. Thus, we apply implicitly the Perron-Frobenius theorem. Moreover the exponentially growing solution $\left(I\left(t\right),U\left(t\right)\right)$ that we consider (which is starting very close to $\left(\mathrm{0,0}\right)$) follows the direction of the positive eigenvector associated with the dominant eigenvalue ${\chi }_2$.

By dividing the first equation of (6.14) by $I\left(t_0\right)$ we obtain

$${\chi }_2=\tau S_0[1+\frac{U\left(t_0\right)}{I\left(t_0\right)}]e^{-{\chi }_2\delta }-\nu$$

and hence

$$\frac{U\left(t_0\right)}{I\left(t_0\right)}=\frac{\left({\chi }_2+\nu \right)}{\tau S_0}{e}^{{\chi }_2\delta }-1.$$ (6.15)

By using the second equation of (6.14) we obtain

$$\frac{U\left(t_0\right)}{I\left(t_0\right)}=\frac{{\nu }_2}{\eta +{\chi }_2}.$$ (6.16)

By using (6.15) and (6.16) we obtain

$$\tau =\frac{\left({\chi }_2+\nu \right)}{S_0}{e}^{{\chi }_2\delta }\frac{\eta +{\chi }_2}{{\nu }_2+\eta +{\chi }_2}.$$ (6.17)

By using (6.12) we compute

$$U\left(t_0\right)=\frac{{\nu }_2}{\eta +{\chi }_2}I\left(t_0\right)=\frac{\left(1-f\right)\nu }{\eta +{\chi }_2}I\left(t_0\right).$$ (6.18)

6.4. Computation of the basic reproductive number ${\mathcal{R}}_0$ of model SEIRUδ

The linearized equation of the infectious part of the system is given by

$$\{\begin{array}{ll}I\text{'}\left(t\right)=\tau S_0[I\left(t-\delta \right)+U\left(t-\delta \right)]-\nu I\left(t\right),& \\ U\text{'}\left(t\right)={\nu }_{2}I\left(t\right)-\eta U\left(t\right).& \end{array}$$ (6.19)

We apply the results in Thieme (Thieme, 2009) to the linear operator $A:D\left(A\right)\subset X\to X$ where

$$X={\mathbb{R}}^2\times C\left([-\delta ,0],{\mathbb{R}}^2\right)$$

$$A\left(\begin{array}{c}{0}_{\mathbb{R}}\\ 0_{\mathbb{R}}\\ I\\ U\end{array}\right)=\left(\begin{array}{c}-I\text{'}\left(0\right)+\tau S_0[I\left(-\delta \right)+U\left(-\delta \right)]-\nu I\left(0\right)\\ -U\text{'}\left(0\right)+{\nu }_{2}I\left(0\right)-\eta U\left(0\right)\\ I\text{'}\\ U\text{'}\end{array}\right)$$

with

$$D\left(A\right)={\left\{0_{\mathbb{R}}\right\}}^2\times C^1\left([-\delta ,0],{\mathbb{R}}^2\right).$$

We split A into

$$C\left(\begin{array}{c}{0}_{\mathbb{R}}\\ 0_{\mathbb{R}}\\ I\\ U\end{array}\right)=\left(\begin{array}{c}\tau S_0[I\left(-\delta \right)+U\left(-\delta \right)]\\ {\nu }_{2}I\left(0\right)\\ 0_C\\ 0_C\end{array}\right)$$

$$B\left(\begin{array}{c}{0}_{\mathbb{R}}\\ 0_{\mathbb{R}}\\ I\\ U\end{array}\right)=\left(\begin{array}{c}-I\text{'}\left(0\right)-\nu I\left(0\right)\\ -U\text{'}\left(0\right)-\eta U\left(0\right)\\ I\text{'}\\ U\text{'}\end{array}\right)$$

By using Theorem 3.5 in (Liu, Magal, & Ruan, 2008) we obtain that $-B$ is invertible and

$${\left(-B\right)}^{-1}\left(\begin{array}{c}\alpha \\ \beta \\ I\\ U\end{array}\right)=\left(\begin{array}{c}0\\ 0\\ \tilde{I}\\ \tilde{U}\end{array}\right)$$

where

$$\begin{array}{c}\tilde{I}\left(\theta \right)={\nu }^{-1}[\alpha +I\left(0\right)]+{\int }_{\theta }^{0}I\left(\sigma \right)d\sigma \\ \tilde{U}\left(\theta \right)={\eta }^{-1}[\beta +U\left(0\right)]+{\int }_{\theta }^{0}U\left(\sigma \right)d\sigma \end{array}$$

Thus we can compute

$$C{\left(-B\right)}^{-1}\left(\begin{array}{c}\alpha \\ \beta \\ I\\ U\end{array}\right)$$

and since the range of C is contained into ${\mathbb{R}}^2\times {\left\{0_C\right\}}^2$ it is sufficient to compute

$$C{\left(-B\right)}^{-1}\left(\begin{array}{c}\alpha \\ \beta \\ 0_C\\ 0_C\end{array}\right)=\left(\begin{array}{c}\tau S_0[\frac{\alpha }{\nu }+\frac{\beta }{\eta }]\\ \frac{{\nu }_2}{\nu }\alpha \\ 0_C\\ 0_C\end{array}\right).$$

Therefore, the next generation matrix is

$$V{S}^{-1}=\left[\begin{array}{cc}\frac{\tau S_0}{\nu }& \frac{\tau S_0}{\eta }\\ \frac{{\nu }_2}{\nu }& 0\end{array}\right]$$

which is a Leslie matrix, and the basic reproductive number ${\mathcal{R}}_0$ is

$${\mathcal{R}}_0=\frac{\tau S_0}{\nu }\left(1+\frac{{\nu }_2}{\eta }\right).$$ (6.20)

By using (6.17) and ${\nu }_2=\left(1-f\right)\nu$, we obtain

$${\mathcal{R}}_0=\frac{{\chi }_2+\nu }{\nu }\frac{\eta +{\chi }_2}{{\nu }_2+\eta +{\chi }_2}{e}^{{\chi }_2\delta }\left(1+\frac{\left(1-f\right)\nu }{\eta }\right).$$ (6.21)

Declaration of competing interest

The authors declare no conflict of interest.

Handling editor. Dr. J Wu