Abstract
Objective
Clinical trials in amyotrophic lateral sclerosis (ALS) continue to rely on survival or functional scales as endpoints, despite the emergence of quantitative biomarkers. Neuroimaging‐based biomarkers in ALS have been shown to detect ALS‐associated pathology in vivo, although anatomical patterns of disease spread are poorly characterized. The objective of this study is to simulate disease propagation using network analyses of cerebral magnetic resonance imaging (MRI) data to predict disease progression.
Methods
Using brain networks of ALS patients (n = 208) and matched controls across longitudinal time points, network‐based statistics unraveled progressive network degeneration originating from the motor cortex and expanding in a spatiotemporal manner. We applied a computational model to the MRI scan of patients to simulate this progressive network degeneration. Simulated aggregation levels at the group and individual level were validated with empirical impairment observed at later time points of white matter and clinical decline using both internal and external datasets.
Results
We observe that computer‐simulated aggregation levels mimic true disease patterns in ALS patients. Simulated patterns of involvement across cortical areas show significant overlap with the patterns of empirically impaired brain regions on later scans, at both group and individual levels. These findings are validated using an external longitudinal dataset of 30 patients.
Interpretation
Our results are in accordance with established pathological staging systems and may have implications for patient stratification in future clinical trials. Our results demonstrate the utility of computational models in ALS to predict disease progression and underscore their potential as a prognostic biomarker. ANN NEUROL 2020;87:725–738
Amyotrophic lateral sclerosis (ALS) is a progressive neurodegenerative condition that is clinically heterogeneous, with considerable variability in survival times after symptom onset.1, 2 From the molecular standpoint, it has been hypothesized that the phosphorylated 43kDa TAR DNA‐binding protein (pTDP‐43) spreads in a "prionlike" manner across the brain in ALS.3, 4, 5 From a macroscale "whole‐brain" perspective, previous cross‐sectional studies have shown that the white matter connections of the motor cortex are impaired in ALS patients.6, 7, 8, 9, 10, 11, 12 This impairment of brain regions is suggested to spread from primary motor regions in a spatially expanding connected manner.9
Brain network analyses have contributed valuable insights into cerebral pathology in vivo and have been extensively applied to various neurodegenerative conditions.13 With increasing availability of noninvasive imaging data for brain structure, including diffusion tensor imaging (DTI), the research area of network neuroscience is able to extend the focus from cross‐sectional comparison studies toward the longitudinal development of brain disorders.14, 15, 16 However, the step toward predicting individual disease progression has yet to be unraveled.
Considering that histopathology is limited to the characterization of postmortem tissues in ALS, magnetic resonance imaging (MRI) measurements have proven their potential to be applied as a biomarker for tracking disease progression and staging in vivo.17, 18 Modeling the disease spreading mechanism in ALS is the next step toward predicting the observed empirical impairment. Network‐based mathematical models can offer a new perspective on the spreading of disease pathology. Computational models can simulate aggregation levels in brain regions using the brain network as an underlying substrate. In silico computational work has suggested that progressive spreading can potentially be predicted based on the topological pattern of the brain's white matter connections, predicting simulated aggregation in line with the Brettschneider stage regions of ALS.19
In this study, we evaluate the use of "computational neurology" approaches to make predictions on disease progression in ALS. We start by exploring network alterations in a large cohort of ALS patients across 4 timepoints using network‐based statistics (NBS). We apply the computational "random walker model" to MRI data of patients to simulate longitudinal disease effects at the group level. We then aim to extend the use of these models toward the estimation of longitudinal disease patterns based on individual MRI scans and to examine the potential of computer simulations for the prediction of disease progression in individual patients. We evaluate the performance of the computer models by comparing simulated aggregation levels with empirical impairment as measured by means of longitudinal MRI scans acquired at 3 later timepoints. We analyze the correlation of the random walker model with clinical decline and thereby assess the applicability of the computational model to forecast disease propagation in individual patients. The prognostic value of the aggregation levels is further explored using deep learning. We validate our method using an external dataset of 30 patients and 30 controls.
Subjects and Methods
MRI Dataset I for Group‐Level Analysis
A set of 60 ALS patients was analyzed at the group level, all of whom underwent 4 longitudinal MRI scans (further denoted as MRI dataset I, demographics and follow‐up interval lengths are displayed in Supplementary Table 1). The 4 longitudinal time points are referred to as T1, T2, T3, and T4. Patients were diagnosed according to the El Escorial criteria20 with either definite or probable ALS and recruited from the outpatient clinic for motor neuron diseases of the University Medical Center Utrecht (UMCU). This study was approved by the medical research ethics committee of the UMCU. For each of the 4 time points, a different subset of 120 controls with the same gender ratio and comparable age distributions was matched (Supplementary Table 2, Fig 1A).
Figure 1.
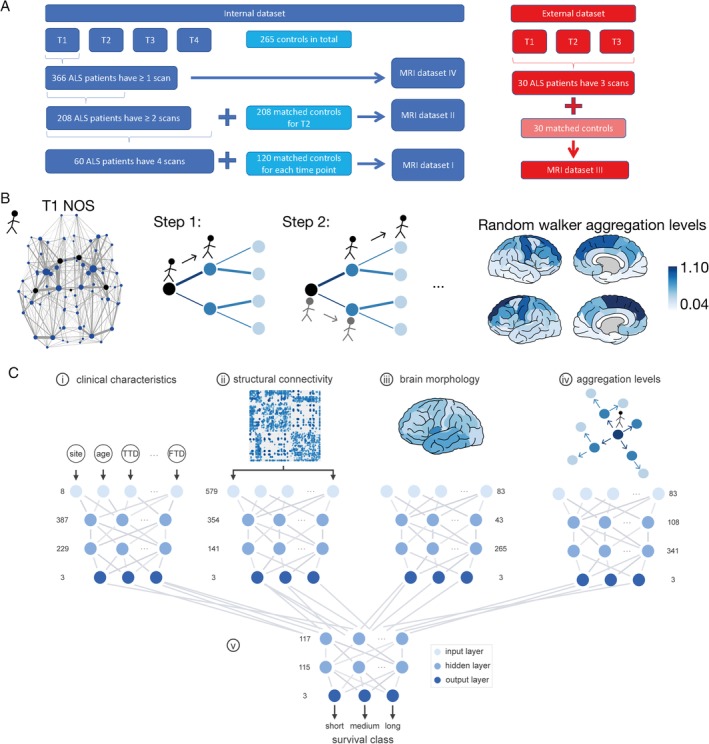
(A) Flowchart of the magnetic resonance imaging (MRI) datasets. The internal dataset of patients and controls is displayed on the left. In total, a data pool of 366 patients and 265 control datasets was included. MRI dataset I: for each time point, T1 to T4, we extracted 120 controls (overlapping sets) from this pool, age‐ and gender‐matched with the 60 amyotrophic lateral sclerosis (ALS) patients who had 4 MRI scans. These data of patients and controls formed MRI dataset I, which was used for the group‐level analysis. MRI dataset II included 148 ALS patients who had 2 scans (T1 and T2) together with the previously mentioned 60 ALS patients, resulting in a total set of 208 ALS patients with at least 2 scans. To calculate the empirical impairment at T2, we matched 208 controls with the same gender ratio and age distribution. The external dataset of 30 controls and 30 ALS patients is described on the right, including the data of patients each having 3 MRI scans (MRI dataset III). The controls were age‐ and gender‐matched for time point T1. Survival predictions were based on the T1 scan; thus, we could use the total of 366 ALS patients in the internal dataset, all of whom had (at least) 1 MRI scan (MRI dataset IV). (B) Schematic overview of the simulations. The far left panel represents the group‐averaged number of streamlines (NOS) connectome, where the thickness of connections represents NOS and the thickness of regions indicates their node strength (ie, sum over all their attached NOS weights). The black dots represent the locations of the possible starting regions, the Brettschneider stage I regions (either right‐hemispheric or left‐hemispheric precentral gyrus, right‐hemispheric or left‐hemispheric superior frontal gyrus, or brainstem). All NOS link weights were resampled with a Gaussian distribution prior to simulations. The initiated random walker selected one of the black starting regions at random (black dots in the NOS network). In every step of the simulations, the random walker chose the next region with a probability proportional to the link weight of the attached links. In the panel "Step 1," the different link weights of the attached links are marked by different thicknesses of the links. In "Step 2," the original random walker selected again randomly a neighboring region with the probability proportional to the NOS of that link. In parallel, a second random walker started from the previously visited starting region and also made 1 step, that is traveled 1 connection. The process continued until the original random walker took 5 steps in total. After 1,000 simulation runs, the number of times that a random walker visited each region was averaged and defined as the (simulated) aggregation level for that region. The results for the random walker simulations on the group‐averaged connectome are visualized in the far right panel; the highest random walker aggregation levels were in the bilateral superior frontal and precentral gyri (displayed as dark regions). The lowest random walker aggregation levels were the right‐ and left‐hemispheric transverse temporal gyri and the entorhinal cortices (light regions). (C) Visualization of the survival prediction process using deep learning. (i) A single model based on 8 clinical characteristics was fitted, consisting of 387 elements in the first hidden layer, 229 in the second hidden layer, and 3 output classes (reflecting short, medium, and long survival). (ii) A model was constructed based on structural connectivity matrices containing fractional anisotropy values (579 input elements), with 354 and 141 hidden elements. (3) The third single model was based on brain morphology in terms of cortical thickness values of 83 brain regions and contained 43 and 265 hidden elements. (iv) The last single model with 108 and 341 hidden elements was fitted using the simulated aggregation levels of the random walker across all brain regions. (v) The output classes of the 4 single models were used as input nodes for the combined model that contained 117 and 115 hidden elements. The combined model, based on single models i–iii, composed of 130 and 101 hidden elements, is not shown. A class label was derived from the output layer and reflected the survival prediction class of the patient. FTD = frontotemporal dementia, TTD = Time to diagnosis. [Color figure can be viewed at http://www.annalsofneurology.org]
MRI Dataset II for Individual‐Level Analysis
We examined the use of the random walker model at the individual level. To avoid a potential bias toward slow progressors in the individual analysis, we added 148 ALS patients with 2 scans to dataset I, resulting in a total size of 208 ALS patients, each with a scan at T1 and T2 (see Supplementary Table 1, MRI dataset II). An age‐ and gender‐matched group of 208 control subjects was extracted for the comparison analysis at T2. Of dataset II, 6 ALS patients had frontotemporal dementia (FTD), one of whom was also included in dataset I.
MRI Dataset III for External Validation
We used a dataset of 30 ALS patients scanned 3 times longitudinally and 30 controls from Trinity College Dublin for external validation (see Supplementary Table 1, MRI dataset III). T1‐weighted images were acquired on a 3T Philips (Best, the Netherlands) Achieva Medical Scanner using a 3‐dimensional inversion recovery prepared spoiled gradient recalled echo sequence, with a spatial resolution of 1mm3, repetition time/echo time (TR/TE) = 8.5/3.9 milliseconds, inversion time = 1,060 milliseconds. DTI images were acquired using a spin‐echo planar imaging sequence with spatial resolution = 2.5mm3, TR/TE = 7,639/59 milliseconds, b values = 0, 1,100 s/mm2, with Spectral Pre‐saturation with Inversion Recovery (SPIR) fat suppression and dynamic stabilization.18 The T1‐weighted images and DTI measurements underwent the same preprocessing steps as the other datasets.
MRI Dataset IV for Survival Prediction
The internal dataset with all patients who had at least 1 MRI scan was enlarged to check whether the random walker model adds to survival prediction for ALS patients, resulting in a total dataset of 366 ALS patients (MRI dataset IV; see Fig 1A). Each of the patients was categorized according to their survival time (ie, time between disease onset and death) as short survivors (<25 months), medium survivors (between 25 and 50 months), and long survivors (>50 months at time of analysis).
Construction of Connectomes
Datasets I, II, and IV were acquired on a 3T Philips Achieva Medical Scanner at UMCU (detailed descriptions can be found in our previous publications8, 10, 21). The Desikan–Killiany atlas and FreeSurfer (v5.3.0) were used to parcellate the brain into 68 cortical regions, 14 subcortical regions, and the brainstem based on the T1‐weighted data.22 Diffusion‐weighted images were corrected for susceptibility and eddy‐current distortions.23, 24 White matter connections between brain areas were determined via Fiber Assignment by Continuous Tracking (FACT) with an initial condition of 8 seeds randomly placed in each voxel.25, 26, 27 The stopping conditions for the fiber tracking were either a fractional anisotropy (FA) value <0.1, a turn of the streamline with an angle >45°, or the border of the brain mask.10 The minimum length to be considered a streamline in our analysis was 30mm. Brain regions and their connections together formed a brain network ("connectome") for each individual, with brain regions represented as "nodes" and pairwise connections represented as "links." FA and number of streamlines (NOS) were used as weights of the network connections ("link weights").28 We used MATLAB R2018a (MathWorks, Natick, MA) for all of the following analysis steps. We generated a group mask for the connections of all patients, considering those connections that were present in at least 50% of all patients, as a compromise between network reliability and preserving the heterogeneity among patients.29 Similarly, we generated a group mask for the control group and combined the group masks from patients and controls, leaving us with only those connections that were common to both group masks for the group‐level analysis. Using group mask thresholds of 40% and 60% led to similar results. At the individual level, as much subject‐specific information as possible was considered, with no additional thresholding applied.
Tracking Empirical White Matter Impairment
A 1‐sided unpaired Student t test was applied to compare the average FA weights in ALS patients with controls. NBS was used to map the largest connected component of affected connections (cutoff α = 0.01 for the p values).30 A null distribution was established to compare to the size of this component using permutations of group labels between patients and controls (10,000 permutations). A similar NBS procedure was applied to compare patients longitudinally, using a paired t test (T1 vs T2, T2 vs T3, etc). All p values were false discovery rate–corrected.
To assign an "impairment level" to each brain region, we calculated a z score (z = [x − μ]/σ; μ = mean, σ = standard deviation) for each connection with respect to the corresponding FA values in controls. We counted the number of connections attached to a brain region with a negative z score (indicating a lower average FA value compared to controls). This number of impaired attached connections was defined as the empirical impairment of that brain region. This analysis was performed at the group and individual levels. For the individual analysis, the control group was split into 2 subgroups depending on their age being below or above the median age of the ALS group of dataset II. Each individual patient was compared to either the younger or older control group depending on his/her age.
Random Walker Model
Brettschneider et al defined 4 stages of cerebral pTDP‐43 aggregation levels based on postmortem observations (displayed in the lower left panel of Fig 2).4 We focused on the measure of NOS (resampled with Gaussian distribution) as an underlying connection weight, because previous studies were able to predict the Brettschneider stages using NOS weights.19 In each run, the random walker started in one of the Brettschneider stage I regions (selected uniformly at random, black dots in Fig 1B). The random walker chose one of the adjacent links with a probability proportional to their link weight in every step. Thus, a link with a higher NOS value had a greater chance of being traversed by the random walker in this model. Additionally, the model was set so that after each step of the random walker, new random walkers started from all previously visited regions in parallel (see Fig 1B, Step 2). The simulations were stopped once the first random walker reached the maximum number of 5 steps, similar to our previous study.19 After simulating these random walks, the number of times a random walker traversed a brain region is further referred to as the (simulated) aggregation level of that region and averaged over 1,000 simulated random walks. We applied the random walker model to the group‐averaged (dataset I) and individual (dataset II) connectomes of ALS patients as well as to the external dataset. We calculated Pearson linear correlation coefficient between the empirical and simulated impairment level over all regions to quantify their relation. To compare the simulated aggregation to controls, we applied the random walker model to the controls of dataset II and calculated the z scores of the aggregation levels per region with regard to the younger or older control group, respectively (same procedure as for tracking the empirical white matter impairment).
Figure 2.
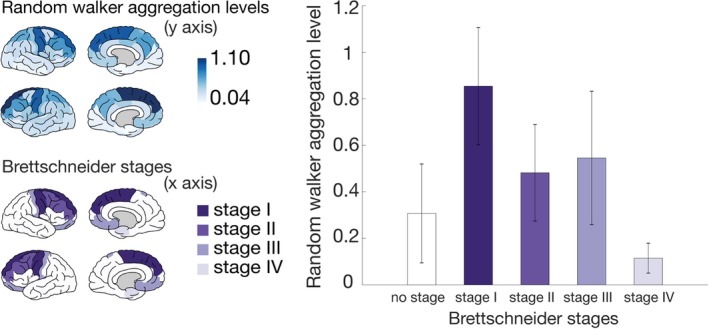
Association between simulated aggregation levels and Brettschneider stages. In the upper left panel, the simulated random walker aggregation levels are visualized based on the group‐averaged connectome with number of streamlines as a link weight (based on 60 amyotrophic lateral sclerosis patients at T1). The Brettschneider stages are visualized on the template brain in the lower left panel. Stage I regions are the precentral and superior frontal gyri and the brainstem. Stage II regions are caudal middle frontal and rostral middle frontal gyri. Stage III regions are medial and lateral orbitofrontal cortices, postcentral gyrus, caudate nucleus, putamen, and nucleus accumbens. Stage IV regions are the entorhinal cortex and the hippocampus. In the bar plot in the right panel, the simulated average aggregation levels per region are visualized when dividing the brain regions into Brettschneider stages. The length of the error bar represents the standard deviation; "no stage" refers to the average aggregation level of all other regions not involved in the neuropathology of Brettschneider (all white regions on the template brain in the lower left panel). [Color figure can be viewed at http://www.annalsofneurology.org]
Clinical Dataset
We used the neurological examination data from 141 patients for the correlation analyses with clinical data (67.8% of dataset II). Upper motor neuron (UMN) burden was calculated for the bulbar region and for each limb at 2 consecutive timepoints. We used UMN scores to categorize the degree of hyperreflexia, hypertonia, and pathological reflexes for the limbs and the degree of pseudobulbar dysarthria, slowing of tongue movements and pseudobulbar reflexes for the bulbar region.31 UMN score ranges from zero (no UMN involvement in that region) to 3 (severe involvement) in each region. Summing up the scores for all regions, we calculated the total whole‐body UMN score for each individual patient.
Deep Learning Predictions of Survival
A deep learning model to predict survival was constructed and trained, as described in detail in our previous publication (see Fig 1C).21 In addition to the previous model, we included the random walker aggregation levels and assessed their added value to the prediction accuracy. We also tested a deep learning model including only aggregation levels. For demographic details of the training (n = 257), validation (n = 55), and test dataset (n = 54), we refer to Supplementary Table 2. The output class with the highest probability was selected as the predicted class label. The overall performance of the deep learning models was assessed as the sum of correctly predicted class labels divided by the total number of patients in the set.
To assess the performance between the different deep learning models, we randomly selected a subset of 27 patients (50%) of the test set and presented them to the trained models. This subsampling process was repeated 10,000 times to obtain a distribution of model accuracies for each of the different models, to which a normal distribution was fitted. Significance between distributions was assessed by a pairwise t test.
Results
In datasets I–III, age and gender did not differ significantly between patients and controls (see Supplementary Table 1). NBS analysis revealed a significantly large impaired connected component at all 4 time points (Fig 3A, p = 0.015 for T1; 2B, p = 0.0147 for T2; 2C, p = 0.0147 for T3; 2D, p = 0.012 for T4). Over the time points T1 up to T4, the number of links in the impaired connected component grew (see Fig 3, from 17 links at T1 [2A], 22 links at T2 [2B], 19 links at T2 [2C], to 29 links at T4 [2D]), indicating a spreading of impairment in a spatiotemporal manner. The number of involved regions in these components also increased over time (see Fig 3, lower panel). None of the longitudinal comparisons showed any significantly impaired connected component.
Figure 3.
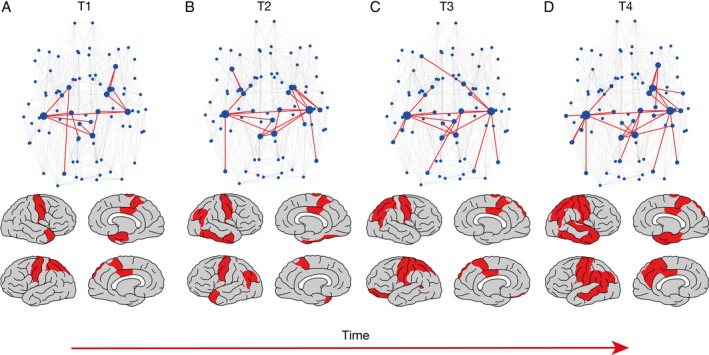
Network‐based statistics (NBS) results for the different time points T1 (A), T2 (B), T3 (C), and T4 (D), based on the connectomes of 60 amyotrophic lateral sclerosis patients compared with their age‐ and gender‐matched control group of 120 subjects. The upper panel represents the links involved in the largest impaired connected component, and the lower panel plots the involved regions on the template brain. In the upper panel, the dark links represent the largest impaired connected component (17 links impaired at T1, p = 0.015; 22 links impaired at T2, p = 0.0147; 19 links at T3, p = 0.0147; and 29 links at T4, p = 0.012 for the cutoff α = 0.01). The light gray lines represent connections not significantly impaired. In the brain plots in the lower panel, the darker regions represent regions involved in the NBS component over the 4 different time points. For T1, subcortical regions involved are bilateral pallida and thalami, left‐hemispheric caudate nucleus, right‐hemispheric amygdala, and putamen; cortical regions involved are bilateral paracentral lobes, precentral gyri, posterior cingulate cortices, left‐hemispheric superior parietal gyri, right‐hemispheric entorhinal cortex, and temporal pole. For T2, subcortical regions involved are bilateral amygdalae, pallida, and thalami, left‐hemispheric caudate nucleus, and right‐hemispheric putamen; cortical regions are bilateral paracentral lobes, precentral gyri, inferior parietal gyri, left‐hemispheric temporal pole, right‐hemispheric fusiform, inferior temporal gyrus, and posterior cingulate cortex. For T3, subcortical regions involved are bilateral caudate nuclei, pallida, and thalami; cortical regions involved are bilateral paracentral lobes, precentral gyri, posterior cingulate cortices, superior parietal gyri, left‐hemispheric banks of the superior temporal sulcus, lateral orbitofrontal cortex, and postcentral and inferior parietal gyri. For T4, subcortical regions involved are bilateral thalami, left‐hemispheric caudate nucleus, right‐hemispheric amygdala, hippocampus, pallidum, and putamen; cortical regions involved are bilateral paracentral lobes, precentral, postcentral, and inferior parietal gyri, posterior cingulate cortices, left‐hemispheric precuneus, banks of the superior temporal sulcus, middle temporal and supramarginal gyri, right‐hemispheric entorhinal cortex, parahippocampal, superior parietal, inferior, and superior temporal gyri, and temporal pole. All other regions are displayed as light gray. [Color figure can be viewed at http://www.annalsofneurology.org]
The aggregation levels for each region resulting from the random walker simulations are illustrated in Figure 2 (upper left panel, simulation results represent the predicted impairment level per brain region at the group level based on dataset I). Categorizing these simulated regional aggregation levels according to the neuropathological stages of Brettschneider revealed a significantly decreasing trend (Jonckheere–Terpstra test p = 0.0006; permutation test of randomly assigning brain areas to Brettschneider stages p = 0.0004).4 All pairwise combinations of the different staging aggregation levels provided significant 2‐sided unpaired t test results (p < 2*10−6), that is, the Brettschneider stage regions differed significantly with regard to their aggregation levels. The simulations were rerun with a different number of steps for the random walker. Because the diameter of the underlying network was 4, we needed the random walker to take at least 4 steps to reach all other regions. From 6 steps onward, the decreasing trend in the Brettschneider regions was not preserved, representing only nodal strength, thus we chose 5 steps.
To test the random walker's potential to predict disease progression, we further compared the simulated aggregation levels as computed on the MRI data at T1 with the empirically measured impairment per brain region (by means of the structural MRI images) at later time points (Fig 4). The aggregation levels of the random walker based on the group‐averaged T1 connectome and the empirical impairment at T4 exhibited a significant positive correlation (corr = 0.7583, p = 1.03*10−16; see Fig 5). Because the degree of the underlying network has a strong influence on the random walker aggregation levels,32 we confirmed the significance of this correlation after normalizing by degree (corr = 0.2174, p = 0.0484).
Figure 4.
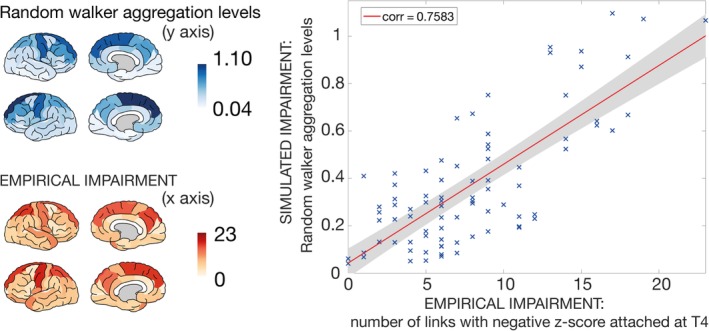
Simulated versus empirical impairment of brain regions at the group level. In the upper left panel, the simulated random walker aggregation levels are visualized based on the group‐averaged connectome with number of streamlines as a link weight (based on 60 amyotrophic lateral sclerosis [ALS] patients at T1). The empirical impairment for each region at T4 is visualized in the lower left panel, where the number of links that possessed a negative z score, with respect to the control group, was counted. The highest empirical impairment was reached in the left‐hemispheric precentral and the right‐hemispheric superior parietal lobule and the left‐hemispheric superior frontal gyrus (darker regions), whereas the right‐ and left‐hemispheric transverse temporal gyri, the left‐hemispheric pericalcarine cortex, and the frontal pole as well as the banks of the superior temporal sulcus were among the least impaired regions (lighter regions). The right panel displays the relation between the 2 left panels. The average random walker aggregation levels on the group‐averaged ALS connectome at T1 are plotted against the empirical impairment for each region at T4. This relation reached a significantly positive correlation of 0.7583 with p = 1.03*10−16. [Color figure can be viewed at http://www.annalsofneurology.org]
Figure 5.
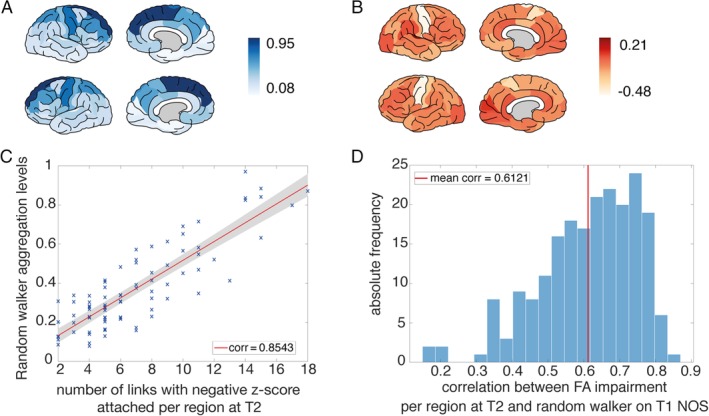
(A) Random walker aggregation levels simulated on the T1 connectome with number of streamlines (NOS) as a link weight averaged over all individuals for each region. The highest average aggregation levels were reached in the superior frontal and precentral gyri (dark regions). (B) Empirical impairment at T2 for fractional anisotropy (FA) based on the dataset of 208 longitudinal individual amyotrophic lateral sclerosis (ALS) patients. For each region, we calculated a z score compared to the respective age‐matched control group and visualized the average over all individuals (dark indicates a positive z score and light indicates a negative z score pointing toward a decrease in FA). The lowest z scores were reached by the precentral gyri and the paracentral lobes (in white). (C) Plot for one example subject of the correlation between the number of impaired links attached per region at T2 (counted as the number of links with a negative z score compared with the respective age‐matched control group) and the average aggregation level of the random walker based on the NOS connectome at T1. This example subject reached the maximum correlation coefficient of 0.8534. (D) Histogram of all correlation coefficients of the random walker results, simulated on the T1 connectome (with NOS as link weights) versus the empirical impairment at T2 for FA based on the dataset of 208 individual ALS patients. The average correlation coefficient was 0.6121, and all individuals reached positive correlations. [Color figure can be viewed at http://www.annalsofneurology.org]
NBS analysis based on axial diffusivity revealed no significant differences between patients and controls, whereas the radial diffusivity (RD) and mean diffusivity (MD) increased significantly in ALS patients (Supplementary Table 3). Interestingly, NBS analysis revealed larger component sizes when taking MD and RD as compared to FA (35–54 links in MD and RD; 17–29 links in FA), suggesting that these measures might be more sensitive than FA for detecting white matter impairment in ALS patients. The correlation analysis at the group level, considering the number of attached links with positive z scores, aligns with the FA results (MD: corr = 0.7946, p = 3.078*10−19; RD: corr = 0.7767, p = 6.21*10−18).
Random walker simulations were repeated on the individual connectomes of 208 ALS patients, and regional aggregation levels were retrieved from individual subjects at their first scan (the average over all individual aggregation levels is visualized on the template brain in Fig 5A). The average z score per region over all individuals at T2 is plotted in Figure 5B. The simulated aggregation levels based on T1 were compared with the empirical impairment per region at T2 (for an example subject see Fig 5C). All individual correlation coefficients between the simulated and empirical disease effects were positive, with an average correlation of 0.6121, and 204 of the 208 were significant. Whereas the group level correlation analysis remained significant after normalizing for degree, this was true for only 22 individuals of 208 (Fig 5D). This result indicates the importance of degree at the individual level, in line with previous analyses.19 To test the effect of FTD patients on the presented results, we repeated the analysis excluding these 6 patients, with the z score distributions recalculated based on the smaller group of 202 patients and 202 age‐ and gender‐matched controls. Exclusion of the FTD patients revealed similar results as the main analysis (mean corr = 0.6106, 198 of 202 patients showed significantly positive correlation, and 23 individuals remained significant after normalizing by the degree), showing a nonsignificant difference with a permutation test (against 1,000 randomly extracted subgroups of the same size: p = 0.7070). Testing the correlation coefficients of the FTD group against the rest of the ALS patients also yielded nonsignificant results (2‐sided t test p = 0.3610; permutation test against 1,000 randomly extracted subgroups of size 6: p = 0.1850). We further examined whether ALS patients with C9ORF72 mutation (C9+) demonstrated significantly different results; a 2‐sided t test of the C9+ group against the rest of the ALS patients (p = 0.33) and a permutation test of the average correlation coefficient of the C9+ group (corr = 0.6119) against 1,000 randomly extracted subgroups of the same size did not reveal differences (p = 0.165). NBS analysis excluding the C9+ patients showed similar results as the main analysis (T1: 14 links, p = 0.0224; T2: 14 links, p = 0.0224; T3: 13 links, p = 0.0224; T4: 31 links, p = 0.0196).
Findings were validated using the external dataset (dataset III); we could confirm the order of the Brettschneider stage regions with regard to the simulated aggregation levels based on T1 (Fig 6C), and a positive correlation was found between these aggregation levels and the empirical impairment at T3 (the last scan in this case) at the group (see Fig 6A, B, D, corr = 0.5508) and at the individual level (see Fig 6E–G).
Figure 6.
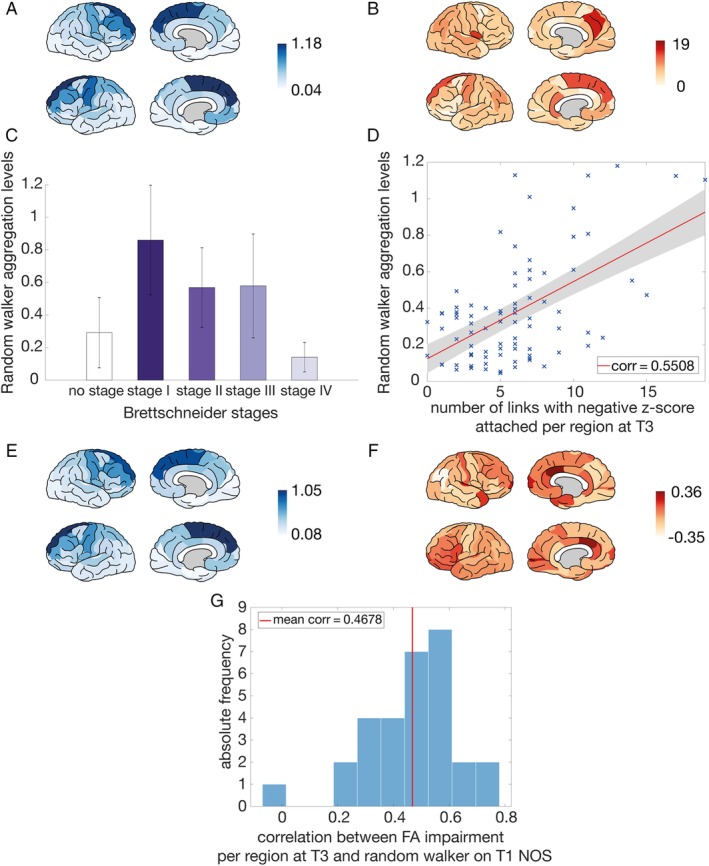
Validation based on an external dataset from the Trinity College Dublin (dataset III). (A) Random walker aggregation levels simulated on the group‐averaged connectome with number of streamlines (NOS) as a link weight based on 30 amyotrophic lateral sclerosis (ALS) patients at T1. (B) The empirical impairment for each region at T3 (determined as the number of links that possessed a negative z score with respect to the control group). (C) Simulated average aggregation levels per region when dividing the brain regions into the Brettschneider stage I, stage II, stage III, and stage IV regions ("no stage" refers to the average aggregation level of all other regions not involved in the neuropathology of Brettschneider). (D) Random walker aggregation levels simulated on the group‐averaged ALS connectome (NOS link weights) at T1 against the empirical impairment for each region at T3 (determined as the number of links that possessed a negative z score with respect to the control group). This relation resulted in a correlation coefficient of 0.5508 (p = 6.8*10−8). (E) Random walker aggregation levels simulated on the T1 connectome with NOS as a link weight averaged over all individuals for each region. (F) Empirical impairment at T3 for fractional anisotropy (FA) for the dataset of 30 longitudinal individual ALS patients. For each region, we calculated a z score compared with the respective control group and visualized the average over all individuals. (G) Histogram of all correlation coefficients of the random walker results, simulated on the T1 connectome (with NOS as a link weight) versus the empirical impairment at T3 for FA for the dataset of 30 longitudinal individual ALS patients. For each region, we counted the number of attached links with a negative z score. The average correlation coefficient was 0.4678, and 23 of 30 individuals reached significant correlations after Bonferroni correction. [Color figure can be viewed at http://www.annalsofneurology.org]
We further calculated the z score of the motor cortex regions (sum of the aggregation levels of the bilateral precentral gyri and paracentral lobes) with respect to controls for each individual patient to compare the random walker aggregation levels of the motor cortex with the UMN score at T2 (see Fig 7A). The lower the z score at T1 (less aggregation than controls), the higher was the UMN score at T2 (corr = −0.2301, p = 0.0075). One explanation of this might include that patients with higher UMN burden have more widespread aggregation; patients with lower UMN burden had a higher variance in aggregation along the cortex (measured as standard deviation) compared to patients with high UMN burden (corr = −0.1928, p = 0.0257; Fig 7B, example subjects displayed in Fig 7C, D).
Figure 7.
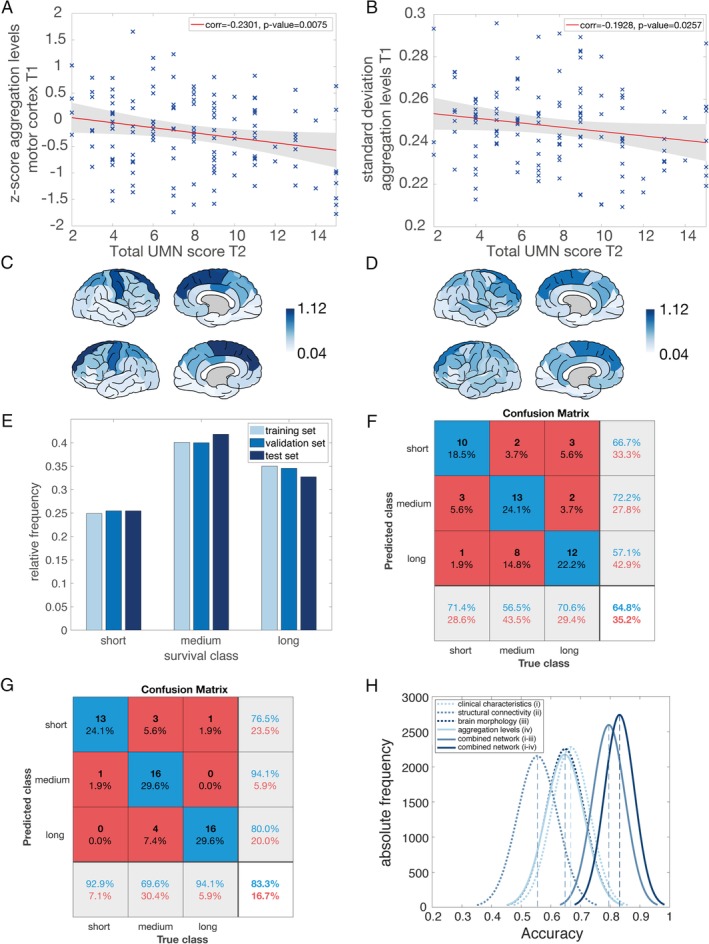
Association between simulated aggregation levels and clinical decline. (A) The z scores of the random walker aggregation levels at T1 in the motor cortex (sum of the aggregation levels of the bilateral precentral gyri and paracentral lobes) were correlated with the total upper motor neuron (UMN) score at T2. The dataset contained 141 amyotrophic lateral sclerosis (ALS) patients as the subset of patients in magnetic resonance imaging (MRI) dataset II, who had a neurological examination on the scan date. The total UMN score in the dataset ranged from 2 (only some involvement of UMN) to 15 (severe involvement). The lower the z score at the first scan (less random walker aggregation than controls), the higher the UMN score at the second time point (corr = −0.2301, p = 0.0075). (B) Total UMN score at T2 correlated negatively with the standard deviation of all random walker aggregation levels at T1 (corr = −0.1928, p = 0.0257). (C) Random walker aggregation levels at T1 of an example subject with a low UMN score at T2 plotted on the template brain. The highest random walker aggregation levels were found in the bilateral superior frontal and precentral gyri (displayed as dark regions). (D) Random walker aggregation levels at T1 of an example subject with a high UMN score at T2 plotted on the template brain. The pattern of random walker aggregation levels was more equally distributed over the whole brain with a lower standard deviation (similar colors over the whole cortex). (E) Survival class distributions of 366 ALS patients across the training, validation, and test sets. The relative frequency was used to display the similarities between sets for each of the 3 survival classes (short, medium, long). (F) The distribution of the prediction results from the neural network are summarized in a confusion matrix. Here, the confusion matrix is shown derived from the model using the random walker aggregation levels of the test set. Correct classifications are displayed on the diagonal, with the overall prediction accuracy 64.8% in the bottom‐right corner. The positive predictive values for each class are displayed in the right, light gray column. The off‐diagonal elements represent incorrect classifications marked by a mismatch between prediction and truth. (G) The confusion matrix derived from the model using a combination of all single modalities (clinical characteristics, structural MRI, brain morphology, and random walker aggregation levels). This combined network reached an overall accuracy of 83.3% for the test set. (H) Distributions of accuracy derived from subsampling the test set 10,000 times for all 6 networks. Mean values are denoted with dashed vertical lines. [Color figure can be viewed at http://www.annalsofneurology.org]
We assessed the added value of aggregation levels as an input for survival class prediction in our deep learning model. The prediction accuracy for a deep learning model only based on aggregation levels was 64.8% (see Fig 7F; see Supplementary Table 4 for accuracies of other single modalities). Adding aggregation levels to the original combined model (based on region morphology, connectivity, and clinical characteristics) increased the accuracy of the previous combined model (83.3% compared to 79.6%; see Fig 7G). The distributions of accuracies between the single networks were significantly different (p = 1*10−32) for all combinations, except for the comparison between morphology MRI and aggregation levels (p = 0.2548; see Fig 7H). More importantly, the accuracies of the 2 combined models differed significantly from each other, indicating the additional value of aggregation levels.
Discussion
This study evaluated the use of computational network models for the prediction of neurodegeneration in ALS. Our findings suggest that a random walker model based on MRI scans can potentially predict longitudinal neurodegeneration observed at follow‐up scans, both at the group level and based on neuroimaging data of individuals. Simulated aggregation levels as derived by the computational models were in line with the pathological Brettschneider stage regions of ALS. Furthermore, these simulated aggregation levels showed overlap with the degree of future upper motor neuron burden and increased the prediction accuracy of the survival class of patients. Our findings suggest that "computational neurology models" may have potential as predictive models to capture individual disease progression in ALS. Computational predictions of disease spread based on the initial MRI scan showed that early stage white matter alterations define subsequent pathology, and that the analyses of early connectivity changes may reliably predict disease burden at later stages.
Our results support the hypothesis that impairment in ALS spreads from the motor cortex along white matter tracts in a spatiotemporal manner. Previous studies have demonstrated progressive and anatomically expanding connectivity alterations in ALS at a group level,6–11,18 and our findings now predict such network integrity changes with a simulation model. Shifting the focus from a group level toward the individual patient may help to advance developing targeted therapy based on precision medicine within the heterogeneous ALS patient population. Furthermore, we demonstrated a consistency between the microscopic pathological staging in ALS4 and its representation on the macroscopic level of brain regions. This overlap may potentially facilitate tracking disease spread and categorizing patients into disease stages in vivo based on MRI.17, 18, 33 This result brings the 2 fields of pathological staging and in vivo MRI staging closer together as a crucial step toward combining all available patient information to understand ALS disease progression. Our study suggests that computational models may help to pave the way to the development of MRI biomarkers for patient stratification and monitoring in clinical trials.18, 34
We used connectome analysis of a large cohort of patients and controls. The validation of our results based on an external independent dataset demonstrates their generalizability. Our study shows evidence that the connectome may be the underlying substrate of disease propagation in ALS. Validating our simulated impairment using the later stage empirical impairment of individual patients, our model offers a new network‐based perspective on ALS as a progressive disease. The impairment level of certain brain regions has been shown to be closely related to clinical outcome measures.10, 17 We demonstrated that the simulated aggregation levels correlate with empirical impairment at the level of brain regions and also with future clinical UMN burden. As our data and those of others indicate, aggregates potentially precede symptoms.35 The individual aggregation patterns based on the first scan may thus aid in making predictions on future UMN burden. As such, computation estimates could be utilized as a biomarker for clinical trials, comparing predicted impairment levels or UMN scores with the actual outcome after, for example, a pharmaceutical intervention that is hypothesized to clear TDP‐43. Such potential applications of computational models require further validation. Objective and quantitative imaging markers can therefore offer an alternative to clinically observed changes, which can possibly be detected at earlier stages of the disease based on MRI scans.
Earlier work using a similar diffusion model in dementia supports our current findings.15 With the help of a mathematical diffusion model, the prevalence rates of Alzheimer disease and behavioral FTD were accurately predicted over the lifespan of patients. The most important clinical implication of the spreading model used for dementia patients has been the potential to predict cognitive decline, enabling patients and their neurologists to make informed choices about treatment and lifestyle.15 The prediction of cognitive decline could also be an interesting topic for future work on ALS data. Successful approaches to modeling disease progression suggest a common underlying mechanism for disease propagation in neurodegenerative conditions, which requires studies using multiple disease cohorts. Random walker models applied to data acquired early in a patient's disease trajectory have the potential to accurately predict late stage disease burden, cognitive decline, and survival in neurodegenerative conditions.
One of the limitations of our approach is that progressive white matter pathology is not the only factor influencing disease progression in ALS. First of all, this study only analyzes degeneration of the central motor neurons at the level of brain regions, whereas future work should link the evidence of both upper and lower motor neuron degeneration in ALS to form a complete picture of the functional loss for patients. A combined approach to studying data on upper and lower motor neuron effects could be designed by analyzing corticomuscular coherence measuring electroencephalography and electromyography simultaneously. Second, a number of established clinical and genetic factors, such as the C9ORF72 mutation or the site of onset, also contribute to disease progression, which may be indirectly represented in an individual connectome.21, 36, 37, 38 As a next step, we intend to analyze the specific network attributes of the connectome structure that accelerate or decrease the speed of disease spread in ALS. These attributes involve the degree distribution of the connectome as well as the overall modular structure, which are both key factors influencing the random walker model and thus the disease progression.32 Whether ALS is a prionlike disease remains a subject of ongoing debate in the field. Correspondences between our simulation results and the clinical decline in patients do not directly expose the nature of the underlying spreading pathology. With the help of the applied spreading model, one can test different adjustments to this wiring architecture in silico, which could lead to future treatment options to slow down disease spread through the white matter connections. Tools like deep brain stimulation could be implemented to realize the needed connectomic adjustments in vivo, which has been suggested as a potential strategy to slow down the progression in other neurological diseases, such as Parkinson disease.39, 40 Furthermore, although Brettschneider et al described the spinal cord in ALS patients as a potential stage I region,4 no spinal cord MRI data were analyzed in the current study. Spinal imaging data could be a potential addition to increase the prediction accuracy of future disease progression models.41, 42, 43 Finally, because ALS patients carrying the SOD1 mutation are known to lack TDP‐43 pathology, this subgroup could be a target for future research to analyze possibly different patterns of connectome dysfunction.
Because ALS is a clinically heterogeneous condition with considerable variation in survival times, accurate prognostic indicators are urgently needed.44 We showed that the simulated aggregation levels based on early imaging data can help to predict survival of individual patients in a large dataset of ALS patients. Using the aggregation levels of the random walker as an additional layer for a previously published machine learning algorithm to predict survival increased classification accuracy significantly.21, 37, 45, 46 Machine learning techniques have been increasingly applied to tackle the complexity and heterogeneity of ALS.47, 48, 49 Accurate prognostication enables patient stratification in clinical trials and may improve quality of life for patients and caregivers.21, 37, 50 However, a well‐known limitation of machine learning results is the "black‐box‐effect," leaving us with only an indirect relation between the input and output data.47 It thus remains difficult to directly decipher the influence of the simulated aggregation levels on the survival of the individual patient.
With our model, we were able to predict to some extent the regional impairment in the central nervous system at later disease stages based on a patient's MRI scan. The simulated aggregation levels correlated with future UMN burden of ALS patients and helped to predict the survival classes for individual patients. Our results demonstrate the applicability of "computational neurology" in ALS to predict disease progression at an individual level and underscore its potential as a prognostic biomarker. Our findings are consistent with established pathological staging systems and may have implications for patient stratification in future clinical trials.
Author Contributions
J.M.M., M.P.v.d.H., and L.H.v.d.B. contributed to the conception and design of the study. J.M.M., P.B., O.H., H.K.v.d.B., A.D.N., and S.C.d.L. helped with the acquisition and analysis of the data. J.M.M. drafted the manuscript and prepared the figures with the help of S.C.d.L. and H.K.v.d.B.
Potential Conflicts of Interest
Nothing to report.
Supporting information
Supplementary Table 1 Demographic and Clinical Characteristics of ALS Patients and Controls in the 4 MRI Datasets
Supplementary Table 2. Demographic and clinical characteristics of the matched control datasets for each time point of MRI dataset I and for the subdivision of MRI dataset IV into training, validation and test dataset.
Supplementary Table 3. Results of the NBS for different time points T1 to T4 (number of links in the largest connected component (LCC) and p‐value) for the different measures of DTI. The NBS analysis was performed based on both one‐sided (unpaired) t‐tests, one testing for an increase in this measure and the other one for a decrease. All p‐values were FDR‐corrected. Significant results are marked in bold. “None < 0.01” means that none of the p‐values resulting from the respective t‐test was lower than 0.01, thus no component could be extracted for the NBS analysis.
Supplementary Table 4. Overall prediction accuracies for six deep learning networks on the training, validation and test sets. The four single networks were based on clinical data, structural connectivity MRI data, brain morphology MRI data and aggregation levels of the random walker. The network clinicalFACTAL was based on the combination of the aforementioned four single networks, while clinicalFACT did not include the aggregation levels as information source and acted as a reference.
Acknowledgment
M.P.v.d.H. is funded by a Vidi Grant of the Dutch Research Council (Netherlands Organization for Scientific Research grant VIDI‐452‐16‐015), an ALWopen grant (ALWOP.179), and an MQ Fellowship. L.H.v.d.B. received funding from the Netherlands Organization for Scientific Research Vici Grant and from the ALS Foundation Netherlands. This work is funded by a Weston Brain Institute Rapid Response grant. P.B. is supported by the Health Research Board (HRB–Ireland; HRB EIA‐2017‐019), the Research Motor Neuron Foundation, and the Irish Motor Neuron Disease Association. O.H. is funded by the Health Research Board and Science Foundation Ireland.
We thank M. de Reus for helping with MRI data analysis, L. Scholtens for helping with the figures, and R. Schmidt for sharing random walker simulation code.
References
- 1. Chiò A, Calvo A, Moglia C, et al. Phenotypic heterogeneity of amyotrophic lateral sclerosis: a population‐based study. J Neurol Neurosurg Psychiatry 2011;82:740–746. [DOI] [PubMed] [Google Scholar]
- 2. Hardiman O, van den Berg LH, Kiernan MC. Clinical diagnosis and management of amyotrophic lateral sclerosis. Nat Rev Neurol 2011;7:639–649. [DOI] [PubMed] [Google Scholar]
- 3. Neumann M, Sampathu DM, Kwong LK, et al. Ubiquitinated TDP‐43 in frontotemporal lobar degeneration and amyotrophic lateral sclerosis. Science 2006;314:130–133. [DOI] [PubMed] [Google Scholar]
- 4. Brettschneider J, Del Tredici K, Toledo JB, et al. Stages of pTDP‐43 pathology in amyotrophic lateral sclerosis. Ann Neurol 2013;74:20–38. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5. Braak H, Neumann M, Ludolph A, Del Tredici K. Does sporadic amyotrophic lateral sclerosis spread via axonal connectivities? Neurol Int Open 2017;1:E136–E141. [Google Scholar]
- 6. Grolez G, Moreau C, Danel‐Brunaud V, et al. The value of magnetic resonance imaging as a biomarker for amyotrophic lateral sclerosis: a systematic review. BMC Neurol 2016;16:155. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7. Agosta F, Pagani E, Petrolini M, et al. Assessment of white matter tract damage in patients with amyotrophic lateral sclerosis: a diffusion tensor MR imaging tractography study. Am J Neuroradiol 2010;31:1457–1461. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8. Verstraete E, van den Heuvel MP, Veldink JH, et al. Motor network degeneration in amyotrophic lateral sclerosis: a structural and functional connectivity study. PLoS One 2010;5:1–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9. Verstraete E, Veldink JH, van den Berg LH, van den Heuvel MP. Structural brain network imaging shows expanding disconnection of the motor system in amyotrophic lateral sclerosis. Hum Brain Mapp 2014;35:1351–1361. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. Schmidt R, Verstraete E, de Reus MA, et al. Correlation between structural and functional connectivity impairment in amyotrophic lateral sclerosis. Hum Brain Mapp 2014;35:4386–4395. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Douaud G, Filippini N, Knight S, et al. Integration of structural and functional magnetic resonance imaging in amyotrophic lateral sclerosis. Brain 2011;134:3467–3476. [DOI] [PubMed] [Google Scholar]
- 12. Buchanan CR, Pettit LD, Storkey AJ, et al. Reduced structural connectivity within a prefrontal‐motor‐subcortical network in amyotrophic lateral sclerosis. J Magn Reson Imaging 2015;41:1342–1352. [DOI] [PubMed] [Google Scholar]
- 13. Braun U, Muldoon SF, Bassett DS. On human brain networks in health and disease. eLS 2015:1–9. Available at https://onlinelibrary.wiley.com/doi/abs/10.1002/9780470015902.a0025783 [Google Scholar]
- 14. Fornito A, Zalesky A, Breakspear M. The connectomics of brain disorders. Nat Rev Neurosci 2015;16:159–172. [DOI] [PubMed] [Google Scholar]
- 15. Raj A, Kuceyeski A, Weiner M. A network diffusion model of disease progression in dementia. Neuron 2012;73:1204–1215. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Baldaranov D, Khomenko A, Kobor I, et al. Longitudinal diffusion tensor imaging‐based assessment of tract alterations: an application to amyotrophic lateral sclerosis. Front Hum Neurosci 2017;11:567. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. Kassubek J, Müller HP, Del Tredici K, et al. Imaging the pathoanatomy of amyotrophic lateral sclerosis in vivo: targeting a propagation‐based biological marker. J Neurol Neurosurg Psychiatry 2018;89:374–381. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18. Bede P, Hardiman O. Longitudinal structural changes in ALS: a three time‐point imaging study of white and gray matter degeneration. Amyotroph Lateral Scler Front Degener 2018;19:232–241. [DOI] [PubMed] [Google Scholar]
- 19. Schmidt R, de Reus MA, Scholtens LH, et al. Simulating disease propagation across white matter connectome reveals anatomical substrate for neuropathology staging in amyotrophic lateral sclerosis. Neuroimage 2016;124:762–769. [DOI] [PubMed] [Google Scholar]
- 20. Brooks BR, Miller RG, Swash M, et al. El Escorial revisited: revised criteria for the diagnosis of amyotrophic lateral sclerosis. Amyotroph Lateral Scler Other Motor Neuron Disord 2000;1:293–299. [DOI] [PubMed] [Google Scholar]
- 21. van der Burgh HK, Schmidt R, Westeneng HJ, et al. Deep learning predictions of survival based on MRI in amyotrophic lateral sclerosis. Neuroimage Clin 2017;13:361–369. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22. Desikan RS, Ségonne F, Fischl B, et al. An automated labeling system for subdividing the human cerebral cortex on MRI scans into gyral based regions of interest. Neuroimage 2006;31:968–980. [DOI] [PubMed] [Google Scholar]
- 23. Andersson JLR, Skare S. A model‐based method for retrospective correction of geometric distortions in diffusion‐weighted EPI. Neuroimage 2002;16:177–199. [DOI] [PubMed] [Google Scholar]
- 24. Andersson JLR, Skare S, Ashburner J. How to correct susceptibility distortions in spin‐echo echo‐planar images: application to diffusion tensor imaging. Neuroimage 2003;20:870–888. [DOI] [PubMed] [Google Scholar]
- 25. Mori S, Crain BJ, Chacko VP, van Zijl PCM. Three‐dimensional tracking of axonal projections in the brain by magnetic resonance imaging. Ann Neurol 1999;45:265–269. [DOI] [PubMed] [Google Scholar]
- 26. Mori S, van Zijl PCM. Fiber tracking: principles and strategies—a technical review. NMR Biomed 2002;15:468–480. [DOI] [PubMed] [Google Scholar]
- 27. Mori S, Kaufmann WE, Davatzikos C, et al. Imaging cortical association tracts in the human brain using diffusion‐tensor‐based axonal tracking. Magn Reson Med 2002;47:215–223. [DOI] [PubMed] [Google Scholar]
- 28. Alexander AL, Lee JE, Lazar M, Field AS. Diffusion tensor imaging of the brain. Neurotherapeutics 2007;4:316–329. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29. de Reus MA, van den Heuvel MP. Estimating false positives and negatives in brain networks. Neuroimage 2013;70:402–409. [DOI] [PubMed] [Google Scholar]
- 30. Zalesky A, Fornito A, Bullmore ET. Network‐based statistic: identifying differences in brain networks. Neuroimage 2010;53:1197–1207. [DOI] [PubMed] [Google Scholar]
- 31. Devine MS, Ballard E, O'Rourke P, et al. Targeted assessment of lower motor neuron burden is associated with survival in amyotrophic lateral sclerosis. Amyotroph Lateral Scler Front Degener 2016;17:184–190. [DOI] [PubMed] [Google Scholar]
- 32. Masuda N, Porter MA, Lambiotte R. Random walks and diffusion on networks. Phys Rep 2017;716–717:1–58. [Google Scholar]
- 33. Schuster C, Hardiman O, Bede P. Development of an automated MRI‐based diagnostic protocol for amyotrophic lateral sclerosis using disease‐specific pathognomonic features: a quantitative disease‐state classification study. PLoS One 2016;11:1–15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34. Keil C, Prell T, Peschel T, et al. Longitudinal diffusion tensor imaging in amyotrophic lateral sclerosis. BMC Neurosci 2012;13:141. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35. Goedert M, Masuda‐Suzukake M, Falcon B. Like prions: the propagation of aggregated tau and α‐synuclein in neurodegeneration. Brain 2017;140:266–278. [DOI] [PubMed] [Google Scholar]
- 36. Gong G, Rosa‐Neto P, Carbonell F, et al. Age‐ and gender‐related differences in the cortical anatomical network. J Neurosci 2009;29:15684–15693. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37. Westeneng HJ, Debray TPA, Visser AE, et al. Prognosis for patients with amyotrophic lateral sclerosis: development and validation of a personalised prediction model. Lancet Neurol 2018;17:423–433. [DOI] [PubMed] [Google Scholar]
- 38. Bede P, Elamin M, Byrne S, Hardiman O. Sexual dimorphism in ALS: exploring gender‐specific neuroimaging signatures. Amyotroph Lateral Scler Front Degener 2014;15:235–243. [DOI] [PubMed] [Google Scholar]
- 39. Gradinaru V, Mogri M, Thompson KR, et al. Optical deconstruction of parkinsonian neural circuitry. Science 2009;324:354–359. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40. Henderson JM. “Connectomic surgery”: diffusion tensor imaging (DTI) tractography as a targeting modality for surgical modulation of neural networks. Front Integr Neurosci 2012;6:1–6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41. Querin G, El Mendili MM, Lenglet T, et al. Spinal cord multi‐parametric magnetic resonance imaging for survival prediction in amyotrophic lateral sclerosis. Eur J Neurol 2017;24:1040–1046. [DOI] [PubMed] [Google Scholar]
- 42. El Mendili MM, Cohen‐Adad J, Pelegrini‐Issac M, et al. Multi‐parametric spinal cord MRI as potential progression marker in amyotrophic lateral sclerosis. PLoS One 2014;9:1–7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43. de Albuquerque M, Branco LMT, Rezende TJR, et al. Longitudinal evaluation of cerebral and spinal cord damage in amyotrophic lateral sclerosis. Neuroimage Clin 2017;14:269–276. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44. Wirth AM, Khomenko A, Baldaranov D, et al. Combinatory biomarker use of cortical thickness, MUNIX, and ALSFRS‐R at baseline and in longitudinal courses of individual patients with amyotrophic lateral sclerosis. Front Neurol 2018;9:614. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45. Fekete T, Zach N, Mujica‐Parodi LR, Turner MR. Multiple kernel learning captures a systems‐level functional connectivity biomarker signature in amyotrophic lateral sclerosis. PLoS One 2013;8:1–8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46. Welsh RC, Jelsone‐Swain LM, Foerster BR. The utility of independent component analysis and machine learning in the identification of the amyotrophic lateral sclerosis diseased brain. Front Hum Neurosci 2013;7:251. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47. Grollemund V, Pradat P‐F, Querin G, et al. Machine learning in amyotrophic lateral sclerosis: achievements, pitfalls, and future directions. Front Neurosci 2019;13:135. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48. Bede P, Iyer PM, Finegan E, et al. Virtual brain biopsies in amyotrophic lateral sclerosis: diagnostic classification based on in vivo pathological patterns. Neuroimage Clin 2017;15:653–658. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49. Schuster C, Hardiman O, Bede P. Survival prediction in amyotrophic lateral sclerosis based on MRI measures and clinical characteristics. BMC Neurol 2017;17:73. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50. Chipika RH, Finegan E, Shing SLH, et al. Tracking a fast‐moving disease: longitudinal markers, monitoring, and clinical trial endpoints in ALS. Front Neurol 2019;10:229. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplementary Table 1 Demographic and Clinical Characteristics of ALS Patients and Controls in the 4 MRI Datasets
Supplementary Table 2. Demographic and clinical characteristics of the matched control datasets for each time point of MRI dataset I and for the subdivision of MRI dataset IV into training, validation and test dataset.
Supplementary Table 3. Results of the NBS for different time points T1 to T4 (number of links in the largest connected component (LCC) and p‐value) for the different measures of DTI. The NBS analysis was performed based on both one‐sided (unpaired) t‐tests, one testing for an increase in this measure and the other one for a decrease. All p‐values were FDR‐corrected. Significant results are marked in bold. “None < 0.01” means that none of the p‐values resulting from the respective t‐test was lower than 0.01, thus no component could be extracted for the NBS analysis.
Supplementary Table 4. Overall prediction accuracies for six deep learning networks on the training, validation and test sets. The four single networks were based on clinical data, structural connectivity MRI data, brain morphology MRI data and aggregation levels of the random walker. The network clinicalFACTAL was based on the combination of the aforementioned four single networks, while clinicalFACT did not include the aggregation levels as information source and acted as a reference.


