Molecule‐Induced Radical Formation (MIRF) Reactions—A Reappraisal

Abstract

Radical chain reactions are commonly initiated through the thermal or photochemical activation of purpose‐built initiators, through photochemical activation of substrates, or through well‐designed redox processes. Where radicals come from in the absence of these initiation strategies is much less obvious and are often assumed to derive from unknown impurities. In this situation, molecule‐induced radical formation (MIRF) reactions should be considered as well‐defined alternative initiation modes. In the most general definition of MIRF reactions, two closed‐shell molecules react to give a radical pair or biradical. The exact nature of this transformation depends on the σ‐ or π‐bonds involved in the MIRF process, and this Minireview specifically focuses on reactions that transform two σ‐bonds into two radicals and a closed‐shell product molecule.

Where radicals come from: Molecule‐induced radical formation (MIRF) processes, where one closed‐shell molecule helps another one dissociate, are viable alternatives for simple unimolecular homolytic bond breaking events.

1. Introduction

Molecule‐induced radical formation (MIRF) reactions occur in a variety of circumstances and describe the reaction of two closed‐shell molecules to give two radicals or a biradical product.1, 2, 3 The same reactions are also referred to as “molecule‐assisted homolysis (MAH)” or “molecule‐induced homolysis (MIH)” reactions, but for the sake of consistency we will in the following restrict ourselves to the “MIRF” acronym originally proposed by Ruechardt et al.3 Three classes of MIRF reactions can be differentiated depending on the bond types involved in this transformation (Scheme 1).

Scheme 1.

MIRF reactions involving different combinations of σ‐ and π‐bonds.

Class A reactions are of the [π+π] type and describe the addition reaction of two π‐bonds to a 1,4‐biradical. Class B covers [σ+π] reactions where σ‐bond homolysis is coupled to the addition of one of the resulting radical fragments to a π‐bond. In contrast to Class A reactions, this transformation yields a radical pair that possibly dissociates into separate and diffusively free species. Class C reactions are of the [σ+σ] type and involve the reaction of two σ‐bonds, such that two radicals are generated together with a new σ‐bonded system. This latter closed‐shell molecule is commonly assumed to position itself between the newly formed radicals and thus hinders their recombination. Further variants of MIRF reactions can be envisioned where the two reacting bonds shown in Scheme 1 are either part of the same larger molecule (intramolecular MIRF reactions) or where the reacting σ‐ and π‐bonds are part of a ring system (which impedes formation of diffusively free species). For the sake of simplicity, in the following we will group all reactions together that involve the same bond types on the reactant side. Class C is the least established MIRF type and also the focus of this Minireview. To set the stage for a more detailed analysis of thermochemical data and bonding aspects of these reactions, we will first look at selected MIRF reactions of Classes A and B.

2. Thermochemical Aspects of MIRF Reactions

Class A is the longest‐known class of MIRF reactions and, according to the “Flory mechanism”, plays an important role in the thermal self‐initiation of the polymerization of alkenes.4, 5, 6, 7 The smallest possible reference system for this transformation is the dimerization of ethylene (1) to “tetramethylene” (or more appropriately butane‐1,4‐diyl diradical 2) as described by reaction R1 (Scheme 2).8 Based on estimates of bond energies available at the time, Flory suggested a reaction enthalpy of approximately +121 kJ mol⁻¹ for this reaction.5 The currently best theoretical studies indicate that diradical 2 is not a true minimum on the potential energy surface, but may best be understood as an “entropy‐locked” species on the free energy surface. In topological terms, radical 2 thus represents a transition state for the asynchronous cycloaddition of two ethylene molecules with an activation enthalpy of ΔH ₂₉₈ ^≠(R1)=+177 kJ mol⁻¹,9 close to the experimental value of +183 kJ mol⁻¹ obtained at higher temperatures.10 The Flory mechanism appears to be particularly relevant for alkene monomers carrying electron‐withdrawing substituents,6, 7 but has also been explored for electron‐rich alkenes such as styrene (3).11 The 1,4‐diradical 4 formed in this latter case is significantly more stable than tetramethylene (2), and theoretical studies by Houk and co‐workers11b predict a reaction enthalpy for the dimerization of styrene (reaction R2, Scheme 2) of ΔH ₂₉₈(R2)=+88 kJ mol⁻¹ on the basis of DFT calculations. This result is easily understood when considering the radical stabilization energy (RSE) of benzyl radicals RSE(PhCH₂ ^.)=−63.2 kJ mol⁻¹,12 and the stabilizing effects of aromatic substituents on C−C double bonds, as reflected, for example, in the differences in the hydrogenation energies of ethylene and styrene (H _hyd(1)=−136.3 kJ mol⁻¹ versus H _hyd(3)=−117.2 kJ mol⁻¹, see the Supporting Information for details).12, 13, 14, 15 The combination of these stabilizing effects with the energetics of tetramethylene formation cited above yields a hypothetical reaction enthalpy for reaction R2 of ΔH ₂₉₈(R2)=+94 kJ mol⁻¹, which is in surprisingly good agreement with the value calculated by DFT. The formation of 1,4‐biradicals such as 2 and 4 competes with formation of zwitterionic adducts as well as the concerted formation of (hetero)cyclohexenes through (4+2) cycloaddition pathways. This latter reaction plays a key role in the “Mayo mechanism” for the self‐initiation of alkene polymerization discussed below.11 The conceptually similar Bergman cyclization (here exemplified through the 1,6‐cyclization of enediyne 5 a to diradical 6 a) is a close relative of the Class A MIRF reactions in that two formally separate π‐bonds react to form a 1,4‐diyl species.16 Current estimates for the gas‐phase reaction enthalpy of this transformation ΔH ₂₉₈(R3a) (Scheme 2) range from +36±417 to +54±14 kJ mol⁻¹.18 These values are closely matched by various high‐level calculations.19, 20 The comparatively favorable reaction enthalpy for the formation of biradical 6 a has been attributed to the simultaneous formation of the “aromatic” 6π‐electron system oriented orthogonally to the 1,4‐biradical orbitals. This unique bonding feature differentiates the Bergman cyclization from the class A MIRF reactions. The same formal characteristics apply to the alternative “Schreiner–Pascal” cyclization mode to give biradical 6 b (reaction R3b) that becomes relevant for terminally substituted derivatives of 5 a.21, 22 The Bergman cyclization plays a major role in enediyne antibiotics, whose mode of action involves the formation of substituted variants of biradical 6 a and their ability to abstract hydrogen atoms from the DNA sugar phosphate backbone in cancer cells.23 This is similarly true for anticancer antibiotics based on the Myers–Saito cyclization of eneyneallenes.24, 25 The parent structure of this compound class 5 b can either cyclize in a C1‐C6 fashion to yield biradical 6 c (reaction R3c) or in a C2‐C6 fashion (also called the Schmittel cyclization)26 to afford biradical 6 d (reaction R3d). This latter cyclization is particularly relevant in terminally substituted derivatives of 5 b.

Scheme 2.

MIRF reactions of the [π+π] type (Class A) for ethylene (1) and styrene (3) together with the reactions of enediyne 5a and eneyneallene 5b.

In Class B we find [σ+π] reactions, where σ‐bond homolysis is coupled to the addition of one of the resulting radical fragments to a π‐bond. An early example of this reaction type was proposed by Walling et al. to be the initiation mechanism for the radical chain addition of tert‐butyl hypochlorite (7) to styrene (3; reaction R4, Scheme 3).27 The initiation reaction proceeds efficiently in the dark even at temperatures of 0–5 °C and involves the formation of the tert‐butyloxy radical (8) and 2‐chloro‐1‐phenylethyl radical (9). The literature value for the Cl−O bond energy in 7 amounts to 198.3 kJ mol⁻¹.28 The current best estimates for the bimolecular reaction of 7 and 3 to give radicals 8 and 9 predict a much smaller endothermicity of ΔH ₂₉₈(R4)=+104.3 kJ mol⁻¹,29 which is in full agreement with the mechanistic hypothesis by Walling et al. The “Mayo mechanism” for the self‐initiation of alkene polymerization has been analyzed for the example of styrene (3) by Pryor et al.11 This involves an initial (4+2) cycloaddition of two styrene molecules to afford cycloadduct 10 with a particularly weak C−H bond (Scheme 3). The reaction enthalpy for transfer of a hydrogen atom to a third equivalent of styrene calculated by DFT amounts to only ΔH ₂₉₈(R5)= +8.4 kJ mol⁻¹. The current best estimates for the C−H bond energy in 10 amount to BDE(C−H,10)=+249.4 kJ mol⁻¹, while the strength of the newly formed C−H bond in radical 12 is BDE(C−H,12)=+182.6 kJ mol⁻¹ (see the Supporting Information). From these bond energies we derive a somewhat higher reaction enthalpy for reaction R5 (Scheme 3) of ΔH ₂₉₈(R5)=+65.8 kJ mol⁻¹.

Scheme 3.

Selected examples of MIRF reactions of the [σ+π] type (Class B).

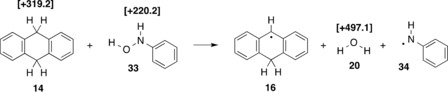
One of the best characterized Class C MIRF reactions was reported by Ruechardt et al. and involves the reaction of fluoride 13 with 9,10‐dihydroanthracene (14) to give tertiary radical 15, hydrogen fluoride, and radical 16 (Table 1, reaction R6).3, 31 This mechanism is supported by the detection of radicals 15 and 16 by EPR spectroscopy and by deuterium isotope effect studies on the reaction rates. As typified by this example, the majority of Class C MIRF reactions involve hydrogen atom transfer (HAT) from activated (e.g. benzylic) positions. The MIRF reaction of fluoride 13 is unusually demanding from a thermochemical point of view. Based on estimates of the heats of formation (Δ_f H ^o) for the reactants and products, Ruechardt et al. calculated a reaction enthalpy of ΔH ₂₉₈(R6)= +157.7 kJ mol⁻¹ (Table 1).31 The combination of these Δ_f H ^o data with currently available bond dissociation energies (BDEs) for hydrogen fluoride15 and the C(9)−H bond in 9,10‐dihydroanthracene (14)28 yields a very similar reaction enthalpy of ΔH ₂₉₈(R6)=+162.4 kJ mol⁻¹ (Table 1). That a process characterized by such an endothermicity proceeds efficiently in practice may thus be due to the forcing reaction conditions (330–360 °C in diphenyl ether as the solvent). A significantly smaller endothermicity of ΔH ₂₉₈(R7)= +90.8 kJ mol⁻¹ can be derived for the reaction of cyclohexanone (17) with cyclohexane hydroperoxide (18), where one molecule of water (20) is formed in addition to the radicals 19 and 21 (Table 1, reaction R7). Although the above value is based on BDE data measured experimentally28 or calculated at the G3B330 level of theory, DFT calculations reported in Ref. 32 predict a much lower value of ΔH ₂₉₈(R7)=+37.7 kJ mol⁻¹. The water molecule formed in this MIRF reaction may not only be beneficial for the overall reaction energy, but may also stabilize the resulting radical pair intermediate by increasing the barrier for radical recombination. This is also an important characteristic of many other MIRF reactions shown in Table 1, such as R8, R9, R10, and R14, where benzyl hydroperoxide (23) reacts with various hydrogen atom donors to yield the respective substrate radicals together with water and benzyloxy radical 25. The reaction enthalpies of these reactions vary as a simple function of the C−H and O−H bond energies of the substrates, and range from ΔH ₂₉₈(R8)=+80.4 kJ mol⁻¹ to ΔH ₂₉₈(R14)=+35.4 kJ mol⁻¹.

Table 1.

Thermochemical data for Class C MIRF reactions.

Entry	MIRF reaction[a]	ΔH 298 [kJ mol−1]	Ref.
R6		+162.4	31
R7		+90.8	32
R8		+80.4	33, 34
R9		+76.0	33, 35
R10		+65.8	33, 34
R11		+62.2	36
R12		+42.3	37
R13		+41.6	38, 39, 40
R14		+35.4	33, 35
R15		+4.5	41

[a] BDE values are given in square brackets in kJ mol⁻¹.

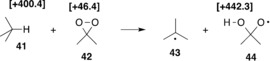
Aside from hydroperoxides as hydrogen atom acceptors, peresters and peracids also appear to be sufficiently potent for MIRF reactions, with the room temperature reaction of N‐hydroxyphthalimide (35, NHPI) with peracetic acid (36) being one of the reported examples (Table 1, reaction R13).38, 39, 40 Provided that a sufficiently good C−H bond donor such as 14 is employed, even the cleavage of N−O bonds, such as in N‐hydroxyaniline (33), is possible (Table 1, reaction R12).37 The reaction of these two components is endothermic by (only) ΔH ₂₉₈(R12)=+42.3 kJ mol⁻¹ and yields radicals 16 and 34 as reaction products together with one water molecule. The thermochemically most favorable MIRF reaction in Table 1 is the reaction of dimethyldioxirane (42, DMDO) with isobutane (41; reaction R15). Despite the high C−H bond energy of BDE(C−H, 41)=+400.4 kJ mol⁻¹ in 41,28 the highly strained peroxide ring system in DMDO provides a sufficient driving force for the overall reaction. Well‐calibrated DFT calculations predict a reaction enthalpy of ΔH ₂₉₈(R15)=+8.9 kJ mol⁻¹ for the formation of the radical pair complex between 43 and 44.38 Theoretical studies by Cremer et al. predicts a dissociation energy of BDE(O−O)=+46.4 kJ mol⁻¹ for the O−O bond in DMDO.42 By combining this value with the BDE(C−H) value for isobutane and the H−O bond energy of 2‐propanol of BDE(H−O)= +442.3 kJ mol^−1[28] as an approximate value for the H−O bond energy in radical 44, we arrive at a very similar reaction enthalpy of ΔH ₂₉₈(R15)=+4.5 kJ mol⁻¹ (Table 1, reaction R15). That C−H bond hydroxylation reactions of hydrocarbons with DMDO proceed quite readily even below 0 °C may thus, at least in part, be due to the rather favorable energetics of the radical‐forming step.43 In contrast to all other reactions in Table 1, the cyclic nature of DMDO binds one of the product radicals and the newly formed O−H bond together in one product molecule. This combination leads to extremely rapid follow‐up reactivity such as the transfer of the hydroxy group between radicals 43 and 44, which is commonly referred to as the “rebound” step.41, 44 The rather low barriers for this process lead to equally small lifetimes of radicals 43/44, and thus substantial challenges in experimental studies to differentiate a concerted45 from a stepwise46 process. In terms of the underlying bond‐making/breaking scheme, this process can be classified as a Class C MIRF reaction.

The question of whether more than two σ‐bonds can participate in Class C MIRF reactions was first raised by Minisci and co‐workers in an attempt to rationalize differences in reactions between NHPI (35) as the hydrogen atom donor and different peracids.39 Noting that reactions are much more efficient with peracetic acid (36; Table 1, reaction R13) than with perbenzoic acid derivatives, the hypothesis was made that decarboxylation of the acetyloxy radical 38 occurs at the same time as homolytic cleavage of the perester O−O bond. In contrast to reaction R13, this now generates two radicals and two closed‐shell molecules (water and CO₂) as the reaction products (Table 2, reaction R16). The decarboxylation of acetyloxy radical 38 alone is a rapid process and known to be exothermic by −66.9±12.6 kJ mol⁻¹.28 The combination of this additional driving force with the reaction enthalpy of ΔH ₂₉₈(R13)=+41.6 kJ mol⁻¹ calculated for reaction R13 leads to ΔH ₂₉₈(R16)=−25.3 kJ mol⁻¹, and thus an exothermic MIRF reaction. A similar situation exists in the reaction of two benzyl hydroperoxide molecules (23), where the terminal hydroxy group of one reactant abstracts the benzylic C−H bond from the other. Assuming that cleavage of the O−O bond in this second reactant occurs concertedly with activation of the benzylic position leads to reaction R17 in Table 2, where again two radicals are formed together with two closed‐shell species (benzaldehyde (26) and water). This makes the reaction energetically more favorable than the reaction of the same two species (Table 1, reaction R10), and yields an overall reaction enthalpy of ΔH ₂₉₈(R17)=−48.0 kJ mol⁻¹.37

Table 2.

Thermochemical data for [σ+σ+σ]‐MIRF reactions.

Entry	MIRF reaction	ΔH 298 [kJ mol−1]	Ref.
R16		−25.3	38, 39, 40
R17		−48.0	33, 35

Surveying the Class C MIRF reactions collected in Table 1 we note that all of these are endothermic, which implies that the reaction enthalpies provide a lower limit for the respective activation enthalpies. We also note that most of the reactions involve the formation of small thermochemically stable molecules (H₂O, HF). The comparatively high O−H bond energy in water of BDE(O−H)=+497.1 kJ mol⁻¹, for example, compensates for the energetic demands of generating two open‐shell product species. The reactant side, in turn, is typically characterized by at least one reactant with a comparatively weak X−Y bond, with the peroxide O−O bond being the most frequent representative here. That the cleavage of two σ‐bonds in the reactants will only proceed with a notable rate if sufficiently strong bonds form on the product side may be expected qualitatively from practically any bimolecular reaction. A comparison of the combined bond energies of the reactant with those of the products in Figure 1 illustrates that this expectation is indeed valid.

Figure 1.

Comparison of BDE values of reactants and products for the Class C MIRF reactions shown in Table 1.

All the MIRF reactions shown in Tables 1 and 2 are bimolecular in nature, and important references for these processes are, therefore, unimolecular radical‐forming reactions. Benzyl hydroperoxide (23), for example, plays the role of hydrogen atom abstractor in bimolecular reactions R8, R9, R10, R14 (Table 1), and R17 (Table 2), but is also considered to co‐initiate the autoxidation of toluene through its unimolecular decomposition to a benzyloxy radical (25) and hydroxyl radical (47; Table 3, reaction R18).35, 47 The current best estimates place the O−O bond energy of 23 at ΔH ₂₉₈(R18)=+202.0 kJ mol⁻¹, a value very similar to other alkylhydroperoxides28 and significantly higher than the reaction enthalpies for the bimolecular MIRF reactions involving this compound. A second reference can be found in the dissociation energies of common radical initiators, a well‐known example being dibenzoyl peroxide (DBPO, 48). The O−O bond energy of 48 amounts to ΔH ₂₉₈(R19)= +181.3 kJ mol⁻¹,33 again a value significantly higher than many of the MIRF reactions in Tables 1 and 2. In practical terms the applicability of peroxide initiators is often described through the temperature required for a decay half‐life of 10 h. For 48 this parameter amounts to 73 °C.48

Table 3.

Selected unimolecular radical‐forming reactions.

Entry	MIRF reaction	ΔH 298 [kJ mol−1]	Ref.
R18		+202.0	33, 35
R19		+181.3	33

3. Transition‐State Structure Requirements for MIRF Reactions

The concerted cleavage and formation of multiple σ‐bonds in a single elementary step requires appropriate alignment of these bonds in the transition states of the Class C reactions described in Tables 1 and 2. A detailed analysis of the respective elementary reaction steps is currently only available for some of these reactions.11, 34 In Scheme 4 we compare the structural details of the transition states for the bimolecular reaction of hydroperoxide 23 with toluene (22; Table 1, reaction R8) and the self‐reaction of two equivalents of hydroperoxide 23 (Table 2, reaction R17).34 To provide an appropriate reference for a simple unimolecular process, we also include results for the O−O bond cleavage in 23 (Table 3, reaction R18).34, 49 The transition‐state structure of this reaction, TS23, is characterized by a largely broken O−O bond, as reflected by the O−O distance of 253.7 pm, accompanied by the formation of a hydrogen bond between the hydroxyl radical (47) and benzyloxy radical 25 as the eventual products of the cleavage process. When we couple O−O bond cleavage in hydroperoxide 23 to hydrogen atom abstraction from the benzylic position in toluene (22), the respective transition state TS2223 is characterized by a significantly shorter O−O bond of 202.2 pm, whereby the hydroxyl fragment separating from the hydroperoxide unit is intimately involved in the hydrogen atom abstraction from the methyl group of 22. All the formal bond angles along the reacting O−O−H−C fragment are larger than 165°, which implies an effective linear alignment of all the reacting σ‐bonds. A further element of conformational control can be seen in the phenyl group of toluene, which aligns orthogonally to the breaking benzylic C−H bond. The enthalpic barrier for the MIRF process through TS2223 is significantly lower than that for the unimolecular O−O bond dissociation through TS23 (ΔH ^≠ ₂₉₈=+127.8 kJ mol⁻¹ versus +177.9). A similarly effective alignment of reacting bonds can also be seen for transition state TS2323 for the self‐reaction of hydroperoxide 23. Even though this reaction is much more exothermic than the reaction of hydroperoxide 23 with toluene because of the simultaneous cleavage of both peroxide O−O bonds, the reaction barrier is very similar at +122.8 kJ mol⁻¹. Structural analysis indicates that only one of the O−O bonds is actively involved in the bond reorganization in transition state TS2323. The O−O bond located in the hydroperoxide unit acting as a hydrogen atom donor is almost the same length in TS2323 (147.4 pm) as in hydroperoxide 23 itself (145.1 pm). This is very much in line with fundamental theoretical analyses of multibond reactions by Dewar50 as well as by Shaik and Shurki,51 where it is found that concerted “zipper reactions” involving multiple covalent bonds are usually not synchronous.

Scheme 4.

Comparison of uni‐ and bimolecular radical‐forming reactions involving benzyl hydroperoxide (23; enthalpy values relative to the reactants are in kJ mol⁻¹; distances are in pm, and angles in degrees).34

A final comment should be made on the product complexes formed in the O−O bond cleavage reactions in Scheme 4. In all three cases, the benzyloxy radical acts as a hydrogen‐bond acceptor, with the hydrogen‐bond donor being a hydroxyl radical in product complex PC23 whereas a newly formed water molecule assumes this role in product complexes PC2223 and PC2323. In all three cases, the hydrogen‐bonding interactions are expected to increase the lifetime of the radical‐pair complexes, as radical recombination requires geometrical changes with reduced hydrogen‐bond strengths.

4. Mechanistic Alternatives to MIRF Reactions

Experimental proof for MIRF reactions is sometimes difficult to obtain because of the numerous mechanistic alternatives leading from the same reactants to the same products. Aside from the above‐mentioned competition with stepwise processes initiated by unimolecular O−O bond cleavage, MIRF reactions also compete with single electron transfer (SET) reactions between the two reaction components. This is particularly relevant for peroxides and peresters, whose O−O bond fragments can serve as one‐electron acceptors. An example is given in Scheme 5 for the reaction of tert‐butyl phenylperacetate (50) with thiophenol (51).52 The proposed mechanism was tailored from earlier studies53 on reactions of neutral nucleophiles (such as sulfides, disulfides, and amines) with esters and anhydrides of peracids. The example chosen here has the advantage that the stepwise and SET processes lead to slightly different products. The stepwise mechanism (A) involves initial O−O bond homolysis in perester 50, followed by (irreversible) decarboxylation of radical 52 to afford benzyl radical 24. Trapping all open‐shell species by hydrogen abstraction from thiophenol generates tert‐butyl alcohol (53), toluene (22), and diphenyldisulfide (54). Analysis of the reaction mixture reveals substantial amounts of phenylacetic acid (59), which can potentially be generated by trapping radical 52, but more likely derives from the SET‐initiated pathway B. The radical anion 56 formed in this step is likely to fragment to tert‐butyloxy radical (8) and phenylacetate (57), whose proton transfer reaction with radical cation 55 then yields acid 59, together with the other products known from pathway A. As indicated in Scheme 5 (pathway C), acid 59 can also be generated directly through a Class C MIRF reaction between perester (50) and thiophenol via transition state TS5051. Further MIRF variants of Class B are conceivable that involve attack of thiophenol at the carbonyl group of peresters 50, and we should also not overlook reaction pathways lacking open‐shell intermediates that generate product 59 through, for example, a series of nucleophilic substitution reactions. All of these variants have to eventually live up to the challenge of rationalizing the reaction rates for phenyl‐substituted derivatives of 50 and its dependence on thiol concentrations. One additional challenge in kinetics studies of decomposition reactions of hydroperoxides, peroxides, and peresters is that their reaction can be “induced” by radicals formed in the decomposition steps. This is best established for hydroperoxides and includes reactions of chain‐carrying radicals, through abstraction of either hydrogen or a HO group from the terminal OOH unit.54, 55, 56 This implies that the decomposition kinetics of hydroperoxides can be especially complex and difficult to analyze in terms of the contributions of individual processes.

Scheme 5.

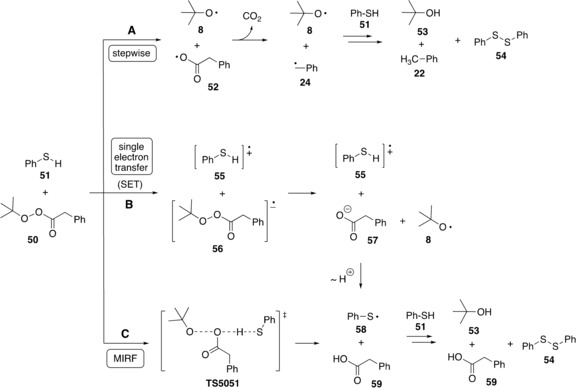
Reaction of tert‐butyl phenylperacetate (50) with thiophenol (51).

A second example, where MIRF reactions may play a role, concerns the chemistry of lipid hydroperoxides (LHPs) and their potential to co‐initiate the autoxidation of polyunsaturated fatty acids (PUFAs) and their esters. This latter process has been studied in great detail because of its enormous role in aging as well as cardiovascular and neurodegenerative diseases.57, 58, 59 There is general agreement that LHP formation results from radical‐mediated autoxidation reactions, whose primary target is the bisallylic position in PUFAs as a result of its comparatively weak C−H bond.59, 60 Formation of a hydroperoxide is accompanied by isomerization of the two C−C double bonds present in the bisallylic fragment; a general structural representation of the resulting hydroperoxides is that of 61 (Scheme 6). To account for the decomposition kinetics of LHPs and related compounds it has been suggested that a combination of unimolecular O−O bond dissociation reactions along pathway D and MIRF reactions may be involved.1 These latter processes may be bimolecular in nature, as described through pathway E (Scheme 6), and generate a water‐separated radical pair 63 in very much the same way as already seen before for benzyl hydroperoxide (23) in reaction R10 (Table 1). However, intramolecular MIRF reactions are equally conceivable, where the diene fragment in 61 serves as the reaction partner for its hydroperoxide unit. This may, for example, involve O−H bond cleavage in 61 coupled to the addition of a hydrogen atom to one of the diene carbon atoms, such that diradical 64 is formed (pathway F), O−O bond cleavage in 61 coupled to addition of a hydroxyl radical to one of the diene carbon atoms to yield diradical 65 (pathway G), or O−O bond cleavage in 61 coupled to abstraction of a hydrogen atom from one of the positions adjacent to the diene unit to yield diradical 66 (pathway H). Unequivocal support for these MIRF pathways is, unfortunately, currently missing as a consequence of the rather complex decomposition kinetics of hydroperoxides.61

Scheme 6.

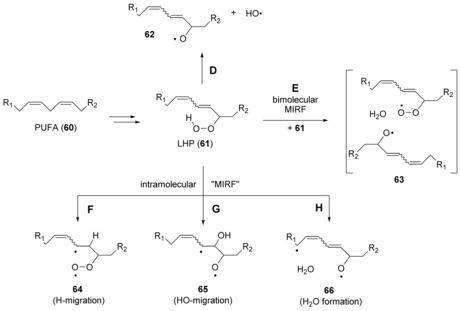
Radical‐forming reactions from lipid hydroperoxides (LHPs).

5. Conclusion

The examples of MIRF reactions collected here from the literature document the widespread occurrence of this reaction type, which is often competitive with established initiation reactions employing purpose‐built initiators. This is particularly true for the reaction of hydroperoxides with hydrocarbons carrying weakly bound hydrogen atoms as well as for self‐reactions of hydroperoxides of benzylic hydrocarbons. The quantitative description of autoxidation reactions, where hydroperoxides occur as transient intermediates, may thus benefit from the consideration of this class of reactions.

Conflict of interest

The authors declare no conflict of interest.

Biographical Information

Harish Jangra obtained his M.S. (Pharmacoinformatics, 2012) from the National Institute of Pharmaceutical Education and Research, S.A.S. Nagar, Punjab, India. He completed his Ph.D. (Computational Chemistry, 2019) at Ludwig‐Maximilians‐Universitaet, Muenchen, Germany, under the supervision of Prof. H. Zipse, and is currently a postdoctoral researcher in the same group. His current research focuses on theoretical studies of chemical and biological radical processes and 1,3‐dipolar cycloaddition reactions.

Biographical Information

Sandhiya Lakshmanan obtained her Ph.D. in Physics from Bharathiar University, Coimbatore, India, in 2014 with Prof. K. Senthilkumar. After postdoctoral research in the group of Prof. H. Zipse, Ludwig‐Maximilians‐Universitaet, Muenchen, Germany, for three years, she was a Research Assistant Professor with Prof. W. L. Hase at Texas Tech University, USA, for two years. She is currently a scientist at CSIR‐National Institute of Science, Technology and Development Studies, New Delhi, India. Her research focuses on quantum chemical modeling and chemical dynamics of reactions important in atmospheric and combustion chemistry.

Biographical Information

Hendrik Zipse completed his Ph.D. in 1991 with Prof. B. Giese at the University of Basel, Switzerland). After postdoctoral research (1992–1993) with Prof. K. Houk at the University of California in Los Angeles (USA), he completed his Habilitation (1997) with Prof. H. Schwarz at the Institut für Organische Chemie at the Technische Universität Berlin (Germany). Since 1998, he has been Associate Professor of Organic Chemistry at Ludwig‐Maximilians‐Universitaet in Muenchen, Germany. His research focuses on mechanistic puzzles in biological and synthetic radical chemistry as well as nucleophilic organocatalysis.

Supporting information

As a service to our authors and readers, this journal provides supporting information supplied by the authors. Such materials are peer reviewed and may be re‐organized for online delivery, but are not copy‐edited or typeset. Technical support issues arising from supporting information (other than missing files) should be addressed to the authors.

Supplementary

L. Sandhiya, H. Jangra, H. Zipse, Angew. Chem. Int. Ed. 2020, 59, 6318.