Abstract
Missing data arise frequently in clinical and epidemiological fields, in particular in longitudinal studies. This paper describes the core features of an R package wgeesel, which implements marginal model fitting (i.e., weighted generalized estimating equations, WGEE; doubly robust GEE) for longitudinal data with dropouts under the assumption of missing at random. More importantly, this package comprehensively provide existing information criteria for WGEE model selection on marginal mean or correlation structures. Also, it can serve as a valuable tool for simulating longitudinal data with missing outcomes. Lastly, a real data example and simulations are presented to illustrate and validate our package.
Keywords: Dropout missingness, inverse probability weight, generalized estimating equations, missing at random, model selection, quasi-likelihood, R
1. Introduction
Longitudinal data are common in clinical trials or observational studies. There exist two major approaches for analysis, generalized estimating equations (GEE) and mixed-effect models, which have different tendencies in model fitting depending on the study objectives. In particular, mixed-effect models adopt an individual-level approach by accommodating random effects to capture the correlation among the observations within-subject (Crowder 1995; Wang 2014; Hedeker and Gibbons 2006); GEE is employed for marginal regression analysis based on a quasi-likelihood function by providing the population-averaged parameter estimates. Due to common research interest in conducting the population-level inference such as overall treatment effect, we focus on GEE, which has several defining features such as the relaxation of distribution assumption with only requirement on the correct specification of marginal mean and variance as well as the link function connecting the covariates of interest and marginal mean, the correlation structure among these dependent responses treated as nuisance parameters which if misspecified will not influence the asymptotic properties of parameter estimates under mild regularity conditions and so on (Liang and Zeger 1986; Wang and Long 2011; Wang 2014; Wang et al. 2016).
Of note is that in longitudinal studies, missing data are frequently encountered. As is well known, three types of missing mechanisms have been summarized and studied (Rubin 1976; Little and Rubin 2014): if the probability of a missing response does not depend on either the observed or unobserved responses conditional on the covariates, the data are said to be missing completely at random (MCAR); it is missing at random (MAR) if conditional on the observed data and the covariates, the probability of a missing response is independent of the unobserved data; also, if the missingness is related to the unobserved responses, the data are said to be missing not at random (MNAR). In practice, subjects often drop out of the study or are lost to follow-up for some reasons such as drug resistance, and the missing data induced by dropouts form a monotone missing pattern which is commonly assumed to be MAR (Preisser et al. 2002; Fitzmaurice et al. 2012). To handle missing data, there are two widely used techniques, inverse probability weight (IPW) and multiple imputation (MI). In some occasions, IPW is preferred by researchers due to several appealing features, for instance, less computational burden and flexible implementation in software, easier to be understood by clinicians in practice and so on (Rubin 1976; Seaman and White 2011).
GEE can lead to consistent parameter estimates only when the data are MCAR in the presence of missing data (Robins et al. 1995; Liang and Zeger 1986). However, when the data are MAR or MNAR, the estimates of the regression parameters will be biased (Laird 1988). Robins et al. (1995) first proposed the weighted GEE (WGEE) method for bias correction under the assumption of MAR, and the WGEE is an extension of GEE by incorporating an IPW matrix. Preisser et al. (2002) and Fitzmaurice et al. (2012) have shown that WGEE can provide valid inference on marginal regression parameters if the mean model and the model for the missingness are correctly specified even without the necessity for correct specification of the within-subject correlation structure. Of note is that there are two types of weights in literature, subject-specific weight (i.e., the same weight assigned to all the observations from a subject) and observation-specific weight (i.e., a specific weight assigned to each observation). The former one was originally developed due to computational convenience, and also Preisser et al. (2002) have shown that observation-level WGEE can provide more efficient estimate than the subject-level WGEE; thus observation-level weights will be applied in our package. Later on, doubly robust GEE was further developed under MAR by incorporating the augmented IPW method for efficiency improvement. The main advantage of this model is that so-called doubly robust estimators are consistent if at least one of the missing model and the outcome model is correctly specified (Bang and Robins 2005; Seaman and Copas 2009; Chen and Zhou 2011; Birhanu et al. 2011; Padilha and Demarqui 2015), and this approach has been widely adopted for clustered randomized trials (CRTs) (Stephens et al. 2012; Prague et al. 2017).
To appreciate the features of wgeesel, we briefly review GEE implementations in existing statistical software R and SAS. The regular GEE with different types of outcomes (Liang and Zeger 1986) has been implemented in SAS with the statements of PROC GENMOD and PROC GEE (SAS Institute Inc. 2016), and the packages yags, gee, repolr and geepack in R (Carey and Ripley 2011; Nooraee et al. 2014; Carey 2015; Parsons 2016; Højsgaard et al. 2016). However, the software implementation of the WGEE approach accommodating missing data under MAR is limited. Recently, SAS (SAS Institute Inc. 2016) launched an experiential version of PROC GEE to fit WGEE for longitudinal data with missing dropout data. Currently, this release does not include all of the capabilities in the REPEATED statement in the GENMOD procedure, and additional features need to be released, such as the weights output from WGEE. Also, SAS is a commercial statistical software; thus, the source code for WGEE fitting in PROC GEE is inaccessible, which poses restriction for researchers on relevant studies if they need to conduct modification on current methods. To our best knowledge, there is no reliable and available R package for implementing WGEE. Even though in several R functions for GEE estimation, there exist options in the arguments to incorporate the weights for WGEE estimation, for instance, the function geeM in geeM (McDaniel et al. 2016) and the function geeglm in geepack, the inference is not reliable under most circumstances because the weight arguments do not properly incorporate the weights for WGEE. Based on our finding, the estimates are only the same as the WGEE estimates from PROC GEE when the “working” correlation structure is independent. To illustrate this, we conducted a simulation study. 250 replicates of correlated binary responses with a sample size of 100 were generated, where the true regression parameter values were β0 = −0.5 and β1 = 0.5, and the true correlation structure is exchangeable with ρ = 0.25 (refer to Section 4 for more details). For each dataset, we estimated the weights and plugged them into geeM and geeglm to obtain the WGEE parameter estimates under the exchangeable “working” correlation structure which is true. We found out that the estimates of β0 and β1 had biases of −0.096 and 0.086 by geeM, and also −0.087 and 0.070 by geeglm, respectively, while the function wgee in our package wgeesel yielded negligible biases of −0.01 and 0.03. Also, the estimates of the standard error were not consistent, where the estimate of standard error for β1 based on geeM and geeglm was 0.6062 and 0.6379, respectively, while it was 0.6226 using both wgee and PROC GEE. More recently, Salazar et al. (2016) provided a sample R program to fit WGEE, in which glm was adopted to estimate the weights, and geeglm was used for WGEE estimation; however, their estimation approach for the weights is problematic. For the data with a monotone missing pattern, that is, MAR, they utilized the data at each individual time for weight estimation, and their estimation did not condition on the previous visit that was not missing (Robins et al. 1995). We applied their R source code on the imps dataset in Section 5 for comparison. For example, for patient 1 with four visits, the weights based on their code at each visit were 1, 1.0000, 1.14251 and 1.3287; however, the weights obtained by both wgee in wgeesel and SAS macro provided by Shen and Chen (2012) were 1, 1.0031, 1.1130, and 1.2005. Obviously, the last two weights calculating by their approach are slightly larger, indicating the inaccuracy of their R program which may lead to invalid inference. Therefore, wgeesel provides valid inference on WGEE with different types of outcomes and “working” correlation structures. Also, with regard to doubly robust GEE model fitting, wgeesel can also be adopted by embedding the existing work such as R packages CRTgeeDR (Prague et al. 2017), which have been popularly applied for marginal regression in CRTs with missing data.
Besides marginal model fitting, the major contribution of our package wgeesel is comprehensively providing existing information criteria particularly for WGEE in the presence of monotone/dropout missingness under MAR. In regression analysis, model selection is important to identify the best model with the traditional information criteria, such as Akaike information criterion (AIC), Bayesian information criterion (BIC), and Mallow’s Cp (Mallows 1973; Akaike 1974; Raftery 1995). However, in longitudinal models with GEE/WGEE, these information criteria cannot be directly applicable because these models are not likelihood based. Besides, the model selection for longitudinal data analysis includes not only the variable selection in the mean model, but also the “working” correlation structure selection because of potential efficiency loss due to in-appropriately specified correlation structures; and the information criteria could be different for these two selection objectives. Pan (2001) proposed a modification of AIC, the quasi-likelihood under the independence model criterion (QIC), for regular GEE model selection where the likelihood was replaced by quasi-likelihood and a proper adjustment was made for the penalty term. QIC can be used for both variable selection and correlation structure selection in GEE analysis, which is available in SAS PROC GENMOD and PROC GEE (SAS Institute Inc. 2016). Also, R packages yags and MuMIn (Carey and Ripley 2011; Bartoń 2015) both provide QIC for GEE model selection. On the other hand, Imori (2013) proposed modified QIC (MQIC) as an asymptotic unbiased estimator of the risk function based on the independent quasi-likelihood. QIC is exactly and asymptotically equivalent to MQIC when the “working” correlation matrix is independent and includes the true correlation structure, respectively. Rotnitzky and Jewell (1990) proposed the Rotnitzky and Jewell criteria (RJC) to examine the adequacy of “working” correlation structure in GEE analysis. The criteria of MQIC and RJC are for GEE model selection, but have not been available in any software except our package wgeesel. Also, we provide an improved RJC in small sample size by utilizing the pooled information from all subjects for variance estimation, which is applicable for balanced longitudinal data (Wang and Long 2011). With regard to information criteria for WGEE model selection, Shen and Chen (2012) proposed the missing longitudinal information criterion (MLIC) for the selection of the mean model based on the quadratic loss function and showed it is superior to QIC when the outcome data are subject to dropout/monotone missingness and are MAR. In addition, they provided the MLIC for correlation (MLICC) for selection of the correlation structure in WGEE. They provided a SAS macro to calculate the MLIC and MLICC. However, their program is not user-friendly with limited outputs unless users manually modify the source code to obtain more results (e.g., weights). Another option is the weighted quasi-likelihood information criterion (QICWp) accommodating the weight matrix proposed by Platt et al. (2013), which usually selects the correct mean model more often than the adjusted R2 in various scenarios. Later on, Gosho (2016) mentioned that QICWp would not be applied to select a “working” correlation structure. To compensate for the imperfection of QICWp, Gosho (2016) proposed QICWr for variable selection and correlation structure selection in WGEE. Until now, none of these have been implemented in R, and our package wgeesel fills up this gap.
Furthermore, this package provides a valuable and essential tool for researchers to simulate longitudinal data with missing responses to different types (i.e., continuous, binary and count). Leisch et al. (1998) proposed an algorithm to generate multivariate binary distributions with a given correlation structure or with given pairwise joint probabilities. Demirtas and Doganay (2012) developed algorithms to generate multivariate random variables with binary and normal/non-normal components. Amatya and Demirtas (2017) generated mixed multivariate count and continuous data from two marginal moments of Poisson and normal distributions. By considering most commonly used correlation structures (i.e., exchangeable, AR1), complete longitudinal data can be first generated based on multivariate distributions, and then given pre-specified drop-out model, the missing probabilities will be calculated. Note that if one observation is missing, the subsequent ones will also be missing to achieve the monotone pattern which is our focus here.
The paper is organized as follows. In Section 2, we outline marginal model fitting (i.e., WGEE, doubly robust GEE), and thus described model selection criteria particularly for WGEE when the outcome data are dropout missing under MAR. Section 3 describes the core functions (wgee, QICW.gee, MLIC.gee, etc.) in wgeesel. Simulation studies are conducted for the data with different types of outcomes or correlation structures in Section 4. Section 5 illustrates the use of wgeesel in a longitudinal data application with repeated binary responses. Lastly, we summarize the features of the package and provide future directions in Section 6.
2. Methodology
2.1. WGEE and doubly robust WGEE
Let Yij represent the jth response on the ith subject with a p × 1 vector of covariates xij, j = 1, …, T, i = 1, …, K. Thus, Yi = (Yi1, …, YiT)T is denoted as a T × 1 vector of outcomes, and Xi = (xi1, …, xiT)T is a T × p matrix of covariates for subject i. For simplicity, we assume balanced data with equal number of observations for all subjects. Let μi = (μi1, …, μiT)T = E(Yi|Xi) and Vi = var(Yi|Xi). Note that μi is usually modeled via a generalized linear model with g(μi) = Xiβ with g as a specified link function (McCullagh and Nelder 1989), β is a p-vector of regression parameters, and Vi is given by . The matrix Ai is a T × T diagonal matrix with diagonal elements var(Yij|xij) = ν(μij), j = 1, …, T, where ν is a known variance function at μij and ϕ is a scale (dispersion) parameter, and Ri(ρ) is a specified “working” correlation matrix depending on a set of parameters ρ. If Ri(ρ) is the true correlation matrix, then Vi is the true covariance matrix of Yi. Denote the indicator rij as 1 if the outcome Yij is observed; otherwise rij = 0 if Yij is missing.
Under MAR assumption, Robins et al. (1995) proposed WGEE method, which extends GEE by incorporating a weight matrix based on the inverse probability of observing each observed outcome (i.e., observation-level weight matrix) to adjust for dropout missingness (Preisser et al. 2002). Given the observed data for subject i, the probability of observing the response Yij is denoted as wij = Pr(rij = 1 | Yi,Xi), which is generally unknown, but can be estimated. For the first time point, we always assume ri1 = 1. Under the monotone missing pattern, wij = λi1 × λi2 × ⋯·λij, where λi1 = 1, and λij = Pr(rij = 1 | ri(j−1) = 1, Yi1, …, Yi(j−1), Xi), for j = 2, …, T. λij can be estimated from the logistic regression model with zij as a vector of predictors such as the time variable, baseline covariates, and/or past outcome variable and α is the vector of corresponding regression parameters.
Under MAR, the estimate of β can be obtained based on the following estimating equation:
| (1) |
where , and the weight matrix Wi = diag(ri1/wi1, … riT/wiT). Robins et al. (1995) have showed that WGEE estimator is consistent estimation of β without requiring correct specification the correlation matrix. We adopt the following algorithm to develop the wgee function, where the observation-specific weight matrix is considered (Lin and Rodriguez 2015):
- Fit a logistic regression model with data (rij, zij) and estimate α by maximizing the following log-partial likelihood:
Thereafter, the conditional probability of observing subject i at the jth time is estimated by , where is the predicted probability obtained from the logistic regression.(2) Assuming independence of the responses Yi, compute an initial estimate of β with an ordinary generalized linear model.
Given the specified “working” correlation structure, estimate the correlation matrix R based on the standardized residuals, the current estimate of β, denoted by , and the specific structure of R, q = 1, 2, …, Q.
Compute the T × T estimated covariance matrix: , based on
- Update by :
(3) Repeat steps 3–5 until convergence.
- Compute the asymptotic covariance matrix of as follows (Preisser et al. 2002):
where , , and .(4)
It is known that WGEE estimators are consistent when the dropout model is correctly specified (Robins et al. 1995). The more appealing method, doubly robust GEE, has gained more attention due to the relaxation of this restriction by combining the imputation method, and doubly robust GEE estimators are still consistent if either of the dropout model and the outcome model for imputation is correctly specified (Seaman and Copas 2009; Prague et al. 2016). There are different versions of doubly robust GEE because of subjective selection of the outcome model under the variety of scenarios, and here we establish a function of drgee based upon the package CRTgeeDR, where more details can be referred to Prague et al. (2016, 2017).
Of note is that both WGEE and doubly robust GEE can achieve valid inference under the assumption of MAR (Shen and Chen 2012; Wang and Long 2011; Gosho 2016; Seaman and Copas 2009; Prague et al. 2016). Therefore, sensitivity analysis is crucial to evaluate the missing mechanism before model fitting in practice. There exist substantial work and discussion on missing data (Little and Rubin 1987; Ibrahim and Molenberghs 2009). Due to the program availability, the most recent work by Moreno-Betancur and Chavance (2016) is recommended, where the pattern-mixture model factorization of the full data likelihood was proposed (Moreno-Betancur and Chavance 2016); however, other programs combining SAS and R functionalities can also be considered (Bunouf et al. 2015).
2.2. Model selection
In this section, we outline the existing information criteria for GEE model selection with particular attention for longitudinal data in the presence of dropout/monotone missingness under MAR. Of note is that two major objective functions are relied on for information criteria derivation, quasi-likelihood function (i.e., QIC, QICW) and quadratic loss function (i.e., MLIC, MLICC) (McCullagh and Nelder 1989; Pan 2001; Shen and Chen 2012).
2.2.1. QIC and QICW
Based on quasi-likelihood, Pan (2001) proposed a criterion, QIC, to select an optimal mean model or “working” correlation structure in GEE, which is shown by
| (5) |
where is a quasi-likelihood function, and . given the “working” correlation structure is independent. In addition, Pan (2001) provided as an approximation to QIC. Because if all model specifications in GEE are correct, and are asymptotically equivalent, thus . Since the validity of the penalty term 2p is unclear under finite samples, the application of QICu is not recommended (Cui and Qian 2007).
Literatures have shown that QIC does not perform satisfactory in the application of longitudinal data with dropout/monotone missingness that is MAR. Shen and Chen (2012) showed that the proportion of correct model selection by QIC decreased as the dropout rate increased. To adjust for missing data under MAR, Platt et al. (2013) proposed a criterion, , where is the weighted quasi-likelihood component with Wi defined in Eq. (1). This criterion is an extension of QICu, but they did not provide comprehensive evaluation. Later on, Gosho (2016) proposed a criterion for model selection based on the weighted quasi-likelihood function given by
| (6) |
where the only difference between QICWp and QICWr is the second penalty term which was extended from QIC in Eq. (5). The model with the smallest QICWr can be used for both variable selection and correlation structure selection. In particular, the author also argued that 2p would be an inappropriate penalty term of QICWp for model selection regardless of the presence or absence of dropout missingness.
2.2.2. MLIC and MLICC
Another alternative criterion for variable selection in WGEE is MLIC proposed by Shen and Chen (2012). Unlike QICWr, MLIC is based on a quadratic loss function, which is employed to measure how well the candidate model predicts the true model. Mallows (1973) also considered this measure for the development of Mallows’ Cp. MLIC is expressed as follows:
| (7) |
where
and
evaluated at and , where with U and S defined in Eq. (4). Here, denotes the true mean for subject i with the estimate denotedby based on the candidate model. In practice, is unknown, which can be estimated from the largest candidate model under consideration (Mallows 1973; Shen and Chen 2012). In addition, with regard to the selection of “working” correlation structure, Shen and Chen (2012) developed the following criterion:
| (8) |
where
Note that Φi is a T × T matrix with the (j, u) element as Φi,j,u = wi,s, s = min(j, u), 1 ≤ j, u ≤ T. (* denotes the element-by-element multiplication of matrices).
2.3. Simulation of longitudinal data with missing responses under MAR
For the simulation of longitudinal data, we consider three types of outcomes (i.e., continuous, binary and count) and potential correlation structures shown in Table 1. The marginal mean μi of the outcome variables Yi is given by
| (9) |
where g is the link function corresponding to types of outcomes, for instance, an identity link function for continuous outcomes, a logit link function for binary outcomes, and a log link function for count data. xi includes cluster-level or subject-level covariates of interest and the associated parameters are denoted by β1. Then, Yi can be generated with a given correlation structure R(ρ) and marginal mean μi. Here, we adopt the functions of “mvrnorm”, “rmvbin” and “genPoisNor” for three types of outcome generation, and the details of the algorithms can be referred to the literature (Demirtas and Doganay 2012; Leisch et al. 1998; Amatya and Demirtas 2017). Afterward, given the pre-specified model for missing data, the probability of missingness at each observation for each subject can be obtained; thus, the missing status can be determined based on the Bernoulli distribution. Note that if one observation is missing, all the subsequent ones will also be missing, and also the assumption of MAR is ensured by the model for missingness which only depends on the observed data.
Table 1.
The list of potential correlation structures in wgee.
| Name | R(ρ) |
|---|---|
| Independence | Cor(Yij, Yij′) = 0, j ≠ j′ |
| Exchangeable | Cor(Yij, Yij′) = ρ, j ≠ j′ |
| First-order Autoregressive (AR1) | Cor(Yij, Yij′) = ρ|j–j’|, j ≠ j′ |
| Unstructured | Cor(Yij, Yij′) = ρjj’, j ≠ j′ |
3. Description of core functions
The main function in wgeesel to implement WGEE approach for longitudinal data with dropout/monotone missing responses under MAR is wgee. In addition, wgeesel provides functions QIC.gee, QICW.gee and MLIC.gee to compute QIC, QICW, and MLIC for model selection in GEE adjusted for potential missing data that is MAR.
3.1. Main functions
The standard code for fitting the marginal model by WGEE is:
wgee (model, data, id, family, corstr, scale=NULL, mismodel=NULL)
model: The model to be fitted by WGEE method. It is the same as the formula argument in the geeglm function.
data: The name of the dataset.
id: Subject id in the dataset.
family: Specify the error distribution and link function in wgee and is identified by the name of the corresponding distribution in a generalized linear model. The available function are: “gaussian”, “binomial” and “poisson”.
corstr: Three pre-defined “working” correlation structures are available, and they are “independence”, “exchangeable”, “ar1” and “unstructured” (Table 1).
scale: A numeric variable giving the value for the scale parameter ϕ. It should be known; otherwise, it needs to be estimated. The default setting is NULL.
mismodel: Specify the logistic regression model for weight estimation.
The wgee function largely follows the syntax and the output style of the geeglm function and provides comprehensive outputs including parameter estimation, weights, scale parameter and so on. Also, with regard to the existing information criteria for model selection, the functions for computing QIC, QICW and MLIC are:
QIC.gee(object);
QICW.gee(object);
MLIC.gee(object, object_full).
The arguments in the model selection function QIC.gee, QICW.gee and MLIC.gee are fitted model objects of class “wgee”. One argument of note in MLIC.gee is object_full, which is the fitted model object of class “wgee” that specifies the largest candidate model under consideration. QIC.gee calculates QIC and QICu. QICW.gee computes the QICWr and QICWp. MLIC.gee outputs MLIC and MLICC.
In addition, the data_sim function in wgeesel is utilized for the simulation of longitudinal data with missing responses under MAR, where normal, Bernoulli or Poisson longitudinal data with monotone missingness are considered. data_sim simulate multivariate random variables depending on the following packages: MASS, bindata and PoisNor (Ripley et al. 2017; Leisch et al. 2012; Amatya and Demirtas 2016). In particularly, multivariate normal data are generated through MASS. Correlated binary data are generated by bindata. Correlated Poisson variables are generated through PoisNor by inverse CDF transformation method. Through specifying the number of lags, y_lag can generate the lagged responses within-subject, which can be included as potential covariates in the dropout model for weight estimation in WGEE.
3.2. Other available functions
Besides the main selection criteria in WGEE, wgeesel also provides the functions to calculate additional information criteria including MQIC, RJC and corrected RJC for regular GEE which are briefly introduced in Section 1 (Imori 2013; Rotnitzky and Jewell 1990; Wang and Long 2011). Note that MQIC.gee computes the MQIC and MQICu; RJC calculates the RJC for selection of “working” correlation structure; RJC2 calculates corrected RJC to select “working” correlation structure for balanced data when the sample size is relatively small. Also, the function of drgee can be used to perform doubly robust GEE model fitting by specifying the dropout model and the outcome model, which is built upon on the package CRTgeeDR (Prague et al. 2016, 2017). In addition, three datasets with different types of outcomes from real applications also available in wgeesel. For research purpose, the simulation function, data_sim, for longitudinal data with monotone missingness are also provided with more details described in Section 4. The objects returned by the functions are detailed in the reference manual (see Value part), which is available from the Comprehensive R Archive Network at https://cran.r-project.org/package=wgeesel.
4. Simulation
In this section, we will conduct simulation studies to evaluate the validity of wgee by comparing the results from PROC GEE (SAS Institute Inc. 2016) and other existing programs. We consider three types of outcomes, continuous, binary and count, and the marginal mean μij is given by g(μij) = β0 + β1xij, i = 1, 2, …, K; j = 1, 2, …, T, where g is the link function described above, xij is a cluster-level covariate following up a Bernoulli distribution, the number of visits T = 3 for each subject, and the sample size K = 100. The true parameter values are β0 = −0.5 and β1 = 0.5, and the true correlation structure is exchangeable with the correlation coefficient ρ = 0.25.
For the dropout model, we assume the following logistic regression model:
| (10) |
where λij = Pr(rij = 1 | ri,j−1 = 1, Yi, xij), α0 = 1, α1 = −0.5 and α2 = −0.5. The overall proportion of missing observations (i.e., the number of missing observations over KT) is between 20% to 35%, which varies across different set-ups.
We use the function data_sim in wgeesel to simulate 250 Monte Carlo datasets for each simulation setting. The sample code for simulating one longitudinal binary data is below:
R> id <- rep (1:100, each = 3) #simulate 100 subjects each with 3 observations
R> x <- cbind (1, rep (rbinom (100, 1, 0.5), each = 3)) #generate covariate x (binary)
R> x_mis <- cbind (1, rep (runif (100), each = 3)) #generate x2 (continuous)
R> sim_data <- data_sim (id, rho = 0.25, phi = 1, x, beta = c (−0.5, 0.5), x_mis,
+ para = c (1, −0.5, −0.5), corstr = “exchangeable”, family = “binary”,
+ lag_level = 1) # simulate the correlated binary data
R> data_final <- sim_data$data [,c (“id”, “response_mis”, “ind”, “ylag1”, “2”, “V2”)]
R> colnames (data_final) <- c (“id”, “response”, “R”, “y_lag”, “x1”, “x2”)
R> head (data_final)
id response R y_lag x x2
1 1 0 1 NA 0 0.7209039
2 1 NA 0 0 0 0.7209039
3 1 NA 0 0 0 0.7209039
4 2 0 1 NA 1 0.8757732
5 2 0 1 0 1 0.8757732
6 2 0 1 0 1 0.8757732
We apply the WGEE method on the datasets with three types of outcomes under exchangeable, AR1 and unstructured “working” correlation structures. The parameter estimates are obtained from wgee and PROC GEE. The results are summarized in Table 2 using the following measures: the difference between the mean of the parameter estimates and the true value (Bias), the mean of the standard error estimates (SE), the Monte Carlo standard deviation of the parameter estimates (SD). It is noted that PROC GEE is still under experimental version and cannot provide the ODS (Output Delivery System) output of the parameter estimates from the dropout model. From the results, we can see that wgee yields satisfactory parameter estimates because of negligible biases. Under the true correlation structure (i.e., exchangeable), the estimates obtained by wgee are exactly the same as the estimates from PROC GEE. When the “working” correlation structure is misspecified (i.e., AR1, unstructured), the estimates from wgee are comparable with those from PROC GEE in terms of bias and SE. Also, as we expect, SDs are close to SEs throughout even though there is some discrepancy for count data which may be due to higher missing rate. Thus, we confirm that our function of wgee provides valid inference, and comprehensive output (e.g., the parameter estimates of the dropout model) can be provided for other research purposes.
Table 2.
Summary of estimation results in WGEE with K = 100 and T = 3.
| Type | Parameters | True | Exchangeable | AR1 | Unstructured | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Bias | SE | SD | Bias | SE | SD | Bias | SE | SD | |||||
| PROC | GEE | β0 | −0.5 | 0.0136 | 0.1113 | 0.1098 | 0.0135 | 0.1118 | 0.1107 | 0.0133 | 0.1111 | 0.1101 | |
| β1 | 0.5 | −0.0087 | 0.1658 | 0.1646 | −0.0082 | 0.1667 | 0.1655 | −0.0115 | 0.1651 | 0.1644 | |||
| Continuous | |||||||||||||
| wgee | β0 | −0.5 | 0.0136 | 0.1113 | 0.1098 | 0.0136 | 0.1118 | 0.1105 | 0.0136 | 0.1108 | 0.1099 | ||
| β1 | 0.5 | −0.0087 | 0.1658 | 0.1646 | −0.0082 | 0.1666 | 0.1655 | −0.0117 | 0.1645 | 0.1642 | |||
| α0 | 1 | −0.0191 | 0.2665 | 0.2833 | −0.0191 | 0.2665 | 0.2833 | −0.0191 | 0.2665 | 0.2833 | |||
| α1 | −0.5 | 0.0216 | 0.3614 | 0.3665 | 0.0216 | 0.3614 | 0.3665 | 0.0216 | 0.3614 | 0.3665 | |||
| α2 | −0.5 | −0.0124 | 0.1882 | 0.1916 | −0.0124 | 0.1882 | 0.1916 | −0.0124 | 0.1882 | 0.1916 | |||
| PROC | GEE | β0 | −0.5 | −0.0066 | 0.2435 | 0.2581 | −0.0060 | 0.2446 | 0.2592 | −0.0065 | 0.2441 | 0.2623 | |
| β1 | 0.5 | 0.0178 | 0.3602 | 0.3620 | 0.0184 | 0.3622 | 0.3638 | 0.0155 | 0.3617 | 0.3689 | |||
| Binary | |||||||||||||
| wgee | β0 | −0.5 | −0.0066 | 0.2435 | 0.2581 | −0.0062 | 0.2446 | 0.2594 | −0.0074 | 0.2435 | 0.2618 | ||
| β1 | 0.5 | 0.0178 | 0.3602 | 0.3620 | 0.0183 | 0.3623 | 0.3638 | 0.0160 | 0.3604 | 0.3675 | |||
| α0 | 1 | −0.0101 | 0.2787 | 0.2904 | −0.0101 | 0.2787 | 0.2904 | 0.0101 | 0.2787 | 0.2904 | |||
| α1 | −0.5 | 0.0337 | 0.3381 | 0.3534 | 0.0337 | 0.3381 | 0.3534 | 0.0337 | 0.3381 | 0.3534 | |||
| α2 | −0.5 | 0.0042 | 0.3383 | 0.3309 | 0.0042 | 0.3383 | 0.3309 | 0.0042 | 0.3383 | 0.3309 | |||
| PROC | GEE | β0 | −0.5 | −0.0012 | 0.1483 | 0.1739 | −0.0030 | 0.1494 | 0.1751 | −0.0077 | 0.1481 | 0.1754 | |
| β1 | 0.5 | −0.0122 | 0.2007 | 0.2262 | −0.0099 | 0.2015 | 0.2301 | −0.0113 | 0.2001 | 0.2348 | |||
| Count | |||||||||||||
| wgee | β0 | −0.5 | −0.0012 | 0.1483 | 0.1738 | −0.0019 | 0.1491 | 0.1750 | −0.0038 | 0.1498 | 0.1733 | ||
| β1 | 0.5 | −0.0121 | 0.2007 | 0.2262 | −0.0115 | 0.2014 | 0.2297 | −0.0188 | 0.2032 | 0.2383 | |||
| α0 | 1 | 0.0045 | 0.2746 | 0.2748 | 0.0045 | 0.2746 | 0.2748 | 0.0056 | 0.2746 | 0.2749 | |||
| α1 | −0.5 | −0.0053 | 0.3458 | 0.3596 | −0.0053 | 0.3458 | 0.3596 | −0.0099 | 0.3457 | 0.3571 | |||
| α2 | −0.5 | 0.0006 | 0.2018 | 0.2114 | 0.0006 | 0.2018 | 0.2114 | 0.0024 | 0.2017 | 0.2112 | |||
Notes: The missing proportion is 28% for the data with continuous outcome, 32% for the data with binary outcomes and 35% for the data with count outcomes. The true correlation structure is exchangeable. Bias is the difference between the mean of the parameter estimates and the true value; SE is the mean of the standard error estimates and SD is the Mont Carlo standard deviation of the parameter estimates.
Moreover, we also evaluate the estimators from WGEE and doubly robust GEE by using our functions of wgee and drgee to compare their performances under correct and misspecified dropout models, where the misspecified dropout model only considers xij as the covariate. The results are summarized in Table 3, where the mean square errors (MSE) of the parameter estimates are reported to assess efficiency. The misspecification of dropout model deteriorates WGEE model fitting but the influence is mild, and similar to the literature (Seaman and Copas 2009; Prague et al. 2016; Stephens et al. 2012), doubly robust estimators are more efficient than WGEE estimators in particularly when the dropout model is misspecified.
Table 3.
Summary of estimation results in WGEE and doubly robust GEE with K = 100 and T = 3.
| Type | Parameters | True | Correct dropout model | Mis-specified dropout model | |||||
|---|---|---|---|---|---|---|---|---|---|
| Bias | SE | MSE | Bias | SE | MSE | ||||
| wgee | β0 | −0.5 | 0.0136 | 0.1113 | 0.0122 | −0.0162 | 0.1094 | 0.0122 | |
| β1 | 0.5 | −0.0087 | 0.1658 | 0.0271 | −0.0180 | 0.1623 | 0.0266 | ||
| Continuous | |||||||||
| drgee | β0 | −0.5 | −0.0198 | 0.0699 | 0.0123 | −0.0093 | 0.0690 | 0.0118 | |
| β1 | 0.5 | −0.0083 | 0.0925 | 0.0220 | −0.0106 | 0.0909 | 0.0218 | ||
| wgee | β0 | −0.5 | −0.0066 | 0.2435 | 0.0664 | −0.0432 | 0.2414 | 0.0665 | |
| β1 | 0.5 | 0.0178 | 0.3602 | 0.1309 | 0.0048 | 0.3560 | 0.1293 | ||
| Binary | |||||||||
| drgee | β0 | −0.5 | −0.0380 | 0.1330 | 0.0615 | −0.0283 | 0.1329 | 0.0609 | |
| B1 | 0.5 | 0.0124 | 0.1769 | 0.1111 | 0.0110 | 0.1764 | 0.1110 | ||
| wgee | β0 | −0.5 | −0.0012 | 0.1483 | 0.0301 | −0.0316 | 0.1451 | 0.0278 | |
| β1 | 0.5 | −0.0121 | 0.2007 | 0.0511 | −0.0231 | 0.1966 | 0.0463 | ||
| Count | |||||||||
| drgee | β0 | −0.5 | −0.0298 | 0.0779 | 0.0240 | −0.0238 | 0.0776 | 0.0239 | |
| B1 | 0.5 | −0.0057 | 0.0956 | 0.0348 | −0.0071 | 0.0950 | 0.0350 | ||
Notes: The missing proportion is 28% for the data with continuous outcome, 32% for the data with binary outcomes and 35% for the data with count outcomes. The true exchangeable correlation structure is used for both models. Bias is the difference between the mean of the parameter estimates and the true value; SE is the mean of the standard error estimates and MSE is the mean square error of the parameter estimates.
5. An illustrative real data application
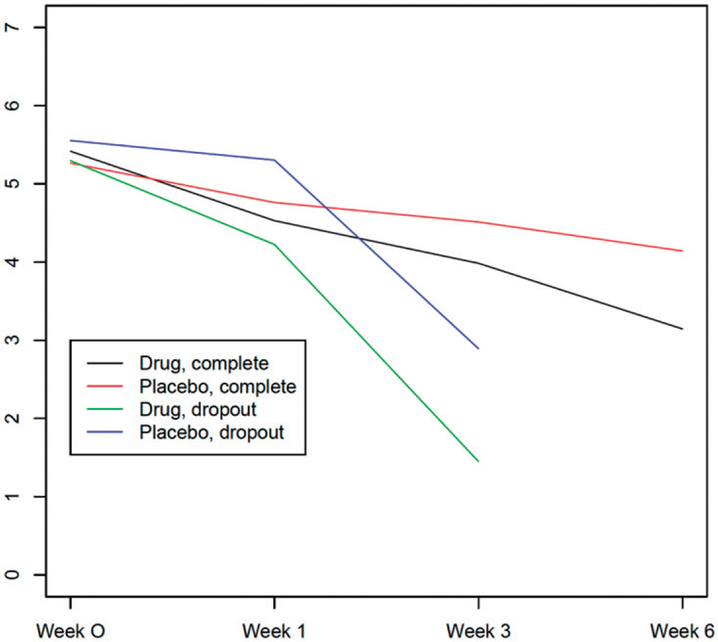
One of real data examples in our package wgeesel is the imps data set, which is from the National Institute of the Mental Health Schizophrenia Collaborative Study (Gibbons and Hedeker 1994). A total of 386 patients were enrolled in this study including 293 patients in treatment group (Drug = 1) and 93 patients in the placebo group (Drug = 0). Each patient was visited four times (Week 0, 1, 3 and 6). During each visit, the severity of the schizophrenia disorder (IMPS79) was measured, which is ranged from 0 to 7. We dichotomize IMPS79 by using the threshold of 4 (Y = 1 if IMPS ≥ 4; otherwise, Y = 0). We are particularly interested in the marginal association between the risk factors (i.e., drug, sex) and the response Y. The missing proportion is 7.3% due to patient dropouts. The missing mechanism needs to be investigated before model fitting. From Figure 1, we can see that the dropout is not MCAR because the trajectory operates differently in the drug and placebo groups, and also dropout does not only depend on covariates because the subjects with complete and missing observations follow different (pre-dropout) trajectories. Therefore, it is reasonable to assume MAR mechanism, and this is also validated by sensitivity analysis (Moreno-Betancur and Chavance 2016).
Figure 1.
Mean IMPS79 across time by the status of dropout.
Here, WGEE models are adopted for analysis, and model selection on marginal mean is conducted given the AR1 “working” correlation structure. Five candidate models shown in Shen and Chen (2012) are considered, and the corresponding information criteria of QIC, QICW and MLIC are calculated for each candidate model. The dropout is considered to be affected by Yi,t−1, Yi,t−2 and Yi,t−3, and the model for missingness is
where I(t > 2) = 1 if t > 2, and 0 otherwise. I(t > 3) = 1 if t > 3, and 0 otherwise. Thus, the first step is to generate a new dataset with Yi,t−1, Yi,t−2I(t > 2) and Yi,t−3I(t > 3) through the following program:
R> library (wgeesel)
R> data (imps)
R> imps$subject <- imps$ID
R> lag1y <- ylag (imps$ID, imps$Y, 1) ###create lagged y(t − 1)##
R> lag2y <- ylag (imps$ID, imps$Y, 2, na=F) ###create lagged y(t−2) I (t>2) ##
R> lag3y <- ylag (imps$ID, imps$Y, 3, na=F) ###create lagged y(t−3) I (t>3) ##
R> imps_new <- cbind (imps, lag1y, lag2y, lag3y)
Then, we fit a full candidate model in WGEE method via the function wgee as follows:
R> fit <- wgee (Y˜Time + Sex + Drug + Time : Sex + Sex : Drug + Drug : Time, imps_new,
+ imps_new$ID, family=“binomial”, corstr = “ar1”, scale = NULL,
+ mismodel =R˜Drug+Time+Sex+lag1y+lag2y+lag3y)
summary of fit, which is the object of class “wgee”, summarizes the fit of the model in WGEE method, including parameter estimates, p-values from hypothesis testing of each parameter in Eq. (1), estimated correlation and scale parameters:
R> summary (fit)
Call:
wgee (model = Y ˜ Time + Sex + Drug + Time:Sex + Sex : Drug + Drug:Time, data = imps_new, id = imps_new$ID, family = “binomial”, corstr = “ar1”, scale = NULL, mismodel = R ˜ Drug + Time + Sex + lag1y + lag2y + lag3y)
Estimates Robust SE z value Pr(>|z|)
(Intercept) 3.2657 0.4931 6.623 < 2e–16 ***
Time −1.1803 0.2387 −4.945 7.6e–07 ***
Sex −0.1877 0.4940 −0.380 0.704
Drug −0.5239 0.4918 −1.065 0.287
Time:Sex 0.0227 0.1712 0.133 0.894
Sex:Drug 0.3449 0.4601 0.750 0.453
Time:Drug −0.2518 0.2289 −1.100 0.271
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘. ‘ 0.1 ‘ ‘ 1
Estimated Scale Parameter: 0.9632
Estimated Correlation: 0.4175
Moreover, the summary of fit$mis_fit, which is the object of class “glm”, summarizes the fit of dropout model including parameter estimates, and p–values from hypothesis testing of each regression parameter in Eq. (2):
R> summary (fit$mis_fit)
Call:
glm (formula = mismodel, family = binomial(), data = data [adjusted_idx,])
Deviance Residuals:
Min 1Q Median 3Q Max
−2.45695 0.08982 0.31660 0.42653 1.26253
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 6.8056 1.2081 5.633 1.77e–08 ***
Drug 0.8357 0.2646 3.158 0.001587 **
Time −2.8870 0.6457 −4.471 7.78e–06 ***
Sex 0.2592 0.2477 1.047 0.295258
lag1y 0.7567 0.2750 2.752 0.005928 **
lag2y −0.6886 0.3653 −1.885 0.059420.
lag3y 1.7137 0.5093 3.365 0.000766 ***---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ‘ 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 561.17 on 1121 degrees of freedom
Residual deviance: 483.96 on 1115 degrees of freedom
AIC: 497.96
Number of Fisher Scoring iterations: 7
We can see that Yi,t−1 and Yi,t−3 are significantly associated with the dropout missigness, and Yi,t−2 has the significant trend. Next step is to conduct model selection, and based on the functions of QIC.gee, QICW.gee, and MLIC.gee in wgeesel, we can have
R> QIC.gee (fit)
QIC QICu Quasi_lik
1 1390 1383.5 −684.7
R> QICW.gee (fit)
QICWr QICWp Wquasi_lik
1 1537.1 1531 −758.5
R> MLIC.gee (fit, fit)
MLIC MLICc Wquad_loss
1 1 257.5 256.9 253.4
The calculation of QIC, QICW and MLIC are returned as well as the quasi-likelihood (Quasi_lik), weighted quasi-likelihood (Wquasi_lik) and weighted quadratic loss (Wquad_loss).
We summary the results of the five candidate models in Table 4. The values in bold are selected as the minimum across the candidate models based on the criterion under consideration. We find out that Model 2 has the smallest MLIC values among all five candidate models given AR1 “working” correlation structure. The selection results based on MLIC are the same as those in Shen and Chen (2012). Compared to the results from MLIC, the model selected by QICWr and the naive QIC seems larger with an redundant interaction term (i.e., Drug × Time, which is non-significant).
Table 4.
Analysis results of imps data for five candidate models.
| Covariate | Model | ||||
|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | |
| Time | −1.34(0.08)*** | −1.37(0.08)*** | −1.37(0.08)*** | −1.17(0.21)*** | −1.18(0.24)*** |
| Drug | −0.85(0.24)** | −0.86(0.24)** | − 0.36(0.44) | − 0.52(0.49) | |
| Sex | 0.12(0.18) | −0.19(0.49) | |||
| Sex × Time | 0.02(0.17) | ||||
| Sex × Drug | 0.34(0.46) | ||||
| Drug × Time | −0.25(0.23) | −0.25(0.23) | |||
| QIC (AR1) | 1401.2 | 1382.1 | 1385.2 | 1381.8 | 1390.0 |
| QICWr (AR1) | 1554.8 | 1529.6 | 1532.7 | 1529.5 | 1537.1 |
| MLIC (AR1) | 261.9 | 255.8 | 256.5 | 256.0 | 257.5 |
p-value < 0.05;
p-value < 0.01;
p-value < 0.001.
6. Conclusion
The key features of this R package wgeesel rely on WGEE model fitting and comprehensive information criteria for WGEE model selection on marginal mean and/or correlation structures. Simulation studies have shown that the function of wgee provides valid inference by comparing to the existing software (i.e., SAS), and comprehensive output including the estimates of the parameters of marginal mean regression as well as the dropout model, scale and correlation coefficients, and the weights matrix. The current version can be applied for correlated data with different types of outcomes (i.e., continuous, binary and count) under commonly used “working” correlation structures (i.e., independence, exchangeable, AR1 and unstructured). More importantly, wgeesel provides a flexible and user-friendly tool to conduct model selection in GEE adjusted to monotone/dropout missing responses that are MAR. We accommodate all existing information criteria (i.e., QIC, QICW, MLIC) in wgeesel to make it possible for identifying the best candidate model in real applications. QICW and MLIC have been shown to have superior performance on model selection compared to QIC in the presence of dropout missingness under MAR (Gosho 2016; Shen and Chen 2012). In addition, we also establish a function to conduct doubly robust GEE based upon the work by Prague et al. (2016, 2017). The doubly robust GEE estimators have more appealing properties than WGEE estimators because they are consistent if either of the dropout and outcome models is correctly specified, which has been validated through simulation studies; however, those information criteria for model selection are not applicable for doubly robust GEE. On the other hand, to ensure valid inference from wgeesel, the assumption of MAR needs to hold; therefore, the investigation on missing mechanism is crucial, and sensitivity analysis can be conducted to evaluate the inference deviance under different missing mechanisms, and further verify the MAR assumption (Bunouf et al. 2015; Moreno-Betancur and Chavance 2016).
Under non-monotone missingness, the MI method has been popularly employed for statistical inference, and the studies on model selection (i.e., doubly robust GEE) in this area are limited. Shen and Chen (2013) recommended the use of the MI-based model selection methods (i.e., MI-based QIC and MLIC), which perform better based on improper (frequentist) imputation than based on proper (Bayesian) imputation (Wang and Robins 1998; Lu et al. 2010). By employing the existing multiple imputation packages, such as mice in R (van Buuren and Groothuis-Oudshoorn 2011), we plan to incorporate multiple-imputation-based model selection approaches into wgeesel to accommodate general patterns of missing data for future studies, and keep adding more features for wide applications in practice and research.
Funding
Wang’s research was partially supported by the National Center for Advancing Translational Sciences, Grant KL2 TR000126 and TR002015. Xue’s research was partially supported by NSF-China Grant (No. 11401095). The content is solely the responsibility of the authors and does not represent the official views of the National Institute of Health, the National Science Foundation and other research sponsors.
References
- Akaike H 1974. A new look at the statistical model identification. IEEE Transactions on Automatic Control 19 (6):716–23. [Google Scholar]
- Amatya A, and Demirtas H. 2016. PoisNor: Simultaneous generation of multivariate data with poisson and normal marginals. R package version 1.1.
- Amatya A, and Demirtas H. 2017. Poisnor: An r package for generation of multivariate data with poisson and normal marginals. Communications in Statistics – Simulation and Computation 46 (3):2241–53. [Google Scholar]
- Bang H, and Robins J. 2005. Doubly robust estimation in missing data and causal inference models. Biometrics 91 (4):962–73. [DOI] [PubMed] [Google Scholar]
- Bartoń K 2015. MuMIn: Multi-model inference. R package version 1.15.6.
- Birhanu T, Molenberghs G, Sotto C, and Kenward M. 2011. Doubly robust and multiple-imputationbased generalized estimating equations. Journal of Biopharmaceutical Statistics 21 (2):202–25. [DOI] [PubMed] [Google Scholar]
- Bunouf P, Molenberghs G, Grouin JM, and Thijs H. 2015. A SAS program combining R functionalities to implement pattern-mixture models. Journal of Statistical Software 68 (1):1–26. [Google Scholar]
- Carey V 2015. gee: Generalized estimation equation solver. R package version 4.13–19.
- Carey V, and Ripley B. 2011. yags: Yet Another GEE Solver. R package version 6.1–13.
- Chen B, and Zhou XH. 2011. Doubly robust estimates for binary longitudinal data analysis with missing response and missing covariates. Biometrics 67 (3):830–42. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Crowder M 1995. On the use of a working correlation matrix in using generalised linear models for repeated measures. Biometrika 82 (2):407–10. [Google Scholar]
- Cui J, and Qian G. 2007. Selection of working correlation structure and best model in gee analyses of longitudinal data. Communications in Statistics – Simulation and Computation 36 (5):987–96. [Google Scholar]
- Demirtas H, and Doganay B. 2012. Simultaneous generation of binary and normal data with specified marginal and association structures. Journal of Biopharmaceutical Statistics 22 (2):223–36. [DOI] [PubMed] [Google Scholar]
- Fitzmaurice GM, Laird NM, and Ware JH. 2012. Applied longitudinal analysis. Vol. 998 New York, NY: John Wiley & Sons. [Google Scholar]
- Gibbons R, and Hedeker D. 1994. Application of random-effects probit regression models. Journal of Consulting and Clinical Psychology 62 (2):285–96. [DOI] [PubMed] [Google Scholar]
- Gosho M 2016. Model selection in the weighted generalized estimating equations for longitudinal data with dropout. Biometrical Journal 58 (3):570–87. [DOI] [PubMed] [Google Scholar]
- Hedeker D, and Gibbons R. 2006. Longitudinal Data Analysis. New York, NY: John Wiley & Sons. [Google Scholar]
- Højsgaard S, Halekoh U, and Yan J. 2016. geepack: Generalized estimating equation package. R package version 1.2–1.
- Ibrahim J, and Molenberghs G. 2009. Missing data methods in longitudinal studies: A review. Journal of the Spanish Society of Statistics and Operations Research 18 (1):1–43. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Imori S 2013. On properties of qic in generalized estimating equations. Hiroshima University, pp. 1–8. [Google Scholar]
- Laird N 1988. Missing data in longitudinal studies. Statistics in Medicine 7 (1–2):305–15. [DOI] [PubMed] [Google Scholar]
- Leisch F, Weingessel A, and Hornik K. 1998. On the generation of correlated artificial binary data. Working Papers SFB “Adaptive Information Systems and Modelling in Economics and Management Science”, Vienna University of Economics and Business, Vienna: http://www.wu-wien.ac.at/am. [Google Scholar]
- Leisch F, Weingessel A, and Hornik K. 2012. bindata: Generation of artificial binary data. R package version 0.9–19.
- Liang K, and Zeger S. 1986. Longitudinal data analysis using generalized linear models. Biometrika 73 (1):13–22. [Google Scholar]
- Lin G, and Rodriguez R. 2015. Weighted methods for analyzing missing data with the gee procedure. Pap SAS166–2015 [Internet], pp. 1–8. [Google Scholar]
- Little R, and Rubin D. 1987. Statistical analysis with missing data. Wiley Series in Probability and Statistics, New York: Wiley. [Google Scholar]
- Little R, and Rubin D. 2014. Statistical analysis with missing data. John Wiley & Sons. [Google Scholar]
- Lu K, Jiang L, and Tsiatis A. 2010. Multiple imputation approaches for the analysis of dichotomized responses in longitudinal studies with missing data. Biometrics 66 (4):1202–08. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mallows C 1973. Some comments on c p. Technometrics 15 (4):661–75. [Google Scholar]
- McCullagh P, and Nelder J. 1989. Generalized linear models, No. 37 in monograph on statistics and applied probability. London: Chapman and Hall. [Google Scholar]
- McDaniel L, Henderson N, and Prague M. 2016. geeM: Solve Generalized Estimating Equations. R package version 0.10.0.
- Moreno-Betancur M, and Chavance M. 2016. Sensitivity analysis of incomplete longitudinal data departing from the missing at random assumption: Methodology and application in a clinical trial with drop-outs. Statistical Methods in Medical Research 25 (4):1471–89. [DOI] [PubMed] [Google Scholar]
- Nooraee N, Molenberghs G, and van den Heuvel E. 2014. Gee for longitudinal ordinal data: comparing r-geepack, r-multgee, r-repolr, sas-genmod, spss-genlin. Computational Statistics & Data Analysis 77:70–83. [Google Scholar]
- Padilha JL, Colosimo E, and Demarqui F. 2015. Doubly robust-based generalized estimating equations for the analysis of longitudinal ordinal missing data. arXiv: 1506.04451.
- Pan W 2001. Akaike’s information criterion in generalized estimating equations. Biometrics 57 (1):120–25. [DOI] [PubMed] [Google Scholar]
- Parsons N 2016. repolr: Repeated measures proportional odds logistic regression. R package version 3.4. [Google Scholar]
- Platt R, Brookhart M, Cole S, Westreich D, and Schisterman E. 2013. An information criterion for marginal structural models. Statistics in Medicine 32 (8):1383–93. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Prague M, Wang R, and DeGruttola V. 2017. Crtgeedr: an r package for doubly robust generalized estimating equations estimations in cluster randomized trials with missing data. The R Journal 9 (2):105–15. [Google Scholar]
- Prague M, Wang R, Stephens A, Tchetgen E, and DeGruttola V. 2016. Accounting for interactions and complex inter-subject dependency in estimating treatment effect in cluster randomized trials with missing outcomes. Biometrics 72:1066–71. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Preisser J, Lohman K, and Rathouz P. 2002. Performance of weighted estimating equations for longitudinal binary data with drop-outs missing at random. Statistics in Medicine 21 (20):3035–54. [DOI] [PubMed] [Google Scholar]
- SAS Institute Inc. 2016. SAS/STAT Software, Version 14.2. Cary, NC. [Google Scholar]
- Raftery A 1995. Bayesian model selection in social research. Sociological Methodology, 111–63. [Google Scholar]
- Ripley B, Venables B, Bates M, Hornik K, Gebhardt A, and Firth D. 2017. MASS: Functions and datasets to support Venables and Ripley, “Modern Applied Statistics with S” (4th edition, 2002). R package version 7.3–47. [Google Scholar]
- Robins J, Rotnitzky A, and Zhao L. 1995. Analysis of semiparametric regression models for repeated outcomes in the presence of missing data. Journal of the American Statistical Association 90 (429):106–21. [Google Scholar]
- Rotnitzky A, and Jewell N. 1990. Hypothesis testing of regression parameters in semiparametric generalized linear models for cluster correlated data. Biometrika 77 (3):485–97. [Google Scholar]
- Rubin D 1976. Inference and missing data. Biometrika 63 (3):581–92. [Google Scholar]
- Salazar A, Ojeda BDM, Fernández F, and Failde I. 2016. Simple generalized estimating equations (gees) and weighted generalized estimating equations (wgees) in longitudinal studies with dropouts: guidelines and implementation in R. Statistics in Medicine 35 (19):3424–48. [DOI] [PubMed] [Google Scholar]
- Seaman S, and Copas A. 2009. Doubly robust generalized estimating equations for longitudinal data. Statistics in Medicine 28 (6):937–55. [DOI] [PubMed] [Google Scholar]
- Seaman S, and White I. 2011. Review of inverse probability weighting for dealing with missing data. Statistical Methods in Medical Research 22 (3):278–95. [DOI] [PubMed] [Google Scholar]
- Shen C, and Chen Y. 2012. Model selection for generalized estimating equations accommodating dropout missingness. Biometrics 68 (4):1046–54. [DOI] [PubMed] [Google Scholar]
- Shen C, and Chen Y. 2013. Model selection of generalized estimating equations with multiply imputed longitudinal data. Biometrical Journal 55 (6):899–911. [DOI] [PubMed] [Google Scholar]
- Stephens A, Stephens A, Tchetgen E, and DeGruttola V. 2012. Augmented gee for improving efficiency and validity of estimation in cluster randomized trials by leveraging cluster and individual-level covariates. Statistics in Medicine 31 (10):915–30. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van Buuren S, and Groothuis-Oudshoorn K. 2011. mice: Multivariate imputation by chained equations in R. Journal of Statistical Software 45 (3):1–67. [Google Scholar]
- Wang M 2014. Generalized estimating equations in longitudinal data analysis: A review and recent developments. Advances in Statistics, Article ID 303728, 10.1155/2014/303728. [DOI] [Google Scholar]
- Wang M, Kong L, Li Z, and Zhang L. 2016. Covariance estimators for generalized estimating equations (gee) in longitudinal analysis with small samples. Statistics in Medicine 35 (10):1706–21. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang M, and Long Q. 2011. Modified robust variance estimator for generalized estimating equations with improved small-sample performance. Statistics in Medicine 30 (11):1278–91. [DOI] [PubMed] [Google Scholar]
- Wang N, and Robins J. 1998. Large-sample theory for parametric multiple imputation procedures. Biometrika 85 (4):935–48. [Google Scholar]