Abstract
Background
Biomechanical properties of intact spinal motion segments are used to establish baseline values during in vitro studies evaluating spinal surgical techniques and implants. These properties are also used to validate computational models (ie, patient-specific finite element models) of human lumbar spine segments. Our laboratory has performed a large number of in vitro mechanical studies of lumbar spinal segments, using a consistent methodology. This provides extensive biomechanical data for a large number of intact motion segments, along with donor demographic variables, bone mineral density (BMD) measurements, and geometric properties. The objective of this study was to analyze how donor demographics, BMD, and geometric properties of cadaveric lumbar spine segments affect motion segment flexibility, including the range of motion (ROM), lax zone (LZ), and stiff zone (SZ), to help improve our understanding of spinal biomechanics.
Methods
A retrospective study examined the relationships between the biomechanical properties of 281 lumbar motion segments from 85 human cadaveric spines, donor demographic variables (age, sex, weight, height, and body mass index), and specimen measurements (vertebral body height, intervertebral disc height, and BMD).
Results
Statistical correlation and regression analyses showed that the flexibility of a lumbar motion segment is affected by lumbar level, donor age, sex, and weight as well as the intervertebral disc height, vertebral body height, and bone quality. Increased disc height was associated with decreased ROM (axial rotation), decreased LZ (flexion-extension and axial rotation), and increased SZ (flexion-extension and lateral bending) in the male group, but increased ROM (lateral bending) in the female group. Increased vertebral body height correlated with increased LZ (lateral bending) in the female group. Increased BMD correlated with decreased ROM overall.
Conclusions
Biomechanical measurements from flexibility testing of cadaveric lumbar spine segments are significantly correlated with donor demographics and specimen measurements. Many of these correlations are sex-dependent.
Keywords: biomechanics, flexibility, lumbar motion segment, regression analysis, range of motion, spine
INTRODUCTION
Biomechanical measurements of intact spinal motion segments are used to establish baseline values during in vitro studies that evaluate the effects of new surgical techniques and spine surgery implants. These measurements are also used to develop computational models (finite element method) of the spine by providing reference values for biomechanical behavior during application of known load conditions. In some published studies involving finite element models of spinal segments, researchers have configured the computer model to mimic experimental behavior seen in limited data sets or to match average behavior from metadata collected using a large number of samples but with inconsistent testing methods.1,2 For instance, some published experimental data describing the biomechanical behavior of intact and normal lumbar spinal motion segments include specimens from only one sex,3 specimens without known material or geometric motion segment properties,3–5 or limited donor demographic variables.6 The load conditions used during these studies vary as well, such as the maximum applied load magnitude (5 to 8 N m), the loading rate, and the possible addition of a compressive preload during bending.
Over the past 25 years, researchers in the Spinal Biomechanics Laboratory at Barrow Neurological Institute have performed numerous in vitro investigations of the lumbar spine. Although each study focused on a different hypothesis or clinical question, nondestructive intact testing to characterize baseline biomechanical properties was common to each. Consequently, biomechanical data for a large number of intact motion segments, with known donor demographics, vertebral material, and geometric properties, have been accumulated. We believe that an improved understanding of relationships between these variables will provide valuable information to the field of spinal biomechanics, especially toward the development and refinement of computational models. Therefore, the objective of this study was to retrospectively analyze the correlations between the biomechanical properties of cadaveric lumbar motion segments with no evidence of disease or abnormalities and specimen demographics (age, sex, weight, body mass index [BMI]), bone mineral density (BMD), and geometric properties (vertebral body height and disc height).
MATERIALS AND METHODS
Specimen Information
As part of the routine experimental protocol, cadaver spines were initially screened by reviewing the donor medical histories. Spines from donors between 18 and 73 years of age, without known histories of metastatic cancers, osteoporosis, spine pathologies (including arthritis), or spine surgeries were considered. Radiographs (anteroposterior and lateral views) were used to further exclude spines with observed osteophytes and disc degeneration. The BMD of L4 of each accepted spine was determined using dual-energy X-ray absorptiometry (DEXA; Hologic Inc., Marlborough, Massachusetts) of spines scanned in the anteroposterior view. Individual vertebral body and disc heights were determined from the DEXA images, which showed calibrated dimensions, in the anteroposterior plane. The methodologies for specimen preparation, dimensional measurements, specimen storage, and testing protocols were consistent among all specimens. In short, specimens (85 spinal segments: T12-S [n = 14], L3-S [n = 15], L2-L5 [n = 48], and L3-L5 [n = 8]) were wrapped and stored at −20°C until tested. Specimens were thawed in normal saline at 21°C and cleaned of muscle tissue while keeping all ligaments, joint capsules, and discs intact. For testing, the caudal end of the distal vertebra was reinforced with household screws, embedded in a metal fixture using fast-curing resin (Smooth-Cast, Smooth-On, Inc., Easton, Pennsylvania), and attached to the base of the testing apparatus. Similarly, the cephalad end of the proximal vertebra was also reinforced with household screws and embedded in resin in a cylindrical metal fixture for pure moment load application.
Flexibility Testing
The well-established protocol for flexibility testing using applied pure moment loads to induce spinal bending with simultaneous optical tracking of vertebral body movements was used. All specimens were subjected to pure moment flexibility tests in a servo-controlled hydraulic testing frame as detailed previously by Crawford et al.7 The advantage of pure moment loading is that the load is distributed evenly to each motion segment, regardless of the distance from the point of loading.8 Loads (7.5 N m maximum) were applied about the appropriate anatomical axes to induce flexion, extension, right and left lateral bending, then right and left axial rotation. Loads were applied quasi-statically in 1.5–N m increments (45 seconds each) after 3 preconditioning cycles at maximum load (60 seconds each) to allow for creep, followed by a resting period (60 seconds). Intervertebral rotations and translations in response to the applied loads were tracked using the Optotrak 3020 system (Northern Digital, Inc., Waterloo, Ontario, Canada), with each opto-electronic marker attached to individual k-wires. Three markers and 3 k-wires were attached to each vertebral body. Local coordinate systems were defined for each motion segment using a digitizing probe.9 Spinal angles in each anatomical plane were calculated using a published technique that has been used to describe angular coupling patterns of a spinal joint.10 During motion in all planes, the angular range of motion (ROM) was determined at each level from angle versus moment data.11
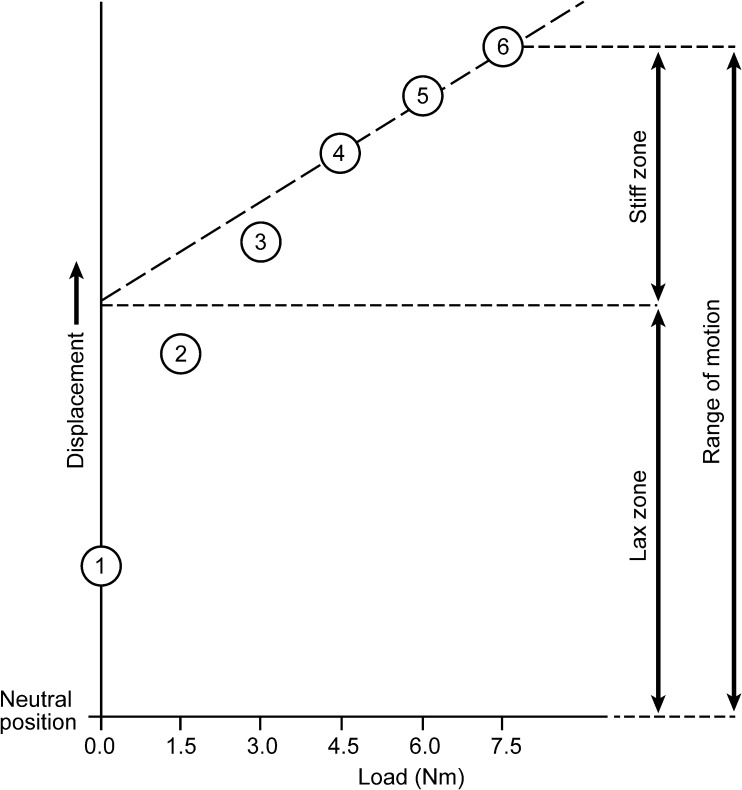
The ROM was further divided into a lax zone (LZ) and stiff zone (SZ), where the LZ is the portion of the ROM in which the ligaments are lax, and the SZ is the portion of the ROM in which ligaments are in tension (Figure 1).
Figure 1.
Graph of biomechanical parameters studied by clinical variables (bone mineral density, age, vertebral body height, and disc height). Each circle represents angular position–data recorded quasi-statically (after holding a steady load for 45 seconds) at the 6 different loads applied. The angular displacement where the lax zone transitions to the stiff zone is found by extrapolating a best-fit to points 4, 5, and 6 to 0 load. The lax and stiff zones sum to provide the range of motion. Used with permission from Barrow Neurological Institute.
Data Analysis
The independent variables considered in this study were donor age, sex, weight (at time of death), height, lumbar level, vertebral body height (superior body of motion segment), intervertebral disc (IVD) height, and BMD. The dependent variables included in the analysis were ROM, LZ, and SZ during flexion-extension (FL-EX; sum of FL and EX), lateral bending (average right and left), and axial rotation (average right and left). Differences in mean values of the variables between females and males were assessed using unpaired 2-tailed Student t tests. Relationships between variables for pooled female + male, female, and male donor groups were evaluated using Pearson correlation analyses and multiple linear regression methods (all variables, with consideration to sex); P values less than .05 were considered significant. All analyses were performed using SigmaStat 12.0 (Systat Software, San Jose, California).
RESULTS
A total of 281 donor lumbar motion segments (L1-L2: 7 female and 6 male; L2-L3: 26 female, 37 male; L3-L4: 38 female, 47 male; L4-L5: 38 female, 47 male; and L5-S: 19 female, 17 male) from 85 cadaver spines (T12-S [n = 14], L3-S [n = 15], L2-L5 [n = 48], L3-L5 [n = 8]) were included in the analysis (Table 1).
Table 1.
Demographics and material properties of lumbar spine motion segmentsa from 85 donor cadaver spines. All data are mean ± SD.
|
Variable |
Donors |
||
|
Women + Men (n = 251) |
Women (n = 116) |
Men (n = 135) |
|
| Age, y | 53.9 ± 10.7 | 52.6 ± 11.8 | 55.0 ± 9.6 |
| Weight, kg | 95.2 ± 32.6 | 97.1 ± 36.9 | 93.6 ± 28.9 |
| Height, cm | 173.4 ± 9.5 | 167.5 ± 8.2 | 178.0 ± 7.6c |
| BMI | 31.8 ± 11.8 | 34.9 ± 14.3 | 29.5 ± 8.95c |
| BMD,b g/cm2 | 0.818 ± 0.171 | 0.793 ± 0.155 | 0.838 ± 0.181c |
| Sup VB height, mm | 26.0 ± 2.3 | 25.7 ± 2.5 | 26.1 ± 2.1 |
| IVD height, mm | 6.5 ± 1.5 | 5.9 ± 1.3 | 6.9 ± 1.5c |
Abbreviations: BMI, body mass index; BMD, bone mineral density; IVD, intervertebral disc; Sup VB, superior vertebral body.
Included 251 motion segments from 85 spines (T12-S [n = 14], L3-S [n = 15], L2-L5 [n = 48], L3-L5 [n = 8]).
BMD of L4.
Significant difference (P < .05) between male and female groups (ANOVA t test).
There were significant differences in terms of donor height, BMI, BMD, and IVD height between the donor women and men (Table 1); the female donors were shorter (167.5 cm versus 178 cm, P < .001), and had higher BMI (34.9 versus 29.5, P < .001), lower BMD (0.793 versus 0.838 g/cm2, P = .045), and narrower IVD height (5.9 mm versus 6.9 mm, P < .001) than the male donors. Similarly, there were significant differences between all biomechanical parameters for the female and male donors, except for SZ during FL-EX (Table 2).
Table 2.
Biomechanical parameters of all lumbar motion segments in donor cadavers (85 spines). All data are mean ± SD.
|
Variable, Degrees |
Women + Men (n = 251) |
Women (n = 116) |
Men (n = 135) |
| ROM (FL-EX) | 8.86 ± 3.45 | 9.7 ± 3.5 | 8.14 ± 3.24a |
| ROM (LB) | 4.74 ± 1.59 | 5.3 ± 1.77 | 4.26 ± 1.25a |
| ROM (AR) | 2.15 ± 1.24 | 2.39 ± 1.42 | 1.94 ± 1.03a |
| LZ (FL-EX) | 5.63 ± 3.18 | 6.56 ± 3.3 | 4.84 ± 2.86a |
| LZ (LB) | 2.69 ± 1.28 | 3.10 ± 1.48 | 2.34 ± 0.96a |
| LZ (AR) | 1.08 ± 0.97 | 1.24 ± 1.14 | 0.94 ± 0.77a |
| SZ (FL-EX) | 3.22 ± 0.92 | 3.17 ± 1.00 | 3.26 ± 0.85 |
| SZ (LB) | 1.87 ± 0.45 | 1.94 ± 0.49 | 1.80 ± 0.40a |
| SZ (AR) | 1.11 ± 0.32 | 1.17 ± 0.33 | 1.06 ± 0.30a |
Abbreviations: AR, axial rotation; FL-EX, flexion-extension; LB, lateral bending; LZ, lax zone; ROM, range of motion; SZ, stiff zone.
Significant difference (P < .05) between male and female groups (ANOVA t-test).
Due to the significant differences between women and men, correlations were analyzed by sex groupings. Correlations between the demographic variables and specimen measurements (Table 3) showed that in the female group, BMD decreased significantly with increased age (r = −0.287, P = .003), BMD increased significantly with increased body weight (r = 0.247, P = .015), and BMD increased significantly with increased donor height (r = 0.275, P = .006). Vertebral body height increased significantly with increased donor height in the male group (r = 0.336, P < .001), whereas there was no such correlation in the female group (r = 0.088, P = .456). Disc height decreased significantly with increased BMD in the male group (r = −0.225, P = .029), but there were no correlations between disc height and any non-biomechanical variable in the female group (P ≥ .42).
Table 3.
Correlation coefficients and P valuesa between donor demographic variables and specimen measurements by sex.
|
Variable |
Weight |
Height |
BMD |
VB Height |
Disc Height |
|||||
|
Men |
Women |
Men |
Women |
Men |
Women |
Men |
Women |
Men |
Women |
|
| Level | ||||||||||
| r | … | … | … | … | … | … | 0.095 | 0.011 | −0.049 | 0.080 |
| P | … | … | … | … | … | … | .316 | .922 | .641 | .518 |
| Age | ||||||||||
| r | −0.230 | −0.127 | −0.120 | −0.008 | −0.196 | −0.287 | 0.032 | 0.025 | −0.078 | −0.012 |
| P | .007 | .197 | .116 | .937 | .023 | .003 | .737 | .822 | .453 | .922 |
| Weight | ||||||||||
| r | … | … | 0.239 | 0.023 | 0.182 | 0.247 | 0.168 | 0.060 | 0.047 | 0.019 |
| P | … | … | .005 | .813 | .034 | .015 | .076 | .609 | .653 | .884 |
| Height | ||||||||||
| r | … | … | … | … | 0.09 | 0.275 | 0.336 | 0.088 | 0.083 | −0.015 |
| P | … | … | … | … | .300 | .006 | <.001 | .456 | .424 | .908 |
| BMD | ||||||||||
| r | … | … | … | … | … | … | 0.048 | 0.004 | −0.225 | −0.101 |
| P | … | … | … | … | … | … | .615 | .970 | .029 | .420 |
| VB height | ||||||||||
| r | … | … | … | … | … | … | … | … | 0.114 | −0.042 |
| P | … | … | … | … | … | … | … | … | .275 | .736 |
Abbreviations: BMD, bone mineral density; VB, vertebral body.
Significant correlations (P < .05) are shown in bold.
Linear relationships between biomechanical variables and the independent variables showed that ROM increased significantly at more caudal lumbar levels during FL-EX in both sex groups (Table 4, P < .001). There were no correlations between ROM and lumbar level during lateral bending in either sex group (P ≥ .848) or during axial rotation in the male group (P = .366). However, the ROM during axial rotation increased at more caudal levels in the female group (P = .003).
Table 4.
Correlation coefficients and P valuesa between biomechanical and independent variables during flexion-extension, lateral bending,b and axial rotationb for men and women.
|
Variable |
Sex |
ROM FL−EX |
ROM LB |
ROM AR |
LZ FL−EX |
LZ LB |
LZ AR |
SZ FL−EX |
SZ LB |
SZ AR |
|||||||||
|
r |
P |
r |
P |
r |
P |
r |
P |
r |
P |
r |
P |
r |
P |
r |
P |
r |
P |
||
| Level | M | 0.51 | <.001 | −0.017 | .848 | 0.078 | .366 | 0.478 | <.001 | −0.039 | .657 | 0.133 | .124 | 0.285 | <.001 | −0.15 | .082 | 0.072 | .408 |
| F | 0.43 | <.001 | 0.014 | .885 | 0.276 | .003 | 0.442 | <.001 | 0.029 | .755 | 0.305 | <.001 | 0.123 | .187 | −0.219 | .018 | 0.249 | .007 | |
| Age | M | 0.044 | .612 | −0.173 | .045 | 0.168 | .051 | 0.16 | .063 | 0.057 | .513 | 0.147 | .090 | −0.414 | <.001 | −0.348 | <.001 | −0.068 | .434 |
| F | 0.02 | .833 | −0.088 | .345 | 0.276 | .003 | 0.182 | .050 | 0.054 | .568 | 0.284 | .002 | −0.488 | <.001 | −0.428 | <.001 | 0.062 | .505 | |
| Weight | M | −0.256 | .003 | −0.283 | <.001 | −0.196 | .023 | −0.247 | .004 | −0.307 | <.001 | −0.127 | .143 | −0.076 | .380 | −0.235 | .006 | −0.228 | .008 |
| F | −0.152 | .120 | −0.172 | .079 | −0.104 | .291 | −0.088 | .373 | −0.004 | .968 | −0.121 | .218 | −0.219 | .025 | −0.128 | .192 | −0.151 | .124 | |
| Height | M | 0.007 | .932 | 0.001 | .993 | −0.084 | .333 | 0.008 | .931 | −0.063 | .468 | −0.071 | .415 | 0.012 | .888 | −0.087 | .317 | −0.009 | .919 |
| F | −0.07 | .479 | −0.123 | .213 | −0.192 | .049 | −0.041 | .678 | −0.182 | .064 | −0.204 | .037 | −0.074 | .455 | −0.084 | .395 | −0.212 | .030 | |
| BMI | M | −0.272 | .001 | −0.289 | <.001 | −0.186 | .031 | −0.267 | .002 | −0.301 | <.001 | −0.121 | .163 | 0.163 | .399 | −0.202 | .019 | −0.234 | .006 |
| F | −0.121 | .225 | −0.144 | .149 | −0.041 | .682 | −0.063 | .527 | 0.033 | .739 | −0.054 | .589 | −0.189 | .057 | −0.136 | .173 | −0.093 | .354 | |
| BMD | M | −0.311 | <.001 | −0.182 | .035 | −0.127 | .143 | −0.296 | <.001 | −0.15 | .082 | −0.126 | .145 | −0.128 | .140 | −0.142 | .100 | −0.225 | .009 |
| F | −0.269 | .005 | −0.15 | .120 | −0.093 | .337 | −0.249 | .009 | −0.167 | .085 | −0.079 | .414 | −0.135 | .163 | 0.014 | .890 | −0.148 | .127 | |
| VB Ht | M | −0.028 | .767 | 0.01 | .916 | −0.02 | .838 | −0.039 | .680 | 0.003 | .977 | 0.016 | .866 | 0.001 | .995 | −0.006 | .950 | 0.031 | .744 |
| F | 0.108 | .329 | 0.173 | .117 | 0.089 | .423 | 0.107 | .337 | 0.23 | .037 | 0.116 | .294 | 0.023 | .836 | 0.035 | .751 | 0.045 | .688 | |
| Disc Ht | M | −0.178 | .087 | 0.127 | .222 | −0.244 | .018 | −0.266 | .009 | 0.072 | .489 | −0.23 | .026 | 0.206 | .046 | 0.358 | <.001 | −0.125 | .228 |
| F | 0.103 | .407 | 0.283 | .020 | 0.12 | .333 | 0.133 | .285 | 0.117 | .346 | 0.119 | .336 | −0.165 | .181 | 0.125 | .313 | 0.237 | .054 | |
| Disc VB Ht | M | −0.179 | .084 | 0.073 | .486 | −0.258 | .012 | −0.26 | .012 | 0.022 | .835 | −0.261 | .011 | 0.19 | .066 | 0.318 | .002 | −0.162 | .119 |
| F | 0.07 | .577 | 0.201 | .103 | 0.103 | .408 | 0.093 | .453 | 0.032 | .796 | 0.091) | .463 | −0.155 | .211 | 0.097 | .434 | 0.215 | .080 | |
Abbreviations: AR, axial rotation; BMD, bone mineral density; BMI, body mass index; F, female; FL-EX, flexion-extension; Ht; height; LB, lateral bending; LZ, lax zone; M, male; ROM, range of motion; SZ, stiff zone; VB, vertebral body.
Significant correlations (P < .05) are shown in bold.
Average of right and left.
During FL-EX, there was no correlation between ROM and age in either sex group (Figure 2A and Table 4; P ≥ .612). However, there were significant relationships between age and both LZ and SZ; in the male group, increased age resulted in increased LZ (Figure 2B and Table 4; P = .063), and in both groups, increased age resulted in decreased SZ (Figure 2C and Table 4 [both P < .001]).
Figure 2.
Mobility of all lumbar levels plotted versus age during flexion-extension for (A) range of motion (ROM), (B) lax zone (LZ), and (C) stiff zone (SZ) including males (M) and females (F). Note the lack of correlation when considering ROM (LZ+SZ) (M: r = 0.044, P = .612; F: r = 0.020, P = .833) but positive correlations considering LZ (M: r = 0.160, P = .063; F: r = 0.182, P = .050) and negative correlations when considering SZ (M: r = −0.414, P < .001; F: r = −0.488, P < .001). Used with permission from Barrow Neurological Institute.
In the male group, increased weight correlated with decreased ROM in all directions of movement (Table 4; P ≤ .023). There were no significant correlations between ROM in any direction and weight in the female group (P ≥ .079). However, SZ decreased significantly with increased weight during FL-EX in the female group (P = .025). There were no significant relationships between height and ROM, LZ, or SZ in any direction of movement in the male group (P ≥ .317). However, increased height in the female group correlated with decreased ROM, LZ, and SZ during axial rotation (P ≤ .049). The relationships between biomechanical variables and BMI were like those for weight, with noticeable differences between the female and male groups (Table 4).
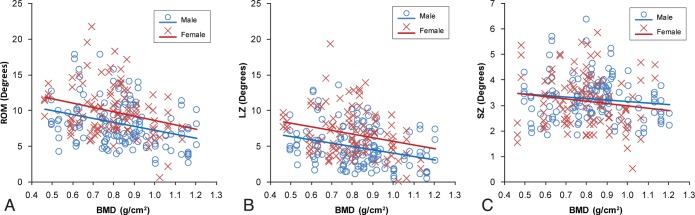
Increased BMD correlated with decreased ROM in both sex groups (Table 4), with significant findings during FL-EX in both groups (Figure 3A; P ≤ .005) and during lateral bending in the male group (P = .035), with the decrease in ROM caused by a decrease in the LZ component of ROM, not in the SZ component (Figures 3B and 3C, respectively). During axial rotation in the male group, SZ decreased significantly with increased BMD (Table 4; P = .009).
Figure 3.
Mobility of all lumbar levels plotted versus bone mineral density (BMD) during flexion-extension for (A) range of motion (ROM), (B) lax zone (LZ), and (C) stiff zone (SZ) including males (M) and females (F). Note the negative correlations when considering ROM (LZ+SZ) (M, r = −0.311, P < .001; F: r = −0.269, P = .005), and LZ (M: r = −0.296, P < .001; F: r = −0.269, P = .009) but lack of correlations when considering SZ (M: r = −0.128, P = .140; F: r = −0.135, P = .163). Used with permission from Barrow Neurological Institute.
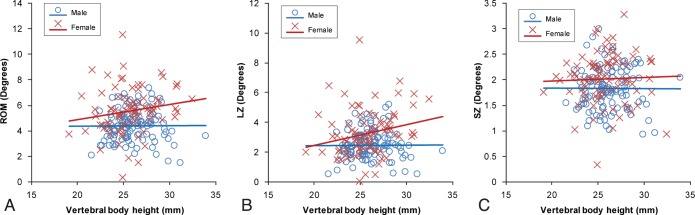
In the male group, vertebral body height did not affect ROM, LZ, or SZ in any direction of movement (P ≥ .68) (Table 4). In the female group, increased vertebral body height was significantly associated with an increased LZ during lateral bending (Figure 4; P = .037).
Figure 4.
Mobility of all lumbar levels plotted versus vertebral body height during lateral bending for (A) range of motion (ROM), (B) lax zone (LZ), and (C) stiff zone (SZ) including males and females. Note the lack of correlations with vertebral body height for male segments (ROM: r = 0.010, P = .916; LZ: r = 0.003, P = .997; SZ: r = −0.006, P = .95), compared with the correlations with vertebral body height for female segments (ROM: r = 0.173, P = .117; LZ: r = 0.230, P = .037; SZ: r = 0.035, P = .751). Used with permission from Barrow Neurological Institute.
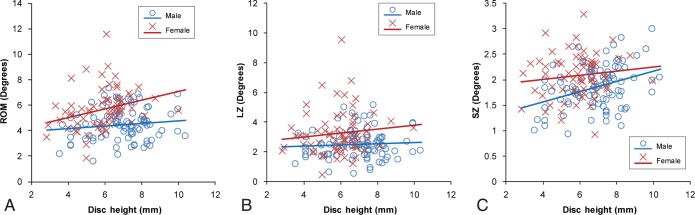
During FL-EX, there were no significant correlations between disc height and ROM for the female or male groups (Table 4 and Figure 5A; P ≥ .087). However, in the male group, there were significant relationships between disc height and both LZ and SZ (Figure 5B-5C); increased disc height was associated with decreased LZ (P = .009) and increased SZ (P = .046) (Table 4). There were no similar correlations in the female group.
Figure 5.
Mobility of all lumbar levels plotted versus disc height during flexion-extension for (A) range of motion (ROM), (B) lax zone (LZ), and (C) stiff zone (SZ) including males and females. Note the slight negative correlations for male segments for ROM (r = −0.178, P = .087) and LZ (r = −0.266, P = .009) while positive for SZ (r = 0.206, P = .046). There were no significant correlations for female segments (ROM: r = 0.103, P = .407; LZ: r = 0.133, P = .285; and SZ: −0.165, P = .181). Used with permission from Barrow Neurological Institute.
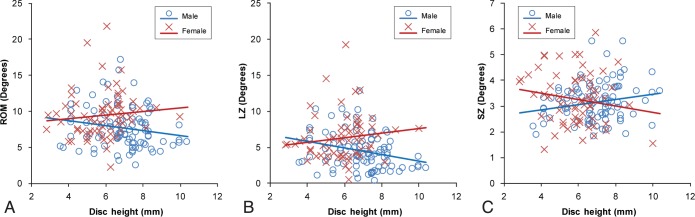
During lateral bending, there was a significant positive correlation between disc height and ROM in the female group (Table 4 and Figure 6A; P = .020) but not in the male group (P = .222). There were no correlations between disc height and LZ in either sex group (Figure 6B, P ≥ .346); however, increased disc height correlated strongly with increased SZ in the male group (Figure 6C; P < .001).
Figure 6.
Mobility of all lumbar levels plotted versus disc height during lateral bending for (A) range of motion (ROM), (B) lax zone (LZ), and (C) stiff zone (SZ) for males (M) and females (F). Note the slightly positive correlation when considering ROM (LZ+SZ) (M: r = 0.127, P = .222; F: r = 0.283, P = .020), lack of correlation when considering LZ (M: r = 0.072, P = .489; F: r = 0.117, P = .346), and positive correlation when considering SZ (M: r = 0.358, P < .001; F: r = 0.125, P = .313). Used with permission from Barrow Neurological Institute.
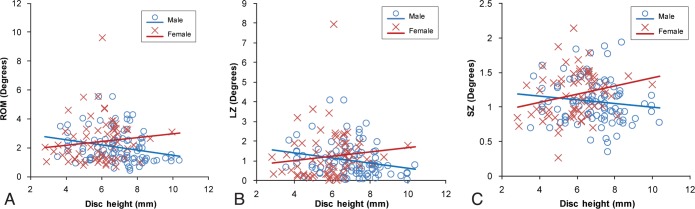
During axial rotation, increased disc height was negatively correlated with ROM, LZ, and SZ in the male group but positively correlated with ROM, LZ, and SZ in the female group (Table 4 and Figure 7). The correlations were significant for ROM and LZ in the male group (P ≤ .026) but were not significant in the female group (P ≥ .054).
Figure 7.
Mobility of all lumbar levels plotted versus disc height during axial rotation for (A) range of motion (ROM), (B) lax zone (LZ), and (C) stiff zone (SZ) for males and females. Note the negative correlations for male segments (ROM: r = −0.244, P = .018; LZ: r = −0.230, P = .026; SZ: r = −0.125, P = .228), and positive correlations for female segments (ROM: r = 0.120, P = .333; LZ: r = 0.119, P = .336; and SZ: r = 0.237, P = .054). Used with permission from Barrow Neurological Institute.
The results of multiple linear regression analysis demonstrated that all 9 measured biomechanical parameters can be predicted using different combinations of the independent variables included in this study (Table 5), with all variables contributing significantly to at least 2 biomechanical parameters.
Table 5.
Summary of correlation coefficients and significant P values from multiple linear regression analyses.
|
Direction |
Parameter |
Level |
Sex |
Age |
Weight |
Height |
BMD |
VB Ht |
Disc Ht |
r |
| Flexion-extension | ROM | <.001 | <.001 | … | .005 | … | <.001 | … | … | .582 |
| LZ | <.001 | <.001 | .012 | … | … | .010 | … | .041 | .594 | |
| SZ | .008 | … | <.001 | <.001 | … | … | … | … | .584 | |
| Axial rotation | ROM | .002 | … | <.001 | … | <.001 | … | … | … | .363 |
| LZ | <.001 | … | .004 | … | … | … | … | … | .451 | |
| SZ | .037 | … | … | .019 | … | .039 | … | … | .269 | |
| Lateral bending | ROM | … | <.001 | .002 | .001 | … | .026 | .044 | … | .458 |
| LZ | … | .009 | … | … | … | … | .016 | … | .368 | |
| SZ | .011 | .009 | <.001 | <.001 | … | … | … | <.001 | .594 |
Abbreviations: Ht, height; LZ, lax zone; ROM, range of motion; SZ, stiff zone; VB, vertebral body.
DISCUSSION
Several factors make this retrospective analysis unique, including: (1) the large number of specimens involved (281 motion segments from 85 spines); (2) known demographics, material and geometric values;(3) biomechanical properties obtained using a consistent and precise test method (including ROM as well as the subcomponents LZ and SZ); and (4) the analysis of correlations between all of these variables. Previous similar studies, some of which also included a large number of specimens,4,6 did not consider all of the variables analyzed in the current study.
Using data from 204 motion segments from 42 lumbar spines evaluated under pure moment loading to 7.5 Nm, Cook et al4 showed that ROM could be predicted using linear combinations of donor demographics including height, weight, and age with reported R2 values between 0.05 and 0.18. In the current study, we have shown that adding BMD, vertebral body height, and disc height measurements to the analysis can substantially increase the predictability of lumbar spine biomechanics. For example, adding these values to the linear regression analysis of ROM during FL-EX resulted in a correlation coefficient of 0.582 (Table 5) or an R2 value of 0.34. We have also shown that ROM subcomponents LZ and SZ can be predicted with similar levels of certainty; a correlation coefficient of 0.594 was calculated for both LZ during FL-EX and SZ during lateral bending (Table 5).
A spinal segment's LZ can be thought of as the portion of ROM when ligaments are lax (ie, during upright posture), whereas SZ can be thought of as the portion when engaged ligaments are in tension toward the limits of the ROM.11 SZ is inversely related to stiffness, with a small SZ indicating that engaged ligaments, together with the IVD they span, are stiff (ie, ligaments and a portion of the disc in tension on one side and in compression on the other), whereas a large SZ means ligaments and the spanned disc are more elastic. In our study, age did not have a quantitative effect on ROM during FL-EX but rather a qualitative effect; LZ increased, and SZ significantly decreased as age increased (Figure 2). In other words, the combination of spinal ligaments and the IVD that they span became increasingly stiff toward their combined terminal ROM, with age. Iida et al12 studied the effects of aging on the mechanical properties of human spinal ligaments and reported significant negative correlations between age and the tensile strength and elastic modulus of explanted supraspinous and interspinous ligaments at L4-L5 (ie, spinal ligaments became less stiff with age). In addition, they did not find a correlation between segmental ROM (determined from functional lateral radiographs of the patient before spinal surgery and of the ligament explant) and the ligament mechanical properties. Thus, the effects of age on SZ in lumbar spinal segments may be caused to a greater extent by changes in the mechanical properties of the IVD than by changes in elasticity of the spinal ligaments.
In this study, we found that in male spines during FL-EX, LZ significantly decreased as disc height increased, whereas SZ significantly increased as disc height increased (Figure 5). This finding suggests that longer or taller disc-ligament combinations tend to be more elastic, which may be related to the effects of geometry (eg, longer ligaments) or the calcification of ligaments and mild degenerative changes in levels with low IVD height, or both. Importantly, lumbar disc height did not correlate with age or donor height in either sex group (Table 3; P ≥ .42). In other words, segmental stiffness (SZ) of lumbar spinal segments during FL-EX was related to both age (older donors had stiffer spinal ligaments) and IVD height; however, IVD height was not related to age or donor height. We may have selectively precluded a relationship between IVD height and age by screening for overtly healthy specimens within the range of 18 to 73 years of age. It is also possible that the observed differences in disc height involved some varying amount of mild disc degeneration. IVD degeneration, which includes loss of disc height along with morphological disc changes, was not quantified in our study. Nonetheless, we believe it is reasonable to compare biomechanical data related to disc height with biomechanical data related to disc degeneration. Muriuki et al5 studied the effects of disc degeneration on lumbar spine kinematics using magnetic resonance imaging and in vitro data from 54 lumbar spine specimens and reported that disc degeneration varied by lumbar level; caudal level discs had more degeneration than cranial discs. They also reported that “low flexibility zone” stiffness (ie, stiffness near terminal ROM) increased as disc degeneration increased during flexion, lateral bending, and axial rotation. In comparison, we did not see correlations between disc height and lumbar level (Table 3; P > .5). However, we noted an increase in SZ (or a decrease in the reciprocal of SZ to compare our data to Muriuki's low-flexibility-zone stiffness data) with increased disc height (ie, decreased disc degeneration) during FL-EX and lateral bending, in males only (Table 4; P ≤ .046), which supports Muriuki's findings. We also noted a significant increase in LZ for caudal levels during FL-EX (Table 4; P < .001), which also supports findings presented by Muriuki et al5 that cranial lumbar discs had a lower “high flexibility zone” (similar to LZ) during flexion. In addition, our finding of increased ROM with increased disc height (ie, decreased ROM with decreased disc height) during lateral bending in females (Table 4; P = .02) is similar to their reported trend of lower ROM with increased disc degeneration. Kettler et al6 also studied the effects of disc degeneration (defined radiographically using disc height, the presence of osteophytes, and sclerosis) on in vitro biomechanics in the lumbar spine and reported a decrease in ROM with increased disc degeneration (ie, decreased disc height), which is similar to our findings. They also reported a trend toward changes in the neutral zone (similar to LZ) with varying degrees of disc degeneration. However, data from male and female spines were grouped, which may have masked statistical significances.
As was seen in this study (Table 2) and other studies,4,5,13 biomechanics in the lumbar spine are sex specific; female spines are more flexible than male spines. Although donor height and disc height were significantly greater for the male than the female groups in this study, vertebral body height was roughly the same between groups (Table 1). It is possible that differences in other anatomic features that were not measured, such as total vertebral body depth, vertebral anterior body depth, and vertebral body width, which in turn may affect lumbar ligament arrangements or disc anatomy, could have contributed to the sex-specific biomechanical differences. In addition, biological differences most likely influence spinal biomechanics, including hormones and history of childbearing, which is linked to increased ligament elasticity.14 BMD was greater in the male specimens than in the female specimens (Table 1). However, significant negative correlations between BMD and ROM (and LZ) during FL-EX were present in both male and female groups (Figure 3; P < .01), illustrating that spinal biomechanics are related to BMD. The study of spinal biomechanics assumes that the vertebrae move as rigid bodies, with all movement limited by surrounding soft tissue, including ligaments and IVDs; therefore, this implies that the material properties of spinal ligaments and discs must be closely related to BMD content.
Spinal morphology15 and tissue material properties are both critical components in computational spine modeling studies. Finite element models of the lumbar spine developed from specimen-specific geometry are often validated using experimental data presented in the literature.1,2 These data are frequently taken from a limited number of spines from both sexes with a high average age, resulting in large standard deviations, which potentially makes validation steps easier. However, based on our current findings, we propose that computational models that use specimen-specific spinal geometry may not be as accurate at predicting biomechanical outcomes as models that incorporate specimen- or at least population-specific material properties. It is plausible that specimen-specific models could predict misleading outcomes when modeling spinal injuries or surgical interventions. In other words, generic models based on small mixed-sex samples may not be robust enough to predict outcomes in specific patient populations. In this light, a modeling approach that focuses on developing a library of patient-specific models may better predict outcomes in matching populations than generic finite element models. We hope that the additional data presented in this study will serve to improve model validation and accuracy of patient- or population-specific models.
LIMITATIONS
This study has several limitations. Information and medical histories provided by tissue banks are limited. The donor body weights and heights may not be correct or representative, given that many donors lose large amounts of body mass near the time of death. In addition, donor tissue was screened to exclude spinal segments with severe disc degeneration; however, tissue specimens with some and varying amounts of disc degeneration were most likely included. Although all of the mechanical tests in this study used a consistent method, the tests applied pure bending moments without any compressive load components, which does not necessarily represent how the spine is loaded during activities of daily living. There may be a limitation of comparing data among specific lumbar levels that were tested as part of multi-segment specimens of different lengths. In this study, the L3-L4 level was common to all 85 spinal segments that were tested. However, disregarding sex, age, and other donor parameters, and based on a 1-way ANOVA, there was no statistical difference in L3-L4 FL-EX ROM when comparing means from the different segment lengths (P = .97). This suggests that ROM for a specific intact lumbar level is independent of the total length of intact segment being tested when using pure moment loads.
FUTURE STUDIES
An additional study including similar analyses involving cervical spinal segments is currently underway. Future studies with large data sets and regression analysis of biomechanical data collected during additional modes of loading (including compression) as well as analyses focused on the effects of instrumentation and surgical techniques are of interest.
CONCLUSIONS
We found significant correlations between the biomechanical behaviors (ROM, LZ, and SZ) of presumably normal cadaver spine segments and the corresponding donor demographics including sex, age, weight, and height. In addition, results from this study showed that geometric properties, including IVD height and vertebral body height, and material properties, specifically BMD, of the cadaveric spine segments are related to spine biomechanics. The biomechanical behavior of the spinal segment is more predictable when all of these variables are considered. Computational models of the spine that ignore patient demographics, geometry, and material properties may be limited.
ACKNOWLEDGMENTS
The authors thank Science Care; Research for Life; and student volunteers Alexander Bhatt, Meaneka Grewel, Wade Savage, Ved Narayan, and Veda Inamdar; and the staff of Neuroscience Publications at Barrow Neurological Institute for assistance with manuscript preparation.
Footnotes
DISCLOSURES and COI: None.
REFERENCES
- 1.Dreischarf M, Zander T, Shirazi-Adl A, et al. Comparison of eight published static finite element models of the intact lumbar spine: predictive power of models improves when combined together. J Biomech. 2014;47(8):1757–1766. doi: 10.1016/j.jbiomech.2014.04.002. [DOI] [PubMed] [Google Scholar]
- 2.Xu M, Yang J, Lieberman IH, Haddas R. Lumbar spine finite element model for healthy subjects: development and validation. Comput Methods Biomech Biomed Eng. 2017;20(1):1–15. doi: 10.1080/10255842.2016.1193596. [DOI] [PubMed] [Google Scholar]
- 3.Panjabi MM, Oxland TR, Yamamoto I, Crisco JJ. Mechanical behavior of the human lumbar and lumbosacral spine as shown by three-dimensional load-displacement curves. J Bone Joint Surg Am. 1994;76(3):413–424. doi: 10.2106/00004623-199403000-00012. [DOI] [PubMed] [Google Scholar]
- 4.Cook DJ, Yeager MS, Cheng BC. Range of motion of the intact lumbar segment: a multivariate study of 42 lumbar spines. Int J Spine Surg. 2015 Mar 5;9:5. doi: 10.14444/2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Muriuki MG, Havey RM, Voronov LI, et al. Effects of motion segment level, Pfirrmann intervertebral disc degeneration grade and gender on lumbar spine kinematics. J Orthop Res. 2016;34(8):1389–1398. doi: 10.1002/jor.23232. [DOI] [PubMed] [Google Scholar]
- 6.Kettler A, Rohlmann F, Ring C, Mack C, Wilke HJ. Do early stages of lumbar intervertebral disc degeneration really cause instability? Evaluation of an in vitro database. Eur Spine J. 2011;20(4):578–584. doi: 10.1007/s00586-010-1635-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Crawford NR, Brantley AG, Dickman CA, Koeneman EJ. An apparatus for applying pure nonconstraining moments to spine segments in vitro. Spine (Phila Pa 1976) 1995;20(19):2097–2100. doi: 10.1097/00007632-199510000-00005. [DOI] [PubMed] [Google Scholar]
- 8.Panjabi MM. Biomechanical evaluation of spinal fixation devices: I. A conceptual framework. Spine (Phila Pa 1976) 1988;13(10):1129–1134. doi: 10.1097/00007632-198810000-00013. [DOI] [PubMed] [Google Scholar]
- 9.Crawford NR, Dickman CA. Construction of local vertebral coordinate systems using a digitizing probe. Technical note. Spine (Phila Pa 1976) 1997;22(5):559–563. doi: 10.1097/00007632-199703010-00020. [DOI] [PubMed] [Google Scholar]
- 10.Crawford NR, Yamaguchi GT, Dickman CA. A new technique for determining 3-D joint angles: the tilt/twist method. Clin Biomech (Bristol, Avon) 1999;14(3):153–165. doi: 10.1016/s0268-0033(98)00080-1. [DOI] [PubMed] [Google Scholar]
- 11.Crawford NR, Peles JD, Dickman CA. The spinal lax zone and neutral zone: measurement techniques and parameter comparisons. J Spinal Disord. 1998;11(5):416–429. [PubMed] [Google Scholar]
- 12.Iida T, Abumi K, Kotani Y, Kaneda K. Effects of aging and spinal degeneration on mechanical properties of lumbar supraspinous and interspinous ligaments. Spine J. 2002;2(2):95–100. doi: 10.1016/s1529-9430(02)00142-0. [DOI] [PubMed] [Google Scholar]
- 13.Rodriguez-Martinez NG, Perez-Orribo L, Kalb S, et al. The role of obesity in the biomechanics and radiological changes of the spine: an in vitro study. J Neurosurg Spine. 2016;24(4):615–623. doi: 10.3171/2015.7.SPINE141306. [DOI] [PubMed] [Google Scholar]
- 14.Marnach ML, Ramin KD, Ramsey PS, Song SW, Stensland JJ, An KN. Characterization of the relationship between joint laxity and maternal hormones in pregnancy. Obstet Gynecol. 2003;101(2):331–335. doi: 10.1016/s0029-7844(02)02447-x. [DOI] [PubMed] [Google Scholar]
- 15.Meijer GJ, Homminga J, Veldhuizen AG, Verkerke GJ. Influence of interpersonal geometrical variation on spinal motion segment stiffness: implications for patient-specific modeling. Spine (Phila Pa 1976) 2011;36(14):E929–E935. doi: 10.1097/BRS.0b013e3181fd7f7f. [DOI] [PubMed] [Google Scholar]