Combining in silico Design and Biomimetic Assembly: A New Approach for Developing High-Performance Dynamic Responsive Bio-nanomaterials

Abstract

Major challenge remains in the design and fabrication of artificial hierarchical materials that mimic the structural and functional features of these natural materials. Here, we demonstrate a novel biomimetic strategy to assemble hierarchical materials from biological nano-building blocks. The constituents and structures of the materials were designed by multiscale modeling and then experimentally constructed by multiscale self-assembly. The resultant materials show nacre-like structures with high mechanical performance. For example, the strength and toughness of 4:16 SNF/HAP:CNF nanocomposites reached 281±14 MPa and 22±2 MJ m⁻³. The strength was approximately 2–3-fold higher than that of natural nacre. The toughness was more than 10 times higher than that of natural nacre and even better than most nacre-like nanocomposites. In addition, these SNF/HAP:CNF nanocomposites can be programmed into “grab and release” actuators due to the gradient structure of the nanocomposites as well as the high water sensitivity of each components, and thus show potential applications in design of novel third generation biomaterials for potential clinical applications. In addition, this “in silico design and biomimetic assembly” route represents a rational, low-cost, and efficient strategy for the design and preparation of robust, hierarchical, and functional nanomaterials to meet a variety of application requirements in bio-nanotechnologies.

Graphical Abstract

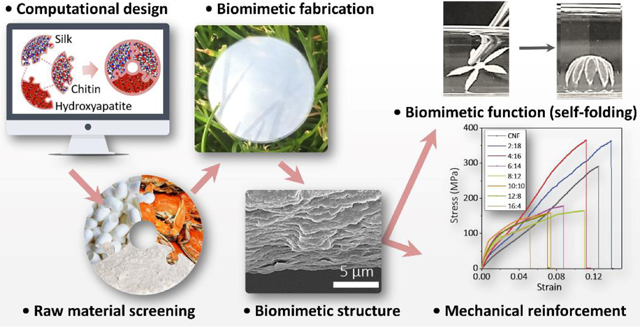
Natural structural materials are built from limited components, but their mechanical performance, such as strength and toughness, exceed artificial counterparts^[1–6]. The secret of success is their multiscale hierarchical structures. Nacre, for example, is composed of biopolymers (e.g., proteins and polysaccharides) and aragonites, which are organized into a hierarchical brick-and-mortar structure to optimize mutual interactions and to combine properties towards longer length scales^[2,7]. Layer-by-layer techniques^[8–10], self-assembly methods^[11–14], and slurry-based freeze-casting/magnetic-field-assisted slip-casting and sintering techniques^[15–19] are common approaches used to replicate the hierarchical structures of nacre. However, these methods are based on synthetic materials and artificial engineering techniques that are tedious and energy-intensive. In contrast, organisms build their structures through more elegant strategies, including self-assembly, biomineralization and alternating deposition of biopolymers and nanominerals^[2]. All of the processes occur at ambient temperature and pressure with optimized energy dissipation. Therefore, “assembly-and-mineralization” methods ^[20], which combine preformed laminated matrices and in situ mineralization techniques, have been accessed to mimic natural processes to generate nacre-like materials, but focus on producing materials with structural and mechanical characteristics similar to natural materials.

In practice, the structural hierarchy of natural materials not only enhances mechanical performance but also endows functions to dynamically interact with the surrounding environment^[3]. For instance, seed pods^[21], conifer pinecone ^[22], and ice plant seed capsules^[23], which are constructed from cellulose nanofibrils with hierarchical and gradient arrangements, can change shape and release seeds upon changes in the humidity of the environment. Some frontiers in biomimicry have gone further to mimic the functionalities of these biological materials. Self-shaping ceramics^[24], self-shaping Al₂O₃/iron oxide based nanocomposites^[25], and 4D printing shape-morphing systems^[26] have been developed, but these systems are derived from synthetic materials and/or artificial engineering techniques. In a word, although a variety of studies have been explored to mimic the structures and/or functions of natural materials, bridging from the nanoscale to the macroscale and using biomimetic processes to create high-performance materials with preprogrammed functions remains a significant challenge^[1]. Herein, we established an “in silico design and biomimetic assembly” strategy to build nacre-like nanomaterials, where multiscale modeling serves to identify material selection and optimization, and three biomimetic processes (i.e., protein self-assembly, biomineralization and vacuum-assist deposition) are used for experimental fabrication. This new strategy was successfully utilized to reproduce the structural hierarchy, mechanics, and functions of natural structural materials, while also mimicking the approaches and methodologies that organisms use to form their materials (i.e., materials selection, design, and assembly).

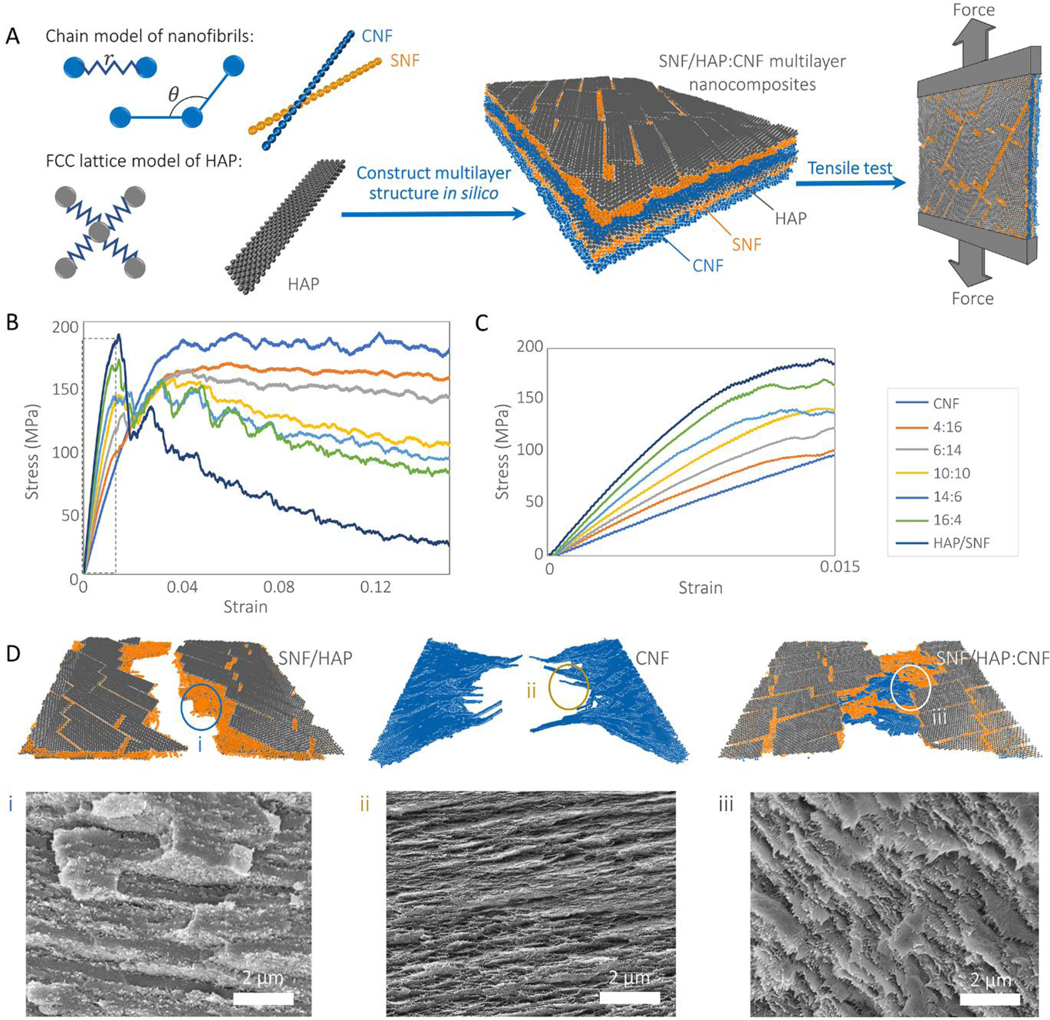
Raw material screening and formula optimization usually are the initial and the essential steps in material design. Proteins and calcium minerals are two of the basic components in bone and nacre. Moreover, our previous studies have predicted that protein/calcium mineral dispersions can form multilayer structures in vitro if the interactions between the protein/calcium minerals are weaker than the interactions between the components themselves^[27]. This prediction was verified by experimental observations, where several protein/hydroxyapatite nanocomposites were successfully assembled into nacre-like structures^[27,28]. Therefore, our raw material screening directly starts from silk nanofibril/hydroxyapatite (SNF/HAP) systems (Scheme 1). The screening was carried out by multiscale modeling (Figure 1 and Experimental section), which predicted the composition-structure-property relationships of a material with atomic-level accuracy. We developed coarse-grained models for SNF and HAP, respectively, according to parameters obtained from full-atomic simulations (Figure S1, S2 and Table S1, Supporting Information), and then were combined to reconstruct multilayer SNF/HAP membranes for tensile stress-strain assessments (Figure 1A). Figure 1B and C disclose the brittle features of SNF/HAP nanocomposites. Although these material systems have high initial stiffness that stems from the rigid characteristics of the HAP phase (Figure 1C), the tensile stress drops dramatically after a strain of ~0.015, followed by failure (breaking) under further tensile load. An examination of the simulation snapshots (Figure 1D) reveals that failure occurred along the edges of HAP nanoplates with fracture of SNFs. These results agree with the rigid feature of SNFs in the dry state^[27,28] and are consistent with previous experimental findings in which the strain of amyloid fibril/HAP and SNF/HAP nacre-like membranes was only ~1.5% and 3±1%, respectively^[27,28]. The strength of these nanocomposites was only ~11.5 MPa and 96±4 MPa, respectively, much weaker than hard bone (150 MPa^[29]) and nacre (140 MPa ^[30]). This gap in mechanical performance between human-engineered vs. native engineered composites drives the desire to rethink initial materials selection, especially, when the focus is on the mechanical properties of the designed materials.

Scheme 1. Guidelines of mechanical-enhanced multilayer SNF/HAP:CNF bio-nanocomposite design.

Figure 1. Multiscale models of SNF/HAP:CNF nacre-like membranes.

(A) SNF and CNF are modeled as chains of beads connected by harmonic bonds and angles. HAP nanoplatelets are modeled as beads in FCC lattice connected by harmonic bonds. These three components are assembled layer-by-layer to mimic the material structure create by experiments, which is further put into tensile loading to assess the mechanical responses. (B) The stress-strain responses of membranes with different mass ratios under tensile loading condition. (C) The stress-strain curves of membranes with different mass ratios under tensile loading condition with stain < 0.015 (the black dashed frame region in figure B). (D) The snapshot shows the blunt fracture surface of CNF/HAP membrane, fibrils pulled towards the loading direction in CNF and chitin fibrils from bridging in SNF/HAP:CNF composite. The insert SEM images are the cross-sectional morphologies of SNF/HAP:CNF membranes after tensile failure. (i) SNF/HAP membrane, (ii) CNF membrane, and (iii) 4:16 SNF/HAP:CNF membrane.

Besides the protein and biomineral components, chitin nanofibrils (CNF) are another fundamental component in biological materials^[31] and are critical for toughening of nacre and shrimp/crab shells^[2,31]. The ductile features of CNFs were confirmed by pristine CNF membrane simulations. Instead of being stressed to fracture as in the SNF and SNF/HAP system, the CNFs were strong enough to induce nanofibril sliding along adjacent neighbors. As a result, the CNF membrane was still intact at the strain of ~0.05, where the SNF/HAP system failed (Figure 1B and C). Afterward, the inter-fibril sliding events provided a sustained stress plateau regime (Figure 1B), which was the major mechanism of consuming energy during the failure process.

The CNF membranes showed a higher and longer stress plateau regime than the SNF/HAP system (Figure 1B). The material was still intact at the strain of ~0.05 where the SNF/HAPs failed (Figure 1B and D). Based on these findings, we built a three-component model by integrating CNF into SNF/HAP to predict the potential mechanical contribution of CNFs for the SNF/HAP:CNF system. The stress level of the plateau regime of the ternary nanocomposites was higher than SNF/HAP system even when only a small number of CNFs was added (Figure 1B). In the stress plateau, a continuous CNF layer held the membrane together even when the SNF/HAP layer failed (Figure 1B). Inter-fibril sliding (Figure S3A, Supporting Information) and CNF pulling (Figure 1D) were observed in the membrane, which dominated the stress plateau regime and toughened the membranes. Additionally, the ternary hybrid membranes showed a higher initial modulus than CNF membranes. These results indicated that the strength and toughness of ternary nanocomposites could be increased synergistically by adding CNF into the SNF/HAP system. We also estimated the effect of adding cellulose nanofibrils (CeNFs) on SNF/HAP membrane performance (Figure S4 and Table S2, Supporting Information). CeNF and CNF have similar structures, and both have high stiffness and strength along the fibril, originating from the continuous covalent bonding^[2]. As presented in Figure S4, CeNF has similar toughening effects as CNF for SNF/HAP system but with higher modulus, because CeNF is much stiffer than CNF^[2]. Therefore, these modeling results confirmed that the introduction of a material phase with sufficient inter-fibril sliding was critical for producing toughness enhanced material.

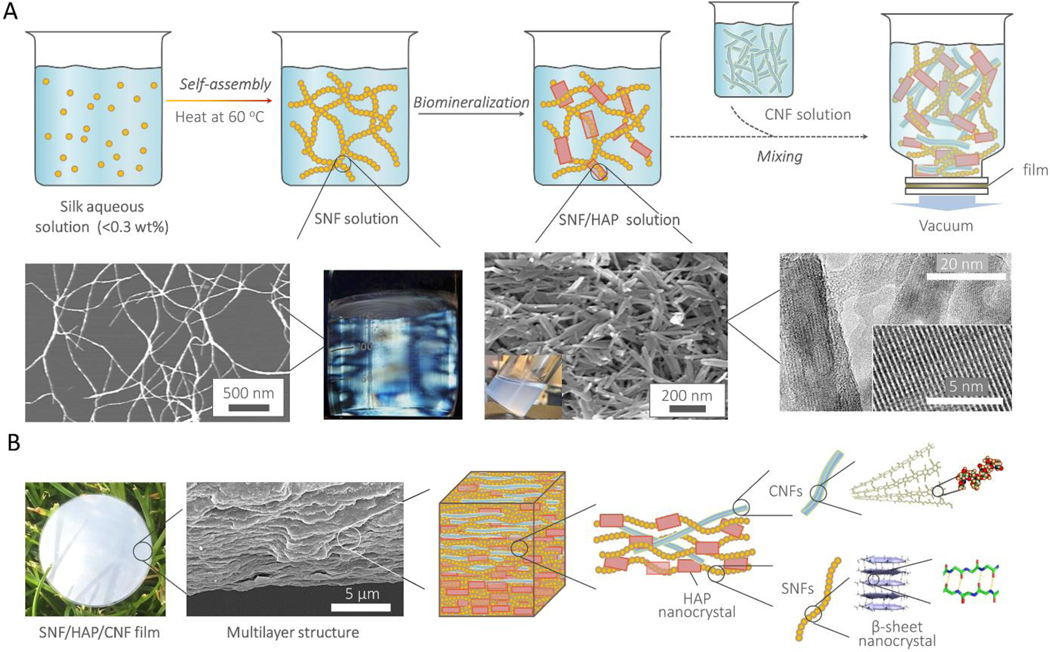
According to the computational predictions, we selected SNF, HAP, and CNF as raw materials to experimentally form nacre-like nanocomposites (Scheme 1). Inspired by natural processes for constructing materials^[2], we developed a three-step biomimetic assembly route for experimental fabrication, which integrated self-assembly, biomineralization, and alternative deposition (Figure 2A). In the first two steps, we followed our recently developed methods for generating multilayer membranes^[27]. Briefly, the aqueous silk solution (0.1–0.2 wt%) was incubated at 60°C for one week to assemble silk proteins into SNFs with a height of 3–5 nm and contour length up to 5 μm (Figure S5, Supporting Information). Then, the SNFs were used as templates to grow HAP nanocrystals, a process akin to biomineralization in bone. The resultant HAP nanocrystals were well-separated in solution and showed uniform morphology with lengths about 100–300 nm (Figure S6, Supporting Information), similar to the morphology of HAP nanocrystals in bones^[2].

Figure 2. The pathway to fabricate the SNF/HAP:CNF nacre-like membranes, and their hierarchical structures.

(A) Scheme of the preparation steps of SNF/HAP:CNF membranes. The first two pictures in the middle row are AFM images of SNFs. The insert visual image is the SNF solution under polarized light. The third and fourth images in the middle row are SEM and TEM images of biomineralized HAP nanocrystals. (B) The hierarchical structures of the SNF/HAP:CNF nacre-like membranes. The first picture is the visual image of the membrane. The second picture is the cross-sectional SEM image of 10:10 SNF/HAP:CNF membrane, which shows nacre-like highly ordered multilayer structures. The molecular and atomic structure of CNF reproduced from permission of ref [5]; the β-sheet and their related atomic structures reproduced from permission of ref [6].

In the third and last step, SNF/HAP hybrids combined with different weight ratios of CNFs (Figure S7, Supporting Information) were assembled into nacre-like membranes via vacuumassisted deposition (Figure 2B and Figure S8, Supporting Information). After these three biomimetic processes, a protein-chitin-biomineral system, as found in natural materials^[2], were assembled into macroscopic materials with structural hierarchies and length scales similar to that of bone and nacre, where nanometer ordering within and with the SNFs and CNFs, and micrometer-scale ordering in the stacking of the nanofibrils and HAPs (Figure 2B).

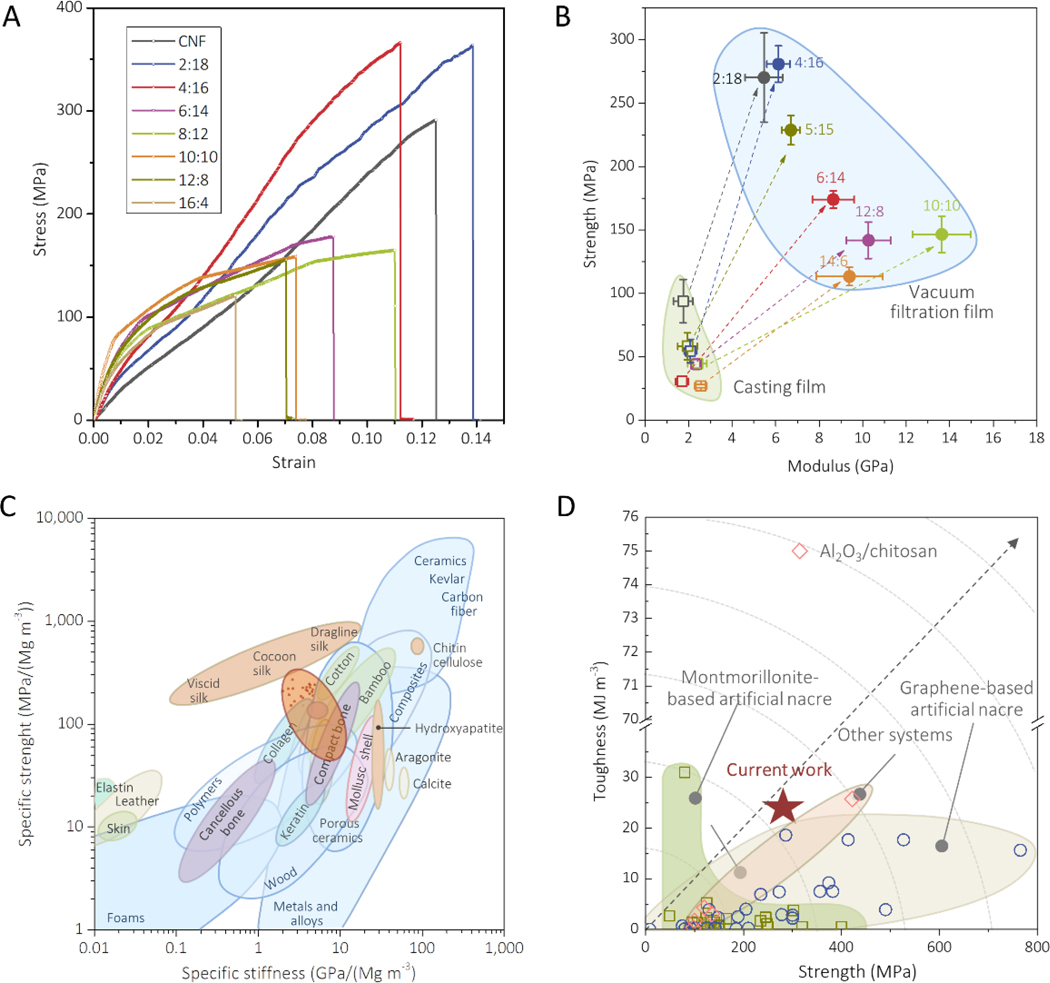
In-plane tensile tests were carried out to determine the mechanical properties of the SNF/HAP:CNF nanocomposites (Figure 3). The hybrid membranes were labeled according to the SNF/HAP:CNF weight ratios. For example, 2:18 means that the weight ratio between (SNF/HAP) and CNF was 2:18. In all cases, the weight ratio of SNF and HAP was fixed as 6:4, because the mineralized HAP crystals appeared most uniform dimension in this ratio. Figure 3A presents typical stress-stain curves of the SNF/HAP:CNF membranes, which agreed with the computational predictions. The composites displayed synergetic improvement of strength, modulus, and toughness. All mechanical parameters were higher than that of the individual materials or the binary components (Table S3, Supporting Information). For example, the tensile strength and toughness of SNF/HAP composites were 96±4 MPa and 2±1 MJ m⁻³, respectively, while the 4:16 SNF/HAP:CNF composites reached 281±14 MPa and 22±2 MJ m⁻³, respectively. For the 4:16 SNF/HAP:CNF composites, the strength was approximately 2–3-fold higher than that of natural nacre and bone. The toughness was more than 12 times higher than that of natural nacre and 18 times higher than that of the bone^[4,32]. By progressively adding CNFs, the toughness of the membranes was increased from 4±1 to 24±6 MJ m⁻³, with a corresponding increase in strength from 113±7 to 270±35 MPa, when the SNF/HAP:CNF weight ratio went from 16:4 to 2:18. The modulus was also modulated by the SNF/HAP:CNF ratio, where HAP promoted stiffness, with the modulus evolving from 4.4±0.7 to 9.1±0.9 GPa when the ratio of SNF/HAP:CNF was changed from 2:18 to 10:10 in the composites. Remarkably, the SNF/HAP:CNF system with ratios between 6:14 and 16:4 even had higher modulus than that of the SNF/HAP composites (7.7±0.2 GPa). The computationally predicted toughening mechanism, namely inter-sliding of each component (Figure S3B, Supporting Information), was observed from the fracture surfaces of the samples, where the nanobuilding blocks pulled towards the load directions (SEM images in Figure 1D). Compared to membranes with a random arrangement prepared by solution casting (Figure 3B, Figure S9 and Table S4, Supporting Information), the strength and modulus of these multilayer membranes were enhanced 4–5 and 5–8 times, respectively, revealing that the hierarchical structure endowed high mechanical performance to the resultant materials.

Figure 3. Mechanical performance of SNF/HAP:CNF nacre-like membranes.

(A) Stress-strain curves of SNF/HAP:CNF membranes with a different weight ratio of SNF/HAP and CNF. (B) Comparison of Young’s modulus and strength of the SNF/HAP:CNF membranes made by casting and vacuum-filtration approaches. (C) Comparison of the specific values (that is, normalized by density) of strength and stiffness (or Young’s modulus) of SNF/HAP:CNF membranes with natural and synthetic materials. Ashby plot of natural and synthetic materials are adapted from ref [32]. (D) Comparison of the strength and toughness of SNF/HAP:CNF membranes with other artificial nacres. The related data is extracted from refs [11,30,33–68].

After normalizing the strength and stiffness of all composites by density (Figure 3C), the values fell to the center of the Ashby plot^[32], indicating the mechanical performance of these composites was comparable with and even superior to natural structural materials. Figure 3D summarizes the mechanical performance of the SNF/HAP:CNF membranes in comparison with other materials with nacre-like structures from the literature^{[11,30,33–68]}. These new composites exhibited an improved balance of strength and toughness than most of the nacre-like materials nanocomposites, such as layered binary GO/polymer^[33–52] and clay/polymer composites^[53–64], except for two nanocomposites consisting of Al₂O₃/chitosan (300 MPa and 75 MJ/m³)^[11] and sodium alginate/tungsten disulfide (422.5 MPa and 25.76 MJ/m³)^[68]. These results demonstrated that through the simplified use of a natural chemical palette of inexpensive ingredients, protein, polysaccharide, HAP, high mechanical performance materials can be achieved, even though the properties of the individual components are relatively meager in comparison to the composite system.

Of note, the mechanical values (such as stiffness) obtained from experiments and modeling are different due to the differences between the modeling and experimental systems of SNF/HAP:CNF nanocomposite. For example, the differences are apparent in the heterogeneity of components and in defect sizes. Owing to high computational costs, it remains a significant challenge to cover the distribution of dimensions of the components in coarse-grained modeling, which required too many fibrils and nanoplatelets that are beyond simulation capacity. As a compromise, in this study the model applied uniform dimensions for each component, but still reached the scale in the experimental approach, and was reliable to study deformation mechanisms. In addition, the introduction of uniform dimensions of the components comes with a drawback in that it was not possible to create a sufficiently dense structure with fully randomly distributed nanofibrils and nanoplatelets, because the stacking of those stiff components would create too many voids. This is not the case in the experimental approach, where shorter nanofibrils can fill the void space created by stacking of longer nanofibrils. Therefore, the nanofibrils or nanoplatelets in the model were placed parallel to each other within the same layer, and the feature of random distribution was then accounted for by arranging the orientations of each component layer so that they did not have a preferred orientation. This arrangement of each component can mostly mimic the fully random orientations in the experiment. As a result, this model effectively revealed a rational strategy for improving the toughness of the SNF/HAP system. Namely, introducing the third component related to inter-fibrillar slip.

Careful examination of the cross-section of the 10:10 SNF/HAP:CNF membranes (Figure 4A-C, and Figure S10, Supporting Information) revealed that the three components formed a gradient distribution along cross-section direction. Most SNF/HAP composites settled at the bottom layer (Figure 4B) and more CNFs remained at the top (Figure 4C) because of the different stiffness, density and interfacial interactions between the components^[27]. As mentioned, the gradient structures in seed pods can trigger dynamic deformations^[3,21–23], thus, we further assessed the self-shaping and self-folding behavior of the SNF/HAP:CNF nanocomposites. As shown in Figure 4D and Movie 1, when a rectangle sample was placed in water, the sample immediately stood up. More remarkably, after the membrane reached the largest angle of deformation, ~25°, it flattened again gradually and self-folded in the opposite direction. The final sample maintained a balance in the crescent shape with a deformation angle of −15°. Such nonlinear folding behavior is proposed as the attribution of the heterogeneous water absorption rate as well as the difference of material volume ratio after full absorption. Accordingly, we established a coarse-grained bilayer model to simulate the heterogeneous swelling of the different material layers. The equilibrium length constant of the lattice structure of each material layer was defined as an explicit exponential function of the simulation time, $a_i(t)=a_{i,end}+(a_0-a_{i,end})\exp (-\frac{t}{t_{i,0}}),$ with different converging rate (t_1,0 < t_2,0) and final equilibrium length $(a_{1,end}<a_{2,end})$ for the different layers (Figure 4E, inserted plot). The simulation snapshots (Figure 4E) showed that the bottom layer swelled faster than the top layer, leading to the upward folding at the beginning. The folded structure yielded the largest deformation at time (t₀), corresponding to the largest mismatch in lattice constant. After t₀, the mismatching strain of the two materials became smaller and was dominated by the final swelling volume of the materials, yielding the refolding in the opposite direction. This folding-unfolding-refolding process can be programmed into a ‘grab-and-release’ device. A four-point-star shape was designed in silico to hold a rigid spherical object with a diameter equal to the half dimension of the device. We have tested the grabbing force in silico, and found that the peak grabbing force can be continuously tunable through regulation of the mismatching strain (ε₀) and stiffness (E) that are governed by the water absorption rate and material composition of the membrane (Figure S11, Supporting Information).

Figure 4. Self-folding behaviors of SNF/HAP:CNF nanocomposites.

(A-C) Cross-section SEM images of 10:10 SNF/HAP:CNF membrane. (B and C) are SEM image of the bottom (B) and the top layer (C) of the 10:10 SNF/HAP:CNF membrane. (D) The relationship of time and deformation angle. The deformation angle is defined by the angle between the horizontal line and the tangent of the left side of the sample. (E) The modeling snapshots of the 10:10 SNF/HAP:CNF nanocomposites in responding to water absorption (left) and “grab and release” design (right). The inserted plot: the lattice constants of the bottom and top material layers as functions of the simulation time, where t₀ in the plot corresponds to the time that the two materials have the largest mismatching strain ε₀ and t₁ correspond to the time that the two materials have no mismatching strain. (F-H) The programmable self-folding process of the 10:10 SNF/HAP:CNF membranes with different thicknesses and shapes. The thicknesses of the membranes in (F), (G), and (H) are 10 μm, 30 μm, and 50 μm, respectively. The time scales of (F), (G), and (H) are ~0.8 s, ~1.75 s, and ~1.8 s, respectively.

These computational programmed ‘grab-and-release’ processes were observed particularly in four-point-star 10:10 SNF/HAP:CNF membranes (Figure 4F-H and Movie 2 and 3). The 10 μm membranes underwent a complete self-folding-unfolding-refolding process once they were immersed in water. In addition, the deformation behavior of 10:10 SNF/HAP:CNF membranes was directly related to the thickness of the membrane. The self-folding behavior was only detected with 1–200 μm thick membranes. In this range, the self-folding processes gradually changed from a three-stage deformation (self-folding-unfolding-refolding) to one stage deformation (self-folding) when the thickness was increased from 10 to 50 μm. The “unfolding and refolding” stages were not detected with 50 μm thick membranes. However, by increasing membrane thickness the self-folding process was more gradual, graceful and controllable (Figure 4F-H). For instance, a 50 μm flower-like pattern was able to self-fold to a perfectly closed “flower” in water (Figure 4H and Movie 4) and all the “petals” were deformed synchronously, while the deformation of “petals” in 10 μm four-point-star specimen was asynchronous. These self-folding processes were reversible once the hydrated membrane was dried and flatted. Furthermore, by controlling the thickness and the shape of SNF/HAP:CNF nanocomposites, different self-folding patterns were achieved, including petals, spirals, and crescents (Movies 1, 5 and 6).

In this study, we exploited a general “in silico design and biomimetic assembly” route to achieve the de novo design of biomimetic materials. This route starts from computational modeling, which provides predictions of the mechanical performance of SNF/HAP composites, which had been measured in our previous experiments. Therefore, the accuracy of the model was initially verified through comparison of modeling and experimental results. Then, these trained models were used to optimize potential component combinations. This ‘virtual prediction’ process saved time and costs of experiments for selecting valid starting components^[69].

At the next stage, according to the optimized outputs from the simulations, we fabricated a SNF/HAP:CNF nanocomposite via biomimetic experimental assembly. The mechanical performance of these nanocomposites verified the in silico predictions. For example, their strength, modulus, and toughness are indeed higher than the individual components or the SNF/HAP composites. Meanwhile, the experimental procedures and material characterization provided further feedback to the modeling designs through an iterative process. This multicycle optimization route represents an advanced predictive tool to improve the efficiency of new material designs and production, avoiding trial and error experiments^[69].

Moreover, the computational model was effective for functional designs. As a prototype in the present study, the modeling successfully programmed the self-folding behavior of SNF/HAP:CNF membranes. This ability to “dial in” specific properties establishes an exciting new opportunity to add multifunctionality to nanocomposite materials, thus enabling unique product designs that efficiently combine mechanical and functional performance. This combination of virtual and experimental design provided a new route for developing cost-effective biomimetic materials, with implications for broader material designs as well.

Experimental Section

Coarse-grained model for SNF/HAP:CNF membranes in-plane tension simulations:

Full atomistic models of each phase were built to evaluate the mechanical properties and interaction strength at the atomistic level, which were set as the targets for training the coarse-grained model. For hydroxyapatite (HAP), a 3.8×3.2×3.4nm block was created from its unit cell. Periodic boundaries were applied in all 3 directions to represent an infinite model. The structure was equilibrated under NPT ensemble at 300 K and 1 a.t.m. It was further loaded in [001] with a strain rate of 10⁸/s. The stress-strain response was then obtained as shown in Figure S1A, Supporting Information. An anti-parallel beta-sheet crystallite was created basing on the Protein Data Bank with identification code 2slk^[70]. The crystallite contained 5 layers of beta-sheet strands. NVT ensemble was applied to control the temperature at 300K. Steered Molecular Dynamics was used to load the crystallite. As shown in Figure S1B, Supporting Information, the left ends of 3 strands were fixed during the simulation, while the right ends of the other two strands were pulled at 0.5m/s with a spring constant of 10 kcal/(mol·Å²). The result in Figure S1B, Supporting Information, shows the modulus to be 12 GPa, which is a linear fit of the elastic region, and the crystallite failed at the strain of 0.0667 (Figure S1B, Supporting Information). A 5 nm long chitin fibril containing 19 polymer chains^[71] was created as shown in Figure S1C, Supporting Information. After equilibration runs at NVT ensemble, the fibril was loaded by pulling the two ends of the fibril with a strain rate of 10⁸/s. The modulus was calculated from the elastic regime, which is 50 GPa. The crystal eventually failed at strain of 0.08 with the cleavage of the glycosidic bonds. The interaction energy between each pair of materials was calculated as the potential energy difference by putting two blocks far from each other and closely attached after equilibrations (Figure S1D, Supporting Information). The [110] surface of crystalline chitin ^[71,72] were chosen as the exposed surfaces that interacting with other phases. A neutral [100] surface of HAP^[73] was constructed. For all the full-atomistic simulations above, the INTERFACE force field^[73] and the CHARMM force field^[74] were used, except that ReaxFF^[75] was applied to the tensile loading on the chitin crystal in order to obtain the fracture strength. The timestep was chosen as 1 fs and the cutoff for the non-bonded interactions was 12 Å. The particle–particle particle–mesh (PPPM) method was used to compute the long-range columbic interactions and the SHAKE algorithm^[76] was applied to constrain high frequency dynamics from hydrogen-related energy terms. All the simulations were performed on the Large-scale Atomic/Molecular Massively Parallel Simulator (LAMMPS)^[77]. Various strain rates have been tested to ensure the rates chosen in the above simulations show converged results, which also compare well with previous simulation studies^[78,79].

In the coarse-grained model, all the materials were modeled by beads connected by bonds (Figure 1A). The size of the beads and the equilibrium distance of the bonds were set to be r₀ = 3nm, which is close to the size of elementary fibrils of chitin and silk^[80–82]. For the HAP nanocrystal model, the beads were arranged into an FCC lattice to form the nanoplates and nearest neighbors were connected by morse bond potential:

$$U_{bond}=D{[1-e^{-\alpha (r-r0)}]}^2$$ (1)

[111] direction was perpendicular to the nanoplate’s surface so that the beads were closed packed in that plane and [110] direction was along the longest axis of the nanoplate. A coarse-grained HAP nanoplate was tensile loaded and the parameters were trained to reproduce the tensile response obtained from full-atomistic simulations (Figure S1A, Supporting Information). For SNF and CNF, the beads were connected by harmonic bonds:

$$U_{bond}=K_t{(r-r_0)}^2$$ (2)

and angles

$$U_{angle}=K_b(1+cos(\theta ))$$ (3)

together to form a chain and the parameters were calculated based on the tensile modulus and geometry of the fibrils:

$$K_t=EA/\left(2r_0\right)=\pi r_{0}E/8$$ (4)

$$K_b=EI/r_0=\pi r_0^{3}E/64$$ (5)

where, E is the tensile modulus of the fibril. The bonds connecting SNF beads and CNF beads broke at r = 3.2 nm and 3.25 nm, respectively, based on the full-atomistic simulations. Non-bonded interactions between different molecules were modeled by a Lennard-Jones potential:

$$\Phi (r)=4\epsilon [{(\sigma /r)}^{12}-{(\sigma /r)}^6]$$ (6)

The energy well depth was calculated from the adhesion energy between each pair of materials:

$$\epsilon =\gamma A,$$ (7)

where γ is the adhesion energy calculated from full-atomistic simulations and $A=r_0^2/\sqrt{3}$ is the interaction area between two beads, by assuming the fibrils were parallelly arranged in triangular lattice. The distance parameter was set as $\sigma =r_0/\sqrt[1/6]{2}$ to ensure the equilibrium distance between neighboring beads was r₀. The cutoff was set to be $\sqrt{3}{r}_0$ to ensure only nearest neighbors interact with each other. The standard Lennard-Jones potential was further shifted by a linear function so that both the energy and force go continuously and smoothly to zero at the cutoff distance^[83]:

$$U=\Phi (r)-\Phi (r_c)-(r-r_c)\frac{d\Phi (r)}{dr}{|}_{r=r_c},$$ (8)

where $r_c=\sqrt{3}{r}_0$ is the cutoff distance. In order to keep the same energy depth and equilibrium beads’ distance after this modification, the Solver tool in Microsoft Excel software was used to calculate new parameters for the modified potential. All the parameters trained for the coarse-grained model were listed in Table S1, Supporting Information.

It is noted that the dimensions of the nanofibrils and nanoplalets are not uniform and have a broad distribution. Due to the limitations of computational cost, the size of the nanoplalet and the length of the nanofibrils were around 5×20×100 nm and 120 nm, respectively, which reached the scale of the samples prepared in the experiments. Although not all dimensions of the materials are covered in the modelling, the conclusions still hold since our model captures the main deformation mechanisms at the molecular scale. The materials were stacked layer-by-layer to form the composites (Figure S1E, Supporting Information). The fibrils and nanoplalets were placed parallel within each layer to obtain a sufficiently dense structure. The orientations of the different layers of each material phase were equally spaced from 0 degree to 180 degrees to account for the non-preference of a particular orientation in the experimentally synthesized samples. The number of layers of each material phase was adjusted to represent different material ratios, while the ratio between SNF and HAP was set at 6:4, the same as the experimentally synthesized composites. Trial simulations were performed on the CNF membrane model with various numbers of layers to verify that the minimum number of layers in the present study (20 layers, that is ~ 45nm in thickness) to ensure reliable results (Figure S2A, Supporting Information). With the fixed ratio of 6:4 between SNF and HAP, every layer of HAP should accompany 7 layers of SNF. Thus, the maximum number of layers of HAP were constrained to be 4. A minimum of 2 layers of HAP was applied to prevent the preferential orientation of HAP nanoplalets. Figure S2B, Supporting Information, shows that 2 layers of HAP are sufficient to capture the brittle response of the HAP/SNF composite. A slab of size ~ 250 nm × 300 nm was cut from the layered assembly to represent the composite membrane (Figure S1E, Supporting Information). Various lateral dimensions have been tested (Figure S2C, Supporting Information) to ensure that the selection of 250 nm × 300 nm is sufficient. After an equilibration running, the samples were loaded by moving two clamped regions at the two ends with a strain rate of 1×10⁷/s. Lower strain rates have been tested and the simulation results didn’t show significant difference (Figure S2D, Supporting Information), indicating the strain rate chosen here is appropriate. The timestep for the coarse-grained simulations was chosen as 10 fs. Stress-strain responses were recorded to assess the material properties and simulation snapshots helped to unravel the underlying molecular mechanisms. All of the simulations were performed under vacuum conditions to be consistent with the dry state in experiments.

Coarse-grained model for structural folding simulations:

FCC lattice was used to model the location of the mass beads (which locate at corners and face centers) and elastic spring was used to model the interaction between the nearest neighboring beads of the nanocomposite. The nanocomposite was simply modeled by two layers of materials. We simply modeled the effect of the water absorption of the two materials on material swelling by tuning the equilibrium length constant of the lattice structure as:

$$a_i(t)=a_{i,end}+(a_0-a_{i,end})\exp (-\frac{t}{t_{i,0}})$$ (9)

Where a_{0 = 0.35} mm is the initial lattice length without water absorption, a_1,end = 0.455mm and a_2,end = 0.555 mm are the equilibrium length constant of the bottom and top layers after full water absorption, respectively, and t_1,0 = 10 s and t_2,0 = 50 s are the time constants of the bottom and top layers used in simulations to reflect how quick the materials absorb water, respectively. The Young’s modulus of the material (E) was defined by the elastic constant of the spring (k) as $E=\frac{16k}{3a}.$ We simply assumed the two materials were of the same Young’s modulus after absorbing water and start with E = 50 MPa to define the spring constant. The value of E was varied from 5 MPa to 50 MPa and no significant effect on the folding-unfolding-refolding process was found. Using this material model, we modelled the nanocomposite of 0.5 mm in thickness (each layer of 0.25 mm in thickness) at the beginning as an expanded pyramid shape. The central square has 7 mm edge length and each triangle on the 4 sides has 20 mm in height. Molecular dynamics simulations of this coarse-grained model were run with time step of 0.000005 s. A spherical nanoindenter was used to represent the spherical object and measure the grabbing force during the simulation.

Preparation of silk nanofibril (SNF) solution:

Bombyx mori (B. mori) silkworm cocoon silk fibers were degummed by boiling in two 30 min changes of 0.5% (w/w) NaHCO₃ solution. Then the degummed silk fibers were washed with distilled water and allowed to air dry at room temperature. Next, a 10 % (w/v) solution of degummed silk fibroin (SF) in aqueous 9.3 mol L⁻¹ LiBr solution was prepared by heating to 60°C for 1 h. This solution was dialyzed with deionized water at room temperature to yield SF solution with a protein concentration ~5 wt %. The detail processes can be found in ref ^[84]. In order to grow SNFs, this solution was further adjusted to 0.1–0.2 wt% SF in aqueous solutions and incubated without perturbation at 60°C over 7 days. The structural details of SNFs were characterized by Atomic Force Microscopy (AFM) (Asylum Research, Oxford Instruments Company, Santa Barbara, CA).

Synthesis of hydroxyapatite (HAP) nanocrystals via biomineralization approach:

SNFs were used as capping agents and templates for mineral formation and growth. Specifically, 6 mL 0.2 M CaCl₂ was added to 100 mL SNF solution (0.1 wt%) under continuous stirring or agitation. Five minutes later, 6 mL 0.2 M Na₂HPO₄ was introduced, and the mixture was incubated at 37°C for one week to grow the HAP nanocrystals. The synthetic HAP nanocrystals were confirmed by X-ray diffraction (XRD) and FTIR spectroscopy measurements (Bruker D8 Discover diffractometer with the 2D detector of GADDS, Bruker, Karlsruhe, Germany. The experiment was performed at MIT Center for Materials Science and Engineering). Their structural features were disclosed by Ultra 55 field emission scanning electron microscopy (SEM) (Carl Zeiss AG, Oberkochen, Germany).

Synthesis of Chitin nanofibril (CNF) via TEMPO-mediated oxidation:

TEMPO-mediated oxidation was carried out with the following steps. First, 1g chitin powder was suspended in 100 mL water with containing 0.016 g TEMPO (0.1 mmol) and 0.1 g sodium bromide (1 mmol). Then, the oxidation reaction was triggered by adding the desired amount of NaClO solution (10 mmol of NaClO per gram of chitin) at room temperature. During the reaction, the pH of the slurry was maintained at 10, achieved via continuous addition of 0.5 M NaOH using a pH-Stat titration system. Once consumption of the alkali was complete, the oxidation was quenched by adding a small amount of ethanol. Afterward, the mixture was adjusted to neutral pH by adding 0.5 M HCl, followed by centrifuged at 12,000 g for 5 min to remove the supernatant. The centrifugation step can be repeated several times to remove all soluble impurities. A water-insoluble TEMPO-mediated oxidized chitin pulp was obtained in this process and the wet pulp was suspended in water at 0.1–0.2 wt% and treated by ultrasonic homogenization at 19.5 kHz and the 300 W output power (7 mm in the probe tip diameter, US-300T, Nihonseiki, Japan) for 15 min to yield CNF aqueous solution.

Preparation of SNF/HAP:CNF membranes:

All of the nacre-like SNF/HAP:CNF membranes were fabricated by vacuum filtration of the SNF/HAP:CNF dispersions through a Sigma-Aldrich vacuum filtration assembly and polycarbonate filtration membranes (pore size, 200 nm; diameter 47 mm; Sigma-Aldrich). After drying, the membranes were easily removed from the support substrate. For the preparation of random distributed SNF/HAP:CNF membranes, the well-mixed SNF/HAP:CNF solution was cast onto a polyethylene plate and allowed to dry at ~25°C and 50% relative humidity to give membranes of an approximate thickness of 10 μm. The SEM tests confirmed no multilayer structure is in these membranes.

Characterization:

Atomic force microscopy (AFM) images of SNFs and CNFs were performed using an Asylum Research MFP-3D-Bio Atomic Force Microscope (Asylum Research, an Oxford Instruments Company, Santa Barbara, CA). Igor Pro 6.36 (WaveMetrics, Inc., Lake Oswego, OR) image analysis software was used to determine the heights of observed structures. Transmission electron microscopy (TEM) images of HAP crystal were collected by JEM-2011 at 200 kV. Scanning electron microscopy (SEM) images of SNF/HAP:CNF membranes were characterized by Ultra 55 field emission scanning electron microscope SEM (Harvard University Center for Nanoscale Systems) at an acceleration voltage of 5 kV. To prevent electrical charging, all the specimens were deposited with a 5-nm-thick Pd/Pt layer before observation. The X-ray diffraction (XRD) spectrum of HAP and SNF/HAP:CNF membranes were obtained using a Bruker D8 Discover diffractometer with the 2D detector of GADDS (MIT Center for Materials Science and Engineering). The experiments were performed using Cu Kα radiation (λ=1.54 Å) at 40 kV and 20 mA. The Fourier transform infrared spectroscopy (FTIR) spectrum of SNF/HAP membrane was collected by using Jasco FTIR-6200 spectrometer (Jasco Instruments, Easton, MD). For each measurement, 64 interferograms were co-added and Fourier-transformed employed a Genzel-Happ apodization function to yield spectra with a nominal resolution of 4 cm-1.