Prediction of Schizophrenia Diagnosis by Integration of Genetically Correlated Conditions and Traits

Abstract

Schizophrenia is genetically heterogeneous and comorbid with many conditions. In this study, we explored polygenic scores (PGSs) from genetically related conditions and traits to predict schizophrenia diagnosis using both logistic regression and deep neural network (DNN) models. We used the combined Molecular Genetics of Schizophrenia and Swedish Schizophrenia Case Control Study (MGS+SSCCS) data for training and testing the models, and used the Clinical Antipsychotic Trials for Intervention Effectiveness (CATIE) data as independent validation. We screened 28 conditions and traits comorbid with schizophrenia to identify traits as potential predictors and used LASSO regression to select predictors for model construction. We investigated how PGS calculation influenced model performance. We found that the inclusion of comorbid traits improved model performance and PGSs calculated from two traits were more generalizable in independent validation. With a DNN model using 19 PGS predictors, we accomplished a prediction accuracy of 0.813 and an AUC of 0.905 in the MGS+SSCCS data. When this model was validated with the CATIE data, it achieved an accuracy of 0.721 and AUC of 0.747. Our results indicate that PGSs alone may not be sufficient to predict schizophrenia accurately and the inclusion of behavioral and clinical data may be necessary for more accurate prediction model.

2. INTRODUCTION

Schizophrenia is a complex psychiatric disorder with heterogeneous etiology. Recent studies have identified more than one hundred risk loci (Schizophrenia Working Group of the Psychiatric Genomics Consortium 2014). However, it is not very clear how to utilize these findings from genome wide association studies (GWASs) to facilitate early and objective diagnosis. In the literature, there are reports that polygenic scores (PGSs) calculated at different P-value thresholds have different power predicting disease status (Vassos et al. 2016; So and Sham 2017). This suggests that PGS may be utilized to help diagnosis.

Schizophrenia, like many other complex disorders, is comorbid with many conditions and traits (Jeste et al. 1996; Buckley et al. 2009; Ferentinos and Dikeos 2012), including bipolar disorder, major depressive disorder, autism, cigarette smoking and other substance use disorders. Additionally, PGSs produced from educational achievement, neuro-cognitive traits, autoimmune disorders and cardiovascular diseases are correlated to that produced from schizophrenia (Bulik-Sullivan et al. 2015). These studies have led to the notion that many comorbid conditions and traits have shared genetic risks (Sivakumaran et al. 2011; Solovieff et al. 2013).

Prediction of schizophrenia is a challenge. In the literature, there are reports of prediction for schizophrenia outcomes using a variety of clinical and behavioral predictors (Bernardini et al. 2017), and many of these studies use only a small sample size. In these studies, logistic regression, Cox regression and support machine vector models are used, and genetic factors are included in some models in the form of family history or parental schizophrenia diagnosis. Because the subjects used in these studies are at risk or clinically high risk individuals, good performances (AUCs between 0.8–0.9) are reported. PGSs are also reported to be able to discriminate schizophrenia cases from controls (Vassos et al. 2016) and are associated with several clinical features (Ruderfer et al. 2014; Jones et al. 2016; Shafee et al. 2018; Sørensen et al. 2018). Although the potential utility of PGSs in the prediction of psychiatric disorders has been reviewed (Wray et al. 2014; So and Sham 2017), direct use of PGSs for schizophrenia diagnosis prediction has not been reported.

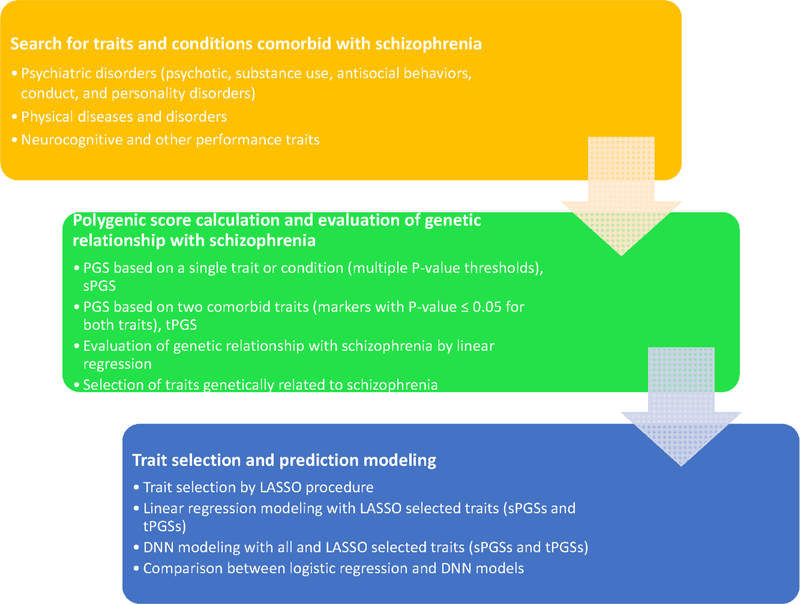
Since PGSs may be a useful tool for diagnosis, and schizophrenia share genetic risks with many other psychiatric conditions and traits, can we combine these partially shared genetic risks with the genetic risks of schizophrenia to build a better and more accurate prediction model for schizophrenia diagnosis? In this report, we explore the possibility that the inclusion of PGSs from comorbid conditions and traits would improve the performance of prediction model for schizophrenia diagnosis. We started with the testing of correlation between PGSs calculated from schizophrenia and other comorbid conditions and traits, and went through the evaluation for models built with logistic regression and artificial deep neural network (DNN) (Figure 1). Our analyses indicated that the inclusion of genetic risks from other comorbid traits did improve the performance. But even with the inclusion of the PGSs from comorbid conditions and traits, the prediction model was not sufficient for clinical application at this time. Some behavioral and clinical information may be necessary to build a clinically useful model.

Figure 1.

A flow chart illustrating the analyses of this study.

3. DATASETS AND METHODS

3.1. Datasets

We utilized the genetic data from two large studies of schizophrenia, the molecular genetics of schizophrenia (MGS)(Shi et al. 2009) and the Swedish Schizophrenia Case Control Study (SSCCS)(Bergen et al. 2012), as training and testing datasets, and utilized the Clinical Antipsychotic Trials for Intervention Effectiveness (CATIE) (Stroup et al. 2003; Sullivan et al. 2008) as independent validation dataset. Details of the datasets were described in supplementary materials.

3.2. Genotype imputation

In order to have the same markers across the MGS, SSCCS and CATIE datasets, we used the IMPUTE2 (Howie et al. 2012) to impute the missing genotypes with the 1000 Genome haplotypes as reference. Markers with the INFO value < 0.4 were filtered out. Details of imputation were described previously (Ware et al. 2016).

3.3. Comorbid trait selection and PGS calculation

Based on literature search, we selected psychiatric and physical diseases/traits that are comorbid with schizophrenia, and downloaded the summary statistics from various sources (Table S1). For each selected trait, we used PrSice (Euesden et al. 2015) to calculate PGSs (International Schizophrenia Consortium et al. 2009) at four thresholds: P-values ≤ 1e-2, 1e-3, 1e-4 and 1e-5. This was the typical way to calculate PGSs. Because it used only those markers associated with the trait of interest alone, we referred it as single trait PGS, or sPGS. We also calculated PGSs using a different strategy. Here we considered those markers showing association with two traits, one was schizophrenia, the other one was those candidate traits comorbid with schizophrenia. A PGS was calculated from those markers showing nominal association with both schizophrenia and the candidate trait, i.e., markers with P-value ≤ 0.05 in both GWASs of schizophrenia and the candidate trait, and the effects from the candidate trait were used as weights. Since this PGS was calculated from two traits, we referred it as two trait PGS or tPGS. The tPGS emphasized the candidate’s relationship with schizophrenia. In contrast, sPGS estimated the risks to the candidate trait alone.

3.4. Variant selection, model testing and validation

With the sPGSs, we evaluated the relationship between these candidate traits and schizophrenia diagnosis using logistic regression where schizophrenia diagnosis was the outcome and the sPGSs were the predictors. We used the LASSO regression to select those traits with a regression P-value ≤ 0.15 in the MGS+SSCCS dataset. These selected traits would be the predictors to be included in our prediction models. For tPGSs, a similar procedure was followed to select potential predictors. The tPGS model included a schizophrenia sPGS calculated at P-value of ≤ 1e-3. To evaluate and compare how much phenotype variation the models explained, we used a logistic regression model and calculated the Nagelkerke’s pseudo r². In the logistic regression model, we considered only additive effect, no interaction terms were included. The MGS+SSCCS dataset was used for model building, training and testing. Specifically, the MGS+SSCCSS sample was randomly divided into training (90%) and testing (10%) parts, and models were trained with the training part, then tested with the testing part. The CATIE data was used as an independent data to validate the model’s performance or generalization.

For the DNN prediction model, we took two approaches. One used all PGSs (sPGSs and tPGSs were used separately). This took advantages of the neuronal network that variable selection was not necessary when the sample size was sufficiently large. The second approach used only those traits selected by the LASSO selection procedure. For both approaches, we used the DNN implemented in Google Tensor Flow package (Abadi et al. 2016). We explored different type of optimizers and activation algorithms, and settled on the AdamOptimizer and elu activation algorithm. More details of DNN modeling were included in the supplementary materials.

4. RESULTS

4.1. Selection of traits genetically related to schizophrenia

Based on our literature search, we obtained GWAS summary statistics for 28 conditions and traits (Table S1), and calculated sPGSs for these traits at multiple P-values thresholds. We then evaluated the relationship between schizophrenia diagnosis and the candidate sPGSs with logistic regression. We conducted variable selection with LASSO regression as using the R package “glmnet” (Friedman et al. 2010). As shown in Table 1, a total of 22 sPGSs from 14 traits (BIP, BIP-II, CAD, CD, MDD, OPPH, UC, BMI, evrSmk, AST, DS, YoS, NEU and SWB) and schizophrenia, was selected, and they all showed statistically significant association with schizophrenia diagnosis. For several traits, multiple sPGSs calculated at different thresholds were selected. It was puzzling that for some traits sPGSs calculated at different thresholds had opposite direction of association. For example, BIP.II showed positive association with schizophrenia at the P-value threshold of 1e-2, but it showed negative association at the threshold of 1e-3. Similar phenomenon was also observed for schizophrenia PGS (SCZ_1e-5) and ever smokers (evrSmk_1e-5). Based on our current knowledge, these should all be positively correlated with schizophrenia risks. For this reason, BIP.II_1e-3, evrSmk_1e-5 and SCZ_1e-5 were excluded, the remaining 19 sPGSs were used in the sPGS model.

Table 1.

LASSO regression selected sPGSs

	Estimate	Std.Err	Z.Value	Pr(>|Z|)	In.Model
BIP_1e-2	573.23	54.88	10.45	< 2.00E-16	Y
CAD_1e-2	−374.85	101.04	−3.71	0.0002	Y
CD_1e-2	−606.36	105.09	−5.77	7.94E-09	Y
MDD_1e-2	−444.17	48.72	−9.12	< 2.00E-16	Y
BIP.II_1e-2	527.50	93.76	5.63	1.84E-08	Y
OPPH_1e-2	−2863.28	841.99	−3.40	0.0007	Y
SCZ_1e-2	11468.94	277.31	41.36	2.00E-16	Y
UC_1e-2	−485.90	108.81	−4.47	7.98E-06	Y
BMI_1e-3	−244.17	85.33	−2.86	0.0042	Y
evrSmk_1e-3	86.32	26.78	3.22	0.0013	Y
MDD_1e-3	−28.64	17.49	−1.64	0.1015	Y
BIP.II_1e-3	−155.38	34.19	−4.55	5.49E-06	N
SCZ_1e-3	1845.42	127.91	14.43	< 2.00E-16	Y
ASD_1e-4	22.30	6.44	3.46	0.0005	Y
BIP_1e-4	11.84	6.84	1.73	0.0835	Y
DS_1e-4	−445.73	63.21	−7.05	1.77E-12	Y
YoS_1e-4	598.37	162.80	3.68	0.0002	Y
earlyLate_1e-5	15.78	7.80	2.02	0.0430	Y
evrSmk_1e-5	−16.29	5.57	−2.93	0.0034	N
NEU_1e-5	169.77	28.52	5.95	2.65E-09	Y
SCZ_1e-5	−292.10	22.91	−12.75	< 2.00E-16	N
SWB 1e-5	74.75	23.54	3.18	0.0015	Y

Abbreviations: BIP, bipolar disorder; CAD, coronary artery disease; CD, Crohn s disease; MDD, major depressive disorder; BIP.II, bipolar disorder, GWAS II; OPPH, one person income per household; SCZ, schizophrenia; UC, ulcerative colitis; BMI, body mass index; evrSmk, ever smoker; ASD, autism spectrum disorder; DS, depressive symptoms; YoS, years of schooling; earlyLate, early person vs late person; NEU, neuroticism; SWB, subjective wellbeing. The suffix after the abbreviation indicated the P-value threshold used to calculate the PGS.

We did the similar analyses with tPGSs. As seen in Table 2, 13 traits were selected by LASSO regression. A comparison between Tables 1 and 2 revealed that except anorexia, cannabis dependence and neo-openness, all other traits were selected by both the sPGS and tPGS selection. That these traits were selected by both sPGSs and tPGSs analyses was comforting that these traits indeed were genetically related to schizophrenia.

Table 2.

LASSO regression selected tPGSs

	Estimate	Std.Err	Z.Value	Pr(>|Z|)
SCZ_1e-3	104.20	14.91	6.99	2.74E-12
ANO	−6.97	2.05	−3.40	0.0007
BIP	65.74	11.53	5.70	1.20E-08
BMI	−442.61	121.83	−3.63	0.0003
CAN	36.86	12.21	3.02	0.0026
earlyLate	7.09	4.24	1.67	0.0944
MEM	1265.04	192.06	6.59	4.50E-11
BIP.II	623.61	30.20	20.65	< 2.00E-16
OPEN	35.62	8.72	4.08	4.42E-05
OPPH	−895.13	157.70	−5.68	1.38E-08
SWB	−997.20	169.64	−5.88	4.15E-09
VNR	−391.85	99.71	−3.93	8.49E-05
YoS	904.81	193.99	4.66	3.10E-06

Abbreviations: SCZ, schizophrenia; ANO, anorexia; BIP, bipolar disorder; BMI, body mass index; CAN, cannabis dependence; earlyLate, early person vs late person; MEM, working memory; BIP.II, bipolar disorder, GWAS II; OPEN, neo openness; SWB, subjective wellbeing; VNR, verbal and numeric reasoning; YoS, years of schooling.

4.2. The effect of PGS thresholds on schizophrenia prediction

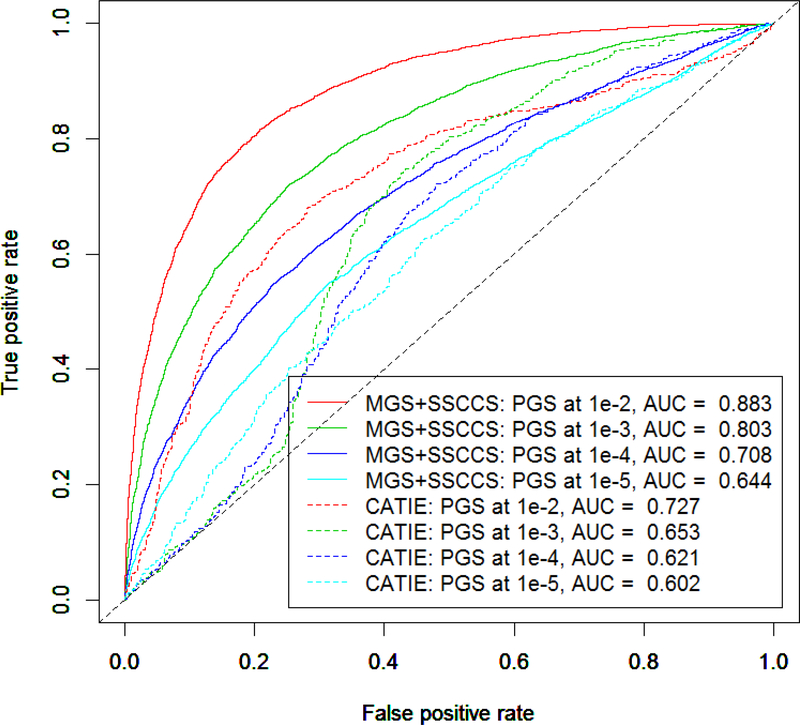
Due to the power of GWASs, most of these studies did not find many loci that were truly associated with the trait of interest. Therefore, it is a common practice that multiple thresholds were used to screen for the threshold that maximally predicted the trait (Euesden et al. 2015). We did these analyses using 4 thresholds: P-value ≤ 1e-2, 1e-3, 1e-4 and 1e-5. In these analyses, we used the sPGSs of schizophrenia alone to predict schizophrenia diagnosis. As shown in Figure 2, the sPGS calculated at a larger P-value performed better in the testing data as measured by the area under the curve (AUC) of receiver operating characteristic. For example, the sPGS calculated at 1e-2 had an AUC of 0.883. The model explained 54% (Nagelkerke’s r² = 0.544) of the variance in the testing part of the MGS+SSCCSS data. The sPGS calculated at 1e-3 had an AUC of 0.803, explaining 35% phenotype variance (Nagelkerke’s r² = 0.348). The same trend was observed in the independent CATIE data. However, the differences between the MGS+SSCCS and CATIE datasets were substantial. For the same P-value thresholds of 1e-2 and 1e-3, the AUCs for the CATIE data were 0.727 and 0.653, and Nagelkerke’s r² = 0.136 and 0.050 respectively. The significant differences between the MGS+SSCCS and CATIE data indicated that there was an overfitting issue with the MGS+SSCCS. The overfitting could be a consequence that the MGS+SSCCS sample (5,576 cases and 6,489 controls) was included in the schizophrenia GWAS (Schizophrenia Working Group of the Psychiatric Genomics Consortium 2014) with which the risk alleles and their weights were used to calculate the sPGSs. Although the CATIE data was also included in the schizophrenia GWAS organized by the Psychiatric Genomics Consortium (PGC), due to its small sample size (741 cases and 751 controls) relative to the total sample size (37,000 cases and 113,000 controls) of the schizophrenia GWAS, its relative contribution to the GWAS summary statistics was limited, therefore, negligible.

Figure 2.

The effect of PGS threshold on prediction power. In a logistic regression model, schizophrenia sPGSs calculated at different thresholds were used to predict schizophrenia diagnosis. The figure showed the AUC curves that sPGSs calculated at different thresholds (indicated by colors) had significant effects on the performance of the prediction models in both the MGS+SSCCS (solid lines) and CATIE (dashed lines) datasets. The differences between the MGS +SSCCSS and CATIE datasets were also noted.

4.3. Inclusion of comorbid traits improved the performance of prediction model

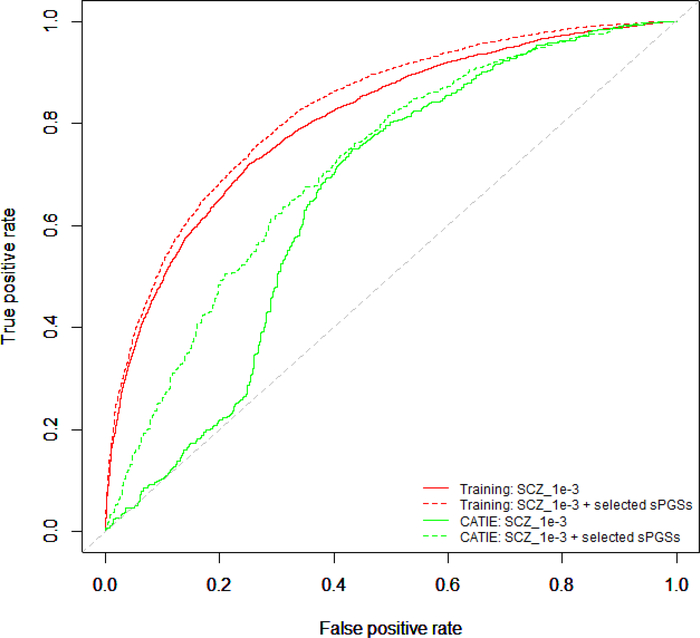
To evaluate whether the inclusion of sPGSs from comorbid traits would improve the performance of prediction model, we used a stepwise procedure to select one sPGS from each comorbid trait. This procedure produced a list of 14 traits (BIP_1e-2, CAD_1e-2, CD_1e-2, MDD_1e-2, OPPH_1e-2, UC_1e-2, evrSmk_1e-3, MEM_1e-3, SCZ_1e-3, DS_1e-4, earlyLate_1e-4, YoS_1e-4, AST_1e-5 and SWB-1e-5). We built a baseline logistic model that used only the SCZ_1e-3 and compared this model with the one that included SCZ_1e-3 and 13 other sPGSs selected by our stepwise procedure. The results were shown in Figure 3. In the MGS+SSCCS data, SCZ_1e-3 alone achieved an AUC of 0.803 (Nagelkerke’s r² = 0.348). With the addition of the other 13 traits, the AUC increased to 0.826 (Nagelkerke’s r² = 0.403), a modest improvement in AUC. When these models were applied to the independent CATIE dataset, the AUCs were 0.653 and 0.715 (Nagelkerke’s r² = 0.050 and 0.178 respectively), the improvement was significant. A similar trend was also observed using SCZ_1e-2, SCZ_1e-4 and SCZ_1e-5 (data not showing).

Figure 3.

Inclusion of PGSs from comorbid traits improved the performance of prediction models. Shown in the figure were receiver operating characteristics (ROC) curves from the schizophrenia sPGS calculated at P-value of 1e-3 alone and the schizophrenia sPGS plus sPGSs from other comorbid traits. Also shown were ROC curves from independent CATIE dataset. In both the MGS+SSCCS and CATIE datasets, the inclusion of sPGSs from comorbid traits improved the performance of the prediction models.

4.4. Models with LASSO selected predictors

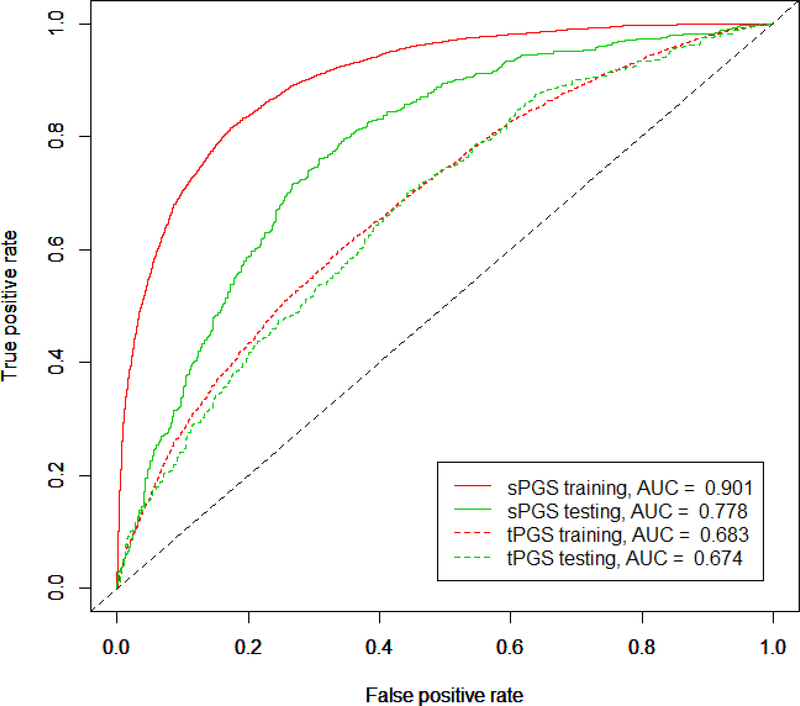
LASSO regression became a popular procedure to select variables from high dimension and correlated data (Frost and Amos 2017; Algamal et al. 2018). We used the LASSO regression implemented in the R package “glmnet” to select PGS predictors from both sPGSs and tPGSs. For the sPGSs, 22 predictors were selected. Of these predictors, there were 3 predictors (BIP.II_1e-3, evrSmk_1e-5, and SCZ_1e-5, Table 1), showing inconsistent association with schizophrenia diagnosis, therefore, these 3 predictors were excluded from the model. We used the remaining predictors to build a logistic regression model to predict schizophrenia diagnosis. With this model, we achieved an AUC of 0.901, which explained about 60% (Nagelkerke’s r² = 0.592) variance in schizophrenia diagnosis for the MGS+SSCCS training data (Figure 4). When this model was applied to the independent CATIE data, we had an AUC of 0.778, and it explained 29% (Nagelkerke’s r² = 0.288) variance.

Figure 4.

Logistic regression models built with LASSO selected predictors. The sPGSs (solid lines) and tPGSs (dashed lines) were tested separately. The MGS+SSCCS data were used as training data, and the independent CATIE sample was used as testing data. The sPGS model had 19 predictors and the tPGS model had 14 predictors. The sPGS model outperformed tPGS model in both training (red lines) and testing (green lines), but it had an issue of overfitting in the training data.

For the tPGS model, a similar logistic model was built. It included the 12 predictors (ANO, BIP, BMI, cannabis, earlyLate, MEM, BIPII, OPEN, OPPH, SWB, VNR and YoS) selected by LASSO regression and the schizophrenia sPGS calculated at P-value ≤ 1e-3. This model had an AUC of 0.683, Nagelkerke’s r² = 0.136 for the MGS+SSCCS data. When the model was applied to the independent CATIE data, the AUC was 0.674, Nagelkerke’s r² = 0.126 (Figure 4). Comparing to the sPGS model, two features stood out: first, tPGS model performed much worse than the sPGS model; and second, the performance between the MGS+SSCCS and the CATIE was similar in the tPGS model. This was in clear contrast to the sPGS model where the overfitting in the training data was obvious. It seemed that the tPGS model was more generalizable.

4.5. DNN model

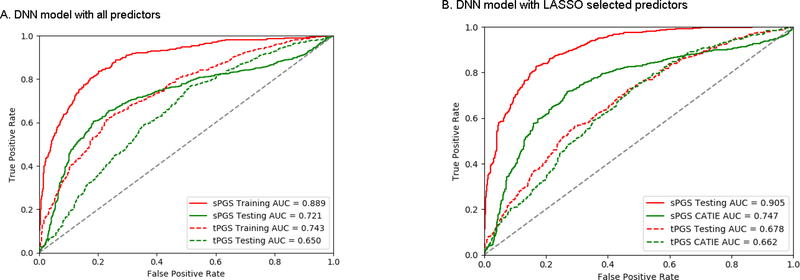
We used tensor flow DNN to build prediction models for schizophrenia diagnosis with sPGSs and tPGSs. Since one of the advantages of DNN is that there is no need to do variable selection when the sample size is sufficiently large, we used all predictors for the DNN models. For the sPGS model, all 116 variable (29 traits each with sPGSs at 4 thresholds) were included in the model. In this model, we fitted the model for 10,000 steps. This model had an accuracy of 81.3% and AUC of 0.889. When this model was applied to the CATIE data, the accuracy was 69.7% and AUC of 0.721 (Figure 5A). For the tPGS model, 25 traits and the sPGS of schizophrenia calculated at P-value ≤ 1e-3 were included. For this model, we also fitted the model for 10,000 steps. This model had an accuracy of 68.9% in the testing data, with an AUC of 0.743 (Figure 5A). When this model was applied to the CATIE data, the accuracy was 61.2% and AUC was 0.650.

Figure 5.

A comparison of performance between the DNN models that used all predictors (A) and LASSO selected predictors (B). LASSO selected predictors had a better performance for both testing (MGS+SSCCS) and validation (CATIE) data.

We also built DNN models with the sPGS and tPGS predictors selected by the LASSO procedure. For the sPGS model, 19 predictors were used. This model achieved an accuracy of 82.1% and AUC of 0.905 (Figure 5B). When the model was applied to the CATIE data, the accuracy was 71.2% and the AUC was 0.747. For the tPGS model, 14 predictors were included. This model had an accuracy of 63.8% and AUC of 0.678 (Figure 5B). For the CATIE data, the accuracy was 61.5% and AUC was 0.662.

By comparing the models that used all PGSs and that used only LASSO selected PGSs, the overall performances were similar. For the sPGS model, LASSO selected predictors had slightly higher accuracy (71.2% vs 68.9%) in the CATIE data. For the tPGS model, the results were virtually the same in the CATIE data.

4.6. Comparison between the linear and DNN models

We conducted a direct comparison between the logistic regression and DNN models using the sPGS and tPGS predictors selected by the LASSO regression. These results were summarized in Table 3. With the sPGS predictors, both logistic regression and DNN models had similar performance in accuracy, but the logistic regression model had slightly better result in discrimination (AUC). When the tPGS predictors were used, the logistic regression and DNN models had similar performances in both accuracy and AUC. In both logistic regression and DNN models, overfitting was observed in the training (MGS+SSCCS) data, likely due to the fact the PGSs were calculated with the GWAS summary statistics that the MGS and SSCCS data contributed for a significant part. It seemed that the tPGSs were more amendable to generalization even their performance was not optimal with current predictors.

Table 3.

A comparison between the logistic regression and DNN models

Dataset		Logistic regression		Neural Network
		Accuracy	AUC	Accuracy	AUC
sPGS Model	MGS+SSCCS	0.820	0	0.823	0
	CATIE	0.72	0	0.723	0
tPGS Model	MGS+SSCCS	0.63	0	0.638	0
	CATIE	0.63	0	0.635	0

5. DISCUSSION AND CONCLUSION

In this study, we evaluated how PGS could be used to predict schizophrenia diagnosis. We took two approaches to calculate the PGSs for schizophrenia and other comorbid traits, and used different models to evaluate their performances. Our major objectives were three-fold: 1) To evaluate whether the inclusion of shared genetic factors from comorbid traits improved the performance of prediction models and by how much; 2) To evaluate which approach was better to calculate PGSs for prediction models; and 3). To compare the logistic regression model with DNN model.

To evaluate whether the inclusion of PGSs from comorbid traits would improve the performance, we compared the model that used SCZ_1e-3 alone with the model that used SCZ_1e-3 and other 13 sPGSs selected by a stepwise procedure. As shown in Figure 3, the inclusion of other 13 comorbid traits had only a modest improvement of AUC in the MGS+SSCCS training data. But the performance was much better when the model was applied to the CATIE dataset, the improvement of AUC was 0.059 (0.712 vs 0.653) and the phenotype variance explained (Nagelkerke’s pseudo r²) increased from 0.050 to 0.178. This was rather remarkable. Similar improvements were also observed for the models with LASSO selected variables. For example, from Figure 2, the observed AUC for SCZ_1e-2 was 0.883. In Figure 4, the model that included SCZ_1e-2 and LASSO selected sPGSs had an AUC of 0.901 in the MGS+SSCCS data. For the CATIE data, the AUC improved from 0.727 to 0.778. From these results, it was clear that the inclusion of PGSs from comorbid traits improved the performance of the prediction model, and this was consistent with the results from other researchers (Li et al. 2014).

We investigated the impact of PGS calculation on prediction model. We took two approaches to calculate the PGSs. The first approach we used to calculate PGSs, i.e. sPGSs, was the standard approach that most researchers used to evaluate the effect of PGS on heritability and genetic correlation (or pleiotropy) between different traits. Here the PGS was the summation of the number of risk alleles to the trait of interest at a specified threshold, weighted by the effect sizes (odds ratio or correlation coefficient) of the risk alleles. The higher the sPGS, the higher the risk to the trait of interest. But its effect on other traits was not clear. The second approach for PGS calculation put emphasis on the shared genetic factors between two traits where only markers showing association with the two traits of interest were used. In our analyses, the results suggested that sPGS outperformed the tPGS in both the logistic regression and DNN models in the combined MGS+SSCCS data (Figure 4 and Table 3). We also observed that models with sPGSs were more susceptible to overfitting. The performance gaps between the MGS+SSCCS training data and independent CATIE data were much larger than that observed in the tPGS models. In Figure 4, the difference in AUCs between the MGS+SSCCS and CATIE data was 0.126 for the sPGS logistic regression model, the corresponding difference in the tPGS model was 0.009. It seemed that the tPGS model had better property for generalization. While sPGSs had a better performance in our analyses, the potential of tPGSs was not fully explored. For example, we calculate tPGSs at only one threshold. What if we do multiple thresholds as we did for sPGSs? Further exploration of tPGSs is warranted.

In our comparison between the logistic regression and the DNN models, we found that the two models had similar performances using either sPGSs or tPGSs (Table 3) in MGS+SSCCS data. But in the independent validation CATIE data, the logistic regression model had slightly better discrimination (AUCs: 0.779 vs 0.747) with the sPGSs predictors. These results may need further investigation.

We also noticed that the best performance of PGS on schizophrenia diagnosis was observed at an accuracy of 72% in the CATIE data, which was achieved using the LASSO selected variables with both logistic regression and DNN models (Table 3). With this accuracy, the current models are not very useful in clinical applications. However, the models have rooms for future improvements. First, we can refine PGS calculation and include more genetic related traits. The results presented in this study and by others have demonstrated this point. Second, the models in this study used PGSs alone, these models did not include any environmental and behavioral factors, or clinical tests or biomarkers. When these factors are included, it is very likely that we can build a model that can predict schizophrenia diagnosis reliably. Therefore, a future direction would be to discover these factors and incorporate them into prediction models.

This study has some limitations. First, the MGS and SSCCS datasets were significant components of PGC schizophrenia GWAS, therefore, PGSs calculated for the MGS and SSCCS subjects are likely inflated. This, we believe, is the single most significant factor leading to the overfitting observed in the MGS+SSCCS data for all models. This confounding effect may impact the interpretation of our results on the MGS+SSCCS data. Second, the tPGSs were calculated at a single threshold. Their underperformance compared to sPGSs might be a consequence of suboptimal selection of threshold. Further refinement may be necessary to clarify this issue. Third, while we screened many conditions and traits that were potentially genetically related to schizophrenia, our screening was by no mean exhaustive. More genetically related traits may be discovered and included in the model, further improving the performance. It may take multiple iterations before an optimal model is found.

In summary, we examined the utility of PGS in a prediction model for schizophrenia diagnosis using both logistic regression and DNN models. With the sPGS predictors selected by LASSO regression, we accomplished an accuracy of 72% with both logistic regression and DNN models when the models were generalized to the independent CATIE data. Given the fact that the models used PGSs alone, there is a great potential for further improvements. A future model would incorporate environmental and behavioral factors, clinical features and biomarkers. This new model has the potential to predict schizophrenia diagnosis and be clinically useful.