Reward-Based Improvements in Motor Control Are Driven by Multiple Error-Reducing Mechanisms

Abstract

Reward has a remarkable ability to invigorate motor behavior, enabling individuals to select and execute actions with greater precision and speed. However, if reward is to be exploited in applied settings, such as rehabilitation, a thorough understanding of its underlying mechanisms is required. In a series of experiments, we first demonstrate that reward simultaneously improves the selection and execution components of a reaching movement. Specifically, reward promoted the selection of the correct action in the presence of distractors, while also improving execution through increased speed and maintenance of accuracy. These results led to a shift in the speed-accuracy functions for both selection and execution. In addition, punishment had a similar impact on action selection and execution, although it enhanced execution performance across all trials within a block, that is, its impact was noncontingent to trial value. Although the reward-driven enhancement of movement execution has been proposed to occur through enhanced feedback control, an untested possibility is that it is also driven by increased arm stiffness, an energy-consuming process that enhances limb stability. Computational analysis revealed that reward led to both an increase in feedback correction in the middle of the movement and a reduction in motor noise near the target. In line with our hypothesis, we provide novel evidence that this noise reduction is driven by a reward-dependent increase in arm stiffness. Therefore, reward drives multiple error-reduction mechanisms which enable individuals to invigorate motor performance without compromising accuracy.

SIGNIFICANCE STATEMENT While reward is well-known for enhancing motor performance, how the nervous system generates these improvements is unclear. Despite recent work indicating that reward leads to enhanced feedback control, an untested possibility is that it also increases arm stiffness. We demonstrate that reward simultaneously improves the selection and execution components of a reaching movement. Furthermore, we show that punishment has a similar positive impact on performance. Importantly, by combining computational and biomechanical approaches, we show that reward leads to both improved feedback correction and an increase in stiffness. Therefore, reward drives multiple error-reduction mechanisms which enable individuals to invigorate performance without compromising accuracy. This work suggests that stiffness control plays a vital, and underappreciated, role in the reward-based imporvemenets in motor control.

Introduction

Motor control involves two main components that may be individually optimized: action selection and action execution (Chen et al., 2018). While the former addresses the problem of finding the best action to achieve a goal, the latter is concerned with performing the selected action with the greatest precision possible (Stanley and Krakauer, 2013; Shmuelof et al., 2014; Chen et al., 2018). Naturally, both processes come at a computational cost, meaning the faster an action is selected or executed, the more prone it is to errors (Fitts, 1954).

Interestingly, both action selection and action execution are highly susceptible to the presence of reward. For instance, introducing monetary reward in a sequence learning task leads to a reduction in selection errors, as well as a decrease in reaction times, suggesting faster computation at no cost to accuracy (Wachter et al., 2009). Similarly, in saccades, reward reduces reaction times and sensitivity to distractors (Manohar et al., 2015). Reports also indicate that reward invigorates movement execution by increasing peak velocity and accuracy during saccades (Takikawa et al., 2002) and reaching movements (Summerside et al., 2018; Carroll et al., 2019; Galaro et al., 2019). Together, these studies suggest that reward can shift the speed-accuracy function, at least in isolation, of both selection and execution. However, it is currently unclear whether reward can simultaneously enhance both the selection and execution components of a reaching movement. As reward has generated much interest as a potential tool to enhance rehabilitation procedures for clinical populations (Goodman et al., 2014; Quattrocchi et al., 2017), it is crucial to determine whether it can improve selection and execution of limb movements without interference. Additionally, punishment has strongly dissociable effects from reward in motor adaptation (Galea et al., 2015), motor learning (Wachter et al., 2009; Abe et al., 2011; Steel et al., 2016; Griffiths and Beierholm, 2017) and saccades (Manohar et al., 2017). However, it remains unclear whether punishment invigorates reaching movements in a similar manner to reward.

Another open question is how reward mechanistically drives improvements in performance. Recent work in eye and reaching movements suggests that reward acts by increasing feedback control, enhancing one's ability to correct for movement error (Carroll et al., 2019; Manohar et al., 2019). However, there are far simpler mechanisms which reward could use to improve execution. For example, the motor system can control the stiffness of its effectors, such as the arm during a reaching task (e.g., through cocontraction of antagonist muscles) (Perreault et al., 2002; Gribble et al., 2003). This results in the limb being more stable in the face of perturbations (Franklin et al., 2007) and capable of absorbing noise that may arise during the movement itself (Selen et al., 2009; Ueyama and Miyashita, 2013), thus reducing error and improving performance (Gribble et al., 2003). Yet, it is unclear whether the reward-based improvements in execution are associated with increased stiffness.

To address these questions, we devised a reaching task where participants were monetarily rewarded depending on their reaction time and movement time. Occasionally, distractor targets appeared, in which case participants had to withhold their movement until the correct target onset, allowing for a selection component to be quantified. In a first experiment, we show that reward improves both selection and execution concomitantly, and that this effect did not scale with reward magnitude. In a second experiment, we demonstrate that, although both reward and punishment led to similar effects in action selection, action execution showed a more global, noncontingent sensitivity to punishment. Behavioral and computational analysis of trajectories revealed that, in addition to an increase in feedback corrections during movement, a second mechanism produced a decrease in motor noise at the end of the movement. We hypothesized that the reduction in motor noise may be achieved through an increase in arm stiffness. We tested this hypothesis and provide empirical evidence that arm stiffness was increased in rewarded trials.

Materials and Methods

Participants

Thirty participants (2 males, median age: 19, range: 18-31 years) took part in Experiment 1. Thirty participants (4 males, median age: 20.5 years, range: 18-30 years) took part in Experiment 2. Thirty participants (10 male, median age: 19.5 years, range: 18-32 years) took part in Experiment 3, randomly divided into two groups of 15. Twenty participants (2 male, median age: 19 years, range: 18-20 years) took part in Experiment 4. All participants were recruited on a voluntary basis and were rewarded with their choice of money (£7.5/h) or research credits. They were informed that this remuneration was in addition to the monetary feedback they would gain by performing well during the tasks. Participants were all free of visual (including color discrimination), psychological, or motor impairments. All the experiments were conducted in accordance with the local research ethics committee of the University of Birmingham (Birmingham, United Kingdom).

Although no power analysis was performed for Experiments 1 and 2, both included relatively large group sizes (N = 30) in comparison with current literature. The sample size for Experiment 3 was preregistered (https://osf.io/qt43b) and based on a previous study using a comparable stiffness estimation technique (Selen et al., 2009). Similarly, we initially tested 15 participants for Experiment 4 and observed an expected null result. However, to ensure this null result was not the consequence of sample size, we collected an additional 5 participants (N = 20).

Task design

Participants performed the tasks on an endpoint KINARM (BKIN Technologies). They held a robotic handle that could move freely on a plane surface in front of them, with the handle and their hand hidden by a panel (Fig. 1A). The panel included a mirror that reflected a screen above it, and participants performed the task by looking at the reflection of the screen (60 Hz refresh rate), which appeared at the level of the hidden hand. Kinematics data were sampled at 1 kHz.

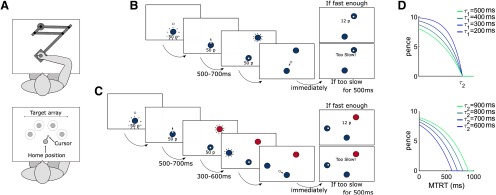
Figure 1.

Reaching paradigm. A, Participants reached to an array of targets using a robotic manipulandum. B, Time course of a normal trial. Participants reached at a single target and earned money based on their performance speed. If they were too slow (MTRT < ${\mathit{\tau }}_2$), a message “Too slow!” appeared instead of the reward information. Transition times are indicated below for each screen. A uniform distribution was used for the transition time jitter. C, Time course of a distractor trial. Occasionally, a distractor target appeared, indicated by a color different from the starting position. Participants were told to wait for the second, correct target to appear and reach toward the latter. D, The faster participants completed their reach to the target, the more money they were rewarded. The speed of the the response was quantified as the sum of movement time and reaction time (i.e., MTRT), and the function mapping MTRT to reward varied based on two parameters ${\mathit{\tau }}_1$ and ${\mathit{\tau }}_2$. ${\mathit{\tau }}_1$ and ${\mathit{\tau }}_2$ enabled the reward function to adjust throughout the task as a function of individual performance history, to ensure all participants received a similar amount of reward (see Task design). Top, Bottom, How how the function varied as a function of ${\mathit{\tau }}_1$ (${\mathit{\tau }}_2$ fixed at 800 ms) and ${\mathit{\tau }}_2$ (${\mathit{\tau }}_1$ fixed at 400 ms), respectively, for a 10 p trial.

Each trial started with the robot handle bringing participants 4 cm in front of a fixed starting position, except for Experiments 3 and 4 to avoid interference with the perturbations during catch trials. A 2-cm-diameter starting position (angular size $\sim$3.15°) then appeared, with its color indicating one of several possible reward values, depending on the experiment. Participants were informed of this contingency during the instructions. The reward value was also displayed in 2-cm-high text (angular size $\sim$3.19°) under the starting position (Fig. 1B,C). Because color luminance can affect salience and therefore detectability, luminance-adjusted colors were used (see http://www.hsluv.org/). The colors used were, in red-green-blue format [76/133/50] (green), [217/54/104] (pink), and [59/125/171] (blue) for 0, 10 and 50 p, respectively, and distractor colors were green, pink, or blue. To ensure that a specific color did not bias the amount of distracted trials, we fitted a mixed-effect model $distracted\sim color+\left(1\right|participant)+(1\left|reward\right)$ with $color$ a 3-level categorical variable encoding the color of the distractor target. Distractor color did not explain any variance in selection error ($p=1.72\hspace{0.17em}\times \hspace{0.17em}10^{-69}$, $p=0.46$ and $p=0.82$ for the intercept, pink and blue colors, respectively), confirming that the observed effect was not driven by distractor colors. From 500 to 700 ms after participants entered the starting position (on average 587 ± 354 ms after the starting position appeared), a 2-cm-diameter target (angular size $\sim$2.48°) appeared 20 cm away from the starting position, in the same color as the starting position. Participants were instructed to move as fast as they could toward it and stop in it. They were informed that a combination of their reaction time and movement time defined how much money they would receive, and that this amount accumulated across the experiment. They were also informed that end position was not factored in as long as they were within 4 cm of the target center.

The reward function was a closed-loop design that incorporated the recent history of performance, to ensure that participants received similar amounts of reward despite idiosyncrasies in individual's reaction times and movement speed, and that the task remained consistently challenging over the experiment (Manohar et al., 2015; Berret et al., 2018; Reppert et al., 2018). To that end, the reward function was defined as follows:

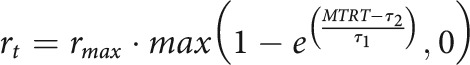where $r_{max}$ was the maximum reward value for a given trial, MTRT was the sum of reaction time and movement time, and ${\tau }_1$ and ${\tau }_2$ adaptable parameters varying as a function of performance (Fig. 1D). Specifically, ${\tau }_1$ and ${\tau }_2$ were the mean of the last 20 trials' 3-4th and 16-17th fastest MTRTs, respectively, and were initialized as 400 and 800 ms at the start of each participant training block. $\tau$ values were constrained so that ${\tau }_1<{\tau }_2<900$ was always true. In practice, all reward values were rounded up (or down in the punishment condition of Experiment 2) to the next penny so that only integer penny values would be displayed. Of note, this reward function (Eq. 1) allows weighting the impact of movement times and reaction times differentially when obtaining MTRTs. However, we did not want to emphasize one over the other, since our aim was to observe how selection and execution performance vary with reward when taking place concomitantly. Therefore, our MTRTs were simply the addition of movement time and reaction time for a given trial, without any weighting bias.

Targets were always of the same color as the starting position (Fig. 1B), and participants were informed of this relationship during the instructions. However, in Experiments 1 and 2, occasional distractor targets appeared, indicated by a different color than the starting position (green, pink, or blue, depending on the correct target's color; Fig. 1C). Participants were informed to ignore these targets and wait for the second target to appear. Failure to comply in rewarded and punished trials resulted in no gains for this trial and an increase in loss by a factor of 1.2, respectively. The first target (distractor or not) appeared 500-700 ms after entering the starting position using a uniform random distribution, and correct targets in distractor trials appeared 300-600 ms after the distractor target using the same distribution. Our task is reminiscent of a go-no-go task where one must execute or inhibit an action, usually a button press, when presented with a “go” cue or a distractor cue (Guitart-Masip et al., 2014), respectively. As the go-no-go paradigm involves pressing a button versus not pressing it, the main differences between a go-no-go task and an action selection task are that a go-no-go task does not include a “response selection” stage (Donders, 1969); and requires participants to inhibit expression of the prepared action. However, the task we used here involves four possible reaching directions (three after the distractor onset) rather than a single action that has to be executed or inhibited, making our paradigm closer to an action selection task, although an inhibitory component remains.

When reaching movement velocity passed below a 0.03 m/s threshold, the end position was recorded, and monetary gains were indicated at the center of the workspace. After 500 ms, the robotic arm then brought the participant's hand back to the initial position 4 cm above the starting position.

In every experiment, participants were first exposed to a training block, where all targets had the same reward value equal to the mean of all value combinations used later in the experiment (e.g., if the experiment had 0 and 50 p trials, the training reward amounted to 25 p per trial). Participants were informed that money obtained during the training would not count toward the final amount they would receive. Starting position and target colors were all gray during training. The $\tau$ values obtained at the end of training were then used as initial values for the actual task.

Experimental design

Experiment 1: reward-magnitude

The purpose of the first experiment was to assess the effect of reward magnitude on the selection and execution components of a reaching movement. There were four possible target locations positioned every 45° around the midline of the workspace, resulting in a 135° span (Fig. 1A). Participants first practiced the task in a 48-trial training block. They then experienced a short block (24 trials) with no distractors, and then a main block of 168 trials (72 distractors, 42.86% of all trials). Trials were randomly shuffled within each block. Reward values used during the task were 0, 10, and 50 p.

Experiment 2: reward versus punishment

The goal of the second experiment was to compare the effects of reward and punishment on the selection and execution components of a reaching movement. The same four target positions were used as in Experiment 1, and participants first practiced the task in a training block (48 trials). Participants then performed a no-distractor block and a distractor block (12 and 112 trials) in a rewarded condition (0 and 50 p trials) and additionally in a punishment condition (−0 and −50 p trials). The order of reward and punishment blocks was counterbalanced across participants. In the distractor blocks, 48 trials were distractor trials (42.86%). Before the punishment blocks, participants were told that they would start with £11 and that the slower they moved, the more money they lost. This resulted in participants gaining on average a similar amount of money on the reward and punishment blocks. They were also informed that, if they missed the target or went to the distractor target, their losses on that trial would be multiplied by a factor of 1.2. The reward function was biased so that:

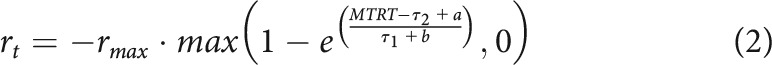With $a=268.5$ and $b=-71.4$. The update rule was also altered, with ${\tau }_1$ and ${\tau }_2$ the mean of the last 20 trials' 15–16th and 17–18th fastest MTRTs, respectively. These changes were obtained by fitting the performance data of the reward-magnitude experiment to a punishment function with free $a$ and $b$ parameters and free updating indexes to minimize the difference in average losses compared with the average gains observed in the reward-magnitude experiment. On average, participants gained £5.40 in the reward condition and lost £5.63 in the punishment condition (paired t test: t₍₂₉₎ = –0.55, p = 0.58, d = –0.1), meaning that this manipulation successfully allowed for a similar amount of gains and losses for a given participant.

Experiment 3: end-reach stiffness

Experiment 3 aimed to examine whether reward was associated with increased muscle stiffness at the end of movement. Because arm stiffness is strongly dependent on arm configuration, stiffness ellipses are usually oriented, with a long axis indicating a direction of higher stiffness. This orientation is influenced by several factors, including position in Cartesian space (Mussa-Ivaldi et al., 1985). If reward affects stiffness as we hypothesized, the possibility that this effect is dependent on a target location must therefore be considered. To account for this, two groups of participants (N = 15 per group) reached for a target located 20 cm from the starting position at either 45° to the right or the left. On occasional “catch” trials (31% trials pseudorandomly interspersed), when velocity passed under a 0.03m/s threshold, a 300-ms-long, fixed-length (8 mm) displacement pushed participants away from their end position and back, allowing us to measure endpoint stiffness (see Data analysis). Because displacements of this amplitude were noticeable, participants were instructed to ignore them and not react, and we used a low proportion of catch trials to reduce anticipation. Importantly, participants were explicitly informed that the accuracy of their reach was defined by their position before the displacement, meaning that the displacement will not impact their monetary gains (e.g., by pushing them away from the target). No distractor trials were used in this experiment. This type of displacement profile was based on previous work showing that it can reliably provide endpoint stiffness measurements (Franklin et al., 2003; Selen et al., 2009).

Participants performed two training sessions: one with no catch trials (25 trials) and one with four catch trials out of 8 trials, with displacements of 0°, 90°, 180°, and 270° around the end position to familiarize participants with the displacement. Participants then performed the main block with 64 catch trials out of 200 trials (32%) and 0 and 50 p reward values. During the main block, displacements were in 1 of 8 possible directions from 0° to 315° around the end position, in step increments of 45° and randomly assigned over the course of the block. We used sessions of 233 trials to ensure session durations remained short, ruling out any effect of fatigue on stiffness as cocontraction is metabolically taxing. To ensure that any measure of stiffness was not due to differences in grip position, a loose finger grip, or postural changes, participants' hands were restrained with a solid piece of plastic, which locked the wrist in a straight position, preventing flexion-extension or radial-ulnar deviations. As the participants held a vertical handle, pronation-supination was also not possible. In addition, a reinforced glove (The Active Hand Company) securely strapped the fingers around the handle during the entire task, preventing any loosening of grip.

Experiment 4: start-reach stiffness

In this last experiment, we tested whether similar differences in endpoint stiffness existed between rewarding and no-reward trials immdiately before the start of the reach. The experiment was essentially similar to Experiment 3, except that the catch trials occurred in the start position at the time the target was supposed to appear. To ensure participants remained in the starting position, two different targets (45° and −45° from midline) were used to maintain directional uncertainty. Participants had 24 trials during the no-catch-trial training, 16 trials during the catch-trial training (8 catch trials), and 200 trials during the main block, with 64 (32%) catch trials. Displacements always occurred 500 ms after entering the starting position, to avoid a jitter-induced bias in stiffness measurement. In noncatch trials, targets also appeared after a fixed delay of 500 ms. Because participants voluntarily moved into the starting position after it appeared, they had sufficient time to process the reward information.

Data analysis

All the analysis code is available on the Open Science Framework website, alongside the experimental datasets at https://osf.io/7as8g/. Analyses were all made in MATLAB (The MathWorks) using custom-made scripts and functions.

Trials were manually classified as distracted or nondistracted. Trials that did not include a distractor target were all considered nondistracted. Distracted trials were defined as trials where a distractor target was displayed, and participants initiated their movement toward the distractor instead of the correct target, based on their reach angle when exiting the starting position. If participants readjusted their reach “mid-flight” to the correct target or initiated their movement to the correct target and readjusted their reach to the distractor, this was still considered a distracted trial. In ambiguous situations, we took a conservative approach and labeled the trial as nondistracted (e.g., if the reach direction was between the correct target and the distractor so that it was challenging to dissociate the original reaching direction). On very rare occasions (<20 trials in the whole study), participants exited the starting position away from the distractor but before the correct target appeared; these trials were not classified as distracted.

Reaction times were measured as the time between the correct target onset and when the participant's distance from the center of the starting position exceeded 2 cm. In trials that were marked as “distracted” (i.e., participant initially moved toward the distractor target), the distractor target onset was used. In trials including a distractor, the second, correct target did not require any selection process to be made, since the appearance of the distractor target informed participants that the next target would be the right one. For this reason, reaction times were biased toward a faster range in trials in which a distractor target appeared, but participants were not distracted by it. Consequently, mean reaction times were obtained by including only trials with no distractor, and trials with a distractor in which participants were distracted. For the same reason, trials in the first block were not included because no distractor was present, and no selection was necessary. For every other summary variable, we included all trials that were not distracted trials, including those in the first block. For normalized data, normalization was performed by substracting the baseline condition to the other conditions for each participant individually.

In Experiments 1 and 2, we removed trials with reaction times >1000 ms or <200 ms, and for nondistracted trials we also removed trials with radial errors >6 cm or angular errors >20. Overall, this resulted in 0.3% and 0.7% trials being removed from Experiment 1 and 2, respectively. Speed-accuracy functions were obtained for each participant individually. For the execution speed-accuracy function, we sorted all trials based on their peak velocity and obtained the average radial error using a sliding window of 30-centile width with 2-centiles (50 quantiles) sliding steps (Manohar et al., 2015). For the selection speed-accuracy function, reaction times and selection accuracy (the proportion of nondistracted trials) were used instead of peak velocity and radial accuracy. Then, each individual speed-accuracy function was averaged by quantile across participants in both the $x$ and $y$ dimension.

To gain a deeper understanding of the control strategy used during reaches under reward, we used a kinematic analysis technique introduced in saccades in Manohar et al. (2019). Briefly, this analysis consists of obtaining the autocorrelation of reaching trajectories over time. We assessed how much the set of positions at time $t$ across all trials correlated with the set of positions at any other time $t\pm n$ (e.g., $t+1$ or $t-5$). If movements are stereotyped across trials, this correlation will be high because the early position will provide a large amount of information about the later or earlier position. On the other hand, if trajectories are variable over time within a trial, the correlation will decrease because there will be no consistency in the evolution of position over time. This can be visualized using a correlation heatmap with time on both the x and y axes (see Figs. 6, 7). Time-time correlation analyses were performed exclusively on nondistracted trials. Trajectories were taken from exiting the starting position to when velocity fell to <0.01m/s. They were rotated so that the target appeared directly in front of the starting position, and $y$-dimension positions were then linearly interpolated to 100 evenly spaced time points. We focused on the $y$ dimensions because it displays most of the variance. Correlation values were obtained on $y$ positions and Fisher-transformed before follow-up analyses (Manohar et al., 2019).

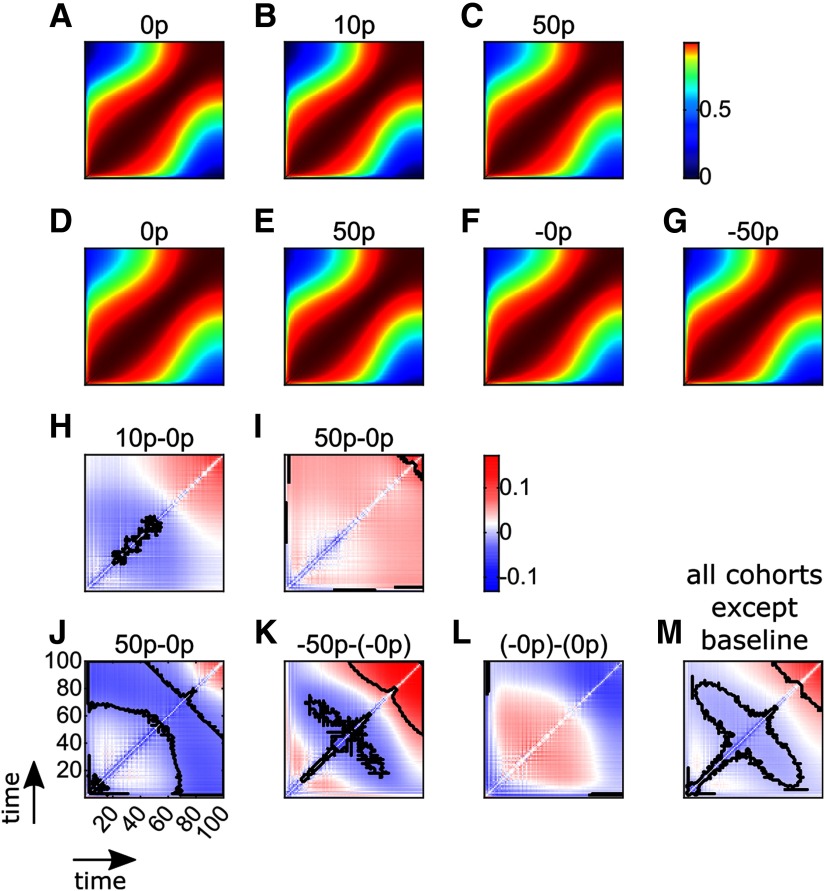
Figure 6.

Time-time correlation maps show that monetary reward and punishment have a biphasic effect on the reach time course. A-C, Time-time correlation maps for all trial types (0, 10, and 50 p) in Experiment 1. Colors represent Fisher-transformed Pearson correlation values. For each map, the bottom left and top right corners represent the start and the end of the reaching movement, respectively. The color maps are nonlinear to enhance readability. D-G, Time-time correlation maps for all trial types (0, 50, −0, −50 p) in Experiment 2. H, I, Comparison of Fisher-transformed correlation maps with the respective baseline map (A) for Experiment 1. Solid black line indicates clusters of significance after clusterwise correction for multiple comparisons. J-L, Similar comparisons for Experiment 2, with each condition's respective baseline (D, F). M, Similar comparison when pooling all contrasts, except the baselines contrast together.

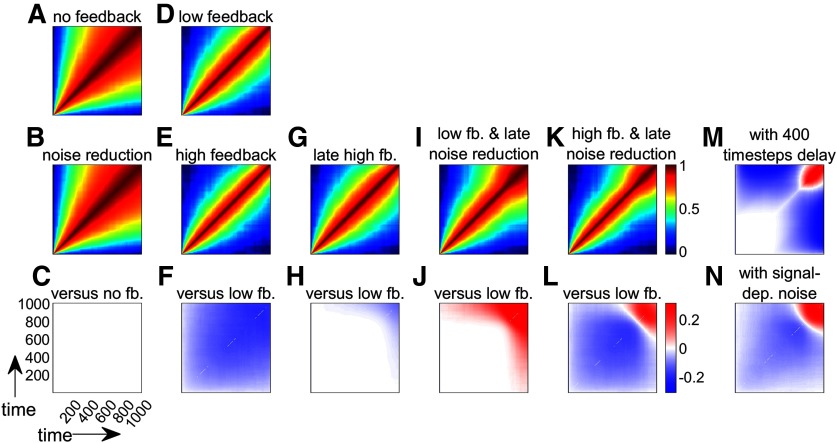
Figure 7.

Simulations of time-time correlation map behavior under different models of the reward- and punishment-based effects on motor execution. A, D, Time-time correlation maps of both control models. Colors represent Fisher-transformed Pearson correlation values. For each map, the bottom left and top right corners represent the start and the end of the reaching movement, respectively. B, E, G, I, K, Time-time correlation maps of plausible alternative models. C, F, H, J, L, Comparison of models with their respective baseline models. M, Same as in L, but with feedback delay of 400 time steps. N, Same as in L, but with a bell-shaped noise term to introduce signal-dependent noise.

For Experiments 3 and 4, the displacements (8 mm) were in 8 possible directions arrayed radially around the participant's hand position at the time of displacement onset. The displacement profile was transient, with a ramp-up, a plateau, and a ramp-down phase to bring the hand back to the original end position. Importantly, the displacement profile was not stepped but controlled at each time step during all three phases. This enabled us to preset the ramp-up and ramp-down profile so as to ensure the smoothest trajectory possible. To this end, we used a sixth-order poly nomial function $x\left(t\right)=20.{\left(\frac{t}{t_{end}}\right)}^3-45.{\left(\frac{t}{t_{end}}\right)}^4+36.{\left(\frac{t}{t_{end}}\right)}^5-10{\left(\frac{t}{t_{end}}\right)}^6$ that minimizes acceleration at the beginning and at the end of the ramp; with $t_{end}$ the time at the end of the displacement and $t$ the current time at which the position $x$ is evaluated. The three phases of displacement (ramp-up, plateau, and ramp-down) were all 100 ms long. As the position was clamped during the plateau phase, velocity and acceleration were on average null, removing any influence of viscosity and inertia. Therefore, the amount of force required to maintain the displacement during plateau was linearly proportional to endpoint stiffness of the arm (Perreault et al., 2002). Positions and servo forces in the $x$ and $y$ dimensions between 140 and 200 ms after perturbation onset were averaged over time for each catch trial (Franklin et al., 2003; Selen et al., 2009). Then, the stiffness values were obtained using multiple linear regressions (function fitlm in MATLAB). Specifically, for each participant, $K_{xx}$ and $K_{xy}^a$ were the resulting $x$ and $y$ coefficients of $F_x\sim 1+x+y$ (with 1 representing the individual interercept in the Wilkonson notation) and $K_{yx}^a$ and $K_{yy}$ were the resulting $x$ and $y$ coefficients of $F_y\sim 1+x+y$. The intercept in the regression parameters were not removed to prevent any possible bias in the stiffness (slope) estimates. Data points whose residual was >3 times the SE of all residuals were excluded (1.56% and 2.27% for Experiment 3 and 4, respectively). Then, we can define the asymmetrical stiffness matrix as follows:

And the symmetrical stiffness matrix that we will use in subsequent analysis as follows:

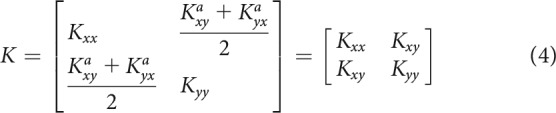These matrices can be projected in Cartesian space using a sinusoidal transform (Eq. 5), resulting in an ellipse.

This ellipse can be characterized by its shape, orientation, and ratio, which we obtained using a previously described method (Perreault et al., 2002).

The displacement was applied by the endpoint KINARM used forthe reaching task. Sampling during the perturbation was the same as during the reaching (1 kHz). The KINARM was equipped with two setsof encoders: a low-resolution primary encoder set and an additional high-resolution secondary encoder set. The error gain feedback matrices during the displacement were as follows: $K_p=\left[\begin{array}{ll}400& 0\\ 0& 400\end{array}\right]$, $K_{v_1}=\left[\begin{array}{ll}2.5& 0\\ 0& 2.5\end{array}\right],$ and $K_{v_2}=\left[\begin{array}{ll}6& 0\\ 0& 6\end{array}\right]$, with $K_p$ the gain matrix (N) for position error and $K_{v_1}$ and $K_{v_2}$ the two gain matrices (N.s) for velocity error. The corrective feedback torques (N.m) were defined as $\tau =K_p.{dx}_2+K_{v_2}.{d\dot{x}}_2+K_{v_1}.{d\dot{x}}_1$with ${dx}_2$ and ${d\dot{x}}_2$ the positional (m) and velocity (m/s) error from the high-resolution secondary encoder, respectively, and ${d\dot{x}}_1$ the velocity error from the low-resolution primary encoder. The feedback torques were then converted to endpoint feedback forces (N) to be applied by the two-link robotic arm of the KINARM using a Jacobian transform matrix $F=\left[\begin{array}{cc}-L1.\text{sin}{\theta }_1& L1.\mathit{cos}{\theta }_1\\ -L2.\text{sin}{\theta }_2& L2.\mathit{cos}{\theta }_2\end{array}\right].\tau$, with $\mathrm{L}1$ and $\mathrm{L}2$ the length of each link, and ${\theta }_1$ and ${\theta }_2$ their angular position. The resulting feedback forces were then low-pass filtered using a second-order Butterworth filter with a 50 Hz cutoff.

Statistical analysis

Although for most experiments we used mixed-effect linear models to allow for individual intercepts, we used a repeated-measure ANOVA in Experiment 1 to compare reward magnitudes with each other independently. This allowed us to assess the effect of reward without assuming a magnitude-scaled effect in the first place. Paired-sample t tests were used when one-way repeated-measure ANOVAs reported significant effects, and effect sizes were obtained using partial ${\eta }^2$ and the Cohen's d method. For Experiment 2, we used mixed-effect linear models. For Experiments 3 and 4, mixed-effect linear models were also used to account for a possible confound between reward and peak velocity in stiffness regulation, while accounting for individual differences in speed using individual intercepts. Since Experiment 3 included a nested design (i.e., participants were assigned either to the right or left target but not both), we tested for an interaction using a two-way mixed-effect ANOVA to avoid an artificial inflation of p values (Zuur, 2009). For all ANOVAs, Bonferroni corrections were applied where appropriate, and post hoc paired-sample t tests were used if ANOVAs produced significant results. Bootstrapped 95% CIs of the mean were also obtained and plotted for every group.

Since trials consisted of straight movements toward the target, we considered position in the $y$ dimension (i.e., radial distance from the starting position) to obtain time-time correlation maps because it expresses most of the variability. To confirm this, reach trajectories were rotated so the target was always located directly in front, and error distribution in the $x$ and $y$ dimension was compared for both Experiments 1 and 2. The $y$ dimension indeed displayed a larger spread in error (Experiment 1: t_(11,156) = –16.15, p < 0.001, d = –0.31; Experiment 2: t_(14,852) = –13.68, p < 0.001, d = –0.22). Time-time correlation maps were analyzed by fitting a mixed-linear model for each time point (Zuur, 2009; Manohar et al., 2019) allowing for individual intercepts using the model $z\sim \mathrm{r}\mathrm{e}\mathrm{w}\mathrm{a}\mathrm{r}\mathrm{d}+\left(1\right|\mathrm{p}\mathrm{a}\mathrm{r}\mathrm{t}\mathrm{i}\mathrm{c}\mathrm{i}\mathrm{p}\mathrm{a}\mathrm{n}\mathrm{t})$, with $z$ the Fisher-transformed Pearson coefficient $\rho$ for that time point. Then clusters of significance, defined as time points with p < 0.05 for reward, were corrected for multiple comparisons using a clusterwise correction and 10,000 permutations (Nichols and Holmes, 2002; Maris and Oostenveld, 2007). This approach avoids unnecessarily stringent corrections, such as Bonferroni correction, by taking advantage of the spatial organization of the time-time correlation maps (Nichols and Holmes, 2002; Maris and Oostenveld, 2007).

Model simulations

We performed simulations of a simple dynamical system to observe how time-time correlation maps are expected to behave under different types of hypothetical controllers. The simulation code is available online on the Open Science Framework URL provided above. Simulation results were obtained by running 1000 simulations and obtaining time-time correlation values across those simulations. The sigmoidal activation function $S\left(t\right)$ used for simulations of the late component was a Gaussian cumulative distribution function such as the following:

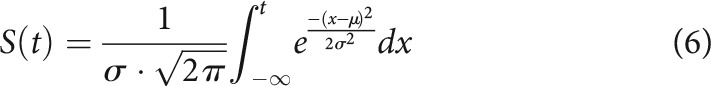with $\sigma =0.5,\mu =0.8\mathrm{s}$ (or 800 ms for our simulation, which is run in ms) and $t_0<t<t_f$ is the simulation time step. It should be noted that the use of a sigmoidal function is arbitrary and may be replaced by any other activation function, such as heaviside, although this will only alter the simulation outcomes quantitatively rather than qualitatively. Values of the feedback control term are taken from Manohar et al. (2019). On the other hand, different noise terms were taken for our simulations because previous work only manipulated one parameter per comparison, whereas we manipulated both noise and feedback at the same time in several models (Eqs. 16, 17) and the model is more sensitive to feedback control manipulation than to noise term manipulation.

Two alternative sets of models were used to assess the effect of signal-dependent noise and delay in feedback corrections, respectively. For the first set, the noise term was redefined as $\mathcal{N}(\mu ,\sigma (t\left)\right)$ with the following:

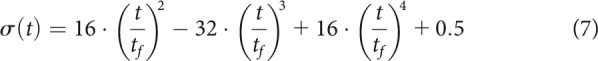with Equation 7 being proportional to the velocity profile of a minimum jerk reaching movement (Flash and Hogan, 1985). Here, the equation was adjusted so that $0.5\le \sigma \left(t\right)\le 1.5$, $\sigma \left(0\right)=\sigma \left(t_f\right)=0.5$ and $\sigma (t_f/2)=1.5$. The second set of models included a delay in feedback corrections, so that the feedback term $\beta \cdot x_t$ and its equivalent in different model variations became $\beta \cdot x_{t-399}$. A 400 time step delay was chosen because observed movement times in the reward-magnitude and reward-punishment experiments were on average between 350 and 400 ms, resulting in a feedback delay of $\sim 350\hspace{0.17em}\times \hspace{0.17em}400/1000\hspace{0.17em}=\hspace{0.17em}140$ms, which is within the range of feedback control delays expressed during reaching tasks (Pruszynski et al., 2011; Carroll et al., 2019).

Regarding model selection, comparisons were performed by fitting each of the five datasets to six candidate models as follows:

with Equation 8 representing a model with noise reduction, Equation 9 a model with increased feedback control, Equation 10 a model with late noise reduction, Equation 11 a model with late increase in feedback control, Equation 12 a model with increased feedback and late noise reduction, and Equation 13 a model with late noise reduction and increased feedback. The free parameters were $\beta$ and $\gamma$, with the last two models including both of them and all others including one. $S\left(t\right)$ was a sigmoidal activation function as indicated in Equation 6 and was fixed. A total of 1000 simulations were done with 1000 time steps per simulation. Time-time correlation maps were then Fisher-transformed and substracted from a control model $x_{t+1}=x_t+\mathcal{N}(\mu ,\sigma )$ for Equation 8 and $x_{t+1}=x_t-0.002\cdot x_t+\mathcal{N}(\mu ,\sigma )$ for all other models to obtain contrast maps. The resulting contrast maps were then fitted to the empirical contrast maps obtained to minimize the sums of squared errors for each individual for individual-level analysis, and across individuals for the group-level analysis. Of note, rather than fitting the model to the across-participant averaged contrast map in the group-level analysis, the model minimized all the individual maps at once, allowing for a single model fit for the group without averaging away individual map features. The optimization process was done using the fminsearch function of the Optimization toolbox in MATLAB. The free parameter search was initialized with ${\beta }_0=0$ and ${\gamma }_0=0$. Model comparisons were performed by finding the model with lowest BIC, defined as $BIC=n\mathrm{l}\mathrm{o}\mathrm{g}(RSS/n)+k\mathrm{l}\mathrm{o}\mathrm{g}n$ with $n=100^2=10\text{,}000$ the number of time points per participant map, $k$ the number of parameters in the model considered, and $RSS$ the model's residual sum of squares.

Results

Reward concomitantly enhances action selection and action execution

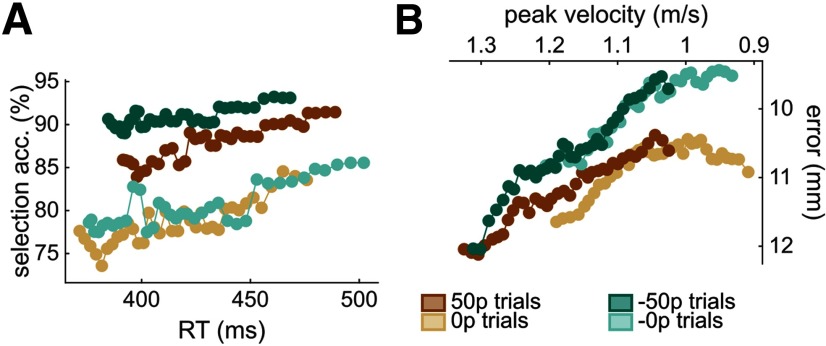
Experiment 1 examined the effect of reward on the selection and execution components of a reaching movement. First, we assessed whether the speed-accuracy functions were altered by reward. As expected, reward shifted the speed-accuracy functions for both selection and execution, underlining augmented motor performance (Fig. 2A,B). Comparing each variable of interest individually, participants showed a clear and consistent improvement in selection accuracy in the presence of reward. Specifically, they were less likely to be distracted in rewarded trials, although this was independent of reward magnitude (repeated-measures ANOVA, F₍₂₎ = 15.8, p = 0.001, partial η² = 0.35; post hoc 0 p vs 10 p, t₍₂₉₎ = –3.34, p = 0.005, d = –0.61; 0 p vs 50 p, t₍₂₉₎ = –5.32, p < 0.001, d = –0.97; 10 p vs 50 p, t₍₂₉₎ = –2.21, p = 0.07, d = –0.49; Fig. 3A). However, this did not come at the cost of slowed decision-making, as reaction times remained largely similar across reward values; if anything, reaction times were slightly shorter if a large reward (50 p) was available compared with no-reward (0 p) trials, although this was not statistically significant (F₍₂₎ = 2.35, p = 0.10, partial η² = 0.07; Fig. 3B,C).

Figure 2.

Speed-accuracy functions for selection (A) and execution (B) shift as reward values increase. The functions are obtained by sliding a 30% centile window over 50 quantile-based bins. A, For the selection panel, the count of nondistracted trials and distracted trials for each bin was obtained, and the ratio (100 × nondistracted/total) calculated afterward. B, For the execution component, the axes were inverted to match the selection panel in A. Top left corner indicates faster and more accurate performance (see Data analysis).

Figure 3.

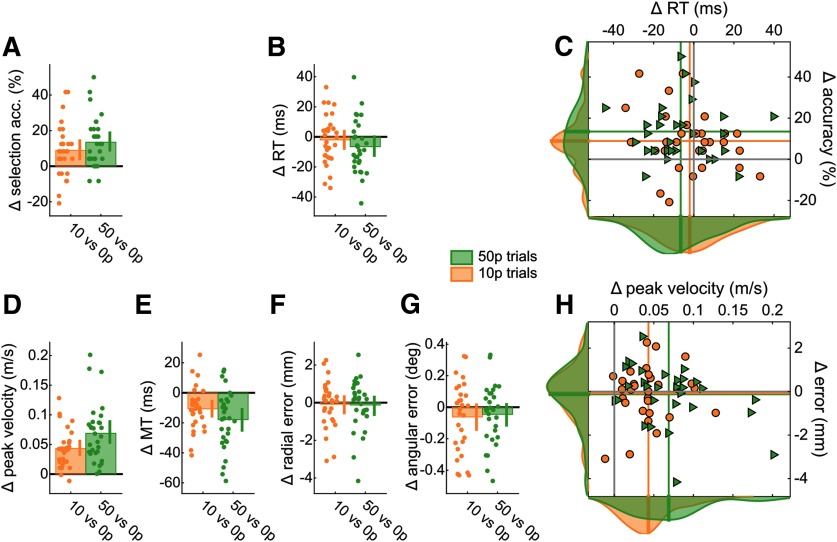
Reward enhances performance in both selection and execution. For all bar plots, data were normalized to 0 p performance for each individual. Bar height indicates group mean. Dots represent individual values. Error bars indicate bootstrapped 95% CIs of the mean. A, Selection accuracy, as the percentage of trials where participants initiated reaches toward the correct target instead of the distractor target. B, Mean reaction times. C, Scatterplot of mean reaction time against selection accuracy. Values are normalized to 0 p trials. Colored lines indicate the mean value for each condition. Solid gray lines indicate the origin (i.e., 0 p performance). Data distributions are displayed on the sides, with transversal bars indicating the mean of the distribution. Triangles represent 50 p trials. D, Mean peak velocity during reaches. E, Mean movement times of reaches. F, Mean radial error at the end of the reach. G, Mean angular error at the end of the reach. H, Scatterplot showing execution speed (peak velocity) against execution accuracy (radial error), similar to C.

In addition, reward led to a marked improvement in action execution by increasing peak velocity that scaled with reward magnitude, although this was driven by three extreme values (F₍₂₎ = 43.0, p < 0.001, partial η² = 0.60; post hoc 0 p vs 10 p, t₍₂₉₎ = –7.40, p < 0.001, d = –1.35; 0 p vs 50 p, t₍₂₉₎ = –7.61, p < 0.001, d = –1.39; 10 p vs 50 p, t₍₂₉₎ = –3.52, p = 0.003, d = –0.64; Fig. 3D). Unsurprisingly, movement time also showed a similar effect; that is, mean movement time decreased with reward, although this did not scale with reward magnitude (F₍₂₎ = 15.3, p < 0.001, partial η² = 0.35; post hoc 0 p vs 10 p, t₍₂₉₎ = 4.07, p < 0.001, d = 0.74; 0 p vs 50 p, t₍₂₉₎ = 4.99, p < 0.001, d = 0.91; 10 p vs 50 p, t₍₂₉₎ = 2.08, p = 0.09, d = 0.38; Fig. 3E). However, this reward-based improvement in speed did not come at the cost of accuracy as radial error (F₍₂₎ = 0.15, p = 0.86, partial η² = 0.005) and angular error (F₍₂₎ = 1.51, p = 0.23, partial η² = 0.05) remained unchanged (Fig. 3F–H).

These results demonstrate that reward enhanced the selection and execution components of a reaching movement simultaneously. Interestingly, these improvements were mainly driven by an increase in accuracy for selection and in speed for execution. However, reward magnitude had only a marginal impact, as opposed to the presence or absence of reward per se. Consequently, for the remaining studies, we used the 0 and 50 p trial conditions to assess the impact of reward on reaching performance.

Punishment has the same effect as reward on selection but a noncontingent effect on execution

Next, we asked whether punishment led to the same effect as reward, as previous reports have shown that they have dissociable effects on motor performance (Wachter et al., 2009; Galea et al., 2015; Song and Smiley-Oyen, 2017; Hamel et al., 2018). The reward block consisted of randomly interleaved 0 and 50 p trials, whereas the punishment block consisted of –0 p and –50 p trials, indicating the maximum amount of money that could be lost on a single trial as a result of slow reaction times and movement times.

First, we obtained speed-accuracy functions for the selection and execution components in the same way as for Experiment 1 (Fig. 4). While punishment had a similar effect on selection (Fig. 4A), it produced dissociable effects on execution (Fig. 4B). Specifically, while peak velocity increased with punishment similarly to reward, it was accompanied by an increase in radial error. Although this could suggest that punishment does not cause a change in the speed-accuracy function relative to its own baseline (−0 p) trials, a clear shift in the speed-accuracy function could be seen between the baseline trials of the reward and punishment conditions (Fig. 4B). Therefore, relative to reward, a punishment context appeared to have a noncontingent beneficial effect on motor execution.

Figure 4.

Reward and punishment affect speed-accuracy functions for selection (A) and execution (B) components. The functions are obtained by sliding a 30% centile window over 50 quantile-based bins. A, For the selection panel, the count of nondistracted trials and distracted trials for each bin was obtained, and the ratio (100 × nondistracted/total) calculated afterward. B, For the execution component, the axes were inverted to match the selection panel in A. Top left corner indicates faster and more accurate performance (see Data analysis).

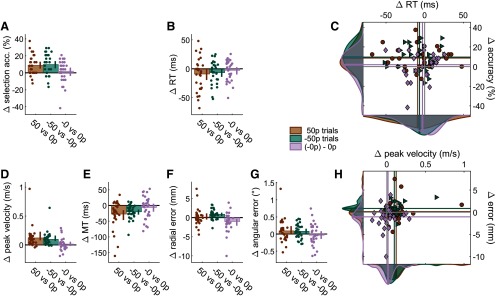
To examine these results further, we fitted a mixed-effect linear model $\mathrm{D}\mathrm{V}\sim 1+\mathrm{R}\mathrm{P}+\mathrm{v}\mathrm{a}\mathrm{l}\mathrm{u}\mathrm{e}+\mathrm{R}\mathrm{P}:\mathrm{v}\mathrm{a}\mathrm{l}\mathrm{u}\mathrm{e}+\left(1\right|\mathrm{p}\mathrm{a}\mathrm{r}\mathrm{t}\mathrm{i}\mathrm{c}\mathrm{i}\mathrm{p}\mathrm{a}\mathrm{n}\mathrm{t})$ that included individual intercepts and an interaction term, where $DV$ is the dependent variable considered, $RP$ indicated whether the context was reward or punishment (i.e., reward block or punishment block), and value indicated whether the trial is a baseline trial bearing no value (0 p and –0 p) or a rewarded/punished trial bearing high value (50 and –50 p). As in Experiment 1, value improved selection accuracy (β = 9.72, CI = [4.51, 14.9], t₍₁₁₆₎ = 3.70, p < 0.001; Fig. 5A) without any effect on reaction times (β = –0.007, CI = [–0.015, 0.002], t₍₁₁₆₎ = –1.53, p = 0.13; Fig. 5B,C) and increased peak velocity and decreased movement time (main effect of value on peak velocity, β = 0.096, CI = [0.045, 0.147], t₍₁₁₆₎ = 3.76, p < 0.001; on movement time, β = –0.02, CI = [–0.033, 0.007], t₍₁₁₆₎ = –3.15, p = 0.002; Fig. 5D,E) at no accuracy cost (radial error, β = –0.085, CI = [–0.001, 0.171], t₍₁₁₆₎ = 1.96, p = 0.052; angular error, β = –0.081, CI = [–0.027, 0.189], t₍₁₁₆₎ = 1.49, p = 0.14; Fig. 5F–H), therefore replicating the findings from Experiment 1. Importantly, context (reward vs punishment) did not alter these effects on selection accuracy (main effect of block, β = –1.94, CI = [–7.15, 3.26], t₍₁₁₆₎ = –0.74, p = 0.46; interaction, β = –0.97, CI = [–8.34, 6.39], t₍₁₁₆₎ = –0.26, p = 0.79; Fig. 5A), reaction times (main effect of block, β = –0.003, CI = [–0.006, 0.011], t₍₁₁₆₎ = –0.66, p = 0.51; interaction, β = –0.002, CI = [–0.014, 0.010], t₍₁₁₆₎ = –0.38, p = 0.70; Fig. 5B), or peak velocity (main effect of block, β = –0.015, CI = [–0.066, 0.036], t₍₁₁₆₎ = –0.59, p= 0.56; interaction, β = –0.024, CI = [–0.047, 0.096], t₍₁₁₆₎ = –0.67, p = 0.50; Fig. 5D). Finally, in line with the observed speed-accuracy functions, the punishment context did affect radial accuracy, with accuracy increasing compared with the rewarding context (main effect of block, β = 0.10, CI = [0.019, 0.19], t₍₁₁₆₎= 2.42, p = 0.017; Fig. 5F), although no interaction was observed (β = –0.07, CI = [–0.19, 0.05], t₍₁₁₆₎ = –1.16, p = 0.25). This can be directly observed when comparing baseline values, as radial error in the –0 p condition was on average smaller than in the 0 p condition (Fig. 5F, pink group).

Figure 5.

Reward and punishment have a similar effect on selection, but not on execution. For all bar plots, data were normalized to baseline performance (0 p or −0 p) for each individual. Bar height indicates group mean. Dots represent individual values. Error bars indicate bootstrapped 95% CIs of the mean. A, Selection accuracy. B, Mean reaction times for each participant. C, Scatterplot of mean reaction time against selection accuracy. Values are normalized to 0 p trials. Colored lines indicate mean values for each condition. Solid gray lines indicate the origin (i.e., 0 p performance, or −0 p, in the punishment condition). Data distributions are displayed on the sides, with transversal bars indicating the mean of the distribution. Circles, triangles and rhombi represent 50 p, −50 p and (−0 p), and −0 p trials, respectively. D, Mean peak velocity. E, Movement times. F, For radial error, punishment did not protect against an increase in error, while reward did. However, a difference can be observed between the baselines (blue bar). G, Angular error. H, Scatterplot showing execution speed (peak velocity) against execution accuracy (radial error), similar to C.

Reward reduces execution error through increased feedback correction and late noise reduction

How do reward and punishment lead to these improvements in motor performance? In saccades, it has been suggested that reward increases feedback control, allowing for more accurate endpoint performance. To test for this possibility, we performed the same time-time correlation analysis as described by Manohar et al. (2019). Specifically, we assessed how much the set of positions at time $t$ across all trials correlated with the set of positions at any other time $t\pm n$ (e.g., $t+1$ or $t-5)$. If movements are stereotyped across trials, this correlation will be high because the early position will provide a large amount of information about the later or earlier position. On the other hand, if trajectories are variable over time within a trial, the correlation will decrease because there will be no consistency in the evolution of position over time. Importantly, the latter occurs with high online feedback because corrections are not stereotyped, but rather dependent on the random error on a given trial (Manohar et al., 2019). If the same mechanism is at play during reaching movements as in saccades, a similar decrease in time-time correlations should be observed.

All time points' correlations were performed by comparing position over trials by centiles, leading to 100 time points along the trajectory (Fig. 6A–G). Across Experiments 1 and 2, we observed an increase in time-time correlation in the late part of movement both with reward and punishment (Fig. 6H–K), although this did not reach significance in the 50 p-0 p condition of the second experiment (Fig. 6J) and the significance cluster size was relatively small in the 10 p-0 p condition (Fig. 6H). In contrast, the early to middle part of movement showed a clear decorrelation that was significant in three conditions but not in the 50 p-0 p condition of the first experiment. Surprisingly, no difference was observed when comparing baseline trials from Experiment 2 (Fig. 6L), which is at odds with the behavioral observations that radial error was reduced in the –0 p condition compared with 0 p (Fig. 5F). Overall, although quantitative differences are observed across cohorts, their underlying features are qualitatively similar (with the exception of the baselines contrast; Fig. 6L), displaying a decrease in correlation during movement followed by an increase in correlation at the end of movement. This suggests that a common mechanism may take place. To assess the global trend across cohorts, we pooled all cohorts together a posteriori, and indeed observed a weak early decorrelation, followed by a strong increase in correlation late in the movement (Fig. 6M). Interestingly, this consistent biphasic pattern across conditions and experiments is the opposite to the one observed in saccades (Manohar et al., 2019). Therefore, this analysis would suggest that reward/punishment causes a decrease in feedback control during the late part of reaching movements. However, a reduction in feedback control should result in a decrease in accuracy, which was not observed in our data. A more likely possibility is that another mechanism is being implemented that enables movements to be performed with enhanced precision under reward and punishment.

One possible candidate is muscle cocontraction. By simultaneously contracting agonist and antagonist muscles around a given joint, the nervous system is able to regulate the stiffness of that joint. Although this is an extremely energy inefficient mechanism, it has been repeatedly shown that it is very effective at improving arm stability in the face of unstable environments, such as force fields (Franklin et al., 2003). Critically, it is also capable of dampening noise (Selen et al., 2009), which arises with faster reaching movements, and therefore enables more accurate performance (Todorov, 2005). Therefore, it is possible that increased arm stiffness could, at least partially, underlie the effects of reward and punishment on motor performance.

Simulation of time-time correlation maps with a simplified dynamical system

To assess whether the correlation maps we observed are in line with this interpretation, we performed simulations using a simplified control system (Manohar et al., 2019) and evaluated how it responded to hypothesized manipulations of the control system. Let us represent the reach as a discretized dynamical system (Todorov, 2004) as follows:

The state of the system at time $t$ is represented as $x_t$, the motor command as $u_t$, and the system is susceptible to a random Gaussian process with mean $\mu =0$ and variance $\sigma =1$. $\alpha$and $\beta$ represent the environment dynamics and control parameter, respectively. For simplicity, we initially assume that $\alpha =1,\beta =0$, and that $x_0=0$. Therefore, any deviation from $0$ is solely due to the noise term that contaminates the system at every time step.

We performed 1000 simulations, each including 1000 time steps, and show the time-time correlation maps of the different controllers under consideration. First, we assume that no feedback has taken place ($\beta =0$, Eq. 14). The system is therefore only driven by the noise term (Fig. 7A). The controller can reduce the amount of noise (e.g., through an increase in stiffness) (Selen et al., 2009). This can be represented as $x_{t+1}=x_t+\gamma \cdot \mathcal{N}(\mu ,\sigma )$ with $\gamma =0.5$. However, this would not alter the correlation map (Fig. 7B,C) as was previously shown (Manohar et al., 2019) because the noise reduction occurs uniformly over time. Now, if a feedback term is introduced with $\beta =-0.002$ and $u_t=x_t$, the system includes a control term that will counter the noise and becomes the following:

With such a corrective feedback term, the goal of the system becomes to maintain the state at 0 for the duration of the simulation. This is equivalent to assuming that $x$ represents error over time and the controller has perfect knowledge of the optimal movement to be performed. Higher feedback control ($\beta =-0.003$) would reduce errors even further. Comparing this high feedback model with the low feedback model (Eq. 15; Fig. 7D,E), we see that the contrast (Fig. 7F) shows a reduction in time-time correlations similar to what is observed in the late part of saccades (Manohar et al., 2019) and in the early part of arm reaches in our dataset(Fig. 6H–K). Since our dataset displays a biphasic correlation map, it is likely that two phenomena occur at different time points during the reach. To simulate this, we altered the original model by including a sigmoidal activation function $S\left(t\right)$ that is inactive early on ($S_0=0$) and becomes active ($S_{t_f}=1$) during the late part of the reach (for details, see Model simulations). This leads to two possible mechanisms, namely, a late increase in feedback or a late reduction in noise as follows:

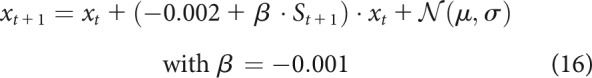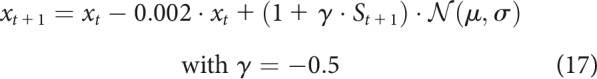The results show that a late increase in feedback causes decorrelation at the end of movement (Eq. 16; Fig. 7G,H), which is the opposite of what we observe in our results. However, similar to our behavioral results, a late reduction in noise causes an increase in the correlation values at the end of movement (Eq. 17; Fig. 7I,J). Therefore, our results (Fig. 6H–K) appear to be qualitatively similar to a combined model in which reward and punishment cause a global increase in feedback control and a late reduction in noise (Eq. 18; Fig. 7K,L) as follows:

The simulations displayed here incorrectly assume that feedback can account for errors from one time step to the next, that is nearly immediately (Bhushan and Shadmehr, 1999) and that the noise term remains the same throughout the reach (Todorov, 2004; Shadmehr and Krakauer, 2008). To explore whether these features would alter our observations, we simulated two alternative sets of models. A first set included a delay of 400 time steps in the feedback response (Fig. 7M), and a second set included a bell-shaped noise term similar to a reach with signal-dependent noise under minimum jerk conditions (Fig. 7N). Both sets of simulation produced results similar to those observed in the original set of models.

Quantitative model comparison

To formally test which candidate model best describes our empirical observations, we fitted each of them to the experimental datasets. Each of the five empirical conditions displayed in Figure 6H–L was kept separate, each condition representing a cohort, and their fit assessed separately. While individually fitted models present several advantages over group-level analysis, it has been argued that the most reliable approach to determine the best-fit model is to assess its performance both on individual and group data and compare the outcomes (Cohen et al., 2008; Lewandowsky and Farrell, 2011) and we will therefore follow this approach. We included six candidate models in our analysis: noise reduction (one free parameter $\gamma$; Fig. 7C), increased feedback (one parameter $\beta$; Fig. 7E), late feedback (one parameter $\beta$; Fig. 7H), late noise reduction (one parameter $\gamma$; Fig. 7J), increased feedback with late noise reduction (two parameters $\beta$ and $\gamma$; Fig. 7L), and an additional model with noise reduction and a late increase in feedback control (two parameters $\beta$ and $\gamma$).

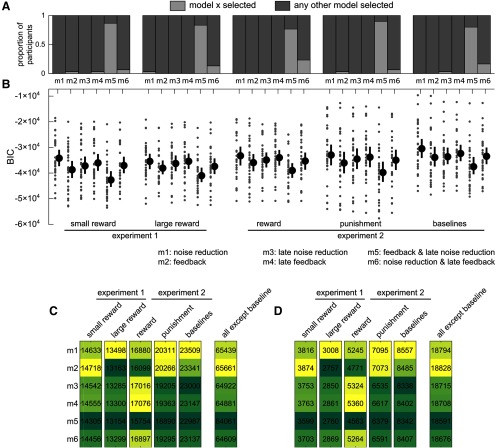
Individual-level analysis resulted in the increased feedback with late noise reduction model being selected by a strong majority of participants for each cohort (Cohorts 1–5: χ² = $[97.6,$ $76.8,$ $74.4,$ $116.8,$ $83.2]$, all $p<0.001$; Fig. 8A), confirming qualitative predictions. The best-fit model for each participant was defined as the model displaying the lowest Bayesian information critetion (BIC) (Fig. 8B). This allowed us to account for each model's complexity because the BIC penalizes models with more free parameters. Of note, the “baselines” cohort displayed the highest BIC for all models considered. However, this should not be surprising, considering that this cohort is the only one that showed no significant trend in its contrast map (Fig. 6L). To confirm that the selected model is indeed the most parsimonious choice, we compared the individual-level outcome with a group-level outcome. Each candidate model was fit to all individual correlation maps at once, thereby allowing for each free parameter to take a single value per cohort. This is equivalent to assuming that the parameters are not random but rather fixed effects, allowing us to observe the population-level trend with higher certainty, although at the cost of ignoring its variability (Cohen et al., 2008; Lewandowsky and Farrell, 2011). Again, for every cohort except the baseline cohort, the model with lowest residuals sum of squares (Fig. 8A) and lowest BIC (Fig. 8B) was the increased feedback with late noise reduction model, although the increased feedback model BIC was marginally lower for the large-reward cohort (Δ BIC = $4$) and therefore was a similarly good fit. Finally, fitting all nonbaseline cohorts yielded the same result. Comparing group-level and invidividual-level model comparisons, we observe that the same model is consistently selected across all experimental cohorts besides the baselines cohort, corroborating the hypothesis that late noise reduction occurs alongside a global increase in feedback control in the presence of reward or punishment. As mentioned previously, one way to increase noise resistance during a motor task is by increasing joint stiffness, a possibility that we test in the following experiment.

Figure 8.

Model comparisons for individual and group fits. A, Proportion of participants whose winning model was the one considered (light gray) against all other models (dark gray) for every cohort. B, Individual and mean BIC values for each participant and each model. Lower BIC values indicate a more parsimonious model. Dots represent individual BICs. Black dot represents the group mean. Error bars indicate the bootstrapped 95% CIs of the mean. C, Residual sum of squares for group-level fits. Darker colors represent lower values. D, Same as in C, but for BIC. fb, Feedback; noise red., noise reduction.

The effect of reward on endpoint stiffness at the end of the reaching movement

Next, we experimentally tested whether the reduction in noise observed in the late part of reward trials was associated with an increase in stiffness. For simplicity, we focused on the reward context only from this point. We recruited another set of participants (N = 30) to reach toward a single target 20 cm away from a central starting position in 0 and 50 p conditions, and used a well-established experimental approach to measure stiffness(Fig. 9A) (Burdet et al., 2000; Selen et al., 2009) (for details, see Materials and Methods).

Figure 9.

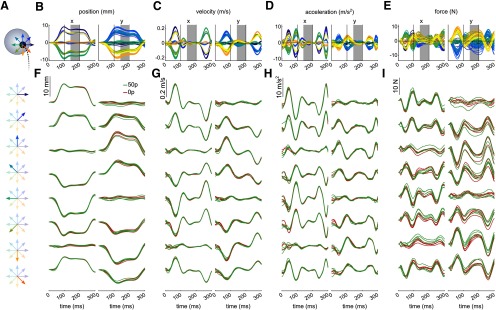
Displacement profiles at the end of the reach for a single participant. A, Schematic of the displacement. Gray circle represents a target. Black circle represents the cursor. Dashed line indicates the past trajectory. At the end of the movement, when velocity decreased behind a threshold of 0.03 m/s, a displacement occasionally occurred in 1 of 8 possible directions. Colored arrow indicates each direction. B, Position over time during the displacement for a participant. Right and left columns indicate the x and y dimensions, respectively. C, Velocity profile. D, Acceleration profile. E, Force profile. Two vertical black solid lines indicate the limit between the ramp-up and plateau, and plateau and ramp-down phase. Values for each variable were taken as the average over time during the 140-200 ms window (gray area), when the displacement is clamped and most stable. F-I, Details of the displacement profiles for each direction independently. 0 and 50 p trials are also represented in red and green, respectively, for comparison.

Figure 9B–E shows the displacement profile of a single participant. Stiffness estimates were assessed during the plateau phase, marked by the gray area, in which the displacement was most stable (Fig. 9B,C). While the y dimension exhibited more variability than the x dimension, this increased variability was within the same range for both the 0 and 50 p trials (Fig. 9F–I). Additionally, while peak velocity was higher during the movement in the reward condition, we can see in Figure 9G that velocity was within similar ranges across conditions at the start of the displacement, underlining that stiffness estimates were unlikely to be biased by velocity through the measurement technique used. A paired t test of mean velocity at displacement onset for each reward condition and across participants yielded a nonsignificant result (x dimension: t₍₂₉₎ = –1.75, p = 0.09; y dimension: t₍₂₉₎ = 1.17, p = 0.25); idem for mean acceleration at displacement onset (x dimension: t₍₂₉₎ = 0.39, p = 0.70; y dimension: t₍₂₉₎ = –0.11, p = 0.91).

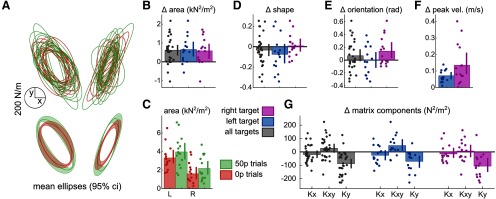
To quantify the global amount of stiffness, we compared the ellipse area across conditions (Fig. 10A–C). In line with our hypothesis, the area substantially increased in rewarded trials compared with non-rewarded trials (Fig. 10A,B). This effect of reward was very consistent across both target positions (Fig. 10B), although absolute stiffness was globally higher for the left target (Fig. 10C). On the other hand, other ellipse characteristics, such as shape and orientation (Fig. 10D,E), showed less sensitivity to reward. However, since reward also increased average velocity (Fig. 10F), in line with our previous results, perhaps this increase in stiffness is a response to higher velocity rather than reward. To avoid this confound, we fitted a mixed-effect linear model, allowing for individual intercepts and target position intercept, where variance in area could be explained both by reward and velocity: $\mathrm{a}\mathrm{r}\mathrm{e}\mathrm{a}\sim 1+\mathrm{r}\mathrm{e}\mathrm{w}\mathrm{a}\mathrm{r}\mathrm{d}+\mathrm{p}\mathrm{e}\mathrm{a}\mathrm{k}\mathrm{v}\mathrm{e}\mathrm{l}\mathrm{o}\mathrm{c}\mathrm{i}\mathrm{t}\mathrm{y}+\left(1\right|\mathrm{p}\mathrm{a}\mathrm{r}\mathrm{t}\mathrm{i}\mathrm{c}\mathrm{i}\mathrm{p}\mathrm{a}\mathrm{n}\mathrm{t})+(1\left|\mathrm{t}\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{e}\mathrm{t}\right)$. As expected, reward, but not peak velocity, could explain the variance in ellipse area (peak velocity: $p=0.46$; reward: $p=0.003$; Table 1), confirming that the presence of reward results in higher global stiffness at the end of the movement. In contrast, fitting a model with the same explanatory variables to the $Ky$ component of the stiffness matrices, which showed the greatest sensitivity to reward compared with the other components (Fig. 10G), revealed that not only reward ($p<0.001$, Bonferroni corrected) but also peak velocity (p = 0.025, Bonferroni-corrected; Table 2) explained the observed variance (model: $Ky\sim 1+\mathrm{r}\mathrm{e}\mathrm{w}\mathrm{a}\mathrm{r}\mathrm{d}+\mathrm{p}\mathrm{e}\mathrm{a}\mathrm{k}\mathrm{v}\mathrm{e}\mathrm{l}\mathrm{o}\mathrm{c}\mathrm{i}\mathrm{t}\mathrm{y}+\left(1\right|\mathrm{p}\mathrm{a}\mathrm{r}\mathrm{t}\mathrm{i}\mathrm{c}\mathrm{i}\mathrm{p}\mathrm{a}\mathrm{n}\mathrm{t})+(1\left|\mathrm{t}\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{e}\mathrm{t}\right)$). In comparison, no significant effects were found to relate to the $Kx$ component (reward: $p=0.21$, peak velocity: $p=1$, Bonferroni-corrected; $Kx\sim 1+\mathrm{r}\mathrm{e}\mathrm{w}\mathrm{a}\mathrm{r}\mathrm{d}+\mathrm{p}\mathrm{e}\mathrm{a}\mathrm{k}\mathrm{v}\mathrm{e}\mathrm{l}\mathrm{o}\mathrm{c}\mathrm{i}\mathrm{t}\mathrm{y}+\left(1\right|\mathrm{p}\mathrm{a}\mathrm{r}\mathrm{t}\mathrm{i}\mathrm{c}\mathrm{i}\mathrm{p}\mathrm{a}\mathrm{n}\mathrm{t})+(1\left|\mathrm{t}\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{e}\mathrm{t}\right)$).

Figure 10.

Reward increases stiffness at the end of movement. A, Individual (top) and mean (down) stiffness ellipses. Shaded areas around the ellipses represent bootstrapped 95% CIs. Right and left ellipses represent individual ellipses for the right and left target, respectively. B, Ellipses area normalized to 0 p trials. Error bars indicate bootstrapped 95% CIs. C, Non-normalized area values are also provided to illustrate the difference in absolute area as a function of target. L, Left target; R, right target. D, Ellipse shapes normalized to 0 p trials. Shapes are defined as the ratio of short to long diameter of the ellipse. E, Ellipse orientation normalized to 0 p trials. Orientation is defined as the angle of the ellipse's long diameter. F, Peak velocity normalized to 0 p trials. Peak velocity increased with reward. G, Stiffness matrix elements for 50 p trials normalized to the stiffness matrix for 0 p trials.

Table 1.

Mixed-effect model for stiffness area at the vicinity of the target

Model:
area ∼ 1 + velocity + reward + (1 | target) + (1 | participant)
No. of observations	60	AIC	1562.1
Fixed effects coefficients	3	BIC	1574.6
Random effects coefficients	32	Log-likelihood	−775.03
Covariance parameters	3	Deviance	1550.1
Fixed effects coefficients (95% CIs):
Variable	Estimate	SE	t statistic	df	p value	Lower	Upper
Intercept	1.58E + 05	1.09E + 05	1.4411	57	0.15501	−61456	3.77E + 05
Velocity	84461	83260	1.0144	57	0.31467	−82266	2.51E + 05
Reward	52737	15180	3.4741	57	0.000986	22340	83134
Random effects covariance parameters (95% CIs):
Variable	Levels	Type	Estimate	Lower	Upper
Target	2	SD	89,384	28,576	279,590
Participant	30	SD	1.2749	96,198	1.69E + 05
Error	60	Residual SD	48,540	37,688	62518

Table 2.

Mixed-effect model for stiffness Ky component at the vicinity of the target

Model:
Ky ∼ 1 + velocity + reward + (1 | target) + (1 | participant)
No. of observations	60	AIC	731.43
Fixed effects coefficients	3	BIC	743.99
Random effects coefficients	32	Log-likelihood	−359.71
Covariance parameters	3	Deviance	719.43
Fixed effects coefficients (95% CIs):
Variable	Estimate	SE	t statistic	df	p value	Lower	Upper
Intercept	−178.28	80.817	−2.206	57	0.031432	−340.11	−16.447
Velocity	−205.92	75.341	−2.7331	57	0.008341	−356.78	−55.049
Reward	−66.893	16.903	−3.9575	57	0.000212	−100.74	−33.046
Random effects covariance parameters (95% CIs):
Variable	Levels	Type	Estimate	Lower	Upper
Target	2	SD	8.6E-05	NA	NA
Participant	30	SD	107.1	79.9	143.6
Error	60	Residual SD	58.18	45.16	74.94

Because interactions with nested elements cannot be compared directly using a mixed-effect linear model (Zuur et al., 2010; Schielzeth and Nakagawa, 2013; Harrison et al., 2018), we used a repeated-measures ANOVA to compare the interaction between reward and target on stiffness. No interaction between reward and target location was observed on area (F₍₁₎ = 0.069, p= 0.79, partial η² < 0.001; Fig. 10A,C).

To better understand the relationship between end-reach stiffness and mid-reach velocity independently of reward value, we took advantage of the fact that participants tend to reach at different speeds compared with one another. We fitted a linear model $Ky\sim \mathrm{p}\mathrm{e}\mathrm{a}\mathrm{k}\mathrm{v}\mathrm{e}\mathrm{l}\mathrm{o}\mathrm{c}\mathrm{i}\mathrm{t}\mathrm{y}$ and $Kx\sim \mathrm{p}\mathrm{e}\mathrm{a}\mathrm{k}\mathrm{v}\mathrm{e}\mathrm{l}\mathrm{o}\mathrm{c}\mathrm{i}\mathrm{t}\mathrm{y}$ for each reward value independently, to assess how stiffness changes as a function of reaching speed across individuals when the reward value is fixed. We found that peak velocity did not explain $Ky$ or $Kx$ ($p=0.30$ and p = $0.30$, respectively; Bonferonni-corrected) for non-rewarded trials, while it explained $Ky$ but not $Kx$ for rewarded trials ($p=0.0147$ and p = $0.37$, respectively). This confirms that velocity only affects end-reach stiffness in the y direction. Interestingly, it also suggests that stiffness variance cannot be explained by peak velocity at all at the lower speeds expressed in 0 p conditions.

We conclude that endpoint stiffness is sensitive to both reward and velocity. However, the velocity-driven increase in stiffness is specific to the dimension that this velocity is directed toward, whereas the reward-driven increase in stiffness is nondirectional, at least in our task. This is likely because our task does not distinguish direction of error (i.e., error in the $y$ dimension is not more punishing than in the $x$ dimension) and so error must be reduced in all dimensions (Selen et al., 2009).

Reward does not alter endpoint stiffness at the start of the movement

Finally, the time-time correlation maps also suggest that the increase in stiffness should only occur at the end of the reaching movement, since the early and middle parts show an opposite effect (decorrelation). Therefore, an increase in endpoint stiffness should not be present immediately before the reach. Unlike the previous experiment, reward and velocity in the subsequent reach had no impact on stiffness, either by the matrix component $Ky$ (reward: $p=0.19$; peak velocity: $p=0.45$; Table 3), or by area (reward: $p=0.35$; peak velocity: $p=0.75$; Table 4), corroborating our interpretation of the correlation map (Fig. 11).

Table 3.

Mixed-effect model for stiffness Ky component at the start of the movement

Model:
area ∼ 1 + velocity + reward + (1 | participant)
No. of observations	40	AIC	1000.4
Fixed effects coefficients	3	BIC	1008.9
Random effects coefficients	20	Log-likelihood	−495.22
Covariance parameters	2	Deviance	990.45
Fixed effects coefficients (95% CIs):
Variable	Estimate	SE	t statistic	df	p value	Lower	Upper
Intercept	176720	105090	1.6817	37	0.10106	−36206	389640
Velocity	−34147	106840	−0.3196	37	0.75107	−250630	182330
Reward	11547	12086	0.95537	37	0.34559	−12942	36036
Random effects covariance parameters (95% CIs):
Variable	Levels	Type	Estimate	Lower	Upper
Participant	20	SD	104260	75922	143160
Error	NA	Residual SD	22268	16332	30360

Table 4.

Mixed-effect model for stiffness area at the start of the movement

Model:
Ky ∼ 1 + velocity + reward + (1 | participant)
No. of observations	40	AIC	460.82
Fixed effects coefficients	3	BIC	469.27
Random effects coefficients	32	Log-likelihood	−225.41
Covariance parameters	2	Deviance	450.82
Fixed effects coefficients (95% CIs):
Variable	Estimate	SE	t statistic	df	p value	Lower	Upper
Intercept	−421.01	134.26	−3.188	37	0.0029121	−700.04	−155.98
Velocity	184.74	138.08	1.3379	37	0.18909	−95.041	464.53
Reward	−12.34	16.319	−0.75617	37	0.45434	−45.406	20.726
Random effects covariance parameters (95% CIs):
Variable	Levels	Type	Estimate	Lower	Upper
Participant	30	SD	97.543	70.244	135.45
Error	NA	Residual SD	32.425	23.767	44.237

Figure 11.

Reward does not alter stiffness at the start of movement. A, Individual (top) and mean (down) stiffness ellipses. Shaded areas around the ellipses represent bootstrapped 95% CIs. Right and left ellipses represent individual ellipses for the right and left target, respectively. B, Ellipses area normalized to 0 p trials. Error bars indicate bootstrapped 95% CIs. C, Stiffness matrix elements for 50 p trials normalized to the stiffness matrix for 0 p trials. D, Peak velocity normalized to 0 p trials. E, Ellipse shapes normalized to 0 p trials. Shapes are defined as the ratio of short to long diameter of the ellipse. F, Ellipse orientation normalized to 0 p trials. Orientation is defined as the angle of the ellipses' long diameter.

Discussion

Here, we demonstrated that reward simultaneously improves the selection and execution components of a reaching movement. Specifically, reward promoted the selection of the correct action in the presence of distractors, while also improving execution through increased speed and maintenance of accuracy, resulting in a shift of each component's speed-accuracy functions. In addition, punishment had a similar impact on action selection and execution, although it enhanced execution performance across all trials within a block; that is, its impact was independent from the current trial value. Computational analysis revealed that the effect of reward on execution involved a combination of increased feedback control and noise reduction, which we then showed was due to an increase in arm stiffness at the end of the reaching movement. Overall, we confirm previous observations that feedback control increases with reward, and propose a new error-managing mechanism that the control system uses under reward: regulation of arm stiffness.

Our results add to the literature arguing that reward increases execution speed in reaching (Chen et al., 2018; Summerside et al., 2018) and saccades (Takikawa et al., 2002; Manohar et al., 2015), but they also deviate in some respects. First, in a serial reaction time study, reward and punishment both reduced reaction times in humans (Wachter et al., 2009), while reaction times are not significantly altered here. However, that study did not include distractors, and serial reaction time tasks strongly emphasize reaction times as a measure of learning. Regardless, the authors showed a punishment-specific noncontingent effect on performance, similar to our results. A possible interpretation is that the motor system presents a “loss aversion” bias similar to prospect theory (Kahneman and Tversky, 1979; Chen et al., 2017, 2020) may have interesting practical implications, as one could imagine training sessions with sparse punishment, enough to signify a punishment context, that will enable faster learning (Galea et al., 2015). Our task is also reminiscent of go-no-go or antisaccade tasks, in which a prepotent response must be inhibited (Guitart-Masip et al., 2014). Consequently, whether reward impacts action selection through improvements of response selection or executive inhibition remains an interesting area of future investigation. Next, radial accuracy has been shown to improve with reward in monkeys (Takikawa et al., 2002; Kojima and Soetedjo, 2017) and humans (Manohar et al., 2015, 2019), but these were studies of saccadic eye movements. One reaching task showed improvements in angular accuracy (Summerside et al., 2018), but their baseline (no-reward) accuracy requirements were minimal, possibly allowing for larger improvements compared with our task, and potentially explaining why we did not observe similar improvements. Finally, while other studies have shown that speed-accuracy functions shift with practice (Reis et al., 2009; Telgen et al., 2014), it is noteworthy that reward has a capacity to do so in what seems a nearly instantaneous time-scale, that is, from one trial to the next, as opposed to hours or even days in skill learning (Telgen et al., 2014).

While it is well established that stiffness has a beneficial effect on motor performance, our work provides the first evidence that this mechanism is used in a rewarding context. Therefore, the current results highlight the need to develop a greater understanding of how the CNS implements stiffness in an intelligent and task-specific manner to maximize reward. Stiffness itself could be regulated through a change in cocontraction of antagonist muscles, which is a simple but costly method to increase stiffness and enhance performance against noise (Gribble et al., 2003; Selen et al., 2009; Ueyama et al., 2011). The presence of reward may make such cost “worthy” of the associated metabolic expense (Todorov, 2004; Ueyama and Miyashita, 2014). Another possibility is that the stretch reflex increases, leading to stronger counter-acting forces produced against the perturbation. For instance, the stretch reflex is sensitive to cognitive factors, such as standing next to a void (Horslen et al., 2018). Nevertheless, the contribution of stiffness in reward-based performance has implications for current lines of research on clinical rehabilitation that focus on improving rehabilitation procedures using reward (Goodman et al., 2014; Quattrocchi et al., 2017). While several studies report promising improvements, excessive stiffness may expose vulnerable clinical populations to increased risk of fatigue and even injury. Therefore, careful monitoring may be required to avoid this possibility.

Previous work on saccades shows that reward had no effect on stiffness (Manohar et al., 2019), meaning that the limb controller uses an additional error-managing mechanism. Why do saccadic and limb control use dissociable control approaches? One possibility may be the difference in motor command profile. Saccadic control displays a remarkably stereotyped temporal pattern of activity, in which the saccade is initiated by a transient burst of action potentials from the motoneurons innervating the extraocular muscles (Robinson, 1964; Joshua and Lisberger, 2015). Critically, this burst reaches its maximum output rate nearly instantaneously in an all-or-nothing fashion (Robinson, 1964; Joshua and Lisberger, 2015), with only marginal variation based on reward and saccade amplitude (Xu-Wilson et al., 2009; Reppert et al., 2015; Manohar et al., 2019). In comparison, motor commands triggering reaching movements present a great diversity of temporal profiles depending on task requirements, and often do not reach maximum stimulation level. This difference may impact the temporal pattern of motor unit recruitment because, according to the size principle (Llewellyn et al., 2010), low-force producing, high-sensitivity motor units are always recruited first during a movement. However, those motor units are also noisier due to their higher sensitivity (Dideriksen et al., 2012). Since saccades always rely on an all-or-nothing input pattern, all motor units are quickly recruited, including high-force, low-sensitivity motor neurons that are normally recruited last. This would drastically reduce the production of execution noise, making stiffness unnecessary (Dideriksen et al., 2012). In line with this argument, previous work has shown that execution noise has a minimal contribution to overall error in eye movements (Van Gisbergen et al., 1981) compared with internally generated (planning) noise (Manohar et al., 2019). Interestingly, the opposite has been reported for reaching, suggesting that execution rather than planning noise is dominant in reaching errors (van Beers et al., 2004). These dissociable activation patterns of motor commands could potentially explain the differences in error-managing mechanisms between saccadic control and reaching. Finally, eye muscles are remarkably more innervated than peripheral skeletal muscles (Porter et al., 1995; Floeter, 2010), leading to a greater quantity of motor units, which scales negatively with noise at the effector stage (Hamilton et al., 2004), which possibly makes stiffness regulation unnecessary.

It is less clear what kind of feedback control is involved in reward-driven improvements. Feedback control encompasses several error-correcting processes that exhibit varying delays. This includes the spinal stretch reflex (∼25 ms delay) (Weiler et al., 2019), transcortical feedback (∼50 ms) (Pruszynski et al., 2011), and visual feedback (∼170 ms) (Carroll et al., 2019). While the spinal stretch reflex is extremely fast, it is difficult to assume an effect of reward or motivation occurring at the spinal level. On the other hand, transcortical feedback includes primary motor cortex processing (Pruszynski et al., 2011), a structure that shows sensitivity to reward (Thabit et al., 2011; Bundt et al., 2016; Galaro et al., 2019). Consequently, an exciting possibility for future research is that transcortical feedback gain is directly enhanced by the presence of reward. Indirect evidence suggests so, as feedback control on similar timescales is sensitive to urgency in reaching (Crevecoeur et al., 2013). This suggests that transcortical feedback gains can also be precomputed beforehand to meet task demands. Finally, recent work shows that reward can indeed modulate visual feedback control in reaching (Carroll et al., 2019). Therefore, it is possible that both transcortical and visual feedback gains increase in the presence of reward, although the former remains to be proved empirically. Additionally, more sophisticated models incorporating several distinct feedback loops may provide further insight on this matter (e.g., Mitrovic et al., 2010).

In saccades, the feedback controller that underlies reward-driven improvements is localized in the cerebellum and adjusts the end part of a saccade trajectory based on errors in the forward model prediction (Van Gisbergen et al., 1981; Chen-Harris et al., 2008; Frens and Donchin, 2009; Manohar et al., 2019). Interestingly, evidence in humans shows that cerebellar forward models do contribute to feedback control in reaching (Miall et al., 2007), and more recently, optogenetics manipulation in mice confirmed its involvement in enhancing reaching endpoint precision (Becker and Person, 2019). Therefore, reward may also enhance the cerebellar feedback loop, although this would only contribute to reducing planning, rather than execution noise (Manohar et al., 2019), and at the end of movement, in contradiction with what we observe here.

In this study, we show that reward can improve the selection and execution components of a reaching movement simultaneously. While we confirm previous suggestions that enhanced feedback control contributes to the improvement in execution, we introduce a novel mechanism by showing that global endpoint stiffness is regulated by the potential reward of a given trial. Therefore, reward drives multiple error-reduction mechanisms, which enable individuals to invigorate motor performance without compromising accuracy.