Topological Linking Drives Anomalous Thickening of Ring Polymers In Weak Extensional Flows

Abstract

Molecular dynamics simulations confirm recent extensional flow experiments showing ring polymer melts exhibit strong extension-rate thickening of the viscosity at Weissenberg numbers $Wi\ll 1$. Thickening coincides with the extreme elongation of a minority population of rings that grows with Wi. The large susceptibility of some rings to extend is due to a flow-driven formation of topological links that connect multiple rings into supramolecular chains. Links form spontaneously with a longer delay at lower Wi and are pulled tight and stabilized by the flow. Once linked, these composite objects experience larger drag forces than individual rings, driving their strong elongation. The fraction of linked rings depends non-monotonically on Wi, increasing to a maximum when Wi ∼ 1 before rapidly decreasing when the strain rate approaches 1/τ_e.

Non-concatenated ring polymers do not entangle like linear polymers, and they tend to have lower Newtonian viscosities than linear melts of similar molecular weight [1–6]. However, recent experiments by Huang et al. [7] show that ring melts are extraordinarily sensitive to extensional flow, exhibiting large, nonlinear growth in the extensional viscosity η_ex even when the strain rate $\dot{\epsilon }$ is small compared to the reciprocal ring relaxation time 1/τ_ring in equilibrium. Such trends are usually due to polymer conformations elongating in the flow field [5, 8–11], but analytic and numerical models for linear response predict this shouldn’t happen when $\dot{\epsilon }\ll 1/{\tau }_{\text{ring}}$ [5, 6].Thus, it appears that new physics emerges and changes how rings dissipate energy in uniaxial extensional flows.

Huang et al. observed an apparent correspondence between the high-rate extensional viscosity η_ex of ring and linear melts of Polystyrene (PS) with the same M_w = 185 kg/mol, leading them to propose that rings transition to behaving like linear chains as they elongate [7]. However, prior simulation studies of unentangled ring and linear melts under planar extension did not observe a clear correspondence at large Wi [12]. In addition, scaling arguments and simulations of linear melts predict that η_ex should scale as ~ N² for linear chains near full extension. [9] and as ~ N²/4 for rings if they behave like linear chains. Thus, extended rings of N monomers should behave like linear chains with N/2 monomers, but this was not observed in experiments.

Here, we use MD simulations to show that the unintuitive rheology of rings under uniaxial extension is driven by a new topological linking mechanism that assembles rings into supramolecular daisy-chains during flow (Fig. 1). We simulate start-up uniaxial extensional flows for ring and linear polymer melts at several molecular weights. Simulations reproduce the strong sensitivity of rings to uniaxial extension reported by Huang et al., and also reveal qualitative differences between the elongation dynamics of rings and linear chains. While chains in linear melts elongate independently during extension, the susceptibility of rings to assemble into supramolecules can drive a minority of rings to elongate and dominate the nonlinear viscosity, even when $W_i\ll 1$. While many quantum materials in applied magnetic fields develop topological interactions that drive nonlinear response, ring polymers linking during extension is the first instance of a similar effect in a classical polymer liquid.

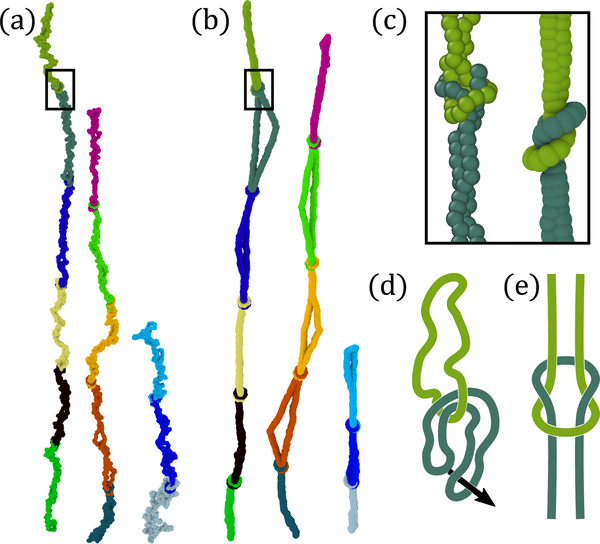
FIG. 1.

(a) Elongated N = 400 rings from the terminal state of the Wi = 0.17 flow. (b) Chains from (a) after PPA, revealing tight-links connecting rings into supramolecules. (c) Close-up of a tight-link framed in (a) and (b) before and after PPA. (d) Diagram of the formation of a link and (e) the final structure once it is pulled taut.

We model polymers with a standard semi-flexible bead-spring model that has been used to study ring melts in equilibrium and under shear [8, 13]. All beads interact with a truncated Lennard-Jones (LJ) potential and results are presented in reduced LJ units. Rings of N = 200, 400, and 800 beads are bound together with a FENE potential with mean bond length b ≈ 0.96. The chain stiffness is controlled by a bond bending potential k_θ(1−cos θ), where θ is the angle between successive bonds. In this study, we fix k_θ = 1.5, which gives a Kuhn segment length n_K ∼ 2.88 beads and an entanglement strand containing N_e ≈ 28 beads [14].

M ring or linear polymers of length N are equilibrated at a temperature T = 1 and density ρ = 0.85 using the methods detailed in Ref. 15 and Ref. 4, respectively. Rings are allowed to diffuse for ∼ 10τ_ring prior to elongation. The majority of our analysis considers a ring melt with M = 5000 and N = 400 (Z = N/N_e ≈ 14) that most closely correspond to the experimental results of Huang et al. on polystyrene (PS) of M_w = 185 kg/mol [7]. In order to compare trends for different molecular weights and compare rings to linear melts, we also model ring melts with: M = 200, N = 200; M = 5000, N = 800; and linear melts with M = 1640, N = 112; M = 250, N = 200; M = 400, N = 400. All simulations are performed using LAMMPS with a time-step Δt = 0.007.

Melts are elongated at constant Hencky strain rate $\dot{\epsilon }\equiv \partial \ln \Lambda /\partial t$ with Λ the stretch along the z-axis. Upper limits of $\dot{\epsilon }$ are chosen to avoid covalent bond stretching. Since polymers are nearly incompressible, the two perpendicular directions contract uniformly to preserve volume. Generalized Kraynik-Reinelt boundary conditions are used to prevent the simulation box from collapsing in the contracting directions [9, 16–18]. Flow is maintained by integrating the G-SLLOD equations of motion with a thermostat damping time of 10 [19, 20]. Like experiments, we record the start-up extensional viscosity ${\eta }_{\text{ex}}(t)={\sigma }_{\text{ex}}/\dot{\epsilon }$ during flow, where the extensional stress ${\sigma }_{\text{ex}}={\sigma }_{zz}-{\sigma }_{rr}$ is the difference in stress between the extension axis (z-axis) and the transverse directions.

Experiments typically analyze data from different chemistries by comparing them in reduced units derived from linear response. The same approach can be used to compare bead-spring simulations to the experiments of Huang et al. [7] For bead-spring simulations, τ_ring (N) is taken from Ge and Rubinstein’s fits of simulation data to the Fractal-Loopy-Globule (FLG) model[6]. For the experiments, we use the empirically measured τ_ring = 52.6 s. Strain rates are reported as a dimensionless Weissenberg number $Wi=\dot{\epsilon }\tau$, with τ = τ_ring for rings and τ = τ_R = τ_eZ² for linear melts. τ_R is the Rouse time which is the longest dissipative relaxation time of a linear chain in the absence of entanglements. It can be related to the entanglement time τ_e and the number of entanglements per chain Z. Prior studies on this bead-spring model have measured τ_e ≈ 1.98 × 10³ [14].

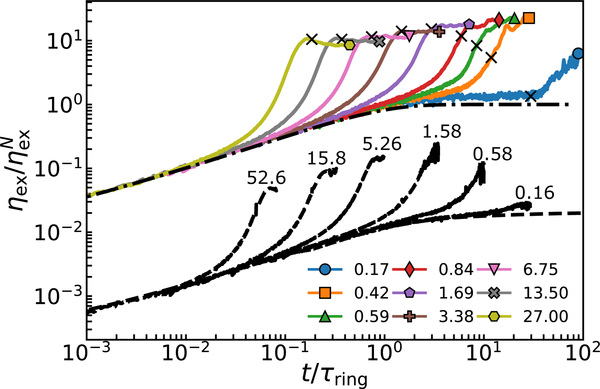
Figure 2 plots the normalized extensional viscosity ${\eta }_{\text{ex}}/{\eta }_{\text{ex}}^N$ versus reduced time t/τ_ring for a bead-spring melt of rings alongside the experimental curves from Huang et al. [7]. Simulation data are smoothed over time with a Gaussian kernel. Both simulation and experiment use rings with $Z~14.{\eta }_{\text{ex}}^N$ is the Newtonian viscosity taken from the plateau of the linear viscoelastic envelope (LVE). The experimental LVE is take from Ref. 7, while the simulated LVE is taken from Eq. 49 of Ref. 6.

FIG. 2.

Start-up extensional viscosity ${\eta }_{\text{ex}}/{\eta }_{\text{ex}}^N$ versus t/τ_ring for a N=400 ring melt (upper data) and PS experiments of Huang et al. [7] (lower data) at the indicated Wi. Dashed and dot-dashed lines show linear envelopes for experiments and simulations, respectively. Both simulations and experiments are for Z ≈ 14 and experiments are shifted down by a factor of 100 for clarity. Experiments terminate at lower Hencky strains (ε ~ 5) then simulations (> 12). Crosses on simulated curves indicate ε = 5.

The simulations reproduce the qualitative trends with Wi that are seen in experiments. Both show a large nonlinear growth in η_ex above the Newtonian viscosity even for $Wi\ll 1$. Extraordinarily, even for the lowest Wi = 0.17, thickening above ${\eta }_{\text{ex}}^N$ is observed in simulations after ~ 30τ_ring. As there is no uncertainty about the homogeneity of composition or flow in the simulated melts, our data support Huang et al.’s conclusion that ring melts exhibit an anomalously large (and seemingly delayed) sensitivity to extensional flow.

Comparing the experimental curves to simulations in Figure 2 shows an apparent difference in the trend of terminal viscosity with Wi. Simulations resolve steady-state plateaus in η_ex for Wi > 0.17 that are a factor ~ 10 larger than ${\eta }_{\text{ex}}^N$ and that weakly decrease with increasing Wi. In contrast, experiments, particularly at lower Wi, do not resolve clear plateaus and give terminal viscosities that decrease towards ${\eta }_{\text{ex}}^N$ as $Wi$ decreases. These differences appear to be due to different maximum strains in simulations and experiments. The average maximum strain in the experiments is ε ∼ 5, while our ring simulations all reach ε > 12. The simulation curves are marked with an “X” at the points corresponding to ε = 5. Simulations truncated at ε = 5 show the same qualitative trends with Wi as seen in experiments. This suggests that the ring experiments at low Wi are likely not resolving steady-state viscosities, so comparing these values to steady-state η_ex for linear melts is difficult. Further, due to the apparent instability of rings towards thickening at times $t>>{\tau }_{\text{ring}}$, current experiments may not be able to reach sufficiently large strains to resolve steady-states at low Wi.

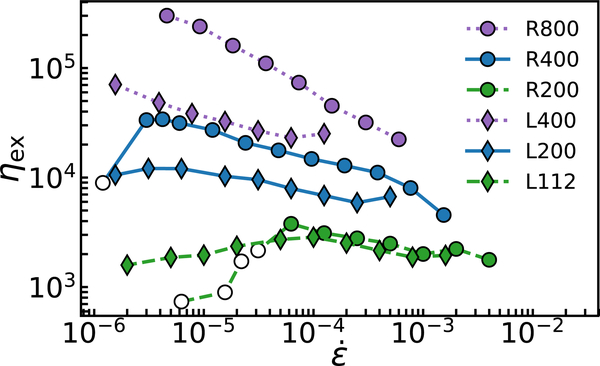
Figure 3 compares steady-state η_ex versus $\dot{\epsilon }$ for three ring and three linear molecular weights. For the smallest N = 200 rings and N = 112 linears, the steady ${\eta }_{\text{ex}}$ converge once $\dot{\epsilon }>{10}^{-4}$. However, this correspondence disappears with increasing molecular weight N. N = 400 rings and N = 200 linears show a similar decrease in η_ex with increasing $\dot{\epsilon }$, but ring η_ex are consistently ∼ 2 – 3 times larger until $\dot{\epsilon }$ > 2 × 10⁻⁴. At higher rates, the linear melt stops thinning while η_ex for rings continue to decrease. N = 800 rings and N = 400 linears exhibit similar behavior, however, the separation between ring and linear η_ex at intermediate rates has grown to a factor ~ 4 – 5.

FIG. 3.

Steady-state η_ex versus $\dot{\epsilon }$ for all three ring molecular weights compared to linear melt data with N_l ≈ N/2. N_l are chosen so elongated rings and linears have similar dimensions at full extension. Unfilled symbols are points that did not reach steady-state by ε = 12.

Prior studies found η_ex ~ N² for linear chains at large Wi [9], the rings do not follow this scaling over our range of $\dot{\epsilon }$. Thus, the viscosity of an elongated melt of N-rings is not simply related to that of an elongated linear melt. The ring-linear correspondence observed by Huang et al. for PS with Z ~ 14 may be a crossing of two different N dependencies at large Wi, like our 200-ring and 112-linear data appear to be.

The different trends in η_ex in Figure 3 imply that rings and linear chains are governed by different physics in extensional flows. This becomes clear when we examine the conformations of chains during flow. A common measure of linear chain elongation is the rms-magnitude of the end-end vector $\overrightarrow{R}$ connecting the two chain ends. Rings do not have chain ends, so instead we define an effective end-end distance for a ring as the maximum distance spanned by any pair of monomers on the ring that are separated by N/2 bonds. With this definition, an N-ring at full extension has approximately the same R as an (N/2)-linear chain.

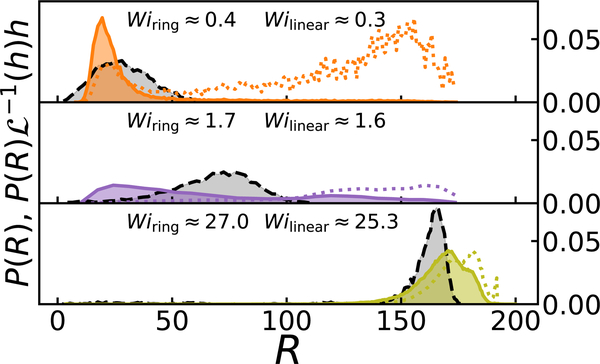
Figure 4 shows steady-state span distribution functions P(R) at three values of Wi for N = 400 rings (solid lines) and N = 200 linear chains (dashed lines). The Wi for the ring and linear chains are approximately the same for the three cases. For linear melts, P(R) exhibits a narrow distribution that shifts to larger R with increasing Wi. This is consistent with the assumption that a deformed entanglement network transmits macroscopic strains independently to each chain. However, the distributions for rings exhibit a fundamentally different behavior. At the low Wi = 0.3, P(R) for the rings develop a long tail corresponding to a small number of highly stretched rings. The tail grows with increasing Wi, producing a broad distribution for Wi ~ 1. For Wi >> 1, the flow becomes fast enough to elongate all rings and P(R) narrows to a single peak centered at large R.

FIG. 4.

Steady-state P(R) for N = 400 rings (solid) and N = 200 linears (dashed) at three Wi. Relative stress contributions $P(R){\mathcal{L}}^{-1}(h)h$ for rings (dotted) are scaled to fit on the same axes.

At low Wi the fraction of highly elongated rings is small, but their contribution to the extensional stress is substantial. This is due to the nonlinear increase in the entropic tension of a ring with increasing R. If we approximate the elongated rings to be under uniform tension, we can estimate the nonlinear increase in entropic tension as $\propto {\mathcal{L}}^{-1}(h)h$, where ${\mathcal{L}}^{-1}$ is the inverse Langevin function and h = R/(bN/2) is the extension ratio of the ring. In Figure 4, the relative contribution of the rings to the stress $\propto P(R){\mathcal{L}}^{-1}(h)h$ is plotted with a dotted line. For Wi = 27, the distributions for rings and linears are similar and all rings contribute substantially to the stress. However, as Wi decreases, the stress contributions become increasingly dominated by the small number of highly elongated rings. This is fundamentally different from linear melts and unprecedented for monodisperse polymers. While linear melt structure can be described with average conformational statistics, outliers dominate the non-linear response of rings.

MD simulations provide the microscopic details necessary to identify the physics driving the strong extension of some rings at low Wi. Rings are susceptible to linking with each-other to form “reef” or “lark’s head” knots, shown in Figure 1(e). These are formed when a ring that has threaded another ring then threads back through itself, as in Figure 1(d). We observe that these links can form when chains are still in compact globular conformations. However, once linked, rings form supramolecules with effectively higher molecular weights and relaxation times, becoming more susceptible to elongation.

We directly observe tight-links in steady-state simulations by applying primitive path analysis (PPA) to our MD trajectories [21]. Adapting techniques from prior ring studies [5, 6], we take a snapshot of the system and fix the coordinates of a single bead on each ring that is closest to the ring’s geometric center. Intramolecular repulsive interactions are then removed, driving rings to collapse into points unless they are topologically linked. Collapsed rings have radii of gyration R_g ∼ 1, much smaller than the average $R_g^{\text{eq}}\approx$ 7.14 in equilibrium. We measure an upper bound ϕ_top for the fraction of topologically linked rings by eliminating any ring that collapses to $R_g<0.5R_g^{\text{eq}}$ < 3.57, which is significantly smaller than the smallest ring conformations observed in equilibrium. While not a direct count of link numbers, this protocol identifies the fraction of chains participating in elongated clusters that are mediated by links (Fig. 1(a)&(b)) and that contribute significantly to the stress.

Figure 1(a) shows several highly elongated clusters of rings from the terminal state of the lowest Wi = 0.17 flow. Figure 1(b) shows the same rings after PPA, revealing many tight-links connecting rings into supramolecules. Figure 1(c) shows a close up of a tight-link between two rings before (left) and after (right) PPA. A supplemental video shows the spontaneous linking of three rings in a Wi = 0.42 flow[22]. Notably, links can form spontaneously during flow between rings that were far apart prior to startup. In addition, supramolecules are not limited to single links, with Figure 1(a) and (b) showing supramolecules of 6, 5, and 3 rings. In fact, we expect nonlinear response to be dominated by larger supramolecules at Wi = 0.17, since they must be be large enough to be pulled tight by low strain rate. The long delay in thickening at low Wi could be due to a long induction time for larger supramolecules to develop.

The effective relaxation times of supramolecules in flow should be significantly larger than for individual rings. Every linked chain adds N monomers to a supramolecule, and we would expect the effective Rouse time of q linked molecules to scale as ~ q². Thus, linked rings experience a much larger drag in flow than unlinked rings at the same $\dot{\epsilon }$, leading to their strong extension. Once elongated, links are pulled tight into reef knots (Figure 1(c)), stabilizing them for as long as flow persists. The ring topology is also important for stabilizing links. Unlike the recently observed transient hooking of rings by linear chains [11], ring-ring links cannot be destroyed by convective-constraint release because rings lack ends.

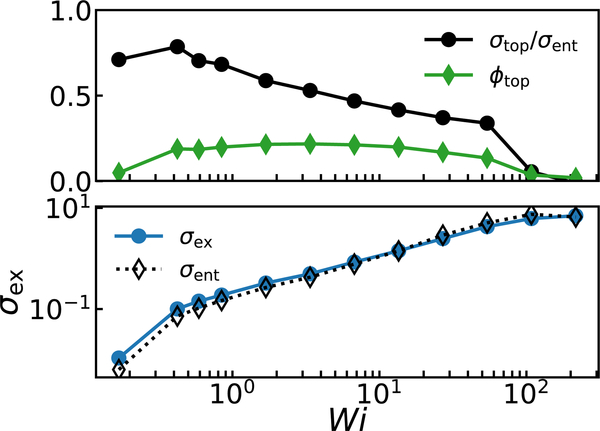
Figure 5(a) plots the fraction of topologically linked rings ${\varphi }_{\text{top}}$ at the terminal strain for all Wi of the N = 400 melt. ϕ_top ~ 0.005 at Wi = 0.17 and increases with increasing Wi up to ϕ_top ~ 0.20 for Wi > 1. This persists until Wi > 50, where ϕ_top rapidly decreases to < 0.01. The sudden decrease at Wi ≈ 50 corresponds to $\dot{\epsilon }{\tau }_e\approx 0.75$, with $\dot{\epsilon }$ approaching the reciprocal of the fundamental loop relaxation time [6]. These trends further imply the existence of an induction time for rings to sample threaded conformations that can form links. Once $\dot{\epsilon }{\tau }_e~1$, we expect rings elongate faster than they can sample such link-forming configurations.

FIG. 5.

(a) Fraction of topologically linked rings ϕ_top and fraction of the entropic stress σ_top/σ_ent they contribute versus Wi for N = 400 rings. (b) Steady-state stress σ_ex versus Wi compared to σ_ent from Eq. 1 for an N = 400 ring melt.

Following previous studies [9], we can approximate an entropic extensional stress σ_ent contributed by elongated rings:

$${\sigma }_{\text{ent}}=\frac{\rho k_{B}T}{n_k}\langle \frac{2R}{Nb}{\mathcal{L}}^{-1}\left(\frac{2R}{Nb}\right)P_2\rangle$$ (1)

Here, ρ is the monomer density, n_k is the Kuhn segment length of the chains and P₂ is the nematic orientational order parameter for the ring span $\overrightarrow{R}$ relative to the extension axis. O’Connor et al. [9] found that Eq. 1 applied to entanglement segments in linear melts predicted the steady σ_ex for a wide range of Wi. Figure 5(b) compares σ_top to σ_ex for the terminal state of the N = 400 ring melt for all Wi. The entropic prediction closely follows σ_ex and agrees especially well at large Wi, as P(R) (Figure 4) becomes a narrow distribution. Deviations are maximum 30–40% at Wi = 0.17; however, this Wi has not reached a steady-state, so P(R) and σ_ent are not yet well defined.

The population ϕ_top drives the nonlinear rise in σ_ex at low Wi. This is seen by measuring the entropic stress contributed by just the topologically linked rings σ_top by only including the ϕ_top population in the expectation value of Eq. 1. The fraction σ_top/σ_ent is shown as circles in Figure 5(a). Consistent with Figure 4, the decreasing fraction ϕ_top of linked rings contributes increasingly to the stress as Wi becomes small. Indeed, at Wi = 0.17, linked chains comprising less than 0.5% of the system contribute ~ 75% of σ_top. In other words, supramolecules contribute most of the anomalous stress observed at low Wi. σ_top/σ_ent decreases with increasing Wi as ϕ_top saturates and then rapidly decreases. Unlinked rings also elongate and contribute substantially to the stress at as Wi increases, further reducing σ_top/σ_ent.

To conclude, MD simulations reproduce the experimental sensitivity of ring melts to extensional flows. Anomalous increases of η_ex at low Wi are caused by a fraction ϕ_top of rings that PPA reveals are topological linking to form supramolecular daisy-chains that elongate at lower Wi than single rings. Microscopic measures of ring entropy directly relate the nonlinear rise in stress to these elongated supramolecules. Unlike the transient “hooking” of rings by linear chains [11], these new ringring links are pulled tight and stabilized by the flow. Thus, supramolecules can persist even if Wi is changed. Our future efforts will study the dynamics of topological link formation during transient flow and stress relaxation. This will require adapting new ring analysis methods [23, 24] to accurately identify and track links as they form.