Genetic Influence on the Sulcal Pits: On the Origin of the First Cortical Folds

Abstract

The influence of genes on cortical structures has been assessed through various phenotypes. The sulcal pits, which are the putative first cortical folds, have for long been assumed to be under tight genetic control, but this was never quantified. We estimated the pit depth heritability in various brain regions using the high quality and large sample size of the Human Connectome Project pedigree cohort. Analysis of additive genetic variance indicated that their heritability ranges between 0.2 and 0.5 and displays a regional genetic control with an overall symmetric pattern between hemispheres. However, a noticeable asymmetry of heritability estimates is observed in the superior temporal sulcus and could thus be related to language lateralization. The heritability range estimated in this study reinforces the idea that cortical shape is determined primarily by nongenetic factors, which is consistent with the important increase of cortical folding from birth to adult life and thus predominantly constrained by environmental factors. Nevertheless, the genetic cues, implicated with various local levels of heritability in the formation of sulcal pits, play a fundamental role in the normal gyral pattern development. Quantifying their influence and identifying the underlying genetic variants would provide insight into neurodevelopmental disorders.

Introduction

The human cerebral cortex is highly convoluted and the process of gyrification starts in utero. To better understand the role of various factors in this phenomenon, detailed models of the cortical folding have been proposed, which include geometric, mechanic, and genetic constraints (Van Essen 1997; Toro and Burnod 2005; Tallinen et al. 2016). A tension-based model proposed that the shape and location of sulci result from the global minimization of the viscoelastic tensions due to the axonal connectivity between cortical areas (Van Essen 1997). Another morphogenetic model underlines the need to include asymmetric gradients of the growth rate to explain the human characteristic brain asymmetries (Toro and Burnod 2005). In the ferret, which is an animal model of the human gyrencephaly, de Juan Romero et al. (2015) recently demonstrated some specific transcriptomic profiles in the germinal cortical layers of the prospective gyrus regions versus the sulcus ones. However, these models and findings have not estimated the proportion of genetic influence on the cortical folds shape. In addition, the formation of the first sulci is supposed to be related to the specialization of the cortex and following the protomap model described by Rakic (1988). The central sulcus materializes such boundary between the primary sensory and motor areas. In order to represent the first folding locations, the notion of sulcal roots was introduced by Régis et al. (2005). They correspond to indivisible units whose shapes and locations are supposed to be stable across individuals, as opposed to sulci that form later. In order to extract these putative first cortical folds, algorithms have been proposed over the past few years to extract the deepest points lying at the bottom of sulcal basins (Im et al. 2010; Meng et al. 2014; Auzias et al. 2015). These points located at the maximum depth in a basin, denoted as sulcal pits, show less intersubject variability than more superficial ones (Lohmann et al. 2008). In addition, these anatomical landmarks were shown to be reliably identified over different scan sessions, scanners, and surface extraction tools (Im et al. 2013). Previous studies have shown that the pattern of the sulcal pits is more consistent in monozygotic twins than unrelated individuals (Lohmann et al. 1999; Im et al. 2011). These results lead to the hypothesis of the pits being under genetic control and having close relationship to functional organization (Lohmann et al. 2008). Furthermore, a longitudinal study has demonstrated that the spatial distribution of the pits already exists at term birth and becomes more pronounced during the first 2 years of life along with the rapid brain volume increase (Meng et al. 2014). This result suggests a genetic plan, which is implemented before birth, as proposed by Rakic (1988). The hemispherical asymmetry of the sulcal pits organization has also been widely studied (Im et al. 2010; Meng et al. 2014; Auzias et al. 2015; Leroy et al. 2015). Consistent results across these studies underline the superior temporal sulcus (STs) as being the most asymmetrical area in term of sulcal pits likely related to language lateralization, in the left hemisphere around the Heschl’s gyrus and planum temporale.

To the best of our knowledge, the heritability of the sulcal pits depth has not been estimated yet. In a recent study (McKay et al. 2013), the depth profile of the central sulcus has been extracted in a pedigree study and the highest heritability estimates were found at the 2 peaks, in sulcal depth position profile. These 2 peaks, close to the hand and mouth cortical regions, actually correspond to the definition of the sulcal pits and reinforced the idea of a tighter genetic control at these points than other parts along the sulcus. Still little is known about the heritability of sulcal pits in the rest of the cortex and the underlying associated genetic variants. Moreover, the potential genetic influence on the asymmetrical distribution of some of the pits remains unknown.

Several studies have already emphasized the feasibility of using sulcal pits as biomarkers to distinguish healthy subjects from diseased ones. Examples of such applications range from quantitatively describing the abnormal sulcal pattern in polymicrogyria (Im et al. 2012) to characterizing the atypical sulcal pattern in children with developmental dyslexia (Im et al. 2016) by using sulcal graph matching. Understanding the genetic underpinnings would provide insight into morphological phenotypes of neurodevelopmental disorders.

Materials and Methods

Subjects

This study relies on the dataset of the Human Connectome Project (HCP) for subjects whose scans and data were released in December 2015 (humanconnectome.org). The details of the release are available in the HCP reference manual. We included all the 897 subjects with structural imaging in the HCP S900 release for the analysis of the sulcal pits. The S1200 release has updated the zygosity, as well as the mother and father identities based on genotyping data available from blood and saliva samples of some HCP subjects. Notably, 36 twins pairs who self-reported as dizygotic (DZ) twins were found to be genetically monozygotic (MZ), and 28 subjects had changes on their father identity (among them 5 also had a change of mother identity). We took these changes into account and included in our analysis all S900 subjects with structural imaging: 897 subjects (393/503/1 M/F/U), containing 179 twin pairs (114 MZ with 99 siblings and 6 half siblings and 65 DZ with 55 siblings and 9 half siblings), 273 siblings, 10 half siblings and 87 unpaired individuals, aged between 22 and 37 years old (μ ± σ = 28.8 ± 3.7 years). The unpaired individuals did not contribute to the genetic parameters estimation, but allowed a more accurate estimation of mean and variance effects. In addition, for the genetic analysis we only included individuals with the most represented values of race/ethnicity variables reported in the HCP dataset among them are 156 subjects labeled “Black or African Am.,” 597 labeled “White, Not Hispanic/Latino,” 54 labeled “White Hispanic/Latino,” 44 labeled “Asian/Nat. Hawaiian/Other Pacific Is.”. Subjects were chosen by the HCP consortium to represent healthy adults beyond the age of major neurodevelopmental changes and before the onset of neurodegenerative changes (Van Essen et al. 2012). They underwent a battery of tests to determine if they met the inclusion/exclusion criteria of HCP, described in (Van Essen et al. 2012). All subjects provided written informed consent on forms approved by the Institutional Review Board of Washington University.

MR Image Acquisition and Processing

MR images were acquired by using a Siemens “Connectome Skyra” 3 T scanner housed at Washington University in St Louis using a 32-channel head coil. For T1-weighted images, 256 slices per slab were acquired with the 3D magnetization-prepared rapid gradient echo (3D-MPRAGE) sequence: TR = 2400 ms, TE = 2.14 ms, TI = 1000 ms, flip angle = 8°, FOV = 224 × 224 mm², and resolution 0.7 mm isotropic. For T2-weighted images, 256 slices per slab were acquired with a 3D-T2SPACE sequence: TR = 3200 ms, TE = 565 ms, variable flip angle, FOV = 224 × 224 mm², and resolution 0.7 mm isotropic. More details on the acquisition and reconstruction can be found in the HCP S900 Reference Manual.

Structural images were first processed by HCP using the HCP structural preprocessing pipeline, whose details can be found in the HCP S900 Reference Manual. We used the preprocessed T1w and T2w volume from each individual subject’s MR data as input of the HCP Freesurfer pipeline, which is based on Freesurfer 5.3.0 (Fischl 2012) with a number of improvements specifically optimized for the HCP data. We additionally performed surface-based interhemispheric registration as proposed in (Greve et al. 2013). First, we created the xhemi of each subject using the xhemireg command of Freesurfer, to transform the right hemisphere into a left one, and then compute the registration to the left side of the symmetric Freesurfer template (fsaverage_sym) using the surfreg command. The Freesurfer outputs needed for the sulcal pits extraction and analysis methods are the white meshes and the registration spheres files, which we converted to the gifti format using Freesurfer command mris_convert.

We are aware of the benefits of the quality control performed by HCP for structural scans. The outputs of the HCP structural pipelines, including Freesurfer surface generation, have been examined by HCP for surface reconstruction quality in the native volume space with the native mesh. However, some Freesurfer outputs needed for interhemispheric registration were not distributed by HCP (list of these files in supplementary material S2), so we decided to re-run the HCP Freesurfer pipeline. We used as inputs the distributed outputs from the PreFreesurfer pipeline and used the HCP Freesurfer pipeline code available on HCP GitHub (github.com/Washington-University/Pipelines/tree/master/FreeSurfer, commit 04/2016). Our study relying mostly on the subjects’ white mesh estimated by the pipelines, we assessed the similarity between the white matter segmentations available from the HCP repository and the ones we computed locally. We compared the correspondence between the white matter segmentation in the wmparc file for all subjects and found 97% of common voxels in average. We visually inspected the differences on few subjects, randomly selected. Using fslview, we assessed whether the white matter mask encompassed properly the folds of the white matter mesh. In some cases the HCP repository data more finely delineate the white matter, whereas in other cases our locally computed data correspond to a better segmentation. Thus, we concluded that the differences in white matter segmentation were negligible between the HCP repository and locally computed data.

Pits Extraction

The BrainVISA process “Sulcal Pits Extraction” (brainvisa.info, version 4.5.0) was used to obtain the sulcal pits from the white meshes of both hemispheres for each individual (Auzias et al. 2015). The procedure first estimates the sulcal depth by computing the depth potential function (DPF) on each white mesh as introduced in (Boucher et al. 2009). The DPF is a scalar field corresponding to the signed traveled distance that quantifies how much a curve is bent inward or outward (i.e., average convexity). It represents the overall shape of a fold as the function whose Laplacian is as close as possible to the mean curvature (κ_mean) of the surface. (αΙ + Δ)D_α = 2κ_mean, where α controls the decay rate of the curvature influence as we move further from a given point. When α tends to infinity, the DPF tends to the mean curvature, when α tends to 0 the DPF tends to the average convexity, and for intermediate values of α, the DPF integrates both types of geometrical information. Thus, the DPF provides a regularized estimation of the depth of the folds based that takes into account information from both convexity and curvature (see Boucher et al. 2009; Auzias et al. 2015 for implementation details). Several advantages, compared to other methods for depth estimation, make it a relevant phenotype to estimate the genetic influence on the sulcal pits. Three main other techniques to estimate the depth may have been used: computing the Euclidean distance to the closest point on the external hull (Im et al. 2010), estimating the geodesic distance to the ridges on the crown of gyri that are in contact with the brain hull (Rettmann et al. 2002), using an adaptive distance transform based on graph-searching algorithm to find the shortest path from each vertex to the brain hull (Kao et al. 2007; Yun et al. 2013). The caveats of these methods are extensively detailed elsewhere (Boucher et al. 2009; Auzias et al. 2015), the main one being the problematic definition of the brain surface hull. The definition of a reference level required by these methods is avoided by the DPF. On this depth map a watershed algorithm is applied to distinguish the different sulcal basins and localize their respective deepest point. During the flooding procedure, the basin merging decision rule was based on the following features: the ridge height (R) which is the height difference between the shallowest pit and the ridge point, the basin area (A) and the geodesic distance between the 2 pits (D). During the flooding the 2 basins were merged if R or D were below corresponding predefined thresholds (ThR, ThD). After the flooding, the small shallow basins for which A was below a given threshold (ThA) were merged with their respective neighbors with which the shared border was the longest. The motivation for this approach as well as the definition of the predefined parameters [ThR = 1.5, ThD = 20, ThA = 50] are described in details in Auzias et al. (2015).

Parcellation Scheme and Areal Nomenclature

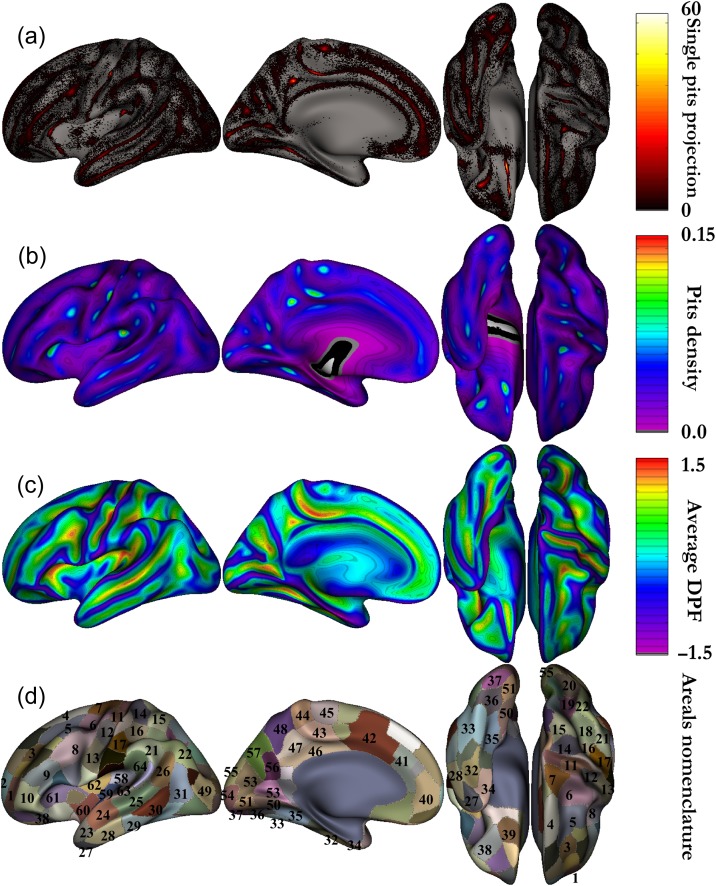
After the extraction of the pits at the individual level, we computed the symmetric group-level cluster regions as proposed by Auzias et al. (2015). Briefly, the correspondences between cortical meshes from the left and right hemispheres were obtained through spherical interhemispheric registration based on the Freesurfer symmetric template fsaverage_sym (Greve et al. 2013). Individual sulcal pit maps were iteratively smoothed corresponding to a Gaussian smoothing keeping a maximum peak height of 1 with 5 mm full width half maximum (FWHM). The smoothed maps from both hemispheres were projected onto the left side of fsaverage_sym, and summed across subjects to obtain the group density map (Fig. 1b). This density map indicates the probability of presence of pits in each location, taking into account information from both hemispheres. A second application of the watershed algorithm was then performed on the pits density map to obtain group-level clusters of pits -denoted in the following as areals. This procedure leads to a parcellation of the template surface into a set of regions where the probability of a having a pit is high. The watershed parameters (gThR = 2, gThD = 15, gThA = 100) were used in order to obtain areals that fit well the geometry of the cortical surface as in (Auzias et al. 2015). The resulting areals were then labeled manually and thus defined the intersubject and interhemispheric correspondence of pits. Note that using a symmetric template was crucial for quantifying the asymmetries: information from both hemispheres was taken into account when computing sulcal pit clusters so that cortical areals of the same size and shape were compared across hemispheres. Figure 1 summarizes the definition of the group map, which includes the projection of all the sulcal pits on the template (Fig. 1a), the density map (Fig. 1b), the average DPF map (Fig. 1c). Figure 1d introduces the nomenclature we used for our areals based on previous names in the literature (Im et al. 2010; Meng et al. 2014).

Figure 1.

Group averages on symmetric template. (a) All the pits from every individual projected onto the left fsaverage_sym template (presented with external, internal, bottom, and top views of the left hemisphere). (b) Density map corresponding to the sum of the smoothed pits map across subjects and across hemispheres. (c) Average DPF map corresponding to the same sum as for the density map. (d) Group-level sulcal basins obtained after performing the watershed on the density map. Nomenclature of our areals mainly based on existing literature (Im et al. 2010; Meng et al. 2014). 1 mid frontal a, 2 sup frontal a, 3 mid frontal b, 4 sup frontal b, 5 mid frontal c, 6 junct sup frontal and precentral, 7 precentral, 8 junct precentral and inf frontal, 9 inf frontal b, 10 inf frontal a, 11 central a, 12 central b, 13 central c, 14 postcentral a, 15 postcentral a bis, 16 postcentral b, 17 postcentral c, 18 intraparietal a, 19 intraparietal b, 20 intraparietal c, 21 supra marginal gyrus, 22 junct intraparietal and sup temporal, 23 sup temporal a, 24 sup temporal b, 25 sup temporal c, 26 sup temporal d, 27 temporale pole, 28 inf temporal a, 29 inf temporal b, 30 inf temporal c, 31 inf temporal d, 32 occipito temporal a, 33 occipito temporal b, 34 collateral a, 35 collateral b, 36 collateral c, 37 collateral d, 38 orbital, 39 olfactory, 40 cingulate a, 41 cingulate b, 42 cingulate c, 43 cingulate d, 44 cingulate e, 45 supplementary motor area, 46 below subparietal and cingulate, 47 subparietal, 48 subparietal b, 49 lateral occipital a, 50 junct collateral and calcarine a, 51 junct collateral and calcarine b, 52 calcarine a, 53 calcarine b, 54 calcarine c, 55 lateral occipital b, 56 parieto-occipital a, 57 parieto-occipital b, 58 circular insular a, 59 circular insular b, 60 circular insular c, 61 circular insular d, 62 circular insular e, 63 planum temporale area, 64 planum parietale.

Heritability Measurements: Analysis of Additive Genetic Variance

In each areal of the symmetric template, we selected, separately for each hemisphere, all subjects having a sulcal pit and considered the DPF value associated to the deepest pit of each subject as our phenotype. The variance components method, as implemented in the Sequential Oligogenic Linkage Analysis Routines (SOLAR) software package (Almasy and Blangero 1998), was used for the heritability estimation of the DPF of the pit in each areal. In SOLAR, the algorithms use maximum variance decomposition methods derived from the strategy developed by Amos (1994). The covariance matrix Ω for a pedigree of individuals is given as follows:

$$\Omega =2·\Phi ·{\sigma }_g^2+\text{I}·{\sigma }_e^2,$$

where σ_g² is the genetic variance due to the additive genetic factors, Φ is the kinship matrix representing the pair-wise kinship coefficients among all individuals, σ_e² is the variance due to individual-specific environmental effects, and I is the identity matrix. In this model named AE, environmental effects are supposed to be uncorrelated among family members (Kochunov et al. 2015). An additional variance parameter can be added to model the effect of common environment, which is associated with any nongenetic factors shared between the individuals like living in the same household. This model is named ACE and the covariance matrix Ω can be written as follows:

$$\Omega =2·\Phi ·{\sigma }_g^2+\text{H}·{\sigma }_c^2+\text{I}·{\sigma }_e^2,$$

where H is the structuring matrix for σ_c², the variance due to common environment effects. H contains zeros and ones depending upon whether a pair of individual shares the same household. The household information is not directly available in HCP data. Thus, we assumed that 2 individuals share the same household if they reported to HCP the same 2 parents (not necessarily the genetic ones for the few half siblings).

Narrow sense heritability is defined as the fraction of the phenotype variance σ_p² attributable to additive genetic factors: h² = σ_g²/σ_p².

The variance parameters are estimated by comparing the observed phenotypic covariance matrix with the covariance matrix predicted by kinship (Almasy and Blangero 1998). Significance of the heritability is tested by comparing the likelihood of the model in which σ_g² is constrained to zero with the one of a model in which σ_g² is estimated. Before testing for the significance of heritability, phenotypes values for each individual within the HCP cohort were adjusted for the following covariates sex, age, age², age × sex interaction, age² × sex interaction, and 4 racial and ethnic groups: Asian, Black, White, Hispanic. Inverse Gaussian transformation was also applied to ensure normality of the measurements. SOLAR computes the heritability value (h²), the significance value (P) and the standard error (SE) for each phenotype.

Given the limitations of using household as a proxy for common environmental influence in a pedigree comprising a large number of siblings like the HCP cohort (Koran et al. 2014; Docherty et al. 2015), we compared the Akaike information criterion (AIC) of the 2 models to discriminate the more suitable, with AIC = 2[number of estimated parameters] – 2 ln(likelihood). We estimated the maximized log-likelihood of each model over all areals with SOLAR and computed the AICs of AE and ACE models to select the one lowering the information criterion for studying the heritability of the pits. We found that on average over the 128 areals (64 on each side) the AIC of ACE model is 754.0 and 752.5 for the AE model, with only 11 areals (8.5%) preferably selecting the ACE model. Unlike population studies containing twins only with controlled household information, the HCP extended twin population with a large number of siblings does not seem to be suitable for adding the household information in the model. Thus, we selected the AE model for our heritability analysis and acknowledge the possible inflation of our heritability estimates due to uncontrolled shared environment as one of the limitations of our study.

Definitions of the Pits Frequency and Asymmetry Index

First, the pits frequency is defined as the number of individuals having at least one pit in this areal divided by the total number of subjects.

We compute the asymmetry index (AI), also known as laterality index (Greve et al. 2013) for any metric, the following way: $\mathrm{AI}=\frac{(L-R)}{(L+R)}$. For instance, L can be the density of pits in the left hemisphere and R for the right hemisphere, both taken in the same group-level cluster of the symmetric template. AI varies from −1 (completely right lateralized) to 1 (completely left lateralized). It is worth noting that this quantification of the asymmetry can also be used for any metric other than the pits frequency. We computed the AI for the heritability values in each areal as well as for the DPF of the pits.

Confidence Interval for Heritability Estimates and Asymmetry Significance

We can compute the confidence interval for heritability estimates under the asymptotic normality assumption of the maximum likelihood estimator where the sample size is ~850 with the following formula: Asymptotic confidence interval at 100 (1 – α)% is $[h^2-Z(\mathrm{\alpha }/2)\times \mathrm{\sigma },{\mathit{h}}^2+Z(\mathrm{\alpha }/2)\times \mathrm{\sigma }]$ (Neale and Miller 1997). For 90%, Z(α/2) = 1.645, for 67%, Z(α/2) = 1.

Using the confidence interval for the heritability estimates in the left and right hemispheres, we deduced that the 2 estimates are significantly different at 100 (1 − α)%, assuming the 2 heritability estimates are independent, if:

$$\mathrm{diff}=\left|{h^2}_{\mathit{right}}-{h^2}_{\mathit{left}}\right|>\mathrm{Z}(\mathrm{\alpha }/2)\times \left({\mathrm{\sigma }}_{h^2\mathrm{right}}+{\mathrm{\sigma }}_{h^2\mathrm{left}}\right).$$

Thresholding Procedure

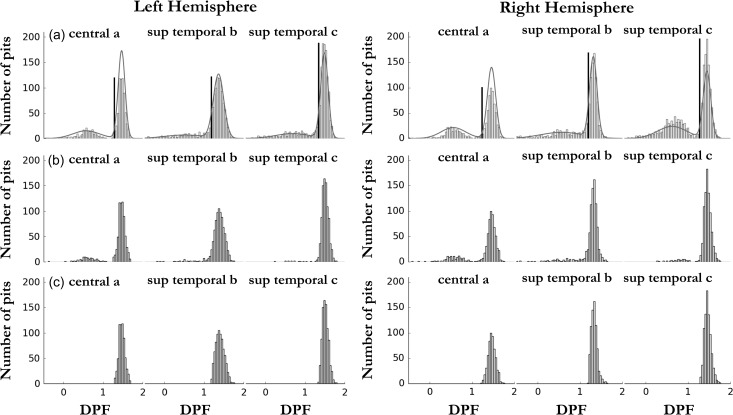
The pits extraction procedure extracts indiscernibly deep and shallower sulcal pits. This distinction can be made in areals corresponding to sulci, in which a clear deep sulcal point can be selected, but also sometimes a bump in the sulcus shape leads to the identification of a shallower pit. The former pits belong to the deep sulcal pits distribution (see Fig. 2a, e.g., in 3 areals) more commonly referred to in the literature and formed early in utero brain development (Régis et al. 2005; Im et al. 2010; Meng et al. 2014). The latter pits are part of the shallower pits distribution (Fig. 2a), that we assumed are formed later in the brain development. The deep sulcal pits are of particular interest because they are supposed to be the phenotypic manifestation of the sulcal roots under tight genetic control (Lohmann et al. 2008). We describe in details in the Supplementary materials a method to filter out the shallower pits, by setting an adaptive threshold per areal (Method S1). Briefly, when we considered the DPF distributions of all pits in an areal we observed either 1 or 2 underlying Gaussian distributions (Fig. 2a, Fig. S2a). Our method consists in fitting a mixture of 2 Gaussians to the whole distribution in the considered areal, in order to set a threshold to separate them while minimizing both the numbers of false positives and false negatives for the deep pits selection. In Figure 2a, we clearly distinguish 2 underlying DPF distributions for the areals considered, some other areals having only one clear Gaussian peak. It also represents how the threshold (the dark line) is set with regard to the pits DPF distribution in each considered areal (Fig. 2a). Two variants of the sulcal root phenotype were studied for each areal: the depth of the deepest pit without applying a threshold and the depth of the deepest pit after applying the adaptive threshold. Notice that in the main text, only the results without thresholding are presented and the others are available in the Supplementary materials. We explain this choice in the discussion.

Figure 2.

(a) Example of the thresholding procedure on all pits DPF per areal in each hemisphere. (b) Phenotypes when selecting the deepest pit for each individual without any thresholding. (c) Phenotypes when selecting the deepest pit for each individual after the adaptive thresholding.

Results

Pits Frequency

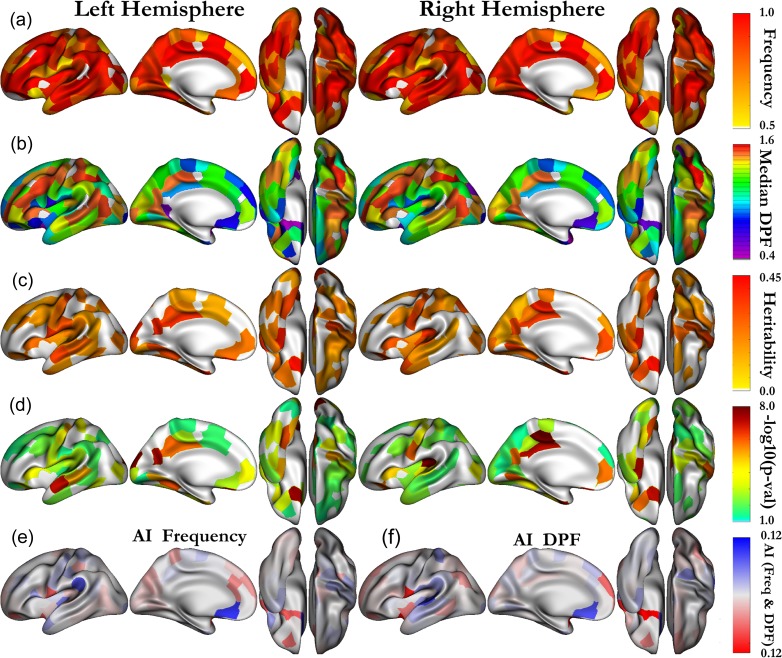
As opposed to previous literature (Im et al. 2010; Meng et al. 2014), we also included in our heritability analysis cluster regions that do not specifically lie at the bottom of the sulci, among them are shallow regions such as the planum temporale area, planum parietal, or the supra marginal gyrus. To include an areal in our analysis, the general constraint we imposed is that the pits frequency must be above 75% in the selected areals on both hemispheres. Nevertheless, a few areas that were present in the previous literature but do not meet this criteria were also included: calcarine (Cal) c, cingulate (Cing) (b, e), collateral (Col) a, superior temporal (ST) a, temporale pole (TP). All of them had a pits frequency above 70% on both sides, except the ST a areal (pits frequency ~55%), that we kept to be consistent with previous nomenclature of the STs. As described in Auzias et al. (2015), the method we used has a higher reliability of extraction resulting in increased pits frequencies compared with Im et al. (2010). We obtained pits frequencies above 90% on both sides in the following areals: “below subparietal (SP) and Cing”, Cal (a, b), central b, Cing (a, c, d), circular insular (Circ) (a, c, d, e), Col (b, c), inferior frontal (IF) (a, b), inferior temporal (IT) (a, c, d), intraparietal (Int) (a, b, c), lateral occipital (LO) (a, b), middle frontal (MF) (a, c), occipito temporal (a, b), olfactory, orbital, parieto-occipital (PO) a, SP (a, b), superior frontal (SF) b, ST (b, c, d), supra marginal gyrus, junction (jct) Int and ST, jct precentral (PreC) and IF, jct SF and PreC; above 80%: central c, Circ b, Col d, IT b, jct Cal and Col, MF b, PO b, planum temporale area, postcentral PostC (a, a bis, c), SF a, supplementary motor area; and above 75%: central a, planum parietale, PostC b, PreC. The frequency in each areal is shown on Figure 3a for all areals with a pits frequency above 50%, notice that results for both the right and left hemispheres are displayed on the symmetric template left side. This representation is complementary to the density map (Fig. 1b), which depicts how the pits are concentrated.

Figure 3.

(a) Deep pits frequency and (b) median DPF of the pits selected as phenotypes in each areal. (c) Heritability and (d) associated –log10(P-values) for all the areals being significant without correction (P < 0.05). The areals which are significant after strict Bonferroni are shown with a color above yellow. Both left and right hemisphere results (a, b, c, d) are presented on the symmetrized (left) template. (e) Asymmetry Index frequency. (f) Asymmetry Index median DPF.

Pits DPF

Figure 2a and Figure S2a introduce the sulcal pits DPF distribution in 6 areals (central [a, b, c] and ST [b, c, d]) corresponding to 2 important primary sulci. We distinguish in central a and ST c, 2 underlying Gaussian distributions, which correspond respectively to pits that have been extracted in a wall cavity of the sulci and pits that lie at the bottom of the sulci. The first Gaussian distribution is of minor interest in our study because it is not reliably extracted across individuals (Fig. 1a). Our phenotype distributions in these areals correspond to Figure 2b and Figure S2b, for which we have selected the deepest pit of each individual in the areal considered. Figure 3b presents the median DPF value of the pit in all parcels to emphasize the regional pit depth differences and summarizes with a discrete representation the average DPF map (Fig. 1c) from the pits point of view. The pits being the putative first cortical folds, the differences observed between various regions might reflect the strength and time course of the folding process regional particularities. We computed the AI for both the frequency of pits and the median DPF for all cluster regions, the results are respectively displayed on Figure 3e,f. We notice that the 2 asymmetry maps are roughly similar, emphasizing the link between the DPF and the frequency of pits. In other words, to be reliably extracted across individuals a pit must be buried deep enough.

Quantitative Genetic Analysis of the Pits DPF

We performed a quantitative genetic analysis of the DPF pit value in each areal named in the nomenclature Figure 1d. We found that more than half of all areals considered on both sides had a heritability estimate significant (P < 0.05) without correction for multiple comparisons. These heritability estimates and their associated P-values are displayed respectively on Figure 3c,d. Tables 1 and 2, for the left and right hemispheres respectively, summarize the significant results after strict Bonferroni correction (P < 0.05/128 ≈ 0.0004) accounting for the multiple tests due to the number of areals considered. These areals, significant after correction, are the ones with a color above yellow on Figure 3d. The full Tables with heritability estimates significant (P < 0.05, uncorrected) are given as Supplementary material (Tables S1 and S2). In the collateral sulcus, we note significant heritability estimates, after correction, for the collateral a, b areals on both sides. Other interesting heritability results are found in the central sulcus, where areals central a, b are found heritable after correction in both hemispheres and central c in the right hemisphere, as well as the areals a, d in the cingulate sulcus. The areals b, c of the STs corresponding to the auditory and semantic networks are noticeably more heritable on the left hemisphere. The olfactory and orbital sulci have relatively symmetric significant heritability estimates, which are respectively about 0.45 and 0.3, which again indicate a genetic influence on the shape of the cortex in these sensory areas.

Table 1.

Results of the additive analysis for the DPF of the pits in the left hemisphere: heritability estimate and associated P-values for each covariate

Trait	h2 ± SE (P)	P-values					h2cov(%)	Subj
		Age	Age2	Sex	Age × Sex	Age2 × Sex
Below subparietal and cingulate	0.37 ± 0.08 (1.9 × 10–6)	0.14	0.59	0.04	0.86	0.64	1.8	817
Central a	0.34 ± 0.07 (5.9 × 10–6)	0.32	0.65	0.16	0.62	0.98	0.0	708
Central b	0.25 ± 0.07 (1.6 × 10–4)	0.6	0.31	0.3	0.93	0.09	1.1	784
Cingulate a	0.23 ± 0.07 (2.0 × 10–4)	0.05	0.24	0.35	0.14	0.26	0.6	845
Circular insular d	0.24 ± 0.07 (1.8 × 10−4)	0.41	0.36	0.13	0.04	0.52	0.3	850
Collateral a	0.4 ± 0.09 (9.2 × 10−6)	0.38	0.82	0.17	0.9	0.62	0.0	608
Collateral b	0.32 ± 0.07 (8.0 × 10−7)	0.93	0.59	0.25	0.52	0.32	0.0	835
Junct collateral and calcarine a	0.32 ± 0.07 (8.7 × 10−6)	0.14	0.23	0.04	0.41	0.71	1.8	728
Lat occipital	0.23 ± 0.07 (3.3 × 10−4)	0.97	0.79	0.25	0.76	0.88	0.0	842
Lateral occipital b	0.39 ± 0.07 (2.6 × 10−8)	0.05	0.33	0.07	0.45	0.4	2.9	804
Olfactory	0.42 ± 0.07 (3.5 × 10−8)	0.67	0.55	0.25	0.3	0.93	0.0	794
Parieto-occipital a	0.38 ± 0.07 (1.0 × 10−7)	0.73	0.61	0.67	0.23	0.95	0.0	779
Postcentral a	0.23 ± 0.07 (2.1 × 10−4)	0.68	0.13	0.17	0.12	0.04	0.1	771
Subparietal	0.31 ± 0.07 (1.5 × 10−6)	0.68	1.0	0.82	0.91	0.25	0.0	840
Sup temporal b	0.33 ± 0.06 (1.0 × 10−7)	0.92	0.23	0.99	0.48	0.2	0.0	818
Sup temporal c	0.26 ± 0.06 (8.0 × 10−6)	0.66	0.48	0.53	0.64	0.47	0.0	843

Only significant results after strict Bonferroni correction P < 0.05/128 are presented here.

h², heritability; SE, standard error; P, associated P-value; h²cov, variance explained by the covariates; Subj, number of subjects. Trait abbreviations are defined in the text.

Ethnicity and race group covariates were not included in this table and had associated P-value close to 1.

Table 2.

Results of the additive analysis for the DPF of the pits in the right hemisphere: heritability estimate and associated P-values for each covariate

Trait	h2 ± SE (P)	P-values					h2cov(%)	Subj
		Age	Age2	Sex	Age × Sex	Age2 × Sex
Below subparietal and cingulate	0.34 ± 0.06 (1.0 × 10−7)	0.96	0.3	0.35	0.69	0.22	0.0	815
Central a	0.3 ± 0.09 (1.9 × 10−4)	0.93	0.81	0.82	0.83	0.69	0.0	666
Central b	0.29 ± 0.08 (9.0 × 10−5)	0.79	0.49	8.5 × 10−3	1.0	0.5	1.3	760
Central c	0.34 ± 0.07 (1.3 × 10−6)	0.84	0.05	0.13	0.55	0.09	0.4	732
Cingulate a	0.31 ± 0.07 (2.1 × 10−6)	0.68	0.38	0.04	0.38	0.53	1.2	847
Cingulate d	0.39 ± 0.06 (3.0 × 10−11)	0.11	0.9	2.4 × 10−3	0.29	0.44	2.7	835
Circular insular a	0.36 ± 0.06 (7.5 × 10−9)	0.67	0.45	1.2 × 10−3	0.7	0.3	4.1	839
Circular insular b	0.3 ± 0.08 (2.1 × 10−4)	0.22	0.66	0.02	0.17	0.96	1.3	699
Circular insular d	0.28 ± 0.07 (2.1 × 10−5)	0.45	0.37	2.1 × 10−5	0.21	0.88	4.4	846
Collateral a	0.4 ± 0.07 (1.0 × 10−7)	0.17	0.31	3.0 × 10−3	0.03	0.08	2.1	587
Collateral b	0.25 ± 0.06 (7.7 × 10−5)	0.81	0.44	0.82	0.37	0.38	0.0	834
Junct collateral and calcarine a	0.35 ± 0.07 (8.0 × 10−7)	0.15	0.19	3.1 × 10−4	0.12	0.32	2.2	751
Lat occipital	0.23 ± 0.06 (1.6 × 10−4)	9.0 × 10−3	0.29	0.41	0.36	0.28	0.5	840
Occipito temporal a	0.26 ± 0.08 (3.2 × 10−4)	6.4 × 10−3	1.6 × 10−5	0.13	0.02	9.5 × 10−3	1.9	793
Olfactory	0.43 ± 0.07 (1.0 × 10−7)	0.54	0.78	8.7 × 10−4	0.37	0.64	2.4	793
Orbital	0.31 ± 0.06 (1.7 × 10−6)	0.68	0.28	0.92	0.77	0.72	0.0	843
Parieto-occipital a	0.33 ± 0.07 (1.6 × 10−6)	0.27	0.87	0.65	0.68	0.97	0.0	803
Planum temporale area	0.27 ± 0.07 (1.0 × 10−4)	0.67	0.08	5.7 × 10−5	0.1	0.45	4.0	769

Only significant results after strict Bonferroni correction P < 0.05/128 are presented here.

h², heritability; SE, standard error; P, associated P-value; h²cov, variance explained by the covariates; Subj, number of subjects. Trait abbreviations are defined in the text.

Ethnicity and race group covariates were not included in this table and had associated P-value close to 1.

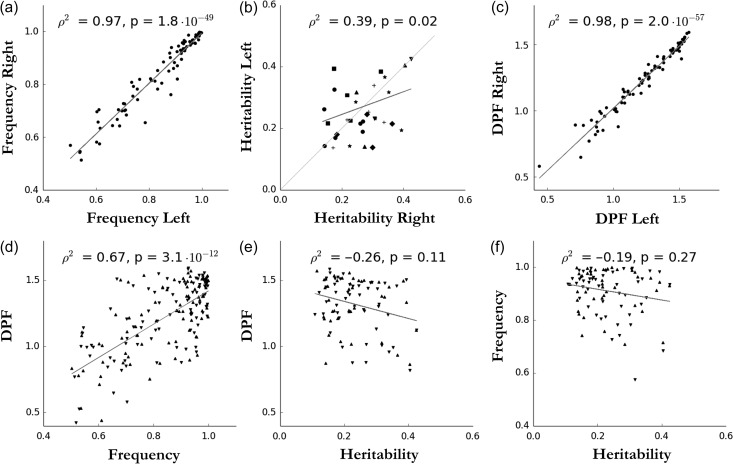
In addition, we quantified the correlation between hemispheres of the frequency and the heritability, as well as the relationship between these 2 and the DPF value. For the frequency-related quantifications, we considered areals with a pits frequency above 50%. For heritability-related quantifications, we kept only areals with a heritability estimate significant (P < 0.05, uncorrected) on both sides. As expected, given the relative symmetry of the brain, the pits frequency on both sides are highly correlated (Pearson correlation: r² = 0.97, P = 10⁻⁴⁹, Fig. 4a), as well as the DPF between hemispheres (r² = 0.98, P = 10⁻⁵⁷, Fig. 4c). The heritability estimates across hemispheres are significantly positively correlated (r² = 0.39, P = 0.02, Fig. 4b), suggesting some symmetric genetic influences over the pits DPF. As observed by Auzias et al. (2015), we note that the DPF and the pits frequency are positively correlated (r² = 0.67, P = 10⁻¹², Fig. 4d), showing a higher reproducibility of the deeper sulcal pits. This might be due do a better registration of the deeper folds. But, it could also reflect a more consistent genetic plan for deeper sulcal pits. However, this second hypothesis seems to be contradicted by the negative correlation trend between the pits DPF and heritability estimates (r² = −0.26, P = 0.11, Fig. 4e). The role of mechanical constraints will be discussed to account for a less important genetic control over pits with higher depth. Besides, the standard errors of the heritability estimates are still relatively large 0.06–0.09 to be compared with the values of these estimates 0.22–0.43. Furthermore, we did not find a significant correlation between the heritability and the frequency (Fig. 4f).

Figure 4.

(a) Correlation between left and right pits frequency for all areals with frequency above 50%. (b) Correlation and comparison of heritability estimates with associated P-values < 0.05 between hemispheres. Significant areals are grouped according to their location with the following legend: light grey line: y = x, star: Cingulate-Calcarine, cross: Central-Frontal, diamond: Sylvian fissure, up triangle: Collateral, disk: Temporal, square: Occipital-Parietal, down triangle: Olfactory-Orbital. (c) Correlation between hemisphere of pits median DPF per areal. (d) Positive correlation between DPF and pits frequency (up: left hemisphere, down: right hemisphere). (e) Negative correlation between pits median DPF and heritability estimates (up: left hemisphere, down: right hemisphere). (f) Correlation not significant between frequency and heritability estimates (up: left hemisphere, down: right hemisphere). For all plots, the regression line is in grey.

In spite of a general symmetric genetic control, we found 6 areals having a significant difference of genetic control between hemispheres, using the criterion previously introduced for a confidence interval of ±σ (67%) (i.e.,  $\mathrm{diff}=|{h^2}_{\mathrm{right}}-{h^2}_{\mathrm{left}}|>1\times {(\mathrm{\sigma }}_{h^2\mathrm{right}}+{\mathrm{\sigma }}_{h^2\mathrm{left}})$). They are the following areals: cingulate d (diff = 0.20), lateral occipital b (0.22), circular insular a, b (respectively 0.15, 0.16) and ST b (respectively 0.15). Reducing the confidence interval to 65% (Z(α/2) = 0.935), we also identified the areal ST c with diff = 0.12. Figure S5 presents a graphic interpretation of this difference presenting the heritability estimates with their confidence intervals in both hemispheres for each areal with associated P-value < 0.05 for h² on both sides.

Discussion

To the best of our knowledge, this quantitative genetic study of the pits depth is the first to estimate the additive genetic effects on the pits, which were for long assumed (Lohmann et al. 2008; Im et al. 2010). First, we confirmed the high reliability of pits extraction in a large population using the procedure described in (Auzias et al. 2015). In addition, we demonstrated the highly symmetric distribution for most pits in term of frequency and DPF, with low values of AI and high correlation between hemispheres. We also emphasized the link between pits DPF and frequency, underlining the fact that deep pits are more consistently extracted across individuals. Second, we reported the heritability estimates for all the pits cluster regions in both hemispheres using the large sample size of the HCP pedigree study enabling to have enough statistical power to estimate the heritability of phenotypes with low genetic influence. We found that pits DPF of areals in the central, cingulate, collateral, occitotemporal, parieto-occipital, and superior temporal sulci, among others, are significantly heritable after strict Bonferroni correction in one or both hemispheres. Finally, we highlighted a few remarkable asymmetrical areals among an overall symmetrical pattern of genetic influence across the brain.

Sulcal Pits Distribution

During the early period of brain development, sulcal roots correspond to the locations where the cortical folding begins (Régis et al. 2005). The sulcal pits associated to these roots are the ones lying at the bottom of the sulci and were previously extracted by imposing a threshold considered as a minimum required depth (Im et al. 2010; Meng et al. 2014). The concept was recently extended (Auzias et al. 2015) to include shallower pits, because algorithmically other vertex points might have fulfilled the requirements of the sulcal pits and might contain information on later periods of brain development or on less deep regions. Including shallower pits offers the opportunity to study folds in shallow region, such as the planum temporale area, planum parietal, or the supra marginal gyrus. The main caveat is that, in areals having already one deep sulcal pits, shallower pits can also be extracted, for example in a sulcus wall cavity. If we consider the 2 types of phenotype distributions: one (Fig. 2b, Fig. S2b) is composed of all deepest pit DPF of individuals having at least one pit and the other one (Fig. 2c, Fig. S2c) being the same distribution after only considering the pits with a DPF above the threshold. We notice that the 2 are almost identical, for the 6 areals under scrutiny in both hemispheres, except that in the second case the left tail of the Gaussian is cut, thus deliberately ignoring part of the population with lower DPF. However, the central a areal phenotype also contains pits from the shallow distribution (Fig. 2b), when we take the deepest pits without thresholding before. Indeed, this specific issue is reflected in the higher heritability estimate and significance for this areal when its distribution has been thresholded (Fig. S3c). Overall, the heritability estimates in other areals (Fig. S3) are identical, except that the standard error increases because the thresholding is conservative and excludes some subject with deep sulcal pits. Despite a better “homogeneity” of the phenotype we decided not to insert this thresholding step in order to include the largest sample possible representative from the general population, which also contains individual belonging to the left tail of the Gaussian distribution. This choice differs from the ones made by (Im et al. 2010; Meng et al. 2014) but avoid the caveat of arbitrarily choosing a threshold (Auzias et al. 2015).

Genetic Influence on the Sulcal Pits

From the current literature, 2 complementary theories emerge that support the genetic influence on the sulcal pits and call for a quantitative genetic study. The first model, based on observations in rhesus macaque, assumed that the morphology of earlier developing brain structures is more genetically controlled (Cheverud et al. 1990). The older the structure ontogenic’s age, the more genetically predetermined it is (Cheverud et al. 1990). A second hypothesis supported by Lohmann and colleagues, who studied the sulcal variability in human twin-pairs and noticed that deeper sulci are more similar than superficial ones, proposed that the deeper cortical structures are more genetically influenced (Lohmann et al. 1999). Since this hypothesis is based on the fact that deep cortical sulci formed earlier in development, this second proposition is actually a consequence of the first model. Both related hypotheses were never formally tested but explained findings in normal cortical variability (Cykowski et al. 2008) as well as in disease-specific difference observed such as in schizophrenia (Narr et al. 2004). Kochunov et al. (2010) tested both of these hypotheses by studying the genetic contribution to regional morphological variability in the cerebral cortex of baboons. They could not replicate the findings of Lohmann and colleagues and rejected this theory. The negative correlation trend we found (Fig. 4e) between the median DPF and the heritability of DPF, means that deeper pits are not necessarily more heritable than more superficial ones and seems to contradict the hypothesis that deeper cortical structures are more genetically influence.

Nevertheless, our study in a human pedigree cohort supports a genetic influence on the sulcal pits, which displays regional variabilities with heritability estimates ranging from 0.2 to 0.5. These results consolidate the hypothesis of a genetic control on these structural landmarks (Lohmann et al. 2008). Our study confirms that the term landmark is appropriate because of the higher pits frequency for pits lying deeper in the cortex (Fig. 4d), thus suggesting a general framework to compare individual sulcal variability. Furthermore, the sulcal pits are key points of the cortical folds, which are often thought to be related to cytoarchitectonic areas (Fischl et al. 2008) and therefore assessing the genetic component of their shape seems particularly relevant. Indeed, the DPF partly includes shape information, because it not only reflects the depth but also the convexity of the pit neighboring white matter. Besides, we note that this range of heritability estimates (below 0.5) suggests pits DPF and thus the cortical structure shape is primarily influenced by nongenetic factors, even though the genetic control over the formation of the gyral pattern is significant. The shape of sulci continues to evolve throughout the adult life as opposed to the total brain volume or the intracranial volume, which are fixed after adolescence and whose heritability estimates are closed to 0.8 (Stein et al. 2012). This conclusion was noticeably reached twenty years ago by Barltey, Jones, and Weinberger with only 10 pairs of MZ and 9 pairs of DZ, who found high heritability for the cerebral size (>0.9) and relatively low heritability for the gyral pattern (<0.2) (Bartley et al. 1997). They underlined the significant role of the genes in shaping the cortical shape by observing that MZ twins were more alike than DZ twins and noticing the interhemispheric symmetry of the gyral pattern within subjects (Bartley et al. 1997).

Focusing on the central sulcus, we found significant heritability estimates, ranging between 0.22 and 0.34, for the sulcal pits in the 3 areals composing central sulcus (a, b, c) in both hemispheres. Moreover, a study on the heritability of the depth position profile found 3 heritability peaks in both left and right hemispheres depth profiles (McKay et al. 2013). Due to the high variability of depth profiles between individuals, the authors could not conclude if the heritability peaks collocated with the maximum depth positions. However, on the average depth trace, the sulcal depth peaks seem to correspond to the heritability peaks. Combined with our results, this would support the importance of the sulcal pits as cleaving points in the genetic plan. Interestingly, the locations of the heritability peak were adjacent to specialized functional areas, with the activations in fMRI tasks activating the hand and mouth regions (McKay et al. 2013). This emphasizes the potential role of the sulcal pits as landmarks separating functional areas, such as the somatotopic arrangement along the central sulcus. Moreover, the average depth in the finger tapping area was pleiotropic with the average reaction time of the corresponding fMRI task. This finding, associated to our heritability estimates, comforts the hypothesis that sulcal pits have close relationship to functional areas (Lohmann et al. 2008) and might suggest a common set of genes influencing the brain function and structure.

We found our highest heritability estimate for the DPF of the sulcal pit in the areal collateral a (h²_left = 0.40, h²_right = 0.40), followed closely by the one in the olfactory sulcus (h²_left = 0.42, h²_right = 0.43). The collateral sulcus showed significant heritability estimates on both sides in 3 areals. These were superior in the anterior areal collateral a in comparison to posterior ones b, d. The anterior areal a corresponds to Rhinal sulcus (Sarnat and Netsky 1981) which is considered, from a phylogenetic point of view, as the second hemispheric sulcus following hippocampal sulcus and demarcates the border between the paleocortex and neocortex (Ribas 2010). In humans, the Rhinal sulcus delineates the parahippocampal uncus from the rest of the neocortical temporal lobe. Thus, the Rhinal sulcus was already present in early mammals (Ribas 2010; Nishikuni and Ribas 2013). Such phylogenetic seniority could explain the higher heritability of the anterior areal of the collateral sulcus.

In addition, we have shown a significant correlation between the heritability of the left and right hemispheres (Fig. 4b), which seems to be in line with initial symmetric morphogenic protein gradients, such as Sonic hedgehog and members of the bone morphogenetic protein family, (Echevarría et al. 2003). This is also in agreement with the “symmetry rule” from McKay and colleagues postulating that a feature in one hemisphere is likely under the control of the same genes or set of genes in the opposite hemisphere (McKay et al. 2013). Genetic clustering based on cortical surface area resumes this rule by showing a genetic organization predominantly bilaterally symmetric across hemispheres (Chen et al. 2012). Similarly, our heritability map of the sulcal pits DPF (Fig. 3e) and the positive correlation found (Fig. 4b), both confirm this postulate.

Asymmetric Genetic Control in Particular Regions

Despite an overall symmetric genetic control, 2 areals in the STs have highly asymmetric heritability estimates, respectively for areals b and c: h²(STb) = 0.33 (P = 10⁻⁷) and h²(STc) = 0.26 (P = 10⁻⁶) in the left hemisphere whereas in the right hemisphere h²(STb) = 0.18 (P = 10⁻⁴), and h²(STc) = 0.14 (P = 0.02) (Tables 1 and 2). These results advocate for a higher genetic control in the left STs. Furthermore, these areals in the left hemisphere might correspond to functional zones involved in language comprehension in adults (Pallier et al. 2011). Specifically, areals ST b and c are located along the linguistic ventral pathway and would map sounds to meaning with phonetic processing in ST c and computations related to larger constituents in ST b (DeWitt and Rauschecker 2012; Skeide and Friederici 2016). Our results suggest genetic cues to increase the genetic control in the lay down of the cortex organization in regions involved in such language functions. These genetic cues, such as differential gene expression, could contribute to the functional gradient of linguistic processes which has been reported along the STs early in life (Dehaene-Lambertz et al. 2006).

Karlebach and Francks (2015) have recently demonstrated in a molecular biology study the lateralization of individual genes expression and gene ontology groups in the human language cortex. These genes are likely to tailor the genetic control over brain particular functions including synaptic transmission and glutamate receptor activity, and pave the way to the nervous system development (Karlebach and Francks 2015). These asymmetrical gene contributions may account for our asymmetric quantitative genetic results, which exhibited a higher heritability in the left hemisphere where the fine-tuning is the most required.

We can also relate this asymmetry of additive genetic effects to various structural asymmetries already demonstrated in the vicinity of the STs. The most notable ones consist of the planum temporale and Heschl’s gyrus larger on the left side (Dorsaint-Pierre et al. 2006); the asymmetry of the STs depth profile, which is more pronounced in humans than chimpanzee (Leroy et al. 2015) and visible in infant brain (Glasel et al. 2011); specifically, plis de passage across areals STs b and c, which are complementary shapes to sulcal pits and are more consistent in the left hemisphere from early in life along the lifespan (Ochiai et al. 2004; Leroy et al. 2015); finally the arcuate fasciculus, which is larger in the left temporal region and whose asymmetry is observed from birth (Dubois et al. 2010). The language lateralization is the main working hypothesis to explain these asymmetries and our findings support stronger genetic control over the underlying structure in the left side of the brain. The left hemisphere temporal area has also been hypothesized to be the side more influenced by in utero environment (Geschwind et al. 2002), which would be coherent with the initial delay in maturation observed in the left hemisphere compared with the right. The hypothesis of Geschwind and colleagues hypothesis was based on results in a cohort of aged twins (61 MZ pair and 67 DZ pair, average age 71 years old), in which they found the temporal lobe volume more heritable in the right hemisphere (Geschwind et al. 2002). However, due to the population size and age, these results, which considered the whole temporal lobe, are to be taken with caution. In addition, the delay formation of the left STs could also be explained by a protracted genetic control to allow the fine tuning of the particular electrophysiological and neurotransmission properties of this key cognitive area. Indeed, Geschwind’s work also supports a genetic contribution to the development of cerebral asymmetry (Geschwind and Miller 2001) and quantitative genetic studies with sufficient statistical power like ours are still needed to validate the importance of the genetic control on each side.

One limitation of our study is that we did not model the shared environment since: first, HCP does not provide direct household information, and second due to the limitations of household as a proxy for common environmental influences in extended pedigree designs. Thus, some of our heritability estimates might be inflated due to unmodeled shared environmental influences. However, the sulcal pits are the putative first cortical folds supposed to be formed early during the cortex development, hence we believe household environmental influence should have a limited effect on their depth.

This study underlines the role of the sulcal pits as good candidates for future genome wide association analysis, using for example the large UK Biobank cohort to have adequate statistical power to detect small effect size variants. Further aim is to build novel polygenic scores in which genotypes at many loci are influencing the sulcal pits. These polygenic scores could be used to investigate the genetic influence of these loci on other phenotypes and neurological disorders.

Supplementary Material

Supplementary data is available at Cerebral Cortex online.