Study of efficiency in five-field and field-by-field intensity modulated radiation therapy (IMRT) plan using DOSXYZnrc Monte Carlo code

Abstract

Implementation of a modern treatment technique, such as IMRT, has been improved. In line with that, Monte Carlo (MC) simulations of this technique require the ability of complex beam configurations modelling with respect to the patient. The source 20 DOSXYZnrc with the dynamic and step and shoot technique can be used to simulate the modality. However, they have a different process to obtain the dose distribution in a certain phantom. This study aimed to compare the simulation efficiency and isodose dose distribution in a water phantom from various beam angles and multileaf collimator (MLC) positions in an IMRT plan using source 20. The 30 × 30 × 30 cm³ phantom was irradiated by Varian Clinac iX10MV photon beam with various field sizes from 2 × 2 to 6 × 6 cm² using some beam angles 5°, 30°, 90°, 180°, and 300° and maintaining the source to surface distance (SSD) of 100 cm. The field-by-field and five-field methods were used to obtain the 3-dimensional (3D) dose distribution. The dose distribution of these methods was compared using the gamma index, DVH analysis, and simulation efficiency. Higher efficiency is better because it implies that it takes less time to reach a given uncertainty. The implementation of source 20 has been validated, with similar results, with validated source in DOSXYZnrc. The identical 3D-dimensions dose distributions using source 20 for dynamic and step and shoot were observed. Two simulations used the same number of histories with the statistical uncertainty of less than 3%. The step and shoot technique was more efficient than the dynamic simulation.

1. Introduction

The goal of radiation therapy is to deliver an appropriate therapeutic dose of radiation to a malignant tumor and minimize side effects in the surrounding normal critical structures. Besides, this treatment is also widely used to treat some kinds of early-stage cancer. To achieve that goal, researchers continue research to develop new techniques. Intensity-modulated radiation therapy (IMRT) is one of the modern techniques routinely used in the treatment of cancers.1, 2, 3, 4 This technique gives high-precision radiotherapy that uses a computer-controlled linear accelerator to deliver precise radiation doses to a malignant tumor or specific areas within the tumor. IMRT allows the radiation dose to conform more precisely to the 3D shape of the tumor by modulating or controlling the intensity of the radiation beam in multiple small volumes. Some studies have been conducted on the small field dosimetry in the IMRT technique,5, 6, 7, 8, 9, 10 but the effect of the step and shoot and sliding window method on such small beams has not been extensively studied. This study was focused on the use of these two methods with Monte Carlo (MC) simulation.

Multi-purpose MC based radiation transport techniques have been used as the most accurate verification tool in radiotherapy, including the IMRT delivery technique, for several years.11, 12, 13, 14, 15, 16 Benhalouche et al. performed the GATE/Geant4 Monte Carlo simulation platform to simulate seven head-and-neck IMRT treatment plans with different beam patterns. They found that the simulated IMRT treatment plans was in agreement with the measurement with difference of less than 1% between the GATE results and corresponding measurements for IMRT plans.¹⁷ The Monte Carlo code used in another work was MCSIM with implementation of several variance reduction techniques. The dose–volume histograms and isodose distributions of 30 prostate cancer cases treated using IMRT treatment plans were calculated using the Monte Carlo method and compared with the measurement results. The step and shoot technique was used during the treatment. The maximum dose differences for the rectum were less than 4% for all the cases.¹⁸ The planning aspects of MLC-based IMRT represent a challenge because the IMRT beams consist of a large number of control points (more than 100 segments for each beam angles) which record the MLC position, coordinates of the isocenter, MU index, etc., depending on the target position. Many studies have demonstrated the feasibility of the MC method in simulating IMRT plan but none of them has explained whether the MC technique used is consistent with treatment techniques (step and shoot or sliding window).^1,13,17, 18, 19, 20, 21 The choice of technique used greatly influences the results obtained.

Therefore, the aim of this work was to evaluate the efficiency and dose distribution of a water phantom in simulating five-field and field-by-field IMRT plan. In order to establish this goal, the Monte Carlo EGSnrc code has been taken as a reference code for our study, which is considered as the potential Monte Carlo code compared to other codes in simulating complex planning and can handle complex geometries concerning the patient used in many physics applications. There were 12 types of sources developed in DOSXYZnrc. Each source can be used to model different simulations. Source 20 (synchronized phase space source) developed by Lobo and Popescu (2010) can be used to simulate an IMRT plan.¹³

2. Methods

2.1. Linear accelerator

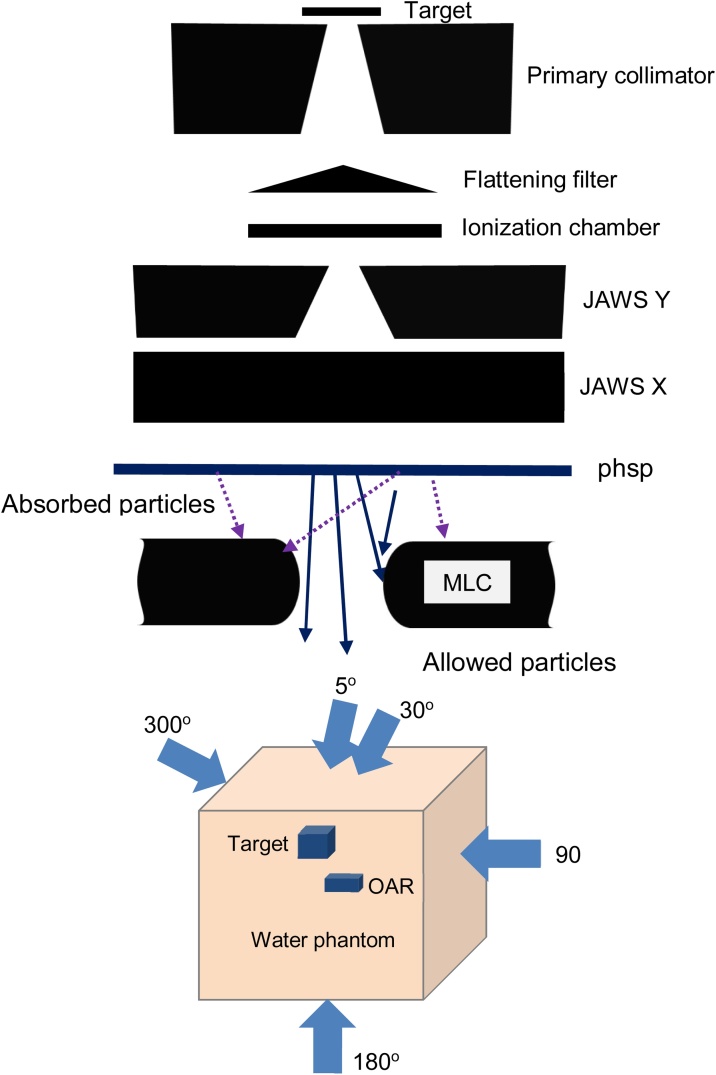
The clinical linear accelerator simulated in this study was Varian Clinac iX10MV photon beam (Varian Oncology Systems, Palo Alto, CA). The dimensions and materials for the accelerator components were incorporated according to the manufacturer’s specifications. A full MC simulation of the treatment head components (target, primary collimator, flattening filter, monitor chamber) is possible as the information is proprietary (Fig. 1). The surrounding space was filled with air of density 0.001293 g/cm³. Varian Clinac iX is equipped with Millenium MLC 60 pair of leaves with a maximum field size of 40 × 40 cm² at the isocenter. The commissioning process for this linac has been done using the EGSnrc-BEAMnrc/DOSXYZnrc Monte Carlo code.²²

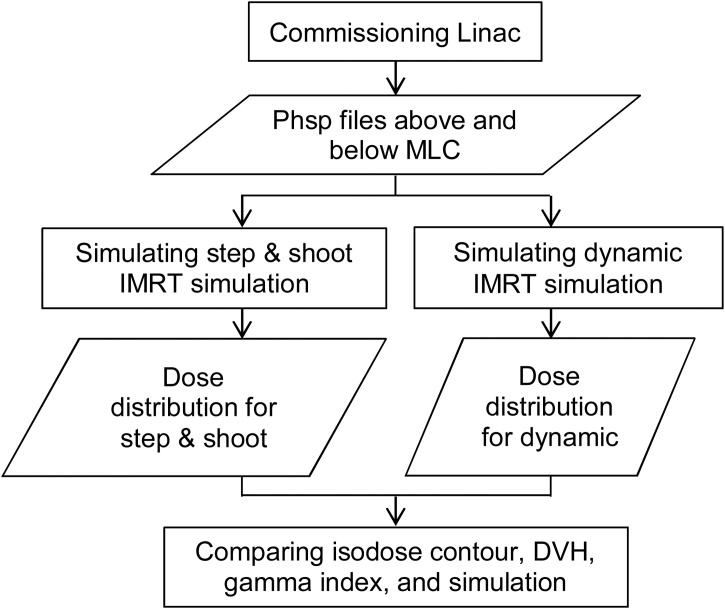
Fig. 1.

A flowchart of the Monte Carlo simulation step.

2.2. Monte Carlo simulation

BEAMnrc and DOSXYZnrc Monte Carlo codes were used for the accelerator head simulation and dose calculation in a water phantom, respectively. Both codes were EGSnrc (Electron Gamma Shower National Research Council Canada, Nelson et al. (1985)) user codes, running under the LINUX operating system. Detailed descriptions of the software can be found in Rogers et al. (2018).^23,24

Overall, the Monte Carlo simulation steps are shown in Fig. 1. The phsp file above MLC was used to simulate the five-field and field-by-field techniques. The dose distribution in the virtual water phantom was obtained from these simulations. The isodose contour, DVH, gamma index, and simulation efficiency was analyzed from the two dose distributions.

In BEAMnrc, the commissioning process allows the user to obtain the output of the particles released by a Linac inform phase space file. The phase-space (phsp) data can be placed anywhere inside the Linac. In this study, the phsp was scored in a scoring plane above the multileaf collimator (MLC) (Fig. 2). Commissioning process of this Linac was carried out in our previous study.¹⁸ This process was done by optimizing initial electron energy and FWHM of sources. The phsp file in this study was obtained during the commissioning process.

Fig. 2.

Illustration of the Varian Clinac iX and phsp file location.

Generally, Monte Carlo simulation uses source 2 (Phase-space (phsp) source, particles incident from any direction) to simulate the dose distribution in a phantom with one field size and one irradiation angle. Lobo and Popescu introduced a new source in DOSXYZnrc that can facilitate simulations with multiple field sizes and several beam angles at the same time and is known as source 20. In this simulation, the phase-space data, as a source input, was collected from a BEAM simulation. This phsp data contained the particles that reached the scoring plane from the target. The phsp can be used as a source more than once. The beam, including syncMLC, was compiled as a shared library using a different input file to eliminate intermediate phase space files (below the MLC) and simulate a continuous beam delivery in a single run. Simulation with source 2 only uses one irradiation angle and one field size, so no sequence file is needed. In source 20, the sequence file including the number of MLC and the MLC leaf opening was put into a file. In this study, the five-field and field-by-field technique are simulated for field sizes of 2 × 2, 3 × 3, 4 × 4, 5 × 5, and 6 × 6 cm². The virtual phantom design, beam arrangement, SSD, theta, phi, and collimator angles were set to the same values for five-field (dynamic) and field-by-field (step and shoot) simulation. The MLC leaves are in continuous movement across the field with certain intensity in the dynamic technique but in the step and shoot technique, there is a time lag between each beam angles with certain MLC leaves position with other angles.

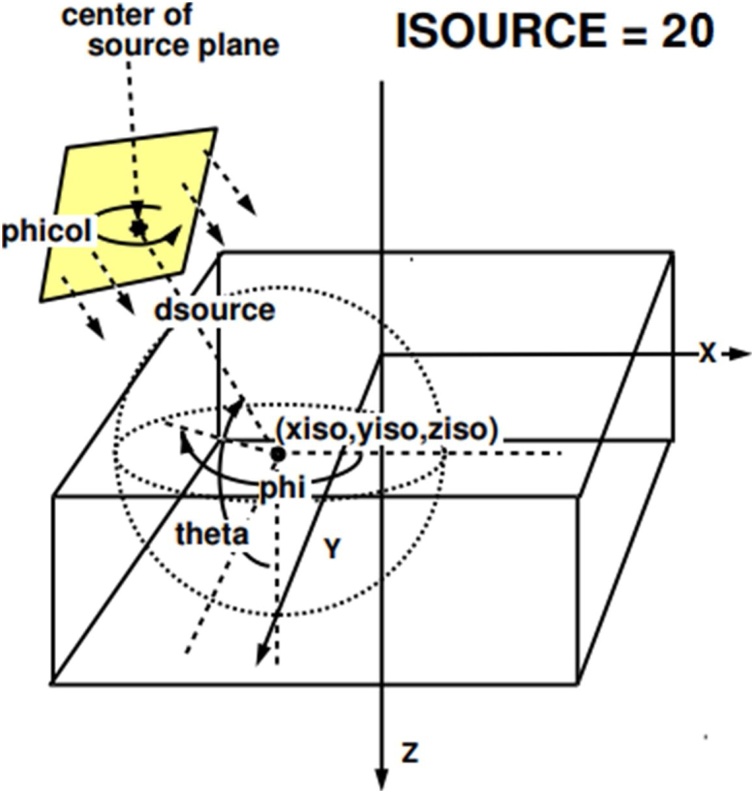
The definition of theta and phi angles is defined in Fig. 3. The theta angle defines the angle between the +z direction and a line joining the center of the beam where it strikes the phantom surface to the isocentere. Meanwhile, the phi angle expresses the angle between the +x direction and the projection on the x–y plane of the line joining the center of the beam on the phantom surface to the isocenter on the xy plane.¹³ In clinical cases, the angle that can be adjusted is gantry angles and can be transformed into the theta and phi angles. The coordinate transformation from gantry angles to theta and phi angles in this study was adopted from Zhan et al.²⁵ The pairs of theta, phi, and field size are described in Table 1.

Fig. 3.

Source 20 of DOSXYZnrc¹³.

Table 1.

List of beam angles and field sizes for field-by field simulation.

Simulation	Gantry angles (o)	Field size (cm2)	Collimator angles (o)	Theta angles (o)	Phi angles (o)
1	5	6 × 6	270	90	275
2	30	5 × 5	270	90	300
3	90	3 × 3	270	90	0
4	180	2 × 2	270	90	90
5	300	4 × 4	270	90	210

DOSXYZnrc simulates dose in Cartesian voxelized geometry in a 3D rectilinear voxel (volume element) (e.g., a phantom or a patient body). The water phantom contains target and organ at risk (OAR) with the dimension of 2 × 2 × 2 cm³ and 1 × 2 × 2 cm³, respectively. Water, target and organ at risk (OAR) were defined as the phantom medium using 700icru PEGS4 cross-section data file. The particle source, phantom geometry, and variance reduction parameters are defined in the input file. Source 20: synchronized phase space source in DOSXYZnrc, was used as a source in this simulation. The number of histories runs in DOSXYZnrc was 5 × 10⁹ particles.

The simulation was divided into 15 steps to obtain good statistical uncertainty. Each part of the simulation used 1 × 10⁸ particles with different seed pairs and at the end of the simulation 1.5 × 10⁹ particles were obtained. The 3D dose distribution was obtained in every simulation step and 15. 3ddose files were obtained at the end of the simulation. The 3ddose files from simulations were combined using our in-house software MATLAB code (license number: 40615480). The simulation steps for field-by-field DOSXYZnrc are shown in Fig. 4. The EGSnrc transport parameters were set to ECUT = AE = 700 keV, PCUT = AP = 10 keV and ESTEPE = 0.04.

Fig. 4.

Simulation step for field-by-field DOSXYZnrc.

2.3. Method of plan comparison

Three parameters were used to compare and verify the five-field and field-by-field simulation: simulation efficiency, isodose distribution, dose volume histogram (DVH), and gamma index analysis.

For all gamma index comparisons, the field-by-field dose distribution was selected as the reference. The criteria were calculated using a local percent dose difference (DD) and distance to agreement (DTA). The recommended gamma criteria based on TG 119 is 3%/3 mm (DD/DTA).

The simulation efficiency was calculated using equation $\epsilon =\frac{1}{s^{2}t}$. This value depends on statistical uncertainty (s) and simulation time (t). A higher efficiency is better because it implies that it takes less time to reach a given uncertainty. DVH analysis was calculated for target and OAR inside the water phantom.

3. Results and discussion

3.1. Dose distributions

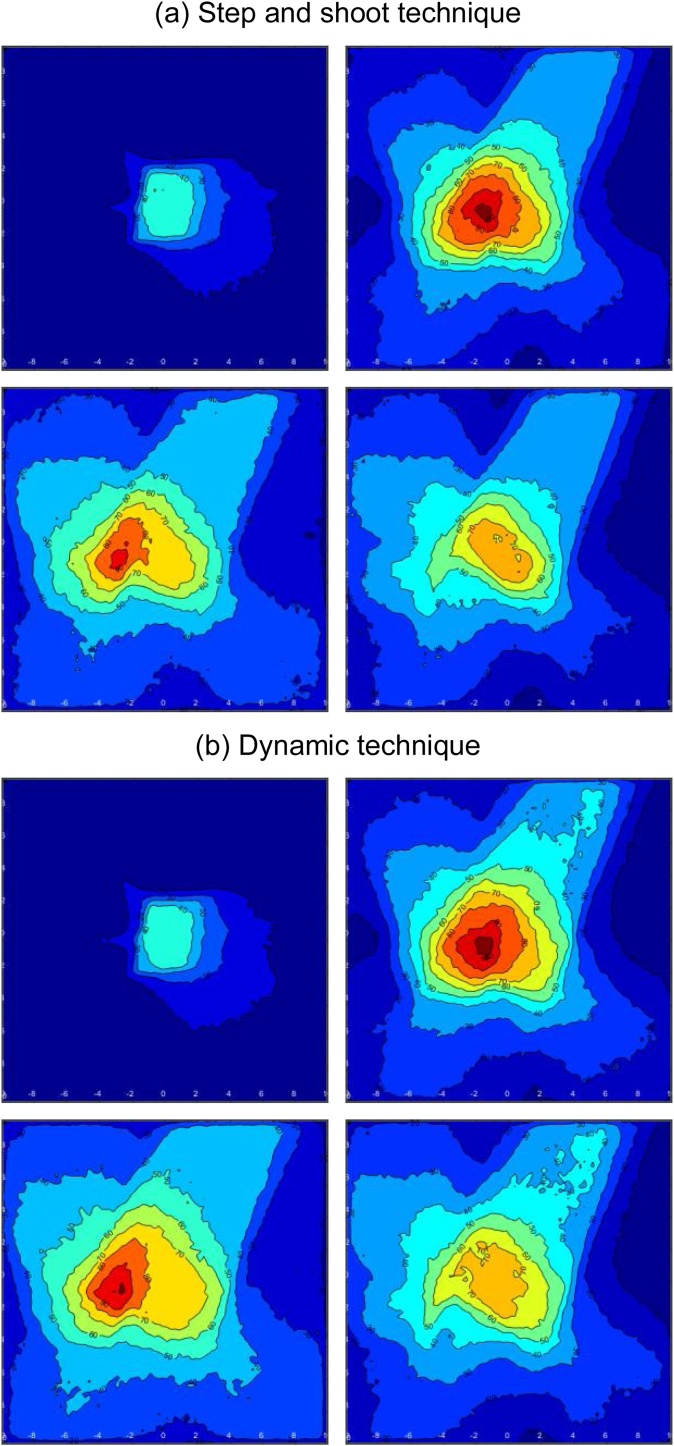
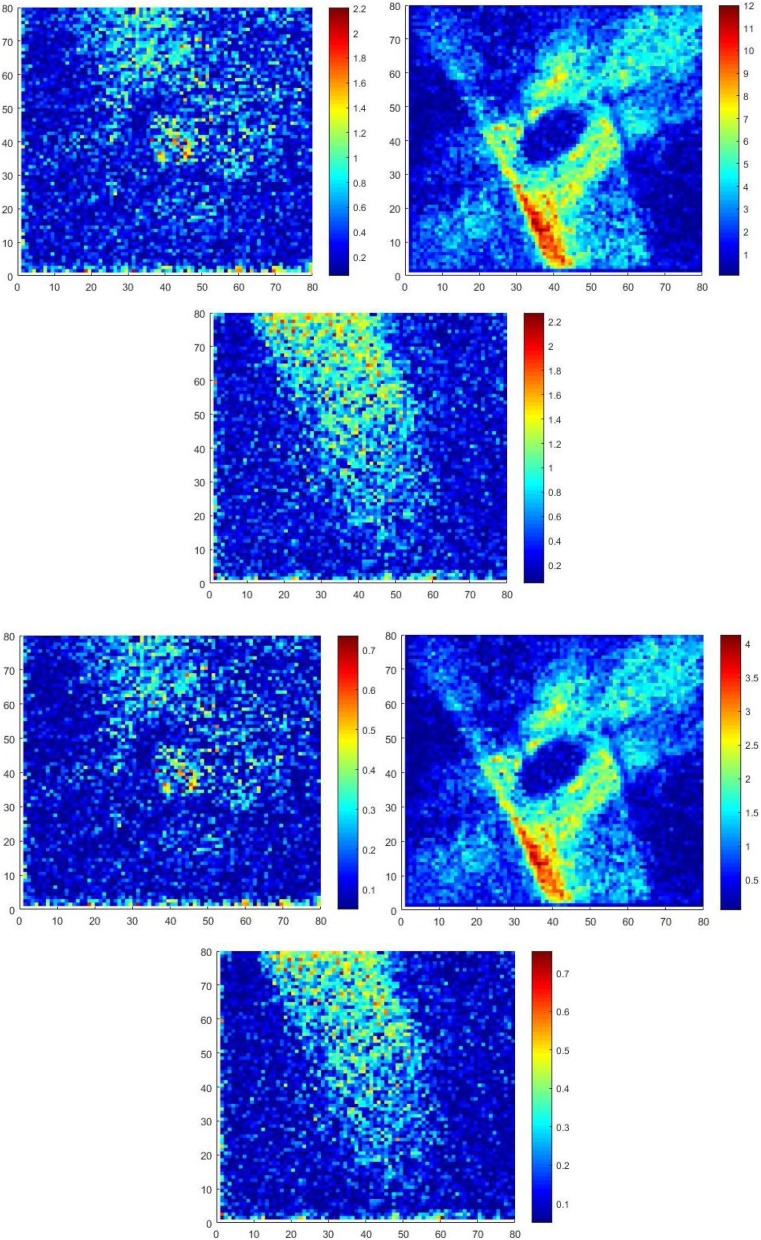
Fig. 5 shows the comparison of Monte Carlo five-field and field-by-field simulation for a multiple beam IMRT plan in DOSXYZnrc, with gantry angles of 5°, 30°, 90°, 180°, and 300° and another parameter lists in Table 1. The figure shows the 100%, 90%, 80%, 70%, 50%, and 20% isodose lines for the axial isocenter slice, normalized to the maximum dose in the entire virtual water phantom. The dose distribution for field-by-field was obtained by adding several dose distributions with different angles using in-house VDOSE GUI based on MATLAB. The five. 3ddose files from each simulation were combined into one 3ddose file for field-by-field simulation.

Fig. 5.

Isodose contour of (a) field-by-field and (b) five-field simulation for slice number 20th, 35th, 40th, and 45th.

This figure shows the isodose contour of field-by-field and five-field simulation for slice number 20, 35, 40, and 45. The dose distribution in the 20th and 45th slice has a similar form and dose value. However, the shape of the isodose curve is very different in the slice in the middle of the phantom (35 and 40). The figure shows that the dose in the 35th and 40th slice for the five-field technique is greater than the dose distribution in the field-by-field technique.

Therefore, it can be said that the five-field and field-by-field dose distributions show a different shape of isodose contour around the isocenter area. This is possible because the location of the phsp file used is also different. The simulation uses a particle source (phsp file) which is above the MLC so that the particles are possibly blocked and absorbed by MLC. Meanwhile, the field-by-field simulations use phsp file in the phantom surface so that no particles will be lost (most of them are allowed) and they will contribute to dose distribution in the phantom.

3.2. Gamma index and DVH

The calculated gamma index maps for slice 20, 40, and 60 with criteria 3%/3 mm and 1%/1 mm is shown in Fig. 6. The map shows that the gamma index was very big in the middle of the phantom.

Fig. 6.

Gamma index maps of step and shoot and dynamic IMRT simulation in slice of 20th, 40th, and 60th with acceptance criteria 1%/1 mm and 3%/3 mm.

Fig. 6 shows the calculated gamma index maps for slice 20, 40 and 60 with criteria 3 mm/3% and 1 mm/1%. The map shows that the gamma index was very big in the middle of the phantom. The hotspot detected in slice 40 in the x-axis around voxel number 30 to 40 and the y-axis around 0 to 40, while in slice 20 and 60 the gamma values are still in the allowed range of 1. The gamma index and gamma pass rate were also tested for an acceptance criterion of 1 mm/1%, 2 mm/2%, 3 mm/3%, and 4 mm/4% (Table 2). The gamma pass rate was calculated using the following equation.²⁶

$$\text{\%}\text{g}\text{a}\text{m}\text{m}\text{a}\text{p}\text{a}\text{s}\text{s}\text{r}\text{a}\text{t}\text{e}=\frac{\text{N}\text{u}\text{m}\text{b}\text{e}\text{r}\text{o}\text{f}\text{p}\text{i}\text{x}\text{e}\text{l}\text{s}with\gamma <1}{\text{N}\text{u}\text{m}\text{b}\text{e}\text{r}\text{o}\text{f}\text{p}\text{i}\text{x}\text{e}\text{l}\text{s}}\times 100\%$$ (1)

Table 2.

Gamma passing rate with different acceptance criteria.

No.	Acceptance criteria	Gamma passing rate (%)	Mean gamma
1	1 mm/1%	69.44	0.99
2	2 mm/2%	84.32	0.50
3	3 mm/3%	90.98	0.34
4	4 mm/4%	95.82	0.26

The acceptance criteria 1 mm/1% and 2 mm/2% show the gamma pass rate of less than 90% (69.44 and 84.32, respectively). In addition, the gamma values for these two criteria were very large, namely 0.99 and 0.5 for 1 mm/1% and 2 mm/2%, respectively (Table 2). These gamma pass rate and gamma value show that these techniques (dynamic and step and shoot) give different dose distribution, even though the gantry angle and the MLC openings are the same.

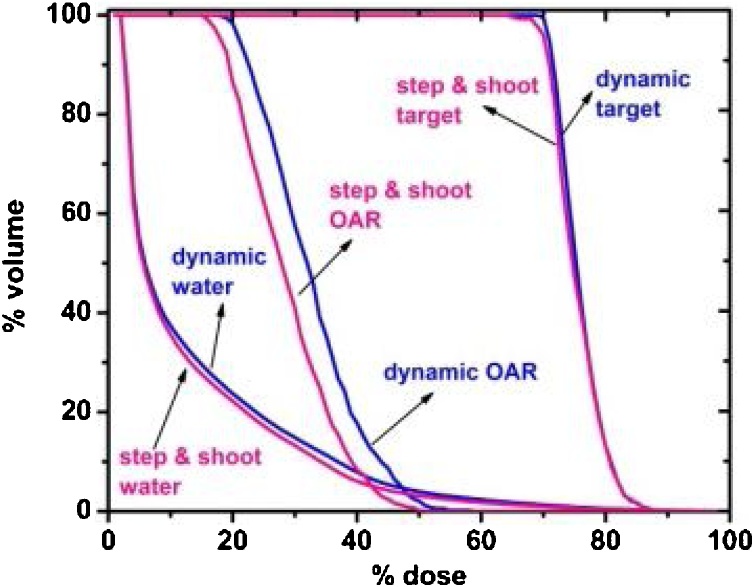
Dose volume histogram was analyzed for water, target, and OAR as shown in Fig. 7. The DVH curve for target and water has an identical shape for dynamic and step and shoot technique. However, the dynamic technique was better than the step and shoot for the OAR.

Fig. 7.

DVH of step and shoot and dynamic technique for water, target, and OAR.

3.3. Simulation efficiency

The statistical uncertainty of the dynamic simulation was bigger than the step and shoot simulation (Table 3). The uncertainty in EGSnrc depends on some factors. This also occurs at simulation time value.

Table 3.

Efficiency of field-by-field and five-field simulation.

Simulations	t (h)	s (statistical uncertainty)	ε (efficiency)
Field-by-field	19.1	2.89	0.0063
Five field	18.3	2.29	0.015

The statistical uncertainty of the dynamic and step and shoot techniques were 2.29% and 2.89%, respectively. The simulation time was 18.3 h for the dynamic and 19.1 h for the step and shoot technique. Hence, the efficiency of dynamic was 0.0105 and step and shoot was 0.0063. The step and shoot technique was more efficient than the dynamic one. The number of particles simulated (N) affected the simulation time and statistical uncertainty (s) $\left(s^2\propto \frac{1}{N}\right)$.²⁷ In Monte Carlo simulation, the entirely possible event will be simulated. Therefore, the simulated event will be close to the actual event. In dynamic techniques, if the first and second gantry angles are set at 5 and 30 degrees respectively, then irradiation will occur between these angles. This can cause some particles will be blocked by MLC and not arrive at the phantom. Whereas in the step and shoot technique, particles will be fired only at the desired angle and certain field size. As a result, the number of particles that arrive at the phantom for the shoot step is more than in the dynamic technique and the number of particles affects the statistical uncertainty.

The value of the statistical uncertainty obtained in this study is still above 1%. This can be overcome by increasing the number of particles simulated and applying several types of variation reduction techniques such as forcing photon interactions, bremsstrahlung splitting, Russian Roulette, bremsstrahlung cross section enhancement, and photon splitting. In addition, it is also recommended that computers with high specifications can shorten the simulation time.

4. Conclusions

The five-field (dynamic) and field-by-field (step and shoot) techniques can be simulated using source 20 in DOSXYZnrc Monte Carlo code with the high-resolution dose distribution. The dose distribution of field-by-field and five-field show a different isodose contour at the isocentere. These different techniques provide different DVH curves for OAR medium. Monte Carlo simulation with the step and shoot technique is more efficient than the dynamic one with a gamma pass rate of 90.98% for the acceptance criterion of 3 mm/3%.

The EGSnrc Monte Carlo code can be used to simulate IMRT planning as in our previous study.²⁸ To simulate the IMRT planning, five-field or field-by-field techniques can be chosen. Therefore, in this study we analyzed the comparison of the dose distribution, dose volume histogram (DVH), gamma index, and simulation efficiency of the two techniques. We recommend the use of field-by-field techniques in simulating IMRT planning based on the results of this study.

Future research will be investigated by validating these techniques with measurement data or comparison with TPS calculations using CT data images.

Financial disclosure

None declared.

Conflict of interest

None declared.