Abstract
Mitochondrial membrane potential (Δψm) plays a key role in vital mitochondrial functions, and its dissipation is a hallmark of mitochondrial dysfunction. The objective of this study was to develop an experimental and computational approach for estimating Δψm in intact rat lungs using the lipophilic fluorescent cationic dye rhodamine 6G (R6G). Rat lungs were excised and connected to a ventilation-perfusion system. The experimental protocol consisted of three single-pass phases, loading, washing, and uncoupling, in which the lungs were perfused with R6G-containing perfusate, fresh R6G-free perfusate, or R6G-free perfusate containing the mitochondrial uncoupler FCCP, respectively. This protocol was carried out with lung perfusate containing verapamil vehicle or verapamil, an inhibitor of the multidrug efflux pump P-glycoprotein (Pgp). Results show that the addition of FCCP resulted in an increase in R6G venous effluent concentration and that this increase was larger in the presence of verapamil than in its absence. A physiologically based pharmacokinetic (PBPK) model for the pulmonary disposition of R6G was developed and used for quantitative interpretation of the kinetic data, including estimating Δψm. The estimated value of Δψm [−144 ± 24 (SD) mV] was not significantly altered by inhibiting Pgp with verapamil and is comparable with that estimated previously in cultured pulmonary endothelial cells. These results demonstrate the utility of the proposed approach for quantifying Δψm in intact functioning lungs. This approach has potential to provide quantitative assessment of the effect of injurious conditions on lung mitochondrial function and to evaluate the impact of therapies that target mitochondria.
NEW & NOTEWORTHY A novel experimental and computational approach for estimating mitochondrial membrane potential (Δψm) in intact functioning lungs is presented. The isolated rat lung inlet-outlet concentrations of the fluorescent cationic dye rhodamine 6G were measured and analyzed by using a computational model of its pulmonary disposition to determine Δψm. The approach has the potential to provide quantitative assessment of the effect of injurious conditions and their therapies on lung mitochondrial function.
Keywords: cationic rhodamine dyes, computational modeling, electrochemical transmembrane potential, fluorescence imaging, mitochondrial uncoupling
INTRODUCTION
Mitochondrial membrane potential (Δψm) is a major component of the proton motive force (mitochondrial electrochemical transmembrane potential), which plays a key role in mitochondrial bioenergetics, metabolic and signaling functions (21, 27). For pulmonary endothelial cells, mitochondria produce ~80–85% of ATP needed for normal cellular functions (13, 25). Dissipation of Δψm is a hallmark of mitochondrial dysfunction observed in various cell types, including pulmonary endothelial cells exposed to oxidative stress (27, 37, 41, 50). In addition, mitochondrial dysfunction has been implicated in the pathogenesis of acute and chronic lung diseases (6, 9, 26, 45, 51, 53, 55). Thus the ability to quantify Δψm in an intact functioning lung is essential to further the understanding of the role of mitochondrial dysfunction in the pathogenesis of lung injury and diseases and to assess the efficacy of potential therapies that target the mitochondria.
Fluorescent lipophilic cations such as rhodamine dyes have been used for monitoring Δψm largely in cultured cells and isolated mitochondria rather than whole organs (2, 24, 26, 27, 33, 44, 52). Only a small number of studies have utilized these dyes to monitor Δψm in intact functioning organs (30, 52). For most studies, measurements of the intensity of fluorescent dyes within cells (cultured cells or specific cells in intact organs) or in isolated mitochondria were obtained. Such measurements are confounded by the propensity of the dyes to undergo self-aggregation and quenching at high concentrations such as occur during accumulation in mitochondria and cytosol (23, 27). In addition, the interpretation of resulting data is confounded by the logarithmic form of the Nernst equation, which specifies that changes in fluorescence intensity are not linearly proportional to changes in Δψm (23, 27).
To overcome the above limitations, Gan et al. developed an experimental and computational approach for estimating mitochondrial and plasma (cellular) membrane potential in cultured pulmonary arterial endothelial cells. The approach was based on the extracellular disposition of the rhodamine dye tetramethylrhodamine ethyl ester (TMRE) or rhodamine 123 (R123) after its addition to the surrounding medium (27). Unlike other studies with cultured cells, Gan et al. quantified the cellular uptake of each dye by measuring changes in its concentration in the surrounding medium instead of in the cells (27). For quantitative interpretation of the measured kinetic data, they developed a computational model that accounted for the dominant processes that determine the uptake of each dye, including plasma and mitochondrial membrane potentials and the multidrug efflux pump P-glycoprotein (Pgp), for which TMRE and R123 are substrates (27).
Motivated by the work of Gan et al. (27), our objective in the present study was to develop an experimental and computational approach for estimating Δψm in intact lungs based on the inlet-outlet concentrations of the lipophilic fluorescent monovalent cationic dye rhodamine 6G (R6G) on passage through the isolated perfused rat lung. The use of the measured inlet-outlet concentrations avoids potential issues that may arise when Δψm is measured directly from lung tissue. For example, R6G aggregation and quenching can occur at high concentrations in the cytoplasm and mitochondria driven by cell and mitochondrial membrane potentials (23) and potentially confound direct intracellular fluorescence intensity measurements. Our choice of R6G for this study was based in part by the work of Roerig et al., who demonstrated significant R6G uptake and retention in isolated perfused rabbit lungs (48), and by R6G’s high permeability in cell membranes of several types of cells, including endothelial cells (39). The results of the present study demonstrate the utility of the experimental and computational approach for quantifying the value of Δψm in intact lungs.
MATERIALS AND METHODS
Materials
R6G, verapamil hydrochloride, carbonyl cyanide p-trifluoromethoxyphenylhydrazone (FCCP), and all other reagents used in experiments were purchased from Sigma-Aldrich (St. Louis, MO).
Isolated Perfused Rat Lung Preparation
Animal protocols described below were approved by the Institutional Animal Care and Use Committees of the Department of Veterans Affairs Medical Center and Marquette University (Milwaukee, WI). Adult male Sprague-Dawley rats [348 ± 3 g (SE), n = 59] were used for this study. Each rat was anesthetized with pentobarbital sodium (40–50 mg/kg ip). The trachea was surgically isolated and cannulated, the chest opened, and heparin (0.7 IU/g body wt) injected into the right ventricle as previously described (8). The pulmonary artery and the pulmonary venous outflow were accessed via cannulas, and then the heart and lungs were removed and connected to a ventilation-perfusion system. The Krebs-Ringer bicarbonate perfusate contained (in mM) 4.7 KCl, 2.51 CaCl2, 1.19 MgSO4, 2.5 KH2PO4, 118 NaCl, 25 NaHCO3, and 5.5 glucose. The perfusate also contained 0.5% to 3% bovine serum albumin (BSA) plus 2.5% to 0% Ficoll to maintain consistent oncotic pressure. The perfusion system was primed with the perfusate maintained at 37°C and equilibrated with a 15% O2, 6% CO2, balance N2 gas mixture resulting in perfusate Po2, Pco2, and pH of ~105 Torr, 40 Torr, and 7.4, respectively. The lung was ventilated (40 breaths/min) with the above gas mixture with end-inspiratory and end-expiratory pressures of ~6 and 3 mmHg, respectively. The pulmonary artery and airway pressures were referenced to atmospheric pressure at the level of the left atrium and monitored continuously during the course of the experiments. Perfusate was pumped (10 mL/min) through the lung until it was evenly blanched and venous effluent was clear of visible blood before switching from single-pass to recirculation mode.
Experimental Protocols
Protocol 1: Effect of R6G input concentration, pump flow, and perfusate %BSA on R6G extraction on passage through the lungs.
For this protocol, the objective was to assess the impact of R6G infused concentration, perfusate flow, perfusate %BSA, and connecting tubing from the perfusate reservoir to the lungs on R6G uptake on its passage through the pulmonary circulation.
For the first set of experiments (n = 7), the perfusate included 0.5% BSA and 2.5% Ficoll. Once the lungs were clear of blood, the pump was stopped and the reservoir emptied and then refilled with 120 mL of perfusate. Two 1-mL reservoir samples were collected before and after the addition of R6G for a final concentration of 0.25 μM. Those samples were used to determine the background signal and the actual R6G concentration in the reservoir. During the 10-min lung perfusion (single-pass mode) with the R6G-containing perfusate, two 1-mL lung venous effluent samples were collected every 20 s for the first 5 min and every minute for the last 5 min, with the first sample collected at time (t) = 40 s, where t = 0 s was the start of the loading phase. Based on the volume (~4 mL) of the system (lung + tubing) and flow, one would expect no R6G signal in the venous effluent sample collected at 20 s. After collection, samples were centrifuged for 1 min (13,000 g, 4°C) to remove cellular components and debris. The sample supernatant was then transferred into a plastic cuvette, and its 565-nm emission signal (525-nm excitation) was measured with a RatioMaster fluorescence system (Photon Technology International, HORIBA Scientific, New Jersey) (8). The emission filter was centered at 565 nm (ET565/30M; Chroma, Vermont) with a bandwidth of 30 nm. R6G optical density was determined and converted to concentration with a standard curve obtained for each perfusate %BSA. The lung R6G extraction ratio (ER), a measure of the fraction of the input extracted on passage through the lungs, was determined with the following equation
| (1) |
where [Cv] is the R6G venous effluent concentration and [Cin] is the infused R6G concentration (0.25 μM).
For some experiments (n = 3), the above protocol was repeated with no lungs attached to the ventilation-perfusion system to assess the impact of the tubing connecting the reservoir to the lungs on the concentration of R6G in the venous effluent.
Based on results from the above experiments (see experimental results), it was determined that the change in R6G concentration in the venous effluent was relatively small (pseudosteady state) after ~6 min at a pump flow of 10 mL/min. Thus, for subsequent experiments under protocol 1, venous effluent was collected only 6 min after the start of the pump for a flow of 10 mL/min and only 3 min and 12 min after the start of the pump for flows of 20 mL/min and 5 mL/min, respectively. This decrease (or increase) in duration accounts for the ~50% decrease (or ~2-fold increase) in transit time though the lungs compared with that when the flow is 10 mL/min.
Using the above protocol with a flow of 10 mL/min, we assessed the impact of R6G input (reservoir) concentration (0.125, 0.5, or 1.25 μM) on R6G ER on passage through the pulmonary circulation. For 0.5 μM and 1.25 μM, venous effluent samples were first diluted with perfusate before the emission signal was measured to keep the intensity within the dynamic range of the fluorescence measuring system. In addition, we assessed the impact of changing perfusate %BSA (1%, 2%, or 3%) on R6G ER at 10 mL/min. For perfusate with BSA concentration of 1%, 2%, or 3%, the Ficoll concentration was 2%, 1% and 0%, respectively, to maintain constant oncotic pressure.
Using the above protocol with perfusate of 0.5% BSA and R6G reservoir concentration of 0.25 μM, we assessed the impact of pump flow (5 mL/min or 10 mL/min) on R6G ER on passage through the pulmonary circulation.
At the end of the above protocol, the lungs were removed from the system and their wet weight was measured. The lungs were then dried, and the dry weight was measured.
Protocol 2: Effect of treating isolated perfused lungs with verapamil and/or FCCP on R6G venous effluent concentration.
Based on results from protocol 1 (see experimental results), the following experimental conditions were used for protocol 2: perfusate with 0.5% BSA +2.5% Ficoll, 10 mL/min pump flow, and 0.25 μM R6G reservoir concentration. These conditions result in lung pseudosteady-state ER of ~0.5, halfway within the dynamic range (0 to 1) of ER.
Protocol 2 consisted of three single-pass perfusion phases: the loading phase, in which the lungs were perfused with R6G-containing perfusate, the washing phase, in which the lungs were perfused with fresh perfusate with no R6G, and the uncoupling phase, in which the lungs were perfused with perfusate containing the uncoupler FCCP and no R6G. Once the lungs were visually clear of blood, the flow was stopped to empty the perfusate in the reservoir and refill with 120 mL of fresh perfusate. Before the perfusate was mixed with the R6G, two 1-mL samples were collected to provide background signal for the loading phase. R6G stock (~42 μM) was then added to the perfusate in the reservoir for a final concentration of ~0.25 μM. Two 1-mL samples were then collected from the reservoir to provide a measure of actual R6G lung input concentration for the loading phase. The remaining perfusate was used to perfuse the lungs during the 10-min loading phase. During this phase, two 1-mL lung venous effluent samples were collected every 20 s for the first 5 min and every minute for the last 5 min, with the first sample collected 40 s after the start of the loading phase.
At the end of the loading phase, the pump was stopped and the reservoir quickly emptied and then refilled with R6G-free perfusate that was used to perfuse the lungs during the 3-min washing phase. Before the pump was restarted for the washing phase, two 1-mL samples were collected from the reservoir and used as background samples for the washing phase. During the washing phase, two 1-mL venous effluent samples were collected every minute.
After the washing phase, the pump was stopped again and the reservoir emptied and then refilled with 75 mL of R6G-free perfusate containing the uncoupler FCCP at a concentration of 67 μM. This concentration is high enough to ensure maximal dissipation of mitochondrial membrane potential (32, 60). This FCCP-containing perfusate was used to perfuse the lungs during the 7-min uncoupling phase. Before the pump was restarted for the uncoupling phase, two 1-mL samples were collected to provide background signal. Venous effluent samples were collected every 20 s for the first 2 min and then every minute for the last 5 min during this phase.
All samples from the three phases of protocol 2 were centrifuged for 1 min (13,000 g, 4°C) to remove any cellular components and debris. The sample supernatant was then transferred into a plastic cuvette, and its 565-nm emission signal (525-nm excitation) was measured (8). The R6G emission signal was determined and converted to concentration with a standard curve.
At the end of protocol 2, the lungs were removed from the system. The lung wet weight was measured, the lungs were dried, and then their dry weight was measured.
Effect of Pgp inhibitor on R6G lung uptake.
For a separate group of lungs, the above protocol was carried out after the inhibition of the Pgp pump that pumps R6G out of the lungs. To inhibit the Pgp pump, protocol 2 was modified as follows. Before the loading phase, perfusate containing verapamil (0.1 mM) (48) was recirculated through the lungs for 3 min at 10 mL/min, after which time the flow was stopped and the reservoir emptied and refilled with perfusate for the loading phase. In addition, perfusate used for all three phases included verapamil (0.1 mM). This concentration is high enough to ensure maximal inhibition of Pgp (48).
Effect of the uncoupler vehicle DMSO on R6G lung uptake.
FCCP is soluble in dimethyl sulfoxide (DMSO). To determine the impact of DMSO alone on the lung uptake of R6G, the protocol was repeated with just DMSO (0.05% of the perfusate volume) added to the perfusate during the uncoupling phase of protocol 2.
Standard Curves
For each experimental day, a proper standard curve was obtained as described below and used to convert R6G emission signal in collected samples to R6G concentration. Six tubes containing perfusate with known concentrations of R6G (0.5 μM, 0.25 μM, 0.125 μM, 0.0625 μM, and 0.03125 μM) were prepared. For each tube, a 2-mL sample was collected and then processed the same way as the samples collected from the lung’s venous effluent. Thus each sample was centrifuged for 1 min (13,000 g, 4°C), after which its 565-nm emission signal was measured. The standard curve was repeated with either verapamil or FCCP added to the samples before the addition of R6G to determine if the inhibitor/uncoupler and/or its vehicle interfered with the R6G emission signal. A standard curve was also obtained for each perfusate %BSA used under protocol 1.
Statistical Analysis
Statistical evaluation of data was carried out with SigmaPlot version 12.0 (Systat Software Inc., San Jose, CA). Values from different groups were compared with unpaired t tests. The level of statistical significance was set at P < 0.05. Values are means ± SE unless otherwise indicated.
EXPERIMENTAL RESULTS
None of the experimental treatments had a significant effect on lung wet weight, wet-to-dry weight ratio, or pulmonary artery pressure.
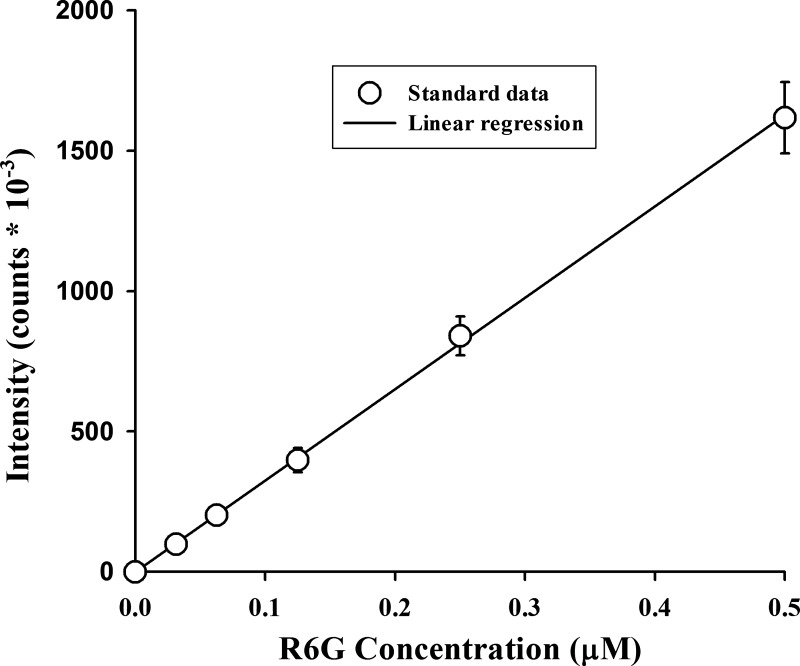
Figure 1 shows an example of the standard curves used to convert R6G emission fluorescent signal to R6G concentration. Neither FCCP (67 μM) nor verapamil (100 μM) had a significant effect on R6G standard curves (data not shown).
Fig. 1.
Standard curve for rhodamine 6G (R6G). Perfusate bovine serum albumin concentration was 0.5%. Values are means ± SE (n = 7).
Protocol 1 Results
R6G lung ER.
Figure 2A shows R6G (0.25 μM) extraction ratio (ER) on passage through the pulmonary circulation at pump flow of 10 mL/min and perfusate containing 0.5% BSA. The results show that ER approaches a pseudosteady-state value ∼6 min [ER = 0.482 ± 0.013 (SE)] after the start of the perfusion of the lungs with R6G-containing perfusate. Thus at 6 min ~48% of the infused R6G was extracted or taken up on a single pass through the lungs.
Fig. 2.
A: Rhodamine 6G (R6G) lung extraction ratio (ER) as a function of sampling time on passage through the pulmonary circulation. R6G reservoir concentration was 0.25 μM, pump flow = 10 mL/min, and perfusate BSA concentration was 0.5%. B: R6G tubing ER as a function of sampling time. R6G reservoir concentration was 0.25 μM, pump flow = 10 mL/min, tubing volume = 4 mL, and perfusate BSA concentration was 0.5%. Solid lines are model predictions using the parameter values in Table 2. Values are means ± SE (n = 7 and 3 for A and B, respectively).
Contribution of perfusion system tubing to R6G ER.
The experimental protocol for Fig. 2A was repeated with the lungs removed from the perfusion system. The results in Fig. 2B show that ER at 6 min is not significantly different from zero. Since the early nonzero ER values in Fig. 2B are due to the transit time it takes R6G-containing perfusate to travel from the reservoir to the outlet (sampling point), perfusion system tubing is not contributing to R6G ER on passage through the pulmonary circulation.
Effect of R6G concentration in reservoir on R6G ER.
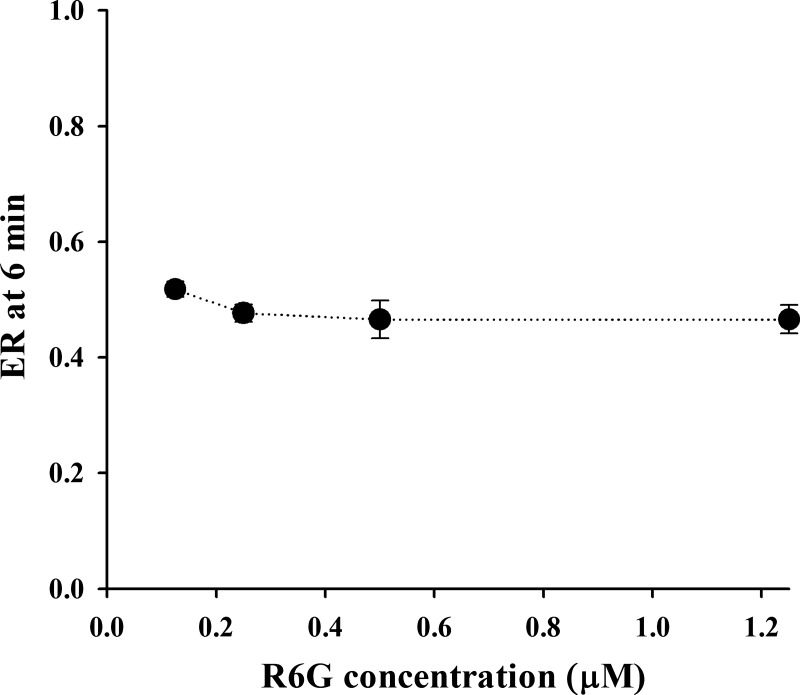
Figure 3 shows R6G ER after 6 min of perfusion of lungs with 0.5% BSA perfusate containing 0.125, 0.25, 0.5, or 1.25 μM R6G at flow of 10 mL/min. These results show that for this concentration range the lung ER is fairly constant (dose independent), consistent with first-order kinetics for the various vascular and cellular processes that contribute to the lung uptake of R6G.
Fig. 3.
Rhodamine 6G (R6G) lung extraction ratio (ER) after 6 min of perfusion (single pass) as a function of R6G input (reservoir) concentration. Pump flow = 10 mL/min, and perfusate bovine serum albumin concentration was 0.5%. Values are means ± SE (n = 6, 7, 4, and 7 for R6G concentrations of 0.125, 0.25, 0.5, and 1.25 μM, respectively).
Effect of perfusate %BSA on R6G ER.
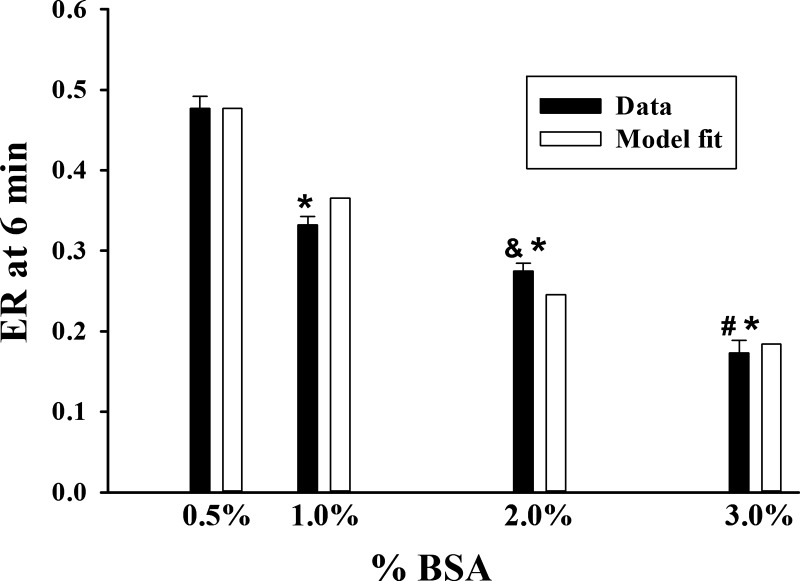
Figure 4 shows R6G ER after 6 min of lung perfusion (10 mL/min) with perfusate containing R6G (0.25 μM) and 0.5%, 1%, 2%, or 3% BSA. The results show that ER decreased as the %BSA in perfusate increased, consistent with a decrease in the fraction of R6G that is available for lung uptake.
Fig. 4.
Rhodamine 6G (R6G) lung extraction ratio (ER) (solid bars) after 6 min of perfusion (single pass) as a function of perfusate %bovine serum albumin (BSA). Pump flow = 10 mL/min. Open bars are model fit values. Values are means ± SE (n = 10, 3, 3, and 4 for perfusate BSA of 0.5%, 1.0%, 2.0%, and 3.0%, respectively). *Significantly different from 0.5% BSA (P < 0.05, unpaired t test); &significantly different from 1.0% BSA (P < 0.05); #significantly different from 2.0% BSA (P < 0.05).
Effect of perfusate pump flow on R6G ER.
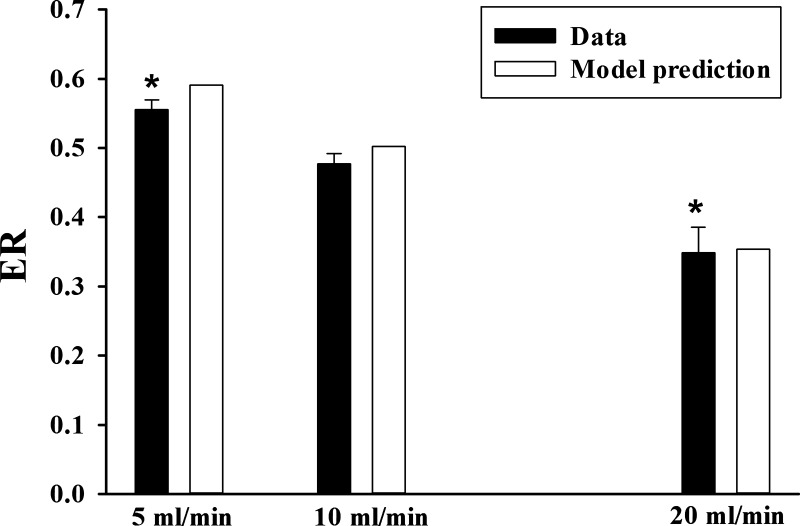
Figure 5 shows that increasing pump flow (from 5 to 20 mL/min) decreased R6G ER, consistent with a decrease in the time available for R6G uptake. The ER was determined at times of 12 min, 6 min, and 3 min after the start of lung perfusion with R6G-containing perfusate at flows of 5, 10, and 20 mL/min, respectively.
Fig. 5.
Rhodamine 6G (R6G) lung extraction ratio (ER) (solid bars) after 12 min, 6 min, and 3 min of perfusion (single pass) with pump flow set at 5, 10, and 20 mL/min, respectively. Open bars are model prediction. Values are means ± SE (n = 4, 10, and 6 for flow of 5, 10, and 20 mL/min, respectively). *Significantly different from ER at flow of 10 mL/min (P < 0.05, unpaired t test).
Protocol 2 Results
Lung venous effluent R6G concentrations during the three phases of protocol 2.
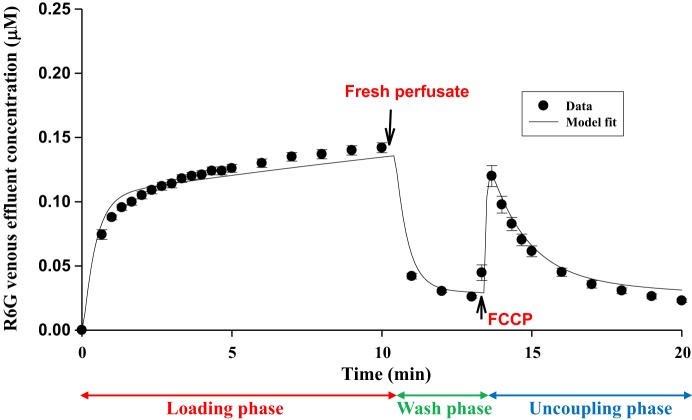
Figure 6 shows R6G venous effluent concentrations during the three phases of protocol 2. Results show that R6G venous effluent concentration decreased from ~0.13 μM during the loading phase to ~0.03 μM during the washing phase after switching from perfusate containing 0.25 μM R6G (loading phase) to perfusate with 0 μM R6G (washing phase). Figure 6 also demonstrates that perfusing the lungs with perfusate containing FCCP (~67 μM) resulted in a rapid increase in the concentration of R6G in the venous effluent samples (uncoupling phase), consistent with the uncoupling of lung tissue mitochondria and the release of R6G that had accumulated in the mitochondria during the loading phase, driven by Δψm. Thus these data contain information about Δψm, which was quantified with the PBPK model as described in mathematical modeling and data analysis.
Fig. 6.
Solid symbols represent rhodamine 6G (R6G) venous effluent concentrations during the loading phase, washing phase, and uncoupling phase with FCCP (67 μM). Values are means ± SE (n = 7 for loading and washing phases and n = 5 for uncoupling phase). Solid line is model fit to data.
Effect of the multidrug efflux pump Pgp inhibitor verapamil on R6G uptake.
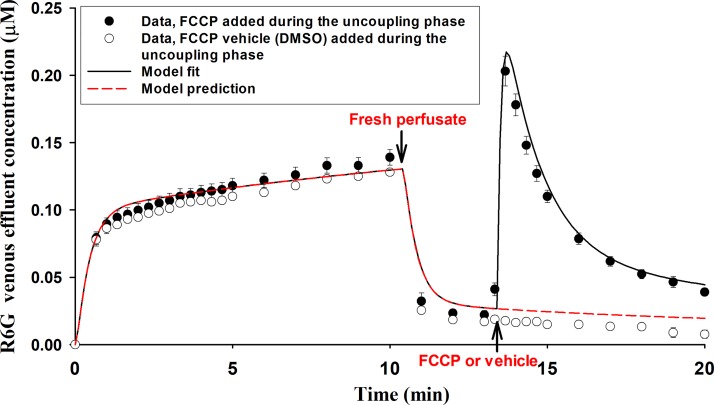
R6G is a known substrate for P-glycoprotein (Pgp) (48). Thus we evaluated the effect of the Pgp inhibitor verapamil on R6G venous effluent concentrations during the three phases of protocol 2. Figure 7 shows the concentrations of R6G in the venous effluent after passage through lungs in which Pgp was inhibited by recirculating verapamil (0.1 mM) for 3 min before carrying out protocol 2. In addition, verapamil (0.1 mM) was added to the perfusate during all three phases of this protocol. The results show no significant change in R6G venous effluent concentration during the loading phase [compared with Fig. 6, 0.142 ± 0.004 (SE) μM vs. 0.139 ± 0.006 μM at the end of the 10-min loading phase] but a large increase in the concentration of R6G released from the lungs after the addition of FCCP to the perfusate (uncoupling phase).
Fig. 7.
Solid symbols represent rhodamine 6G (R6G) venous effluent concentration in lungs after treatment with verapamil in protocol 2. Values are means ± SE (n = 6, 5, and 5 for loading phase, washing phase, and uncoupling phase, respectively). Open symbols represent R6G venous effluent concentration in lungs after treatment with verapamil in protocol 2 with DMSO (FCCP vehicle) instead of FCCP added to the perfusate during the uncoupling phase. Values are means ± SE (n = 2). Solid line is model fit to mean of the solid symbols. Dashed line is model prediction of the open symbols.
Figure 7 also shows that adding only the vehicle (DMSO) for FCCP to the perfusate during the uncoupling phase had no effect on the concentration of R6G in the venous effluent compared with that during the washing phase.
MATHEMATICAL MODELING AND DATA ANALYSIS
PBPK Model of R6G Pulmonary Disposition
For mechanistic and quantitative interpretation of the R6G kinetic data, we developed a physiologically based pharmacokinetic (PBPK) model for the pulmonary disposition of R6G. The model was used to estimate parameters descriptive of the dominant factors that determine the lung uptake and retention of R6G, including Δψm.
The PBPK model (Fig. 8) includes four regions, namely, the tubing region, consisting of the tubing connecting the reservoir to the pulmonary artery, the lung vascular region, the extravascular (intracellular, nonmitochondrial) region, and the mitochondrial region, each with volume Vtub, Vc, Ve, and Vm, respectively. The model accounts for the hypothesized dominant vascular and/tissue processes that determine the lung uptake and retention of R6G on passage through the pulmonary circulation. Within the tubing and vascular region, the model accounts for the binding of R6G to BSA, which is assumed to be rapidly equilibrating with dissociation constant Kd1. The model also accounts for the electrochemical gradients that drive the uptake of R6G from the vascular region to the extravascular region and from the extravascular to the mitochondrial region. R6G flux across the plasma membrane (J1) or inner mitochondrial membrane (J2) is represented by a modified Goldman–Hodgkin–Katz equation that is based on a one-dimensional Nernst–Planck equation under the assumption of a constant electric field (27, 31). Furthermore, the model accounts for the Pgp pump, which pumps R6G from the nonmitochondrial extravascular region back to the vascular region (48). The PBPK model makes no assumptions regarding the anatomical location of the Pgp protein, although it is assumed that Pgp transports R6G from the extravascular region back to the vascular region (48). At the concentration of R6G used (0.25 μM), we assume that the pump follows first-order kinetics based on the data in Fig. 3. Within the extravascular region, the model allows for slowly equilibrating R6G interactions (48). This could represent intracellular binding or sequestration in organelles (48). Thus the process is assumed to follow first-order kinetics based on the data in Fig. 3. Within the mitochondrial region, the model accounts for the binding of R6G to various proteins (52), which is assumed to be rapidly equilibrating with dissociation constant Kd3. The inhibitor verapamil is assumed not only to inhibit (competitive inhibition) Pgp-mediated R6G efflux but also to compete (noncompetitive inhibition) with R6G for binding sites in the extravascular region (48) (see discussion).
Fig. 8.
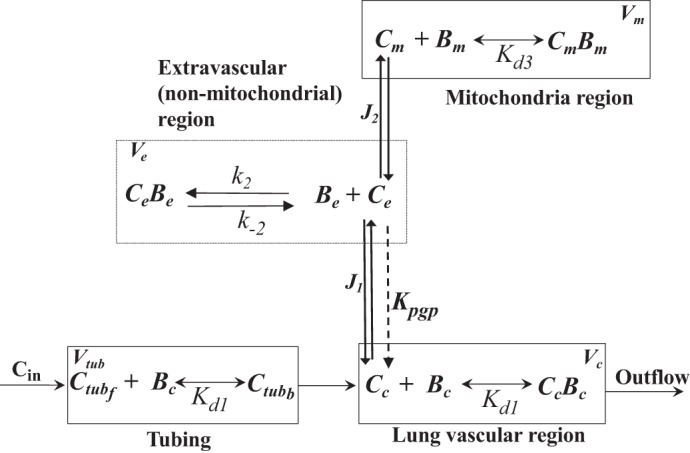
Physiologically based pharmacokinetic (PBPK) model of rhodamine 6G (R6G) lung uptake and retention on passage through the rat pulmonary circulation. The model consists of 4 regions: tubing, vascular, extravascular (nonmitochondrial), and mitochondrial with volumes Vtub, Vc, Ve and Vm, respectively. See appendix and glossary for definitions of symbols and parameters.
The rate of change of the concentrations of R6G in each of the four regions is described by the following system of ordinary differential equations (ODEs), which were derived with the laws of mass balance and mass action. See appendix for details regarding the derivation of these equations.
| (2) |
| (3) |
| (4) |
| (5) |
| (6) |
where
| (7) |
| (8) |
[Ctub](t) and [C̄e](t) are R6G total (free + bound) concentrations (μM) at time t in the tubing and vascular regions, respectively; [Ce](t) and [Cm](t) are R6G free concentrations at time t in extravascular and mitochondrial regions, respectively; [CeBe](t) is R6G bound concentration in the extravascular region at time t; [Cin] is the R6G concentration in the reservoir; [Bc] is %BSA in the perfusate; [Bm] is the concentration of R6G binding sites within the mitochondrial region; Q (mL/min) is pump flow; P1S1 (mL/min) and P2S2 (mL/min) are products of R6G permeability (P) across plasma and mitochondrial membranes, respectively, and the surface area (S) of these membranes; Kpgp is Pgp-mediated dye efflux rate (mL/min); (%BSA) is the dissociation equilibrium constant for R6G-BSA binding in the vascular region; is the dissociation constant for R6G-Bm binding within the mitochondrial region; is the apparent volume (mL) of the mitochondrial region; ki and k−i are R6G and protein/binding site association and dissociation rate constants, respectively, with Bc (i = 1) and Bm (i = 3), respectively; k̄2 = k2[Be] (min−1) and k−2 (min−1) are rate constants for R6G binding and unbinding with binding sites Be within Ve, respectively, and [Be] is the concentration of those binding sites; α = ZF/RT (mV−1) is a constant dependent on gas constant (R), Faraday constant (F), dye valence (Z = 1 for monovalent R6G), and absolute temperature (T); and Δψm and Δψp are mitochondrial and plasma membrane potential (mV), respectively.
To reduce the number of unknown model parameters, the lung vascular volume (Vc) was set at 0.85 mL (5) and the lung extravascular volume (Ve) was set at 1.0 mL based on lung tissue water volume estimated from lung wet weight and wet-to-dry weight ratio (7). To break the correlation between Vm and Δψm, the ratio Vm/Ve was set to 0.02, consistent with a lower bound measured for this ratio in rat pulmonary endothelium (27). To break the correlation between P1S1 and Δψp, the value of Δψp was set to that (−43 mV) estimated by Gan et al. in cultured pulmonary arterial endothelial cells (27). Furthermore, we assumed complete dissipation of Δψm in the presence of FCCP at the concentration used (67 μM) (32, 60) and complete inhibition of Pgp in the presence of verapamil at the concentration used (0.1 mM) (48). Then, Δψm, Kpgp, Kd1, Kd3, k̄2, k−2, P1S1, and P2S2 are the unknown model parameters (Table 1). The model-governing ODEs were solved numerically with the MATLAB (MathWorks) function “ode45,” which is based on an explicit Runge–Kutta formula. The equations were solved with the following initial (t = 0) conditions: [C̄c](0) = [Ce](0) = [Cm](0) = 0 and [Ctub](0) = [Cin] for protocol 1 and loading phase of protocol 2 and [Ctub](0) = 0 for the washing and uncoupling phases of protocol 2.
Table 1.
Model parameters
| Symbol | Description | Units |
|---|---|---|
| Kd1 = k−1/k1 | Dissociation constant for R6G-BSA binding in the vascular region | %BSA |
| k̄2 | Apparent rate constant for R6G-Bc binding within the cytoplasm region | min−1 |
| k−2 | Dissociation rate constant of R6G-Bc binding within the cytoplasm region | min−1 |
| Kd3 | Dissociation constant for R6G-Bm binding within the mitochondria region | |
| Kpgp | Rate of efflux of R6G via Pgp pump from cytoplasm to the vascular region | mL/min |
| P1S1 | R6G permeability-surface area product across the plasma membrane | mL/min |
| P2S2 | R6G permeability-surface area product across the inner mitochondrial membrane | mL/min |
| Δψm | Mitochondrial membrane potential | mV |
BSA, bovine serum albumin; Pgp, P-glycoprotein R6G; rhodamine 6G.
Estimation of PBPK Model Parameters
The first step in the procedure to estimate the unknown parameters was to fit the mean kinetic data of protocol 2 in the absence of verapamil (Fig. 6) and the ER values at the four different perfusate %BSA (Fig. 4) simultaneously. The objective was to obtain an estimate of Kd1 for R6G binding with perfusate BSA and initial estimates of the other unknown parameters (Table 1). The model fitting was done in MATLAB by using the “lsqcurvefit” function to implement the trust-region-reflective algorithm, an iterative optimization algorithm that readily incorporates bounds on the values of the parameters.
The estimated values of model parameters that best fit the data along with the model fits are shown in Table 2 and Figs. 4 and 6, respectively. Based on the estimated values of Kd1 (0.32% BSA; Table 2), R6G is ~61% bound to BSA in perfusate that includes 0.5% BSA.
Table 2.
| P1S1, mL/min | P2S2, mL/min | Kpgp, mL/min | k̄2, mL/min | k−2, min−1 | Kd3 | Δψm, mV | Kd1, %BSA | CV, % |
|---|---|---|---|---|---|---|---|---|
| 45.40 | 0.71 | 6.19 | 11.13 | 0.1223 | 0.0327 | −118.21 | 0.32 | 11.5 |
CV, coefficient of variation.
Next, Kd1 was fixed at the value in Table 2, and the other model parameters were estimated from the kinetic data from individual protocol 2 experiments without or with verapamil added to the perfusate (Figs. 6 and 7). In the presence of verapamil, the value of Kpgp was set to zero. The estimated values of the model parameters are shown in Table 3. Model simulations using the mean values of the estimated model parameters (Table 3) are shown in Figs. 6 and 7. The estimated values of the model parameters show that verapamil not only inhibited Pgp but also had a significant effect on the binding of R6G in the extravascular region (see discussion).
Table 3.
Values of model parameters estimated by fitting the model to protocol 2 kinetic data from individual lungs in the absence or presence of verapamil in the perfusate
| P1S1, mL/min | P2S2, mL/min | Kpgp, mL/min | k̄2, mL/min | k−2, min−1 | Kd3 | Δψm, mV | CV, % | |
|---|---|---|---|---|---|---|---|---|
| R6G | 48.56 ± 1.03 | 0.75 ± 0.09 | 5.77 ± 0.50 | 11.25 ± 0.67 | 0.117 ± 0.007 | 0.030 ± 0.004 | −117.5 ± 0.3 | 10.2 ± 1.1 |
| R6G + verapamil | 46.54 ± 0.35 | 1.07 ± 0.19 | 0 | 6.90 ± 0.45* | 0.178 ± 0.023* | 0.018 ± 0.003* | −131.2 ± 5.8 | 9.3 ± 0.4 |
Values are means ± SE (n = 6 and 5 without and with verapamil, respectively). Kd1 (%BSA) was fixed at the value in Table 2. CV, coefficient of variation; R6G, rhodamine 6G.
Different from without verapamil (t test, P < 0.05).
One measure of the model fit to the data is the coefficient of variation (CV) (47) given by
| (9) |
where and are the measured and model fit R6G venous effluent concentrations, respectively, and N and P are the number of data points and the number of model parameters, respectively. The CV for the model fits (Figs. 4–7) ranged between 9.3% and 11% (Tables 2 and 3).
PBPK Model Validation
To validate the model, we assessed its ability to predict experimental data that were not used for model development, including estimation of the values of the unknown model parameters. To that end, we evaluated the ability of the model to predict the experimental data in Fig. 5 at the different pump flows. The kinetic model and the mean of the estimated best fit values of model parameters without verapamil (Table 3) were evaluated by predicting the effect of pump flow on R6G ER at flows of 5 mL/min and 20 mL/min (Fig. 5). The results in Fig. 5 show that the predicted ER values are close to the measured values, providing support for the model and the estimated values of the model parameters (Table 3).
Measures of Estimability of the Model Parameters in Table 3 from data in Figs. 6 and 7
The estimability of the model parameters from the protocol 2 kinetic data in Figs. 6 and 7 was evaluated with a Monte Carlo approach and sensitivity analysis (12, 22). For the Monte Carlo approach, the model was fit to the protocol 2 mean data without (Fig. 6) or with (Fig. 7) verapamil and was repeated 100 times with different initial values for the model parameters. The initial values were determined as the mean of the estimated best fit values given in Table 3 (without or with verapamil) + a uniformly distributed random value within ±30% of this mean. The resulting estimated values from the 100 fits are shown in Table 4. The results show smaller standard deviation (SD) for Δψm from data with verapamil (Fig. 7) compared with no verapamil (Fig. 6) added to the perfusate (see discussion).
Table 4.
Estimated values of model parameters (Monte Carlo approach)
| P1S1, mL/min | P2S2, mL/min | Kpgp, mL/min | k̄2, mL/min | k−2, min−1 | Kd3 | Δψm, mV | |
|---|---|---|---|---|---|---|---|
| R6G | 48.04 ± 7.05 | 0.683 ± 0.154 | 10.80 ± 5.38 | 13.93 ± 2.56 | 0.121 ± 0.013 | 0.031 ± 0.009 | −144.26 ± 23.93 |
| R6G + verapamil | 49.69 ± 8.78 | 1.123 ± 0.291 | 0 | 7.30 ± 0.73 | 0.170 ± 0.019 | 0.016 ± 0.004 | −130.70 ± 14.67 |
Values are mean ± SD estimated values of model parameters (Monte Carlo approach): 100 different fits to the mean data in the absence or presence of verapamil with the initial values of model parameters equal to the mean values of the fits to individual experiments (Table 3) ± a uniformly distributed random value within ±30% of this mean error. R6G, rhodamine 6G.
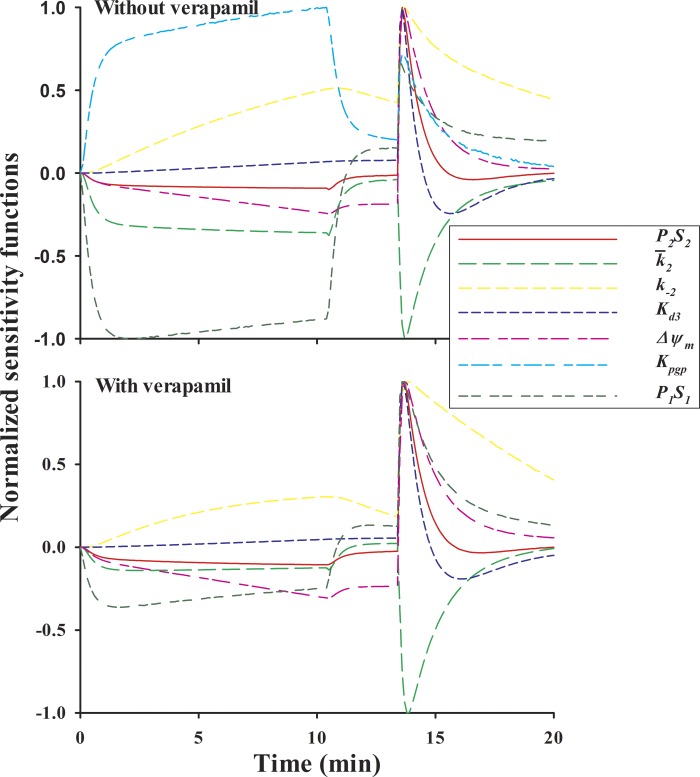
The estimability of the model parameters from the protocol 2 kinetic data in Figs. 6 and 7 was also evaluated with sensitivity analysis. Parameters values were set to the mean of the best fit values estimated from the individual experiments (Table 3). Figure 9 shows the corresponding sensitivity functions representing the normalized change in the model fit for a 1% change in the value of each free parameter. Both an increase in P2S2 and a more negative value of Δψm (more depolarized) drive more R6G into the mitochondria and hence result in negative sensitivity functions during the loading phase. As such, the results show similarly shaped sensitivity functions for P2S2 and Δψm during the loading phase of protocol 2. For the washing phase, the sensitivity function for P2S2 is close to zero but different from zero for Δψm. During the uncoupling phase, an increase in P2S2 and the uncoupling of a more depolarized Δψm results in more R6G diffusing from lung tissue to lung vascular region and hence larger R6G venous effluent concentration. Thus Δψm and P2S2 are positively correlated during a portion of this phase. This relative similarity between the sensitivity functions of P2S2 and Δψm during the loading phase and most of the uncoupling phases may reflect correlation between these two parameters and is consistent with the relatively large SD for both parameters in Table 4. See discussion for potential approaches to reduce this correlation.
Fig. 9.
Model parameter sensitivity functions with protocol 2 without (top) or with (bottom) verapamil. The sensitivity functions show the change in the model solution given a 1% increase in the value of a given model parameter. Each plot is normalized to its maximum value.
Sensitivity of Protocol 2 Experiments to Depolarization and Hyperpolarization of Δψm
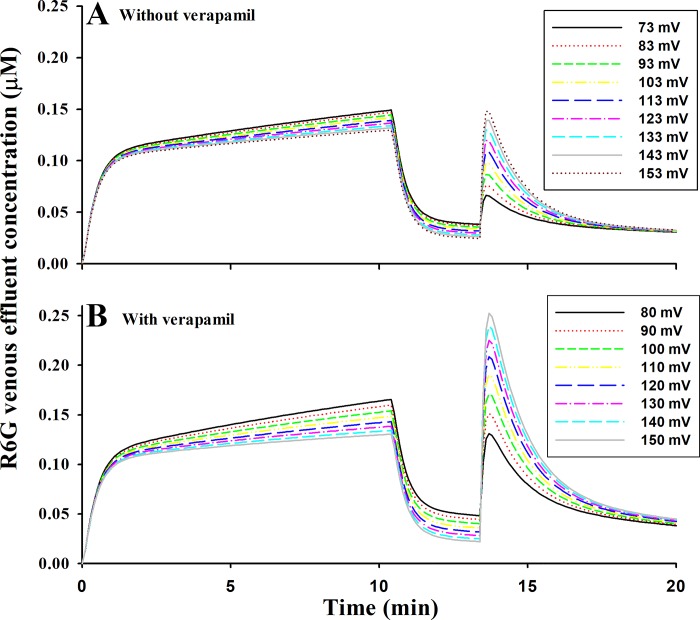
To assess the ability of protocol 2, without and with verapamil added to the perfusate, to detect a change in Δψm, model simulations (Fig. 10) were generated with the mean values of the estimated parameters in Table 3. The value of Δψm was decreased (depolarization) or increased (hyperpolarization), with the values of the other model parameters set to the mean values in Table 3. Results show that the uncoupled phase is highly sensitive to a change in Δψm and that the sensitivity to Δψm depolarization is larger in the presence of verapamil than in its absence.
Fig. 10.
Model predictions of the sensitivity of lung rhodamine 6G (R6G) venous effluent concentrations with protocol 2 to depolarization or repolarization of mitochondrial membrane potential without (A) or with (B) verapamil. Mean values of model parameters in Table 3 were used to generate these simulations.
DISCUSSION
Our study describes a fluorometric experimental and computational approach for evaluating lung tissue Δψm in isolated perfused rat lungs with the lipophilic cationic dye R6G. The approach is based on changes in the lung R6G inlet-outlet perfusate concentrations before and after uncoupling the lung tissue mitochondria. A PBPK model was developed and used for quantitative interpretation of the resulting kinetic data and for estimating parameters that describe the dominant processes that determine the disposition of R6G on passage through rat lungs, including Δψm. The model and estimated parameters were validated by determining their ability to reasonably predict the effect of pump flow on the extraction ratio of R6G on passage through the lungs over a wide range of flows. The estimated value of Δψm is consistent with that estimated from cultured pulmonary arterial endothelial cells (27). These results demonstrate the utility of this approach for quantifying tissue Δψm in isolated perfused lungs.
The lung is a complex organ with multiple vascular and tissue processes determining the pulmonary disposition of R6G. To overcome this complexity, we used inhibitors and a variety of perfusion conditions to target the dominant processes that are hypothesized to determine the pulmonary disposition of R6G. This provided us with discriminating information about those processes. In addition, we used a PBPK model to interpret the data. Computational modeling provides a mechanistic and quantitative framework that accounts for those processes and allows us to estimate parameters descriptive of those processes, including Δψm (27, 28, 48). The PBPK model developed in the present study is an extension of the model developed by Roerig et al. for the disposition of R6G in rabbit lungs to evaluate the lung activity of Pgp (48). Unlike the model developed in the present study, the PBPK model in the study by Roerig et al. did not account for the role of Δψm and Δψp in the lung uptake or retention of R6G (48). For that study, the objective was to evaluate the kinetics of the Pgp pump in isolated perfused rabbit lungs by using R6G as a Pgp substrate.
Generally speaking, a single experimental condition or data set of the type presented here does not contain sufficient information to estimate the parameters of the PBPK model (27, 28, 48). Instead, a diverse set of experimental conditions was needed to provide sufficiently discriminating information about the dominant processes that determine R6G uptake and retention in the lung. This approach is needed to break the correlation between some of the model parameters that describe these processes. Both measures of estimability of model parameters from the kinetic data with protocol 2 without or with verapamil (Fig. 9 and Table 4) suggest a relatively high correlation between Δψm and P2S2 during the loading phase and a portion of the uncoupling phase but not during the washing phase. This observation is consistent with the relatively high standard deviation of the estimated values of Δψm and P2S2 with the Monte Carlo approach (Table 4). One approach to reduce this correlation would be to extend the duration of the washing phase or to include additional experimental data, such as protocol 2 under a different flow.
For the present study, R6G was chosen since its uptake is rapid enough to accumulate within the lung tissue on a single pass through the pulmonary circulation (48). This is in part due to its relatively high octanol/water partition coefficient compared with that of other rhodamine dyes such as R123 (42). Our data are consistent with the large (relative to flow) estimated values of P1S1 for R6G (Table 3) and its high permeability in cell membranes in a wide range of cells, including endothelial cells (36, 39). Furthermore, under the experimental conditions used in the present study (10 mL/min flow, 0.5% BSA, and 0.25 μM input concentration), R6G ER is ~0.5 (Fig. 2), which is midway within the 0 to 1 dynamic range for ER, and hence optimal for detection of depolarization or repolarization of Δψm.
Previous studies using cationic dyes to probe Δψm have predominantly been carried out in isolated mitochondria and cultured cells (1, 2, 9, 11, 16, 19, 27, 31, 33, 39, 44, 52). Gan at al. developed an approach for quantifying Δψm and plasma membrane potential in cultured pulmonary endothelial cells based on the disposition of rhodamine dyes in the medium surrounding the cultured cells (27). The experimental and computational approach described in the present study uses a strategy similar to that used by Gan et al. in cultured endothelial cells by measuring the dye lung inlet-outlet concentrations rather than lung tissue/cellular concentrations to estimate Δψm. The estimated values of Δψm in the present study [−118 ± 1 (SE) mV and −131 ± 6 mV without and with verapamil, respectively] are comparable to those estimated by Gan et al. in cultured pulmonary endothelial cells [−130 ± 3 (SE) mV and −133 ± 1 mV with rhodamine 123 and TMRE, respectively] (27).
Previous studies evaluated the effect of R6G on mitochondrial functions (29, 56). Using isolated rat liver mitochondria, Gear showed that R6G at concentrations > 1 μM can have a significant inhibitory effect (Ki ~3 μM) on mitochondrial membrane potential and ATP-supported calcium accumulation (29). Williams et al. showed that human skin fibroblasts cultured in R6G-containing culture medium for 3–8 days experienced poor growth for R6G concentrations as low as 1.2 μM (56). In addition, this prolonged cell treatment with R6G significantly decreased the number of intact mitochondria and electron transport chain enzyme activities (56). For the present study, the concentration of R6G in the lung perfusate was 0.25 μM, well below the 1 μM at which toxic effects on mitochondrial functions were observed, and the lungs were perfused with this concentration for 10 min. In addition, the binding of R6G to BSA in perfusate decreased the concentration of perfusate R6G available for cellular uptake to ~0.125 μM. Thus for the present study the experimental conditions, including R6G concentration, were chosen to minimize R6G cytotoxic effects.
Fluorescent lipophilic cations such as rhodamine dyes have been used for monitoring Δψm largely in cultured cells and isolated mitochondria. Such studies are essential for elucidating fundamental mechanisms. However, they cannot reproduce the multicellular environmental in an intact organ under physiological and pathophysiological conditions. To the best of our knowledge, the use of cationic dyes to measure Δψm in intact lungs is limited to the present study and a recent study by Hough et al. (30). The present study reports a global lung measure of Δψm and permits absolute quantification of Δψm in units of millivolts. Hough et al. used TMRE to assess the effect of acute chemical lung injury on Δψm in isolated perfused mouse lungs (30) with an alveolar micropuncture technique. Confocal microscopy was used to measure TMRE fluorescent intensity in microvascular endothelial cells in the local injured region before and after injury with HCl, where the change in measured TMRE fluorescence was used as a measure of change in Δψm. Although this approach allows for assessing a change in endothelial TMRE fluorescence in an intact lung, it measures a local change in TMRE fluorescence as an index of Δψm, which may not be reflective of the overall change in lung Δψm. This is especially true for lung disease or injury, which generally is heterogeneous, affecting some lung regions/lobes more than others. Moreover, this approach does not account for the fact that dyes such as TMRE are also Pgp substrates (27). For cell types that have few or no multidrug transporters, this may be of minimal importance, but multidrug transporters perform a key function in the pulmonary endothelium (27, 48). A disease- or injury-induced change in Pgp activity will have an effect on TMRE mitochondrial fluorescence intensity (27, 58), which could be misinterpreted to represent a change in Δψm.
Comparison of the data in Figs. 6 and 7 shows that lung treatment with verapamil had no significant effect on the uptake and retention of R6G during the loading phase, although it had a significant effect during the uncoupling phase of protocol 2. The estimated values of the model parameters (Table 3) suggest that verapamil not only inhibited the Pgp pump but also competed with R6G for the slowly equilibrating binding sites in the extravascular region. This effect countered the increase in lung uptake of R6G due to the inhibition of the Pgp pump and allowed the R6G released from the mitochondrial region into the extravascular region during the uncoupling phase to diffuse quickly into the vascular region driven by the increase in the concentration gradient of free R6G across the plasma membrane (17, 48). Previously, we reported competition between the sequestration of R6G and another Pgp inhibitor (GF120918) in rabbit lungs (48). In addition, both verapamil and R6G are lipophilic amines (48), and the inhibition of the intracellular sequestration of one lipophilic amine by another in the lung has been previously reported (4, 49, 57).
Model simulations (Fig. 11) using the mean values of the estimated model parameters in Table 3 revealed that the increase in R6G venous effluent concentration during the uncoupling phase in the presence of verapamil compared with that in the absence of verapamil cannot be explained by just the inhibition of the Pgp pump, and in fact the R6G efflux concentration was predicted to decrease during the uncoupling phase. For Fig. 11, we simulated the R6G venous effluent concentrations assuming that Pgp is inhibited and where the inhibitor either does or does not compete with R6G for binding in the cytoplasm region. The simulations show that if the inhibitor does not compete then the R6G venous effluent concentration is decreased during the loading phase and at the peak of the curve during the uncoupling phase. When the inhibitor does compete with R6G for binding in the cytoplasm, the difference between the R6G venous effluent concentration during the loading phase without and with the inhibitor is minimized, but the peak of the concentration during the uncoupling phase is increased compared with that without Pgp inhibitor. These results are consistent with experimental results obtained with verapamil (Figs. 6 and 7). To elucidate further the effect of this competition between R6G and verapamil in the cytoplasm, we simulated the dynamics of R6G concentrations in the various model regions in the absence and presence of verapamil (Fig. 12), using the mean values of the model parameters in Table 3. Again, these simulations demonstrate that binding competition between R6G and verapamil in the cytoplasm leads to a significant increase in the concentration of free R6G in the cytoplasm during the uncoupling phase, which in turns leads to an increase in the concentration of R6G in the venous effluent.
Fig. 11.
Model simulations of protocol 2 rhodamine 6G (R6G) venous effluent concentrations in the absence (solid line) of a P-glycoprotein (Pgp) inhibitor and under conditions in which the Pgp inhibitor inhibited Pgp without (dotted line) or with (dashed line) competition with R6G binding in the cytoplasm. Mean values of model parameters in Table 3 (without verapamil) were used to generate these simulations.
Fig. 12.
Model simulations of protocol 2 rhodamine 6G (R6G) concentrations in the various regions of the model in the absence (solid line) and presence (dashed line) of verapamil. Mean values of model parameters in Table 3 were used to generate these simulations.
Unlike the results of the present study, Roerig et al. showed a significant increase in R6G lung uptake in the presence of verapamil compared with that in its absence in isolated perfused rabbit lungs (48). This could be due to the relatively large rate of Pgp-mediated R6G efflux compared with that for cytosolic R6G binding in rabbit lungs (1.44 min−1 vs. 0.23 min−1) (48). For rat lungs, the rate of Pgp-mediated R6G efflux was smaller than that for cytosolic R6G binding (5.8 min−1 vs. 11.3 min−1) (Table 3). In addition, for rabbit lungs the rate of Pgp-mediated R6G efflux is an order of magnitude larger than the rate of R6G efflux by diffusion across the cell membrane, whereas in the rat lungs P1S1 is much larger than the rate of Pgp-mediated efflux (Kpgp; Table 3).
One question that could be addressed with the proposed PBPK model is the sensitivity of protocol 2 to a change in Δψm in the presence or absence of verapamil. Model simulations (Fig. 10) show that protocol 2 in the presence of verapamil has a higher sensitivity to depolarization of Δψm than in the absence of verapamil. This is in part due to a decrease in the competition between cytoplasm binding and mitochondria for free R6G in the cytoplasm. This fact and a reduction in the number of unknown parameters for protocol 2 in the presence of verapamil suggest that protocol 2 in the presence of verapamil is preferable for evaluating Δψm in isolated perfused lungs for conditions expected to cause dissipation of Δψm.
Scaduto and Grotyohann attempted to probe Δψm in isolated perfused rat hearts by monitoring the surface emission fluorescence of the cationic rhodamine dye tetramethylrhodamine methyl ester perchlorate (TMRM) after its addition to perfusate that was recirculated through the heart (52). However, the results with a mitochondrial uncoupler and substrate-free perfusate were difficult to interpret in part because of alteration in the fluorescent properties of TMRM in heart tissue due to accumulation of TMRM in both mitochondria and cytosol (52). The approach described in the present study overcame this limitation by 1) determining the lung uptake of R6G from the lung inlet and outlet R6G perfusate concentrations on passage through the pulmonary circulation instead of from lung surface measurements and 2) using computational modeling for quantitative interpretation of the resulting kinetic data and for estimating parameters descriptive of the dominant vascular and tissue processes that determine lung uptake and accumulation of R6G, including Δψm.
For the present study, the value of Δψp was fixed to that estimated by Gan et al. from cultured pulmonary endothelial cells (27). Previous studies have demonstrated a key role for Δψp in regulating channel-mediated calcium entry in response to mechanical stimuli, oxidative stress, ischemia, and hypoxia (14, 15, 34, 43, 54). As such, Δψp could be altered by injury or disease. One could obtain information about Δψp by evaluating the impact of its depolarization on R6G lung uptake and retention. This could be done by perfusing the lungs with perfusate containing high potassium as was done by Gan et al. in cultured endothelial cells (27) or by Al-Mehdi et al. in isolated perfused rat lungs (3). Another approach would be to use fluorescent dyes sensitive to Δψp such as the anionic probe bis-oxonol (3, 59).
Aggregation of R6G in the cell membrane, cytoplasm, or intracellular organelles, including the mitochondria, could result in significant non-potential-dependent (non-Nernstian) R6G cellular accumulation (23). Previously, Ehrenberg et al. assessed R6G cellular aggregation and reported R6G intracellular-to-extracellular concentration ratios ranging between 35 and 77 in three different cultured cell types under conditions of dissipated Δψp and Δψm (23). We note that our proposed PBPK model (Fig. 8) allows for R6G binding in the perfusate (binding to albumin), cytoplasm, and mitochondrial regions. For each region, the model lumps all of the various binding processes, including aggregation. Thus the model allows for both free and bound forms of R6G to exist in all regions and accounts for both forms in the quantitative interpretation of the data. To demonstrate the suitability of this approach, we simulated R6G vascular and tissue concentrations, using the estimated values of the model parameters (Table 3) under conditions of dissipated Δψp and Δψm. Specifically, we simulated the infusion of R6G (single-pass lung perfusion with perfusate containing 0.25 μM R6G) for 120 min (to reach steady state). Then as a measure of R6G lung binding/aggregation we computed the ratio of intracellular R6G concentration to perfusate R6G concentration at steady state. This ratio was ~38 for perfusate containing 0.5% BSA and ~86 for perfusate containing 0.05% BSA. These values are within the range of values of R6G concentration ratios reported by Ehrenberg et al. (23), suggesting that binding/aggregation is appropriately accounted for in the model.
In our modeling analysis, the lung vascular volume (Vc) was fixed to that estimated previously from normal rat lungs (5). However, lung injury, including oxidative stress, has been shown to change lung vascular and extravascular volumes (6, 18). An independent estimate of Vc could be obtained with lipophilic amines and indicator dilution methods in isolated perfused lungs as previously described (6, 47).
The lung consists of 40 different resident cell types (20, 35). In addition, other cell types (e.g., leukocytes) are recruited to the lungs after injury (7, 9, 18). For the present study, the results with R6G provide no direct information regarding the contributions of the different cell types to the measured R6G lung uptake and estimated Δψm. However, endothelial cells would be expected to dominate because of their large surface area and high fraction (~50%) of total cells in normal lungs and their direct contact with R6G in perfusate (18). Although the question regarding the contributions of specific cell types will be important for future studies, alteration in the lung R6G uptake and estimated Δψm as an index of pulmonary mitochondrial dysfunction has functional implications regardless of the lung cell types involved.
We and others have reported various measures of mitochondrial dysfunction in intact lungs, pulmonary endothelial cells in culture, and isolated mitochondria in response to oxidative stress (9, 10, 27, 28, 37, 40, 46, 53). The proposed approach will allow us to quantify the effect of oxidative stress on Δψm in intact functioning lungs.
In conclusion, we present a novel experimental and computational approach for probing and estimating Δψm in isolated perfused rat lungs. The approach has the potential to provide quantitative assessment of the effect of various injurious conditions on lung mitochondrial function and to evaluate the impact of therapies that target the mitochondria. The proposed approach can also be easily adapted for other organs or cationic dyes. The MATLAB code for the computational model is available for download at the model sharing website https://www.physiome.org or upon request to the corresponding author.
GRANTS
This work was supported by NIH Grant 2R15 HL-129209-02 and Department of Veterans Affairs Merit Review Award BX001681.
DISCLOSURES
No conflicts of interest, financial or otherwise, are declared by the authors.
AUTHOR CONTRIBUTIONS
S.H.A. and E.R.J. conceived and designed research; S.H.A. and A.C. performed experiments; S.H.A., A.C., A.V.C., and R.K.D. analyzed data; S.H.A., A.C., A.V.C., R.K.D., and E.R.J. interpreted results of experiments; S.H.A. and A.C. prepared figures; S.H.A. drafted manuscript; S.H.A., A.C., A.V.C., R.K.D., and E.R.J. edited and revised manuscript; S.H.A., A.C., A.V.C., R.K.D., and E.R.J. approved final version of manuscript.
ENDNOTE
At the request of the authors, readers are herein alerted to the fact that additional materials related to this manuscript may be found at: https://www.physiome.org/. These materials are not a part of this manuscript and have not undergone peer review by the American Physiological Society (APS). APS and the journal editors take no responsibility for these materials, for the Web site address, or for any links to or from it.
ACKNOWLEDGMENTS
We thank Carlos Marquez Barrientos and Lucy Hatfield for help with the experiments.
GLOSSARY
- [Bc]
[BSA] Vascular BSA concentration (%BSA)
- [Be]
Concentration of extravascular R6G binding sites (μM)
- [Bm]
Concentration of mitochondrial R6G binding sites (μM)
- [Cc]
Free R6G concentration within the vascular region (μM)
- [CcBc]
Concentration of bound R6G within the vascular region (μM)
- [C̄c]
Total concentration of R6G within the vascular region (μM)
- [Ce]
Free R6G concentration within the extravascular region (μM)
- [CeBe]
Concentration of bound R6G within the extravascular region (μM)
- [Cin]
Infused R6G concentration (μM)
- [Cm]
Free R6G concentration within the mitochondrial region (μM)
- [CmBm]
Concentration of bound R6G within the mitochondrial region (μM)
- [Ctub]
Free R6G concentration within the tubing region (μM)
- CV
Coefficient of variation
- J1
Dye flux across the plasma membrane [nmol/(cm2·min)]
- J2
Dye flux across the inner mitochondrial membrane [nmol/(cm2·min)]
- k1
Association rate constant of R6G-BSA binding in the vascular region (%BSA−1·min−1)
- k−1
Dissociation rate constant of R6G-BSA binding within the vascular region (min−1)
- k2
Association rate constant of R6G-Be binding in the extravascular region (μM−1·min−1)
- k−2
Dissociation rate constant of R6G-Be binding in the extravascular region (min−1)
- k̄2
k2[Be] Apparent rate constant for R6G-Be binding in the extravascular region (min−1)
- k3
Association rate constant of R6G-Bm binding in the mitochondrial region (μM−1·min−1)
- k−3
Dissociation rate constant of R6G-Bm binding in the mitochondrial region (min−1)
- k̄3
k3[Bm] Apparent rate constant for R6G-Bm binding in the mitochondrial region (min−1)
- Kd1
k−1/k1 Dissociation constant for R6G-BSA binding in the vascular region (% BSA)
- Kd3
k−3/k̄3 Dissociation constant for R6G-Bm binding in the mitochondrial region
- Kpgp
Rate of efflux of R6G via Pgp pump from extravascular to vascular region (mL/min)
- P1
R6G permeability across plasma membrane (cm/min)
- P2
R6G permeability across inner mitochondrial membrane (cm/min)
- Q
Flow rate (mL/min)
- S1
Surface area of plasma membrane (cm2)
- S2
Surface area of inner mitochondrial membrane (cm2)
- Vc
Physical volume of vascular region (mL)
- Ve
Physical volume of extravascular region (mL)
- Vm
Physical volume of mitochondrial region = 0.02Ve (mL)
- Vm_app
Apparent volume of mitochondrial region (mL)
- Vtub
Physical volume of tubing region (mL)
- α
ZF/RT Constant dependent on the universal gas constant (R), Faraday constant (F), R6G valence (Z = 1), and absolute temperature (T) (mV−1)
- Δψm
Mitochondrial membrane potential (mV)
- Δψp
Plasma membrane potential (mV)
APPENDIX
The PBPK model (Fig. 8) describing the pulmonary disposition of R6G includes four regions, namely, the tubing region, which consists of the tubing connecting the reservoir to the pulmonary artery, the lung vascular region, the extravascular (intracellular, nonmitochondrial) region, and the mitochondrial region, with volumes Vtub, Vc, Ve, and Vm, respectively. Within the vascular region, the model accounts for the binding of R6G to BSA. The model also accounts for electrochemical gradients that drive the uptake of R6G from the vascular to the extravascular region and from there to the mitochondrial region. R6G flux across the plasma membrane (J1) or inner mitochondrial membrane (J2) is represented by a modified Goldman–Hodgkin–Katz equation that is based on a one-dimensional Nernst–Planck equation under the assumption of a constant electrostatic field (27, 31). Furthermore, the model accounts for pumping of R6G from the extravascular region back to the vascular region via the Pgp pump (48). Within the extravascular region, the model allows for slowly equilibrating interactions for R6G (48). Within the mitochondrial region, the model accounts for the binding of R6G to protein (52).
The rates of change in the concentrations of R6G in each of the four regions are described by the following system of ordinary differential equations (ODEs), which were derived with the laws of mass balance and mass action.
Tubing Region
| (A1) |
where [Cin] and [Ctub] are total (free + bound) concentration of R6G in reservoir and tubing regions, respectively.
Vascular Region
Rates of change in the concentrations of free ([Cc]) and BSA-bound ([CcBc]) R6G within the vascular region are
| (A2) |
| (A3) |
where Bc = perfusate % BSA and [Ctub]f and [Ctub]b are the free and BSA-bound R6G concentrations in the tubing region such that
| (A4) |
and
| (A5) |
Under the assumption of rapidly equilibrating interactions between R6G and perfusate BSA,
| (A6) |
| (A7) |
where Kd1 is the R6G-to-BSA binding dissociation constant. Let
| (A8) |
then the addition of Eqs. A2 and A3 after substituting Eqs. A7 and A8 for free and bound forms of R6G in the vascular region results in
| (A9) |
and
| (A10) |
Extravascular Region
Rates of change in the concentrations of free ([Ce]) and protein-bound ([CeBe]) R6G within this region are
| (A11) |
| (A12) |
where k̄2 = k2[Be] and
| (A13) |
Mitochondrial Region
Rates of change in the concentrations of free ([Cm]) and protein-bound ([CmBm]) R6G within this region are
| (A14) |
| (A15) |
where [Bm] = protein concentration within the mitochondrial region.
Under the assumption of rapidly equilibrating interactions between R6G and Bm,
| (A16) |
| (A17) |
whereis R6G and Bm binding dissociation constant.
The addition of Eqs. A14 and A15 after substituting Eq. A17 for [CmBm] results in
| (A18) |
where is the apparent volume of the mitochondrial region.
Thus the governing ODEs for the R6G PBPK model (Fig. 8) are
| (A19) |
| (A20) |
| (A21) |
| (A22) |
| (A23) |
where
| (A24) |
| (A25) |
REFERENCES
- 1.Agard C, Rolli-Derkinderen M, Dumas-de-La-Roque E, Rio M, Sagan C, Savineau JP, Loirand G, Pacaud P. Protective role of the antidiabetic drug metformin against chronic experimental pulmonary hypertension. Br J Pharmacol 158: 1285–1294, 2009. doi: 10.1111/j.1476-5381.2009.00445.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Aiuchi T, Daimatsu T, Nakaya K, Nakamura Y. Fluorescence changes of rhodamine 6G associated with changes in membrane potential in synaptosomes. Biochim Biophys Acta 685: 289–296, 1982. doi: 10.1016/0005-2736(82)90070-0. [DOI] [PubMed] [Google Scholar]
- 3.Al-Mehdi AB, Shuman H, Fisher AB. Oxidant generation with K+-induced depolarization in the isolated perfused lung. Free Radic Biol Med 23: 47–56, 1997. doi: 10.1016/S0891-5849(96)00574-6. [DOI] [PubMed] [Google Scholar]
- 4.Anderson MW, Orton TC, Pickett RD, Eling TE. Accumulation of amines in the isolated perfused rabbit lung. J Pharmacol Exp Ther 189: 456–466, 1974. [PubMed] [Google Scholar]
- 5.Audi SH, Bongard RD, Dawson CA, Siegel D, Roerig DL, Merker MP. Duroquinone reduction during passage through the pulmonary circulation. Am J Physiol Lung Cell Mol Physiol 285: L1116–L1131, 2003. doi: 10.1152/ajplung.00185.2003. [DOI] [PubMed] [Google Scholar]
- 6.Audi SH, Bongard RD, Krenz GS, Rickaby DA, Haworth ST, Eisenhauer J, Roerig DL, Merker MP. Effect of chronic hyperoxic exposure on duroquinone reduction in adult rat lungs. Am J Physiol Lung Cell Mol Physiol 289: L788–L797, 2005. doi: 10.1152/ajplung.00064.2005. [DOI] [PubMed] [Google Scholar]
- 7.Audi SH, Clough AV, Haworth ST, Medhora M, Ranji M, Densmore JC, Jacobs ER. 99MTc-hexamethylpropyleneamine oxime imaging for early detection of acute lung injury in rats exposed to hyperoxia or lipopolysaccharide treatment. Shock 46: 420–430, 2016. doi: 10.1097/SHK.0000000000000605. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Audi SH, Friedly N, Dash RK, Beyer AM, Clough AV, Jacobs ER. Detection of hydrogen peroxide production in the isolated rat lung using Amplex red. Free Radic Res 52: 1052–1062, 2018. doi: 10.1080/10715762.2018.1511051. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Audi SH, Jacobs ER, Zhang X, Camara AK, Zhao M, Medhora MM, Rizzo B, Clough AV. Protection by inhaled hydrogen therapy in a rat model of acute lung injury can be tracked in vivo using molecular imaging. Shock 48: 467–476, 2017. doi: 10.1097/SHK.0000000000000872. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Audi SH, Merker MP, Krenz GS, Ahuja T, Roerig DL, Bongard RD. Coenzyme Q1 redox metabolism during passage through the rat pulmonary circulation and the effect of hyperoxia. J Appl Physiol (1985) 105: 1114–1126, 2008. doi: 10.1152/japplphysiol.00177.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Baracca A, Sgarbi G, Solaini G, Lenaz G. Rhodamine 123 as a probe of mitochondrial membrane potential: evaluation of proton flux through F0 during ATP synthesis. Biochim Biophys Acta 1606: 137–146, 2003. doi: 10.1016/S0005-2728(03)00110-5. [DOI] [PubMed] [Google Scholar]
- 12.Bassingthwaighte JB, Chaloupka M. Sensitivity functions in the estimation of parameters of cellular exchange. Fed Proc 43: 181–184, 1984. [PMC free article] [PubMed] [Google Scholar]
- 13.Bongard RD, Yan K, Hoffmann RG, Audi SH, Zhang X, Lindemer BJ, Townsley MI, Merker MP. Depleted energy charge and increased pulmonary endothelial permeability induced by mitochondrial complex I inhibition are mitigated by coenzyme Q1 in the isolated perfused rat lung. Free Radic Biol Med 65: 1455–1463, 2013. doi: 10.1016/j.freeradbiomed.2013.07.040. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Campbell DL, Strauss HC, Whorton AR. Voltage dependence of bovine pulmonary artery endothelial cell function. J Mol Cell Cardiol 23, Suppl 1: 133–144, 1991. doi: 10.1016/0022-2828(91)90032-H. [DOI] [PubMed] [Google Scholar]
- 15.Chatterjee S, Levitan I, Wei Z, Fisher AB. KATP channels are an important component of the shear-sensing mechanism in the pulmonary microvasculature. Microcirculation 13: 633–644, 2006. doi: 10.1080/10739680600930255. [DOI] [PubMed] [Google Scholar]
- 16.Chen LB. Mitochondrial membrane potential in living cells. Annu Rev Cell Biol 4: 155–181, 1988. doi: 10.1146/annurev.cb.04.110188.001103. [DOI] [PubMed] [Google Scholar]
- 17.Cho CW, Liu Y, Yan X, Henthorn T, Ng KY. Carrier-mediated uptake of rhodamine 123: implications on its use for MDR research. Biochem Biophys Res Commun 279: 124–130, 2000. doi: 10.1006/bbrc.2000.3916. [DOI] [PubMed] [Google Scholar]
- 18.Crapo JD, Barry BE, Foscue HA, Shelburne J. Structural and biochemical changes in rat lungs occurring during exposures to lethal and adaptive doses of oxygen. Am Rev Respir Dis 122: 123–143, 1980. doi: 10.1164/arrd.1980.122.1.123. [DOI] [PubMed] [Google Scholar]
- 19.Davis S, Weiss MJ, Wong JR, Lampidis TJ, Chen LB. Mitochondrial and plasma membrane potentials cause unusual accumulation and retention of rhodamine 123 by human breast adenocarcinoma-derived MCF-7 cells. J Biol Chem 260: 13844–13850, 1985. [PubMed] [Google Scholar]
- 20.Dinh PC, Cores J, Hensley MT, Vandergriff AC, Tang J, Allen TA, Caranasos TG, Adler KB, Lobo LJ, Cheng K. Derivation of therapeutic lung spheroid cells from minimally invasive transbronchial pulmonary biopsies. Respir Res 18: 132, 2017. doi: 10.1186/s12931-017-0611-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Duchen MR, Surin A, Jacobson J. Imaging mitochondrial function in intact cells. Methods Enzymol 361: 353–389, 2003. doi: 10.1016/S0076-6879(03)61019-0. [DOI] [PubMed] [Google Scholar]
- 22.Dutta S, Ebling WF. Parameter estimability of biphasic response models. J Pharm Sci 86: 44–51, 1997. doi: 10.1021/js960248f. [DOI] [PubMed] [Google Scholar]
- 23.Ehrenberg B, Montana V, Wei MD, Wuskell JP, Loew LM. Membrane potential can be determined in individual cells from the nernstian distribution of cationic dyes. Biophys J 53: 785–794, 1988. doi: 10.1016/S0006-3495(88)83158-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Farkas DL, Wei MD, Febbroriello P, Carson JH, Loew LM. Simultaneous imaging of cell and mitochondrial membrane potentials. Biophys J 56: 1053–1069, 1989. doi: 10.1016/S0006-3495(89)82754-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Fisher AB. Intermediary metabolism of the lung. Environ Health Perspect 55: 149–158, 1984. doi: 10.1289/ehp.8455149. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Fu C, Dai X, Yang Y, Lin M, Cai Y, Cai S. Dexmedetomidine attenuates lipopolysaccharide-induced acute lung injury by inhibiting oxidative stress, mitochondrial dysfunction and apoptosis in rats. Mol Med Rep 15: 131–138, 2017. doi: 10.3892/mmr.2016.6012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Gan Z, Audi SH, Bongard RD, Gauthier KM, Merker MP. Quantifying mitochondrial and plasma membrane potentials in intact pulmonary arterial endothelial cells based on extracellular disposition of rhodamine dyes. Am J Physiol Lung Cell Mol Physiol 300: L762–L772, 2011. doi: 10.1152/ajplung.00334.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Gan Z, Roerig DL, Clough AV, Audi SH. Differential responses of targeted lung redox enzymes to rat exposure to 60 or 85% oxygen. J Appl Physiol (1985) 111: 95–107, 2011. doi: 10.1152/japplphysiol.01451.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Gear AR. Rhodamine 6G. A potent inhibitor of mitochondrial oxidative phosphorylation. J Biol Chem 249: 3628–3637, 1974. [PubMed] [Google Scholar]
- 30.Hough RF, Islam MN, Gusarova GA, Jin G, Das S, Bhattacharya J. Endothelial mitochondria determine rapid barrier failure in chemical lung injury. JCI Insight 4: e124329, 2019. doi: 10.1172/jci.insight.124329. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Huang M, Camara AK, Stowe DF, Qi F, Beard DA. Mitochondrial inner membrane electrophysiology assessed by rhodamine-123 transport and fluorescence. Ann Biomed Eng 35: 1276–1285, 2007. doi: 10.1007/s10439-007-9265-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Huang Y, Kwan KK, Leung KW, Wang H, Kong XP, Dong TT, Tsim KW. The extracts and major compounds derived from Astragali radix alter mitochondrial bioenergetics in cultured cardiomyocytes: comparison of various polar solvents and compounds. Int J Mol Sci 19: 1574, 2018. doi: 10.3390/ijms19061574. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Johnson LV, Walsh ML, Bockus BJ, Chen LB. Monitoring of relative mitochondrial membrane potential in living cells by fluorescence microscopy. J Cell Biol 88: 526–535, 1981. doi: 10.1083/jcb.88.3.526. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Koliwad SK, Kunze DL, Elliott SJ. Oxidant stress activates a non-selective cation channel responsible for membrane depolarization in calf vascular endothelial cells. J Physiol 491: 1–12, 1996. doi: 10.1113/jphysiol.1996.sp021191. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Kotton DN, Morrisey EE. Lung regeneration: mechanisms, applications and emerging stem cell populations. Nat Med 20: 822–832, 2014. doi: 10.1038/nm.3642. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Loetchutinat C, Saengkhae C, Marbeuf-Gueye C, Garnier-Suillerot A. New insights into the P-glycoprotein-mediated effluxes of rhodamines. Eur J Biochem 270: 476–485, 2003. doi: 10.1046/j.1432-1033.2003.03403.x. [DOI] [PubMed] [Google Scholar]
- 37.Ma C, Beyer AM, Durand M, Clough AV, Zhu D, Norwood Toro L, Terashvili M, Ebben JD, Hill RB, Audi SH, Medhora M, Jacobs ER. Hyperoxia causes mitochondrial fragmentation in pulmonary endothelial cells by increasing expression of pro-fission proteins. Arterioscler Thromb Vasc Biol 38: 622–635, 2018. doi: 10.1161/ATVBAHA.117.310605. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Mandalà M, Serck-Hanssen G, Martino G, Helle KB. The fluorescent cationic dye rhodamine 6G as a probe for membrane potential in bovine aortic endothelial cells. Anal Biochem 274: 1–6, 1999. doi: 10.1006/abio.1999.4253. [DOI] [PubMed] [Google Scholar]
- 40.Merker MP, Audi SH, Lindemer BJ, Krenz GS, Bongard RD. Role of mitochondrial electron transport complex I in coenzyme Q1 reduction by intact pulmonary arterial endothelial cells and the effect of hyperoxia. Am J Physiol Lung Cell Mol Physiol 293: L809–L819, 2007. doi: 10.1152/ajplung.00448.2006. [DOI] [PubMed] [Google Scholar]
- 41.Merker MP, Bongard RD, Gan Z, Audi SH. Mitochondrial bioenergetics in intact normoxic and hyperoxia-adapted pulmonary arterial endothelial cells (BAEC) (Abstract). Free Radic Biol Med 47, Suppl 1: S98, 2009. [Google Scholar]
- 42.Mottram LF, Forbes S, Ackley BD, Peterson BR. Hydrophobic analogues of rhodamine B and rhodamine 101: potent fluorescent probes of mitochondria in living C. elegans. Beilstein J Org Chem 8: 2156–2165, 2012. doi: 10.3762/bjoc.8.243. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Paffett ML, Naik JS, Resta TC, Walker BR. Reduced store-operated Ca2+ entry in pulmonary endothelial cells from chronically hypoxic rats. Am J Physiol Lung Cell Mol Physiol 293: L1135–L1142, 2007. doi: 10.1152/ajplung.00432.2006. [DOI] [PubMed] [Google Scholar]
- 44.Perry SW, Norman JP, Barbieri J, Brown EB, Gelbard HA. Mitochondrial membrane potential probes and the proton gradient: a practical usage guide. Biotechniques 50: 98–115, 2011. doi: 10.2144/000113610. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Piantadosi CA, Suliman HB. Mitochondrial dysfunction in lung pathogenesis. Annu Rev Physiol 79: 495–515, 2017. doi: 10.1146/annurev-physiol-022516-034322. [DOI] [PubMed] [Google Scholar]
- 46.Pruijn FB, Schoonen WG, Joenje H. Inactivation of mitochondrial metabolism by hyperoxia-induced oxidative stress. Ann NY Acad Sci 663: 453–455, 1992. doi: 10.1111/j.1749-6632.1992.tb38699.x. [DOI] [PubMed] [Google Scholar]
- 47.Ramakrishna M, Gan Z, Clough AV, Molthen RC, Roerig DL, Audi SH. Distribution of capillary transit times in isolated lungs of oxygen-tolerant rats. Ann Biomed Eng 38: 3449–3465, 2010. doi: 10.1007/s10439-010-0092-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Roerig DL, Audi SH, Ahlf SB. Kinetic characterization of P-glycoprotein-mediated efflux of rhodamine 6G in the intact rabbit lung. Drug Metab Dispos 32: 953–958, 2004. doi: 10.1124/dmd.104.000042. [DOI] [PubMed] [Google Scholar]
- 49.Roerig DL, Kotrly KJ, Ahlf SB, Dawson CA, Kampine JP. Effect of propranolol on the first pass uptake of fentanyl in the human and rat lung. Anesthesiology 71: 62–68, 1989. doi: 10.1097/00000542-198907000-00012. [DOI] [PubMed] [Google Scholar]
- 50.Ruchko M, Gorodnya O, LeDoux SP, Alexeyev MF, Al-Mehdi AB, Gillespie MN. Mitochondrial DNA damage triggers mitochondrial dysfunction and apoptosis in oxidant-challenged lung endothelial cells. Am J Physiol Lung Cell Mol Physiol 288: L530–L535, 2005. doi: 10.1152/ajplung.00255.2004. [DOI] [PubMed] [Google Scholar]
- 51.Ryter SW, Rosas IO, Owen CA, Martinez FJ, Choi ME, Lee CG, Elias JA, Choi AM. Mitochondrial dysfunction as a pathogenic mediator of chronic obstructive pulmonary disease and idiopathic pulmonary fibrosis. Ann Am Thorac Soc 15, Suppl 4: S266–S272, 2018. doi: 10.1513/AnnalsATS.201808-585MG. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Scaduto RC Jr, Grotyohann LW. Measurement of mitochondrial membrane potential using fluorescent rhodamine derivatives. Biophys J 76: 469–477, 1999. doi: 10.1016/S0006-3495(99)77214-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Sepehr R, Audi SH, Staniszewski KS, Haworth ST, Jacobs ER, Ranji M. Novel flurometric tool to assess mitochondrial redox state of isolated perfused rat lungs after exposure to hyperoxia. IEEE J Transl Eng Health Med 1: 1500210, 2013. doi: 10.1109/JTEHM.2013.2285916. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Stevens T, Cornfield DN, McMurtry IF, Rodman DM. Acute reductions in Po2 depolarize pulmonary artery endothelial cells and decrease [Ca2+]i. Am J Physiol Heart Circ Physiol 266: H1416–H1421, 1994. doi: 10.1152/ajpheart.1994.266.4.H1416. [DOI] [PubMed] [Google Scholar]
- 55.Ten VS, Ratner V. Mitochondrial bioenergetics and pulmonary dysfunction: current progress and future directions. Paediatr Respir Rev. In press. doi: 10.1016/j.prrv.2019.04.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Williams AJ, Murrell M, Brammah S, Minchenko J, Christodoulou J. A novel system for assigning the mode of inheritance in mitochondrial disorders using cybrids and rhodamine 6G. Hum Mol Genet 8: 1691–1697, 1999. doi: 10.1093/hmg/8.9.1691. [DOI] [PubMed] [Google Scholar]
- 57.Wilson AG, Pickett RD, Eling TE, Anderson MW. Studies on the persistence of basic amines in the rabbit lung. Drug Metab Dispos 7: 420–424, 1979. [PubMed] [Google Scholar]
- 58.Yao C, Jiang J, Tu Y, Ye S, Du H, Zhang Y. β-elemene reverses the drug resistance of A549/DDP lung cancer cells by activating intracellular redox system, decreasing mitochondrial membrane potential and P-glycoprotein expression, and inducing apoptosis. Thorac Cancer 5: 304–312, 2014. doi: 10.1111/1759-7714.12093. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Zhang Q, Matsuzaki I, Chatterjee S, Fisher AB. Activation of endothelial NADPH oxidase during normoxic lung ischemia is KATP channel dependent. Am J Physiol Lung Cell Mol Physiol 289: L954–L961, 2005. doi: 10.1152/ajplung.00210.2005. [DOI] [PubMed] [Google Scholar]
- 60.Zhao Z, Gordan R, Wen H, Fefelova N, Zang WJ, Xie LH. Modulation of intracellular calcium waves and triggered activities by mitochondrial Ca flux in mouse cardiomyocytes. PLoS One 8: e80574, 2013. doi: 10.1371/journal.pone.0080574. [DOI] [PMC free article] [PubMed] [Google Scholar]