Development and binocular matching of orientation selectivity in visual cortex: a computational model

Abstract

In mouse visual cortex, right after eye opening binocular cells have different preferred orientations for input from the two eyes. With normal visual experience during a critical period, these preferred orientations evolve and eventually become well matched. To gain insight into the matching process, we developed a computational model of a cortical cell receiving orientation selective inputs via plastic synapses. The model captures the experimentally observed matching of the preferred orientations, the dependence of matching on ocular dominance of the cell, and the relationship between the degree of matching and the resulting monocular orientation selectivity. Moreover, our model puts forward testable predictions: 1) The matching speed increases with initial ocular dominance. 2) While the matching improves more slowly for cells that are more orientation selective, the selectivity increases faster for better matched cells during the matching process. This suggests that matching drives orientation selectivity but not vice versa. 3) There are two main routes to matching: the preferred orientations either drift toward each other or one of the orientations switches suddenly. The latter occurs for cells with large initial mismatch and can render the cells monocular. We expect that these results provide insight more generally into the development of neuronal systems that integrate inputs from multiple sources, including different sensory modalities.

NEW & NOTEWORTHY Animals gather information through multiple modalities (vision, audition, touch, etc.). These information streams have to be merged coherently to provide a meaningful representation of the world. Thus, for neurons in visual cortex V1, the orientation selectivities for inputs from the two eyes have to match to enable binocular vision. We analyze the postnatal process underlying this matching using computational modeling. It captures recent experimental results and reveals interdependence between matching, ocular dominance, and orientation selectivity.

INTRODUCTION

Animals receive information about the world through multiple modalities (vision, audition, touch, etc.). For these information streams to provide a meaningful representation of the sensory world they have to be merged in a coherent fashion; only then do they enable the brain to better detect events, analyze the corresponding situations, and then make decisions accordingly. Typically, this coherence is only acquired during a postnatal critical period (Stein and Rowland 2011).

The merging of across-modality information has been extensively investigated in the cat superior colliculus (SC) (Fuentes-Santamaria et al. 2009; Huerta and Harting 1984; Stein and Meredith 1993; Wallace et al. 1993) as well as the optic tectum of the barn owl (Brainard and Knudsen 1998), where multisensory neurons integrate the information they receive from upstream unisensory neurons in different sensory channels (e.g., visual and auditory). Like in other sensory systems, the capability of SC multisensory neurons to engage in multisensory integration is not innate but is learned gradually during postnatal life as a consequence of normal multisensory experience. Two main results of the multisensory neurons’ learning process in SC are the initial development of large, unisensory receptive fields for visual and auditory input and their subsequent contraction and matching across modalities. This can enhance the degree to which the neurons’ receptive fields for visual and auditory inputs pertain to the same spatial location and enables the neuron to extract coherent information from the different modalities.

Matching of different information streams can also play an important role within a single modality. In the visual system, for instance, neurons in the visual cortex prefer similar orientations through the two eyes. As in the multisensory case, this binocular matching requires normal sensory experience. Shortly after eye opening cortical cells in layer 2/3 of mouse visual cortex V1 have quite different monocular preferred orientations through each eye (Wang et al. 2013). With normal binocular visual experience these preferences become binocularly matched to the adult level by postnatal day 31 (P31) (Wang et al. 2013), which corresponds to the end of the critical period for ocular dominance plasticity (Gordon and Stryker 1996).

Inspired by these experimental results and to gain insight into general matching mechanisms, we developed a computational model for the development and matching of input preferences of neurons receiving multichannel input via plastic synapses. In the case of multisensory SC neurons the input preferences would correspond to visual and auditory receptive fields. For concreteness, we will focus here on the binocular matching in V1, where the input preferences correspond to orientation preferences.

The development of visual cortex has been studied extensively over the years. Many studies have used a firing-rate framework for the neurons as well as for the synaptic plasticity (e.g., Miller et al. 1989), which assumes, in particular, that the pre- and postsynaptic spike trains are uncorrelated. Since the spiking of cortical cells is driven by fluctuations in the input rather than its mean (e.g., Hansel and van Vreeswijk 2012), it is not clear whether the correlations are sufficiently negligible. We therefore considered a single spiking neuron with synapses whose plasticity is spike dependent (Clopath et al. 2010). It received separate inputs from each eye. Motivated by the fact that in a multisource system upstream neurons gain selectivity before the downstream neurons (Stein and Rowland 2011; Wang et al. 2010), we chose the inputs from the upstream neurons to be orientation selective. This is consistent with complex cells in V1 receiving oriented inputs from simple cells. The evolution of the synaptic weights was driven by stimuli representing gratings with randomly switching orientation. In an initial phase these inputs were uncorrelated between the two eyes to mimic spontaneous retinal or thalamic activity before eye opening (Espinosa and Stryker 2012). After eye opening the inputs were chosen to be perfectly correlated between left and right. Our aim was to keep the model as simple as possible, while still capturing a wide range of experimental observations. We therefore did not modify the plasticity rules when switching between these two phases and did not include a transition period (P15–P20) during which the input changes from being dominated by spontaneous activity to being dominated by visually evoked activity (Toyoizumi et al. 2013).

Our model captures key experimental observations (Levine et al. 2017; Wang et al. 2010):

• 1) the matching is predominantly achieved by shifting the preferred orientation for input from the weaker eye.
• 2) the resulting binocular orientation selectivity increases with decreasing mismatch.

In addition, the model provides insight into a number of further experimental observations and puts forward testable predictions:

• 1) The matching speed increases with initial ocular dominance, suggesting ocular dominance as a key driver of the binocular matching process.
• 2) While the matching improves more slowly for cells that are more orientation selective, the selectivity increases faster for better matched cells during the matching process. This suggests that matching drives orientation selectivity but not vice versa.
• 3) The initial binocular preferred orientation is a good predictor for the matching outcome.
• 4) There are two main routes to matching: the preferred orientations either drift toward each other or one of the orientations switches quite suddenly, involving a transient loss of binocularity, which can become permanent if it occurs toward the end of the critical period. While drifting occurs for small initial mismatch, switching is specific for large mismatch.

We expect that these results provide insight more generally into how neuronal systems can develop to integrate inputs from multiple sources coherently to generate normal neuronal function.

METHODS

Neuron model.

We used an adaptive exponential integrate-and-fire model (Brette and Gerstner 2005) with an additional current describing an afterpotential depolarization (Badel et al. 2008). In this model the evolution of the postsynaptic membrane potential u(t) was given by

$$C\frac{d}{dt}u=-g_L\left(u-E_r\right)+g_L{\text{Δ}}_T{e}^{\frac{u-V_T}{{\text{Δ}}_T}}-w_{ad}+z+I,$$ (1)

where E_r was approximately the resting potential, C the membrane capacitance, g_L the leak conductance, and I the current stimulation. The exponential term mimicked the activation of sodium current. Upon reaching the peak voltage V_peak, the voltage u was reset to the fixed value V_reset. The parameter Δ_T was the slope factor and V_T was the (variable) threshold potential. The variable w_ad represented a hyperpolarizing adaptation current with dynamics given by

$${\tau }_{w_{ad}}\frac{d}{dt}{w}_{ad}=a\left(u-E_r\right)-w_{ad},$$ (2)

where τ_wad was the time constant of the adaptation of the neuron and a controlled the strength with which ω_ad was driven. On firing, ω_ad was increased by an amount b. The afterpotential depolarization was captured by the variable z. It was set to I_sp immediately after a spike and decayed then with a time constant τ_z,

$${\tau }_z\frac{d}{dt}z=-z.$$ (3)

Refractoriness was modeled by employing an adaptive threshold V_T, which was set to $V_{T_{max}}$ immediately after a spike and decayed then to $V_{T_{rest}}$ with a time constant ${\tau }_{V_T}$,

$${\tau }_{V_T}\frac{d}{dt}{V}_T=-\left(V_T-V_{T_{rest}}\right).$$ (4)

Parameters for the neuron were taken from Clopath et al. (2010) and kept fixed throughout all simulations (see Table 1).

Table 1.

Parameters used in the model for the neuron

Parameter	Value	Parameter	Value
C, membrane capacitance	281 pF	a, subthreshold adaptation	4 nS
gL, leak conductance	35 nS	b, spike triggered adaptation	0.0805 nA
Er, approximated resting potential	−70.6 mV	Isp, spike current after a spike	400 pA
ΔT, slope factor	2 mV	τz, spike current time constant	40 ms
VT, threshold potential at rest	−50.4 mV	${\tau }_{v_T}$, threshold potential time constant	50 ms
Vreset, resetting voltage	−50.4 mV	$V_{T_{max}}$, threshold potential after a spike	30.4 mV
Vpeak, spiking threshold	20 mV	k, argument of modified Bessel function for synaptic input	1.7
τwad, adaptation time constant	144 ms	A, amplitude of the orientation-selective response of synapses	0.14
gex, excitatory synaptic conductance	35 nS	Vex, reversal potential of the excitatory synapse	0 mV
ginh, inhibitory synaptic conductance	40 nS	Vinh, reversal potential of the inhibitory synapse	−80 mV

All parameters were set in advance on the basis of Clopath et al. (2010).

To test the robustness of our results we also used a simplified neuron model with both the adaptation current and afterdepolarization removed, with which we obtained very similar results.

Synaptic inputs.

Our model consisted of one postsynaptic binocular cell modeling a cortical cell in V1 receiving excitatory, tuned synaptic inputs (Fig. 1A), driven by independent Poisson spike trains. In the first set of simulations these inputs were taken to be monocular. They were divided equally into 250 inputs from the left and 250 from the right eye, respectively. In addition, inhibitory, untuned synaptic inputs were introduced to capture the sublinear binocular integration observed experimentally (Zhao et al. 2013) (Fig. 2). The monocular preferred orientations of the tuned excitatory synapses were linearly spaced between 0° and 180°. To mimic visual input consisting of gratings oriented at an angle θ₀ each excitatory synapse i with preferred orientation θ_i received as input a Poisson spike train with an average firing rate given by the von Mises distribution with center 2θ₀,

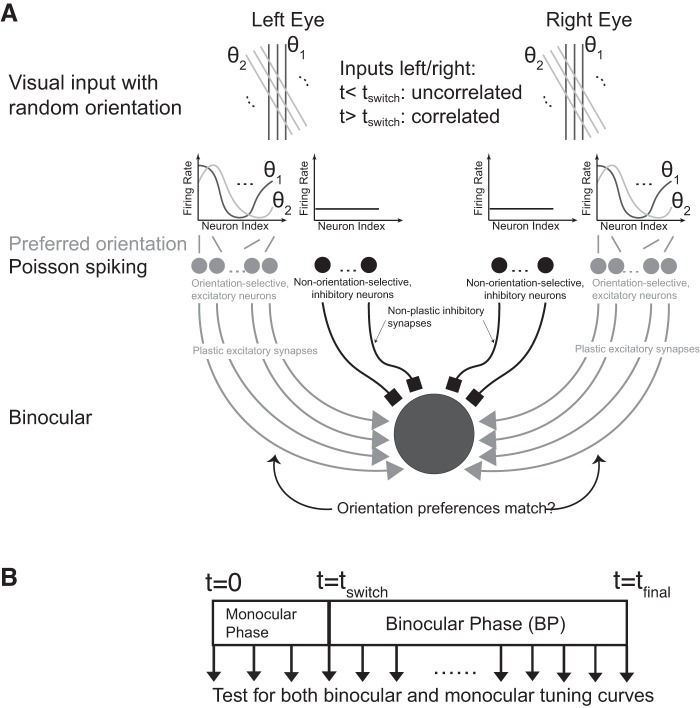
Fig. 1.

Computational model. A: the postsynaptic neuron received synaptic inputs as Poisson spike trains from excitatory, orientation-selective synapses and conductance-based current inputs from nonselective inhibitory synapses, divided equally into inputs from the left and the right eye. Random sequences of oriented visual input characterized by orientation θ were presented to each eye. Only excitatory synapses were plastic. B: simulation protocol. The orientation of the simulated visual input was randomly shifted every 225 ms. The left and right inputs were uncorrelated until a time t_switch (monocular phase), then left and right inputs were identical (binocular phase).

Fig. 2.

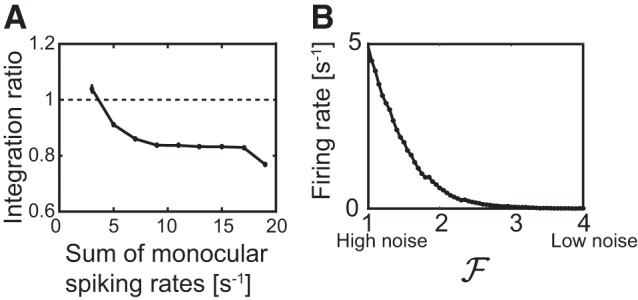
A: sublinear integration ratio of the spiking rate. The ratio of the firing rate for binocular input during the binocular phase and the sum of the corresponding monocular rates is plotted against the sum of the monocular spiking rates. B: fluctuations drive the spiking. The firing rate of the cell goes to 0 when the fluctuations in the excitatory inputs are reduced by increasing the rates of the Poisson trains by a factor $\mathcal{F}$, while keeping the mean current fixed.

$${\nu }_i=A\frac{e^{k\text{cos}\left(2\left({\theta }_i-{\theta }_0\right)\right)}}{2\pi I_0\left(k\right)}.$$ (5)

Here the modified Bessel function of order 0, I₀(k), provided the normalization and A controlled the overall amplitude of the input. The value of k was determined by matching the tuning width of ν_i to that observed for neurons in layer 4 (Hoy and Niell 2015; Niell and Stryker 2008). All excitatory and inhibitory synapses delivered conductance-based currents. The total synaptic current I_syn was given by

$$I_{syn}={{\displaystyle \sum }}_{i=1}^{i=500}{X}_i\hspace{0.17em}{w}_i\hspace{0.17em}{g}_{ex}\hspace{0.17em}\left(V_{ex}-u\right)+g_{inh}\hspace{0.17em}\left(V_{inh}-u\right),$$ (6)

where g_ex (g_inh) was the excitatory (inhibitory) synaptic conductance and V_ex (V_inh) the reversal potential of the excitatory (inhibitory) synapses. The presynaptic Poisson spike trains were given by X_i(t) = ∑_nδ(t−t_i⁽ⁿ⁾) with i the index of the synapse and n counting the spikes in the train. The conductance g_inh of the inhibitory synapses was chosen to match the experimentally observed binocular sublinear integration ratio (Zhao et al. 2013) (Fig. 2). Since the inhibitory synapses were not plastic, the timing of that input was not essential and we modeled it as a steady current rather than driven by spike trains. The difference in the strength of input from the ipsilateral eye and from the contralateral eye was not included in the model. Note that, effectively, the visual inputs in our model were all presented with the same spatial phase. Therefore, the difference in the phase dependence of the response of complex cells and simple cells in V1 was not considered in the model.

Besides the scenario with monocular input, we performed additional numerical simulations for scenarios with binocular inputs having various input characteristics. We used various distributions of the ocular dominance index (ODI) and allowed various degrees of mismatch. Specifically, we investigated the following scenarios:

• 1) the binocular inputs to each synapse are perfectly matched and the distribution of their ocular dominance is peaked at ODI = 0.
• 2) the binocular inputs to each synapse are unmatched with independent, uniformly distributed preferred orientations and the distribution of their ocular dominance is peaked at ODI = 0.
• 3) the binocular inputs to each synapse are perfectly matched and the distribution of their ocular dominance rises toward positive and negative ODI.
• 4) the binocular inputs to each synapse are unmatched with independent, uniformly distributed preferred orientations and the distribution of their ocular dominance rises toward positive and negative ODI.
• 5) same as 3) except the 40% of the inputs that had the most biased ODI in case 3 are made monocular.
• 6) same as 4) except the 40% of the inputs that had the most biased ODI in case 4 are made monocular.

We present mostly results for cases 1 and 2. In case 1, the excitatory inputs were provided by 500 tuned synapses. For each of the 25 equally spaced preferred orientations there were 20 synapses, the ODI values of which were spaced to obtain the distribution f(x) = 0.75–0.75x², xϵ[−1, 1]. Thus, the ODI of cell j was given by $F^{-1}\left(\frac{j-1}{19}\right)$, j = 1,… 20, with F(x) being the CDF of f(x), F(x) = 0.5+0.75x−0.25x³. Case 3 was as case 1 except f(x) = 0.125+1.125x², xϵ[−1, 1]. In case 2, the cell received 490 excitatory, tuned synaptic inputs. For each ODI value there were 49 synapses with independently chosen preferred orientations. The ODI values were chosen as in case 1. Case 4 is as case 2 except f(x) = 0.125+1.125x², xϵ[−1, 1]. With binocular inputs, given a visual input oriented at θ₀ each excitatory synapse i with preferred orientation θ_il through the left eye and θ_ir through the right eye received a Poisson spike train with an average firing rate given by the linear combination of the monocular firing rates (cf. case 5),

$${\nu }_i=\frac{L}{L+R}A\frac{e^{k\text{cos}\left(2\left({\theta }_{il}-{\theta }_0\right)\right)}}{2\pi I_0\left(k\right)}+\frac{R}{L+R}A\frac{e^{k\text{cos}\left(2\left({\theta }_{il}-{\theta }_0\right)\right)}}{2\pi I_0\left(k\right)},$$ (7)

where $\frac{R-L}{R+L}=\text{ODI}$. In cases 1–6 we applied the same plasticity model and simulation protocol as in the monocular case.

Plasticity model.

The excitatory synapses were chosen to be plastic while the strength of the inhibitory synapses was kept fixed. As plasticity model we chose the well-validated model of voltage-based spike-timing-dependent plasticity (STDP) with homeostasis introduced in Clopath et al. (2010), which exhibited separate additive contributions to the plasticity rule for long-term depression (LTD) and for long-term potentiation (LTP),

$$\frac{d}{dt}{w}_i=-A_{\text{LTD}}\left(\overline{\overline{u}}\right)\hspace{0.17em}{X}_i\hspace{0.17em}{\left[{\overline{u}}_{-}-{\theta }_{-}\right]}_{+}+A_{\text{LTP}}\hspace{0.17em}{\overline{x}}_i\hspace{0.17em}{\left[u-{\theta }_{+}\right]}_{+}{\left[{\overline{u}}_{+}-{\theta }_{-}\right]}_{+}.$$ (8)

The weights were limited by hard bounds, w_min ≤ w_i ≤ w_max. The LTP component depended on the postsynaptic membrane potential and a low-pass filtered version of the presynaptic spike train obtained via

$${\tau }_x\frac{d}{dt}{\overline{x}}_i=-{\overline{x}}_i+X_i\left(t\right).$$ (9)

The low-pass filtered, postsynaptic membrane potentials ū_± were obtained via

$${\tau }_{\pm }\frac{d}{dt}{\overline{u}}_{\pm }=-{\overline{u}}_{\pm }+u\left(t\right)$$ (10)

and entered the plasticity rule through the rectifier denoted by […]₊. The amplitude $A_{\text{LTD}}\left(\overline{\overline{u}}\right)=A_{\text{LTD}}^{\left(0\right)}\frac{{\overline{\overline{u}}}^2}{u_{ref}^2}$ captured a homeostatic process based on the low-pass filtered square of the deviation of the membrane potential from the resting potential,

$${\tau }_{th}\frac{d\left({\overline{\overline{u}}}^2\right)}{dt}=-{\overline{\overline{u}}}^2+{\left(u\left(t\right)-E_r\right)}^2.$$ (11)

Thus, the key features of this plasticity model are that depression occurs when a presynaptic spike arrives and the average voltage ū₋ surpasses the threshold θ₋, while a synapse is potentiated if the momentary postsynaptic voltage u(t) is above the threshold θ₊ and the average voltage ū₊ is above θ₋ during a time of order τ_x after a presynaptic spike.

Parameters for the plasticity model were kept fixed throughout all simulations (see Table 2).

Table 2.

Parameters of the plasticity model

Parameter	Value	Parameter	Value
θ+, threshold potential for voltage	−45.3 mV	τ−, time constant for filtered voltage ū−	10 ms
θ−, threshold potential for filtered voltage	−70.6 mV	τ+, time constant for filtered voltage ū+	7 ms
ALTD(0), amplitude of LTD	7∗10−4 mV−2	τx, time constant for the presynaptic spiking trace	15 ms
ALTP, amplitude of LTP	12∗10−4 mV−2	τth, time constant for the homeostasis	1.2 s
wmin, lower bound for the synaptic weight	0	wmax, upper bound for the synaptic weight	1.6

Parameters as used in Clopath et al. (2010) for visual cortex, except for $A_{LTD}^{(0)}$ and $A_{LTP}$, which have been increased to speed up the simulations. LTD, long-term depression; LTP, long-term potentiation.

Simulation.

The initial strengths of the excitatory synapses were chosen randomly from a uniform distribution within [w_min, w_max]. For the first stage from t = 0 to a time t = t_switch, we simulated monocular vision by presenting a random sequence of oriented visual inputs that were uncorrelated between the left and the right eye. The orientation of the visual input was randomly changed every 225 ms. This represented the monocular phase (MP) of the simulation (Fig. 1B). Then, in the second, binocular phase (BP) from t = t_switch to a time t = t_final, we simulated binocular vision by presenting a random sequence of oriented visual inputs that were identical for the two eyes. The orientation of the visual input was again changed randomly at the same frequency as in MP. Note that for cases 1, 3, and 5 we did not include in our model an early phase during which the preferred orientations of upstream neurons become matched. We omitted the transition period (P15–P20) during which spontaneous activity and visually evoked activity are both driving plasticity (Toyoizumi et al. 2013). To monitor the evolution of the preferred orientation we recorded all synaptic strengths every 250 ms. Monocular and binocular tuning curves were generated by testing the spiking response of the postsynaptic cell for the recorded synaptic strengths every 20 s. To gather statistics, we ran the simulations multiple times (n = 5,600 trials). Each trial produced an effectively different cell with different response properties.

To generate a well-controlled initial mismatch for the BP we shifted, right after MP, the synaptic strengths for inputs from one eye from 0° to 80° in steps of 10°.

All numerical simulations were performed with MATLAB.

Data analysis.

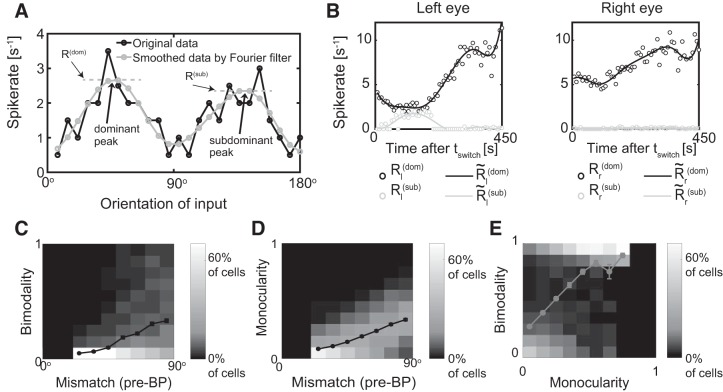
We characterized the response of the postsynaptic neuron using the average spiking rate during windows with a duration of 1 s, both monocularly and binocularly. The tuning curve was generated by plotting the response magnitude against the orientation of the visual input. We defined the preferred orientation of the cell as the orientation that gave the largest response. This was done for monocular input yielding separate preferred orientations O_L,R for the left and right eye, respectively, and for binocular input resulting in O_bino. The monocular/binocular spiking rate was defined as the response for the preferred orientations O_L,R and O_bino, respectively. The mismatch ΔO in the preferred orientation was calculated as the smaller of the two values |O_L−O_R| and 180°−|O_L−O_R|. The global orientation selectivity index (gOSI) was computed as the magnitude of the sum $\frac{\sum R\left(\theta \right)e^{2i\theta }}{\sum R\left(\theta \right)}$ over all angles with R(θ) giving the firing rate response at orientation θ. The ODI for each cell was calculated as $\frac{R-L}{R+L}$, where R and L represent the maximum response magnitude for input from the right and left eye, respectively. The ODI ranges from −1 to 1, where positive values indicate right bias and negative values indicate left bias. The prediction error for the matching outcome was the difference between the predicted and the measured binocular preferred orientation. The decay rate of mismatch during binocular vision at time t [with mismatch ΔO(t)] was determined by $-\frac{\text{Δ}O\left(t+\text{Δ}t\right)-\text{Δ}O\left(t\right)}{\text{Δ}O\left(t\right)\hspace{0.17em}\text{Δ}t}$ with Δt = 45 s. To reduce the impact of noise, we included in the computation of the matching rate only cells for which ΔO(t) was larger than 30°. To analyze the evolution of the monocular tuning curves, we developed two quantifications, the bimodality index and the monocularity index. The bimodality index B quantified the maximal degree of bimodality of the monocular tuning curves throughout BP by measuring at each timepoint t during BP the response amplitude for the dominant and the subdominant preferred orientations. At each time t, for the left and right eye the dominant preferred orientation was defined as the orientation evoking the maximal response R_l^(dom) and R_r^(dom), respectively, after smoothing the tuning curves with a four-mode Fourier filter (Fig. 11A below). If the tuning curves exhibited an additional peak R_l,r^(sub), it defined the subdominant preferred orientation. If there was no such subdominant peak we set the corresponding amplitudes R_l^(dom) to 0. The bimodality index B was then computed as

$$\mathcal{B}=\underset{t\ge t_{switch}}{\text{max}}\left(\max \left(\frac{\widetilde{R_l^{\left(sub\right)}}\left(t\right)}{\widetilde{R_l^{\left(dom\right)}}\left(t\right)},\frac{\widetilde{R_r^{\left(sub\right)}}\left(t\right)}{\widetilde{R_r^{\left(dom\right)}}\left(t\right)}\right)\right),$$

where $\tilde{R}\left(t\right)$ was obtained by smoothing the corresponding R(t) in time using a piecewise cubic spline with five nodes to reduce noise. A bimodality index close to 1 characterized a cell whose tuning curve was quite bimodal at some time during the matching (Fig. 11A and Fig. 11B, left).

Fig. 11.

The type of matching depends on the initial mismatch, the bimodality index B, and the monocularity index M. A: identifying dominant and subdominant preferred orientations in each eye at time t. Black, noisy monocular tuning curve; gray, smoothed data using a four-mode Fourier filter (data from Fig. 4B). B: temporal evolution of the dominant and the subdominant monocular response amplitudes ${\tilde{R}}_{l,r}^{(dom,sub)}$ of each eye (circles). ${\tilde{R}}_{l,r}^{(dom,sub)}$ (lines) denotes the data smoothed by a piecewise cubic spline with five nodes. The cell is bimodal through the left eye near time t = 150 s and monocular through the right eye. C: histogram of the bimodality index B for different values of the mismatch at the onset of binocular phase (BP). D: histogram of the monocularity index M for different values of the mismatch at the onset of BP. E: combined histogram of the bimodality index B and the monocularity index M. The lines in C, D, and E denote the mean of the bimodality index B for different values of the mismatch (C) and the monocularity (E) and the mean of the monocularity index M for different values of the mismatch (D). Error bars denote the SE, some of which were smaller than the symbol size.

The monocularity index M measured the maximal degree of monocularity of the cell during BP. It was computed as

$$\mathcal{M}=1-\underset{t\ge t_{switch}}{\text{min}}\left\{\min \left[\frac{R_l^{\left(dom\right)}\left(t\right)}{R_l^{\left(dom\right)}\left(t_{switch}\right)},\frac{R_r^{\left(dom\right)}\left(t\right)}{R_r^{\left(dom\right)}\left(t_{switch}\right)}\right]\right\}$$

where the left and right monocular response amplitudes R_l,r^(dom)(t_switch) for the dominant preferred orientation at the onset of BP were used to scale the later response amplitudes. The closer this index is to 1, the more monocular the cell was at some time during BP (Fig. 11B). We were particularly interested in how relatively strong monocular orientational receptive fields (ORF) matched. Here we loosely defined ORFs as those orientations to which the neuron responded significantly, i.e., the orientations for which the tuning curve is significantly above baseline. Focusing on relatively strong ORFs we calculated the bimodality and monocularity index only for cells that, at the onset of BP, had monocular gOSIs through each eye above 0.3, monocular maximal response above 0.8/s, and mismatch larger than 20°.

Robustness test.

We tested the sensitivity of our results with respect to the five key parameters of the plasticity model (i.e., A_LTP, A_LTD, τ_x, τ₊, τ₋) by varying them by ± 20%. To do so the main results were condensed into correlations between different quantities characterizing the cells (Table 3). For instance, to test whether the matching rate decreased with increasing gOSI we measured the correlation between the matching rate and the gOSI across all cells and determined to what extent the correlation changed when changing the parameters. To assess the significance of these changes we compared them with the 95% confidence interval of the correlation for the standard parameter set. Most correlations did not change significantly with these parameter changes. Even when the changes were quantitatively significant, the results still agreed qualitatively with those from the standard parameter set. The core MATLAB code used is available at http://modeldb.yale.edu/262465.

Table 3.

Robustness test

A Figure	B Quantity 1	C Quantity 2	D No. of Parameter Sets Outside the 95% Confidence Interval	E 95% Confidence Interval for the Standard Set
Fig. 5A	OL, change in the left preferred orientation during BP	|ODI| at tswitch	0/10	(0.19, 0.29)
Fig. 5B	OR, change in the right preferred orientation during BP	|ODI| at tswitch	0/10	(−0.29, −0.19)
Fig. 6A	Mean monocular gOSI at tswitch	Mismatch at tswitch	0/10	(−0.05, 0.03)
Fig. 6B	Mean monocular gOSI (t = 192.5 s)	Mismatch (t = 192.5 s)	5/10	(−0.29, −0.19)
Fig. 6D	Matching rate	Mean monocular gOSI	0/10	(−0.24, −0.08)
Fig. 6F	Growth rate of gOSI	Mismatch	1/10	(−0.41, −0.31)
Fig. 8B	Accuracy of predicting matching outcome with preferred binocular orientation (Obino) at t = 192.5 s	Mismatch at t = 192.5 s	0/10	(−0.45, −0.34)
Fig. 8C	Accuracy of predicting matching outcome with preferred binocular orientation (Obino) at tswitch	Mismatch at tswitch	0/10	(−0.24, −0.15)
Fig. 10B	Matching rate	|ODI|	0/10	(0.02, 0.13)
Fig. 8B	Monocularity index M	Mismatch at tswitch	3/10	(0.29, 0.45)
Fig. 8A	Bimodality index B	Mismatch at tswitch	1/10	(0.30, 0.41)
Fig. 8C	Bimodality index B	Monocularity index M	2/10	(0.39, 0.53)

For each figure listed (column labeled A), the correlation between 2 quantities characterizing the cell (columns B and C) was computed with a 95% confidence interval for the standard parameter set (column E) and the number of parameter sets was determined for which the correlation is outside that confidence interval (column D). BP, binocular phase; gOSI, global orientation selectivity index; ODI, ocular dominance index; t_switch, beginning of the binocular phase.

RESULTS

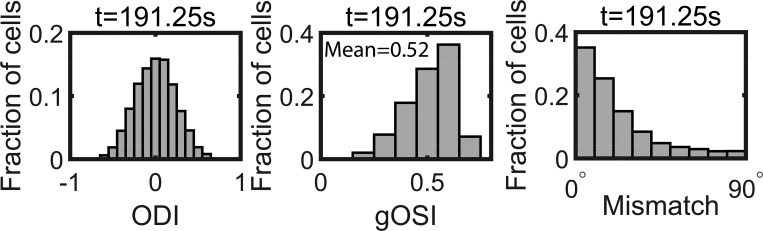
The computational model consisted of one hypothetical binocular cell receiving excitatory, orientation-tuned inputs from each eye via plastic synapses (Clopath et al. 2010) and inhibitory, untuned inputs from each eye via nonplastic synapses (Fig. 1A). Through the inhibitory inputs the model captured the experimentally observed sublinear binocular integration (Zhao et al. 2013) (Fig. 2A). In analogy to the cortical balanced state (e.g., Hansel and van Vreeswijk 2012), the firing of the cells was driven by fluctuations in the inputs rather than their mean value (Fig. 2B) The computation involved a monocular (MP) and a binocular (BP) phase (Fig. 1B). Since the stimulus sequence in both phases was random, repeated trials effectively generated an ensemble of cells with different response properties. The resulting distributions for the ocular dominance (ODI), the orientation selectivity (gOSI), and the remaining mismatch of the preferred orientations (ΔO) were consistent with the experimental data reported by Hoy and Niell (2015) (Fig. 3).

Fig. 3.

Distribution of the properties of the cells at the end of the binocular phase. Left: ocular dominance index (ODI). Middle: global orientation selectivity index (gOSI). Right: mismatch of monocular preferred orientations (ΔO).

Synaptic plasticity captures binocular matching.

The results obtained in our model are consistent with key aspects of previous experiments (Levine et al. 2017; Wang et al. 2010, 2013). Using a tuning width for the inputs that corresponds to that of cells in layer 4 (Niell and Stryker 2008), our model reproduced the development of orientation selectivity for V1 cells with global orientation selectivity index (gOSI) and tuning width similar to those found experimentally in layer 2/3 (Hoy and Niell 2015; Niell and Stryker 2008). Also, the experimentally observed sublinear binocular integration (Zhao et al. 2013) was captured in our model (Fig. 2).

Moreover, while right after eye opening a fraction of V1 cells has been observed to have well-developed orientation selectivity, their monocular preferred orientations for input from the left and the right were poorly matched (Wang et al. 2010). In fact, in some cells, they were nearly 90° apart, the maximal possible difference. This mismatch decreased substantially with age to reach the adult level by P30–P36 (Wang et al. 2010, 2013).

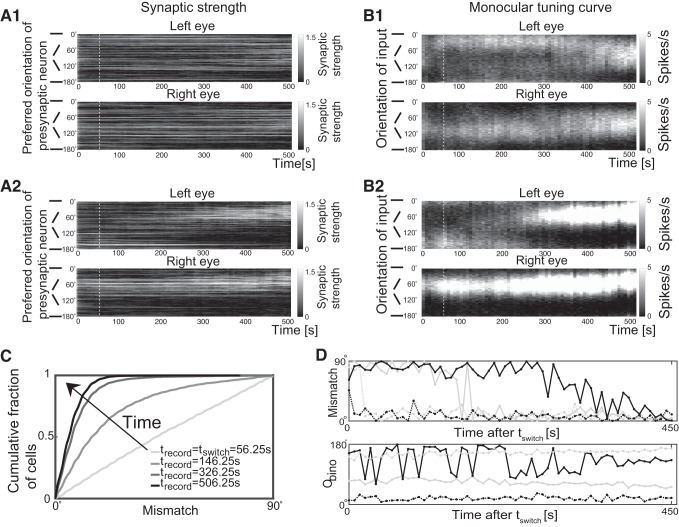
In our model, during the initial phase of MP multiple sets of synapses were potentiated. Due to the random distribution of the initial synaptic strengths, the randomly chosen orientations, as well as the variability of the number of spikes in the input Poisson spike trains the synaptic strengths did not vary smoothly with orientation. Nevertheless, the sets of potentiated synapses roughly specified monocular orientational receptive fields (ORFs) of the postsynaptic neuron, defined as those orientations for which the tuning curve is significantly above baseline. During MP these ORFs for input from the left and the right eye did not match (Fig. 4A, 1 and 2 up to t = t_switch, marked by white dashed lines), which manifested itself also in non-matching orientation tuning curves (Fig. 4B, 1 and 2).

Fig. 4.

Binocular vision reduces the mismatch of the monocular preferred orientations. A1 and A2: two examples of the temporal evolution of the synaptic strengths. The presynaptic neurons are ordered according to their preferred orientation (vertical axis), and their synaptic strengths are illustrated in grayscale as a function of time (horizontal axis). B1 and B2: corresponding evolution of the monocular tuning curves through each eye. Grayscale indicates the firing rate of the cell in response to monocular input with an orientation as indicated along the vertical axis. In A1 and B1 the two monocular preferred orientations drifted toward each other while in A2 and B2 one monocular preferred orientation switched to the other discontinuously to achieve binocular matching. White dashed lines mark t = t_switch. C: the cumulative distribution function of the mismatch at different times (t_switch = 56.25 s; n = 5,600 cells). D: the evolution of the mismatch and the binocular preferred orientation O_bino for 4 cells during the binocular phase (BP), showing representative trajectories. The solid black line represents the cell shown in A1 and B1. The solid gray line represents the cell shown in A2 and B2.

During BP both eyes received the same inputs. This allowed the potentiation of weak synapses that by themselves were not strong enough to drive a postsynaptic spike, if the synapses with the same preferred orientation but receiving input from the other eye were sufficiently strong to trigger a spike. This slowly modified the ORFs and the tuning curves (Fig. 4, A and B for t>t_switch), decreasing the mismatch between the two monocular preferred orientations. Eventually, in almost all cells the preferences became matched within 20° (Fig. 4C). The variability in the evolution of the cell properties was extremely high: cells could match early (dashed lines in Fig. 4D) or late (solid lines), their preferred orientation could shift gradually (black lines) or it could switch suddenly (gray lines).

The effect of ODI on the matching outcome.

It has been shown that 3 wk of environmental enrichment can rescue the disrupted binocular mismatch caused by visual deprivation during the critical period (Levine et al. 2017). These experiments revealed that ocular dominance plays a key role in the binocular matching process. In cells whose response was dominated by one of the two eyes, binocular matching was achieved by the orientation preference for input from the nondominant eye changing, while the orientation preference for input from the dominant eye did not change much.

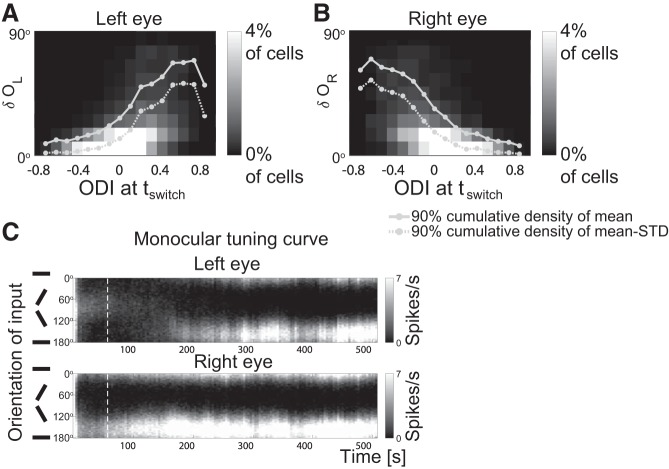
Motivated by this experimental result, we determined for each cell the change δ_L,R in the left and right monocular preferred orientations during BP as well as the ocular dominance index (ODI) right before BP. The statistics of δ_L,R and ODI across many cells are shown in histograms of δ_L,R for each value of the ODI (Fig. 5, A and B). As in the experiments, the range in the change of preferred orientation for input from the nondominant eye was much wider than that for the dominant eye. This asymmetry becomes very clear when considering—for each value of the ODI—the range in δ_L,R that includes 90% of the cells; its upper limit is shown as solid lines in Fig. 5, A and B. Since the preferred orientation is measured using Poisson spike trains it exhibits fluctuations. To illustrate that they do not reduce the asymmetry impact we also considered the cumulative distribution across cells of the mean of δ_L,R minus the standard deviation of δ_L,R. Its 90% point is given by the dashed lines. Figure 5C shows an illustrative example in which at t_switch (white dashed line) the cell was dominated by the input from the right eye (ODI = 0.415). During BP the preferred orientation for input from the nondominant (left) eye changed substantially, while that for input from the dominant (right) eye did not evolve much.

Fig. 5.

Preferred orientation mostly changes for nondominant eye. A: two-dimensional histogram in which the grayscale of each square bin indicates the percentage of cells whose monocular preferred orientation through the left eye changed by δO_L (vertical axis) during the binocular phase (BP) and that had an ocular dominance index (ODI) at t_switch as given on the horizontal axis. B: same plot as A, except for the right eye. In both A: and B: t_switch = 56.25 s, t_final = 506.25 s, n = 5,600 cells. C: the evolution of the monocular tuning curve for input from the left and right eye (cf. Fig. 4B). White dashed lines mark t = t_switch. The scale of the grayscale map is capped to better show the difference between the left and right monocular firing rates at t_switch (ODI>0).

The interaction between orientation selectivity and matching.

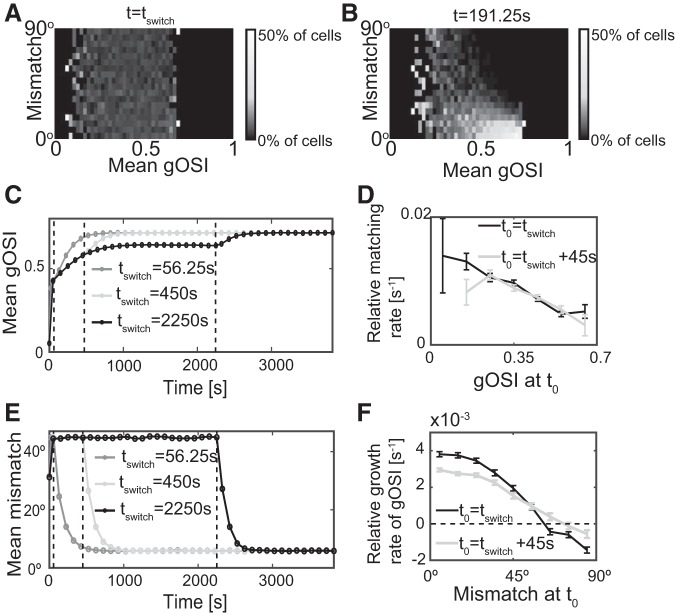
Previous experimental results revealed an inverse relationship between mismatch and gOSI: cells with smaller orientation mismatch had greater orientation selectivity. This did not hold in mice whose binocular matching process was compromised by visual deprivation; their ΔO values spanned the entire 0°–90° range for all gOSI values (Levine et al. 2017). The histograms in Fig. 6 show the relationship between mismatch and gOSI obtained in the model at the onset of BP at t_switch (Fig. 6A) and at an intermediate time during BP (Fig. 6B). Most cells were neither well matched nor very selective at the end of MP (Fig. 6A). Consistent with the experimental results, at intermediate times during BP the mismatch was small in highly orientation-selective cells (Fig. 6B).

Fig. 6.

Matching leads the development of orientation selectivity during binocular phase (BP). A and B: histogram of the mismatch for different values of the mean monocular global orientation selectivity index (gOSI) at t = t_switch = 56.25 s. The histogram is normalized for each value of the mean monocular gOSI. B: as A, but for t = 192.5 s during BP. Lower mismatch is correlated with higher orientation selectivity (n = 5,600 cells). C: binocular vision enhances orientation selectivity. The evolution of gOSI for t_switch = 56.25 s, 450 s, 2,250 s (marked by dashed lines) (n = 5,000 cells). D: less selective cells match faster. The relative matching rate is given by $-\frac{\text{Δ}O\left(t_0+\text{Δ}t\right)-\text{Δ}O\left(t_0\right)}{\text{Δ}O\left(t_0\right)\text{Δ}t}$, where t₀ = t_switch (black line) and t₀ = t_switch+45 s (gray line) with Δt = 45 s. E: binocular vision matches monocular preferred orientations. The evolution of mismatch for t_switch = 56.25 s, 450 s, 2250 s (marked by dashed lines) (n = 5,000 cells, t_final = t_switch+562.5 s). F: the growth rate of the global orientation selectivity index (gOSI) decreased with increasing mismatch. The relative growth rate of the gOSI is given by $\frac{\text{Δ}gOSI\left(t_0+\text{Δ}t\right)-\text{Δ}gOSI\left(t_0\right)}{\text{Δ}gOSI\left(t_0\right)\hspace{0.17em}\text{Δ}t}$, where t₀ = t_switch (black line) and t₀ = t_switch+45 s (gray line) with Δt = 45 s. In D and F the error bars denote the SE.

To gain insight into the relationship between the matching process and the sharpening of the orientation selectivity, we measured the evolution of the gOSI and the mismatch for different durations of the MP (Fig. 6, C and E). For t_switch>1,250 s the gOSI reached a steady state during MP (Fig. 6C). Remarkably, its saturation value was significantly lower than the value reached during BP, even if that BP followed an MP with short duration. This indicates that binocular vision enhanced the development of orientation selectivity. Further analysis showed that the mismatch decayed exponentially to its final value faster than the gOSI. By employing initial conditions with well-controlled mismatch (see methods), we showed that less selective cells matched faster (Fig. 6D) and the growth rate of the gOSI decreased with increasing mismatch (Fig. 6F). Strikingly, for cells with large mismatch the growth rate could even be negative and the cells became less selective. With time, however, the mismatch of these cells decreased as it did for the other cells and eventually reached values for which the gOSI increased. This suggests that the matching process enhanced the orientation selectivity, while orientation selectivity was not a driving force of binocular matching but had, instead, a negative effect on matching speed.

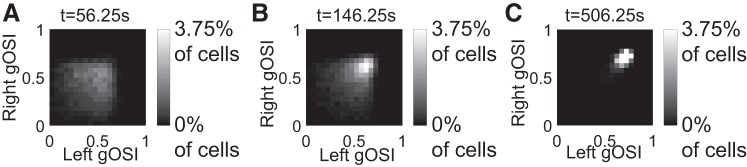
Moreover, at the onset of BP the left and right orientation selectivities were often quite different from each other, leading to a broad distribution across cells (Fig. 7A). But binocular vision enhanced the selectivities and drove them to the same large value (Fig. 7, B and C).

Fig. 7.

Binocular vision enhances and matches monocular orientation selectivity. Two-dimensional histograms of right and left global orientation selectivity index (gOSI) at the onset (A, t_switch = 56.25 s) and two intermediate times during binocular phase (BP) (B and C) (n = 5,600 cells).

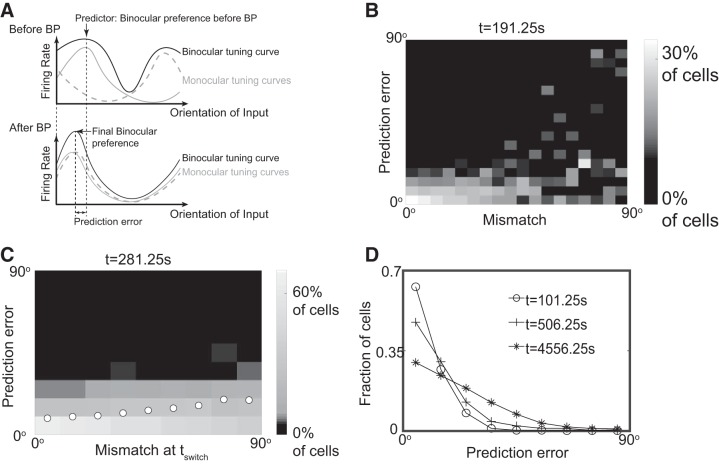
Prediction of matching outcome.

Next, we put forward testable predictions based on our model. We hypothesized that the binocular preferred orientation right before BP could predict the eventual matching outcome. We therefore defined the prediction error as the difference between the final binocular preferred orientation and that at the beginning of BP (Fig. 8A). Overall, the binocular preferred orientation at t_switch was a quite good predictor for the preferred orientation at all time points during BP that we investigated (Fig. 8B). Note that in Fig. 8B the histogram of the prediction error was normalized separately for each value of the mismatch. This revealed that for small mismatch almost all cells had a prediction error of less than 20°, while for large mismatch the distribution of prediction errors was almost uniform. Thus, the mismatch that remained at a given time during BP indicated quite well whether the binocular preferred orientation at t_switch was a good predictor for the binocular preferred orientation at that later time.

Fig. 8.

Binocular preferred orientation at the onset of binocular phase (BP) predicts the preference after matching. A: the prediction error was calculated as the difference between the binocular preferred orientation before and after BP. B: the quality of the prediction decreased with increasing mismatch. Histogram of the prediction error for different values of the mismatch, both at the same time t = 191.25 s. The histogram is normalized separately for each value of the mismatch. C: the accuracy of prediction decreased with the initial mismatch. Like B, but at t = 281.25 s and using the initial mismatch. Circles represent the mean prediction error of the trials for each value of initial mismatch. D: the mean prediction error increased with time. The distribution of the prediction error from well-matched cells (mismatch <20°) at three intermediate times during BP. In all figures, t_switch = 56.25 s and n = 5,600 cells.

Can the reliability of the prediction for the preferred orientation already be anticipated at t_switch? Indeed, already the initial mismatch was a good indicator for this reliability (Fig. 8C): the prediction was quite accurate when the initial mismatch was small, while it became less reliable for large initial mismatch.

Since in the experiments the monocular, rather than the binocular, tuning curves were measured Levine et al. (2017), we tested how well the superposition of two monocular tuning curves at the onset of BP could predict the final, matched orientation. We found that at each time point the preferred orientation determined by the linear superposition of two monocular curves was close to the binocular preferred orientation and therefore it was also a good predictor for the matching outcome (Fig. 9).

Fig. 9.

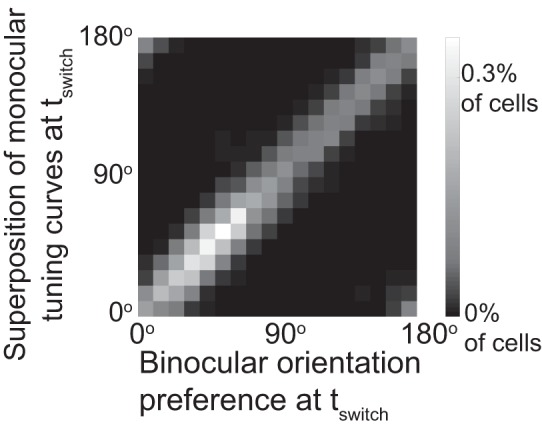
Binocular tuning is well approximated by the sum of the monocular tuning curves. Histogram of the binocular preferred orientation and the preferred orientation obtained from the sum of the two monocular tuning curves.

The matched preferred orientation that emerges in a given cell reflects the initial synaptic weights as well as the sequence of presented visual inputs. Since in our simulations the synapses were plastic throughout the simulation and the sequence of inputs was random, the binocular preferred orientation evolved on a slow time scale, wandering around in a diffusive manner. The distribution of the prediction error across cells therefore broadened with time as shown in Fig. 8D for well-matched cells (mismatch less than 20°), implying a growing mean prediction error.

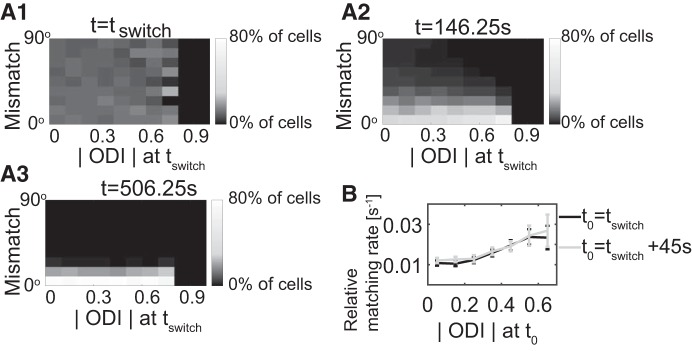
The speed of matching depends on the initial ODI.

We next examined how initial ocular dominance affected the speed of the matching process. Figure 10A, 1, 2, and 3 shows the histogram of the mismatch for various time points as a function of the magnitude |ODI| of the ocular dominance index at t_switch. For high initial |ODI| the mismatch decreased rapidly, while in many cells that had a lower initial |ODI| the matching proceeded more slowly (most clearly seen comparing t = 146.25 s with t = t_switch). We quantified this in terms of the decay rate of the mismatch at time t given by $-\frac{\text{Δ}O\left(t_0+\text{Δ}t\right)-\text{Δ}O\left(t_0\right)}{\text{Δ}O\left(t_0\right)\hspace{0.17em}\text{Δ}t}$ with Δt = 45 s. Figure 10B shows the mean of the decay rates across cells for different ranges of the |ODI| at t₀ = t_switch and t₀ = t_switch+45 s. This result is consistent with the intuition that cells with a low initial |ODI| have two monocular ORFs with similar overall synaptic strengths, which compete with each other during BP, slowing down the matching process. This effect of ocular dominance on the binocular matching rate reveals ocular dominance as a driver of the binocular matching process. Note that cells with an initial mismatch less than 40° were not included in Fig. 10B, since here we were only interested in the matching processes starting with a state that was not well matched. Similar values for the decay rates as shown in Fig. 10B were obtained at other intermediate times during BP, suggesting an exponential decay of mismatch during BP.

Fig. 10.

Binocular matching speed increases with the absolute value of initial ocular dominance index (ODI) (A1–A3). Histograms of mismatch at different times for different values of the magnitude of ODI at t_switch (t_switch = 56.25 s, n = 5,600 cells). The histograms are normalized for each value of initial |ODI| separately. B: the average relative matching rate during the time interval [56.25 s, 146.25 s] against the ODI at t_switch = 56.25 s and t_switch+45 s (3,537 out of 5,600 cells; error bar gives SE).

The type of matching process depends on the initial mismatch.

Finally, we investigated whether there are qualitatively different processes through which the binocular matching was obtained. There were at least two such processes: the two monocular preferred orientations could shift gradually toward each other (Fig. 4B1), or one of the preferred orientations could switch to the other one discontinuously (Fig. 4B2). The latter case was characterized by a period during which the tuning curve for one eye was bimodal, with the dominance switching from one peak to the other, leading to a discontinuity in the preferred orientation. During this time the cell responded only weakly to input from that eye; the cell was effectively monocular. In contrast, when the matching was achieved by shifting, the tuning curves of both eyes had only a single peak, which gradually shifted, and the cell remained binocular throughout BP (Fig. 4B1).

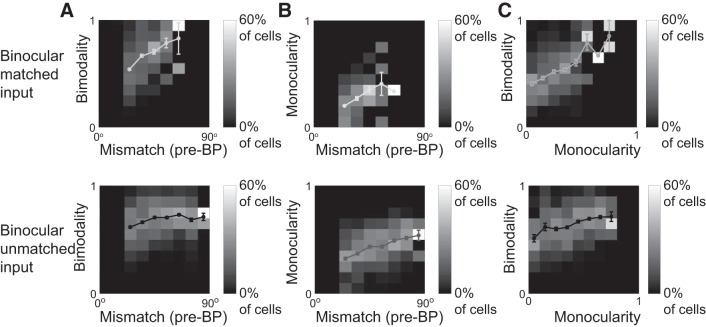
Based on these observations we introduced a bimodality index B and a monocularity index M to characterize the matching process (see methods and Fig. 11, A and B) and related it to the mismatch at t_switch (Fig. 11, C and D). For small initial mismatch, the cells showed little monocularity or bimodality throughout the matching process, implying that binocular matching was achieved by the monocular preferred orientations shifting toward each other. If the initial mismatch was large, however, bimodality and monocularity were both larger and it was more likely that one of the two preferred orientations switched to the other. Thus, both bimodality and monocularity were equally suited to characterize the matching process; in fact, they were positively correlated (Fig. 11E).

The dependence of matching on the input characteristics.

So far we assumed for simplicity that all excitatory input synapses are monocular. However, cells in V1 vary substantially in their ocular dominance. To go beyond this simplification we therefore performed extensive additional numerical simulations to determine how the learning process and outcome depends on the input characteristics. We included inputs that were more realistic for the visual system but covered also other situations that might be relevant for matching processes in multimodal sensory processing. Specifically, we made the inputs binocular using various distribution of the ODI and allowed various degrees of mismatch. Here we illustrate the results for the following scenarios:

• 1) The binocular inputs to each synapse are perfectly matched and the distribution of their ocular dominance is peaked at ODI = 0.
• 2) The binocular inputs to each synapse are unmatched with independent, uniformly distributed preferred orientations and the distribution of their ocular dominance is peaked at ODI = 0.

Complex cells in the visual system are presumably best described by inputs in between these two cases, since under natural conditions simple cells match before complex cells (Wang et al. 2013) and exhibit a peaked ODI-distribution (Gordon and Stryker 1996; Mrsic-Flogel et al. 2007). Thus, complex cells receive quite well, but not perfectly, matched inputs.

We found that, in all cases with binocular and potentially unmatched inputs, key features of the matching process were qualitatively the same. In particular, matching predominantly occurred via shifting of the preferred orientations if the mismatch was small, while switching of the orientations occurred mostly for large mismatch (Fig. 12).

Fig. 12.

Shifting and switching depend on mismatch also for binocular inputs. Top: binocular, perfectly matched inputs. Bottom: binocular, unmatched inputs. A: histogram of the bimodality index B for different values of the mismatch at the onset of binocular phase (BP). C: histogram of the monocularity index M for different values of the mismatch at the onset of BP. C: combined histogram of the bimodality index B and the monocularity index B. The lines indicate the respective means with error bars denoting the SE; the single point without error bar in the top panel of B and C for the initial mismatch belonging to (60°, 70°] represents a single cell.

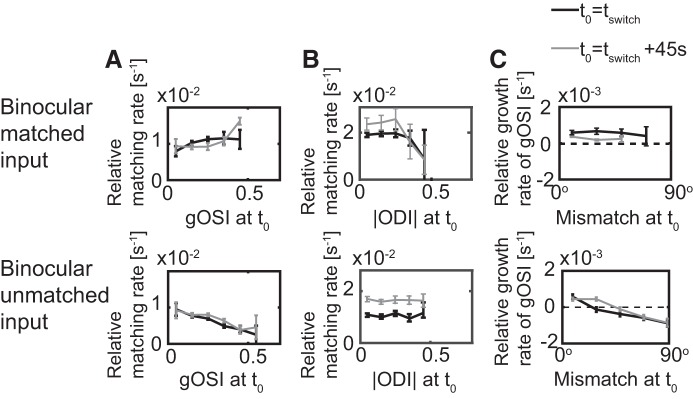
The only significant differences arose for matched binocular inputs. While for unmatched binocular inputs the matching rate decreased with increasing gOSI, as was the case for the monocular inputs, this was not the case for matched binocular inputs (Fig. 13A). In the latter case the mismatch of the cell response arises because different synapses provide inputs with different preferred orientations and different ODI. Thus, even though the left and right preferred orientations of a given synapse are the same, the strengths of the inputs from the left and right eye are not balanced. As a result, the orientation that dominates the overall input is in general not the same for the two eyes. For the mismatch of the cell to decrease it is then sufficient if its orientation selectivity increases, because this implies that the range of orientations that contribute to its input is reduced. This increase in the selectivity and the associated matching occurs already during the monocular phase. The difference in the matching mechanism also led to a difference in the dependence of the matching rate on the ODI (Fig. 13B) and the dependence of the growth rate of the gOSI on the mismatch (Fig. 13C). Performing additional simulations (see scenarios 3–6 listed in methods), we found that this mechanism was less relevant when the inputs to each synapse were less matched or less binocular (i.e., more of the inputs to the cells had ODIs closer to 1 or −1).

Fig. 13.

The interaction between ocular dominance index (ODI), global orientation selectivity index (gOSI), and mismatch with binocular inputs. Top: binocular matched inputs. Bottom: binocular, unmatched inputs. A: the dependence of the matching rate on the gOSI. B: the dependence of the matching rate on the |ODI|. C: the dependence of the growth rate of the gOSI on the mismatch; error bars give the SE. Results are shown for t₀ = t_switch and for t₀ = t_switch+45 s. (See Fig. 6, D and F, Fig. 10B). With binocular, unmatched inputs the behavior is as for monocular inputs. For binocular, matched inputs qualitative differences arise, particularly for the dependence of the matching rate on the gOSI (cf. Fig. 6, E and F).

DISCUSSION

The role of plasticity in the development of the brain has been investigated extensively, with the visual system, particularly V1, serving as a prime example. Many of these studies were motivated by findings in cats, ferrets, and monkeys, where cellular response properties like ocular dominance and preferred orientation vary quite smoothly with position in visual cortex, leading to ocular dominance columns and orientation maps. The formation of these maps and columns has been described using Hebbian, correlation-based models (Erwin and Miller 1998; Miller 1994; Miller et al. 1989; Piepenbrock et al. 1997). From the perspective of multisensory integration the matching of the two monocular preferred orientations is of particular interest. As shown by Erwin and Miller (1998), this matching requires that the strengths of the two input-correlation modes are not too similar. The temporal evolution toward the matched configuration and the relation of this evolution to that of the orientation selectivity and ocular dominance has, however, not been addressed in (Erwin and Miller 1998). In modeling synaptic plasticity using the Bienenstock–Cooper–Munro (BCM) model (Bienenstock et al. 1982), the combined evolution of preferred orientation and ocular dominance has been investigated with focus on the impact of monocular and binocular deprivation (Clothiaux et al. 1991). To model strabism, this study also considered the case of uncorrelated inputs to the left and right eye. In that case all cells eventually became purely monocular in their model.

Our study has been motivated by recent experiments in mice (Levine et al. 2017; Wang et al. 2010, 2013), which focused on the process by which the two monocular preferred orientations become matched. We aimed to investigate to what extent these experimental findings can be captured in a relatively simple computational model. We therefore considered a single spiking neuron that receives orientation-selective inputs via plastic synapses.

For the plasticity mechanism we chose a well-accepted, biophysically somewhat detailed model (Clopath et al. 2010), which has been validated under quite a few, varied plasticity protocols, including in visual cortex. It reduces to the BCM model (Bienenstock et al. 1982), if the pre- and postsynaptic spike trains are uncorrelated and if their evolution is captured adequately within a firing-rate model. Since cortical cells in the balanced state respond to fluctuations in the input rather than its mean (Hansel and van Vreeswijk 2012), it is not clear, however, whether the correlations are sufficiently negligible. Moreover, the stimuli used in the experiments varied on a time scale that is not much longer than the interspike intervals (Niell and Stryker 2008). We therefore did not perform that reduction.

For simplicity, we assumed that the synaptic plasticity mechanism does not change with eye opening and the subsequent onset of the critical period for ocular dominance; only the inputs to the cortical neuron, which drive the synaptic plasticity, were taken to change from being uncorrelated between the two eyes before eye opening to being correlated after eye opening. This simplification is consistent with a number of experimental findings. In cats, orientation selectivity emerges already before eye opening, driven by vision-independent spontaneous activity in the retina (Chapman and Stryker 1993), and continues to increase after eye opening. Until the onset of the critical period this increase does not depend on visual input (Crair et al. 1998). Correspondingly, the onset of the critical period has been identified not as a change in the plasticity mechanism but as a transition from synaptic plasticity being driven predominantly by spontaneous activity to being driven mostly by visually evoked input (Toyoizumi et al. 2013). This change results from an increase in inhibition, which reduces the weaker, spontaneous activity—but not the stronger, visually evoked activities—to magnitudes that are not sufficient to drive synaptic plasticity. Note that this scenario may vary across species (Chapman and Stryker 1993; Hagihara et al. 2015).

We focused on complex cells, which receive orientation-selective inputs from simple cells, a situation that is analogous to that in multisource systems in which upstream neurons gain selectivity before the downstream neurons (Stein and Rowland 2011; Wang et al. 2013). We explored a number of different scenarios. In the simplest situation, each synapse provided purely monocular, well-tuned input, corresponding to a situation in which each synapse represents a single source. In V1 of the mouse, simple cells in the binocular zone are binocular and their monocular preferred orientations can be quite well matched already during the period of interest (Wang et al. 2013). However, this does not imply that the monocular preferred orientations of the complex cells are already well matched at that point, since the simple cells feeding into the complex cell, which have different preferred orientations, are dominated by different eyes, reflecting their broad distribution of the ODI. We investigated this situation for different ODI distributions. The results are qualitatively similar to those obtained in the monocular case, unless synapses providing inputs with ODI close to 0 dominate. In that case an additional matching mechanism becomes relevant.

Despite its simplicity, our model captured a number of fundamental experimental results for the development of orientation tuning in mouse V1 (Levine et al. 2017; Wang et al. 2010, 2013). During the monocular phase a fraction of the cells became orientation selective with respect to inputs from both eyes, but the preferred orientations were rarely matched. The matching occurred during the binocular phase and depended strongly on the ocular dominance of the neuron: for cells that were dominated by the input from one eye the matching process typically involved only small changes in the preferred orientation of the dominant eye, while the orientation of the weaker eye could change substantially (Levine et al. 2017). For those cells the initial preferred orientation of the dominant eye is a good predictor for the preferred orientation after matching. Considering all cells, in the model the initial binocularly preferred orientation predicts the final preferred orientation well. As in the experiment (Levine et al. 2017), the orientation selectivity was higher in well-matched cells and enhanced by correlated visual input (Hoy and Niell 2015). Both results reflect the enhanced drive the cells receive once the monocular tuning curves overlap, which leads to stronger plastic changes as well as enhanced selectivity due to the synaptic homeostasis (Clopath et al. 2010).

In the model the development of orientation selectivity and its matching are driven by different types of correlations in the inputs to the cells and therefore differ in their time course. Orientation selectivity starts to emerge already before eye opening. After eye opening visual input is expected to enhance cortical activity and with it the learning speed for orientation selectivity, consistent with the results of Hoy and Niell (2015). In the model the matching process requires correlated inputs from both eyes. It therefore suggests that matching does not start until eye opening and persists then throughout the critical period. Indeed, experimental results suggest that at P15–P18, i.e., shortly after eye opening, the matching of V1 cells is still close to chance level (Wang et al. 2013), which is consistent with the lack of matching in dark-reared mice (Wang et al. 2010). However, already at the beginning of the critical period (P19–P21) the preferred orientations are somewhat matched (Wang et al. 2013). Due to the presence of uncorrelated spontaneous activity during the phase between eye opening and the critical period (Fagiolini and Hensch 2000), the model suggests that during that phase the matching proceeds more slowly than during the critical period.

In the model, cells whose left and right monocular tuning curves overlap match more rapidly. Thus, for a given mismatch less selective cells are predicted to match faster. This is consistent with results obtained in mice that were reared in the dark from P1 to P30 (Wang et al. 2010). At P30 the distribution of their mismatch was not statistically different from a uniform distribution and their selectivity was lower than that observed at the beginning of the critical period. As found in the model, their matching progressed faster than was the case for undeprived animals during the critical period. Conversely, binocular deprivation between eye opening and the onset of the critical period has been found to increase the fraction of cells that have strong orientation selectivity (Crair et al. 1998) but large mismatch (Wang et al. 2010). Our model predicts that their matching process will be slower.

Conversely, the model predicts that the mismatch affects the orientation selectivity. By manipulating the initial mismatch at fixed orientation selectivity, we showed that during the binocular matching process cells did not become more orientation selective unless the mismatch was small enough to allow the monocular tuning curves to overlap.

Moreover, the overlap of the tuning curves is predicted to affect the matching process in a qualitative manner. For small mismatch, for which the tuning curves overlap significantly, the monocular preferred orientations are predicted to shift smoothly toward each other. For large mismatch, however, the model predicts that the response to input from one eye and its selectivity drop substantially during the evolution. If the plasticity period continues sufficiently long beyond that phase, this reduction in response is only transient and the response eventually recovers with a preferred orientation that has switched to that of the input from the other eye. This switching process is predicted to be more likely after binocular deprivation between eye opening and the onset of the critical period. If the switching occurs, however, late in the critical period, the remaining duration of the plastic period may not suffice for the recovery and the cell may remain essentially monocular. This has been reported experimentally for a fraction of L2/3 cells (Tan et al. 2018).

When the plasticity period in the model was sufficiently long, all cells became highly selective and very well matched, more so than observed experimentally (Wang et al. 2010). This could result from an oversimplification of the plasticity mechanism or of the stimuli used in the simulations. Alternatively, it could suggest that biologically the overall plasticity process and its duration are not optimized specifically for orientation selectivity and matching but could have additional objectives. This interpretation is supported by the observation that in the model the best orientation selectivity and matching would be achieved in the shortest time if there was no monocular period at all. However, it has been pointed out that such a monocular period during which contra- and ipsilateral inputs are uncorrelated is necessary to form retinogeniculate and geniculocortical connections with segregated eye-specific areas in lateral geniculate nucleus (reviewed by Arroyo and Feller 2016).

In our model the plasticity resulted from changes in the synaptic weights that were driven by correlations between presynaptic spikes and the evolution of the postsynaptic voltage, combined with a homeostatic mechanism based on the postsynaptic long-term activity (Clopath et al. 2010). We expect that most of our results do not depend qualitatively on the specific details of the plasticity mechanism as long as it has a Hebbian component that is based on the correlations between pre- and postsynaptic activities and that does not change the weights for low presynaptic activity, in combination with homeostatic regulation. Conceivably, the plasticity mechanism could have a strong structural component (Sailor et al. 2016), which may be quite likely at this developmental stage of the animal.

We have considered in our model only a single neuron and its feedforward inputs. In the mammalian V1 the L2/3 and the L4 neurons are, however, part of a recurrent network. This recurrent connectivity plays a key role in the development of the ocular dominance columns and orientation maps (Erwin and Miller 1998; Miller 1994; Miller et al. 1989) that are found in higher mammals like cats, ferrets, and monkeys (Hubel and Wiesel 1968; Mountcastle 1997). Mouse V1, however, does not exhibit such maps, suggesting that the recurrent connectivity plays a less important role during development. Computational modeling has shown that in the cortical balanced state the recurrent connectivity does play a role in enhancing the orientation selectivity of the cells by providing feedback that reduces the untuned components in the input (Hansel and van Vreeswijk 2012; Pattadkal et al. 2018). Whether and how the recurrent, seemingly random connectivity affects the matching process is, however, still an open question.

The framework of our model can readily be applied to neurons in other multichannel systems such as binaural auditory neurons or multisensory neurons to capture the development and matching of multiple, single-channel receptive fields that represent corresponding physical properties (e.g., orientation, position). For multisensory neurons in superior colliculus, for example, it has been shown that the selectivity of multisensory neurons develops after the development of selectivity of its upstream unisensory neurons (Stein and Rowland 2011), which is similar to the setup in our model. The binocular vision and its ensuing matching of orientation selectivity through binocular vision in our visual cortex model corresponds to sensing the same event through different modalities simultaneously and the matching of their corresponding receptive fields. Thus, the ideas and results developed here may readily carry over to explain experimental results for the development and matching of receptive fields in other sensory cortices integrating inputs across modalities (Stein and Rowland 2011).

To conclude, by modeling the development and binocular matching for a hypothetical cell in visual cortex V1, we captured a host of experimental results in mouse and give several predictions. Key elements of the model are the evolution and competition of two monocular receptive fields in the presence of correlated inputs. The simplicity of this framework makes it a good candidate to investigate the interaction between selectivity, channel dominance, and mismatch of a specific physical property at the single neuron level during the matching process in multisource experience-dependent sensory systems.

GRANTS

This work was supported by National Institute on Deafness and Other Communication Disorders Grant R01DC015137 (H. Riecke) and National Eye Institute Grant R01EY020950 (J. Cang).

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the authors.

AUTHOR CONTRIBUTIONS

X.X., J.C., and H.R. conceived and designed research; X.X. performed experiments; X.X. and H.R. analyzed data; X.X. and H.R. interpreted results of experiments; X.X. prepared figures; X.X. and H.R. drafted manuscript; X.X., J.C., and H.R. edited and revised manuscript; X.X., J.C., and H.R. approved final version of manuscript.

ENDNOTE

At the request of the authors, readers are herein alerted to the fact that additional materials related to this manuscript may be found at https://modeldb.yale.edu/262465. These materials are not a part of this manuscript, and have not undergone peer review by the American Physiological Society (APS). APS and the journal editors take no responsibility for these materials, for the website address, or for any links to or from it.