Skip to main content
NCBI home page
ACS Omega logoLink to ACS Omega
. 2020 Apr 14;5(16):9510–9516. doi: 10.1021/acsomega.0c00732

New Approach Combining Molecular Fingerprints and Machine Learning to Estimate Relative Ionization Efficiency in Electrospray Ionization

Alfred W Mayhew †, David O Topping ‡, Jacqueline F Hamilton †,*
PMCID: PMC7191837  PMID: 32363303

Abstract

graphic file with name ao0c00732_0003.jpg

Electrospray ionization (ESI) is widely used as an ionization source for the analysis of complex mixtures by mass spectrometry. However, different compounds ionize more or less effectively in the ESI source, meaning instrument responses can vary by orders of magnitude, often in hard-to-predict ways. This precludes the use of ESI for quantitative analysis where authentic standards are not available. Relative ionization efficiency (RIE) scales have been proposed as a route to predict the response of compounds in ESI. In this work, a scale of RIEs was constructed for 51 carboxylic acids, spanning a wide range of additional functionalities, to produce a model for predicting the RIE of unknown compounds. While using a limited number of compounds, we explore the usefulness of building a predictor using popular supervised regression techniques, encoding the compounds as combinations of different structural features using a range of common “fingerprints”. It was found that Bayesian ridge regression gives the best predictive model, encoding compounds using features designed for activity coefficient models. This produced a predictive model with an R2 score of 0.62 and a root-mean-square error (RMSE) of 0.362. Such scores are comparable to those obtained in previous studies but without the requirement to first measure or predict the physical properties of the compounds, potentially reducing the time required to make predictions.

Introduction

Electrospray ionization (ESI) is an ionization technique commonly employed prior to mass spectrometric (MS) analysis. The high sensitivity and low ion fragmentation of the technique, along with its suitability for coupling to liquid chromatography (LC), have led to its widespread adoption for complex mixture analysis in a wide variety of fields, including food sciences, environmental sciences, metabolomics, and proteomics. However, the responses of compounds to ESI are difficult to predict and can vary by many orders of magnitude depending on the compound structure.1 This leads to issues for quantitative analysis where authentic standards are not available, as is common in environmental analysis.

Since the introduction of ESI, an effort has been made to quantify the effect of ion source parameters and analyte properties on mass spectra.2−5 This work was important for establishing the impact of matrix effects on the signal acquired from an ESI source but only focused on the effect of changes in the concentration for one analyte and not on variations between analytes.

One method to overcome the issues surrounding quantitative ESI analysis is to construct relative ionization efficiency (RIE) scales, first introduced by Leito et al.6 and investigate which chemical or structural features influence the instrument response.6−11 If the parameters that dictate RIE could be fully understood, then the chemical properties of an entirely novel analyte could be used to predict the response of that compound in MS. The majority of previous studies aiming to predict RIE use either measured or calculated physical properties. For example, Henriksen et al.12 found that the octanol–water partition coefficient (log P) was a much better predictor of instrument response than pKa, due to the requirement for compounds to reside in the surface layer of an ESI droplet to ionize. However, when a mixture of solvents was used (as often is for chromatographic separations), the trend with log P was significantly weaker. Chalcraft et al.13 and Hermans et al.14 corroborated the importance of log P, along with the significance of molecular volume, in their papers investigating ionization efficiencies for MS coupled to separation processes: capillary electrophoresis (CE) and LC. The aim of such papers has been to determine the chemical and physical factors that influence ionization efficiency. Since no single parameter is sufficient to characterize the complex processes occurring during ionization, multivariate analysis is more appropriate and is commonly used.12

In the previous studies presented, the measurement or calculation of physicochemical properties is essential to correlate the RIE value with the compound structure. In this study, we have bypassed this step by using a molecular fingerprint of each compound to build the RIE scale. Molecular fingerprints are a way of encoding the structure of a molecule. The most common type of fingerprint is a series of binary digits (bits) that represent the presence or absence of particular substructures or functionalities in the molecule. These can be rapidly created from the simplified molecular-input line-entry system (SMILES) string of a chemical structure. This method has previously been used to predict electron impact ionization (EI) mass spectra.15 In this study, we have combined the fingerprints with measured RIE values to construct a negative-mode RIE scale containing 51 carboxylic acids, a common functional group targeted in negative-mode ESI, with a wide range of structures and additional functionalities. Rather than using multiple linear regression, we have tested a series of machine learning regression models and compared their predictive power for different fingerprints and model combinations.

Experimental Section

Experimental Procedure

Mass spectra were obtained on an ultrahigh-resolution mass spectrometer (QExactive Orbitrap, Thermo Scientific). The heated ESI parameters used were the defaults for a 20 μL min–1 flow rate: a sheath gas flow rate of 19 (arb.), aux gas flow rate of 6 (arb.), a capillary temperature of 250 °C, and an aux gas heater temperature of 113 °C. Data were collected for the 57 compounds shown in the Supporting Information (Table S1). All samples were dissolved with 80:20 water/methanol as the solvent. Standard solutions of each compound with benzoic acid were made up at five concentrations between approximately 2 and 20 μmol dm–3. Spectra were collected for 3 min (344 data points), and the average intensity of the deprotonated molecular ion peak (and any significant fragmentation peaks) was obtained using the “XCalibur Qual Browser” software. Where fragmentation did occur, the sum of the intensities of the molecular ion peak and fragmentation peaks was taken for each concentration.

Calculation of RIE

RIE is calculated by taking the ratio of the response of the analyte to the response of a reference compound, in this case, benzoic acid, as shown in eq 1.7,16 RIE(B1, B2) is the RIE of compound 1 relative to compound 2, R1 and R2 are the responses of compounds 1 and 2, and c1 and c2 are the concentrations of compounds 1 and 2, respectively

graphic file with name ao0c00732_m001.jpg 1

However, in more recent work, RIE has been calculated by instead taking the ratio of the concentration–response curve gradients according to eq 2.17,18 In this work, RIE was calculated according to eq 2

graphic file with name ao0c00732_m002.jpg 2

Calibration curves were plotted for each compound from the intensity of the signal at five different concentrations. A straight line of best fit was obtained by linear regression, giving an equation in the form y = mx + c for the best-fit line of each compound. The regression lines were not forced through the origin. The ratio of gradients from concentration–response curves of the reference compound and the compound of interest was used to give RIE. This is demonstrated in the Supporting Information (Figure S1), which shows the procedure for calculating the RIE for azelaic acid, using benzoic acid as the reference compound.

Predicting Physical Properties

Our initial investigations into predicting RIE focused on multiple linear regression against several predicted physical properties (as listed in the Supporting Information Table S1). Predicted values were obtained from four sources. Boiling point and melting point were calculated using the U.S. Environmental Protection Agency’s EPI suite, a tool designed to predict a range of physical properties of compounds that has been reviewed by a panel of the EPA’s Independent Science Advisory Board.19 log P and pKa values were calculated using the ChemDraw Prime 16.0 software. Molecular volume and topological polar surface area (TPSA) were calculated using the Molinspiration website, an online tool used for predicting the bioactivity of compounds based on their structure.20 The UManSysProp tool was used to calculate the liquid “subcooled density” of the compounds at 298.15 K. Since most of the compounds analyzed are solid at room temperature, the “subcooled liquid density” refers to a prediction of that compound’s density if it were a liquid at room temperature.21 UManSysProp is a tool designed to aid in the prediction of the behavior of compound and aerosol properties.

Molecular Fingerprints and Machine Learning

A molecular fingerprint for each compound was generated using the UManSysProp package for python in tandem with the Python wrapper for the openbabel package (Pybel).21,22 The molecular structure of each compound was inputted to Pybel as a SMILES string. This parsing by Pybel allowed the UManSysProp package to generate a fingerprint for each compound. A selection of fingerprint types are available within UManSysProp including “composition”, “Stein and Brown”, “Nannoolal primary”, “Nannoolal secondary”, “Nannoolal interactions”, “evaporation”, “Girolami”, “Schroeder”, “Le Bas”, “UNIFAC”, and “AIOMFAC”. Full details of the fingerprints can be found in the UManSysProp source code as made available via a GitHub repository (https://github.com/loftytopping/UManSysProp_public.git). Each fingerprint is constructed by counting the occurrence of specific functionalities within the molecule and recording them into a python dictionary. The simplicity of these fingerprints means that they are easier to attain than the physical properties of each compound, particularly when using the Pybel and UManSysProp packages to generate the fingerprints directly from SMILES strings for each compound. However, the downside of using such fingerprints is that there is no distinction between structural isomers. For example, both 3,4-dihydroxybenzoic acid and 2,3-dihydroxybenzoic acid would have identical fingerprints.

The scikitlearn package was used for constructing and testing the predictive models based on the laboratory data.23 Scikitlearn allows for the simple use of a range of machine learning techniques within the python programming language. A selection of the model types available in the package were tested: linear regression, Bayesian ridge regression, decision tree regression, multilayer perceptron (MLP) regression, passive aggressive regression, random forest regression, stochastic gradient descent (SGD) regression, and Epsilon-support vector regression (SVR). Prior to constructing the models, the fingerprint values were scaled through the “Robust Scaler” that comes as part of the scikitlearn package. Scaling is often required for a good fit for many model types and can decrease the time required for training.24 A range of scalers were trialed, and while the scalers made little impact on the model scores, the Robust Scaler produced a more standard distribution of fingerprint parameters and so was chosen for use. To determine the best parameters for each model, validation curves were constructed where the model score was calculated while varying each parameter. The parameter value that gave the best R2 score was then used.

Model Validation

Once a machine learning model is built, it must be tested by providing the model with a test set of data. In this case, the model is tested by predicting the RIE for compounds for which the RIE is known and comparing the predicted RIE to the measured value. To prevent overfitting of models, they should be tested on a different set of data than the model training set. Often, this validation will be done by splitting the data into training data (used to build the model) and test data (used to test the model after it is built). However, this approach becomes untenable when only a small amount of data is available, as the training set becomes too small to build a reliable model.25 For this reason, the models built in this work all used leave-one-out cross validation (LOOCV). This method aims to test the predictive capability of a model built using all of the available data. For n compounds, the model is run n times. Each time the model is run, a different compound is selected as the “test set”, and the model is trained on the remaining n – 1 compounds.26 A list of predicted values for each compound is then compiled, where all of the other compounds were used to train the model each time. An overall score for the model can then be determined by calculating the R2 using eq 3 and the root-mean-square error (RMSE) using eq 4. It is these R2 and RMSE values, obtained from LOOCV with the model applied to each molecule in turn, that are used to assess the quality of each model-fingerprint combination. These metrics are used to evaluate the quality of an RIE prediction from a model trained on all of the available data previously used in LOOCV, for an entirely novel compound.

Scikitlearn calculates R2 using eq 3, where yi is the RIE of compound i, ŷi is the predicted RIE based on the model, and y̅i is the average RIE. From this formula, a negative R2 value is possible and corresponds to a model that predicts worse than simply taking an average RIE value and applying that as the “predicted RIE” each time

graphic file with name ao0c00732_m003.jpg 3

Many of the previous investigations into predicting RIE have relied on R2 as an indicator of model quality. However, it has been noted that R2 alone is not sufficient for assessing the quality of predictive models, particularly those validated with LOOCV.27,28 As a result, the root-mean-square error (RMSE) values have also been quoted for models produced in this investigation. RMSE was obtained by taking the square root of the mean-squared error (MSE) metric output from the Scikitlearn package

graphic file with name ao0c00732_m004.jpg 4

The code used to test all of the available models, along with the code utilizing just Bayesian ridge regression, has been made available via a GitHub repository (https://github.com/AlfredMayhew/RIE-Prediction).

Results and Discussion

The measured log RIE values for 51 compounds are illustrated in Figure 1 (and the values are given in the Supporting Information Table S1). Data for the remaining six compounds were not used due to poor linearity in the calibration curves. The measured log RIE values range between −2.59 and 1.46, covering 4 orders of magnitude.

Figure 1.

Figure 1

Open in a new tab

Scale of measured log relative ionization efficiencies (log RIEs), relative to benzoic acid. A table of log RIEs can be found in the Supporting Information, Table S1.

To initially compare the results with previous RIE prediction scales, we compared subsets of compounds to the calculated physical properties listed in the Experimental Section. There are clear correlations between the RIE of linear dicarboxylic acids and molecular mass, log P, and pKa (R2 of 0.73, 0.68, and 0.90, respectively), as shown in the Supporting Information (Figures S2–S4). This result is in agreement with Henriksen et al. who noted that RIE increased with increasing log P and that for “some compounds (primarily carboxylic acids) [response] decreases at lower pKa values”.12 A correlation was also observed between the measured RIE in para-substituted benzoic acids and the electron-withdrawing character of substituents, as defined by the Hammett parameter (σp) (see the Supporting Information Figure S5).29 These results show that the measured RIE values are consistent with the previous work and so are a useful data set to develop the molecular fingerprint method. However, no single parameter was suitable for the prediction of RIEs when structures become more complex and multiple functionalities are included.

Multiple linear regression attempts to overcome the complexity by including multiple physical properties. However, when we performed multiple linear regression against the seven predicted physical properties (boiling point, melting point, log P, pKa, molecular volume, TPSA, and subcooled density), the R2 value for correlation between the measured and predicted RIEs was only 0.38. The magnitude of the coefficients for each parameter in the linear regression (given in the Supporting Information Table S2) can give insight into the relative importance of each physical property on ionization, though the relatively low R2 of predictions obtained means that caution should be applied in such investigations. A larger magnitude means that a parameter is given a larger weighting in the linear regression model and so potentially has more of an impact on RIE. log P was found to be a major predictive factor (confirming findings previously mentioned), along with subcooled density. It does not seem intuitive that the density should have such a large influence on the RIE, but this significance may be due to a further property that dictates the liquid density. For example, the density of a liquid is influenced by intermolecular interactions, and such interactions will also influence ionization. Previous investigations into the density as a predictor of RIE have only been performed in the recent literature insofar as density is being used to calculate surface tension14 and the use of solid density as a parameter.10,30 Alymatiri et al.30 noted the effect of solid density on ionization but found that increased density resulted in increased RIE. The negative sign of the coefficient for subcooled density shown in Table S2 would indicate that the reverse is true in our study.

The low R2 obtained by multiple linear regression likely resulted from the wide range of structures and functionalities present in our set of compounds, and so a fingerprint machine learning approach was investigated.

Machine Learning Models

Initially, the models were run on the entire set of compounds for which data was available. However, it was found that RIE was predicted very poorly for compounds with low RIE and that the predictions of the model as a whole were significantly improved by removing the data for compounds with an RIE < 0.1 (i.e., 3,3-dimethylacrylic acid, p-hydroxybenzoic acid, sorbic acid, PABA). The removal of these compounds means that the developed model is only applicable for predicting the response of compounds with an RIE > 0.1 (log RIE > −1).

While investigating the predictive capability of different model and fingerprint combinations, it was found that using log RIE as an input parameter resulted in far better model scores than simply using RIE. This is due to log RIE showing a more standard distribution than RIE, where the distribution is skewed toward low values. The best R2 score obtained using the RIE values was 0.39 (from the aiomfac fingerprint with an MLP model). This increased to 0.62 (using the aiomfac fingerprint with a Bayesian ridge regression model) by simply converting RIE values to log RIE prior to model training. The same improvement does not come about by the conversion of RIE values to log RIE after model training, indicating that the closer predictions are a result of improvements in the model.

Table 1 shows the calculated R2 scores for a selection of the model-fingerprint combinations. The RMSE values for the same selection of model-fingerprint combinations are given in the Supplementary Information (Table S3).

Table 1. R2 Scores for a Selection of Fingerprint-Model Combinations for the log RIE Predictionsa.

  composition Nannoolal primary Nannoolal secondary Le Bas UNIFAC AIOMFAC
linear regression –0.046 –2.8 × 1022 –0.19 –0.068 –3.2 × 1023 –8.3 × 1022
Bayesian ridge –0.090 0.42 –0.078 –0.026 0.60 0.62
decision tree –0.21 0.32 –0.37 0.44 0.30 0.27
MLP –0.61 –0.38 –0.033 –0.37 –0.080 –0.30
passive aggressive –3.5 0.16 –1.3 –1.6 0.090 –0.18
random forest 0.37 0.12 –0.073 0.43 0.069 0.16
SGD –0.066 –0.0025 –0.085 –0.16 0.030 0.038
SVR –43 0.078 –0.56 –92 –0.51 –0.41
Open in a new tab
a

Note that R2 is calculated using eq 3; hence, the R2 can be negative, indicating a prediction worse than using the average log RIE value.

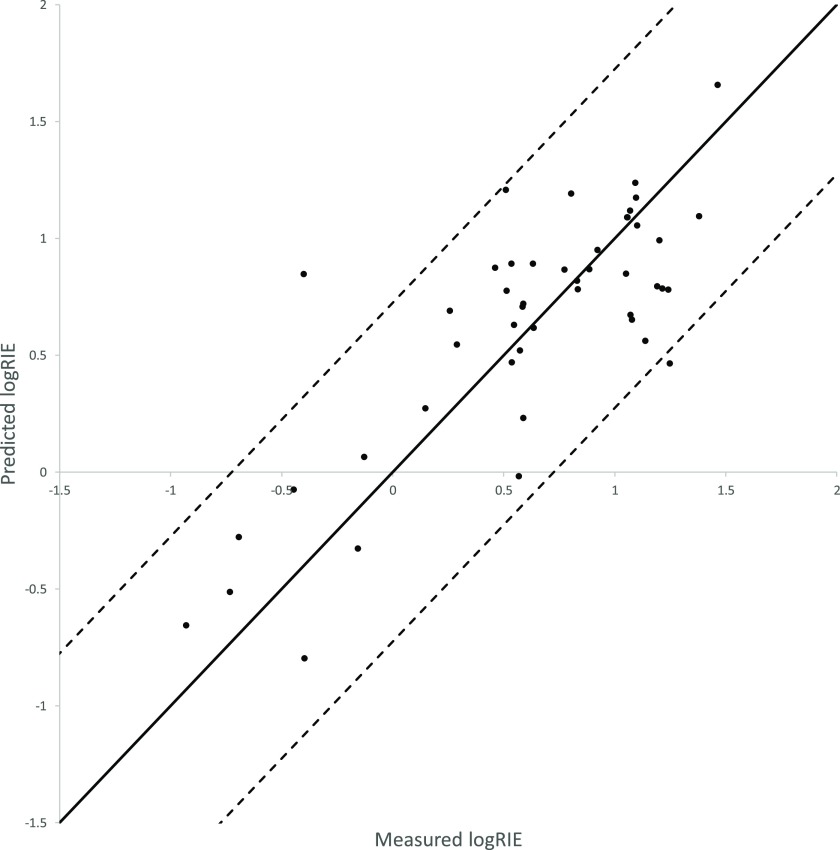
Bayesian ridge regression models combined with the aiomfac (R2 = 0.62, RMSE = 0.362) or UNIFAC (R2 = 0.60, RMSE = 0.375) fingerprints gave the best scores. The AIOMFAC and UNIFAC fingerprints are similar, with AIOMFAC being based on UNIFAC, but with more parameters. The best predictive model results are compared to the measured RIE values in Figure 2.

Figure 2.

Figure 2

Open in a new tab

Predictions produced by Bayesian ridge regression with compounds represented as aiomfac fingerprints. The solid black line = 1:1 (perfect predictions would lie along this line). The dotted black lines = 2 × RMSE from the 1:1 line.

One advantage of the Bayesian ridge regression model is the ability to obtain the coefficients used by the model for each parameter. This gives an idea as to the relative importance the model places on each functionality. From these coefficients (given in the Supporting Information Table S4), it is revealed that the Bayesian ridge regression model places high importance on aromatic groups, double bonds, and oxygenated groups. Any functionalities not represented in the test set of compounds are disregarded by the model, with a coefficient of 0. Interestingly, the “carboxylic acid” functionality gave a coefficient of 0, despite mono-, di-, and triacids all being present in the set of 51 compounds. This poses an issue for basing predictions off this training set as the model has no recognition of the need for acidic hydrogen for ionization to occur because all compounds in the training set have this functionality. This problem would likely be solved with the inclusion of compounds with other types of acidic hydrogen atoms or those with no acidic hydrogen that do not ionize in negative-mode ESI.

Some fingerprint types consistently produce poor models. For example, the Nannoolal secondary fingerprint fails to produce any model with a score greater than 0. This indicates that the fingerprint does a poor job at representing the compounds and fails to pick out the relevant structural properties that dictate RIE, which were picked out by other fingerprint types. Alternatively, some model types, such as MLP, do not produce good scores regardless of the fingerprint used.

Comparison to Previous Work

The prediction of log RIE values obtained in this work is of comparable quality to other papers aiming to predict RIE. For example, Oss et al. obtained an R2 of 0.67 for analysis of their validation set by multiple linear regression.7 Kruve and Kaupmees obtained an R2 of 0.77 for a group of 61 compounds in different solvents.31 Liigand et al. obtained R2 values of between 0.55 and 0.81 for predictions in different biological matrices; the reported RMSE values of between 0.36 and 1.31 also compare favorably to our obtained RMSE.32 All of these studies used multiple linear regression to produce predictions, whereas here we have shown that predictions of similar quality can be obtained without the need to measure or predict the physical properties of the compounds.

As a further test of the technique, the measured RIE values presented by Kruve et al.18 were used as inputs to the different models, representing the molecules with each fingerprint type. This data was chosen as it was also focused on negative-mode ESI and determined RIE for a higher number of compounds (62 compounds). To make their predictions, Kruve et al. sorted compounds into separate “bins” based on their functionality, performed multiple linear regression on each bin, and then combined the predictions to obtain an R2 of 0.83 between measured and predicted log RIEs. By using a Bayesian ridge regression model and representing compounds as UNIFAC fingerprints, we were able to predict log RIE without the need for the binning of compounds (which would become untenable if compounds with multiple functionalities were included in the data set). The measured log RIE and our predicted log RIE showed a good correlation, with an R2 = 0.68 (RMSE = 0.648). The data from Kruve et al. spans a much wider range of measured log RIE values (−2.46 to 3.49), indicating that the model is able to provide reasonable predictions over a large range of log RIE values. However, Kruve et al. also make use of compounds with a more limited range of functionalities, perhaps accounting for the quality of predictions obtained.

Conclusions

Through the use of molecular fingerprints in tandem with machine learning techniques, predictions comparable to those made by other studies can be made on a set of carboxylic acids with a diverse range of functionalities. The best predictions were made by encoding the compounds as aiomfac fingerprints and performing Bayesian Ridge Regression. The technique outlined here provides a route to constructing predictive models for eventual use in quantitative ESI analysis.

Further work is needed to develop more useful fingerprints for ESI prediction, taking into account additional molecular properties, and allowing isomers to be differentiated. Additionally, the predictive models developed in this work have only been applied to carboxylic acids, so they would likely not predict RIEs well for species not containing this functionality.

Work into the transferability of RIE scales between instrument setups and solvent systems offers a promising insight into potential practical uses of RIE scales, with laboratories calibrating their ESI–MS setups with a series of readily available compounds to allow them to apply RIE scales to their own research.16,31 Further work is needed to build on the method developed in this work, including analyzing a larger data set, incorporating a chromatographic separation step, investigating a wider range of functionalities, and applying the technique to positive-mode ESI.

Acknowledgments

A.W.M. acknowledges an NERC PANORAMA Ph.D. studentships and the University of York UG student bursary. The work was funded by the Natural Environment Research Council (NE/S010467/1), and the Orbitrap-MS was funded by a Natural Environment Research Council strategic capital grant (CC090). The authors acknowledge the help of Kelly Pereira, Daniel Bryant, and Martyn Ward for technical help and discussions.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsomega.0c00732.

  • List of the compounds analyzed, their physical properties, and measured and predicted RIEs (Table S1); example procedure for calculating RIE (Figure S1); plots of molecular properties vs RIE (Figures S2–S5); linear regression coefficients (Table S2); RMSE values for a selection of model-fingerprint combinations (Table S3); Bayesian ridge regression coefficients (Table S4) (PDF)

Author Contributions

Practical work was carried out by A.W.M. and supervised by J.F.H. and D.O.T. The manuscript was primarily written by A.W.M., with contributions from J.F.H. and D.O.T.

The authors declare no competing financial interest.

Supplementary Material

ao0c00732_si_001.pdf (582.3KB, pdf)

References

  1. Constantopoulos T. L.; Jackson G. S.; Enke C. G. Effects of salt concentration on analyte response using electrospray ionization mass spectrometry. J. Am. Soc. Mass Spectrom. 1999, 10, 625–634. 10.1016/S1044-0305(99)00031-8. [DOI] [PubMed] [Google Scholar]
  2. Tang L.; Kebarle P. Effect of the Conductivity of the Electrosprayed Solution on the Electrospray Current. Factors Determining Analyte Sensitivity in Electrospray Mass Spectrometry. Anal. Chem. 1991, 63, 2709–2715. 10.1021/ac00023a009. [DOI] [Google Scholar]
  3. Raffaelli A.; Bruins A. P. Factors affecting the ionization efficiency of quaternary ammonium compounds in electrospray/ionspray mass spectrometry. Rapid Commun. Mass Spectrom. 1991, 5, 269–275. 10.1002/rcm.1290050605. [DOI] [Google Scholar]
  4. Cech N. B.; Enke C. G. Relating electrospray ionization response to nonpolar character of small peptides. Anal. Chem. 2000, 72, 2717–2723. 10.1021/ac9914869. [DOI] [PubMed] [Google Scholar]
  5. Enke C. G. A Predictive Model for Matrix and Analyte Effects in Electrospray Ionization of Singly-Charged Ionic Analytes. Anal. Chem. 1997, 69, 4885–4893. 10.1021/ac970095w. [DOI] [PubMed] [Google Scholar]
  6. Leito I.; Herodes K.; Huopolainen M.; Virro K.; Künnapas A.; Kruve A.; Tanner R. Towards the Electrospray Ionization Mass Spectrometry Ionization Efficiency Scale of Organic Compounds. Rapid Commun. Mass Spectrom. 2008, 22, 379–384. 10.1002/rcm.3371. [DOI] [PubMed] [Google Scholar]
  7. Oss M.; Kruve A.; Herodes K.; Leito I. Electrospray ionization efficiency scale of organic compound. Anal. Chem. 2010, 82, 2865–2872. 10.1021/ac902856t. [DOI] [PubMed] [Google Scholar]
  8. Kiontke A.; Oliveira-Birkmeier A.; Opitz A.; Birkemeyer C. Electrospray ionization efficiency is dependent on different molecular descriptors with respect to solvent pH and instrumental configuration. PLoS One 2016, 11, e0167502 10.1371/journal.pone.0167502. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Wu L.; Wu Y.; Shen H.; Gong P.; Cao L.; Wang G.; Hao H. Quantitative structure-ion intensity relationship strategy to the prediction of absolute levels without authentic standards. Anal. Chim. Acta 2013, 794, 67–75. 10.1016/j.aca.2013.07.034. [DOI] [PubMed] [Google Scholar]
  10. Mandra V. J.; Kouskoura M. G.; Markopoulou C. K. Using the partial least squares method to model the electrospray ionization response produced by small pharmaceutical molecules in positive mode. Rapid Commun. Mass Spectrom. 2015, 29, 1661–1675. 10.1002/rcm.7263. [DOI] [PubMed] [Google Scholar]
  11. Ehrmann B. M.; Henriksen T.; Cech N. B. Relative Importance of Basicity in the Gas Phase and in Solution for Determining Selectivity in Electrospray Ionization Mass Spectrometry. J. Am. Soc. Mass Spectrom. 2008, 19, 719–728. 10.1016/j.jasms.2008.01.003. [DOI] [PubMed] [Google Scholar]
  12. Henriksen T.; Juhler R. K.; Svensmark B.; Cech N. B. The relative influences of acidity and polarity on responsiveness of small organic molecules to analysis with negative ion electrospray ionization mass spectrometry (ESI-MS). J. Am. Soc. Mass Spectrom. 2005, 16, 446–455. 10.1016/j.jasms.2004.11.021. [DOI] [PubMed] [Google Scholar]
  13. Chalcraft K. R.; Lee R.; Mills C.; Britz-McKibbin P. Virtual Quantifcation of Metabolites by Capillary Electrophoresis-Electrospray Ionization-Mass Spectrometry: Predicting Ionization Ef ciency Without Chemical Standards. Anal. Chem. 2009, 81, 2506–2515. 10.1021/ac802272u. [DOI] [PubMed] [Google Scholar]
  14. Hermans J.; Ongay S.; Markov V.; Bischoff R. Physicochemical Parameters Affecting the Electrospray Ionization Efficiency of Amino Acids after Acylation. Anal. Chem. 2017, 89, 9159–9166. 10.1021/acs.analchem.7b01899. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Topping D. O.; Allan J.; Rami Alfarra M.; Aumont B. STRAPS v1.0: Evaluating a methodology for predicting electron impact ionisation mass spectra for the aerosol mass spectrometer. Geosci. Model Dev. 2017, 10, 2365–2377. 10.5194/gmd-10-2365-2017. [DOI] [Google Scholar]
  16. Liigand J.; Kruve A.; Liigand P.; Laaniste A.; Girod M.; Antoine R.; Leito I. Transferability of the Electrospray Ionization Efficiency Scale between Different Instruments. J. Am. Soc. Mass Spectrom. 2015, 26, 1923–1930. 10.1007/s13361-015-1219-6. [DOI] [PubMed] [Google Scholar]
  17. Liigand P.; Kaupmees K.; Kruve A. Influence of the amino acid composition on the ionization efficiencies of small peptides. J. Mass Spectrom. 2019, 54, 481–487. 10.1002/jms.4348. [DOI] [PubMed] [Google Scholar]
  18. Kruve A.; Kaupmees K.; Liigand J.; Leito I. Negative electrospray ionization via deprotonation: Predicting the ionization efficiency. Anal. Chem. 2014, 86, 4822–4830. 10.1021/ac404066v. [DOI] [PubMed] [Google Scholar]
  19. EPA U.Estimation Programs Interface Suite for Microsoft Windows; United States Environmental Protection Agency: Washington, DC, USA, 2012.
  20. Molinspiration. https://www.molinspiration.com/cgi-bin/properties.
  21. Topping D.; Barley M.; Bane M. K.; Higham N.; Aumont B.; Dingle N.; McFiggans G. UManSysProp v1.0: an online and open-source facility for molecular property prediction and atmospheric aerosol calculations. Geosci. Model Dev. 2016, 9, 899–914. 10.5194/gmd-9-899-2016. [DOI] [Google Scholar]
  22. O’Boyle N. M.; Morley C.; Hutchison G. R. Pybel: A Python wrapper for the OpenBabel cheminformatics toolkit. Chem. Cent. J. 2008, 2, 5 10.1186/1752-153x-2-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Pedregosa F.; Varoquaux G.; Gramfort A.; Michel V.; Thirion B.; Grisel O.; Blondel M.; Prettenhofer P.; Weiss R.; Dubourg V.; Vanderplas J.; Passos A.; Cournapeau D.; Brucher M.; Perrot M.; Duchesnay É. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
  24. Juszczak P.; Tax D. M. J.; Duin R. P. W. Feature scaling in support vector data description. Proc. ASCI 2002, 95–102. [Google Scholar]
  25. Cawley G. C.; Talbot N. L. C. Gene selection in cancer classification using sparse logistic regression with Bayesian regularization. Bioinformatics 2006, 22, 2348–2355. 10.1093/bioinformatics/btl386. [DOI] [PubMed] [Google Scholar]
  26. Good P. I.Resampling Methods: A Practical Guide to Data Analysis, 3rd ed.; Birkhäuser, 2005. [Google Scholar]
  27. Alexander D. L. J.; Tropsha A.; Winkler D. A. Beware of R(2): Simple, Unambiguous Assessment of the Prediction Accuracy of QSAR and QSPR Models. J. Chem. Inf. Model. 2015, 55, 1316–22. 10.1021/acs.jcim.5b00206. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Golbraikh A.; Tropsha A. Beware of q(2). J. Mol. Graphics Modell. 2002, 20, 269–276. 10.1016/S1093-3263(01)00123-1. [DOI] [PubMed] [Google Scholar]
  29. Hansch C.; Leo A.; Taft R. W. A Survey of Hammett Substituent Constants and Resonance and Field Parameters. Chem. Rev. 1991, 91, 165–195. 10.1021/cr00002a004. [DOI] [Google Scholar]
  30. Alymatiri C. M.; Kouskoura M. G.; Markopoulou C. K. Decoding the signal response of steroids in electrospray ionization mode (ESI-MS). Anal. Methods 2015, 7, 10433–10444. 10.1039/C5AY02839F. [DOI] [Google Scholar]
  31. Kruve A.; Kaupmees K. Predicting ESI/MS Signal Change for Anions in Different Solvents. Anal. Chem. 2017, 89, 5079–5086. 10.1021/acs.analchem.7b00595. [DOI] [PubMed] [Google Scholar]
  32. Liigand P.; Liigand J.; Cuyckens F.; Vreeken R. J.; Kruve A. Ionisation efficiencies can be predicted in complicated biologicalmatrices: A proof of concept. Anal. Chim. Acta 2018, 1032, 68–74. 10.1016/j.aca.2018.05.072. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ao0c00732_si_001.pdf (582.3KB, pdf)

Articles from ACS Omega are provided here courtesy of American Chemical Society

RESOURCES