Planning High-Quality Motions for Concentric Tube Robots in Point Clouds via Parallel Sampling and Optimization

Abstract

We present a method that plans motions for a concentric tube robot to automatically reach surgical targets inside the body while avoiding obstacles, where the patient’s anatomy is represented by point clouds. Point clouds can be generated intra-operatively via endoscopic instruments, enabling the system to update obstacle representations over time as the patient anatomy changes during surgery. Our new motion planning method uses a combination of sampling-based motion planning methods and local optimization to efficiently handle point cloud data and quickly compute high quality plans. The local optimization step uses an interior point optimization method, ensuring that the computed plan is feasible and avoids obstacles at every iteration. This enables the motion planner to run in an anytime fashion, i.e., the method can be stopped at any time and the best solution found up until that point is returned. We demonstrate the method’s efficacy in three anatomical scenarios, including two generated from endoscopic videos of real patient anatomy.

I. Introduction

Motion planning can enable surgical robots such as concentric tube robots [1] to automatically reach a desired surgical target while avoiding anatomical obstacles. Composed of nested, pre-curved tubes, concentric tube robots can curve around anatomical obstacles to reach targets in highly constrained environments such as the skull base, the lungs, and the heart [2], Enabling the robot to safely avoid anatomical obstacles (such as blood vessels, critical nerves, sensitive organs, and bones) requires a fast and effective motion planner, as well as an accurate model of the patient anatomy. In previous work, such an anatomical model is typically generated from the segmentation of preoperative 3D volumetric imaging, such as Computed Tomography (CT) [3], [4], [5], However, for surgical procedures that modify the anatomy, anatomical models created from preoperative images may quickly become out-of-date and inaccurate, significantly hindering safe motion planning. By contrast, a variety of intra-operative endoscopic sensors can be used to quickly produce point cloud representations of the anatomy. In this work, we introduce a new motion planning method, Parallel Sampling and Interior point optimization Motion Planning (PSIMP). PSIMP quickly produces high-quality motion plans for concentric tube robots operating in point cloud anatomical representations.

Point clouds that represent patient anatomy can be generated during minimally-invasive surgery in a variety of ways, including via small laser scanners [6], structured light sensors [7], and generated directly from endoscopic video (see Fig. 1) using computer vision techniques [8], [9], [10], In contrast to CT imaging, such sensors and techniques can be repeatedly used intra-operatively, acquiring point clouds in seconds rather than minutes, and do not rely on ionizing radiation (i.e., x-rays), which may be harmful to patients and clinical staff when used repeatedly. Such techniques also have advantages over fluoro imaging due to the reduced radiation exposure and are much cheaper than MRI. As the anatomy changes, new point clouds can be generated and used by the motion planner. In this work, we evaluate our method using point clouds generated via endoscopic video using a technique called “structure from motion” [11], [12], but the method can be used directly with point clouds from any source.

Fig. 1.

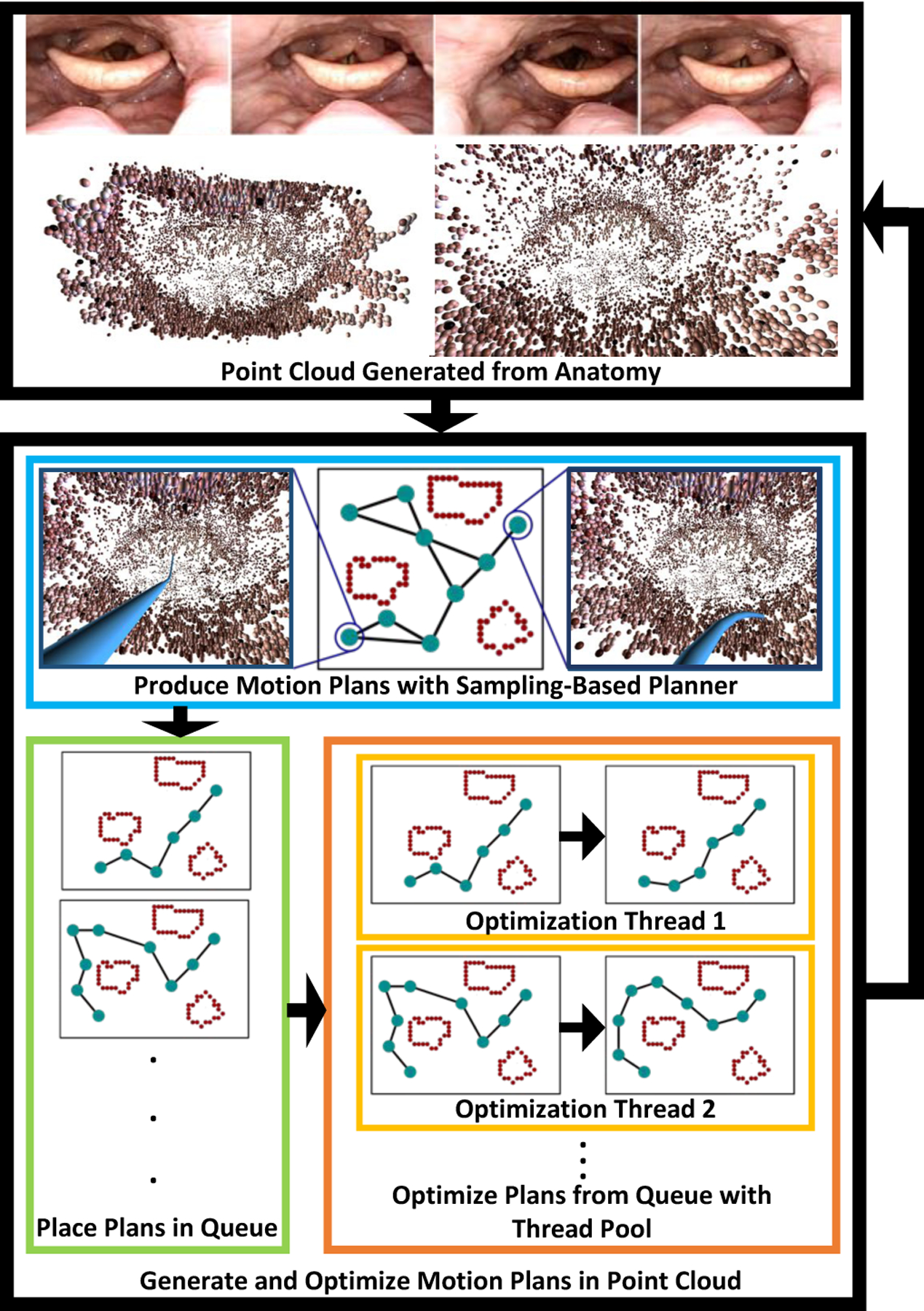
Our method, PSIMP, takes as input a point cloud representing patient anatomy (top). PSIMP generates and optimizes motion plans for the robot to move safely through the point cloud (bottom). A sampling-based motion planner runs constantly in its own thread (blue box), generating motion plans over time—represented as collision-free sequences of configurations (2D cartoon representations of the plans are included here for illustrative purposes). As the motion plans are generated they are placed in a queue (green box). A thread pool (orange box) then takes each of the motion plans, and optimization threads (yellow boxes) perform interior point local optimization on the plans, improving their quality according to a cost based on clearance from obstacles. If the anatomy has not changed significantly, multiple motion planning queries can be solved for the initial point cloud, in real time, allowing the physician to move the robot through the anatomy safely. If the anatomy changes significantly (e.g., due to the surgical procedure), a new point cloud can be generated to be used by the motion planner in subsequent queries.

To enable high-quality, fast motion planning for concentric tube robots when obstacles are represented using point clouds, PSIMP combines sampling-based motion planning with local optimization (see Fig. 1). This combines the benefits of sampling-based motion planning, such as the exploration of multiple homotopic classes (see Fig. 2), with the benefits of local optimization, namely the ability to produce high-quality plans very quickly. We introduce a parallel, multi-threaded framework, that combines a sampling-based motion planning thread with a pool of local optimization threads. As the sampling-based motion planner generates motion plans, those solutions are placed in a queue of motion plans that are then locally optimized by a pool of threads that are running the local optimization method in parallel. This allows the sampling-based motion planner to run uninterrupted, ensuring that it continues exploring globally, while the local optimizers are iteratively improving the quality of the motion plans more quickly than the sampling-based motion planner is capable of doing on its own.

Fig. 2.

A top down view of an example scenario wherein the robot is tasked with passing between vertical columns represented as point clouds. The sampling-based motion planning phase of the planner allows for the discovery of different homotopic classes. (Left) The planner may initially find a solution to the goal point (green) for the robot (blue) that passes very close to the point cloud (red). (Right) The planner may later in the planning process find a better homotopic class in which the robot is able to reach the goal in a safer way, further from points in the point cloud.

PSIMP plans motions at rates suitable for interactive use, returning the first valid motion plan in a fraction of a second on average, and rapidly improving upon that initial solution in fractions more. Our local optimization uses interior point optimization, a class of optimization techniques that guarantee intermediate solutions satisfy constraints (e.g., obstacle avoidance and joint limits) during optimization [13]. This property enables the method to run in an anytime fashion, i.e., the method can be stopped at any time and the best solution found up until that point will be returned. Our method leverages a cost function, similar to that in [14], based on the robot’s clearance from the point cloud that encourages the avoidance of anatomical obstacles and helps to produce motions robust to incomplete obstacle knowledge.

We demonstrate the efficacy of PSIMP in three scenarios in which obstacles are represented via point clouds: an upper airway environment (near the epiglottis), a colon environment, and a skull base environment. The upper airway and colon environments are generated from real endoscopic video of real patients, while the skull base environment is generated from synthetic data. We show that combining local optimization with sampling-based motion planning outperforms sampling-based motion planning by itself in each of the anatomical settings. We also demonstrate the ability of PSIMP to react to a change in the point cloud when the anatomy is modified during a surgical procedure, which is not feasible when obstacle representations are generated solely from pre-operative imaging such as CT scans.

II. Related Work

Point clouds have been used in medical procedures in a variety of ways. Point clouds from stereoscopic cameras have been used for virtual fixtures in haptic interfaces [15] and for the registration of a digital overlay for teleoperation [16]. Soft tissue deformation has been tracked using 3D plenoptic imaging during autonomous suturing [17]. Point clouds generated by structure from motion in nasal endoscopy have been used for registering endoscopic images to CT data and overlaying areas of interests on the endoscope images [8], [10]. We propose the use of point clouds as the anatomical representation during motion planning, enabling the obstacle representation to be regularly updated during a surgical procedure and hence enabling the motion planner to adapt to changes in the anatomy during surgery.

Concentric tube robots have been proposed for a variety of surgical tasks [2]. The control of concentric tube robots has primarily considered computing controls based on desired tip movements. This includes methods that compute controls based on the robot’s Jacobian [18], [19] and a Fourier series based approximation of the robot’s kinematics [20].

Motion planning can enable robots to automatically move in an environment while avoiding obstacles. A popular motion planning paradigm is sampling-based motion planning, which includes methods such as Probabilistic Roadmaps (PRM) [21] and Rapidly-exploring Random Trees (RRT) [22], in which a collision-free graph or tree data structure is incrementally constructed. Many such algorithms provide a property called probabilistic completeness, i.e., the probability the algorithm finds a valid motion plan, if one exists, approaches 1 as the number of samples approaches infinity. Extensions to these methods have the stronger guarantee of asymptotic optimality, i.e., the method will converge to a globally optimal motion plan under some objective function as the number of samples approaches infinity. Such methods include RRT*, PRM* [23], BIT* [24], and FMT* [25].

Optimization-based motion planning methods work by locally optimizing plans numerically in a high dimensional trajectory space. Such methods include CHOMP [26], ITOMP [27], and Traj-Opt [28]. Recently, we presented ISIMP, a method that combines local optimization with sampling-based motion planning in point clouds for serial link manipulator arms [29]. Our motion planner in this work, PSIMP, differs from these prior methods in that we optimize a different metric. These prior methods optimize either for path smoothness [26], [27], [28] or for path length [29]. By contrast, here we introduce an anatomical clearance cost function that encourages motions that avoid anatomical obstacles by larger distances, increasing plan safety. This also allows us to simplify the constraint set by leveraging the new cost function for obstacle avoidance. Additionally, as in [29], PSIMP employs both sampling-based motion planning and interior point local optimization, but rather than interleaving the two, we utilize parallelism to perform both optimization and sampling simultaneously.

When computing motions for concentric tube robots that avoid obstacles, a few approaches have been studied. This includes simplifying the kinematics for fast computation [30], [31]. Sampling-based motion planning for concentric tube robots has been studied for skull base surgery. However, until recently, the previous methods either provided planning rates that were much slower than required for an intra-operative setting [32], or required preoperative imaging and extensive precomputation of a roadmap over the course of many hours prior to motion planning [4], [33]. The desire for a reactive anatomical representation precludes the use of methods that require extensive precomputation. Recently, a template-based, fast kinematic model was developed for concentric tube robots, based on an unloaded torsionally compliant kinematics model, in conjunction with a PRM-style motion planner which achieves much faster planning rates [34]. PSIMP uses this new kinematic model to enable fast shape computations during motion planning. PSIMP efficiently solves motion planning problems in environments represented by point clouds by leveraging local optimization to improve upon PRM-style motion planning alone.

III. Problem Definition

We consider a point cloud P, where P = {p₁, p₂,…, p_j}, $p_k\in {ℝ}^3$ for k ∈ {1,…,j}, is an unordered set of j 3D points in the global coordinate frame lying on the surface of patient anatomy. In the anatomical environment represented by this point cloud, we consider a concentric tube robot. The concentric tube robot consists of N telescoping pre-curved tubes numbered in order of increasing cross-sectional radius, such that T₁ is the innermost tube, and T_N is the outermost tube. Each tube consists of a straight segment followed by a pre-curved segment reaching to its tip. We define the location of the robot in the global coordinate frame, i.e., the position from which the tubes extend, as ${\text{x}}_{\text{start}}\in {ℝ}^3$ with orientation v_start ∈ SO(3). Each tube can be inserted linearly starting at x_start and rotated axially at its base. We define the length of insertion for tube k as ${\beta }_k\in ℝ$ and the rotational value as θ_k ∈ [−π, π). A configuration for the robot then becomes q = (θ_i, β_i : i = 1,…,N) with configuration space $\mathcal{Q}={\left(S^1\right)}^N\times {ℝ}^N$.

Given a configuration $\mathbf{q}\in \mathcal{Q}$, we define the robot’s backbone shape function as $\text{backbone}\left(q,s\right):{\left(S^1\right)}^N\times {ℝ}^N\times ℝ\mapsto {ℝ}^3$. This function describes the centerline of the robot as a space curve parameterized by s ∈ [0,1] where backbone(q, 0) = x_start and backbone(q, 1) maps to the 3D position of the tip of the robot in the global frame for configuration q. This function, combined with knowledge of the cross-sectional radii of the tubes, allows us to estimate the shape of the robot shape(q) as the volume in space occupied by the robot in configuration q. To compute backbone we use the mechanics-based model developed by Leibrandt et al. [34].

We define a path as a continuous function $\sigma :\left[0,1\right]\to \mathcal{Q}$. The motion planning problem then becomes one of finding a path such that σ(0) = q_start and backbone(σ(1), 1) = x_goal, the 3D location of the goal point in the global frame. Intuitively, this states that σ(0) is the starting configuration of the robot and σ(1) is a configuration for which the tip of the robot is at the goal point. We then define a collision-free path as a path such that p ∉ shape(σ(s)), ∀p ∈ P, ∀s ∈ [0, 1], i.e., one such that the shape of the robot along the entire path does not contain any points in P. Conceptually, this defines each point in the point cloud as an obstacle, precluding the need for a more complex geometric representation of the anatomy. Defining the kinematic constraints of the robot, such as joint limits, as the general inequality g(σ) ≥ 0, we can then combine these to define a valid motion plan as one such that the following constraints are satisfied:

$$\begin{array}{l}p\notin \text{shape}\left(\sigma \left(s\right)\right),\forall p\in P,\forall s\in \left[0,1\right]\\ g\left(\sigma \right)\ge 0\\ \sigma \left(0\right)=q_{\text{start}}\\ \text{backbone}\left(\sigma \left(1\right),1\right)=x_{\text{goal}}.\end{array}$$ (1)

To enable the computation of high quality motion plans, we introduce the notion of cost. We choose a cost function that facilitates safe motion planning by favoring plans that move the robot’s geometry far from the patient’s anatomy. This has the benefit of increasing the safety of the plans by making them robust to actuation noise and to the possibility of small holes and gaps in the point cloud. Specifically, we define a function clear(q) = min_p∈P sd(shape(q), p), where sd(shape(q), p) is the signed distance between the shape of the robot at configuration q and point cloud point p. The function sd is defined as the positive distance if p is external to the robot’s geometry, and negative penetration depth if p is internal to the robot’s geometry. clear(q) is the minimum such value over all the points in the point cloud, for a specific configuration. We define the cost of a configuration q as:

$$\text{cost}\left(q\right)\{\begin{array}{rr}\hfill \frac{1}{\text{clear}\left(q\right)},& \hfill \text{clear}\left(q\right)>0\\ \hfill \infty ,& \hfill \text{clear}\left(q\right)\le 0.\end{array}$$ (2)

The cost of a path σ then becomes

$$\text{Cost}\left(\sigma \right)={\int }_0^1\text{cost}\left(\sigma \left(s\right)\right)ds.$$ (3)

We next define a motion planning query as the tuple (P, q_start, x_goal, t_max), where t_max is the maximum time allotted for the motion planner to solve the query. The goal is then to produce a valid motion plan that solves the query, satisfies (1), and has as low of a cost as possible, as defined by (3).

Multiple queries can be performed, as the physician desires, and P can be updated appropriately as the patient’s anatomy changes during the procedure. We compute motion plans with respect to the most recent P.

IV. Method

To plan motions for the concentric tube robot in the point cloud representing the patient’s anatomy, we propose Parallel Sampling and Interior point optimization Motion Planning (PSIMP). PSIMP combines sampling-based methods (to globally explore different routes around anatomical obstacles) with local optimization (to facilitate fast computation of high quality plans).

A. Method Overview

We begin by using the sampling-based motion planner PRM* [23], which allows for the discovery of multiple homotopic classes (see Fig. 2) while planning using an objective function, (3) in our case, returning better and better motion plans as computation time increases. It does so while enforcing that paths obey obstacle avoidance constraints as well as other kinematic constraints. For the concentric tube robot model we use, we have kinematic constraints, i.e., g(σ) ≥ 0 in (1), associated with maximum and minimum insertion values for each tube.

At a high level, our method works by continuously running a PRM* thread which discovers better-and-better paths over time. PRM* generates paths as a discretized sequence of n configurations (q₀, q₁,…, q_n–1), such that q₀ = q_start and backbone(q_n–1,1) = x_goal, and n can vary depending on the path. A continuous motion plan is derived from such a representation by moving from one configuration to the next, via linear interpolation in configuration space. Each time PRM* discovers a better path than it had previously, that path is placed in a queue of paths that are awaiting local optimization. Simultaneously, a thread pool of local optimization threads are continuously taking motion plans from the queue and improving the plans in parallel via interior point optimization. Interior point optimization iteratively optimizes a path generated by PRM* by moving the configurations in configuration space to lower the overall cost of the motion plan. For example, consider Fig. 3, which shows a discretized motion plan as a set of configurations, pre-optimization (Fig. 3, top) and post-optimization (Fig. 3, bottom). Interior point optimization is used due to its property of maintaining a solution that is collision-free and satisfies the kinematic constraints during optimization. This process continues for as long as time allows (i.e., until t_max) and the best path found up to any given time is retained (see Fig. 1).

Fig. 3.

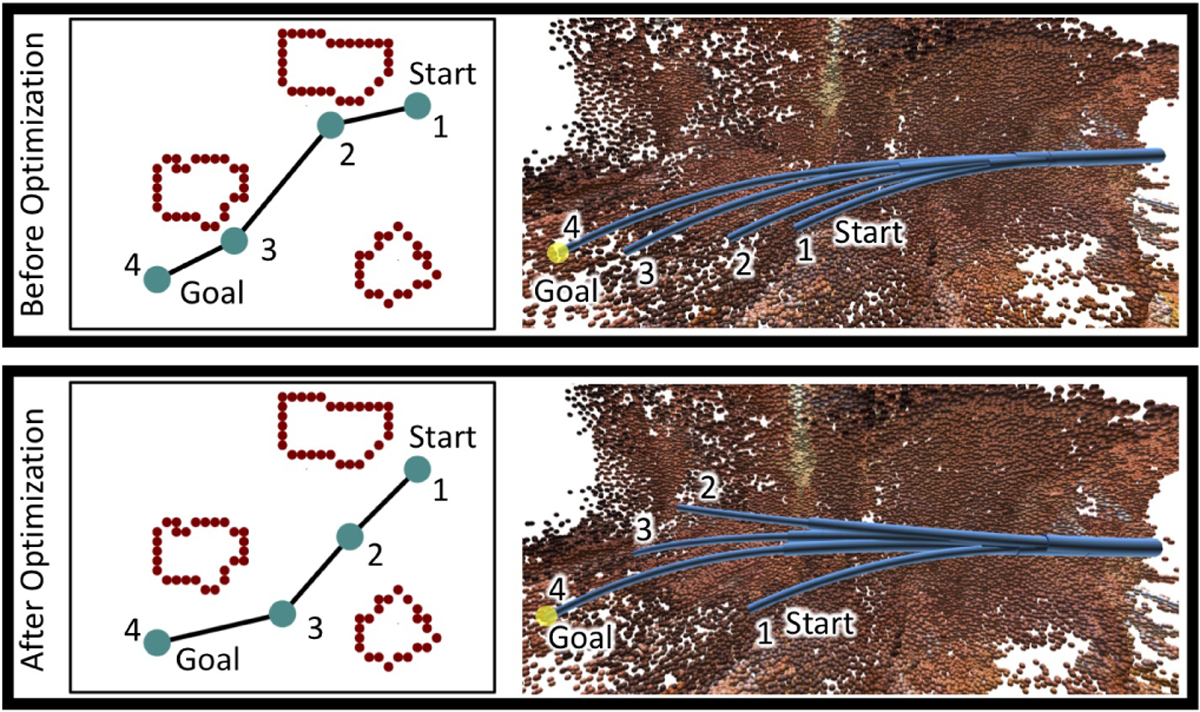
Top: A plan produced early on by the sampling-based planner passes close to obstacles on its way to a configuration who’s tip touches the goal point (yellow). Observe that during the motion the robot’s tip stays near the point cloud (the configurations are overlaid on each other in the image on the right). Bottom: The intermediate configurations of that plan after optimization will travel further from obstacles as the robot moves toward the goal point. Observe that the robot’s tip moves toward the center of the point cloud, far away from the anatomy, as it travels toward the goal point. For demonstrative purposes, to the left of each plan visualization is a 2-dimensional drawing illustrating the concepts. Note, however, that the actual plan exists as a sequence of configurations in the robot’s 6-dimensional configuration space.

We next further describe the method’s two submethods, global exploration through sampling and interior point local optimization.

B. Global Exploration through Sampling

In our method, we utilize a constantly running PRM* motion planning thread to explore the configuration space and discover paths in multiple homotopic classes. Specifically, we utilize the k-nearest variation of PRM*. PRM* works by iteratively constructing a graph $\mathcal{G}=\left(\mathcal{V},\mathcal{E}\right)$ as a motion-planning roadmap, embedded in $\mathcal{Q}$, where $\mathcal{V}$ is a set of vertices which represent collision-free configurations of the robot and $\mathcal{E}$ is a set of edges, where an edge represents a valid transition between two robot configurations. PRM* randomly samples configurations in $\mathcal{Q}$, and adds the collision-free configurations to $\mathcal{V}$ (we explicitly limit the sampling to configurations that respect the kinematic constraints). It then attempts to connect each newly sampled configuration to its k nearest neighbors in $\mathcal{V}$, where k is a parameter that scales with $\left|\mathcal{V}\right|$ as in [23]. If two configurations can be connected in a collision-free way via linear interpolation in configuration space, an edge between the two configurations is added in $\mathcal{E}$. Because the goal is defined as a location in ${ℝ}^3$ and not as a configuration, multiple configurations can satisfy the goal. In order to discover such a configuration quickly, our method performs goal biasing by attempting to ensure that a user-specified percentage of the samples are configurations that touch the goal with their tip and connect them to $\mathcal{G}$. This is done using a damped least-squares inverse kinematics (DLS-IK) controller [35], [36], [18], and allows the method to find an initial solution quickly.

For each motion planning query, PRM* starts by running until it finds the first path in $\mathcal{G}$ that connects the start configuration to a configuration that places the tip of the robot within some radius around the goal point. When that first valid path is found, it is placed in the optimization queue. PRM* then continues sampling configurations, adding to $\mathcal{G}$, discovering lower cost paths and other configurations who’s tips reach the goal point. Each time it finds a path with lower cost than it has found before, that path is placed in the optimization queue and sampling continues. This process continues as time allows, i.e., until t_max has been reached. It is worth noting that although we use PRM* in our implementation, many sampling-based motion planning algorithms could be used in a similar way instead.

C. Interior Point Local Optimization

We maintain a queue of motion plans generated by the PRM* thread. This queue is being operated on by a pool of local optimization threads in parallel. Anytime one of the local optimization threads is available, it retrieves the next motion plan from the queue and performs local optimization on it. When the thread completes the optimization of a plan, it returns to the pool and optimizes the next plan in the queue, if the queue is non-empty. These threads locally optimize plans generated by the PRM* thread using an interior point constrained optimization method [13]. At a high level, this works by taking the initial path, representing it in a high dimensional path space, and performing gradient descent with respect to the path’s cost, defined by (3), while keeping each iteration interior to the feasible set, i.e., respects the kinematic constraints and is collision-free.

More formally, given a discretized path generated by the PRM*, (q₀, q₁,…, q_n–1), we concatenate q₁ through q_n–2 into a vector of dimensionality 2 * N * (n − 2), which represents the intermediate configurations in the path. This ensures that the start and goal configurations remain unchanged by the optimization. We then perform gradient descent with backtracking line search using the Armijo condition [13] on this vector with respect to the cost in (3). Note that we use only first-order gradient information, computed numerically, as computing higher-order derivatives can be computationally expensive for concentric tube robots. In order to compute the cost of the intermediate configurations vector, the first and last configurations must be added back into the path. To ensure there is at least one intermediate configuration, if an initial path has only a start and goal configuration, a third is added halfway between the two.

We use a cost metric that assigns infinite cost to paths that collide with the environment, and which encourages paths to be as far from collision as possible. For this reason, we do not need to formulate the point cloud into the constraint set, enabling us to consider a much simpler set of constraints. This allows us to use a simpler interior point method than in [29]. At each step of descent, if the configurations violate the kinematic constraints, they are projected back into the convex feasible set by clamping the configurations between their maximum and minimum values defined by the robot’s tube lengths, ensuring g(σ) ≥ 0 is satisfied. In this way, a path is locally optimized with respect to the path cost, and the constraints are enforced at each iteration. This frequently results in a large improvement in path cost compared to the pre-optimized path.

D. Keeping Track of the Best Plan Found

The PRM* thread and the optimization threads are working in parallel to generate better and better plans as time allows, i.e., until t_max has elapsed, at which time the best plan found is returned for execution on the robot. However, even prior to t_max, the best plan found at any given time, by any of the threads, is maintained. In this way, if for any reason the algorithm must be stopped early, the best plan found up until that time can be used.

It is worth noting that the choice of an interior point optimization strategy augments the ability to stop the method early and return a high-quality solution. The interior point optimization is an iterative process, i.e., the optimization is occurring as a sequence of small steps in the intermediate configurations’ vector space described above. Unlike many other constrained optimization methods, interior point methods have the property that the plan at each of its iterations is valid and collision-free. This implies that we do not need to wait for the interior point optimization to complete before we can leverage the improvements it has found. If PSIMP must stop in the middle of an optimization, the last iterate of the optimization is itself a valid plan, and as such can be used if it is of the lowest cost found by any of the threads up until that time.

V. Results

We evaluate PSIMP in two ways. First, we compare it to a pure sampling-based motion planner PRM* by itself, in three anatomical scenarios, and demonstrate that PSIMP is able to find motion plans with significantly lower cost in a fraction of a second, and which continue to improve as time allows. Second, we demonstrate the method’s ability to adapt to changes in the anatomy during the surgical procedure.

All results were generated on an 3.40GHz Intel Xeon E5–1680 CPU with 64GB of RAM, and 4 threads were allocated for the local optimization thread pool in all experiments.

A. Comparison and Analysis

We evaluate our method in three point cloud scenarios, two generated from real patient data using the structure from motion library COLMAP [11], [12] (see Fig. 4) and one generated from a synthetic skull model (see Fig. 7). The real patient point cloud scenarios are generated from endoscopic video of (1) a patient’s upper airway (UA) near the epiglottis, and (2) a patient’s colon. Note that although the point clouds used for evaluation are generated via structure from motion, point clouds generated by other methods or sensors can be used by the method and the method remains unchanged.

Fig. 4.

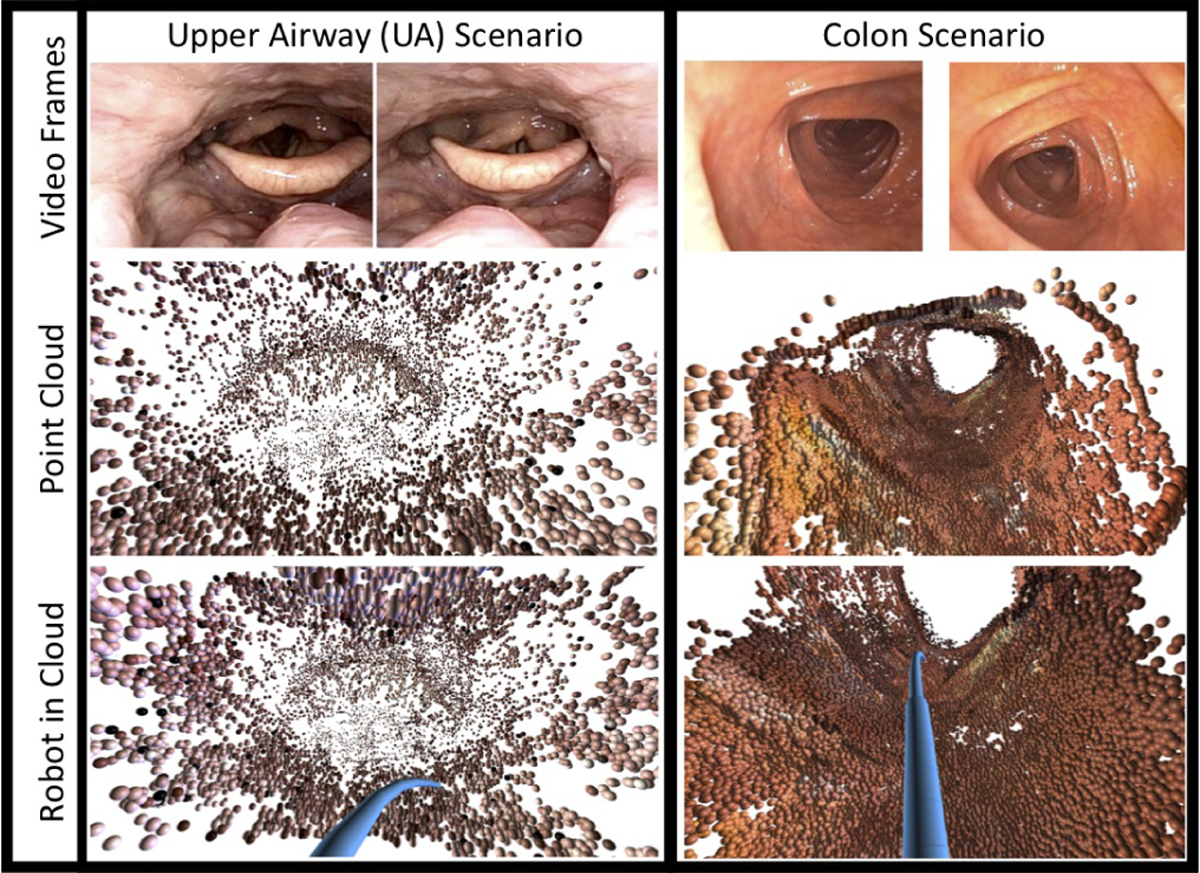
We evaluate our method using two point clouds generated from real patient anatomy. Left: The first is generated from an endoscopic video of the upper airway (UA). Right: The second is generated from an endoscopic video of a colon. A simulated version of the concentric tube robot is shown in blue in both point clouds in the bottom row. Both point clouds are generated from endoscopic video using COLMAP [11], [12]. In addition to these two point clouds generated from real patient data, we also evaluate in a point cloud generated from simulated skull base anatomy, which is shown in Fig. 7.

Fig. 7.

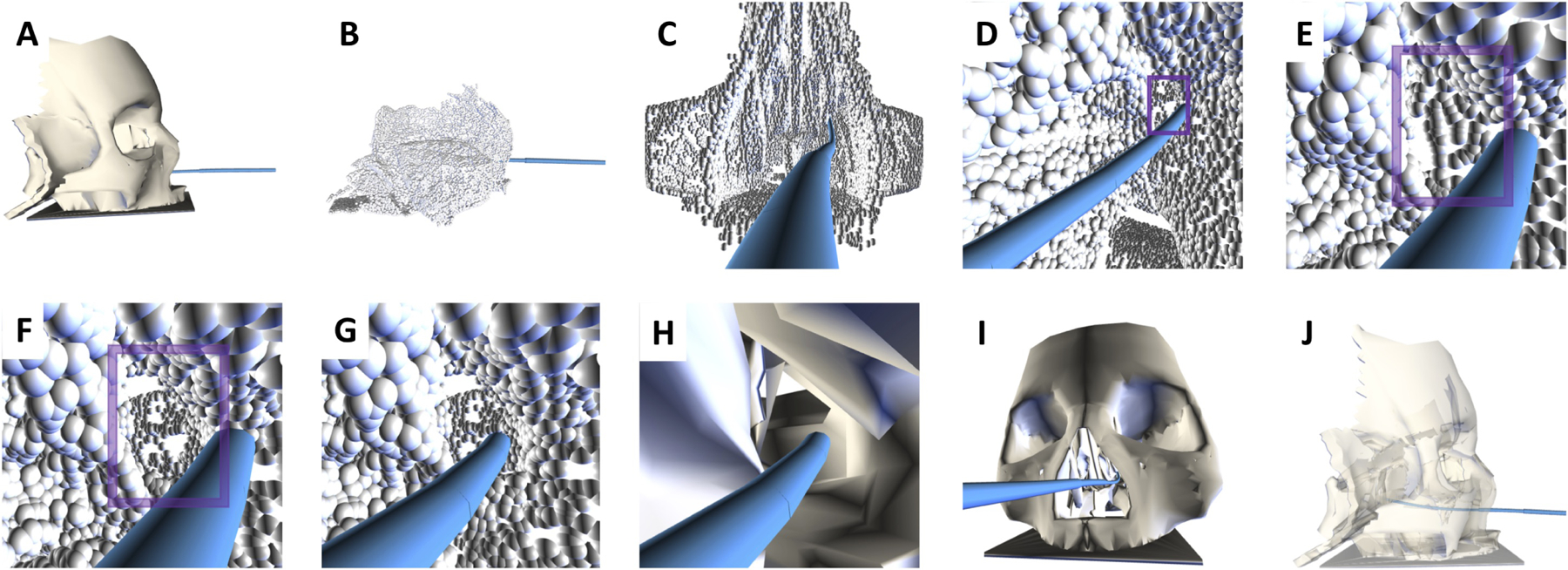
PSIMP plans collision-free motions for a concentric tube robot in anatomy represented using a point cloud, and it can quickly replan motions based on a new point cloud when the anatomy changes. (A) An anatomical model of the skull base from which we derive the initial point cloud. (B) The point cloud derived from the model using a virtual camera moving through the sinuses and skull base. (C) Motions are planned for the robot (blue) deep into the sinuses using our method. (D) In the model, an obstruction exists in the sinuses. The point cloud reflects the obstruction with points on its surface (in the purple window). We plan a motion for the robot to a point at the obstruction. (E) A closer view of the obstruction. (F) The obstruction is removed from the anatomy, and we generate a new point cloud which reflects the new opening (in the purple window). (G) Our method generates a motion plan for the robot to move through the new opening in the point cloud to a point behind the opening. (H,I) Two views of the anatomical model that has the obstruction removed, with the robot passing through the obstruction. (J) The anatomical model rendered semi-transparent for visualization of the final configuration. Our method was able to find a collision-free solution both to the obstruction and beyond.

In all three scenarios, 100 random queries are generated with different collision-free start configurations, and goal points within the reachable workspace of the robot, for 300 total. To ensure we are evaluating queries that simulate surgical tasks, we construct goal points near the point cloud by randomly sampling collision-free configurations that place the tip of the robot within 3 mm of the point cloud, and set the goal point to be the robot’s tip position in that configuration. The configuration that generated the goal point is not recorded, only the ${ℝ}^3$ goal point and we do not ensure that a valid motion plan exists between the randomly generated start configuration and the tip position prior to evaluating the methods. We evaluate PSIMP’s ability to compute high-quality paths over time, and compare the cost of the best computed paths to those generated by a PRM* algorithm without our interior point optimization added. The motion planners were able to successfully plan motions in 98 queries in the UA scenario, 99 queries in the colon scenario, and 98 queries in the skull base scenario. The results presented here are averaged over the successful queries for each scenario.

First, we demonstrate how the quality of the paths improve as computation time increases. In Fig. 5, we compare the cost of the best plan found by PSIMP and PRM* up until a given time, with the cost of the best path found after 100 seconds. Because the queries have different start configurations and goal points, the costs between the queries in each scenario can vary greatly making them difficult to compare directly. As such, for each query we compute the ratio of cost at a given time over the best cost found after 100 seconds, and plot the average over all the queries. In Fig. 5 we show the ratios as they improve over time. We present the time axis in log scale to provide more detail at earlier times. On average the best plans found by PSIMP start improving upon those found by PRM* after ≈ 0.1 seconds, and are 10% – 30% better by ≈ 0.5 seconds, depending on the scenario. Prior to ≈ 0.1 seconds, the methods are comparable as the first plan found by both methods will be identical, and the first optimization of PSIMP has yet to occur.

Fig. 5.

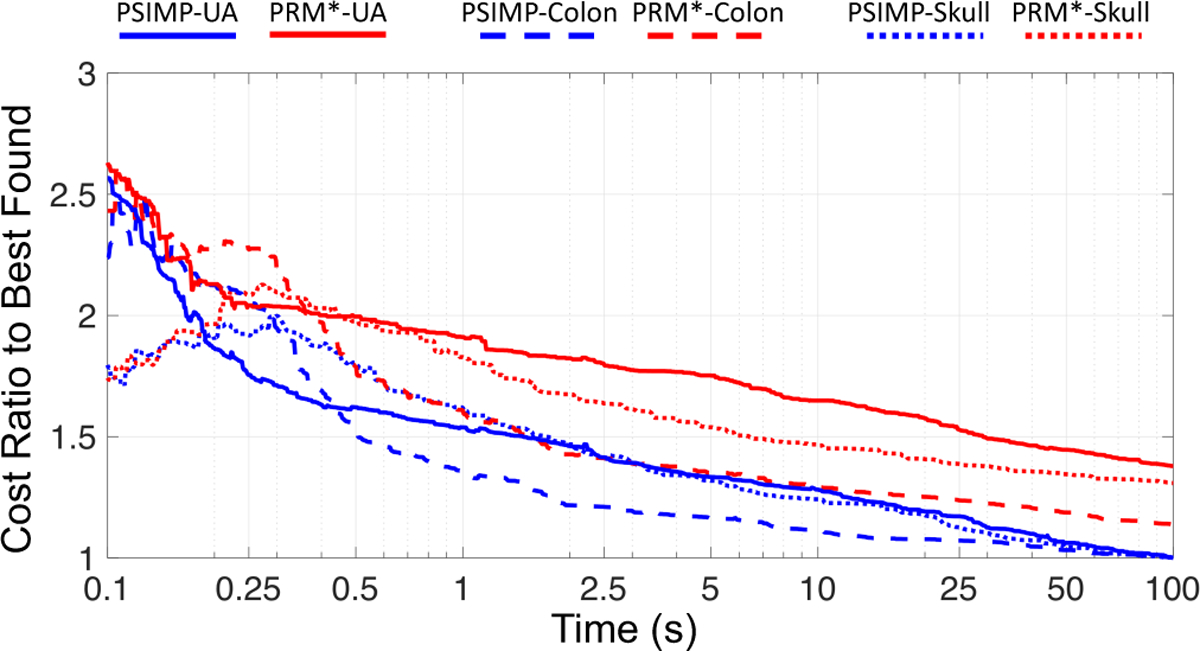
We evaluate the performance of PSIMP (blue) and PRM* (red) over time for all three scenarios, UA (solid lines), colon (dashed lines), and skull base (dotted lines). Shown here is the ratio of the cost of the best plan found by each method up to a given time divided by the cost of the best plan found at any time, by either method, shown for 100 total seconds of computation. At any time after ≈ 0.25 seconds, the cost of the best plan found by PSIMP is significantly lower than that of PRM*. The results are averaged over 99 different queries for the colon scenario, and 98 different queries for the UA and skull base scenario. Note that the time axis is plotted on a log scale to show more detail at earlier times.

In Fig. 6, we compare the costs of the plans found by the methods directly to each other, plotting the ratio of the cost of the best plan found by PRM* divided by the cost of the best plan found by PSIMP, for any point in time. Similar to the previous results, this shows that PSIMP has found, on average, a plan that is between 10 and 40 percent better than that found by PRM* at any point in time after ≈ 0.5 seconds, with improvements beginning around ≈ 0.1 seconds. Prior to that time, the two methods produce very similar results due to the reasons described above. This demonstrates the efficacy of the local optimization performed by PSIMP to improve the quality of solutions found at very short timescales.

Fig. 6.

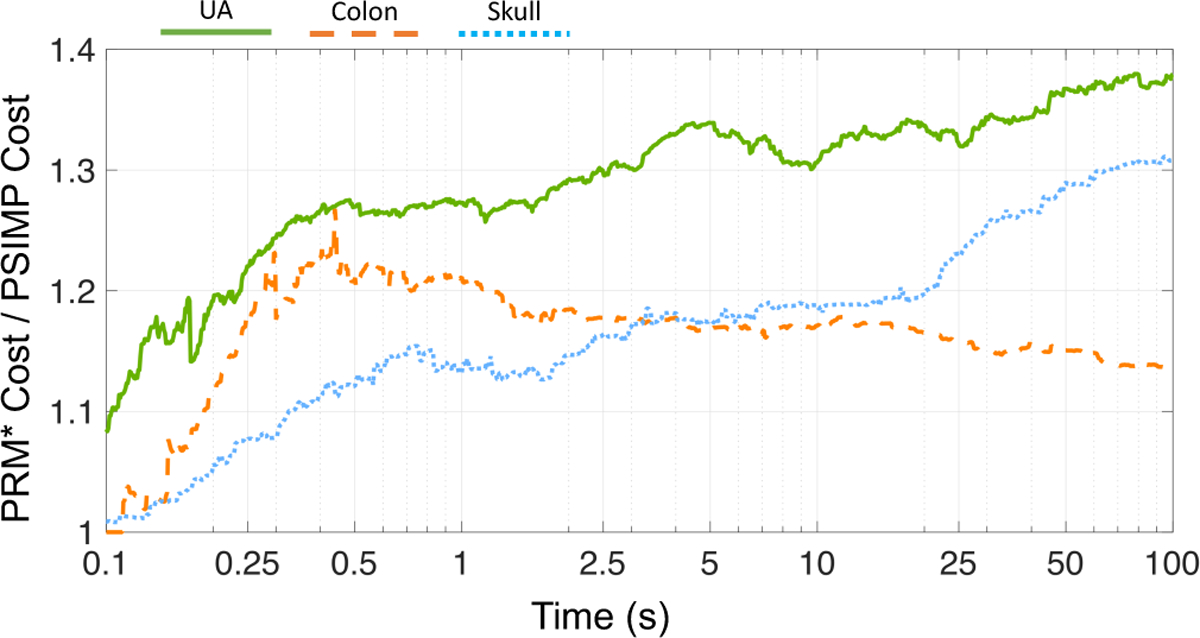
We compare the two methods directly. Here we show the cost of the best plan found by PRM* divided by the cost of the best plan found by PSIMP over time. At any time after ≈ 0.5 seconds, PSIMP has found a plan that is 10–30 percent lower in cost than the best plan found by PRM*. The results are averaged over 99 queries for the colon scenario and 98 queries for the UA and skull base scenario. Note that the time axis is plotted on a log scale to show more detail at earlier times.

In order to be effective in a surgical setting, the motion planner used must produce a valid path quickly. This is the case for PSIMP. The first path is found by PSIMP in a fraction of a second, with a median value of 0.12 seconds. This is the time required by the sampling-based thread in PSIMP to find its first solution. Furthermore, our results demonstrate that if you are willing to allow a small amount of extra computation, PSIMP will significantly improve the plan via local optimization, making it safer to execute. For instance, given 0.15 seconds longer of computation time, PSIMP improves the cost of the best plan found by 13.2% on average across all queries in all scenarios. Further, as more time is allowed to plan, the quality will continue to improve, allowing for safer motion plans.

B. Adapting to Changing Anatomy

To demonstrate our method adapting to changing anatomy, we use a point cloud constructed from an anatomically inspired model of the human skull base and nasal passageways. For visualization of the entire process, see Fig. 7. We generate the point cloud from the model by moving a virtual camera through the nasal passageways, and recording the points on the surface of the model visible to the camera. These points are then concatenated into a point cloud.

We consider an example surgical scenario in the skull base, wherein the robot must move through the sinuses, remove an obstruction in the sinus passageways on the patient’s left side, and then move deeper into the skull base to continue the procedure. The point cloud anatomical model initially reflects this blockage by containing points on the surface of the blockage, and not containing points behind it (due to occlusion caused by the blockage). We first plan a motion for the concentric tube robot that brings the tip of the robot up to the blockage. Next we remove the blockage from the model, as if it were done during the surgical procedure. We then generate a new point cloud with the blockage removed, adding points that can be viewed from near the robot’s tip, as if it were carrying a small chip tip camera. This new cloud is then used as the obstacle representation for the robot, and a motion is planned for it to proceed beyond where the blockage was previously.

Planning the second motion through the opening would not be possible in the case where the obstacle representation remains static, such as is the case when segmenting obstacles only from pre-operative imaging. By updating the model, as we do through updating the point cloud, the obstacle representation accurately represents the patient’s changed anatomy and safe motions can be planned with respect to the changed anatomy.

This is a demonstrative example showing the value of using an obstacle representation that can be generated quickly intra-operatively, compared with using pre-operative imaging to generate the obstacle representation for planning.

VI. Conclusion

Planning motions for concentric tube robots in point clouds allows for adaptation with respect to changing patient anatomy during the course of a surgical procedure. We presented PSIMP, a method that effectively and safely plans motions in point cloud representations of anatomy using a combination of sampling-based global exploration and interior point local optimization. We evaluated our method in three anatomical scenarios, an upper airway scenario and colon scenario generated from endoscopic video of real patients, and a skull base scenario with point clouds generated from simulated images. We evaluated the efficacy of our method, showing that it succeeds in quickly finding collision-free motion plans and significantly improves upon the initial motion plans in fractions of a second. We demonstrated the ability of PSIMP to react to changing point clouds and to plan motions based on the updated information.

In future work we plan to consider the impact of uncertainty in the robot’s motion. As such, we plan to evaluate PSIMP on a physical robot in ex vivo or phantom anatomy using closed-loop control based on sensed tip position to follow motion plans computed by PSIMP. We also plan to consider accounting for the uncertainty associated with concentric tube robot mechanical models during the motion planning process.