MECHANICAL STRESSES ASSOCIATED WITH FLATTENING OF HUMAN FEMOROPOPLITEAL ARTERY SPECIMENS DURING PLANAR BIAXIAL TESTING AND THEIR EFFECTS ON THE CALCULATED PHYSIOLOGIC STRESS-STRETCH STATE

Abstract

Planar biaxial testing is commonly used to characterize the mechanical properties of arteries, but stresses associated with specimen flattening during this test are unknown. We quantified flattening effects in human femoropopliteal arteries (FPAs) of different ages, and determined how they affect the calculated arterial physiologic stress-stretch state. Human FPAs from 472 tissue donors (age 12-82 years, mean 53±16 years) were tested using planar biaxial extension, and morphometric and mechanical characteristics were used to assess the flattening effects. Constitutive parameters for the invariant-based model were adjusted to account for specimen flattening, and used to calculate the physiologic stresses, stretches, axial force, circumferential stiffness, and stored energy for the FPAs in 7 age groups. Flattened specimens were overall 12±4% stiffer longitudinally and 19±11% stiffer circumferentially when biaxially tested. Differences between the stress-stretch curves adjusted and non-adjusted for the effects of flattening were relatively constant across all age groups longitudinally, but increased with age circumferentially. In all age groups these differences were smaller than the intersubject variability. Physiologic stresses, stretches, axial force, circumferential stiffness, and stored energy were all qualitatively and quantitatively similar when calculated with and without the flattening effects. Stresses, stretches, axial force, and stored energy reduced with age, but circumferential stiffness remained relatively constant between 25 and 65 years of age suggesting a homeostatic target of 0.75±0.02 MPa. Flattening effects associated with planar biaxial testing are smaller than the intersubject variability, and have little influence on the calculated physiologic stress-stretch state of human FPAs.

1. INTRODUCTION

Peripheral Arterial Disease (PAD) usually manifests as an atherosclerotic obstruction of the femoropopliteal artery (FPA) that reduces blood flow to the lower limbs. It is one of the leading causes of morbidity, mortality, and impairment in quality of life with annual hospitalization costs of more than $21 billion(Mahoney et al. 2008). The high cost is primarily attributed to the large number of peripheral operations and interventions that fail and require reintervention(Adam et al. 2005; Schillinger et al. 2006; Conte et al. 2006; Schillinger et al. 2007). High failure rates of PAD interventions and reconstructions are often attributed to the severe mechanical environment of the flexing limb resulting in adverse interactions between the repair device and the artery(MacTaggart et al. 2014; Desyatova et al. 2017b; Poulson et al. 2018; Maleckis et al. 2018; Desyatova et al. 2018). Computational modeling can be used to simulate these interactions and design devices with optimized performance, but it requires accurate input data on arterial mechanical properties.

Human FPAs have anisotropic structure with primarily circumferentially-oriented smooth muscle cells (SMCs) in the media, longitudinally-oriented elastic fibers in the external elastic lamina (EEL) at the border of media and adventitia, and helically-oriented collagen fibers in the adventitia(Kamenskiy et al. 2015; Kamenskiy et al. 2016). The complexity of this structure requires multiaxial tests for the characterization of mechanical properties. The two most commonly performed experiments are inflation/extension and planar biaxial extension tests(Humphrey 2002). In combination with residual deformations, these two types of tests theoretically provide equivalent data(Holzapfel and Ogden 2009) for constitutive modeling, but while former is generally preferred for testing small tubular specimens, the latter is more commonly used with larger arteries, like human FPAs, in part due to wider equipment availability and more straightforward testing protocols that do not require branch ligation or estimation of longitudinal pre-stretch. However, one of the challenges of planar biaxial testing is necessity to flatten the specimen. In a tubular form, arteries contain residual stretches and stresses that are thought to be released by opening of the arterial ring into a sector(Humphrey 2002) and curving of the axial strip(Kamenskiy et al. 2015; Sommer et al. 2017). Flattening of the curved specimen prior to planar biaxial testing likely introduces additional stresses into the sample(Keyes et al. 2013), but their magnitudes and variation with age have not been characterized. Furthermore, mechanical properties determined from planar biaxial tests usually do not account for the flattening effects(Kamenskiy et al. 2017), which may affect assessment of physiologic stresses and stretches.

The goal of the current work was to test the hypothesis that flattening of the FPA specimens for planar biaxial testing changes their mechanical response, and affects the assessment of physiologic stress-stretch state. This was achieved by quantifying stretches and stresses associated with flattening of the FPA specimens prior to planar biaxial testing, adjusting the constitutive parameters, and calculating the physiologic stress-stretch state with and without the flattening effects by using constitutive modeling.

2. METHODS

Arteries in vivo experience a complex loaded stress-stretch state that is influenced by the internal pressure, longitudinal pre-stretch, and circumferential and longitudinal residual stresses and stretches that change through the thickness of the FPA wall(Holzapfel and Ogden 2010b; Kamenskiy et al. 2014; Kamenskiy et al. 2016)(Figure 1C). When the artery is excised, it axially contracts releasing the longitudinal pre-stretch(Bustamante and Holzapfel 2010). In this load-free configuration, the internal pressure and the longitudinal pre-stretch vanish, but the artery still possesses circumferential and longitudinal residual stresses and stretches (Figure 1B). These residual characteristics can be assessed by measuring the circumferential (α) and longitudinal (β) opening angles in a radially-opened arterial ring and longitudinal sections. Since these manipulations are assumed to release most of the residual stresses(Vaishnav and Vossoughi 1983; Humphrey 2002), arterial configuration in this state is considered to be stress-free (Figure 1A). Importantly, although separate measurements of circumferential and longitudinal opening angles are convenient and are commonly used in the literature(Humphrey 2002; Holzapfel et al. 2007; Holzapfel and Ogden 2010b; Holzapfel and Ogden 2010a), it is a simplification of the actual complex three-dimensional shape that results from the mutual directional coupling(Sommer and Holzapfel 2012).

Figure 1:

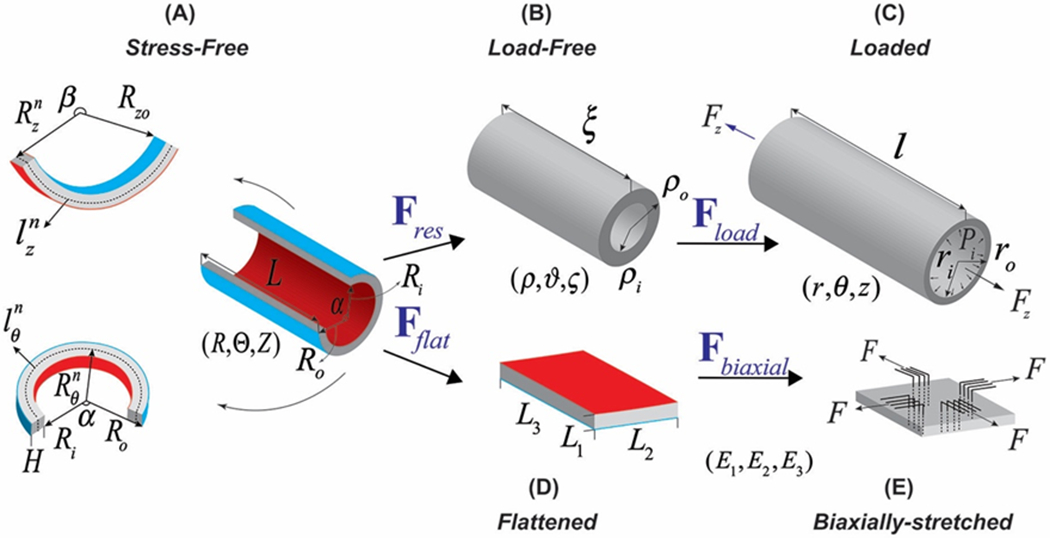
Kinematics of the FPA demonstrating (A) stress-free configuration obtained by radially opening the arterial ring and cutting out a longitudinal strip, (B) load-free configuration with no internal pressure or longitudinal pre-stretch, (C) in vivo loaded state, (D) flattened configuration, and (E) biaxially-stretched state. Note that in the stress-free state (A) longitudinal strip curves intima outward, likely due to tension in the longitudinally-oriented elastic fibers in the external elastic lamina(Kamenskiy et al. 2017), while opened ring curves intima inward.

In order to be biaxially tested, the arterial sample needs to be further flattened and attached to an experimental setup. Assuming that axial and circumferential flattenings are independent, one can calculate the total deformation gradient F_flat associated with flattening. This F_flat then produces a flattened configuration (Figure 1D) that contains non-zero stresses and stretches in both directions. After attaching the specimen to the biaxial device a small preload (typically 0.01 N) is applied to maintain tension during the test, and then the artery is biaxially stretched (Figure 1E) with different loading ratios to obtain sufficient data density for constitutive parameter determination. Once these parameters are determined, they are used in combination with flattening and residual deformation gradients, longitudinal pre-stretch, and internal luminal pressure to calculate the in vivo stress-stretch state. This kinematics will be addressed in the reverse order below.

2.1. Planar biaxial testing

FPAs from 472 subjects (age range 12 – 82 years, mean age 53 ± 16 years, 78% male) were obtained from Live On Nebraska within 24 hours of subject’s death. Prior to excision from the body, the in situ length of the FPA segment was measured using an umbilical tape. The tape was placed alongside the surgically exposed artery between the locations at which the artery was transected representing the true in situ length of the arterial segment. The artery and the tape were then cut together, and while the umbilical tape maintained its length, the artery typically shortened due to in situ pre-stretch. Pre-stretch was then defined as the ratio of the in situ arterial length (umbilical tape length) to the excised artery length(Kamenskiy et al. 2016). Geometric data including arterial wall thickness (H), outer radius of the load-free ring (ρ_o), inner and outer radii of the stress-free circumferential strip (R_i, R_o), inner radius of the longitudinal strip (R_zo), and circumferential (α) and longitudinal (β) opening angles were measured optically.

Planar biaxial tests were performed on 13 × 13 mm arterial segments (when permitted by vessel size) submerged into 0.9% phosphate-buffered saline at 37°C. A total of 19 different protocols were used to obtain sufficient data density for constitutive modeling. For additional details of these tests, please refer to Kamenskiy et al(Kamenskiy et al. 2017) or Desyatova et al(Desyatova et al. 2017a).

2.2. Constitutive relations

FPA stress-stretch characteristics measured during planar biaxial tests are portrayed well by the four-fiber family invariant-based constitutive model that phenomenologically accounts for the contribution of isotropic ground substance, longitudinal elastic fibers, circumferential smooth muscle cells, and helical collagen fibers(Kamenskiy et al. 2014; Kamenskiy et al. 2015; Kamenskiy et al. 2016; Kamenskiy et al. 2017; Desyatova et al. 2017a). The strain energy function for such material can be defined as

$$W=W_{gr}+W_{el}+W_{smc}+W_{col,1}+W_{col,2},$$ Eq. 1

where

$$\begin{gathered} W_{\mathit{gr}}=\frac{C_{\mathit{gr}}}{2}(I_1^{\mathit{gr}}-3), \\ {W}_{\mathit{el}}=\frac{C_1^{\mathit{el}}}{4C_2^{\mathit{el}}}\left(e^{C_2^{\mathit{el}}{\langle I_4^{\mathit{el}}-1\rangle }^2}-1\right), \\ {W}_{\mathit{smc}}=\frac{C_1^{\mathit{smc}}}{4C_2^{\mathit{smc}}}(e^{C_2^{\mathit{smc}}{\langle I_4^{\mathit{smc}}-1\rangle }^2}-1), \\ {W}_{\mathit{col},j}=\frac{C_1^{\mathit{col}}}{4C_2^{\mathit{col}}}\left(e^{C_2^{\mathit{col}}{\langle I_4^{\mathit{col},j}-1\rangle }^2}-1\right)j=1,2. \end{gathered}$$ Eq. 2

Here c_gr, $c_1^i$, $c_2^i$ (i = el, smc, col) are constitutive parameters that determine the passive FPA mechanical behavior, and Macaulay brackets $\langle (\cdot )\rangle =\frac{1}{2}[(\cdot )+\mid (\cdot )\mid ]$ are used to filter positive values so fibers only contribute to stress during tension. The total Cauchy stress can then be written as a summation of the volumetric and isochoric parts

$$\mathit{t}=-p\mathit{I}+\overline{\mathit{t}}=-p\mathit{I}+\stackrel{\overline{\mathit{t}}}{\overbrace{2\frac{\partial W}{\partial I_1}\mathit{B}+2\sum _i\frac{\partial W}{\partial I_4^i}{\mathit{m}}_i\otimes {\mathit{m}}_i,}},$$ Eq. 3

where i stands for each group of structurally significant fibers with m_i = FM_i, I₁ = trC, $I_4^i={\mathit{M}}_i\cdot ({\mathit{CM}}_i)$, M_i the unit vector in the direction of the fibers in the reference configuration, and F, B and C are the deformation gradient, and the left and right Cauchy-Green stretch tensors, respectively. Further, in the absence of shear, $I_4^i$ has the forms:

$$I_4^{el}={\mathit{\lambda }}_z^2,I_4^{smc}={\mathit{\lambda }}_{\theta }^2,I_4^{col,1}=I_4^{col,2}=I_4^{col}={\mathit{\lambda }}_z^2{\mathit{cos}}^2\gamma +{\mathit{\lambda }}_{\theta }^2{\mathit{sin}}^2\gamma ,$$

where γ is the angle between the collagen fibers and the longitudinal direction. Note that θ, z in λ_θ and λ_z are used only to point out that these directions align with the circumferential and longitudinal directions of the artery and they need to be substituted with the appropriate stretches in each case described in Figure 1.

Constitutive parameters are then determined by minimizing the error function

$$e=|{\mathit{t}}^{th}({\mathit{F}}_{total},P)-{\mathit{t}}^{\mathit{exp}}|,$$

where t^exp is the experimental Cauchy stress calculated by dividing the measured force by the area during the biaxial test, t^th is the theoretical Cauchy stress which is a function of the total deformation gradient the specimen is experiencing during the test (please see the next section) and the constitutive parameters P that include c_gr, $c_1^i$, $c_2^i$ in Eq. 2 and the angle γ between the collagen fibers and the longitudinal direction which are all determined using nonparametric bootstrapping(Ferruzzi et al. 2011; Kamenskiy et al. 2017). Briefly, this included 2000 iterations of random resampling and fitting, followed by the analysis of the probability distribution of each parameter to determine the global minimum. The bootstrapping was performed both before and after accounting for the flattening effects, which resulted in two different sets of constitutive parameters for each specimen. Relations for the Cauchy stresses are provided in the Appendix 7.1

To determine age-group specific mechanical responses, we followed the approach described previously(Kamenskiy et al. 2017). Specifically, since constitutive parameters in Eq. 1 are interrelated, it is not appropriate to average them across specimens to obtain average age group-specific mechanical properties. Instead, the average stress-stretch responses, and the 25^th and 75^th percentile responses for each age group were generated first, and then the resulting curves were used to determine constitutive parameters representing these age groups again using nonparametric bootstrapping(Ferruzzi et al. 2011; Kamenskiy et al. 2017).

2.3. Kinematics of flattening and planar biaxial experiment

Before arterial specimen can be biaxially tested, it needs to undergo flattening deformation F_flat that takes the artery from the stress-free (Figure 1A) configuration to the flattened (Figure 1D) state. Assuming incompressibility and independence of longitudinal and circumferential deformations, F_flat can be written as

$${\mathit{F}}_{flat}=diag\left[\frac{1}{{\mathit{\lambda }}_2{\mathit{\lambda }}_3},{\mathit{\lambda }}_2,{\mathit{\lambda }}_3\right],$$

where λ₂ and λ₃ are stretches corresponding to the circumferential and longitudinal directions, respectively.

When flattened for planar biaxial testing, part of the arterial specimen undergoes tension, while the opposite side experiences compression. This implies the existence of a neutral axis that does not change its length during flattening. Neutral axis is typically assumed to be located in the middle of the section, i.e. half-way between intima and adventitia(Sommer and Holzapfel 2012).

From Figure 1, the flattening stretches can be expressed in terms of the neutral axes radii of the circumferential and longitudinal sections, $R_{\theta }^n$ and $R_z^n$ respectively, as(Ogden 1997; Sommer and Holzapfel 2012)

$${\mathit{\lambda }}_2=\frac{l_{\theta }^n}{l_{\theta }}=\frac{R_{\theta }^n}{R_{\theta }},{\mathit{\lambda }}_3=\frac{l_z^n}{l_z}=\frac{R_z^n}{R_z},$$ Eq. 4

where $l_{\theta }^n$ and $l_z^n$ are equal to L₂ and L₃, respectively, in the flattened state (Figure 1D) and

$$R_i\le R_{\theta }\le R_i+H,R_{zo}\le R_z\le R_{zo}+H.$$

Since loads during planar biaxial tests are applied uniformly to the specimen’s cross-sections, average stretches are used in F_flat, and details of averaging are summarized in the Appendix 7.2. The total deformation gradient experienced by the artery during planar biaxial test therefore includes F_flat and F_biaxial:

$${\mathit{F}}_{total}={\mathit{F}}_{biaxial}{\mathit{F}}_{flat}.$$ Eq. 5

2.4. Kinematics of residual and physiologic deformations

Constitutive parameters determined from the experimental data were then used to describe physiologic arterial behavior by implementing a kinematic framework that considers residual stresses, longitudinal pre-stretch, and the internal pressure (Figure 1C). This framework has been described previously(Ogden 1997; Holzapfel et al. 2000; Humphrey 2002; Sommer and Holzapfel 2012; Kamenskiy et al. 2014), but will also be briefly summarized below for clarity. More details are provided in the Appendices 7.3 and 7.4.

Deformation gradient associated with the residual deformation in the cylindrical coordinate system can be written as

$${\mathit{F}}_{res}=diag[{\mathit{\lambda }}_{\rho },{\mathit{\lambda }}_{\vartheta },{\mathit{\lambda }}_{\zeta }],$$

where λ_ρ, λ_ϑ and λ_ζ are the radial, circumferential and longitudinal residual stretches respectively. Using incompressibility one can find

$${\mathit{\lambda }}_{\vartheta }(\rho )=\frac{\rho }{R}\mathrm{K}=\frac{\rho \mathrm{K}}{\sqrt{R_o^2-\mathrm{K}{\mathit{\lambda }}_{\zeta }\left({\left(\frac{1}{\mathrm{K}}{R}_o{\mathit{\lambda }}_{\vartheta }^o\right)}^2-{\rho }^2\right)}},$$ Eq. 6

where $\mathrm{K}=\frac{2\pi }{2\pi -\alpha }$ is a measure of the circumferential opening angle and ${\rho }_o=\frac{1}{\mathrm{K}}{R}_o{\lambda }_{\vartheta }^o$. Note that the residual stretch λ_ζ contains both the flattening and the $\frac{\xi }{L}$ stretch of the axial strip, and the unknown stretches ${\lambda }_{\vartheta }^o$ and $\frac{\xi }{L}$ in λ_ζ can be determined using the boundary conditions of no axial force and zero luminal pressure in the load-free state.

Further, deformation F_load, which takes the load-free configuration to the loaded (current) configuration, is given by

$${\mathit{F}}_{load}=diag[{\mathit{\lambda }}_r,{\mathit{\lambda }}_{\theta },{\mathit{\lambda }}_z],$$

where ${\mathit{\lambda }}_{\theta }=\frac{r}{\rho }$ and λ_z is equal to the measured in situ longitudinal (axial) pre-stretch, i.e. ${\mathit{\lambda }}_z^{\text{in situ}}$.

Therefore, the total deformation that the FPA experiences when progressing from the stress-free to the in vivo loaded state (Figure 1A,B,C) can be expressed as

$${\mathit{F}}_{phys}={\mathit{F}}_{load}{\mathit{F}}_{res}=diag[{\mathit{\lambda }}_r^{phys},{\mathit{\lambda }}_{\theta }^{phys},{\mathit{\lambda }}_z^{phys}],$$

where the longitudinal physiologic stretch is given by

$${\mathit{\lambda }}_z^{phys}={\mathit{\lambda }}_z^{insitu}{\mathit{\lambda }}_{\zeta },$$

and the circumferential stretch can be calculated as

$${\mathit{\lambda }}_{\theta }^{phys}={\mathit{\lambda }}_{\theta }{\mathit{\lambda }}_{\vartheta }=\frac{r}{R}\mathrm{K}=\frac{r\mathrm{K}}{\sqrt{R_o^2-\mathrm{K}{\mathit{\lambda }}_{\zeta }{\mathit{\lambda }}_z\left({\left(\frac{1}{\mathrm{K}}{R}_o{\mathit{\lambda }}_{\vartheta }^o{\mathit{\lambda }}_{\theta }^o\right)}^2-r^2\right)}},$$ Eq. 7

where ${\mathit{\lambda }}_{\theta }^o=\frac{r_o}{{\rho }_o}$. Assuming no perivascular tethering, boundary condition of zero pressure on the outer surface of the artery, and the average internal luminal pressure of 100 mmHg in the loaded state, one can calculate the ${\mathit{\lambda }}_{\theta }^o$.

2.5. FPA physiologic conditions

Cauchy stresses and stretches as a function of thickness at systolic (120 mmHg), diastolic (80 mmHg), and average (100 mmHg) pressures and in situ longitudinal pre-stretch ${\mathit{\lambda }}_z^{\text{in situ}}$ were calculated to assess physiologic FPA function and determine how it changes with age. Physiologic circumferential stiffness was assessed as the change in the average circumferential stress between systole and diastole divided by the change in the average circumferential stretch

$$E_{\theta }=\frac{t_{\theta \theta }^{phys,avg}(sys)-t_{\theta \theta }^{phys,avg}(dias)}{{\mathit{\lambda }}_{\theta }^{phys,avg}(sys)-{\mathit{\lambda }}_{\theta }^{phys,avg}(dias)},$$ Eq. 8

where $t_{\theta \theta }^{\mathit{phys},\mathit{avg}}$ and ${\mathit{\lambda }}_{\theta }^{\mathit{phys},\mathit{avg}}$ are the average through-thickness circumferential physiologic stress and stretch, respectively, calculated by integrating them over the current volume and dividing by the total current volume (see Appendix 7.2).

In addition, for each sample we have calculated longitudinal pre-stretch at which axial tethering force and internal pressure decouple, i.e. the change in the axial force is minimal as the artery experiences changes in pressure(Van Loon et al. 1977; Weizsacker et al. 1983; Brossollet and Vito 1995; Humphrey 2002; Stålhand and Klarbring 2005; Holzapfel and Ogden 2010a). This decoupling suggests energy efficient function(Sommer et al. 2010) which was further assessed by calculating change in the average through-thickness strain energy between systole and diastole as

$$\Delta W_{avg}=W_{avg}^{sys}-W_{avg}^{dias},$$

where the strain energy W is a function of ${\mathit{\lambda }}_{\theta }^{\mathit{phys}}$ given by Eq. 7 and ${\mathit{\lambda }}_z^{\mathit{phys}}$.

2.6. Statistical Analysis

Pearson correlation coefficient r was used to assess the strength of linear relation between continuous variables, with values closer to ±1 demonstrating stronger relations. Statistical significance of the observed correlations was assessed by testing the hypothesis of no correlation against the alternative hypothesis of nonzero correlation using the corr function of MATLAB. Value of p<0.05 was considered statistically significant.

3. RESULTS

Changes in the FPA morphometric characteristics with age are demonstrated in Figure 2. Opening angles α, β and FPA thickness H were measured experimentally, while ρ_i, ρ_o, r_i, and r_o were calculated using boundary conditions for each corresponding defosrmation.

Figure 2:

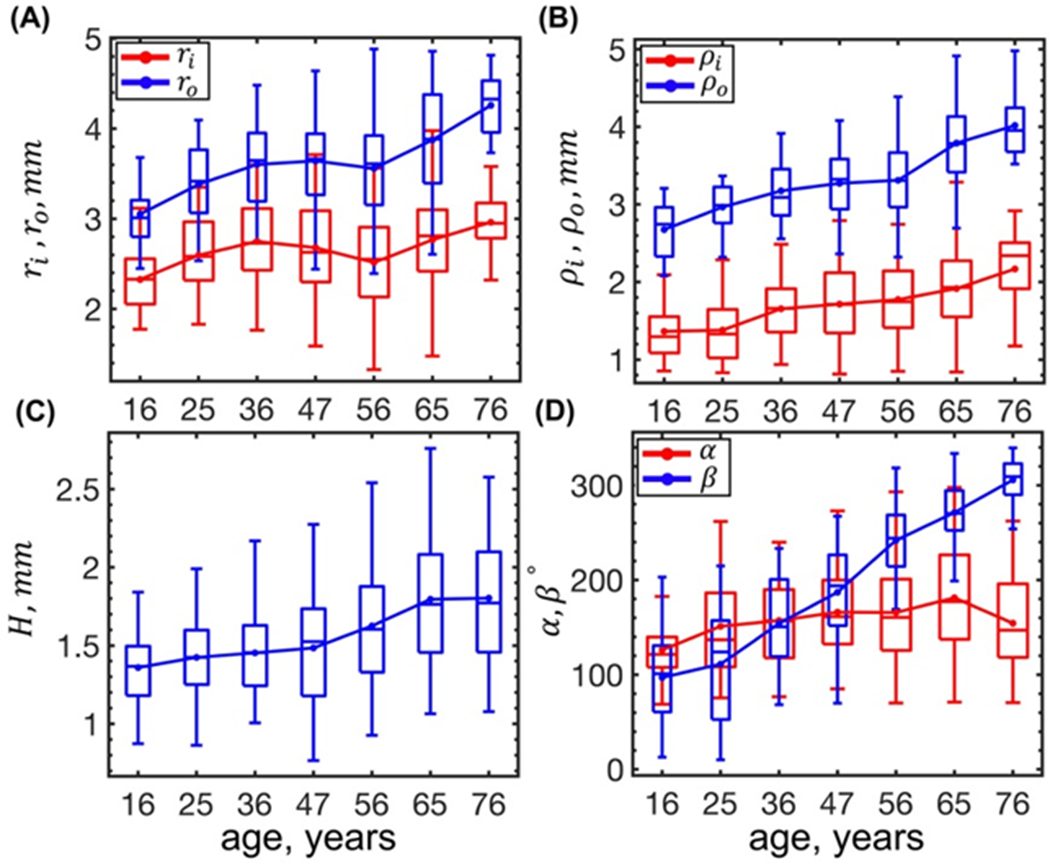
Changes with age of the FPA radii in the (A) loaded and (B) load-free configurations, (C) stress-free thickness H, and (D) circumferential and longitudinal opening angles. Here boxes bound 25^th and 75^th percentiles for each age group, median and average values are marked with a line and a dot within each box, and whiskers extend to the 5^th and 95^th percentiles.

Both the inner and the outer FPA radii in the loaded and load-free configurations increased with age (p < 0.01), but the outer radius increased at a higher rate (r = 0.36 and r = 0.56) than its inner counterpart (r = 0.14 and r = 0.35), suggesting an increase in the in vivo wall thickness due to outward remodeling. In the stress-free configuration, the FPA wall thickness (r = 0.36, p < 0.01), the circumferential α and longitudinal β opening angles increased with age (p < 0.01) (Figure 2), but the correlation with age was stronger for the β (r = 0.83) than for the α (r = 0.19).

Constitutive parameters representing average FPAs in each age group are summarized in Table 1, and Figure 3 shows the stress-stretch responses plotted using these parameters (solid lines). For comparison, the same graphs are plotted using the parameters not adjusted for the flattening effects (dashed lines). Variability within each age group was assessed by calculating the 25^th and 75^th percentiles, and the corresponding graphs are plotted in Figure 3 as shaded semi-transparent regions. Constitutive parameters adjusted for the flattening effects and representing FPAs at the 25^th and 75^th percentiles for all age groups are summarized in the Appendix 7.5. Aging resulted in stiffening of the FPAs in both longitudinal and circumferential directions, but longitudinal stiffening occurred faster, resulting in the overall more isotropic response of older FPAs.

Table 1:

Parameters for the four-fiber family constitutive model describing the isochoric response of human FPAs in 7 age groups. Parameters represent the average FPA within each age group and are adjusted for the effects of flattening. Here n is the sample size in each age group that was used to derive these parameters. The coefficient of determination R²=0.99 for all age groups.

Age group (years)	n	Cgr(kPa)	$C_1^{\mathit{el}}(kPa)$	$C_2^{\mathit{el}}$	$C_1^{\mathit{smc}}(kPa)$	$C_2^{\mathit{smc}}$	$C_1^{\mathit{col}}(kPa)$	$C_1^{\mathit{col}}$	γ°
16.3 (11-20)	30	3.41	40.78	0.04	0.13	4.18	10.46	0.97	61.66
25.0 (21-30)	37	12.55	29.80	0.32	6.62	3.37	3.66	3.68	56.55
36.0 (31-40)	56	9.38	34.43	0.75	6.88	4.03	4.00	4.60	55.11
46.5 (41-50)	64	9.63	39.41	1.82	10.93	6.31	5.40	7.21	50.58
56.1 (51-60)	125	5.05	41.09	2.91	14.75	8.24	7.72	10.16	50.23
65.0 (61-70)	135	3.96	45.24	6.30	15.91	10.51	8.19	18.84	48.35
75.5 (70-80)	25	3.05	38.53	10.34	26.55	10.42	7.56	24.82	50.96

Figure 3:

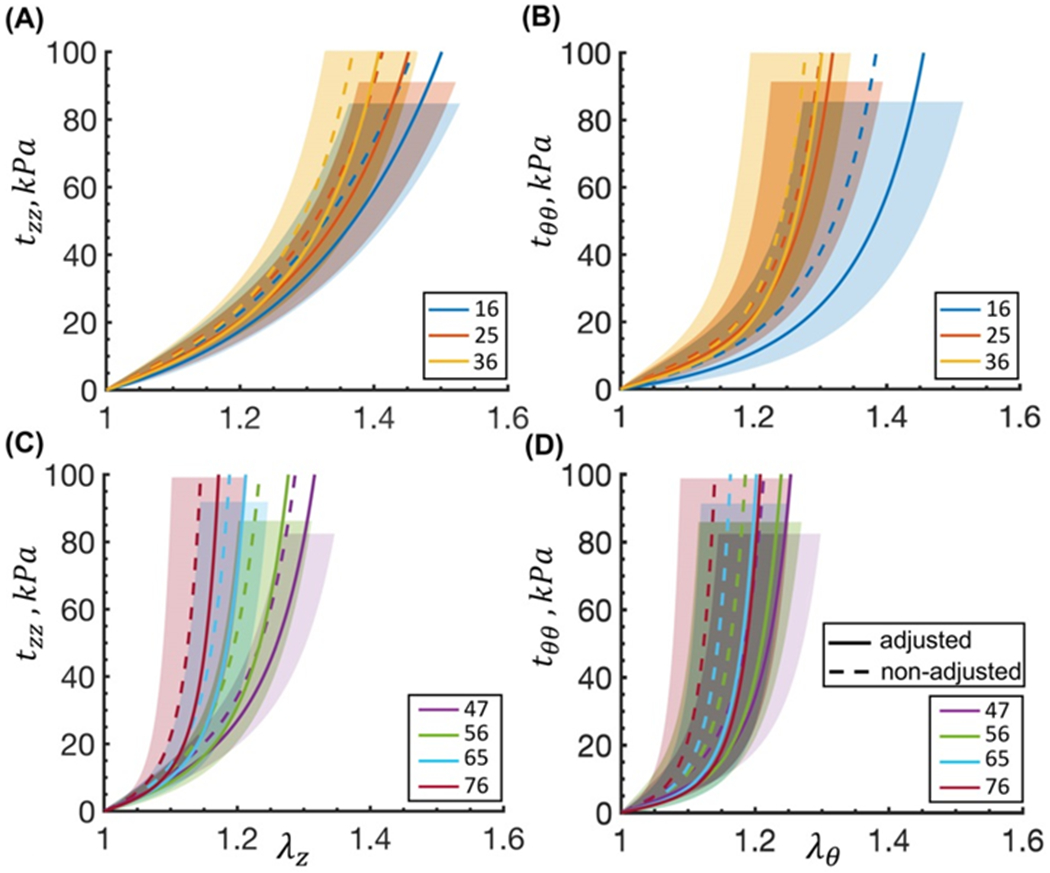
Cauchy stress-stretch responses for the average FPA in each age group plotted in the (A,C, z) longitudinal and (B,D, θ) circumferential directions using adjusted (sold lines) and the non-adjusted (dashed lines) constitutive parameters. Legend indicates average age in each group (years). For clarity the graphs are separated into 4 panels. Variability within each age group for the adjusted parameters is demonstrated by the shaded semi-transparent regions that bound 25^th and 75^th percentile ranges. They have different heights for better visual representation.

Taking flattening deformations into account resulted in the overall softer response in both directions (Figure 3), but the difference in stretches at 100 kPa stress was relatively small, i.e. 19 ± 11% in the circumferential direction and 12 ± 4% in the longitudinal direction, which was less than the variation in the stress-stretch responses within the age groups.

Aging was associated with reduction in the longitudinal and circumferential flattening stretches (r = −0.71 and r = −0.22, p<0.01, respectively) and stresses (r = −0.21 and r = −0.08, p<0.01, respectively) averaged through thickness (Figure 4). Longitudinal flattening stress decreased with age from 8.7 to 4.7 kPa due to larger longitudinal opening angle β (i.e. flatter longitudinal strips in older subjects), and circumferential flattening stress decreased from 3.4 to 2 kPa due to the slight increase in the circumferential opening angle α with age.

Figure 4:

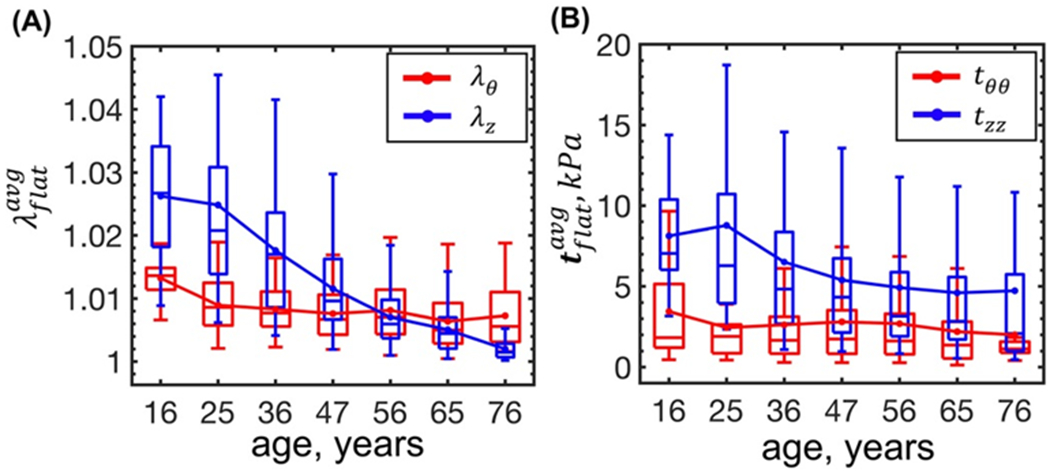
Change in the (A) flattening stretches and (B) stresses averaged through the FPA wall thickness with age. Boxes bound 25^th and 75^th percentiles for each age group, median and average values are marked with a line and a dot within each box, and whiskers extend to the 5^th and 95^th percentiles.

The averaged through-thickness longitudinal and circumferential residual stresses were almost zero because of their opposite tensile and compressive nature but similar absolute values at the intimal and adventitial surfaces.

Change in the physiologic stress-stretch state with age calculated using both the adjusted and the non-adjusted parameters is demonstrated in Figure 5. Adjustment for the flattening deformations had minor effect on the results. Largest difference between the stresses plotted using the adjusted and the non-adjusted parameters, was observed for the longitudinal direction in young FPAs (~14 kPa) while the longitudinal and circumferential stretches were, respectively, ~0.02 and ~0.05 higher across all age groups after adjusting for the flattening effects. Taking flattening effects into account also somewhat decreased the axial force F_z (~0.11 N), but had little effect on the circumferential stiffness E_θ, with a difference of < 35 kPa.

Figure 5:

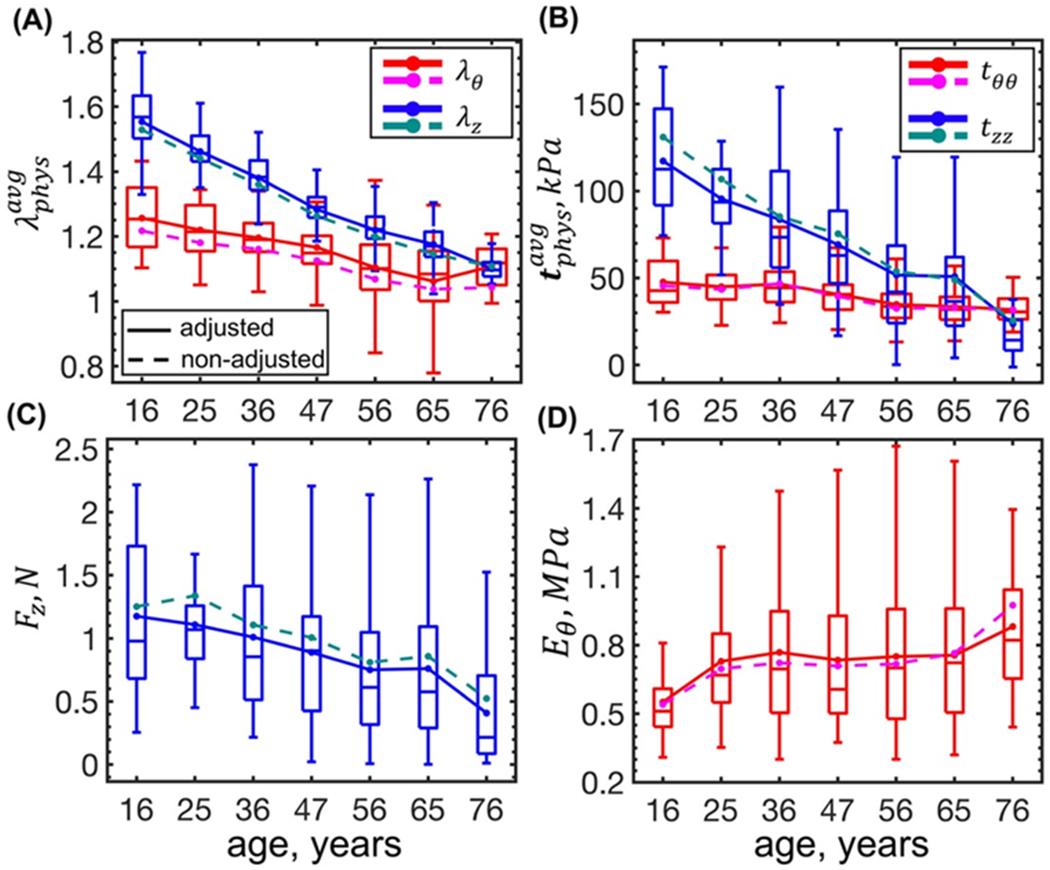
Changes in the physiologic stress-stretch state with age calculated using the adjusted (solid lines) and the non-adjusted (dashed lines) constitutive parameters. Panel (A) illustrates changes in stretches (red, magenta – circumferential; blue, dark cyan – longitudinal), and panel (B) in stresses with age, both calculated using through-thickness averaging. Panels (C) and (D) demonstrate changes in the axial force and circumferential stiffness with age, respectively. Boxes bound 25^th and 75^th percentiles for each age group, median and average values are marked with a line and a dot within each box, and whiskers extend to the 5^th and 95^th percentiles. Boxes are plotted for the data adjusted for the flattening deformations. Note that the results obtained using the adjusted and the non-adjusted constitutive parameters follow the same trends, and the differences are much smaller than the variability within the age groups.

Figure 5 demonstrates that all physiologic stretches and stresses, calculated as through-thickness averages, decreased with age (p < 0.01). Physiologic circumferential stretch decreased from ${\mathit{\lambda }}_{\theta }^{\mathit{phys},\mathit{avg}}=1.26$ in the youngest to ${\mathit{\lambda }}_{\theta }^{\mathit{phys},\mathit{avg}}=1.1$ in the oldest age group (r = −0.48), and the associated physiologic circumferential stress decreased from $t_{\theta \theta }^{\mathit{phys},\mathit{avg}}=48\mathrm{kPa}$ to $t_{\theta \theta }^{\mathit{phys},\mathit{avg}}=32\mathrm{kPa}$ (r = −0.42), respectively. In the longitudinal direction, reduction in the physiologic stretch ${\mathit{\lambda }}_z^{\mathit{phys},\mathit{avg}}$ and the associated stress $t_{\mathit{zz}}^{\mathit{phys},\mathit{avg}}$ was much more pronounced (r = −0.84 and r = −0.48, respectively). Physiologic longitudinal stretch decreased from ${\mathit{\lambda }}_z^{\mathit{phys},\mathit{avg}}=1.57$ in the youngest to ${\mathit{\lambda }}_z^{\mathit{phys},\mathit{avg}}=1.1$ in the oldest age group, and the longitudinal stress decreased from $t_{\mathit{zz}}^{\mathit{phys},\mathit{avg}}=117\mathrm{kPa}$ to $t_{\mathit{zz}}^{\mathit{phys},\mathit{avg}}=24\mathrm{kPa}$, respectively. Reduction in the longitudinal stretch and stress with age was followed by the reduction in the axial force F_z (Figure 5C, r = −0.27, p < 0.01) that changed from 1.18 N to 0.41 N, and a slight increase in the circumferential stiffness E_θ (Figure 5D, r = 0.15 and p < 0.01) from 0.55 MPa to 0.88 MPa, although latter appeared to maintain its value of ~0.75 ± 0.02 MPa from 25 to 65 years of age.

Decrease in the longitudinal stress with age was also observed at the intimal and adventitial surfaces (r = −0.54, r = −0.33, p < 0.01) (Figure 6A). At the adventitial surface it changed from 106 kPa in the youngest age group to 51 kPa in the oldest age group, and at the intimal surface longitudinal stress decreased from 116 kPa to 17 kPa. Circumferential stress at the intimal surface also decreased with age (r = −0.59, p < 0.01) from 104 kPa to almost zero, but at the adventitial surface it increased (r = 0.43, p < 0.01) (Figure 6B) from 24 kPa to 102 kPa, which changed the nature of stress distribution through the FPA wall thickness. Specifically, in young FPAs circumferential stress at the intimal surface was higher than that at the adventitial surface, but the opposite was observed for the older FPAs, with the switch appearing at the age of 30-40 years (Figure 6B). Similarly to the results obtained using through-thickness averages (i.e. Figure 5), flattening did not substantially alter stresses at the intimal or adventitial surfaces with the largest difference observed for the $t_{\theta \theta }^{\mathit{int}}$ in young FPAs that was ~18 kPa higher after adjusting for flattening.

Figure 6:

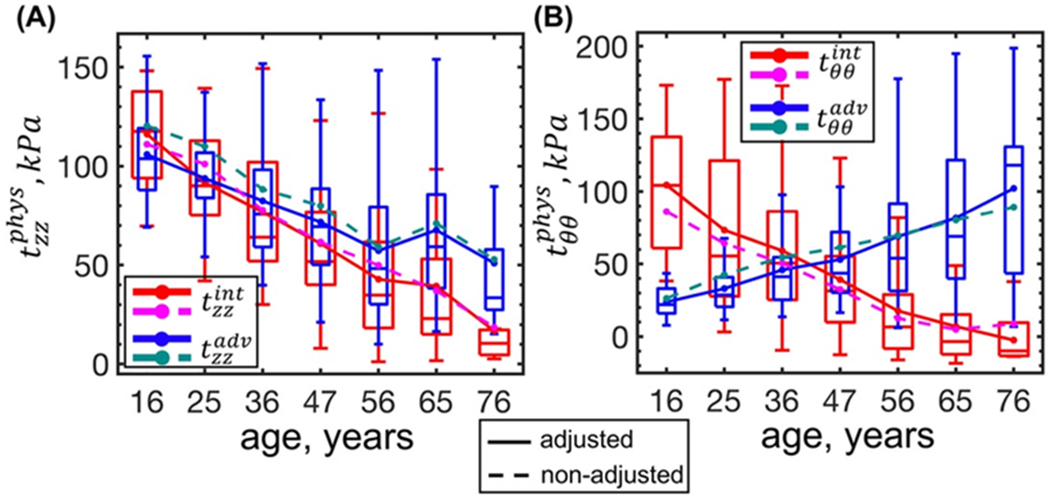
Changes in the physiologic stress-stretch state with age at the intimal and adventitial surfaces calculated using parameters adjusted (solid lines) and non-adjusted (dashed lines) for the flattening effects. Panels (A) and (B) describe changes in the longitudinal and circumferential stresses at the intimal (red, magenta) and adventitial (blue, dark cyan) surfaces, respectively. Boxes bound 25^th and 75^th percentiles for each age group, median and average values are marked with a line and a dot within each box, and whiskers extend to the 5^th and 95^th percentiles. Boxes are plotted for the data adjusted for the flattening deformations.

Adjustment for the flattening effects also did not notably change the calculated in situ pre-stretch at which the internal pressure and the longitudinal force decoupled(Sommer et al. 2010) (${\mathit{\lambda }}_z^{\text{decoupling}}$), nor did it markedly influence the stored physiologic energy W (Figure 7). Figure 7A demonstrates that for the young FPAs the calculated pre-stretch ${\mathit{\lambda }}_z^{\text{decoupling}}$ was 0.18 higher than the measured in situ pre-stretch ${\mathit{\lambda }}_z^{\text{in situ}}$, but the difference decreased with age, and for the old FPAs the two values were closer (0.04 difference). The average stored energy ΔW decreased with age (Figure 7B) (r = −0.65, p < 0.01) from 2.3 kPa to 0.4 kPa, suggesting that older FPAs had an almost 6-fold less stored energy available for elastic deformation compared with younger FPAs.

Figure 7:

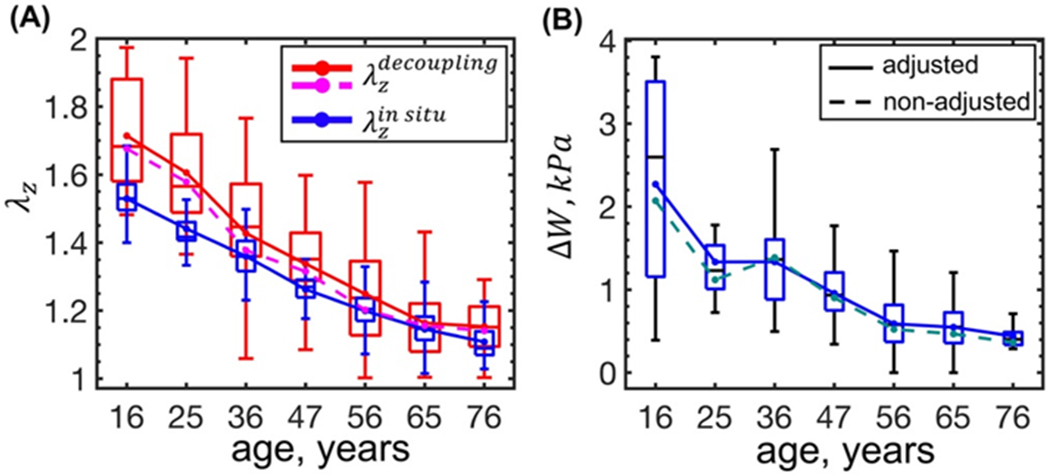
(A) In situ longitudinal pre-stretch (${\mathit{\lambda }}_z^{\text{in situ}}$, blue) compared with the decoupling pre-stretch (${\mathit{\lambda }}_z^{\text{decoupling}}$, red and magenta) at which the internal pressure becomes independent of the axial force; (B) change in the FPA stored energy (i.e. ΔW = W_sys − W_dias) with age calculated using the adjusted parameters (solid lines) and the non-adjusted parameters (dashed lines). Boxes bound 25^th and 75^th percentiles for each age group, median and average values are marked with a line and a dot within each box, and whiskers extend to the 5^th and 95^th percentiles. Boxes are plotted for the data adjusted for the flattening deformations.

4. DISCUSSION

Planar biaxial extension is a common test to characterize the complex mechanical properties of arterial tissue, particularly when studying large human or porcine arteries. It is more popular and generally easier to perform than inflation-extension testing because it does not require branch ligation, pre-stretching of the sample to its in situ length to avoid buckling, or tackling image analysis issues associated with tracking the fuzzy adventitial surface. But despite its advantages, planar biaxial test has two major limitations. First, it requires the tubular specimen to be radially cut, which releases the intramural residual stresses. Second, the radially-cut specimen needs to be flattened to be attached to the biaxial device. This introduces additional stresses to the specimen that may influence constitutive parameter determination, and affect calculation of the physiologic stress-stretch state. The goal of the current study was to quantify the effects associated with specimen flattening during planar biaxial testing, and determine how they affect the calculated physiologic stress-stretch state and the stored elastic energy. We have focused our analysis on human FPAs because of the importance to understand their mechanical characteristics for computational modeling aimed at improving the outcomes of PAD interventions and reconstructions. Since flattening characteristics may be a function of age, we have analyzed a large database of human FPAs 12-82 years old, and have reported constitutive parameters adjusted for the effects of flattening that can be directly used in computational and constitutive modeling.

Our results demonstrate that the FPAs were overall 12 ± 4% stiffer longitudinally and 19 ± 11% stiffer circumferentially when biaxially tested, suggesting that most specimens experienced tension in both directions when flattened. Though flattening stretches reduced with age as the longitudinal and circumferential opening angles became wider, the arteries also stiffened in both directions. Longitudinally, increase in stiffness with age balanced the increase in the longitudinal opening angle β, which resulted in a relatively constant difference between the adjusted and the non-adjusted longitudinal stress-stretch curves across all age groups. Circumferentially, higher stiffness trumped the increase in the circumferential opening angle α, resulting in the overall larger differences in the stress-stretch curves plotted using the adjusted and the non-adjusted parameters. Nevertheless, despite these differences that persisted across all age groups and both directions, the effects of flattening were substantially smaller than the intersubject variability within each age group.

Observed increase in the longitudinal and the circumferential opening angles with age agrees well with other studies(Saini et al. 1995; Alford et al. 2008; Kamenskiy et al. 2017; Desyatova et al. 2017a). Growth and remodeling of the intramural constituents produces multiaxial residual stretches and stresses that change as a function of age(Valentín et al. 2011; Kamenskiy et al. 2015) and alter both the circumferential and the longitudinal opening angles. In the FPA, longitudinally-oriented elastic fibers in the EEL are under significant tension in maturity, which makes them primarily responsibe for both curving of the axially-cut strip intima outward(Kamenskiy et al. 2017), and for the in situ longitudinal pre-stretch(Cardamone et al. 2009; Kamenskiy et al. 2017). Degradation and fragmentation of these elastic fibers with age releases the tension and results in wider β and flatter longitudinal strips(Kamenskiy et al. 2015; Kamenskiy et al. 2017). Circumferentially, increase in the opening angle α may be associated with hypertrophy of the medial SMCs and the greater accumulation of collagen in the inner (as opposed to the outer) part of the media(Feldman and Glagov 1971).

Differences in the stress-stretch responses obtained using constitutive parameters adjusted and non-adjusted for the flattening effects, did not translate into large differences in the physiologic variables. Physiologic stresses, stretches, axial force, circumferential stiffness, and stored energy were all qualitatively and quantitatively similar when calculated with and without the flattening effects. At the same time, the kinematic framework that considered both the flattening and the residual effects, permitted detailed description of changes experienced by human FPAs with age.

Our data demonstrate that the physiologic stresses and stretches decreased with age, and this decrease was much more pronounced in the longitudinal direction (almost 5-fold), than circumferentially (1.5-2.5-fold). To facilitate reduction in the longitudinal stress, the FPAs elongated, which reduced the in situ longitudinal pre-stretch, and decreased the associated axial force(Kamenskiy et al. 2016). Circumferentially, FPA stiffening was compensated by increased thickness, which resulted in the overall constant physiologic stiffness E_θ for the arteries between 25 and 65 years of age, but a decreasing stored energy ΔW available for elastic deformation.

Constant physiologic circumferential stiffness E_θ in the setting of decreasing physiologic intramural stresses, stretches, and elastic energy with age, suggests the existence of the homeostatic state that is regulated by the physiologic stiffness rather than the intramural stresses(Humphrey 2008; Humphrey et al. 2014). It is important to distinguish this stiffness from the one measured experimentally with planar biaxial (i.e. Figure 3) or inflation-extension testing because it incorporates longitudinal pre-stretch and residual stresses. This result demonstrates the importance of ex vivo mechanical characterization and constitutive modeling to assess the in vivo FPA physiology, as most of the involved parameters cannot be directly measured in vivo.

Conversely, the presented framework can help estimate some of the FPA characteristics that require arterial excision, such as the in situ longitudinal pre-stretch. Our data demonstrate that the longitudinal pre-stretch at which the axial force decouples from the luminal pressure is close to the measured in situ longitudinal pre-stretch in older FPAs. This agrees with previous findings in animal and human arteries from other locations(Van Loon et al. 1977; Schulze-Bauer et al. 2003), and suggests that in the elderly the in situ longitudinal pre-stretch serves to minimize the axial work done by the artery during the cardiac cycle. This finding is particularly interesting in the context of the observed decrease in the FPA elastic stored energy with age, suggesting that as the artery stiffens and has less available energy for physiologic pulsation, the in situ pre-stretch adapts to support the energy efficiency. In younger FPAs, the decoupling stretch needs to be significantly higher than the in situ longitudinal pre-stretch to achieve energy efficiency, which may be associated with a substantial axial force that can be damaging to the tissue. At the same time, young artery has significantly more available energy for pulsation, which may make the energy efficiency less critical.

While presented results demonstrate the utility of planar biaxial testing in studying the in vivo physiologic stress-stretch state of the FPA, and provide a set of constitutive parameters that can be readily used for computational modeling, it is important to compare them with the results of inflation-extension testing in the future. It is also important to consider these results in the context of study limitations. First, we assumed homogeneity of the FPA wall, but the medial and adventitial layers are known to be significantly different in structure. In the FPA, tunica media is composed primarily of circumferentially-oriented smooth muscle cells and amorphous collagen, while tunica adventitia has undulated collagen fibers with preferred orientation. Furthermore, the interface between the media and the adventitia, the EEL, contains longitudinally-oriented elastic fibers that are under tension(Kamenskiy et al. 2016). Due to complexity of this structure, flattening of the circumferential and longitudinal strips likely produces more complex stresses at the interfaces and through the thickness of the FPA wall, than those calculated using one set of constitutive parameters determined for the entire specimen. Nevertheless, layer separation and their individual testing may not be the best solution to this issue for at least two reasons. First, adequate and atraumatic layer separation is challenging, and may be impossible in younger healthier FPAs. In older and more diseased arteries, layers themselves become highly inhomogeneous which likely requires further compartmentalization. Second, layer separation changes the state of the arterial wall and disrupts the interfaces, which raises the question of whether arterial layers tested separately and combined computationally will produce similar mechanical responses as a non-separated specimen.

Another limitation is that current analysis neglected the effects of perivascular tethering on the outer surface of the FPA wall, which likely affected the assessment of physiologic stress-stretch conditions. Additional experiments are needed to quantify perivascular tethering effects(Ferruzzi et al. 2018) in human FPAs, and to determine whether they change with age and disease. While these and other limitations are being addressed, current analysis provides a better understanding of the effects associated with flattening of the FPA specimens during planar biaxial testing, and offers a set of adjusted constitutive parameters that can be used to model the physiologic FPA behavior in subjects of different ages.

7. APPENDIX

7.1. Cauchy stresses

The components of the isochoric Cauchy stress tensor $\stackrel{‒}{\mathit{t}}$ associated with each of the residual, physiologic, and flattening deformations can be calculated by taking the appropriate derivatives in Eq. 3 and using a form of strain energy function defined by Eq. 1 and Eq. 2. This produces Cauchy stresses in the form

$$\begin{gathered} {\overline{t}}_{rr}=c_{gr}{\mathit{\lambda }}_r^2=c_{gr}\frac{1}{{\mathit{\lambda }}_z^2{\mathit{\lambda }}_{\theta }^2}, \\ {\overline{t}}_{\theta \theta }=c_{gr}{\mathit{\lambda }}_{\theta }^2+c_1^{smc}\langle {\mathit{\lambda }}_{\theta }^2-1\rangle e^{c_2^{smc}{({\mathit{\lambda }}_{\theta }^2-1)}^2}{\mathit{\lambda }}_{\theta }^2+2c_1^{col}\langle I_4^{col}-1\rangle e^{c_2^{col}{(I_4^{col}-1)}^2}{\mathit{\lambda }}_{\theta }^2{\mathit{sin}}^2\gamma , \\ {\overline{t}}_{zz}=c_{gr}{\mathit{\lambda }}_z^2+c_1^{el}\langle {\mathit{\lambda }}_z^2-1\rangle e^{c_2^{el}{({\mathit{\lambda }}_z^2-1)}^2}{\mathit{\lambda }}_z^2+2c_1^{col}\langle I_4^{col}-1\rangle e^{c_2^{col}{(I_4^{col}-1)}^2}{\mathit{\lambda }}_z^2{\mathit{cos}}^2\gamma , \end{gathered}$$

with

$$I_4^{col}={\mathit{\lambda }}_z^2{\mathit{cos}}^2\gamma +{\mathit{\lambda }}_{\theta }^2{\mathit{sin}}^2\gamma$$

where r, θ, z are used to point out that these directions align with the radial, circumferential and longitudinal directions of the artery in vivo. When considering specimen flattening, stretches λ_r, λ_θ, λ_z need to be substituted with λ₁, λ₂, λ₃. When considering residual deformations, they need to be substituted with λ_ρ, λ_ϑ, λ_ζ. Finally, when considering physiologic deformations, these stretches need to be substituted with ${\mathit{\lambda }}_r^{\mathit{phys}},{\mathit{\lambda }}_{\theta }^{\mathit{phys}},{\mathit{\lambda }}_z^{\mathit{phys}}$.

7.2. Obtaining through-thickness values of stretch and stress

Through-thickness average values of stretch and stress were calculated by integrating them over the current volume and dividing the result by the total current volume. In Cartesian coordinates, since the stretches and the stresses vary through specimen thickness, this takes the form:

$$\begin{gathered} {\mathit{\lambda }}_{2,3}^{ave}=\frac{\int \int \int {\mathit{\lambda }}_{2,3}dv}{\int \int \int dv}=\frac{{\int }_0^{L_1}{\mathit{\lambda }}_{2,3}d{x}_1}{{\int }_0^{L_1}d{x}_1}=\frac{{\int }_0^{L_1}{\mathit{\lambda }}_{2,3}d{x}_1}{L_1}, \\ {t}_{22,33}^{ave}=\frac{\int \int \int t_{22,33}dv}{\int \int \int dv}=\frac{{\int }_0^{L_1}{t}_{22,33}d{x}_1}{{\int }_0^{L_1}d{x}_1}=\frac{{\int }_0^{L_1}{t}_{22,33}d{x}_1}{L_1}, \end{gathered}$$

where L₁ is the thickness of the flattened specimen. Similarly in the cylindrical coordinates:

$$\begin{gathered} {\mathit{\lambda }}_{\theta }^{avg}=\frac{\int \int \int {\mathit{\lambda }}_{\theta }^{phys}rdrd\theta dz}{\int \int \int rdrd\theta dz}=\frac{{\int }_{r_i}^{r_o}{\mathit{\lambda }}_{\theta }^{phys}rdr}{{\int }_{r_i}^{r_o}rdr}, \\ {t}_{\theta \theta }^{avg}=\frac{\int \int \int t_{\theta \theta }^{phys}rdrd\theta dz}{\int \int \int rdrd\theta dz}=\frac{{\int }_{r_i}^{r_o}{t}_{\theta \theta }^{phys}rdr}{{\int }_{r_i}^{r_o}rdr}. \end{gathered}$$

7.3. Kinematics of the residual and physiologic deformations

The stress-free (reference) configuration (Figure 1A) is defined in terms of cylindrical coordinates (R, Θ, Z) as

$$R_i\le R\le R_o,0\le \Theta \le 2\pi -\alpha ,0\le Z\le L,$$

where R_i, R_o, α and L are the inner and outer radii, opening angle, and the length of the stress-free arterial segment, respectively. The deformation gradient F_res takes this configuration into the load-free state (Figure 1B) geometrically defined as

$${\rho }_i\le \rho \le {\rho }_o,0\le \vartheta \le 2\pi ,0\le \zeta \le \xi ,$$

in which

$$\rho =\rho \left(R\right),\vartheta =\frac{2\pi }{2\pi -\alpha }\Theta ,\zeta ={\mathit{\lambda }}_{\zeta }Z.$$

In cylindrical coordinates F_res is then given by

$${\mathit{F}}_{res}=diag\left[\frac{\partial \rho }{\partial R},\frac{\rho }{R}\frac{\partial \vartheta }{\partial \Theta },\frac{\partial \zeta }{\partial Z}\right]=diag\left[{\mathit{\lambda }}_{\rho },{\mathit{\lambda }}_{\vartheta },{\mathit{\lambda }}_{\zeta }\right],$$

where λ_ρ, λ_ϑ and λ_ζ are the radial, circumferential and longitudinal residual stretches respectively, with λ_ϑ given by(Ogden 1997; Holzapfel et al. 2000; Humphrey 2002; Sommer and Holzapfel 2012; Kamenskiy et al. 2014)

$${\mathit{\lambda }}_{\vartheta }=\frac{\rho }{R}\mathrm{K}$$ Eq. 9

and $\mathrm{K}=\frac{2\pi }{2\pi -\alpha }$ is a measure of the circumferential opening angle. Assuming incompressibility, one can write

$${\rho }_o^2-{\rho }_i^2=\frac{1}{\mathrm{K}{\mathit{\lambda }}_{\zeta }}(R_o^2-R_i^2),$$ Eq. 10

and similarly

$${\rho }_o^2-{\rho }^2=\frac{1}{\mathrm{K}{\mathit{\lambda }}_{\zeta }}(R_o^2-R^2).$$ Eq. 11

By substituting R form Eq. 11 in Eq. 9, the circumferential residual stretch λ_ϑ can be calculated at each point through thickness as a function of ρ, R_o, K, ${\mathit{\lambda }}_{\vartheta }^o$, λ_ζ, given by Eq. 6.

Further, deformation F_load takes the load-free configuration to the loaded (current) configuration (Figure 1C) which in cylindrical coordinates is defined as

$$r_i\le r\le r_o,0\le \theta \le 2\pi ,0\le z\le l,$$

where

$$r=r\left(\rho \right),\theta =\vartheta ,z={\mathit{\lambda }}_z\zeta .$$

F_load is given by

$${\mathit{F}}_{load}=diag\left[\frac{\partial r}{\partial \rho },\frac{r}{\rho }\frac{\partial \theta }{\partial \vartheta },\frac{\partial z}{\partial \zeta }\right]=diag\left[{\mathit{\lambda }}_r,{\mathit{\lambda }}_{\theta },{\mathit{\lambda }}_z\right],$$

in which ${\mathit{\lambda }}_{\theta }=\frac{r}{\rho }$ is the circumferential stretch. Assuming incompressibility, similar to Eq. 11

$$r_o^2-r^2=\frac{1}{{\mathit{\lambda }}_z}({\rho }_o^2-{\rho }^2).$$ Eq. 12

The total deformation gradient with respect to the stress-free configuration is then given by

$${\mathit{F}}_{phys}={\mathit{F}}_{load}{\mathit{F}}_{res},$$

in which, the circumferential stretch is calculated as

$${\mathit{\lambda }}_{\theta }^{phys}={\mathit{\lambda }}_{\vartheta }{\mathit{\lambda }}_{\theta }=\frac{\rho }{R}\mathrm{K}\times \frac{r}{\rho }=\frac{r}{R}\mathrm{K}$$

By substituting ${\rho }_o^2-{\rho }^2$ from Eq. 10 in Eq. 12, one can find ${\mathit{\lambda }}_{\theta }^{\mathit{phys}}$ as a function of r, R_o, K, ${\mathit{\lambda }}_{\vartheta }^o$, λ_ζ, λ_z, given by Eq. 7.

7.4. Equilibrium and boundary conditions

The total Cauchy stress in Eq. 3 (i.e. $\mathit{t}=-p\mathit{I}+\stackrel{‒}{\mathit{t}}$) contains both volumetric and isochoric parts(Ogden 1997; Humphrey 2002; Holzapfel and Ogden 2010a). Constitutive parameters define the isochoric stress tensor $\stackrel{‒}{\mathit{t}}$ (Section 2.2), but the volumetric component −pI needs to be determined from the equilibrium and boundary conditions(Humphrey 2002; Holzapfel and Ogden 2010a).

Assuming quasi-static motions(Humphrey 2002), in the absence of body forces, for each of the deformations depicted in Figure 1, the equilibrium equation is

$$div\mathit{t}=0,$$ Eq. 13

where div represents the spatial divergence. Eq. 13 can then be used to find the Lagrange multiplier p in Eq. 3, along with the unknown stretches.

For the deformation associated with the specimen flattening Eq. 13 reduces to(Ogden 1997) t₁₁ = 0, and from Eq. 3 the volumetric part of the Cauchy stress can then be determined as $p={\stackrel{‒}{t}}_{11}$.

In the load-free configuration, the only non-trivial component of Eq. 13 is(Humphrey 2002; Holzapfel and Ogden 2010a)

$$div\mathit{t}=0\Rightarrow \frac{\partial t_{\rho \rho }}{\partial \rho }+\frac{t_{\rho \rho }-t_{\vartheta \vartheta }}{\rho }=0$$

which reduces to

$$t_{\rho \rho }\left(\rho \right)={\int }_{{\rho }_i}^{\rho }\frac{{\overline{t}}_{\vartheta \vartheta }-{\overline{t}}_{\rho \rho }}{\rho }d\rho ,$$ Eq. 14

for t_ρρ(ρ_i) = 0. The Lagrange multiplier can then be calculated at each point through the thickness of the artery by substituting t_ρρ into Eq. 3, i.e.

$$p\left(\rho \right)={\overline{t}}_{\rho \rho }-t_{\rho \rho }.$$

In addition, since axial force vanishes in the load-free configuration due to release of longitudinal pre-stretch, the axial global equilibrium can be written as(Humphrey 2002; Holzapfel and Ogden 2010a)

$$F_{\zeta }=2\pi {\int }_{{\rho }_i}^{{\rho }_o}{t}_{\zeta \zeta }\rho d\rho =0,$$ Eq. 15

where F_ζ denotes the axial force. The above equation can be further reduced to(Humphrey 2002)

$$F_{\zeta }=\pi {\int }_{{\rho }_i}^{{\rho }_o}\left(2{\overline{t}}_{\zeta \zeta }-{\overline{t}}_{\rho \rho }-{\overline{t}}_{\vartheta \vartheta }\right)\rho d\rho =0.$$ Eq. 16

Eq. 14 and Eq. 16 combined with the boundary condition t_ρρ(ρ_o) = 0 are then solved together to calculate the unknown stretches ${\mathit{\lambda }}_{\vartheta }^o$ and $\frac{\xi }{L}$ in Eq. 6.

Similar to Eq. 14, for the loaded configuration (Figure 1C) one can write

$$t_{rr}\left(r\right)={\int }_{r_i}^r\frac{{\overline{t}}_{\theta \theta }-{\overline{t}}_{rr}}{r}dr-P_i,$$ Eq. 17

where P_i is the internal luminal pressure, and the Lagrange multiplier is determined according to

$$p(r)={\stackrel{‒}{t}}_{\mathit{rr}}-t_{\mathit{rr}}.$$

Furthermore, assuming no pressure on the outer surface of the artery one can find

$$t_{rr}\left(r_o\right)={\int }_{r_i}^{r_o}\frac{{\overline{t}}_{\theta \theta }-{\overline{t}}_{rr}}{r}dr-P_i=0,$$ Eq. 18

which can be used to find ${\mathit{\lambda }}_{\theta }^o$ in Eq. 7. Finally, the axial force in the loaded configuration can be calculated from(Humphrey 2002)

$$F_z=\pi {\int }_{r_i}^{r_o}\left(2{\overline{t}}_{zz}-{\overline{t}}_{rr}-{\overline{t}}_{\theta \theta }\right)rdr.$$ Eq. 19

7.5. Variability of the mechanical properties within age groups

The four-fiber family constitutive parameters adjusted for the effects of flattening and representing the 25^th and 75^th percentiles within each age group, are summarized in Table 2 and Table 3, respectively.

Table 2:

Parameters for the four-fiber family constitutive model describing the isochoric behavior of human FPAs in 7 age groups at the 25^th percentile. Parameters are adjusted for the effects of flattening. Here n is the sample size in each group that was used to derive these parameters. The coefficient of determination R²=0.99 for all age groups.

Age group (years)	n	Cgr(kPa)	$C_1^{\mathit{el}}(kPa)$	$C_2^{\mathit{el}}$	$C_1^{\mathit{smc}}(kPa)$	$C_2^{\mathit{smc}}$	$C_1^{\mathit{col}}(kPa)$	$C_1^{\mathit{col}}$	γ°
16.3 (11-20)	30	11.33	26.22	0.43	13.81	0.01	3.55	4.84	1.18
25.0 (21-30)	37	15.99	16.28	0.72	7.00	7.33	1.32	7.96	1.03
36.0 (31-40)	56	15.98	17.85	1.17	11.89	10.47	4.32	6.08	0.84
46.5 (41-50)	64	18.98	17.04	2.59	13.39	21.87	3.31	9.76	0.81
56.1 (51-60)	125	20.13	7.88	9.64	20.60	27.67	5.14	23.97	0.85
65.0 (61-70)	135	14.37	9.31	18.14	10.14	32.62	11.02	31.89	0.77
75.5 (70-80)	25	0.02	25.11	31.28	33.92	30.04	23.22	61.82	0.82

Table 3:

Parameters for the four-fiber family constitutive model describing the isochoric behavior of human FPAs in 7 age groups at the 75^th percentile. Parameters are adjusted for the effects of flattening. Here n is the sample size in each group that was used to derive these parameters. The coefficient of determination R²=0.99 for all age groups.

Age group (years)	n	Cgr(kPa)	$C_1^{\mathit{el}}(kPa)$	$C_2^{\mathit{el}}$	$C_1^{\mathit{smc}}(kPa)$	$C_2^{\mathit{smc}}$	$C_1^{\mathit{col}}(kPa)$	$C_1^{\mathit{col}}$	γ°
16.3 (11-20)	30	0.00	19.03	0.00	2.86	0.79	4.85	0.59	0.95
25.0 (21-30)	37	2.86	16.17	0.09	6.30	1.42	4.77	1.12	0.95
36.0 (31-40)	56	6.79	13.83	0.42	4.73	2.80	2.93	2.36	0.95
46.5 (41-50)	64	7.79	14.03	1.20	5.56	3.34	1.69	5.26	0.90
56.1 (51-60)	125	0.01	18.86	1.47	7.84	4.34	4.95	4.90	0.86
65.0 (61-70)	135	1.56	19.64	2.98	8.39	5.16	1.77	11.83	0.81
75.5 (70-80)	25	4.27	25.31	4.20	10.81	4.06	1.08	15.43	0.80