Abstract
The thermal-based Two-Source Energy Balance (TSEB) model partitions the evapotranspiration (ET) and energy fluxes from vegetation and soil components providing the capability for estimating soil evaporation (E) and canopy transpiration (T). However, it is crucial for ET partitioning to retrieve reliable estimates of canopy and soil temperatures and net radiation, as the latter determines the available energy for water and heat exchange from soil and canopy sources. These two factors become especially relevant in row crops with wide spacing and strongly clumped vegetation such as vineyards and orchards. To better understand these effects, very high spatial resolution remote-sensing data from an unmanned aerial vehicle were collected over vineyards in California, as part of the Grape Remote sensing and Atmospheric Profile and Evapotranspiration eXperiment and used in four different TSEB approaches to estimate the component soil and canopy temperatures, and ET partitioning between soil and canopy. Two approaches rely on the use of composite Trad, and assume initially that the canopy transpires at the Priestley–Taylor potential rate. The other two algorithms are based on the contextual relationship between optical and thermal imagery partition Trad into soil and canopy component temperatures, which are then used to drive the TSEB without requiring a priori assumptions regarding initial canopy transpiration rate. The results showed that a simple contextual algorithm based on the inverse relationship of a vegetation index and Trad to derive soil and canopy temperatures yielded the closest agreement with flux tower measurements. The utility in very high-resolution remote-sensing data for estimating ET and E and T partitioning at the canopy level is also discussed.
Introduction
The use of unmanned aerial vehicles (UAVs) for estimating water use and crop stress has been gaining much interest in recent years. This is due in part to a tremendous increase in the availability of UAVs and advancement in sensor technology that supports UAV platforms. The very high-resolution data obtained with UAVs can provide estimates of both leaf canopy temperatures and background soil/ground cover temperatures. Methods are under development to apply very high-resolution UAV imagery for precision ET monitoring (e.g., Zipper and Loheide 2014; Hoffmann et al. 2016; Ortega-Farías et al. 2016). Others are using high-resolution thermal imagery in a crop water stress index (CWSI) approach for estimating leaf water potential for irrigation scheduling (Bellvert et al. 2016).
Few models have had the capability to compute robust fluxes over a variety of surface conditions and at the same time partition fluxes from the vegetated canopy and underlying soil/substrate layer. One such modeling approach is the Two-Source Energy Balance (TSEB) land surface scheme that contains a level of complexity that makes it robust for many different landscapes (Kustas and Anderson 2009). The TSEB land surface scheme has been integrated into a multi-scale model operating at regional scales (Anderson et al. 2011) and recently implemented in a data fusion scheme allowing for daily ET estimates at 30 m resolution (Cammalleri et al. 2013, 2014), much more useful for agricultural water management.
However, for certain high-valued crops, such as vineyards as well as orchards, information needs to be at plant or irrigation sector level to identify levels of plant stress and how it varies at the vine/tree level over a field. Water deficit, nutrient deficiencies, or disease/pest infestation which all lead to plant stress can be detected from elevated plant temperatures that deviate from the surrounding observed plant temperatures. This allows for variable rate application of water, nutrients, or fungicide/pesticide within a field. For irrigation management in vineyards, knowing the water use of the inter-row (consisting of a cover crop or bare soil) and vine crop is important, since it relates to water availability in the root zone. Thus, having thermal and visible/near-infrared imagery that is fine enough resolution to discriminate between interrow and vine will provide the means to properly partition the energy fluxes and ET between the two sources. In addition, compared to moderate-resolution data from Landsat, for example, the finer resolution imagery can more accurately identifying features in a vineyard affecting overall water use (Xia et al. 2016).
TSEB partitions the surface energy fluxes between nominal soil and canopy sources using estimates of soil (TS) and canopy temperatures (TC). Because direct measurements of canopy temperatures are rarely available, in most applications, these component temperatures have been derived from a measurement of the bulk composite surface radiometric temperature Trad. When only a single observation of composite Trad is available (i.e., measurement at a single angle), the estimation of TC or TS requires some assumptions. One approach developed for TSEB (Norman et al. 1995) starts with an initial estimate of TC that assumes plants are transpiring at a potential rate, as defined by the Priestley and Taylor (1972) formulation, and thus requires a reasonable estimate of the energy used for transpiration. The green fraction of vegetation (fg) has become an important parameter within this approach, since it acts as a scaling factor for the potential transpiration, by taking into account the phenological development of the vegetation. For example, Guzinski et al. (2013) showed an improvement of TSEB accuracy by adjusting the magnitude of fg in forested ecosystems and in crops during senescence. In alternate forms of the TSEB model, direct estimates of soil and canopy temperatures obtained without employing any assumptions based on the canopy transpiration have been used (Chehbouni et al. 2001; Kustas and Norman 1997; Morillas et al. 2013; Song et al. 2015). Several approaches for such retrieval have been proposed by measuring soil and canopy temperatures separately (Morillas et al. 2013) or by analytically solving Eq. 1 with observations of Trad at two different viewing angles (Kustas and Norman 1997).
In this paper, the TSEB land surface scheme is applied to UAV high-resolution data collected during Intensive Observation Periods (IOPs) for the Grape Remote sensing and Atmospheric Profile and Evapotranspiration eXperiment (GRAPEX). Our hypothesis is that using high enough spatial resolution imagery, both TS and TC can be estimated directly without the need for an initial assumption of potential transpiration or greenness status, and hence compute better estimates of turbulent fluxes than using coarser scale composite Trad. However, because of the much finer resolution of the UAV data, associated with this is an increase in complexity of modeling of key processes which include the radiation transmission and wind attenuation through the vine canopy, which has non-uniform vertical leaf area distribution (e.g., often most of the LAI is concentrated in the upper half of the vine canopy). In addition, the original TSEB formulations were developed to be applied at the micrometeorological scale with variables for aerodynamic resistance terms relating to scales on the order of 102 m and radiation and radiometric temperatures at resolutions that contain a mixture of canopy and soil/substrate contributions (Xia et al. 2016). Therefore, it is of interest to evaluate TSEB (or any other resistance energy-based model) at finer scales which are required in precision irrigation (Bellvert et al. 2016).
Materials
The UAV imagery was collected over two Pinot noir blocks located within the Borden vineyard near Lodi, CA (38.29 N 121.12 W), in Sacramento County as part of the GRAPEX project. The two adjacent vineyards differ in the age and maturity of the vines, with the north and south vineyards being planted in 2005 and 2008, respectively. The management of the two vineyards, which include the timing and amount of irrigation, pruning activities, cover crop management, and application of agrochemicals, also differed from season to season and between the blocks due to variation in weather and climate conditions.
In both fields, the configuration of the trellising system and interrow is the same. The vine trellises are 3.35 m apart and run east–west. There is an individual vine planted every 1.52 m, with the two main vine stems attached to the first cordon at a height of 1.45 m above ground level (agl). There is a second cordon at 1.9 m agl, where vine shoots are managed. Typically, the vines reach a maximum height of between 2.0 and 2.5 m agl during the growing season with the vine biomass concentrated in the upper half of the total canopy height. The typical vine canopy width is nominally 1 m mid-season. Pruning of the vines is mainly performed to remove shoots growing significantly into the interrow. However, the amount and timing of pruning have varied between growing seasons, so that leaf area and its vertical distribution were not the same in each growing season. Finally, a crop covering the interrow is present in spring; then, it is usually mowed between May and June and cured in summer becoming dead stubble.
Three-to-four Intensive Observation Periods (IOPs) were conducted every year since 2014 (typically in April June, July, and/or August) coinciding with different grapevine phenological stages. However, due to the UAV system availability as well as budget constraints, not all years had the same number of IOPs or had UAV imagery collected. For this study, UAV imagery was collected in 2014 during the early August IOP, in 2015 during the early June IOP as well as in the late July IOP, and in 2016 during the early May IOP (see Table 1). The times of acquisition were approximately 1–2 h after local sunrise (07:00–08:00 PDT), during the Landsat 7/8 overpass time (nominally 11:45 PDT) and in the afternoon near peak atmospheric demand (between 15:00 and 16:00 PDT). The UAV system flew at 450 m agl, resulting in 0.15 m pixel resolution in the visible and near-infrared bands and 0.60 m resolution in the thermal infrared. The visible and near-infrared sensors wavebands are similar to the Landsat blue, green, red, and near-infrared channels, while the thermal-infrared spans the 8–14 micrometer wavelengths, with a Field of View of 49°and a reported accuracy of 1 K. Before the flight, the thermal camera onboard the UAV was calibrated by comparing its values with a NIST traceable blackbody. Later, during the flight, in situ blackbody temperatures were acquired over homogeneous warm and cold reference targets using a second thermal camera, to evaluate the atmospheric contribution at the UAV mounted camera. Finally, an assessment of temperature was also performed using both Trad derived from pyrgeometers on the EC system and concomitant Landsat Trad. More details about the a vicarious calibration/validation of the atmospheric effects on the UAV thermal camera is described by Torres-Rua (2017). Finally, the structure from motion approach used for the image ortho-rectification and mosaicking allowed the generation of a photogrammetric 3D point cloud that was also used in this study.
Table 1.
Dates and times (launch and landing) of AggieAir GRAPEX flights
| Date | IOP | Morning flight | Landsat flight | Afternoon flight | |||
|---|---|---|---|---|---|---|---|
| Launch | Landing | Launch | Landing | Launch | Landing time | ||
| August 09, 2014 | 4 | 7:10 AM | 7:30 AM | 11:30 AM | 11:50 AM | No flight planned | |
| June 02, 2015 | 2 | 6:51 AM | 7:32 AM | 11:21 AM | 12:06 PM | 2:54 PM | 3:20 PM |
| July 11, 2015 | 3 | 6:37 AM | 7:11 AM | 11:26 AM | 12:00 PM | 2:58 PM | 3:31 PM |
| May 02, 2016 | 1 | 8:13 AM | 8:35 AM | 12:53 PM | 1:17 PM | 3:52 PM | 4:16 PM |
| May 03, 2016 | 1 | 8:40 AM | 9:06 AM | No flight due to clouds | 1:35 PM | 2:00 PM | |
All times are expressed in Pacific Daylight-Saving Time zone
The eddy covariance/energy balance systems were located approximately 20 m inside the vineyard at the east edge to have an adequate fetch for the prevailing winds from the west. A detailed description of the measurements and their post-processing is described by Alfieri et al. (2018). Briefly, the tower at each site is instrumented with an infrared gas analyzer (EC150, Campbell Scientific,1 Logan, Utah) and a sonic anemometer (CSAT3, Campbell Scientific) co-located at 5 m agl to measure the concentrations of water and carbon dioxide and wind velocity, respectively. The full radiation budget was measured using a four-component net radiometer (CNR-1, Kipp and Zonen, Delft, The Netherlands) mounted at 6 m agl. Air temperature and water vapor pressure at 5 m agl were measured using a Gill-shielded temperature and humidity probe (HMP45C, Vaisala, Helsinki, Finland). Subsurface measurements include the soil heat flux measured via a cross-row transect of five plates (HFT-3, Radiation Energy Balance Systems, Bellevue, Washington) buried at a depth of 8 cm, soil temperature measured via thermocouples buried at a depth of 2 cm and 6 cm, and soil moisture content measured via a soil moisture probe (HydraProbe, Stevens Water Monitoring Systems, Portland, OR) buried at a depth of 5 cm. Overall closure error of both EC system during the 3 year study period is around 85%. When looking at the individual closure errors during the UAV acquisitions, a larger variability in the energy balance closure is observed, with the largest closure error occurring for the afternoon flight on May 2nd 2016 (66%). For the rest of overpasses in Table 1, the closure is above 80%.
Methodology
The TSEB land surface energy balance scheme was developed to explicitly account for the differences in aerodynamic coupling between the soil/substrate, the canopy layer (Norman et al. 1995), and the surface layer above the canopy. Figure 1 illustrates the basic set of equations used in TSEB to solve for the energy balance of both the soil/substrate and vegetation canopy layers, assuming that canopy and soil resistances to heat and water transport are in “series”. The TSEB “series” version was chosen over the Norman et al. (1995) “parallel” version based on two main reasons: (i) overall the “series” version has shown larger robustness than the “parallel” version in a wide range of environments and conditions (Guzinski et al. 2014; Kustas et al. 2016; Li et al. 2005) and (ii) we expect that the turbulence created by the row-interrow system will enhance the heat and water exchange between soil and canopy, i.e., the hotter and drier bare soil will add extra heat to the canopy–air interface, which is explicitly (and mathematically) represented by a resistance system in series. Key inputs are the surface radiometric temperature (Trad) at a view angle (θ) and the canopy cover fraction (fC) which is related to the leaf area index (LAI). The system of equations for the energy balance of the soil/substrate and canopy is constrained through the effective soil (TS) and canopy (TC) temperatures estimated from radiometric temperature balance equation in Fig. 1 and constrained by the soil (Rs) and canopy (Rx) aerodynamic resistances to sensible (H) heat fluxes from the soil and canopy surfaces. These combine to yield the total sensible heat flux determined by the temperature difference between the canopy air space TA and the surface layer TAC and associated surface layer aerodynamic resistance (RA). The soil and canopy temperatures constrain the sensible heat fluxes, net radiation (Rn), and soil heat flux (G) with the added initial estimate of canopy latent heat flux (λEC) or transpiration based on either the Priestley–Taylor (PT), Penman–Monteith (PM), or light-use efficiency (LUE) parameterization (see Kustas and Norman 1999; Colaizzi et al. 2014; Anderson et al. 2008). Finally, the latent heat flux from the soil, λES, is computed as the residual flux. Although a crop cover is present, and photosynthetically active in sprint, for this study, this layer is considered together with the underlying soil as an ensemble source of heat and water exchange, i.e., TC corresponds to the grapevine temperature, whereas TS represents the background/interrow (soil+cover crop) temperature.
Fig. 1.
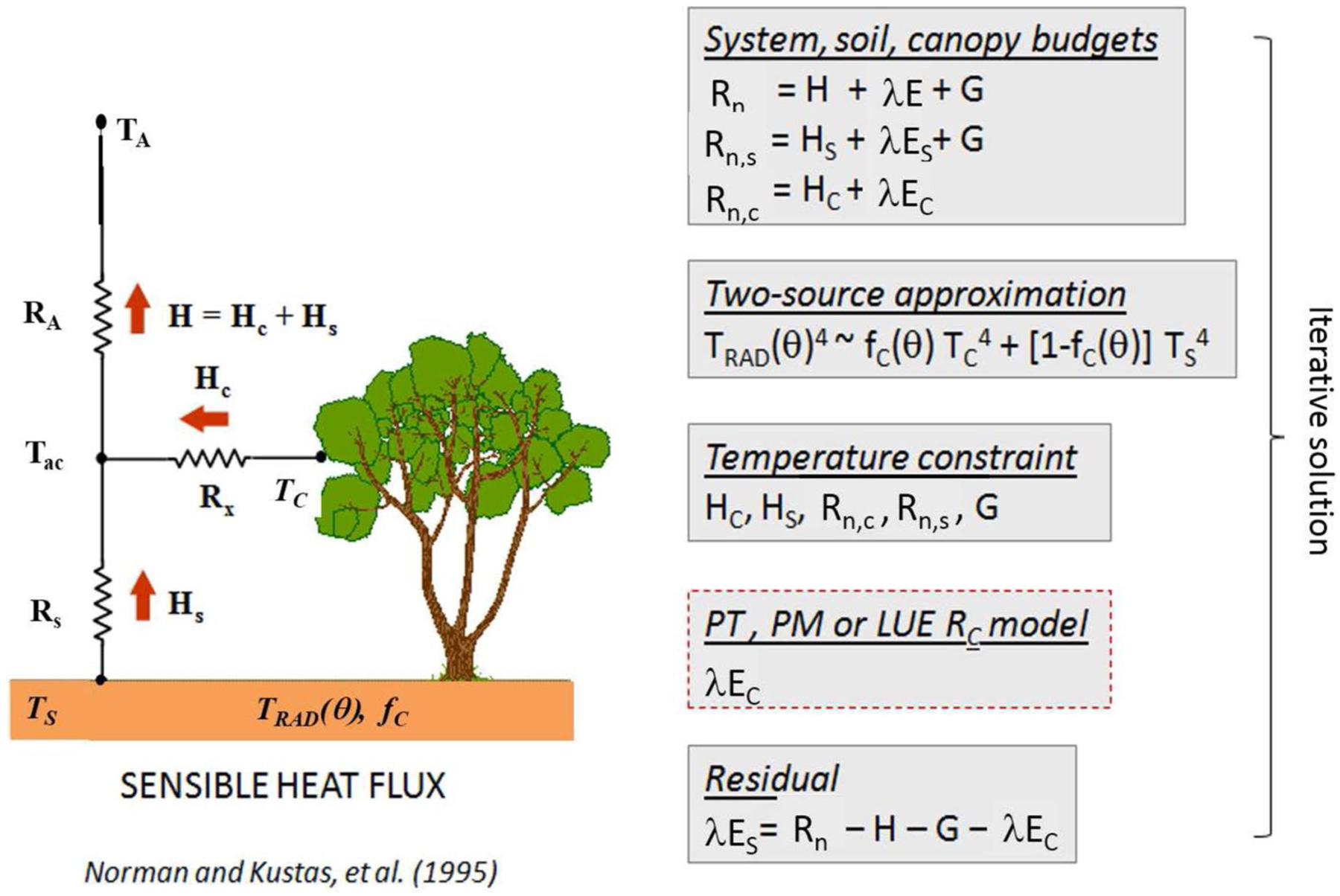
Schematic representation of the two-source energy balance model
Retrieval of canopy and soil temperatures
We evaluated two TSEB approaches that make use of composite radiometric temperature, namely, TSEB-PT (PT for Priestley–Taylor) and DTD (Dual-Temperature Difference) along with two other approaches that exploit fine-scale spatial imagery, thermal infrared, and multispectral, to derive estimates of canopy and soil temperature.
Priestley–Taylor iterative retrieval, TSEB‑PT
Given the difficulty of obtaining pure component temperatures, Norman et al. (1995) found a solution to retrieve TS and TC using a single observation of the directional radiometric temperature Trad(θ). Assuming that a composite Trad containing temperature contributions from the plant canopy and soil/substrate is what is typically provided by a radiometer, Eq. 1 decomposes the composite Trad(θ) temperature between its components TS and TC :
| (1) |
with fC(θ) being the fraction of vegetation observed by the sensor. Since Eq. 1 consists of two unknowns and only one equation, an iterative process to find HS, TS,, HC, and TC is defined based upon an initial guess of potential canopy transpiration, and under the assumption that during daytime hours, condensation should not occur. The canopy sensible heat flux is estimated based on the Priestley and Taylor (1972) potential transpiration (Eq. 2):
| (2) |
where αPT is the Priestley–Taylor coefficient, initially set to 1.26, fg is the fraction of vegetation that is green and hence capable of transpiring, Δ is the slope of the saturation vapor pressure vs. temperature, and λ is the psychrometric constant. TC is then computed by inverting the equation for turbulent transport of heat (see Norman et al. (1995)) between the surface and the reference height above the surface. With a first estimate of TC, soil temperature is computed from Eq. 1, and then, soil sensible and latent heat fluxes are estimated. At this stage, if the soil latent heat flux is non-negative, a solution is found; otherwise, canopy transpiration is reduced via an incremental decrease in αPT which effec tively increases TC and reduces TS until a realistic solution is found (no condensation-negative values of λE occurring on either the soil or the canopy). For more details, the reader is referred to Norman et al. (1995) and Kustas and Norman (1999).
Dual‑time‑difference TSEB, DTD
The DTD model described in Norman et al. (2000) is a further development of the TSEB-PT modeling scheme. DTD similarly divides the observed composite Trad into TC and TS and computes surface energy balance components following virtually the same procedure. However, DTD uses two Trad observations, one nominally 1.5 h after sunrise (Trad,0) and another during the daytime (Trad,1) with the TSEB formulation to reduce errors in deriving an atmospherically and emissivity-corrected Trad and availability of local air temperature observations. Using both tower-based and satellite observations, the utility of DTD has been evaluated over a variety landscapes showing advantages in reducing errors compared to applying TSEB when there is uncertainty in local air temperature observations (Kustas et al. 2012; Guzinski et al. 2013). In the more recent “series” implementation of DTD (Guzinski et al. 2014, 2015), the sensible heat flux at these two times, assuming that H after sunrise is minimal, is expressed as in Eq. 3:
| (3) |
Similar to TSEB-PT, Eq. 3 requires an a priori value of canopy latent or sensible heat flux (HC,i). Therefore, the same iterative process based on a first guess of potential Priestley–Taylor transpiration is needed in DTD.
In the application of TSEB with composite radiometric temperature, Trad for TSEB-PT and DTD is derived by taking the original 0.6 m thermal UAV images and aggregating the 0.6 m pixels to 3.6 m using average of the 0.6 m blackbody radiances. The value of 3.6 m corresponds to the minimum pixel size from the original 0.6 m that incorporates radiative temperature contributions from both the vine and interrow sources existing within the 3.35 m row width dimension.
Contextual TSEB for component temperature estimation, TSEB‑2T
If the soil and canopy temperatures can be derived from the LST imagery collected at high enough resolution, then the energy fluxes can be derived directly from the component temperatures without the need for a separate parametrization for the canopy transpiration (Norman et al. 1995). In this case, we obtained canopy and soil temperatures by searching for pure vegetation and soil pixels in a contextual spatial domain (Fig. 2). That is, in a 3.6 × 3.6 m grid, we assign for each of these cells the canopy and soil temperatures corresponding to the average temperature for the 0.6 m pixels that are considered, respectively, bare soil/cover crop stubble and pure vegetation. The selection criterion for detecting pure soil NDVIsoil is based on the empirical relationship between NDVI and in situ LAI, with NDVIsoil is LAI = 0 the extrapolation of that curve for. On the other hand, pure vegetation NDVI (NDVIveg) is the mean value of pixels classified as pure vegetation using a support vector machine binary supervised classification of the 0.15 m multispectral imagery. However, it may be the case that no pure pixels at the native resolution (0.6 m) are found in a 3.6 m spatial domain, either due to very dense vegetation (e.g., lack of bare soil/substrate pixels) or very sparse vegetation (e.g., lack of pure vegetation pixels). If that is the case, and assuming that there is a linear relationship between NDVI and Trad, we extrapolate to the pure vegetation or soil NDVI value the linear fit of the NDVI-Trad pairs within the 3.6 m mixed-pixel to estimate the Trad extrapolated value for the pure vegetation (or soil) within the 3.6 m aggregated pixel resolution.
Fig. 2.
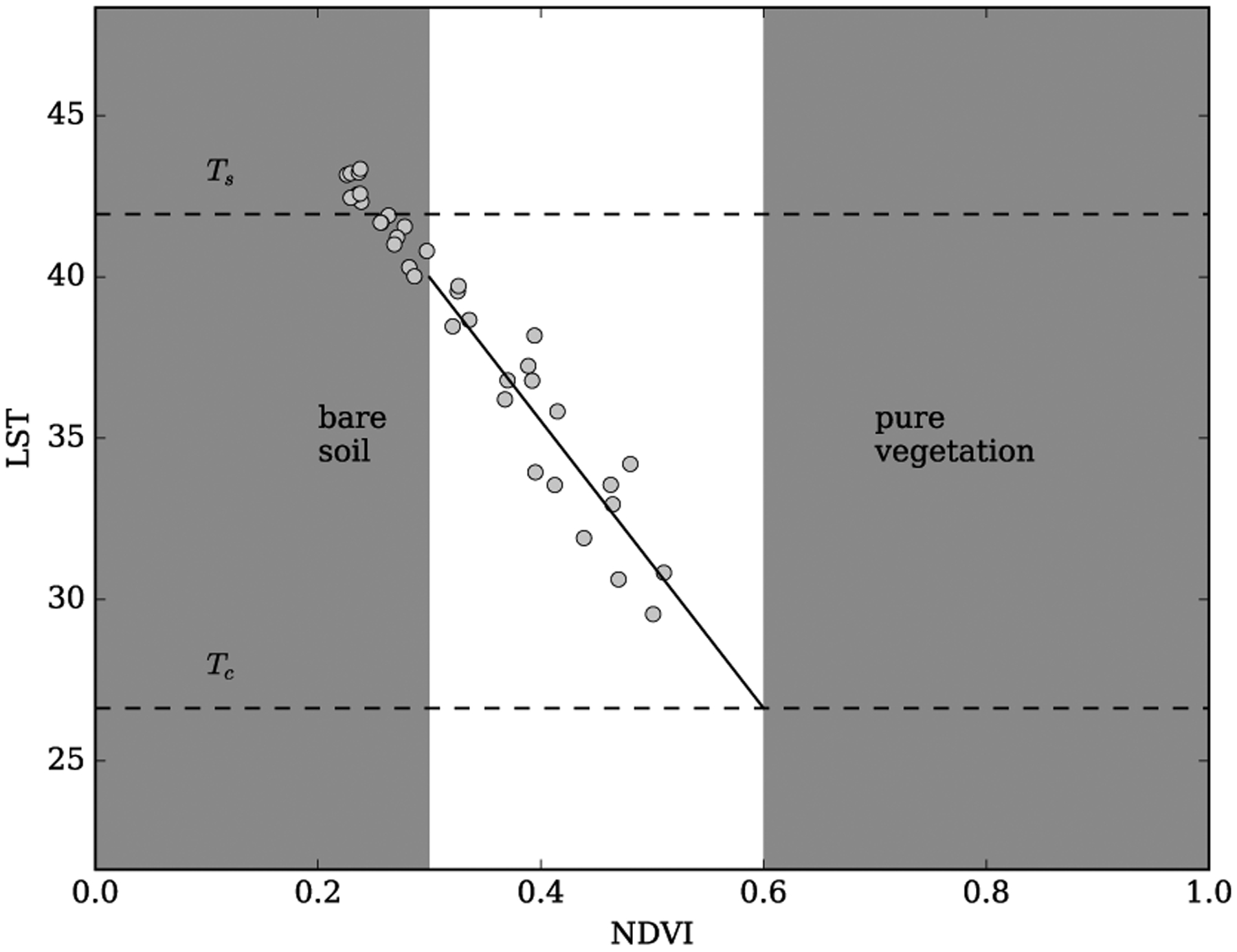
Example of contextual NDVI-Trad scatterplot used for finding canopy and soil temperatures for a 3.6 m grid. Each point corresponds to a 0.6 m pixel NDVI-Trad pair within a 3.6 m spatial domain. Canopy (soil) temperatures are retrieved first by averaging the Trad values above (below) a pure vegetation (soil) NDVI threshold, which corresponds to the greyed areas in the plot. If no pure pixels are found in those areas, the canopy (soil) temperature is found by extrapolating the linear fit between all NDVI-Trad pairs in the domain to the pure vegetation (soil) NDVI threshold
Data‑mining sharpening of temperature, TSEB‑2T‑DMS
We made use of a data-mining fusion algorithm (Gao et al. 2012) to sharpen the original LST imagery (0.60 m) and to match the finer spatial resolution of the (VIS/NIR) UAV images (0.1 5 m). This was performed under the assumption that sharpened temperature would allow a better discrimination between soil and canopy temperatures. Once Trad was produced at 0.15 m, soil and canopy temperatures were then derived at 3.6 m using the same approach described above and summarized in Fig. 2.
TSEB submodels
There have been additional modifications and refinements suggested to algorithms of TSEB for row crops related to radiation partitioning (Colaizzi et al. 2012a, c) and soil heat flux (Colaizzi et al. 2014). A description of the refinements made for application to vineyards is described below. One pertains to the radiation modeling similar to Colaizzi et al. (2012a), while another incorporates a new within canopy wind profile formulation that accounts for non-uniform vertical profile of leaf area (Massman et al. 2017). Finally, the aerodynamic soil-resistance term uses new coefficients based on results from Kustas et al. (2016) over rough soil surfaces.
Radiation formulation partitioning for row crop submodel
We developed a simplified method to derive the clumping index in row crops such as vineyards. The new clumping index is based on the geometric model by Colaizzi et al. (2012a, c), but instead of considering the crops as elliptical hedgerows, we assumed a rectangular canopy shape, which simplifies the trigonometric calculations. A comparison of a different radiation models with ground truth radiation measurements described by Parry et al. (2018) supports the use of this modified radiation scheme. The clumping index is defined as the factor that modifies the leaf area index (LAI) of a real canopy (F) in a fictitious homogeneous canopy with LAIeff= ΩF such as its gap fraction is the same as the gap fraction of the actual canopy (G(θ,ϕ)). This effective LAI is then used as input in the Campbell and Norman (1998) canopy radiative transfer model to estimate soil and canopy net radiation. The inputs needed in the revised radiation model are described in Fig. 3.
Fig. 3.
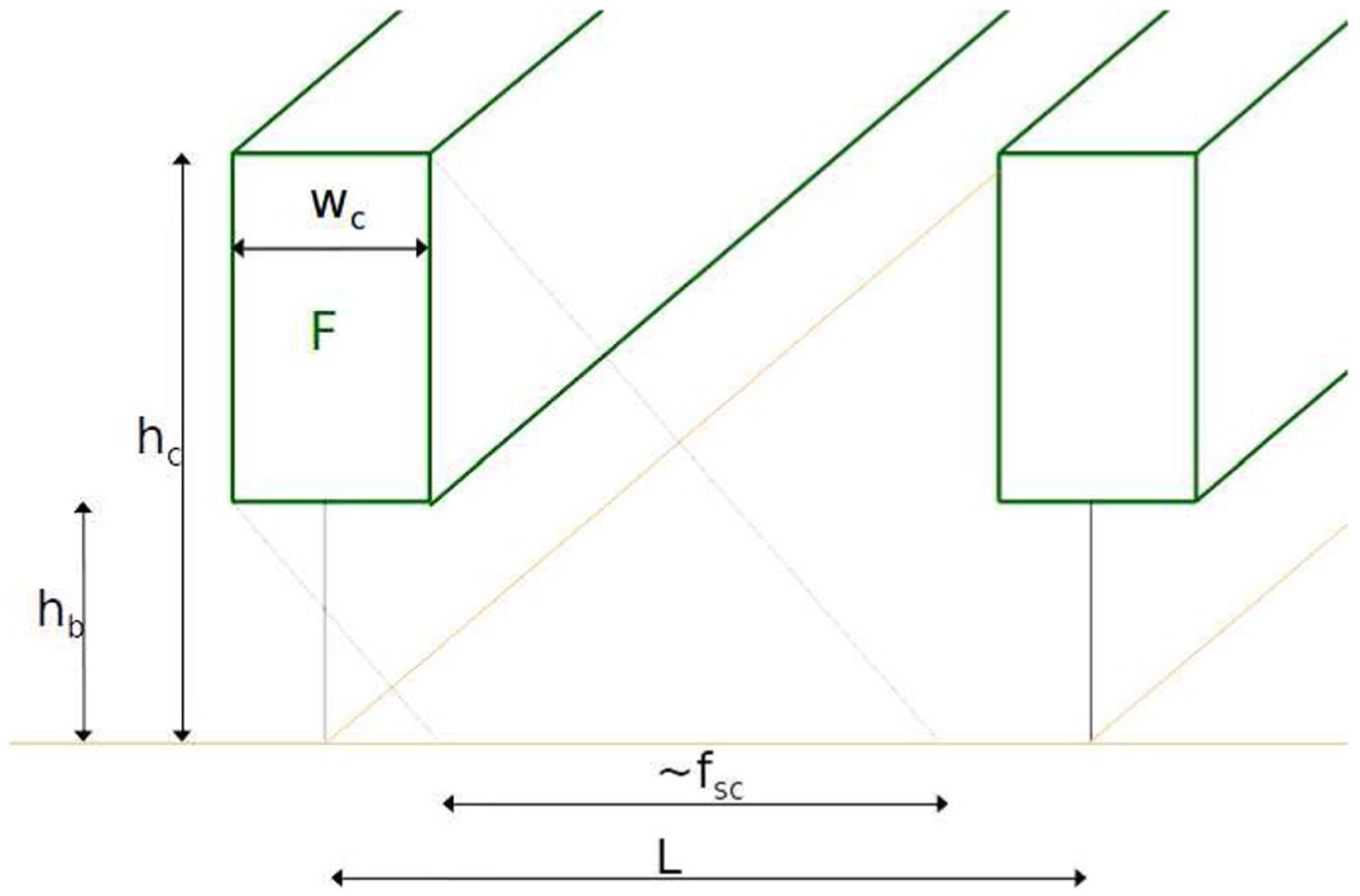
Canopy structure model for estimating the clumping index for incident radiation. hc and hb are the heights for the top and the base of the green canopy, respectively; wc is the canopy average width; F is the local leaf area index; L is the width between rows; and fsc, is solar canopy view factor, i.e., the fraction of soil that is cast by shadows
Wind profile attenuation formulation submodel
The new canopy wind profile model proposed by Massman et al. (2017) eliminates the assumptions of uniform vertical distribution of leaf area and wind attenuation with depth throughout the canopy layer. Therefore, this model provides a more physically realistic method for calculating wind speed attenuation for canopies with arbitrary foliage distribution and leaf area. An additional input compared to previously used canopy wind profiles, such as Goudriaan (1977) used in the TSEB formulation to date, is the relative canopy foliage distribution. In our study site, with an overstory comprised of grapevines clumped due to the trellis system, we estimated our canopy foliage distribution using the histogram of height fields obtained from the photogrammetric dense cloud points. Such foliage distribution could also be estimated using full-waveform LiDAR data (Mallet and Bretar 2009) or by fitting the foliage density from discrete-return LiDAR systems (Coops et al. 2007). Nieto et al. (2018) found that when Massman et al. (2017) wind attenuation model is embedded within TSEB using 2015 in situ tower-based land surface temperature data, there is an improvement in the agreement with measured H fluxes, specially early in the growing season when canopy grapevine in not fully developed.
Soil‑resistance parametrization
Kustas et al. (2016) showed that in the case of sparse and heavily clumped vegetation and/or when the soil surface is very rough, the values for the coefficients in the soil and canopy (Rx) aerodynamic resistance parameters for heat transport (see Fig. 1) are likely to deviate from the typical values proposed in Kustas and Norman (1999) and Norman et al. (1995). For these vineyards, the soil aerodynamic resistance is assumed to be affected by the presence of a grass layer which turns to senescent grass stubble in June. Therefore, we used in the estimation for RS the value for a rough soil surface suggested in Kondo and Ishida (1997) and supported by the results in Kustas et al. (2016) for a rocky soil surface.
Soil heat flux
Some of the UAV images were acquired later in the afternoon when the assumption of a constant ratio between G and Rn,S is less reliable (Santanello and Friedl 2003; Colaizzi et al. 2012b). Agam et al. (2018) showed the uncertainties and challenges in modeling soil heat flux in this type of open canopy surface. Nevertheless, based on comparisons Rn,S between the measured soil heat flux and the estimated Rn,S in Nieto et al. (2018), a modified G vs. formulation was adopted that takes into account the daily temporal behaviour of the G∕Rn,S ratio. We found that a double asymmetric sigmoid function better fits the observations than the sinusoidal function proposed by Santanello and Friedl (2003) (Fig. 4).
Fig. 4.
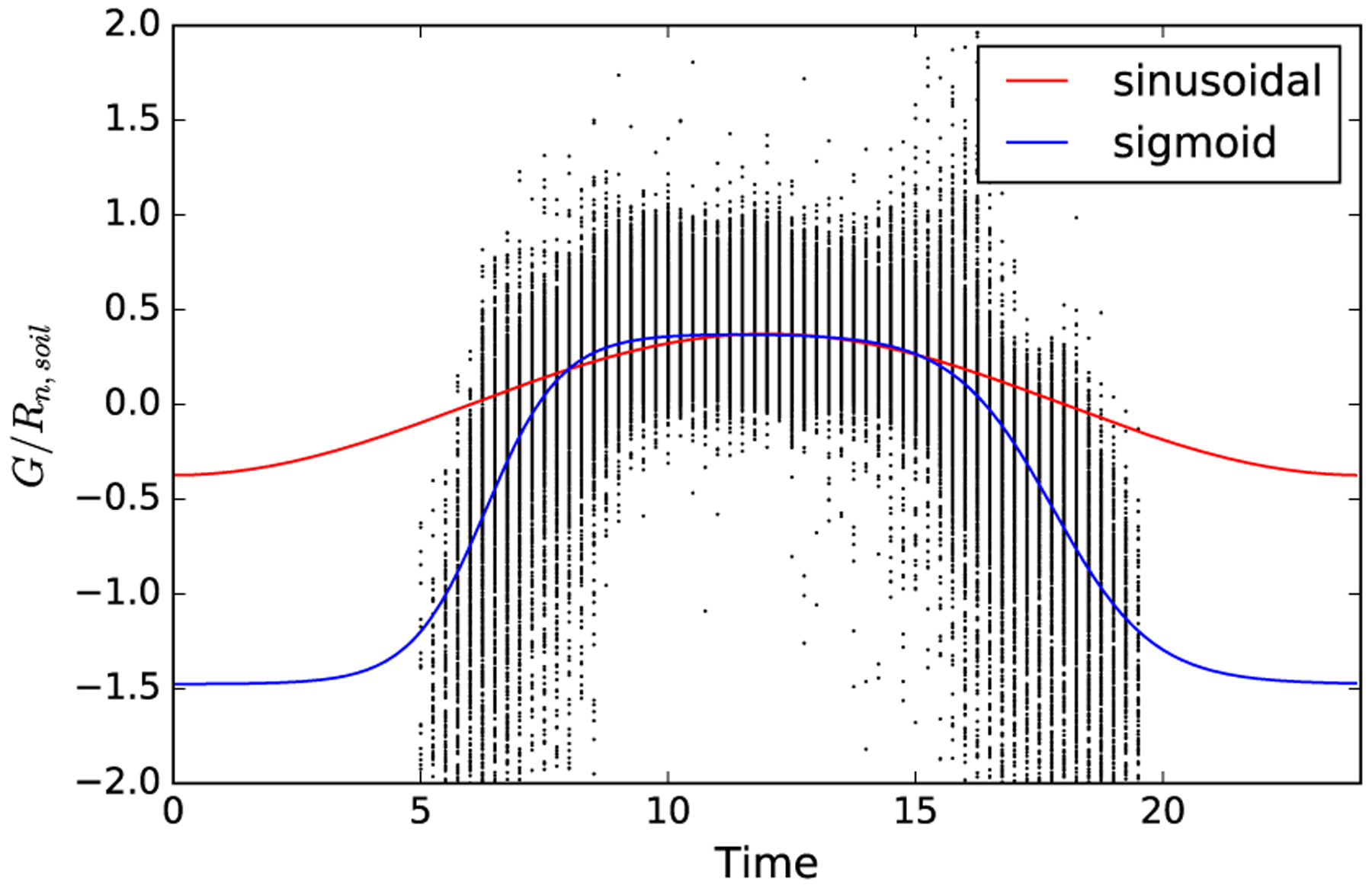
Empirical G∕Rn,S curve fit as a function of time of the day.Red line corresponds to the fitted Santanello and Friedl (2003), and blue line corresponds to the fitted curve used in this study. Following Colaizzi et al. (2012b), the regression curves were fitted only with the cases in which Rn,S > 0
Estimation of ancillary inputs with UAV data
All spatial distributed inputs (i.e., temperatures and canopy properties) used in TSEB were provided at 3.6 m spatial resolution. This magnitude was chosen as the closest multiple of the 0.6 m TIR resolution that covers the width between grapevine rows (3.35 m). Furthermore, we assume that this spatial resolution is compatible to the micrometeorological length scales appropriate for application of the aerodynamic and radiation formulations developed for TSEB (Xia et al. 2016). Therefore, it is assumed the calculation of the resistances to heat transport, radiation, and wind attenuation within the canopy layer follow the TSEB procedure in partitioning of fluxes and temperatures between interrow and vine canopy sources.
Leaf Area Index and fractional cover
Multiple linear regression between in situ LAI measured with a LiCOR plant canopy analyzer at multiple locations (including southeast to northwest transects of both north and south vineyards (Kustas et al. in press)) and metrics derived from the UAV imagery (Pope and Treitz 2013; Zhao and Popescu 2009) were used to derive spatial maps of LAI. The most significant metric was the NDVI computed from the multispectral imagery, but other covariates derived from the 3D point cloud were also included in these empirical models. These other 3D structural metrics were especially relevant in the flights in May 2016, in which a significant amount of photosynthetically active cover crop in the inter-row was present, and hence, NDVI by itself could not fully explain the variability in canopy LAI.
On the other hand, fractional cover was estimated as the proportion of grapevine/bare soil within each 3.6 m cell, based on a binary supervised classification of the 0.15 multispectral imagery. Canopy width, which is used as input for radiation transmission submodel (Fig. 3), was then computed as 3.35fC, with 3.35 being the width between rows.
Canopy height and relative foliage density
Canopy height (hC), required for estimating radiation transmission in row crops (Fig. 3) and the relative foliage density (fa(z∕hC), required for the Massman et al. (2017) canopy wind attenuation model, were both estimated from the 3D UAV photogrammetric point cloud described by Aboutalebi et al. (2018). Estimates of hC were derived as the difference between the 99th and 1st percentile height of all point clouds within each 3.6 m cell. The relative foliage density, on the other hand, was computed as the frequency histogram of all point heights between the 99th and 1st percentile, and nor malized so at the maximum frequency value. A percentile was used instead of absolute minimum and maximum heights to remove possible outliers in the photogrammetric point cloud.
Results
The UAV spatially distributed TSEB fluxes were evaluated against the measured EC fluxes (Fig. 5) after pixel aggregation, considering the estimated pixel contribution from the EC footprint at the time of the flight overpass, which was estimated using the two-dimensional flux footprint developed by Detto et al. (2006). Although there are diverging arguments on which energy balance closure method is more robust, based on current and previous measurements observed in arid and more humid and advective environments, we consider that λE is not as reliably measured as H, see Li et al. (2005) for a more extensive discussion on this topic. Therefore, the lack of closure in the EC fluxes was compensated by adding the residual closure to the latent heat flux.
Fig. 5.
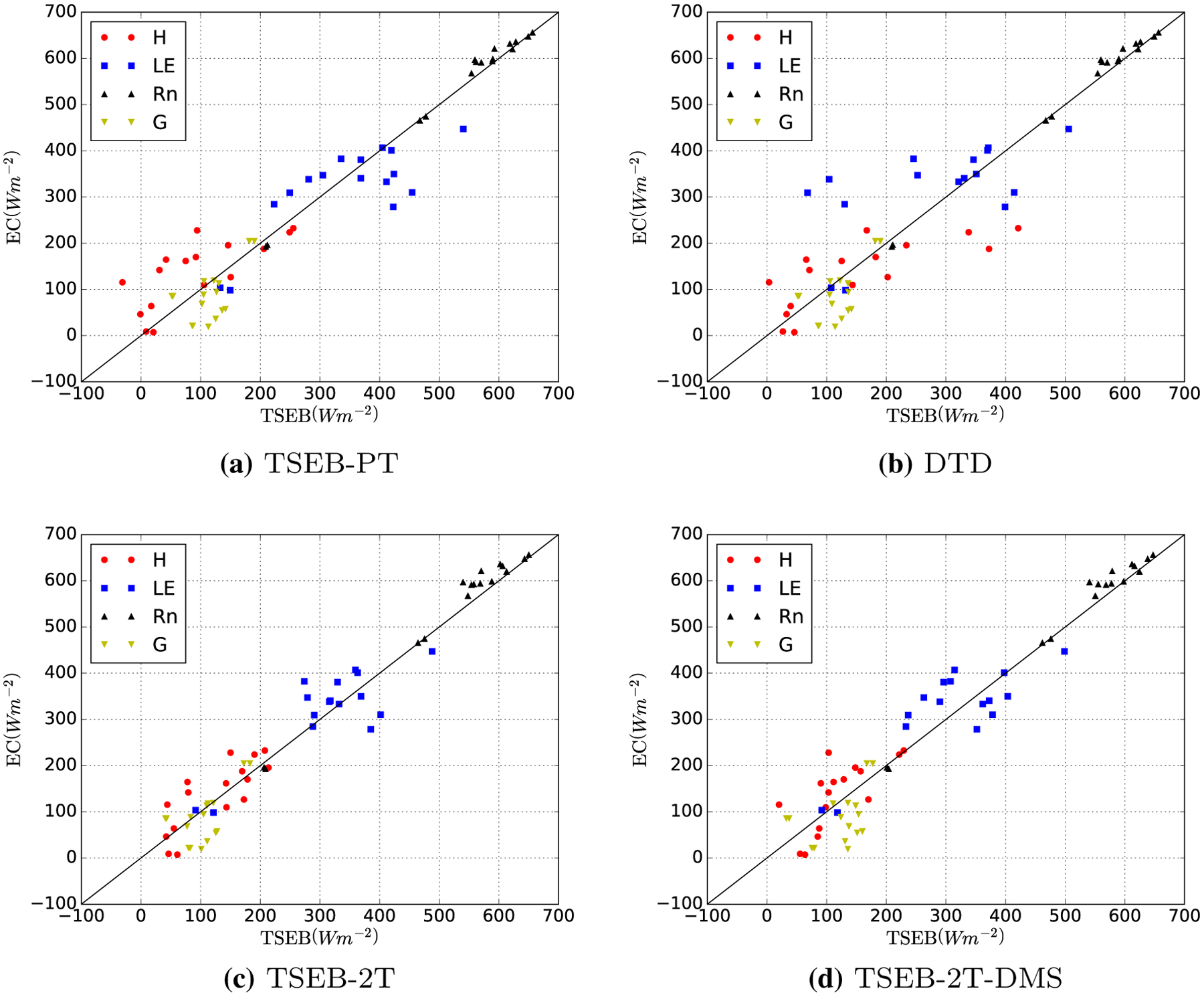
Scatterplot of observed vs. predicted fluxes using the different TSEB model approaches. (a)TSEB-PT. (b)DTD. (c)TSEB-2T. (d)TSEB-2T-DMS
Table 2 lists the error statistics for the estimated turbulent fluxes using the different proposed models, while Fig. 5 illustrates the agreement between the various TSEB model outputs and the EC measurements at the overpass time. Overall, the models that used the estimated the component temperatures soil/interrow and canopy temperatures (TSEB-2T and TSEB-2T-DMS) yielded a closer agreement with measured H as indicated by the lower RMSE values in H (50 and 58 vs. 70 and 78 Wm−2 for TSEB2T and TSEB2T-DMS vs. DTD and TSEB-PT, respectively). A similar result was obtained for λE, where RMSE in component temperature models yielded values lower than 65 Wm−2, while composite-based models showed larger RMSE around 80 Wm−2. In particular, TSEB2T with RMSE for H and λE on the order of 50 Wm−2, and correlation of 0.8 to 0.9 with observed fluxes, appears to outperform all other models. No significant differences were found between models in estimating G and Rn, with only TSEB2T giving slightly lower RMSE and bias than the other three approaches.
Table 2.
Flux error assessment between the eddy covariance and the different TSEB approaches for estimating TC and TS. Bias (Wm−2) is the mean difference between the TSEB modelled flux and the EC. RMSE (Wm−2) is the root mean square error, which is as well decomposed between its unsystematic (RMSEu) and systematic (RMSEs) parts (Willmott 1981). r is the correlation coefficient between the TSEB modelled flux and the EC, rounded to two decimal digits
| Variable | Model | Bias | RMSE | RMSEu | RMSEs | r |
|---|---|---|---|---|---|---|
| H | TSEB-PT | −58 | 78 | 48 | 61 | 0.74 |
| DTD | −7 | 70 | 69 | 11 | 0.76 | |
| TSEB2T | −27 | 52 | 37 | 37 | 0.78 | |
| TSEB2T-DMS | −28 | 57 | 41 | 40 | 0.72 | |
| λE | TSEB-PT | 51 | 75 | 54 | 52 | 0.89 |
| DTD | −2 | 80 | 79 | 7 | 0.78 | |
| TSEB2T | 22 | 49 | 44 | 23 | 0.91 | |
| TSEB2T-DMS | 12 | 58 | 57 | 13 | 0.87 | |
| G | TSEB-PT | 30 | 50 | 36 | 34 | 0.72 |
| DTD | 31 | 51 | 36 | 35 | 0.72 | |
| TSEB2T | 18 | 43 | 35 | 25 | 0.73 | |
| TSEB2T-DMS | 35 | 62 | 46 | 42 | 0.57 | |
| Rn | TSEB-PT | −8 | 17 | 12 | 12 | 1 |
| DTD | −8 | 17 | 12 | 12 | 1 | |
| TSEB2T | −18 | 27 | 16 | 22 | 0.99 | |
| TSEB2T-DMS | −14 | 23 | 15 | 17 | 0.99 | |
| Rn,sw | TSEB-PT TSEB-PT | −21 | 23 | 5 | 23 | 1 |
| DTD | −21 | 23 | 5 | 23 | 1 | |
| TSEB2T | −21 | 23 | 6 | 22 | 1 | |
| TSEB2T-DMS | −21 | 23 | 6 | 22 | 1 | |
| Rn,lw | TSEB-PT | 9 | 16 | 13 | 9 | 0.81 |
| DTD | 9 | 16 | 13 | 9 | 0.82 | |
| TSEB2T | 3 | 16 | 15 | 5 | 0.86 | |
| TSEB2T_DMS | 6 | 14 | 13 | 7 | 0.87 |
Spatio‑temporal trends in evapotranspiration partitioning
In Fig. 6, the frequency histograms of evapotranspiration partitioning (i.e., λEC∕λE) between models for each flight and site are illustrated. Except for the flight in May 2016, the distribution of λEC∕λE is considerably different between models. In general, TSEB2T and DTD usually compute larger values of λEC∕λE compared to TSEB2T-DMS and TSEB-PT. Furthermore, the models compute a higher λEC∕λE for the flights in June and July 2015, for the south site.
Fig. 6.
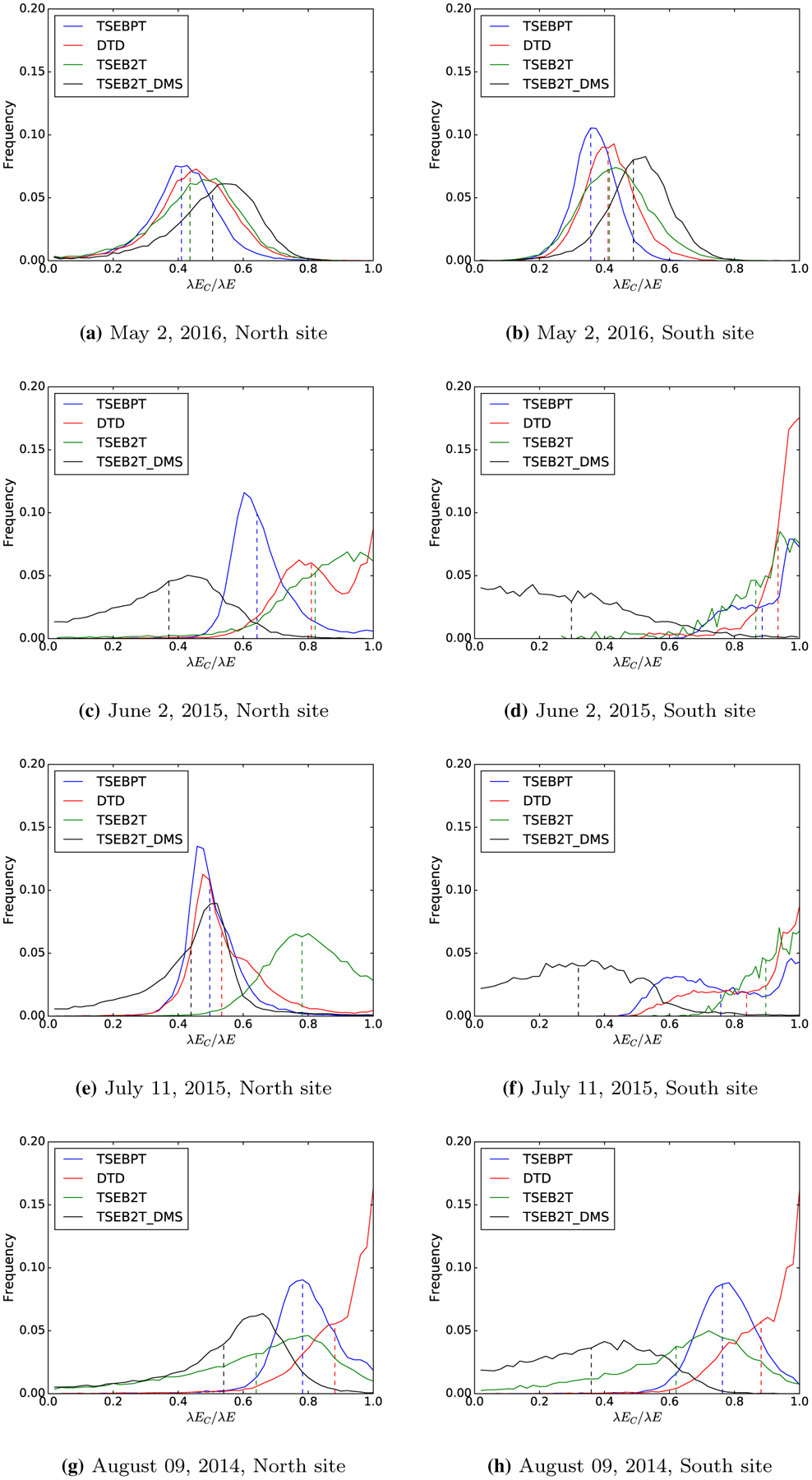
Frequency histograms for the modelled latent heat flux partitioning (λEC∕λE) with vertical dashed lines correspond to the average value of the distribution. Left panels correspond to the mature grapevine site (north), and right panels show the young grapevine site (south). Figures are sorted by month instead of chronologically
Likewise, Fig. 7 shows the comparison of ET partitioning using the UAV imagery and the corresponding tower-based TSEB-PT used in Kustas et al. (2018) and Nieto et al. (2018) for the 4 flights illustrated in Fig. 6 with the output extracted from the flux tower footprint.
Fig. 7.
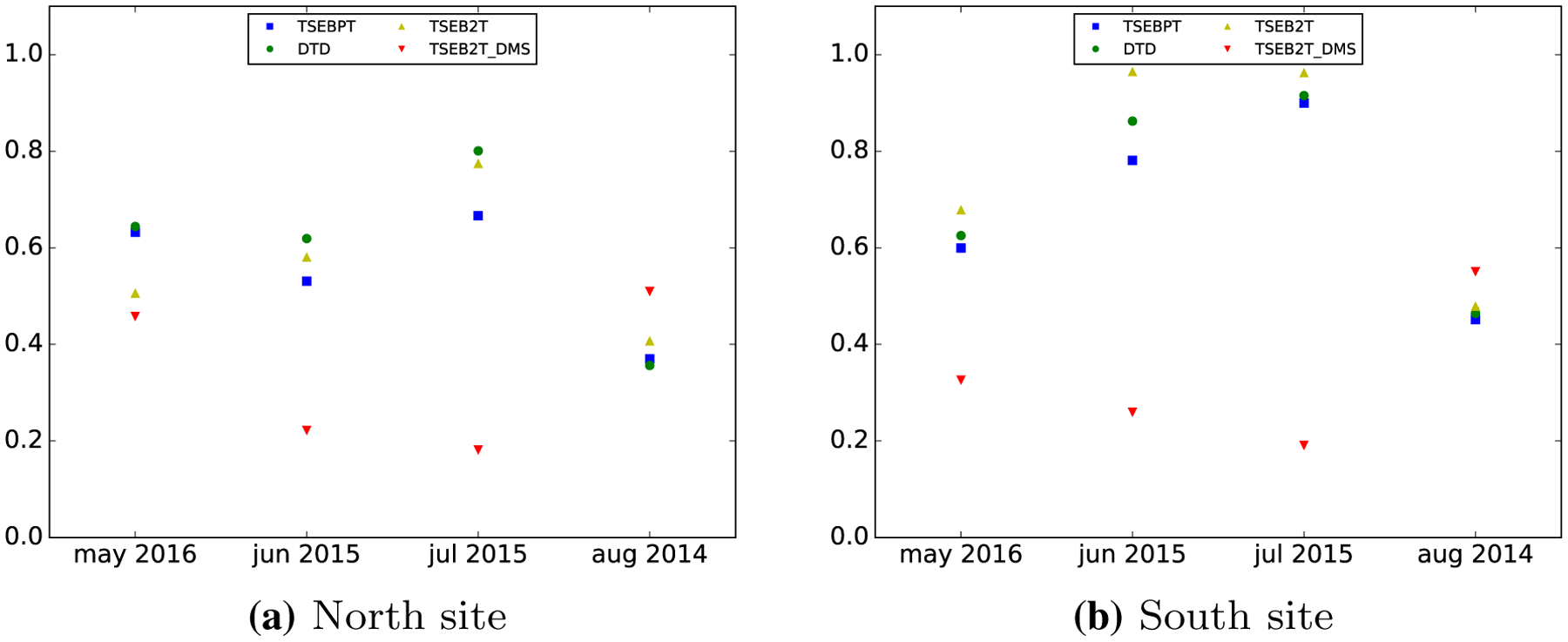
Footprint average of ET (λE/λE) partitioning for the different models tested (colored points) compared to the tower-based TSEB-PT used in Kustas et al. (this issue), (black line). Left, north vineyard. Right, south vineyard
Discussion
The results of this study show a better agreement in turbulent flux partitioning when using the component temperatures as input to TSEB, particularly TSEB2T (see Table 2). Although this result was also shown in a recent study using satellite data (Song et al. 2016), this was not observed by Colaizzi et al. (2012b) using ground-based radiometric temperature observations. However, Colaizzi et al. (2012b) pointed out that one of the possible reasons of the poorer performance found using TSEB2T was the difficulty in measure TC during the earlier stages of crop development (cotton in their case). With the methodology used in our study, it is possible to overcome this issue and retrieve TC in sparse canopies, by combining multispectral and thermal-infrared data in a contextual algorithm. Finally, since the error statistics for the other two fluxes (Rn and G) did not show larger differences among models, one could assume that the use of component temperatures made an impact in better partitioning the available energy between sensible and latent heat fluxes. Actually, Ortega-Farías et al. (2016) used UAV thermal-infrared imagery an irrigated olive orchard to measure directly TC and TS and found similar errors to our study (56 and 50 for Wm−2 for H and λE, respectively) with a patch (or parallel) resistance dual source energy balance model.
For GRAPEX, Xia et al. (2016) also tested TSEB-PT over the same site, in their case using manned airborne imagery collected in 2013. They obtained somewhat lower errors than those reported here, with 42 and 43 Wm−2 RMSE for H for the North and South sites, respectively)and 37 and 51 Wm−2 for λE. One possible explanation might be due to the larger uncertainty in Trad when using miniaturized thermal cameras onboard UAV systems, which usually require in situ calibration (Torres-Rua et al. 2018; Berni et al. 2009). Indeed, when applying TSEB with a time-difference temperature to remove possible bias in Trad, there is an improvement in the estimates of H using DTD compared to TSEB-PT. This, together with the similar results shown by Hoffmann et al. (2016), seems to confirm the utility of using the morning temperature rise of temperatures instead of absolute temperatures, as pointed out in other studies (Norman et al. 2000; Anderson et al. 2011; Guzinski et al. 2013). Finally, Fig. 5 shows that in this study, a larger range of conditions (e.g., Rn ranging from 200 to 700 Wm−2) is observed compared to the data set of Xia et al. (2016), which might also be contributing generally larger RMSE in the current study.
Regarding evapotranspiration partitioning between grapevine transpiration and ground evaporation, one of the most noticeable issues shown in Fig. 6 is the large difference in distribution and average values between the north and south sites during the flights of June 2015 (Fig. 6c, d) and July 2015 (Fig. 6e, f). Inspecting the observed UAV Trad images for these two flights (Fig. 8), one can observe a significant difference in temperatures between the north and the south vineyards. These differences are not as evident for the flights in May 2016 and August 2014, but for June and July, the differences are mostly likely due to warmer surface temperatures in the interrow for the south vineyard. This is due to the combined effect of a lower vegetation cover and generally drier soil conditions in this younger vineyard which received less irrigation than the more mature north vineyard (Knipper et al. 2018). Both factors lead to a reduced soil evaporation and likely a more efficient irrigation.
Fig. 8.
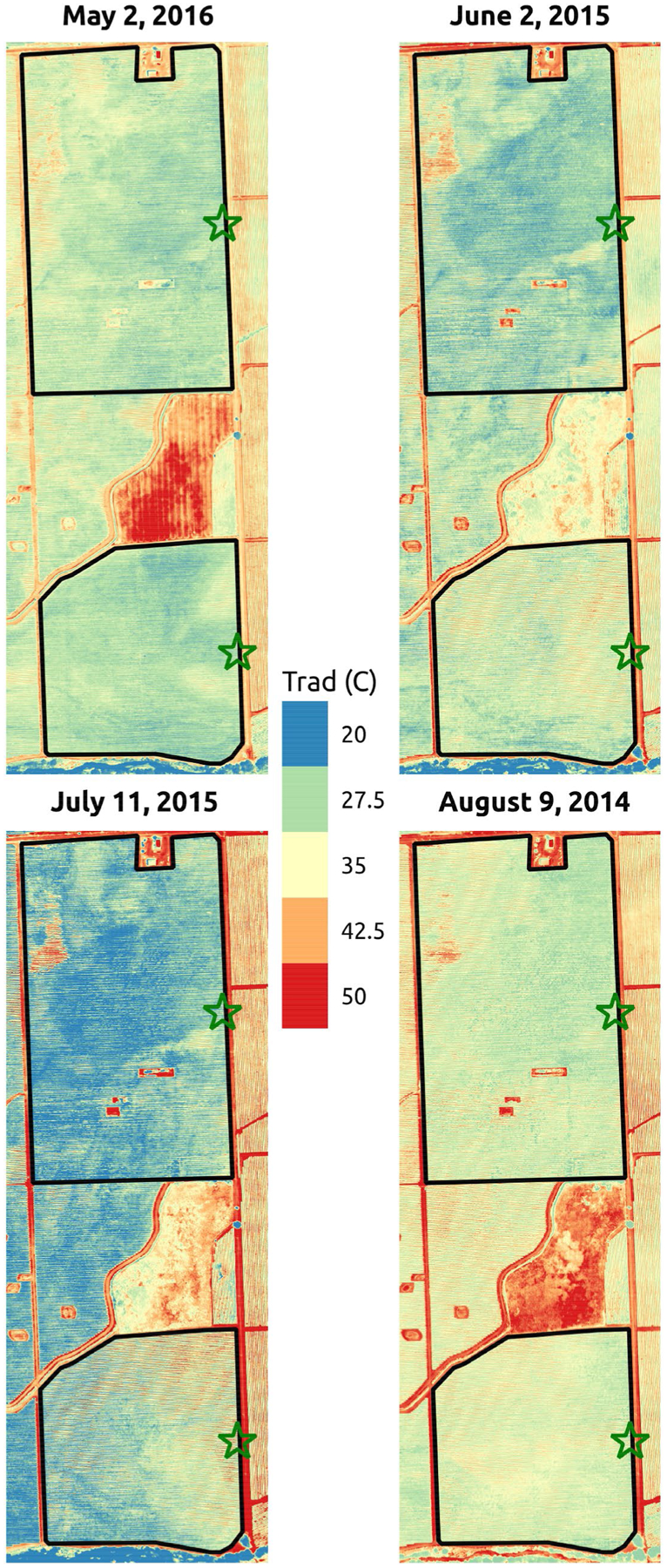
Measured radiometric temperatures with the UAV system for the flights corresponding to Fig. 6. Two black outlines represent both vineyard limits, whereas the green stars show the location of the eddy covariance towers
Kustas et al. (this issue) applied the correlation-based flux partitioning method to the high-frequency eddy covariance data to compare monthly values of λEC∕λE with TSEB estimates using tower-based T rad values derived from pyrgeometer upwelling and downwelling hemispherical longwave radiation. Monthly values for June and July 2015 were 0.83 and 0.82 for the north vineyard, while the south vineyard yielded values of 0.84 and 0.9, respectively. Pixels extracted from the tower footprint area using TSEB2T yielded values most similar values to the findings of Kustas et al. (this issue) (results not shown). However, with only two dates and two sites, we cannot reach any definitive conclusion regarding partitioning performance. We can also see that the May 2016 acquisition tends to have lower λEC∕λE values than the June or July 2015 overpasses, most significantly for TSEB2T. This likely due to higher soil moisture from winter rains, a photosynthetically active cover crop but a relatively low vine biomass. For June and July acquisitions, the cover crop has gone through senescence and has been mowed (grass stubble) with a dry soil in the interrow (except for a bare soil area under the grapevine canopies staying relatively wet from frequent irrigation) all of which would increase λEC∕λE. The decrease in λEC∕λE value in August is not easily understood, although both the tower-based TSEB output and the values derived from the UAV imagery are in agreement regarding this trend. Ground and remote-sensing observations do indicate a decreasing in LAI from June to August, so this is contributing to the reduction in λEC∕λE. The monthly values of λEC∕λE from the correlation-based flux partitioning method with the high-frequency eddy covariance data for August 2015 does decrease from June and July, but not as markedly [see Kustas et al. (2018)]. That magnitude and trend in λEC∕λE observed by Kustas et al. (2018) seem to be in close agreement with TSEB2T for the north vineyard and closer to TSEB-PT for the south vineyard.
Figure 9 illustrates the histograms of TC and TS for the flights in July 2015 and August 2014 at the north site, where the differences in λEC∕λE between TSEB-PT and TSEB2T are significant (in July 2015) and are similar (August 2014), respectively. The temperature distributions in Fig. 9 confirm that the larger λEC∕λE values from TSEB2T shown in Fig. 6 are in agreement with a lower TC (i.e., higher λES) and higher Ts (i.e., lower λES) in TSEB2T compared to TSEB-PT. Similarly, the close agreement in λEC∕λE between TSEB2T and TSEB-PT for the August 2014 flight also agrees with the significant overlap in the TC and TS distributions, as illustrated in Fig. 9. Nevertheless, more independent measurements of λEC∕λE over the growing season are required to provide a thorough evaluation of the reliability of the various TSEB approaches in estimating ET partitioning Kustas et al. (2018)
Fig. 9.
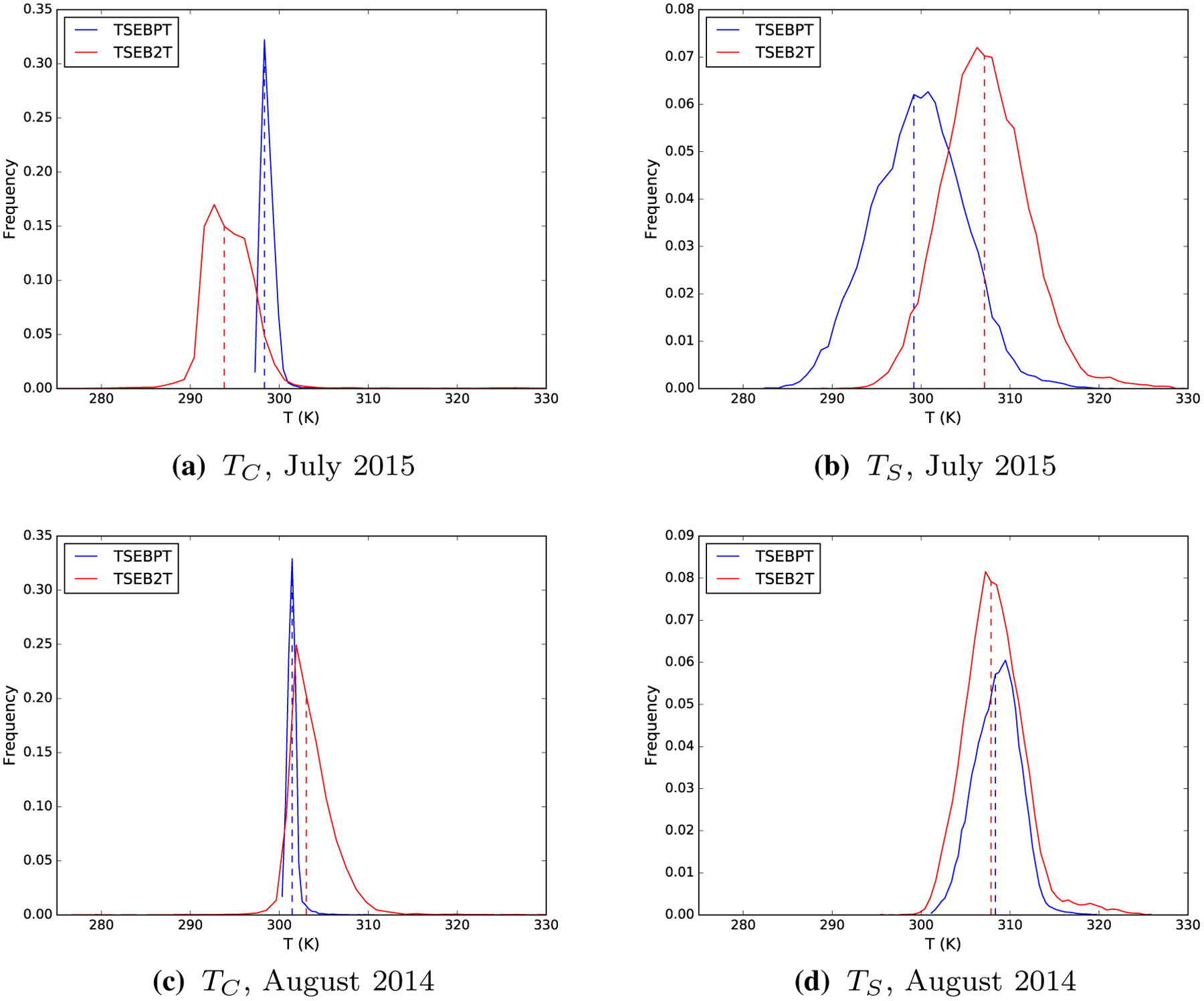
Frequency histograms for the component temperatures (TC and TS) estimated in TSEB-PT (blue histogram) and TSEB2T (red histogram).Vertical dashed lines correspond to the average value of the distribution.
Conclusions
This study explored different approaches to estimate the component soil and canopy temperatures to be used in the Two-Source Energy Balance Model. In addition to the Priestley–Taylor TSEB described in Norman et al. (1995) and its time-differencing approach the Dual-Temperature Difference model (Norman et al. 2000), we proposed two novel methods to derive soil and canopy temperatures from very high spatial resolution imagery, only available from airborne manned or unmanned platforms. Results showed that the use of a simple contextual algorithm based on the correlation between NDVI and the radiometric temperature (TSEB2T) outperformed the other approaches when estimating the bulk turbulent fluxes (H and λE).
Due to the increasing interest in deriving crop stress and transpiration metrics for irrigation management, a qualitative analysis was done as well to evaluate the robustness of the methods in estimating ET partitioning. The TSEB2T approach seemed to produce λEc/λE estimates consistent with Kustas et al. (2018) running TSEB-PT using tower-based Trad observations for the north vineyard, less so for the south vineyard. However, more independent measurements are needed to confirm the utility of the various TSEB approaches in partitioning ET to T and E.
Surprisingly, using sharpening of temperatures (TSEB2TDMS) to achieve a more detailed map of temperatures (0.15 m) did not provide any greater benefit in estimating λE, although yielded similar results to TSEB2T, but in many cases, computed λEc/λE values tend to be much lower than the other TSEB approaches (Figs. 6 and 7). It is possible that the DMS-sharpening method adds noise to the original 0.6 m thermal imagery making the retrieval of canopy and soil temperature more uncertainty and consequently less robust. Nevertheless, this method might still be useful for sharpening coarser imagery, for instance, when flying at higher altitudes to reduce costs, or over crops with narrower canopies
It is worth noting as well that TSEB model assumes a layer of more or less photosynthetically active vegetation (controlled by parametrizing its green fraction, fg), with a bare soil (or at least non-photosynthetic active) layer underneath. This issue presents a challenge in retrieving the soil and canopy temperatures and the λE partitioning when there is a photosynthetically active cover crop layer in the inter-row. Such is the case in many managed vineyards in California, where they use a crop cover to deplete the soil moisture after the winter rains, or in natural environments such as wooded savannahs having a grass understory. This study assumed that the crop cover contribution to the water fluxes is negligible, and thus, the crop was included in an bulk layer together with the underlying soil. However, in more humid areas, the water flux rate from the crop cover could be larger, likely making TSEB flux estimates more uncertain. Therefore, future research is planned for implementation of a simplified three-source model for flux partitioning between grapevine, crop cover, and soil.
Finally, a question that still remains unanswered and thus is a topic for future research is the number of flights and dates for operational irrigation scheduling, which would depend as well on grapevine variety and irrigation management strategy (Bellvert et al. 2016). Nevertheless, we think that these measurements should be complemented in all cases by satellite data (see Knipper et al. 2018), and the application of the multi-scale data fusion system in vineyards has been shown to provide significant information about the spatial variability in ET at 30 m resolution on a daily basis which is critical for accurate water use accounting (Semmens et al. 2016; Knipper et al. 2018). Therefore, the potential synergy of the unique information that can be provided by satellite (daily ET) and by airborne systems (canopy level ET and E and T partitioning) needs to be thoroughly investigated to determine when there are situations, particularly for high-valued crops, that would greatly benefit crop yield and sustainability from combining information from both platforms.
Acknowledgements
Partial funding provided by E.&J. Gallo Winery made possible the acquisition and processing of the high-resolution manned aircraft and UAV imagery collected during GRAPEX IOPs. In addition, thanks are given to the Utah Water Research Laboratory for the use of the AggieAir UAV platform, support personnel and partial funding. In addition, we would like to thank the staff of Viticulture, Chemistry and Enology Division of E.&J. Gallo Winery for the collection and processing of field data during GRAPEX IOPs. Finally, this project would not have been possible without the cooperation of Mr. Ernie Dosio of Pacific Agri Lands Management, along with the Borden/ McMannis vineyard staff, for logistical support of GRAPEX field and research activities. USDA is an equal opportunity provider and employer.
Appendix
A. TSEB model
The basic equation of the energy balance at the surface can be expressed following Eq. 4:
| (4a) |
| (4b) |
| (4c) |
with Rn being the net radiation, H is the sensible heat flux, λE is the latent heat flux or evapotranspiration, and G is the soil heat flux. “C” and “S” subscripts refer to canopy and soil layers, respectively. The symbol “≈” appears, since there are additional components of the energy balance that are usually neglected, such as heat advection, storage of energy in the canopy layer, or energy for the fixation of CO2 (Hillel 1998)
The key in TSEB models is the partition of sensible heat flux into the canopy and soil layers, which depends on the soil and canopy temperatures (TS and TC, respectively). If we assume that there is an interaction between the fluxes of canopy and soil, due to an expected heating of the in-canopy air by heat transport coming from the soil, the resistances network in TSEB can be considered to be in series. In that case, H can be estimated as in Eq. 5 (Norman et al. 1995, Eqs. A1–A3):
| (5) |
where ρair is the density of the air (kghboxm−3),Cp is the heat capacity of the air at constant pressure (Jkg−1K−1), and TAC is the air temperature at the canopy interface, equivalent to the aerodynamic temperature T0, computed with Eq. 6 (Norman et al. 1995, Eq. 4):
| (6) |
Here, Ra is the aerodynamic resistance to heat transport (sm−1),Rs is the resistance to heat flow in the boundary layer immediately above the soil surface (sm−1), and Rx is the boundary layer resistance of the canopy of leaves (sm−1). The mathematical expressions of these resistances are detailed in Eq. 7 and in Norman et al. (1995) and Kustas and Norman (2000) and discussed in Kustas et al. (2016):
| (7a) |
| (7b) |
| (7c) |
where u*is the friction velocity (ms−1) computed as
| (8) |
In Eq., zu and zT are the measurement heights for wind speed u (ms−1) and air temperature TA (K), respectively. d0 is the zero-plane displacement height, and z0M and z0H are the roughness length for momentum and heat transport, respectively (all those magnitudes expressed in m), with z0H = z0M. exp (−kB−1) In the series version of TSEB, z0H is assumed equal to z0M, since the term Rx already accounts for the different efficiencies between heat and momentum transport (Norman et al. 1995), and therefore, kB−1 = 0. The value of κ′ = 0.4 is the von Karman’s constant. The ψm(ζ) terms in Eqs. 7a and are the adiabatic correction factors for momentum. The formulations of these two factors are described in Brutsaert (1999) and Brutsaert (2005). These corrections depend on the atmospheric stability, which is expressed using the Monin–Obukhov length L (m):
| (9) |
where H is the bulk sensible heat flux (Wm−2), E is the rate of surface evaporation (kgs−1), and g is the acceleration of gravity (ms−2)
The coefficients b, c in Eq. 7b depend on turbulent length scale in the canopy, soil-surface roughness, and turbulence intensity in the canopy, which are discussed in Sauer et al. (1995), Kondo and Ishida (1997) and Kustas et al. (2016). C′ is assumed to be 901/2 m−1 and lw is the average leaf width (m)
B. Modifications to TSEB model for row crops
B.1. Radiation transmission in row crops
The clumping index for row crops is defined as the factor that modifies the leaf area index of a real canopy (F) in a fictitious homogeneous canopy with LAIeff˙ = ΩF such as its gap fraction is the same as the gap fraction of the real-world canopy (G(θ,ϕ))
| (10) |
where κbe(θ) is the beam extinction coefficient through a plant with an ellipsoidal inclination distribution (Campbell 1986, 1990), θ is the zenith incidence angle, and Ψ is the relative azimuth angle between the incidence beam and the row direction
Our modelled real canopy consists of a horizontally infinite long prism with a total height hc (i.e., the canopy height) and a width wc (i.e., canopy width) that is placed above the ground at hb (i.e., the height of the first living branch). This canopy contains finite-sized leaves randomly placed (no clumping within the canopy) oriented according to a ellipsoidal leaf angle distribution function (Campbell 1990) with a total leaf area index F (Fig. 3).
Then, the real canopy gap fraction consists of the sunlit part of the bare soil that is not shaded by the canopy plus the gaps caused by the solar beam passing through the crop canopy (Eq. 11):
| (11) |
The solar canopy view factor fsc(θ,ϕ) is the fraction of soil that is cast by shadows (Colaizzi et al. 2012a) and in our case is estimated as
| (12) |
where L is the row separation (m). For a vertical projection (θ= 0), Eq. 12 reduces to wc∕L, the fractional cover.
B.2. Massman et al. (2017) wind attenuation profile
Compared to previously used canopy wind profiles such as Goudriaan (1977) or Massman (1987), the additional key input required in Massman et al. (2017) wind attenuation model is the relative canopy foliage distribution, computed as in Eq. 13:
| (13) |
where is the relative canopy shape (i.e., and ξ = z/hc and PAI is the plant (leaves+stems) area index. Massman et al. (2017) modelled fa(ξ) as a combination of asymmetric Gaussian curves, but fa(ξ) can also be estimated as a continuous curve obtained from canopy structure measurements or three-dimensional cloud points, such as in Nieto et al. (2018).
The canopy wind speed profile is then the product of two terms: one logarithmic profile (Ub) that is dominant near the ground and a second a hyperbolic cosine profile (Ut) that dominates near the top of the canopy, where the canopy foliage distribution plays a major role. Ancillary input in Ut is the the drag coefficient of the individual foliage elements (Cd), which is usually considered equal to 0.2 (Massman et al. 2017; Goudriaan 1977). Massman et al. (2017) model has as well the ability to consider variations of the drag coefficient due to either wind sheltering between foliage elements, or vertical variations independently of wind blocking. This effect can usually be disregarded in most canopies (Massman et al. 2017), so was it in this study.
Footnotes
The use of trade, firm, or corporation names in this article is for the information and convenience of the reader. Such use does not constitute official endorsement or approval by the US Department of Agriculture or the Agricultural Research Service of any product or service to the exclusion of others that may be suitable
References
- Aboutalebi A, Torres-Rua A, Nieto H, Kustas W (2018) Assessment of different methods for the shadows detection in high-resolution imagery and shadows impact on calculation of NDVI, LAI, and evapotranspiration. Irrig Sci (this issue) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Agam N, Alfieri J, Kustas W, Jones S, McKee L, Prueger J (2018) Spatial variability in soil heat flux from a detailed soil heat flux plates array. Irrig Sci (this issue) [Google Scholar]
- Alfieri J, Kustas W, Gao F, Prueger J, Nieto H, Hipps L (2018) Influence of wind direction on the effective surface roughness of vineyards. Irrig Sci (this issue) [Google Scholar]
- Anderson MC, Norman JM, Kustas WP, Houborg R, Starks PJ, Agam N (2008) A thermal-based remote sensing technique for routine mapping of land-surface carbon, water and energy fluxes from field to regional scales. Remote Sens Environ 112(12):4227–4241. 10.1016/j.rse.2008.07.009 [DOI] [Google Scholar]
- Anderson MC, Kustas WP, Norman JM, Hain CR, Mecikalski JR, Schultz L, González-Dugo MP, Cammalleri C, d’Urso G, Pimstein A, Gao F (2011) Mapping daily evapotranspiration at field to continental scales using geostationary and polar orbiting satellite imagery. Hydrol Earth Syst Sci 15(1):223–239. 10.5194/hess-15-223-2011 [DOI] [Google Scholar]
- Bellvert J, Zarco-Tejada P, Marsal J, Girona J, González-Dugo V, Fereres E (2016) Vineyard irrigation scheduling based on airborne thermal imagery and water potential thresholds. Aust J Grape Wine Res 22(2):307–315. 10.1111/ajgw.12173 [DOI] [Google Scholar]
- Berni JAJ, Zarco-Tejada PJ, Suarez L, Fereres E (2009) Thermal and narrowband multispectral remote sensing for vegetation monitoring from an unmanned aerial vehicle. IEEE Trans Geosci Remote Sens 47(3):722–738. 10.1109/TGRS.2008.2010457 [DOI] [Google Scholar]
- Brutsaert W (1999) Aspects of bulk atmospheric boundary layer similarity under free-convective conditions. Rev Geophys 37(4):439–451 [Google Scholar]
- Brutsaert W (2005) Hydrology: an introduction. Cambridge University Press, Cambridge [Google Scholar]
- Cammalleri C, Anderson MC, Gao F, Hain CR, Kustas WP (2013) A data fusion approach for mapping daily evapotranspiration at field scale. Water Resour Res 49(8):4672–4686. 10.1002/wrcr.20349 [DOI] [Google Scholar]
- Cammalleri C, Anderson M, Gao F, Hain C, Kustas W (2014) Mapping daily evapotranspiration at field scales over rainfed and irrigated agricultural areas using remote sensing data fusion. Agric For Meteorol 186:1–11. 10.1016/j.agrformet.2013.11.001 [DOI] [Google Scholar]
- Campbell G (1990) Derivation of an angle density function for canopies with ellipsoidal leaf angle distributions. Agric For Meteorol 49(3):173–176. 10.1016/0168-1923(90)90030-A [DOI] [Google Scholar]
- Campbell GS (1986) Extinction coefficients for radiation in plant canopies calculated using an ellipsoidal inclination angle distribution. Agric For Meteorol 36(4):317–321 [Google Scholar]
- Campbell GS, Norman JM (1998) An introduction to environmental biophysics, 2nd edn Springer, New York [Google Scholar]
- Chehbouni A, Nouvellon Y, Lhomme J, Watts C, Boulet G, Kerr Y, Moran M, Goodrich D (2001) Estimation of surface sensible heat flux using dual angle observations of radiative surface temperature. Agric For Meteorol 108(1):55–65 [Google Scholar]
- Colaizzi P, Evett S, Howell T, Li F, Kustas W, Anderson M (2012a) Radiation model for row crops: I. Geometric view factors and parameter optimization. Agron J 104(2):225–240 [Google Scholar]
- Colaizzi P, Agam N, Tolk J, Evett S, Howell T, Gowda P, O’Shaughnessy S, Kustas W, Anderson M (2014) Two-source energy balance model to calculate E, T, and ET: Comparison of Priestley-Taylor and Penman-Monteith formulations and two time scaling methods. Trans ASABE 57:479–498 [Google Scholar]
- Colaizzi PD, Kustas WP, Anderson MC, Agam N, Tolk JA, Evett SR, Howell TA, Gowda PH, O’Shaughnessy SA (2012b) Two-source energy balance model estimates of evapotranspiration using component and composite surface temperatures. Adv Water Resour 50:134–151. 10.1016/j.advwatres.2012.06.004 [DOI] [Google Scholar]
- Colaizzi PD, Schwartz RC, Evett SR, Howell TA, Gowda PH, Tolk JA (2012c) Radiation model for row crops: II. Model evaluation. Agron J 104(2):241–255. 10.2134/agronj2011.0083 [DOI] [Google Scholar]
- Coops NC, Hilker T, Wulder MA, St-Onge B, Newnham G, Siggins A, Trofymow JAT (2007) Estimating canopy structure of Douglas-fir forest stands from discrete-return LiDAR. Trees 21(3):295 10.1007/s00468-006-0119-6 [DOI] [Google Scholar]
- Detto M, Montaldo N, Albertson JD, Mancini M, Katul G (2006) Soil moisture and vegetation controls on evapotranspiration in a heterogeneous mediterranean ecosystem on Sardinia. Italy. Water Resour Res 42(8):w08419 10.1029/2005WR004693 [DOI] [Google Scholar]
- Gao F, Kustas WP, Anderson MC (2012) A data mining approach for sharpening thermal satellite imagery over land. Remote Sens 4(11):3287 10.3390/rs4113287 [DOI] [Google Scholar]
- Goudriaan J (1977) Crop micrometeorology: a simulation stud Center for Agricultural Publications and Documentation, Wageningen, Tech. rep [Google Scholar]
- Guzinski R, Anderson MC, Kustas WP, Nieto H, Sandholt I (2013) Using a thermal-based two source energy balance model with time-differencing to estimate surface energy fluxes with day-night MODIS observations. Hydrol Earth Syst Sci 17(7):2809–2825. 10.5194/hess-17-2809-2013 [DOI] [Google Scholar]
- Guzinski R, Nieto H, Jensen R, Mendiguren G (2014) Remotely sensed land-surface energy fluxes at sub-field scale in heterogeneous agricultural landscape and coniferous plantation. Biogeosciences 11(18):5021–5046. 10.5194/bg-11-5021-2014 [DOI] [Google Scholar]
- Guzinski R, Nieto H, Stisen S, Fensholt R (2015) Inter-comparison of energy balance and hydrological models for land surface energy flux estimation over a whole river catchment. Hydrol Earth Syst Sci 19(4):2017–2036. 10.5194/hess-19-2017-2015 [DOI] [Google Scholar]
- Hillel D (1998) Environmental soil physics. Academic Press, New York [Google Scholar]
- Hoffmann H, Nieto H, Jensen R, Guzinski R, Zarco-Tejada P, Friborg T (2016) Estimating evaporation with thermal UAV and two-source energy balance models. Hydrol Earth Syst Sci 20(2):697–713. 10.5194/hess-20-697-2016 [DOI] [Google Scholar]
- Knipper KR, Kustas WP, Anderson MC, Alfieri JG, Prueger JH, Hain CR, Gao F, Yang Y, McKee LG, Nieto H, Hipps LE, Alsina MM, Sanchez6 L (2018) Evapotranspiration estimates derived using thermal-based satellite remote sensing and data fusion for irrigation management in california vineyards. Irrig Sci (this issue) [Google Scholar]
- Kondo J, Ishida S (1997) Sensible heat flux from the earth’s surface under natural convective conditions. J Atmos Sci 54(4):498–509 [Google Scholar]
- Kustas W, Anderson M (2009) Advances in thermal infrared remote sensing for land surface modeling Agric For Meteorol 149(12):2071–2081 (Environmental Biophysics - Tribute to John Norman; ) [Google Scholar]
- Kustas W, Norman J (2000) A two-source energy balance approach using directional radiometric temperature observations for sparse canopy covered surfaces. Agron J 92(5):847–854 [Google Scholar]
- Kustas W, Alfieri J, Nieto H, Gao F, Anderson M (2018) Utility of the two-source energy balance model TSEB in vine and inter-row flux partitioning over the growing season. Irrig Sci. 10.1007/s00271-018-0586-8 (this issue) [DOI] [Google Scholar]
- Kustas WP, Norman JM (1997) A two-source approach for estimating turbulent fluxes using multiple angle thermal infrared observations. Water Resour Res 33(6):1495–1508. 10.1029/97WR00704 [DOI] [Google Scholar]
- Kustas WP, Norman JM (1999) Evaluation of soil and vegetation heat flux predictions using a simple two-source model with radiometric temperatures for partial canopy cover. Agric For Meteorol 94(1):13–29. 10.1016/S0168-1923(99)00005-2 [DOI] [Google Scholar]
- Kustas WP, Alfieri JG, Anderson MC, Colaizzi PD, Prueger JH, Evett SR, Neale CM, French AN, Hipps LE, Chávez JL, Copeland KS, Howell TA (2012) Evaluating the two-source energy balance model using local thermal and surface flux observations in a strongly advective irrigated agricultural area. Adv Water Resour 50:120–133. 10.1016/j.advwatres.2012.07.005 [DOI] [Google Scholar]
- Kustas WP, Nieto H, Morillas L, Anderson MC, Alfieri JG, Hipps LE, Villagarcía L, Domingo F, García M (2016) Revisiting the paper “using radiometric surface temperature for surface energy flux estimation in mediterranean drylands from a two-source perspective”. Remote Sens Environ 184:645–653 [Google Scholar]
- Kustas WP, Anderson MC, Alfieri JG, Knipper K, Torres-Rua A, Parry CK, Nieto H, Agam N, White A, Gao F, McKee L, Prueger JH, Hipps LE, Los S, Alsina M, Sanchez L, Sams B, Dokoozlian N, McKee M, Jones S, McElrone A, Heitman JL, Howard AM, Post K, Melton F, Hain C (2018) The grape remote sensing atmospheric profile and evapotranspiration eXperiment (GRAPEX). Bull Am Meteorol Soc. 10.1175/BAMS-D-16-0244.1 (in press) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li F, Kustas WP, Prueger JH, Neale CM, Jackson TJ (2005) Utility of remote sensing-based two-source energy balance model under low-and high-vegetation cover conditions. J Hydrometeorol 6(6):878–891 [Google Scholar]
- Mallet C, Bretar F (2009) Full-waveform topographic lidar: state-ofthe-art. ISPRS J Photogramm Remote Sens 64(1):1–16. 10.1016/j.isprsjprs.2008.09.007 [DOI] [Google Scholar]
- Massman W (1987) A comparative study of some mathematical models of the mean wind structure and aerodynamic drag of plant canopies. Bound-Layer Meteorol 40(1):179–197 [Google Scholar]
- Massman W, Forthofer J, Finney M (2017) An improved canopy wind model for predicting wind adjustment factors and wildland fire behavior. Can J For Res 47(5):594–603. 10.1139/cjfr-2016-0354 [DOI] [Google Scholar]
- Morillas L, García M, Nieto H, Villagarcía L, Sandholt I, González-Dugo M, Zarco-Tejada P, Domingo F (2013) Using radiometric surface temperature for surface energy flux estimation in Mediterranean drylands from a two-source perspective. Remote Sens Environ 136:234–246. 10.1016/j.rse.2013.05.010 [DOI] [Google Scholar]
- Nieto H, Kustas W, Gao F, Alfieri J, Torres A, Hipps L (2018) Impact of different within-canopy wind attenuation formulations on modelling sensible heat flux using TSEB. Irrig Sci. 10.1007/s00271-018-0611-y [DOI] [Google Scholar]
- Norman J, Kustas W, Prueger J, Diak G (2000) Surface flux estimation using radiometric temperature: a dual-temperature-difference method to minimize measurement errors. Water Resour Res 36(8):2263–2274 [Google Scholar]
- Norman JM, Kustas WP, Humes KS (1995) Source approach for estimating soil and vegetation energy fluxes in observations of directional radiometric surface temperature. Agric For Meteorol 77(3–4):263–293. 10.1016/0168-1923(95)02265-Y [DOI] [Google Scholar]
- Ortega-Farías S, Ortega-Salazar S, Poblete T, Kilic A, Allen R, Poblete-Echeverría C, Ahumada-Orellana L, Zuñiga M, Sepúlveda D (2016) Estimation of energy balance components over a drip-irrigated olive orchard using thermal and multispectral cameras placed on a helicopter-based unmanned aerial vehicle (UAV). Remote Sens 8(8):638 10.3390/rs8080638 [DOI] [Google Scholar]
- Parry C, Nieto H, Guillevic P, Agam N, Kustas B, Alfieri J, McKee L, McElrone A (2018) An intercomparison of radiation partitioning models in vineyard row structured canopies. Irrig Sci (this issue) [Google Scholar]
- Pope G, Treitz P (2013) Leaf area index (LAI) estimation in boreal mixedwood forest of Ontario, Canada using light detection and ranging (LiDAR) and WorldView-2 imagery. Remote Sens 5(10):5040–5063. 10.3390/rs5105040 [DOI] [Google Scholar]
- Priestley CHB, Taylor RJ (1972) On the assessment of surface heat flux and evaporation using large-scale parameters. Mon Weather Rev 100(2):81–92. [DOI] [Google Scholar]
- Santanello J Jr, Friedl M (2003) Diurnal covariation in soil heat flux and net radiation. J Appl Meteorol 42(6):851–862 [Google Scholar]
- Sauer TJ, Norman JM, Tanner CB, Wilson TB (1995) Measurement of heat and vapor transfer coefficients at the soil surface beneath a maize canopy using source plates. Agric For Meteorol 75(1–3):161–189. 10.1016/0168-1923(94)02209-3 [DOI] [Google Scholar]
- Semmens KA, Anderson MC, Kustas WP, Gao F, Alfieri JG, McKee L, Prueger JH, Hain CR, Cammalleri C, Yang Y, Xia T, Sanchez L, Alsina MM, Vélez M (2016) Monitoring daily evapotranspiration over two california vineyards using Landsat 8 in a multi-sensor data fusion approach. Remote Sens Environ 185:155–170. 10.1016/j.rse.2015.10.025 [DOI] [Google Scholar]
- Song L, Liu S, Zhang X, Zhou J, Li M (2015) Estimating and validating soil evaporation and crop transpiration during the HiWATER-MUSOEXE. IEEE Geosci Remote Sens Lett 12(2):334–338. 10.1109/LGRS.2014.2339360 [DOI] [Google Scholar]
- Song L, Liu S, Kustas WP, Zhou J, Xu Z, Xia T, Li M (2016) Application of remote sensing-based two-source energy balance model for mapping field surface fluxes with composite and component surface temperatures. Agric For Meteorol 230231:8–19. 10.1016/j.agrformet.2016.01.005 [DOI] [Google Scholar]
- Torres-Rua A (2017) Vicarious calibration of sUAS microbolometer temperature imagery for estimation of radiometric land surface temperature. Sensors 17:1499 10.3390/s17071499 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Torres-Rua A, Nieto H, Parry C, Alarab M, McKee M (2018) Inter-comparison of thermal sensors from ground aircraft, and satellite. Irrig Sci (this issue) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Willmott CJ (1981) On the validation of models. Phys Geogr 2(2):184–194. 10.1080/02723646.1981.10642213 [DOI] [Google Scholar]
- Xia T, Kustas WP, Anderson MC, Alfieri JG, Gao F, McKee L, Prueger JH, Geli HME, Neale CMU, Sanchez L, Alsina MM, Wang Z (2016) Mapping evapotranspiration with high-resolution aircraft imagery over vineyards using one- and two-source modeling schemes. Hydrol Earth Syst Sci 20(4):1523–1545. 10.5194/hess-20-1523-2016 [DOI] [Google Scholar]
- Zhao K, Popescu S (2009) Lidar-based mapping of leaf area index and its use for validating GLOBCARBON satellite LAI product in a temperate forest of the southern USA. Remote Sens Environ 113(8):1628–1645. 10.1016/j.rse.2009.03.006 [DOI] [Google Scholar]
- Zipper SC, Loheide SP II (2014) Using evapotranspiration to assess drought sensitivity on a subfield scale with HRMET, a high resolution surface energy balance model. Agric For Meteorol 197:91–102. 10.1016/j.agrformet.2014.06.009 [DOI] [Google Scholar]


