MAIN-BELT ASTEROIDS OBSERVED FROM CS3: 2019 JULY TO SEPTEMBER

Abstract

CCD photometric observations of 25 main-belt asteroids were obtained at the Center for Solar System Studies (CS3) from 2019 July to September.

The Center for Solar System Studies (CS3) has seven telescopes which are normally used in program asteroid family studies. The focus is on near-Earth asteroids, but when suitable targets are not available, Jovian Trojans and Hildas are observed. When a nearly full moon is too close to the family targets being studied, targets of opportunity amongst the main-belt families were selected.

Table I lists the telescopes and CCD cameras that were used to make the observations. Images were unbinned with no filter and had master flats and darks applied. The exposures depended upon various factors including magnitude of the target, sky motion, and Moon illumination.

Table I:

List of CS3 telescope/CCD camera combinations.

Telescope	Camera
0.30-m f/6.3 Schmidt-Cass	FLI Microline 1001E
0.35-m f/9.1 Schmidt-Cass	FLI Microline 1001E
0.35-m f/9.1 Schmidt-Cass	FLI Microline 1001E
0.35-m f/9.1 Schmidt-Cass	FLI Microline 1001E
0.35-m f/11 Schmidt-Cass	FLI Microline 1001E
0.40-m f/10 Schmidt-Cass	FLI Proline 1001E
0.50-m F8.1 R-C	FLI Proline 1001E

Image processing, measurement, and period analysis were done using MPO Canopus (Bdw Publishing), which incorporates the Fourier analysis algorithm (FALC) developed by Harris (Harris et al., 1989). The Comp Star Selector feature in MPO Canopus was used to limit the comparison stars to near solar color. Night-tonight calibration was done using field stars from the CMC-15 or the ATLAS catalog (Tonry et al., 2018), which has Sloan griz magnitudes that were derived from the GAIA and Pan-STARR catalogs, among others. The authors state that systematic errors are generally no larger than 0.005 mag, although they can reach 0.02 mag in small areas near the Galactic plane. BVRI magnitudes were derived by Warner using formulae from Kostov and Bonev (2017). The overall errors for the BVRI magnitudes, when combining those in the ATLAS catalog and the conversion formulae, are on the order of 0.04–0.05 mag.

Even so, we found in most cases that nightly zero point adjustments for the ATLAS catalog to be on the order of only 0.02–0.03 mag were required during period analysis. There were occasional exceptions that required up to 0.10 mag. These may have been related in part to using unfiltered observations, poor centroiding of the reference stars, and not correcting for second-order extinction terms. Regardless, the systematic errors seem to be considerably less than other catalogs, which reduces the uncertainty in the results when analysis involves data from extended periods or the asteroid is tumbling.

The Y-axis for some lightcurves may be given as “Reduced Magnitude” instead of “Magnitude.” Both are Johnson V with the former corrected to a unity distance by applying −5*log (rΔ) to the measured sky magnitudes with r and Δ being, respectively, the Sun-asteroid and the Earth-asteroid distances in AU. Otherwise, the values are the sky magnitudes. The magnitudes were normalized to the phase angle given in parentheses using G = 0.15. The X-axis rotational phase ranges from −0.05 to 1.05.

In the lightcurve plots, the Y-axis may be labeled “Reduced Magnitude” or “Magnitude.” Unless otherwise indicated, the values are Johnson V. The latter are sky (catalog-derived) magnitudes while “Reduced Magnitude” indicates that sky magnitudes were corrected to unity distances by applying −5*log (rΔ) to the measured sky magnitudes, with r and Δ being, respectively, the Sun-asteroid and the Earth-asteroid distances in AU. The magnitudes were normalized to the phase angle given in parentheses using G = 0.15. The X-axis rotational phase ranges from −0.05 to 1.05.

The amplitude indicated in the plots (e.g. Amp. 0.23) is the amplitude of the Fourier model curve and not necessarily the adopted amplitude of the lightcurve.

For brevity, only some of the previously reported rotational periods may be referenced. A complete list is available at the lightcurve database (LCDB; Warner et al., 2009).

855 Newcombia.

Per the LCDB, this inner main-belt asteroid has been observed several times in the past. Cooney et al. (2007); Klinglesmith et al. (2014, 2016, 2017); and Stephens (2014) all found periods near 3.004 h, in agreement with this year’s result.

The Klinglesmith data were available in the ALCDEF asteroid photometry database (http://www.alcdef.org/) (Warner et al. 2011), so we attempted a pole and shape model.

Sparse data observations were obtained from the Catalina Sky Survey and USNO-Flagstaff survey using the AstDyS-3 site (http://hamilton.dm.unipi.it/asdys2/). These sparse data were combined with our dense data using MPO LCInvert, (Bdw Publishing). This Windows-based program incorporates the algorithms developed by Kassalainen et al (2001a, 2001b) and converted by Josef Durech from the original FORTRAN to C. A period search was made over a sufficiently wide range to assure finding a global minimum in x² values.

The modeling processing using lightcurve inversion has been detailed previously (e.g., Warner et al., 2017, and references therein). The idea is to find a shape and its orientation such that its modeled lightcurves closely match the original data. Main-belt asteroids usually require data from at least three oppositions at different phase angle bisector longitudes before a reliable model can be developed.

In the PAB longitude plot, green circles represent dense lightcurves while red squares represent sparse data from one or more of the surveys. The green line in the period plot lies 10% above the lowest x² value. This was an ideal solution as it has a well-defined shape with only one data point below the line.

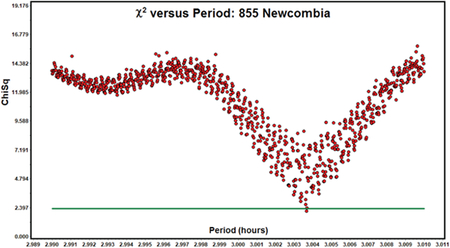
In the pole plot, dark red represents a solution that is more than 10% above the lowest x² value. A “perfect” solution is when there is only one dark blue region and all the others are dark red. This result shows a strong solution of ecliptic coordinates (287°, −72°, 3.003687 h) and a weak, competing solution of (61°, −73°, 3.003687 h), which is about 180° apart. The longitude mirroring is a common trait of the inversion process.

We chose (287°, −72°, 3.003687 h) because it had the lowest x² value. In both cases, the estimated error for the pole is a circle of about 10° radius and 0.000001 h for the period.

The solid black line in the lightcurve plots is the model lightcurve and the red dots are the original data. The model curves in are from the solution for ecliptic coordinates (287°, −72°) although the fits to the model based on (61°, −73°) are essentially identical.

1355 Magoeba.

This Hungaria has been observed numerous times by Warner (2007; 2010a; 2011a; 2013a; and 2015a). With each new set of observations, the solution seemed to favor a new period. Eventually, they settled to an ambiguous solution of about 2.9 h or 5.9 h. The observations in 2014 (Warner, 2015a), indicated the possibility of a satellite with an orbital period of about 15 h.

The raw data from the 2019 campaign, with observing runs of 6 hours or more, virtually assure that a rotation period of 5.9452 h is correct because of the asymmetry of the lightcurve.

Since a satellite was suspected from the 2014 data (Warner, 2015e), a dual-period search was done using the 2019 data. The result was an unconvincing lightcurve with P = 16.376 h and A = 0.04 mag. This period and the adopted one of 5.9466 h have an almost exact 11:4 ratio. This would often indicate that the second period is the result of harmonics in the Fourier search. A cleaner result for the preferred solution was produced by using the “P2” solution as a “noise reduction filter.”

1727 Mette.

This Hungaria was observed in 2019 to extend the time range of the available data, which serves to refine the sidereal period in spin axis modeling. The latest result of P = 2.9804 h agrees with previous ones found by Warner (2011a; 2015b) for the primary of this known binary (Warner et al., 2013b; 2013c). There were no indications of the satellite in the 2019 data set.

2150 Nyctimene.

This is another Hungaria member that has been studied numerous times by the authors (e.g., Warner, 2007; 2013a; 2017; Stephens, 2016). As with 1355 Magoeba, a dual-period search found a result that, while improbable but not impossible, served to improve the fit of the data to the Fourier model curve.

2432 Soomana.

Waszczak et al. (2015) using sparse data found a period of 3.207 h, rated U = 2. Our period agrees with that result.

2511 Patterson.

This member of the Vesta family has been observed several times in the past. Juarez et al. (2005); Hasegawa et al. (2012); Waszczak et al. (2015) all found rotational periods near 4.14 h. Durech et al. (2018) found a pole solution with ecliptic coordinates of (194°, 50°) and a sidereal period of 4.14065 h. They found an alternate pole solution of (10°, 31°). This year’s period is in good agreement with those results.

4125 Lew Allen.

The apparition in 2019 was the fifth one that Warner observed this Hungaria (Warner 2015c and references therein) each time finding a period neat 4.62 h. Both authors observed it in 2019, Warner in July and then Stephens in August.

Both periods are in good agreement with prior results. While the overall shape of the lightcurve did not change significant, its amplitude decreased from 0.41 to 0.36 mag as the phase angle decreased from about 29° to 23°. This is a common phenomenon (Zappala et al., 1990).

4569 Baerbel.

Brinsfield (2010) observed this inner main-belt asteroid in 2010, finding a rotational period of 2.737 h. The Brinsfield observations were on two nights spaced seven days apart and the resulting lightcurve, although having an amplitude of 0.24 mag, was somewhat noisy. This year’s result differs from Brinsfield by 0.05 h. The period spectrum does not show a possibility of a shorter period, which was probably caused by an alias resulting from the seven day gap between sessions.

4868 Knushevia.

Adding data from the 2019 apparition did more to confuse than refine the solution for this Hungaria. At three previous apparitions (Warner, 2009; 2010b; Warner et al., 2012a), the period ranged from 4.45 and 4.72 h. Observations in 2013 (Warner and Stephens, 2015) found a period of 3.1422 h and the possibility of a satellite with an orbital period of 11.9 or 23.8 h. The data from 2019 supported none of these results.

The best fit was found at P = 2.784 h, but there was a small gap in the coverage, which indicated the possibility of a “fit by exclusion,” which is where a local minimum is found by the Fourier analysis by minimizing the number of overlapping data points. A search between 3–4 hours found a very symmetric quadramodal solution at about 3.7 h. This is entirely possible (Harris et al., 2014). So is the half-period, bimodal solution at 1.856 h (Alt).

While the shorter period puts the asteroid (D ~ 2.3 km) above the so-called “spin barrier” at about 2.2 h, it would be in good company in that region of the frequency-diameter plot from the LCDB (Warner et al., 2009). For example, (60716) 2000 GD65, rated U = 3, has a period of 1.953 h and diameter of 2.25 km (Warner et al., 2009). High-quality observations at future apparitions are encouraged.

6485 Wendeesther.

Warner (2012) found a period of 74.82 h. The 2019 data set was more extensive and allowed finding a refined period of 75.56 h.

6558 Norizuki.

This appears to be the first reported lightcurve period for Norizuki, which is a member of the Flora group/family with an estimated diameter of 3.9 km.

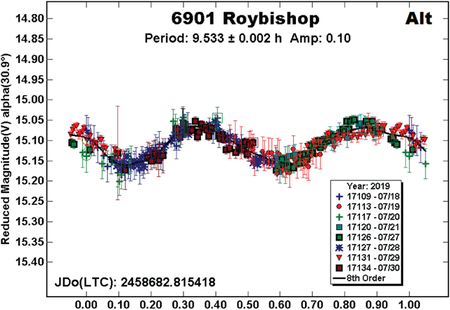
6901 Roybishop.

This 5.8 km Hungaria is another example of ambiguous solutions as a result of low amplitude (0.04–0.09 mag) lightcurves. Previous results (Warner 2009; 2015d; Warner et al. 2012b) were close to 4.7 h, the same result found from the 2019 data. However, the bimodal solution with a period of 9.533 h cannot be formally excluded.

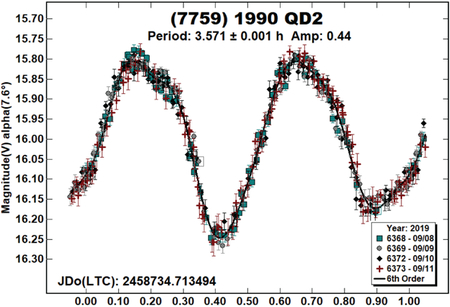
(7759) 1990 QD2.

This appears to be the first reported lightcurve period in the LCDB for this inner main-belt asteroid.

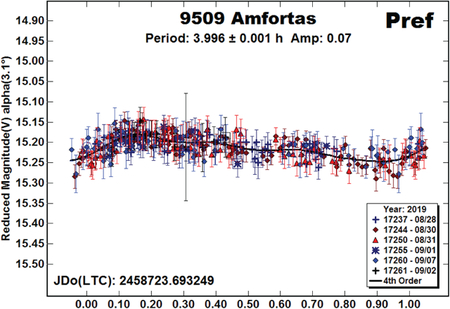
9509 Amfortas.

There were no previously reported periods in the LCDB for this Flora member to guide the analysis of the 2019 data. The period spectrum shows several likely candidates.

We have adopted the monomodal solution of 3.996 h over the bimodal, double-period solution of 7.989 h based mostly on the possible fit by exclusion (large gap in lightcurve) and the nearly symmetrical split-halves lightcurve. Both solutions are possible (Harris et al., 2014) and so neither can be formally excluded.

9565 Tikhonov.

There are no previously reported lightcurves in the LCDB for this member of the Flora family, which is estimated to have an effective diameter of 4.5 km.

(11116) 1996 EK.

Pravec et al. (2019) reported this member of the Flora family as a likely binary asteroid candidate from the Photometric Survey for Asynchronous Binary Asteroids. Marginal attenuation detections were found in 2006; inconclusive attenuations were seen in 2009 with a primary rational period reported of 4.4018 h. The survey did not see any attenuations in May 2019, and none are seen in our data. Our period is consistent with their reported results.

(18890) 2000 EV26.

This Hungaria is a known binary (Warner, 2015a). The asteroid was moving through rich star fields, forcing rejecting of nearly half the data points. The primary (“P1”) period is in good agreement with previous results. The orbital (“P2”) period is similar to those found on two previous occasions.

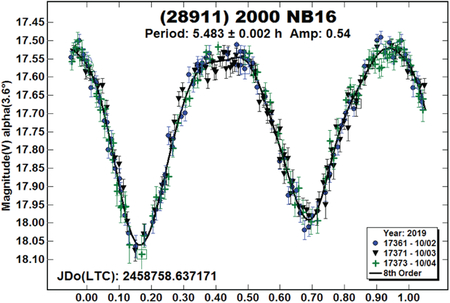
(28911) 2000 NB16.

Waszczak et al. (2015) reported a period of 5.486 h for this outer main-belt object.

(51229) 2000 JF27.

This looks to be the first rotation period found for this 4.8 km outer main-belt object. The period spectrum shows several likely candidates. The limited data set and low SNR did not allow doing better. We adopted the solution closest to a bimodal lightcurve. Given the 0.25 mag amplitude, this seems a safe assumption (Harris et al., 2014).

(58285) 1993 YN.

There are no rotation periods posted for this Mars-crosser in the LCDB. The period we were able to find is close to an integral multiple of Earth days, requiring almost two weeks of observing time to complete the lightcurve.

The period is close to where tumbling would be more likely than not (Pravec et al., 2005). However, we saw no obvious signs such as data from a given night not matching the slope of the Fourier curve.

(75464) 1999 XM159.

Despite a noisy data set but because of the large amplitude, we were able to find a reasonably secure solution for this Flora member. There were no previously reported periods listed in the LCDB.

(80593) 2000 AG144.

No records were found in the LCDB for this Mars-crosser, so this is another new discovery of an asteroid rotational period. With a period close to the spin barrier of about 2.2 h, it’s prudent to be on the lookout for a possible secondary period due to a satellite. We found no evidence of such.

(141808) 2002 NV38.

This Mars-crosser also did not have any previous rotation periods posted in the LCDB. It is rotating a little faster than the accepted 2.2 h spin barrier, although that is more of a guideline than a hard and fast rule. Again, no secondary periods were noted over six nights of observations.

(218322) 2003 YC65.

For various reasons, it was not possible to follow this Flora member longer than the three nights in late August. Each night’s data clearly showed a short period of P < 6 h. The raw plot of all three nights shows what appears to be a long period lightcurve near a minimum. On this assumption, a low-order dual-period search was done. This found a possible long period of 41 h. Once this was subtracted, a noisy but clear solution of 5.13 h was found. We believe this may be a candidate for member in the rare class of very wide binary asteroids (see, e.g., Warner, 2016).

(248824) 2006 SA281.

This 1.8 km Eunomia member had no previously reported period in the LCDB.

Table II.

The two pole solutions for 855 Newcombia. It is common in lightcurve inversion to get two solutions that differ by about 180° in longitude.

855 Newcombia	Eclipitic Long/Lat	Sidereal Period (hours)
Preferred	(287°, −72°)	3.003687 ± 0.000001
Alternate	(61°, −73°)

Table III.

Observing circumstances and results. The phase angle is given for the first and last date. If preceded by an asterisk, the phase angle reached an extrema during the period. L_PAB and B_PAB are the approximate phase angle bisector longitude/latitude at mid-date range (see Harris et al., 1984). Grp is the asteroid family/group (Warner et al., 2009). For a binary, the first line gives the rotation period of the primary and the second line gives the orbital period of the satellite.

Number	Name	2019 mm/dd	Phase	LPAB	BPAB	Period(h)	P.E.	Amp	A.E.	Grp
855	Newcombia	09/12–09/15	20.9, 20.6	53	5	3.004	0/001	0.4	0.02	MB-I
1355	Magoeba	09/13–09/22	26.9, 24.1	37	12	5.9466	0.0006	0.13	0.01	H
1727	Mette	07/14–07/16	14.8, 13.7	314	4	2.9804	0.0004	0.35	0.02	H
2150	Nyctimene	07/17–08/01	25.0, 22.3	324	33	6.1254	0.0002	0.56	0.02	H
2432	Soomana	09/12–09/15	27.4, 27.2	56	4	3.206	0.001	0.42	0.02	V
2511	Patterson	08/13–08/16	23.0, 22.2	7	−10	4.139	0.0005	0.95	0.02	V
4125	Lew Allen	07/17–07/28	28.9, 26.2	330	21	4.6283	0.0001	0.41	0.02	H
4125	Lew Allen	08/14–08/16	23.0, 22.7	334	27	4.635	0.001	0.36	0.02	H
4569	Baerbel	07/20–07/22	9.8, 10.0	293	19	2.79	0.002	0.14	0.02	MB-I
4868	Knushevia	08/21–08/23	19.1, 18.1	353	14	2.784	0.002	0.08	0.02	H
	Alternate					1.856	0.002	0.06	0.02
6485	Wendeesther	08/16–08/31	33.0, 30.1	6	27	75.56	0.02	1.13	0.03	H
6558	Norizuki	08/28–09/02	3.1, 4.0	335	5	2.4507	0.0006	0.11	0.01	FLOR
6901	Roybishop	07/18–07/30	30.9, 29.6	349	24	4.766	0.002	0.09	0.01	H
7759	1990 QD2	09/08–09/11	7.6, 5.8	356	−2	3.571	0.001	0.44	0.02	MB-I
9509	Amfortas	08/28–09/07	3.1, 6.1	335	5	0.001	0.07	0.07	0.01	FLOR
9565	Tikhonov	07/06–07/14	20.9, 18.1	319	9	7.8448	0.0006	0.56	0.02	FLOR
11116	1996 EK	07/17–07/22	27.1, 28.2	257	10	4.387	0.002	0.17	0.02	FLOR
18890	2000 EV26	06/26–07/14	19.5, 21.4	271	32	3.8151	0.0002	0.13	0.02	H
	Satellite orbit					14.248	0.002	0.08	0.02
28911	2000 NB16	10/02–10/04	3.6, 3.4	12	8	5.483	0.02	0.54	0.03	MB-O
51229	2000 JF27	08/28–09/08	6.7, 3.5	355	−4	4.78	0.01	0.25	0.03	MB-O
58285	1993 YN	07/27–08/09	13.2, 11.0	314	13	51.53	0.04	0.28	0.03	MC
75464	1999 XM159	09/09–09/10	1.6, 1.1	349	0	5.054	0.008	0.53	0.07	FLOR
80593	2000 AG144	09/17–09/22	20.7, 23.3	343	22	2.747	0.001	0.12	0.02	MC
141808	2002 NV38	09/17–09/22	10.0, 12.6	347	7	2.068	0.001	0.17	0.02	MC
218322	2003 YC65	08/30–09/01	3.4, 4.0	335	5	41	4	0.44	0.05	FLOR
248824	2006 SA281	08/30–09/02	3.3, 3.9	335	5	5.537	0.003	0.7	0.05	MB-O