Skip to main content
PMC home page
Wiley - PMC COVID-19 Collection logoLink to Wiley - PMC COVID-19 Collection
. 2004 Dec 15;168(1):233–243. doi: 10.1111/j.1467-985X.2004.00345.x

A comparison study of realtime fatality rates: severe acute respiratory syndrome in Hong Kong, Singapore, Taiwan, Toronto and Beijing, China

Paul S F Yip 1, K F Lam 1, Eric H Y Lau 1, Pui‐Hing Chau 1, Kenneth W Tsang 1, Anne Chao 2
PMCID: PMC7194100  PMID: 32367908

Abstract

Summary.  In an outbreak of a completely new infectious disease like severe acute respiratory syndrome (SARS), estimation of the fatality rate over the course of the epidemic is of clinical and epidemiological importance. In contrast with the constant case fatality rate, a new measure, termed the ‘realtime’ fatality rate, is proposed for monitoring the new emerging epidemic at a population level. A competing risk model implemented via a counting process is used to estimate the realtime fatality rate in an epidemic of SARS. It can capture and reflect the time‐varying nature of the fatality rate over the course of the outbreak in a timely and accurate manner. More importantly, it can provide information on the efficacy of a certain treatment and management policy for the disease. The method has been applied to the SARS data from the regions affected, namely Hong Kong, Singapore, Toronto, Taiwan and Beijing. The magnitudes and patterns of the estimated fatalities are virtually the same except in Beijing, which has a lower rate. It is speculated that the effect is linked to the different treatment protocols that were used. The standard estimate of the case fatality rate that was used by the World Health Organization has been shown to be unable to provide useful information to monitor the time‐varying fatalities that are caused by the epidemic.

Keywords: Competing risk, Counting process, Severe acute respiratory syndrome, Time‐varying fatality rate

1. Introduction

Severe acute respiratory syndrome (SARS) is a highly contagious and severe atypical pneumonia which is caused by a new coronavirus and is predominantly transmitted by droplets and contact with contaminated fomites (Tsang, Ho, Ooi et al., 2003; Rota et al., 2003; Seto et al., 2003; Riley et al., 2003). SARS has rapidly spread worldwide and there were in total 8098 reported cases with 774 fatalities at July 31st, 2003 (World Health Organization, 2003a). An on‐going controversial topic is the estimation of the fatality rate of SARS. The usual definition of the fatality rate that has been adopted by the World Health Organization (WHO) is the ratio of the cumulative number of deaths to the cumulative number of infected people in the course of the epidemic (World Health Organization, 2003b). This is often called the case fatality rate and is assumed to be a constant.

While the outbreak was on going and there were patients still in hospitals over the course of the epidemic, the WHO estimate assumed implicitly that all remaining SARS in‐patients would eventually recover. It therefore led to an underestimation of the true case fatality rate. For example, in the midst of the SARS outbreak at April 15th, 2003, the fatality rate in Hong Kong was 4.5% according to the WHO estimate, but it hit a record high of 17.0% at the end of the epidemic. Furthermore, the WHO estimate cannot reflect the changing fatality rate over the course of the epidemic in a timely manner owing to the use of cumulative data in the calculation. The WHO estimates of the fatality rates of Hong Kong, Singapore, Taiwan, Beijing and Toronto were 17.0%, 13.9%, 10.7%, 6.5% and 15.8% at July 31st, 2003, respectively. Hong Kong appeared to have the highest fatality rate.

Donnelly et al. (2003) were the first to apply a survival analysis framework to analyse the SARS data and to estimate the time delay distributions of the times since infection to onset, onset to admission, admission to death and admission to discharge. They assumed a fixed probability π (the case fatality rate) and 1−π for the respective outcomes of death and recovery for each in‐patient on admission during the whole course of the epidemic. Their approach projected an estimate of the case fatality rate, and the estimate depends on whether the age of the patient is over 60 years or not. Their formulation can also be easily extended to a mixture of regression or threshold models to incorporate exogenous variables. In this setting, the constant case fatality rate is often interpreted as a measure of the severity or virulence of an infectious disease.

For a completely new disease like SARS, it would be worthwhile and informative to inves‐ tigate how the rate of death (given that a patient either dies or recovers) varies with time as clinical experience on diagnosis and management improve over time. When modelling this rate, there is no need to model the infectious process as our interest is in measuring the fatality that is inflicted by the epidemic. Also, the duration of hospitalization of individual patients is not taken into account since the initiation of hospitalization of an SARS patient is dependent on several factors, including the very early screening of hospital staff who are exposed, leading to detection and hospitalization of very early and asymptomatic disease, which is in contrast with the reluctance of some cases to seek medical attention, thereby delaying their hospitalization in the process. In this paper, we call this rate the realtime fatality rate. The rapid accumula‐ tion of experience and knowledge on the diagnosis, investigation and management, along with different age groups being affected at different times, compounded by differences in viral loads and other confounding factors, do not permit the assumption of a constant rate throughout the period of the outbreak . To monitor the fatality of an emerging epidemic, an estimator for such a time‐specific rate at the population level should be used to assess the efficacy of treatment in realtime, especially when the disease is rapidly evolving. For instance, there is also considerable controversy on the treatment of SARS (Wenzel and Edmond, 2003). The efficacy of ribavirin and corticosteroids, which were commonly used in Hong Kong for an empirical treatment of SARS, is not proven by controlled trial studies that were impossible to organize during the initial outbreak. In the absence of large scale clinical trials to assess the efficacy of various treatments, investigators are interested in the estimation of the realtime fatality rate over the course of the epidemic with a broad assessment of the effect of other factors, including variation in clinical management and other exogenous (including unidentified or unspecified) factors over the course of the outbreak.

In this paper, a counting process in a competing risk set‐up is used to model the transitions from in‐patient to death and from in‐patient to recovery (Andersen et al., 1993; Yip and Lam, 1992, 1993). The in‐patients are subject to death, or recovery or to remain in the hospital over the course of the epidemic. Here, the timescale of interest is the calendar time, rather than the usual time to event from admission in standard survival analysis studies as in Donnelly et al. (2003). A new measure termed the realtime fatality rate is proposed in this paper and is defined as the probability of death conditioned on a transition to death or recovery at time t. This formulation can therefore model the fatality rate in realtime for the infected community in a macro perspective. Since rate estimates from survival models are usually estimated as step functions, a kernel method is used to smooth the estimates of the transition rates for recovery and death at time t, and for the realtime fatality rate. This realtime fatality rate is also useful in providing information on the efficacy of certain treatments and on the management of the disease during the outbreak of the disease. The approximate pointwise confidence limits of the respective transition and the realtime fatality rates are readily available. The method is applied to the SARS data from the regions affected, namely Hong Kong, Singapore, Toronto, Taiwan and Beijing.

2. Method

2.1. Clinical data collection

The daily data on admission, discharge and death for all SARS patients in Hong Kong, Singapore, Taiwan, Beijing and Toronto were obtained from the Web sites of the respective Government agencies and authorities: Hong Kong, http://www.info.gov.hk/info/sars/c_news.htm; Singapore, http://app.moh.gov.sg/sars/news/updates.asp; Taiwan, http://sars.doh.gov.tw/news/; Beijing, http://www.moh.gov.cn/zhgl/yqfb/index.htm; Toronto, http://www.hc-sc.gc.ca/pphb-dgspsp/sars-sras/eu-ae/index.html. All patients with probable SARS were diagnosed according to the criteria that were established by the WHO (World Health Organization, 2003b). Briefly, patients with probable SARS presented with high fever (temperature above 38°C), coughing or breathing difficulty, contact history with SARS patients and pulmonary infiltrates that were consistent with pneumonia on chest radiographs or high resolution computed tomog‐raphy of the thorax that could not be explained by an alternative diagnosis (Tsang, Mok, Wong and Ooi, 2003). The criteria from the WHO and Centers for Disease Control and Prevention (2003) do not require microbiological confirmation although most patients with SARS in Hong Kong have positive serological evidence of SARS coronavirus infection, i.e. a significant rise in immunoglobulin G after a period of 21 days (Peiris et al., 2003).

2.2. Statistical model

For each in‐patient, the final outcome must be either death or recovery. The primary target of most medical treatments and policies for lethal epidemics such as SARS is to lower the fatality rate during the outbreak of the epidemic, i.e. to lower the force of death relative to recovery, rather than necessarily to shorten the period of hospitalization. Hence a measure of treatment efficacy should be time sensitive (calendar time but not chronological time) and focus on their effects on death and recovery. By considering these two outcomes as competing ‘risks’ as in Yip and Lam (1992), we can obtain a realtime fatality rate which serves well for treatment or policy evaluation during the epidemic. The two risks, which are not necessarily independent, are assumed to operate simultaneously on the in‐patients. Since the times of the outbreak in SARS‐affected areas are different, we have different time origins (different calendar times) for different regions depending on the time of onset of the SARS epidemic and the availability of the data, with all areas followed longitudinally up to June 30th, 2003. The method proposed makes use of the information only on the cumulative number of deaths, cumulative number of discharges and SARS patients who are still in hospital on day t (for the Hong Kong region, t=0 for March 1st, 2003, t=1 for March 2nd, 2003 and so on), denoted by N 1(t),N 2(t) and I(t) respectively. Suppose that N 1(t) and N 2(t) are counting processes with intensity processes or cause‐specific instantaneous transition rates for a transition to death and to recovery on the tth day, denoted by γ 1(t) and γ 2(t) respectively, that satisfy the multiplicative intensity model

graphic file with name RSSA-168-233-e002.jpg

where F t={I(u),N i(u), for i=1,2;0u<t}, the σ‐field representing the history of the epidemic process up to but not including time t. By the Doob–Meyer decomposition (see Yip and Lam (1992) and Andersen et al. (1993), we have that

graphic file with name RSSA-168-233-e011.jpg

are zero‐mean martingales with respect to the increasing family of σ‐fields {F t,t≥0}.

On the basis of standard martingale theories, the cumulative cause‐specific transition rates can be estimated easily by the usual Nelson–Aalen estimator. A smoothed version of the cause‐specific transition rates can be estimated by the Ramlau‐Hansen (1983) estimator given by

graphic file with name RSSA-168-233-e001.jpg (1)

where t i1<t i2<… denote the ordered exit times due to cause i, b is the window width of a kernel function, which determines the degree of smoothing, and B is a kernel function. One frequently used kernel function is the Epanechnikov kernel function

graphic file with name RSSA-168-233-e012.jpg

Details on the estimation of γ 1(t) and γ 2(t) can be found in Yip and Lam (1992, 1993). Since the time unit is days, there were situations where several people recovered or died on the same day. For simplicity we assume that all the deaths occurred before the discharges on each day. This assumption has very little effect on the estimates. It should be noted that only those exit times t il for which t−b<t il<t+b would contribute to the estimation of γ i(t),whereas the information on those days that are outside the range would have no contribution. Under some mild regularity conditions, estimator (1), suitably normalized, is distributed according to a normal distribution asymptotically (see Andersen et al. (1993), pages 241–243) and the variance of the estimator is consistently estimated by

graphic file with name RSSA-168-233-e013.jpg

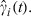Hence approximate 100(1−α)% pointwise confidence limits can be constructed for the γ i easily. The choice of the bandwidth b for the kernel function in equation (1) leads to a trade‐off between the variance and bias of Inline graphic The optimal bandwidth for γ can be obtained by minimizing the integrated mean‐square error (Andersen et al., 1993) in theory. However, a subjective value of b by visually examining the fitted γ would be sufficient for our purpose. After many trials of different bandwidths, window widths of 5, 7, 6, 3 and 12 days were chosen for Hong Kong, Singapore, Taiwan, Beijing and Toronto respectively, depending on the volatility and sparseness of the data. A natural estimator for the ratio of the transition rates θ(t)=γ 2(t)/γ 1(t) was given by

graphic file with name RSSA-168-233-e015.jpg

By the martingale theories, it can be shown that the estimates of the cumulative intensities 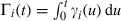Inline graphic, for i=1,2, are nearly orthogonal and hence the covariance is 0. The delta method can be used to estimate the variance of Inline graphic and is thus given by

graphic file with name RSSA-168-233-e018.jpg

Finally, we propose a new measure of the fatality rate π(t) defined as the probability of death conditioned on a transition to death or recovery at time t. Mathematically

graphic file with name RSSA-168-233-e003.jpg

A natural estimator for π(t) is thus

graphic file with name RSSA-168-233-e004.jpg

and, again using the delta method, the variance estimator for 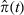Inline graphic is given by

graphic file with name RSSA-168-233-e006.jpg

Approximate 100(1−α)% confidence limits for π(t) can also be obtained in a similar manner to that for γ(t). Also, it is important to note that, as mentioned earlier, there is no need to model the complex hospitalization process I(u) in our formulation as far as the estimation of the realtime fatality rate is concerned.

3. Results

For the entire Hong Kong region up to July 31st, 2003, altogether 1755 cases were hospitalized. Of these, 1456 and 299 cases were discharged and died from SARS respectively. Figs 1(a) and 1(b) depict the estimates of γ 1(t) and γ 2(t) respectively, together with the associated 95% confidence bands. Both transition rates increased with time since the beginning of the epidemic. The estimated intensity of transition to death, 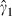Inline graphic, peaked around March 20th, decreased and then increased again around May 15th, 2003. The estimated intensity of recovery, 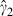Inline graphic, peaked around April 1st, where most of the SARS patients who were medical health workers from a regional hospital (Prince of Wales Hospital) were discharged, and another two peaks were also found around the end of April and on May 19th. Fig. 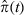1(c) depicts the ratio estimate of the two rates, Inline graphic, while Fig. 1(d) shows the plot of the estimated realtime fatality rate at time t, Inline graphic, over the course of the epidemic together with the WHO estimate. The WHO methodology estimated the case fatality rates of SARS in Hong Kong at March 30th, April 15th and May 25th, 2003, as 2.5%, 9.9% and 15.8% respectively and started to stabilize thereafter, with a final estimate of 17% at June 30th. In contrast, the realtime fatality rate was chaotically high at the beginning of the outbreak, since few patients were discharged in the early stages of the outbreak. The realtime fatality rate seemed to have stabilized from early April, fluctuating between 15% and 20%. Similar figures for the estimated realtime fatality rates (with different origins) for Singapore, Taiwan, Beijing and Toronto are given in Fig. 2.

Figure 1.

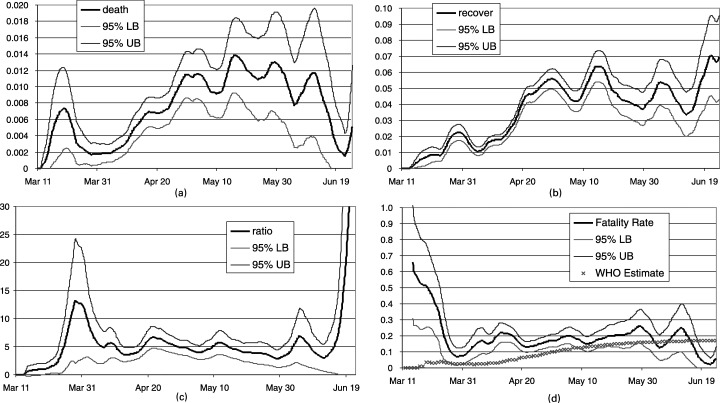
Figure 1

Open in a new tab

Kernel estimates of the SARS outbreak in Hong Kong: (a) instantaneous death‐rate γ 1(t); (b) instantaneous recovery rate γ 2(t); (c) ratio of instan‐taneous recovery and death‐rates θ(t); (d) realtime fatality rate π(t) and WHO estimate of case fatality rate

Figure 2.

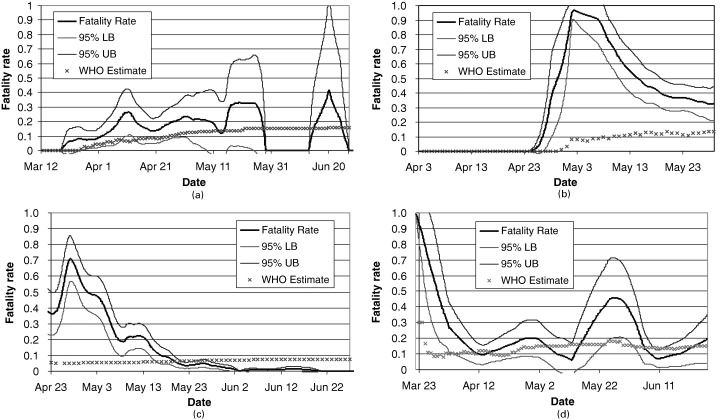
Figure 2

Open in a new tab

Realtime fatality rate and WHO estimate of the case fatality rate for the regions (a) Singapore, (b) Taiwan, (c) Beijing and (d) Toronto

The number of SARS cases in Singapore was smaller than that of Hong Kong probably because of the confinement of outbreaks within hospitals and the lack of major community outbreaks, such as that occurring in Amoy Gardens in Hong Kong. There were altogether 238 cases with 33 deaths with a WHO‐estimated case fatality rate of 13.9%. Fig. 2(a) shows that the realtime fatality rate appeared to stabilize approximately 4 weeks after the outbreak, which was similar to what happened in Hong Kong. The fatality rates fluctuated between 15% and 19% after the middle of April.

Data from Taiwan became available from April 4th, 2003. Altogether 37 deaths were found out of the 346 cases with a WHO case fatality rate of 10.7%. However, the time‐varying rate suggested an unusually high rate in the early part of the outbreak, which subsequently improved. Most of the major outbreaks were found within hospitals in Taiwan.

For Toronto the data were available from March 18th, 2003, with a total of 39 deaths from 247 infected cases giving a WHO case fatality rate of 15.8%. SARS had made a come‐back in the community (http://www.hc-sc.gc.ca/pphb-dgspsp/sars-sras/eu-ae/index.html). The most recent date of onset of illness and isolation among probable cases was June 12th. Most of the SARS cases in Canada were found in Toronto.

For Beijing, a special hospital was built within two weeks to treat the SARS patients in May 2003. The Government implemented very effective measures to prevent infection in the community and in hospital, including the removal of the Minister of Health and the Mayor of Beijing City, who failed to deal with the epidemic control. A very high level working group was set up and headed by a Vice‐Premier. The realtime fatality rate was estimated to be high in the early stage of the epidemic and continuously improved over the course of the epidemic such that the rate was less than 5% by June 10th. However, the WHO case fatality rate was much higher than this June estimate of the time‐varying rate, since the former was very much affected by the early data.

4. Discussion

An estimation of the fatality rate in the situation of an emerging outbreak or epidemic is never straightforward. This is particularly true for SARS, when clinicians all over the world had to deal with this highly contagious and frightening pneumonic illness with no idea of its aetiology, pathogenesis, clinical features, management issues or prognosis, other than anecdotal information from colleagues from mainland China (Tsang and Lam, 2003; Lee et al., 2003). The original estimate of the fatality rate for SARS was only about 4.5%, by both the WHO and the Hong Kong Health Authority (Department of Health of Hong Kong Government, 2003), even as late as the beginning of April 2003. This was later adjusted to about 10% in May 2003. This underestimation of the fatality rate from SARS must have undoubtedly affected the health care planning measures that were taken to contain SARS, and thus the outcome of the SARS outbreak at the community level.

Our comparison of the estimated realtime fatality rates among the SARS‐affected areas shows that the SARS fatality rate appears to be changing with time in all regions. Besides Beijing, the realtime fatality rates of all other areas seem to fluctuate around 12–20%. The constant fatality assumption, which was adopted by Donnelly et al. (2003), does not reflect the situation at the population level. Indeed the approach of Donnelly et al. (2003) can be extended easily to regression models set up to allow for differences in the diagnosis and management of patients by allowing the (time constant) case fatality rate to depend on relevant (possibly time‐varying) explanatory variables. However, a time‐varying fatality rate at a population level is always helpful and meaningful to medical researchers.

In addition, this changing fatality pattern is not reflected by the definition of case fatality rate that has been adopted by the WHO that derives from the ratio of cumulative deaths to the total number of cases diagnosed. Any variation in clinical outcome measures, e.g. as a result of improved treatment modalities, would not be depicted by such a definition. By using the actual calendar timescale, rather than duration of hospitalization, the method proposed provides a visual assessment of the effect of other factors, including variation in clinical management and other exogenous (including unidentified) factors over the course of the outbreak. A stable estimate of the fatality rate could reflect a more mature approach to the diagnosis and treatment of SARS, although the efficacy of using high dose corticosteroid and ribavirin, to deal with the lung parenchymal inflammation and coronavirus itself, are largely controversial (Booth et al., 2003; Wenzel and Edmond, 2003; Cyranoski, 2003). The constant case fatality assumption is more suitable for some well‐known infectious diseases such as rabies or smallpox because the aetiology, pathogenesis and treatment have been well studied with a standard treatment protocol. It is recommended that the realtime fatality rate be investigated at the outbreak of an emerging epidemic. It can serve as an indicator of the change in the fatality rate over time and can provide information on the effectiveness of the policy and treatment that are adopted.

Our data show that SARS fatality rates among Hong Kong, Singapore and Toronto were similar, whereas Beijing appeared to have a lower rate after the first month of the epidemic. In the absence of data from controlled clinical trials for the treatment of SARS, it would be interesting to speculate whether the time‐varying fatality rates that are calculated by our model could be related to the different clinical treatment protocols that were used by these areas. For instance, the use of ribavirin was essentially forbidden in Canada by late April 2003, whereas it has consistently been the standard empirical practice in Hong Kong. The use of continuous positive airway pressure, delivered by nasal masks, to patients with hypoxia has been partly attributed as a cause of the low case fatality and low intensive care unit admission in mainland China (personal communication from Professor N. S. Zhong of Guangdong). The use of traditional Chinese medicine has also been claimed to be the cause of low case fatalities in Beijing, and glycyrrhizin, an active component of liquorice roots, has been shown to inhibit the replication of SARS‐associated coronavirus (Cinatl et al., 2003). The Singaporian practice of using ribavirin and corticosteroid in the treatment of SARS is not uniform, and the standard protocol that is practised in Taiwan has not been fully published (Twu et al., 2003; Hsu et al., 2003). Although these differences in clinical practices could contribute to a difference in case fatalities, it should be cautioned that they do not necessarily equate to conclusions that are drawn from controlled clinical trials. Not withstanding these limitations, especially acknowledging the insensitivity of the case fatality rate as a clinical outcome and the possible discrepancy in the diagnostic stringency, it is possible that ribivarin treatment could have no effects in the clinical outcome of SARS patients.

There is increasing concern about emerging infections all over the world, and SARS is only an example of how ignorant we are in dealing with the statistical–epidemiological and clinical management of this condition. Our model of using the realtime fatality rate should allow epidemiologists to monitor not only SARS but also other emerging infections and conditions in the future.

Corrigendum for this article in Journal of the Royal Statistical Society Series A, Volume 168, Issue 2, http://www.blackwell-synergy.com/links/doi/10.1111/j.1467-985X.2005.00359.x/

Acknowledgements

The authors pay tribute to all the front line medical health workers in those affected areas who have contributed to the control of SARS. The authors also thank the reviewers, an Associate Editor and the Joint Editor for their helpful comments and suggestions that improved the pres‐ entation of the paper.

References

  1. Andersen, P. K. , Borgan, Ø. , Gill, R. D. and Keiding, N. (1993) Statistical Models based on Counting Processes. New York: Springer. [Google Scholar]
  2. Booth, C. M. , Matukas, L. M. , Tomlinson, G. A. , Rachlis, A. R. , Rose, D. B. , Dwosh, H. A. , Walmsley, S. L. , Mazzulli, T. , Avendano, M. , Derkach, P. , Ephtimios, I. E. , Kitai, I. , Mederski, B. D. , Shadowitz, S. B. , Gold, W. L. , Hawryluck, L. A. , Rea, E. , Chenkin, J. S. , Cescon, D. W. , Poutanen, S. M. and Detsky, A. S. (2003) Clinical features and short‐term outcomes of 144 patients with SARS in the greater Toronto area. J. Am. Med. Ass., 289, 2801–2809. [DOI] [PubMed] [Google Scholar]
  3. Centers for Disease Control and Prevention (2003) Severe acute respiratory syndrome (SARS): diagnosis/evalu‐ ation. Centers for Disease Control and Prevention, Atlanta. (Available from http://www.cdc.gov/ncidod/sars/diagnosis.htm.) [Google Scholar]
  4. Cinatl, J. , Morgenstern, B. , Bauer, G. , Chandra, P. , Rabenau, H. and Doerr, H. W. (2003) Glycyrrhizin, an active component of liquorice roots, and replication of SARS‐associated coronavirus. Lancet, 361, 2045–2046. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Cyranoski, D. (2003) Critics slam treatment for SARS as ineffective and perhaps dangerous. Nature, 423, 4. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Department of Health of Hong Kong Government. Latest figures on severe acute respiratory syndrome. Department of Health of Hong Kong Government, Hong Kong. (Available from http://www.info.gov.hk/dh/diseases/ap/eng/infected.htm.) [Google Scholar]
  7. Donnelly, C. A. , Ghani, A. C. , Leung, G. M. , Hedley, A. J. , Fraser, C. , Riley, S. , Abu‐Raddad, L. J. , Ho, L. M. , Thach, T. Q. , Chau, P. , Chan, K. P. , Lam, T. H. , Tse, L. Y. , Tsang, T. , Liu, S. H. , Kong, J. H. , Lau, E. M. , Ferguson, N. M. and Anderson, R. M. (2003) Epidemiological determinants of spread of causal agent of SARS in Hong Kong. Lancet, 361, 1761–1766. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Hsu, L. Y. , Lee, C. C. , Green, J. A. , Ang, B. , Paton, N. I. , Lee, L. , Villacian, J. S. , Lim, P. L. , Earnest, A. and Leo, Y. S. (2003) Severe acute respiratory syndrome (SARS) in Singapore: clinical features of index patient and initial contacts. Emerg. Infect. Dis., 9, 713–717. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Lee, N. , Hui, D. , Wu, A. , Chan, P. , Cameron, P. , Joynt, G. M. , Ahuja, A. , Yung, M. Y. , Leung, C. B. , To, K. F. , Lui, S. F. , Szeto, C. C. , Chung, S. and Sung, J. J. Y. (2003) A major outbreak of severe acute respiratory syndrome in Hong Kong. New Engl. J. Med., 348, 1986–1994. [DOI] [PubMed] [Google Scholar]
  10. Peiris, J. S. M. , Chu, C. M. , Cheng, V. C. C. , Chan, K. S. , Hung, I. F. N. , Poon, L. L. M. , Law, K. I. , Tang, B. S. F. , Hon, T. Y. W. , Chan, C. S. , Chan, K. H. , Ng, J. S. C. , Zheng, B. J. , Ng, W. L. , Lai, R. W. M. , Guan, Y. , Yuen, K. Y. and members of the HKU/UCH SARS Study Group (2003) Clinical progression and viral load in a community outbreak of coronavirus‐associated SARS pneumonia: a prospective study. Lancet, 361, 1767–1772. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Ramlau‐Hansen, H. (1983) Smoothing counting process intensities by means of kernel functions. Ann. Statist., 11, 453–466. [Google Scholar]
  12. Riley, S. , Fraser, C. , Donnelly, C. A. , Ghani, A. C. , Abu‐Raddad, L. J. , Hedley, A. J. , Leung, G. M. , Ho, L. M. , Lam, T. H. , Thach, T. Q. , Chau, P. , Chan, K. P. , Lo, S. V. , Leung, P. Y. , Tsang, T. , Ho, W. , Lee, K. H. , Lau, E. M. , Ferguson, N. M. and Anderson, R. M. (2003) Transmission dynamics of the etiological agent of SARS in Hong Kong: impact of public health interventions. Science, 300, 1961–1966. [DOI] [PubMed] [Google Scholar]
  13. Rota, P. A. , Oberste, M. S. , Monroe, S. S. , Nix, W. A. , Campagnoli, R. , Icenogle, J. P. , Penaranda, S. , Bankamp, B. , Maher, K. , Chen, M. H. , Tong, S. , Tamin, A. , Lowe, L. , Frace, M. , DeRisi, J. L. , Chen, Q. , Wang, D. , Erdman, D. D. , Peret, T. C. , Burns, C. , Ksiazek, T. G. , Rollin, P. E. , Sanchez, A. , Liffick, S. , Holloway, B. , Limor, J. , McCaustland, K. , Olsen‐Rasmussen, M. , Fouchier, R. , Gunther, S. , Osterhaus, A. D. , Drosten, C. , Pallansch, M. A. , Anderson, L. J. and Bellini, W. J. (2003) Characterization of a novel coronavirus associated with severe acute respiratory syndrome. Science, 300, 1394–1399. [DOI] [PubMed] [Google Scholar]
  14. Seto, W. H. , Tsang, D. , Yung, R. W. , Ching, T. Y. , Ng, T. K. , Ho, M. , Ho, L. M. , Peiris, J. S. and Advisors of Expert SARS Group of Hospital Authority (2003) Effectiveness of precautions against droplets and contact in prevention of nosocomial transmission of severe acute respiratory syndrome (SARS). Lancet, 361, 1519–1520. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Tsang, K. W. , Ho, P. L. , Ooi, G. C. , Yee, W. K. , Wang, T. , Chan‐Yeung, M. , Lam, W. K. , Seto, W. H. , Yam, L. Y. , Cheung, T. M. , Wong, P. C. , Lam, B. , Ip, M. S. , Chan, J. , Yuen, K. Y. and Lai, K. N. (2003) A cluster of cases of severe acute respiratory syndrome in Hong Kong. New Engl. J. Med., 348, 1977–1985. [DOI] [PubMed] [Google Scholar]
  16. Tsang, K. W. and Lam, W. K. (2003) Management of severe acute respiratory syndrome—the University of Hong Kong experience. Am. J. Respir. Crit. Care Med., 168, 417–424. [DOI] [PubMed] [Google Scholar]
  17. Tsang, K. W. , Mok, T. Y. , Wong, P. C. and Ooi, G. C. (2003) Severe acute respiratory syndrome (SARS) in Hong Kong. Respirology, 8, 259–265. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Twu, S. J. , Chen, T. J. , Chen, C. J. , Olsen, S. J. , Lee, L. T. , Fisk, T. , Hsu, K. H. , Chang, S. C. , Chen, K. T. , Chiang, I. H. , Wu, Y. C. , Wu, J. S. and Dowell, S. F. (2003) Control measures for severe acute respiratory syndrome (SARS) in Taiwan. Emerg. Infect. Dis., 9, 718–720. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Wenzel, R. P. and Edmond, M. B. (2003) Managing SARS amidst uncertainty. New Engl. J. Med., 348, 1947–1948. [DOI] [PubMed] [Google Scholar]
  20. World Health Organization (2003a) Cumulative number of reported probable cases of SARS. World Health Organization, Geneva. (Available from http://www.who.int/csr/sars/country/2003_06_23/en/.) [Google Scholar]
  21. World Health Organization (2003b) Case definitions for surveillance of severe acute respiratory syndrome (SARS). World Health Organization, Geneva. (Available from http://www.who.int/csr/sars/casedefinition/en/.) [Google Scholar]
  22. Yip, P. and Lam, K. F. (1992) A class of non‐parametric tests for the equality of failure rates in competing risks model. Communs Statist. Theory Meth., 21, 2541–2556. [Google Scholar]
  23. Yip, P. and Lam, K. F. (1993) A multivariate nonparametric test for the equality of failure rates in a competing risks model. Communs Statist. Theory Meth., 22, 3199–3222. [Google Scholar]

Articles from Journal of the Royal Statistical Society. Series A, (Statistics in Society) are provided here courtesy of Wiley

RESOURCES