Healthcare Costs of Treating Privately Insured Patients with Acute Myeloid Leukemia in the United States 2004–2014: A Generalized Additive Modeling Approach

Abstract

Objectives

To predict healthcare cost trajectories for patients with newly diagnosed acute myeloid leukemia (AML) receiving allogeneic hematopoietic cell transplantation (alloHCT), as a function of days since chemotherapy initiation, days relative to alloHCT and days before death or last date of insurance eligibility (LDE). An exploratory objective examined patients with AML receiving chemotherapy only.

Methods

We used Optum’s de-identified Clinformatics® Data Mart Database to construct cumulative cost trajectories from chemotherapy initiation to death or LDE (through December 31, 2014) for United States patients aged 20–74 years diagnosed between March 1, 2004 and December 31, 2013 (n=187 alloHCT; n=253 chemotherapy only). We used generalized additive modeling (GAM) to predict expected trajectories and bootstrapped confidence intervals (CI) at user-specified intervals conditional on dates of alloHCT and death or LDE relative to chemotherapy initiation.

Results

Expected costs for a hypothetical patient receiving alloHCT 60 days after chemotherapy initiation and followed for five years were $572,000 (95% CI:$517,000-$633,000); $119,000 (95% CI:$51,000-$192,000); $102,000 (95% CI:$0-$285,000); $79,000 (95% CI:$0-$233,000), for years 1–4 respectively, and either $494,000 (95% CI:$212,000-$799,000) or $108,000 (95% CI:$0-$230,000) in year 5, whether the patient died or was lost to follow-up on day 1,825, respectively.

Conclusions

Rates of cost accrual varied over time since chemotherapy initiation with accelerations around the time of alloHCT and death. GAM is a potentially useful approach for imputing longitudinal costs relative to treatment initiation and one or more intercurrent or terminal events in randomized controlled trials or registries with unrecorded costs or for dynamic decision-analytic models.

Introduction

Acute myeloid leukemia (AML) is a cancer of the bone marrow, characterized by proliferation of cancerous cells that prevent the marrow from producing healthy blood cells [1,2]. Following initial chemotherapy, consolidation chemotherapy is recommended for patients with favorable risk disease whereas those with intermediate or poor risk disease are considered candidates for allogeneic hematopoietic cell transplantation (alloHCT) [3].

AlloHCT is resource-intensive [4–7]. Several studies have examined costs and utilization associated with alloHCT or chemotherapy but not alloHCT (chemotherapy only) for patients with AML [8–11]. A recent study estimated total costs in the first year after AML diagnosis for patients age 50–64 years who received chemotherapy only to be $280,799 (95% confidence interval [CI]:$258,473-$305,030) or who received alloHCT to be $544,178 (95% CI:$489,994-$604,353) [12]. However, this study was limited by its short time horizon and inability to account for the relationship between mortality and cost. All else equal, patients who survive longer are expected to incur higher total costs simply because they receive additional healthcare while alive. From the perspective of third-party payers, the healthcare system or society, costs associated with increased longevity are real costs that must be considered [13]. However, intensive resource use around the time of death may incur substantial costs [14–16] with little therapeutic benefit [17,18].

Our primary objective was to estimate healthcare cost trajectories as a function of days since chemotherapy initiation, days relative to alloHCT and days before death or loss to follow-up for patients with newly-diagnosed AML receiving alloHCT. An exploratory objective examined trajectories for patients with AML receiving chemotherapy only. Better understanding of the dynamics of healthcare costs may shed light on the potential value of alloHCT and may further help identify future research opportunities for higher quality end-of-life care for patients with AML.

To best inform decision-making, cost-effectiveness and budget impact analyses should account for variation in healthcare costs over the course of treatment. Treatment intensity, and therefore the rate at which costs accumulate, is likely to vary over time for complex conditions with heterogeneous clinical courses such as AML. Common approaches to estimating costs for patients with cancer [19] stratify total costs by phase of care (initial, continuing and terminal) [20–22] or over specific windows of time since diagnosis such as the first year after diagnosis [12,23]. Analysis by fixed time windows since diagnosis combines the heterogeneous experiences of patients who die within the period (potentially contributing substantial end-of-life costs, but lower costs of continuing care) with those who survive. Analysis by phase of care also typically uses fixed windows of time since diagnosis but adds a fixed window of time before death and defines the continuing phase of care as all time in-between. For example, Brown et al (2002) define the initial phase of colorectal cancer care to be the month of diagnosis and five months afterwards and defines the terminal phase as the last twelve months of life [20]. The treatment phase approach blends potentially heterogeneous patient experiences within phases, varying by timing of initial and potentially subsequent treatments. Cost analysis by phase also requires patients in the initial treatment phase to have survived into the continuing phase; patients dying within the specified initial phase window are assigned to the terminal phase despite having initiated treatment in that same timeframe.

Longitudinal approaches estimating trajectories of costs conditional on survival time offer potentially more useful information for decision-makers relative to analyses of the total cost of care over wide time windows or by phase of care [24–27]. Such approaches are useful for imputing costs for dynamic decision analytic models -- particularly discrete event simulation [28] or partitioned survival models [29] that simulate individual times to events. We introduce an approach to analyzing trajectories of cumulative healthcare costs from claims data using natural cubic splines in a generalized additive modeling (GAM) framework assuming gamma-distributed costs and a log link function. We then apply our approach to predict expected cost trajectories of patients with AML who were treated with either alloHCT or chemotherapy only, conditional on when alloHCT was received as well as when death or loss to follow-up occurred.

Methods

Data Source

Optum’s de-identified Clinformatics® Data Mart Database (Optum) included commercial and Medicare Advantage inpatient, outpatient, professional, ancillary services, and pharmacy claims from January 1, 2004 through December 31, 2014, for members from all 50 states in the United States (U.S.). Optum linked claims to the Social Security Administration Death Master File (DMF), allowing joint investigation of cost and survival. While specificity for deaths reported in the DMF is nearly 100% [30], due to lack of a deterministic link to the death master file some deaths among patients are unreported [31]. Because Optum reported month and year of death only, we imputed death dates following an algorithm using claims information at the last date of service (see Appendix Table A1).

Our study was considered exempt by the National Marrow Donor Program’s Institutional Review Board.

Study Population and Patient Selection

Our primary study population comprised U.S. commercially insured and Medicare Advantage adults aged 20–74 years with de novo AML diagnosed between March 1, 2004 and December 31, 2013 who received alloHCT; an exploratory aim included patients of the same age range and diagnosis who received chemotherapy only. Cohort identification followed procedures from a previous claims-based study of patients with newly-diagnosed AML treated with alloHCT or chemotherapy only [12]. Patients were identified by International Classification of Diseases, Ninth Revision, Clinical Modification (ICD-9-CM) diagnosis and procedure codes (see Appendix Table A2). Inclusion and exclusion criteria (see Appendix Table A3) were designed to balance sensitivity (including as many patients with newly-diagnosed AML who underwent treatment with curative intent as possible) with specificity (excluding patients who had spurious AML-related codes, AML likely to be secondary to other diseases, or recurrent previously-diagnosed AML) [32].

Cumulative Healthcare Cost Trajectories

We constructed cumulative healthcare cost trajectories as daily running totals for each patient. Trajectories for each individual i began at their date of chemotherapy initiation (t_CI[i] ≡ 0), and ended at the earlier of their date of death t_D[i] or last date of eligibility (LDE) t_LDE[i] (capped at the end of the study period, December 31, 2014). Trajectories for patients with LDE preceding death or who had no recorded date of death ended at t_LDE[i]. Dates of alloHCT (t_HCT[i]), death, and eligibility were counted relative to chemotherapy initiation. Individual cost trajectories therefore ranged from t ∈ [0,min {t_D[i],t_LDE[i]}], and overall expected cost trajectories ranged from t ∈ [0,max_i{min {t_D[i],t_LDE[i]}}].

Let j = 1,…J_i index the set of all J_i claims of patient i sorted by service date. Then $\ell =1,\dots {\mathcal{L}}_{i,j,t}$ indexes the line items for claim j of patient i having date of service t relative to the date of chemotherapy initiation. Line-item service dates for outpatient facility, professional and ancillary services, and pharmacy services were considered reliable, since such services are delivered on a single date. Line-item inpatient facility costs observed during an inpatient stay were summed and divided by the length of stay in days, and then allocated equally to each day of the inpatient stay:

$$c_{i,j,t}=\frac{1}{\left(t1-t0\right)}\sum _{t=t0}^{t1}\left(\sum _{\ell =1}^{{\mathcal{L}}_{i,j,t}}{c}_{\ell }\right)$$ (1)

for t = t0,…,t1, where t0 and t1 are the admission and discharge dates, respectively. Costs were then summed across claims by date:

$$\{c_{i,t}\}={\sum }_{j=1}^{J_i}{c}_{i,j,t}$$ (2)

for t = 0,…min {t_D[i],t_LDE[i]} to obtain a daily sequence of costs {c_i,t}. By convention, c_i,j,t = 0 for all dates t in which no service was provided under claim j. Given each patient’s cost sequence, we defined the cumulative cost trajectory as the daily running total of all healthcare costs:

$$\{C_{i,t}\}=\sum _{T=1}^t{c}_{i,T}$$ (3)

Note that if each element of {c_i,t} ≥ 0, then the cumulative cost trajectory {C_i,t} is non-decreasing.

Optum applied administrative cost adjustments as negative values on either the same or a separate claim. We used an algorithm matching negative line-items with their corresponding positive line-items, if possible, and adjusted the date of each negative claim accordingly to match its associated positive claim. If no match was observed, negative claims were applied on the date indicated. Optum provided inflation-adjusted to the year 2017 standardized line-item costs, which account for variations in payment rates, contract terms, and geographic areas and therefore can be considered representative of the U.S. third-party payer perspective.

Statistical Analysis

For an introduction to GAM, see the Methodological Appendix. Our specification used four time-varying covariates, each of which can be thought of as a running stopwatch with different reference points measuring time relative to chemotherapy initiation and the dates of alloHCT, and death or loss to follow-up. Specifically, we modeled:

$$C_{i,t}\sim \text{Gamma}(\frac{{\mu }_{i,t}}{\gamma },\gamma )$$ (4a)

$$\begin{gathered} \ln ({\mu }_{i,t})=\sum _{k\in K_t}^{}{\beta }_{1k}{N}_k\left(t_i\right)+1[t_{HCT[i]}\ne NA]\sum _{k\in K_{HCT}}^{}{\beta }_{2k}{N}_k(t_i-t_{HCT[i]}) \\ +1[t_{D[i]}\le t_{LDE[i]}]\cdot \sum _{k\in K_D}^{}{\beta }_{3k}{N}_k(t_i-t_{D[i]}) \\ +1[t_{D[i]}=\text{NA}\text{or}{t}_{LDE[i]}<t_{D[i]}]\cdot \sum _{k\in K_D}^{}{\beta }_{4k}{N}_k(t_i-t_{LDE[i]}) \end{gathered}$$ (4b)

where γ is an estimated shape parameter, N() is the natural cubic spline basis function, β_1k, β_2k, β_3k, and β_4k are sets of estimated natural spline coefficients for each time covariate, and K_t = {0,30,60,90,120,150,180,365,550,730,1095,max_i t_D[i]}, K_HCT = {−30,−14,0,14,30,100,180,365}, and K_D = {−30,−14,−7,0} are sets of knots representing time since chemotherapy initiation t_i, time relative to alloHCT (t_i − t_HCT[i]), and time before death (t_i − t_D[i]) or loss-to-follow-up (t_i − t_LDE[i]), respectively, whichever comes first. The indicator function 1[t_HCT[i] ≠ NA] turns on the additive component for time relative to alloHCT only for patients who received alloHCT (i.e., had a date of transplant that was not missing). Similarly, indicator functions 1[t_D[i] ≤ t_LDE[i]] and 1[t_D[i] = NA or t_LDE[i] < t_D[i]] turn on the appropriate additive component for time relative to whichever terminal event occurred (death and loss-to-follow-up, respectively). Knots were chosen by our transplant hematologist-oncologist co-authors to represent clinically relevant time points. Models were estimated separately by treatment received using the ‘gam’ package [33] in R (3.6.0) [34].

We used the ‘predict.gam’ method to predict expected cumulative cost through any date of interest. Given estimated $\widehat{\beta }$ and $\widehat{\gamma }$ and an input vector of known dates of alloHCT and death or loss to follow-up for a hypothetical representative individual j, the tool predicted expected cumulative costs $E[C_{j,t_{*}}|t_{HCT\left[j\right]},t_{D\left[j\right]},t_{LDE\left[j\right]};\widehat{\beta },\widehat{\gamma }]$ through any specified date t_* ∈ [0,min {t_D[j],t_LDE[j]}]. To predict expected costs incurred in a time period, we took first-differences of a sequence of expected cumulative costs evaluated at specified time points t_n, for n = 1,2,…N: $E\left[c_{j,t_n}|\cdot \right]=E[C_{j,t_n}|\cdot ]-E[C_{j,t_{n-1}}|\cdot ]$, where $E[C_{j,t_{n-1}}|\cdot ]=0$ if t_n−1 = 0 by definition. For illustration and comparison with other published alloHCT cost analyses, we generated predictions on an annual basis, although any regular or irregular sequence of dates could be chosen.

To quantify uncertainty, we conducted 1,000 unweighted bootstrap replications by resampling trajectories with replacement, separately by treatment group. We constructed 95% confidence intervals (CI) for spline smooths using the percentile method. 95% CIs for predicted trajectories using the lookup tool imposed a monotonicity constraint by recursively choosing $E\left[C_{j,t_n}|\cdot \right]=\mathrm{m}\mathrm{a}\mathrm{x}\left\{E\left[C_{j,t_n}|\cdot \right],E\left[C_{j,t_{n-1}}|\cdot \right]\right\}$, for n = 2,…N, thus requiring each bootstrapped sequence to be non-decreasing.

RESULTS

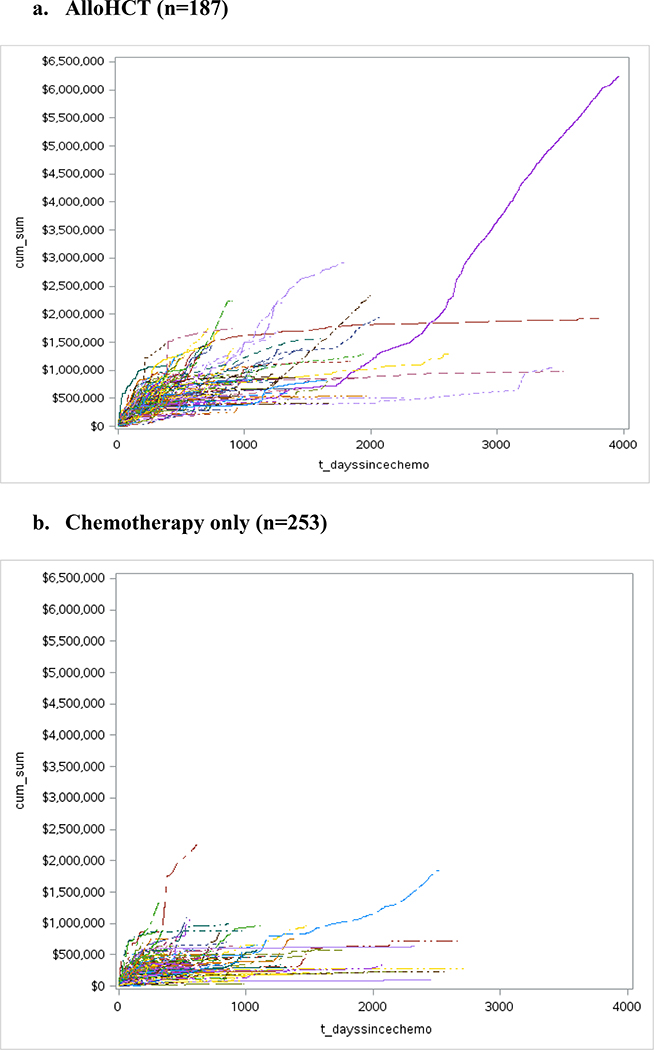
Four hundred forty patients met inclusion criteria (n=187 alloHCT; n=253 chemotherapy only), (see Appendix Figure A1 and Appendix Table A3). Plots of observed cumulative cost trajectories for alloHCT and chemotherapy only recipients are presented in Figure 2. Due to data sparsity beyond 5 years, we truncated all model plots and predictions at 1,825 days post-chemotherapy initiation.

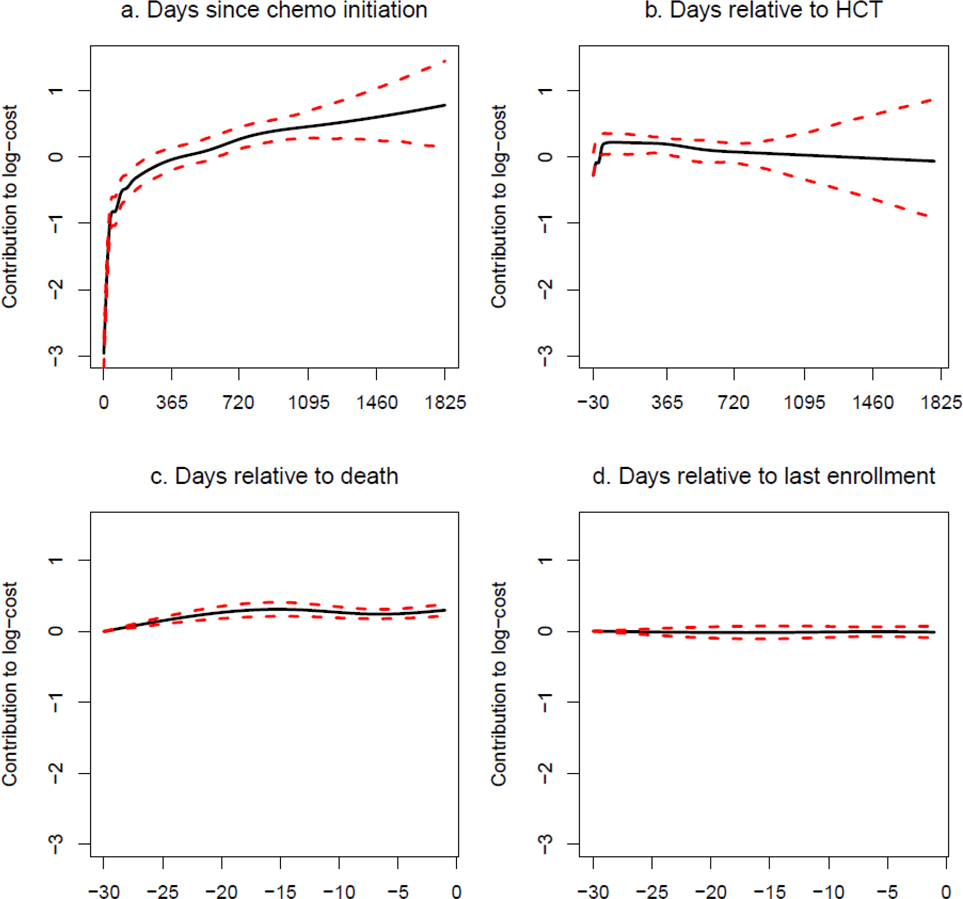
Figure 2. GAM modeling: AlloHCT Group.

Generalized Additive Model Results

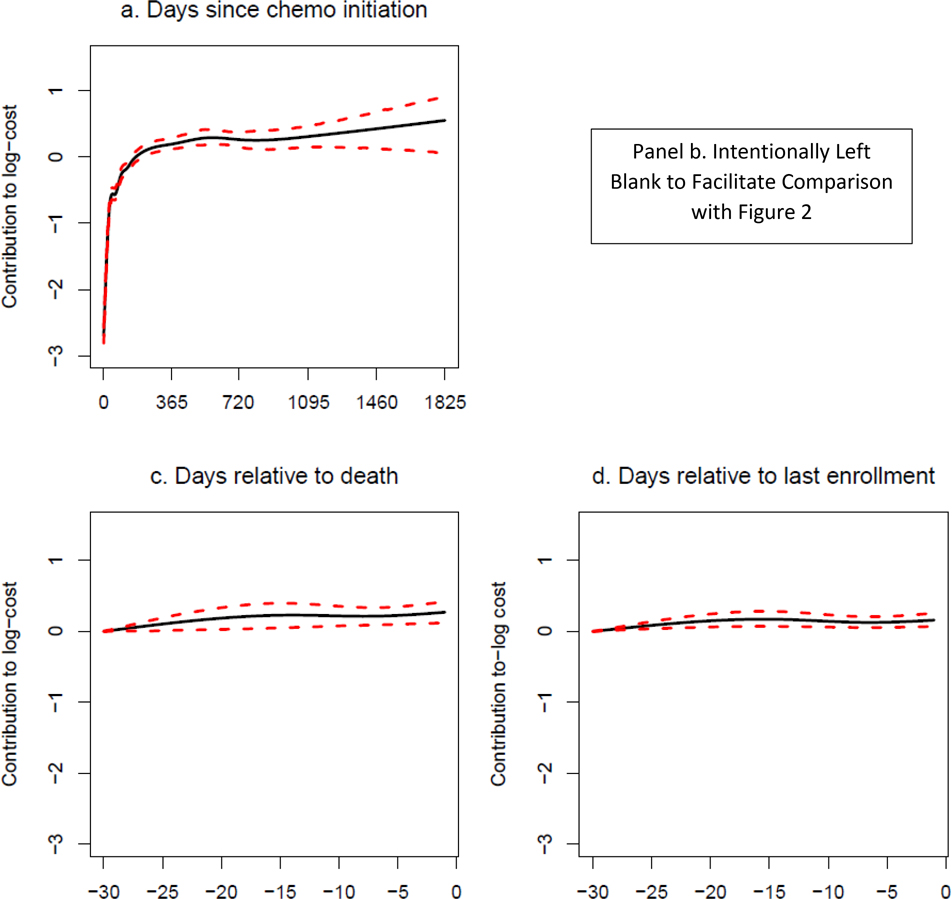
GAM results are shown in Figure 2 for alloHCT recipients and Figure 3 for patients receiving chemotherapy only. Each panel represents the weighted sum of basis functions for each running time covariate and therefore corresponds to one of the Σ terms in (4b). Confidence intervals widen markedly approximately 1,000 days after chemotherapy initiation and 800 days after receipt of alloHCT due to small numbers of observed trajectories in which individuals have survived or were not lost to follow-up at that time. Base expected costs (i.e., not attributed by the GAM model to timing of alloHCT, death or loss to follow-up) rapidly accrue within the first three months after chemotherapy initiation and accrue less rapidly beginning around six months (Figures 2a, 3a). For patients treated with chemotherapy only surviving beyond approximately 500 days, the base rate of cost accrual reduces appreciably, while for patients treated with alloHCT, the base rate of cost accrual stabilizes, with cumulative costs increasing at a higher rate than for chemotherapy only.

Figure 3. GAM modeling: Chemotherapy only group. Note: panel b. intentionally left blank to facilitate comparison with Figure 2.

For patients receiving alloHCT, the additive component for time relative to the date of alloHCT (Figure 2b) indicates rapidly increasing costs beginning 30 days prior to transplant and continuing at a high rate for the first 100 days. Cost accrual relative to the date of alloHCT then abates significantly and remains stable for approximately the first year, after which it begins to decline.

Both for patients receiving alloHCT and those receiving chemotherapy only, rates of cost accrual during the 30 days prior to death are significantly elevated (Figures 2c, 3c). While the magnitude of results may look small relative to the base rate of cost accrual, these plots are on the log-dollar scale, so the effect on the dollar scale is multiplicative. For patients receiving alloHCT, there appears to be little change in the rate of cost accumulation around the time of loss to follow-up (Figure 2d). However, for patients receiving chemotherapy only, the pattern of cost accrual around loss to follow-up (Figure 3d) is qualitatively similar to the pattern around time of death.

Expected Cost Trajectories

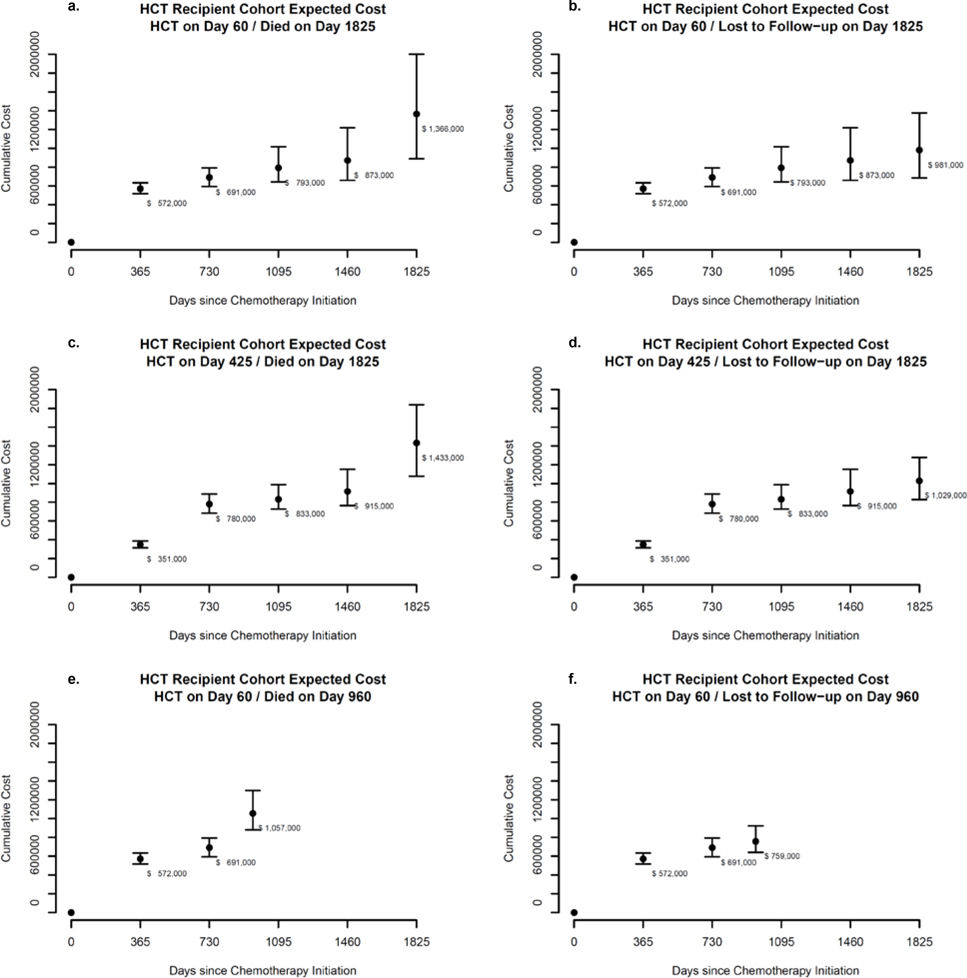
Allowing time for initial therapy and evaluation for alloHCT candidacy, we evaluated estimated cost trajectory equations at annual intervals for a hypothetical representative patient receiving alloHCT 60 days after chemotherapy initiation who either died (Figure 4a) or was lost to follow-up (Figure 4b) on day 1,825 after chemotherapy initiation. Yearly (non-cumulative) expected costs (rounded to the nearest $1,000) for patients receiving alloHCT on day 60 and surviving up to day 1,825 were $572,000 in year one (95% CI: $517,000-$633,000); $119,000 in year two (95% CI: $51,000-$192,000); $102,000 in year three (95% CI: $0-$285,000); and $79,000 in year four (95% CI: $0-$233,000). Expected costs in year five were substantially larger if death occurred on day 1,825: $494,000 (95% CI: $212,000-$799,000) than if the patient was lost to follow-up on day 1,825: $108,000 (95% CI:$0-$230,000), indicating costs of approximately $386,000 attributable to end-of-life for alloHCT recipients.

Figure 4. Expected costs since chemotherapy initiation: AlloHCT Group.

Figures 4c and 4d assume the same scenario as 4a and 4b, except alloHCT occurs on day 425. While year one costs were approximately $221,000 lower than if alloHCT occurred on day 60, cumulative costs in years two through five are approximately $60,000 to $90,000 higher, suggesting that later transplantation is associated with slightly higher long-run cumulative costs.

Figures 4e and 4f represent scenarios where patients received alloHCT at day 60 but died or were lost to follow-up on day 960. Comparing 4f to 4b shows slightly lower cumulative costs at three years, reflecting loss to follow-up occurring 135 days before the full third year. Markov models with fixed cycle length should use appropriate methods to account for death or loss to follow-up occurring prior to the end of the full cycle.

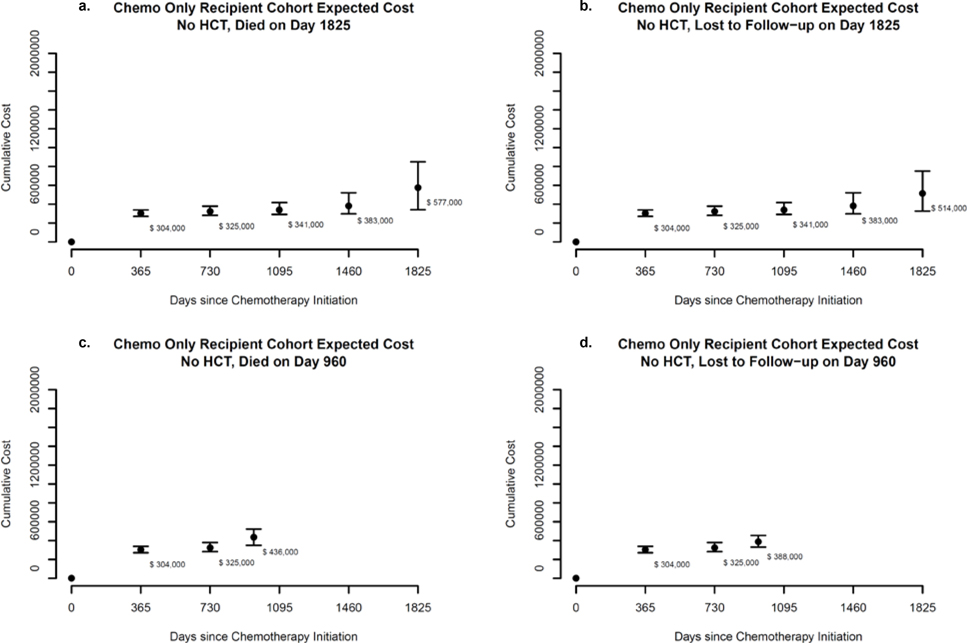
Figure 5 represents scenarios where a hypothetical representative patient receiving chemotherapy only died (Figure 5a) or was lost to follow-up (Figure 5b) on day 1,825; or died (Figure 5c) or was lost to follow-up (Figure 5d) on day 960. Yearly costs for patients receiving chemotherapy only and surviving up to day 1,825 were $304,000 in year one (95% CI: $271,000-$339,000); $21,000 in year two (95% CI: $0-$61,000); $16,000 in year three (95% CI: $0-$69,000); and $43,000 in year four (95% CI: $0-$120,000). For patients receiving chemotherapy only, expected costs in year five were predicted to be higher than in year four, regardless of whether the patient died on day 1,825: $194,000 (95% CI: $0-$376,000) or was lost to follow-up: $131,000 (95% CI: $0-$260,000). Differences suggest expected end-of-life costs of approximately $63,000 for patients receiving chemotherapy only.

Figure 5. Expected costs since chemotherapy initiation: Chemotherapy only group.

Discussion

Our analysis provides the longest follow-up to date of costs for patients with newly-diagnosed AML receiving alloHCT or chemotherapy only. Notably, our estimates for a hypothetical patient receiving alloHCT on day 60 after chemotherapy initiation are close to published one-year post-diagnosis costs using data from Truven [12], which included patients surviving less than one year: $572,000 vs. $544,178 for patients receiving alloHCT and $304,000 vs. $280,788 for patients receiving chemotherapy only.

Costs associated with end-of-life appear lower among patients treated with chemotherapy only than patients treated with alloHCT. However, end-of-life costs could be underestimated for patients receiving chemotherapy only if such patients are more likely than those receiving alloHCT to have unreported deaths. We note recent development of an algorithmic approach to identifying under-reported deaths in claims data [35]. While we can think of no plausible mechanism why patients receiving chemotherapy only who died would be less likely to have deaths reported in the DMF, we note that Optum uses clinical information including hospital discharge disposition to supplement the DMF. If patients receiving alloHCT are more likely to use healthcare, and particularly to die while hospitalized, then we might expect more accurate death status for alloHCT patients. We find suggestive evidence in our results. For patients receiving alloHCT, healthcare cost trajectories in the 30 days before death (Figure 2c) and loss to follow-up (Figure 2d) were markedly different. However, for patients receiving chemotherapy only, the trajectories before death (Figure 3c) and loss to follow-up (Figure 3d) were qualitatively similar. The pattern we observe for alloHCT is what we would expect if loss to follow-up were unrelated to the intensity of healthcare use around the time of the last date of insurance eligibility. Overall, year five costs for chemotherapy only patients who are lost to follow-up on day 1,825 were predicted to be about $88,000 higher than year four costs, while the difference between cost in years four and five was only $29,000 for patients receiving alloHCT.

In our case study, confidence intervals become wider over time uncertainty due to decreasing numbers of trajectories lasting through later dates. Indeed, uncertainty in later years is substantial enough that in the absence of a monotonicity constraint, some of the 95% CIs for annual (non-cumulative) costs would have included negative numbers. We recommend when estimates are incorporated into decision-analytic models in practice that bootstrapped trajectories be used directly in second-order Monte Carlo probabilistic sensitivity analysis rather than treating expenditures at each time point as independent draws matching the point estimates and confidence intervals. This will preserve correlation among the parameters and ensure monotonicity of cumulative expenditures.

Another substantial limitation of our analysis was its inability to infer causality from directly observed differences in cost trajectories between non-randomized treatments. Patients receiving alloHCT and surviving to day 1,825 are unlikely to have the same clinical characteristics as patients who survive to day 1,825 receiving chemotherapy only, and therefore direct comparison of the two trajectories is not appropriate. However, we note that it is possible in other applications with larger datasets to account for observed potential confounders by adding them as additional covariates in the GAM specification. As GAM is simply a generalization of GLM, other covariates, whether continuous, ordinal or factor, can be incorporated if there are enough observations with variation to support their estimation. We also note that propensity scores could be used as inverse probability of treatment weights in GAM to achieve balance on observable factors. The two approaches could be combined in doubly-robust estimation [36]. However, we caution that administrative claims may not provide enough clinical information (such as cytogenetic risk in the case of AML) to balance patients on all important confounders between treatments.

GAM is a flexible semi-parametric approach with many applications in medical research [37], ecology [38], epidemiology [39] and geospatial analysis [40]. However, its use in health economics and outcomes research has so far been limited. We were unable to find any published applications of GAM to modeling of cumulative healthcare costs. One study by Pullenayegum et al (2012) demonstrated the potential usefulness of GAM for modeling the association of EQ-5D utility as a quasi-continuous measure with diabetes-related complications in a cross-sectional study of adults with diabetes [41]. GAM and restricted splines have been proposed as an alternative to fractional polynomials [42] for the modeling of time-varying non-proportional hazard curves in survival analysis [43,44], including network meta-analysis [45].

Our analysis shows GAM to be a potentially useful approach for imputing cost trajectories where variation in the intensity of health care utilization occurs around known events (such as receipt of subsequent treatment and death or loss to follow-up). Target applications include imputing costs in studies where RCTs or registries record relevant clinical events but do not track costs – a common situation faced by applied health economics and outcomes researchers. Imputation of cost trajectories with GAM is also potentially useful for dynamic decision analytic modeling, where simulated events occur with probability and timing dictated by parameters obtained through synthesis of secondary data sources. As demonstrated in Figures 4 and 5, we can evaluate expected cumulative cost trajectories at one or more user-specified time points, conditional on timing of intercurrent and terminal events. Such conditional cost curves can be used directly in decision-analytic models based on discrete event simulation or partitioned survival analysis, where simulated event times are drawn from empirical or parametric distributions. Alternatively, the trajectories can be evaluated at regular intervals and first-differenced for inclusion in Markov-like models. Of course, analysts would still need access to administrative data with sufficient sample sizes representing relevant treatments and populations. Fortunately, such data sources are widely available from several commercial vendors and government databases.

Our approach can be compared with other longitudinal cost models [24–27]. Wilson et al. (2006) used mixed effects recurrent event regression to estimate a “mean cumulative function,” which accumulated average costs per patient per six-month period, excluding patients who were censored in each period [27]. Liu et al. (2007) jointly modeled survival and monthly cost using shared random effects to account both for censoring and for higher costs near death [26]. Liu (2009) expanded upon their previous work to incorporate two-part models accounting for periods with zero costs [25]. Recent work by Li et al. (2018) also jointly modeled survival and costs, in this case using Kaplan-Meier estimates to obtain the marginal distribution of survival followed by a bivariate penalized spline to model monthly cost conditional on estimated survival [24].

In comparison, our approach accounted for censoring by incorporating additive terms in GAM allowing the shape of cost trajectories to vary smoothly by time before death or loss to follow-up. While our approach cannot jointly predict survival and cost as in Liu et al. (2007), Liu (2009) or Li et al. (2018), our target applications (imputation of cost trajectories when event times are known) only require prediction of costs conditional on survival. The joint survival-cost models discussed above are fairly highly parameterized and require relatively sophisticated estimation techniques including the EM algorithm [24,26] and gaussian quadrature [25]. Furthermore, the additive nature of GAM allows us to predict cost trajectories conditional on more than one event – i.e., in addition to survival, we can also condition on loss to follow-up among patients who were not observed to have died as well as timing of alloHCT. In other applications, this approach could account for timing of multiple events, including treatment escalations, development of complications, disease recurrence or progression. GAM also easily accommodated non-normality of cost data, in our case using a gamma distribution with a log link function [46]. By using cumulative trajectories, we were also able to avoid the need to “bin” costs into monthly (or other fixed length) periods and/or use two-part models to account for periods with zero expenditures.

Conclusions

Our study demonstrated a novel approach to analysis of healthcare cost trajectories using generalized additive models. We found the rates at which costs accrue for patients diagnosed with AML vary substantially over time since chemotherapy initiation and around the time of alloHCT. We also found evidence of substantially increased costs in the 30 days prior to death, particularly for patients treated with alloHCT. Because treatment is self-selected in our claims-based dataset, causal interpretation of observational cost-differences between treatments is not warranted. However, our approach may have general application for imputing cost trajectories conditional on known intercurrent and terminal events, such as in randomized controlled trials where cost data were not collected or for decision dynamic decision-analytic models where such events are simulated based on synthesized evidence.

Figure 1. Cost trajectories from chemotherapy initiation until death or loss to follow-up for patients diagnosed with AML between March 2004 and December 2013.

• For patients with newly diagnosed acute myeloid leukemia (AML), receipt of allogeneic hematopoietic cell transplantation (alloHCT) is associated with increased intensity of healthcare cost accumulation from 30 days before transplant through about 100 days after, remaining elevated for about the first year.

• For patients with AML receiving alloHCT, the rate at which healthcare costs are incurred accelerates substantially in the last 30 days of life.

• Generalized additive models may be useful for imputing trajectories of healthcare costs that vary with respect to the timing of treatment initiation and receipt of subsequent treatment as well as death or other events.