Comparison of computational to human observer detection for evaluation of CT low dose iterative reconstruction

Abstract

Model observers were created and compared to human observers for the detection of low contrast targets in computed tomography (CT) images reconstructed with an advanced, knowledge-based, iterative image reconstruction method for low x-ray dose imaging. A 5-channel Laguerre-Gauss Hotelling Observer (CHO) was used with internal noise added to the decision variable (DV) and/or channel outputs (CO). Models were defined by parameters: (k1) DV-noise with standard deviation (std) proportional to DV std; (k2) DV-noise with constant std; (k3) CO-noise with constant std across channels; and (k4) CO-noise in each channel with std proportional to CO variance. Four-alternative forced choice (4AFC) human observer studies were performed on sub-images extracted from phantom images with and without a “pin” target. Model parameters were estimated using maximum likelihood comparison to human probability correct (PC) data. PC in human and all model observers increased with dose, contrast, and size, and was much higher for advanced iterative reconstruction (IMR) as compared to filtered back projection (FBP). Detection in IMR was better than FPB at 1/3 dose, suggesting significant dose savings. Model(k1,k2,k3,k4) gave the best overall fit to humans across independent variables (dose, size, contrast, and reconstruction) at fixed display window. However Model(k1) performed better when considering model complexity using the Akaike information criterion. Model(k1) fit the extraordinary detectability difference between IMR and FBP, despite the different noise quality. It is anticipated that the model observer will predict results from iterative reconstruction methods having similar noise characteristics, enabling rapid comparison of methods.

1. INTRODUCTION

Ionizing radiation from x-ray computed tomography (CT) contributes the greatest per capita medical exposure of all medical imaging procedures, which has raised concerns as to the dose delivered in imaging procedures [1–4]. The introduction of iterative reconstruction (IR) techniques in CT imaging has both improved image quality and allowed for reductions of radiation dose in a variety of clinical tasks [5–12]. Such techniques are continuing to improve, such as statistical IR, which may further reduce dose [13, 14]. Aside from reducing dose in current tasks, IR may enable CT applications which are otherwise infeasible due to high dose such as dynamic CT myocardial perfusion imaging [15, 16]. The extent to which an IR algorithm can lower dose is task-dependent, and task-based metrics have been suggested as more appropriate assessments of image quality for IR instead of the contrast-to-noise ratio (CNR) or signal-to-noise ratio (SNR) [17]. Low contrast detectability (LCD) is one such task-based metric which provides a quantitative assessment of image quality and is well-established in the literature [18, 19].

LCD is typically measured across several human observers, a time consuming process which can slow progress. A widely used experimental method is the multiple alternative forced-choice (MAFC) paradigm which directly compares noise-only images to signal-plus-noise images [18, 19]. LCD is quantified by observers’ ability to detect and select signal images instead of noise images. Due to intra-observer variability, an MAFC experiment requires hundreds of trials per observer. Due to inter-observer variability, multiple observers are required. This would be much alleviated by a model observer predictive of human LCD [20–22]. One such model is the Channelized Hotelling Observer (CHO) which models human perception using several frequency-selective channels through which the observer makes detection decisions [20, 23]. The choice of these channel filters will impact the model’s performance, and should be considered according to the signal shape [24]. The CHO captures overall trends in human detection, but often largely over-estimates human performance [25]. To address this, internal noise has been used as a way to model a known inefficiency in human performance [26, 27]. The addition of internal noise can have large effects on CHO detectability outputs, and internal noise distributions can be sampled in a variety of ways with differing effects [28, 29]. The ideal internal noise sampling method remains unclear for general applications. This motivates our work in which we aim to develop a robust computational model observer able to assess LCD similar to human observers in both FBP and IR which span a wide range of noise characteristics. We compared a Laguerre-Gauss CHO with internal noise (CHO-IN), using six different internal noise sampling methods, to human performance in 4AFC experiments across signal size, contrast, and x-ray dose, reconstructed with conventional FBP and advanced iterative reconstruction (Philips IMR). A model observer matched to human observer performance in both traditional FBP and IR would aid task-based dose optimization and reconstruction parameter tuning processes by rapid, automated evaluation of low contrast lesion detectability.

2. METHODS

In this section we discuss the LCD studies performed including phantoms used, human and model observer studies, the CHO and internal noise models, and data fitting methods.

2.1. Phantom and Images

CT images were generated using a simulated phantom with added cylindrical low-contrast pins. Signal images were taken from a slice containing the pins of 1mm reconstructed thickness. Noise images were taken from a slice without pins. Images were simulated at three different dose levels: 63% (62 mAs), 40% (39 mAs), and 20% (20 mAs), relative to 98 mAs (100%) dose. Full dose (100%) was tested but yielded saturated detection values, not useful for detection studies. FBP and IMR images were reconstructed from the same raw projection data on a Philips reconstruction system. For each dose setting, 200 signal image acquisitions and 600 noise image acquisitions were obtained. These images were used for both human and model observer experiments.

The phantom contains 12 pins at different contrast and size combinations, labeled as pins #1–12 (Fig. 1). The phantom has a diameter of 15cm with an image resolution of 512×512 pixels and mean background of 0 HU. Sub-image patches containing a signal were taken as 64×64 pixel patches with the signal at the sub-image center. These signal sub-images were used for the human and model observer detection experiments. For the noise images, corresponding sub-image patch locations were taken. These noise sub-images were used as the noise images in the observer experiments. For the dose experiment, pin #6 (6mm, 0.5% contrast) was used at 63%, 40%, and 20% dose (Fig. 2). For the size experiment, dose and contrast were fixed to 20% dose and 0.5% contrast and pins #5, #6, and #7 were used. For the contrast experiment, dose and size were fixed at 20% dose and 6mm and pins #2, #6, and #10 were used.

Figure 1. Phantom used for the human and model observers and sample 4 Alternate Forced Choice trials.

(Left) The simulated phantom has twelve cylindrical signals at varied diameters and contrasts. Signals appear circular in the axial slice. Starting from 12 o’clock and moving clockwise, they are pin #1 (4mm 0.3%), pin #2 (6mm 0.3%), pin #3 (8mm 0.3%), pin #4 (15mm 0.3%), pin #5 (4mm 0.5%), pin #6 (6mm 0.5%), pin #7 (8mm 0.5%), pin #8 (15mm 0.5%), pin #9 (4mm 1.0%), pin #10 (6mm 1.0%), pin #11 (8mm 1.0%), and pin #12 (15mm 1.0%). (Center) A 4AFC trial for FBP is shown with one signal image and three noise images. (Right) A 4AFC trial for IMR is shown. All 4AFC experiments used a window of 100 and level of 0 HU. Contrast has been enhanced in these images for display purposes.

Figure 2. FBP and IMR sample images from dose experiment.

Signal images are shown with dose decreasing from left to right from 63% to 20% dose with (Top) FBP reconstruction and (Bottom) IMR reconstruction. Noise becomes more aggressive as dose is reduced. Note the drastic difference in noise characteristics between FBP and IMR reconstructed images.

2.2. Human Observer Study

4-Alternative Forced Choice (4AFC) experiments were used to assess LCD, a well-established technique [18, 19]. Experiments were performed by three trained observers with normal or corrected-to-normal vision in an IRB-exempt protocol. The experiment was performed in a darkened room using a calibrated Barco© MDRC1119 perceptually linear display. Observers performed 4AFC experiments for each dose, size, and contrast condition and both reconstruction techniques. In each 4AFC trial, one signal image and three noise images were shown as in Figure 1. Observers were shown the signal image prior to each 4AFC experiment and given 20 test trials. Then, each subject performed the 200 trial 4AFC experiment for one IMR condition and one FBP condition. In each 4AFC experiment, probability correct (PC) was obtained. There were a total of 14 experiment blocks per observer. The order of FBP and IMR experiments, first or second, was randomized to minimize bias. Experimental conditions (dose, size, contrast) were similarly randomized. Observers were blind to experimental conditions. A window width of 100 HU and level of 0 HU was used in all experiments.

2.3. Model Observer Study

The CHO-IN model was used with six different internal noise sampling approaches, as described in section 2.5. The inputs to the model were the same 200 signal and 600 noise sub-image patches as used in the 4AFC human observer study. Each image is passed through five rotationally-symmetric Laguerre-Gauss channel filters to obtain channel outputs. Channel weights are determined by the channel output covariance. The channel weights are multiplied by corresponding channel outputs and summed to obtain a decision variable for the image. This decision variable can be interpreted as the relative probability that an image contains the signal. From the distribution of signal and noise decision variables, the detectability index (d’) can be computed. A corresponding PC for 4AFC is calculated from this d’ [19, 30]. Thus, model PC can be compared directly to human PC as in previous works [28, 31].

2.4. Channelized Hotelling Observer (CHO)

We use the CHO as described in previous works [20, 23, 31, 32]. Five Laguerre-Gauss channels were selected since signals were rotationally symmetric [24]. The CHO can be understood by two general steps: channel filtration and Hotelling. In the channel filtration step, each image is passed through the channel filters to obtain a channel output (denoted CO). These outputs are multiplied by channel weights and summed to yield a decision variable, λ, given as:

$$\mathrm{\lambda }=\sum _{m=1}^M{w}_m\cdot C{O}_m.$$ (1)

M is the number of channels and m is the channel index. The channel weights are determined by the Hotelling process, the multiplication of the inverse scatter matrix and the mean difference of the signal and noise channel outputs

$$S_c=\frac{1}{2}\left(cov\left({\mathit{\text{CO}}}_S\right)+cov\left({\mathit{\text{CO}}}_N\right)\right),$$ (2)

$$\mathit{\text{w}}={\mathit{\text{S}}}_c^{-\text{1}}[\overline{{\mathit{\text{CO}}}_S}-\overline{{\mathit{\text{CO}}}_N}],$$ (3)

where CO_S and CO_N are MxM channel output covariance matrices and $\overline{{\mathit{\text{CO}}}_S}$ and $\overline{{\mathit{\text{CO}}}_N}$ are Mx1 channel output means. Detectability is then calculated from the distribution of signal and noise decision variables as described in section 2.6.

2.5. Internal noise sampling and detectability calculation

Six internal noise models were tested with noise added to the decision variable (denoted λ) or the channel outputs (denoted CO) sampled as:

1. Model(k1): decision variable noise is proportional to background decision variable standard deviation, σ_in,λ = k₁σ_λ, where σ_in,λ is calculated for both σ_λ,S and σ_λ,N, the signal and noise decision variable standard deviations.

2. Model(k2): decision variable noise is constant, σ_in,λ = k₂.

3. Model(k1,k2): decision variable noise has both constant and proportional terms, σ_in,λ = k₁σ_λ + k₂.

4. Model(k3): channel noise is uniform across channels, ${\mathbf{\sigma }}_{\mathit{\text{in}},\mathit{\text{co}}}^2=k_3{\mathit{\text{I}}}_{\mathit{\text{M}}}$,I_M is a M × 1 identity vector, with length the same as the number of channels (five in this work).

5. Model(k4): channel noise is proportional to variance in channel output, ${\sigma }_{\mathit{\text{in}},\mathit{\text{co}}}^2=k_4\mathit{\text{diag}}\left({\mathit{\text{K}}}_{\mathit{\text{S}}}\right)$.

6. Model(k1,k2,k3,k4): channel and decision variable internal noise, σ_in,λ = k₁σ_λ + k₂ and ${\sigma }_{\mathit{\text{in}},\mathit{\text{co}}}^2=k_3{\mathit{\text{I}}}_5+k_4\mathit{\text{diag}}\left({\mathit{\text{K}}}_{\mathit{\text{S}}}\right)$, calculated for both signal and noise distributions.

Internal noise was sampled in a Monte Carlo fashion by adding noise to the decision variable or channel outputs as in previous works [28, 29, 31]. Noise is added either to the decision variable by λ_CHO−IN = λ_CHO + λ_IN, where λ_IN is sampled from the normal distribution with zero mean of N(0; σ_in,λ) or in the channel output by λ_CHO−IN,j = R_CHO,j + ε_IN,j where ε_IN,j is sampled from (0; σ_in,CO,j) for channel j, repeated for each channel and each image.

To calculate the detctability of the CHO [30],

$$d\prime =\frac{\langle {\lambda }_S\rangle -\langle {\lambda }_N\rangle }{\sqrt{\frac{1}{2}{\sigma }_S^2+\frac{1}{2}{\sigma }_N^2}},$$ (4)

where ${\sigma }_S^2$ is the decision variable variance for signal images, ${\sigma }_N^2$ is the decision variable variance for noise images and <. > denotes the mean. Adding internal noise to the CHO using the described models increases the decision variable variance, thereby reducing the detectability. Internal noise must be sampled many times for each image to stabilize the stochastic output from the Monte Carlo process. In this work, we used 100 internal noise realizations per image. This allows for the calculation of detectability which can be converted to PC for a 4AFC experiment and compared to human observer data [19].

2.6. Parameter fitting

Model internal noise parameters are fitted by maximum-likelihood (ML) to average human PC for all 14 conditions (recon, dose, size, contrast). All conditions are used for parameter fitting to minimize bias toward a single condition, which may lead to under- or over-estimation of detectability in other cases. ML accounts for the underlying binomial distribution of the 4AFC experiment. High PC measurements have less variance than low PC measurements and the PC measurement probability density function is skewed toward higher PCs for a given expected value. Fitting model parameters using maximum-likelihood accounts for these aspects, whereas least-squared error minimization does not. The likelihood of obtaining k = PC_human * N correct selections given PC_model for N trials is given by

$$P\left(k;N,P{C}_{\text{mod}el}\right)=\left(\begin{array}{c}N\\ k\end{array}\right)P{C}_{\text{mod}el}{}^k{\left(1-P{C}_{\text{mod }el}\right)}^{N-k}.$$ (5)

The probability of obtaining human performance across M conditions is given by

$$P_{\mathit{\text{total}}}=\prod _{m=1}^{M}P\left(k_m;N,p_m\right).$$ (6)

Which can be written in log form,

$$P_{\mathit{\text{total}},\mathit{\text{log}}}=\sum _{m=1}^M\mathrm{\text{log}}(P\left(k_m;\text{N},p_m\right)).$$ (7)

Finally, we can formulate the cost function simply by the negative log-likelihood,

$$C=-P_{\mathit{\text{total}},\mathit{\text{log}}},$$

Which we minimized using a direct search algorithm. The tradeoff between model complexity and fit was evaluated by the Akaike Information Criterion, corrected for a finite number of samples, AIC_C [33],

$$AI{C}_C=2k+2C+\frac{2k(k+1)}{n-k-1},$$ (9)

with k as the number of parameters and n as the number of conditions.

3. RESULTS

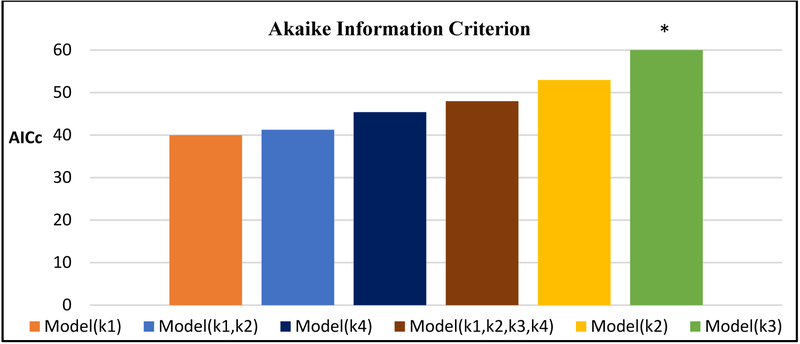
Human and model observer experiment results are shown in Figure 3. Model(k1,k2,k3,k4) gave the best performance with the lowest negative log-likelihood error of 17.8, while Model(k3) gave the most error, 202.5. Model(k1) and Model(k1,k2) performed nearly as well as Model(k1,k2,k3,k4). In fact, when considering model complexity according to AICc, Model(k1) performed best (Fig. 4). Model(k1,k2) and Model(k1,k2,k3,k4) gave the lowest average PC error overall, 0.024±0.025 and 0.025±0.022, respectively. In general, models tended to overestimate PC in FBP and underestimate in IMR.

Figure 3. Human and Model observer results.

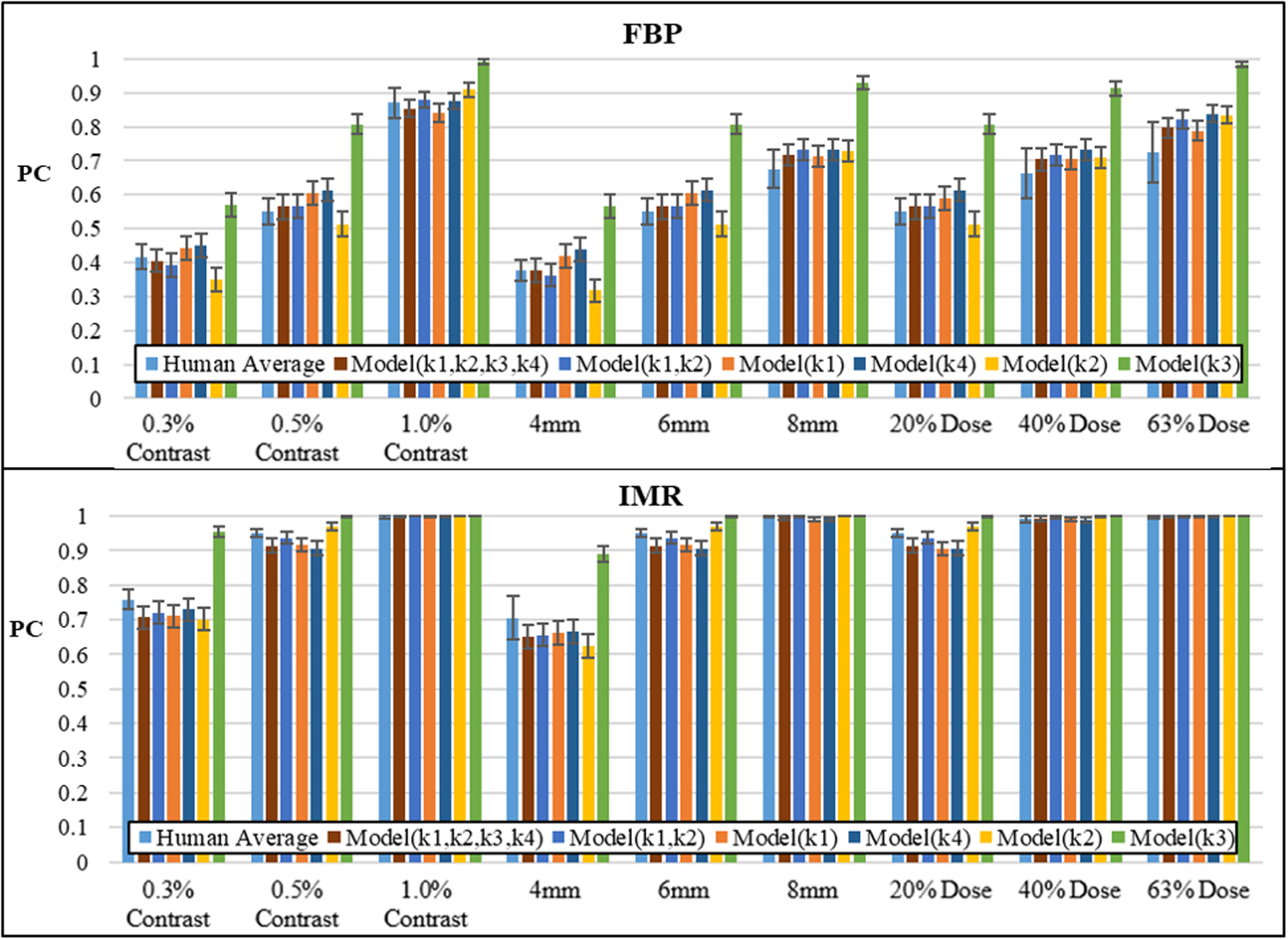
(Top) Results of FBP and (bottom) IMR detection studies in conditions of varied contrast, size, and dose. Models are organized by increasing ML error from left to right. Error bars indicate standard deviation of human observers and standard deviation of the model from the binomial distribution.

Figure 4. Assessment of model observer fit and complexity by AICc.

Lower AICc indicates better performance, with models listed by increasing AICc from left to right. *Model(k3) has an AICc of 407.4, not shown on this scale.

All observers performed better with IMR reconstructed images compared to FBP reconstructions. In the dose study, it was found that IMR gave better LCD at 20% dose than FBP at 63% dose, suggesting at least a 3x dose savings. At this low dose, IMR did not lose performance compared to FBP when considering reduced size (4mm) and reduced contrast (0.3% contrast).

4. DISCUSSION

The choice of internal noise method affected the performance of the CHO-IN model as compared to human observers. CHO-IN with decision variable internal noise generally performed better than the channel output noise. From our analysis, the decision variable standard deviation proportionality parameter, k1, appears to be the most important determinant of model agreement to human observers. This is perhaps due to the relationship of the decision variable to the image noise, which is reconstruction-dependent. The combined decision variable and channel output internal noise model performed slightly better than the decision variable only model, although when considering model complexity and propensity to overfit, the AICc suggests Model(k1) is more appropriate. The models were able to capture trends across target size, contrast, and dose in both reconstructions despite very different image noise characteristics. Slight over-estimation in FBP and under-estimation in IMR indicates that there is still room for improving the model. Further, the 4AFC task is arguably not as clinically relevant as a detection plus localization task, but the CHO framework presented here has extensions to localization tasks [34].

Several considerations should be made for model parameter optimization. Clearly, fitting across multiple variables reduces the likelihood of bias in the model, whereas fitting only to one condition in our data would cause over- or under-estimation of detectability in other conditions. This appears to be a more considerable effect when comparing next-generation IR algorithms, such as IMR, which significantly changes noise characteristics. The selection of the cost function also impacts model fitting, as least squares will seek only to minimize the PC error without considering the lower variation at high PCs, such as IMR. Alternatively, one may fit by detectability to avoid this problem. The optimal internal noise parameters, and perhaps even internal noise model, will depend on the selected channel filters (Gabor, Difference of Gaussians, Band Pass, etc), so care should be taken to select channels appropriate for the signal detection task [24, 29].

Predictive ability of the decision variable model was not tested in this work, but would be of interest in future studies. A model observer for reconstruction comparisons should be robust in terms of spanning a wide range of noise characteristics, as IR/FBP blending is common in hybrid reconstructions and model-based IR algorithms have several parameters which impact noise effects. Additional studies on new data would provide more insight as to the model’s predictive power and generalizability.

Lastly, we observed that IMR gave better performance than FBP across all observers in all conditions, with better LCD in the smallest pin (4mm) and lowest contrast pin (0.3% contrast) at 20% dose. In the dose study, IMR gave better detection at 20% dose than FBP at 63% dose, suggesting at least a 3x dose savings. The CHO-IN model evaluated here could be applied to additional phantom studies with goals of reconstruction algorithm parameter tuning or task-dependent dose reduction, thereby reducing the number of human observer experiments required.