Impact of Electronic Polarizability on Protein-Functional Group Interactions

Abstract

Interactions of proteins with functional groups are key to their biological functions, making it essential that they be accurately modeled. To investigate the impact of the inclusion of explicit treatment of electronic polarizability in force fields on protein-functional group interactions, the additive CHARMM and Drude polarizable force field are compared in the context of the Site-Identification by Ligand Competitive Saturation (SILCS) simulation methodology from which functional group interactions patterns with five proteins for which experimental binding affinities of multiple ligands are available, were obtained. The explicit treatment of polarizability produces significant differences in the functional group interactions in the ligand binding sites including overall enhanced binding of functional groups to the proteins. This is associated with variations of the dipole moments of solutes representative of functional groups in the binding sites relative to aqueous solution with higher dipole moments systematically occuring in the latter, though exceptions occur with positively charged methylammonium. Such variation indicates the complex, heterogeneous nature of the electronic environments of ligand binding sites and emphasizes the inherent limitaiton of fixed charged, additive force fields for modeling ligand-protein interactions. These effects yield more defined orientation of the functional groups in the binding pockets and a small, but systematic improvement in the ability of the SILCS method to predict the binding orientation and relative affinities of ligands to their target proteins. Overall, these results indicate that the physical model associated with the explicit treatment of polarizability along with the presence of lone pairs in a force field leads to changes in the nature of the interactions of functional groups with proteins versus that occurring with additive force fields, suggesting the utility of polarizable force fields in obtaining a more realistic understanding of protein-ligand interactions.

Introduction

Computer simulations have become an important tool to model physical phenomena on the molecular scale in the biological, chemical, and material sciences. Such simulations have benefited from advancements in computational resources, methods and algorithms. Ideally, quantum chemistry methods can be employed for molecular simulations. However, these methods are limited to relatively small system sizes and moderately sized molecules.^1–3 Accordingly, for most condensed phase applications, the molecular simulations are performed using molecular mechanical (MM) techniques allowing access to larger system sizes and longer time scales.⁴ These techniques, particularly Monte Carlo (MC) or molecular dynamics (MD) simulations, are based on intra/inter molecular potential energies or forces of the given coordinates obtained from an additive or polarizable force field.^5–7

Force fields use an analytical potential energy function to study the behaviour of any given system and predict a range of properties. These functions are parametric in nature. The accuracy of the results obtained from the MM methods relies on the sampling of the conformations, which may be facilitated using enhanced sampling methods,⁸ as driven by the accuracy of the force field. Currently, there are a number of highly specialized molecular force fields based on an additive, fixed or non-polarizable treatment of the partial atomic charges, such as CHARMM,^{9, 10} AMBER,^11–13 GROMOS,^{14, 15} OPLS,^{16, 17} and others which are well established and extensively used.¹⁸ The greatest advantage with additive force fields is their ability to handle large system sizes even for millions of atoms. However, keeping the partial atomic charges on the atomic nucleus fixed represents a significant approximation as in reality the charge distribution in a molecule varies in response to their environment. To overcome this, polarizable force fields for molecular simulations have been developed and are becoming more widely used with examples including ion-protein binding, ion permeations, ionic liquids, and hydrogen bond dynamics.^19–25 Examples of polarizable force fields under various levels of development include the CHARMM Drude polarizable force field,²⁶ AMBER ff02,²⁷ AMOEBA,^28–30 and CHEQ.^{31, 32} While polarizable force fields offer multiple advantages in modeling environmental responses, using these increases the computational time as compared to simulations using the additive force fields.^33–35

The Drude polarizable force field is based on the classical Drude oscillator model³⁶ and has been undergoing active development.^{26, 33, 37–44} The Drude oscillators (or particles) are connected to the polarizable non-hydrogen atom nuclei via a harmonic spring. In the Drude force field, the hydrogen atoms are considered to be non-polarizable. The Drude particle carries some negative charge with a small mass of 0.4 amu. Most importantly, the Drude particle can move around the non-hydrogen atom in response to the electric field, making the way for the induced dipole moment. Moreover, the model also includes lone pairs modelled as virtual particles on the hydrogen bond acceptor atoms for improving hydrogen bonding in polar compounds.⁴⁵ While the Drude force field is still under development, it has been used to predict thermodynamic, transport and structural properties in selected chemical and biomolecular systems, though the true potential of the force field is largely unexplored.^46–53

In this study, our aim is to demonstrate the impact of electronic polarizability on the interactions of functional groups with proteins in the context of the Site Identification by Ligand Competitive Saturation (SILCS)^{54, 55} framework. The SILCS methodology is based on a precomputed ensemble of water and small solutes representing a range of different types of functional groups around a target macromolecule typically a protein. This ensemble is then converted to free energy maps for the different functional groups and water, termed FragMaps, that may be used to discover and/or design new molecules as well as for protein-protein interactions.^56–60 Similar to SILCS, other co-solvents based simulation methods are increasingly applied in the context of a variety of applications.^61–70 To directly understand the impact of polarizability, the SILCS MD-based simulations were performed with both the CHARMM36 additive and Drude polarizable force fields with the FragMaps extracted for the two models for five proteins. The FragMaps are then analyzed to determine the similarities of the maps based on overlap coefficients, prediction of the relative affinities of ligand binding, dipole moment distribution plots of solutes used in the simulations, and vector maps for those solutes to monitor their orientation in selected binding sites. The SILCS methodology has previously been used on a diverse set of proteins using a combined Grand canonical Monte Carlo (GCMC)-MD sampling approach with the additive CHARMM36 and CHARMM General Force Field.^{58, 71, 72} However, as the GCMC methodology has yet to be extended to the Drude polarizable force field the goal of the present study is achieved through the use of MD sampling alone in the SILCS simulations.

The next section explains the computational methodology for the SILCS system setup, SILCS MD simulation, and SILCS-MC ligand sampling details along with other terms. In the results and discussion section, we discuss and compare various outcomes obtained from additive and Drude force field-based simulations, and the last section presents concluding remarks.

Computational Methodology

A. SILCS System Setup

Five diverse proteins for which experimental data in relation to the ligand binding affinities are available were selected for the present study. These include (1) Farnesoid X acceptor (Factor Xa, 1FJS),⁷³ (2) p38α Mitogen-Activated protein kinase (P38, 3FLN),⁷⁴ (3) tyrosine kinase 2 (TYK2, 4GIH),⁷⁵ (4) tRNA m1G37 methyltransferase enzyme TrmD (TRMD, 4YPW),⁷⁶ and (5) mouse double minute 2 homolog (HDM2, 4JV7).⁷⁷ For each protein, the ligands were accessed from our previous works yielding a total of 175 ligands. Additional details regarding ligand preparation can be found in Ustach et al.⁵⁸ (for P38, HDM2, TYK2, and TRMD) and Raman et al.(Factor Xa).⁷⁸ The crystal water, ligands, and cofactors were removed from each protein. The simulation system for the SILCS methodology involves a protein, multiple solutes, and water. In order to have efficient sampling of the system, 10 independent simulations are performed on each protein. The initial structure of the proteins was altered by setting the χ¹ dihedral in ten individual orientations in 36° increments for solvent accessible residues based on a solvent accessibility of 0.005 nm² determined based on solvent accessible surface area (SASA)⁷⁹ from GROningen MAchine for Chemical Simulation (GROMACS).⁸⁰ Each of those 10 structures were then solvated by water at 55 M along with the eight solutes, each at a concentration of 0.25 M, keeping a minimum distance of 10 Å from the edge of the simulation box. The solutes include benzene, propane, methanol, formamide, acetaldehyde, methylammonium, imidazole and acetate, as previously performed.⁵⁸ An in-house script comprising several GROMACS utilities is used to perform the system setup with different initial positions and orientations of protein, solutes and water. Each system is energy minimized using the steepest descent algorithm⁸¹ for 5000 steps followed by equilibration and production. The additive system set up for each protein were converted to the Drude polarizable model using the CHARMM⁸² program. During this conversion, the Drude particles were added to all the non-hydrogen atoms of the system along with the lone pairs to hydrogen bond acceptors.

B. SILCS MD Details

Protein force field parameters were from the additive CHARMM36⁸³ model or Drude-2013 polarizable force field³⁷. Additive force field parameters for the solutes and ligands were derived from the CHARMM general force field (CGenFF)⁸⁴ program. Drude parameters for the solutes were from the original publications^{26, 85, 86} and modified parameters for selected solutes are included in the final section of the Supporting Information. For water, the additive simulation uses CHARMM TIP3P water model,^{87, 88} which was converted to the polarizable SWM4-NDP⁸⁹ model for Drude simulations. For all the additive simulations, GROMACS software version 5.1.0 was used for the energy minimization, equilibration and production runs. The additive simulation employed the Nosé-Hoover thermostat^{90, 91} and Parrinello-Rahman barostat⁹² for maintaining the system temperature and pressure at 298 K and 1 atm, respectively, and the LINCS algorithm⁹³ was used to constrain all bonds with hydrogen atoms including water. The backbone Cα atoms were restrained with a force constant of 0.12 kcal mol⁻¹Å⁻² for the production simulations. The nonbonded interaction was computed with a cutoff of 8.0 Å by using the Verlet cutoff scheme. The Lennard-Jones (LJ) interactions were switched off smoothly in the range of 5.0 to 8.0 Å along with the long-range isotropic dispersion correction to the energy and pressure for LJ interaction beyond 8.0 Å. The particle mesh Ewald (PME)⁹⁴ method is used to handle the long-range electrostatics with a real space cutoff of 8.0 Å, maximum grid spacing 1.2 Å, and fourth order B-spline interpolation. The time constant for temperature and pressure coupling was set to 1 ps. The equilibration was carried out for 1 ns followed by the production run for 200 ns for each of the 10 systems for each protein with a timestep of 2 fs.

The Drude simulations were performed with the OpenMM⁹⁵ toolkit which was recently customized to handle Drude polarizable force field based simulations.³³ Simulation details were identical to those used for the additive force field with the following differences. The Drude particles were optimized using steepest descent⁸¹ (1000 steps) and adopted-basis Newton-Raphson (2000 steps) energy minimization methods followed by MD equilibration in the NPT ensemble for 10,000 steps with a timestep of 1 fs at the temperature and pressure of 298 K and 1 bar, respectively. A hard wall restraint of 0.2 Å between the parent atom and the Drude was applied to prevent instability and large displacements of Drude particles.⁹⁶ The hard wall is designed to avoid polarization catastrophe that may occur due to low frequency close interactions between atoms that may occur during the MD simulation leading to over polarization. In the present study, the hard wall was only encountered in the C and O atoms of the FORM solute in 5.7E-5 % of the time steps. The Drude polarizable simulations used the extended Lagrangian dynamics scheme⁹⁷ where the real atoms and the Drude particles are coupled to two thermostat responsible for uniting their dynamics. The “physical” and Drude thermostats were maintained at temperatures of 298 K and 1 K with the friction coefficients of 5 ps⁻¹ and 20 ps⁻¹, respectively. Periodic boundary conditions (PBC)⁹⁸ were used in all the simulations with the nonbonded interactions and Cα atom restraints treated as described above for the additive model. The pressure was regulated using a Monte Carlo barostat in OpenMM. The production simulations were carried out for 200 ns for each of the 10 systems for each protein with a timestep of 1 fs. The total sampling time for additive and Drude simulation is 2 μs. Simulation snapshots were saved every 10 ps during the production runs.

C. FragMaps, GFE, and Overlap Coefficients

FragMaps were generated from the simulation trajectories by binning selected solute and water non-hydrogen atoms into 1 × 1 × 1 ų cubic volume elements (voxels) and the occupancy of the selected atoms determined. Selected atoms of the solutes are categorized into the FragMaps as described below. The probability distributions are normalized for the concentration of the solutes in solution and converted into the grid free energies (GFE) via Boltzmann transformation⁹⁹ yielding FragMaps defined based on free energies of the selected solute or water atoms relative to being in bulk solution. GFE is an atom-based metric which allocates a free energy score to selected ligand atoms in correspondence to the overlap of those atoms with the FragMaps. In the present study selected solute atom types were combined into generic FragMaps as follows by merging voxel occupancies of the different solutes and converting the normalized distributions into GFE.⁵⁸ They are generic nonpolar or apolar (GENN, benzene and propane), generic acceptor (GENA, formamide O, acetaldehyde O, imidazole acceptor N, and methanol O), generic donor (GEND, formamide N and imidazole donor N, and methanol O). In addition, specific maps for methylammonium nitrogen (DPOS, MAMN), acetate oxygen (ANEG, ACEO) and methanol (MEOO) were used, with the latter used for calculating the GFE scores of alcohols. All visualization of the FragMaps was presented using visual molecular dynamics (VMD)¹⁰⁰ program.

Analysis of the similarity of the FragMaps was performed based on the overlap coefficient. The overlap coefficient (OC) provides a quantitative evaluation of the similarity of two sets of FragMaps. OCs values greater than 0.8 indicate a high degree of similarity and values of 0.6–0.8 depicts reasonable level of similarity⁷⁸ with lower values indicating significant differences. The overlap coefficient (OC) ⁹⁹ is defined as

$$\text{Overlap}\hspace{0.17em}\text{coefficient}=\sum _{i=1}^{N}min\left(\frac{Q_i^1}{{\sum }_{j=1}^N{Q}_j^1};\frac{Q_i^2}{{\sum }_{j=1}^N{Q}_j^2}\right)$$

where N is the number of voxels in the FragMaps and $Q_j^1$ and $Q_j^2$ are their occupancies of voxel i. The OCs were calculated individually for each FragMap and vary between 0 to 1, with 1 signifying equivalent FragMaps.

D. LGFE and SILCS-MC Sampling

SILCS-MC sampling method is utilized to predict the binding conformation of the ligands in the presence of FragMaps.⁷⁸ The SILCS-MC is a Monte Carlo sampling method where ligand moves are accepted/rejected based on the Metropolis¹⁰¹ criteria. The Metropolis criteria is based on the ligand grid free energy (LGFE) scores combined with intramolecular conformational energies associated with the CGenFF energy function. LGFE scores are obtained by classifying selected ligand atoms into different FragMaps types, as mentioned above, based on their chemical similarity to the different type of FragMaps. Based on the overlap of the ligand atoms with the FragMaps each atom is assigned a GFE score, with the LGFE score being the summation of the atomic GFE scores. Details of current implementation of the GFE and LGFE scoring is detailed in Ustach et al.⁵⁸ The LGFE scores are representative of binding free energies; however, as they are a sum of the GFE scores of the classified atoms in each ligand and, therefore, are missing contributions such as the configurational entropy associated with connecting the atoms to make the full ligand, they are not formal free energies of binding. For the SILCS-MC the temperature was initially set to 300 K for the normal MC run and gradually lowered it to 0 K. The CGenFF contribution to the Metropolis criteria, in addition to the LGFE scores, includes van der Waals (vdW), electrostatic and dihedral terms. All the force field parameters for the ligands were derived from the CGenFF program.⁸⁴ The SILCS-MC method does not contain any protein and solvent environment explicitly, therefore, a distance dependent dielectric (=4|r|) was employed to compute intramolecular electrostatics.^102–104 Before starting the SILCS-MC run, each ligand structure was optimized in the context of CGenFF by employing energy minimization for 10,000 steps. During the SILCS-MC sampling involved translations, rotations and rotations of dihedrals about rotatable bonds. The CGenFF intramolecular energy used in the SILCS-MC Metropolis criteria is the additive form for both the additive and Drude FragMap calculations. Moreover, we performed five independent runs of SILCS-MC cycles for each ligand to thoroughly identify a minimum free energy binding conformation.

Two types of SILCS-MC protocols were used, namely Local and Exhaustive. The protocols differ in the number of MC cycles, types of attempted moves and initial placement of the ligand. The starting conformation and orientation for the Local protocol involves a user defined position of the ligand, typically based on the crystallographic location, whereas in the Exhaustive protocol the ligand is positioned randomly within a radius defined by the user. The Exhaustive protocol explores a larger region of conformational space as compared to the Local due to initial placement of the ligand in a random conformation and orientation in the binding pocket. For the Exhaustive protocol, a 10 Å radius was used. Each ligand was then subjected to 100 MC steps and 1000 annealing steps for the Local protocol and 10,000 MC steps and 40,000 annealing steps for the Exhaustive protocol with the final ligand orientation being selected based on the most favorable LGFE score. Final scoring of each ligand is based solely on the LGFE score. Additional details about the SILCS MC protocols can be accessed from the recent work by Ustach et al.⁵⁸ We note that while the SILCS simulations are performed using the Drude polarizable force field and, therefore, are computationally more demanding than the additive SILCS simulations by ~4 fold, once the SILCS FragMaps are available the ligand SILCS-MC docking calculations have the identical computational requirements for the two models as the SILCS-MC sampling is performed directly in the field of the FragMaps.

Results and discussion

SILCS FragMaps are 3D probability distributions of selected solute atoms that define the functional group affinity pattern of the target protein. The FragMaps quantify regions of both favorable and unfavorable affinities of the functional groups relative to being in aqueous solution. The utility of the SILCS methodology is largely based on the accuracy of the FragMaps with respect to the true functional group distributions that would be observed experimentally (if such experiments were available). Accordingly, it may be assumed that improvements in the underlying potential energy function may lead to more accurate distributions of solutes and water around the target protein and, therefore, improved FragMaps. To test this, in the present study SILCS simulations are applied to 5 proteins using both the CHARMM36 additive and Drude-2013 polarizable force fields. As the Drude force field explicitly treats electronic polarization as well as lone pairs in the case of hydrogen bond acceptors, it is anticipated that the force field will more accurately model the distribution of solute functional groups around the protein. In addition, the proposed calculations allow for details of variations in dipole moments and the orientation of functional groups that occur in ligand binding sites associated with the explicit treatment of polarizability and lone pairs to be investigated.

Analysis of the overlap coefficient (OC) values of the FragMaps from simulations 1–5 and 6–10 from each of the systems for all 5 proteins was performed to determine the extent of convergence of the SILCS MD simulations (Table S1 of the supporting information). The OC values are all 0.8 or greater, indicating high convergence. With respect to treatment of the ligands, the SILCS method offers the advantage that once the FragMaps are available the SILCS-MC ligand docking is primarily based on the FragMaps themselves rather than the underlying potential energy function. Thus, for SILCS-MC of the ligands the combined CGenFF/MolCal⁷⁸ engine used to convert mol2 files into the SILCS atom classification used for the additive-based FragMaps may also be used for the Drude-based FragMaps. Essentially, once the polarization contributions are embedded in the FragMaps, the same tools for ligand sampling, and the same computational demand, may be used for the Drude SILCS-MC calculations.

A. FragMap Analyses

Initial comparison of the FragMaps from the additive and Drude force fields involved OC analysis. Results, shown in Table S2 of the Supporting Information, shows the values of OC for different solutes for all the protein targets for the entire simulation box. The majority of values are > 0.8 with the lowest value being 0.71 indicating the overall maps to be similar. The overall high OC values between the additive and Drude FragMaps are expected given that majority of 3D space defining the FragMaps is in the solution around the proteins. To determine if the FragMaps are similar in the regions important for ligand binding the OC values in the binding pockets were evaluated.

Table 1 represents the OC values for regions centered on the binding pocket of size 20×20×20 ų for P38 and Factor Xa and 16×16×16 ų for the other proteins; the sizes were selected based on the spatial extent of the known ligands. Interestingly, there are major differences observed between the additive and Drude models for the majority of FragMaps and proteins. Some of the protein show OC values close to 0.3 in particular for charged solutes. The OC values for HDM2 show a reasonable level of similarity for all FragMaps and the agreement for the water tipo maps is also high in all cases. Thus, the OC values in the majority of binding pockets indicates that there are significant differences present in the FragMap distributions between the two force fields. Additional analysis focused on the details of these differences.

Table 1:

Overlap coefficients for the different solutes in a cubic box encompassing the binding pockets in the Drude versus additive simulation for each protein target.

	P38	Factor Xa	HDM2	TRMD	TYK2
FragMap
meoo	0.58	0.74	0.79	0.63	0.59
imin	0.49	0.62	0.75	0.48	0.53
iminh	0.50	0.61	0.75	0.52	0.54
foro	0.55	0.63	0.79	0.54	0.47
forn	0.55	0.62	0.80	0.61	0.50
mamn	0.52	0.47	0.77	0.57	0.34
aceo	0.54	0.53	0.79	0.34	0.60
benc	0.49	0.55	0.63	0.53	0.57
prpc	0.46	0.54	0.62	0.58	0.66
aalo	0.61	0.65	0.73	0.65	0.61
tipo	0.71	0.81	0.89	0.78	0.75
aalc	0.62	0.66	0.75	0.65	0.67
gehc	0.54	0.64	0.78	0.51	0.60
acec	0.48	0.49	0.75	0.32	0.56
Average	0.55	0.61	0.76	0.55	0.57

meoo: methanol O, imin: imidazole acceptor N, imih, imidazole donor N, foro: formamide O, forn, formamide N, mamn: methylammonium N, aceo, acetate O, benc, benzene Cs, prpc, propane Cs, aalo, acetaldehyde O, tipo, Tip3P O, aalc, acetaldehyde carbonyl C, gehc: imidazole Cs and acec: acetate carbonyl C.

Qualitative evaluation of the FragMap distributions obtained from the Drude and additive simulations in the bindings sites was based on the data shown in Figures 1 and S2. Included are ligands from the crystal structures used to initiate the SILCS simulations, allowing for determination of the ability of the FragMaps to qualitatively recapitulate the location of different functional groups of the ligands. Discussion of results for Factor Xa, P38 and TRMD are below with those for HDM2 and TYK2 in the Supporting Information. The present discussion is based on visualization of the maps at a GFE contour level of −1.2 kcal/mol unless noted.

Figure 1:

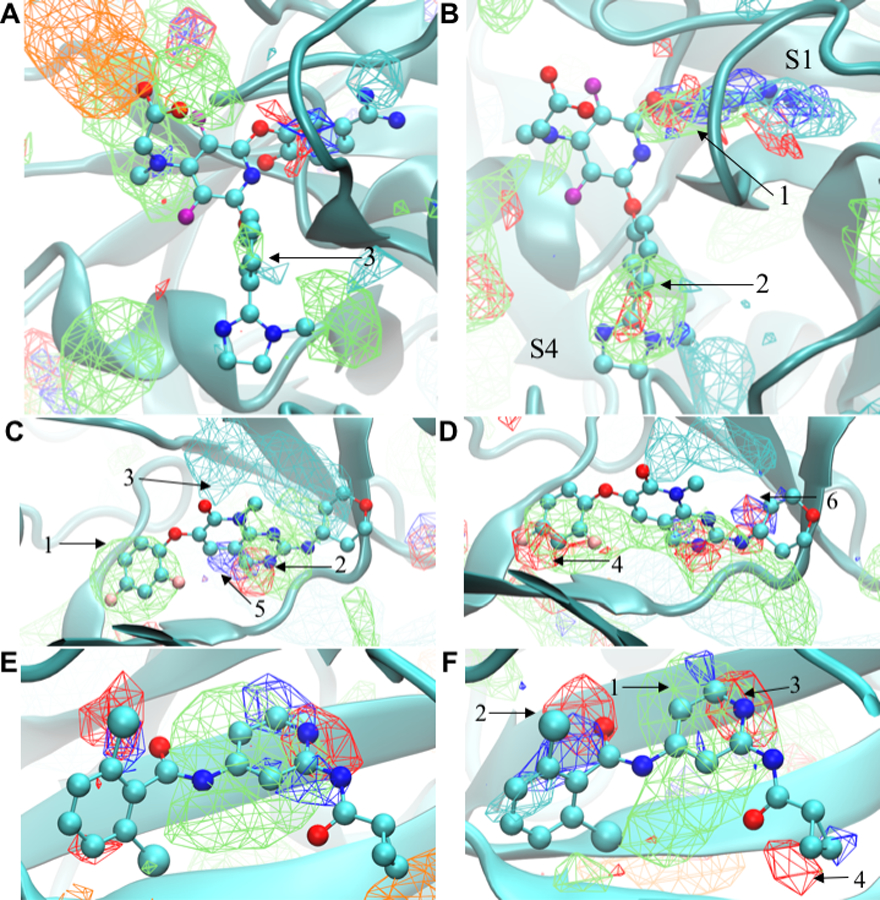
FragMaps overlaid on the proteins Factor Xa, P38 Map kinase and TYK2. Cartoon representations are shown based on the crystal conformations (PDB 1FJS, PDB 3FLN, and PDB 4GIH, respectively) with portions of the protein occluding the binding pocket view omitted. The ligands from the respective crystal structures are shown in CPK representation with atom type color. Panels A, C and E show the FragMaps for Factor Xa, P38 Map kinase and TYK2 obtained from the additive simulations while panels B, D, and F show the FragMaps for Factor Xa, P38 Map kinase and TYK2, respectively, obtained from the Drude simulations. The FragMaps color are GENN or APOLAR (green), GENA (red), GEND (blue), MAMN (cyan), and ACEO (orange). All FragMaps isocontour surfaces are displayed at a cutoff of −1.2 kcal/mol. 2D images of the ligands are shown in Figure S1 of the Supporting Information.

Factor Xa: The FragMaps in the active site are shown in Figure 1A and 1B for additive and Drude simulations, respectively. Beginning with the apolar FragMaps, the Drude FragMaps clearly replicate both aromatic phenyl rings of the ligand as shown by the arrow 1 in the S1 pocket and arrow 2 in the S4 pocket. In contrast, the additive apolar FragMaps entirely miss the aromatic ring in the S1 pocket (Figure 1A). The additive FragMaps indicate the presence of the benzene ring in pocket S4 (arrow 3); however, their extent is lower than with the Drude FragMap. Hydrogen bond acceptor or donor (GENA/GEND) FragMaps are evident in the S1 and S4 pockets, with the extent of those maps larger with the Drude FragMaps. With the S4 pocket, the ligand’s imidazole group is captured by the Drude GENA FragMaps while these are not present with the additive model at the contour level of −1.2 kcal/mol. The charged amidine group in the S1 pocket is correctly mapped by positive MAMN FragMaps for both force fields. In addition, the Drude MAMN FragMaps are present in the lower region of the S4 pocket which is consistent with the presence of an imidazole or ammonium group on ligands in the 1EZQ, 1MQ5, and 1Z6E crystal structures.⁷⁸ The additive simulation also shows certain FragMaps for negative (ACEO) and apolar groups in the upper left corner of Figure 1A . The apolar maps (green) are overlaid on the crystallographic structure whereas the negative maps (orange) are adjacent to the apolar maps. The ligand does contain a carboxylate group in that region, consistent with the presence of the ACEO FragMaps. With the Drude force field ACEO FragMaps are present in that region when visualized at a contour of −0.4 kcal/mol.

P38 MAP Kinase: The P38 FragMaps are shown in Figure 1C and 1D for additive and Drude simulations, respectively. The apolar FragMaps for both models are similar as shown by arrows 1 and 2 in Figure 1C recapitulating the locations of the aromatic rings. However, the Drude apolar FragMaps form a continuous distribution across the binding site, better representing the central bicyclic heterocycle of the ligand. The positive (MAMN) FragMaps are similar for the Drude and additive models as shown by arrow 3 in Figure 1C. Finally, significant differences are observed in the hydrogen bond donor and acceptor (GEND and GENA) FragMaps. Arrow 4 in Figure 1D denotes the hydrogen bond acceptor FragMaps from the Drude model which overlap with the fluorine atoms of ligand; these FragMaps are not evident in the additive results. Additional GENA/GEND FragMaps, shown by arrow 5 in Figure 1C, are present for both force fields. However, the additive FragMaps are quite limited as compared to the Drude results, where the FragMaps recapitulate more of the donor and acceptor atoms in the ligands as indicated by arrow 6 in the Figure 1D.

TYK2: The TYK2 FragMaps are shown in Figure 1E and 1F for additive and Drude models, respectively. The apolar FragMaps for both models capture the central region of the ligand overlapping with the aromatic ring of the ligand as shown by the arrow 1 in Figure 1F. These apolar maps extend beyond the pyridine ring, indicating that larger ring systems or hydrophobic functional groups could be accommodated in this region, consistent with the presence of an additional pyridine ring in this region in known inhibitors.⁷⁵ Both the force fields largely fail to have apolar maps overlapping with the dichloro aromatic ring of the ligand (left side of Figures 1E and 1F). A small region of Drude apolar FragMaps is present at the lower portion of that region, which correspond to one of the chlorine atoms on the ring. However, significant hydrogen-bond donor and acceptor maps are present in the vicinity of one of the chlorine atoms (arrow 2) and a small acceptor region is present adjacent to the second chlorine with the Drude FragMaps. The presence of these maps may indicate that the chlorines are interacting favorably with the protein via halogen bond or halogen-hydrogen bond donor interactions. ^{43, 105} Better modelling of these types of interactions may be performed using SILCS simulations that include halogenated solutes, as recently performed.⁵⁸ Additional hydrogen bond donor or acceptor FragMaps capture other heteroatoms on the ligand (arrow 3). In addition, the Drude FragMaps show the possibility of having polar groups in the vicinity of the isopropyl group (arrow 4 on Figure 1F). The acceptor FragMap is adjacent to the oxygen in the peptide bond and both the donor and acceptor maps indicate the potential for adding polarity to the isopropyl ring.

B. SILCS-MC Ligand Binding Predictions

Quantitative predictions centered upon the ability of both force fields to rank the order of ligand affinities based on LGFE scores to further evaluate the impact of the inclusion of polarizability on the SILCS method. The LGFE scores approximate experimental binding affinities though they are not true binding free energies, as discussed above. Two SILCS-MC sampling protocols, Local and Exhaustive, were applied for both the Drude and additive FragMaps of the five proteins. Local sampling is based on a known initial ligand conformation while Exhaustive is based on randomization of the ligand orientation in the binding site followed by more extensive MC conformational sampling. In the present study, comparisons were initially performed based on the predictive index (PI), root mean square error (RMSE), and the percent correct (PC).⁵⁸ The PI correlation for ligand scoring ranges between 1 for 100% true relative predictions and −1 for 100% false predictions, and 0 for the random predictions.¹⁰⁶ It is designed to be a metric of the ability of the method to rank order the ligands based on their affinities. The weighting term in the PI increases with the increment in the magnitude of the differences in affinities. The sum of true positive and true negative comparisons is referred to as the PC for each series of ligands. The PC values should be maximal for lead optimization purposes and is simply indicating the percentage of occurrences when correct predictions in the direction of the binding affinity are made. The reported PC values are average values over individual PC values with each ligand in the series taken as the reference ligand. RMSE is based on the root-mean-square difference between the LGFE and the experimental binding free energies over all the ligands of each protein.

The PI, RMSE and PC values obtained from SILCS-MC simulation for both sets of FragMaps with Exhaustive and Local protocols are listed in Table 2. For the Drude FragMaps, the averaged values of PI, RMSE and PC for Exhaustive protocol are 0.44 ± 0.09, 2.18 ± 0.28 and 0.65 ± 0.03, respectively, where the errors are the standard errors over the 5 proteins. In comparison, the Exhaustive protocol for additive FragMaps results in 0.36 ± 0.10, 2.36 ± 0.53, and 0.61 ± 0.03 for PI, RMSE and PC, respectively. For the Local protocol the Drude FragMap averaged values for PI, RMSE and PC are 0.46 ± 0.13, 3.50 ± 0.51 and 0.64 ± 0.04, respectively, while for the additive FragMaps the results are 0.47 ± 0.05, 4.33 ± 1.21, and 0.64 ± 0.02 for PI, RMSE and PC, respectively. Thus, the Exhaustive and Local protocol results show overall improvements with the Drude FragMaps versus the additive, although the PI and PC values are close to each other with the Local sampling. However, as is evident from Table 2 in certain cases the additive FragMaps (e.g. TRMD with both the Exhaustive and Local protocols) yield better agreement with experiment, consistent with the system specific nature of CADD methods.

Table 2:

Comparison of SILCS-MC LGFE scores and docked orientations with experimental data for the Exhaustive and Local SILCS_MC docking protocols in Drude and additive FragMaps for different protein targets. The PI, RMSE, PC, RMSD and COMD signifies the predictive index, root mean square error, percent correct, root mean squared distance (Å), and center of mass difference (Å), respectively, along with the average LGFE-∆Gbind (kcal/mol) difference.

System	Protocol	PI	RMSE	PC	RMSD	COMD	Average LGFE-∆Gbind
P38	Exhaustive (Drude)	0.44	2.04	0.67	6.11	2.10	1.80
	Exhaustive (Additive)	0.36	2.09	0.63	7.28	1.69	1.77
	Local (Drude)	0.59	3.97	0.71	1.84	1.29	3.89
	Local (Additive)	0.55	3.93	0.69	1.26	0.88	3.85
Factor Xa	Exhaustive (Drude)	0.09	2.73	0.55	5.35	2.70	2.07
	Exhaustive (Additive)	−0.01	4.28	0.51	10.50	7.40	3.95
	Local (Drude)	−0.02	4.13	0.51	1.69	0.98	3.56
	Local (Additive)	0.27	9.06	0.58	2.68	1.56	8.83
HDM2	Exhaustive (Drude)	0.58	1.15	0.69	5.87	2.82	−0.55
	Exhaustive (Additive)	0.36	1.33	0.60	5.70	2.59	0.64
	Local (Drude)	0.75	1.47	0.75	1.84	1.16	1.14
	Local (Additive)	0.57	2.88	0.70	2.10	1.09	2.64
TYK2	Exhaustive (Drude)	0.61	2.61	0.69	5.66	2.80	2.41
	Exhaustive (Additive)	0.55	2.61	0.67	5.16	2.02	2.40
	Local (Drude)	0.56	3.80	0.63	2.53	1.74	3.63
	Local (Additive)	0.50	3.50	0.63	1.81	1.04	3.33
TRMD	Exhaustive (Drude)	0.46	2.35	0.64	6.45	4.82	1.91
	Exhaustive (Additive)	0.52	1.48	0.66	2.69	1.07	0.64
	Local (Drude)	0.43	4.11	0.60	1.28	0.85	3.79
	Local (Additive)	0.45	2.29	0.61	1.53	0.89	1.68

The final orientations of the ligands obtained from the SILCS-MC are an additional yardstick to quantify the Drude or additive force fields. For this purpose, we calculated the root mean squared distance (RMSD) and center of mass difference (COMD) of the final orientations of the ligands relative to the initial crystal structure-based orientations. The RMSD and COMD values for each protein with both protocols are listed in Table 2. For the Exhaustive SILCS-MC docking with the Drude set, the averaged values of RMSD and COMD are 5.89±0.19 and 3.05±0.46 Å, respectively while the additive values are 6.27±1.29 and 2.95±1.14 Å, respectively. The lower value of RMSD for the Drude set shows a small improvement in the prediction capability of the ligand orientation when compared to the additive values while the averaged COMD values are similar. Thus, the Drude model leads to a small improvement in the orientation of the ligands in the binding sites though their overall locations are similar with the two model. With the Local protocol, the RMSD and COMD averaged values for Drude are 1.84±0.20 and 1.20±0.15 Å, respectively while the additive values are 1.88±0.24 and 1.09±0.12 Å, respectively, indicating similar behaviour for the two FFs.

Shown in Figure 2 are the minimum LGFE conformations for Factor Xa, P38, and TYK2 based on the Exhaustive protocol. The analogous results for HDM2 and TRMD are shown in Figure S3. As is evident in the large majority of cases, despite the radius of 10 Å of the sphere used for initial ligand placement, the docked ligands are within the binding pockets. However, in all the systems variations in the orientations among all the ligands are observed to varying degrees and, with HDM2 and TRMD (Figure S2), a couple of the ligands occupy regions outside the binding pocket. In such cases use of a smaller radius may be applied in the Exhaustive protocol to avoid departure of the ligand from the binding pocket. This was not performed in the present study as we simply applied the two default SILCS-MC approaches as previously presented.⁵⁸

Figure 2:

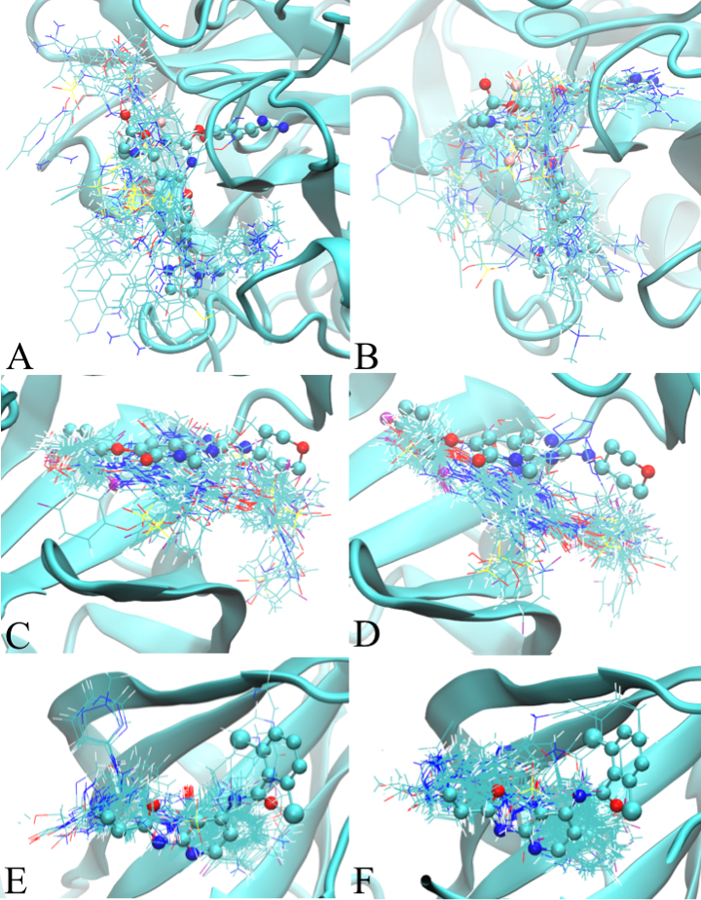
Ligand minimum LGFE conformations from the Exhaustive SILCS-MC protocol for targeted proteins. The left (A, C, and E) and right (B, D, and F) panels shows the ligand conformations obtained from the additive and Drude SILCS-MC docking, respectively. Figures A/B, C/D, and E/F represent Factor Xa, P38, and TYK2, respectively. The crystallographic position of the ligand from the crystal structures are displayed in CPK model to show the location of the binding pocket. 2D images of the ligands are shown in Figure S1 of the supporting information.

The final metric subjected to quantitative analysis was the magnitude of the LGFE scores. The LGFE scores do not directly correspond to the binding energy due to exclusion of energy terms associated with the covalent connectivity of the ligands such as the configurational entropy as well as additional terms. However, the LGFE should approximate the experimental binding affinity as they are based on the contributions of all individual functional group GFE that include contributions from desolvation, loss of rotational and translational degrees of freedom as well as functional group-protein interactions. The averaged differences between the binding affinity and the LGFE values are provided in the last column of the Table 2. For Exhaustive SILCS-MC the Drude and additive average differences are 1.53±0.53 and 1.88±0.62 kcal/mol, respectively, while with the Local sampling the values are 3.20±0.52 and 4.07±1.25 kcal/mol. In addition, the Drude and additive LGFE values obtained from Exhaustive protocol are plotted with respect to the experimental binding energy for all the ligands of all the protein as shown in Figure 3. All the data points related to Drude LGFE are closer to the linear line as compare to additive data sets except a few points. The smaller difference with the Drude model indicates that the free energies of the interactions of the solutes with the protein are more accurately modelled by the polarizable force field over the additive model. Notable, the Drude values are systematically less unfavorable than the additive values with respect to the experimental affinities, indicating that the polarizable force field is leading to overall enhanced binding of the solutes to the protein. Such improvements are associated with the electronic response of the solutes upon going from the aqueous solution to protein bound environments.

Figure 3:

Correlation between the experimental binding data and the predicted LGFE scores for Drude and additive set with Exhaustive protocol.

C. Dipole Moment Distributions

The binding of a particular solute to the protein corresponds with a change in its electrostatic environment from aqueous solution to the variety of environments in and around the protein. Such a change leads to alteration of the electron distribution of the solute, an effect that is accessible to the Drude polarizable force field. In order to quantify the polarization effects occurring upon the interaction of the solutes with the protein, we computed the dipole moment distributions of all the solutes from the SILCS simulations. The dipole moments were computed in the ligand binding pockets for all solutes within 3 Å of the selected residue and in the bulk phase as defined as 6 Å away from the protein surface based on the non-hydrogen atoms. The dipole moments for each solute were computed by orienting the solute to the same axis and center in the bulk and binding pocket for all different proteins, respectively, with the x, y and z vectors aligned on each solute shown in Figure S4. Figure 4 shows the dipole moment distribution for all the solutes in the binding pocket and the bulk phase with the pockets defined by glycine 106 of P38 Kinase, serine 184 of Factor Xa, and lysine 40 of TYK2 from the Drude SILCS simulations. For comparison purposes, Figure S5 shows the dipole moment distributions for all the solutes from the Drude and additive simulations. Moreover, the x, y, and z components of the dipole moment distribution for all solutes from the Drude simulations are presented in Figure S6, S7 and S8, respectively.

Figure 4:

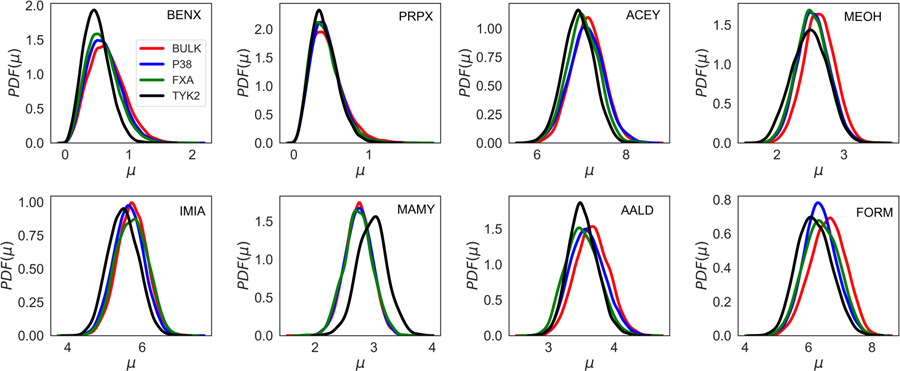
Total Dipole moment distribution obtained from the Drude simulations for all the eight solutes from the P38, Factor Xa, and TYK2 protein simulations. The red color shows the dipole moment for the solute in the bulk phase and the blue, green, and black color represents dipole moment in the ligand binding pocket of P38, Factor Xa, and TYK2 protein, respectively. The BENX, PRPX, ACEY, MEOH, IMIA, MAMY, AALD and FORM represents solutes for benzene, propane, acetate, methanol, imidazole, methylammonium, acetaldehyde, and formamide, respectively.

For most of the solutes, the dipole distributions obtained from the Drude simulations show noticeable differences between the bulk and the binding pocket as shown in Figure 4. For the solutes the extent of variations between the bulk and protein environments differ. Minimal changes occur with propane with a similar effect seen in MAMY for bulk and two of the proteins while a significant difference is present in the binding site of TYK2, where an increase in the dipole moments occur. With the other solutes there is generally a decrease in the dipole moment distributions in the binding sites of the proteins. The difference, which often ranges from 0.1 to 0.5 D, shows the extent by which the aqueous and protein environment perturb the electron distribution of the solutes. These results differ significantly from those with the additive force field, as expected, where no evident differences in the distributions are observed in the different environments and those distributions are more narrow than with the Drude force field (Figure S5).

Table 3 presents the average and standard errors for the dipole moments of all solute in the binding pockets versus in bulk solution for Drude model of P38, Factor Xa and TYK2 protein. Consistent with the distributions, there is a systematic decrease in the dipole moments in the binding sites as compared to bulk. The only exception occurs with MAMY where the differences are negligible or larger in the binding pocket with TYK2. Similar effects have been observed in studies of base flipping from DNA¹⁰⁷ and in proteins^{37, 39} using the Drude force field where increases in bases or amino acid side chains, respectively, upon increased exposure to aqueous solution have been shown to occur. Such overall trends are interesting as they further emphasize the limitation of the approximation associated with the use of fixed charges in additive force fields and how it will tend to underestimate the equilibrium of the solutes in solution versus in the bound state. In addition, given the variability in the percent differences, even between individual solutes in the different proteins, it’s evident that selection of a common scaling factor for the charges to account for the condensed phase environment is not possible.

Table 3:

Comparison of the averaged dipole moment values for all the solutes in the binding pockets versus in bulk solution for Drude model of P38, Factor Xa, and TYK2 protein.

Protein	Solute	Pocket		Bulk		Difference	% Difference
		Average	Std. Error	Average	Std. Error
P38 Kinase	BENX	0.616	0.005	0.656	0.003	−0.041	−6.60
	PRPX	0.431	0.003	0.447	0.002	−0.016	−3.74
	MAMY	2.741	0.005	2.740	0.001	0.001	0.05
	IMIA	5.634	0.029	5.731	0.003	−0.097	−1.72
	MEOH	2.546	0.003	2.630	0.002	−0.083	−3.27
	AALD	3.595	0.010	3.664	0.002	−0.068	−1.90
	ACEY	7.108	0.033	7.137	0.003	−0.029	−0.40
	FORM	6.368	0.014	6.606	0.005	−0.238	−3.74
Factor Xa	BENX	0.582	0.016	0.654	0.003	−0.072	−12.37
	PRPX	0.418	0.012	0.443	0.002	−0.025	−5.98
	MAMY	2.737	0.018	2.739	0.002	−0.002	−0.07
	IMIA	5.715	0.071	5.727	0.004	−0.012	−0.21
	MEOH	2.526	0.008	2.630	0.003	−0.104	−4.12
	AALD	3.515	0.027	3.666	0.002	−0.151	−4.30
	ACEY	7.023	0.030	7.132	0.003	−0.109	−1.55
	FORM	6.402	0.038	6.600	0.006	−0.198	−3.09
TYK2	BENX	0.495	0.009	0.656	0.003	−0.161	−32.55
	PRPX	0.407	0.008	0.449	0.001	−0.042	−10.29
	MAMY	2.970	0.026	2.738	0.002	0.232	7.82
	IMIA	5.488	0.042	5.732	0.003	−0.244	−4.45
	MEOH	2.489	0.032	2.627	0.002	−0.139	−5.57
	AALD	3.523	0.015	3.669	0.003	−0.146	−4.15
	ACEY	6.931	0.012	7.134	0.003	−0.204	−2.94
	FORM	6.180	0.032	6.599	0.004	−0.419	−6.78

More detailed analyses of the impact of interactions with proteins on the dipoles of the solutes are presented in Figures S6, S7 and S8 showing the x, y and z component distributions of the dipole moments. Results are shown for both the additive and Drude simulations. The trends are similar to that with the total dipole moments with respect to the degree of variation of the solute types in the bulk versus protein environments. However, interesting specific variations are observed. With FORM there is a peak in the all three distributions in the binding site of Tyk2 that leads to an overall downshift in the total dipole moment distribution (Figure 4). Large peaks also occur with MAMY in Factor Xa and, to a smaller extent, with P38. These effects are associated with specific interactions between the solutes and the unique environments of the individual binding sites. Together, these results indicate complex electrostatic effects upon moving from the bulk to the binding pockets with shifts in the dipole distributions ranging from decreases through minimal changes to increases depending on the solute and binding pocket, with the effects occurring with both polar and apolar solutes. In addition, in certain cases specific interactions occur that lead to anisotropic perturbations of the dipole moments. These results, along with the wide distributions of the Drude versus additive dipoles indicates the physical forces dictating the equilibrium between the bulk phase and binding sites differ significantly between the additive and Drude models.

D. Vector Maps

Additional analysis of the impact of the inclusion of polarizability and lone pairs focused on the orientation of the solutes in the ligand binding pockets. This was performed by calculating vectors of selected solutes that were within 3 Å of a residue in the binding site. Vectors were based on the ND1 to HD1 bond for IMIA, OG to HG1 bond for MEOH, and C to O bond for AALD, with analysis performed on Factor Xa for IMIA and MEOH, P38 kinase for IMIA and MEOH, and TYK2 for AALD and MEOH. Figure 5 shows the comparison of the Drude and additive vector maps for these solutes.

Figure 5:

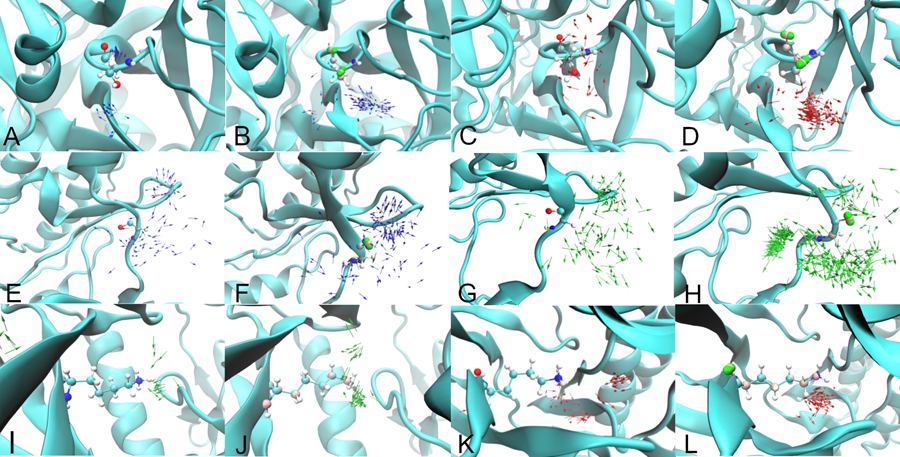
Vector maps for IMIA (Figure A and B) and MEOH (Figure C and D) adjacent to serine 184 of Factor Xa, IMIA (Figure E and F) and AALD (Figure G and H) adjacent to glycine 106 of P38 MAP kinase, AALD (Figure I and J) and MEOH (Figure K and L) adjacent to lysine 40 of TYK2. Panels A, C, E, G, I and K show the vector maps obtained from the additive simulations and Panels B, D, F, H, J, and L show the vector maps from the Drude simulations. With the Drude the visualization of the targeted binding-site residues includes the Drude particles (pink) and the lone pairs (green). The blue, red, and green color arrow represents the IMIA, MEOH, and AALD fragments.

With Factor Xa (Figure 5A and B), the Drude has a large number of IMIA N-H vectors towards the serine 184 hydroxyl oxygen, associated with an N-H…O hydrogen bond, whereas with the additive a smaller number of vectors are in this orientation. This scenario was also observed for IMIA with glycine 106 hydroxyl oxygen of P38 kinase (Figure 5E and F). Similar behaviour occurred for the Drude MEOH solute in Factor Xa (Figure 5C and D) and TYK2 (Figure 5K and L) where the MEOH O-H vector orients towards the hydroxyl in Factor Xa and away from the amino group in TYK2 thereby participating in hydrogen bonds. In both cases the orientation effect is less pronounced with the additive force field. The Drude AALD C=O vectors are dominated by interactions with the backbone amino group of glycine 106 for P38 kinase (Figure 5G and H) whereas no specific orientations are observed with the additive model. For TYK2 (Figure 5I and J) with the Drude, the majority of AALD C=O vectors point towards the amino group of lysine 40 consistent with a C=O…H-N hydrogen bond. In contrast, the additive vectors are not near the amino group, showing a clear distinction between the two force fields. These examples show the impact of lone pairs and electronic polarizability on the location and orientation of the solutes in the ligand binding sites, effects that contribute to the differences in the FragMaps in the ligand binding pockets between the two force fields (Table 1).

Conclusions

The present results indicate a large impact associated with the inclusion of electronic polarization and lone pairs on the nature of the interactions of functional groups with proteins. This points to the importance of the improved treatment electrostatic interactions in force fields in more accurately modelling intermolecular interactions. Such improvements, which we anticipate will be achieved with other polarizable force fields, are related to variations in dipole moments upon moving between bulk and protein bound states that, along with lone pairs (or atomic multipoles in the case of AMOEBA²⁹) lead to more defined orientations of the functional groups in the binding sites and produce increased occupancy of the functional groups in the bound state. Notably, these effects lead to a small, but systematic improvement in the prediction of the affinity of ligands to the protein in the context of the SILCS methodology. This observation is consistent with improvements in calculated binding affinities previously reported in free-energy perturbation studies using both the Drude and AMOEBA polarizable force fields,^108–111 and speaks to the utility of polarizable force fields in more accurately model molecular interactions.