Abstract
Background:
Changes in patient-reported seizure frequencies are the gold standard used to test efficacy of new treatments in randomized controlled trials (RCTs). Recent analyses of patient seizure diary data suggest that the placebo response may be attributable to natural fluctuations in seizure frequency, though the evidence is incomplete. Here we develop a data-driven statistical model and assess the impact of the model on interpretation of placebo response.
Methods:
A synthetic seizure diary generator matching statistical properties seen across multiple epilepsy diary datasets was constructed. The model was used to simulate the placebo arm of 5000 RCTs. A meta-analysis of 23 historical RCTs was compared to the simulations.
Results:
The placebo 50%-responder rate (RR50) was 27.3 ± 3.6% (simulated) and 21.1 ± 10.0% (historical). The placebo median percent change (MPC) was 22.0 ± 6.0% (simulated) and 16.7 ± 10.3% (historical).
Conclusions:
A statistical model of daily seizure count generation which incorporates quantities related to the natural fluctuations of seizure count data produces a placebo response comparable to those seen in historical RCTs. This model may be useful in better understanding the seizure count fluctuations seen in patients in other clinical settings.
Keywords: epidemiology, clinical trials, statistics, seizures, diary
1. Background:
There is a pressing need for RCTs (randomized clinical trials) to identify new effective drugs for people with epilepsy. However, the large (and growing) placebo response found in many RCTs reduces their statistical efficiency[1], necessitating larger numbers of RCT participants to identify an effective candidate drug. Put more simply, large placebo response is a direct contributor to higher costs for RCTs. There is a need for a publicly available seizure diary simulator in order to investigate the placebo response of RCTs; any such seizure diary simulator would need to account for possible contributors to the placebo response in order to investigate the magnitude of their respective contributions.
The placebo response (i.e., the estimated effect size for the placebo arm of an RCT) has been attributed to some combination of regression-to-the-mean, various psychological effects which are collectively referred to as the ‘placebo effect’, and the natural fluctuations of seizure count data[1]. Our group previously found that the patient-reported diaries of seizure counts alone, analyzed as if they came from an RCT, can generate a robust placebo response[2]. As that work was based on seizure diaries in patients whose antiseizure regimens were being actively managed by their physicians, we further validated this effect in three independently collected datasets using both forward and reverse time analysis. That study also identified large placebo responses independent of temporal direction, suggesting natural fluctuations as the cause[3]. These findings suggest that the natural variability of seizure count data (i.e., their natural fluctuations) are potentially a significant contributor to the placebo response seen in RCTs, and any seizure diary simulator which is used to study the placebo response of RCTs should incorporate quantifiable aspects of the natural variability in order to account for its influence.
Three recent findings can help quantify natural variability: firstly, seizure diaries have been observed to have statistical features of negative binomial (NB) distributions[4–6]. Second, the heterogenous distribution of seizure frequencies across a cohort of 12,946 subjects was recently published[7]. Third, the average and the standard deviation in seizure counts for each individual patient were consistently found to have a specific positive log-linear relationship across multiple datasets[8]. The present work combines these three features to create the NV (natural variability) model, a tool for generating realistic synthetic seizure diaries. The objective of this paper is to explore the consequences of a realistic, data-driven seizure-diary simulator on interpreting the placebo response of RCTs.
2. Methods:
2.1. NV Model - daily seizure count generation:
Any simulated patient or simulated patient population generated by the NV model is referred to here as a synthetic patient to distinguish them from actual patients/patient populations. Daily seizure counts for each individual synthetic patient are generated by an NB (negative binomial) distribution via a hierarchical model. There were several possible distributions which could have been used, but NB was chosen due to previous research showing that it fit well to various datasets[4–6] as well as the NB distribution’s compatibility with the properties described in section 2.2. The NB distribution has two parameters: n, whose domain is restricted to be ≥0, and p, whose domain is restricted to the interval (0, 1), with both interval endpoints being exclusive. The NB distribution was implemented via a Gamma-Poisson mixture so that n could be allowed to be any positive number instead of being constrained to just being a positive integer. Setting n as a continuous parameter facilitates switching between different timescales (see Appendix A for details). Additionally, a continuous domain for n enhances the optimization procedure which is introduced in section 2.2.3 and described in detail in Appendix B.
In order to incorporate heterogeneity into the synthetic patient population, we randomly generate n and p for each patient separately. We chose the Gamma distribution as the Bayesian prior distribution for n, and the Beta distribution as the Bayesian prior for p. The prior distributions were chosen in order to accommodate the domain restrictions on their respective parameters. The Gamma distribution is parameterized by shape and scale, while the Beta distribution is parameterized by α and β. Those four group-level parameters all have their domains restricted to be >0 and fully parameterize the model used to generate daily seizure count data for multiple patients. Figure 1A illustrates the essential components of how the NV model uses the group-level parameters to generate daily seizure counts. Appendix A explains how NV model algorithmically generates daily seizure counts for multiple patients in more detail.
Figure 1:
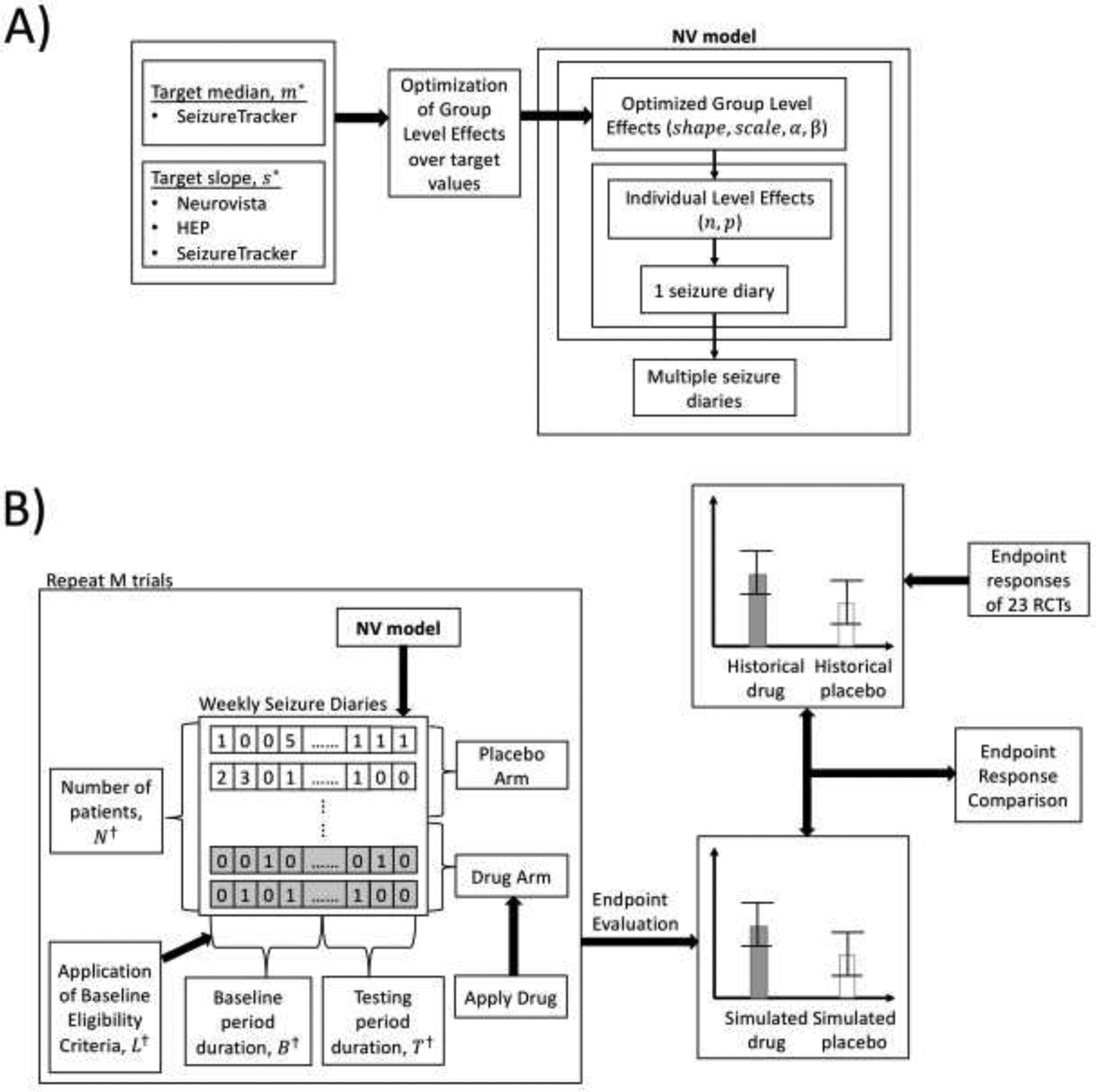
A) Flow diagram of generation of synthetic seizure diaries corresponding to a simulated patient population via utilization of NV model, shown with optimization over group level parameters. None of the 23 RCTs in the endpoint response comparison were used to optimize over the group level parameters. B) Flow diagram of the endpoint response comparison, where two statistical summarizations of the endpoint responses from 5000 simulated RCTs and 23 historical RCTs were compared against each other. †All four of these RCT design parameters (N, B, T, L) were taken from the ezogabine RCT [13].
2.2. Properties expected of the synthetic patient population
In order to have a realistic synthetic patient population, the group level parameters were fitted such that two statistical features matched target values found in actual patient populations. The two features (further described below) reflect the heterogeneity in patient average seizure frequency, and the close relationship between average seizure count and count variability.
2.2.1. The L relationship:
In order to quantify the natural variability of seizure count data, there needs to be a mathematical relationship which predicts a quantity related to variability, such as the standard deviation. The “L relationship” (4), represents the connection between the standard deviation (σ) of two-week seizure count data and the two-week average (μ) seizure count using the following equations [8]:
| (1) |
| (2) |
| (3) |
| (4) |
Our prior work plotted the base-10 log of the average two-week seizure count vs. the base 10 log of the standard deviation of the two-week seizure counts, one point per patient, for multiple patients, and then fitted a line of best fit to those points. This was done for multiple patient populations: The first population consisted of 15 patients from the Neurovista trial with confirmed focal drug-resistant epilepsy who had implanted subdural electrodes [9]. The second population consisted of 263 patients with new-onset epilepsy with diaries screened by the Human Epilepsy Project (HEP)[10]. The third population consisted of 12,946 patients who provided self-reported seizure diaries on Seizuretracker.com[7]. The slope, m, was consistently found to be ≈0.7 while the intercept, b, was found to be ≈0. This finding is consistent with the NB distribution, where any type of count data has slope >0.5. The correlation coefficients for the analyzed patient populations ranged from 0.804 to 0.971, which indicated a highly linear relationship. The fact that multiple datasets fit to a common slope suggested a generalizable finding. Therefore, the log-linear slope of the patient population was fitted to be as close to 0.7 as possible. A visualization of the L relationship can be found in Appendix B.
2.2.2. Median of Monthly Seizure Counts:
The L relationship can predict the amount of natural variability to expect for any patient’s seizure frequency, but it cannot predict what that patient’s seizure frequency should be; another observed property which can be used to predict seizure frequencies is required. SeizureTracker.com is an online and mobile longitudinally collected database of self-reported seizure count data. Our prior analysis of the patient-reported seizures from SeizureTracker.com found the median of summarized average monthly seizure frequencies for the entire patient population (12,946 patients at the time of analysis) to be 2.7[7] with a long tail to the distribution. The monthly median seizure frequency for NV Model was therefore fitted to be as close to a target value of 2.7 as possible.
2.2.3. Optimization over parameters
Due to domain restrictions of the NB distribution parameters, an analytic solution is not possible. Therefore, an optimization was performed to approximate both features as closely as possible. The goal was to optimize the group-level parameters such that the median and the slope which were estimated from a population of 10,000 synthetic patients fit their respective target values (0.7 for the slope, 2.7 for the median) as closely as possible. In order to fulfill this goal, a “discretized gradient descent” algorithm was designed in order to explore the parameter space of the group-level parameters for an optimal solution, with the optimal solution defined as the set of parameters with the lowest possible cost as according to a pre-defined cost function. Typical gradient-descent/optimization methods were not usable due to a lack of explicit formulas for some estimated quantities. Of note, the two target parameters (0.7 slope, and 2.7 median) were derived as above in section 2.2.1 and 2.2.2, and did not come from any historical RCT dataset. Therefore, it can be stated that the optimization was independent of any RCT data.
This optimization algorithm was run 1000 times on the O2 High Performance Compute Cluster, supported by the Research Computing Group, at Harvard Medical School[11] to generate 1000 sets of ‘optimal’ parameters. The set of parameters with the lowest cost was chosen from among those ‘optimal’ parameters as the true optimal set of parameters. The pseudocode in Appendix C describes this optimization algorithm in more detail.
2.2.4. Testing the NV Model
A group of 10,000 NV Model patients with variable length diaries was generated to closely approximate clinical scenarios in which patients provide diaries of different lengths[12]. The diary lengths were randomly generated to reflect between 24 and 120 weeks according to a uniform distribution. The histogram of seizure frequencies and slope of the log-log curve was tested from this group.
2.3. RCT simulations:
RCT simulation software was created in order to compute the drug and placebo responses from NV Model patients. The RCTs were composed of a “placebo” and a “drug” arm with patients randomly chosen in equal numbers for each arm. The duration of baseline and test periods (8 and 12 weeks), the number of patients (306), and the number of minimum required seizures in the baseline period (4) were replicated from a typical RCT with the anti-seizure medication ezogabine[13].
2.3.1. Drug and placebo response
Drug effect in the simulated RCTs was implemented as a probabilistic reduction in the weekly seizure counts for each individual patient[14]. An artificial simulated drug efficacy (i.e. expected difference between drug and placebo response) of 20% was used, similar to what has been seen in multiple meta-analyses of epilepsy drug RCTs[12, 15, 16]. No changes were made to the placebo arm patients during placebo treatment. In this way, the RCT simulated a situation where psychological effects do not impact placebo or drug responses[2, 3, 14]. The pseudocode in Appendix D outlines the details of how the drug efficacy was simulated.
2.4. Comparing RCT simulations to historical RCTs:
Typical trial endpoint responses were computed for each simulated trial: the 50-percent responder rate (RR50) and median percentage change (MPC)[17]. The endpoint responses calculated from 5000 simulated trials were compared to a meta-analysis of the same endpoints extracted from 23 historical RCTs[13, 18–39] in an endpoint response comparison. For each historical RCT the drug arm with the highest RR50 (when multiple doses were tested) and the placebo arm were considered. RCTs which compared different drugs against each other in two separate drug arms were treated as two separate RCT results. Figure 1B shows a flow diagram of how the endpoint response comparison was carried out.
2.5. Implementation and Availability:
The open source code for NV Model and the RCT simulation were implemented in Python (v3.6.5), and are available for download on GitHub[40].
3. Results:
3.1. Patient simulation results:
The optimized shape, scale, α, and β parameters that were found were 24.143, 297.366, 284.366, and 369.628 respectively. Figure 2 shows the distribution of seizure frequencies, and that the median seizure frequency was similar to the target 2.7 seizures/month. Figure 3 shows the log-log plot of average 2-week seizure count to the standard deviation of counts from the same population. It also shows that the best-fit slope was close to the target 0.7. The linear fit had an R2 of 0.66 suggesting a moderately strong linear relationship. Figure 4 shows the weekly seizure diary of one synthetic patient, which resembles a typical patient diary seen in clinical practice. This patient was found by manually searching through less than 1% of all the seizure diaries.
Figure 2:

Histogram of monthly seizure frequencies of 10,000 simulated patients, shown with fitted median and historically derived target median of monthly seizure frequencies. The fitted median is 2.9, while the target median is 2.7. The fitted and target median are close to each other, suggesting that the seizure frequencies of the simulated and actual patient populations are similar.
Figure 3:
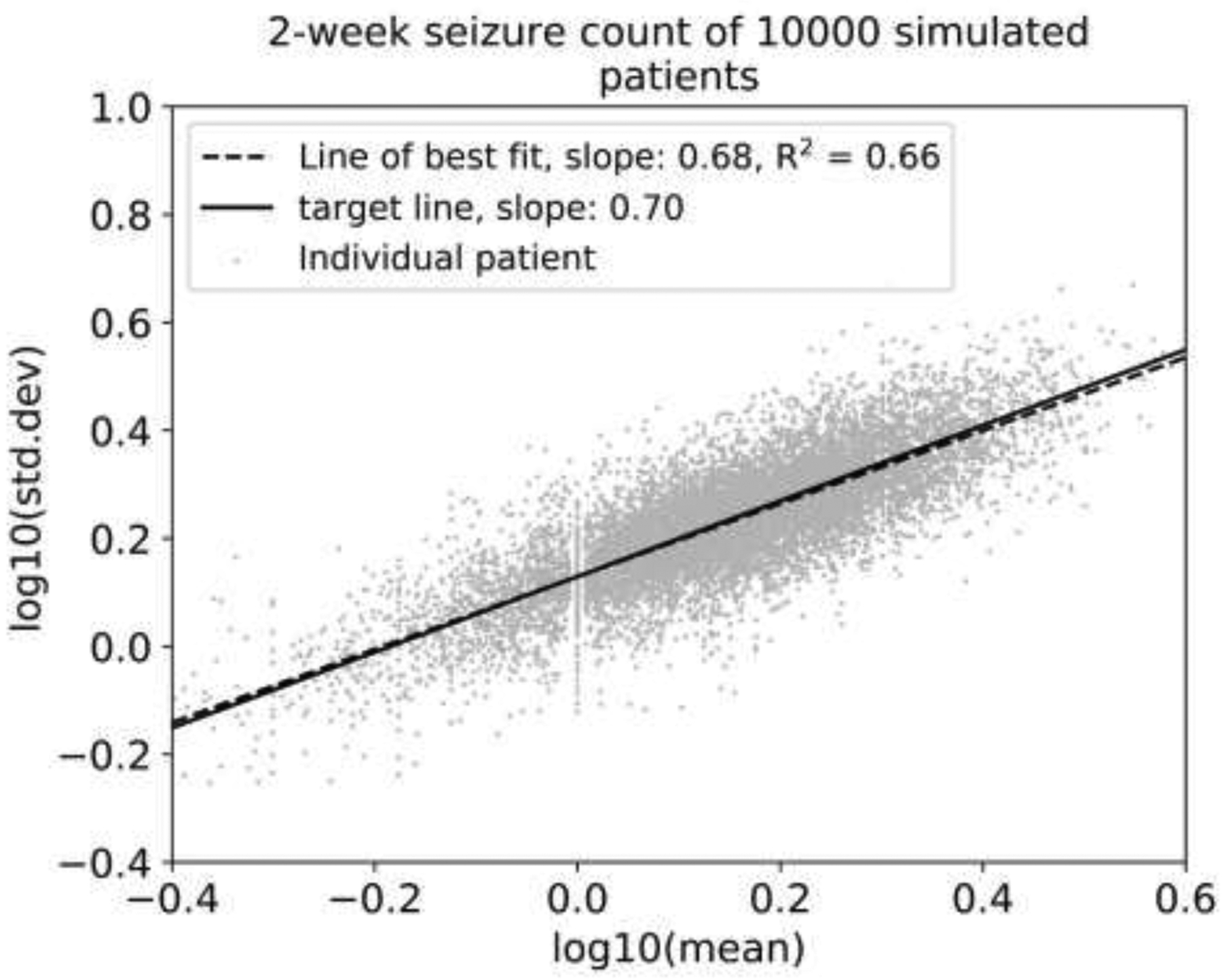
Base-10 logarithm of the standard deviation of seizures count per two-week period vs. base-10 logarithm of the average seizure count of two-week periods, shown with the line of best fit for the simulated patient population. The fitted slope is 0.68 with an R2 value of 0.66, and the target slope, based on historical seizure diaries and intracranial seizure monitoring studies was 0.70. This shows that the simulated diaries have the “L relationship” on this plot that was noted in other datasets [8].
Figure 4:

Weekly seizure diary of a synthetic patient over 119 weeks (~30 months). This simulated diary is similar to those seen by clinicians. It is interesting to note that while some weeks show no seizures, others show more 6 or more seizures. The model did not explicitly include provisions for clusters, yet, they happened anyway due to random chance.
The average baseline monthly median seizure frequency published across the 23 RCTs[13, 18–39] was found to be 8.7, compared to the target value of 2.7 used for developing NV Model.
3.2. RCT simulation results:
Figure 5 shows the comparison beween the simulated RCTs and historical RCTs. The comparison between the simulated and historical RCT endpoints was done by calculating the mean and standard deviation of the endpoints for both the placebo and drug arm over all available trials. Predictions from the simulations matched the historical RCT endpoints. Figure 8 in Appendix E shows the RR50 and MPC for the placebo and drug arms of a single representative simulated trial.
Figure 5:

Horizontal bar chart of RR50 (50% responder rate) and MPC (median percentage change) from 5000 simulated trials with an artificial drug effect of 20% compared to a meta-analysis of 23 historical trials. The bars show the mean of the trials, and the error bars show the standard deviation. This bar chart shows the similarity between the simulated and historical RCTs, suggesting that the model can make reasonable predictions about RCT outcomes.
4. Discussion:
The NV Model and RCT simulations were designed without any psychological “placebo effects”, yet they were able to reproduce typical placebo response values. RCT simulations yielded a reduction in the measured drug effect compared to the true drug effect, which can only be due to natural variability acting as statistical noise in the estimation of treatment efficacy. The difference in typical seizure frequencies between NV Model and the historical RCTs suggests that typical RCT patients may be sicker than the general patient population, such as those seen in clinic[41]. The NV Model predicts that for any patient given a new treatment, there is an approximately 1 in 5 chance that the seizure frequency will be reduced by more than 50% during the first three months due to random fluctuations. If psychological factors can play a role, that percentage could be even higher. This result is relevant when judging the efficacy of any treatment (medication, device, diet, etc.).
Although NV Model did not explicitly generate clusters, they occurred nonetheless. (e.g. Figure 4). It would be common for a patient or a provider to attribute those weeks with high seizure counts to something such as stress, lack of sleep, or other factors[42, 43]. However, any clustering noted in this simulation must be an epiphenomenon and not a reflection of underlying disease states. Further study is required to determine how often such pseudo-clusters are misclassified as true clusters.
The main utility of NV model is its ability to generate data sets for the purposes of testing hypotheses related to natural variability in seizure counts. These include hypotheses about placebo response, trial design, trial analysis, and issues related to seizure clustering. NV model is capable of generating an arbitrarily large amount of realistic seizure diaries, the size of which is limited only by available computational resources. This makes it simpler to conduct studies which need a large amount of seizure diaries without needing to rely on limited data sets.
4.1. Model optimization and target value selection:
The optimal slope was chosen to be 0.7 according to data observed across three patient populations[8]. The seizure diaries coming from these three populations were very different: the SeizureTracker.com population spanned a much longer length of time than the other datasets, and had far more patients[7]. However, the diaries suffer from many biases attributed to self-reported data[2]. The HEP diaries, while physician curated, are fundamentally self-reported data from new onset epilepsy patients[10]. The Neurovista diaries can be considered to be as accurate as possible given that the seizures were confirmed by intracranial EEG data, but the population size is very small, and only seizures at the electrodes could be detected[9]. Despite these differences and biases, the L-relationship was consistently found across all of these datasets[8]. This provides evidence of universality of the target value for the slope across patient populations.
For the median seizure frequency, the target value of 2.7 seizures/month was based on data from SeizureTracker.com[7], one of the largest available databases and is presumed to be representative of the general epilepsy population. A strength of NV Model is that the range of realistic seizure frequencies was derived from this vast, diverse population.
4.2. Comparison to other previous simulations of daily seizure counts:
There have been previous statistical models of daily seizure count data: several models incorporated clusters and memory[4, 6, 44–47], cycles[44], and other features (e.g., linear time trends and dropout)[5, 44, 45, 48–50]. Six of these models were fitted to seizure diaries from less than 100 patients[44, 50–53], 5 models were fitted to seizure diaries from over 100 patients who were eligible for RCT participation[6, 45, 46, 48, 49], and 1 model was based on seizure diaries from 1526 users of SeizureTracker[4].
All prior modeling studies (except one[4]) validated their model on the same data used to produce the model. This practice can lead to “overfitting” and lack of generalizability[54]. Given the numerous causes and subtypes of epilepsy[55], it is important to consider the generalizability of features beyond specific datasets. None of the prior studies address this problem. In contrast, NV model was fit to heterogeneous datasets[7, 9, 10], and was validated on 23 separate historical RCTs. Also, none of the previous models incorporated the L-relationship[8], which persists across diverse datasets. Therefore, the performance metrics of our study may be more generalizable than prior work.
There are two other aspects to NV Model which make it novel and unique compared to previous models. Firstly, the NV Model is more parsimonious than other models, making it simpler to extend, and to derive insights into the inner workings of the model. Secondly, usage of NV Model is facilitated through open-source availability on Github[40].
4.3. Limitations
Seizure clustering is a clinically observed phenomenon in which multiple seizures occur close in time to each other, in the absence of status epilepticus[56]. There is no consistent quantitative definition of seizure clusters[56], nor a clear pathophysiological basis. One hypothesis is that seizures increase the probability of future seizures[56]. Another hypothesis suggests that the results of severe epilepsy at different periods of time are misinterpreted as distinct physiological events[57]. The lack of consensus about cluster definitions and features precludes inclusion of them in the NV Model.
Multidien cycles are a recently re-discovered phenomenon in which seizures occur according to a cyclical pattern over time (the lengths of time involved include days or weeks)[58, 59]. Multidien cycles were not built into this model because they have not yet been fully characterized. It is currently unknown what factors (including stochastic ones) contribute to the existence of one or more cycles, what drives them, and how persistent they are. The lack of cycles in NV Model could prove useful when evaluating candidate multi-cycle models.
A study of longitudinal intracranial EEG data in 8 patients found evidence of long-term “memory” processes in 6 patients[60], meaning that future seizure counts may be informed by previous seizure counts. However, the small size of the examined patient population makes it unclear if this is a widespread trend. Furthermore, a study derived and validated multiple statistical models of daily seizure counts over patients from SeizureTracker.com[4]. The models which included memory showed an insignificant improvement when compared to models without memory. Therefore, the NV Model uses a “memoryless” statistical distribution.
4.4. Future Work
Multiple studies have noted that placebo responses have risen within recent RCTs over the years[61, 62]. NV model currently is unable to explain this effect, additional features are likely required to model this. Also, a difference in placebo responses between different geographic locations has been observed[20], although not in meta-analysis[62]. Future extensions to NV model may incorporate geographic location as well. There is also evidence that the parameters involved in designing RCTs (e.g., inclusion/exclusion criteria, number of baseline weeks, number of treatment weeks, etc.) may influence the placebo response, as shown by meta-analyses[12, 63] and by simulation[14]. The NV Model could assist with estimating the effects of RCT parameters on the placebo and drug responses.
NV model is capable of generating a large placebo response in the general patient population due to natural variability, but there are other hypothesized components of the placebo response discussed in section 1 such as psychological effects and regression-to-the-mean which were not included[1]. Furthermore, typical RCTs tend to include patients with a much higher average seizure rate than the target used for NV model, which would change the statistical properties seen here. Our choice of target rate reflected a very large population-based study, and therefore may be useful for considering a broad based epilepsy population. Therefore, when considering RCT populations, further refinements to NV model will be required. Future research could involve quantifying the contributions of various potential placebo response components (including natural variability) amongst more typical RCT patients.
5. Conclusions
The NV Model is able to replicate the placebo response as seen in a meta-analysis of 23 actual RCTs. Clinicians should be aware that some patients may appear to improve on ineffective treatments in a manner analogous to what the NV Model demonstrates. The model was optimized such that a generated population of synthetic patients statistically resembles multiple real patient populations. It also allows for inferences about the placebo response within the general patient population to be made. NV Model is parsimonious, facilitating extensions but also deeper insights into the system.
We elected to use a very large patient population that was well characterized, therefore our target seizure frequency distribution was lower than typical RCT values. Consequently, the model may not be directly applicable to RCTs. Several phenomena such as seizure clustering, multidien cycles, and memory within the seizure count data are not explicitly built into the NV Model due to unclear quantitative definitions and/or lack of evidence of necessity.
Highlights.
Trial simulations utilize a model of seizure count data to produce simulated placebo
The model is able to replicate placebo response as seen in 23 actual RCTs
The model is parsimonious, facilitating extensions
Acknowledgements
This project was made possible in part by the International Seizure Diary Consortium (https://sites.google.com/site/isdchome/), and the ongoing collaboration between SeizureTracker.com and our lab. This work was supported in part by NINDS grant T32NS048005. We would like to thank Zarina Nip for help with some of the Python coding. Portions of this research were conducted on the O2 High Performance Compute Cluster, supported by the Research Computing Group, at Harvard Medical School. See http://rc.hms.harvard.edu for more information. D. Goldenholz reports grants from NIH and BIDMC.
Appendix A: Daily seizure count statistical model
Appendix A.1: Daily seizure count generation figure
Figure 6:
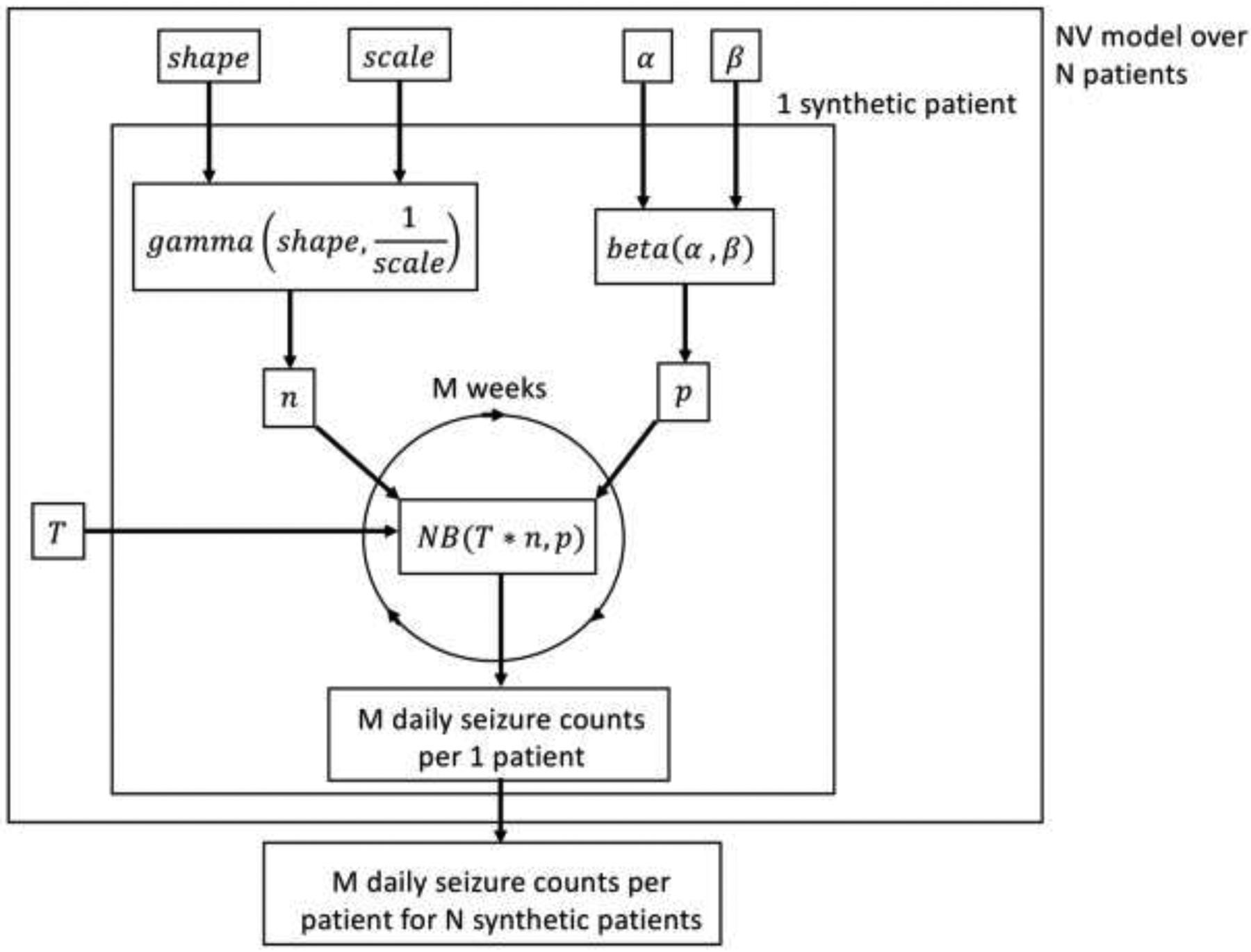
Graphical representation of NV model seizure diary generation via a flow diagram. For every patient, n and p are randomly generated according to the Gamma and Beta distributions, respectively, which are themselves parameterized by the group level parameters. The patient-specific n and p are then used to generate daily seizure counts from a Negative Binomial distribution via an equivalent Gamma-Poisson mixture. The default time scale is daily, but that can be modified by setting the T parameter to be anything other than 1.
Appendix A.2: Daily seizure count generation pseudocode:
Ci,j = seizure count on ith day of jth patient
T = time-scale conversion factor (default value is 1)
For jth patient:
nj ~ Gamma(shape, scale)
pj ~ (α, β)
For ith day:
Appendix A.3: Procedure for converting between timescales
For the NV model, shape, scale, α, and β are optimized to produce realistic daily seizure counts. If, however, weekly or even monthly seizure counts are needed instead, then all that is needed is to change the time-scale conversion factor, T, from 1 to whatever amount of days are in the interval of time that is desired (e.g., T = 7 for weekly counts, T = 14 for bi-weekly counts, T = 28 for monthly counts, etc.).
It is also possible to go from time-scales with larger intervals to time-scales with shorter intervals: if shape, scale, α, and β were instead optimized to produce weekly or even monthly counts, and one wanted to produce daily seizure counts, then all that would be needed is to divide by the necessary factor instead (e.g., for going from weekly counts to daily counts, for bi-weekly counts to daily counts, for monthly counts to daily counts, etc.).
This division would be much more restricted and difficult to accomplish if the domain of nj was discrete instead of continuous, particularly with the optimization procedure done over the group-level parameters.
In general, the continuity of nj allows for simplistic switching between different timescales for the seizure counts: just have the correct time-scale conversion factor in order to change between timescales.
Appendix B: The L relationship
Figure 7:

The base-10 log of the average two-week seizure count vs. the base 10 log of the standard deviation of the two-week seizure counts, with one point per patient, across three datasets (SeizureTracker, HEP, Neurovista)[8]. For each dataset, a line of best fit was plotted with correlation coefficients shown in the legend. Both the correlation coefficients and the plotted points for all three heterogeneous datasets strongly suggest that there is a generalizable relationship between the average seizure count and the standard deviation.
Appendix C: NV Model parameter optimization
Appendix C.1: Optimization algorithm description
There are 4 parameters that are outputted by the optimization algorithm when it is finished: shapec[t], scalec[t], αc[t], and βc[t] (the t index refers to the current iteration of the algorithm). These four parameters are collectively labelled as the central point parameters, and can be summarized in one vector, called the central point vector:
| (C.1) |
There is a 4-dimensional 3×3×3×3 grid which has the central point vector as its central point. In order to define this grid, 4 more quantities and 4 more indices are needed. The i, j, k and l indices refer to which direction a point on the grid is in the shape, scale, α, and β directions, respectively. The Δshape, Δscale, Δα, and Δβ parameters quantify the magnitude the other vectors have to step away from the central point vector in the parameter space for their respective axes.
| (C.2) |
| (C.3) |
| (C.4) |
| (C.5) |
| (C.6) |
One point in the 4-dimensional grid gives rise to a synthetic patient population, which in turn will have a given estimated median seizure frequency and an estimated log-log slope. The log-log slope was estimated via linear regression between the base 10 logarithms of the biweekly seizure count mean and standard deviations. The variance of both the monthly median and the log-log slope can be large enough to confuse the algorithm and cause it to converge on a non-optimal solution, so in order to lower the variance, the average of the median monthly seizure frequency and the log-log slope over multiple, separate, independently generated synthetic patient populations are used instead of individual estimates:
| (c.7) |
| (C.8) |
| (C.9) |
| (C.10) |
The N parameter refers to the number of synthetic patient populations that the median and the log-log slope were estimated over. It was empirically determined that both estimates had reached the lower bound of their variance after N = 30.
The target values for the median and the log-log slope are referred to as m* and s*, respectively. A cost function which uses the square of the differences between the estimates and their target values is used to quantify how far a set of parameters is from the optimal solution:
| (C.11) |
Note that the cost includes a weight scaling term of 100 that corrects for the different scales of the two target values.
The algorithm works by choosing the vector within the grid with the lowest cost to be the new central point for the grid in the next iteration:
| (C.12) |
| (C.13) |
The algorithm continues to find the new central point for each iteration until the cost function reaches below a boundary ϵ, at which point the algorithm returns the current central vector as the optimal set of parameters. If the algorithm reaches a grid where the central point vector is the lowest point in the grid, then it cannot move anymore and has reached a local minimum, at which point the algorithm returns that vector as the optimal set of parameters instead with a warning that a local minimum was reached. The initial central point vector at t = 0 is randomly generated.
Appendix C.2: Optimization algorithm pseudocode:
t = 0
while (C[t | i, j, k, l] > ϵ): for i = [0, 1, 2]: for j = [0, 1, 2]: for k = [0, 1, 2]: for l = [0, 1, 2]:
t := t + 1
return
Appendix D
Appendix D.1: Drug Efficacy Seizure Count Removal pseudocode
Ti,j = ith day of jth patient in testing period
collection of all M days in testing period for jth patient
placeboj = placebo effect as percentage for jth patient
μplacebo = mean placebo effect percentage over all patients
σplacebo = standard deviation of placebo effect percentage over all patients
efficacyj = drug efficacy as percentage for jth patient
μefficacy = mean drug efficacy as percentage over all patients
σefficacy = standard deviation of drug efficacy percentage over all patients
abs(·) = absolute value function
sgn(·) = sign function
For jth patient:
if(patient belongs to placebo arm)
placeboj ~ N(μplacebo, σplacebo)
if(patient belongs to drug arm):
efficacyj ~ N(μefficacy, σefficacy)
apply_effect(effect, ):
For ith day in testing period:
num = 0
For k = 1: Ti,j
prob ~ uniform(0, 1)
if( prob < abs(effect) ):
num = num + sgn(effect)) * 1
Ti,j := Ti,j – num
return
Appendix D.2: Description of efficacyj
In general, the drug efficacy for each jth patient, efficacyj, can be randomly generated for each different patient as according to a normal distribution, and the placebo effect is normally distributed in the same manner. For this paper, μefficacy = 0.2 and σefficacy = 0.05 such that the drug efficacy for each patient in the drug arm was distributed normally with a mean of 20% and a standard deviation of 5%. Also, μplacebo = 0 and σplacebo = 0 such that there were no psychological effects happening in neither the placebo arm nor the drug arm of the simulated trials.
Appendix E
One representative simulated trial:
Figure 8:

(Left) 50%-responder rate (RR50) endpoints from one randomly simulated trial for placebo and drug arm, p-value calculated using Fisher exact test. (Right) Median percentage change (MPC) endpoints from one simulated trial for placebo and drug arm, p-value calculated using Wilcoxon Signed Rank Test. This graph shows the RR50 and MPC from one trial of the RCT simulations which are both within 1 standard deviation of the estimated RR50 and estimated MPC of 5000 simulated trials, i.e. typical of the larger simulated trial set (Figure 5).
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Disclosure of Conflicts of Interest
D. G. is an advisor for Magic Leap. J.R., B.C., P.L. and S.G have no conflicts to report.
Ethical Publication Statement
We confirm that we have read the Journal’s position on issues involved in ethical publication and affirm that this report is consistent with those guidelines.
References
- [1].Goldenholz DM, Goldenholz SR. Response to placebo in clinical epilepsy trials-Old ideas and new insights. Epilepsy Res 2016; 122: 15–25. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [2].Goldenholz DM, Moss R, Scott J, et al. Confusing placebo effect with natural history in epilepsy: A big data approach. Ann Neurol 2015; 78: 329–36. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [3].Goldenholz DM, Strashny A, Cook M, et al. A multi-dataset time-reversal approach to clinical trial placebo response and the relationship to natural variability in epilepsy. Seizure 2017; 53: 31–36. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [4].Tharayil JJ, Chiang S, Moss R, et al. A big data approach to the development of mixedeffects models for seizure count data. Epilepsia; 58 Epub ahead of print 2017. DOI: 10.1111/epi.13727. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5].Hougaard P, Lee ML, Whitmore GA. Analysis of overdispersed count data by mixtures of Poisson variables and Poisson processes. Biometrics 1997; 53: 1225–38. [PubMed] [Google Scholar]
- [6].Trocóniz IF, Plan EL, Miller R, et al. Modelling overdispersion and markovian features in count data. J Pharmacokinet Pharmacodyn 2009; 36: 461–477. [DOI] [PubMed] [Google Scholar]
- [7].Ferastraoaru V, Goldenholz DM, Chiang S, et al. Characteristics of large patient-reported outcomes: Where can one million seizures get us? Epilepsia open 2018; 3: 364–373. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [8].Goldenholz DM, Goldenholz SR, Moss R, et al. Is seizure frequency variance a predictable quantity? Ann Clin Transl Neurol; 5 Epub ahead of print 2018. DOI: 10.1002/acn3.519. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [9].Cook MJ, O’Brien TJ, Berkovic SF, et al. Prediction of seizure likelihood with a long-term, implanted seizure advisory system in patients with drug-resistant epilepsy: A first-in-man study. Lancet Neurol 2013; 12: 563–571. [DOI] [PubMed] [Google Scholar]
- [10].French JA, Kuzniecky R, Lowenstein D. The Human Epilepsy Project, http://www.humanepilepsyproject.org/.
- [11].Harvard Medical School O2 High Performance Compute Cluster web page, https://rc.hms.harvard.edu/ (2019).
- [12].Rheims S, Perucca E, Cucherat M, et al. Factors determining response to antiepileptic drugs in randomized controlled trials. A systematic review and meta-analysis. Epilepsia 2011; 52: 219–233. [DOI] [PubMed] [Google Scholar]
- [13].JA F, BW A-K, RF L, et al. Randomized, double-blind, placebo-controlled trial of ezogabine (retigabine) in partial epilepsy. Neurology 2011; 76: 1555–1563. [DOI] [PubMed] [Google Scholar]
- [14].Goldenholz DM, Tharayil J, Moss R, et al. Monte Carlo simulations of randomized clinical trials in epilepsy. Ann Clin Transl Neurol 2017; 4: 544–552. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [15].Rheims S, Cucherat M, Arzimanoglou A, et al. Greater response to placebo in children than in adults: A systematic review and meta-analysis in drug-resistant partial epilepsy. PLoS Med 2008; 5: 1223–1237. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [16].Beyenburg S, Stavem K, Schmidt D. Placebo-corrected efficacy of modern antiepileptic drugs for refractory epilepsy: Systematic review and meta-analysis. Epilepsia 2010; 51: 7–26. [DOI] [PubMed] [Google Scholar]
- [17].Siddiqui O, Hershkowitz N. Primary Efficacy Endpoint in Clinical Trials of Antiepileptic Drugs: Change or Percentage Change. Ther Innov Regul Sci 2010; 44: 343–350. [Google Scholar]
- [18].Naritoku DK, Warnock CR, Messenheimer JA, et al. Lamotrigine extended-release as adjunctive therapy for partial seizures. Neurology 2007; 69: 1610–1618. [DOI] [PubMed] [Google Scholar]
- [19].Krauss GL, Serratosa JM, Villanueva V, et al. Randomized phase III study 306: adjunctive perampanel for refractory partial-onset seizures. Neurology 2012; 78: 1408–15. [DOI] [PubMed] [Google Scholar]
- [20].French JA, Krauss GL, Biton V, et al. Adjunctive perampanel for refractory partial-onset seizures: randomized phase III study 304. Neurology 2012; 79: 589–96. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [21].French JA, Kugler AR, Robbins JL, et al. Dose-response trial of pregabalin adjunctive therapy in patients with partial seizures. Neurology 2003; 60: 1631–7. [DOI] [PubMed] [Google Scholar]
- [22].Lee BI, Yi S, Hong SB, et al. Pregabalin add-on therapy using a flexible, optimized dose schedule in refractory partial epilepsies: a double-blind, randomized, placebo-controlled, multicenter trial. Epilepsia 2009; 50: 464–74. [DOI] [PubMed] [Google Scholar]
- [23].Ben-Menachem E, Biton V, Jatuzis D, et al. Efficacy and safety of oral lacosamide as adjunctive therapy in adults with partial-onset seizures. Epilepsia 2007; 48: 1308–17. [DOI] [PubMed] [Google Scholar]
- [24].Berkovic SF, Knowlton RC, Leroy RF, et al. Placebo-controlled study of levetiracetam in idiopathic generalized epilepsy. Neurology 2007; 69: 1751–60. [DOI] [PubMed] [Google Scholar]
- [25].Biton V, Berkovic SF, Abou-Khalil B, et al. Brivaracetam as adjunctive treatment for uncontrolled partial epilepsy in adults: a phase III randomized, double-blind, placebo-controlled trial. Epilepsia 2014; 55: 57–66. [DOI] [PubMed] [Google Scholar]
- [26].Klein P, Schiemann J, Sperling MR, et al. A randomized, double-blind, placebo-controlled, multicenter, parallel-group study to evaluate the efficacy and safety of adjunctive brivaracetam in adult patients with uncontrolled partial-onset seizures. Epilepsia 2015; 56: 1890–8. [DOI] [PubMed] [Google Scholar]
- [27].French JA, Krauss GL, Steinhoff BJ, et al. Evaluation of adjunctive perampanel in patients with refractory partial-onset seizures: results of randomized global phase III study 305. Epilepsia 2013; 54: 117–25. [DOI] [PubMed] [Google Scholar]
- [28].Baulac M, Leon T, O’Brien TJ, et al. A comparison of pregabalin, lamotrigine, and placebo as adjunctive therapy in patients with refractory partial-onset seizures. Epilepsy Res 2010; 91: 10–9. [DOI] [PubMed] [Google Scholar]
- [29].Lim KS, Lotay N, White R, et al. Efficacy and safety of retigabine/ezogabine as adjunctive therapy in adult Asian patients with drug-resistant partial-onset seizures: A randomized, placebo-controlled Phase III study. Epilepsy Behav 2016; 61: 224–230. [DOI] [PubMed] [Google Scholar]
- [30].Beydoun a Uthman BM, Kugler a R, et al. Safety and efficacy of two pregabalin regimens for add-on treatment of partial epilepsy. Neurology 2005; 64: 475–80. [DOI] [PubMed] [Google Scholar]
- [31].Elger CE, Brodie MJ, Anhut H, et al. Pregabalin add-on treatment in patients with partial seizures: a novel evaluation of flexible-dose and fixed-dose treatment in a double-blind, placebo-controlled study. Epilepsia 2005; 46: 1926–36. [DOI] [PubMed] [Google Scholar]
- [32].V. B, J.C. S, A. V, et al. Double-blind, placebo-controlled study of lamotrigine in primary generalized tonic-clonic seizures. Neurology 2005; 65: 1737–1743. [DOI] [PubMed] [Google Scholar]
- [33].Arroyo S, Anhut H, Kugler AR, et al. [3]Pregabalin Add-on Treatment: A Randomized, Double-blind, Placebo-controlled, Dose-Response Study in Adults with Partial Seizures. Epilepsia 2004; 45: 20–27. [DOI] [PubMed] [Google Scholar]
- [34].Biton V, Di Memmo J, Shukla R, et al. Adjunctive lamotrigine XR for primary generalized tonic-clonic seizures in a randomized, placebo-controlled study. Epilepsy Behav 2010; 19: 352–358. [DOI] [PubMed] [Google Scholar]
- [35].Brodie MJ; Lerche H; Gil-Nagel A; Elger C; Hall S; Shin P; Nohria V; Mansbach H Efficacy and safety of adjunctive zonisamide therapy for refractory partial seizures. Epilepsy Res 2010; 75: 75–83. [DOI] [PubMed] [Google Scholar]
- [36].Porter RJ, Partiot A, Sachdeo R, et al. Randomized, multicenter, dose-ranging trial of retigabine for partial-onset seizures. Neurology 2007; 68: 1197–1204. [DOI] [PubMed] [Google Scholar]
- [37].Chung S, Sperling MR, Biton V, et al. Lacosamide as adjunctive therapy for partial-onset seizures: a randomized controlled trial. Epilepsia 2010; 51: 958–67. [DOI] [PubMed] [Google Scholar]
- [38].Ryvlin P, Werhahn KJ, Blaszczyk B, et al. Adjunctive brivaracetam in adults with uncontrolled focal epilepsy: results from a double-blind, randomized, placebo-controlled trial. Epilepsia 2014; 55: 47–56. [DOI] [PubMed] [Google Scholar]
- [39].Halász P, Kälviäinen R, Mazurkiewicz-Beldzińska M, et al. Adjunctive lacosamide for partial-onset seizures: Efficacy and safety results from a randomized controlled trial. Epilepsia 2009; 50: 443–53. [DOI] [PubMed] [Google Scholar]
- [40].Romero J, Nip Z. Seizure Diary Simulator Github Page, https://github.com/GoldenholzLab/patientSimulator (2018).
- [41].Tlusta E Clinical relevance of patients with epilepsy included in clinical trials. Epilepsia 2008; 49: 1479–80. [DOI] [PubMed] [Google Scholar]
- [42].Haut SR, Shinnar S, Moshé SL. Seizure clustering: Risks and outcomes. Epilepsia 2005; 46: 146–149. [DOI] [PubMed] [Google Scholar]
- [43].Mackay M, Mahlaba H, Gavillet E, et al. Seizure self-prediction: Myth or missed opportunity? Seizure 2017; 51: 180–185. [DOI] [PubMed] [Google Scholar]
- [44].Balish M, Albert PS, Theodore WH. Seizure Frequency in Intractable Partial Epilepsy: A Statistical Analysis. Epilepsia 1991; 32: 642–649. [DOI] [PubMed] [Google Scholar]
- [45].Ahn JE, Plan EL, Karlsson MO, et al. Modeling Longitudinal Daily Seizure Frequency Data From Pregabalin Add-On Treatment. J Clin Pharmacol 2012; 52: 880–892. [DOI] [PubMed] [Google Scholar]
- [46].Delattre M, Savic RM, Miller R, et al. Analysis of exposure-response of CI-945 in patients with epilepsy: Application of novel mixed hidden Markov modeling methodology. J Pharmacokinet Pharmacodyn 2012; 39: 263–271. [DOI] [PubMed] [Google Scholar]
- [47].Albert PS. A Two-State Markov Mixture Model for a Time Series of Epileptic Seizure Counts. Biometrics 1991; 47: 1371. [PubMed] [Google Scholar]
- [48].Nielsen JC, Hutmacher MM, Wesche DL, et al. Population dose-response analysis of daily seizure count following vigabatrin therapy in adult and pediatric patients with refractory complex partial seizures. J Clin Pharmacol 2015; 55: 81–92. [DOI] [PubMed] [Google Scholar]
- [49].Deng C, Plan EL, Karlsson MO. Approaches for modeling within subject variability in pharmacometric count data analysis: dynamic inter-occasion variability and stochastic differential equations. J Pharmacokinet Pharmacodyn 2016; 43: 305–314. [DOI] [PubMed] [Google Scholar]
- [50].Alosh M The impact of missing data in a generalized integer-valued autoregression model for count data. J Biopharm Stat 2009; 19: 1039–1054. [DOI] [PubMed] [Google Scholar]
- [51].Albert PS, Follmann DA. Modeling repeated count data subject to informative dropout. Biometrics 2000; 56: 667–677. [DOI] [PubMed] [Google Scholar]
- [52].Thall PF, Vail SC. Some Covariance Models for Longitudinal Count Data with Overdispersion. Biometrics 1990; 46: 657. [PubMed] [Google Scholar]
- [53].Molenberghs G, Verbeke G, Demétrio CGB. An extended random-effects approach to modeling repeated, overdispersed count data. Lifetime Data Anal 2007; 13: 513–531. [DOI] [PubMed] [Google Scholar]
- [54].Ng A Machine Learning Yearning: Technical Strategy for AI Engineers, In the Era of Deep Learning. Kindle Direct Publishing, 2019. [Google Scholar]
- [55].Wyllie E, Gidal BE, Goodkin HP, et al. Wyllie’s treatment of epilepsy : principles and practice.
- [56].Haut SR. Seizure clusters: Characteristics and treatment. Curr Opin Neurol 2015; 28: 143–150. [DOI] [PubMed] [Google Scholar]
- [57].Jafarpour S, Hirsch LJ, Gaínza-lein M, et al. Seizure cluster : Definition, prevalence, consequences, and management. Seizure Eur J Epilepsy. DOI: 10.1016/j.seizure.2018.05.013. [DOI] [PubMed] [Google Scholar]
- [58].Karoly PJ, Goldenholz DM, Freestone DR, et al. Circadian and circaseptan rhythms in human epilepsy: a retrospective cohort study. Lancet Neurol 2018; 4422: 1–9. [DOI] [PubMed] [Google Scholar]
- [59].Baud MO, Kleen JK, Mirro EA, et al. Multi-day rhythms modulate seizure risk in epilepsy. Nat Commun 2018; 9: 1–10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [60].Cook MJ, Varsavsky A, Himes D, et al. The dynamics of the epileptic brain reveal long memory processes. Front Neurol 2014; 5: 1–8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [61].Ryvlin P, Cucherat M, Rheims S. Risk of sudden unexpected death in epilepsy in patients given adjunctive antiepileptic treatment for refractory seizures: A meta-analysis of placebo-controlled randomised trials. Lancet Neurol 2011; 10: 961–968. [DOI] [PubMed] [Google Scholar]
- [62].Zaccara G, Giovannelli F, Cincotta M, et al. Adverse events of placebo-treated, drugresistant, focal epileptic patients in randomized controlled trials: a systematic review. J Neurol 2015; 262: 501–515. [DOI] [PubMed] [Google Scholar]
- [63].Zaccara G, Giovannelli F, Schmidt D. Placebo and nocebo responses in drug trials of epilepsy. Epilepsy Behav 2015; 43: 128–134. [DOI] [PubMed] [Google Scholar]


