The sensitivity and specificity analyses of ambient temperature and population size on the transmission rate of the novel coronavirus (COVID-19) in different provinces of Iran

Abstract

On 10 April 2020, Iran reported 68,192 COVID-19 cumulative cases including 4232 death and 35,465 recovery cases. Numerous factors could influence the transmission rate and survival of coronavirus. On this basis and according to the latest epidemiological researches, both ambient temperature (AT) and population size (PS) can be considered as significant transmissibility factors for coronavirus. The analysis of receiver operating characteristics (ROC) allows measuring the performance of a classification model using the confusion matrix. This study intends to investigate the sensitivity of AT and PS on the transmission rate of the novel coronavirus in different provinces of Iran. For this purpose, the information of each province of Iran including the annual average of AT and the number of healthy and diseased cases are categorized. Subsequently, the sensitivity and specificity analyses of both AT and PS factors are performed. The obtained results confirm that AT and PS have low sensibility and high sensitivity, respectively. Thus, there is no scientific reason to confirm that the number of COVID-19 cases in warmer climates is less than that of moderate or cold climates. Therefore, it is recommended that the cities/provinces with a population of over 1.7 million people have stricter inspections and more precise controls as their management policy.

Graphical abstract

1. Introduction

The coronavirus disease 2019 (COVID-19) first manifested itself in Wuhan city, Hubei province, China (Wang et al., 2020). Afterward, as an epidemic illness, the coronavirus disease spread swiftly to other provinces of China (Abdi, 2020). Finally, COVID-19 crossed the boundaries of China and spread to all regions of the world (Faridi et al., 2020). The data of the World Health Organization (WHO) show that from 22 January 2020 to 10 April 2020, almost 1.7 million coronavirus cases have been identified with over 100,000 cases of deaths and 377,000 cases of recovery all over the world (https://www.worldometers.info/coronavirus). This robust transmission rate of the coronavirus disease has led to the substitution of the epithet ‘epidemic’ with ‘pandemic’ in the description of this disease (Layne et al., 2020; Yang et al., 2020).

The coronavirus disease has had a high transmission rate in Iran compared with its neighboring countries including Bahrain, Iraq, Kuwait, Oman, Afghanistan, and Pakistan (Zhuang et al., 2020). From 15 February 2020 to 10 April 2020, Iran has acknowledged 68,192 COVID-19 cumulative cases encompassing 4232 death and 35,465 recovery cases. Although the cumulative statistics of the patients in Iran have been reported up to 10 April 2020, the number of the patients in the provinces is available only until 22 March 2020 (https://www.behdasht.gov.ir).

Many different factors could influence the transmission rate and survival of coronavirus. Based on the latest epidemiological researches and laboratory studies (Dalziel et al., 2018; Guo et al., 2020; Ma et al., 2020; Tan et al., 2005; Tosepu et al., 2020; Yuan et al., 2006; Zhu and Xie, 2020), the ambient temperature (AT) and population size (PS) can be considered as the crucial transmissibility factors. For instance, the AT and PS parameters could increase or decrease the transmissibility risk and survival period of coronavirus in the air and on surfaces. Hence, the sensitivity analyses of AT and PS parameters on the transmission rate of the novel coronavirus is immensely crucial for improving the safety and survival of mankind. The analysis of the receiver operating characteristics (ROC) allows measuring the performance of a classification model using the confusion matrix. This research intends to examine the sensibility of AT and the sensitivity of PS on the transmission rate of the novel coronavirus in different provinces of Iran. To this end, the information of each province of Iran including the annual average of AT and the number of healthy and diseased cases are collected. Subsequently, the sensitivity and specificity analyses of both AT and PS parameters are performed.

The present work is organized as follows. The materials and data (including data collection and the study area) are described in Section 2. The analysis details of the ROC curve are presented in Section 3. Afterwards, the effectiveness and efficiency of the AT and PS parameters on thirty-one numerically simulated provinces of Iran are evaluated. Moreover, the results of sensitivity and specificity analyses are demonstrated in Section 4. Finally, the concluding remarks of this work are summarized in Section 5.

2. Materials and data

2.1. Data collection

The numbers of daily confirmed cases were collected from the official websites of Iran including those of the Ministry of Health and Medical Education (MHME) (https://www.behdasht.gov.ir), Iran Meteorological Organization (IMO) (http://www.irimo.ir/far/index.php), and the Statistical Center of Iran (SCI) (https://www.amar.org.ir).

It is worth mentioning that the number of patients in each province of Iran has only been reported until 22 March 2020, although the cumulative statistics of patients in Iran is updated on a daily basis. Hereupon, in this research, the statistical data of Iran have been collected and classified in each province from 15 February 2020 to 22 March 2020.

2.2. Study area

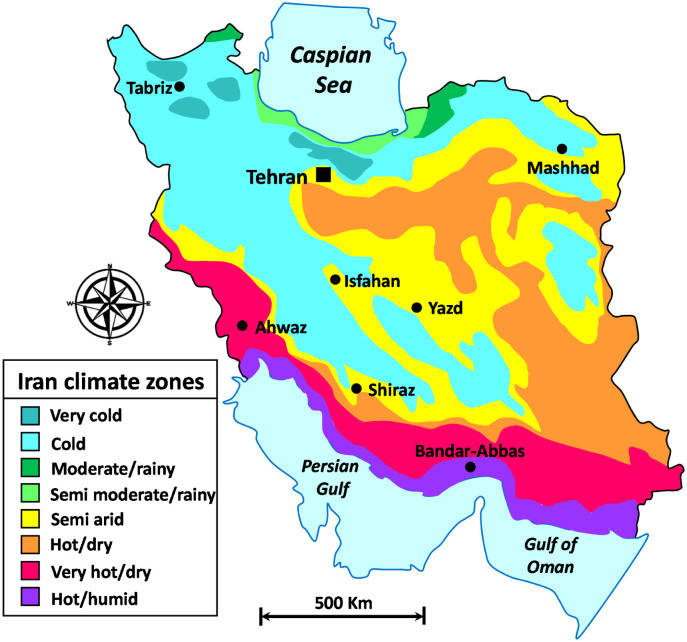
The Islamic Republic of Iran is a country in western Asia with approximately 80 million inhabitants and a territory of 1,648,195 km². Although Iran has only 31 provinces, it has a wide diversity of climate and population. The contour map of the climate zones of Iran have been illustrated in Fig. 1 (Roozitalab et al., 2018).

Fig. 1.

The contour map of the climate zones in Iran.

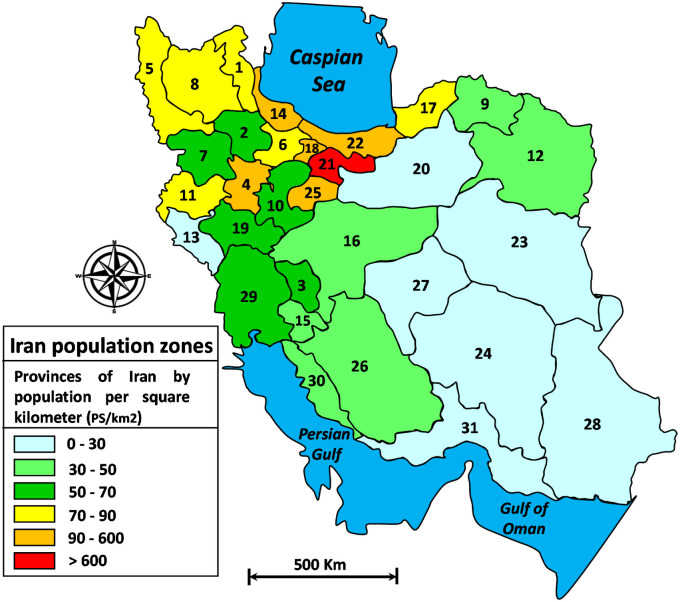
Similarly, the classification of the population zones of Iran have been depicted in Fig. 2 (https://fanack.com/iran/population).

Fig. 2.

The classification of the population zones in Iran (Note: The numbering of Iran provinces is based on the Table 1).

The statistical data of each province of Iran including mean annual AT, PS, the number of coronavirus cases (NCC), and the rate of coronavirus cases (RCC) from 15 February 2020 to 22 March 2020 have been tabulated in Table 1 . From 15 February 2020 to 22 March 2020, Iran has reported 21,638 COVID-19 cases including 1685 death and 7783 recovery cases (https://www.behdasht.gov.ir). As shown in Fig. 1, Fig. 2 and Table 1, the maximum values of PS, AT, and NCC belong to Tehran, Hormozgan, and Tehran provinces, respectively. Moreover, the minimum values of PS, AT, and NCC belong to Ilam, Ardabil, and Bushehr provinces, respectively.

Table 1.

The statistical data of each province of Iran from 15 February 2020 to 22 March 2020.

No.	Province	AT (°C)	PS (person)	NCC (person)	RCC (%)
1	Ardabil	9	1,270,420	287	0.023
2	Zanjan	10	1,057,461	397	0.038
3	Charmahal va Bakhtiari	11	947,763	70	0.007
4	Hamedan	11	1,758,268	240	0.014
5	West Azarbaijan	12	3,265,219	397	0.012
6	Qazvin	12	1,273,761	670	0.053
7	Sanandaj	12	1,603,011	240	0.015
8	East Azarbaijan	12	3,909,652	810	0.021
9	North Khorasan	13	863,092	170	0.020
10	Markazi	13	1,429,475	880	0.062
11	Kermanshah	14	1,952,434	180	0.009
12	Central Khorasan	14	6,434,501	880	0.014
13	Ilam	14	580,158	180	0.031
14	Guilan	15	2,530,696	1187	0.047
15	Kohgilouyeh va Bouirahmad	15	713,052	70	0.010
16	Esfahan	16	5,120,850	1976	0.039
17	Golestan	17	1,868,619	400	0.021
18	Alborz	17	2,712,400	1196	0.044
19	Lorestan	17	1,760,649	480	0.027
20	Semnan	17	702,360	630	0.090
21	Tehran	17	13,267,637	5100	0.038
22	Mazandaran	17	3,283,582	1700	0.052
23	South Khorasan	18	768,898	178	0.023
24	Kerman	18	3,164,718	170	0.005
25	Qom	18	1,292,283	1176	0.091
26	Fars	18	4,851,274	500	0.010
27	Yazd	18	1,138,533	719	0.063
28	Sistan va Balouchestan	20	2,775,014	127	0.005
29	Khuzestan	25	4,710,509	450	0.010
30	Bushehr	25	1,163,400	60	0.005
31	Hormozgan	27	1,776,415	118	0.007

3. The analysis of receiver operating characteristics (ROC)

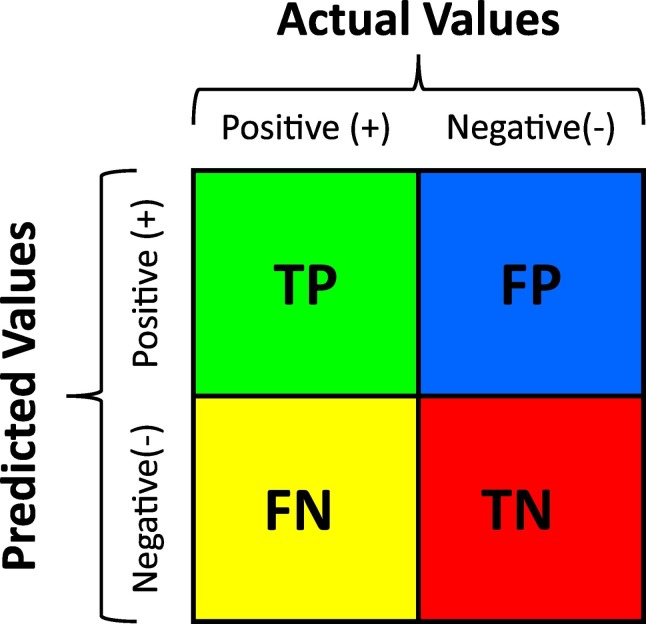
In statistics, as a probability curve, ROC demonstrates the true positive rate (TPR) or sensitivity versus the false positive rate (FPR) or specificity. In other words, the ROC curve is a performance measurement for classification problems at various threshold settings (Fawcett, 2006). As a classification model with 4 different combinations of predicted and actual values, the confusion matrix has been depicted in Fig. 3 (Powers, 2011).

Fig. 3.

The bivariate classification with 4 different combinations of predicted and actual values.

Herein TP, FP, FN, and TN represent true positive, false positive, false negative, and true negative, respectively. The explanation of these indices is as follows:

• • TP: The model predicted that a person is sick and it is true.
• • FP: The model predicted that a person is sick and it is false.
• • FN: The model predicted that a person is healthy and it is false.
• • TN: The model predicted that a person is healthy and it is true.

The predicted (as positive or negative) and actual (as true or false) values have been categorized. Sensitivity is defined as the ratio of true positives to all positives. In the same way, specificity is defined as the ratio of true negatives to all negatives. Based on the predicted and actual values, the mathematical relationships of sensitivity and specificity have been formulated in Eq. (1) and Eq. (2), respectively (Gönen, 2007).

$$\text{Sensitivity}=\frac{\mathrm{TP}}{\mathrm{TP}+\mathrm{FN}}$$ (1)

$$\text{Specificity}=\frac{\mathrm{TN}}{\mathrm{TN}+\mathrm{FP}}$$ (2)

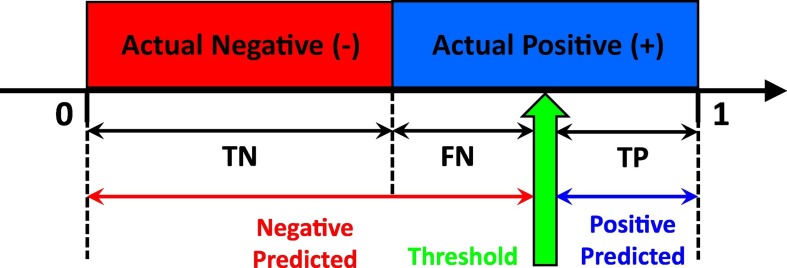
In order to calculate the ROC curve, the threshold must be moved step by step from 0 to 1 (see Fig. 4 ). The values higher and lower than the threshold value are classified as predicted positive and negative values, respectively. The sensitivity (TPR) and specificity (FPR) values have been computed at each threshold, becoming one point on the ROC curve. The set of the computed points forms the ROC curve for each sensitivity and specificity analysis (Gönen, 2007).

Fig. 4.

The conceptual illustration of the threshold movement in each step.

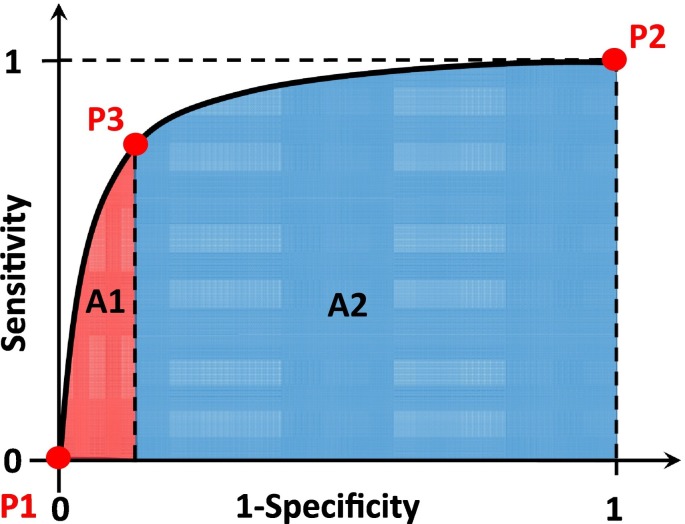
As shown in Fig. 5 , each ROC curve has two main regions (A1 and A2) and three critical points (P1 through P3). In general, A1 and A2 are the high and low sensitive regions, respectively. The summation of A1 and A2 regions is called the ‘area under the curve’ (AUC = A1 + A2). The AUC of an ideal model is near 1 which means that it can measure separability in the best way possible. Conversely, the AUC of an imperfect model is near 0 which implies that it can measure separability in the worst way possible. At P1, the threshold is more than one and only FN and TN are activated. Reciprocally, at P2, the threshold is less than zero and only TP and FP are activated. In the ROC curve, P3 which is called the optimum or cut-off point has the minimum distance from the point (0, 1). This point is considered as the boundary of high (A1) and low (A2) sensitive regions (Gönen, 2007).

Fig. 5.

The ROC curve.

4. The sensitivity and specificity analyses

The sensitivity and specificity analyses of the AT and PS variations in all the provinces of Iran have been performed in this section. In the ROC curves, the sensitivity axis is based on the true positive rate and the specificity axis is based on the true negative rate. In other words, the horizontal axis signifies the design variable and the vertical axis implies the sensitivity of the same variable.

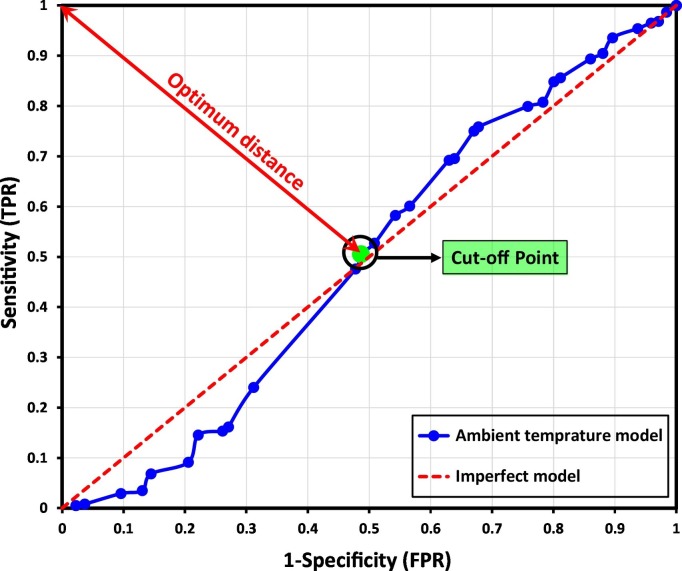
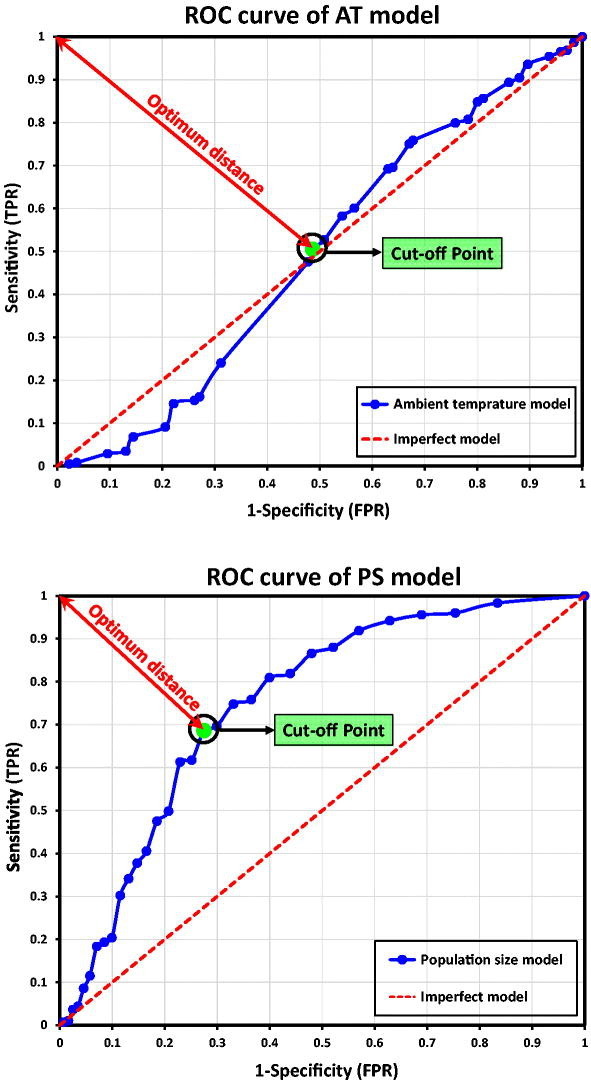
Fig. 6 demonstrates the ROC curve of the transmission rate of coronavirus based on the AT variations in different provinces of Iran. The AUC of the AT model is approximately 0.5. It can be observed that the AT model has no capacity to distinguish between positive and negative classes. Moreover, it can be seen that the behavior of the AT model is similar to that of an imperfect model which indicates that the AT model does not have a high performance. As marked in Fig. 6, the accurate coordinates of the cut-off or optimum point are P3 (0.486, 0.505). The cut-off point confirms that the spread level of coronavirus in provinces with a temperature of less than 17 °C is slightly more than that of the other provinces. It can be concluded that the transmission rate of coronavirus does not have a high sensibility versus the AT parameter in different provinces of Iran since the AT parameter has a linear relationship with the number of people afflicted with COVID-19. Therefore, there is no scientific reason to assume that the number of people afflicted with COVID-19 in warmer climates is less than that of moderate or cold climates.

Fig. 6.

The sensitivity analysis of the transmission rate of coronavirus based on the variations of AT in different provinces of Iran.

In both Fig. 6, Fig. 7 , the red dash lines are weak models and the AUCs of these models are exactly 0.5. These models predict the patient people as healthy ones and vice versa. The higher the AUC, the better the model is able to distinguish between the patient people and the healthy ones.

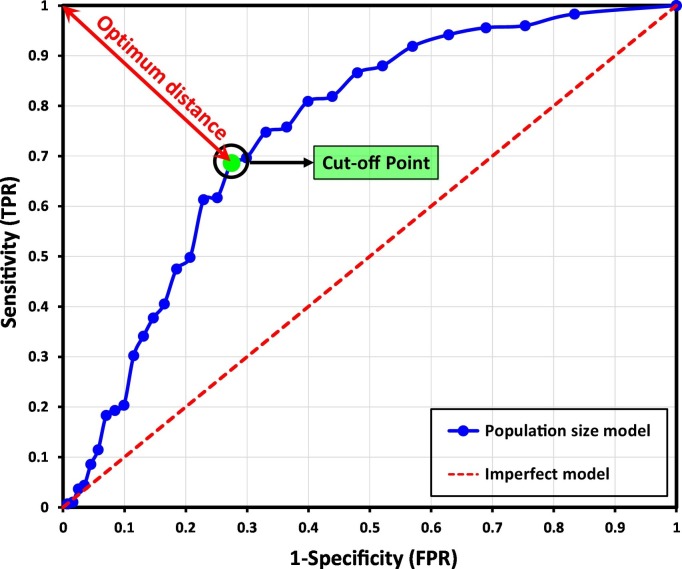
Fig. 7.

The sensitivity analysis of the transmission rate of coronavirus based on the variations of PS in different provinces of Iran.

Fig. 7 shows the ROC curve of the transmission rate of coronavirus based on the variations of PS in different provinces of Iran. The AUC of the PS model is approximately 0.8. It can be understood that the PS model has a relative capacity to distinguish between the positive and negative classes. In contrast to the AT model, the PS model has a nonlinear behavior which indicates that it has a higher sensitivity than the AT model. Therefore, it can be deduced that the transmission rate of coronavirus has a high sensitivity to the PS parameter in different provinces of Iran since it has a nonlinear relationship with the number of people afflicted with COVID-19. As marked in Fig. 7, the precise coordinates of the cut-off or optimum point are P3 (0.274, 0.686). The cut-off point confirms that the transmission rate of coronavirus in provinces with a population of over 1.7 million people is more than that of the other provinces. According to the findings of the current paper, it is recommended that the cities/provinces with a population of over 1.7 million people have stricter inspections and more precise controls as their management policy.

5. Conclusions

In this research, the sensibility of the AT parameter and the sensitivity of the PS parameter on the transmission rate of the novel coronavirus were investigated in different provinces of Iran. To evaluate the effectiveness of both the AT and PS parameters, their ROC curves were analyzed.

The obtained results indicated that the AT parameter had a linear relationship with the number of people afflicted with COVID-19 in different provinces of Iran and that the transmission rate of coronavirus did not have a high sensibility to it. Thus, there is no scientific reason to assume that the number of people afflicted with COVID-19 in warmer climates is less than that of moderate or cold climates. Reciprocally, the PS parameter had a nonlinear relationship with the number of people afflicted with COVID-19 in different provinces of Iran and the transmission rate of coronavirus had a high sensitivity to it. Based on the findings of the current research, it is suggested that the cities/provinces with a population of more than 1.7 million people have stricter inspections and more precise controls as their management policy.

Declaration of competing interest

The authors declared that they have no conflict of interests.

CRediT authorship contribution statement

Mehdi Jahangiri: Visualization, Investigation. Milad Jahangiri: Conceptualization, Methodology, Software, Validation. Mohammadamir Najafgholipour: Writing - review & editing.

Editor: Jianmin Chen