A spatio-temporal analysis for exploring the effect of temperature on COVID-19 early evolution in Spain

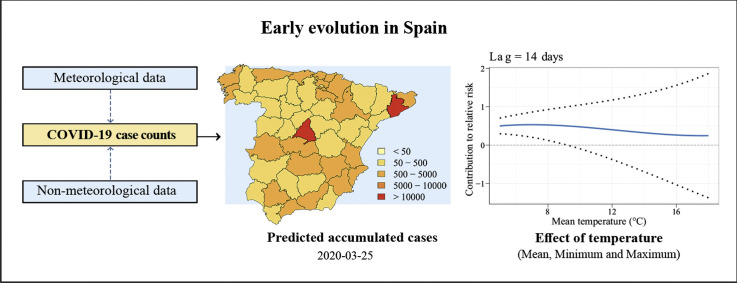
Abstract

The new SARS-CoV-2 coronavirus, which causes the COVID-19 disease, was reported in Wuhan, China, in December 2019. This new pathogen has spread rapidly around more than 200 countries, in which Spain has one of the world's highest mortality rates so far. Previous studies have supported an epidemiological hypothesis that weather conditions may affect the survival and spread of droplet-mediated viral diseases. However, some contradictory studies have also been reported in the same research line. In addition, many of these studies have been performed considering only meteorological factors, which can limit the reliability of the results. Herein, we report a spatio-temporal analysis for exploring the effect of daily temperature (mean, minimum and maximum) on the accumulated number of COVID-19 cases in the provinces of Spain. Non-meteorological factors such as population density, population by age, number of travellers and number of companies have also been considered for the analysis. No evidence suggesting a reduction in COVID-19 cases at warmer mean, minimum and maximum temperatures has been found. Nevertheless, these results need to be interpreted cautiously given the existing uncertainty about COVID-19 data, and should not be extrapolated to temperature ranges other than those analysed here for the early evolution period.

Graphical abstract

1. Introduction

History has demonstrated that pathogens may cause devastating consequences in our health and economy. Thus, the rapid spread of the new SARS-CoV-2 pathogen, causing the Coronavirus disease 2019 (COVID-19) is a clear current example. In this regard, the Director-General of the World Health Organization (WHO) has recently declared COVID-19 a global pandemic on 11 March 2020 starting in Wuhan, Hubei Province, China in December 2019 (WHO, 2020c). According to the WHO, the current COVID-19 outbreak situation has confirmed 1,812,734 cases and 113,675 deaths involving 213 countries (WHO, 2020a) where Spain is one of the leading countries of this global health crisis with 172,541 confirmed cases and 18,056 confirmed deaths (ISCIII, 2020) (data reported on April 14th 2020) in a population of about 47 million people. Nonetheless, experts are warning that there could be many more cases that have not been detected and/or informed, especially in undeveloped countries. This strain continues to spread globally, overwhelming intensive care units and health system capacity. The present outbreak of this coronavirus-associated acute respiratory disease is the third documented spillover of an animal coronavirus to humans in only two decades and has been identified as a zoonotic coronavirus, similar to SARS coronavirus and MERS (Liu et al., 2020). Thus, SARS-CoV-2 is closely related (88–89% similarity) to two bat-derived severe acute respiratory syndrome-like coronaviruses, bat-SL-CoVZC45 and bat-SL-CoVZXC21 (Lai et al., 2020). However, it is more distant from SARS-CoV (~79% similarity) and Middle East respiratory syndrome coronavirus (MERS-CoV) (~50% similarity) (Jiang et al., 2020; Lu et al., 2020; Ren et al., 2020). The SARS-CoV-2 coronavirus is stable from several hours to days in aerosols and on surfaces, according to a new study from the National Institute of Allergy and Infectious Diseases, Centers for Disease Control and Prevention, UCLA and Princeton University scientists (van Doremalen et al., 2020). These scientists have found that SARS-CoV-2 was detectable in aerosols for up to 3 h, up to 4 h on copper, up to 24 h on cardboard and up to two to three days on plastic and stainless steel. These results provide key information about the stability of this strain and suggest that people may acquire the virus through the air and after touching contaminated objects. Thus, this pathogen is easily spread by human-to-human transmission via droplets or direct contact, and this type of infection has shown a basic reproduction number of about 2.24–3.58 (Lai et al., 2020; Remuzzi and Remuzzi, 2020). It is often spread via coughing, sneezing, touching or even breathing, and those who do not exhibit symptoms can also spread the illness (American Lung Association, 2020). In fact, this coronavirus has been reported to spread faster than its two ancestors SARS-CoV and MERS-CoV (Vellingiri et al., 2020), probably due to the high transmission rate produced by asymptomatic carriers (Bai et al., 2020; Singhal, 2020). Standard recommendations to prevent infection spread include regular hand washing and covering mouth and nose when coughing and sneezing. It has also been recommended to avoid close contact with anyone showing symptoms of respiratory illness such as coughing and sneezing and keep a distance of 1–2 m from them (WHO, 2020b).

The lockdown for the SARS-CoV-2 epidemic in Italy and Spain after one month follow up has shown positive results in flattening the epidemic curve (Tobías, 2020). However, even though these unprecedented containment and mitigation policies implemented to limit the spread of COVID-19 in most countries, including travel restrictions, screening and testing of travellers, isolation and quarantine, and school and university closures, the new SARS-CoV-2 coronavirus continues to spread. Indeed, a recent study has demonstrated that under certain combinations of an individual patient's physiology and environmental conditions, such as humidity and temperature, the gas cloud and its payload of pathogen-bearing droplets of all sizes can travel 7–8 m (Bourouiba, 2020). Viruses can be transmitted by being influenced by several factors, including climatic conditions (temperature and humidity), and population density (Dalziel et al., 2018). In this regard, previous studies have suggested a correlation between weather and COVID-19 pandemic in a similar way that it occurs with other viral infectious diseases such as influenza (Ficetola and Rubolini, 2020; Liu et al., 2020; Ma et al., 2020; Oliveiros et al., 2020; Tosepu et al., 2020). However, other studies have reported contradictory results showing that meteorological conditions may not be associated with COVID-19 in terms of absolute humidity (Shi et al., 2020) or temperature (Jamil et al., 2020; Xie and Zhu, 2020). According to these last authors, the previous results showing evidence for a correlation between meteorological factors with COVID-19 transmission was likely to be an artifact, reflecting the pathways of spread. In fact, several of these previous studies have been performed considering only meteorological factors, without accounting for non-meteorological variables that might be more decisive.

Spatio-temporal spread of COVID-19 has been recently reported for China (Huang et al., 2020; Kang et al., 2020) and Italy (Giuliani et al., 2020). In the present paper, we focus on the case of Spain. Spain is located in a temperate zone of the world. However, it is the most climatically diverse country in Europe and it is classified within the 10 most climatically diverse countries in the world (Ministerio de Medio Ambiente y Medio Rural y Marino. AEMET, 2011). Spain is currently a country with the third-highest life expectancy of the world (WHO, 2020b), which explains somehow the high impact which is causing COVID-19 in this country, especially in old people for whom this disease represents a major threat (Morley and Vellas, 2020). In addition, according to the World Tourism Organization, Spain was the country in the world with the second highest international tourist arrivals in 2019 (UNWTO, 2019). The climate in Spain varies across the entire country with five main climatic zones: the hot-summer Mediterranean climate, which is dominant on the Iberian Peninsula; the warm-summer Mediterranean climate in parts of north-western Spain and mostly inland the central-northern Spain; the oceanic climate in the northern part of Spain; the semiarid climate in the south-eastern part of the country; the warm-summer continental climate in many areas of the north-eastern zones located over 1000 m above sea level (Kottek et al., 2006).

In this study, a spatio-temporal analysis of the early evolution of COVID-19 across the provinces of Spain is carried out. The main goal is to explore the existence of a relationship between temperature at the province level and the evolution of the accumulated number of COVID-19 cases for approximately the first month of the epidemic in Spain.

2. Data

2.1. Study area

The provinces of Spain located in the Iberian Peninsula have been considered for the analysis. The Balearic and Canary islands were discarded for the analysis in order to focus entirely on a more homogeneous area. For the same reason, the cities of Ceuta and Melilla, which are located in the north of Africa, were also not included in the analysis.

2.2. COVID-19 data

COVID-19 data corresponding to the provinces of Spain was downloaded from a repository publicly available and accessible through this link: https://code.montera34.com:4443/numeroteca/covid19. This repository is being maintained by multiple volunteers that are extracting and homogenising COVID-19 data from multiple web sources belonging to both official and private media.

February 25th 2020 has been chosen as the starting date for this early evolution study because it was when the first COVID-19 cases were identified in Spain. The study period spans from this date to March 28th 2020, which corresponds to two weeks after Spain's lockdown started. Hence, for each province belonging to the study area, a time series of length 33 (days) with the number of daily accumulated COVID-19 cases is formed.

2.3. Temperature data

Temperature data has been obtained from 172 automatic weather stations installed across the study area. The data was downloaded from the OpenData platform of the State Meteorological Agency (AEMET) via the API provided by this institution. Concretely, the daily mean, minimum and maximum temperatures (in °C) measured by each of these weather stations from the beginning of February to the end of March have been collected for the analysis.

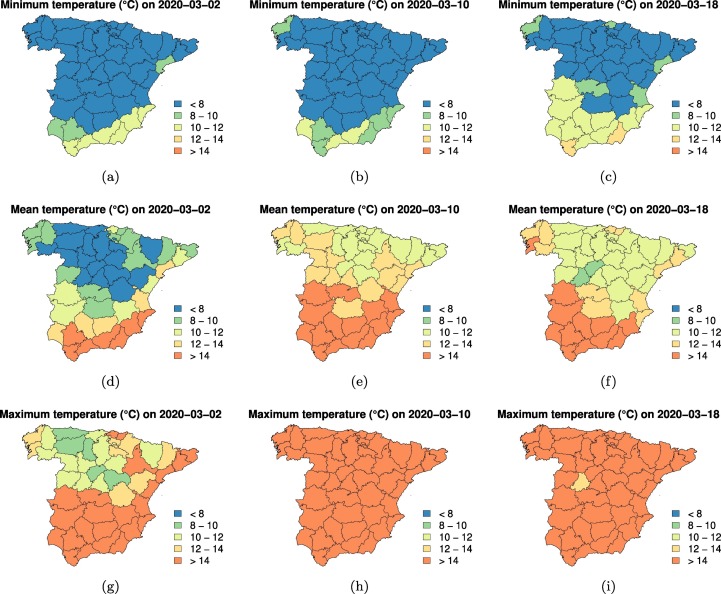
Temperature data at the province level has been estimated in two stages. First, ordinary kriging (Cressie, 1988) was used to estimate temperature values over a spatial grid of points covering the whole area under investigation. Points within the grid were separated by 5 km, resulting in a total of nearly 20,000 points. Secondly, province-level daily estimations for the variables of interest have been obtained as the average of the estimations corresponding to points of the grid lying within the province. Table 1 displays a summary of the three temperature-related variables that have been investigated at the province level. Fig. 1 shows the province-level estimations corresponding to mean, minimum and maximum temperatures for three days within the period under investigation.

Table 1.

Statistical summary of the meteorological covariates used for the analysis.

Variable	Min.	1st Qu.	Median	Mean	3rd Qu.	Max.
Minimum temperature (°C)	−3.19	3.13	5.57	5.39	7.69	13.51
Mean temperature (°C)	0.62	8.70	10.81	10.83	12.88	20.02
Maximum temperature (°C)	3.14	13.66	16.03	16.29	18.59	29.26

Fig. 1.

Minimum (a–c), mean (d–f) and maximum (g–i) temperatures estimated at the province level for three days within the period under investigation.

Since this coronavirus has shown a mean incubation period of approximately 5 days (ranging from 2 to 14 days) (Nishiura et al., 2020; Rasmussen et al., 2020), the effect of these temperature-related variables has been considered with a time delay of 2 to 14 days. Hence, these temperature-related variables are referred to as temporally-lagged variables in subsequent sections.

2.4. Non-meteorological data

In addition to the effect of temperature on the accumulated number of COVID-19 cases, other covariates unrelated to meteorological conditions available at the provincial level were also included in the analysis. Population data by age group corresponding to the start of the year 2020 has been obtained from the Spanish Statistical Office (INE) at the province level. The total population has been used to obtain the population density (in hab/km²) for each province. The population by age group has been utilised to estimate the expected number of COVID-19 cases in each province on March 28th 2020, according to the age distribution of all the cases that had been recorded in Spain by this date. Following the official reports that are being published by the Ministry of Health from Spain, the number of expected cases for province i (on March 28th 2020), which is denoted by E _i, was estimated as follows (Carella, 2020):

$$E_i=\sum _j{f}_j{P}_{\mathit{ij}}$$ (1)

where P _ij is the population of province i corresponding to age group j, and f _j is the incidence of cases in the age group j for the whole population of the country. As COVID-19 affects the elderly population more severely, the probability of testing and hence detecting COVID-19 among people from certain age groups is higher. Hence, accounting for the age structure of each province is convenient for data modelling purposes.

Finally, the number of travellers that have stayed in each province during February 2020 and the number of companies by province were also obtained from the INE. The number of travellers was estimated by the INE through survey procedures. In this analysis, a traveller is consider someone that came from other province or country to spend at least one night in the corresponding province during the month of reference. Thus, a higher number of travellers arriving at some provinces in February 2020 could have increased the risk of the spread of COVID-19 in subsequent weeks. Similarly, the fact that a province has a higher number of active companies can induce intranational mobility during working days.

3. Methodology

3.1. Software

The R programming language (R Core Team, 2020) has been used to carry out the statistical analyses involved in the present investigation. In particular, the R packages automap (Hiemstra et al., 2008), ggplot2 (Wickham, 2016), gstat (Pebesma, 2004; Gräler et al., 2016), INLA (Rue et al., 2009; Lindgren and Rue, 2015), rgdal (Bivand et al., 2019), spdep (Bivand et al., 2008) were required for the analysis.

3.2. Statistical modelling approach

The number of accumulated COVID-19 cases at the province level has been investigated through spatio-temporal modelling techniques. Specifically, the accumulated number of COVID-19 cases detected in each province, i, on a day, t, from February 25th 2020 to March 28th 2020 has been assumed to follow a Poisson distribution with mean E _i μ _it, where E _i represents the expected number of cases (on March 28th 2020, following Eq. (1)), and μ _it the relative risk for province i on day t. Several fixed and random effects are considered to model the natural logarithm of the relative risk, which finally yields to the following modelling structure used for the analysis:

$$\begin{array}{l}{O}_{\mathit{it}}\sim \mathrm{Po}\left(E_i{\mu }_{\mathit{it}}\right)\\ log\left({\mu }_{\mathit{it}}\right)=\alpha +\sum _k{\beta }_k{X}_i^k+\sum _{j}p\left(X_{\mathit{it}-\mathit{Lag}}^j,3\right)+s_i+u_i+{\delta }_t+{\epsilon }_t\end{array}$$ (2)

where O _it represents the accumulated number of cases recorded for province i (i=1,...,47) on day t (t=1,...,33), E _i is the expected number of cases for province i (log(E _i) is the offset term of the linear predictor), α is the global intercept of the model, β _k the fixed effect that covariate X _i ^k defined at the province level has on μ _it, p( ⋅ ,3) represents a third-degree polynomial that allows establishing a non-linear relationship between temporally-lagged covariates, X _it−Lag ^j, and μ _it, s _i is a spatially-structured effect for province i, u _i is a spatially-unstructured effect for province i, δ _t is a temporally-structured effect for day t and ε _t is a temporally-unstructured effect for day t.

The statistical model described in Eq. (2) has been fitted using the Integrated Nested Laplace Approximation (INLA) (Rue et al., 2009; Lindgren and Rue, 2015) (which approximates Bayesian inference for latent Gaussian models). This model has enabled us to consider several fixed and random effects of a different nature. Non-meteorological province-level covariates can be included as fixed effects, each of whom is represented by a β _k parameter. The temperature-related covariates are temporally-lagged for their inclusion in the model. This specification allows establishing a direct relationship between relative risks on the day t, μ _it's, and the values of temperature that were measured some days before (Lag days before), which correspond to the moment at which some of the COVID-19 cases detected on the day t were actually infected by the virus. Following the existing literature on the incubation time of COVID-19, the parameter Lag was varied from Lag=2 to Lag=14 days. The use of a third-degree polynomial allows the model to capture non-linear relationships between the covariate and the number of accumulated COVID-19 cases.

The rest of the parameters appearing in Eq. (2) (s _i, u _i, δ _t, ε _t) represent pure spatial and temporal random effects. The inclusion of these effects is rather convenient to account for unobserved spatial heterogeneity (unavailable or non-measurable variables at the province level) or temporal trends. The spatially-structured effect, s _i, follows the Besag's spatial model (Besag et al., 1991). This effect accounts for the spatial dependence between the provinces of Spain, which is measured through a binary neighbourhood matrix that represents the contiguity relationships between provinces (two provinces are defined as neighbours if they share a common geographical border). The temporally-structured effect δ _t is defined through a second-order random walk. Finally, the spatially-unstructured (u _i) and the temporally-unstructured effect (ε _t) were defined as two different independent and identically distributed Gaussian random effects to account for specific province-level and daily-level variability that may be skipped by the two structured effects, s _i and δ _t.

4. Results

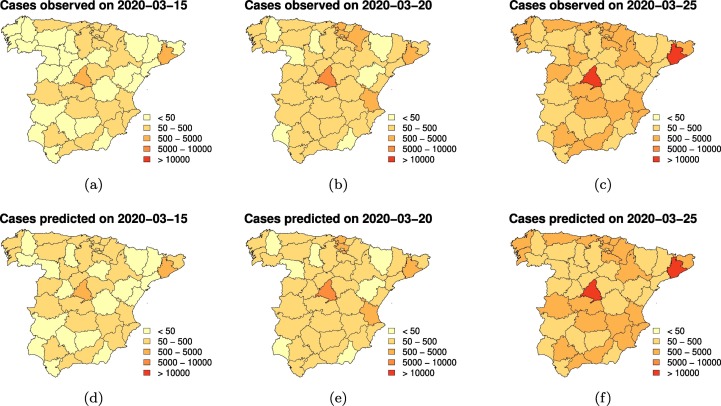
The model described by Eq. (2) allows for the inclusion of several non-meteorological (population density, number of visitors and number of companies) and lagged meteorological covariates (mean, minimum and maximum temperature) considered for this study. Furthermore, the age structure of each province is accounted through the offset term, E _i. However, some of these covariates are highly correlated to each other, for which reason it is convenient to use them separately, or to make a selection of them, to avoid multicollinearity issues. Population density, the number of visitors and the number of companies all show a Pearson's correlation above 0.85 at the province level (Table 2 ). Fitting three independent models with each of these covariates alone yielded very similar results. Therefore, population density was chosen for being the most common and accessible variable of the three. Similarly, the three temperature-related covariates are also highly correlated, which led us to define three different models each of whom only included one of them. The rest of the random effects indicated in Eq. (2) were considered for the three models. Fig. 2 shows the accumulated number of COVID-19 cases observed for three days within the period under study, and the accumulated number of cases predicted by the model that considers mean temperature and Lag=14 days. The model correctly captures the evolution of the epidemic across the provinces of Spain.

Table 2.

Correlation matrix for the non-meteorological covariates considered for the analysis at the province-level.

	Companies	Population density	Visitors
Companies	1.00	0.89	0.97
Population density	0.89	1.00	0.86
Visitors	0.97	0.86	1.00

Fig. 2.

Accumulated number of COVID-19 cases observed (a–c) and accumulated number of cases predicted by the model described by Eq. (2) considering mean temperature and Lag=14 days (d–f), for three days within the period under investigation.

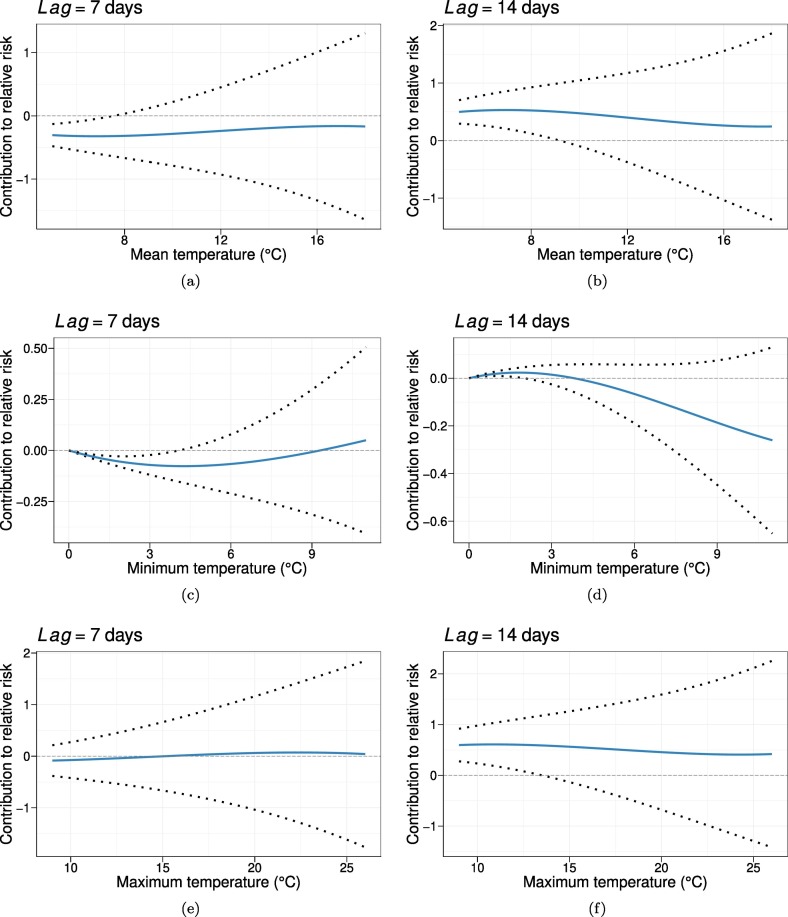
Fig. 3 shows the third-degree polynomials that were estimated by each of the three models, considering Lag=7 and Lag=14 days. The results for other Lag values are very similar, so only these two are displayed. The range of temperatures displayed in each of the six plots provided in Fig. 3 covers the 95% of the mean, minimum or maximum temperatures available in the dataset. The solid curves in each of them correspond to the polynomial that can be built according to the coefficients of the first-, second- and third-degree terms that are estimated by the model in each case. The dotted lines correspond to the polynomials that are defined by the 2.5 and 97.5 percentiles of the posterior distributions of these three coefficients. No trend is observed neither with increasing mean, minimum nor maximum temperature. Specifically, the fact that the dotted lines do not lie consistently within the upper (or lower) half-plane indicates that there is no clear evidence of a contribution to relative risks by any range of the temperature-related variables.

Fig. 3.

The solid line represents the third-degree polynomial that is defined by the three estimated coefficients (corresponding to first-, second- and third-order terms) that are found following the statistical model described by Eq. (2), considering mean (a–b), minimum (c–d) and maximum temperatures (e–f). Dotted lines represent the two polynomials that are defined by the 2.5 and 97.5 percentiles of the posterior distributions associated to each of the coefficients of the polynomial.

5. Discussion and conclusions

The analysis of how certain meteorological conditions may have affected the initial spread of COVID-19 at the country, city or regional level has become an important line of research in recent weeks. In many of these studies, non-meteorological factors have not been included in the analysis. We highlight the need for considering non-meteorological factors, such as population density, to get more reliable results. In addition, we have also accounted for the age structure of each region under study, which seems very convenient because of the existing age-group differences in detection rates.

In this study, no consistent evidence has been found regarding the existence of a relationship between the accumulated number of COVID-19 cases in the provinces of Spain and temperature values at the province level. This conclusion is in good agreement with a previous study on the association between mean temperature and COVID-19 spread performed in 122 cities of China (Xie and Zhu, 2020). Although the authors of this study found that mean temperature was positively associated with newly confirmed cases when temperature was below 3°, this association was not observed for temperatures above 3°, which is close to the range of mean temperature measured in Spain for the period that we have investigated: 95% of the daily mean temperature values observed ranged from 5° to 18°. In this regard, it is important to note that the period under study is months ahead from the summer season, where temperatures will be considerably higher. Future studies may lead to different findings, but no extrapolation to warmer periods should be done from current investigations.

In conclusion, further research would be needed to better elucidate the role of several meteorological variables on the expansion of the COVID-19 epidemic, for several reasons. Currently available data on the epidemic is subject to a large degree of uncertainty. The number of confirmed cases is globally underestimated, and comparisons across countries, cities or regions are difficult to be determined due to differences in data collection procedures or health policies, among others. Under these circumstances, every statistical analysis of COVID-19 data needs to be interpreted with caution (Royal Statistical Society, 2020). It is also important to remark that measuring the effect of weather-related covariates on the virus transmission is highly complex. Indeed, weather usually affects several aspects of human daily life such as commuting choices or leisure activities, among many others. Therefore, the interaction between weather conditions and human behaviour can be a confounder of the true relationship between environmental conditions and virus propagation.

CRediT authorship contribution statement

Álvaro Briz-Redón: Conceptualization, Methodology, Formal analysis, Software, Investigation, Writing - original draft, Writing - review & editing. Ángel Serrano-Aroca: Conceptualization, Methodology, Investigation, Writing - original draft, Writing - review & editing.

Declaration of competing interest

The authors declare no conflict of interest.