A new approach to modeling the fade-out threshold of coronavirus disease

On 21 December of 2019, four lower respiratory tract samples were collected from patients with pneumonia of unknown cause in Wuhan, China [1]. This disease was later diagnosed as a coronavirus disease. The World Health Organization (WHO) named the coronavirus disease as COVID-19 on 11 February and declared a pandemic on 11 March 2020. The COVID-19 is a previously unknown disease with no tools available for pharmaceutical management at the early stage of its outbreak. On 23 January 2020, Wuhan was locked down and all provinces and regions across China imposed antiviral prophylaxis, quarantines, school closures, travel restrictions, and social distancing by implementing the “first-level response to major public health emergencies” during the period 23–25 January 2020. The case confirmation speed during this period improved due to development of new coronavirus nucleic acid-based detection technologies [2].

The goal of modeling the fade-out threshold is to gain insight into how to calculate the mean die-out time of the epidemic, which improves our understanding of the dynamics of the spread of the epidemic. When the infectious disease spreads in a population, a model may help to provide real-time forecasting [3], [4]. Epidemic modeling is one of the essential tools for both developing strategies in preparation for the outbreak and evaluating the effectiveness of control policies during the outbreak. Furthermore, the model can also assist in decision-making by making projections regarding intervention-induced changes in the spread of disease.

Regarding the infectious disease dynamics, the basic reproduction number $R_0$ is a critical indicator. Ross [5] first proposed the concept of $R_0$ and defined it as the average number of new infections caused by a single infected individual when introduced into a wholly susceptible population over the duration of the infection of this individual. This concept has been widely used and improved since then. The $R_0$ provides an indication of whether the introduction of the disease will result in a localized burnout or signal the beginning of an epidemic that could move through all geographic scales [6]. A timely estimation on $R_0$ of the COVID-19 epidemic may prove beneficial in understanding how to control the worldwide spread of the epidemic [7].

In the formula of $R_0$, the transmission rate β is not directly observable and can be difficult to measure due to its dependence on the probability of transmission between individuals and social contact rates [8]. The transmission rate of an infectious disease is defined as the per capita rate of infection given contact, which can be expressed as the product of the number of daily contacts that a susceptible individual has with other individuals and the probability of transmission during each contact [9]. In other words, a more highly infectious disease has a higher transmission rate. However, we need to know the transmission rate if we want to predict the changes of an epidemic disease. Determining the time-dependent transmission function that exactly reproduces disease incidence data can yield useful information about disease outbreaks, including a range of potential values for the recovery rate of the disease. If the time-dependent transmission function is constructed, information regarding intervention and stopping the outbreak can be obtained.

The time-dependent transmission rate (TDTR) is used to account for intervention effects, such as raising awareness in the population about the current severity of the epidemic, implementing measures of quarantine and isolation of patients, and providing access to effective and affordable medicines. We constructed an algorithm to compute the TDTR from the well-known Susceptible-Infected-Recovered (SIR) model based on the reported data. The SIR model was first proposed in 1927 [10] in order to incorporate the possibility of switching transmission rates when the prevention strategy was changed and has been widely modified and applied since 1927 (e.g., [9], [11]).

Based on the improved SIR model [9], we developed a new TDTR as follows:

$$\beta \left(t\right)=\frac{\frac{\mathrm{d}I\left(t\right)}{\mathrm{d}\mathit{t}}-\frac{\mathrm{d}S\left(t\right)}{\mathrm{d}\mathit{t}}+\left(\mu \left(t\right)+\gamma \left(t\right)\right)·I\left(t\right)-\mu \left(t\right)·S\left(t\right)+\mu \left(t\right)}{2·I\left(t\right)·S\left(t\right)}\text{,}$$ (1)

where $S\left(t\right)$ represents susceptible fractions of the population at time $t$; $I\left(t\right)$ represents the infected fractions of the population; $\beta \left(t\right)$ denotes the TDTR; $\gamma \left(t\right)$ is the recovery rate; and $\mu \left(t\right)$ refers to the fatality rate.

The basic reproduction number [11] can be formulated as

$$R_0\left(t\right)=\frac{\beta \left(t\right)}{\gamma \left(t\right)+\mu \left(t\right)}\text{,}$$ (2)

where $R_0\left(t\right)$ is the $R_0$ at time $t$.

Plugging these elements into our newly developed TDTR, we can derive a new formula of $R_0$ as follows:

$$R_0\left(t\right)=\frac{\frac{\text{d}I\left(t\right)}{\text{d}\mathit{t}}-\frac{\text{d}S\left(t\right)}{\text{d}\mathit{t}}+\left(\mu \left(t\right)+\gamma \left(t\right)\right)·I\left(t\right)-\mu \left(t\right)·S\left(t\right)+\mu \left(t\right)}{2·\left(\mu \left(t\right)+\gamma \left(t\right)\right)·I\left(t\right)·S\left(t\right)}\text{.}$$ (3)

It has been universally accepted that if $R_0$ is < 1, the introduction of an infected individual would not result in an outbreak, but only a localized infection. Therefore, even though the new infections cannot be completely prevented, measurements of $R_0$ < 1 indicate that an epidemic can still be under control [12], meaning that treating each individual in order to control the disease outbreak is not necessary. However, when $R_0$ > 1, then an epidemic will occur and the infection will spread in the population no matter how small the initial number of infected individuals is. When $R_0$ > 2, a major outbreak is possible [13]. If $R_0$ > 3, the emergence of a pandemic is generally considered to be inevitable.

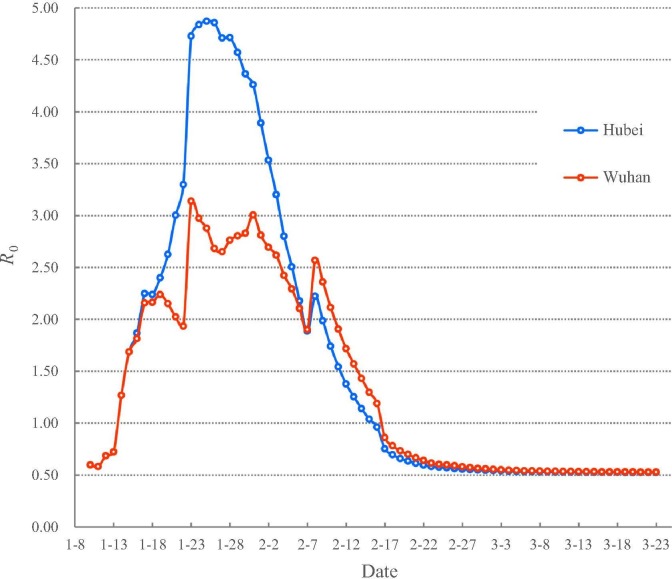
Our calculation began on 10 January 2020 when data became available. As is shown in Fig. 1 , the results from $R_0\left(t\right)$ indicate that the stage of natural transmission of COVID-19 can be divided into three sub-stages from 10 January to 23 February 2020. The first sub-stage is when $R_0$ exceeded one from 10 to 14 January 2020 in Wuhan city and Hubei Province, meaning that COVID-19 spread quickly in the population. The second sub-stage, on 17 January 2020, $R_0$ exceeded two and a major outbreak occurred in Wuhan and Hubei. Given the different population sizes, $R_0$ exceeded four and three on 23 January 2020 for Hubei and Wuhan respectively. Hubei faced an extremely dangerous situation before the implementation of the intervention policy.

Fig. 1.

The $R_0$ values based on the new model in Wuhan and Hubei.

After the intervention of locking down Wuhan city on 23 January 2020, $R_0$ started to have an oscillatory decrease in Wuhan city. The implementation of the “first-level response to major public health emergencies” in all provinces of China from 23 to 25 January, 2020 monotonously decreased $R_0$ in Hubei Province since 26 January 2020. $R_0$ decreased to < 2 on 9 and 11 February 2020 in Hubei Province and Wuhan city respectively. The decline of $R_0$ to below 2 indicates that they have passed the major outbreak. However, COVID-19 continued to spread across Hubei until $R_0$ dropped below 1 on 16 February 2020 for Hubei and on 17 February 2020 for Wuhan, meaning that the COVID-19 has been under control since 17 February 2020. The fitted equations (see the Supplementary materials online) demonstrate that R ₀ is decreasing to its minima and will stay on stable levels in a short time for Hubei and Wuhan, respectively.

We should note that a substantial fraction of the transmission of COVID-19 was caused by individuals without symptoms, which adds considerable uncertainty to the fade-out threshold derived from the model. In addition, both the temporal and spatial models need to be improved methodologically. A robust temporal model for the spread of an infectious disease should incorporate the following information [14]: the patterns of contacts among infectious and susceptible individuals, the latency period from being infected to becoming infectious, the duration of infectiousness, and the extent of immunity acquired following infection. Once all of these factors are formulated in a model, we will be able to construct the entire epidemic curves describing the expected number of individuals who will be infected, the duration of the epidemic, the peak incidence, and the expected number of cases at each point in time.

Conflict of interest

The authors declare that they have no conflict of interest.

Biographies

Tianxiang Yue is the head of Department for Eco-Environmental Informatics, Institute of Geographical Sciences and Natural Resources Research, Chinese Academy of Sciences. He received Ph.D. degree in system ecology from Chinese Academy of Sciences in 1992. He has been a professor of State Key Laboratory of Resources and Environment Information System since 2000. He is a pioneering expert in the method for high accuracy surface modelling and the fundamental theorem for eco-environmental surface modelling.

Zemeng Fan is an associate professor of State Key Laboratory of Resources and Environmental Information System, Institute of Geographical Science and Natural Resources Research, Chinese Academy of Sciences. He received his Ph.D. degree in Cartography and Geographical Information System. His research activities mainly focus on eco-environmental surface modelling.

Appendix A. Supplementary data

The following are the Supplementary data to this article: