Lifetime fitness in wild female baboons: tradeoffs and individual heterogeneity in quality

Abstract

Understanding the evolution of life histories requires information on how life histories vary among individuals, and how such variation predicts individual fitness. Using complete life histories for females in a well-studied population of wild baboons, we tested two non-exclusive hypotheses about the relationships among survival, reproduction, and fitness: the quality hypothesis, which predicts positive correlations between life history traits, mediated by variation in resource acquisition, and the tradeoff hypothesis, which predicts negative correlations between life history traits, mediated by tradeoffs in resource allocation. In support of the quality hypothesis, we found that females with higher rates of offspring survival were themselves better at surviving. Further, after statistically controlling for variation in female quality, we found evidence for two types of tradeoffs: females who produced surviving offspring at a slower rate had longer lifespans than those who produced surviving offspring at a faster rate, and females who produced surviving offspring at a slower rate had a higher overall proportion of offspring survive infancy than females who produced surviving offspring at a faster rate. Importantly, these tradeoffs were evident even when accounting for: (i) the influence of offspring survival on maternal birth rate, (ii) the dependence of offspring survival on maternal survival, and (iii) potential age-related changes in birth rate and/or offspring survival. Our results shed light on why tradeoffs are evident in some populations, while variation in individual quality masks tradeoffs in others.

INTRODUCTION

Measuring within-species variation in survival and reproduction is essential for understanding the selection pressures that influence phenotypic traits. Studies that measure how variation in behavioral phenotypes leads to differences in individual survival and reproduction have both confirmed and challenged assumptions about the evolution of many behavioral traits, including cooperation, foraging, and inbreeding avoidance (e.g., Krakauer 2005; Altmann 1991; Reid et al. 2015). At the same time, understanding the relationships between life history traits and fitness itself sheds light on the evolutionary significance of within-species variation in life history traits and other fitness components, and on how such variation is maintained in natural populations (e.g., Gaillard et al. 2000; Weladji et al. 2006).

Trade-offs between fitness components are a fundamental assumption of life history theory (Stearns 1989; Roff 2002). For instance, individuals who invest highly in reproduction are expected to face costs in terms of survival and/or future reproduction (Reznick 1985; Stearns 1989; Viallefont et al. 1995; Visser and Lessells 2001; Blomberg et al. 2013). However, inter-individual variation in quality (e.g., in the ability to acquire or efficiently use resources) may mask variation in resource allocation strategies if high-quality individuals show both high birth rates and high survival (Cam et al. 1998; Cam and Monnat 2000; Beauplet et al. 2006; Sanz-Aguilar et al. 2008; Weladji et al. 2008; Hamel et al. 2009a, 2010a; Torres et al. 2011). Variation in individual quality may mask tradeoffs, or even produce positive correlations between traits that are expected to trade off (e.g., Weladji et al. 2008; Olijnyk and Nelson 2013).

The roles of both tradeoffs and individual heterogeneity in life history variation have been examined in a number of studies (see Hamel et al. 2010b, 2017a; Vedder and Bouwhuis 2017 for recent reviews) and methods have been developed for identifying tradeoffs in the presence of significant individual heterogeneity (e.g., Hamel et al. 2014, 2017b; Descamps et al. 2016). This work has revealed that both the strength of tradeoffs and the role of individual heterogeneity in modulating tradeoffs vary across environmental conditions (e.g., Pilastro et al. 2003; Cubaynes et al. 2011; King et al. 2011), across the life course of individuals (e.g., Beauplet et al. 2006; Descamps et al. 2008), and between species and populations (e.g., Hamel et al. 2009, 2010b). However, why tradeoffs are evident in some populations, while variation in individual quality masks tradeoffs in others, is not yet completely understood (see Descamps et al. 2009). Answering this question will require extensive longitudinal, individual-based data on survival, reproduction, and fitness in natural populations of multiple taxa.

Here, we examine tradeoffs and individual heterogeneity using a large, long-term dataset of complete life histories from the well-studied, wild, Amboseli baboon population. This population lives in a natural savannah ecosystem with a full complement of predators and no food provisioning. Thus, the birth and death rates reflect natural processes of intra-specific competition and predation. Further, baboons breed non-seasonally, and females show considerable variation in birth rates both within and between individuals; this variation in birth rates is strongly linked to variation in the ability to acquire resources (Gesquiere et al. 2018). In addition, the 47-year study includes unusually detailed data not only on lifespan, but also on every reproductive event of the female study subjects (fig. 1). Most relevant here are our data on pregnancy outcomes (live birth versus fetal loss or still birth), survival status of offspring, and time to next conception and birth.

Figure 1.

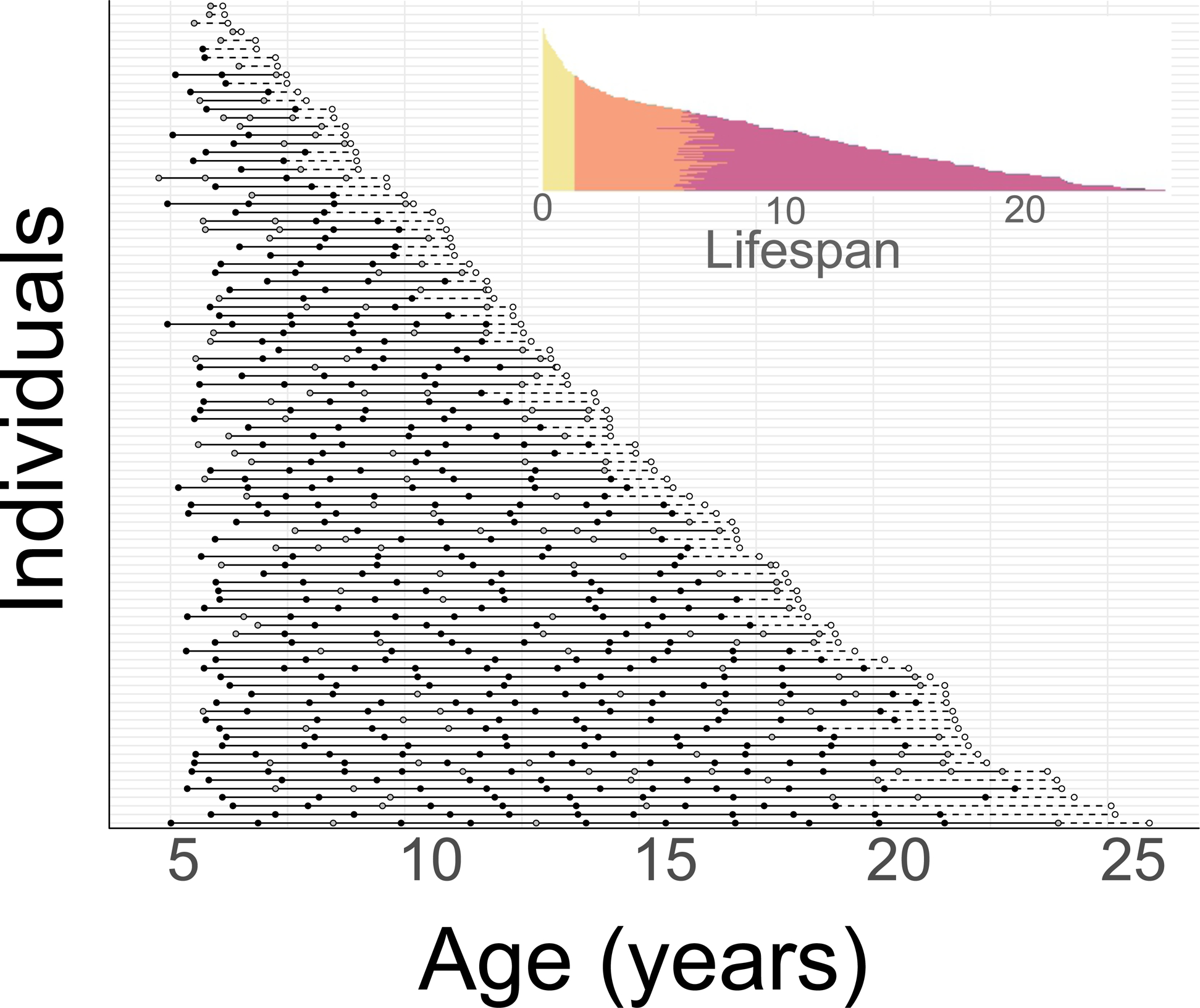
Visualization of complete female life histories. The main panel includes only females that experienced at least one live birth (N=96). Each line represents a distinct female, and each filled dot represents a live birth; black dots represent offspring who survived to weaning age, gray dots represent offspring who died before the average age of weaning in our population. Solid black line segments represent interbirth intervals (some of which represent live interbirth intervals, and some surviving interbirth intervals: see text and Table S2). Open dots indicate the female’s age at death and dashed lines represent the time between her last birth and death. The inset panel shows all females in the dataset, including those who died without reproducing (N=199). Infancy (to average weaning age) is shown in yellow, the juvenile period (between weaning and age at first reproduction) in orange, the reproductive period in magenta, and post reproductive life in dark purple (considered to begin 915 days after a female’s last live birth; i.e., the mean live interbirth interval plus 2 standard deviations).

In analyzing the relationships among maternal rate, offspring survival, and maternal reproductive lifespan, our dataset allowed us to address three potential complications. First, in baboons, like many species with extended periods of maternal care, maternal birth rate is accelerated when an offspring dies before being weaned, so that fast birth rates will generally be associated with poor offspring survival. Second, offspring survival depends on maternal survival; when a mother dies before an offspring is sufficiently weaned, that offspring almost certainly will not survive (Tung et al. 2016). Third, birth rate and/or offspring survival could vary systematically with maternal age (e.g., Descamps et al. 2008; Hayward et al. 2015), producing a phenotypic correlation between one or both of these reproductive phenotypes and reproductive lifespan. These potential complications reflect the fact that offspring survival is partly a function of maternal traits and behaviors. Thus, although we followed standard procedures for measuring fitness, and did not consider offspring survival as a component of maternal fitness (Wolf and Wade 2001; Wilson et al. 2005), we nonetheless statistically controlled for the relationships between (i) offspring survival and maternal birth rate and (ii) offspring survival and maternal survival. We also (iii) included maternal age in our models to control for variation in offspring survival and maternal birth rate accros the lifespan of the mother.

We evaluated two non-exclusive hypotheses regarding the nature of the phenotypic relationship between reproduction and survival. The “tradeoff” hypothesis posits that environmentally or genetically mediated differences in individual resource allocation drive a negative relationship between reproduction and adult female survival. Under the tradeoff hypothesis, individuals who allocate highly towards reproduction, via high birth rates or high offspring survival, will have shorter lives than individuals with lower allocation to reproduction. Similarly, individuals who allocate resources towards one component of reproduction will have reduced output in other reproductive traits. In contrast, the “quality” hypothesis posits that differences in individual quality, resulting from either genetic or environmental differences between individuals, drive a positive relationship between reproduction and survival. Under this hypothesis, individuals with high allocation to reproduction will have longer lives than individuals with low allocation to reproduction, because their high phenotypic quality allows them to maintain high levels of reproduction without compromising survival. These hypotheses are not mutually exclusive (Oli et al. 2002; Weladji et al. 2008; Hamel et al. 2009a, 2010a; Wilson and Nussey 2010; Théoret-Gosselin et al. 2015): the observed phenotypic relationships between reproductive phenotypes and survival reflects the contributions of both tradeoffs and inter-individual variation in quality.

METHODS

Study population

We studied a population of wild savannah baboons in the Amboseli ecosystem of southern Kenya that has been the subject of ongoing research for more than four decades (Alberts and Altmann 2012). This population is composed primarily of yellow baboons with some naturally occurring admixture from neighboring anubis baboon populations (Alberts and Altmann 2001; Tung et al. 2008). Savannah baboons live in stable social groups containing multiple adults and juveniles of both sexes, ranging in size from approximately 20–100 animals. The Amboseli Baboon Research Project monitors multiple such groups (‘study groups’) in the Amboseli ecosystem (Alberts and Altmann 2012). All subjects are individually recognized based on unique morphological and facial features. All demographic and life-history events (births, maturation events, immigrations, deaths and emigrations) are recorded on a routine basis as part of the near-daily monitoring of the study groups.

Our study subjects were all of the female baboons born into study groups between 1971 (the start of continuous observation on this population) and 1996 (the latest year from which no females born were still alive at the time of analysis), yielding 205 complete female life histories. We excluded females born after 1996 because including them would bias our dataset against individuals with long lifespans. We knew the birth and death dates for all 205 subjects to within a few days. For the study subjects who reproduced, we also knew the birth dates of all of their offspring to within a few days, with a few exceptions (N=7) where the uncertainty in birthdate was >= 1 month. We ran all analyses of interbirth intervals with and without these uncertain cases and found no difference in magnitude, direction, or significance of results. Death dates were known for all offspring who died before the study ended. We also excluded 6 outliers from all analyses presented in the main text: 3 with early cessation of reproduction, 1 with late age at first birth (associated with a near-fatal injury sustained in late puberty), 2 with exceedingly slow birth rates (table S1). These outliers had phenotypes that were > 3 standard deviations from the mean and/or exerted a disproportionate influence on the results of a regression model (Cook’s distance > 0.5; details in table S1). See the supplement for analyses that include these outliers, leading to some minor changes in the significance of some tests (see tables S3–S5, Results, and Discussion). Our final dataset included 199 individuals.

In baboons, births are non-seasonal, occurring frequently in all months of the year. Female baboons remain in their natal group throughout their lives, and our study subjects were observed several times each week for their entire lives, with occasional exceptions. It is very unlikely that any pregnancies were missed; female baboons exhibit external indicators of reproductive state that make it easy for observers to detect cycling, conception, and pregnancies (see Altmann 1973; Beehner et al. 2006; Gesquiere et al. 2007 for details). The onset dates for all pregnancies are assigned using visual assessment of these reproductive indicators. Endocrinological analyses in our study population, combined with decades of close observation, confirm that these visual methods are greater than 97% accurate for identifying the timing of the onset of pregnancy, and in turn pregnancy due dates (Beehner et al. 2006).

Life history traits

Age at death (AD).

Death is assigned when a carcass is found, or at the time a female disappears from the study population, as no female has ever permanently dispersed to a new group during the 47-year study (table S2). Our study population represents approximately half of the baboon population in the Amboseli ecosystem, suggesting that we would be very likely to detect even rare cases of permanent female movement between groups.

Age at first live birth (AFLB).

During each observation day on a study group, all members of that group are registered as present or not, and the reproductive state of all adult females is assessed based on external indicators (see Beehner et al. 2006; Gesquiere et al. 2007). New infants are identified on the first observation day on which they are seen, typically within 0 – 3 days of birth. We mark the start of a female’s reproductive life as the age at which she first gives birth to a live offspring (table S2).

Reproductive Lifespan (RL).

We define reproductive lifespan as the age at death minus age at first live birth (table S2). We use age at death as the endpoint instead of age at last birth because nearly all baboon females (94.75% of our dataset, fig. 1) are reproductively active (cycling, pregnant or lactating) at the time of their death and baboon females do not experience systematic reproductive cessation towards the end of life (fig. 1; Altmann et al. 2010; Alberts et al. 2013b). We re-ran the analyses presented here with an alternative definition of reproductive lifespan (age at last live birth minus age at first live birth) and found only small differences in effect sizes, with no differences in the direction or significance of any of our results (tables S3–S5).

Offspring Survival (OS).

We measured offspring survival as the proportion of a female’s live born offspring that survived to 70 weeks of age, the estimated age at weaning in our population (Altmann 1998, table S2). We refer to individuals that are between birth and 70 weeks of age as infants.

Live Interbirth interval (IBI_L).

To estimate birth rate, we counted the number of days between live births (the live interbirth interval) for each female that had at least two live births in our dataset (n=87). The time between two live births is strongly influenced by offspring survival: mothers experience much shorter post-partum amenorrhea when their offspring dies before weaning and resume cycling, conceive, and give birth again more quickly after the death of an unweaned infant (Altmann et al. 1978).

Surviving interbirth interval (IBI_S).

Because the interval between live births is heavily determined by offspring survival, we also calculated the average duration (in days) of the interval between the birth of an infant who survived at least 70 weeks (the entire period of infant dependence, hereafter the infancy period) and the next birth, for all mothers with at least one such interval (n=82). This interval, termed the surviving interbirth interval, represents the average time required by each mother to raise an infant successfully to weaning and subsequently conceive, gestate and birth another live infant. This metric is correlated with the live interbirth interval (R=0.81, p<0.0001) but the two metrics are distinct; we interpret the surviving interbirth interval as a direct reflection of a female’s ability to recover from a reproductive event (production of an offspring that survives infancy). Therefore, we used IBI_S when we were considering heterogeneity in individual quality, and when we were investigating tradeoffs between allocation to reproduction and allocation to survival (table S2).

Measures of individual fitness

Lifetime reproductive success (LRS).

Lifetime reproductive success for each female was defined as the total number of live offspring born to her, regardless of the offspring’s subsequent survival. The ability of a mother to raise an offspring to independence can be treated as a component of maternal fitness (e.g., Clutton-Brock 1988), but we removed offspring survival – a phenotype that combines maternal and offspring characteristics – entirely from our measure of mother’s LRS. This allowed us to investigate the relationship between offspring survival and individual fitness and follows the strict bookkeeping practices suggested by quantitative evolutionary biologists for estimating measures of selection (Arnold 1983; Lande and Arnold 1983; Cheverud 1984; Wolf and Wade 2001).

λ_ind. λ_ind is the individual-level analogue to λ_pop, the population rate of increase, and incorporates two fitness components: (i) the number of liveborn offspring produced by an individual, and (ii) the year of life during which these offspring are produced, to estimate each individual’s rate of increase. λ_ind is calculated separately for each observed individual life history. Specifically, λ_ind is the dominant eigenvalue of each individual’s age-structured population projection matrix (see McGraw and Caswell 1996 for details). We constructed these matrices from our longitudinal individual-level data on births and deaths, and calculated λ_ind using the ‘popbio’ package in R v3.3.1. The individual with the highest λ_ind (i.e., fastest growth rate) is considered to have the highest fitness.

Variance in LRS explained by survival to age at first live birth.

We had two classes of individuals in our dataset: females who died without reproducing (non-breeders, n=103) and females who gave birth to at least one live offspring (breeders, n=96). We followed the methods detailed by Brown (1988) and calculated the contribution to variance in LRS of females who reproduced successfully as p(σ²_LRS) and the contribution of females who failed to reproduce as p(1-p)$\left({\overline{\text{x}}}^2{}_{\text{LRS}}\right)$, where p is the proportion of individuals who gave birth to at least one live offspring (p =0.49) and σ²_LRS and ${\overline{\text{x}}}^2{}_{\text{LRS}}$ are the variance and squared mean of those breeders’ LRS, respectively.

Relationships among offspring survival, reproductive lifespan, live interbirth interval, and fitness

We constructed a path analysis to examine the pairwise relationships between the proportion of offspring surviving, reproductive lifespan, live interbirth interval, and lifetime reproductive success. This analysis produced partial correlation coefficients between all pairs of our variables of interest, while simultaneously controlling for effects of the other variables in the model. Given the biological constraints of this model (i.e., one cannot continue producing offspring after death), we view these path coefficients as simply partial correlation coefficients and we caution against interpreting this path coefficients as indicative of “causal” relationships, per se.

We calculated the variance-covariance matrix between all standardized predictor and response variables and performed path analysis in the structural equation modelling package (‘sem’) in R v3.3.1. We used variance-standardized variables, including variance-standardized LRS, so that we could directly compare path coefficients between variables. We modeled the proportion of offspring surviving, a priori, as an exogenous variable (with no prior links in the causal pathway) because of its known effects on live interbirth interval. In contrast, we modeled reproductive lifespan, live interbirth interval, and LRS as endogenous variables (i.e., with prior links in the causal pathway). Because the large majority of infant deaths occur in the first few months of life, and shorten the interbirth interval by more than a year, we only modeled an effect of offspring survival on interbirth interval and did not model the reverse effect of interbirth interval on offspring survival (Altmann et al. 1978). We present the results for the model with the lowest BIC, as determined by backwards stepwise model selection.

Addressing effects of maternal age, maternal survival, and offspring survival on life history traits

Our path analysis supported the quality hypothesis (namely, we found a positive correlation between offspring survival and maternal survival). However, as discussed in the introduction, three complications plague analyses of the relationship between lifetime reproduction and survival in baboons, and any other long-lived, non-seasonally breeding mammal (including humans): (i) offspring survival influences maternal birth rate, (ii) offspring survival depends on maternal survival, and (iii) birth rate and/or offspring survival could vary systematically with maternal age.

To address these concerns and their potential effects in the path analysis, we constructed two linear mixed models to examine the relationship between maternal reproductive lifespan (RL, which represents survival), and two reproductive traits in our path analysis: offspring survival (OS) and the live interbirth interval (IBI_L). The first linear model, the ‘OS model’, was a GLMM with the survival status of each offspring in our dataset as the response variable (table S4). The second linear model, the ‘IBI_L model’, was an LMM with the length of each live birth interval in our dataset (IBI) as the response variable (table S4). Maternal age at offspring birth and maternal reproductive lifespan were continuous predictors in both models. Because the relationship between maternal age and reproductive phenotypes may not be linear in our population (Gesquiere et al. 2018) we added an additional categorical predictor of maternal parity (nulliparous or not) to both models. We did not include a quadratic effect of maternal age, because quadratic models are often not the most appropriate way to model age-dependence in traits (see Berman et. al 2009 for a discussion). However, by modeling the effects of maternal parity, we allow for the outcome that inexperienced (and generally young) mothers may have reproductive phenotypes similar to old, senescent mothers. Because offspring will generally not survive infancy if their mother dies, we included an additional categorical predictor in the offspring survival (OS) model indicating whether the mother died before the offspring during the 70-week infancy period. Because offspring survival greatly influences the duration of post-partum amenorrhea, we included an additional categorical predictor in the IBI_L model indicating whether or not the offspring was alive for the entire 70-week infancy period. Both models included random effects of maternal ID and year the offspring was born. The OS model allowed us to measure the relationship between offspring survival and reproductive lifespan controlling for the effects of maternal death during infancy. The IBI_L model allowed us to measure the relationship between live interbirth interval and reproductive lifespan, controlling for the effect of offspring death during infancy.

The results of the OS model indicated that the relationship between offspring survival and reproductive lifespan resulted from the selective disappearance (i.e., early mortality) of females with low offspring survival (Van de Pol and Verhulst 2006) rather than from a positive correlation between maternal age and offspring survival. Similarly, the results of the IBI_L model confirmed that the relationship between live interbirth interval and reproductive lifespan was not statistically significant, even after considering effects of maternal age and parity (table S4). The results of these two linear mixed models also allowed us to rule out the possibility that changes with age in OS and IBI could produce spurious correlations between reproductive lifespan and these two phenotypes in our path analysis. We ran these models in R v3.3.1, using the lme4 package (Bates et al. 2015); we ran the offspring survival model with a binomial distribution and a logit link.

Detecting survival costs and reproductive costs of reproduction by considering heterogeneity in female quality

Both our path analysis and the mixed effects models of OS and IBI_L failed to detect tradeoffs between survival and reproduction, suggesting marked differences in female quality. Consequently, we hypothesized that the relationship between survival and reproduction might be influenced by individual quality. To test this hypothesis, we used a multivariate index of phenotypic quality (Hamel et. al 2009a; Wilson and Nussey 2010). We used four fitness-associated phenotypes as indicators of quality: age at first live birth (AFLB), surviving interbirth interval (IBI_S), proportion of offspring surviving to weaning (OS), and reproductive lifespan (RL). Specifically, we used principal components analysis to identify independent axes of covariation among these fitness-associated phenotypes (AFLB, IBI_S, OS, and RL). A principal component of trait covariation can be interpreted as reflecting substantial variance in individual quality if each trait loads onto the PC in a direction consistent with increasing fitness, if the PC accounts for a large part of observed variation in traits, and if it is positively correlated with variance in individual fitness (Hamel et al. 2009b). Alternatively, a principal component of trait covariation may reflect tradeoffs if some traits load onto the PC in a direction that reflects increasing fitness, while others load in a direction that reflects decreasing fitness or if the PC is not strongly correlated with individual fitness (Hamel et al. 2009b).

Our results indicated that the covariance between AFLB, IBI_S, OS and RL was consistent with variation in quality (see below), and we subsequently designated the first principal component (PC1) of the PCA as our quality index (table 1). In contrast, we found that the second principal component of covariation (PC2) captured negative covariation among several of our traits, consistent with the idea that it reflects tradeoffs (table 1; Hamel et al. 2009b).

Table 1.

Summary of putative indicators of multivariate female quality from principal components analysis

Component	Variable loadings*	Variance Explained	Description	Correlation with measures of fitness
				LRS	λIND
PC1	AFLB: −0.87 IBIs: −0.79 RL: 0.20 OS: 0.27	38%	Females with early ages at first reproduction and short interbirth intervals (fast birth rates) versus females with late ages at first reproduction and long interbirth intervals (slow birth rates). This axis represents a ‘quality’ axis.	0.31 p=0.005	0.36 p=0.0008
PC2	AFLB: −0.03 IBIs: −0.39 RL: −0.70 OS: −0.69	28%	Females with short lives and low offspring survival but short interbirth intervals (fast reproduction) versus females with long lives and high offspring survival but long interbirth intervals (slow reproduction). This axis thus describes both tradeoffs with interbirth interval length and evidence of quality differences (seen in the covariation between offspring survival and reproductive lifespan).	0.54 p<0.001	0.33 p=0.003

We examined the relationship between our quality index (PC1) and fitness in two ways. First, we calculated a simple correlation between quality and individual fitness (measured as both LRS and λ_IND). Second, we calculated selection differentials and selection gradients (partial regression coefficients) for each phenotype in the quality index (see Supplementary Methods and table S6). We then used these selection gradients (i.e., multivariate vectors of selection) to determine Θ, the angle between the vector of multivariate selection and the principal component representing our quality index; we report the values of Θ in the supplement (table S7; see Supplementary Methods and Wilson and Nussey 2010 for details). Small values of Θ (representing a close alignment between the vector of multivariate selection and the quality index) are characteristic of populations in which selection may act upon variation in phenotypic quality (Wilson and Nussey 2010).

Finally, to test the hypothesis that the relationship between survival and reproduction is influenced by individual quality we constructed two sets of linear models, designated the ‘tradeoff models,’ both of which had individual quality and IBI_S as the sole predictors. The first tradeoff model had reproductive lifespan (RL) as the response variable; the second tradeoff model had offspring survival (OS) as the response variable. We note that the two response variables, RL and OS, were also among the measures that contributed to individual quality (i.e., to PC1 of our PCA). Thus, we expect a positive relationship between quality and RL and between quality and OS. However, such a positive relationship still allows for tradeoffs between RL and IBI_S, and between OS and IBI_S, as demonstrated by the loadings onto PC2 (table 1).

Our tradeoff models explicitly test for the relationship between IBI_S and RL (first set of tradeoff models) and between IBI_S and OS (second set of tradeoff models) while controlling for variation in quality (i.e., for PC1). This approach is conceptually related to the principal components analysis itself, which describes multiple axes of covariation among variables. Specifically, PC1 in our PCA describes significant covariation among our four life history traits in a direction consistent with increasing fitness (with a considerable range of values in the loadings for each trait; table 1), and PC2 describes some negative covariation among some of the variables, once PC1 is accounted for, reflecting likely tradeoffs (again, with a range of values for trait loadings; table 1). In our tradeoff models, we seek to explicitly examine the tradeoffs that are suggested in the PCA by asking whether individuals with long reproductive lifespans for their quality (first tradeoff model) or high offspring survival for their quality (second tradeoff model) also tend to have relatively long birth intervals after a surviving birth.

To confirm the statistical validity of our regressions, we examined the variance inflation factors of the tradeoff models and found that collinearity between predictors was low (all variance inflation factors < 5) indicating that these models are stable. In addition, we designed a permutation test to examine the possibility that the covariation between our response variables (RL or OS) and our predictor variable (IBI_S) may have influenced our quality metric in such a way as to bias our tradeoff models in favor of detecting tradeoffs. Specifically, we assigned a second p-value to each model via a permutation test in which we retained the actual pattern of IBI_S and RL values (for tradeoff model 1) and IBI_S and OS values (for tradeoff model 2), but in which other relationships among the life history variables occurred at random. This procedure removed evidence of any tradeoffs, indicating that the tradeoff outcome was not an inevitable outcome of the existing data structure (see supplemental methods for more details).

RESULTS

Females vary considerably in life history phenotypes and fitness

Age at death, age at first live birth, reproductive lifespan, birth intervals, and offspring survival.

The median age at death in the full data set (n = 199) was 5.41 years (range 0.01y to 25.89y; fig. S1A). Ninety-six of these 199 females gave birth to at least one live offspring (fig. 1). The median age at death for these 96 ‘breeders’ was 14.31 years (range 6.12y – 25.89y, fig. S1A) and the median reproductive lifespan was 8.27 years (range 0.18y to 20.88y, fig. S1E). The median age at first live birth was 5.9; this trait was the least variable of all of our life history phenotypes, ranging from just 4.75y to 7.98y (fig. S1C). The median interval between live births in our dataset was 1.67 years (608.6 days, range 269.5 to 959 days, fig. S1B). The median interval between surviving births in our dataset was 1.75 years (638.5 days, range 392 to 960 days, fig.S1D). The median proportion of offspring that survived to 70 weeks was 0.75 (range 0 to 1, fig. S1F). The generation time, estimated from our empirical data and defined as the average age of a mother at the birth of a daughter (Coale 1972), was 11.41 years.

Measures of fitness.

The mean lifetime reproductive success considering all 199 females was 2.71 ± 3.59 (mean ± SD) live offspring (range 0 to 14). For the 96 breeders, the mean LRS was 5.61 ± 3.21 live offspring (range 1 to 14) (fig. S2A). The mean value of λ_ind for the 199 females in our dataset was 0.52 ± 0.55 (mean + SD, range 0 to 1.18). For the 96 breeders, the mean λ_ind was 1.09 ± 0.08 (range 0.87 to 1.18) (fig. S2B). Note that the population average of λ_ind is not the same as the population rate of increase (λ_pop) because the mean of a set of eigenvalues (a set of λ_ind in this case) is not the same as the eigenvalue of the mean matrix (λ_pop) (Lenski and Service 1982). LRS and λ_ind were positively associated (R²=0.68, p<0.001), and the relationship between the two fitness measures was curvilinear (fig. S3), consistent with findings in other species (Brommer et al. 2002, 2004; Robbins et al. 2011).

Following Brown (1988), we partitioned the variance in LRS among females of different classes (non-breeders and breeders) and found that 61.3% of the variance in LRS among all females was attributable to females who never reproduced. Consistent with previous work in our population (Alberts and Altmann 2003) and expectations for a long-lived species, survival also explained the majority of the variance in LRS among the individuals who did survive to reproduce. The parameter estimate in the path analysis indicates that an increase of one standard deviation in reproductive lifespan increases lifetime reproductive success by 2.90 live births (i.e., by 0.97 standard deviations for LRS). In contrast, an increase of one standard deviation in live interbirth interval increases lifetime reproductive success by only 0.63 births (less than 1/4 of a standard deviation for LRS).

Evidence for the quality hypothesis: the longest-lived females had the highest offspring survival

Our path analysis revealed a positive relationship between offspring survival and reproductive lifespan (fig.2, table S3): females with higher rates of offspring survival were themselves more successful at surviving. The results from our GLMM of offspring survival (the ‘OS model’, see Methods and table S4) also support this finding. Specifically, even while controlling for other important effects, including maternal loss (β=−1.42, p<0.001), maternal parity (β=−0.62, p=0.056), and maternal age (β=−0.37, p=0.018) on offspring survival, females who would ultimately lead long reproductive lives produced offspring with a higher probability of surviving than females who would ultimately lead shorter reproductive lives (β=0.35, p=0.017, fig. 3A, table S4). This result suggests that quality differences among females may have contributed to differences both in reproductive lifespan and offspring survival.

Figure 2.

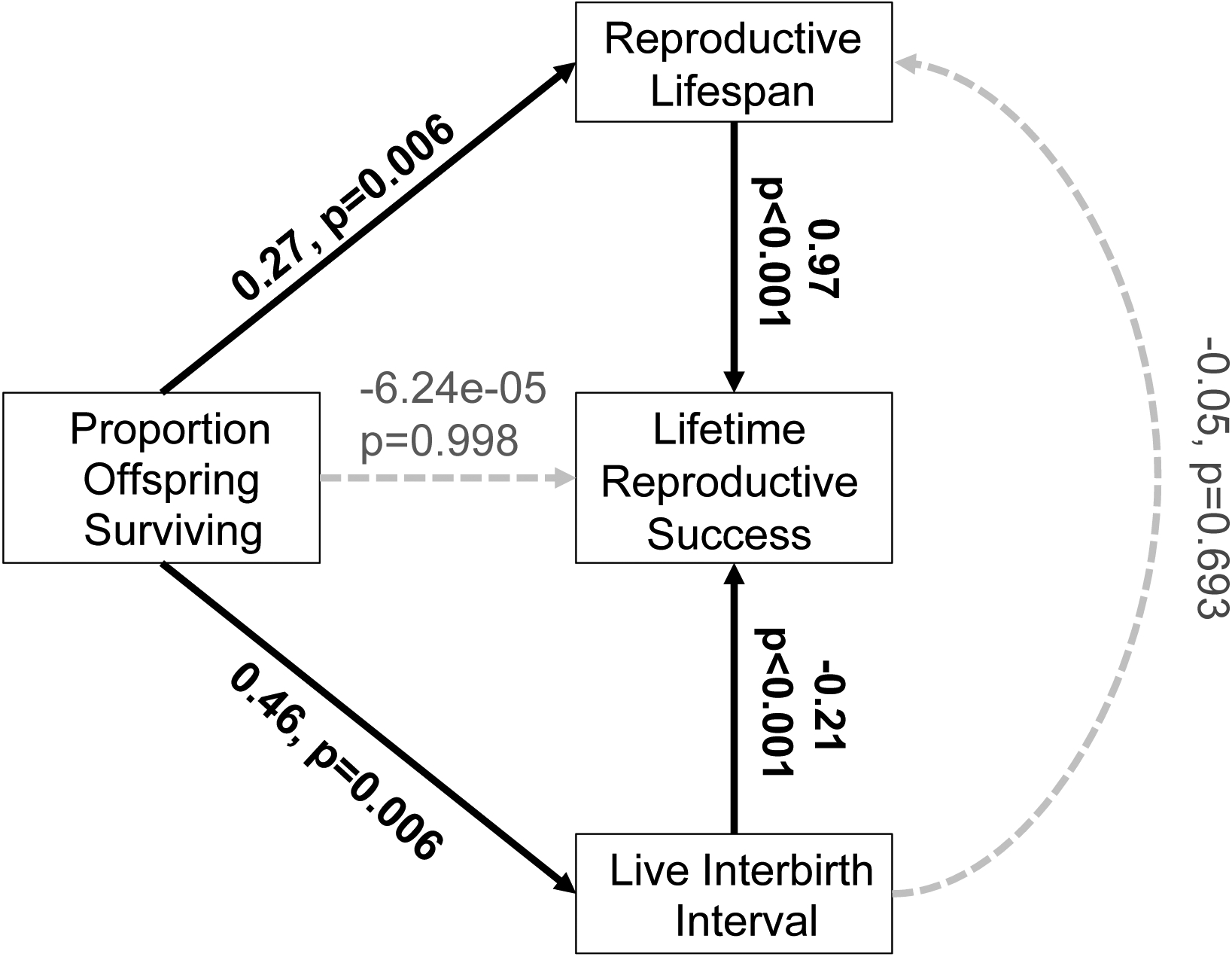
Path analysis with standardized pairwise partial correlation coefficients between life history traits and fitness. Significant partial correlation coefficients are in bold. Paths that are included in the full model, but not in the best-supported model (as determined by backwards stepwise selection) are shown in light gray with dashed lines. Longer IBI_L (slower production of live offspring) is associated with higher offspring survival and lower LRS. Longer reproductive lifespan is associated with higher offspring survival and higher LRS.

Figure 3.

Reproductive lifespan is correlated with offspring survival (A) but not with live interbirth interval (B). The regression lines in both panels represent visualizations of (G)LMMs. (A). Probability of offspring survival as a function of mother’s age at birth and reproductive lifespan. The trendlines show predicted values with 95% confidence intervals from a model that also includes maternal parity, maternal death in the weaning period, and random effects of maternal identity and offspring birth year. The model indicates a statistically significant relationship between offspring survival and maternal age, as well as between offspring survival and maternal reproductive lifespan (which is depicted as categorical but modeled as continuous). The small vertical lines show our actual offspring survival data. (B) Live interbirth interval as a function of mother’s age and reproductive lifespan. The trendlines show predicted values with 95% confidence intervals from a model that also includes maternal parity, offspring death in the weaning period, and random effects of maternal identity and offspring birth year; the model indicates no statistically significant relationship between live interbirth interval and maternal age, or between live interbirth interval and reproductive lifespan. The points show our observed interbirth interval data.

Our path analysis also revealed the negative relationship between offspring survival (OS) and live interbirth interval (IBI_L) that one expects for non-seasonal breeders (fig.2). Our LMM of live interbirth interval (the ‘IBI_L model’, see Methods and table S4) confirmed that this relationship was caused by females’ immediate responses to offspring death. Specifically, if their current offspring died in infancy, females reproduced again quickly: live birth intervals in which the offspring survived to weaning were 171 ± 15 days longer (p<0.0001) than live birth intervals in which the offspring died before 70 weeks of age (table S4). The IBI_L model also confirmed that interbirth interval was unrelated to other life history variables, although nulliparous females showed a trend towards longer intervals (especially when including outliers, see table S4). The IBI model also revealed considerable heterogeneity among females in interbirth interval lengths (table S4).

Detecting tradeoffs depends on measuring individual quality

Our finding that the longest-lived females had the highest offspring survival suggests that variation in female quality is a salient feature in this population, and that it may obscure tradeoffs between reproduction and survival. To test for evidence of tradeoffs between reproduction and survival while controlling for variation in female quality, we developed a multivariate index of female quality, PC1 from a principal components analysis of covariation among life history traits (see Methods). The variables that loaded most heavily on PC1 were AFLB and IBI_S (see table 1, table S8, fig. S4 for more details), Both AFLB and IBI_S had negative loadings on our quality index, because early ages at first live birth and short surviving birth intervals are consistent with features of high quality females. Our quality index, PC1, showed a statistically significant positive correlation with individual fitness measured both by LRS and λ_ind (R=0.31, p=0.005; R=0.36, p=0.0008, respectively).

After controlling for variation in female quality (i.e., after including PC1 as a predictor in a multiple regression), our ‘tradeoff model’ of reproductive lifespan revealed a negative relationship between surviving birth interval and reproductive lifespan. That is, females with long lifespans had longer surviving birth intervals than those with short lifespans, a tradeoff that was evident only when accounting for variation in female quality (fig. 4A,4B, table 2). Our permutation tests revealed that this tradeoff was not an inevitable outcome of the existing data structure (fig. S5). However, this tradeoff was not statistically significant when we included outliers (see tables S1, S5).

Figure 4.

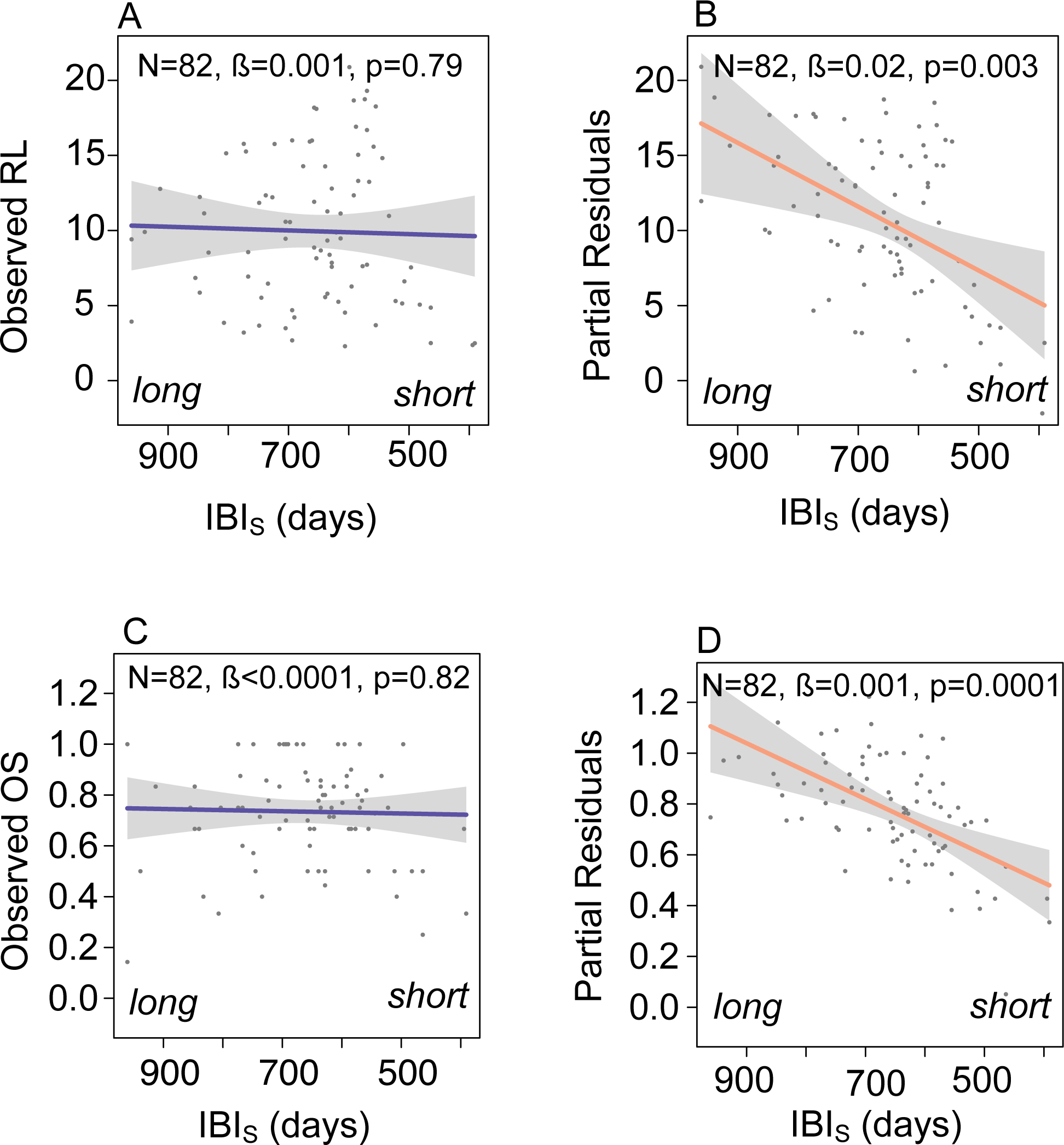
Survival and reproductive costs of reproduction are apparent after accounting for individual heterogeneity in quality. (A) The observed population-level relationship between surviving interbirth interval (IBI_S) and reproductive lifespan (RL). (B) The population-level relationship between surviving interbirth interval and reproductive lifespan after accounting for variation in phenotypic quality. The points in (B) represent the partial residuals from a regression of our quality metric (i.e., PC1) against reproductive lifespan, plotted as a function of surviving interbirth interval (i.e., the average length of time between the birth of an offspring who survived infancy and the mother’s next live birth). (C) The observed population-level relationship between surviving interbirth interval (IBI_S) and proportion offspring surviving (OS). (D) The population-level relationship between surviving interbirth interval and proportion offspring surviving after accounting for variation in quality. The points in (D) represent the partial residuals from a regression of our quality metric (i.e., PC1) against proportion offspring surviving, plotted as a function of surviving interbirth interval.

Table 2.

Results of four ‘tradeoff models’ of the relationships between surviving interbirth interval and reproductive lifespan, and between surviving interbirth interval and offspring survival, controlling for individual quality (see fig 4; see also table S5 for tradeoff models including outliers and using alternative definition of reproductive lifespan).

Model description*	Predictor	Effect size (Std. Err.)	p value
1. Reproductive Lifespan ~ Surviving interbirth interval (fig. 4A)	IBIs	0.001 (0.004)	0.791
2. Reproductive Lifespan ~ Surviving interbirth interval + Quality score (fig. 4B)	IBIs	0.02 (0.007)	0.003
	Quality score	2.47 (0.69)	0.0006
3. Proportion offspring surviving ~ Surviving interbirth interval (fig. 4C)	IBIs	0 (1.89e-04)	0.815
4. Proportion offspring surviving ~ Surviving interbirth interval + Quality score (fig. 4D)	IBIs	0.001 (2.67e-04)	0.0001
	Quality score	0.13 (0.03)	5.4e-06

^*The tilde (~) in each model indicates that that model tests the dependence of the response variable on the predictor variables (which are listed after the tilde).

Similarly, after controlling for variation in female quality, our ‘tradeoff model’ of offspring survival revealed a negative relationship between surviving interbirth interval and offspring survival. That is, females with long intervals after a surviving birth had higher overall rates of offspring survival than those with shorter intervals after a surviving birth (fig. 4C, 4D, table 2, see table S5 for results with outliers). Again, our permutation test revealed that this tradeoff was not an inevitable outcome of the existing data structure (fig. S5).

Maternal age affects offspring survival but not live interbirth interval

Finally, our GLMM of offspring survival revealed that maternal age strongly influenced offspring survival: older mothers were less successful at producing surviving offspring (β=−0.37, p=0.018; fig. 3A), as were first time mothers (β=−0.62, p=0.056; table S4). In contrast, females showed no statistically significant change in live interbirth intervals with age.

DISCUSSION

We demonstrated considerable variance in lifetime fitness among wild female baboons. As expected for long-lived organisms, individual survival (measured both as survival to first reproduction and length of reproductive lifespan) was the primary determinant of individual fitness (see also Clutton-Brock 1988; Newton 1989). We also found evidence that both heterogeneity in female quality and tradeoffs drive the phenotypic relationships between reproduction and survival in wild baboons. Specifically, female baboons who led long reproductive lives also achieved high rates of offspring survival, indicating early mortality of lower quality females and suggesting the existence of a quality ‘syndrome’ among female baboons that promotes the survival of both high-quality females and their offspring. Similar selective disappearance of individuals with lower reproductive success has been documented in other long-term studies (e.g., Weladji et al. 2006; McCleery et al. 2008; Bouwhuis et al. 2009; Hayward et al. 2013). By accounting for individual heterogeneity in phenotypic quality, we also found evidence for two tradeoffs that females experience if they produce surviving offspring (as opposed to simply live births) at a relatively high rate: (i) such females die younger, and (ii) such females produce fewer surviving offspring overall. We discuss each of these results in more detail below.

Survival, Reproduction, and Fitness

Sixty-one percent of the variance in LRS in the study population was attributable to individuals who died at or before the average age of first reproduction. We attributed variance in LRS due to these individuals as variance in LRS explained by survival. However, it is possible that some of this variance in LRS is linked to the ‘reproductive potential’ of an individual. For instance, individuals with below average reproductive systems, destined to have low fertility, may also tend to be below average in other physiological functions and less likely to survive to reproductive age. Our evidence that variation in female quality drives the relationship between survival and reproduction in adult females lends support to this idea. However, no reproductive phenotypes can be measured for individuals who die before reproducing; they thus represent an ‘invisible fraction’ of the population with regards to reproductive phenotypes (Grafen 1988).

Among the ‘visible fraction’ of reproductive phenotypes, survival again explains the majority of the variance in individual fitness. That is, little of the population-wide variance in fitness is explained by differences among individuals in live interbirth interval, even though individuals with shorter live interbirth intervals tend to have higher fitness (fig. 2). Thus, using live interbirth interval (or other similar measures) as proxies for fitness may fail to accurately reflect the ways in which selection is acting on this system. Though these results are consistent with our expectations and the findings of prior studies, we highlight them here because studies in natural populations (including ours) sometimes use reproductive variables as proxies for fitness when investigating environmental and/or genetic sources of variance in fitness (reviewed in Kingsolver et al. 2001 - see table 3; Hereford et al. 2004 - see table 1; Siepielski et al. 2009 - see appendix S1; Altmann et al. 1998, Altmann and Alberts 2003, but see Tinbergen and Sanz 2004; Morrissey et al. 2012; Bonnet et al. 2017 for illustrative counter-examples).

Variation in quality masks tradeoffs at the population level

In contrast to the predictions of the tradeoff hypothesis, we found that females with long reproductive lives had high offspring survival, suggesting that these females were of higher phenotypic quality than the females with short lives and poor offspring survival. We also found statistically significant inter-individual variance in live interbirth intervals that was not associated with reproductive lifespan, suggesting that the best metric of female quality may involve multiple phenotypes. Indeed, using a multivariate index of female quality, we found that higher quality females performed better in both survival and reproduction than females of lower quality, but that females did indeed face survival and reproductive costs of reproduction. Specifically, a 4-month increase in the duration of the surviving interbirth interval (i.e., a slower surviving birth rate by one standard deviation of the mean IBI_S; table S2) corresponded to an additional 2.5 years of reproductive life, and to an increase in overall offspring survival of about 13% (fig. 4, table S5).

Our study adds to the growing number of mammalian populations in which the effects of individual heterogeneity have been documented to modulate the effects of life-history tradeoffs (e.g., Beauplet et al. 2006; Weladji et al. 2008; Hamel et al. 2009a; Vedder and Bouwhuis 2018). The multivariate approach we employed here is useful for identifying variation in quality, but as our analysis only considered life history traits that are generally directly associated with fitness, they do not shed light on the sources of this variation in quality. These observations raise the question, what causes differences in female quality? In cercopithecine primates, female dominance rank is an intuitively appealing explanation for variance in female quality; however, given the system of nepotistic maternal rank ‘inheritance’ (Lea et al. 2014) and limited evidence of a relationship between dominance rank and lifespan in our population (Archie et al. 2014) we suggest that while dominance rank may influence female quality (perhaps by providing access to higher value resources), dominance rank alone is not a sufficient causal explanation for variance in female quality.

Another intriguing possible driver of variation in female quality is the early life environment. Conditions in early life affect lifespan and/or reproduction in a range of other taxa (e.g., in red-billed choughs: Reid et al. 2003; red deer: Nussey et al. 2007; Mauritius kestrels: Cartwright et al. 2014; humans: Hayward et al. 2014; goshawks: Herfindal et al. 2015; bighorn sheep: Pigeon et al. 2017). In Amboseli baboons, we have shown that early life conditions affect both survival and reproduction in females (Tung et al. 2016; Lea et al. 2015). We also know from previous analyses that early life adversity influences adult social connectedness: females with higher levels of early adversity show lower levels of social connectedness to other adult females (Tung et al. 2016). Low social connectedness, in turn, is linked to poor offspring survival and poor maternal survival (Silk et al. 2003, Archie et al. 2014). This set of results suggests that early life adversity may influence female quality. More work is needed to investigate these and other potential sources of variance in female quality and how they may interact with dominance rank to influence life history traits.

Stronger evidence for senescence in maternal competence than in birth rate

Our results provide evidence of maternal age-dependent variation in offspring survival, a finding demonstrated in a range of other taxa (for instance, see Kern et al. 2001; Torres et al. 2011; Hayward et al. 2014). However, the dynamics of the relationship between maternal age and offspring survival depend on the biology of the species considered, with evidence in some species suggesting a role for maternal experience in increasing offspring survival with age (e.g., Hastings and Testa 1998) and in other species a role of maternal senescence in decreasing offspring survival with age (e.g., Descamps et al. 2008). The cognitive complexity of baboons, combined with the ecological complexity of the environment in which they live, strongly suggest a role for maternal experience in promoting offspring survival (Pusey 2012; see also: Kornberg et al. 1997; Muller et al. 2006). The current study is consistent with these results, as nulliparous mothers have lower offspring survival than more experienced mothers. However, the current study also suggests that maternal competence declines as females age, resulting in lower offspring survival among older mothers. Notably, offspring survival in our study decreases at a similar rate for mothers of both short and long lifespans, indicating that maternal competence declines as the probability of maternal survival declines (fig. 3).

In contrast to the results for offspring survival, we found no evidence of a linear decline in live birth rate with maternal age (table S4), although reproductive senescence has been widely documented in a range of other taxa (see Nussey et al. 2013; Lemaitre and Gaillard 2017; Gesquiere et al. 2018 for recent reviews). Our evidence for reproductive senescence in the Amboseli baboons is ambiguous, as other work in the population has detected evidence of linear and/or quadratic age effects on some reproductive phenotypes (Beehner et al. 2006, Alberts and Altmann 2010, Alberts et al. 2013, Gesquiere et al. 2018) and the current study documents potential for age related decline in maternal competence. These mixed results demonstrate the pressing need for further, detailed investigations into both the age-dependence of live interbirth intervals and the possibility that individual quality contributes to variation in the age at onset or the rate of reproductive senescence (for example, see Nussey et al. 2007; Bouwhuis et al. 2010).

Our results motivate future work to dissect the contributions of genetic and environmental differences among individuals to the phenotypic variation we have observed here. Such work would be feasible using the animal model (Lynch and Walsh 1998; Kruuk 2004; Wilson et al. 2010), which would also allow for the investigation of genetic contributions to variance in female quality and the estimation of the genetic correlation between our traits of interest and fitness (Rausher 1992; Morrissey et al. 2010). As investigation into the physiological, molecular and genetic mechanisms underlying life history traits increases, we highlight the importance of considering heterogeneity in individual quality – both in deciding where to look for the mechanisms of tradeoffs (probably in individuals of low quality) and as a field of investigation in its own right.