Personalized Risk Prediction in Clinical Oncology Research: Applications and Practical Issues Using Survival Trees and Random Forests

Abstract

A crucial component of making individualized treatment decisions is to accurately predict each patient’s disease risk. In clinical oncology, disease risks are often measured through time-to-event data, such as overall survival and progression/recurrence-free survival, and are often subject to censoring. Risk prediction models based on recursive partitioning methods are becoming increasingly popular largely due to their ability to handle non-linear relationships, higher order interactions, and/or high dimensional covariates. The most popular recursive partitioning methods are versions of the Classification and Regression Tree (CART) algorithm, which builds a simple interpretable tree structured model. With the aim of increasing prediction accuracy, the random forest algorithm averages multiple CART trees, creating a flexible risk prediction model. Risk prediction models used in clinical oncology commonly use both traditional demographic and tumor pathological factors as well as high-dimensional genetic markers and treatment parameters from multi-modality treatments. In this article, we describe the most commonly used extensions of the CART and random forest algorithms to right-censored outcomes. We focus on how they differ from the methods for non-censored outcomes, and how the different splitting rules and methods for cost complexity pruning impact these algorithms. We demonstrate these algorithms by analyzing a randomized phase III clinical trial of breast cancer. We also conduct Monte Carlo simulations to compare the prediction accuracy of survival forests with more commonly used regression models under various scenarios. These simulation studies aim to evaluate how sensitive the prediction accuracy is to the underlying model specifications, the choice of tuning parameters, and the degrees of missing covariates.

1. Introduction

With the development of “omics”-based technology, different cancer types are no longer narrowly and purely defined based on clinical and pathologic taxonomic systems. As elaborated in the 2011 US Institute of Medicine’s National Research Council report Toward Precision Medicine: Building a Knowledge Network for Biomedical Research and a New Taxonomy of Disease (Desmond-Hellmann et al., 2011), the key of precision medicine is to precisely identify patients with different risks of developing a disease, different disease prognoses, or different responses to treatment, by integrating the ever-increasing magnitude of data collected from different sources more rapidly if not simultaneously. In oncology research, precision medicine is reshaping disease diagnosis and management in many ways. New standards of care have been and will continue to be developed for the newly (re)defined disease subtypes, which are collectively defined through clinical/pathological factors and biomarkers. For example, epidermal growth factor receptor (EGFR)-positive metastatic non-small cell lung cancer (mNSCLC) is now widely considered as a separate disease subtype as opposed to being included in the general mNSCLC and treated with different standard of care. Another example is the development and use of 70-gene signature in early stage breast cancer treatment management. The 70-gene signature has been shown to be an important prognostic tool to stratify patients based on the predicted disease recurrence risks (Van De Vijver et al., 2002).Recently, the landmark MINDACT trial further demonstrated its role to aid treatment decision making in early-stage breast cancer (Cardoso et al., 2016).

Development and application of analytic tools that can precisely and robustly predict and stratify disease risks thus stand for one of the key infrastructures in the era of precision medicine. Only after we identify patients’ disease risks and prognoses, we are able to evaluate and apply innovative interventions that are appropriate to patients’ benefit-risk profiles. Predicting and stratifying disease risks for complex diseases like cancer is often further complicated by the presence of censoring. Unlike vast majority of genetic studies on other complex disease where the outcomes are typically binary (e.g., disease vs. non-disease), the disease risks in oncology are most commonly measured in terms of time to event occurrence, such as overall survival (time from treatment initiation or randomization to death) or progression/recurrence-free survival (time from treatment initiation or randomization to the first occurrence of progression or death). All of these endpoints are frequently subject to censoring, especially right censoring.

In the absence of censoring, methods based on Classification and Regression Trees (CART) are increasingly becoming a popular alternative to more traditional regression methods. CART is a class of nonparametric models which construct risk prediction models by recursively partitioning the covariate space (Breiman et al., 1984). Regression trees stratify patients into different risk groups based on a continuous outcome creating a prediction model that is both easy to interpret and visualize. The hierarchical nature of the tree building process can result in an unstable model with low prediction accuracy. With the aim of improving prediction accuracy, Breiman (2001) proposed the random forest procedure which averages multiple regression trees creating a more flexible risk prediction model. The usually improved prediction accuracy of random forests, when compared to regression trees, comes at the price that the random forest algorithm creates a “black-box” model that is hard to interpret or visualize.

Several papers extend the regression tree and random forest algorithms to censored data and the resulting algorithms are respectively referred to as survival trees and survival forests. There are several advantages of these methods compared to more traditional regression models such as the Cox and accelerated failure time models. Survival trees and forests do not make any parametric or semi-parametric assumptions and have the ability to detect and account for higher order interactions as well as non-linear relationships. The functional form of the covariates is also not pre-specified so the user does not need to decide which main effects or interactions to include in the model. They can also easily account for the situation when the covariate dimension is larger than the sample size. An important disadvantage of regression tree based methods compared to the Cox model is that theoretical properties as well as inferential procedures are not well understood. For survival forests, another disadvantage is the lack of interpretability of the resulting model.

CART based methods, which are sometimes referred to as recursive partition analysis (RPA) methods in the clinical oncology literature, have been used in some diseases areas to advance our understanding of diagnosis and prognosis. For example, when treating glioblastoma multiforme (GBM), the most aggressive primary brain cancer, the prognostic groups being widely used in clinical trials and disease management for risk stratifications were developed based on an early survival tree method (Ciampi et al., 1988) and thus called GBM-RPA classes (Curran et al., 1993). After having been validated and used repeatedly for more than two decades, the prognostic groups have been recently refined by incorporating biomarker information (Bell et al., 2017) based on a commonly used survival tree method proposed by LeBlanc and Crowley (1992). In contrast, to the best of our knowledge, it appears that survival forests have not been adopted widely in the clinical oncology literature so far.

The remainder of this paper is organized as follows. Sections 2 and 3 introduce some commonly used survival tree and survival forests algorithms with an emphasis on their rationale, applications, and some practical issues when implementing them in translational research. In section 4 we give an overview of available implementations in the software R. Section 5 demonstrates how survival trees and forests can be used to analyze data from a randomized phase 3 trial on breast cancer treatment. In section 6 we use simulations to illustrate the improvements in prediction accuracy compared to a Cox model in settings where the proportional hazard assumption is violated and when the Cox model fails to correctly include interactions. We furthermore explore how prediction accuracy is impacted both by the choice of tuning parameters and methods for dealing with missing data. We conclude this paper with discussions and some remarks in Section 7.

2. Survival Tree Methods

Section 2.1 briefly describes the CART algorithm for continuous uncensored outcomes and Section 2.2 describes the most popular survival tree algorithms.

2.1. Regression Trees in Absence of Censoring

In this subsection, the dataset is assumed to consist of n i.i.d. observations of the form (T W, ), where $T\in ℝ$ is a continuous outcome and $W\in {ℝ}^p$ is a p dimensional covariate vector. We only present a high level overview, for more details we refer to Breiman et al. (1984).

The first step in the regression tree algorithm is to recursively split the covariate space into smaller and smaller rectangles until a predetermined criteria is met. At the beginning of the process all the data is in a single group (called a node). The dataset is split into two groups (called daughter nodes) using the covariate splitpoint combination that results in the largest reduction in L₂ loss. This process is repeated recursively within each of the two daughter nodes until a pre-determined criteria is met. This step builds a complex prediction model that usually substantially overfits the data.

The second part of the regression tree algorithm, commonly referred to as cost-complexity pruning, aims to avoid overfitting. For a fixed $\alpha \in {ℝ}_{+}$ the cost complexity of a tree ψ(W) is defined by

$$C{C}_{\alpha }(\psi )=\sum _{i=1}^n{\left(T_i-\psi \left(W_i\right)\right)}^2+\alpha |\psi (W)|,$$ (1)

where | ψ(W) | is the number of distinct groups, referred to as terminal nodes, that the tree splits the covariate space into. The cost complexity consists of two terms, the training error and a term penalizing the size of the tree, where the size of the penalty depends on the tuning parameter α. When comparing several trees we say that a tree is optimal with respect to the cost complexity for a fixed α if it minimizes CC_α. Varying α over the interval [0, ∞) results in different optimal subtrees w.r.t. CC_α. This algorithm creates a finite sequence ψ₁,…,ψ_K of candidate trees to become the final prediction model, where each tree in the sequence is optimal w.r.t. some interval corresponding to α. The final tree is then selected from the sequence using L₂ loss cross-validation. The final estimator within a terminal node is calculated as the mean restricted to using observations falling in that terminal node.

2.2. Survival Trees

In presence of censoring (denoted by C), the observed data on each subject consists of $(\tilde{T}=\min (T,C),\mathrm{\Delta }=I(T\le C),W)$. For uncensored responses, the CART algorithm uses L₂ loss to calculate the reduction in loss and perform the cost complexity pruning and cross-validation. With time-to-event outcomes, calculating the L₂ loss requires knowledge of the true failure time for all observations, which is unknown for all censored observations. How to replace the L₂ loss by a quantity that can be calculated when there is censoring has been the main driving force behind methodological developments extending the CART algorithm to censored data.

Survival tree methods can be grouped into two categories (Molinaro et al., 2004). The first category makes splitting decisions by minimizing the risk within nodes, which intuitively is maximizing some measure of homogeneity within a node (e.g.,Gordon and Olshen (1985); LeBlanc and Crowley (1992); Molinaro et al. (2004); Steingrimsson et al. (2016a)). The associated pruning and stopping algorithms are largely based on extensions of the cost-complexity and cross-validation steps to handle censored outcomes.

The second category deviates from the traditional CART methods in that the splitting criteria are meant to maximize the between-node heterogeneity (e.g., Ciampi et al. (1986); Segal (1988); Leblanc and Crowley (1993)). Table 0 summarizes the key ideas of splitting and selection used for several survival tree methods. For a recent review of survival tree based methods we refer to Bou-Hamad et al. (2011). Now we will describe two of the most commonly used survival trees, the Relative Risk Trees proposed in LeBlanc and Crowley (1992) and extensions of conditional inference trees to censored data (Hothorn et al., 2006).

The starting point of the development in LeBlanc and Crowley (1992) is a likelihood for the tree structure assuming that the failure time distribution within a node follows a proportional hazard model with a common baseline hazard across nodes. An one-step estimator for the likelihood is calculated using a one-step estimator of the Breslow estimator for the unknown cumulative hazard. The one-step deviance of a node is then calculated as twice the difference between the likelihood of a saturated model and the likelihood of that node. Splits are based on finding the covariate splitpoint combination that maximizes the reduction in one-step deviance. The cost-complexity of a tree is defined in the same manner as formula (1) with the training error replaced by the one step deviance. This deviance based cost complexity criteria is used to create a sequence of candidate trees and the final tree model is selected from that sequence by finding the tree that minimizes the cross-validated one step deviance.

Hothorn et al. (2006) proposed conditional inference survival trees. The key idea is to replace the splitting and cost-complexity pruning step by a permutation test based splitting and stopping criteria. The p-value from a global null hypothesis test serves both as the splitting and stopping criteria. If the global test is not rejected at a pre-specified significance level the node is not split further. If the global hypothesis test is rejected the node is split using the covariate and splitpoint combination which is most strongly associated with the outcome. For censored data the authors propose to use either a log-rank test or tests based on inverse probability censoring weighted (IPCW) methods to calculate the association between covariates and the outcome. The authors demonstrated that the conditional inference algorithm offers comparable predictive performance as competing methods, and can effectively overcome a long-standing challenge in CART based extension, i.e., the final tree selection tends to favor predictors with many potential splits.

3. Random Forests for Survival Data

3.1. Random Forests in Absence of Censoring

With the aim of improving prediction accuracy, Breiman (1996) proposed the bagging algorithm which averages multiple fully grown regression trees (no cost-complexity pruning) to create a more flexible prediction model. To de-correlate the individual regression trees used in the bagging algorithm, Breiman (2001) proposed the random forest algorithm. When a splitting decision is made in the random forest algorithm, instead of searching over all splitpoint and covariate combinations only mtry ≤ p of the covariates are considered. The individual trees in the random forest algorithm are often referred to as the building blocks or base learners of the algorithm.

The basic random forest algorithm can be summarized by the following three steps: (1) draw M different bootstrap samples from the original dataset; (2) for each bootstrap sample build a fully grown tree (without cost complexity pruning), where at each splitting decisions the search for the best split is restricted to mtry covariates which are randomly selected from the p different covariates.; (3) the final prediction model is obtained by averaging the predictions from each of the M trees built in step (2).

Each bootstrap sample selects approximately 63.2% of observations referred to as the “in-bag” data, and the remaining 36.8% of observations which are not selected in the bootstrap sample is referred to as the “out-of-bag” (OOB) data. Measures based on OOB prediction error have been used in random forests to simultaneously assess model validation and variable importance.

3.2. Extensions to Censored Data

Several extensions of the random forest algorithms to censored data have been developed. Zhu and Kosorok (2012) proposed the recursively imputed survival trees algorithm which makes splitting decisions using log-rank test statistics and uses extremely randomized trees instead of CART trees as building blocks. Steingrimsson et al. (2016b) base splitting decisions on censoring unbiased transformations which are unbiased estimators of the L₂ risk.

Ishwaran et al. (2008) developed the random survival forest (RSF) algorithm where splitting decisions are made to maximize the between-node heterogeneity, such as a log-rank test statistic (Segal, 1988; Leblanc and Crowley, 1993) or a standardized log-rank (score) statistic (Hothorn and Lausen, 2003). For the j -th bootstrap sample (j =1,…,M), denote the total number of events until time s by ${\tilde{N}}_j^{*}(s,W)$ and the number at risk at time s by ${\tilde{Y}}_j^{*}(s,W)$, both restricted to the terminal node which W falls into in the tree built from bootstrap sample j. The random survival forest algorithm aggregates the Nelson-Aalen terminal node estimators of all bootstrap-based trees to obtain the predicted survival functions ${\widehat{S}}^{\mathrm{r}}(t|W)$ as

$${\widehat{S}}^{\text{r}}(t|W)=\exp \left(-\frac{1}{M}\sum _{j=1}^M{\int }_0^t\frac{{\tilde{N}}_j^{*}(ds,W)}{{\tilde{Y}}_j^{*}(s,W)}\right).$$

Hothorn et al. (2017) implement conditional inference forests using conditional inference trees as base learners, calculating weighted Kaplan-Meier estimators at each terminal node. As for the random survival forest algorithm, the final prediction is an estimator for the conditional survival function S₀ (u | W) = P(T > u | W ). The predicted survival function ${\widehat{S}}^{\mathrm{c}}(t|W)$ can be expressed as

$${\widehat{S}}^{\mathrm{c}}(t|W)=\prod _{s\le t}\left(1-\frac{{\sum }_{j=1}^M{\tilde{N}}_j^{*}(ds,W)}{{\sum }_{j=1}^M{\tilde{Y}}_j^{*}(s,W)}\right).$$

As pointed out by mogensen 2012 evaluating, the two approaches to obtain predicted survival functions, e.g., ${\widehat{S}}^{\mathrm{r}}(t|W)$ and ${\widehat{S}}^{\mathrm{c}}(t|W)$, only differ in whether to assign more weights to terminal nodes with more subjects are at risk, by showing

$$\frac{{\sum }_{j=1}^M{\tilde{N}}_j^{*}(ds,W)}{{\sum }_{j=1}^M{\tilde{Y}}_j^{*}(s,W)}=\frac{1}{M}{\sum }_{j=1}^M{\omega }_j\frac{{\tilde{N}}_j^{*}(ds,W)}{{\tilde{Y}}_j^{*}(s,W)},$$

where ${\omega }_j=\frac{{\tilde{Y}}_j^{*}(s,W)}{1/M{\sum }_{j=1}^M{\tilde{Y}}_j^{*}(s,W)}$.

3.3. Evaluating Prediction Accuracy, Variable Importance Measures, and Missing Data

Prediction Accuracy

One of the key motivations for the random forest algorithm is to improve the prediction accuracy. In the absence of censoring, prediction accuracy of any prediction model can be evaluated using several methods such as cross-validation, concordance index (C-index), or ROC-based estimators. As the true failure time is unknown for censored observations, evaluating prediction accuracy is harder for failure time data than for fully observed continuous or binary outcomes.

Now we describe the censored data Brier score, a commonly used method to evaluate prediction accuracy when some observations are censored. The Brier risk for an estimator S (t | W) at fixed time t is defined by E[(I(T > t) – S(t | W)) ²]. Graf et al. (1999) proposed to use IPCW to account for censoring when estimating the Brier risk and the resulting censored data Brier Score estimator at a given time t is given by

$$\frac{1}{n}\sum _{i=1}^n\frac{{\mathrm{\Delta }}_i(t){(I({\tilde{T}}_i(t)>t)-\widehat{S}(t|W_i))}^2}{\widehat{G}(\min (t,{\tilde{T}}_i)|W_i)}.$$

Here, $\tilde{T}(t)=\min (T,t,C)$, $\mathrm{\Delta }(t)=I(\tilde{T}(t)\le C)$, and $\widehat{G}(u|W)$ is an estimator for the censoring curve P(C > u | W). When evaluating the prediction accuracy of a prediction model cross-validation is commonly used to avoid overfitting.

Variable Importance Measures (VIMP)

Variable selection and evaluating which variables influence prediction accuracy is another important aspect in survival forest analysis. Permutation and minimal depth VIMPs are both commonly used to evaluate importance of a variable on prediction accuracy.

The rational for permutation based VIMPs is that the more “important” a covariate is, the larger the anticipated increase in prediction error is when its relationship with the outcome is destroyed. Formally, permutation based VIMPs for a covariate W^(j) is defined as the average differences between the prediction errors when W^(j) is randomly permuted, and the prediction errors under the observed values of W^(j), using the out-of-bag data and across all trees within the (Breiman, 2001; Ishwaran et al., 2008). The larger the permutation VIMP is, the more important a covariate is with respect to the prediction error. Practically, VIMP appears to asymmetrically favor continuous covariates or categorical covariates with many levels, although it becomes less biased when conditional inference trees are used as the base learner (Gröomping, 2009).

Minimal depth VIMPs (Ishwaran and Kogalur, 2010) is another intuitive idea to quantify the relative importance of variables in random forests. If a covariate frequently splits close to the root node that covariate is considered more importance. Formally, within each tree if we rank all nodes based on their relative “distance” to the root node (i.e., 0 for root node, 1 for first-level daughter node, etc.), we can obtain the distribution of minimal depth for any covariate by recording its first splits across all trees within the forest. Chen and Ishwaran (2012) argued that minimal depth has several advantages over permutation based VIMPs, including (1) it is independent from the terminal node estimators; (2) it has nice theoretical properties including closed-form distributions. They also suggested using the mean of the minimal depth distribution as an optimistic threshold for variables to be considered as important in prediction.

Missing Data

Random forests involves two levels of randomization, bootstrap and randomly selecting a subset of covariates when making splitting decisions. Therefore the conventional surrogate splitting approach used in CART trees to handle missing data becomes problematic. Ishwaran et al. (2008) proposed an adaptive imputation procedure, which imputes missing data right before each node splits, instead of imputing before growing the forest. At each node split, this approach imputes missing values by randomly drawing from non-missing cases within the same node. These imputed values are only used when observations need to be further sorted into subsequent nodes. However they don’t contribute to impact the split decision, nor are used again at other nodes. This process is repeated until the stopping criteria are met.

4. Computer Software Implementations

The R package rpart (Therneau et al., 2015) implements the relative risk trees and allows for multiple options such as incorporating case weights and controlling the minimum size of the terminal node. The package allows the user to write their own user written splitting criteria, a useful feature when implementing a new survival tree method. The package rpart.plot allows for nice plotting options.

The R package party (Hothorn et al., 2017) implements the conditional inference tree method. The option mincriterion specifies the threshold to trigger splits which controls the tree size. The R package partykit also converts a tree fitted using rpart to a party compatible tree, so that the trees fitted by different packages can be visualized in the same fashion.

The random survival forest algorithm is implemented in the random ForestSRC R package (Ishwaran and Kogalur, 2016). Among other things, the users can choose different values of ntree to control the numbers of bootstrap samples, mtry to control the number of covariates randomly selected for each split, nodesize to control the minimum number of failure times at each terminal node, and splitrule to control if a log-rank test statistic (Segal, 1988; Leblanc and Crowley, 1993) or a log-rank score statistic (Hothorn and Lausen, 2003) to be used as the splitting rule. User-defined custom splitting rule is also permitted. The package ggRandomForests (Ehrlinger, 2016) offers nice visual tools for intermediate data objects from randomForestSRC, including permutation VIMPs, minimal depth VIMPs, and various variable dependency plots. The package party provides a unified random forest implementation for categorical, continuous and survival outcomes, based on conditional inference trees (Hothorn et al., 2006) as the base learners. The package pec (Mogensen et al.,2012) calculates prediction error curves for survival trees and forest.

5. Analysis of the German Breast Cancer Dataset

In this section we use both survival trees and forests to analyze the German Breast Cancer dataset which is publicly available in the R package TH.data. The R code used for analysis is provided in the supplementary material. The dataset is from a prospective randomized clinical trial on the treatment of node positive breast cancer in 686 patients. The covariates we use in the analysis are hormonal therapy (horTh), age, menopausal status (menostat), tumor size (tsize), tumor grade (tgrade), number of positive nodes (pnodes), and levels of progesterone (progrec) and estrogen (estrec) receptor, where the last two variables are measured in fmol. Previous analysis in Schumacher et al. (1994) suggests that the number of positive nodes and the levels of progesterone receptor are important predictors.

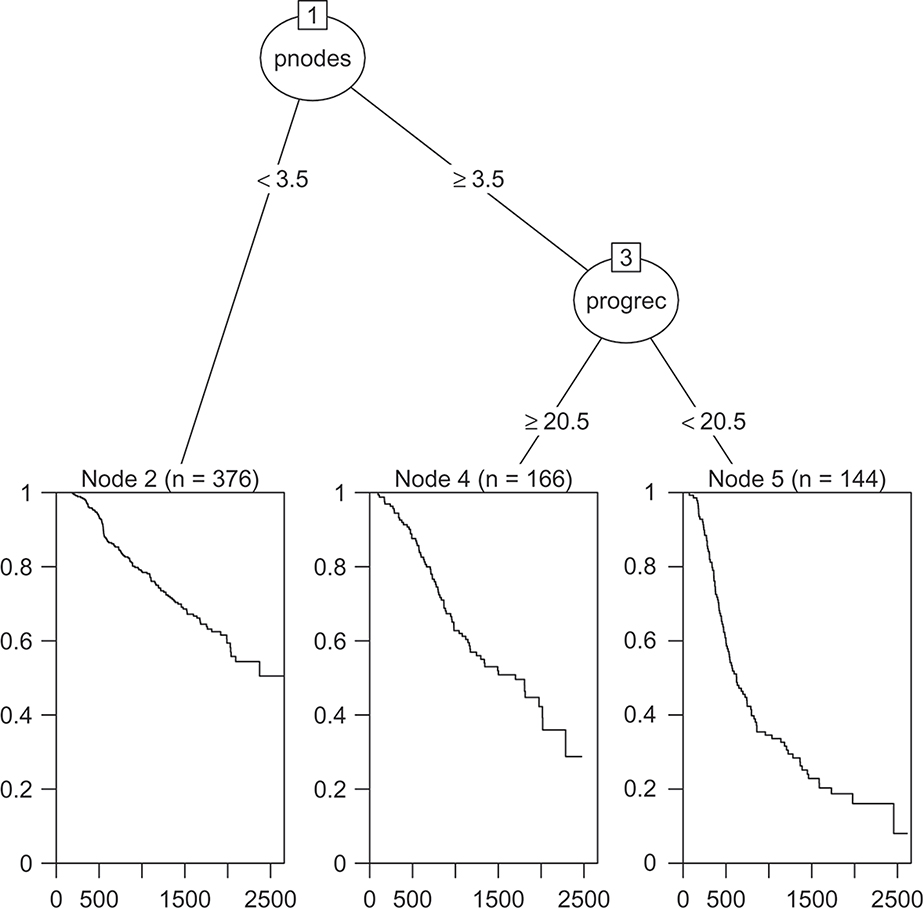
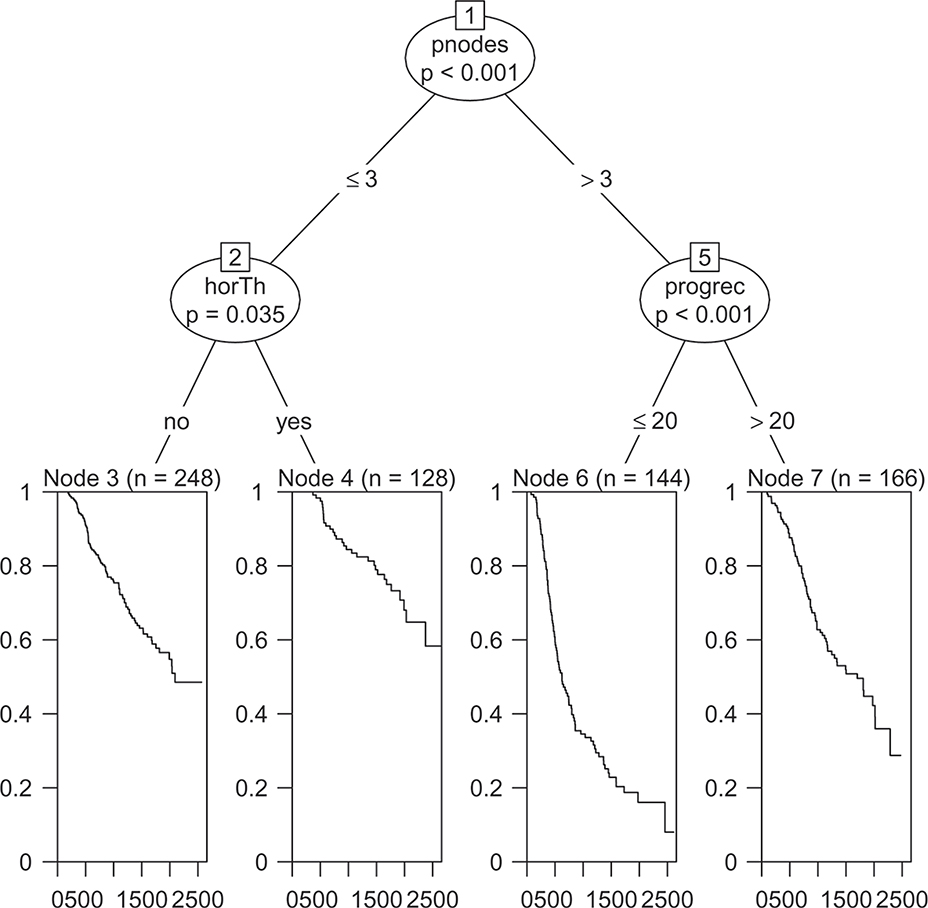
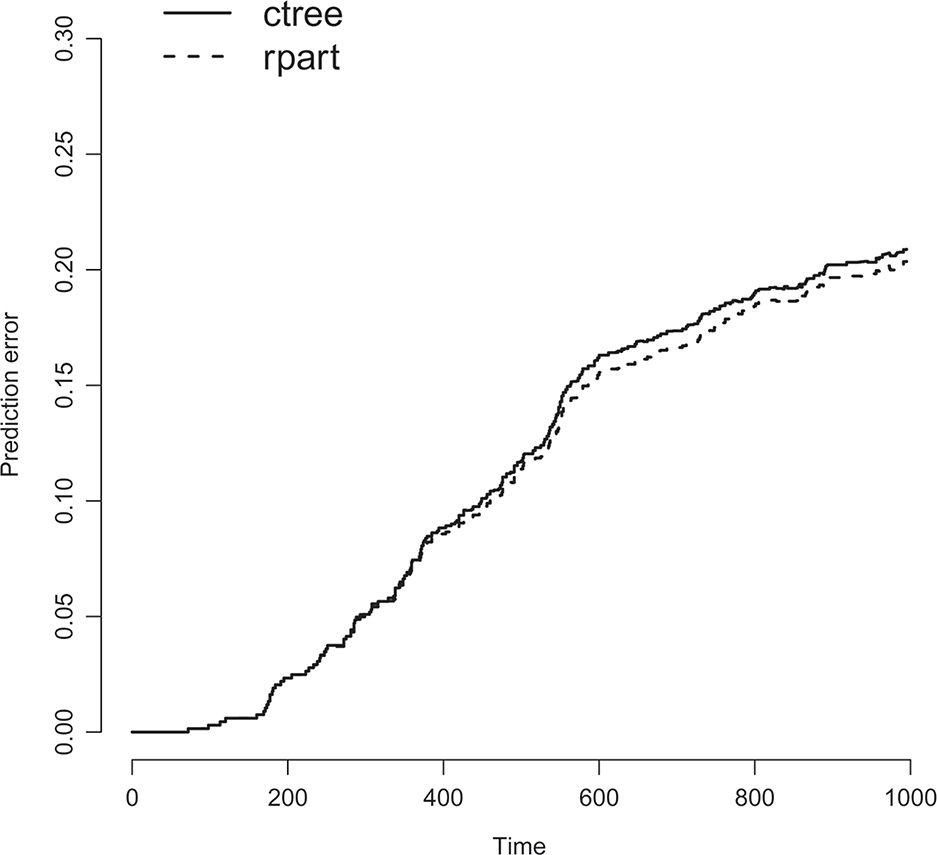
Figures 1–2 show the final trees fitted using the default methods for censored data in the rpart and party packages. From the figures we see that both trees split first on if the number of positive nodes is greater than three or not. Both trees also split the group with more than three positive nodes according to if the level of progesterone receptor is larger than 20. The only other split made is that the conditional inference tree splits the group with less than four positive nodes according to if the participant had undergone hormonal therapy or not. Figure 3 compares the prediction accuracy of the two trees calculated using the cross-validated censored data Brier score as a function of time, calculated using the R package pec. Here, lower values imply better performance.

Figure 1:

Default rpart algorithm for censored data fit to the German breast cancer data.

Figure 2:

Default ctree algorithm for censored data fit to the German breast cancer data.

Figure 3:

Prediction accuracy for the rpart and ctree trees.

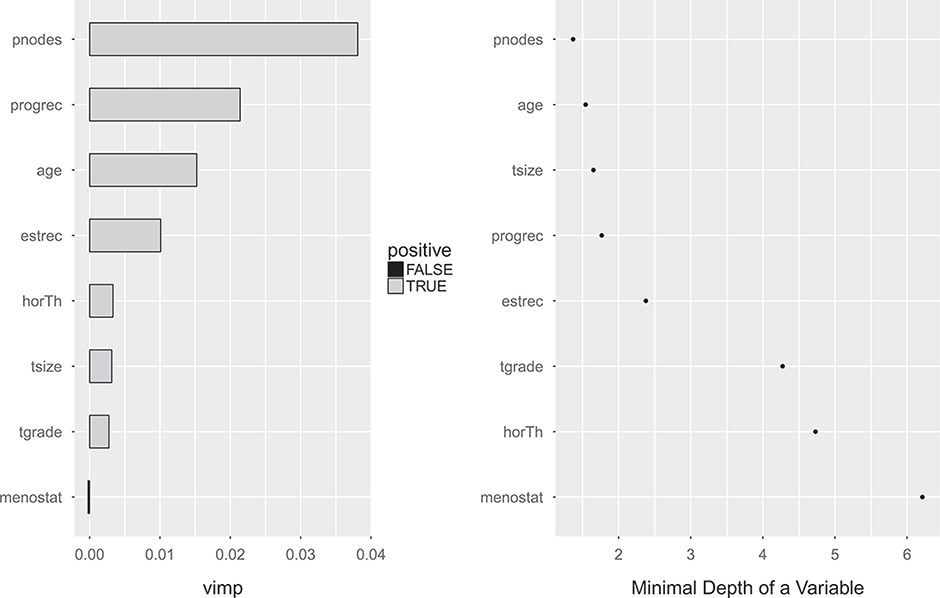
Figure 4 shows the permutation (left) and minimal depth (right) variable importance measures corresponding to the random survival forest procedure. For the permutation based variable importance measure, the number of positive nodes and the levels of progesterone receptor are the two most important variables. Age, number of positive nodes, tumor size, and the levels of progesterone receptor have substantially lower minimal depth variable importance measures than the other variables.

Figure 4:

Permutation (left) and minimal depth (right) variable importance measures for the German breast cancer dataset. Higher values imply more important variables for the permutation based variable importance measure. Lower values imply more important variables for the minimal depth variable importance measure.

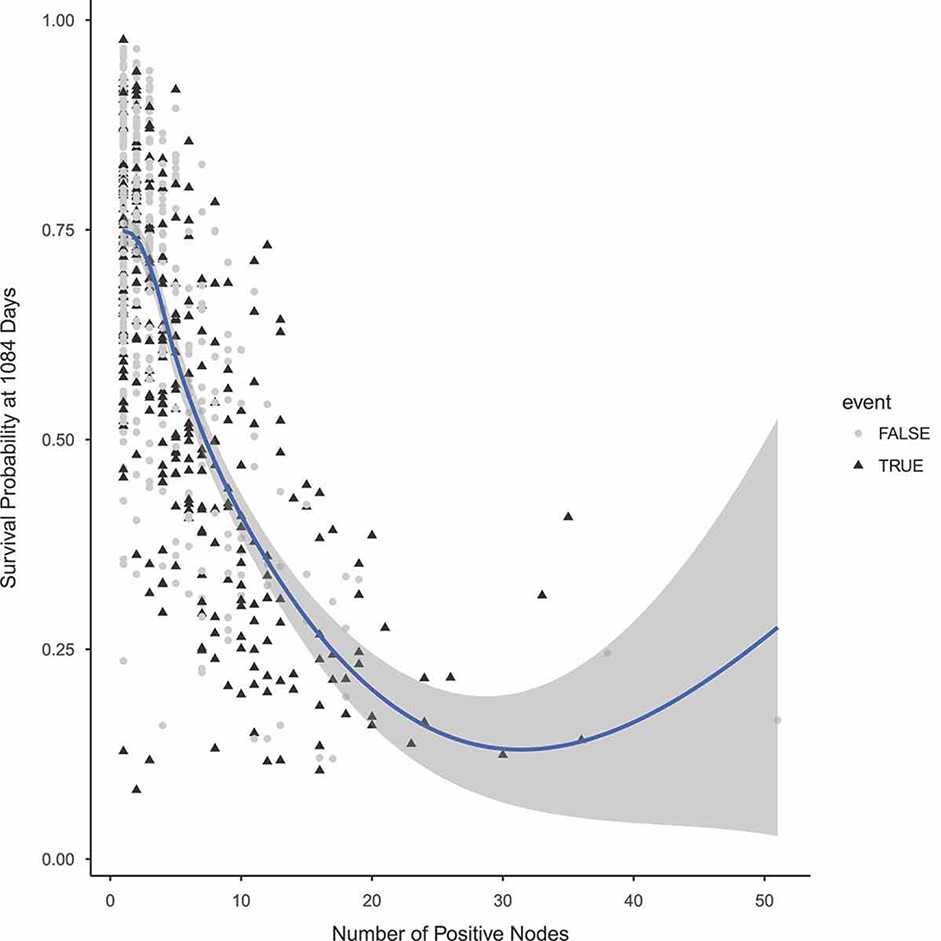
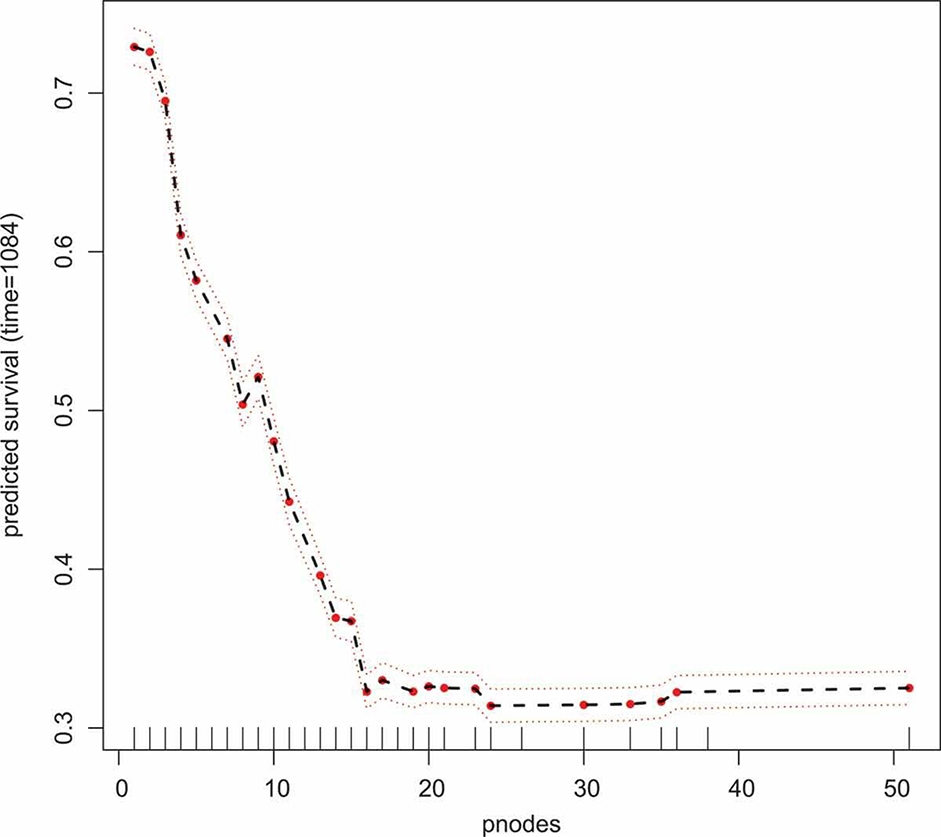
To further investigate the effect of number of positive nodes on predicted survival, we use variable dependency and partial dependency plots. A variable dependency plot shows the predicted survival probability at a pre-specified timepoint as a function of a specific covariate, here the number of positive nodes. Each point on the plot represents one datapoint in the training set. Partial dependency plots are created by integrating (averaging) over the effect of other covariates. To calculate the partial dependency for a fixed value a of number of positive nodes, predictions are calculated for all observations in the training set by setting the number of positive nodes to a. The partial dependency at number of positive nodes equal to a is then calculate as the average of these predictions. Figures 5 and 6 are variable dependency and partial dependency plots, which show the effect of number of positive nodes on the probability of surviving beyond 1084 days. Here, 1084 days is the median of the observed times in the dataset. From both figures we see that more positive nodes correspond to lower survival probabilities.

Figure 5:

A variable dependency plots for the effect of number of positive nodes on surviving beyond 1084 days in the German Breast Cancer dataset.

Figure 6:

A partial dependency plot showing the effect the number of positive nodes has on the probability of surviving beyond 1084 days in the German Breast Cancer dataset.

For comparison, Table 2 shows the results from a main effects Cox model. From the table we see that the number of positive nodes and levels of progesterone receptor levels are the two most influential covariates.

Table 2:

Estimates and test statistics from a main effects Cox model fit to the German breast cancer study.

	HR	Wald Statistics	p-value
Hormonal therapy	0.71	−2.68	0.007
Age	0.99	−1.02	0.31
postmenopausal	0.26	1.41	0.16
Tumor size	1.00	1.98	0.048
Tumor grade II vs. I	1.89	2.55	0.01
Tumor grade III vs. I	2.18	2.90	0.004
Number of positive nodes	1.05	6.55	< .001
Levels of progesterone receptor	1.00	−3.87	< .001
Levels of estrogen receptor	1.00	0.44	0.66

6. Simulations

In this section we aim to quantitatively evaluate the prediction accuracy of survival forests, focusing on practical issues that may arise in clinical oncology translational research: (1) the impacts of model mis-specification, in comparison with Cox models (regular and penalized); (2) the impacts of various tuning parameters; (3) the impact of missing covariates. The survival forest methods under evaluation include random survival forest (as implemented in R package randomForestSRC), and extensions of conditional inference forests to censored data (as implemented in R package party). The penalized Cox model is implemented in the R package glmnet.

The default tuning parameters are used for all methods and the optimal λ for the L₁ penalized Cox model is selected using ten fold cross-validation. In addition, we also include random survival forests with a feature selection. Before the algorithm is implemented, variable selection is performed using minimal depth variable importance measures as described in Ishwaran et al. (2010) and implemented using the function var.select in the package randomForestSRC. The random survival forest algorithm is then run using only the selected covariates.

As previously stated, one of the advantages of survival forest algorithms is that complex model specification, such as interactions between main effects, do not need to be pre-specified by the users. Survival forest algorithms, due to their non-parametric nature, should also be robust to specific model assumptions such as the proportional hazards assumption. To evaluate the practical performance of the different algorithms, we therefore considered the following two simulation settings: (1) when the proportional hazard (PH) assumptions holds and an interaction term is present; (2) when the PH assumption is violated.

In both settings, we assume the covariate dimension p = 50 and the covariate vector is normally distributed with mean zero and covariance matrix with element (i,j) equal to 0.9^|i-j|. Such an assumption is meant to mimic a reasonable translational research study, where a moderate number of possibly correlated biomarkers are simultaneously of interest. In Setting 1, the failure time is simulated from a proportional hazard model with hazard rate $\lambda (t|W)=e^{W_2+W_1{W}_2}$. The remaining covariates W₃,···,W₅₀ are independent of the failure time.The censoring time follows an exponential distribution with rate 1, which results in 37% censoring. In Setting 2, the failure time follows a gamma distribution with shape parameter $\frac{1}{2}+\frac{1}{3}|{\sum }_{j=1}^{10}{W}_j|$ and scale parameter 1. The remaining W₁₁,···,W₅₀ are assumed to have null effects. The censoring variable is exponentially distributed with rate 0.2, which results in 37% censoring rate. In both settings, all the algorithms were fit on a training set consisting of 200 and 500 i.i.d. observations and used to predict P(T > t_j | W_i) for a fixed t_j, j =1,2,3 on an independent test set of size n =1,000. In both settings the landmark times of interest t _j are the 25,50, and 75th quantile of the marginal survival distribution. A total of 1,000 simulations are used for all the simulations reported in this section.

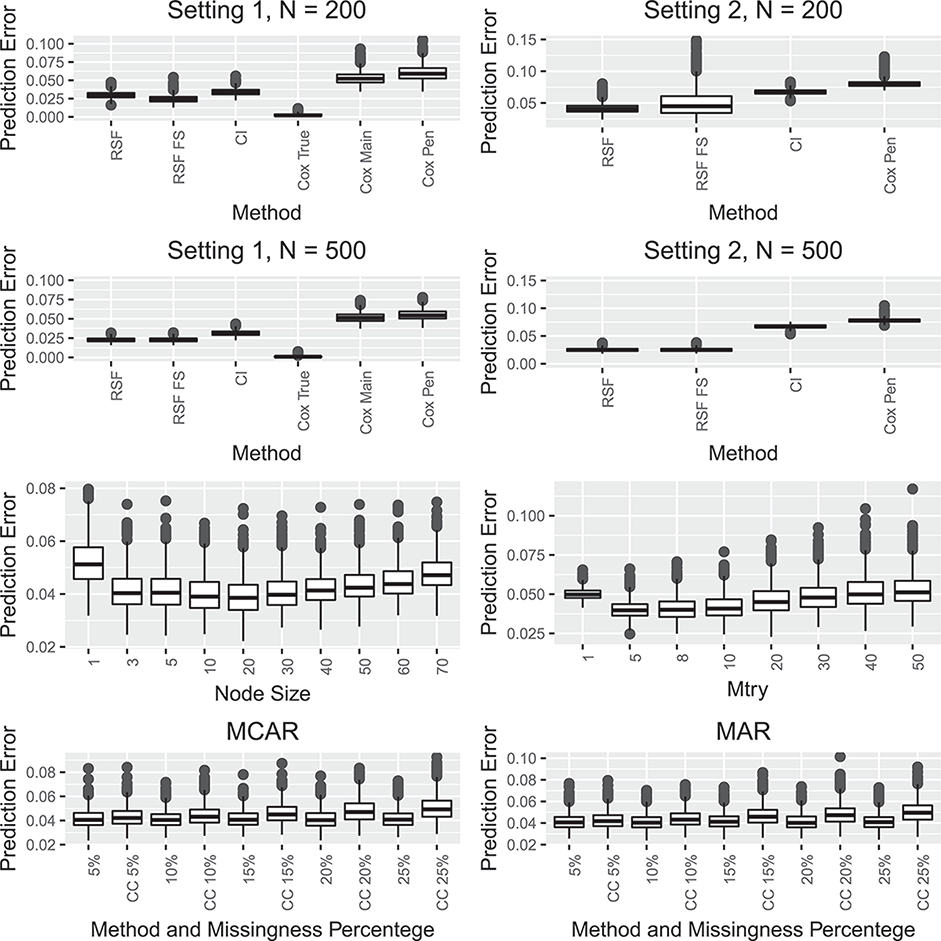
The top row in Figure 7 shows the prediction errors, defined as

$$\frac{1}{3}\sum _{j=1}^3\frac{1}{1000}\sum _{i=1}^{1000}{(\widehat{P}\left(T>t_j|W_i\right)-P\left(T>t_j|W_i\right))}^2,$$

for all algorithms considered under both simulation settings when the sample size is 200. The second row shows the prediction errors for a sample size of 500. All trends seen in the plots were similar for both sample sizes.

Figure 7:

The first two rows shows simulation results comparing prediction error for random survival forests (RSF), random survival forests with feature selection (RSF FS), conditional inference forests (CI), and a penalized cox model (Cox Pen) in two settings described in Section 6. The first row shows the results when the sample size is 200 and the second row for the sample size 500. For the first setting Cox True and Cox Main refer to the true underlying Cox model and a Cox model that includes the correct main effects. The third row shows the impact of the choice of the tuning parameters mtry and node size on the prediction error for the random survival forest algorithm. The fourth row shows the impact of missing data on the prediction error for the random survival forest algorithm both when the missing is completely at random and when the missingness is at random.

In Setting 1, the correctly specified Cox model (which includes the correct main effects and interactions) is included to serve as a benchmark when comparing with other algorithms. Not surprisingly, it outperforms all other algorithms and has the smallest prediction errors. Any of the non-parametric survival forest procedures show a better prediction accuracy than the mis-specified Cox models, which include a model with correctly specified main effects but not the interaction. The penalized Cox model which selects from all main effects shows the worst prediction accuracy among all algorithms evaluated.

Similarly, when the proportional hazard assumption is violated (Setting 2), the penalized Cox model performs substantially worse than all the non-parametric survival forest procedures. These findings highlight that the prediction accuracy of the Cox models highly depends on if the model is correctly specified, and thus the survival forest algorithms may be preferred to avoid the potential model mis-specification risks.

In both settings, the random survival forest procedures (with or without feature selection) perform better than the conditional inference forests. Whether to perform variable selection prior to the random survival forest algorithm appears to depend on how strong underlying covariate effects are. When the signal is strong (Setting 1), the prediction error for performing upfront variable selection is lower. In contrast, when the signal is weak (Setting 2), the variability of prediction errors for random survival forest with feature selection is larger than the regular random survival forest.

The third row of Figure 7 shows the impacts of tuning parameters mtry (right) and the node size (left) on prediction errors for the random survival forest procedure under Setting 2 and sample size 200. For both parameters the default values $mtry=\lceil \sqrt{p}\rceil =8$ and node size equal to three perform well.

In the presence of missing data, it is common to perform a complete case analysis which completely ignores observations with at least one missing covariate. The fourth row in Figure 7 summarizes the impacts of missing data under Setting 2 with a sample size of 200. We are interested in comparing the prediction accuracy of the adaptive imputation approach (implemented for random survival forests using rfsrc function) for handling missing data and a complete case analysis approach. Recall that under Setting 2, the failure time follows a gamma distribution with shape parameter $\frac{1}{2}+\frac{1}{3}|{\sum }_{j=1}^{10}{W}_j|$ and scale parameter 1, and W₁₁,···, W₅₀ do not affect the failure time.

Here we consider two different types of missingness mechanisms, missing completely at random (MCAR) and missing at random (MAR). Covariates that are subject to being missing are W₁ and W₄₆,···,W₅₀, with W₁ also affecting the failure time distribution and W₄₆,···,W₅₀ being noise variables. The other covariates W₂,···,W₄₅ are always observed in the simulations.

For the MCAR scenario, the missing indicators of the covariates subject to missing (e.g, W₁,W₄₆,···,W₅₀) are randomly simulated using a Bernoulli distribution which is calibrated to obtain the desired rate of marginal missingness. Similarly, for the MAR scenario, the probability of being missing for each of W₁,W₄₆,···,W₅₀ follows a logistic regression model log(p_miss / (1- p_miss)) = β₀ + 0.1W₂ + 0.1W₁₁, where the intercept β₀ is calibrated to obtain the desired missingness rates. For both scenarios, the overall missingness probabilities, i.e., proportion of observations with at least one covariate missing, are set to be 5,10,15,20, and 25%.

As shown in the fourth row of Figure 7, the prediction errors based on complete case analysis are positively correlated with the probability of missingness. Meanwhile, the prediction errors using the adaptive imputation approach (implemented for function rfsrc) are rather robust to different proportions of missingness, and consistently lower than the prediction errors based on complete case analysis.

7. Discussions

This paper aims to provide a gentle introduction to survival trees and forests, with an emphasis on the rational and applications of some commonly used algorithms. For illustration purposes, we present a data analysis of the German Breast Cancer Group Study to contrast the various survival tree and forest algorithms we reviewed. We also conducted Monte Carlo simulations to evaluate the impacts of model misspecification, choice of tuning parameters, and missing data when using survival forests. These results showcase how tree-based methods may offer robust alternatives to more traditional regression based methods.

We focus on clinical oncology translational research. These studies often involve retrospectively analyzing archived specimens collected from completed clinical trials. Frequently it is of great interest to combine clinical and pathological information with putative prognostic, or even predictive, biomarker information to jointly refine the disease risk stratification and prediction. The work by Bell et al. (2017) may serve as a useful motivating example to elaborate the unique challenges encountered in these studies, and why survival tree and forest analyses may sometimes be more informative than conventional regression analysis.

When fitting a Cox model it is often difficult to decide on which main effects and interactions to include and what their functional form should be. From the simulations in Section 6 we see that the Cox model can suffer from poor prediction accuracy when the model is misspecified either by not including the correct interactions or if the proportional hazard assumption is not satisfied. Datasets often consist of moderate or large number of predictors and a relatively small sample size, in which case a Cox model would have a low power to detect interactions.

In the study of Bell et al. (2017), due to the availability of specimens, the number of available cases decreased to less than 50% of the original study sample size when combining with at least one biomarker data, and the available cases further decreased to about 20% when limiting to those with all six biomarkers of interest. In translational research it is rather common that the number of observations with complete biomarker information decreases substantially compared to the original sample size. When there is missing covariate information, using only observations with complete data is in general not preferred for risk prediction purposes. The simulation results in Section 6 show that the prediction accuracy from random survival forests can suffer greatly if only complete observations are used. In contrast, adaptive tree imputation performs reasonably well and the prediction accuracy seen in the simulations was relatively robust against moderate level of missingness.

For selected classification and regression trees and random forest algorithms, there have been some systematic investigations conducted and various imputation approaches proposed (e.g., Ding and Simonoff (2010); Hapfelmeier et al. (2014)), which showed certain improvements from naive approaches under various scenarios. To the best of our knowledge, there are very few specific and systematic investigations on the treatment of missing data with either survival trees or survival forests. This issue remains an open question and deserves further investigations.

For survival trees, the splitting rule is an essential part and may play a key role in its prediction performance. A recent investigation reported by Shimokawa et al.(2015) suggests that it is difficult to recommend a particular survival tree splitting and pruning algorithm that performs uniformly optimal under different situations. Depending on the shape of underlying hazard function (constant, increasing, decreasing or bathtub-shaped), the survival trees’ performance may differ greatly. For the random forest algorithm, however, the splitting rules are generally considered as a less sensitive parameter, because the ensembles aggregate trees and the two-step randomization procedure substantially improves their robustness.

Competing risks data are also frequently encountered in clinical oncology research, where individuals under study may experience one of two or more different types (causes) of failure after initial diagnosis and treatment. An important quantity in competing risks analysis is the cumulative incidence function (CIF), which is the cumulative probability of a particular event type having occurred by time t in the presence of other competing events. The problem of constructing tree-based methods for competing risks data has not been widely studied. Callaghan (2008) proposed two survival tree methods for CIF, one which maximizes between-node heterogeneity in terms of a modified two-sample Gray’s test statistic (Gray, 1988), one which maximizes within-node homogeneity based on the sums of event-specific martingale residuals. To the best of our knowledge, these methods are not implemented by any publicly available software.

Extensions of the random forest algorithm have been developed to estimate the CIF. The rfsrc function of randomForestSRC package implements two different splitting rules for competing risk data. One is rooted in the differences in CIF and can be expressed as a modified weighted log-rank type Gray’s statistic when the censoring time is known, and the other is rooted in the difference in cause-specific hazards and can be expressed as weighted log-rank statistic where competing events are treated as censored (Ishwaran et al., 2014). Mogensen and Gerds (2013) proposed an alternative approach to apply the random forests procedure of Breiman (2001), where they directly jackknife pseudovalues (Klein and Andersen, 2005) to estimate the CIF at a time-point t. To the best of our knowledge, we are not aware of any systematic investigations across these proposed competing risks trees and forests.

Table 1:

Summary of Selected Survival Tree Methods.

Splitting Rule	Stopping Rule	Reference
KM-based Impurity	Cost-complexity, cross-validation	Gordon and Olshen (1985)
Node deviance	Cost-complexity, cross-validation	LeBlanc and Crowley (1992)
IPCW loss function	Cost-complexity, cross-validation	Molinaro et al. (2004)
Doubly-robust loss function	Cost-complexity, cross-validation	Steingrimsson et al. (2016a)
Log-rank test statistics	NA	Segal (1988)
Log-rank test statistics	Resampling, permutation	Leblanc and Crowley (1993)
p-value	p-value	Hothorn et al. (2006)