Graph Theoretic Analysis of Brain Connectomics in Multiple Sclerosis: Reliability and Relationship with Cognition

Abstract

Research suggests that disruption of brain networks might explain cognitive deficits in multiple sclerosis (MS). The reliability and effectiveness of graph theoretic network metrics as measures of cognitive performance were tested in 37 people with MS and 23 controls. Specifically, relationships with cognitive performance (linear regression against the paced auditory serial addition test-3 seconds [PASAT-3], symbol digit modalities test [SDMT], and attention network test) and 1-month reliability (using the intraclass correlation coefficient [ICC]) of network metrics were measured using both resting-state functional and diffusion magnetic resonance imaging data. Cognitive impairment was directly related to measures of brain network segregation and inversely related to network integration (prediction of PASAT-3 by small worldness, modularity, characteristic path length, R² = 0.55; prediction of SDMT by small worldness, global efficiency, and characteristic path length, R² = 0.60). Reliability of the measures for 1 month in a subset of nine participants was mostly rated as good (ICC >0.6) for both controls and MS patients in both functional and diffusion data, but was highly dependent on the chosen parcellation and graph density, with the 0.2–0.5 density range being the most reliable. This suggests that disrupted network organization predicts cognitive impairment in MS and its measurement is reliable for a 1-month period. These new findings support the hypothesis of network disruption as a major determinant of cognitive deficits in MS and the future possibility of the application of derived metrics as surrogate outcomes in trials of therapies for cognitive impairment.

Introduction

Dysfunction of brain networks is increasingly thought to contribute to cognitive impairment in multiple sclerosis (MS; Schoonheim et al., 2015). This occurs through a loss of capacity for information transfer between distal gray matter regions by degradation of the interconnecting white matter (WM) tracts (Catani and ffytche, 2005; Dineen et al., 2009). Because of this, and due to the distributed nature of focal and diffuse damage in the MS brain, a holistic model of connectivity disruption is appropriate. The network model based on graph theory (Bullmore and Sporns, 2009) has been widely applied in the study of MS, with many studies now showing whole brain abnormalities at the group level (reviewed by Filippi et al., 2013; Schoonheim et al., 2015).

In graph theoretic analysis, brain regions are modeled as “nodes” and the connections between them are modeled as “edges” (Bullmore and Sporns, 2009). The edges, representing anatomical connections or functional synchronizations within the brain, have an associated number describing their strength. With a thresholding procedure, sometimes based on the density of the graph (i.e., the ratio of edges to the total possible edges), weak connections can be ignored. From this structure, summary descriptors of the graph's organization can be extracted; commonly, these include the clustering coefficient, characteristic path length, global efficiency, small worldness, and modularity (Bassett and Bullmore, 2017). These metrics describe the overall topology of the network using standard formulae, as described in Rubinov and Sporns (2010). The graph theoretic model can, therefore, look beyond local changes at how the topology of an entire network is impacted and is not dependent on regional hypotheses about relevant seed regions or networks.

Studies comparing MS patients with controls have shown that brain network metrics are altered in people with MS (Fleischer et al., 2017; Kocevar et al., 2016; Li et al., 2013; Liu et al., 2017; Schoonheim et al., 2012, 2013; Shu et al., 2016; Tewarie et al., 2014b). There is some evidence of a consensus that information transfer across networks in people with MS is less efficient than in controls (He et al., 2009; Shu et al., 2011), that graph measures of network segregation are increased, and that measures of network integration are decreased (Gamboa et al., 2014; Llufriu et al., 2017; Richiardi et al., 2012; Rocca et al., 2010; Tewarie et al., 2014a). However, the effect of brain network disorganization on cognitive performance in MS is much less well understood. A small number of studies have found relationships between functional and structural brain network measures and cognitive performance (Hardmeier et al., 2012; Llufriu et al., 2017; Meijer et al., 2017; Miri Ashtiani et al., 2018; Van Schependom et al., 2014), but these studies show heterogeneity in terms of the direction and nature of the relationships, and the variety of imaging measures used.

By providing summary measures of whole brain network integrity, network metrics have potential to be used as intermediate outcome measures for therapies aiming to improve (or at least slow degradation of) brain network integrity in people with MS. However, before use in this way, it is essential that the reliability of the commonly applied summary brain network metrics applied in people with MS is known. In the context of neurological disease, more abnormal anatomy and a presumed greater level of in-scanner head motion have the potential to degrade the quality and reliability of the resulting magnetic resonance imaging (MRI) measurements (Van Dijk et al., 2012). Although reliability of network organization measures has been reported previously in healthy volunteer studies (Andreotti et al., 2014; Welton et al., 2015), reliability of these measures in people with MS has not been reported.

It is, therefore, pertinent to investigate whether MRI-based measures of network integrity in MS are relevant for cognitive performance and reliable over time. We hypothesized that graph theoretic brain network metrics based on both diffusion and functional MRI (fMRI) would (1) correlate with commonly used standardized neuropsychological tests for cognitive performance (specifically those sensitive to information processing speed) in people with MS (Korakas and Tsolaki, 2016), (2) be reliable for a 1-month time period (as defined by intraclass correlation coefficient [ICC] scores above a conventional threshold), and (3) confirm previous findings that graph theoretic brain network metrics based on both diffusion and fMRI significantly differ in people with MS relative to controls, with measures of segregation being higher and measures of integration being lower in MS.

Materials and Methods

Recruitment

The study protocol was approved by the U.K. National Research Ethics Service Nottingham 2 Committee (Ref 14/EM/0064). People with MS were recruited from MS clinics at the Nottingham University Hospitals NHS Trust, a regional clinical neurosciences center. Details of the sample size calculation are given in the Supplementary Data. MS participants met the following criteria: aged 18–65 years; clinically definite diagnosis of relapsing-remmiting MS or secondary progressive MS (as defined by the treating neurologist using standard clinical guidelines); no other neurological, neurosurgical, or psychiatric conditions, no relapses or changes in medication within the past 30 days; and no contraindication to MRI. For the purposes of this study, depression, which is a common association with MS, did not exclude participation. Healthy participants were recruited through posters placed on approved notice boards in specific hospital areas, according to the following criteria: aged 18–65 years; no current or past neurological, neurosurgical, or psychiatric conditions; and no contraindication to MRI. During recruitment, we attempted to match control and MS groups for mean age, gender, and education level. We planned for 15 of the MS group to return for a follow-up after 4–6 weeks (assuming no clinical relapses), in which the same protocol as the initial visit would be followed.

Neuropsychological testing protocol

All MS and control participants underwent neuropsychological assessment on the same day as the imaging. The protocol comprised the following tests: (1) the multiple sclerosis functional composite (MSFC; Fischer et al., 1999), which includes the Nine-Hole Peg Test (measures finger dexterity), timed 25-foot walk (measures mobility and leg function), and paced auditory serial addition test-3 seconds (PASAT-3; rate and capacity for auditory information processing), (2) attention network test (ANT; sustained attentional performance) and its subscores: alerting, orienting, and conflicting (Fan et al., 2002), (3) symbol digit modalities test (SDMT; visual information processing speed; Smith, 1982), (4) modified fatigue impact scale (MFIS; Fisk et al., 1994), (5) Neurological Fatigue Index (NFI-MS; Mills et al., 2010), (6) Beck depression inventory 2nd edition (BDI-II; Beck et al., 1996), and (7) Pittsburgh Sleep Quality Index (PSQI; Buysse et al., 1989). Quantification of sleep quality and depressive symptoms was included to identify any potential confounding effect on cognitive performance (Hammar and Årdal, 2009; Nebes et al., 2009). The MSFC, ANT, and SDMT were chosen as commonly used tests spanning multiple cognitive domains. The BDI and PSQI were used to test known confounds of cognitive performance with relevance to MS. MFIS and NFI-MS were reported for further characterization of the cohort. Demographic details were also recorded at this time (gender,, ethnicity, age, handedness, education, subtype, age of onset, and disease duration).

Imaging protocol

Magnetic resonance imaging was performed at 3T on a GE Discovery 750 (General Electric Healthcare, Milwaukee, WI) with 32-channel head coil. The protocol included T1-weighted axial fast-spoiled gradient echo (flip angle = 8°, matrix 256 × 256 × 156, voxel size 1 × 1 × 1 mm, TE = 3.17 ms, TI = 900 ms, TR = 8200 ms, FOV = 256 mm, number of excitations = 1), T2-weighted fluid attenuated inversion recovery (FLAIR; flip angle = 111°, TE = 120 ms, TR = 8000 ms, TI = 2250 ms, matrix 512 × 512 × 46, voxel size 0.46 × 0.46 × 3 mm, FOV = 235.5 mm), diffusion tensor imaging (DTI; 4 b = 0 volumes and 32 diffusion-weighted volumes, matrix 128 × 128 × 66, voxel size 2 × 2 × 2 mm), and resting-state fMRI (flip angle = 80°, TE = 36 ms, TR = 2200 ms, matrix 64 × 64 × 37, voxel size 3.75 × 3.75 × 3.6 mm, 191 volumes, ∼7 min).

Image processing

The volume of T2-hyperintense lesions was measured on the FLAIR images using the JIM software package (version 5.0; Xinapse Systems, Essex, UK) fuzzy semiautomatic lesion segmentation tool, by filling lesions in three dimensions, given a manually created set of points placed in the center of lesions. All T1-weighted images underwent segmentation using the FreeSurfer software package (version 5.3.0; Fischl, 2012) to generate sets of 164 cortical and subcortical gray matter regions of interest (ROIs) defined in the Destrieux atlas (Destrieux et al., 2010). The data used for the analysis of reliability were also segmented using the Harvard-Oxford Atlas (Desikan et al., 2006) for 126 cortical and subcortical ROIs. WM and CSF masks were extracted using FSL FAST (version 4.0; Zhang et al., 2001).

The quality of the fMRI data was ascertained using a custom script implemented in MATLAB (version 2013a; TheMathWorks, Natick, MA) that incorporated data quality best practices from other studies like the Function Biomedical Informatics Research Network initiative (Friedman and Glover, 2006), and included inspection of power spectra. Processing of the fMRI data was performed using tools in FSL (version 5.0.7; Jenkinson et al., 2012). The first two volumes (4.4 sec) of each data set were removed to allow for the brain tissue to reach a steady state of radiofrequency excitation. Head motion was corrected for by affine registration to volume 96 (the center of the resting state) using MCFLIRT. Data sets were checked for excessive motion (defined as a cumulative rotation of >3° or translation >4 mm). Brain extraction tool was applied to remove nonbrain structures. Spatial smoothing was not applied, so that local correlations between adjacent ROIs were not introduced. The skull-stripped T1-weighted images were registered to the skull-stripped fMRI data sets using a rigid-body transformation in FSL FLIRT and the resulting transformation was applied to the FreeSurfer ROI volumes to map them to fMRI space.

The mean blood oxygen level dependent signal within each ROI over the timecourse was extracted. Using MATLAB, the linear trend was removed from the extracted time series to account for scanner drift. The following variables were then regressed from the time series: three translation and three rotation parameters, the mean signal from the ventricles, and the mean signal from the WM. The WM and ventricle ROIs were from the FAST segmentation already described but eroded to ensure that no partial volumes were included and to avoid global demeaning and introduction of spurious anticorrelations. These regressors were used because they represent a good balance between denoising and signal loss for data sets of a similar number of time points as ours (Bright and Murphy, 2015). To create association matrices, functional connectivity between every pair of ROIs was quantified by the Pearson correlation coefficient. Finally, Fisher's r-to-Z transformation was applied to linearize the r values.

Diffusion data were processed using FMRIB's Diffusion Toolbox (Behrens et al., 2003). First, eddy current-induced distortions and subject motion were corrected using Eddy (Andersson and Sotiropoulos, 2016). All image volumes were registered to the average b = 0 image by affine transformation. BET was applied to remove nonbrain structures. Diffusion parameters were estimated and ROIs from the two atlases were registered to the DTI space by registering the T1 brain image to the average b = 0 image by affine transformation and applying the transformation matrix to the ROIs. Deterministic fiber tracking was applied to every pair of ROIs to create matrices of the number of reconstructed streamlines between them. This was measured twice (A-to-B and B-to-A) because the number of streamlines between seed and terminal ROIs could vary depending on direction, that is, the connectivity matrix was not symmetric. The following standard formula was then applied, which sums the streamline counts for each direction and scales the result by their volumes (Buchanan et al., 2014; Cheng et al., 2012; Owen et al., 2013):

$$a_{ij}=\frac{s_{ij}+s_{ji}}{m_i+m_j},$$

where a_ij is the corrected summary streamline count, s_ij and s_ji are streamline counts in each direction between ROIs i and j, and m_i and m_j are voxel counts in each ROI.

Graph analysis

The association matrices contained all the information necessary to describe graphs where each ROI is modeled by a node and each connectivity value is modeled by a weighted edge. To remove spurious or weak connections and retain the strong connections, we applied a minimum density threshold to each graph (density was defined as the ratio of the number of existing edges to the number of possible edges). To avoid arbitrarily selecting a single threshold and to improve the robustness of the results, a range of density thresholds was applied. The range of thresholds used was 0.2–0.5, in increments of 0.02, giving 15 total densities. This range was chosen with the aim of producing results that were reliable and were not based on graphs that were (1) fragmented and (2) too dense to have small world properties (Bassett and Bullmore, 2006; Fornito et al., 2010). The integral of each metric score across this range produced a summary score, as in Hosseini et al. (2012). Once a graph had been appropriately thresholded, it was used to calculate a set of global metrics using the Brain Connectivity Toolbox (Rubinov and Sporns, 2010). The chosen metrics were selected based on their reliability and frequency of use in previous literature (Welton et al., 2015): clustering coefficient, characteristic path length, global efficiency, small worldness, and modularity (each detailed in the appendix to Rubinov and Sporns, 2010). The data used for the analysis of reliability underwent the same procedure using the additional range of densities 0–1, so that the impact of graph density on reliability over time could be investigated.

We verified that the thresholded graphs followed the defining properties of small world networks: a low characteristic path length, a high clustering coefficient, and the presence of high-degree hubs (Watts and Strogatz, 1998). Deviation from these characteristics may indicate pathological networks (Stam, 2014). To investigate this, 1000 random and 1 regular lattice graph of the same average size and order as the brain MRI graphs for MS participants were first generated at each density using MATLAB and the BCT methods for randomization. The same integration procedure as for the human MRI data was then applied to ascertain a summary score for the random and lattice graphs to serve as controls.

Statistical analysis

All variables were first tested for normality using Kolmogorov–Smirnov tests and by visual inspection of histograms. The level of statistical significance for all tests was set at 5%. For the analysis of group differences in summary network metrics, the normalized metric scores were entered into a two-way analysis of covariance (ANCOVA) with group and metric type as factors and age, gender, and education as covariates.

To test for relationships between network metrics and neuropsychological measures in the MS group, we first checked for linear relationships between the variables of interest using scatter plots and tests for correlation. We then performed linear regression analyses with the neuropsychological measures (PASAT-3, SDMT, and ANT subscores) as the dependent variables and the network metrics entered into the model in one block as the independents. Supplementary Figure S1 illustrates fulfillment of assumptions for linear regression.

We performed a second set of regression analyses that were the same but with covariates of no interest (age, gender, education, PSQI, and BDI) entered as a first block of independents and the network metrics entered as a second block. This was done separately because of the potential for overfitting when the number of subjects per independent variable is low; therefore, there was a likelihood of overestimating the model R² in these tests (Austin and Steyerberg, 2015).

Reliability between the first and second visits was quantified using the ICC statistic (two-way random effects, single measures, and consistency) and compared with the ICCs reported in our previous systematic review of reliability of network metrics in healthy people (Welton et al., 2015). Reliability was tested under both parcellation schemes and at each density interval, as well as using the area-under-the-curve between the densities 0.2–0.5 as a summary measure. The formula for the ICC used was

$$ICC\left(consistency\right)=\frac{BMS-MSE}{BMS+\left(k-1\right)MSE},$$

where k is the number of observers, BMS is the between-subjects mean squared, and MSE is the mean squared error. The ICCs are generally interpreted as follows: <0.40, “poor”; 0.40–0.59, “fair”; 0.60–0.74, “good”; >0.74, “excellent” (Shrout and Fleiss, 1979).

Results

Sample characteristics

A total of 37 people with MS and 23 control subjects were recruited. A summary of demographic and neuropsychological data is given in Table 1. Of the MS group, 12 (37%) were taking disease modifying drugs, 17 (46%) were taking antidepressants, and 18 (49%) were taking other medications for symptom relief. One-way analysis of variance (Table 1) confirmed significant differences between MS and control groups for all tests of cognition and fatigue and suggested that the groups were adequately matched for age, gender, and education (i.e., without significant group differences). A comparison of our neuropsychological test scores with normative MS samples showed that our sample performed significantly worse in all tests of cognition and fatigue but was not significantly different in terms of physical disability, sleep quality, or depression (Supplementary Table S1).

Table 1.

Demographic and Neuropsychological Data for the Sample

	Multiple sclerosis	Control	One-way ANOVA for the group difference: p
Gender (%, female)	81	73	n/s
Handedness (%, Right)	84	87	n/s
Ethnicity	WE = 37	WE = 21, A = 1, BI = 1
TWMLL (mL)	7.77 (8.87)	0.42 (0.87)	<0.001
Age at date of first scan (years)	48 (11)	42 (12)	n/s
Years of full-time education after age 16 (years)a	2 (2)	3 (2)	n/s
MS subtype	RR = 22, SP = 15
Age of onset (years)	31 (6)
Disease duration (years)	17 (10)
Use of disease modifying drugs, n (%)	12 (37)
MSFC	−0.38 (0.69)	0.64 (0.43)	<0.001
PASAT	36.31 (2.44)	44.87 (2.43)	0.020
9HPT	25.03 (7.09)	22.23 (6.71)	<0.001
T25FW	7.5 (3.3)	4.6 (0.8)	<0.001
PSQI	8.35 (3.42)	4.50 (1.41)	0.003
MFIS	54.25 (19.98)	11.00 (10.08)	<0.001
BDI	18.21 (12.37)	2.00 (3.22)	<0.001
SDMT	41.91 (13.09)	57.00 (10.74)	<0.001
NFI-MS	48.24 (10.57)	13.95 (12.16)	<0.001
ANT
Alerting	−0.97 (14.53)	17.33 (18.57)	<0.001
Orienting	20.58 (24.19)	36.29 (23.95)	0.023
Conflicting	99.12 (49.05)	170.90 (72.45)	<0.001

All measures of center and spread are given as mean (SD) except where indicated.

^aCompulsory schooling in the United Kingdom lasts until age 16 years.

9HPT, Nine-Hole Peg Test; A, Arabic; ANOVA, analysis of covariance; ANT, attention network test; BDI, Beck depression inventory II; BI, British Indian; MFIS, Modified Fatigue Impact Scale; MSFC, multiple sclerosis functional composite; n/s, nonsignificant; NFI-MS, Neurological Fatigue Index; PASAT, paced auditory serial addition test; PSQI, Pittsburgh Sleep Quality Index; RR, relapsing-remitting; SD, standard deviation; SDMT, symbol digit modalities test; SP, secondary progressive; T25FW, timed 25-foot walk; TWMLL, total white matter lesion load; WE, white European.

Data quality

The mean relative displacement between successive fMRI volumes was 0.203 mm (standard deviation [SD] 0.344) for the MS group and 0.125 mm (SD 0.051) for the control group (t = 1.08, p = 0.286). Based on the outputs of the fMRI quality script, two data sets were excluded from the MS group and all further analyses due to excessive motion. After removal of these data sets, the mean relative displacement of the MS group was 0.159 mm. No data sets were excluded based on inspection of power spectra. Supplementary Figure S2 demonstrates the small world structure of the brain networks by comparison with random and lattice networks.

Group differences in network organization

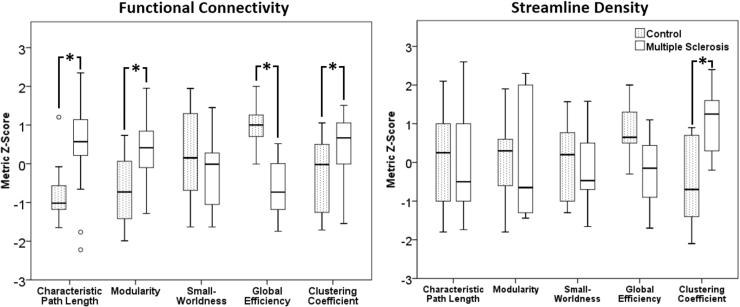
The distribution of network metrics did not significantly differ from a normal distribution as assessed by Shapiro–Wilk test. ANCOVA revealed that, for resting functional connectivity, when correcting for age, gender, and education, there were significant differences in network metrics between groups (Table 2; Fig. 1) in the clustering coefficient, characteristic path length, global efficiency, and modularity metrics, but not in small worldness. For streamline density networks, only the clustering coefficient was significantly different (Table 2).

Table 2.

Outcome of the Analysis of Covariance Analysis

Metric	Functional connectivity				Streamline density
	MS mean (95% CI)	Control mean (95% CI)	F	p	MS mean (95% CI)	Control mean (95% CI)	F	p
Characteristic path length	1.268 (1.262–1.275)	1.249 (1.241–1.258)	15.944	<0.001	0.122 (0.120–0.126)	0.122 (0.120–0.125)	0.821	0.369
Modularity	5.254 (5.162–5.346)	5.017 (4.896–5.138)	7.063	<0.001	3.511 (3.394–3.571)	3.508 (3.486–3.529)	0.241	0.625
Small worldness	0.928 (0.916–0.940)	0.921 (0.902–0.939)	2.670	0.056	0.343 (0.336–0.349)	0.341 (0.332–0.348)	0.072	0.790
Global efficiency	1.573 (1.546–1.600)	1.723 (1.667–1.779)	29.289	<0.001	1.385 (1.373–1.397)	1.413 (1.364–1.463)	3.112	0.083
Clustering coefficient	0.618 (0.612–0.623)	0.598 (0.549–0.687)	3.146	0.032	0.294 (0.289–0.297)	0.299 (0.296–0.303)	8.223	0.006

The results show significant group differences in network metrics with age, gender, and education as covariates.

FIG. 1.

Boxplots of the normalized metric scores for each group. (Left) functional connectivity and (right) streamline density. Asterisks indicate significant differences.

Relationship with cognitive impairment

For people with MS, the linear regression models using network metrics derived from functional connectivity networks were significantly predictive for the PASAT-3 and SDMT but not for the ANT subscores (Table 3). The variables that significantly contributed to predicting 55.6% of the variance for the PASAT-3 were small worldness, modularity, characteristic path length, and clustering coefficient (each having p < 0.05 in a one-sample t-test on the unstandardized coefficients). The direction of the relationships indicated that individuals with greater levels of impairment on the PASAT-3 had increased clustering and modularity, longer average path lengths, and less small worldness. The variables that significantly contributed to predicting 60% of the variance for the SDMT were small worldness, global efficiency, and characteristic path length. The direction of the relationships indicated that individuals with greater levels of impairment on the SDMT had less small worldness, lower global efficiency, and longer average path lengths. For the tests using streamline density data, no model was significant (Table 3). In the tests including the covariates of no interest (age, gender, education, PSQI, and BDI), the R² estimates were higher, suggesting that the demographic variables were strong predictors, but were likely overestimated (Supplementary Table S2). In controls, the linear regressions showed no significant predictions for any of the independents (Supplementary Table S3).

Table 3.

Outcomes from the Multiple Linear Regressions for Cognitive Measures in People with Multiple Sclerosis, Not Including Covariates

Cognitive test, dependent	Functional connectivity network metrics model			Streamline density network metrics model
	F	p	R2	F	p	R2
PASAT	8.752	<0.001	0.556	1.980	0.115	0.276
SDMT	16.384	<0.001	0.600	0.244	0.939	0.134
ANT alerting	1.675	0.175	0.237	2.005	0.110	0.136
ANT orienting	0.583	0.713	0.097	1.796	0.147	0.111
ANT conflicting	0.760	0.586	0.123	0.677	0.644	0.053

All independents were entered into the model in one step.

Reliability

Follow-ups were carried out in 10 individuals with MS (selected as the first 10 recruited, with another 5 subjects who did not attend follow-up), but the data from one were excluded due to motion, thus 18 MRI data sets from 9 individuals were included in the reliability analysis. This subgroup had a mean age of 41 years (SD 9), the mean follow-up time was 46.6 days (SD 14.8), and included seven females (78%). No participant had clinical evidence of relapse during this interval.

For functional connectivity data and the Harvard-Oxford atlas, reliability of network metrics over time in people with MS over the range of densities 0.2–0.5 was graded as “good” for clustering coefficient and global efficiency, and “fair” for characteristic path length (Shrout and Fleiss, 1979; Table 4). For the Destrieaux parcellation, clustering coefficient and characteristic path length were graded as “fair,” whereas global efficiency was graded as “good.” For tests with streamline density data, all ICCs were graded as “good,” except the characteristic path length reliability ICC using the FreeSurfer atlas, which was graded as “excellent.”

Table 4.

Intraclass Correlation Scores for Consistency of Network Metrics Under Two Different Parcellation Schemes

	Harvard-Oxford	FreeSurfer	Previous studies in healthy people (mean ± SD)
Functional connectivity
Clustering coefficient	0.635*	0.499	0.644 ± 0.231
Characteristic path length	0.489	0.573	0.710 ± 0.164
Global efficiency	0.659*	0.676*	0.750 ± 0.112
Streamline density
Clustering coefficient	0.722*	0.733*	0.644 ± 0.231
Characteristic path length	0.714*	0.800**	0.710 ± 0.164
Global efficiency	0.707*	0.689*	0.750 ± 0.112

Previous studies data from Welton et al. (2015).

^*ICCs in the “good” range.

^**ICCs in the “excellent” range. All others were in the “fair” range.

ICC, intraclass correlation.

Compared with studies in healthy people, as we previously reviewed (Welton et al., 2015), reliability of network metrics in people with MS was only slightly lower in both atlases (Fig. 2). Plots of reliability for the three metrics over the range of densities, shown in Supplementary Figure S3, support the chosen density range of 0.2–0.5 for our other analyses, in that reliability is generally high for all metrics across this range.

FIG. 2.

Bar chart comparing reliability between network metrics in the cohort of MS participants and in healthy volunteers from previously reported studies. A higher ICC reflects greater reliability. The bars for the Harvard-Oxford Atlas and Destrieaux atlas are from people with MS. (Left) functional connectivity and (right) streamline density. Previous studies data from Welton et al. (2015). ICC, intraclass correlation; MS, multiple sclerosis.

Discussion

Using graph theory and MRI data, we were able to assess summary measures of brain network organization for relationships with cognitive impairment and reliability in people with MS. Group differences in functional network metrics and relationships with cognitive measures were in accordance with findings of previous studies: the brains of cognitively impaired people with MS had longer average path lengths, lower network efficiencies, and lower small worldness. The impact of disease status on reliability was low. These results support the future use of network measures in clinical studies and may provide insights into the underlying mechanisms of cognitive impairment in MS.

Disrupted network topology in multiple sclerosis

Graph theoretic approaches using both functional and structural networks are now widely applied in research on neurological disease; for example, in epilepsy (Bernhardt et al., 2011), Alzheimer's (Tijms et al., 2013), albinism (Welton et al., 2017), and traumatic brain injury (Sharp et al., 2014). In each of these examples, the observed network reorganization represents a general deviation from the optimal small world structure. However, so far, there is little consensus on the exact nature of the deviation (Stam, 2014). In MS, structural network disruption in comparison with healthy controls has been characterized by reduced small worldness (He et al., 2009); increased modularity localized to the cerebellum, cingulum, and temporoparietal regions (Fleischer et al., 2016); reduced efficiency in frontal, parahippocampal, motor, and occipital regions (Li et al., 2013); and decreased efficiency in regions subserving motor, visual, and language functions (Shu et al., 2011). The observed differences in our findings between functional connectivity-based and structural-based networks, and their relationship with cognitive performance, are crucial for our understanding of brain networks, how function emerges from structure, and how it is impacted by disease (Park and Friston, 2013). In our data, we found inverse group differences in characteristic path length and modularity between functional and structural networks, whereas in other metrics, differences were absent (small worldness), or followed the same direction (global efficiency and clustering). In terms of reliability, there was a slight bias toward structural networks being more reliable (Fig. 2). However, it is currently difficult to interpret these differences at a high level.

Our findings of longer average path lengths, increased modularity, increased clustering, and reduced global efficiency in functional networks in MS than controls are, therefore, compatible with previous studies and with our hypothesis. These changes imply a network that is more segregated, with more distinct subnetworks that are, compared with controls, relatively weakly connected between themselves but more strongly connected within themselves. We were able to verify the small world structure of our data compared with randomized and regular graphs. Our results on group differences, therefore, support the theory of the efficient neuronal architecture in MS being disrupted.

Cognitive performance, as measured by both the PASAT-3 and SDMT, was significantly predicted by network organization as hypothesized. For the PASAT-3, the best predictor was the clustering coefficient. Three previous studies of cognitive impairment in MS using an fMRI network model also found that PASAT-3 performance in MS was related to increased clustering (Schoonheim et al., 2013; Shu et al., 2016; Van Schependom et al., 2014). Others found relationships with increased nodal strength (Llufriu et al., 2017), increased local and global efficiency (Shu et al., 2016), lower mean degree (Rocca et al., 2016), lower hierarchy scores (Rocca et al., 2016), longer average path lengths (Rocca et al., 2016), and increased modularity (Gamboa et al., 2014). A more highly clustered brain network indicates that nodes' neighbors become more closely connected within themselves. This may be the brain's response to the attenuation of signals in WM tracts by focal lesions: as long-range connections or connections between subnetworks become disrupted, networks may instead become more tightly connected to their strongest remaining neighbors.

In contrast, the SDMT focuses on fast processing of visual information. The best predictors for the SDMT were small worldness, efficiency, and path length. These differences may, therefore, be related to the type of task that was performed and may suggest that the relationships between the network metrics (representing increased network segregation) and cognitive performance are specific to tasks that involve fast complex processing of information and production of speech. This is further reinforced by the tests with ANT scores, which are mostly based on reaction time, and which were not significantly predicted by network organization measures.

Reliability of the network measures over time was good. The reliability scores were comparable with those from previous studies in healthy individuals, suggesting a negligible effect of disease status; although our sample size was small for this test. Although an increased propensity for motion in diseased cohorts is expected, for example, due to muscle spasms in MS, this was not a large factor for reliability. It is also known that even motion within the normal range for healthy young adults significantly impacts individual connectivity measurements (Van Dijk et al., 2012). This presumably impacts network measurements to some degree; however, no studies have specifically investigated the impact of motion on network measurements. Overall, this evidence supports the applicability of network measures in future clinical studies. The reliability of these measures between different sites has not yet been investigated, but will be crucial for applications in multicenter studies. The large degree of variability in reliability scores over the density range 0–1 demonstrates the importance of testing a range of thresholds, rather than arbitrarily selecting one fixed threshold. Accordingly, our findings are specific to the chosen density range (0.2–0.5), which appeared to be most reliable.

There were methodological issues that should be acknowledged. First, there are some questions over the interpretation of network topology measures. It is not known what drives differences in specific metrics, and further studies should be conducted toward that end. Until we have a stronger basic understanding, researchers should be cautious when drawing conclusions based on network topology. Our results may be less generalizable to the noncognitively impaired MS population due to the bias in our sample toward cognitively impaired individuals and use of disease-modifying or antidepressant drugs. We also acknowledge the small number of enrolled subjects, especially for the follow-up analysis, which should qualify interpretation of these findings.

Conclusion

Our findings show that functional deficits in MS are associated with disruption to macroscopic brain networks. We present evidence that summary measures of network organization may be valid and reliable markers of cognitive impairment in MS.

Authors' Contributions

All listed authors contributed significantly to the conception, design, analysis, and article writing for this study.

Author Disclosure Statement

No competing financial interests exist.

Funding Information

Project costs and T.W. were funded by a PhD studentship grant from the UK MS Society (registered charity numbers 1139257/SC041990; grant reference number 988).

Supplementary Material

Supplementary Data

Supplementary Figure S1

Supplementary Figure S2

Supplementary Figure S3

Supplementary Table S1

Supplementary Table S2

Supplementary Table S3