Logistic growth modelling of COVID-19 proliferation in China and its international implications

Highlights

• •This study applied a logistic growth model with parameters estimated by a non-linear least squares (NLS) method to daily new COVID-19 cases.
• •The model fitted time-series data exceedingly well for the whole of China, eleven selected Chinese provinces and municipalities, South Korea and Iran.
• •This study provided key estimates and a 95% confidence interval for parameters K, r, and P ₀.
• •This study found that the growth rates of outbreaks differed between provinces in China and between South Korea and Iran.
• •As of March 13, 2020, this study's model suggested that countries such as the U.S.A., France, Italy, and Spain were still in the early stages of outbreaks.

Abstract

Objective

As the coronavirus disease 2019 (COVID-19) pandemic continues to proliferate globally, this paper shares the findings of modelling the outbreak in China at both provincial and national levels. This paper examines the applicability of the logistic growth model, with implications for the study of the COVID-19 pandemic and other infectious diseases.

Methods

An NLS (Non-Linear Least Squares) method was employed to estimate the parameters of a differentiated logistic growth function using new daily COVID-19 cases in multiple regions in China and in other selected countries. The estimation was based upon training data from January 20, 2020 to March 13, 2020. A restriction test was subsequently implemented to examine whether a designated parameter was identical among regions or countries, and the diagnosis of residuals was also conducted. The model's goodness of fit was checked using testing data from March 14, 2020 to April 18, 2020.

Results

The model presented in this paper fitted time-series data exceedingly well for the whole of China, its eleven selected provinces and municipalities, and two other countries - South Korea and Iran - and provided estimates of key parameters. This study rejected the null hypothesis that the growth rates of outbreaks were the same among ten selected non-Hubei provinces in China, as well as between South Korea and Iran. The study found that the model did not provide reliable estimates for countries that were in the early stages of outbreaks. Furthermore, this study concured that the R² values might vary and mislead when compared between different portions of the same non-linear curve. In addition, the study identified the existence of heteroskedasticity and positive serial correlation within residuals in some provinces and countries.

Conclusions

The findings suggest that there is potential for this model to contribute to better public health policy in combatting COVID-19. The model does so by providing a simple logistic framework for retrospectively analyzing outbreaks in regions that have already experienced a maximal proliferation in cases. Based upon statistical findings, this study also outlines certain challenges in modelling and their implications for the results.

1. Introduction

An outbreak of severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2), a zoonotic coronavirus similar to severe acute respiratory syndrome coronavirus (SARS-CoV) and Middle East respiratory syndrome-related coronavirus (MERS-CoV), has rapidly spread across China and various regions of the world. As of April 17, 2020, the cumulative numbers of confirmed cases had reached 82 719 in China (NHCPRC, 2020) and 2 074 529 in 210 countries and territories worldwide (World Health Organization, 2020).

In light of these recent developments, the scientific community has sought understanding of coronavirus disease 2019 (COVID-19), the disease caused by SARS-CoV-2, and many have undertaken statistical and modelling approaches. The R ₀ value for virus transmissibility has been evaluated through stochastic Markov chain Monte Carlo (MCMC) methods (Wu et al., 2020a), a mathematical incidence decay and exponential adjustment (IDEA) model (Majumder and Mandl, 2020), and a statistical exponential growth model adopting the serial interval from severe acute respiratory syndrome (SARS) (Zhao et al., 2020). Researchers have also utilized several models to generate short-term forecasts for cumulative case counts (Roosa et al., 2020), and have developed a ‘susceptible, un-quarantined infected, quarantined infected, confirmed infected’ (SUQC) model to characterize the dynamics of outbreaks (Zhao and Chen, 2020).

This study applied a logistic growth function with parameters estimated by a non-linear least squares (NLS) method to model and analyze time-series data from eleven provinces and municipalities in China (Anhui, Beijing, Chongqing, Guangdong, Henan, Hubei, Hunan, Jiangsu, Jiangxi, Shanghai, and Zhejiang) and nine other countries (Iran, South Korea, France, Germany, the U.S.A., Italy, Spain, Singapore and Japan). The implications of the results for the study of infectious diseases are discussed.

2. Methods

Devised by Belgian mathematician Pierre-François Verhulst (1804–1849) and corroborated by others in later years, the logistic function has become one of the essential tools for bio-assays and has been increasingly applied in a variety of fields, including statistics, economics, and epidemiology (Cramer, 2004). Specifically, it has been used to model population growth in a region and bacterial growth in a broth, and has been implemented in binary decision-making processes in economics and finance.

The equation of the logistic function, following a common sigmoid curve, takes the mathematical form

$$P\left(t\right)=\frac{K{P}_0{e}^{rt}}{K+P_0(e^{rt}-1)}$$ (1)

where P(t), or the number of cumulative cases of COVID-19, is expressed as a function of time, t, with parameters $\beta =(K,P_0,r)$. To be exact, K represents carrying capacity, P ₀ represents the initial value of the function at t  = 0, and r represents the growth rate, or the speed of proliferation.

This study did not, however, use a logistic function to directly estimate a model for cumulative cases. Previous studies have suggested that fitting deterministic models to cumulative cases, due to serial correlation in the error terms (measurement errors), creates biased parameters and overfitting of the model to data, and underestimates the uncertainty associated with parameters (King et al., 2015). Therefore, the derivative of the logistic growth function was adopted to model the daily new cases. The general differential logistic equation takes the following form:

$$P^{\text{'}}\left(t\right)=rP\left(t\right)\left(1-\frac{P\left(t\right)}{K}\right)$$ (2)

Substituting Equation (1) into Equation (2) gives the logistic differential equation

$$f(t,\beta )=\frac{dP}{dt}=\frac{rK{P}_0{e}^{rt}(K-P_0)}{{(K+P_0{e}^{rt}-P_0)}^2}$$ (3)

Specifically, the number of observed daily new cases, I(t), is equal to f(t,β) plus an error term ε, as shown in the statistical model below, where t  = 1, 2, …T, and T is the number of observations.

$$I(t)=f(t,\beta )+\epsilon (t)$$ (4)

Equation (4) is the key equation for modelling time-series data. The study assumed that the error terms were independent and identically distributed (i.i.d.), and used the NLS method to estimate β by minimizing the residual sum of squares, ${\sum }_t{(I(t)-f(t,\beta ))}^2$.

After estimation, this study set $\hat{I}$, or$f(t,\hat{\beta })$, as the predicted value at a given t using estimated parameters $\hat{\beta }$. The residual is defined as $w(t)=I(t)-I(\hat{t})$. The study defined $TSS=\sum I{(t)}^2,RSS=\sum I{(\hat{t})}^2$, and $ESS=\sum w{(t)}^2$, representing the total sum of squares, regression sum of squares, and the residual (error) sum of squares, respectively. According to the statistical identity TSS  =  RSS  +  ESS (Pindyck and Rubinfeld, 1991), the coefficient of determination is expressed as

$$R^2=\frac{RSS}{TSS}=\frac{\sum I{(\hat{t})}^2}{\sum I{(t)}^2}$$ (5)

The study calculated the F-statistic value through $F=\frac{RSS/n}{ESS/(T-n)}$, given that n is the number of parameters, or three, T is the number of observations, and that F asymptotically follows an F-distribution with n and (T–n) degrees of freedom.

This study established matrix X as equivalent to the partial derivative of f(t·β) or such that $X=\partial f/\partial \beta$. The estimate of the asymptotic covariance matrix of β is $VCOV(\beta )=MSE*{(X^{\prime }X)}^{-1}$ (Greene, 1997), wherein MSE is the estimate of the residual variance, equal to $ESS/(T-n)$. The confidence interval of ${\hat{\beta }}_l$ is determined by equating

$${\hat{\beta }}_l\pm stderr*t\left(T-n,1-\frac{\alpha }{2}\right)$$ (6)

wherein α is the significance level, substituted with 5% when calculating the 95% confidence interval (95% CI).1

In order to test certain restrictions upon parameters β, this study compared the ESS of a free model (ESS _f) to the ESS of a restricted model (ESS _r) and calculated a test static F _R with q constraints on β, where

$$F_R=\frac{(ES{S}_r-ES{S}_f)/q}{ES{S}_f/(T-n)}$$ (7)

The test asymptotically follows an F-distribution with q and (T–n) degrees of freedom (Schabenberger and Pierce, 2002).

Estimation was completed using the SAS software package. The method of optimization utilized a Gauss–Newton algorithm, which is advantageous as it does not require a second derivative and converged quickly with this study's estimations. The Gauss–Newton algorithm iteratively finds the values of parameters β that minimize the sum of squares of the residuals. It starts from an initial estimate β ⁽⁰⁾ and proceeds by iterations ${\beta }^{(s+1)}={\beta }^{(s)}+{(X^{\prime }X)}^{-1}{X}^{\prime }w({\beta }^{(s)})$ expressed in terms of $w$ and β, which are column matrices, and in terms of s, which is the iteration step during the optimization process.

The daily times-series data of cumulative COVID-19 cases from January 20, 2020 to April 18, 2020 were retrieved from the National Health Commission of the People's Republic of China and its respective health commissions in the selected eleven provinces and municipalities. Time-series data for the nine other countries up until April 18, 2020 were obtained through WIND DATA, a leading financial data services provider in China.

This study took measures to adjust the time-series data for cumulative cases in China. It should be noted that on February 12, 2020, clinical evidence and radiographic confirmation were introduced into the diagnosis guidelines for new cases, causing a jump of nearly 15 000 new cases in Hubei, China.2 On April 16, 2020, health officials announced a one-time re-adjustment of the number of cumulative cases in Wuhan, Hubei — an increase by 325 cases — which were originally omitted from the public amidst the epidemic. For data consistency, this study removed all cases that were added on those two days. To further ensure consistency, this study removed all confirmed cases that were imported from abroad (1575 cases nationally, including 741 cases in many of the ten non-Hubei provinces of China). In addition, 305 cases in the prison system reported on February 20, 2020 (271 in Hubei and 34 in Zhejiang) where the spread was relatively independent and not within the coverage of the provisional health authorities were also removed (Wu et al., 2020b).

The time-series data for daily new cases in China, derived from cumulative cases, were split into two time periods for training and testing. The study fit a logistic growth model for time-series data from January 20, 2020 up until March 13, 2020 (defined as training data), when the manuscript was originally written. It estimated all parameters and related statistics of the model based upon the training data only. The estimated model was then fitted to the time-series data from March 14, 2020 to April 18, 2020 (defined as testing data).

The regression model took the assumption of i.i.d. error terms. This study performed several residual diagnosis tests to check whether such an assumption was appropriate for the fitted errors or not. Previous papers have found that using the raw residuals, w(t), of non-linear models for diagnosis may be misleading, as they may have non-zero means and different variances. These papers have, consequently, suggested that the use of alternative residuals, referred to as projected residuals, may overcome many of the shortcomings of the raw residuals (Cook and Tsai, 1985). To test whether the error terms in the regression model were independent as per the suggestion by Cook and Tsai, a Durbin–Watson (DW) statistic (Durbin and Watson, 1950) was employed for both the raw residuals and projected residuals.3 Similarly, to test for homoskedasticity, this study carried out the White test (White, 1980) for both types of residuals.4

3. Results and discussion

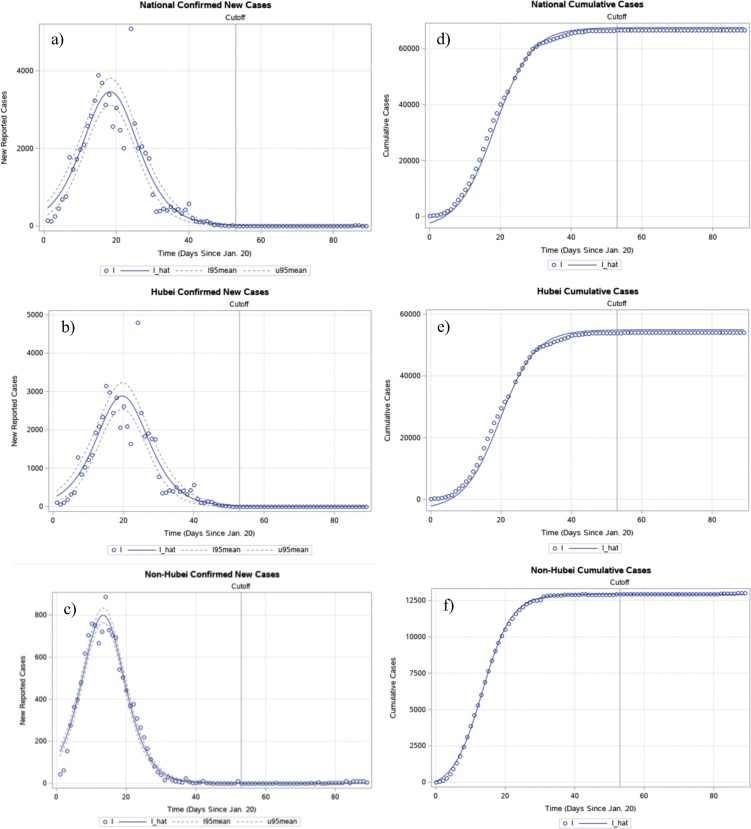
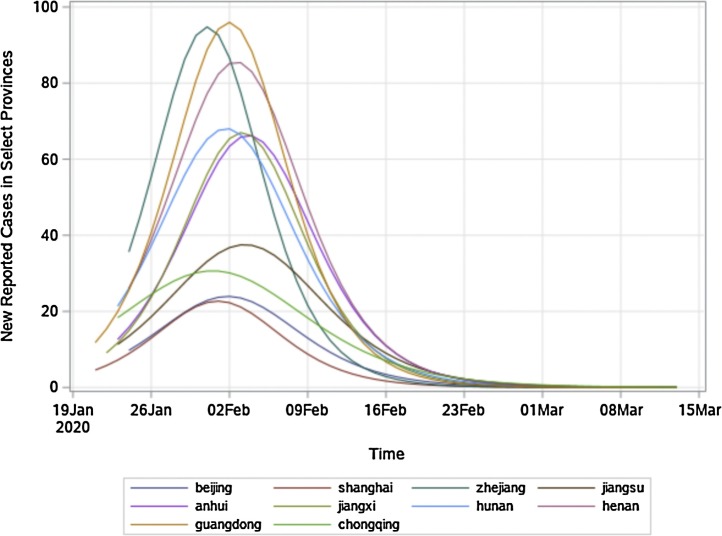
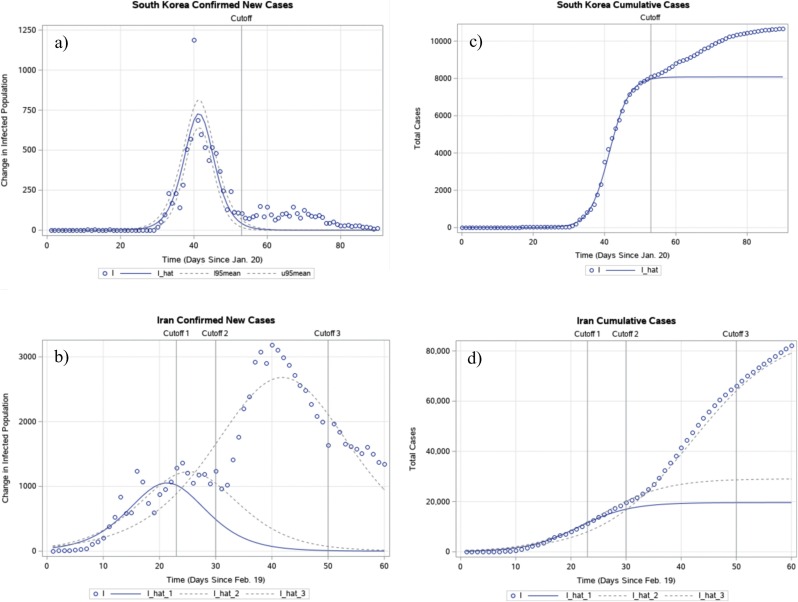
Equation (4) was first fitted for the training data for the whole of China, as well as for Hubei Province and non-Hubei provinces; the results are displayed in Table 1 and Fig. 1 . The same model was then fitted for training data from ten selected non-Hubei provinces and municipalities, with the results shown in Table 2 and Fig. 2 . The model was subsequently fitted for the training data from the nine other countries as well, for which the results are shown in Table 3 and Fig. 3 . After the parameters of the model had been estimated, they were fitted in the corresponding testing data, and the results are illustrated in Tables 1, 2 and 3 and Figs. 1, 2 and 3.5

Table 1.

Modelling results for national, Hubei, and non-Hubei time-series data

Regional classification	T	$\hat{K}$	95% CI of $\hat{K}$		$\hat{r}$	95% CI of $\hat{r}$		$\widehat{P_0}$	F statistic	Approx. Pr > F	Estimated date of maximal increase	R2
			Lower	Upper		Lower	Upper					Train	Test	Total
National	53	71 954.6	64 640.2	79 268.9	0.1927	0.1683	0.2170	0.2170	213.77	<0.0001	2020/2/7	0.929	0.851	0.929
Hubei	52	58 221.3	51 319.0	65 123.5	0.1984	0.1691	0.2277	1156	151.5	<0.0001	2020/2/9	0.903	13.271	0.903
Non-Hubei	53	13 426.1	12 810.6	14 041.6	0.2386	0.2248	0.2524	530.7	1116.33	<0.0001	2020/2/2	0.985	0.000	0.986

CI, confidence interval.

Table 1 shows the modelling results of Equation (4) estimated for time-series data of new COVID-19 cases in China, Hubei, and non-Hubei provinces. While the study includes the calculations for the 95% confidence interval for P₀, it is not provided within Tables 1, 2 and 3 due to space limitations. The training period lasted from January 20, 2020 to March 13, 2020, whereas the testing period lasted from March 14, 2020 to April 18, 2020. The ‘Train’ column includes the training data, the ‘Test’ column includes the testing data, and the ‘Total’ column includes the training and testing data combined.

Fig. 1.

Graphical representation of the modelling results in Table 1. The estimated logistic growth function and actual values for new reported cases nationally (a), in Hubei Province (b), and in non-Hubei provinces (c), and the estimated and actual values for cumulative cases nationally (d), in Hubei Province (e), and in non-Hubei provinces (f) are represented. I is the observed value and I_hat is $\hat{I}$. Graphing Equation (1) using estimated parameters from Equation (3) involved more than plugging parameters $\hat{\beta }$ in. When integration occurs, one needs to add some constant C, and therefore this study added a constant that was the difference between the mean of all observed data points and that of all predicted data points. The cutoff day, namely March 13, 2020, distinguished the training period from the testing period. The dotted lines of l95mean and u95mean show the 95% confidence interval of the mean predicted value at a given time (t).

Table 2.

Modelling results for ten selected non-Hubei provinces and municipalities in China

Province/municipality	T	Date of first observation	$\hat{K}$	95% CI of $\hat{K}$		$\hat{r}$	95% CI of $\hat{r}$		$\widehat{P_0}$	F statistic	Approx. Pr > F	Estimated date of maximal increase	R2
				Lower	Upper		Lower	Upper					Train	Test	Total
Anhui	51	22-Jan	1052.8	973.7	1131.9	0.2518	0.2279	0.2757	41.49	416.86	<0.0001	2020/2/3	0.963	0.000	0.963
Beijing	50	23-Jan	415.5	369.3	461.8	0.2304	0.1974	0.2634	38.869	232.06	<0.0001	2020/2/2	0.937	0.000	0.935
Chongqing	51	23-Jan	695.4	601.1	789.6	0.1764	0.1463	0.2064	109.90	212.24	<0.0001	2020/1/31	0.930	0.000	0.930
Guangdong	54	19-Jan	1347.2	1243.2	1451.3	0.2846	0.2572	0.312	24.89	372.66	<0.0001	2020/2/2	0.956	0.000	0.955
Hunan	51	22-Jan	1116.7	1027.2	1206.2	0.2438	0.2188	0.2689	76.54	404.48	<0.0001	2020/2/1	0.962	0.000	0.962
Henan	50	23-Jan	1366.1	1269.9	1462.3	0.2507	0.2281	0.2733	89.91	519.54	<0.0001	2020/2/2	0.971	0.000	0.971
Jiangsu	51	22-Jan	707	657.9	756.1	0.2124	0.1935	0.2313	47.69	534.04	<0.0001	2020/2/2	0.971	0.000	0.971
Jiangxi	52	21-Jan	983.7	890.7	1076.7	0.2725	0.2402	0.3048	26.59	254.12	<0.0001	2020/2/3	0.940	0.000	0.940
Shanghai	53	20-Jan	345.7	313.9	377.6	0.2625	0.2319	0.2932	14.33	278.07	<0.0001	2020/2/1	0.943	0.000	0.943
Zhejiang	50	23-Jan	1241.7	1054.7	1428.7	0.3053	0.2462	0.3644	98.836	120.92	<0.0001	2020/1/31	0.885	0.000	0.885

CI, confidence interval.

Table 2 shows the modelling results of Equation (4) estimated for time-series data of new COVID-19 cases in ten non-Hubei provinces. The ten provinces chosen were those that had the highest numbers of cumulative cases or those that were significant to China's economy. The ‘Train’ column includes the training data, the ‘Test’ column includes the testing data, and the ‘Total’ column includes the training and testing data combined.

Fig. 2.

Graphical representation of the modelling results in Table 2 for time-series data of ten provinces in China. Due to space limitations, this figure does not present the scatter plot data of observed values for each province/municipality. The scatter plot and fitted curves for each province/municipality have been drawn, and they are available upon request.

Table 3.

Modelling results for nine selected countries

Country	T	Date of first observation	$\hat{K}$	95% CI of $\hat{K}$		$\hat{r}$	95% CI of $\hat{r}$		$\widehat{P_0}$	F statistic	Estimated date of maximal increase	R2
				Lower	Upper		Lower	Upper				Train	Test	Total
Iran	23	19-Feb	19 604.5	10378.3	28830.8	0.2151	0.1237	0.3066	197.20	79.87	11-Mar	0.923	0.030	0.085
South Korea	53	20-Jan	8080	7126.2	9033.8	0.3610	0.3082	0.4138	0.0026	157.34	1-Mar	0.904	0.007	0.858
France	49	24-Jan	57 021.5	−1.26E7	12718836	5.3E–4	−1.133	1.1343	51 631	0.35	Convergence criterion unmet
Germany	45	28-Jan	70 247.7	−5.84E6	5.98E6	9.4E–4	−0.979	0.9814	64 905	0.36	Convergence criterion unmet
U.S.A	51	22-Jan	5530.3	−4.728E9	4.7282E9	5.6E–3	−132.6	132.6	5444.5	0.04	Convergence criterion unmet
Italy	41	1-Feb	42 896.4	−1.449E8	1.4498E8	5.4E–3	−14.10	14.11	12 572	0.85	Convergence criterion unmet
Spain	41	1-Feb	49 407.6	−2.498E9	2.4981E9	6.2E–3	−22.53	22.55	47 464	0.31	Convergence criterion unmet
Singapore	50	23-Jan	15 679.8	−5.834E7	58373740	0.0104	−0.779	0.8007	118.3	10.29	Convergence criterion unmet
Japan	50	20-Jan	29 78.6	−5022426	5028383	0.0070	−1.602	1.616	157.0	7.13	Convergence criterion unmet

CI, confidence interval.

Table 3 shows the modeling results of Equation (4) estimated for time-series data of new COVID-19 cases in nine nations. Apart from Iran and South Korea, the model failed to reach optimal results for the other seven nations. Six of the listed nations (France, Germany, Iran, Italy, Spain, and the USA) represented those with the most cumulative cases as of March 13, 2020. The three others (Japan, South Korea, and Singapore) are nations that are situated close to China and underwent early outbreaks. The ‘Train’ column includes the training data, the ‘Test’ column includes the testing data, and the ‘Total’ column includes the training and testing data combined.

Fig. 3.

Graphical representation of the modelling results in Table 3 for time-series data of South Korea and Iran. The estimated logistic growth function and actual values for new cases in South Korea (a) and Iran (b), and the estimated growth function and actual values for cumulative cases in South Korea (c) and Iran (d) are represented. I is the observed value and I_hat is $\hat{I}$. As in Fig. 1, this study added a constant that was the difference between the mean of all observed data points and that of all predicted data points in the integration process. The cutoff day in (a) and (c), namely March 13, 2020, distinguished the training period from the testing period. This is also the case for cutoff 1 in graphs (c) and (d). However, for Iran, this study developed two other models, shown with dotted lines, based on different cutoff dates at t = 30 (cutoff 2, March 21, 2020) and t = 50 (cutoff 3, April 9, 2020).

Based on Figures 1, 2 and 3, the regression model fits the testing data well. However, its R ² values in the testing period, as indicated in Table 1, Table 2, do not show consistent results. This is due to the fact that the testing and training time-series data inherently occupy two distinct portions of the non-linear curve, wherein the training period covers the peak of the outbreak with most of the cases, and the testing period covers only the flat, right-end tail with few cases. This study identified that when the predicted value reached close to 0 in the testing period and new cases became sporadic, the R ² value ended up unstable - sometimes almost 0 and other times surpassing 1 - a finding also consistent with Greene (Greene, 1997). As a result, the R ² may be different between distinct sections of the non-linear curve, and may be misleading when it is used to compare goodness-of-fit between these portions.6

The model may not carry the strikingly high R ² values that appear when fitted to cumulative data. However, the results avoid the problem of bias and the underestimation of uncertainty, yielding more realistic estimates. Notably, as shown in Fig. 1, national COVID-19 cases will be around 71 954.6 (95% CI 64 640.2–79 268.9), the Hubei, China cases will be around 58 221.3 (95% CI 51 319–65 123.5), and the non-Hubei, China cases will be around 13 426.1 (95% CI 12 810.6–14 041.6). It is important to note that the confidence intervals exclude the cases removed during the data adjustment process, as mentioned in the Methods section.

While parameters K and P ₀ reflect innate regional differences in population and size, this study demonstrated that the growth rate r might differ between provinces in China resulting from variations in local control measures and policies. Through the restriction test, the study showed that the calculated test statistic was 3.84863 with a corresponding p-value of 0.00010, and rejected the null hypothesis that r was the same among provinces and municipalities (Table 4 ). These findings corroborate previous studies showing that the degree of success in the control of proliferation has been influenced by a host of factors, ranging from individual patient response (Lau et al., 2016) to control and precautionary measures taken. More specifically, these may include differences in quarantine protocols, city-wide lockdowns, and travel restrictions, as well as distinctions in local cultures and behavior. Therefore, there is potential for others to study COVID-19 proliferation in various regions in China with the aim of strengthening viral prevention measures as cases surge internationally.

Table 4.

Parameter restriction test results

Restriction test	Restricted parameter	ESSr	ESSf	q	T–n	Test statistic	p-Value	Test results
10 Provinces/Municipalities	r	26 777.3	24 985.5	9	483	3.84863	0.00010	Reject null hypothesis
South Korea – Iran	r	1 370 869	1 185 307	1	70	10.9586	0.00083	Reject null hypothesis

Table 4 shows the restriction test results on growth rate r. The null hypothesis was that the growth rates were the same among the ten provinces or the same between South Korea and Iran. ESS_r is the residual sum of squares with restrictions, ESS_f is the residual sum of squares without restrictions, and qrepresents the number of restrictions imposed upon the growth rates. The Test statistic is calculated based upon Equation (7).

In regards to the modelling process for the nine countries listed in Table 3, the model failed to generate reliable estimates for seven out of the nine countries when no clear, discernable date of maximal increase in COVID-19 cases existed according to the data as of March 13, 2020. Consequently, when a model based on Equation (4) failed to reach optimal results, the corresponding region was likely in the early stages of an outbreak as of March 13, 2020.7 In the two nations that did yield reliable estimates, South Korea and Iran, this study predicted COVID-19 cases to reach 8080 (95% CI 7126.2–9033.8) and 19 604.5 (95% CI 10 378.3–28 830.8), respectively. A restriction test was also conducted for the growth rate r between these two countries, the results of which are displayed in Table 4. The test statistic was 10.9586 and the p-value was 0.00083, and this study, again, rejected the null hypothesis that r was the same between South Korea and Iran. In the case of South Korea, the regression model provided a good fit in the training data, but the fitness in the testing period was less satisfactory because the model failed to capture the additional new cases in the testing period. Modelling the data for Iran was a significantly more complicated process. Fig. 3 indicates a multitude of peaks in the time-series data of confirmed new cases of COVID-19 in Iran. As a result, the initial logistic model built using data up to March 13, 2020 failed to capture new peaks after that date. When estimating the regression model using more data and a cutoff date set at t  = 30 and t  = 50 (March 21, 2020 and April 9, 2020, respectively), this study demonstrated how the logistic regression model had evolved and fitted the data better as new information became available.

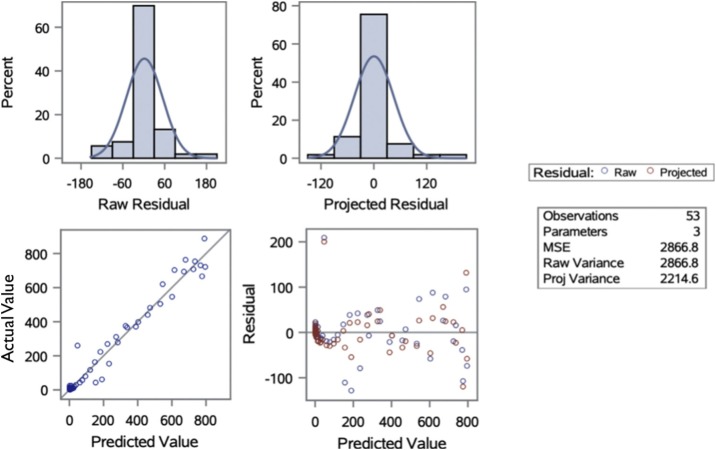
The results of the residual diagnosis tests from Table 5 and Fig. 4 show both the raw and projected residuals have their distributions centered around 0, and their predicted values closely follow a 45-degree line with their corresponding actual values. This study identifies the existence of positive serial correlation in two of the ten selected non-Hubei provinces (Zhejiang and Jiangsu) and in Iran based on either the raw or projected residuals. In the rest of the non-Hubei provinces of China as well as in South Korea, the DW test failed to reject the null hypothesis of no serial correlation in residuals. Furthermore, with the exception of Beijing, Guangdong and Shanghai, China, this study identified the existence of heteroscedasticity in all other selected non-Hubei provinces and cities, suggesting the variance in error terms largely existed and that it may vary depending on different stages of the proliferation. Accordingly, whereas this study's estimates are still consistent, they are not efficient (Pindyck and Rubinfeld, 1991). The findings suggest that further research may be needed to develop more efficient estimators of the model.

Table 5.

Durbin–Watson and White test results

Country/province	Type of residual	Durbin–Watson test		White test
		DW statistic	Result	Chi-square value	Result
National	Raw	1.796	Fail to reject	3.198	Fail to reject
	Projected	2.123	Fail to reject	2.558	Fail to reject
Hubei	Raw	1.911	Fail to reject	3.198	Fail to reject
	Projected	2.196	Fail to reject	2.558	Fail to reject
Non-Hubei	Raw	1.043	Reject	19.244	Reject
	Projected	1.629	Fail to reject	5.120	Fail to reject
Anhui	Raw	2.280	Fail to reject	14.810	Reject
	Projected	2.461	Fail to reject	16.203	Reject
Beijing	Raw	2.041	Fail to reject	3.855	Fail to reject
	Projected	2.232	Fail to reject	3.295	Fail to reject
Chongqing	Raw	1.941	Fail to reject	21.915	Reject
	Projected	2.090	Fail to reject	21.986	Reject
Guangdong	Raw	2.120	Fail to reject	4.0863	Fail to reject
	Projected	2.482	Fail to reject	5.406	Fail to reject
Hunan	Raw	1.993	Fail to reject	6.115	Reject
	Projected	2.190	Fail to reject	7.609	Reject
Henan	Raw	1.937	Fail to reject	13.720	Reject
	Projected	2.259	Fail to reject	20.010	Reject
Jiangsu	Raw	0.767	Reject	6.980	Reject
	Projected	1.531	Indeterminate	9.280	Reject
Jiangxi	Raw	1.549	Indeterminate	8.200	Reject
	Projected	1.826	Fail to reject	8.112	Reject
Shanghai	Raw	1.850	Fail to reject	1.850	Fail to reject
	Projected	1.901	Fail to reject	1.901	Fail to reject
Zhejiang	Raw	1.301	Reject	20.455	Reject
	Projected	1.650	Fail to reject	23.465	Reject
Iran	Raw	1.193	Reject	3.712	Reject
	Projected	2.088	Fail to reject	5.329	Reject
South Korea	Raw	1.776	Fail to reject	2.253	Fail to reject
	Projected	2.100	Fail to reject	2.798	Fail to reject

Table 5 shows the results of the Durbin–Watson test and White test conducted on both raw and projected residuals. The critical value for the DW test with the number of explanatory variables being 1 was 1.51 to 1.59, and ‘Reject’ indicated serial correlation issues. The critical value for the White test was 5.99, and ‘Reject’ indicated heteroskedasticity. Both the DW test and White test were conducted at the 5% significance level. The residual diagnosis was not performed for the seven other nations not listed in this table due to the lack of optimal model estimates.

Fig. 4.

Residual diagnosis for the non-Hubei regression model. The results in this figure are based on the non-Hubei time-series data; the results for other regions are available upon request.

In conclusion, this simple, three-parameter logistic growth function for reported COVID-19 cases estimated by an NLS method presents certain insights for current and future studies of outbreaks. This study's findings demonstrate that the model fitted the data in China exceedingly well, and the study was able to provide estimates for COVID-19 cases and compare the speed of proliferation among regions. However, the model failed to provide estimates for outbreaks in their early stages, and only yielded results after there was a definitive day of maximal increase in cases. Conducting a restriction test on the r parameter, the study found that between provinces in China and between other countries alike, the growth rates of COVID-19 differed and the study conjectured that this was due to disparities in local public health policies, societal behavior, patient response, etc. Accordingly, there is potential for this model to contribute to formulating better policies towards combatting COVID-19 by retrospectively analyzing the outbreaks in regions such as provinces in China. This study also observed that in non-linear regressions, the R ² value varied between different sections of the non-linear curve, and that the existence of heteroscedasticity and serial correlation in some provinces and countries warrant further research.

In summary, the study's findings show that in a relatively isolated environment such as China, where control measures are consistently strict and regulatory, the logistic regression model fits very well. However, when other factors become prevalent — such as diverging public health control practices and imported cases from abroad — the proliferation of infectious diseases may complicate research methods and a single logistic growth model may not suffice.

Declarations

Funding: Not applicable.

Ethical approval and consent to participate: The need for ethical approval or individual consent was not applicable.

Availability of data and materials: All data and materials used in this work are publicly available.

Consent for publication: Not applicable.

Conflict of interest: No conflict of interest to declare.