Toward Understanding the Risk of Secondary Airborne Infection: Emission of Respirable Pathogens

Abstract

Certain respiratory tract infections are transmitted through air. Coughing and sneezing by an infected person can emit pathogen-containing particles with diameters less than 10 μm that can reach the alveolar region. Based on our analysis of the sparse literature on respiratory aerosols, we estimated that emitted particles quickly decrease in diameter due to water loss to one-half the initial values, and that in one cough the volume in particles with initial diameters less than 20 μm is 6 × 10⁻⁸ mL. The pathogen emission rate from a source case depends on the frequency of expiratory events, the respirable particle volume, and the pathogen concentration in respiratory fluid. Viable airborne pathogens are removed by exhaust ventilation, particle settling, die-off, and air disinfection methods; each removal mechanism can be assigned a first-order rate constant. The pathogen concentration in well-mixed room air depends on the emission rate, the size distribution of respirable particles carrying pathogens, and the removal rate constants. The particle settling rate and the alveolar deposition fraction depend on particle size. Given these inputs plus a susceptible person's breathing rate and exposure duration to room air, an expected alveolar dose μ is estimated. If the infectious dose is one organism, as appears to be true for tuberculosis, infection risk is estimated by the expression: R = 1 − exp(−μ). Using published tuberculosis data concerning cough frequency, bacilli concentration in respiratory fluid, and die-off rate, we illustrate the model via a plausible scenario for a person visiting the room of a pulmonary tuberculosis case. We suggest that patients termed “superspreaders” or “dangerous disseminators” are those infrequently encountered persons with high values of cough and/or sneeze frequency, elevated pathogen concentration in respiratory fluid, and/or increased respirable aerosol volume per expiratory event such that their pathogen emission rate is much higher than average.

Individuals with certain respiratory tract infections (e.g., tuberculosis, smallpox, pneumonic plague) may transmit the infection through the air. When the individual coughs, sneezes, or speaks, particles of saliva and mucus containing the pathogen are emitted. Prior to the evaporative water loss that these particles undergo, many particles are sufficiently small to remain suspended in air for several minutes or more. In addition, owing to evaporation, some fraction of the larger particles becomes sufficiently small to remain suspended in air for a similar duration. If particles carrying pathogens are inhaled by a susceptible individual and deposit in a suitable location in the respiratory tract, infection and disease can ensue. Susceptible persons include personal contacts of the diseased individuals and health care workers who attend diseased patients in institutional settings.

Although airborne infection is simple in concept, the literature reveals disagreement regarding the ability of respiratory aerosol to transmit infection via inhalation. Because a great majority of emitted pathogens are in large particles termed “droplets,” which rapidly settle out of air, some believe there is a negligible chance of inhaling any pathogens, especially if the exposure is brief. Rather, it is argued that prolonged exposure in close proximity to the infectious case is required to elevate infection risk to an appreciable degree. For some pathogens it is thought that airborne transmission requires the infectious case to directly spray droplets by coughing or sneezing onto conjunctiva or mucous membranes,⁽¹⁾ an inoculation route termed “droplet transmission.” There is no consensus on the size criterion of a droplet, but one might consider a particle with an aerodynamic diameter d_a on the order of a few tens of μm or larger to be a droplet.

As an alternative, some believe that most droplets quickly evaporate down to the size of “droplet nuclei,” which settle from air slowly. The size criterion for a droplet nucleus is commonly taken to be d_a less than about 5 μm.^(2,3) Infection via inhalation of pathogen-carrying droplet nuclei is termed “airborne transmission.” W.F. Wells⁽⁴⁾ argued that droplets derived from respiratory fluid with d_a < 100 μm rapidly evaporate to become droplet nuclei before they can be removed from air by gravitational settling. However, we will show that the overall concentration of the nonvolatile components of respiratory fluid is not consistent with the idea that an emitted particle with d_a > 20 μm can become a droplet nucleus.

Our purpose here is to summarize the sparse data on the size distribution of respiratory aerosol, and to consider evaporative water loss in creating respirable pathogen-carrying particles. We show that while the vast majority of emitted pathogens are carried by particles that will not be inhaled even after water loss, the number of pathogens carried by small particles can still pose an appreciable infection risk for a susceptible person.

BASIC IDEAS

For this discussion, we assume that the alveolar region of the lung is the target site of infection, in which case, interest focuses on those pathogen-carrying particles with d_a ≤ 10 μm. Particles with d_a > 10 μm generally do not reach the alveolar region, and those in the 2 μm to 10 μm range reach the alveolar region with variable efficiency.⁽⁵⁾ Indeed, the idea of droplet nuclei involvement in airborne infection assumes that the alveolar region is the target site.⁽¹⁾ Because the density of a respiratory particle should be close to that of water, we will make no distinction between the physical and aerodynamic diameter. We note evidence that M. tuberculosis bacilli when carried on particles with d_a = 2 μm are one to two orders of magnitude more infective than when carried on particles with d_a ≈ 12 μm.⁽⁶⁾ More extreme is the case of Streptococcus Group C bacteria, which show an inhalation LD50 in mice of 200 when carried on particles with d_a = 2 μm, compared with an inhalation LD50 of 20 × 10⁶ when carried on particles with d_a = 12 μm.⁽⁷⁾ Still, it is invalid to broadly assert that respirable particles are required to transmit infection via inhalation, because for some pathogens the upper respiratory tract may be a target tissue. For example, there is evidence that subsequent to inhalation exposure to variola virus (smallpox) and Yersinia pestis bacilli (pneumonic plague), primary infection can occur in either the alveolar region or the upper respiratory tract.^(8–11)

Predicting infection risk for a susceptible person involves considering a set of factors including the airborne concentration of pathogens carried on particles with d_a ≤ 10 μm. This concentration depends on the pathogen concentration in respiratory fluid, the numbers and initial sizes of respiratory fluid particles emitted per unit time, the rate of particle removal from room air by mechanisms that include deposition onto surfaces and exhaust ventilation, the viability loss rate of the airborne pathogen, and distance from the point of emission. The concentration also depends on the size of the pathogen and its degree of aggregation. For example, if some fraction of organisms is associated with approximately spherical clusters of diameter 20 μm, these clusters cannot be carried by particles with d_a ≤ 10 μm; in this case, the pathogen concentration (number per mL) in respiratory particles with d_a ≤ 10 μm will be less than the pathogen concentration in the original respiratory fluid.

Let G denote the emission rate of pathogens (h^{− 1}) carried on particles that initially have, or quickly attain, d_a ≤ 10 μm. As we will show, an emitted particle can rapidly undergo water loss to attain an equilibrium diameter that is approximately one-half the initial diameter. Therefore, expelled particles with d_a ≤ 20 μm constitute the inhaled particles with d_a ≤ 10 μm. G is the product of the expulsion event rate E (event h^{− 1}), the pathogen concentration in respiratory fluid C_F (mL^{− 1}), and the volume of the emitted particles per expulsion event that have initial diameters less than 20 μm, denoted V₂₀ (mL event^{− 1}):

(1)

It has been suggested that respiratory particle diameters are approximately lognormally distributed.^(6,12) It would be convenient if the lognormal model were a good descriptor, because V₂₀ could be estimated using the geometric mean (GM) and geometric standard deviation (GSD) of the particle count distribution by diameter. As will be discussed, however, there are problems with using the lognormal model for respiratory particle diameters. In the alternative, we use a nonparametric method to estimate V₂₀. The latter volume is the sum of the number of particles in different diameter ranges or “bins” up to d_a = 20 μm, multiplied by the mean particle volume in the respective bins:

(2)

where N_i is the number of particles in the ith diameter size bin emitted per expulsion event, and v_i is the mean volume (mL) of a particle in the ith bin. If d_min and d_max denote the bin's lower and upper diameter values, respectively, the mean particle volume for the bin is estimated as follows:

(3)

Equation 3 assumes that particle diameters are uniformly distributed by count across the interval d_min to d_max. The quantities G and V₂₀ summarize in general terms the source strength of an infectious person. However, due to the dependence of particle settling and pulmonary deposition on particle diameter, estimating airborne infection risk should account in finer detail for the size distribution of pathogen-carrying particles. To this end, the emission rate of pathogens in different diameter bins up to d_a = 20 μm will be considered.

EVAPORATIVE WATER LOSS

Respiratory particles are composed of an aqueous solution containing inorganic and organic ions and glycoproteins; microbes are suspended in the medium. When expelled, the particles enter an environment that usually is at a lower relative humidity (RH) and temperature than in the respiratory tract. Therefore, the evaporation of some water, with concomitant particle shrinkage, is to be expected. Although we have found no literature that directly addresses evaporation from respiratory particles, the scientific literature on the equilibrium and kinetic aspects of aqueous aerosols, when combined with information on mucus composition, provides a basis to make reasonable estimates of the expected degree and rate of evaporation.

Table I summarizes data on mucus composition.⁽¹³⁾ The ion content is dominated by monovalent species, and the molar concentration of cations and anions is each approximately 150 mM. If we treated the ion content as 150 mM of NaCl (molecular weight 58.5 g/mol), the mass concentration of ions would be 8.8 g/L. According to Table I, the protein concentration of 76 g/L is about an order of magnitude higher. Because of its large contribution to the equilibrium particle size, the effect of protein on final particle size must be considered.

TABLE I. Major Components of Mucus.

Species	Molecular Weight or Atomic Mass	Concentration
Na+	23 g	91 ± 8 mM
K+	39.1 g	60 ± 11 mM
Cl−	35.5 g	102 ± 17 mM
Lactate	89 g	44 ± 17 mM
Glycoprotein	not given	76 ± 18 g/L

Source: Data from Effros et al., “Dilution of Respiratory Solutes in Exhaled Condensates.” American Journal of Respiratory and Critical Care Medicine 165:663–669 (2002).

Equilibrium Size with Complete Desiccation

Maximum shrinkage occurs if a particle loses all its water and retains nonvolatile solutes. The equilibrium size can be estimated, although the unknown dry density of the complex mixture of solutes in the respiratory fluid, denoted ρ_nonvolatile, introduces uncertainty. By equilibrium size we mean the diameter of a particle for which there is no net change in water content, that is, there is a balance between any evaporation of water vapor from and condensation to the particle. The mass concentration (g/L) of each nonvolatile chemical species in respiratory fluid is the product of its molar concentration (mol/L) and its molecular or atomic weight (g/mol). The total mass concentration C_nonvolatile of the five nonvolatile species in Table I is:

Let d₀ denote the initial particle diameter, and let d_eq denote the equilibrium particle diameter. If the particle becomes completely desiccated at equilibrium, the mass of nonvolatile species in the dry particle must be the same as in the emitted particle:

(4)

By rearrangement, the equilibrium diameter of the completely desiccated particle is related to the initial diameter as follows:

(5)

For ρ_nonvolatile a reasonable estimate is 1000 g/L, the density of water. Given C_nonvolatile = 88 g/L, we find d_eq = 0.44 × d₀. Therefore, the diameter of a completely desiccated respiratory particle is estimated to be a little less than one-half its initial diameter. If we considered only the ions in respiratory fluid, and treated the ion content as 150 mM of NaCl with ρ_NaCl = 2200 g/L, then C_nonvolatile = 8.8 g/L and d_eq = 0.16 × d₀.

Equilibrium Size with Incomplete Desiccation

Evaporation is driven by the difference in the water vapor pressure at equilibrium above the particle surface and in the ambient air. The presence of solutes in an aqueous respiratory particle causes a depression of the vapor pressure relative to that above pure water. The net effect is that some water will remain in the particle at equilibrium unless the RH is very low (below the crystallization RH). This retained water will cause the equilibrium diameter to be larger than estimated for complete drying.

The deliquescence relative humidity (DRH) is the minimum RH at which a solid salt particle undergoes a phase change to become an aqueous salt solution. For NaCl, the DRH is 75%.⁽¹⁴⁾ The crystallization RH (CRH) is the maximum relative humidity at which a wet salt droplet undergoing drying makes the phase change from an aqueous solution to a solid. The CRH is always less than the DRH. Seinfeld and Pandis⁽¹⁴⁾ reported CRH and DRH values of 40% and 80%, respectively, for ammonium sulfate. They did not report a CRH for NaCl, but given the similarity of the DRH values, it seems reasonable to expect that the CRH for NaCl is in the vicinity of, and perhaps somewhat less than, 40%. The result is that for indoor RH values > 40%, we expect some water to remain in the respiratory particles at equilibrium, even if they were to behave as salt droplets. At indoor RH values far below 40%, complete drying is feasible.

If a particle of respiratory fluid were treated as a simple NaCl solution at 150 mM, and if the indoor RH were 50%, it can be shown that after evaporative water loss d_eq = 0.19 × d₀, which is 19% greater than d_eq = 0.16 × d₀, as for a completely desiccated salt particle. If a particle of respiratory fluid containing glycoprotein in addition to ions were to retain water to a proportionate degree, the equilibrium diameter of the incompletely desiccated particle would be d_eq = (1.19) × (0.44 d₀) = 0.52 × d₀. Using a similar adjustment over the typical range of indoor RH (30% to 70%), the equilibrium diameter would range from 0.47 ×d₀ (30% RH) to 0.61 ×d₀ (70% RH). Given uncertainty in the estimate, we use the approximation d_eq = 0.5 × d₀ for our subsequent discussion. We stress that the reduction of a respiratory particle's initial diameter by one-half owing to evaporation is a rough estimate, in part because the solutes in respiratory fluid may be hygroscopic; however, we found no studies that have directly investigated the shrinkage of expelled respiratory particles.

Kinetics

In addition to the extent of the particle diameter decrease owing to evaporation, the rate of decrease must be considered. For airborne infection by droplet nuclei, there are three additional time scales of interest: (1) transport from the near field to mixing throughout a room, (2) settling of particles onto surfaces, and (3) removal of particles by air exchange or by active filtration. These time scales vary from many seconds to a few hours for typical indoor settings. If the evaporation rate is much faster than each of the other processes, then the details of the rate need not be considered and one can reasonably treat the new equilibrium as being attained instantaneously. At the other extreme, if the evaporation rate is much slower than all other important processes, one can neglect evaporation altogether. Intermediate conditions would necessitate a careful analysis of evaporation kinetics.

The analysis of evaporation entails computing the net flux of water vapor molecules by diffusion through a boundary layer adjacent to the particle. The driving force is the difference in partial pressure between the vapor immediately above the particle surface and the ambient air far from the surface. The net loss of water molecules is related to a net rate of particle shrinkage by material balance. A key result is the time-dependent equation for the particle diameter d(t) subsequent to time zero:

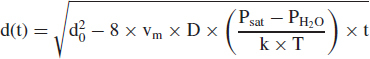(6)

In this expression, P_sat is the partial pressure of water vapor (dyne/cm²) in equilibrium with the surface of the droplet, which is assumed to equal water's saturation vapor pressure at ambient temperature T (kelvin). For simplicity, the decrease in P_sat owing to solutes is neglected. The term P_H2O is the partial pressure of water vapor in ambient air, equal to (RH/100) × P_sat. The initial particle diameter at time t = 0 is d₀ (cm). The parameter k is Boltzmann's constant (1.38 × 10^{− 16} erg/K), the term v_m is the condensed-phase volume occupied by a single water molecule (3 × 10^{− 23} cm³), and D is the molecular diffusivity of water vapor in air (0.18 cm²/sec).

Equation 6 can be rearranged to estimate the time needed for a particle's diameter to reach one-half its initial diameter, or d_eq = 0.5 × d₀. For T = 293 K (20°C) and the stated values of k, v_m, and D, the equation is:

(7)

where ϵ = 9.35 × 10⁸ g/(cm³− sec). At 50% RH (P_sat− P_H2O = 11,600 dyne/cm²), the estimated time for a particle with d₀ = 20 μm to attain d_eq = 10 μm is 0.24 sec; over the typical range of indoor RH, this estimated time is 0.17 s (30% RH) to 0.4 sec (70% RH). Particles with smaller d₀ values will attain their equilibrium diameters more rapidly. Given this relatively short time scale, we treat evaporation from respiratory particles with an initial diameter d₀ ≤ 20 μm as an instantaneous process. We note, however, that the presence of glycoprotein and other solutes in respiratory fluid will decrease P_sat below the saturation vapor pressure of pure water; as a result, t_eq will be somewhat longer than the times we have presented in this analysis. Experiments of the evaporation kinetics of respiratory fluid would be needed to determine whether these estimates are correct.

PARTICLE SIZE STUDIES

We located only three studies that have reported in a detailed manner the sizes and numbers of particles emitted during coughing and sneezing; the latter are the expulsion events generating the greatest number of particles. These studies were published by Duguid⁽¹⁵⁾ in 1946, Louden and Roberts⁽¹⁰⁾ in 1967, and Papineni and Rosenthal⁽¹⁶⁾ in 1997. Given the 50-year time span, it is not surprising that the studies employed different methods that likely contributed to inconsistency in the findings.

Duguid

Two techniques were used to describe the sizes and numbers of particles emitted during coughing, sneezing, and talking. A dye was introduced into the mouth, and a subject coughed or sneezed at a celluloid-surfaced slide held 6 inches in front of the mouth. The stain marks on the slide were measured by microscopy, and the stain diameters were reduced by one-half to estimate the airborne particle diameters. The reduction accounted for the spreading of the aqueous particles when they impacted on the slide; it was assumed that these particles had lost negligible water prior to impaction. Because only 1% of the particles on the slides had airborne diameters < 10 μm, it was assumed that most smaller particles were carried past the slide in the deflected air stream. To collect the latter particles, the cough or sneeze was directed into a chamber from which air was collected through a slit sampler onto an oil-coated slide. Air sampling was conducted for one minute, starting at half a minute after the expulsion event. The stained particles on the slide were measured by microscopy and appeared roughly spherical (not flattened). Duguid increased the measured stain diameters four-fold to estimate the airborne particle diameters; this adjustment assumed the sampled particles were completely desiccated and that d_eq = 0.25 × d₀. Less than 1% of the particles collected by air sampling had airborne diameters greater than 20 μm.

Using criteria that were not well explained or justified, Duguid combined the particle size distributions found by the two methods. In Figure 1, the circles show Duguid's cough data as cumulative percentile by count versus initial (expelled) particle diameter; the line labeled “D” shows the expected cumulative percentiles given the estimated lognormal parameters GM = 14 μm and GSD = 2.6. For Duguid's sneeze data, the estimated lognormal distribution parameters were GM = 8.1 μm and GSD = 2.3. In estimating the GM and GSD parameters, it was assumed that all of the emitted particles were observed. Table II lists the particle counts in different diameter ranges as reported by Duguid for a cough and a sneeze. The average number of particles emitted per cough and per sneeze was 5 × 10³ and 1 × 10⁶, respectively. We note that the number of test subjects and their health status were not described.

FIGURE 1. Log-probability plots of particle diameter (μm) versus cumulative percentile by count. The circles show Duguid's cough data, where the diameters are the initial particle diameters. The line labeled “D” shows the expected cumulative percentiles for Duguid's data given a fitted two-parameter lognormal distribution with estimated parameters of GM = 14 μm and GSD = 2.6. The diamonds show the Louden and Roberts cough data, where the diameters are the equilibrium particle diameters. The line labeled “L&R” shows the expected cumulative percentiles for the Louden and Roberts data given a fitted two-parameter lognormal distribution with estimated parameters of GM = 12 μm and GSD = 8.4.

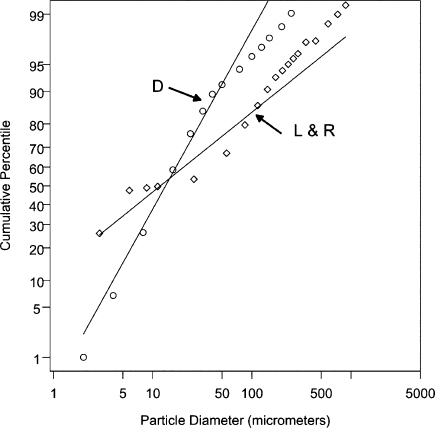
TABLE II. Numbers of Particles in Different Initial Diameter Ranges Emitted in One Cough and One Sneeze According to Duguid.

Diameter Range (μm)	Number of Particles in a Cough	Number of Particles in a Sneeze
1–2	50	26,000
2–4	290	160,000
4–8	970	350,000
8–16	1600	280,000
16–24	870	97,000
24–32	420	37,000
32–40	240	17,000
40–50	110	9000
50–75	140	10,000
75–100	85	4500
100–125	48	2500
125–150	38	1800
150–200	35	2000
200–250	29	1400
250–500	34	2100
500–1000	12	1000
1000–2000	2

Source: Data from Duguid, “The Size and Duration of Air-Carriage of Respiratory Droplets and Droplet-Nuclei.” Journal of Hygiene 4:471–480, Table 3 (1946).

Louden and Roberts

Two techniques were used to describe the sizes and numbers of particles emitted during coughing and talking. In a chamber of volume 0.057 m³, bond paper was placed on each equal surface area section of the chamber floor and walls. A dye was introduced into the mouth, and a subject coughed three times into the chamber. The chamber was then sealed for 30 min to permit particles to deposit onto surfaces. After 30 min, air was drawn from inside the chamber at 0.028 m³/min through a 0.45-μm pore Millipore filter to collect the particles that had remained suspended in air. The duration of sampling was not stated; however, we note that two minutes would suffice to sample a volume equal to that of the entire chamber. This procedure was repeated until five sets of three coughs were made for a subject, at which point the stain marks on the bond paper and the Millipore filter were measured by microscopy.

For particles with stain diameters greater than 10 μm, the measured diameters were adjusted slightly downward using a regression equation to obtain the airborne particle diameters. The equation was derived from the results of a separate study that evaluated the stain diameters of liquid particles with initial diameters in the 35 to 280 μm range after impaction onto bond paper.⁽¹⁷⁾ Because the regression equation did not apply to smaller particles, it was assumed that a particle with a stain diameter less than 10 μm had the same airborne diameter. The authors stated that all particles with stain diameters less than 10 μm were found on the Millipore filter, while all particles with stain diameters greater than 10 μm were found on the bond paper. The regression equation did not account for water loss from the larger particles prior to deposition onto bond paper,⁽¹³⁾ and there was no adjustment for evaporative water loss from the smaller particles collected on the Millipore filter.

In Figure 1, the diamonds show the Louden and Roberts cough data as cumulative percentile by count versus final (presumed equilibrium) particle diameter. The line labeled “L&R” shows the expected cumulative percentiles given the estimated lognormal parameters GM = 12 μm and GSD = 8.4. In estimating the GM and GSD parameters, it was assumed that all of the emitted particles were observed. Table III lists the cough particle counts in different diameter ranges as reported by Louden and Roberts; the numbers are aggregated across 90 coughs (two cough experiments for each of three subjects). The average number of particles emitted per cough was 470, which is an order of magnitude below Duguid's estimate. The health status of the test subjects was not described.

TABLE III. Numbers of Particles in Different Presumed Equilibrium Diameter Ranges Emitted in 90 Coughs According to Louden and Roberts.

Diameter Range (μm)	Number of Particles in 90 Coughs
1–2.9	10,879
2.9–5.8	9026
5.8–8.7	562
8.7–11.2	300
11.2–26	1650
26–55.5	5760
55.5–85	5205
85–114	2775
114–144	1785
144–173	1050
173–203	480
203–232	390
232–262	315
262–291	240
291–350	450
350–439	45
439–586	450
586–734	165
734–881	120
881–1029	30
1029–1176	60
1176–1471	150
> 1471	60

Source: Data from Loudon and Roberts, “Droplet Expulsion from the Respiratory Tract.” American Review of Respiratory Disease 95:435–442, Table 1 (1967).

Papineni and Rosenthal

Two techniques were used to describe the sizes and numbers of particles emitted during coughing and speaking. A subject coughed into a funnel connected to an optical particle counter (OPC), which sized and counted the particles before evaporative water loss occurred. The OPC was reported to have a lower diameter detection limit of 0.3 μm. Cough particle measurements for five subjects were made using the OPC method; all subjects were described as healthy. Electron microscopy was also used to count and size particles that impacted onto a grid placed on a glass slide, but this technique was used for normal exhalation only. The cough data were not tabulated according to particle count by size, but instead were graphically displayed for one subject only. Table IV lists the particle counts in different diameter ranges for this subject. No diameter above 2.5 μm was reported, although it appears that other subjects may have expelled particles with diameters up to 8 μm. Approximately 85% of the particles detected had diameters less than 1 μm. There were 420 particles emitted in the subject's cough, which is similar to the average number of 470 particles found in the Louden and Roberts study.

TABLE IV. Estimated Numbers of Particles in Different Initial Diameter Ranges Emitted in One Cough According to Papineni and Rosenthal.

Diameter Range (μm)	Number of Particles in a Cough
< 0.6	290
0.6–0.8	50
0.8–1.0	25
1.0–1.5	35
1.5–2.0	10
2.0–2.5	10

Source: Data from Papineni and Rosenthal, “The Size Distribution of Droplets in the Exhaled Breath of Healthy Human Subjects.” Journal of Aerosol Medicine 10:105–116, 1997, Figure 5.

DISCUSSION

Large Particles in Respiratory Aerosol

The Papineni and Rosenthal findings substantially differ from the data reported by Duguid and by Louden and Roberts (hereafter denoted L&R). The former contain no particles with diameters greater than 8 μm, while the latter two data sets contain many particles with diameters greater than 100 μm. This discrepancy is important because in the Duguid and L&R distributions, particles with diameters greater than 8 μm contain more than 99.9% of the aerosol volume (and therefore more than 99.9% of the pathogens) emitted. The absence of large particles from the data reported by Papineni and Rosenthal signifies that the potential pathogen emission rate would be several orders of magnitude lower than suggested by the other two data sets. The deficit of large particles in the Papineni and Rosenthal study may be a result of limitations in quantitatively sampling these particles using OPCs. Although OPCs can size particles up to 10 μm and larger, sampling and transmission losses become progressively more important with size for particles larger than about 2 μm.^(18,19) Moreover, we judge the results of a bioaerosol study described below to be inconsistent with the particle size data offered by Papineni and Rosenthal, but consistent with the Duguid and L&R data.

A study by Hamburger and Robertson⁽²⁰⁾ used subjects who were nose and throat culture positive for group A hemolytic streptococci. Each subject sat in the corner of a room (2.4 m × 3.0 m × 2.4 m) while facing into the room. Blood agar plates were placed on the floor in front of the subject at distances of 0.36, 1.7, and 2.9 m, respectively. A broth bubbler air sampler with its air inlet 0.9 m above the floor was also placed at each of these locations. The plates were intended to assay large droplets that settled, while the air samplers were intended to assay small particles suspended in air. A subject coughed 12 times, sneezed several times (median 3 times), or counted numbers while trying to direct the expulsion in a horizontal direction. When the expiratory activities started, the air samplers were operated for 5 min, at which point the subject left the room and the agar plates and bubbler samples were retrieved.

For sneezing, the most common result (13 of 20 subjects) was that relatively few streptococci were found in the air samples, but many were expelled in large droplets that settled to the floor. The large majority of streptococci were found on the settling plate at 0.36 m from the subject, far fewer were found at 1.7 m, and usually none were found at 2.9 m. In contrast, the streptococci collected by air sampling were more evenly distributed across the sampler locations. Two subjects expelled streptococci that were found only in the air samples and not on the settling plates. Twenty different subjects were used for the cough experiments, of whom only eight were found to expel streptococci; there was no consistent pattern in terms of the relative number of streptococci on the settling plates versus the air samples. Among 40 subjects tested, the number of group A hemolytic streptococci in saliva ranged from 2 × 10³ to 7.6 × 10⁶ mL^{− 1}.

To explain the markedly different results for sneezing versus coughing, the investigators argued that saliva is expelled during sneezing but typically not during coughing. They asserted that coughing expels fluid from the back of the pharynx but not in sufficient volume to emit large numbers of pathogens. An alternative explanation is that coughing emits far fewer particles (and pathogens) than does sneezing, and that the study design was not sufficiently sensitive to quantify the numbers of pathogens in large versus small particles emitted by coughing. According to Duguid, a sneeze releases 200-fold more particles than does a cough, such that three sneezes emit fiftyfold more particles than do 12 coughs. Most sneeze subjects also had higher concentrations of streptococci in saliva than did cough subjects; the respective median values were 4.3 × 10⁵ mL^{− 1} versus 1.6 × 10⁵ mL^{− 1}. Given that the number of streptococci colonies assayed on settling plates exceeded 35 for only two sneeze subjects, an approximate 100-fold reduction in the number of bacteria expelled by cough subjects indicates that no settled streptococci would be expected to be found for the latter subjects.

The Hamburger and Robertson sneeze data showed that most streptococci are carried by large particles that rapidly settle from air. According to Duguid, the particle size distributions for coughing and sneezing are similar, and the Duguid and L&R studies found large particles emitted in coughs. Overall, we judge the bioaerosol study findings to be consistent with the Duguid and L&R particle size distributions but inconsistent with the Papineni and Rosenthal distribution in which no large particles were present. As already alluded to, the underlying reason may be that Papineni and Rosenthal simply did not measure large particles.

If the Duguid and L&R data reflect the distribution of particle sizes in coughs and sneezes, it follows that the vast majority of emitted pathogens are carried by particles with d_eq > 50 μm. For example, according to the L&R cough data, > 99.999% of the aerosol volume (and, therefore one expects, pathogens) are in particles with d_eq > 50 μm. These particles will rapidly settle from air and even if inhaled will not reach the alveolar region. Hence, the argument that most pathogens are in large droplets not available for inhalation (or more strictly, not able to reach the alveolar region) is correct. However, as we will explain, this finding does not imply that infection by the inhalation route is highly unlikely.

The Respirable Particle Volume

We have argued that the emission rate of pathogens that can reach the alveolar region depends on the volume of the particles that initially have d_a ≤ 20 μm, denoted V₂₀. To estimate this quantity for a cough, we use the L&R data (Table III) and not the Duguid data (Table II) for several reasons. First, Duguid increased the observed diameters of the smaller particles by fourfold to account for evaporative water loss, whereas we have argued that a twofold increase is more appropriate, or d₀ = 2 ×d_eq. Second, owing to the lack of detail provided in Duguid's paper, we cannot discern what percentage of the particles in each of the first five diameter ranges in Table II were inappropriately size-adjusted by this factor of four. In contrast, the only adjustment applied by Louden and Roberts involved correcting for the slight spreading of the larger particles when impacting onto the bond paper; they did not adjust for evaporative water loss. Third, Duguid's data involved an unspecified number of subjects and an unspecified number of coughs in the range 10 to 22, whereas the L&R data involved observations known to be from three subjects and 90 coughs. Finally, another study in which cough particles were photographically enumerated reported that a cough releases on the order of several hundred particles.⁽²¹⁾ This estimate is in line with the L&R data but is an order of magnitude less than Duguid's particle count.

Because Louden and Roberts did not adjust their observed particle diameters for water loss, we believe it is reasonable to treat the Table III data as a distribution of equilibrium particle diameters. Given that we desire the initial particle diameters to compute V₂₀, we increase the reported diameters by a factor of two. This adjustment is shown in Table V for the first four L&R diameter ranges that contain particles contributing to V₂₀. Columns 3 and 4 list the lower and upper limits of the reported (presumed equilibrium) particle diameter bins, denoted as d_eq,min,i and d_eq,max,i, respectively, where i indexes a specific bin. Note that the upper limit of the fourth bin is listed as 20 μm rather than 2 × 11.2 μm = 22.4 μm. Columns 1 and 2 list the lower and upper limits of the bins for the initial particle diameters, where d_0,min,i = 2 ×d_eq,min,i and d_0,max,i = 2 ×d_eq,max,i.

TABLE V. Parameters for the First Four Particle Diameter Bins for the Louden and Roberts Cough Data.

Column 1	Column 2	Column 3	Column 4	Column 5	Column 6	Column 7	Column 8	Column 9
d0,min,i (μm)	d0,max,i (μm)	deq,min,i (μm)	deq,max,i (μm)	Initial vi (10− 10 mL)	Number Particles	Bin Volume 10− 8 mL	(μm)	Alveolar Deposition Fraction
2	5.8	1	2.9	0.38	120	0.47	2.1	0.32
5.8	11.6	2.9	5.8	3.8	100	3.8	4.5	0.21
11.6	17.4	5.8	8.7	17	6.2	1.0	7.3	.023
17.4	20	8.7	10	34	1.7	0.6	9.4	.006

Note: The reported (presumed) equilibrium diameters in Columns 3 and 4 are the same values shown in Table III, except for the fourth bin's upper limit, which is 10 μm rather than 11.2 μm. The reported particle diameters are multiplied by 2 to obtain the initial diameters prior to evaporative water loss. The initial diameters are listed in Columns 1 and 2. Column 5 lists the initial mean particle volume in each bin. Column 6 lists the number of particles emitted per cough in each bin, which equals the number of particles listed in Table III divided by 90. The exception is the fourth bin for which the number is proportionately decreased to account for the truncated bin range. Column 7 lists the initial particle volume in each bin. Column 8 lists the diameter corresponding to the mean equilibrium particle volume in each bin. For each bin, Column 9 lists the alveolar deposition fraction of a particle with the corresponding diameter in Column 8.

The initial mean volume of the particles in the ith bin, v_i, is computed by Equation 3 based on d_0,min,i and d_0,max,i; the value is listed in Column 5. The number of particles in each bin is listed in Column 6, and is set equal to the number of particles in the second column of Table III divided by 90. The exception is that for the fourth bin, the particle number is further adjusted by the fraction 0.52, because 52% of the 17.6 to 22.4 μm range is covered by the smaller interval 17.6 to 20 μm; the assumption is that particles are uniformly distributed by diameter across the larger range. The total volume of the particles in each bin is listed in column 7, and is the product of the initial mean particle volume (column 5) and the number of particles in the bin (column 6). The sum of the column 7 entries is V_20, which equals 6 × 10^{− 8} mL; this summation is the same operation shown in Equation 2 for i = 1,2,3,4.

In our V₂₀ calculations for a cough, we assumed an average of 470 particles (of equilibrium diameter greater than 1 μm) emitted per cough as reported by Louden and Roberts and did not rely on Duguid's estimate of 5000 particles per cough. At the same time, Duguid reported that a sneeze emits about 200-fold more particles than a cough. Therefore, a rough estimate of V₂₀ for a sneeze is 200 × (6 × 10^{− 8} mL) = 1.2 × 10^{− 5} mL.

Although we choose to rely on the L&R cough data, we note two inconsistencies in those findings. First, the investigators stated that all particles with stain diameters greater than 10 μm were found on the bond paper covering the chamber surfaces, while all particles with stain diameters less than 10 μm were collected on the Millipore filter air samples. However, air sampling was commenced 30 min after a subject coughed into the chamber, and in that 30-min interval a large fraction of particles with d_eq < 10 μm should have deposited onto the bond paper. For example, a particle with a 5 μm equilibrium diameter has a terminal settling velocity of 2.8 m h⁻¹. Given that the chamber height was 0.3 m, we would expect nearly all 5 μm particles to have settled onto the bond paper prior to the air sampling. The assay method was apparently not a factor since the same light microscopy technique with a resolving power of 0.5 μm was used to examine the bond paper and Millipore filters. We cannot resolve the discrepancy, which leaves open the possibility that the L&R cough data underestimate the number of particles with initial diameters less than 20 μm, and thereby lead to underestimating the value of V₂₀.

Second, it is likely that the methods used by Louden and Roberts failed to detect particles with equilibrium diameters less than 1 μm; as shown in Table III, these investigators did not report submicron diameter particles. However, the observations of Papineni and Rosenthal shown in Table IV indicate that many particles with diameters less than 1 μm are present in respiratory aerosol. The absence of submicron diameter particles in the L&R data causes a negative error in our estimate of V₂₀, although the error should be small because submicron particles likely contribute relatively little volume. For example, a 0.5 μm diameter particle has 1000-fold less volume than a 5 μm diameter particle. In addition, bacilli with a length or width aspect greater than 1 μm could not be carried by submicron diameter particles. On the other hand, virus particles and rickettsiae could be associated with submicron particles.

A final issue is the unknown health status of the three test subjects in the L&R study and its effect on our estimate of V₂₀ for a cough. We believe it is more likely that the subjects were healthy (had no frank respiratory disease) than unhealthy, because it is reasonable to assume that obvious respiratory disease among the cough subjects would have been noted in the published report. Of course, the failure to mention ill health does not prove its absence. In turn, an estimate of V₂₀ based on the coughs of healthy subjects would likely underestimate V₂₀ for coughs by individuals with certain respiratory infections generating greater amounts of sputum than normal.

The Lognormal Model

We stated earlier that if particle diameters were lognormally distributed, V₂₀ could be found using the parameters of the diameter count distribution. Unfortunately, the deviations from the expected cumulative percentile line for the L + R data in Figure 1 visually indicate that a lognormal distribution model does not provide a good fit. In the alternative, we found that a mixture of two lognormal distributions provides a better fit. As before, in estimating the GM and GSD parameters, it was assumed that all of the emitted particles were observed. For the adjusted L&R particle diameters (2 × reported value), the mixture model indicates there is a count distribution of “small” emitted particles with GM = 9.8 μm and GSD = 9.0, and a count distribution of “large” emitted particles with GM = 160 μm and GSD = 1.7. The former distribution contains 71% of all the cough particles, while the latter distribution contains 29%. For the adjusted L&R data, Figure 2 depicts the cumulative percentile by count versus initial particle diameter. The straight line shows the expected cumulative percentiles given a two-parameter lognormal distribution model with GM = 24 μm and GSD = 8.4, whereas the dashed curve shows the expected cumulative percentiles given a weighted mixture of the two lognormal distributions just described.

FIGURE 2. Log-probability plots of particle diameter (μm) versus cumulative percentile by count for the adjusted Louden and Roberts cough data, where the diameters are the presumed initial particle diameters (2× the reported values). The diamonds show the observed cumulative percentiles. The solid line shows the expected cumulative percentiles given a fitted two-parameter lognormal distribution model for the data with the estimates GM = 24 μm and GSD = 8.4. The dashed curved line shows the expected cumulative percentiles given a fitted mixture model of two lognormal distributions for the data. There is a distribution of “small” particles with estimates GM = 9.8 μm and GSD = 9.0, and a distribution of “large” particles with estimates GM = 160 μm and GSD = 1.7. The small particle distribution contains 71% of all the cough particles, and the large particle distribution contains 29%.

Although the mixture model improves the fit to the data, we note two problems that cause us not to rely on the estimated model parameters. The first is the aforementioned problem of the lower truncation of observed equilibrium diameter particles at 1 μm. If submicron diameter particles represent a substantial fraction of the particle count in emitted respiratory aerosol, then the estimated parameters of the mixture model for the diameter count distribution could be substantially biased. The second problem is that the combination of GSD = 9.0 for the “small” particle distribution, and the unbounded right tail of a lognormal distribution, leads to predicting an impossible aerosol volume. Given 470 particles in a cough, the fitted parameters correspond to an aerosol volume per cough of 450 mL.

Because it was adequate for our purposes to use a nonparametric estimate of V₂₀, we did not explore other statistical models that might adequately fit the observed data and permit reasonable extrapolation to particle sizes beyond the observations. At the same time, we offer the following comment. If an upper particle size limit were assumed, one could apply a bounded distribution such as a beta distribution or a mixture of beta distributions to model the count distribution of particle diameters. For small particles below the detection limit, if there was independent information on the volume of aerosol emitted in a cough, one might apply constrained maximum likelihood or Bayesian techniques to extrapolate the estimated diameter count distribution to these small particle sizes. In general, the particular question of interest should dictate the class of statistical model that is used. If the interest is infection via inhalation, only particles with equilibrium diameters less than 100 μm are relevant, and thus the appropriate models should give optimal estimates of the distribution in that range, for example, distributions with natural boundaries such as beta distributions or other truncated distributions. If extrapolation beyond the data is of primary interest, a different class of models is warranted. For all such estimation problems, given a particular subset of candidate models, model selection techniques such as density-based cross-validation should be used to pick the model best supported by the data.

An Airborne Infection Risk Model

For simplicity in illustrating the potential for inhalation infection by pathogens carried on particles with d_eq ≤ 10 μm, we use the well-mixed room (WMR) dispersion construct. In a WMR, particles are instantaneously and uniformly mixed throughout the air of the room. Although mixing requires finite time, the WMR model reasonably estimates exposure intensity for persons not near the emission source, and the widely used Wells-Riley model for M. tuberculosis infection assumes the WMR construct.^(6,22) We note that if infection by large nonrespirable particles (e.g., d_eq = 50 μm) were considered, relying on the WMR dispersion model would be inappropriate. The reason is that large particles have a terminal settling velocity sufficiently high to cause most to settle out of room air close to the release point; because large particles do not disperse throughout room air, exposure intensity to pathogens carried on large particles (and hence, infection risk) is extremely sensitive to a person's location in the room relative to the emission source.

Pathogens in respirable particles are added to room air at overall rate G (h^{− 1}) per Equation 1. However, because the rate of particle removal from room air and the probability of particle deposition in the alveolar region depend on particle diameter, we separately account for the particles in each of the four diameter bins shown in Table V. For the ith diameter bin, the pathogen emission rate is given by the expression:

(8)

where N_i is the number of particles per expiratory event in the bin, and v_i is the mean volume (mL) of a particle in the bin as computed by Equation 3 based on the initial bin limits d_0,min,i and d_0,max,i (Columns 1 and 2, Table V). The v_i and N_i values are listed in Columns 5 and 6, respectively, of Table V. The total respirable pathogen emission rate G is the sum of the bin-specific G_i values, as shown by Equations 1 and 2.

Viable pathogens can be removed from room air by several mechanisms. First, particles (and pathogens) are removed by dilution air with first-order rate constant α₁ equal to the room supply/exhaust airflow rate Q (m³ h⁻¹) divided by the room volume V (m³), or α₁ = Q/V (h^{− 1}); the rate constant α₁ is also termed the number of air changes per hour (ach). Second, particles with aerodynamic diameter d_a (μm) are removed by gravitational settling with first-order rate constant α₂ = ⌊0.108d_a²[1 + (0.166/d_a)]⌋H (h^{− 1}), where H (m) is the room height. The numerator in the expression for α₂ is the terminal settling velocity of the particle in m h^{− 1}; division of the terminal settling velocity by H gives the removal rate due to stirred settling.⁽⁵⁾ Third, airborne pathogens are biologically inactivated with first-order rate constant α₃ (h^{− 1}), which depends on the sensitivity of the pathogen to environmental stress. Finally, the application of in-room air filtration and upper room air ultraviolet germicidal irradiation can remove viable pathogens with a rate constant denoted α₄ (h^{− 1}).

Let α_2,i denote the settling rate constant for a particle in the ith diameter bin. The value of the aerodynamic diameter used to compute α_2,i is the diameter of that particle corresponding to the equilibrium particle of mean volume. To explain, when the particles have reached their equilibrium size after water loss, the lower limit for the ith diameter bin is d_eq,min,i and the upper limit is d_eq,max,i, which are listed, respectively, in Columns 3 and 4, Table V. The mean volume of the equilibrium particles in the ith bin, denoted , is computed by Equation 3 based on d_eq,min,i and d_eq,max,i. The diameter corresponding to this mean particle volume, denoted 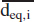, equals [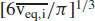; this diameter value is listed in Column 8 of Table V.

Given the addition and removal rates in the WMR construct, the time-averaged airborne pathogen concentration carried by particles in the ith diameter bin, denoted C_AV,i (m^{− 3}) is estimated as follows:

(9)

The overall respirable pathogen concentration in room air, denoted C_AV, is the sum of the bin-specific C_AV,i values. Next, consider a visitor to the room who inhales at rate B m³ h⁻¹ and is present for T hours. The expected number of inhaled pathogens contained in particles in the ith diameter size bin is C_AV,i× B × T. Of this number, some fraction f_i deposit in the alveolar region. To assign this fraction, we used the d_eq,i value for the bin, and averaged the alveolar deposition fractions of this particle size for mouth breathing and nose breathing, respectively, as read from a graph of alveolar deposition fraction versus d_a value and breathing mode.⁽⁵⁾ For example, for particles with d_a = 4.5 μm, 32% and 11% deposit in the alveolar region with mouth breathing and nose breathing, respectively; we assigned the average value of 21%.

The total expected number of pathogens deposited in the visitor's alveolar region, denoted μ, is computed by the expression:

(10)

where i = 1,2,3,4 indexes the four diameter bins listed in Table V. The actual integer number of pathogens deposited would follow a Poisson probability distribution. If the deposition of just one pathogen can initiate infection, the risk of infection R is given by the expression:

(11)

The term exp(−μ) is the Poisson probability that no pathogens deposit in the alveolar region. The complement, 1 − exp (−μ), is the Poisson probability that one or more pathogens deposit, in which case infection is assumed to occur.

Equation 11 is essentially the same as the traditional Wells-Riley “one-hit” risk model for infection by M. tuberculosis,^(6,22) which we use subsequently in an illustrative example. Although Wells and Riley inappropriately generalized the equation to the circumstance in which the infectious dose is greater than one,⁽²³⁾ Equation 11 is expected to apply to M. tuberculosis and to variola virus (smallpox) because published data for these two pathogens support an inference that the infectious dose is one organism.^(6,24–27) A discussion of the evidence is beyond the scope of this article; instead, we refer the reader to the cited references. We note that if the infectious dose is more than one organism, as appears to be the case for the pneumonic plague agent Yersinia pestis,⁽²⁸⁾ Equation 11 is not valid. Instead, if n organisms are required to infect, the risk of infection is the Poisson probability that n or more pathogens deposit, which is given by the “multiple-hit” expression:

(12)

where μ is again defined by Equation 10. The sum term on the right-hand side of Equation 12 is the probability that fewer than n organisms deposit.

The Potential for Inhalation Infection

A hypothetical but plausible scenario for airborne tuberculosis (TB) transmission is presented to illustrate the risk model. Consider a pulmonary TB source case who coughs 10 times per hour, or E = 10 h^{− 1}. Among a series of 96 pulmonary TB patients, one-fifth coughed an average of 12 times or more per hour.⁽²⁹⁾ Assume the bacilli concentration in respiratory fluid is C_F = 5 × 10⁶ mL^{− 1}. Among a series of 22 pulmonary TB patients, the mean concentration of viable M. tuberculosis bacilli in sputum was 8.4 × 10⁶ mL^{− 1} (range 6.6 × 10⁴ to 3.4× 10⁷ mL^{− 1}).⁽³⁰⁾ Assume that cough particles adhere to the adjusted L&R distribution shown in Table V for particles with d_eq ≤ 10 μm. Given these inputs, the total respirable pathogen emission rate G is 3 h^{− 1}.

Assume the source case occupies a residential bedroom for which V = 50 m³, H = 3 m, and Q = 25 m³/h, such that α₁ = (25 m³/h) / (50 m³) = 0.5 h^{− 1}. A 50 m³ volume is reasonable for a bedroom, and 0.5 ach is a typical residential air exchange rate.⁽³¹⁾ Airborne M. tuberculosis bacilli are reported to lose viability with a half-time of 6 h,⁽³²⁾ which corresponds to α₃ = ln(2)/(6 h) = 0.1 h^{− 1}. Assume no air disinfection controls are used in the bedroom such that α₄ = 0. For this set of inputs, and resulting G_i and α_2,i values, C_AV = 0.04 m^{− 3}. Assume that a susceptible visitor to the room has breathing rate B = 1.0 m³/h, which corresponds to light activity,⁽³³⁾ and is present for T = 1 h. Based on Equation 10 and the bin-specific C_AV,i and f_i values, μ = .008. Based on Equation 11, R = 1 − exp (−.008) = .0079, or 0.79%.

We judge that a 0.79% risk of infection for 1 h of exposure is substantial. If the visitor had repeated exposures such that T = 10 h, the risk of infection would be 7.7%. In addition, the WMR construct ignores the higher exposure intensity (and higher infection risk) that would pertain close to the emission source.^(34,35) We also note that our hypothetical G = 3 h^{− 1} is not so different from the mean respirable M. tuberculosis emission rate of 1.25 h^{− 1}, and falls within the emission rate range of 0 to 60 h^{− 1}, as reported by Riley and colleagues for a series of pulmonary TB patients as biologically assayed with guinea pigs.⁽³⁶⁾ In fact, the pathogen emission rates reported by Riley are underestimates because they did not account for a pulmonary deposition fraction less than one for the bacilli inhaled by guinea pigs.

Clearly, infection risk depends on the true values for the input parameters in Equations 11 and 12, and these factors can vary across pathogens, across infectious source cases, across rooms, across susceptible persons, and across time. We suggest that source cases termed “superspreaders” or “dangerous disseminators” are those infrequently encountered persons with high values for the factors C_F, E, and/or V₂₀, such that their emission rate of respirable pathogens is very much higher than average. For example, among the 96 pulmonary TB patients who were studied for cough frequency, one-half coughed 3 times per hour or less, but two patients coughed more than 48 times per hour.⁽²⁹⁾ In the previous scenario, a five-fold increase in C_F to 2.5 × 10⁷ mL^{− 1}, a five-fold increase in cough frequency E to 50 h^{− 1}, and a five-fold increase in V₂₀ to 3 × 10^{− 7} mL, would yield G = 370 h^{− 1}, C_AV = 5 m^{− 3}, and μ = 1. Infection risk via airborne transmission would then increase to 63% with just 1 h of exposure.

As previously noted, if the infectious dose is more than one organism, Equation 11 is not valid and infection risk will be substantially lower given the same input factors. For example, assume that the alveolar deposition of n = 10 pathogens is required to initiate infection. Based on Equation 12, the risk of infection is given by the expression:

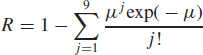where μ is defined by Equation 10. Next, consider a scenario with μ = 1. If the infectious dose is one organism, infection risk is 0.63 according to Equation 12. However, if the infectious dose is 10 organisms, infection risk is only 1.1 × 10^{− 7} according to the above expression based on Equation 14. This latter value could well be considered a de minimus risk.

CONCLUSIONS

Limited published data on the number and size distribution of respiratory fluid particles in a cough, combined with an estimated rapid decrease in particle sizes to one-half the initial diameters, leads to our estimating 6 × 10^{− 8} mL as the fluid volume per cough initially contained in particles with d_eq ≤ 10 μm. The corresponding volume for a sneeze is 1.2 × 10^{− 5} mL. We stress that these are rough estimates, and confirming their validity would require new experimental research efforts. Given these numbers however, if information is available on the pathogen concentration in respiratory fluid and the rate of expiratory events, an average emission rate for pathogens carried on respirable particles can be estimated. With further information on the room air supply rate and resistance of aerosolized pathogen to environmental stress, a simple well-mixed room model may be used to estimate the respirable pathogen concentration in general room air. In turn, infection risk for a susceptible room occupant is a function of the expected pulmonary dose, which depends on the airborne concentration, breathing rate, exposure duration, the alveolar particle deposition fraction for different particles sizes, and the infectious dose.

This approach to evaluating airborne infection risk requires multiple data inputs. For any given pathogen, infectious source case, and susceptible room occupant, there may be substantial uncertainty in the true values. Even so, we believe the approach provides a useful framework for identifying the most important information needs, and for evaluating the relative efficacy of alternative infection control measures.

ACKNOWLEDGMENTS

The authors thank Rachael Jones for conducting a literature search for pertinent articles. This work was funded by the National Institute for Occupational Safety and Health, Centers for Disease Control and Prevention, via collaborative agreement S2148-22/22 with the Association of Schools of Public Health. The ideas expressed are solely the responsibility of the authors and do not necessarily reflect the official views of the funding agency.