Curling of epithelial monolayers reveals coupling between active bending and tissue tension

Significance

Epithelial monolayers are sheet-like tissues composed of cells connected to one another that line the surface of all organs. These tissues change shape and bend during developmental morphogenesis or early in tumor formation. Yet, the amplitude of bending forces and how they integrate with tensile and compressive forces within the plane of the tissue remain largely unknown. By revealing the ability of epithelial monolayers to curl, we demonstrate that the polarization of contractile molecular motors within the tissue thickness generates high spontaneous curvature of the sheet. We quantify the corresponding torques and show that stretch and compression within the tissue plane can substantially impact curling. Such mechanical coupling could be at play during epithelial morphogenesis.

Abstract

Epithelial monolayers are two-dimensional cell sheets which compartmentalize the body and organs of multicellular organisms. Their morphogenesis during development or pathology results from patterned endogenous and exogenous forces and their interplay with tissue mechanical properties. In particular, bending of epithelia is thought to result from active torques generated by the polarization of myosin motors along their apicobasal axis. However, the contribution of these out-of-plane forces to morphogenesis remains challenging to evaluate because of the lack of direct mechanical measurement. Here we use epithelial curling to characterize the out-of-plane mechanics of epithelial monolayers. We find that curls of high curvature form spontaneously at the free edge of epithelial monolayers devoid of substrate in vivo and in vitro. Curling originates from an enrichment of myosin in the basal domain that generates an active spontaneous curvature. By measuring the force necessary to flatten curls, we can then estimate the active torques and the bending modulus of the tissue. Finally, we show that the extent of curling is controlled by the interplay between in-plane and out-of-plane stresses in the monolayer. Such mechanical coupling emphasizes a possible role for in-plane stresses in shaping epithelia during morphogenesis.

At all scales, from the cell plasma membrane to the petals of flowers, living systems use the ability of thin sheets to form curved shapes adapted to their functions (1, 2). At the tissue scale, epithelial monolayers bend and fold as part of developmental morphogenesis. This process requires the regulated activity of biological actors to generate spatially patterned physical forces. So far, fold formation in epithelial monolayers on the minute time scale has been shown to result from local contraction of the acto-myosin cytoskeleton. In particular, bending moments arise either through the formation of apicobasal acto-myosin cables (3, 4) or through constrictions caused by an asymmetric distribution of Myosin II along the apicobasal axis (5, 6). This latter process drives tissue morphogenesis during development (7–9), for instance, during the mesoderm invagination in Drosophila (10–12), but can also accompany disruption of epithelial architecture in disease, for example, during tumor growth in the pancreatic duct (13). Epithelial folding can also occur in response to in-plane compressive deformations, when their magnitude is sufficient to dissipate tissue pretension generated by Myosin II contractility (14). Although each of these mechanisms in isolation can give rise to folding, theoretical and experimental insights suggest that variations of in-plane stresses at the tissue scale can act in parallel to apical or basal constrictions to define the three-dimensional (3D) shape of epithelia (15–17). Yet, in contrast to the mechanical properties and active forces generated by epithelial monolayers within the plane (14, 18–23), methods to characterize out-of-plane forces and mechanical properties of epithelia (active torques and bending modulus) have only recently started to be developed (24). Consequently, the relative magnitudes of forces acting in plane and out of plane remain unknown, making the contribution of out-of-plane stresses to morphogenesis challenging to assess.

Here we use epithelial curling to characterize out-of-plane tissue mechanical properties. Curling is a mechanical phenomenon which occurs at the free edge of elastic materials endowed with a spontaneous curvature. For example, curling has been observed in the cell membrane during malaria parasite egress (25) or on a sheet of paper swelling at a liquid surface (26). In this article, we find that curling occurs at the free edge of epithelial monolayers devoid of substrate in vivo during Drosophila leg eversion and in vitro in suspended Madin–Darby Canine Kidney (MDCK) monolayers. We show that the high curvature of the curls is controlled by the asymmetric localization of Myosin II motors along the apicobasal axis. By unfurling the tissue via micromanipulation, we measure the amplitude of the resulting active torques as well as the bending modulus of the monolayer. Finally, we find a coupling between the in-plane and out-of-plane tissue shape, which can be understood quantitatively by modeling the tissue as a continuous thin sheet endowed with a spontaneous curvature. Altogether, these findings show that high spontaneous curvature generated by an apicobasal asymmetry of contractility allows epithelial monolayers to regulate their 3D shapes according to dynamic in-plane boundary conditions.

Results

Epithelial Monolayer Curling Depends on Myosin II Polarization.

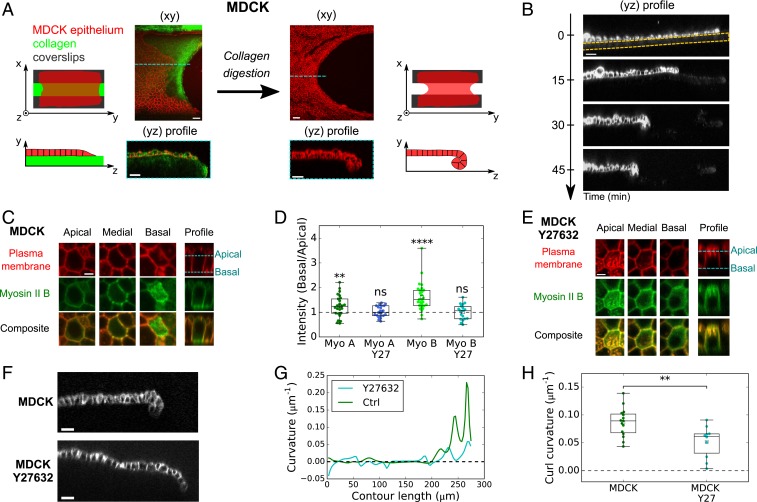
To investigate the importance of out-of-plane forces in shaping epithelia, we examined curling in monolayers. We hypothesized that epithelial tissues possessing an apicobasal asymmetry in myosin distribution along with a free edge and negligible matrix foundation should curl. Suspended epithelial monolayers meet these conditions. Indeed, these tissues are generated by culturing the epithelium on a scaffold of type I collagen, which is polymerized between two parallel glass plates and is then removed via enzymatic digestion (Fig. 1A and Materials and Methods) (18, 27). Upon matrix removal, we noticed that the free edge of MDCK monolayers retracted and took on a parabolic shape (n = 14/14; Fig. 1A and SI Appendix, Fig. S1A and Movie S1). These shape changes in the plane of the tissue were accompanied by shape changes in the transverse direction (yz plane) where the tissue curled toward its basal side (Fig. 1 A and B and SI Appendix, Movie S2). We extracted the radius of curvature of the curls $R_c=\left(12.7\pm 1.1\right)\hspace{0.17em}\mathrm{\mu }$m (see SI Appendix, Fig. S1 B and C, for method) which was comparable to the monolayer thickness measured in this region, $h=\left(18.6\pm 1.3\right)\mathrm{\mu }$m. Together with the lack of interstice observable within the curl (SI Appendix, Fig. S1D), this shows that MDCK epithelial monolayers curl as much as volume exclusion and steric interactions allow. We thus hypothesized that such high curvature stems from torques actively generated by an apicobasal asymmetry in the distribution of Myosin II molecular motors. To test this hypothesis, we imaged the distribution of GFP-tagged Myosin II-A and -B in MDCK monolayers devoid of substrate. Both myosins were enriched at the basal surface and lateral junctions compared to the apical surface (Fig. 1 C and D and Fig. S1E). This asymmetry of contractility along the apicobasal axis is consistent with the orientation of the curl toward the basal side of the epithelium. To directly prove that active forces were at the origin of tissue curling, we treated monolayers with Y27632, an inhibitor of Rho-kinase. In these conditions, the tissues showed a reduced asymmetric localization of Myosin II, which was significant only for Myosin II-B (Fig. 1 D and E and Fig. S1F). Concomitantly, the curvature at the tip of the tissue was reduced twofold (Fig. 1 F–H).

Fig. 1.

Curling at the free edge of MDCK epithelial monolayers is controlled by asymmetry in Myosin II across tissue thickness. (A) Effect of substrate digestion on the free edge of an epithelial monolayer. (Left) An MDCK monolayer (red) grows on a device composed of two parallel coverslips (black) connected by a collagen bridge (green). (Right) After collagen digestion, the monolayer has retracted in the xy plane and curled in the yz plane. (Scale bars: 30 $\mathrm{\mu }$m.) (B) Profile view (yz plane) of an MDCK monolayer as digestion of the collagen substrate proceeds. Collagenase is introduced in the medium at t = 0 min. Cell membrane is marked with CellMask. The initial thickness of the collagen substrate is indicated by the dashed yellow line. (Scale bar: 30 $\mathrm{\mu }$m.) (C) Localization of Myosin II-B–GFP in the apical, medial, and basal regions of an MDCK monolayer devoid of substrate. Plasma membrane is marked with CellMask (red). (Scale bar: 5 $\mathrm{\mu }$m.) (D) Ratio of Myosin II-GFP average fluorescence intensity in the basal surface to the apical surface (see method in SI Appendix). Myo A, Myosin II-A (n = 25 cells); Myo B, Myosin II-B (n = 27); Myo A Y27, Myosin II-A treated with 25 $\mathrm{\mu }$M Y27632 (n = 21); Myo B Y27, Myosin II-B treated with 25 $\mathrm{\mu }$M Y27632 (n = 18). Significance tests are one-sample t tests comparing the mean of the distribution to a value of 1 (SI Appendix, SI Methods). Two-sided Mann–Whitney tests comparing treated and nontreated samples: $p=7.4\hspace{0.17em}\times \hspace{0.17em}10^{-2}$ for Myosin II-A and $p=7.8\times 10^{-5}$ for Myosin II-B. Data extracted from n = 3 monolayers minimum for each condition. (E) Localization of Myosin II-B–GFP in the apical, medial, and basal regions of an MDCK monolayer devoid of substrate treated with 25 $\mathrm{\mu }$M Y27632. Plasma membrane is marked with CellMask (red). (Scale bar: 5 $\mathrm{\mu }$m.) (F) Profile view (yz plane) of the free edge of a suspended MDCK monolayer in untreated conditions (Top) and after treatment with 25 $\mathrm{\mu }$M Y27632 (Bottom). Cell junctions are marked with E-Cadherin-GFP. (Scale bars: 20 $\mathrm{\mu }$m.) (G) Local curvature along contour length of the monolayers shown in F. (H) Boxplot of curled tissue curvature, measured at the monolayer free edge in untreated (n = 15) and Y27632-treated tissues (n = 10).

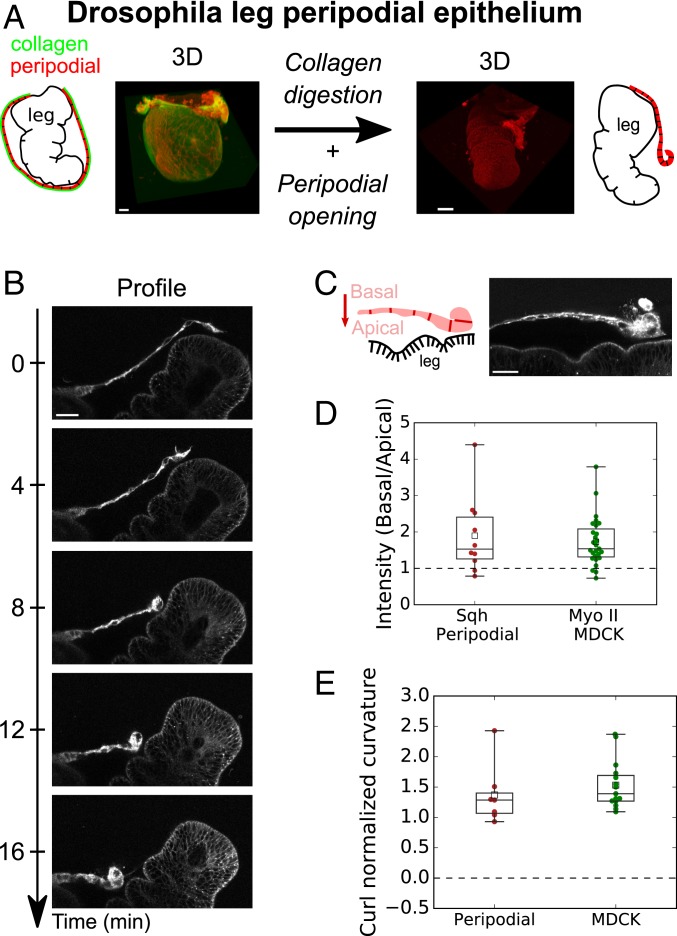
To establish whether epithelial curling occurs in vivo, we searched for an in vivo tissue which possesses a free edge and detaches from its extracellular matrix. The peripodial epithelium enclosing the Drosophila leg imaginal disc is known to meet these conditions. During early metamorphosis (28), the leg imaginal disc turns itself inside out (everts) (29, 30). To allow eversion, the peripodial epithelium first detaches from its basal extracellular matrix before rupturing, which generates a free edge that expands through Myosin II-dependent retraction (31) (SI Appendix, Fig. S2 and Movie S3). To focus on the mechanism of retraction at the cell scale, we recorded cell shape changes during peripodial retraction. Together with a large reduction of cell area, the peripodial epithelium curled (n = 9/13) toward the basal side (n = 9/9) (Fig. 2 A and B and SI Appendix, Movie S4), suggesting that the basal surface of the epithelium is more contractile than the apical surface. This was consistent with enrichment at the basal domain of Sqh, the homolog of Myosin II in Drosophila, and the magnitude of the asymmetry was comparable to what we observed in suspended monolayers (Fig. 2 C and D). Accordingly, the radius of curvature $R_c$ of the peripodial epithelium was close to its thickness, as found in MDCK suspended monolayers (Fig. 2E). These results show that in the absence of substrate interference, a Myosin II asymmetry along the apicobasal axis can control the out-of-plane curvature at the free edge of epithelial monolayers in vivo and in vitro.

Fig. 2.

The peripodial epithelium curls in vivo during Drosophila leg disk eversion. (A) Fate of peripodial epithelium during Drosophila leg disk eversion. Before eversion (Left), the leg epithelium is encapsulated in the squamous peripodial epithelium whose basement membrane (Vkg-GFP; green) is intact. After collagen digestion, the peripodial epithelium ruptures and withdraws (Right) allowing leg eversion. Cell membranes are marked with CellMask (red). (Scale bars: 20 $\mathrm{\mu }$m.) (B) Time series of a retracting peripodial epithelium imaged with confocal microscopy. Profile view in the plane perpendicular to the retraction front. Cell membranes are marked with CellMask (red). (Scale bar: 20 $\mathrm{\mu }$m.) (C) Distribution of Sqh-RFP (Myosin II homolog) during Drosophila leg eversion. (Scale bar: 20 $\mathrm{\mu }$m.) (D) Ratio of average fluorescence intensity in the basal surface to the apical surface (see method in SI Appendix). Intensity of Sqh-RFP for the peripodial epithelium (n = 10) and Myosin II-GFP (pooled for Myosin II-A and II-B, n = 52 cells from nine monolayers) for MDCK suspended monolayers. Significance tests are one-sample t tests comparing the mean of the distribution to a value of 1 (SI Appendix, SI Methods). (E) Boxplot of normalized curvature (ratio of average tissue height $h$ over average radius of curvature $R_c$) at the monolayer free edge in the peripodial epithelium (n = 7) and in MDCK monolayers (n = 15).

Characterization of Active Torques and the Bending Modulus.

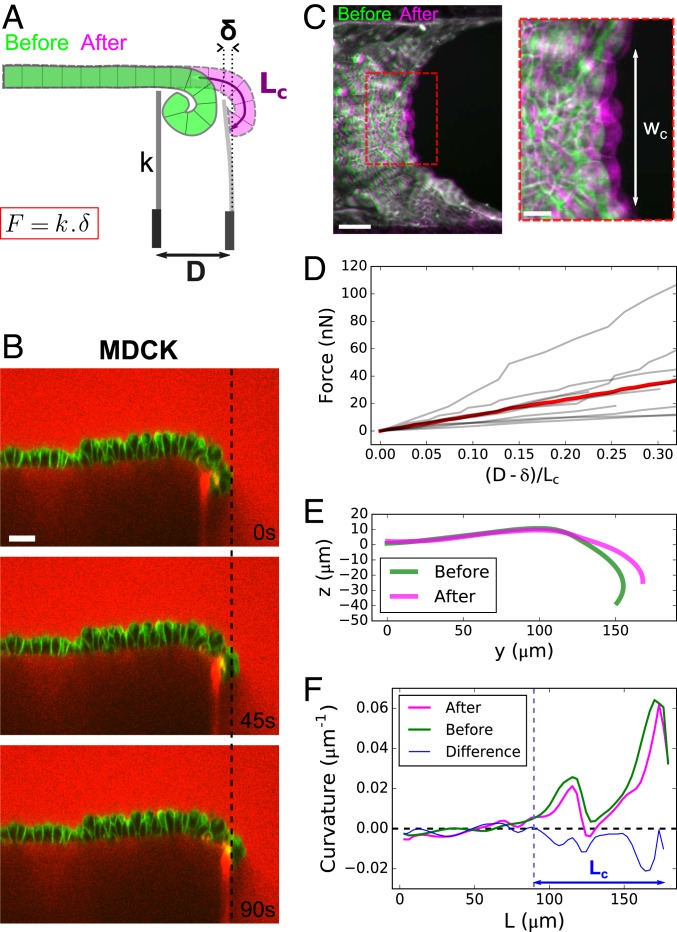
We then aimed to directly test if curls were generated by active torques by measuring the force necessary to unfurl MDCK epithelia. To do this, we brought a glass needle of stiffness $k$ into contact with the curled region of a monolayer and imposed a displacement $D\left(t\right)$ at its base via a motorized micromanipulator (SI Appendix, SI Methods). Simultaneously, we imaged the change of curvature of the tissue in the yz plane and measured the deflection $\delta \left(t\right)$ of the cantilever using confocal microscopy (Fig. 3 A and B and SI Appendix, Fig. S3A and Movie S5). The force required to unfurl the tissue $F\left(t\right)=k\delta \left(t\right)$ was on the order of tens of nano-Newtons (Fig. 3D). In the plane, the force propagated over a region of width $w_c$ and induced a small stretch of the bulk of the tissue, as shown by confocal stacks of the tissue acquired before and after unfurling (Fig. 3C and SI Appendix, Fig. S3D). Out of plane, the displacement of the cantilever resulted in a change of curvature of the curled region (Fig. 3 E and F).

Fig. 3.

Characterization of active torques and bending modulus of epithelial monolayers. (A) Diagram of the setup to measure the bending modulus of an epithelial monolayer. A flexible glass capillary of stiffness $k$, serving as a force cantilever, is approached close to a tissue edge (green) of curled length $L_c$. The displacement $D$ imposed at the base of the cantilever generates a deflection $\mathrm{\delta }$ of the cantilever, due to the restoring force of the flattened tissue (pink). (B) Time series of an MDCK monolayer imaged in profile during a ramp of displacement of the force cantilever. Dextran-Alexa647 was added to the medium (red). Note that this dye also stains the tip of the cantilever underneath the monolayer, which facilitates the measurement of its displacement. Cell membranes are marked with CellMask (green). (Scale bar: 30 $\mathrm{\mu }$m.) (C) Overlay of projected confocal stacks showing the free edge of an MDCK suspended monolayer before (green) and after (magenta) unfurling of the monolayer by the force cantilever. $w_c$ denotes the width of unfurled tissue. (Scale bar: 50 $\mathrm{\mu }$m.) Inset shows a zoom on the deformed region of width $w_c$. (Scale bar: 20 $\mathrm{\mu }$m.) (D) Force variation along a ramp of displacement imposed at the cantilever base. The displacement of the cantilever tip is quantified by the ratio $\frac{D-\delta }{L_c}$, which is equal to 1 when the tissue is fully unfurled. The gray lines represent n = 9 separate experiments; the red line represents the average. (E) Typical profile of monolayer before (green) and after (pink) unfurling of the tissue by the cantilever. (F) Typical variation of curvature of the monolayer along its contour length L before (green) and after (pink) unfolding by the cantilever. The difference between the two curves is plotted in blue. The dashed blue line indicates the transition between curled and noncurled regions of the tissue corresponding to the position where the blue curve departs from the x axis.

Because the force applied on the cantilever by the tissue did not relax after unfurling (SI Appendix, Fig. S3C), we could use this method to define a bending modulus for the epithelial monolayer by using a thin film approximation. Thus, the work transferred to the tissue via the cantilever displacement is equal to the sum of the variation of bending energy of the curled tissue and the stretching energy of the bulk (see details in SI Appendix, Appendix 1). We could then estimate a bending modulus of the tissue, $B=\left(1.9\pm 0.3\right)\times 10^{-13}$ N$\cdot$m, close to that predicted by the classical Kirchhoff–Love model of thin plate, $B_{KL}=\left(3.1\pm 0.2\right)\times 10^{-13}$ N$\cdot$m and consistent with a recent estimate extracted from buckling of MDCK monolayers due to tissue growth in long-time scale experiments (32).

Spontaneous Curvature Is Homogeneous Throughout the Epithelium.

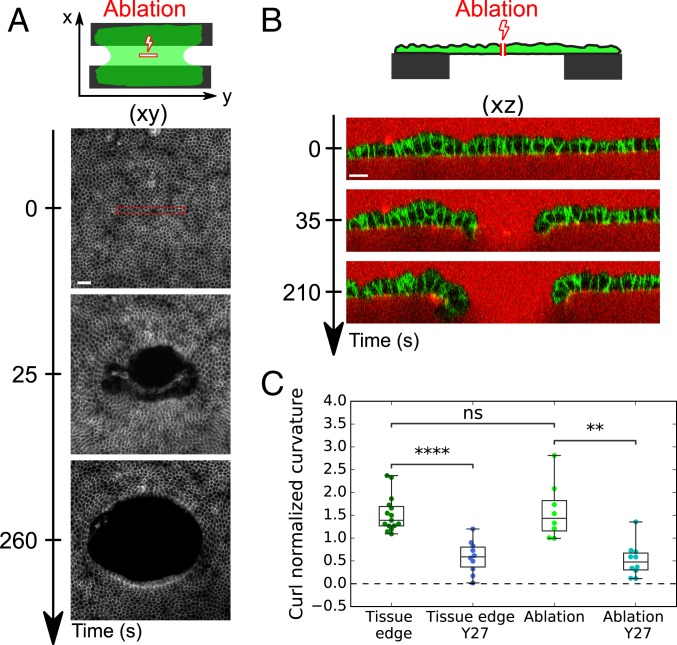
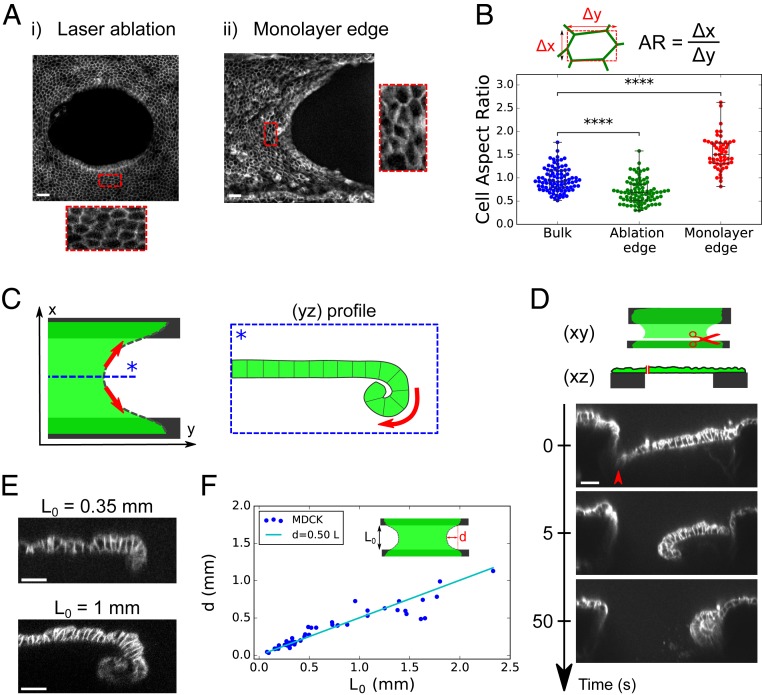
During wound healing, cells at the free edge acquire different characteristics from those in the bulk (33). Therefore, we asked whether curling emerged from specific cell properties at the edge of the tissue or from a spontaneous curvature present everywhere in the bulk of the tissue. For this, we used laser ablation to generate a rectangular cut in the center of MDCK monolayers (150 × 15 $\mathrm{\mu }{\text{m}}^2$, $\simeq$16 × 2 cells) whose long axis was oriented parallel to the coverslips (Fig. 4A). Ablation of monolayers growing on a collagen substrate was followed by wound healing (SI Appendix, Fig. S4A and Movie S6), whereas ablation of suspended monolayers induced retraction of the tissue which took on an elliptical shape in the xy plane (Fig. 4A and SI Appendix, Movie S7). Simultaneously, the monolayer curled basally in the plane perpendicular to the longest axis of the cut (xz plane) (Fig. 4B and SI Appendix, Movie S8). Despite the difference of orientation and location, the curvature at the tip of ablated tissue was similar to curls occurring at the free edge of monolayers after collagen digestion (Fig. 4C). The fast time scale (approximately tens of seconds) at which the new free edge could curl indicates that all cells in MDCK monolayers are endowed with a constant isotropic spontaneous curvature which can bend the tissue and lead to curling wherever a free edge is generated. Thus, curling is not a specific property of cells at the tissue edge in our culture conditions. Furthermore, the tissue spontaneous curvature possesses an active origin since Rho-kinase inhibition led to the same reduction of curvature at the ablated site as at the tissue boundary (Fig. 4C and SI Appendix, Fig. S4 B and C and Movie S9).

Fig. 4.

Active spontaneous curvature is a bulk property of the tissue. (A) Time series of the ablation of a suspended MDCK monolayer. Laser ablation was performed inside the red rectangle at time t = 0 s. Cell junctions are marked with E-Cadherin-GFP. (Scale bar: 50 $\mathrm{\mu }$m.) (B) Time series of the profile view (xz plane) of an MDCK suspended monolayer before and after laser ablation. Cell junctions are marked with E-Cadherin-GFP. The medium is marked with Dextran-Alexa647 (red). (Scale bar: 15 $\mathrm{\mu }$m.) (C) Boxplot of the curled tissue normalized spontaneous curvature ($h/R_c$) of suspended MDCK monolayers at the free tissue edge or at the edge created by laser ablation in presence (n = 10) or not (n = 8) of Y27632 (Y27).

The Extent of Curling Is Controlled by Tissue Boundaries.

Together our results show that Myosin II asymmetry controls the spontaneous curvature of the tissue, but the parameter limiting the extent of curling at the free edge remains unclear. Notably, in both free edges created in the bulk by ablation and free edges at the tissue boundary, we observed that cells are elongated along the axis tangential to the edge (Fig. 5 A and B). Thus, we hypothesized that curling could be limited by the in-plane tissue tension. Indeed, sheet-like materials with a spontaneous curvature tend to curl naturally to relax their bending energy. This effect deflects the tissue inward. However, when the sheet is clamped at two of its ends, such deflection of the free edge created by curling will also stretch the free edge. Stretching could ultimately limit tissue curling via an elastic in-plane response of the monolayer (Fig. 5C). In sum, the balance between bending and in-plane elastic energies may define the equilibrium 3D shape of the monolayer. This is in line with the parabolic shapes observed at the free edge of the tissue in the xy plane or after laser ablation (Fig. 5A).

Fig. 5.

Tissue boundaries control the extent of curling. (A) Maximum projection of confocal stacks showing the free edge of an MDCK suspended monolayer: (A, i) 260 s after laser ablation in the tissue bulk and (A, ii) at the tissue boundary free edge. Insets show stretched cells in the direction tangential to the edge. Cell junctions are marked with E-Cadherin-GFP. (Scale bars: 30 $\mathrm{\mu }$m.) (B) Boxplot of cell aspect ratio: in the bulk before ablation (blue; n = 89 cells), in the vicinity of the ablation site (green; n = 87) as in A, i, and in the vicinity of the free edge (red; n = 53) as in A, ii. n = 5 different monolayers in each condition. The aspect ratio (AR) is computed as described in the diagram above the graph. (C) Diagram illustrating the proposed balance of forces in the plane and out of plane. The monolayer (green) possessing a spontaneous curvature naturally curls at the free edge to relax its bending energy. Curling deflects the tissue inward (box). Such deflection generates stretching of the free edge (red arrows), which ultimately limits curling because of monolayer elasticity. (D) Representative time series of a profile view (xz plane) of an ablated suspended MDCK monolayer (n = 12). Ablation was performed along the full length of the tissue at the interface with the coverslip (see diagram). Red arrowhead shows the location of the cut. (Scale bar: 30 $\mathrm{\mu }$m.) (E) Representative profiles (yz plane) of MDCK suspended monolayers acquired by confocal microscopy for monolayers of different lengths $L_0$ (n = 15 for $L_0$ = 0.35 mm; n = 5 for $L_0$ = 1 mm). (Scale bars: 30 $\mathrm{\mu }$m.) (F) Deflection $d$ of MDCK monolayers free edge as a function of initial length $L_0$. The line in cyan shows the linear fit as suggested by our model (SI Appendix, Appendix 2).

To directly test this, we first completely abolished tissue tension by cutting monolayers along the full length of the tissue–coverslip interface. After the cut, the tissue curled over its entire length, especially in the xz plane perpendicular to the cut (Fig. 5D and SI Appendix, Movie S10), confirming that tissue clamping and the resulting in-plane tension could prevent tissue curling.

Spontaneous Curvature Induces a Coupling Between In-Plane and Out-of-Plane Tissue Shape.

To further assess this idea, we designed a mechanical model of the epithelium. Because the in-plane (14) and out-of-plane (SI Appendix, Fig. S3C) mechanical responses of the tissue appear elastic within the time scale of our experiments (30 s to 15 min), we modeled the epithelium as a continuous rectangular elastic sheet endowed with a spontaneous curvature (SI Appendix, Appendix 2). In this framework, the extent of curled tissue at the free edge is a function of the sheet’s initial length $L_0$, its in-plane deformation $ϵ=\frac{L-L_0}{L_0}$, and the mechanical properties of the tissue: the 2D elastic modulus $E$, the bending modulus $B$, and the spontaneous curvature $C_s=\frac{1}{R_c}$. Importantly, all these parameters have been measured in our setup (see SI Appendix, Fig. S5 A and B, for the method to determine E). A first prediction of the model, which was confirmed experimentally, is that the deflection $d$ (corresponding to the length of tissue that curls at the center of the free edge) increases proportionally to the unstrained tissue length $L_0$ (SI Appendix, Appendix 2, and Fig. 5 E and F).

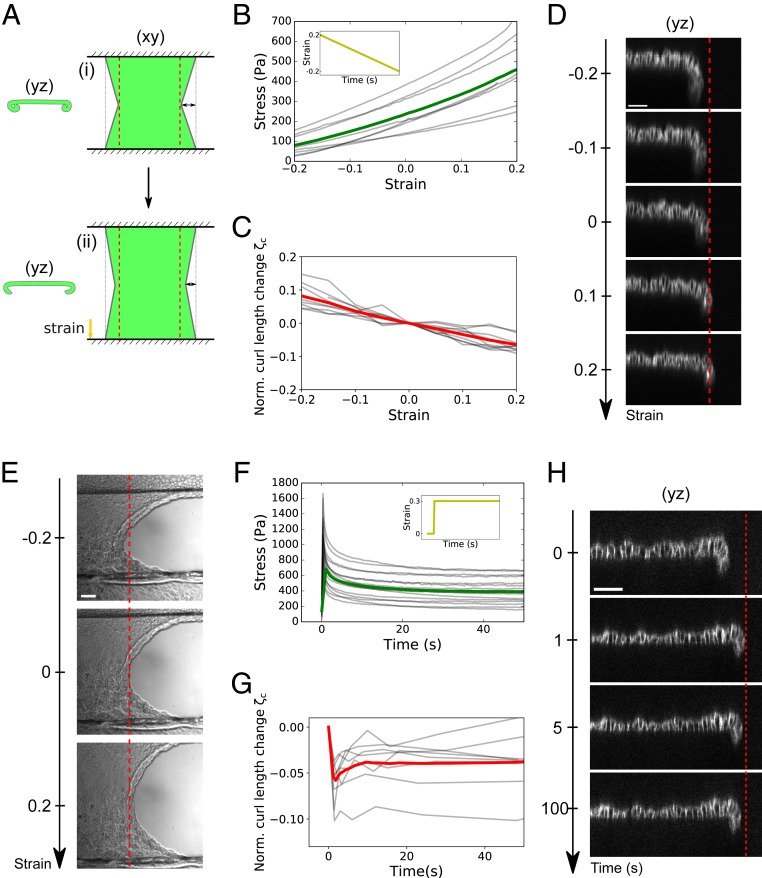
Conversely, our model predicts that in response to uniaxial stretch, the curled tissue should unfurl. This is because unfurling reduces the length of the free edge and the in-plane elastic energy of the sheet (Fig. 6A). To directly reveal such coupling, we dynamically controlled the length of the tissue along the x axis (SI Appendix, Fig. S5A) and monitored the effect on the curled length at the monolayer free edge (yz plane). We first imposed a slow ramp of deformation ranging from +20 to −20% at a strain rate of $0.5\%\cdot {\text{s}}^{-1}$. In this regime, MDCK monolayers behave elastically with stress increasing proportionally to strain (Fig. 6B) (14). Here we found that the curled tissue length increased as tissue stress and strain decreased (Fig. 6 C and D and SI Appendix, Movie S11). To compare this out-of-plane deformation to the in-plane strain imposed, we extracted the adimensional number ${\zeta }_c=\frac{L_c-L_c^0}{L_0}$, where $L_c$ and $L_c^0$ are the curled tissue length and curled tissue length for an in-plane strain $ϵ=0$, respectively. Remarkably, ${\zeta }_c$ is of the same order of magnitude as the in-plane strain $ϵ$, indicating a strong coupling between in-plane and out-of-plane tissue shapes. These shape changes were in quantitative agreement with predictions from our model parametrized with the mean measured values of the mechanical parameters ($B$, $E$, and $C_s$) (SI Appendix, Fig. S5C). In the model, coupling results from the high spontaneous curvature of the tissue since decreasing $C_s$ by an order of magnitude led to a lower change of curled length (SI Appendix, Fig. S5D). Therefore, we conclude that the coupling between in-plane and out-of-plane monolayer deformation originates from the high spontaneous curvature of the tissue controlled by the asymmetric distribution of Myosin II.

Fig. 6.

In-plane stress and spontaneous curvature interplay to control the extent of curling. (A) Diagram describing the model of 2D elastic sheet used to predict the coupling between in-plane (stretch) and out-of-plane (curling) tissue shape (SI Appendix, Appendix 2). (A, i) Curled and retracted state naturally reached by the sheet due to spontaneous curvature. For simplicity, the free edge is modeled as a straight diagonal line. (A, ii) Curled state reached after uniaxial stretching $\mathrm{ϵ}$ along the x axis. (B) Evolution of monolayer stress with in-plane strain during a ramp of compression performed at a rate of $0.5\%\cdot {\text{s}}^{-1}$ after an initial 25% stretch and 5 min period of rest (Inset). The gray lines represent eight individual experiments; the green line represents the average. (C) Evolution of normalized curled tissue length as a function of in-plane monolayer strain $\mathrm{ϵ}$ for the same ramp of deformation as in B. The gray lines represent nine individual experiments; the red line represents the average. ${\zeta }_c$ is defined in the main text. (D) Typical evolution of MDCK monolayer profile during a ramp of in-plane strain. Cell–cell junctions are shown by E-Cadherin-GFP staining. The red dashed line indicates tissue edge at null strain to emphasize the unfurling of the monolayer at positive strain (stretching) and increased curling at negative strain (compression). (Scale bar: 50 $\mathrm{\mu }$m.) (E) Typical DIC images of monolayer free edge in various strain conditions (−20, 0, and +20% strain). The red dashed line indicates tissue edge at zero strain. (Scale bar: 50 $\mathrm{\mu }$m.) (F) Time evolution of monolayer stress after a 30% step of stretch (Inset). The gray lines represent 16 individual datasets; the green line represents the average. (G) Evolution of normalized curled tissue length as a function of time after a 30% step of stretch. The gray lines represent eight individual datasets; the red line represents the average. (H) Typical evolution of MDCK monolayer profile after a step of in-plane strain. Cell–cell junctions are shown by E-Cadherin-GFP staining. The red dashed line indicates tissue edge immediately after stretch to emphasize the curling of the monolayer as stress relaxes. (Scale bar: 50 $\mathrm{\mu }$m.)

Interestingly, this coupling also implies that stretching a suspended monolayer causes an increase of its projected width, while compression induces a decrease in tissue width (Fig. 6E and SI Appendix, Movie S12). This behavior is not due to a bulk negative Poisson ratio (i.e., cells in the bulk do not change width; SI Appendix, Fig. S5 E and F) but rather to a behavior of the interface only.

In the above experiment, stress and strain evolve in proportion to one another. Yet our model suggests that in-plane stress controls tissue curling. In previous work, we have shown that following a step deformation of the monolayer, a substantial portion of stress is relaxed within tens of seconds (23) (Fig. 6F). We thus applied a fast step of stretch (+30% strain at $400\%\cdot {\text{s}}^{-1}$), maintaining strain constant while monitoring the curled length as in-plane stress decreases. Immediately upon application of stretch (i.e., in less than $\sim$0.8 s), the length of curled tissue decreased. Then, during stress relaxation, curled length increased for n = 6/8 samples before reaching a plateau in a time scale of about 10 s (Fig. 6 G and H and SI Appendix, Movie S13). Comparing curling relaxation with stress relaxation (Fig. 6F) showed that curled length and stress evolved in proportion to one another during about 60% of the stress relaxation process (SI Appendix, Fig. S5G). Therefore, out-of-plane tissue shape is influenced by in-plane tissue stress, even in absence of in-plane deformation.

Discussion

Active torques have long been known to induce out-of-plane deformation during epithelial morphogenesis, with some tissues showing Myosin II enrichment in the apical domain (7, 10) and others in the basal domain (8, 9). However, because of a lack of direct measurements, their importance relative to other forces in epithelia has been challenging to assess. Here, by measuring the stress required to flatten naturally curled MDCK tissues in vitro, we provide a direct demonstration of the existence of out-of-plane stresses generated by an asymmetric distribution of Myosin II. The spontaneous radius of curvature associated to these torques was on the order of the monolayer thickness in the MDCK epithelium and in the retracting peripodial epithelium of the Drosophila leg embryo. Such high spontaneous curvature is rare in inert materials, although at a different scale it can be observed in the cell membrane under the action of specialized proteins (1).

One important effect of spontaneous curvature in thin films is that it induces a coupling between tissue deformations in plane and out of plane (17, 34). Accordingly, we show here in the MDCK epithelium that changes in boundary conditions in the plane result in a visible change of curled tissue length at the free edge. Although we cannot exclude other potential mechanical feedback (for example, myosin flows in response to the variation of in-plane stresses), this effect is likely independent of cell signaling. Indeed, curling decreased immediately after the tissue was stretched at very high strain rate leading to out-of-plane deformation on a subsecond time scale (Fig. 6H). Furthermore, our mechanical model could predict changes of tissue shape out of plane (curled length) in response to a ramp of in-plane deformation by minimizing the elastic energy of a 2D sheet endowed with a constant and isotropic spontaneous curvature. This indicates that the coupling exists without any change of the tissue spontaneous curvature, which could occur in response to signaling. Even though the two systems studied here exhibit a basal enrichment of Myosin II, this effect should be valid regardless of the orientation of the torques and thus could be applied to in vivo systems showing either higher basal or apical contractility. In fact, it was shown recently that disruption of in-plane tension anisotropy in the Drosophila embryo can prevent mesoderm invagination driven by apical constriction (35), while compression generated by cell migration is required to correctly shape the optic cup alongside basal recruitment of Myosin II in zebrafish (36).

From our measurements, we could also estimate the bending stiffness of epithelial tissues. The value extracted was consistent with predictions from thin plate theory and from now on can be used to test the predictions of continuous mechanical models in specific biological contexts. For example, it was shown recently that depending on duct radius, early pancreatic tumor lesions either evaginate or invaginate, and the transition radius $R^{*}$ was predicted to be equal to the ratio between the bending modulus and the bending moment of the epithelium (13). Using our measurements yields $R^{*}\simeq \frac{B}{F_u}\simeq 10\hspace{0.17em}\mathrm{\mu }$m, which is on the order of magnitude of the in vivo measurements (with $F_u\simeq 30$ nN the typical force required to unfurl a commensurate section of epithelium), and thus suggests that the mechanical properties measured in vitro could be relevant to epithelia in general.

Importantly, rather than being a curiosity restricted to in vitro settings, we have shown that curling also occurs in vivo as part of developmental morphogenesis, during Drosophila leg eversion. In this process, the peripodial epithelium detaches from its matrix, fractures, and curls as it retracts to allow leg extension. Since the apical side of the peripodial epithelium faces the apical surface of the leg columnar epithelium, basal curling of the peripodial epithelium may facilitate leg eversion by limiting frictional forces between the two tissues. Furthermore, epithelial curling has also been reported in pathological conditions. During age-related macular degeneration, the retinal epithelium detaches from its basement membrane, ruptures, and retracts, leading to partial blindness of the patient (37). Curling, which has also been reported in this case, might have a negative impact by amplifying the opening of the retina (38). Thus, we expect epithelial curling to be involved in other physiological or pathological phenomena where a substrate-free epithelial monolayer exhibits a free edge and Myosin II polarization creates a spontaneous curvature of the tissue.

Materials and Methods

MDCK Cell Culture.

MDCK cells were cultured at ${\mathrm{37}}^{○}$C in an atmosphere of 5% ${\mathrm{C}\mathrm{O}}_{\mathrm{2}}$. Cells were passaged at a 1:5 ratio every 3 to 4 d using standard cell culture protocols and disposed of after 25 passages. The culture medium was composed of high-glucose Dulbecco’s Modified Eagle Medium (Thermo Fisher Scientific) supplemented with 10% FBS (Sigma) and 1% penicillin-streptomycin (Thermo Fisher Scientific).

Generation of Suspended MDCK Tissues.

Suspended monolayers of MDCK cells were generated as described in (18, 27). Briefly, a drop of collagen was placed between two test rods and left to dry at ${\mathrm{37}}^{○}$C. This collagen was then rehydrated before cells were seeded onto it and cultured for 72 h. Immediately before each experiment, collagen was removed via enzymatic digestion with collagenase leaving a suspended monolayer without extracellular matrix.

Supplementary Material and Methods.

Additional material and methods can be found in SI Appendix.