Determining the correct stoichiometry of Kv2.1/Kv6.4 heterotetramers, functional in multiple stoichiometrical configurations

Significance

Voltage-gated potassium (Kv) channels play a key role in cellular electrical excitability. While various Kv subunits assemble to homotetrameric functional channels, the silent subfamilies KvS exclusively form heterotetramers with Kv2 subunits and thus regulate their biophysical properties in a tissue-specific way. Despite the vast functional research, key aspects of the heterotetrameric architecture remain controversial, including the stoichiometry with which KvS and Kv2 can assemble. We used concatemers and single subunit counting in combination to show that Kv2/Kv6 assemble in a 2:2 stoichiometry following the general dimer-of-dimer mechanism for channel formation. We demonstrate how to objectively choose the most likely model for single subunit counting data, which is applicable for any multimeric complex and will help choosing models confidently.

Abstract

The electrically silent (KvS) members of the voltage-gated potassium (Kv) subfamilies Kv5, Kv6, Kv8, and Kv9 selectively modulate Kv2 subunits by forming heterotetrameric Kv2/KvS channels. Based on the reported 3:1 stoichiometry of Kv2.1/Kv9.3 channels, we tested the hypothesis that Kv2.1/Kv6.4 channels express, in contrast to the assumed 3:1, in a 2:2 stoichiometry. We investigate the Kv2.1/Kv6.4 stoichiometry using single subunit counting and functional characterization of tetrameric concatemers. For selecting the most probable stoichiometry, we introduce a model-selection method that is applicable for any multimeric complex by investigating the stoichiometry of Kv2.1/Kv6.4 channels. Weighted likelihood calculations bring rigor to a powerful technique. Using the weighted-likelihood model-selection method and analysis of electrophysiological data, we show that Kv2.1/Kv6.4 channels express, in contrast to the assumed 3:1, in a 2:2 stoichiometry. Within this stoichiometry, the Kv6.4 subunits have to be positioned alternating with Kv2.1 to express functional channels. The variability in Kv2/KvS assembly increases the diversity of heterotetrameric configurations and extends the regulatory possibilities of KvS by allowing the presence of more than one silent subunit.

Single subunit counting, the progressive stepwise photobleaching of fluorescently labeled monomers in a biological complex, has been the method of choice to determine stoichiometries in biological assemblies (1). This technique is based on the irreversible photobleaching of green fluorescent protein (GFP) tags, which are fused to the protein of interest (Fig. 1 A and F) (1). During prolonged excitation, each GFP progressively loses its ability to fluoresce by photochemical destruction, leading to stepwise bleaching events. Since only a fraction of the GFPs mature to become fluorescent, one obtains a binomial distribution of N-th order, where N is the number of monomers in the biological assembly. More rigorous evaluation revealed GFP-maturation rates in the range between 0.4 and 0.9 (1–12). With increasing N, it becomes difficult to distinguish between the different orders of binomial distributions in this range. Often, one must rely on the highest step count; for instance, observation of a small number of five bleaching steps automatically leads to a pentamer and excludes a tetramer. While this logic is theoretically true, it can be misleading if more than one complex colocalize within one diffraction-limited spot. This situation is unavoidable, even in fully stochastic distribution of the single complexes. What has been lacking to date is an objective manner of selecting the correct model based on a posteriori probabilities. Here, we show how to evaluate different models and use this method to determine the stoichiometry of Kv2.1/Kv6.4 complexes.

Fig. 1.

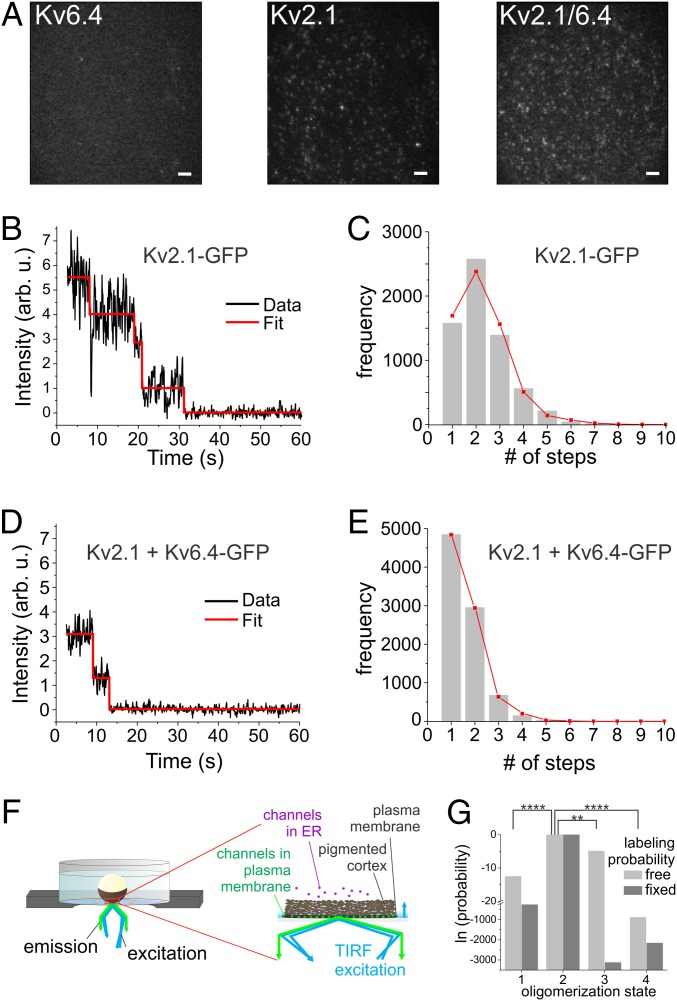
Single-channel subunit counting. (A) Representative frames of a recorded movie of Kv6.4–GFP (Left), Kv2.1–GFP (Center), and Kv2.1/6.4–GFP (Right; 1:8 ratio) expressed in the Xenopus oocyte membrane recorded in TIRF configuration. (Scale bars: 2 µm.) (B and D) Representative intensity time traces from single Kv2.1–GFP homomeric (B) and Kv2.1/Kv6.4–GFP heteromeric (D) channels with four and two bleaching steps, respectively. Arb. u., arbitrary units. (C and E) PIF automated analysis: Each spot was analyzed, and the number of steps was recorded. The resulting distribution histograms (gray bars) from Kv2.1–GFP (C) and Kv2.1/Kv6.4–GFP (E) were fitted to binomial distributions of fourth order (tetramer) and second order (dimer), respectively. The probability to detect fluorescence from GFP was P = 0.48, and the fraction of colocalization was 10% and 29%, respectively. The ratio of Kv2.1:Kv6.4–GFP was 1:8 (weight:weight). (F) Oocytes were illuminated by TIRF, and fluorescence was recorded by using an EMCCD camera. The pigmented cortex in Xenopus oocytes is positioned between the plasma membrane and ER such that fluorescence from the ER is efficiently blocked. (G) Log likelihoods for the distribution in E for 3:1, 2:2, 1:3, and 4:0 Kv2:Kv6 stoichiometries. Significance was determined by AIC with respect to 2:2 stoichiometry. **P > 0.99; ****P > 0.9999.

Voltage-gated K⁺ (Kv) channels regulate the selective flux of K⁺ ions across the cell membrane by opening, closing, and/or inactivating in response to changes in membrane voltage (13). A fully assembled Kv channel consists of four α-subunits, with the NH₂ terminus containing the T1 domain as a key determinant in controlling tetramerization of compatible subunits (14, 15). To tune the native Kv currents to tissue-specific requirements, each tissue expresses a characteristic set of α-subunits, which are divided into several subfamilies based on sequence homology. In the case of the Shaker-related subunits, eight different subfamilies can be distinguished: Kv1–Kv6 and Kv8–Kv9 (16). Within each of the Kv1–Kv4 subfamilies, subunits cannot only oligomerize into homotetramers, but also into heterotetramers, increasing the diversity of Kv channel complexes. Members of the Kv5, Kv6, Kv8, and Kv9 subfamilies, on the other hand, are unable to form functional channels, even though they have the typical topology of a Kv α-subunit and are therefore designated silent Kv (KvS) subunits (17). However, they do selectively interact with members of the Kv2 subfamily, forming functional Kv2/KvS heterotetramers that possess unique biophysical and pharmacological properties. Generally, they slow the activation and deactivation kinetics, shift the voltage dependency of activation and inactivation, and reduce in heterologous expression systems the current density relative to Kv2 homotetramers. Therefore, these KvS subunits are considered modulatory α-subunits of the Kv2 subfamily.

Oligomerization of Kv subunits into a functional channel is thought not to occur by the sequential addition of monomers to the channel complex, but by dimerization of dimers, in which the dimeric interaction sites differ from those mediating monomer–monomer interactions (18). Therefore, heterotetramers are expected to assemble with a 2:2 stoichiometry, which has been confirmed in the case of the Kv4 homolog jShal1 and jShalγ1 (19). In contrast, for Kv2.1/Kv9.3 heterotetramers, a stoichiometry of three Kv2.1 subunits and one Kv9.3 subunit has been reported (20), alluding that a similar 3:1 stoichiometry could be applicable to all Kv2/KvS channels. This would imply assembly of each one homodimer and one heterodimer, assuming the channels are assembled from dimers (21).

On the other hand, several studies have shown subunit stoichiometry of heteromeric Kv channel complexes to vary dependent on the relative expression of the different subunits (22–26). It is also important to study only the configuration of functionally expressed Kv2/KvS channel complexes, excluding temporary aggregations that might be formed due to overexpression but that are retained in the endoplasmic reticulum (ER) in a physiological context. Therefore, KvS subunits might be more diverse than assumed, leading to the idea that, in addition to a 3:1 ratio, Kv2/KvS channels assemble in a 2:2 ratio, i.e., as a dimer of dimers.

We explored the distribution of stoichiometries with two experimentally independent approaches. To probe the internal arrangement of the different stoichiometries, we compared the biophysical properties of concatemers with corresponding monomeric constructs. With the latter approach, ion-channel stoichiometries have been successfully studied (27–29). Possible stoichiometries are 3:1, 2:2, or a population mixing both stoichiometries. In single subunit counting experiments, we directly counted the number of Kv6.4 subunits in Kv2.1/Kv6.4 heteromers expressed in Xenopus oocytes. Since maturation of GFP, whose photobleaching steps are detected, is not complete, each stoichiometry will lead to a characteristic bleaching-step distribution histogram. Choosing the most likely distribution is, therefore, a prominent problem for the analysis and interpretation of single subunit counting data. Here, we provide the framework for objectively choosing the most likely (mixture of) stoichiometry of a multimeric arrangement, applicable to any single subunit counting experiments of multimeric complexes.

Results

Kv2.1/Kv6.4 Heterotetramers Coexpress in a 2:2 Stoichiometry.

Kv6.4 is a representative member of the KvS family, given its profound modulating effect on the Kv2 channel properties (30). The direct way to investigate the stoichiometry of Kv2.1/Kv6.4 heterotetramers is by single subunit counting experiments, which provide directly the number of fluorescently labeled Kv6.4 subunits within a single channel assembly. For our studies, we chose the Xenopus oocyte expression system for the single subunit counting experiments because injection of RNA provides accurate control over expression level and expression-level ratios (31), not easily achieved by DNA transfection in mammalian cells. Furthermore, fluorescence originating from nontrafficked channel assemblies retained in the ER is efficiently blocked by the melanin pigmentation located between membrane and ER in Xenopus oocytes (Fig. 1F). We initially carried out the experiments in human embryonic kidney 293 (HEK293) cells and obtained high background fluorescence from Kv6.4–GFP-transfected cells trapped in the ER in the absence of Kv2.1 (9).

Not every GFP-fusion protein is detected. While photobleaching before the measurement can be limited by protecting the samples from light, the chromophore matures (i.e., develops its fluorescent properties) only in a fraction of the GFP population after protein folding. The fraction of mature GFP depends on the experimental conditions, but not on the protein the GFP is fused to (9). Therefore, we initially determined the probability of GFP maturation for the experimental conditions used here by studying the Kv2.1 homotetramer in the absence of any silent subunits. The expression level was adjusted such that individual channels were clearly distinguishable as single spots, which is a prerequisite for reliably determining the stoichiometry of single channels (Fig. 1 A–E; please refer to Methods for a detailed explanation of the exclusion criteria). As a homotetramer, each Kv2.1 contains four GFP proteins per channel. Accordingly, the homogenous tetrameric population showed a step-number distribution following a binomial distribution of fourth order, consistent with each GFP having a finite probability of fluorescence p_f = 0.48 of being observed (Fig. 1C; n = 6,388 spots, 16 oocytes).

The histogram showed some spots with more than four bleaching steps. Intuitively, this may seem unexpected, but it is a result of the stochastic distribution of the channels. In order to obtain sufficient spots for a meaningful analysis, there is a 10 to 20% probability of finding two channels within the same diffraction-limited spot (∼300-nm diameter). This colocalization of more than one channel within a diffraction-limited spot was consistently found in all our experiments independent of the protein of interest. While one might be tempted to exclude spots with more than the theoretically possible number of steps per protein from analysis as an artifact, such a selective exclusion would distort the determination of the remaining distribution; e.g., two tetramers would lead to a binomial distribution of eighth order, which have a finite probability not only for five to eight, but also for one to four steps. Excluding the five to eight as an artifact would misrepresent the one to four distribution. As a result, the fluorescence probability p_f of the fluorophore would be overestimated. We will discuss below that colocalization is also essential to obtain reliable information if observing heterogenous populations.

We next studied the stoichiometry of the Kv2.1/Kv6.4 heteromers. To exclude any background of Kv2.1 homotetramers from our analysis, a Kv6.4–GFP fusion protein was coexpressed with wild-type (WT) Kv2.1, rendering the latter monomers invisible. Xenopus laevis oocytes were injected with untagged Kv2.1 and Kv6.4–GFP RNA in a 1:8 ratio. The ratio was biased toward the Kv6.4 subunit to be consistent with the electrophysiological experiments, where higher Kv2.1 fractions would result in a majority of homotetrameric Kv2.1 channels that would superpose the electrical signal of the heteromers. The majority of the photobleaching time traces showed one or two bleaching events, consistent with a 2:2 stoichiometry (Fig. 1D). This observation was confirmed when fitting the step-distribution histogram to a binomial distribution (Fig. 1E). The histogram (n = 8,675 spots, 28 oocytes) was fitted to binomial distributions of second, third, and fourth order as well as a Poisson distribution, representing expression of two, three, four, and one Kv6.4 subunit per tetramer, respectively (see Methods for details).

With the colocalization of spots, we obtained typically up to four to eight bleaching steps per histogram. To evaluate the different stoichiometries against each other, we calculated weighted-likelihood ratios (for details, see Single Subunit Counting Analysis). When the probability of fluorescence was fixed to the previously determined value p_f = 0.48, we found that a 2:2 stoichiometry best fit our data (P > 0.9999). Despite the relatively stable maturation rate, we preferred not to rely on a fixed parameter but, rather, let the fit confirm the previous knowledge. For this reason, we also fit the data, leaving the probability of fluorescence p_f free to vary. Under these conditions, the binomial distribution of second order was the best fit, and the 2:2 stoichiometry remained the most likely stoichiometry (P > 0.99; Fig. 1G). Although left free to vary, the p_f of the 2:2 stoichiometry did not alter significantly (p_f = 0.49), whereas it was inconsistent with the values for the other possible Kv2:Kv6 ratios: p_f (3:1) = 1; p_f (1:3) = 0.36; and p_f (0:4) = 0.3.

Kv2.1/Kv6.4 Heterotetramers Are Functional in a 2:2-Stoichiometrical Configuration.

While the single subunit counting experiments indicated a 2:2 stoichiometry, they cannot provide an answer as to how the subunits are arranged within the tetramer. Therefore, we investigated the functionality of Kv2.1/Kv6.4 heterotetramers with different stoichiometry using concatemeric constructs. Since Kv channels assemble by the dimerization of dimers (18), we started by analyzing the dimeric constructs Kv2.1–Kv2.1, Kv2.1–Kv6.4, and Kv6.4–Kv2.1 (Fig. 2A) and compared their electrophysiological properties with those of the corresponding channels assembled from the WT monomeric subunits (Fig. 3A). To avoid limitations on channel assembly and conformational flexibility due to the covalent linking of subunits, a 10- to 12-amino-acid linker was inserted between them (Fig. 2A). Such a linker has prevented this potential problem in previous studies (27, 28, 32, 33). Western blot analysis confirmed that all dimeric constructs were expressed as an intact polypeptide (Fig. 2B), indicating that the dimeric constructs were not cleaved, and no single subunits were expressed. We did not draw any conclusions from the band intensities about expression levels, as transfection efficiencies typically varied widely.

Fig. 2.

Overview and Western blot analysis of dimeric Kv2.1 and Kv2.1/Kv6.4 constructs. (A) Design of Kv2.1–Kv2.1 (Left), Kv2.1–Kv6.4 (Center), and Kv6.4–Kv2.1 (Right) dimers. The Kv2.1 and Kv6.4 subunits are shown in white and black, respectively. Neighboring subunits had a common, unique RE site enabling the linkage of subunits using specific RE digests. Subunits were covalently joined by a peptide linker, of which the nucleotide and amino acid sequences are shown below in lowercase and uppercase, respectively. (B) Expression of dimers as a single polypeptide was examined with Western blotting using Kv2.1 antibodies. As a positive control, lysates of HEK293 cells (co)transfected with Kv2.1 and Kv6.4 or with Kv2.1 alone were used. In all lysates containing the positive controls or the dimers, a single band was noticeable which corresponded to the predicted molecular mass, while no signal was detected in lysates of nontransfected HEK293 cells. All dimeric constructs yielded one dominant protein band when probed with Kv2.1 antibodies with a molecular mass that approached their estimated weight.

Fig. 3.

Biophysical properties of Kv2.1 monomers and dimers. (A and B) Whole-cell current recordings of Kv2.1 channels composed of Kv2.1 monomers (Left; 0.5 µg of Kv2.1 transfected) or Kv2.1 dimers (Right; 1 µg transfected) used to determine the activation (A) and inactivation (B) properties. Voltage protocols are shown on top. (C) Voltage dependence of activation for Kv2.1 channels composed of monomers (filled circles) or Kv2.1 dimers (open circles) derived from plotting the normalized tail current amplitudes at −25 mV (from recordings as shown in A) as a function of the prepulse potential. (D) Voltage dependence of inactivation obtained from plotting the normalized peak current amplitude at +60 mV (from recordings as shown in B) as a function of the prepulse potential. (E) Time constants of activation and deactivation obtained as described in Methods. Note that the biophysical properties of Kv2.1 channels composed of dimers were similar to those assembled from Kv2.1 monomers.

To evaluate the effect of our concatemeric design, the Kv2.1 dimeric construct was studied first. The Kv2.1 dimer yielded functional channels with biophysical properties closely resembling those of Kv2.1 monomer-derived channels (Fig. 3 A and B). No significant differences were observed in the voltage dependencies of activation and inactivation or in the time constants of activation and deactivation (Fig. 3 C–E and Table 1), confirming that the covalent linker between the Kv2.1 subunits allowed enough conformational flexibility to yield functional channels without affecting their biophysical properties.

Table 1.

Biophysical properties of homotetrameric Kv2.1 and heterotetrameric Kv2.1/Kv6.4 channels composed of monomers, dimers, or tetramers

	Activation			Inactivation
	V1/2	k	n	V1/2	k	n
Monomer
Kv2.1	6.1 ± 2.2	9.0 ± 0.4	7	−18.2 ± 2.3	6.4 ± 0.5	7
Kv2.1 + Kv6.4	3.4 ± 2.2	18.9 ± 0.9	6	−63.2 ± 2.2	9.1 ± 0.8	10
Dimer
Kv2.1–Kv2.1	5.6 ± 2.4	10.9 ± 1.5	7	−23.4 ± 2.2	5.6 ± 0.9	7
Kv2.1–Kv6.4	−4.6 ± 1.0	18.4 ± 0.6	3	−58.4 ± 0.7	7.3 ± 0.3	3
Kv6.4–Kv2.1	2.4 ± 2.7	21.6 ± 2.5	4	−62.5 ± 1.9	7.3 ± 0.2	4
Tetramer
Kv2.1–Kv2.1–Kv2.1–Kv2.1	1.8 ± 2.8	9.4 ± 0.6	5	−21.0 ± 1.9	5.6 ± 0.4	6
Kv2.1–Kv6.4–Kv2.1–Kv2.1 (3:1)	1.7 ± 2.9	14.9 ± 1.8	4	−54.8 ± 2.4	8.6 ± 0.7	10
Kv2.1–Kv6.4–Kv2.1–Kv6.4 (2:2)	5.7 ± 3.1	21.9 ± 0.3	5	−62.8 ± 1.6	9.4 ± 0.9	9
Kv2.1–Kv6.4–Kv6.4–Kv2.1 (2:2)	ND

Values are given as mean ± SEM, and n is the number of cells analyzed. The midpoints of activation and inactivation (V_1/2), represented in millivolts, and the slope factor (k) were obtained from a single Boltzmann fit. ND, no data.

It was demonstrated previously that the biophysical properties of dimers containing two different subunits can be affected by the position of these subunits within the dimeric construct (34). Therefore, two different dimeric constructs were designed to investigate the functionality of Kv2.1/Kv6.4 channels in a 2:2 configuration: Kv2.1–Kv6.4 and Kv6.4–Kv2.1. Coexpression of Kv2.1 and Kv6.4 monomers yielded Kv2.1/Kv6.4 heterotetramers with biophysical properties that differed clearly from those of Kv2.1 homotetramers, and the obtained kinetics were comparable to what has been reported before (Table 1) (30, 35–40). The most significant difference with Kv2.1 homotetramers is an approximately −40-mV shift in the voltage dependence of inactivation and an activation curve with a shallower slope factor k (Table 1). Both the Kv2.1–Kv6.4 and Kv6.4–Kv2.1 dimers each produced currents with characteristic Kv2.1/Kv6.4 heterotetrameric properties (Fig. 4 A and B and Table 1). Furthermore, also the activation and deactivation kinetics of both dimers were similar to those of Kv2.1/Kv6.4 heterotetramers assembled from coexpressing Kv2.1 and Kv6.4 monomers (Fig. 4C). The order of Kv2.1 and Kv6.4 within the dimer did not play a significant role, consistent with our finding that the Kv2.1 concatemer behaves like the monomer (Fig. 4).

Fig. 4.

Biophysical properties of Kv2.1–Kv6.4 and Kv6.4–Kv2.1 dimers. (A) Whole-cell current recordings after (co)transfection of Kv2.1 and Kv6.4 in 1:10 ratio (Top; black circles in B and C), 5 µg of Kv2.1–Kv6.4 (Middle; white squares in B and C), and 5 µg of Kv6.4–Kv2.1 (Bottom; gray inverted triangles in B and C) used to determine the activation (Left) and inactivation (Right) properties. Voltage protocols are shown on top. (B) Voltage dependence of activation (normalized conduction G/G_max; right y axis) and inactivation (normalized current I/I_max, left y axis) for Kv2.1/Kv6.4 channels assembled from monomers (black circles), Kv2.1–Kv6.4 dimer (white squares; V_1/2 = −58.4 ± 0.7 mV, k = 18.4 ± 0.6 mV/e-fold), and Kv6.4–Kv2.1 dimer (gray inverted triangles; V_1/2 = −62.5 ± 1.9 mV, k = 21.6 ± 2.5 mV/e-fold). Voltage dependence of activation was derived from plotting the normalized tail current amplitudes at −35 mV as a function of the prepulse potential. Voltage dependence of inactivation was obtained from the normalized peak current amplitude at +60 mV in function of the prepulse potential. (C) Time constants of activation and deactivation obtained as described in Methods. Note that the biophysical properties of the Kv2.1–Kv6.4 and Kv6.4–Kv2.1 dimers were similar to those of the coexpressed Kv2.1 and Kv6.4 monomers.

Kv2.1/Kv6.4 Heterotetramers Are Functional in an Alternating Arrangement.

The results obtained from the dimer constructs indicated that Kv2.1/Kv6.4 channels are functional in a 2:2 configuration, consistent with the findings from the single subunit counting data. It remains unclear whether the arrangement of the silent subunits within the tetramer influences the function. Assuming that the channels are assembled as a dimer of dimers, the Kv2.1 and Kv6.4 subunits are likely arranged alternately within the heterotetrameric channel. However, the Kv6.4 subunits can be positioned side by side instead of being separated from each other by Kv2.1 subunits. We will refer to these configurations as adjacent (side by side) and alternating, respectively. To evaluate the functional effect of different geometrical arrangements of Kv2.1/Kv6.4 channels with a 2:2 stoichiometry, the following tetrameric constructs were created: Kv2.1 tetramer, Kv2.1–Kv6.4–Kv2.1–Kv6.4, and Kv2.1–Kv6.4–Kv6.4–Kv2.1 (Fig. 5A). Similar to the dimeric constructs, neighboring subunits were covalently coupled with a 10- to 12-amino-acid linker. As for the dimeric constructs, band intensities of the Western blot analysis using Kv2.1 antibodies differed due to variation in transfection efficiencies, but revealed that all tetrameric constructs were expressed as a single polypeptide (Fig. 5B).

Fig. 5.

Overview and Western blot analysis of tetrameric constructs. (A) Design of different tetrameric constructs composed of different unique rearrangements of Kv2.1 and Kv6.4 subunits, which are shown in white and black, respectively. (B) Expression of tetramers as a single polypeptide was examined with Western blotting by using Kv2.1 antibodies. The blot in B, Left was obtained after an exposure time of 1 min. Because of an overload of Kv2.1 monomer and Kv2.1–Kv2.1 dimer protein compared to the different tetramers, the blot was cut, and the lanes with the different tetramer proteins were exposed for 10 min extra, yielding the blot in B, Right. In all lysates loaded (different lanes), a band was expected at the predicted molecular mass.

The functionality of the tetramers that represented the adjacent (Kv2.1–Kv6.4–Kv6.4–Kv2.1) and alternating (Kv2.1–Kv6.4–Kv2.1–Kv6.4) configurations were assessed, and their biophysical properties were compared with those of the Kv2.1 tetrameric construct. Tetramers in the alternating configuration produced ionic currents that displayed the biophysical signature of Kv2.1/Kv6.4 heterotetramers (Fig. 6 A–C and Table 1). Moreover, the kinetics of activation and deactivation differed from those of the Kv2.1 tetramer (Fig. 3D). The current density decreased from 360 ± 76 pA/pF (n = 7) to 160 ± 57 pA/pF (n = 6) at +30 mV for the Kv2.1 tetramer and Kv2.1–Kv6.4–Kv2.1–Kv6.4 (Fig. 6E), respectively. In contrast, tetramers representing the adjacent configuration produced no ionic currents, yielding a current density of only 9 ± 3 pA/pF (n = 9; Fig. 6E). The results demonstrate that Kv2.1/Kv6.4 heterotetramers in a 2:2 stoichiometry function only when the Kv2.1 and Kv6.4 subunits alternate and not when the Kv6.4 subunits are positioned side by side (i.e., adjacent).

Fig. 6.

Biophysical properties of Kv2.1/Kv6.4 tetrameric concatemers. (A, Lower) Whole-cell current recordings after transfection of 5 µg of Kv2.1 tetramer (Left) (filled circles in B–D), Kv2.1–Kv6.4–Kv2.1–Kv6.4 (Center) (open circles in B–D), and Kv2.1–Kv6.4–Kv6.4–Kv2.1 (Right) elicited by the voltage protocol shown in A, Upper. (B) Plot shows the voltage dependence of activation determined for the Kv2.1 tetramer (filled circles; V_1/2 = −1.8 ± 2.8 mV, k = 9.4 ± 0.6 mV/e-fold) and Kv2.1–Kv6.4–Kv2.1-Kv6.4 tetramer (open circles; V_1/2 = −5.7 ± 3.1 mV, k = 21.9 ± 0.3 mV/e-fold). (C) The voltage dependence of inactivation is displayed for both the Kv2.1 (V_1/2 = −21.8 ± 2.5 mV, k = 5.1 ± 0.4 mV/e-fold) and Kv2.1–Kv6.4–Kv2.1–Kv6.4 tetramer (V_1/2 = −62.2 ± 1.7 mV, k = 9.3 ± 1.3 mV/e-fold). (D) Time constants of activation and deactivation obtained as described in Methods. (E) Current density of tetramers determined by normalizing the steady-state current at the end of a 500-ms pulse at +30 mV to the cell capacitance. The number of cells analyzed is indicated above every bar plot.

Kv2.1/Kv6.4 Channels Are Functional in a 3:1 Stoichiometrical Configuration.

Since the above results suggested that the Kv6.4 subunits have no compatible interaction sites, it seems very unlikely that functional Kv2.1/Kv6.4 channels containing more than two Kv6.4 subunits can be formed under physiological conditions. However, it would leave the possibility to combine a homodimer with a heterodimer, leading to a 3:1 stoichiometry, as proposed for Kv2.1/Kv9.3. Although our single subunit counting data suggest a predominant 2:2 arrangement, we explored the functionality of Kv2.1/Kv6.4 channels in a 3:1 stoichiometry by constructing a Kv2.1–Kv6.4–Kv2.1–Kv2.1 tetramer. Under similar incubation conditions, this construct yielded ionic currents that displayed some hallmarks of Kv2.1/Kv6.4 heterotetrameric channels (Fig. 7). Compared to the Kv2.1 tetramer, the voltage dependence of inactivation was shifted into hyperpolarized direction, and the voltage dependence of activation had a shallower slope factor k (Fig. 7 C and E and Table 1). Also, the time constants of activation displayed a fast and a slow component (Fig. 7D), typical for Kv2.1/Kv6.4 heterotetramers. However, comparing the properties to both the Kv2.1 homotetramer and the concatemers in 2:2 stoichiometry highlighted that the slope factor of activation and the shift of the inactivation of the concatemer in 3:1 stoichiometry differed significantly (P ≤ 0.003; SI Appendix, Fig. S1) from the WT Kv2.1 tetramer and the Kv2.1–Kv6.4–Kv2.1–Kv6.4 tetramer (2:2 stoichiometry). The values of the 3:1 stoichiometry fell between both (Table 1). Thus, both parameters progressively alter with incorporation of more Kv6.4 subunits.

Fig. 7.

Biophysical properties of Kv2.1–Kv6.4–Kv2.1–Kv2.1 (3:1 stoichiometry). (A and B, Lower) Representative whole-cell current recordings of Kv2.1–Kv6.4–Kv2.1–Kv2.1 used to determine the activation (A) and inactivation (B) properties. Voltage protocols are shown in A and B, Upper, and horizontal bar at the start of the recordings indicates the zero-current level. (C) Plot displays the voltage dependence of activation for the Kv2.1–Kv6.4–Kv2.1–Kv2.1 (3:1) tetramer (gray circles; V_1/2 = 1.7 ± 2.9, k = 14.9 ± 1.8 mV/e-fold). As comparison, the voltage dependence of activation for the Kv2.1+Kv6.4 heterotetramers assembled from monomeric subunits (Kv2+Kv6) and that of the Kv2.1–Kv6.4–Kv2.1–Kv6.4 (2:2) tetramer is retaken from Figs. 4 and 6 and represented with black and white circles, respectively. (D) Time constants of activation and deactivation of the Kv2.1–Kv6.4–Kv2.1–Kv2.1 tetramer are represented. (E) Plot displays the voltage dependence of inactivation for the Kv2.1–Kv6.4–Kv2.1–Kv2.1 (3:1) tetramer (gray circles) compared to that of Kv2.1+Kv6.4 heterotetramers assembled from monomeric subunits (Kv2+Kv6; black circles) and that of the Kv2.1–Kv6.4–Kv2.1–Kv6.4 (2:2) tetramer (white circles). (F) Box plot represents the midpoint of channel inactivation values of Kv2.1+Kv6.4 heterotetramers assembled from monomers (Kv2+Kv6) and the Kv2.1–Kv6.4–Kv2.1–Kv6.4 (2:2) and Kv2.1–Kv6.4–Kv2.1–Kv2.1 (3:1) tetramers. One-way ANOVA with pairwise analysis between the three models was performed, and the statistical significance was added to the figure. Values between parentheses indicate the number (n) of cells analyzed.

In comparison, the electrophysiological data of the Kv2.1/Kv6.4 heterotetramers assembled from monomeric subunits corresponded well to those of the 2:2 stoichiometry (Table 1 and Fig. 7 C and E). Statistical analysis indicated that the midpoint of inactivation of Kv2.1/Kv6.4 heterotetramers assembled from monomers resembled that of the Kv2.1–Kv6.4–Kv2.1–Kv6.4 tetramer (2:2 stoichiometry), and both differed significantly from that of the Kv2.1–Kv6.4–Kv2.1–Kv2.1 tetramer (3:1 stoichiometry; P < 0.005; Fig. 7F). This suggests that—although a 3:1 stoichiometry is perfectly functional—coexpression of monomers prefers a 2:2 stoichiometry, consistent with an assembly as a dimer of dimers. The vast majority of the population has two silent Kv6.4 subunits, and only few (if any) have one Kv6.4.

Tetraethylammonium Sensitivity Confirms Proper Assembly of Concatemers.

Concatemers have been used successfully to investigate the stoichiometry of Kv channels (28, 29). However, due to the occurrence of T1–T1 interactions while the proteins are still attached to the ribosomes (41), it may be possible that multiple concatemers associate with each other, excluding some of the covalently attached subunits to be incorporated in the channel complex. In this case, the phenotype of the subunit positioned first in the construct will predominate, as they are more likely to be incorporated into the channel complex (34). The dimers used in this study did not seem to encounter this problem, as the biophysical properties of both Kv2.1–Kv6.4 and Kv6.4–Kv2.1 dimers were similar and comparable with those of coexpressed Kv2.1 and Kv6.4 monomers (Fig. 4 and Table 1).

Compared to the dimers, the tetrameric constructs might suffer more from this potential folding problem. However, two observations favor that the positional arrangement of the subunits were well constrained in our tetrameric constructs. First, the slope factor of the voltage dependence of activation becomes shallower, and the midpoint of inactivation shifts toward more hyperpolarized potentials when more Kv6.4 subunits are included, and, second, the functionality of the tetrameric construct representing a 2:2 stoichiometry was abolished by changing the position of the Kv6.4 subunits from an alternating to an adjacent configuration. To unequivocally prove the proper folding of the tetramers, the sensitivity of the tetrameric constructs to extracellular applied tetraethylammonium (TEA) was determined. The binding site of extracellular TEA is well characterized in Kv channels, and a threonine residue in the pore loop of the Shaker-type Kv channel (residue T449, respectively) was identified as an important binding determinant (42). Kv2.1 and Kv6.4 have at the equivalent position a tyrosine and valine residue, respectively (Y384 in Kv2.1 and V425 in Kv6.4; Fig. 8A). Consequently, it was expected that Kv6.4 subunits are less sensitive to TEA than Kv2.1 subunits, which will decrease TEA sensitivity of the Kv2.1/Kv6.4 heterotetramers compared to Kv2.1 tetramers. Indeed, the concentration response curve of the Kv2.1–Kv6.4–Kv2.1–Kv2.1 and the Kv2.1–Kv6.4–Kv2.1–Kv6.4 tetramer shifted gradually toward higher TEA concentrations with more Kv6.4 subunits being included (Fig. 8). Plotting the normalized remaining current as a function of applied TEA concentration yielded concentration effect curves with a half-maximal inhibitory concentration value of 2.5 ± 0.5 mM (n = 5), 5.4 ± 0.2 mM (n = 6), and 9.5 ± 1.3 mM (n = 5) for the Kv2.1, the Kv2.1–Kv6.4–Kv2.1–Kv2.1 (3:1), and the Kv2.1–Kv6.4–Kv2.1–Kv6.4 tetramer, respectively (SI Appendix, Fig. S1). These data strengthen the argument that all four covalently coupled subunits of our tetrameric constructs were incorporated into the Kv2.1/Kv6.4 channels and that these heterotetrameric channels have, indeed, a different drug response compared to Kv2.1 homotetramers (40).

Fig. 8.

TEA sensitivity of tetrameric constructs. (A, Upper) An alignment of a partial pore loop sequence of human Kv2.1 and hKv6.4 is shown. The corresponding residue identified to be important for TEA binding in Shaker-type Kv channels is highlighted in bold (Y385 and V425 in Kv2.1 and Kv6.4, respectively). (A, Lower) Representative steady-state current recordings are shown for the Kv2.1 (Left) and the Kv2.1–Kv6.4–Kv2.1–Kv6.4 tetramer (Right) in the presence of different extracellular TEA drug concentrations. Whole-cell ionic currents were elicited by repetitively applying a +80-mV depolarizing step, followed by a −35 mV repolarization before stepping to −80-mV holding potential (interpulse interval was 15 s). (B) Concentration-effect curves for the Kv2.1 (white circles), the (3:1) Kv2.1–Kv6.4–Kv2.1–Kv2.1 (gray circles), and the (2:2) Kv2.1–Kv6.4–Kv2.1–Kv6.4 tetramer (black circles) obtained by normalizing the remaining steady-state currents from recordings shown in A as a function of applied TEA drug concentration. Note that the curve gradually shifts toward higher TEA concentrations when more Kv6.4 subunits are present in the tetramer.

Kv2.1/Kv6.4 Channels Intrinsically Prefer a 2:2 Stoichiometry.

Considering that the concatemer containing a single silent subunit was functional, we should not exclude ad hoc the possibility of mixed populations. We demonstrated above that Kv2.1/Kv6.4 assemble predominantly in a 2:2 stoichiometry; however, it has been suggested previously that the expression-level ratio between compatible Kv subunits can influence the stoichiometry of heterotetrameric channel complexes in heterologous expression systems (22–26). Our results above may, thus, be a consequence of the ratio in which Kv2.1 and Kv6.4(–GFP) were expressed. A fixed 3:1 stoichiometry has been suggested for Kv2.1/Kv9.3, and, recently, a preference for a 3:1 stoichiometry was also suggested for Kv2.1/Kv6.4 (43).

A pure or preferential 3:1 stoichiometry for Kv2.1/Kv6.4 would contradict our above results. However, if the assembly of the Kv2/KvS heteromers was concentration-dependent, then the distributions in the single subunit counting data should alter in a concentration-dependent manner, and we did not observe 3:1 stoichiometries because of an elevated Kv6.4 concentration. In this context, it is important to reflect upon the question of whether the single subunit counting data represent physiological conditions. To be able to observe single channels, we have to work at a relatively low expression level. However, the assembly of the channels into tetramers occurs already in the ER (41). It is, therefore, not the absolute number of channels expressed, but the Kv2.1/Kv6.4 ratio which is decisive for the biological assembly.

To test whether 3:1 stoichiometries occurred if less Kv6.4 subunits were present, we carried out the single subunit counting experiments at different expression ratios, altering the ratio of Kv2.1:Kv6.4 from 1:8 to 1:1, effectively increasing the relative amount of Kv2.1 (Fig. 9). In contrast to electrophysiological experiments, excess of Kv2.1 is possible here since the homotetrameric Kv2.1 channels are not fluorescently labeled and are, hence, silent in the optical measurements. No fluorescent spots were observed at the plasma membrane upon further increase of the Kv2.1:Kv6.4 ratio above 1:1, suggesting that Kv2.1 homotetramers were the ubiquitous form under those conditions.

Fig. 9.

Concentration dependence of Kv2.1/Kv6.4 stoichiometry. Step distribution obtained from Kv2.1/Kv6.4-GFP heteromers expressed in Xenopus oocytes in weight:weight ratios 1:8 (A), 1:4 (B), 1:2 (C), and 1:1 (D) are shown. (Left) The gray bars indicate the observed distribution, and the red trace is the best fit for a 2:2 stoichiometry for fixed p_f and variable p_col. (Right) The relative likelihoods for homogenous populations for the given stoichiometries for fixed (dark gray) and free (light gray) probability of fluorescence p_f. **P > 0.99; ***P > 0.999; ****P > 0.9999. n = 8,675 (A), 3,301 (B), 2,759 (C), and 610 (D).

To quantify the preference of a 2:2 over 3:1 stoichiometry, we calculated the weighted relative likelihoods at the different expression ratios. Under all conditions, including with probability of GFP fluorescence p_f free to vary, the probability of a 2:2 stoichiometry was P > 0.9, while it increased to even P > 0.9999 for expression ratios Kv2.1:Kv6.4 = 1:2 and 1:4 (Fig. 9). At the 1:1 ratio, we only observed a low number of spots (n = 610), which led to the lower certainty, indicating that, at all concentrations, the 2:2 stoichiometry was predominant.

We then evaluated the possibility of a mixed population of 3:1 and 2:2 stoichiometry, as suggested in Pisupati et al. (43). We assumed that channels of both compositions were able to colocalize, as colocalization occurs stochastically, and not due to a specific interaction. We used a convoluted distribution (see Single Subunit Counting Analysis for details). As we outline below (Model Selection of Single Subunit Counting Data), it is essential to have a sufficiently high expression to observe colocalization. Without it, the number of free parameters supersedes the number of data points, allowing any apparent ratio between the stoichiometries. The convoluted distribution of colocalized channels prevents this artifact. Our experimental results were best fitted by the resulting distribution function if the fraction of 3:1 channels was zero, i.e., by a pure 2:2 stoichiometry for all Kv2.1:Kv6.4 expression ratios tested (Table 2).

Table 2.

Distribution of heterogenous populations

Kv2.1/Kv6.4 ratio	Stoichiometry			pcol	pf	Significance
	3:1	2:2	1:3
1:8	0	1	−	0.30	0.49
	0	0.669	0.331	0.14	0.46	>0.999
1:4	0	1	−	0.30	0.57
	0.01	0.741	0.252	0.18	0.55	>0.999
1:2	0.001	0.999	−	0.32	0.45	0.731
	0	1	0	0.32	0.45	0.269
1:1	0	1	−	0.29	0.53	0.58
	0.008	0.813	0.180	0.20	0.52	0.42

The single subunit counting distributions were fitted to distributions accounting for heterogenous populations. Each ratio was evaluated as a combination of 3:1 and 2:2 in the absence (−) and presence of 1:3 stoichiometries. p_f represents the probability of GFP fluorescence and p_col the colocalization probability. The different stoichiometries were assumed to colocalize (e.g., one spot could contain one 2:2 and one 3:1 for a total of three potentially labeled Kv6.4). Significance was calculated as weighted likelihood ratios as done previously.

We previously rejected the possibility of having three Kv6.4 and a single Kv2.1 subunit (i.e., a 1:3 Kv2.1:Kv6.4 stoichiometry) because T1 domains of Kv6.4 are not compatible, and it has been suggested that only heteromers with opposing silent subunits are functional (30, 38, 43–46). However, 1:3 channels might express as nonfunctional channels that are trafficked to the membrane as silent channels and, thus, appear in the single subunit counting data, leading to a heterogenous mixture of 3:1, 2:2, and 1:3 heteromers. We, therefore, also evaluated the possibility of a mixed population as above, now allowing 3:1, 2:2, and 1:3 stoichiometries (Table 2). While at expression ratios 1:1 and 1:2 the fit did not improve significantly compared to a pure 2:2 population, at high Kv6.4–GFP amounts (1:4 and 1:8), the fit improved when including a fraction up to 33% of Kv2.1/Kv6.4–GFP heteromers in the 1:3 stoichiometry. It should be noted that these distributions have an additional degree of freedom (the fraction of trimers), so it is not clear whether the improvement is owed to this. The results, thus, leave open the possibility that, at very high Kv6.4 expression levels, nonfunctional heteromers in the 1:3 stoichiometry are trafficked to the plasma membrane. It is doubtful, however, that this has any physiological relevance. So, under physiological conditions, we propose that Kv2.1/Kv6.4 express in a preferred 2:2 stoichiometry consistent with both the single subunit counting and the electrophysiological data.

Model Selection of Single Subunit Counting Data.

While our study suggests a fixed 2:2 Kv2.1/Kv6.4 stoichiometry, Pisupati et al. (43) reported a preferential 3:1 stoichiometry for the identical heteromer. Considering that the experimental data of both studies were quite similar, these contradicting interpretations raise the question how to objectively extract the correct stoichiometry (or mixture thereof) from the experimental data.

Single subunit counting data have, in general, the disadvantage of a low number of experimental data points (typically one to eight bleaching steps) and a strong similarity between the resulting distributions. The statistics have been improved after introduction of automated detection and analysis algorithms, which allowed a large number of spots to be analyzed, and, incidentally, also removed unconscious user bias to the “best-looking” spots. To find the true stoichiometry, it is essential to not only show that a chosen model (stoichiometry or mixture thereof) fits the data well, but also that an alternative model, i.e., a different stoichiometry, shows less agreement. Our considerations of the heterogenous populations above also demonstrate that hidden populations (like 1:3) may be overlooked if no further alternatives are explored.

Model Selection in a Homogenous Population.

When choosing the most likely model in a homogenous population, the task is to determine the true number of subunits N contained in each macromolecule with the highest probable confidence. Due to the probability of fluorescence (p_f), a single macromolecule can show 0 to N bleaching steps, which means that a dimeric protein would only show two nonzero data points. For a higher number of subunits, more nonzero data points would be observed, which prevents a direct comparison of different models. This problem is circumvented by allowing colocalization of two or more macromolecules within one diffraction-limited spot. Even if the colocalization probability is close to zero, this allows an easier comparison among different models. All resulting distributions are described by three free parameters and contain an infinite number of nonzero points independent of the number of subunits per macromolecule N (Methods and Eq. 5). Accordingly, a posteriori likelihoods can be directly compared, and we can determine the relative probabilities of the different models with weighted relative likelihoods, as described in Methods.

Characterizing Heterogenous Populations.

The situation is different in heterogenous populations. Here, we do not decide which model is the most appropriate, but, rather, combine the different stoichiometries into a single function. The challenge for heterogenous populations is to determine the correct fractions of all three stoichiometries that best describe the heterogenous population (parameter fitting).

A mixture between monomers and dimers (as is the case here) is particularly challenging because two colocalized monomers are equivalent to a single dimer, and, vice versa, a dimer with only one fluorescent fluorophore is equivalent to a monomer. Consequently, a superposition of one- and two-step distributions can analytically be converted into a pure two-step population. This leads to the situation that, in the absence of colocalization, the distribution is described by more free parameters than it contains data points. Therefore, an infinite number of exact solutions exist. In the presence of colocalization, on the other hand, a single solution exists for the correct distribution between stoichiometries, as shown in the minimum of the error landscape of a simulated distribution (Fig. 10 A and B).

Fig. 10.

Model for channel assembly. (A and B) Error landscape for the step histogram from single subunit counting data obtained from simulated data (10,000 spots). The error is given in logarithmic scale and denotes the deviation of the correct from the calculated step histogram for any given set of parameters p_f and the ratio between a 2:2 and 3:1 stoichiometry in a heterogenic population. Colocalization allows for a single minimum in the error landscape. The red line in B indicates the correct p_f. (C) Accuracy of finding the correct parameters. Shown is the 1-σ width of the normal distribution of the found values (e.g., D) with a midpoint in the correct value for the 2:2/3:1 ratio. With a fixed (±0.005) p_f, the ratio can be determined with 1% accuracy when analyzing 100,000 points. (D) Ratios found by fitting the histograms of simulated 10,000 spots when restricting the p_f to the correct (Left) and 5% too low (Right) value. P_f was allowed to vary 0.5% (red) or 5% (blue).

But even in the presence of colocalization, the stochastic variations may be too large to obtain the correct parameters. Since the stochastic variations reduce with increasing sample size, we asked how many spots need to be analyzed to obtain a reliable result. We simulated heterogenous populations of a given ratio (0.7) between 3:1 and 2:2 stoichiometries comprising a variable number of channels, which were stochastically labeled (probability of fluorescence p_f) and colocalized (p_col). If we leave all three parameters free to vary within realistic values (0 ≤ ratio ≤ 1, 0.4 ≤ p_f ≤ 0.8, and 0 ≤ p_col ≤ 0.3), the ratios found were broadly distributed around the correct value with a 1-σ (68%) variation (or SD) of ±0.25 if 100 spots are analyzed (Fig. 10C, black). This improves to only ±0.2 if 10⁶ spots are analyzed.

Restricting p_f improves the accuracy significantly, but only if at least 1,000 spots were analyzed. One hundred spots would not improve better than ±0.18, even if we had exact knowledge of p_f. If we allow p_f to vary by 10% and 5% around its predetermined value and increase the number of spots to 1,000, the SD reduces to ±0.13 and ±0.08, respectively (Fig. 10C, green and purple). For Δp_f = ±5%, the value obtained for the ratio would lie between 0.62 and 0.78.

Further improvement is only possible by increasing the number of spots to 10⁶ or by fixing p_f within 1% (Fig. 10C, red; and Fig. 10 D, Left) and observing 10,000 spots (±0.02). However, this assumes that p_f is known exactly, as we do in the simulations. Under experimental conditions, a 2 to 5% variation in p_f is often observed due to variations in prebleaching or GFP maturation rate. If we fix p_f to a value 5% too high, the result for the ratio would be consistently off by ∼10% (Fig. 10 D, Right, red). Here, it would be advisable to leave p_f free to vary within ±5%, which would find the correct ratio in most cases (Fig. 10 D, Right, blue).

To summarize, most accurate results would be obtained when 1) collecting sufficient data points (>1,000), 2) allowing for some colocalization (<30%), and 3) fitting the data both with a fixed p_f and a variable p_f that varies within a small range (±5% of the predetermined value), since it is unlikely that p_f is constant in an experimental setting.

Discussion

KvS subunits display, compared to the ubiquitously expressed Kv2 subunits, a more restricted expression pattern. It is, therefore, expected that the KvS subunits tune the expression and localization of Kv2 currents in order to meet the tissue-specific requirements, as has been confirmed by the involvement of different KvS subunits in several (patho-)physiological processes (for review, see ref. 47). This makes them potential therapeutic targets, especially since it was demonstrated that Kv2.1/Kv6.4 channels are modulated differently by the well-characterized drug 4-aminopyridine compared to Kv2.1 homotetramers and other Kv2/KvS heterotetramers (40). It has been shown and confirmed by our TEA experiments (Fig. 8) that the pharmacological characteristics of heteromeric Kv channel complexes are affected by the stoichiometry of the subunits involved (23, 48, 49). The differential pharmacological response underlines the importance to know the exact stoichiometries of these heterotetrameric Kv2/KvS channels. Furthermore, our data show that there is also a significant 8-mV hyperpolarizing shift in the voltage dependence of inactivation between a 2:2 or 3:1 stoichiometry (Table 1 and Figs. 6 and 7). Although this shift seems on first sight small, the amount of inactivated channels at physiological relevant resting membrane potentials almost doubles. At −70 and −60 mV, the amount of inactivated channels is in a 3:1 stoichiometry ∼10 and 20% (Fig. 7), whereas in the 2:2 stoichiometry, it amounts to ∼20 and 35%, respectively (Fig. 6). A recent paper on Kv2.1-related neurodevelopmental disorders documented a spectrum of Kv2.1 mutations (50). Among pathogenic mutations that did not affect current density, negative shifts in the voltage dependence of inactivation in the order of 10 to 20 mV were observed that would sufficiently reduce channel availability, resulting in a loss of function (50).

Tetramerization of Kv channels is guided by the N-terminal T1 domain, which facilitates the assembly of compatible subunits and prevents the addition of incompatible subunits into the channel tetramer (51–54). For example, removal of the T1 domain from the incompatible subunits Kv2.1 and Kv1.4 resulted in the coassembly of these subunits into a functional channel (51). Yeast two-hybrid assays and Förster resonance energy transfer analysis have shown that the T1 domain of KvS subunits interacts with that of Kv2.1, but not with their own, suggesting that no functional KvS homotetramers can be formed and that Kv2/KvS heterotetramers cannot contain more than two KvS subunits (30, 38, 44–46). This has been supported by the observation that Kv2.1/Kv9.3 heterotetramers consist of three Kv2.1 subunits and one Kv9.3 subunit (20), proposing that a similar 3:1 stoichiometry applies to all Kv2/KvS heterotetramers. While our results confirmed that concatemeric Kv2.1/Kv6.4 channels with a 3:1 stoichiometry are functional (Fig. 7), they also showed that Kv2.1/Kv6.4 channels adopt a 2:2 configuration independent of the expression ratio when assembled from monomers (Figs. 1 and 9). The functionality of Kv2.1/Kv6.4 channels with a 2:2 configuration was further evidenced with dimeric and tetrameric constructs that indicated that the position of the silent Kv6.4 and Kv2.1 subunit have to alternate to yield functional channels. Although it was previously not reported that Kv2.1/KvS channels with a 2:2 configuration are functional, it agrees with the general scheme that Kv channels assemble by dimerization of dimers in which the dimeric interaction sites differ from those mediating monomer–monomer interactions (18).

Since Kv6.4 subunits do not interact directly, it is very unlikely that Kv6.4 dimers are formed, which implies that not more than two Kv6.4 subunits can be incorporated into a Kv2.1/Kv6.4 heterotetramer, although the single subunit counting data did not explicitly exclude this possibility at high Kv6.4 levels. The subsequent assembly of two Kv2.1/Kv6.4 dimers into a functional channel can occur by at least two possible ways: The Kv2.1/Kv6.4 dimers assemble into a tetramer without any interaction between the two Kv6.4 subunits, or the dimerization of the Kv2.1 and Kv6.4 monomers induces conformational changes that allows the Kv6.4 subunits to interact with each other. However, in the latter case, it might be expected that the Kv6.4 subunits can be positioned side by side in the Kv2.1/Kv6.4 heterotetramer. Our data indicate that such a positional arrangement does not produce functional Kv2.1/Kv6.4 heterotetramers (Fig. 6A) and disfavors this scenario. The adjacent position of two Kv6.4 subunits would also be difficult to reconcile with the specific interactions between N and C termini in the heteromeric complex (38), and it has been shown that parts of the S6 play a key role in stable heteromer formation (43).

Other heterotetrameric Kv channels can assemble with a random subunit stoichiometry and arrangement, depending on the ratio between the involved subunits (22–26). For example, Kv7.2/Kv7.3 heterotetramers display a fixed 2:2 stoichiometry when cells express an equal amount of both subunits, but varying this ratio results in Kv7.2/Kv7.3 heterotetramers with a variable stoichiometry (24). This raises the possibility that cells can modulate Kv currents through endogenous changes in subunit expression level. Our present study demonstrated that Kv2.1/Kv6.4 channels can functionally express in variable 3:1 or 2:2 stoichiometry when using concatemers, but predominantly expresses in 2:2 stoichiometry when coexpressed. The predominant 2:2 stoichiometry in the single subunit counting data are reflected in the electrophysiological properties of the Kv2.1–Kv6.4 dimer and Kv2.1–Kv6.4–Kv2.1–Kv6.4 tetramer constructs, which strongly resemble the properties of Kv2.1+Kv6.4 coexpression. A detailed analysis of the electrophysiological data (SI Appendix) describes how the contribution of each subunit to the properties of the channel can be estimated. This analysis suggests that the behavior of Kv2.1 and Kv6.4 subunits in the coexpressions is consistent with the behavior observed in the concatemeric constructs in 2:2 stoichiometry.

The analysis also shows that the voltage dependence of Kv6.4 subunits is far shifted toward more polarized potentials compared to Kv2.1, in agreement with previous findings (36). Consequently, Kv6.4 subunits control inactivation. Activation, on the other hand, is controlled by the Kv2.1 subunits, since all subunits need to be activated to open the channel.

Interestingly, the Kv6.4 subunits seem to influence the apparent gating charge of the Kv2.1 subunits associated with activation—cutting them in half—without changing the midpoint of activation. We should note here that the apparent gating charges were determined from channel opening, assuming a single voltage-dependent step for activation, and therefore does not directly reflect the actual gating charges found in the primary sequence of the voltage-gated ion channels. As the actual charges remain unaltered and allosteric influence of the electric field is highly unlikely, the reduced apparent charge suggests that the Kv6.4 subunits do not allow the gating charges responsible for the final pore opening to move through the entire electric field. This steric hindrance of the Kv2.1 subunits to reach their final state is consistent with the mismatch in the S6 of Kv2.1 and Kv6.4, as suggested by Pisupati et al. (43).

The thorough analysis of the electrophysiological data thus confirmed the findings from the single subunit counting measurements. Our subunit counting analysis introduced a method to reliably interpret any single subunit counting data and thereby eliminated any ambiguity in model selection. In particular, the inclusion of colocalization—in addition to increasing the number of data points—allows direct evaluation of the likelihoods among different models and removes the ambiguity in the probability of fluorescence. We expect that the analysis algorithm provides clear criteria for model selection and will make single subunit counting useful in the interpretation of heteromeric macromolecules such as ion channels but also the large family of G-protein-coupled receptors.

Methods

Electrophysiology.

Ltk⁻ cells (mouse fibroblasts; ATCC CCL 1.3), which showed low endogenous K⁺ currents, were cultured in Dulbecco’s modified Eagle medium supplemented with 10% horse serum and 1% penicillin/streptomycin under a 5% CO₂ atmosphere. Cells were transiently transfected by using Lipofectamine 2000 (ThermoFisher) with the appropriate amount of channel complementary DNA (cDNA), as indicated in the figure legends. A total of 0.5 µg of enhanced GFP (eGFP) was cotransfected as transfection marker. Cells transfected with dimeric constructs were incubated at 37 °C for 16 to 24 h. Tetrameric constructs were incubated at 25 °C for 48 h to aid protein folding. Cells were subsequently enzymatically dissociated with trypsin and used for electrophysiological analysis.

Whole-cell currents were recorded at ∼21 °C by using an Axopatch-200B amplifier and digitized by using a Digidata-1440A acquisition system. Command voltages and data storage were controlled with the pClamp (Version 10.2) software (all Molecular Devices). Patch pipettes were pulled from 1.2-mm borosilicate glass (WPI) and subsequently heat polished. This yielded patch pipettes with a resistance of 1 to 3 MΩ in the solutions used. Extracellular bath solution contained (in mM): 145 NaCl, 4 KCl, 1 MgCl₂, 1.8 CaCl₂, 10 Hepes, and 10 glucose, with the pH adjusted to 7.35 with NaOH. The patch pipettes were filled with an intracellular solution containing (in mM): 110 KCl, 5 K₂ATP, 2 MgCl₂, 10 Hepes, and 5 K₄-BAPTA adjusted to pH 7.2 with KOH. Junction potentials were zeroed with the filled pipette in the bath solution. Cells were excluded from analysis if the voltage error exceeded 5 mV after series resistance compensation. Cells were continuously superfused with extracellular solution.

Concatemer Design.

Human Kv2.1 and Kv6.4 were both cloned in the mammalian expression vector peGFP-N1 (Clontech) as described (30). Concatemeric constructs were created by the sequential insertion of individual subunits into peGFP-N1. Adjacent subunits shared a unique restriction-enzyme (RE) site and were segregated by a linker sequence of 30 to 36 bp, which was added to the individual subunits before they were inserted into the concatemer. Both the appropriate RE sites and the linker sequences were introduced by PCR amplification using the QuikChange site-directed mutagenesis kit (Agilent) and mutant primers. The presence of the desired modifications and the accuracy of the final sequence were confirmed by DNA sequencing.

Western Blot.

Concatemeric constructs (10 µg of cDNA per 75-cm² culture dish) were transiently transfected into HEK293 cells by using Lipofectamine 2000, according to the manufacturer’s guidelines. Cells were cultured in minimal essential medium supplemented with 10% fetal bovine serum, 1% penicillin/streptomycin, and 1% nonessential amino acids under a 5% CO₂ atmosphere in a humidified 37 °C incubator. After harvesting, the cells were lysed by adding lysis buffer, consisting of phosphate-buffered saline (PBS) supplemented with 5 mM ethylenediaminetetraacetic acid, 1% Triton X-100, and a complete protease inhibitor mixture (Roche Diagnostics). The lysed cells were denatured in NuPAGE lithium dodecylsulfate sample buffer for 30 min at 37 °C. The samples were separated on a NuPAGE 3 to 8% Tris–acetate gel and then transferred to a poly(vinylidene fluoride) membrane, which was subsequently blocked with 5% nonfat milk powder in PBS. Concatemers were detected by overnight incubation of mouse Kv2.1 antibodies (K89/34, University of California Davis/NIH NeuroMab Facility), followed by incubation with horseradish peroxidase-labeled anti-mouse immunoglobulin G (GE Healthcare) and enhanced chemiluminescence detection by using the WesternBright Sirius Chemiluminescent Detection kit (Advansta), according to the manufacturer’s guidelines.

Pulse Protocols and Data Analysis.

Voltage protocols were adjusted based on the biophysical properties of the channels, as shown in the figures. Holding potential was −80 mV, and the interpulse interval ranged from 15 to 30 s to prevent channels from accumulating in the inactivated state. The voltage dependence of activation and inactivation was fitted to a Boltzmann equation: y = 1/1/[1 + exp(−(V − V_1/2)/k)], in which V represents the applied voltage, V_1/2 the voltage at which 50% of the channels are open or inactivated, and k the slope factor. Activation and deactivation time constants were determined by fitting the activating and deactivating currents with a single- or double-exponential function. Results are presented as mean ± SEM with n the number of analyzed cells. One-way ANOVA with pairwise comparison between groups was used to find statistical significance in the midpoint of channel inactivation and in TEA sensitivity between WT Kv2.1 tetramer, the Kv2.1–Kv6.4–Kv2.1–Kv2.1 tetramer (3:1 stoichiometry) and the Kv2.1–Kv6.4–Kv2.1–Kv6.4 tetramer (2:2 stoichiometry). P values lower than 0.05 were considered statistically significant. Data were analyzed by using pClamp10 and Sigmaplot (Version 11; Systat).

Expression of Kv2/KvS in Xenopus oocytes.

Kv2.1 and Kv6.4–GFP were fused into the pBSta and pSP64 vector, respectively, as described (55), and cRNA was in vitro transcribed by using a T7 mMachine kit (Invitrogen), according to the manufacturer’s protocol. Oocytes from X. laevis were surgically obtained, according to protocols approved by the Comité de déontologie de l'expérimentation sur les animaux de l'Université de Montréal. Follicular membrane was removed enzymatically with collagenase type 1A (1 mg/mL; catalog no. C9891, Sigma) in a Ca²⁺-free solution. Oocytes were injected with varying ratios of Kv2.1 and Kv6.4–GFP RNA (in ng: 23+0, 23+23, 3+6, 3+12, and 3+24) and incubated for 18 to 48 h at 18 °C.

Oocytes were treated with neuraminidase (1 U/mL) and hyaluronidase (1 mg/mL) for 4 to 5 min at room temperature to enzymatically remove the extracellular matrix. Subsequently, oocytes were transferred into a hyperosmotic solution (in mM: 250 KCl, 1 MgCl, 1 ethylene glycol tetraacetic acid, 50 sucrose, and 10 Hepes, pH 7.4), and the vitelline membrane was manually removed.

N^o 1 glass coverslips were cleaned in the sequence: sonication (at 37 kHz and T = 60 °C) in Alconox 1% in H₂O and two times in anhydrous ethanol. Coverslips were rinsed with H₂O after each sonication step and, finally, dried under a steady-filtered nitrogen stream. For imaging, the injected and pretreated oocytes were placed onto the cleaned coverslips with the animal pole facing down (in mM) 115 N-methyl glucamine, 50 sucrose, 10 Hepes, and 2 Ca(OH)₂, adjusted to pH 7.4 with methyl-sulfonic acid.

Imaging Photobleaching Using Total Internal Reflection Fluorescence.

Fluorescence was recorded by using an Axiovert-200 microscope (Zeiss). Excitation was achieved in total internal reflection fluorescence (TIRF) configuration using a 488-nm laser (PhoXx, Omicron). For TIRF imaging, the laser light was reflected at an angle sufficient to achieve total reflection and only evanescent excitation in the region within ∼300 nm above the coverslip, thus eliminating background fluorescence emerging from the cytosol. Excitation intensity was 3.7 mW/mm². Emission was collected with a 60× numerical aperture-1.49 objective (Olympus) and filtered by a bandpass emission filter (ET525/50 nm) in combination with a laser line reflecting dichroic mirror (Z405/488/561/635, Chroma). Images were recorded with a backlit 128×128-pixel electron-multiplying charge-coupled device (EMCCD) camera (iXon+ 860BV, Andor) at a sampling rate of 20 Hz.

Single Subunit Counting Analysis.

Spot detection and trace analysis were carried out by using the automated algorithm PIF (Progressive Idealization and Filtering) (9) to achieve objective criteria for acceptance and rejection of movies and single spots and to avoid user bias. PIF was specifically designed to automatically detect fluorescent spots; filter fluorescence traces to remove background, thus increasing signal-to-noise ratio; and, finally, count bleaching steps (9). The following parameters were used for spot detection: The selection of a spot was limited to one neighbor (3 × 3 pixels), and the minimum signal/noise ratio (dF/F) was set to 10%. Since noninjected oocytes did not add fluorescent spots beyond the background of the cleaned coverslips, the minimum fluorescence intensity amplitude was set to 0. The spot overlap limit was restricted to sigma = 1.25. The following parameters were used for step detection: Changes in the minimal and maximal step amplitude did not influence the final histograms, so they were left at 0 and 1 × 10⁶, respectively. The total fluorophore photobleach length was set to 100%. All other trace quality-control parameters were kept at their default setting.

The region of interest (ROI) function was used to remove out-of-focus areas. Once the initial analysis was completed, step-frequency histograms were accepted according to the following criteria: 1) No spot movement was detected; 2) the global photobleaching decay displayed an exponential decay with three time constants; 3) spot density was below 0.04 spots/(total number of pixels) in ROI; and 4) not more than 70% of the traces were rejected. The final histogram was fitted to a binomial distribution of fourth order for Kv2.1–GFP, resulting in a probability of fluorescence (GFP maturation efficiency) of p_f = 0.48. This parameter reflects the fact that the chromophore matures only in a fraction of all GFP proteins. The distribution histograms of Kv2.1/Kv6.4–GFP measurements were best fitted with a binomial distribution of second order while maintaining a fixed p_f of 0.48. Results are presented with n as the number of accepted spots.

The models for different stoichiometries were evaluated by weighted relative likelihoods (56, 57) given by

$${}^{w}r{L}_i=\frac{r{L}_i}{{\displaystyle {\sum }_{k}r{L}_k}},$$ [1]

with i indexing the stoichiometry, and the sum over k includes all possible stoichiometries and the relative likelihoods rL_i

$$r{L}_i=\exp \left(\frac{AI{C}_{min}-AI{C}_i}{2}\right).$$ [2]

Here, AIC defines the Akaike information criterion (58)

$$AI{C}_i=2\cdot f-2\text{ln}\left(L_i\right),$$ [3]

with f the number of free parameters in the model i and Li the likelihood of the model i:

$$\text{ln}\left(L_i\right)=\sum _{k=\#steps}{n}_k\cdot ln\left(p_{k,i}\right).$$ [4]

n_k represents the absolute number of experimentally observed events with k photobleaching steps, and p_k,i describes the probability to find k photobleaching steps according to model (stoichiometry) i,

$$p_{k,i}={\displaystyle \sum _{w\ge \frac{k}{i}}\frac{p_{col}^{w-1}}{\left(w-1\right)!}{e}^{-p_{col}}\left(\begin{array}{c}w\cdot i\\ k\end{array}\right)p_f^k\cdot {\left(1-p_f\right)}^{w\cdot i-k}},$$ [5]

representing a Poisson-weighted sum of binomials, with p_col the probability of finding two channels within a diffraction-limited spot and w the number of channels in the spot. p_f is, again, the probability of fluorescence.

We chose to use the weighted relative likelihoods and AIC instead of Bayesian-based estimators since the number of free parameters for all models remains constant. In this context, the penalty for additional free parameters in the Bayesian Information Criterion disappears.

The distribution for heterogenous populations had to consider the colocalization of channels with different stoichiometry. Noncolocalized spots (i.e., single channels) were calculated as a linear superposition of the distributions respective for the three stoichiometries 3:1 $\left(\overrightarrow{M}\right)$, 2:2 $\left(\overrightarrow{D}\right)$, and 1:3 $\left(\overrightarrow{T}\right)$. Colocalized spots with two or more channels were calculated by exponentiation of the original distribution weighted by a Poisson distribution representing the probability of finding more than one channel in one spot. The final distribution $\overrightarrow{S}$ was thus

$$\overrightarrow{S}=\left[{\displaystyle \sum _{i=1}^{\infty }\frac{p_{col}^{i-1}}{\left(i-1\right)!}{e}^{-p_{col}}\cdot {\left(p_{3:1}\overrightarrow{M}+p_{2:2}\overrightarrow{D}+p_{1:3}\overrightarrow{T}\right)}^i}\right]\cdot \stackrel{\rightharpoonup }{x},$$ [6]

where p_j:k represent the fraction of the three populations with

$$p_{3:1}+p_{2:2}+p_{1:3}=1.$$ [7]

$\overrightarrow{M}$ signifies the monomer (3:1) stoichiometry. It is a square matrix with

$${\stackrel{\rightharpoonup }{M}}_{i,j}=\{\begin{array}{ll}{p}_f\hfill & if\hspace{0.17em}i=j\hfill \\ 1-p_f\hfill & if\hspace{0.17em}i=j+1\hfill \\ 0\hfill & else\hfill \end{array}.$$ [8]

$\overrightarrow{D}\hspace{0.17em}\mathrm{and}\hspace{0.17em}\overrightarrow{T}$ signify the dimer (2:2) and trimer (3:1) stoichiometries with $\overrightarrow{D}={\overrightarrow{M}}^2$ and $\overrightarrow{T}={\overrightarrow{M}}^3$.

The matrices are converted into a vector containing the distributions via multiplication with the vector $\stackrel{\rightharpoonup }{x}$

with $x_i=\{\begin{array}{cc}1& if\hspace{0.17em}i=1\\ 0& else\end{array}.$

Simulations.

Simulated data were generated according to the above equations, assuming Poisson (shot) noise for each probability. We chose different conditions; shown here are p_f = 0.55, p_col = 0.1, and dimer/monomer ratio = 0.7. We simulated 10,000 distributions each for 100; 1,000; 10,000; 100,000; and 1,000,000 spots. For randomly picked distributions from each ensemble (>1,000), we determined the best-fitting parameters. Since the parameters were not normally distributed, we determined the interval within which 68% (1-σ) of the data were found. All simulations and analysis was done in Matlab (Mathworks) with in-house-written routines.

Data Availability.

All data discussed in the paper will be available upon request.