The Neural Basis for Response Latency in a Sensory-Motor Behavior

Abstract

We seek a neural circuit explanation for sensory-motor reaction times. In the smooth eye movement region of the frontal eye fields (FEF_SEM), the latencies of pairs of neurons show trial-by-trial correlations that cause trial-by-trial correlations in neural and behavioral latency. These correlations can account for two-third of the observed variation in behavioral latency. The amplitude of preparatory activity also could contribute, but the responses of many FEF_SEM neurons fail to support predictions of the traditional “ramp-to-threshold” model. As a correlate of neural processing that determines reaction time, the local field potential in FEF_SEM includes a brief wave in the 5–15-Hz frequency range that precedes pursuit initiation and whose phase is correlated with the latency of pursuit in individual trials. We suggest that the latency of the incoming visual motion signals combines with the state of preparatory activity to determine the latency of the transient response that controls eye movement.

Impact statement

The motor cortex for smooth pursuit eye movements contributes to sensory-motor reaction time through the amplitude of preparatory activity and the latency of transient, visually driven responses.

Introduction

Timing is everything. In preparing to jump for a rebound in a basketball game, the difference of a few milliseconds may make the difference between success and failure. Jump too early, and you are back on the ground before the ball bounces off the rim. Jump too late and your opponent snatches the ball away from your outstretched hands. The temporal precision and accuracy of highly skilled movements focuses attention on the neural mechanisms that decide exactly when to initiate a movement.

In the present paper, we ask what features of neural responses control behavioral latency of visually guided smooth pursuit eye movements. Pursuit is driven by visual motion with latencies just under 100 ms and is initiated in the rich form we study only in the presence of visual motion. The visual inputs that drive pursuit arise from the middle temporal visual area (area MT, Newsome et al. 1988), where latencies to visual motion are between 40 and 60 ms (Lisberger and Movshon 1999). Thus, only a short time is available to transform visual motion signals into movement. We tend to think of the latency of pursuit in terms of the times required for visual signals to arrive in MT, traverse the cortex to the smooth eye movement region of the frontal eye field (FEF_SEM), reach neurons in the pontine nuclei and the nucleus reticularis tegmenti pontis, and drive the simple-spike activity of Purkinje cells in the floccular complex of the cerebellum.

From first principles, however, multiple features of neural responses might control behavioral latency. One popular model posits that neural activity at a key site ramps up to a threshold that triggers movement (Asrress and Carpenter 2001). Faster ramps will reach threshold more quickly and trigger a movement with a shorter latency. This model appears to be true for the role of the frontal eye fields in saccadic eye movements (Hanes and Schall 1996) and is related to current thinking about decision-making, where one theory posits that accumulation of evidence leads to ramping activity, triggering a movement to report the decision when the ramp crosses a threshold (Ratcliff 2002; Gold and Shadlen 2007). However, ramp-to threshold may not apply for all kinds of movements. For example, as we found in area MT (Lee et al. 2016), the latency of the visually driven transient response might be the key feature of neural responses that determines behavioral latency. This may be true to some degree even for saccades, especially in subcortical parts of the relevant circuits (Marino et al. 2012; Chen et al. 2018).

FEF_SEM is known from stimulation, lesion, recording, and anatomical studies to be important for the generation of pursuit eye movements (Brodal 1980; Gottlieb et al. 1993, 1994; Keating 1991; MacAvoy et al. 1991; Tian and Lynch 1996; Shi et al. 1998; Tanaka and Fukushima 1998; Tanaka and Lisberger 2001, 2002b, 2002a; Ono and Mustari 2009; Lisberger 2010). Its anatomical connections suggest that FEF_SEM has a central role in pursuit through disynaptic connections to relevant regions of the cerebellum (Tian and Lynch 1997; Brodal 1980). It is a combined sensory and motor area and plays a role in setting the strength of the pursuit response (Tanaka and Lisberger 2001) based on the signal-to-noise ratio of the sensory signal and previous experience (Darlington et al. 2018). The responses of neurons in FEF_SEM include both transient pulses of firing related to the initiation of pursuit and preparatory activity that evolves before a moving target initiates pursuit, and therefore are rich enough to allow tests of multiple neural correlates of pursuit latency. Thus, we can test the ramp-to-threshold theory (to see if it generalizes from saccades to pursuit) as well as the potential roles of the amplitude of preparatory activity versus the latency of the pursuit-related response in determining behavioral latency.

We find evidence for multiple computations that may control pursuit latency, with at best weak evidence in favor of the ramp-to-threshold theory for pursuit eye movements. Neuron–neuron correlations in the latencies of FEF_SEM neurons cause the trial-by-trial variation in the latency of pursuit-related FEF_SEM responses to be linked closely to variation in the behavioral latency, and can account for two-third of the variation in behavioral latency. The amplitude of preparatory activity is negatively correlated with pursuit latency in many neurons and could contribute to the latency computation. We also find a low-frequency component in the local-field potential (LFP) that shifts in time (or phase) but not in power in relation to pursuit latency. We suspect that both the latency of the incoming visual motion signals and the expectation represented by preparatory activity contribute to neural and behavioral latency, and that the low-frequency LFP holds a key to understanding how they combine.

Materials and Methods

Two adult male rhesus monkeys were trained to pursue a circular dot that executed a step-ramp trajectory of target position (Rashbass 1961), in exchange for juice or water reward. Before training, we performed two separate surgeries using sterile procedure. In the first surgery, we implanted a head holder on the skull for head restraint and a stainless-steel chamber on the skull. The chamber was aimed stereotaxically at the point that was anterior 24 mm and lateral 20 mm relative to ear bar zero, but angled so that electrodes entered orthogonal to the surface of the cortex. In the second surgery, we sutured a scleral search coil to the sclera of one eye (Ramachandran and Lisberger 2005). After finishing behavioral training, we performed a craniotomy inside the chamber for introducing quartz-insulated platinum/iridium electrodes into the brain. All experiments were conducted at Duke University using methods that had been approved in advance by the Institutional Animal Care and Use Committee at Duke University. Methods conformed to the National Institutes of Health Guide for the Care and Use of Laboratory Animals. The latency distribution for neurons and the relationship between spikes and LFP in area MT were obtained by reanalyzing the data reported in previous papers (Lee and Lisberger 2013; Lee et al. 2016). We also performed a few analyses on data collected from the same two monkeys in previous experiments on FEF_SEM (Darlington et al. 2018).

Data Acquisition

Visual stimuli were presented on a gamma-corrected 24-inch CRT color monitor (Sony Trinitron), whose spatial resolution was 2304 × 1440 pixels and vertical refresh rate was 80 Hz. The monitor was placed 60 cm from the monkey and the screen covered 44 × 29 deg of horizontal and vertical visual fields. Accurate measurement of visual motion onset timing was guaranteed by corrections after collection of the primary data. Since we did not use a photodiode system to determine exact stimulus motion onset during recording experiments, all the visual motion onset timing was corrected by the reference data collected after the experiments. This was possible because the timing of our stimulus control and data acquisition program is extremely precise. Horizontal and vertical eye position and velocity were sampled at 1 kHz. Eye velocity was obtained by differentiating and low-pass filtering eye position at a cut-off frequency of 25 Hz using an analog circuit. The filter was linear and causal and so it incorporated a small-time delay relative to the eye velocity obtained digitally with a zero-phase, noncausal filter. It is the same circuit that we have used for more than 40 years.

During experiments, we slowly lowered one to three electrodes or tetrodes in the FEF_SEM and recorded spikes and local field potentials (LFP) using the Tetrode Mini-matrix System (Thomas Recording GmbH). The input impedance and gain of the Mini-matrix preamplifier were 1GΩ and ×19 individually. The input impedance of the preamplifier was much higher than the impedance of the single electrodes and tetrodes that we used (Thomas Recording GmbH, 2–4 MΩ and 1–2 MΩ individually), ensuring that our recordings would be relatively free from phase distortion in low-frequency LFPs (Nelson et al. 2008). For LFPs, signals were low-pass filtered with a cut-off frequency of 170 Hz and digitized at a sampling rate of 2 kHz. For action potentials, signals were high-pass filtered with a cut-off frequency of 150 Hz and those that crossed a preset threshold were digitized at a sampling rate of 40 kHz. Digitization, filtering, and amplification of signals were done with a Plexon MAP system (Plexon Inc.).

We isolated single neural spikes online, using a window discriminator for analyzing and displaying neural response properties. We performed more accurate offline discrimination of single neural responses later, using spike waveforms that exceeded a certain threshold. We took exceptional care in spike sorting because any significant sorting errors might add noise in trial-by-trial correlation analyses. First, we performed initial spike sorting using principal component analysis. Then, we refined the sorting by visually inspecting the waveforms in a smaller time chunk, to detect any waveform changes caused by the slow drift of electrodes. We used Plexon Offline Sorter (Plexon Inc.) for the offline spike sorting procedure. Sorted spikes were converted to time stamps with a time resolution of 1 ms and were inspected again visually to look for obvious sorting errors.

Experimental Design

We recorded neural activity in FEF_SEM, while two rhesus monkeys were engaged in smooth pursuit eye movement tasks. We identified FEF_SEM using functional markers. As we advanced electrodes through the areas known stereotaxically to be close to the arcuate sulcus, we first looked for the area that showed oculomotor responses. We then advanced the electrodes past saccade-related neurons until we found neurons that were strongly modulated by smooth pursuit eye movements. Then, we isolated single neuron responses and performed two experiments.

In the first experiment, we tested the direction tuning of the neurons under study during smooth pursuit eye movement. We randomly interleaved saccade trials and pursuit trials, where saccade trials required the monkeys to make saccades to a target at 15 deg eccentricity in one of eight directions (45 deg interval), and pursuit trials required them to track a target moving at 15 deg/s in one of eight directions (45 deg interval). We used a white circular dot as a saccade target and random dot stimulus and/or grating as pursuit targets. The random dot stimulus was made from white and black dots to control luminance contrast of the stimulus (see Yang et al. 2012). Typically, the luminance contrast of the random dot stimulus was 100%, and the contrast of the grating stimulus was 12%. We usually used both stimuli, but either sufficed for determining the direction tuning of FEF_SEM neurons. All the visual stimuli were presented on a uniform gray background. We obtained saccade and pursuit direction tuning curves online as least-square fits to a Gaussian function and used the tuning curves to choose the preferred pursuit direction of the neurons under recording, and to test whether the neurons were more strongly tuned to smooth pursuit or saccadic eye movement. Only the 133 neurons with larger responses during pursuit than during saccades were admitted for further data acquisition.

In the second experiment, we recorded neural responses while monkeys tracked a yellow circular dot that moved in a step-ramp trajectory. Typically, we chose two pursuit directions that provided good compromises among the preferred directions of the neurons under study and one target speed (10 deg/s or 20 deg/s); sometimes, we used both target speeds and more than two directions. The size of the step in the step-ramp target motion was 1 and 3 deg for target speeds of 10 and 20 deg/s. After the experiment, we screened all trials visually and excluded from further analysis any pursuit trials that contained saccades or microsaccades in the interval from 100 ms before to 210 ms after target motion onset. For most of our analyses, we selected one direction of target motion that matched most closely with the preferred direction of each neuron, usually within ±30 deg of the preferred direction.

Estimation of Pursuit Latency and FEF _SEM -Pursuit Latency Correlation

We used an objective method that was developed in our previous study to quantify the latency of pursuit for each trial (Lee and Lisberger 2013; Lee et al. 2016). Briefly, we computed the average horizontal and vertical eye velocities across trials and used the averages from 20 ms before to 80 ms after the initiation of pursuit as templates. Here, we used the initial 80 ms of smooth pursuit, instead of 100 ms to include more trials in the analysis. The overall result for pursuit latency was the same whether we used 80 or 100 ms for the analysis. We shifted and scaled the templates in every trial and estimated the best match using the least-square method. The best time shift defined the pursuit latency in each trial. We included a trial in the further analysis only if the best-fitted estimate accounted for more than 80% of eye-velocity variance. We proceeded to further analysis only if 80 or more trials passed this test.

We estimated the latencies of the average responses of FEF_SEM neurons through a statistical method. First, we obtained spike density functions by convolving spike trains with a Gaussian window of a 10-ms standard deviation (SD) and averaging the individual spike density functions across trials. Then, we set a baseline by averaging neural activity in the interval ± 25 ms from motion onset. If the average spike density between 30 and 300 ms from motion onset exceeded the baseline activity plus 20% of the SD of the baseline and continued to do so for more than 50 ms, then we selected the first time bin of the 50 ms as the latency of the average firing rate.

We estimated trial-by-trial FEF_SEM-pursuit latency correlations using a method developed in our previous study (Lee et al. 2016). First, we excluded any neurons whose responses in the interval from 1 to 100 ms after neural response latency failed to reach 20 spikes/s, leaving 99 FEF_SEM neurons from the two monkeys for further analysis. Then, we selected one pursuit condition per neuron that provided the largest average response across the interval from 1 to 100 ms after the time chosen as the neural response latency. By taking advantage of the fact that the correlation coefficient is a regression slope of Z-transformed data (Rodgers and Nicewander 1988), we obtained the correlation by taking a geometrical mean of the two regression coefficients—one coefficient with pursuit latency as independent variable and neural latency as dependent variable, and the other with neural latency as independent variable and pursuit latency as dependent variable.

To calculate a regression coefficient when pursuit latency is the independent variable, we divided the trials from each neuron into five equal-sized groups (quintiles) according to the estimated pursuit latency. We computed the spike density functions by averaging across the trials in each quintile of trials. Using the mean spike density function for all trials as a template, we estimated the best-fitting values of time shift for each quintile by shifting and scaling the template to match the quintile’s spike density. Then, we calculated the regression coefficient for graphs that plotted the estimated time shift of the mean spike density as a function of the mean pursuit latency for each quintile.

To calculate a regression coefficient when neuronal latency is an independent variable, we used an iterative process to estimate neuronal latency in individual trials. Using the mean spike density function for all trials as the template, we estimated time shifts and scaling factors for the spike density from each individual trial. We then updated the template using a Bayesian procedure (Bollimunta et al. 2007) and repeated the estimation procedure two more times. Then, we divided trials into quintiles according to the final estimates of neural latency and computed mean spike density function for each quintile of trials. We estimated the five best-fitting values of time shifts by shifting and scaling the template along the mean spike density function of each quintile. Finally, we calculated the regression coefficient for pursuit latency as a function of the estimated neural latencies for the 5 quintiles. We obtained the Pearson’s correlation coefficient by taking geometrical mean of the two regression coefficients. We applied the same procedure using the responses of pairs of neurons to estimate neuron–neuron latency correlations. We started from 134 unique pairs, and again selected pairs where the average of the two average responses across the interval from 1 to 100 ms after each neural latency exceeded 20 spikes/s. This left 93 pairs for further analysis.

Note that the regression slope for the z-scored data, and therefore the correlation coefficient for the actual data, could be zero even if there were only 2 (or 5) points, and so the z-scored regression analysis provided a good estimate of correlation. The analysis approach and the use of quintiles of the data did not average away neural noise but only estimation noise. It guarantees a reliable estimate of correlation.

Local Field Potential Analysis

Spike-Field Coherence

We preprocessed the LFP data with a Butterworth filter to remove 60-Hz line noise, using a function in the Fieldtrip MATLAB toolbox (Oostenveld et al. 2011). Then, we analyzed the “spike-field coherence” between the spikes and the LFP recorded from the same electrode. We used the Chronux MATLAB toolbox (Bokil et al. 2010) for all the spike-field coherence analysis. For the low frequencies (1–20 Hz), we used a Hanning window as a taper. For frequency ranges between 20 and 170 Hz, we used five spheroidal tapers with 15 Hz of spectral smoothing. We calculated the spike-field coherence in 150-ms sliding windows with a step size of 10 ms. We calculated coherence and transformed the coherence using the variance stabilization method (Bokil et al. 2007). To correct a potential confound that can occur at the low frequencies due to the transient responses (Jarvis and Mitra 2001), we shuffled trials and calculated the variance stabilized coherences 1000 times and generated the “null distributions” of coherences across frequencies. Then, we obtained a z-score as a function of frequency using the shuffle analysis as in our previous study (Lee and Lisberger 2013).

LFP Phase-Pursuit Latency Correlation

First, we used a sixth-order Butterworth filter to band-pass filter the LFP and isolate frequency in bandwidths of 2–1 Hz steps from 0 to 160 Hz. We obtained power and phase information from each band-pass-filtered component by applying a Hilbert transformation. Then, across trials and for each millisecond within trial, we calculated the correlation between instantaneous phase/power at that instant and estimated pursuit latency. From the correlation map, we selected the frequency range that maximized the correlation, isolated the LFP in the 5–15-Hz range using a sixth-order Butterworth filter, and calculated the correlation between instantaneous phase/power and pursuit latency after Hilbert transformation. Because phase information has a circular form and pursuit latency has a linear form, we used the correlation coefficient calculation for circular and linear data (Berens 2009).

Underlying Probability of Spiking and Computer Simulations

As we showed in our previous study (Lee et al. 2016), variation in neural latency has two components, one created by variation in the timing of the underlying probability of spiking, and the other created by the stochastic nature of spike timing. To estimate the SD of the latency of the underlying probability of spiking, we used a computational simulation approach separately for each FEF_SEM neuron. (1) We calculated the coefficient of variation (CV) using interspike intervals in a time window from 100 to 300 ms after the average neural latency. (2) We recalculated the spike density function to estimate a template for the underlying probability of spiking by aligning each trial according to its estimated neural latency and applying a Gaussian filter (3 ms SD) to the realigned spike density function. (3) In different runs where the SD of the latency variation was an independent variable, we jittered the template of underlying probability in latency across trials using random values from a Gaussian distribution with a mean of zero and SD chosen from predetermined values (1, 2, 4, 6, 8, 10, 12, 16, 20, 24, 28, 32, 36, 40). (4) For each run, we used the neuron’s CV as the basis for creating simulated spike trains that followed a renewal Gamma process (Brown et al. 2002; Koyama and Shinomoto 2005). (5) We estimated latency SD from the simulated spike train using the same procedure that we used for real data. (6) We used the simulated relationship between latency SD for spikes and underlying probability of firing to estimate the actual latency SD of the underlying probability given the latency SD measured from each neuron’s spiking. In this step, we included neurons only if the regression explained more than 40% of the variance, reducing the number of neurons included in the further analysis from 99 to 94.

Once we had estimated SD of latency for spiking and underlying firing probability, we could estimate the latency correlation between underlying firing probability and behavior or between two underlying firing probabilities:

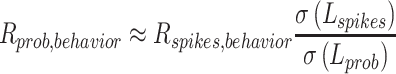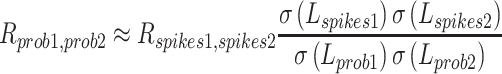where L represents latency. When we estimated the latency correlation between underlying firing probability and behavior, we selected neurons with estimated latency SDs of underlying probability of spiking equal to or larger than one, to avoid over-estimation of the correlation. This resulted in sample reduction for the estimation of latency correlation between underlying probability and behavior, from 94 to 76.

Computer Simulations

To estimate how much of pursuit latency variation could originate from FEF_SEM, we conducted a computational analysis. We simulated a population of 1000 spiking FEF_SEM neurons with responses and correlation structures that were statistically the same as our sample of FEF_SEM neurons. We used realigned time-varying mean spike density functions of our FEF_SEM recordings to determine the underlying probability of spiking. We also randomly selected the latency SD of the underlying firing probability of spiking from a Gamma distribution fitted to our observed distribution of latency SD with a shape parameter of 1.39 and scale parameter θ of 10.16. For each model neuron, we selected a value of SD from the Gamma distribution, drew 200 latencies from a Gaussian distribution with that SD, and shifted the underlying firing probability of spiking in time by those values for our 200 simulated trials. In the population of 1000 model FEF_SEM neurons, we also retained the structure of the neuron–neuron latency correlations for the underlying probability of firing derived from our data: the distribution of pairwise latency correlation followed a Gaussian distribution with a mean of 0.19. For each trial in each model neuron, we modeled the interspike interval distribution by using the shape of the latency-jittered time-dependent underlying firing probability to scale a renewal Gamma process based on the CV of interspike interval distribution in our data (Brown et al. 2002; Koyama and Shinomoto 2005). We estimated the spike density of each simulated neuron by applying a Gaussian filter with SD of 10 ms and computed the population average across the 1000 simulated neurons’ spike density functions in each trial. From these population spike density functions, we estimated the latency in individual trials. We simulated the added downstream noise by generating random numbers that follow a Gaussian distribution, with zero mean and SD that ranged from 0 to 10 ms in 0.5-ms steps. We repeated the whole simulation process 10 times to calculate the mean and SD of simulated neuron-behavior latency correlation for the underlying firing probability and SD of simulated latencies.

Results

Our goal is to understand the neural circuit mechanisms that determine sensory-motor latency. Here, our analysis focuses on the trial-by-trial variation in neural and behavioral responses because trial-by-trial correlations provide a powerful tool for understanding the processing that occurs within a sensory-motor system. For example, our previous paper (Lee et al. 2016) implies that variation in the latency of responses in area MT could account for up to 70% of the trial-by-trial variation in the latency of pursuit.

Our strategy was to record local field potentials (LFP) and the spiking activity of multiple single neurons in the smooth eye movement region of the frontal eye fields (FEF_SEM), while monkeys pursued a spot target that underwent step-ramp motion (Figure 1A, after Rashbass 1961). The step-ramp target motion reduces the frequency of saccades in the initiation of pursuit and cleanly separates pursuit and saccadic eye movements in time, enabling analysis of the initiation of pursuit uncontaminated by saccades. Because we were interested in evaluating single-trial data and revealing trial-by-trial correlations between neural and behavioral responses, we typically collected more than 100 repetitions of a few target motions (Figure 1B).

Figure 1.

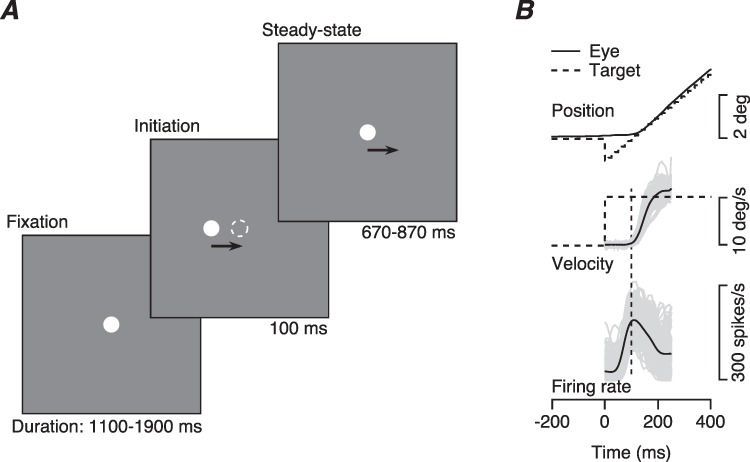
Structure of the task and example traces of step-ramp target motion and smooth pursuit eye movements. A: The three components of step-ramp target motion. B: Superimposed eye and target motion and spike density function traces. Dashed and continuous traces in the top two panels show target and eye motion. The black and gray traces for eye velocity and firing rate show averages across trials and data from individual trials. Data are from a representative recording in FEF_SEM.

Here, we present new results on the features of responses in FEF_SEM that contribute to neural and behavioral latency, and we compare our results in FEF_SEM with additional analyses of the data from prior recordings in area MT (Lee et al. 2016). We report three main findings. (1) The local field potentials in both FEF_SEM and MT include low-frequency components that are linked tightly to the latency of smooth pursuit eye movements and that are a signature of trial-by-trial correlations between the latencies of neighboring neurons. (2) The trial-by-trial variation in the latency of spiking responses in FEF_SEM is tightly correlated with the latency of pursuit eye movements, with the expected commensurate neuron–neuron latency correlations for pairs of FEF_SEM neurons (Schoppik et al. 2008). (3) The amplitude of preparatory activity is correlated negatively with behavioral latency and could play an important role in determining the latencies of FEF_SEM responses and pursuit eye movement.

Trial-by-Trial Correlation Between Neural Latency and Pursuit Latency

In response to target motion in their preferred direction, FEF_SEM neurons fire a transient burst of spikes followed by a sustained plateau, frequently at a lower rate (Figure 1B). As illustrated in Figure 1B, the onset of FEF_SEM responses usually precedes the onset of pursuit eye velocity, and both the firing rate response and the eye velocity of pursuit vary considerably from trial-to-trial in both latency and amplitude. Here, we leverage those variations to discover features of the neural computations that could determine sensory-motor latency in the pursuit system.

Trial-by-trial correlations between the latency variations of FEF_SEM neurons and pursuit eye movements provide evidence that the latency of responses in FEF_SEM controls sensory-motor reaction time to some degree. We used a procedure described elsewhere to estimate trial-by-trial latencies for pursuit eye movements (Lee and Lisberger 2013; Lee et al. 2016) and to sort behavioral trials into 5 quintiles based on the estimated latency of pursuit in each trial (Figure 2A). We then revealed coordinated shifts in the latencies of eye movements and neural responses in FEF_SEM by averaging the time-varying firing rates in each quintile (Figure 2B).

Figure 2.

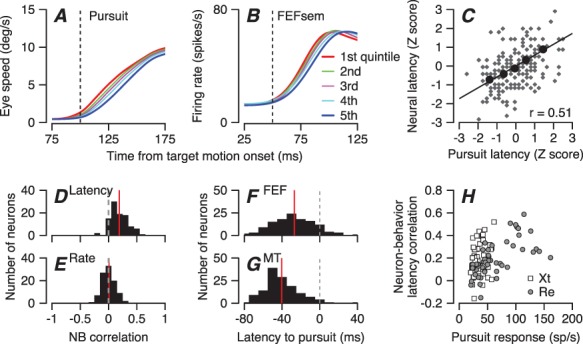
Trial-by-trial relationships between latency variation in pursuit behavior and firing of FEF _SEM neurons. A: Eye speed versus time during the initiation of pursuit. B: Population average firing rate of FEF_SEM neurons in the same intervals. In (A, B), the five traces in each panel show data for quintiles of trials sorted by the latency of pursuit. Red and blue traces show data for the shortest and longest latency group. Green, purple, and cyan show data for the middle groups. C: Plot of z-scored neural latency versus z-scored pursuit latency for an example neuron. Black circles show data for the 5 quintiles based on pursuit latency and small gray symbols show measurements for individual trials. Line was obtained by regression on large black symbols. D: Distribution of response latency-pursuit latency correlations for 99 FEF_SEM neurons. E: Distribution of response amplitude-pursuit latency correlations. F, G: Distributions of latency from neural responses in MT and FEF_SEM to the onset of pursuit. H: Relationship between FEF_SEM neural response amplitudes and neuron-behavior latency correlations. The correlation between neural responses and neuron-behavior latency correlations was 0.46 (Pearson’s correlation, P = 1.4×10⁻⁶). Different symbols in H show data recorded in different monkeys.

To quantify the trial-by-trial latency correlations between FEF_SEM responses and behavior for each neuron, we applied the estimation method detailed in our previous publication (Lee et al. 2016). Briefly, we used an iterative Bayesian method to estimate the latency and gain of firing rate and eye velocity on each individual trial relative to a template created by averaging across groups of trials. We made these estimates on the basis of the trajectory of firing rate from −20 to 100 ms from the onset of neural response and of eye velocity from −20 to 80 ms after the initiation of smooth pursuit eye movement. By basing our estimates on the full transition of each variable from baseline to peak value, we ensured that our estimates of latency were based on the left–right shift of the full waveform relative to the average, and the estimate of response amplitude was based on the full transition from baseline to peak. We then obtained the correlation coefficient between the latencies of firing rate and eye movement by taking advantage of the fact that the Pearson’s correlation coefficient is defined by the regression slope of Z-transformed data (Figure 2C).

The trial-by-trial correlation between neural and behavioral latency (Figure 2D) formed a distribution across all our neurons with a mean of 0.19 that was significantly different from zero (t-test P = 3.4×10⁻²², 99 neurons, t(98) = 12.59). The mean correlation coefficients were 0.196 and 0.183 in the two monkeys individually and were significantly different from zero (t-test P = 7.13×10⁻¹² and 1.46×10⁻¹¹, n = 50 and 49 neurons, t(49) = 8.94, t(48) = 8.79) and statistically the same in the two monkeys (two-sample t-test, P = 0.68, t(97) = 0.41). In contrast, for the same sample of neurons, the correlation between the amplitude of the pursuit-related responses and behavioral latency had means of 0.007 and 0.01 in the two monkeys. The means were not significantly different from zero (t-test P = 0.61, t(49) = 0.51 and P = 0.61, t(48) = 0.51, Figure 2E).

The absolute response latencies of FEF_SEM neurons (n = 125) fit well within the expectations for a sensory-motor circuit. They preceded the initiation of pursuit by an average of 27 ms (Figure 2F) and followed the responses of MT neurons (n = 135) by an average of 13.3 ms (Figure 2G). The latencies in FEF_SEM for pursuit target motion agreed well with the latencies for flashed visual stimuli (Schmolesky et al. 1998), supporting our previous suggestion (Darlington et al. 2018) that the pursuit-related response is driven by visual inputs. The responses of neurons in area MT preceded the onset of pursuit by an average of 40.3 ms, and the distributions of response latency for MT and FEF_SEM were statistically different (two-sample t-test, P = 4.3×10⁻⁷_,t(258) = 5.2).

To verify that the small magnitude of neuron-behavior latency correlations was not an artifact of the vagaries of estimating single-trial neural latency from a handful of spikes, we evaluated the relationship between neural response amplitude and neuron-behavior latency correlation. Our premise was that artifacts of latency estimation would mitigate against large correlations in neurons with weak responses. However, we found in both monkeys that neurons with weaker responses during pursuit (<50 spikes/s) could have either strong or weak neuron-behavior latency correlations (Figure 2H). Thus, we think that the values of neuron-behavior latency correlation document a genuine relationship. We also note that a population of neurons with stronger responses recorded mainly in monkey Re had uniformly strong neuron-behavior latency correlations.

Local Field Potential in the 5–15-Hz Range is Linked to Pursuit Latency

In many (but not all cases), local field potential (LFP) probably provides an index of the neural processing within the localized region around the tip of the recording electrode. We reasoned that analysis of the LFP in our recordings should reveal correlates to confirm the phenomena we measured in spikes, and that the LFP might reveal special features of the neural computation that determines sensory-motor reaction time.

For the example recording in Figure 3, the timing of the LFP was aligned with the onset of pursuit. We show this by ordering the > 200 trials in the dataset according to pursuit latency in each trial and plotting the raw LFP (Figure 3A) as a function of time as a horizontal line for each trial. The same alignment appeared (Figure 3B) after the LFP data had been filtered to emphasize the frequency content between 5 and 15 Hz. In Figure 3C, we plot the trial-by-trial correlation between the phase of the LFP and the pursuit latency in colors for each frequency in the LFP and each time in the trial for the example recording. The plot reveals positive correlations that exceeded 0.4 in a tight range around 100 ms after target motion onset in time and between 6 and 17 Hz in frequency. As outlined in the Materials and Methods, the data analysis in Figure 3C applied the Hilbert transform to LFPs that had been filtered with narrow pass bands at different frequencies and obtained instantaneous phase for each frequency and every millisecond in every trial. Then, we calculated the trial-by-trial correlation between pursuit latency and the instantaneous phase and power as a function of time. We used a correlation coefficient for circular data for phase (Berens 2009) and a Pearson’s correlation for power.

Figure 3.

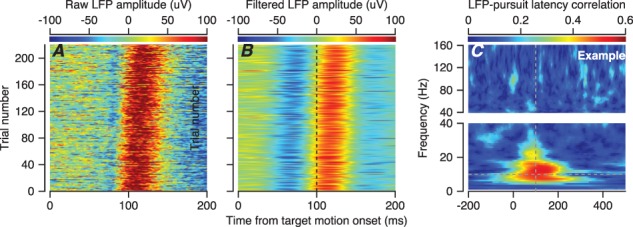
Example recording session showing the temporal alignment of LFP with the onset of pursuit. A: Each line of the plot shows the LFP for one trial as a function of time, and colors show the amplitude of the LFP. B: The data from A have been replotted after filtering with a 5–15-Hz bandwidth. In both A and B, the trials have been ordered by the behavioral latency of pursuit. C: The color of each pixel plots the trial-by-trial correlations between pursuit latency and the phase of the LFP for this example recording session as function of LFP frequency in 1-Hz bands and time from the onset of target motion. We have broken the y-axes in C into two segments with different scales to improve the visibility of the larger values of correlation in the lower frequency ranges.

A large trial-by-trial correlation between the phase of different frequency components of the LFP and the pursuit latency appeared regularly, with a peak correlation of 0.2 averaged across neurons at the best time and frequency (Figure 4A). For FEF_SEM, the correlations had peaks for frequencies in the 5–15-Hz range and at times around 100 ms after the onset of target motion, near the time of the initiation of pursuit. Analysis of LFP data from earlier recordings in area MT (Figure 4B) revealed a similar correlation, albeit with a slightly smaller value of peak correlation in MT. Thus, the phase of the LFP around the time of pursuit initiation is predictive of pursuit latency in both FEF_SEM and MT.

Figure 4.

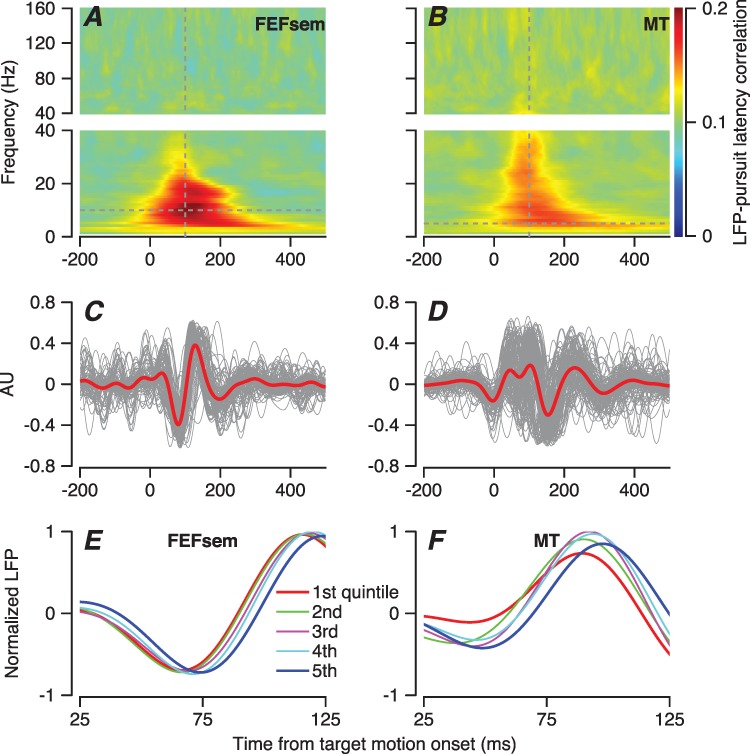
Local field potential and its correlation with the latency of pursuit. A, B: The color of each pixel plots the trial-by-trial correlations between pursuit latency and the phase of the LFP averaged across 123 sites in FEF_SEM (A) and 138 sites in MT (B) as function of LFP frequency in 1-Hz bands and time from the onset of target motion. We have broken the y-axes in A and B into two segments with different scales to improve the visibility of the larger values of correlation in the lower frequency ranges. C, D: Traces for local field potential filtered with a bandpass of 5–15 Hz for FEF_SEM (C) and MT (D). Red and gray traces show averages across all the recordings and data from individual average recordings for the FEF_SEM. Data have been plotted in arbitrary units to improve visibility of recordings with different amplitudes of LFP. E, F: LFP sorted into quintiles according to pursuit latency, after normalizing individual-filtered LFPs from individual trials by the maximum peak to trough distance. Red and blue traces show data for the shortest and longest latency group. Green, purple, and cyan traces show data for the middle groups. Example neurons recorded in FEF_SEM (E) and MT (F).

The finding of a correlation between LFP phase and pursuit latency stimulated us to identify the component of the LFP that is linked to pursuit initiation. We band-pass filtered the raw LFP from each behavioral trial to extract the 5–15-Hz frequency component. When synchronized on the onset of target motion, the single-trial LFP in FEF_SEM contained a brief wave that started about 30 ms after the onset of target motion and underwent a negative–positive–negative fluctuation that ended about 200 ms after the onset of target motion. The shape of the LFP wave was consistent across the 123 LFP recordings, as shown in Figure 4C where we normalized the averages to arbitrary units to improve the visibility of the superimposed traces. In MT, the same analysis yielded a somewhat smaller and more complicated set of deflections, but otherwise the results in the two areas were remarkably similar (138 LFP recordings, Figure 4D).

We next asked whether the LFP shifted in time in relation to pursuit latency by grouping the filtered LFP according to the quintiles of pursuit latency for each recording. For two example sessions, this analysis revealed a relationship between the phase shift of the LFP and the latency of pursuit, both in FEF_SEM (Figure 4E) and MT (Figure 4F), consistent with the trial-by-trial correlations shown in Figure 4A and B.

Quantitative analysis of all recording sites from FEF_SEM and MT revealed that behavioral latency is much better correlated with the phase shift of the LFP than with its power. Now, we correlated the behavioral latency on each trial with the power and phase in the LFP after filtering with a 5–15-Hz frequency window and plotted the results as a function of the time during the LFP. For an example LFP recorded in FEF_SEM (Figure 5A), the correlation between latency and LFP phase reaches a maximum correlation of ~ 0.6, while the correlation between latency and LFP power is smaller and negative. Population averages across 123 LFPs in FEF_SEM show the same effects (Figure 5C). In the population average, the correlation reaches a peak of 0.25 just more than 100 ms after the onset of target motion, which corresponds to the time of initiation of smooth pursuit. The results are similar for the LFP in area MT, although the effects are smaller (Figure 5B and D). We conclude that LFP in the 5–15-Hz frequency range is tightly linked to the latency of pursuit and may be related to neural processing in both MT and FEF_SEM that is contributing to sensory-motor reaction time. The differences in the details of the LFP wave in MT and FEF_SEM and its systematic relationship with behavioral latency imply that the LFPs we found in the two areas are not simply an artifact of the procedures we used for filtering the LFP.

Figure 5.

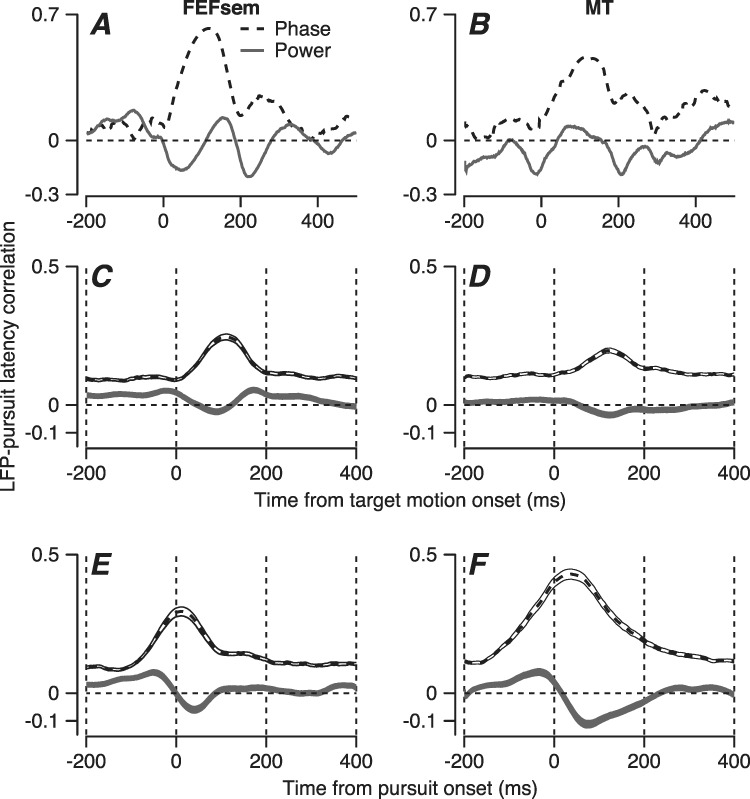
Quantitative analysis of the relationship between local field potential and pursuit latency. Graphs show example recordings in FEF_SEM (A) and MT (B) and averaged across all recording sites in FEF_SEM (C) and MT (D) as a function of the time during the wave. E and F show the same analysis as in C and D, but now with the time of the phase and power measurements aligned relative to the onset of pursuit instead of the onset of target motion. Dashed and black traces show correlations of the LFP phase versus power, and the ribbons around the traces in (C, F) show the standard error of the mean across recordings.

We obtained different, but expected results when we calculated the correlations based on the phase of the LFP relative to the onset of pursuit instead of relative to the onset of target motion. In FEF_SEM, the results were little changed and the time of peak phase correlation aligns with the onset of pursuit (compare Figure 5C and E). If LFP phase always occurred at exactly the same time relative to the onset of pursuit, then we would expect the phase difference between LFP and pursuit onset to be the same in all trials and correlations between LFP phase relative to pursuit onset and pursuit latency to be zero. This is different from the intuition that average firing rates across trials should get larger and narrower if firing rates were averaged aligned on pursuit onset versus target motion onset. Thus, we interpret Figure 5E as evidence that the LFP in FEF_SEM is aligned to some degree with both the onset of target motion and pursuit. In contrast, the growth of the correlations in Figure 5F relative to Figure 5D implies that the LFP in MT is more aligned with the onset of target motion.

Relationships Among LFP, Neuron Behavior, and Neuron–Neuron Latency Correlations

The existence of neuron-behavior latency correlations in FEF_SEM implies that each neuron acts as a proxy for many other neurons with correlated response latencies. The predictive power of the latency of a single neuron results from the combined effect of it and its partners on behavior. The relationship between LFP and response latency supports this interpretation. To better understand the neural processing that creates these relationships, we next explored the interactions among neuron-behavior latency correlations, neuron–neuron latency correlations, and LFP.

The coherence of its spikes with the LFP predicts the magnitude of each neuron’s neuron-behavior latency correlation (Figure 6), supporting the conclusion that responses in any individual neuron are related to responses in multiple neighbor neurons. For the two example neurons in Figure 6A and B, one (A) has a neural latency that is weakly correlated with the behavioral latency, while the other (B) has a neural latency that is strongly correlated with the behavioral latency. The spike-field coherences of the two neurons differed the most in 5–15-Hz frequency range when we plotted the z-scored spike field coherences as a function of frequency at 100 ms after the onset of target motion (Figure 6C).

Figure 6.

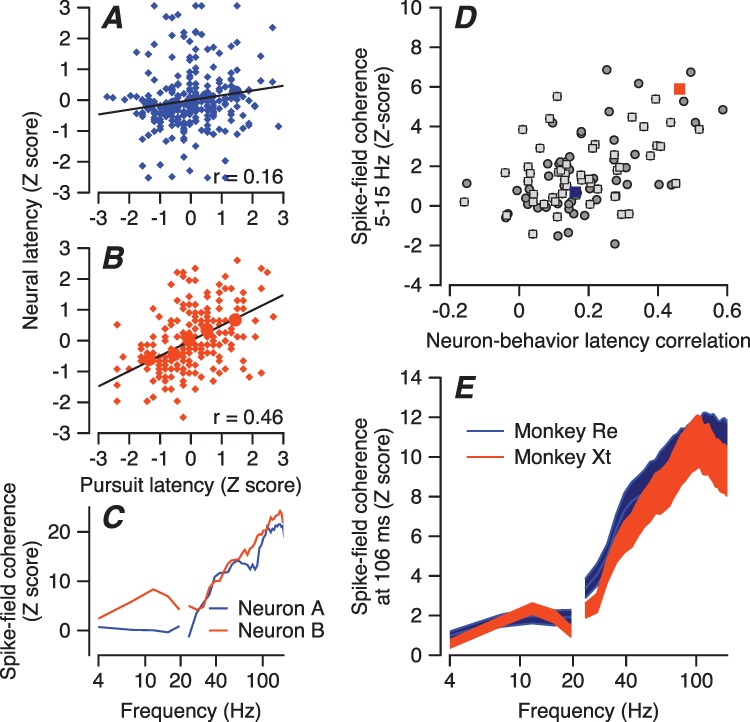
Relationship between spike-field coherence and FEF _SEM -pursuit latency correlation. A, B: Plots of z-scored neural latency versus z-scored pursuit latency for two example neurons. Navy blue and orange circles show data for the 5 quintiles based on pursuit latency, and smaller diamond symbols show measurements for individual trials. Lines were obtained by regression on the large filled symbols. FEF_SEM-pursuit latency correlation of the neurons in panels A and B are low versus high. C: Z-scored spike-field coherences of the two example neurons as a function of frequency measured at a time window centered at 106 ms from motion onset. Colors match A and B. D: Each symbol shows data for a different neuron, and the scatter plot shows the correlation between z-scored spike-field coherences and FEF_SEM-pursuit latency correlations. Orange and navy-blue squares are data of example neurons. Dark gray circles and light gray squares are data from monkeys Re and Xt. E: Spike field coherence as a function of LFP frequency, plotted in different colors for the two monkeys.

Across all FEF_SEM neurons, we found a strong relationship between the z-scored spike-field coherence and the neuron-behavior latency correlation in a time window centered at 106 ms and a frequency window centered at 7.8 Hz (Figure 6D). The Pearson’s partial correlation (controlling for firing rate) of 0.43 and 0.36 for monkeys Re and Xt (P = 0.0023 and 0.012, n = 50 and 49 neurons) suggests that the LFP in the frequency range from 5–15 Hz represents an aspect of neural processing in FEF_SEM that is related in some way to behavioral latency. Even though the amplitudes of the spiking responses during pursuit initiation were somewhat different for the two monkeys, the spike-field coherences were almost identical (Figure 6E).

The predictive value of spike-field coherence for neuron-behavior latency correlation is modulated as a function of both LFP frequency and time of the LFP relative to the onset of target motion. Figure 6 shows results only for a single time. Therefore, we next show this correlation across all times and frequencies and include comparison with the same experiment in area MT. In FEF_SEM, the correlation between spike-field coherence and neuron-behavior latency correlation appears as a red blob in the frequency range from 5–15 Hz and surrounding a time about 100 ms after the onset of visual target (Figure 7A). Reanalysis of the neural data collected from area MT for our earlier paper (Lee et al. 2016) reveals that the correlation describing this relationship is weaker in MT (Figure 7B). Furthermore, direct comparison as a function of frequency in Figure 7D shows that the peak in the frequency range from 5 to 15 Hz for FEF_SEM (red trace) is broader for MT (blue trace).

Figure 7.

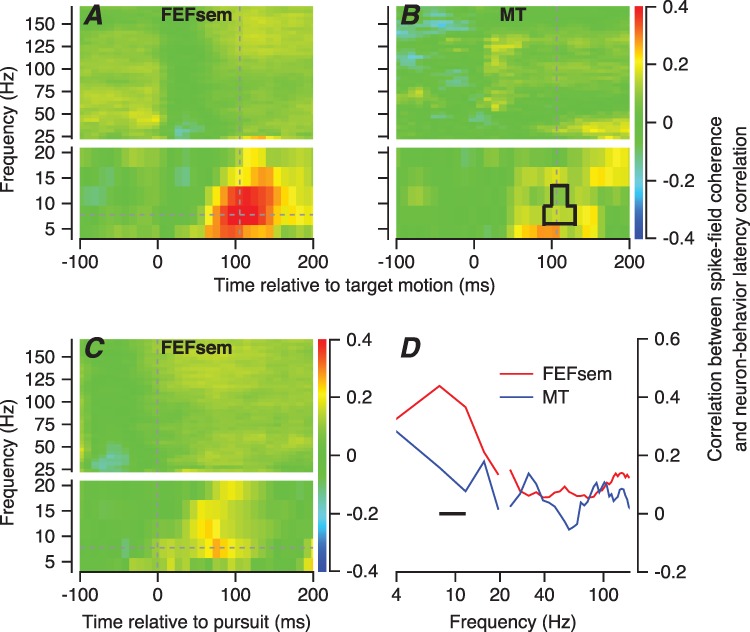
Relationship between spike-field coherence and neuron-behavior latency correlation in FEF _SEM and MT, averaged across the full sample of neurons. A, B: The color of each pixel shows the correlation between z-scored spike-field coherence and neuron-behavior latency correlations averaged across all recording sites in FEF_SEM (A) and MT (B), plotted as a function of frequency in the coherences and time from the onset of target motion. The area within the black shape in B is the region of statistically significant differences between FEF_SEM and MT. The intersection of the dashed lines in A shows the time and frequency used for panel D. C: The same analysis as in A, except that the time in the LFP and spikes was taken relative to the onset of pursuit. We have broken the y-axes in (A, C) into two segments with different scales to improve the visibility of the larger values of correlation in the lower frequency ranges. D: Red and blue lines show the correlation between z-scored spike-field coherences and neuron-behavior latency correlations measured at a time window centered at 106 ms averaged across all recording sites in FEF_SEM and MT.

Figure 7 shows averages across the full samples of neurons in both areas, allowing us to verify that the differences between MT and FEF_SEM were statistically significant over the frequency range from 6 to 12 Hz (horizontal line in Figure 7D), when evaluated using the Fisher’s r-to-z transformation (P < 0.05, n = 99 for FEF_SEM, n = 115 for area MT). The differences between FEF_SEM and MT were statistically significant in the pixels surrounded by the black rectangle in Figure 7B (Fisher’s r-to-z transformation, P < 0.05). The differences again support our suggestion that the 5–15-Hz LFP in FEF_SEM is a product of the underlying biology and not simply an artifact of the signal processing, which was identical in the two areas.

The correlations between spike-field coherence and the neuron-behavior latency correlation for FEF_SEM were reduced in magnitude by a factor of 2 when we followed the advice of a reviewer and redid the analysis using the time in the LFP and spikes relative to the onset of pursuit, rather than the onset of target motion (Figure 7C). The correlations are weakly positive in the interval from about 0–100 ms after the onset of pursuit. This result is expected if a narrow band of predictive synchrony is aligned on the onset of target motion and is shuffled in time and weakened when aligned on pursuit onset. It suggests that the synchrony between spikes and LFP that is informative about the neuron-behavior latency correlation is time locked to visual target onset.

The relationships among neuron-behavior latency correlations, behavioral latency, and the low-frequency LFP component suggest that the neural synchronization with the LFP could be a consequence of synchrony in the responses of FEF_SEM neurons, that is to their degree of neuron–neuron latency correlation. Indeed, numerous other studies have demonstrated a relationship between neuron–neuron and neuron-behavior correlations in analyses of other parameters (Shadlen et al. 1996; Schoppik et al. 2008; Huang and Lisberger 2009; Hohl et al. 2013; Lee and Lisberger 2013; Gu et al. 2014; Zandbelt et al. 2014; Lee et al. 2016; Liu et al. 2012). We verified that the same is true for latency correlations in FEF_SEM by measuring neuron–neuron latency correlations between pairs of FEF_SEM neurons and comparing them with the neuron-behavior latency correlations (Figure 8A and B). In our sample of 93 pairs of simultaneously recorded neurons that satisfied criteria outlined in the Materials and Methods, pairwise neuron–neuron latency correlations had a distribution with a mean of 0.04 (Figure 8A). A given neuron had a stronger neuron-behavior latency correlation if it also had a stronger neuron–neuron latency correlation with a neighbor neuron recorded simultaneously (Figure 8B). The relationship between neuron-behavior latency correlation and neuron–neuron latency correlation was statistically significant (r = 0.27, P = 0.0002). The relationship in Figure 8B is consistent with the conclusion that neuron–neuron latency correlations cause neuron-behavior latency correlations. We also found a strong correlation (Pearson’s r = 0.4, P = 2.23×10⁻⁴, n = 93) between neuron–neuron latency correlation and the mean of the spike-field coherences for the pair of neurons under study (data not shown).

Figure 8.

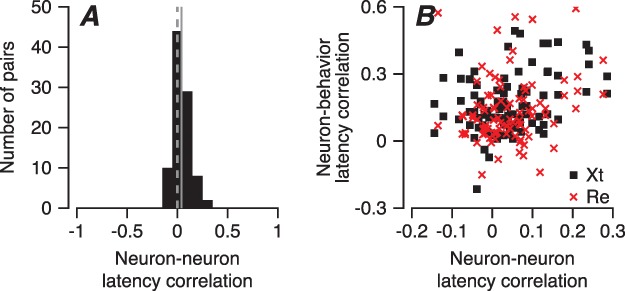
Neuron–neuron latency correlations in pairs of FEF _SEM neurons. A: Distribution of neuron–neuron latency correlations between pairs of FEF_SEM neurons. The vertical solid line shows the mean correlation, and the vertical dashed line denotes zero correlation. B: Each point plots data for a different FEF_SEM neuron, and the scatter plot shows the relationship between that neuron’s FEF_SEM-pursuit latency correlation and its neuron–neuron latency correlation with a simultaneously recorded neuron. Red x’es and black squares are data from monkeys Re and Xt.

Other Features of Neural Responses that may Contribute to Pursuit Latency

It makes sense that the correlated latency of the transient responses of neurons in the FEF_SEM plays a role in determining the latency of pursuit initiation. But, what mechanisms control the neural latencies in FEF_SEM? Several possibilities exist: (1) the correlated latency of visual motion inputs from the population response in MT (Lee et al. 2016); (2) the time when a ramp increase in firing rate reaches a threshold (“ramp-to-threshold,” Hanes and Schall 1996) and (3) the amplitude of preparatory activity that ramps up during fixation before the onset of target motion (Darlington et al. 2018). Below, we use analyses of trial-by-trial correlations with behavioral latency, first to show a possible role of preparatory activity and second to show that the responses of many neurons in FEF_SEM fail to agree with the predictions of the ramp-to-threshold mechanism. To bolster the generality of our findings, we present results separately for both the samples of FEF_SEM neurons obtained for the present paper using a “multiple-direction” task where the target moved randomly on different trials in one of two to four directions and the sample from a prior paper (Darlington et al. 2018) using a “single-direction” task where the target moved in the same direction repeatedly for many trials.

A Role for Preparatory Activity

We observed trial-by-trial correlations between the duration of fixation and behavioral latency and between the amplitude of preparatory activity and behavioral latency, as have others in the past (Teichner 1954; Findlay 1981; Niemi and Näätänen 1981). The time from the onset of the fixation point to the start of target motion varied between 1100 and 1900 ms in these experiments, and the trial-by-trial correlation between the duration of fixation and the latency of pursuit was negative (average Pearson’s r = −0.18, t-test, P = 2.68×10⁻⁴⁷, n = 153, t(152) = −21.22), meaning that longer fixation is associated with shorter behavioral latency. The correlations between the duration of fixation and behavioral latency in the present paper using the multiple-direction pursuit task (Figure 9D) agreed well with those obtained earlier from the same monkeys for the single-direction pursuit task (Figure 9A) (average Pearson’s r = −0.238, t-test P = 2.25×10⁻¹³⁰, n = 95 sessions with four speed/contrast conditions, t(379) = −37.72).

Figure 9.

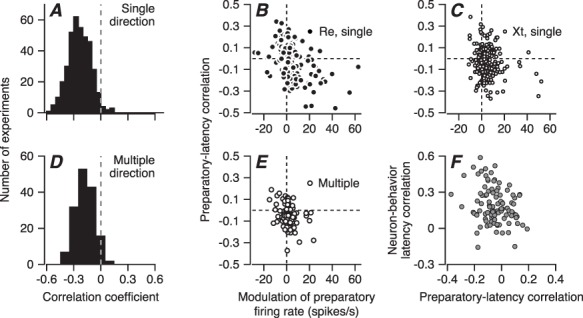
Relationship between preparatory activity and behavioral latency. A, D: Distributions of trial-by-trial correlations between duration of fixation and pursuit latency. A reanalyzes previously reported single-direction experiments in monkeys Xt and Re, while D reports results for the experiments in this paper, from the same two monkeys but for blocks of trials with two or four directions of randomly interleaved target directions. B, C, E: Scatter plots showing the trial-by-trial correlation of preparatory activity at the end of fixation with pursuit latency versus the modulation of preparatory activity across fixation. Each symbol shows results for a different experiment. Again, B and C show data for previous single-direction experiments in monkeys Re and Xt, and E shows data for multiple-direction experiments from both monkeys in the present paper. The dashed lines are the same in all three panels, allowing comparison of the samples. F: Scatter plot showing the relationship between neuron-pursuit latency correlation and correlation of preparatory activity with pursuit latency.

We found a possible effect on the latency of pursuit in the preparatory activity that accumulates during fixation by evaluating the trial-by-trial correlation between behavioral latency and firing rate at the end of fixation. In both the multiple-direction and the single-direction tasks, the correlation averaged close to zero. However, the correlation tended to be more positive for neurons with negative modulation of preparatory activity and more negative for neurons with positive modulation of preparatory activity (Figure 9B, C, and E). The Pearson’s correlation between the amplitude of preparatory modulation and the preparatory-latency correlation was −0.32 (P = 0.001, n = 99 neurons) in the multidirection task (Figure 9E), and agreed well with the data from the single-direction task (r = −0.44 and − 0.18 in Figure 9B and C, P = 1.43×10⁻⁷, n = 131 directions in B and P = 0.01, n = 190 directions in C). Also, the correlation for pursuit latency versus preparatory activity was in a direction that was compatible with the neuron-behavior latency correlations in individual neurons: stronger negative correlations, meaning higher preparatory activity for shorter behavioral latencies, in neurons with larger neuron-behavior latency correlations (Figure 9F, Pearson’s r = −0.25, P = 0.011, n = 99).

No Support for Ramp-to-Threshold

The ramp-to-threshold hypothesis predicts that firing rate in advance of movement onset should increase up to a threshold that, when crossed, triggers movement after a latency. It follows that firing rate at that latency before movement onset should be the same across trials for a given target motion and also across different target motions. The ramp-to-threshold hypothesis is not really tested by the finding that the size of the pursuit-related response does not have any predictive power for the pursuit latency variation (Figure 2E), because this measures peri-movement rather than premovement firing rate. Therefore, we conducted two analyses as explicit tests that, in the end, failed to support strongly the ramp-to-threshold theory of movement latency for FEF_SEM.

In the first analysis, we divided all the trials for a single condition of target motion in a single neuron into quintiles according to the latency of pursuit in each trial and computed the time-varying average of firing rate within each quintile. We analyzed the firing rate in the interval from 20 to 40 ms before the behavioral latency in each quintile (Figure 10A), where the analysis interval was chosen to represent the latency between pursuit-related responses in FEF_SEM and eye movement onset (Figure 2F). We then tested the ramp-to-threshold hypothesis by plotting the firing rate as a function of the latency, and fitted the data with a regression line (Figure 10D). The ramp-to-threshold theory posits that the slope of the regression line for these plots should be zero.

Figure 10.

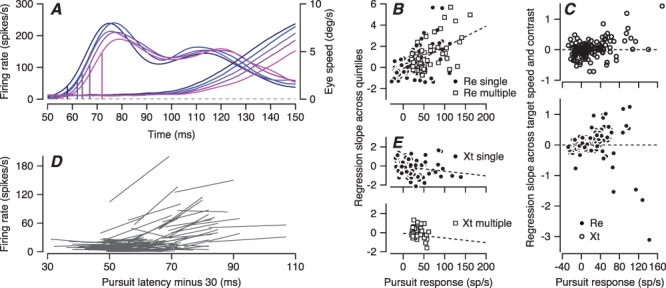
Direct tests of the ramp-to-threshold hypothesis for individual neurons in FEF _SEM . A: Firing rate (left-hand traces) and eye velocity (right-hand traces) for an example neuron divided into quintiles according to pursuit latency in individual trials and plotted as a function of time from the onset of target motion. The five vertical lines on the firing rate traces show the values of firing rate 30 ms before the latency of eye velocity in each quintile. B, E: Slope of the regression line versus amplitude of the pursuit-related response. A slope of zero would support the ramp-to-threshold hypothesis. Each symbol shows a different neuron. Filled circles show data from earlier single direction experiments and open squares show data from the current multiple directions experiments. Panel B shows data from monkey Re and panel E shows data from monkey Xt. C: Same plot as (B, E), but now using data solely from our earlier single-direction experiments and plotting the regression slopes for points taken from targets of high- or low-contrast moving at 2, 10, or 20 deg/s. D: Linear regression lines fitted to each FEF_SEM neuron’s plots of firing rate 30 ms before the onset of pursuit versus pursuit latency for the 5 quintiles of pursuit latency. Each line shows data for a different neuron.

For the population of FEF_SEM neurons, the slopes were close to zero for neurons with relatively weak pursuit-related responses, but did not follow the predictions of ramp-to-threshold by being positive for neurons with stronger pursuit-related responses in monkey Re and negative in monkey Xt (Figure 10B and E). For monkey Re, the data from the multidirection task used in this paper (Figure 10B, open squares) agreed with those from the single direction task used in a previous paper (filled circles). For monkey Xt, the data for the multidirection tasks had a much narrower range of pursuit-related response amplitudes, making comparison of the two tasks more difficult.

We provide statistics for the single-direction task because in both monkeys, it provided a wider range of pursuit-related responses and therefore more neurons with nonzero values of slope. In monkey Re, the regression slopes were significantly positive (average regression slope = 0.21, t-test P = 0.006, n = 190, t(189) = 2.79). In this monkey, neurons with larger pursuit responses had positive slopes and a regression analysis of Figure 10B revealed a statistically significant Spearman’s correlation of 0.41 (P = 3.3×10⁻⁹, n = 190 experiments). In monkey Xt, (Figure 10E), regression slopes were negative on average (−0.138, t-test P = 0.0283, n = 131, t(130) = −2.22), which means that firing 20–40 ms before pursuit onset was lower when pursuit was delayed. The negative regression slopes were more pronounced when the average pursuit response was higher and the relationship between average pursuit responses and regression slopes has a Spearman’s correlation = −0.2 (P = 0.02, n = 131 experiments, Figure 10E).

In the second analysis, we computed the time-varying trajectories of mean eye velocity and firing rate separately for target motions at 2, 10, and 20 deg/s at high and low contrast for each individual neuron. We then measured the average behavioral latency and the firing rate in the interval from 20 to 40 ms before the onset of pursuit and plotted the firing rate as a function of the latency. Again, the ramp-to-threshold theory predicts slopes of zero, and we found mostly positive slopes for neurons with large pursuit-related responses and again slopes near zero for neurons with smaller responses (Figure 10C). Here, the data from the two monkeys overlap almost perfectly, save a few outliers in monkey Re, and both monkeys showed statistically significant Spearman’s correlations in Figure 10C (Xt: r = 0.29, P = 8.16×10⁻⁴, n = 131; Re: r = 0.44, P = 1.59×10⁻¹⁰, n = 190). Together, these results do not support, and in most cases, they speak against the ramp-to-threshold theory for control of pursuit latency by FEF_SEM. We do not have data from the saccadic FEF and we have no reason to doubt the veracity of prior results that supported the ramp-to-threshold theory in that area (Hanes and Schall 1996). The control of pursuit latency might be different from the control of saccade latency.

Contribution of the Correlated Latency Variation in FEF _SEM to Trial-by-Trial Variation in Smooth Pursuit Latency

Our data document relationships among a low-frequency component of LFP, neuron-behavior latency correlations, and neuron–neuron latency correlations of FEF_SEM neurons. These results indicate that the latency variation of the FEF_SEM neural population, which arises from the correlated latency variation between neurons, has an impact on behavioral latency variation. Therefore, we developed a computational model to ask how much of smooth pursuit latency variation can be accounted for by the correlated neural latency variation in FEF_SEM neurons.

We followed the same procedure that we used previously for estimating the contribution of the correlated latency variation of area MT neurons to latency variation in the initiation of smooth pursuit (Lee et al. 2016). The main feature of the procedure is that we need to estimate what we call the “underlying probability of firing” and compute realistic correlations between the latencies of the underlying probabilities of spiking for pairs of model FEF_SEM neurons so that we can generate properly correlated model spike trains (details below). We might think of the underlying probability of firing in terms of the summed postsynaptic current in each FEF_SEM neuron.

Our analysis has multiple steps.

• (1) We calculate the underlying probability of firing from the spiking data for each FEF_SEM neuron by averaging spike density across multiple repetitions of the same target motion.

• (2) We estimate the SD of the latency of the underlying firing probability by assuming different values of SD, assembling 100 trials with the underlying firing probability shifted in time according to the SD, laying down simulated spikes with realistic discharge irregularity for each specific neuron, and performing our analysis of the latency of spike trains to estimate the SD of spiking latency. Then, we find the SD of the underlying spiking probability that matches the SD of spiking probability we measured from the actual data through the linear regression function between SD of underlying firing probability and estimated SD of simulated spikes. Figure 11A shows the relationship between SD of spiking and SD of underlying firing probability from our sample of FEF_SEM neurons.

• (3) We use a similar procedure to estimate the correlation between the neural latency variation of the underlying firing probability of spiking and the behavioral latency variation. Again, we create model neurons with different degrees of correlation between the latencies of the underlying probability of spiking and of pursuit, lay down simulated spikes with realistic discharge irregularity for each neuron in our sample, and perform our analysis of the trial-by-trial correlation between the latencies of the simulated spike trains and the behavior. We then use the neuron-behavior latency correlation for each neuron’s actual spikes to estimate its neuron-behavior latency correlation for the underlying probability of firing (Figure 11B). The average neuron-behavior latency correlations were 0.19 for spikes and 0.3 for the underlying probability of firing.

• (4) We estimate neuron–neuron latency correlations between underlying probabilities of spiking of pairs of simultaneously recorded neurons using the same procedure outlined above, except with the underlying probability of firing for pairs of neurons. The range of actual correlations is wider for the underlying probability of firing versus the spikes (Figure 11D vs. C), and neither shows a compelling relationship to the latency difference between the two neurons. Neuron–neuron latency correlations for spiking and the underlying probability of spiking averaged 0.057 and 0.19.

• (5) Using model parameters based on the distribution of parameters derived for our sample of FEF_SEM neurons, we simulated a population of 1000 spiking FEF_SEM neurons. The model neurons had realistic properties, including time-dependent shapes of underlying firing probability of spiking, coefficient of variation (CV) of interspike interval, neural latency SD, and neuron–neuron latency correlations. We ran the simulation 200 times to represent the responses to 200 trials of target motion. For each trial, we created a population spike density function by convolving each spike train with a Gaussian function having an SD of 10 ms and then averaging across the responses of 1000 model neurons. We decoded behavioral latency from the population spike density function using the same procedure we had used for estimating latency from the smooth pursuit data.

Figure 11.

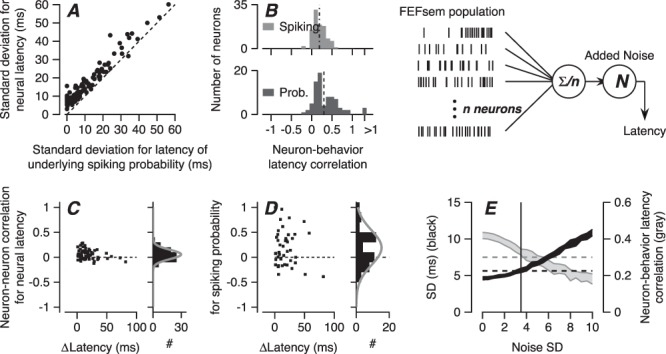
Computational analysis for the effect of neuron–neuron latency correlation on behavioral latency variation. A: Relationship between latency SD of firing rate and latency SD of underlying firing probability of spiking. Each symbol shows one neuron. Dashed line is the unity line. B: Top and bottom graphs show distributions of FEF_SEM-pursuit latency correlations based on spike density functions and on the underlying probability of spiking. The number of neurons included on this analysis is different from the previous figures. Model schematic: The model deploys n model spiking neurons, computes an average spike density function across the full population, and adds latency noise to predict pursuit latency on each simulated trial. C: Distribution of neuron–neuron latency correlation for firing rate as a function of the mean latency differences between neurons. D: Distribution of neuron–neuron latency correlation for underlying probability of spiking in relation to mean neural latency differences. E: Predictions for pursuit behavior based on decoding a model FEF_SEM population for different values of downstream noise. Black- and gray-filled areas show SD of latency and neuron-behavior latency correlation averaged across 10 simulations. Vertical line shows SD of 3.5 ms for Gaussian noise added downstream.

For the model FEF_SEM population, the predicted SD of behavioral latency was 4.6 ms in the absence of downstream noise and increased as a linear function of Gaussian noise applied downstream (Figure 11E). Therefore, correlated variation in the latency of responses in FEF_SEM can account alone for at least 40% of the nominal behavioral latency variation SD of 10 ms (Osborne et al. 2005). In the experiments reported here, the average SD of pursuit latency was 5.6 ms (Figure 9E, black dashed line), so that FEF_SEM could actually be contributing almost all of the behavioral latency variation.

In the model FEF_SEM population, the predicted neuron-behavior latency correlation for underlying firing probability averaged 0.42 in the absence of downstream noise and decreased as a function of the noise-added downstream increased (Figure 9E, gray dashed line). In our data, the neuron-behavior latency correlation for the underlying probability of firing in our FEF_SEM neurons averaged 0.3. When we added random noise from a Gaussian distribution with SD of 3.5 ms (Figure 9E, vertical line), the SD of predicted behavioral latency was 5.7 ± 0.3 ms and the predicted neuron-behavior latency correlation for underlying firing probability was 0.33 ± 0.02, both comparable to what we observed in the data. Our model shows that under certain assumptions, the latency variation in FEF_SEM, its neuron–neuron latency correlations, plus modest downstream latency noise could account for all of the behavioral variation in pursuit latency.

Discussion

We think that FEF_SEM has a central role in pursuit behavior and therefore a crucial role in determining pursuit latency because of many observations showing its tight relationship with pursuit eye movements (Brodal 1980; Keating 1991; MacAvoy et al. 1991; Gottlieb et al. 1993, 1994; Shi et al. 1998; Tanaka and Fukushima 1998; Tanaka and Lisberger 2001, 2002b, 2002a; Ono and Mustari 2009; Lisberger 2010). While many of the relevant observations are “correlative,” the known anatomical pathways from FEF_SEM to the pursuit-related regions of the cerebellum (Tian and Lynch 1997; Brodal 1980) and the profound and quite precise behavioral effects of electrical stimulation and inactivation in the FEF_SEM (MacAvoy et al. 1991; Gottlieb et al. 1993, 1994; Tian and Lynch 1996; Shi et al. 1998; Tanaka and Lisberger 2001) imply that activity in FEF_SEM neurons directly impacts the behavioral output.

Our analysis reveals four important findings that help us to understand how FEF_SEM controls sensory-motor reaction time for smooth pursuit eye movements. (1) Latency variation of the pursuit-related spiking response in FEF_SEM is correlated with latency variation of pursuit behavior because the latencies of FEF_SEM neurons are correlated with each other. The model in Figure 11 shows that the neuron–neuron latency correlation between FEF_SEM neurons alone could account for two-third of the SD in behavioral latency of 6 ms in these experiments and 40% of the SDs reported before (Osborne et al. 2005). Modest downstream latency noise allows the model to account for the rest of the variation in behavioral latency and also brings the predicted neuron-behavior latency correlations into line with the experimental data from FEF_SEM. (2) The amplitude of preparatory activity could contribute to the regulation of neural and behavioral latency, but the data do not support the ramp-to-threshold theory strongly for pursuit eye movements. (3) When a neuron’s trial-by-trial fluctuations in latency are highly correlated with the fluctuations in pursuit behavioral latency, the neuron’s latency variation is likely to be correlated with that of neighboring neurons. (4) The latency of pursuit and the correlated variation of neuronal latencies in the FEF_SEM both are linked tightly to the phase of the local field potential in the 5–15-Hz frequency range, and this feature of the LFP seems likely to reflect essential features of the neural control of latency. We propose two features of responses in FEF_SEM that contribute to neural and behavioral latency: the state of preparation and the timing of visual motion-related inputs.

Control of Pursuit Latency

The timing of the overall envelope of firing rate in FEF_SEM (present data) and MT (Lee et al. 2016) encodes the latency of the impending pursuit eye movement. The correlation of the phase, rather than the power, of the LFP with behavioral latency emphasizes the likely functional importance of the timing of the inputs and outputs of FEF_SEM rather than the amplitude of firing rates. We found little evidence in the FEF_SEM for the ramp-to-threshold theory applies for saccadic eye movements in other parts of the frontal eye fields (Hanes and Schall 1996). However, there is little reason to think that the premotor mechanisms are the same for pursuit and saccades, and it now seems likely that they also use different mechanisms for determining when a movement begins. In pursuit, the trial-by-trial correlation between the amplitude of preparatory activity that is present before target motion and the latency of pursuit after target motion raises the possibility that preparatory activity plays a role in determining the latency of the pursuit-related responses in FEF_SEM and therefore also of pursuit itself.

The neural signals that control pursuit latency have both similarities and differences with those that control saccade latency. To make this comparison, it is important to recognize that preparatory activity in the FEF_SEM is present before the visual motion that drives pursuit and therefore is analogous to the baseline activity of saccade neurons in the saccadic FEF and the superior colliculus. For each movement, any ramp-to-threshold will appear after the onset of a visual stimulus for movement and may be part of the movement-related activity. Hauser et al. (2018) showed that the baseline activity of FEF neurons before the visual target onset is negatively correlated with the saccade latency, just as we found for preparatory activity in FEF_SEM. They found correlations between saccadic latency and the rate of rise of the movement-related firing, while we did not find evidence for a ramp-to-threshold nor any relation between pursuit latency and pursuit-related response amplitude in FEF_SEM. Dorris et al. (1997) demonstrated preparatory activity in the superior colliculus and found a correlation between preparatory activity and saccade latency, just as we did for pursuit. In both the saccadic FEF and the superior colliculus, changes in the properties of the visual stimulus caused parallel changes in the latency of neural responses and saccades (Marino et al. 2012; Chen et al. 2018) in agreement with our findings of strong relationships between neural latency in FEF_SEM and pursuit latency.

We have now reported significant trial-by-trial neuron-behavior latency correlations in three major nodes for smooth pursuit eye movement: extrastriate visual area MT, FEF_SEM, and the floccular complex of the cerebellum. The presence of the 5–15-Hz LFP in both MT and FEF_SEM suggests that they are not completely independent, but simultaneous recordings from MT and FEF_SEM will be required to determine the extent to which FEF_SEM and MT control pursuit latency jointly or independently. We admit that our current understanding of the role of FEF_SEM in pursuit eye movements somewhat clouds the question of its contribution to pursuit latency. Our correlation analysis indicates that the outputs from MT and FEF_SEM both contribute to pursuit initiation, while previous data indicate that FEF_SEM modulates the strength of visual-motor transmission from MT, potentially without actually driving pursuit eye velocity itself (Tanaka and Lisberger 2001). We do not know how a multiplicative modulation would affect pursuit latency. However, one possible answer is that the gain control signal emanating from FEF_SEM is critically important in determining pursuit latency because the visual motion signal from MT cannot initiate the movement until gain has become nonzero.

Origin of Correlated Variation of FEF _SEM Neural Latency and Pursuit Latency

Our data imply that the correlated latency variation across neurons in FEF_SEM contributes to the actual trial-by-trial variation in the latency of pursuit and leads to the impressive neuron-behavior latency correlations we recorded in FEF_SEM. Thus, the same framework seems to apply for correlated latencies and response amplitudes in many areas of the brain, including area MT for smooth pursuit eye movements (Huang and Lisberger 2009; Hohl et al. 2013; Lee and Lisberger 2013; Lee et al. 2016), area MT for perceptual decisions (Shadlen et al. 1996), FEF_SEM for pursuit eye movements (Schoppik et al. 2008), and subcortical vestibular neurons (Liu et al. 2012) and area MSTd (the dorsal subdivision of the medial superior temporal area, Gu et al. 2014) for heading discrimination. The relationship between the size of the neuron-behavior correlations for a given neuron and its spike-field coherence with the LFP supports the conclusion that neural activity acquires trial-by-trial predictive power for behavioral variation because the neuron under study is part of a population of neurons with correlated variation.

Noise correlation across the relevant population is a necessary, but not sufficient, condition to create neuron-behavior correlations in either latency or response amplitude. Absent noise correlations and the trial-by-trial fluctuations in the activity of any one neuron will be averaged away by the large size of the relevant population of neurons. Even with noise correlations, the amount of behavioral-variation-added downstream from the area under study must be small, because downstream noise will inevitably reduce neuron-behavior correlations (Schoppik et al. 2008). In the neural circuit for pursuit eye movements, it is striking that downstream noise does not eliminate neuron-behavior correlations in either latency or response amplitude. We conclude, as we did before (Osborne et al. 2005), that the trial-by-trial variation in pursuit latency and amplitude is a consequence of correlated noise in cortical areas, and that subcortical components of the circuit loyally follow the instructions given by the cortex without judging their veracity. Indeed, the presence of neuron-behavioral correlations limits the amount of noise that can be injected downstream, challenging to some degree the conclusions of Bakhtiari and Pack (2019) about how much noise is created by noise correlations in MT versus downstream from MT.

The Possible Meaning of 5-15-Hz LFP

We found relationships among neuron–neuron latency correlation, neuron-behavior latency correlation, and spike-field coherence in the 5–15-Hz frequency range. The three measures covary across neurons that we recorded: a neuron with high synchrony with 5–15-Hz LFP has high neuron–neuron latency correlation and high neuron-behavior latency correlation. Their covariation implies that the three factors originate from one mechanism.

The 5–15-Hz frequency range of the LFP overlaps with the alpha range of neural oscillation, but we do not think this is a meaningful piece of information. We find it challenging to reconcile the linkage between the LFP wave and pursuit initiation with the relationship of alpha wave to feedback signaling (Michalareas et al. 2016), attention (Saalmann et al. 2012), attentional gating (Foxe and Snyder 2011), or working memory (Gevins et al. 1997). We also note but cannot reconcile our findings with the LFP suppression in the beta range that precedes arm movement (Best et al. 2017), or the correlation between beta power and reaching reaction time in the primary motor cortex (Khanna and Carmena 2017). A previous study reported a traveling beta wave in macaque area V4 that is correlated with the parameters of saccadic eye movements (Zanos et al. 2015), including an interesting phase relationship between beta-frequency LFP and the timing of saccade offset. Our findings differ in the specific frequency of LFP (beta vs. 5–15 Hz), the behavior (saccade vs. smooth pursuit), the brain area (area V4 vs. FEF_SEM), and the time epochs for the correlation (after saccade offset vs. before pursuit initiation). In many ways, the predictive value of the LFP wave component in FEF_SEM for neural and pursuit latency resembles that for gamma synchrony in the LFP in area MT for neuron–neuron spike count correlations (Lee and Lisberger 2013). It is curious that latency and spike rate are related to LFP in such different frequency ranges.

Finally, we are struck by the fact that the LFP wave in the 5–15-Hz frequency range shifts in time in parallel with pursuit latency, and that its phase is so well correlated with pursuit latency on a trial-to-trial basis. However, we still regard the LFP as a consequence of neural activity and we do not ascribe any causal role to it. We view the 5–15-Hz frequency components in the LFP as a consequence of critical neural activity, where the activity itself gets synchronized in the FEF_SEM to facilitate initiation of a pursuit eye movement. The LFP could reflect internal activity in FEF_SEM, could be a correlate of a trigger for pursuit initiation projecting to FEF_SEM from another node in the pursuit circuit, or might be simply a passive consequence of latency correlations in inputs from area MT that report the sensory estimate of target speed and direction. We suspect that understanding the latency-related component of the LFP might point us to the neural mechanisms that determine behavioral latency in our particular sensory-motor system, and possibly in other systems as well.

Funding

Research supported by National Institutes of Health grant (R01-EY027373) (S.G.L.) and (F30-EY027684) (T.R.D.). J.L. was supported in part by the Institute for Basic Science, Republic of Korea (IBS-R015-D1).

Notes:

We thank S. Tokiyama, S. Ruffner, and S. Happel for technical assistance. We also thank Dr J. Patrick Mayo for help in visual stimulus timing calibration. Conflict of Interest: The authors declare no competing financial interests.

Author Contributions

Conceptualization is formed by J. L and S.G.L.; methodology is adopted by J.L. and S.G.L.; investigation is carried out by J.L. and T.R.D.; formal analysis is done by J.L. and T.R.D.; writing—original draft is made by J.L. and S.G.L.; writing—review and editing is done by J.L., T.R.D, and S.G.L.; and funding acquisition is obtained by S.G.L.