Distinct Manifestations of Cooperative, Multidimensional Stimulus Representations in Different Auditory Forebrain Stations

Abstract

Classic spectrotemporal receptive fields (STRFs) for auditory neurons are usually expressed as a single linear filter representing a single encoded stimulus feature. Multifilter STRF models represent the stimulus-response relationship of primary auditory cortex (A1) neurons more accurately because they can capture multiple stimulus features. To determine whether multifilter processing is unique to A1, we compared the utility of single-filter versus multifilter STRF models in the medial geniculate body (MGB), anterior auditory field (AAF), and A1 of ketamine-anesthetized cats. We estimated STRFs using both spike-triggered average (STA) and maximally informative dimension (MID) methods. Comparison of basic filter properties of first maximally informative dimension (MID1) and second maximally informative dimension (MID2) in the 3 stations revealed broader spectral integration of MID2s in MGBv and A1 as opposed to AAF. MID2 peak latency was substantially longer than for STAs and MID1s in all 3 stations. The 2-filter MID model captured more information and yielded better predictions in many neurons from all 3 areas but disproportionately more so in AAF and A1 compared with MGBv. Significantly, information-enhancing cooperation between the 2 MIDs was largely restricted to A1 neurons. This demonstrates significant differences in how these 3 forebrain stations process auditory information, as expressed in effective and synergistic multifilter processing.

Introduction

The spike-triggered average (STA) represents the average stimulus spectrogram preceding spikes from a neuron (de Boer and Kuyper 1968) and characterizes response properties including temporal and spectral modulations, and feature selectivity, in a largely linear manner (Aertsen and Johannesma 1981; deCharms et al. 1998; Theunissen et al. 2000; Miller et al. 2001; Depireux et al. 2001; Hsu et al. 2004b; Woolley et al. 2005; Klein et al. 2006).

Before reaching cortex, sound information passes through brainstem, midbrain, and thalamic nuclei and undergoes transformations in sound representation due to changes in neural processing, which may be substantially nonlinear (Young 1998; Escabí and Schreiner 2002; Woolley et al. 2006; Williamson et al. 2016; Lee et al. 2017; Kuchibhotla and Bathellier 2018). One strategy for modeling nonlinear processing has been to pair a linear receptive field (RF) with a spiking nonlinearity (NL) (Steveninck and Bialek 1988; Marmarelis 1997; Ringach 2004;Simoncelli et al. 2004). However, even this approach is not sufficient to capture the information conveyed by the neurons (Atencio et al. 2008).

The maximally informative dimension (MID) analysis extends the linear–nonlinear framework by employing more than one linear filter (Sharpee et al. 2004), and, with a sufficient number of filters, such a multilinear framework can capture more fully nonlinear systems (Marmarelis and Orme 1993; Marmarelis 1997). Multiple filters can be derived by maximizing the amount of mutual information they jointly convey. MIDs have the advantage that they are not biased by stimulus correlations when non-Gaussian stimuli are applied, including environmental and communication sounds (Steveninck and Bialek 1988; Yamada and Lewis 1999; Slee et al. 2005; Fairhall et al. 2006; Schwartz et al. 2006; Maravall et al. 2007; Sharpee et al. 2011a). Alternative approaches, which may incorporate processing constraints, have also been shown to yield conjoint, multidimensional RFs of auditory cortical neurons that capture more information and enable better response predictions (Harper et al. 2016; Kozlov and Gentner 2016; Atencio and Sharpee 2017).

In cat primary auditory cortex (A1), a 2-filter MID model showed significant improvements over both the STA and the single-filter MID model (Atencio et al. 2008, 2009). In contrast, responses in the central nucleus of the inferior colliculus (ICC) essentially could be accounted for by a single MID with, on average, insubstantial contributions of a second filter (Atencio et al. 2012).

Here, we apply MID analysis to neurons in the ventral division of the cat medial geniculate body (MGBv), the core cortical field A1, and the anterior auditory field (AAF) to examine the progression of nonlinear, multidimensional processing from subcortical to core forebrain areas. MGBv receives direct input from the ICC and is a primary source of direct inputs to A1 and AAF (Middlebrooks and Zook 1983; Morel and Imig 1987; Lee and Winer 2005; Winer et al. 2005). By comparing midbrain, thalamic, and cortical filter contributions, we can determine whether the benefits of a multifilter model are restricted to cortical processing or whether they already exist subcortically and thereby provide a more complete picture of the emergence, character, and functional specificity of early auditory cortical processing.

In all 3 stations, the first MID filter (MID1) captures significantly more information than the STA. We confirm that A1 responses are better modeled by 2, synergistic MID filters (Atencio et al. 2008, 2009), and that MGBv neurons, similar to ICC neurons (Atencio et al. 2012), can be sufficiently described by single-filter RFs with little contribution from multifilter synergy. AAF neurons, similar to A1, have higher synergy than MGBv neurons although the mean prediction gain for the 2-filter model appears to be smaller than for A1.

Our findings reveal a dichotomy in the dimensionality and cooperativity of thalamic and cortical RFs, indicating a transformation between subcortical and cortical auditory processing. General functional differences between MID1 and MID2 filters are maintained across forebrain stations.

Materials and Methods

Electrophysiological methods and stimulus design have been described in previous reports (Atencio et al. 2008, 2016; Atencio and Schreiner 2010; Miller et al. 2001). A brief description follows.

Electrophysiology

All procedures were carried out in compliance with the University of California, San Francisco Institutional Animal Care and Use Committee as well as the guidelines of the National Institutes of Health. Adult cats (n = 3) were initially sedated with ketamine (30 mg/kg) and acepromazine (0.15 mg/kg) and then anesthetized with pentobarbital sodium (15–30 mg/kg) for the surgical procedure. During recording, animals were held in a stereotaxic frame, and an areflexic state was maintained by constant infusion of ketamine (2–11 mg/kg/h) and diazepam (0.05–0.2 mg/kg/h). Diazepam reduces stress-induced release of neurotransmitter in cortex, thus providing a more stable state for recording. While it acts as an inhibitory agonist, the relatively low dose is unlikely to create differing, nucleus-specific effects.

Recordings were made in a sound-shielded anechoic chamber and stimuli were delivered via a closed speaker system to the contralateral ear. Extracellular recordings in A1 and AAF were made using linear 16-channel microelectrode arrays (150 μm spacing; NeuroNexus Technologies). Recordings in the ventral nucleus of the medial geniculate body (MGBv) used bundles of 1 to 3 tungsten electrodes (MicroProbes,) with impedances of ~4.0 MΩ. The ventral division was typically found approximately 5 mm anterior to the interaural plane and 10 mm lateral of the midline and identified by its distinct tonotopic organization and narrow frequency tuning.

Neural traces, bandpass filtered between 600 and 6000 Hz, were recorded with a Neuralynx Cheetah recording system at sampling rates between 24 and 31 kHz. Offline spike sorting used a Bayesian spike-sorting algorithm (Lewicki 1994). The sorter only considers events that surpass 5 standard deviations above the background noise level, and the number of spikes in the refractory period is always below 1%. It also allows the separation of overlapping spikes from the same contact, thus increasing the yield (see Atencio and Schreiner 2013; Atencio et al. 2016).

Stimuli

Dynamic moving ripple (DMR) stimuli (Escabí and Schreiner 2002), a broadband stimulus spanning frequencies between 500 and 40 000 Hz with 50 sinusoidal carriers per octave, were presented for 15 min. For cortical recordings, the stimuli spanned a temporal modulation range between −40 and 40 Hz (sign refers to the direction of the frequency sweeps with positive values corresponding to upward sweeps). For thalamic recordings, the temporal modulation range spanned from −150 to 150 Hz. For all recording sites, spectral modulations ranged between 0 and 4 cycles/octave at a maximum modulation depth of 40 dB.

Spiking Nonlinearities

RF models consisted of either 1 or 2 linear filters with 25 frequency bins and 20 time bins each. For each filter, an empirical spiking nonlinearity NL f(x) was estimated via Bayes’ theorem: where x is the projection value between the filter and a stimulus segment, P(spk) is the average driven spike rate, P(x) is the prior distribution of projection values, and P(x|spk) is the spike-conditioned distribution of projection values. In the case of 2-filter models, the 2-dimensional spiking NL was calculated as

where x₁ and x₂ are the projection values for the first and second filters of the model, respectively.

RF Models

Different methods were used to estimate filters for each model. Reverse correlation was used to construct the STA (Aertsen and Johannesma 1981; deCharms et al. 1998; Klein et al. 2000; Theunissen et al. 2000; Escabí and Schreiner 2002). In addition, MIDs were obtained to construct 1- and 2-filter models for each neuron (Sharpee et al. 2004). In the 1-dimensional model, the filter is estimated by maximizing the mutual information captured by the RF. RF information was calculated as:

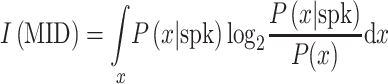The RF information was maximized via an iterative approach utilizing gradient ascent combined with simulated annealing. Overfitting was avoided by jackknifing the estimation set. The mean of 4 jackknifed filter estimations was used in the final model.

The 2-filter model was obtained by holding the first filter (MID1) constant and estimating the second filter (MID2) that captured the most information when considered jointly with MID1. The joint information yield by the 2 filters was calculated by 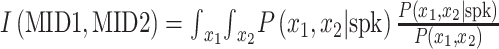where x₁ and x₂ are projection values between stimulus segments and MID1 and MID2, respectively. P(x₁,x₂) is the joint prior distribution of MID1 and MID2 projection values, and P(x₁,x₂|spk) is the spike-conditioned joint distribution of MID1 and MID2 projection values. Information maximization was achieved, as in the one-filter MID model, by an iterative approach combining gradient ascent and simulated annealing. The same jackknifing approach was used to avoid overfitting.

Single-Spike Information

The mutual information conveyed by single spikes I_spk was determined as follows (Brenner et al. 2000; Sharpee et al. 2004): 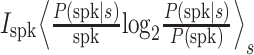where s is a discrete stimulus condition. In the case where a time-varying stimulus s(t) is repeated over several trials, the above equation is equivalent to with r(t) as the time-varying mean firing rate, and is the average of r(t) over time.

Response Predictions

Neural responses were modeled as inhomogeneous Poisson processes. For each RF model, the time-varying rate r(t) of the process was estimated within a linear-nonlinear-Poisson (LNP) framework. r(t) was calculated by

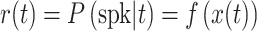where x(t) was the set of projection values over time between the model filter and the stimulus, and f(x) was the spiking NL function (as defined above). In the case of the 2-filter model, r(t) was calculated using the 2-dimensional spiking NL function as follows:

where x₁(t) and x₂(t) were the sets of projection values over time for MID1 and MID2, respectively. A RF model’s response prediction performance was evaluated by finding the coefficient of determination (R²) between r(t) and the real, observed peristimulus time histogram (PSTH) of each neuron.

Intrinsic trial-to-trial variability contributes noise that makes measuring the true time-varying rate function impossible using finite data. It is possible, however, to estimate the maximum possible R² that can be expected to be obtained with PSTHs constructed from the presentation of a finite number of stimulus trials. This maximum expected R² was estimated for each neuron using an approach adapted from previously reported methodologies (Sahani and Linden 2003; Hsu et al. 2004a). Prediction gain is calculated as:

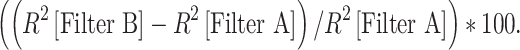Results

RF Models

Spectro-temporal RF models of single units were obtained for 3 auditory forebrain areas: the MGBv (N = 61 neurons), AAF (N = 116), and A1 (N = 312). The yield of neurons in AAF was highest from middle layers and not sufficient to derive layer-specific statistics. Therefore, we combined data across recording depth. For each neuron, the stimulus-response relationship was characterized by 3 different RF models.

The first model was the STA, representing the average stimulus spectrogram preceding a spike. The STA, widely used to characterize sensory neurons (Atencio and Schreiner 2013), serves as a reference point for comparing the utility of other models.

The second RF model was the MID1, representing the filter that captures the highest mutual information between the stimulus and response. The one-filter MID model has several theoretical advantages over the STA. It is unbiased by stimulus correlations of any order, and can thus be applied to any stimulus paradigm, including natural stimuli. It is also able to characterize neurons whose responses are invariant to spectral and temporal phase; the STA would fail to register a significant filter for these neurons because stimuli that are countermatched in phase (i.e., 180° out of phase) would cancel each other out.

On its own, however, MID1 may not capture the total stimulus information conveyed by a neuron if other stimulus information, independent from that captured by the MID1, modulates the neuron’s activity. A third RF model, the 2-filter MID, incorporates an additional linear filter, MID2, to capture potential additional RF information. The first component of the 2-filter MID model is the MID1. The second MID component (MID2) is estimated as the filter that captures the highest mutual information when considered jointly with MID1.

All RFs were estimated from neural responses to dynamic moving ripple stimuli (Escabí and Schreiner 2002). Figure 1 shows the RF models for 3 exemplar neurons, one each from MGBv, AAF, and A1. Each RF filter is accompanied by its associated spiking NL, which relates the firing rate response to the similarity between a stimulus and the RF filter. This similarity is measured in terms of projection values, that is, the dot product between stimulus and filter. Large positive projection values indicate high correlation between the stimulus and the filter, and large negative values indicate high anticorrelation. The 2-dimensional spiking NL (Fig. 1, last column) shows the joint spiking relationship of MID1 and MID2 for the 2-filter MID model.

Figure 1.

STRF examples. First and second columns: STA filters and associated spiking NL functions. Third and fourth columns: MID1 component filters and associated spiking nonlinearities. Fifth and sixth columns: MID2 component filters and associated spiking nonlinearities. Seventh column: 2-dimensional spiking NL function for the joint 2-filter MID model.

Qualitatively, the structures of STA and MID1 filters appear highly correlated, with dominant excitatory (red) and inhibitory (blue) components occupying similar regions in spectrotemporal space in all 3 stations.

The shapes of the STA and MID1 spiking nonlinearities were also highly similar with predominantly asymmetrical shapes (Fig. 1, second and fourth columns), indicating that only positive projection values between the filter and the stimulus are leading to spiking responses. That is, anticorrelation between stimulus and filter resulted in no increase in firing rate and could reduce the response below the average firing rate (horizontal line, Fig. 1). In contrast, MID2 spiking nonlinearities (Fig. 1, sixth column) were more symmetrical. Stimuli that were either highly correlated or highly anticorrelated with the MID2 filter had heightened chances of eliciting a spike.

The similar filter structures and equally asymmetric nonlinearities of the STA and MID1 RFs suggest that STA and MID1 encode similar stimulus features. MID2 filters, with their distinct filter structures and symmetrical spiking nonlinearities, represent stimulus processing distinct from the STA and MID1. The symmetric NL reflects an invariance of the response with regard to the envelope phase. Comparison of the magnitude of the firing rate reflected in the MID1 and MID2 NL (Fig. 1, fourth and sixth columns) indicates a larger contribution of MID2 to the firing rate of cortical neurons relative to thalamic neurons.

Filter Correlations

The degree of RF similarity between the 3 models in different processing stations can be quantified by filter correlation. Figure 2 shows the correlations between the STA and MID1 and between MID1 and MID2 for MGBv, AAF, and A1 neurons. For comparison, we also include previous data for ICC neurons, the main input to the MGBv (Atencio et al. 2012). In all areas, the STA and MID1 are highly correlated whereas MID2 is generally uncorrelated to MID1 (and by implication to the STA) since this filter captures information not represented by the STA or MID1. ICC and MGBv neurons show higher STA/MID1 correlation values than AAF and A1 neurons (P < 0.01, rank-sum test, Bonferroni-corrected), with ICC neurons having even higher STA and MID1 correlations than MGBv units (P < 0.01, rank-sum test, Bonferroni-corrected). MGBv neurons displayed a median correlation value of 0.91 between the STA and MID1, significantly higher than for AAF (0.83) and A1 (0.84) neurons (P < 0.01, rank-sum test, Bonferroni-corrected). Median correlations between MID1 and MID2 for MGBv, AAF, and A1 neurons are 0.01, −0.02, and −0.01, respectively. No significant differences were found for MID1 and MID2 correlation values for all 4 areas. The high correlation between STA and MID1 across all areas indicates that the 2 filters convey similar spectrotemporal features. The high STA-MID1 correlations for ICC and MGBv neurons suggest that the STA is a reasonably accurate representation of the first-order feature processing performed by midbrain and thalamic neurons. In contrast, the low correlations between MID1 and MID2 in all 4 auditory areas suggest that the information/prediction improvements yielded by the 2-filter MID model come from representing additional feature components that were hitherto unincorporated into the filter analysis.

Figure 2.

RF filter correlations. Average correlation strength between STRF filters is shown for neurons in ICC (Atencio et al. 2012), MGBv, AAF, and A1. Error bars: SD.

While MID filters appear to convey the same spectrotemporal features as the STA model, they provide a more accurate representation of that feature. For example, unlike the STA, filters obtained via MID analysis are not biased by stimulus correlations (Sharpee et al. 2004; Atencio et al. 2008). Stimulus correlation effects may be removed from the STA if Gaussian stimuli are used to estimate the filters, because they are completely described by their second-order correlations. More complex stimuli such as natural sounds often have higher-order correlations whose effects cannot be removed (Ringach et al. 2002; Paninski 2003). An MID filter could provide improved predictive power over an STA filter that is biased by correlations that are present in the stimulus.

RF Information

One way of comparing the utility of our models is to estimate the RF information, measured by the mutual information, which quantifies the ability of the filter to describe the relationship between the stimulus and the neuron’s spiking response. Figure 3 shows the range of information captured by each of the 3 different models in MGBv, AAF, and A1. Scatterplots of STA information versus MID1 information (Fig. 3A–C) and of MID1 information versus the joint MID1,2 information (Fig. 3D–F) are shown. For all neurons, the information yielded by MID1 was always greater than or equal to that of the STA. Likewise, the 2-filter MID model (MID1,2) always yielded at least as much information as MID1 alone.

Figure 3.

RF information. (A–C) Information captured by the STA versus MID1 information for MGBv, AAF, and A1. (D–F) MID1 information versus the joint 2-filter MID model (MID1,2) information for the 3 stations. (G) Median percentages of total single-spike information I_spk for neurons in MGBv, AAF, and A1 captured by 3 filter field models. Error bars: standard error (SE) about the median.

The mutual information conveyed by single spikes can also be calculated in a model-independent fashion if stimuli are repeated over many trials (Brenner et al. 2000; Sharpee et al. 2004). Using the spiking responses to 50 repetitions of a short dynamic moving ripple, we calculated the total single-spike information I_spk conveyed by each neuron. I_spk serves as an upper limit on the amount of mutual information that a RF model can possibly capture.

Figure 3G shows median information values as a percentage of each neuron’s I_spk value. In MGBv, the median percentage of I_spk captured by the STA was 31% compared with 23% and 25% of I_spk in AAF and A1, respectively. This indicated that the STA was superior in capturing the available single-spike information in thalamic neurons relative to cortical neurons. MID1 filters in A1 and AAF captured significantly more information than STAs with increases of 35% and 27%, respectively. A similar increase in MGBv was statistically not significant. Compared with the single-filter MID, MGBv neurons were modeled only marginally better by the 2-filter MID, improving from a median value of 37% to 40% of I_spk with MID1,2 (an 8% increase). Cortical neuron models, however, benefitted markedly from the inclusion of a second filter. Single-filter MIDs yielded median values of 31% and 33% in AAF and A1, respectively, whereas 2-filter MIDs improved both AAF and A1 median information values to 39% of I_spk, a 26% and 18% increase, respectively. Thus, while the information captured jointly by MID1 and 2 is approximately the same for all 3 stations, the contribution of MID2 is significantly larger for A1 and AAF as compared with MGBv. Thus, it becomes more difficult to capture cortical responses without relying on increasingly more sophisticated models.

Sufficiency

To elucidate further the advantage of a 2-filter MID model, we calculated 2 RF sufficiency values: STA sufficiency and MID1 sufficiency. STA sufficiency is the percentage of the information captured by MID1,2 that is also captured by the STA. A high STA sufficiency indicates that a neuron is already well-characterized by the STA, and applying MID models to the cell may be unnecessary. Correspondingly, MID1 sufficiency measures the percentage of MID1,2 information that is already captured by MID1. Figure 4 shows STA and MID1 sufficiency values for neurons in MGBv, AAF, A1 and again ICC (Atencio et al. 2012). ICC and MGBv neurons both have significantly higher values of both STA and MID1 sufficiency compared with AAF and A1 neurons (P < 0.01, rank-sum test, Bonferroni-corrected), suggesting that single-filter RF models are reasonably sufficient for characterizing subcortical responses. In fact, ICC and MGBv neurons, respectively, have median STA sufficiencies of 79% and 80%, indicating a 20% average increase in information by estimating MID1,2. In contrast, 2-filter models of cortical neurons stand to gain nearly 40% in information over the STA. Thus, cortical neurons display more multifeature processing than subcortical neurons.

Figure 4.

RF model sufficiency. STA and MID1 RF information relative to the information captured by the 2-filter MID model. SE bars about the median; starred horizontal bars: significant differences in medians (P < 0.01, rank-sum test, Bonferroni-corrected).

Synergy

The information results for the 2-filter MID model establish the presence of significant multifeature processing in cortical neurons, yet the manner in which these features interact has yet to be addressed. There are 3 possibilities for how the 2 RF features combine to yield information. First, the features could be treated independently; in this case, information yielded jointly by the 2 features would be the sum of their independent information contributions. Second, the features could contribute redundant information; the joint information would be less than the sum of their independent contributions. Third, the features could combine synergistically; the joint information would be greater than the sum of their independent contributions.

Synergy, or positive cooperativity, for MID models has been shown previously for A1 neurons (Atencio et al. 2008, 2009). Synergy is defined as 100 times the ratio of the joint, 2-filter information and the sum of the individual information contributions from each filter component. Synergy values greater than 100 indicate that the features represented by MID1 and MID2 combine synergistically, conveying more information than the sum of their parts. Values below 100 indicate a degree of redundancy.

Figure 5A–C show the distribution of synergy values for MGBv, AAF, and A1 neurons. The median synergy values for the 2-filter MID models of the 3 areas and ICC (Atencio et al. 2012) are depicted in Fig. 5D. AAF and A1 neurons exhibited significantly more synergy between the MID1 and MID2 features compared with neurons in ICC and MGBv (P < 0.01, rank-sum test, Bonferroni corrected). Thus, for a significant proportion of cortical neurons, the features represented in the 2-filter MID model do not simply encode stimulus information independently. Rather, the 2 features interact nonlinearly, giving cortical—but not subcortical—neurons sensitivity to particular combinations of the 2 spectro-temporal features. These complex, cooperative interactions are expressed in the 2-dimensional spiking nonlinearities of the cortical 2-filter MID models (see Fig. 1).

Figure 5.

Synergy between MID1 and MID2. (A–C) Distribution of synergy values for MGBv, AAF, and A1. The dashed reference line at 100 indicates no information synergy. (D) Median 2-filter MID synergy for ICC, MGBv, AAF, and A1 (with SE bars). Starred horizontal bars: significant differences in medians (P < 0.01, rank-sum test, Bonferroni-corrected).

NL Asymmetry

In a linear-nonlinear RF framework, the linear filter accounts for only part of the model. The other part consists of the spiking NL function that relates the match between the spectrotemporal structure of the stimulus and filter to the spiking activity of the neuron. This spiking NL is important because it is possible for 2 neurons with highly similar RF filters to display dissimilar spiking patterns to the same stimulus. For example, consider 2 neurons with identical linear filters. One neuron is sensitive to the spectral envelope phase of the preferred stimulus feature while the other neuron responds without regard to spectral phase. The first neuron will have a spiking NL that is highly asymmetrical, with spikes occurring only for stimuli in phase with the filter and thus yielding a large, positive stimulus-filter projection value. The second neuron, on the other hand, will have a symmetrical NL function such that stimuli highly matched or countermatched with the RF filter will both elicit spikes.

For each neuron, we calculate an asymmetry index (ASI) for the spiking nonlinearities associated with each model filter (see Material and Methods). ASI values near 1.0 indicate that a neuron spikes only when a stimulus is highly matched with the filter. Values near 0.0 indicate that a neuron will spike even when a stimulus is unmatched. Negative values indicate that a neuron preferentially spikes when stimuli are countermatched to the filter. Figure 6A shows mean ASI values for nonlinearities associated with STA, MID1, and MID2 filters for neurons in MGBv, AAF, and A1. Cumulative distribution functions (CDFs) of the ASI values in the 3 areas are shown in Fig. 6B–D. We found that in all 3 auditory areas, MID2 nonlinearities were significantly more symmetrical compared with the highly asymmetric nonlinearities associated with STAs and MID1s (P < 0.01, rank-sum test, Bonferroni-corrected). The median value for MID2s (Fig. 6D) is near 0, with equal distribution of negative and positive ASIs. Both STA and MID1 ASIs were positive with significantly higher asymmetry in MGBv neurons compared with those of AAF and A1 neurons (P < 0.01, rank-sum test, Bonferroni-corrected; Fig. 6B,C).

Figure 6.

Asymmetry of the filter nonlinearities. (A) ASI of filter nonlinearities for MGBv, AAF, and A1. SE bars about the median. (B–D) Cumulative probability function for STA, MID1 and MID2. Significant differences are indicated by stars (^**P < 0.01; ^***P < 0.001; Kolmogorov–Smirnov test, Bonferroni-corrected).

These results suggest that the stimulus features described by MID2 filters have a strong tendency toward response invariance with regard to spectral or temporal envelope phase. In contrast, the features represented by the STA and MID1 generally require more precise alignment of stimulus and filter in spectral and temporal dimensions in order to drive neural responses. The latter was especially true in MGBv neurons, where ASI values for the STA and MID1 were higher than in AAF and A1.

NL Threshold and Transition

We next assessed the shape of the NL curve by parametric fits for the asymmetric nonlinearities of STAs and MID1s (see Fig. 1 for actual examples and Fig. 7A,B for schematic examples). Threshold values (Θ) indicate the minimal match that is required between stimulus and STA/MID for the neuron to respond. High threshold values indicate higher stimulus feature selectivity. Threshold values for STA and MID1 nonlinearities (Fig. 7C,D) were fairly similarly distributed across MGBv, AAF, and A1 with slightly higher thresholds for MGBv versus A1.

Figure 7.

NL parameters. (A) Schematic illustration of 2 NL thresholds (Τ) for a transition value (S) of 0. (B) Schematic illustration of 2 NL transitions (S) for a threshold value (T) of 20. (C–F) Cumulative probability functions for STA and MID1 thresholds and transition values. Dashed reference line at the mean value.

The transition parameter (σ) indicates the noise in the response. The lower the value, the more the NL approximates a hard rectification. Again, the transition distributions for the 3 stations were quite similar with slightly lower transition values for MGBv nonlinearities of the STA (re A1, Fig. 7E) and MID1 (re AAF, Fig. 7F). Together, these data indicate that neurons in all 3 stations require at least a moderate match between filter and stimulus to respond at an elevated rate. When this threshold is reached, the response increases approximately linearly with increasing stimulus-filter correlations.

Spectral Filter Aspects

All 3 filters, STA, MID1 and MID2, reflect a neurons’s specific spectral and temporal stimulus preferences. To characterize potential differences in these filters across neurons and between stations, we identified the peak in the spectrotemporal structure (see Methods and Fig. 8A for details of filter peak identification) and measured its location in time and frequency for every model filter. We focused on the peak of each filter because it was the strongest component in the RF structure and thus represented the stimulus element with the greatest influence on the neuron’s spiking activity. We called the temporal location of the peak the peak latency and the spectral location the peak frequency.

Figure 8.

Peak frequency distribution. (A) Schematic illustration of defining peak frequency, spectral integration window (blue lines) and peak latency, temporal integration window (red lines) from a STRF. (B) Cumulative probability function of peak frequency for the 3 filters in MGBv, AAF, and A1. (C) Difference between STA and MID1 peak frequency for MGBv, AAF, and A1. (D) Difference between MID1 and MID2 peak frequency for MGBv, AAF, and A1. Dashed reference line for zero difference.

Figure 8 shows results for peak frequencies of each filter model. The left column (Fig. 8B) displays the CDFs of peak frequencies for each model in neurons from MGBv, AAF, and A1. We did not find statistically significant differences between the distributions for each model in any of these 3 auditory areas, reflecting a fairly unbiased (or equally biased) sampling of the tonotopic space (P > 0.3, Kolmogorov–Smirnov test, Bonferroni-corrected). In pairwise comparisons, however, we found that for a given neuron, MID2 often had a different peak frequency than the STA and MID1. Figure 8C displays the differences in peak frequencies between MID1 and STA filters within neurons. Figure 8D displays the peak-frequency differences between MID2 and MID1 filters. The vast majority of MID1 and STA filters were well-matched in peak frequency; in all areas, the median absolute difference in peak frequency between the STA and MID1 was no more than one-tenth of an octave. In contrast, the median absolute differences between MID1 and MID2 peak frequencies were over half of an octave. We use the measure of median absolute differences rather than SDs due to the comparative robustness of median absolute difference measures in distributions with non-Gaussian tails. In all 3 auditory areas, the median absolute difference in peak frequency between MID2 and MID1 was greater than that between MID1 and the STA (P < 0.01, rank-sum test). We found no significant bias in any filter model toward either lower or higher peak frequencies (P > 0.2, rank-sum test).

Neurons do not only process stimulus information at the peaks of their spectrotemporal filters. Each peak is also associated with temporal and spectral integration windows that together represent the portion of a stimulus that influences the spiking activity of the neuron. We identified the limits of the temporal and spectral integration windows as the points at which the amplitudes of the marginal absolute tuning curves dropped below the lowest quarter of the dynamic range (see Material and Methods and Fig. 8A for details of filter integration window identification). We used the absolute values of the RF filters because we wished to include suppressive regions (such as inhibitory sidebands) within the integration windows. The temporal and spectral integration windows thus represent the ranges over which neurons integrate both excitatory and inhibitory stimulus information.

Figure 9 shows results for the bandwidth of the spectral integration windows. Figure 9A shows CDFs of the spectral integration windows for each of the 3 filter types. STAs and MID1s in AAF had a larger spectral bandwidth than A1 (P < 0.01, signed-rank test). In pairwise filter comparisons within each field (Fig. 9B), we found that MID2s generally had larger spectral integration windows than MID1 filters in MGBv and A1. In MGBv neurons, MID2 filters had median bandwidths that were 0.30 octaves wider than MID1 filters compared with a difference of only 0.15 octaves in A1 (P < 0.01, signed-rank test). We found no significant differences in pairwise model filter comparisons for neurons in AAF (P > 0.2, signed-rank test).

Figure 9.

Spectral integration. (A,B) Cumulative probability function of spectral integration bandwidth for the 3 filters in MGBv, AAF, and A1. Significant differences are indicated by stars (^*P < 0.05; ^**P < 0.01; Kolmogorov–Smirnov test, Bonferroni-corrected).

Our spectral integration results showed that in MGBv and A1, MID2 filters integrated stimulus information over a broader frequency range than MID1 filters. Interestingly, we did not see the same differences between MID2 and MID1 filters for AAF neurons. This may be because MID1 filters in AAF already had broader spectral integration windows (median width: 0.80 octaves) compared with MID1 filters in MGBv and A1 (median widths: 0.65 and 0.60 octaves, respectively).

The peak frequencies of MID2 filters further support the idea that MID2 represents influences from a separate set of input connections than for MID1 (Atencio et al. 2008, 2009). MID2 filters commonly display frequency processing ~2/3 octaves away from the peak frequencies of the STA and MID1 (based on peak difference plus bandwidth difference). This suggests that MID2s may encode contextual, off-frequency influences from longer-range connections relative to the main frequency focus encoded by STAs and MID1s.

Temporal Filter Aspects

Peak latencies reflect the timing relationship between stimulus and response. Figure 10A displays the CDF of peak latency for each filter type across the 3 stations. No significant latency differences across the sampled population were seen for either STAs or MID1s between the 3 stations. However, MID2 latencies in A1 and AAF were significantly longer than in MGBv (P < 0.01, Kolmogorov–Smirnov test, Bonferroni-corrected). In each area, a greater proportion of MID2s exhibited significantly longer peak latencies compared with the STA and MID1 (Fig. 10B). We found that in AAF, the peak latency of the MID2 filter typically occurred 30 ms (median value) later than the peak latency of the MID1 filter. Similarly, in A1, we found that neurons had a median MID2 peak latency 24 ms later than the MID1 peak latency. In both AAF and A1, we found these latency differences to be significant (P < 0.01, paired signed-rank test). We did not find a significant difference in median MID2 and MID1 peak latencies for MGBv neurons (P > 0.2, paired signed-rank test).

Figure 10.

Peak latency. (A,B) Cumulative probability function of peak latency for the 3 filters in MGBv, AAF, and A1. Significant differences are indicated by stars (^*P < 0.05; ^**P < 0.01; Kolmogorov–Smirnov test, Bonferroni-corrected).

The differences in MID2 and MID1 peak latencies in cortical cells may suggest that the 2 filters are sensing short-term sequential aspects in the stimulus with MID2 filters reacting to stimulus segments 20–40 ms before the stimulus portion relevant for MID1. The observed synergy between the filters may be a reflection of this sequence sensitivity. The latency difference may represent influences from different sources of neural input. For example, MID2, with its longer peak latency, may reflect the influences of corticocortical input from nonprimary auditory areas or from nonlemniscal thalamic inputs whereas MID1 appears to be dominated by influences from short-latency thalamic inputs. Alternatively, MID2 may reflect relatively weak synapses on a neuron that require prolonged or repeated excitation from presynaptic neurons before driving a spiking response.

Figure 11 shows results for the length of the temporal integration windows of each model and area. Figure 11A compares CDFs of the temporal integration windows by filter type. Only MID2s showed a difference between the fields, namely longer integration windows for AAF compared with MGBv (P < 0.05, Kolmogorov–Smirnov test, Bonferroni-corrected). Significant differences in the CDFs between filter types for each field (Fig. 11B) were observed in AAF between the STA and MID1 and in A1 between the STA and MID1 and between the STA and MID2 (P < 0.01, Kolmogorov–Smirnov test, Bonferroni-corrected). These differences came in the form of longer temporal integration windows for the STAs. In AAF and A1, STA filters had temporal integration windows 5 and 6 msec longer (respectively) than MID1s for the same neuron (P < 0.01, signed-rank test). A1 also showed longer STA integration windows compared with MID2s (P < 0.01, signed-rank test).

Figure 11.

Temporal integration. (A,B) Cumulative probability function of temporal integration window for the 3 filters in MGBv, AAF, and A1. Significant differences are indicated by stars (^*P < 0.05; ^**P < 0.01; Kolmogorov–Smirnov test, Bonferroni-corrected).

Combined, the spectral and temporal differences between MID1 and MID2 filter features suggests a potential role of MID2s in spectrotemporal context detection and the representation of multidimensional feature conjunctions.

Model Validation: Response Predictions

With any RF model, there is a chance that the measured results are only valid for the stimulus set used for estimation. In order to test if its utility extends past the estimation set, a model must be validated on a novel stimulus. To this end, we presented our neurons with 50 trials of a 30-s dynamic moving ripple segment. Although the dynamic moving ripple segment had the same spectrotemporal and modulation parameters as the estimation stimulus, the stimulus was generated from a random starting state and thus was uncorrelated to estimation stimulus.

We chose to validate our RF models by using them to predict these response PSTHs. We generated predicted PSTHs using a LNP rate model (see Materials and Methods). In this model, the RF filter is first convolved with the stimulus to generate a set of projection values over time. These projection values are then translated into spike rates via the experimentally obtained spiking NL function. These spike rates constitute the PSTH prediction for the model. Predictions for all 3 of our RF models are shown along with the real, observed PSTH for an A1 example neuron in Figure 12A.

Figure 12.

Example model predictions for an A1 neuron. First row: example PSTH observed by averaging over 50 trials of 30 s Dynamic Moving Ripple stimulus. Second, third, and fourth rows: PSTH predictions generated from the STA, one-filter MID, and 2-filter MID models, respectively. Prediction performance is indicated as coefficients of determination (R²).

We measured the similarity of each predicted PSTH with the observed PSTH by calculating the square of the correlation coefficient (R²) between the 2 signals. R², also known as the coefficient of determination, measures the proportion of the variance in the observed PSTH that is captured by each model prediction. Due to intrinsic neural variability, however, it is virtually impossible to obtain an R² value of 1 for any neuron using real data. With an infinite number of trials, we could theoretically average out this intrinsic trial-to-trial variability, but even if our model perfectly predicts the true time-varying rate function of a neuron, with finite data we will still obtain R² values less than 1. Additionally, neurons often display differing degrees of trial-to-trial variability, so it is difficult to compare R² values directly for different neurons.

It is possible to measure the maximum R² value that can be obtained within the limits of finite data sets. We estimated this value by adapting previously reported methodologies (Sahani and Linden 2003; Hsu et al. 2004a) to relate the average R² value between PSTHs obtained for subsets of the real data to the maximum possible R² we would expect to obtain if we possessed a perfect prediction of the time-varying firing rate. The MGBv neurons had a median maximum R² of 0.63 while AAF and A1 neurons had median values of 0.41 and 0.43, respectively (Fig. 12B). The median maximum expected R² value for MGBv neurons was significantly higher than for neurons in AAF or A1 (P < 0.01, ranked-sum test, Bonferroni-corrected). No significant difference was found between the distributions of maximum R² values for A1 and AAF neurons (P > 0.15, Kolmogorov–Smirnov test). These results indicate that MGBv neurons generally display significantly less trial-to-trial variability compared with cortical neurons. In all auditory areas, however, the maximum expected R² varied considerably across neurons, and there were several neurons in both AAF and A1 with maximum expected R² values of over 0.8, demonstrating that some cortical neurons maintain highly precise trial-to-trial spiking comparable to that of the better thalamic neurons.

In order to compare the prediction performance of our models for different neurons, we normalized prediction R² values by the maximum R² values for each neuron. These normalized R² values can be interpreted as the proportion of PSTH variance captured by the prediction model that could possibly have been captured. For example, if a neuron has a maximum R² of 0.5, and a RF model generates a predicted PSTH with an R² of 0.4 with the observed PSTH, then our prediction model will have captured 80% of the variance that is possible to predict. The mean normalized prediction values for the 3 areas and filter configurations are shown in Table 1.

Table 1.

Normalized predictions (R², mean and SD)

	N	STA	MID1	MID1,2
MGB	53	0.03 ± 0.04	0.05 ± 0.11	0.05 ± 0.12
AAF	108	0.11 ± 0.11	0.14 ± 0.13	0.15 ± 0.13
A1	261	0.08 ± 0.09	0.12 ± 0.13	0.13 ± 0.14

Figure 13A,C,E display scatterplots comparing the prediction performance of our 3 RF models across MGBv, AAF, and A1. We note that for many AAF and A1 neurons and for a handful of medial geniculate body (MGB) neurons, some RF models achieved prediction performances approaching 1, indicating that those models had captured as much of the response variance as was possible. In particular, the 2-filter MID model achieved near maximal prediction performance in many AAF and A1 neurons.

Figure 13.

Comparisons of the prediction performances and gains. (A,C,E) Prediction performance. Scatter plots of coefficient of determination (R²) comparing MID1 to STA prediction (left panel), MID1,2 to MID1 prediction (middle panel), and MID1,2 to STA prediction (right panel) for MGBv, AAF, and A1, respectively. (B,D,F) Prediction gain. Percent increase in R² prediction performance of the MID1 over the STA (left panel); percent increase in R² prediction performance of the 2-filter MID model over MID1 alone (middle panel); percent increase in R² prediction performance of the 2-filter MID model over the STA (right panel). Asterisks denote histograms displaying significant prediction gains (^*P < 0.01, signed-rank test, Bonferroni-corrected).

From the scatterplots, we also observe that the one-filter MID model generally had superior prediction performance over the STA in AAF and A1, but this trend was less clear in MGBv. The 2-filter MID model, MID1,2, generally produced slightly better predictions than MID1 in A1, but this trend was not apparent in MGBv or AAF. These trends are more clearly illustrated in Figure 13B,D,F, where the model comparisons are plotted as histograms of prediction gains. Only values R² > 0.02 were compared to limit the influence of meaningless predictions. A few outliers >500% were observed but are not further considered in this comparison. MID1 had significant prediction gains over the STA in AAF and A1 (P < 0.01, signed-rank test, Bonferroni-corrected), but not for neurons in MGBv. MID1,2 had superior prediction performance to the STA in all studied areas (P < 0.01, signed-rank test, Bonferroni corrected). MID1,2 predicted better than MID1, however, only in A1 (P < 0.01, signed-rank test, Bonferroni corrected).

These results indicate that A1 is the only auditory area studied here with clearly significant multifeature processing. Most of the prediction gains for AAF neurons were achieved by using the one-filter MID model rather than the STA. Interestingly, the 2-filter MID model displayed significant prediction improvements over the STA despite the fact that MID1 showed no prediction gains over the STA and the MID1,2 showed no prediction gain over MID1. We take this result to indicate that the 2-filter MID model is predominantly useful for characterizing MGBv neurons that are not already adequately modeled by MID1.

Discussion

Multifeature processing by individual neurons has been demonstrated in a variety of sensory systems and in many different animal models. At least 2 relevant RF filters have been identified for fly H1 neurons (Brenner et al. 2000), salamander retinal ganglion cells (Fairhall et al. 2006), rat barrel cortex (Maravall et al. 2007), and macaque visual neurons (Rust et al. 2005; Fitzgerald et al. 2011; Rowekamp and Sharpee 2011). Several studies have also shown the presence of multidimensional filters in A1 of cats (Atencio et al. 2008, 2009, 2012; Atencio and Sharpee 2017) and ferrets (Harper et al. 2016; Rahman et al. 2019) as well as in birds (Sharpee et al. 2011b; Kozlov and Gentner 2016).

Specifically, MID RF analysis was applied to recover multiple features in cat A1 neurons (Atencio et al. 2008, 2009, 2012), and our current A1 results showed good correspondence to our previous results. MID models, however, had not been derived for MGBv or cortical fields other than A1. Our goal was to assess the potential emergence and/or transformation of multifeature processing across 3 auditory forebrain areas, MGBv, AAF, and A1, in comparison to observations in the auditory midbrain that had yielded little evidence of multidimensional RFs (Atencio et al. 2012).

Our results show that 2-filter models in cat core auditory fields A1 and AAF capture significantly more stimulus information than in the lemniscal midbrain and thalamus, indicating a qualitative transformation of signal processing at the cortical stage. AAF neurons display information gains from the 2-filter MID model similar to those observed in A1, but the gains are slightly less than for A1 relative to the one-filter models in ICC and MGBv neurons. Unlike for the cortical fields, the one-filter model for MGBv neurons captures most of the explainable information, similar to results found for ICC neurons (Atencio et al. 2012). It should be noted that we previously (Atencio et al. 2009) had observed higher MID1,2 synergy values and lower MID1 contributions in A1 than in the current sample. In the first studies, we noted that we estimated MIDs for neurons that had a significant STA. In the current study, we were more conservative, and merely incorporated neurons if they modulated their firing rates to repeated trials of the same stimulus, without regard to whether we obtained an STA for the neuron.

Three general aspects of signal processing captured by multiple neuronal filters and their associated nonlinearities can be identified and compared across the studied forebrain stations (Tables 2 and 3): cooperativity, manner, and content.

Table 2.

Filter-property differences within 3 forebrain stations

Processing aspect	Parameter	MG	A1	AAF
Cooperation	Sufficiency	MID1 > STA	MID1 > STA	MID1 > STA
Cooperation	Synergy
Manner	NL asymmetry	STA, MID1 > MID2	STA, MID1 > MID2	STA, MID1 > MID2
Manner	NL threshold
Manner	NL transition
Content	Information	MID1 > STA, MID2	MID1 > STA, MID2	MID1 > STA, MID2
Content	Spectral integration	MID2 > MID1	MID2 > MID1
Content	Latency	MID2 > STA, MID1	MID2 > STA, MID1	MID2 > STA, MID1
Content	Temporal integration	STA > MID1	STA > MID1, MID2

Note: MG, ventral medial geniculate body. Statistical difference at P < 0.05 (either Kolmogorov–Smirnov test or ranked-sum test).

Table 3.

Filter-property differences between 3 forebrain stations

Processing aspect	Parameter	STA	MID1	MID2	MID1,2
Cooperation	Sufficiency	MG > A1, AAF	MG > A1, AAF
Cooperation	Synergy				A1, AAF > MG
Manner	NL asymmetry	MG > A1, AAF	MG > A1, AAF
Manner	NL threshold	MG > A1	MG > A1
Manner	NL transition	A1 > MG	AAF > MG
Content	Information	MG > A1, AAF	MG > A1, AAF	A1, AAF > MG
Content	Spectral integration	AAF > A1	AAF > A1
Content	Latency			A1, AAF > MG
Content	Temporal integration		AAF > MG

Statistical difference at P < 0.05 (either Kolmogorov–Smirnov test or rank-sum test).

“Cooperative processing” is expressed in the emergence and synergistic combination of multifilter features in cortical neurons and is a key aspect of processing transformations between subcortical and cortical neurons. This is demonstrated by the sufficiency measure that compares the stimulus information accounted for by a single filter to that jointly captured by 2 simultaneously acting filters. Both, in the ICC and the MGBv, the information captured by a single filter is nearly as high as that of a 2-filter model indicating that a second filter does not add significantly to the information processing (Table 3). By contrast, the second filter observed in A1 and AAF adds a significant amount of information that is not accounted for by the first filter alone. In addition, the active cooperation between the 2 filters, measured as synergy between the filters, is substantial in cortical neurons but essentially absent in ICC and MGBv. This lack of feature synergy in ICC and MGBv neurons likely reflects the weak information contributions by MID2 in these subcortical structures. Thus, if an ICC/MGBv neuron receives convergent input from neural populations encoding multiple features, but is not selective for any particular combination of those features, it can be adequately summarized in a single-filter model. The information gain and synergy results indicate that AAF and A1 both gain multifeature processing characteristics lacking in MGBv/ICC neurons. Thus, there appears to be a hierarchical evolution of RF dimensionality and feature cooperativity as neurons exhibit stronger multifeature processing at progressively higher levels in the ascending auditory pathway, with the main transition taking place between MGBv and cortex. This progression is expected on computational grounds because the invariant or at least robust representation of auditory objects in various background conditions requires that neural responses be tuned to conjunctions of features (Atencio et al. 2012). Because these findings are based on population averages, it is possible that portions of tectal and thalamic neurons do show stronger nonlinear response features (Escabí and Schreiner 2002; Williamson et al. 2016) that would benefit from modeling with second feature filters, especially in nonlemniscal regions.

“Manner of processing” is captured by the nonlinear relationship that determines how the match between stimulus and filter is converted into a firing rate. The asymmetry of the spiking NL function differed between STA/MID1 and MID2 (Table 2; Atencio et al. 2008). We observed highly asymmetric functions for STA/MID1s and a more symmetric form for MID2s in all 3 structures, indicating that MID2 filters were generally less sensitive than the STA/MID1 to the particular phase of spectrotemporal envelope feature. We interpreted these results as indicating that MID2 filters not only represent stimulus features distinct from the STA and MID1, but also process these features in a distinct manner as well. The high asymmetry of STA and MID1 nonlinearities in all 3 stations indicate that these filters act like feature detectors with high sensitivity to the envelope phase and tuned to a narrow range of stimulus constellations. The higher STA/MID1 asymmetry in MGBv (Table 2) shows that thalamic neurons are less tolerant of stimulus/filter mismatches than are cortical neurons.

Threshold values of the nonlinearities quantify the match required between spectrotemporal receptive field (STRF) and stimulus for the neuron to respond. High threshold values indicate high stimulus feature selectivity and reduced transmission noise. Thresholding with different values results in trade-offs in spiking fidelity and response throughput (Escabí et al. 2005). Thus, thresholding affects not only the average driven activity of a neuron, but also constrains the rate and specificity of the communicated information. The threshold distribution of MGBv neurons was shifted to higher values than in A1, indicating a higher thalamic feature selectivity. AAF and A1 had similar threshold distributions for STA/MID1 filters.

The transition parameter of the spiking NL relates neuronal stimulus preferences and intrinsic membrane properties. The smoothness of the transition point reflects the noise in spike generation mechanism (Ringach and Malone 2007). Low transition smoothness indicates that neurons respond in a manner that approximates hard rectification with little added ‘leakage’ noise. Higher values result in a noisier, more graded response to stimuli. For MID1 filters, MGBv neurons showed lower transition values, that is, less leakage noise, than AAF neurons, reflecting a more faithful signal transmission. This was also the case for STA filters when comparing MGBv to A1 neurons.

The third aspect of multidimensional RFs, “content processing”, relates to what stimulus characteristics are reflected in the 2 filters. First, the stimulus-based information captured by the filters differs between the 3 stations (Table 3). The STA and MID1 of MGBv neurons capture more information than those for A1 and AAF. This is potentially related to the fact that temporal processing in thalamic neurons is more precise and covers a wider bandwidth than in cortical neurons (Miller et al. 2002). By contrast, MID2 captures significantly more information both in A1 and AAF than in MGBv and, as previously shown, in the ICC (Atencio et al. 2012). This adds critical support for the notion that multifilter processing essentially emerges, or is significantly strengthened at the cortical level (Atencio et al. 2012).

We found that in MGBv, AAF, and A1 neurons, MID1 filters typically represented spectrotemporal features highly similar to those conveyed by the STA but with higher information content (Table 2). MID2 filters, on the other hand, represented stimulus features generally in a similar frequency region but uncorrelated to those of the STA and MID1, and thus captured feature processing previously unaccounted for by single-filter models. Other spectrotemporal processing differences between the stations include the wider spectral integration range of STAs and MID1s in AAF relative to A1 and a longer temporal integration of MID1s in AAF relative to MGBv, consistent with previous studies (Imaizumi et al. 2004; Miller et al. 2001). Furthermore, the weak MID2 filters in MGBv have a significantly shorter temporal integration range than those found in A1 and AAF. Overall, however, it appears that the content differences among filters across the 3 stations are less compelling than differences in relative strength of the 2 filters.

Potential Sources for Multiple Filter Generation

While our study does not serve to directly address the question how the 2 MIDs are generated, some of our results suggest likely hypotheses. A1 receives a wide range of corticocortical connections in addition to thalamocortical connections (Lee and Winer 2011) and is thus ideally situated to integrate sound information from a variety of feature sources. The origin of the 2-MID model likely is linked to convergent and cooperative thalamic and cortical inputs although the local or distributed contributing sources still need to be determined.

We found that MID2 processing in cortical areas typically had longer latencies compared with STA and MID1 processing. One possible explanation for this is that cortical MID2 filters reflect the influence of corticocortical and/or nonlemniscal thalamic connections while cortical STA and MID1 are dominated by feed-forward influences from the auditory thalamus. AAF and A1 both receive significant corticofugal projections from other auditory cortical areas (Rouiller et al. 1991; Lee and Winer 2011), and these projections are likely to provide long-latency input that contributes to shaping the stimulus processing of the neuron. As AAF and A1 share a fair degree of reciprocal connectivity (Rouiller et al. 1991; Lee and Winer 2011), MID2 filters in A1 may even be capturing influences from AAF, and vice versa.

Another possible explanation for the longer latencies in MID2 filters is that they capture influences from weak synapses while the STA and MID1 capture influences from stronger input connections. For most synapses, pairs of presynaptic spikes are more likely to drive spikes than isolated, single spikes (Usrey et al. 1998, 2000; Kara and Reid 2003; Shih et al. 2011). In weaker synapses that require pairs of spikes in order to elicit significant postsynaptic activity, registering the effect of the input spike pair requires waiting for the arrival of the second presynaptic spike, resulting in longer-latency responses from these connections.

Further supporting the suggestion that MID2 filters reflect influences from a different set of input connections than STA and MID1 filters, MID2 processing is often centered on frequencies over half an octave away from the peak frequencies of the STA and MID1. As MGBv, AAF, and A1 are all tonotopically organized and receive input from other tonotopic areas (Lee and Winer 2011), the STA and MID1 may represent the effects of nearby, frequency-matched connections, while MID2 represents the effects of more distal, off-frequency connections. This is compatible with our hypothesis that MID2 filters may be constructed from more remote inputs forming weaker or less synchronous synaptic activity. The density of synaptic connections is generally inversely related to the distance from a neuron (Yuan et al. 2011), so the more distal, off-frequency influences reflected in MID2 filters would generally come from a sparser collection of connections that may require more coincident presynaptic spiking in order to drive postsynaptic activity.

We also found that MID2 filters often integrate information over a broader spectral range than MID1 filters, indicating that MID2 may be particularly important for capturing the neural processing of broadband stimuli. Natural sounds, whether textured background sounds, speech, or music, are characteristically broadband (McDermott and Simoncelli 2011), so the broader spectral and temporal integration of MID2 filters as well as their envelope phase tolerance is an important complement to the narrower tuning and faster integration of MID1s.

MID2 components of AAF neurons were less effective than in A1 and may imply that AAF occupies a somewhat lower position in the auditory processing hierarchy than A1. This notion is supported by AAF’s slightly shorter response latencies and slightly higher temporal modulation preferences than A1 (Schreiner and Urbas 1988; Kowalski et al. 1995; Linden et al. 2003; Rutkowski et al. 2003).

We recorded only from the ventral division of the MGB, as the primary contributor of afferents to AAF and A1, which exhibits clear tonotopic organization (Imig and Morel 1985). However, projections from nonlemniscal thalamic stations to core cortical regions exist (Lee and Winer 2011) and may contribute to the formation of additional, cooperative filters. The medial and dorsal divisions of the MGB receive greater corticofugal input from nonprimary A1 than the ventral divisions (Winer et al. 2001). It is conceivable that neurons from these divisions may display significant multifeature processing properties due to cortical feedback that are less evident in ventral division neurons.

We used 2 MID filters as the maximum number of dimensions tested in our models, largely because of the heavy computational load required for MID analysis. We do not imply, though, that 2 filters are sufficient to model A1 neurons. Theoretically, the linear-nonlinear framework used in MID analysis can accurately model the entire set of dynamical, nonlinear, time-invariant systems classified as a Volterra series system, when using a sufficient number of linear filters (Marmarelis and Orme 1993; Marmarelis 1997). It is important to note, however, that the relative information and prediction gain of moving to the 2-filter model is significantly smaller than what is gained by using the one-filter MID instead of the STA. This suggests that there may be diminishing benefits from incorporating additional MID filters. Moreover, on a computational level, it has been suggested that MID analysis is only practical for recovering stimulus-response relationships of relatively low-dimensionality, that is, by employing only a few jointly activated filters. High-dimensional MID models, that is, with a larger number of joint filters, would require the collection of an exorbitant amount of data in order to adequately sample the distribution of spike-conditioned stimulus probabilities (Fitzgerald et al. 2011).

Our study demonstrates that the information benefits previously observed for A1 neurons also apply to another core cortical field, AAF. We find that A1 neurons display significantly stronger evidence of multifilter processing compared with neurons from MGBv and AAF. These results have implications for how sound information may be represented even further along the auditory pathway.

Multifilter processing is a manifestation of complex, nonlinear properties and is not unique to A1 but seems to first become relevant in the auditory forebrain; there were subsets of MGBv and, in particular, AAF neurons that benefited from the multidimensional model. Given that forebrain neurons with significant 2-filter MID models exist, an open question remains concerning what the advantages are for specific functional processing aspects, and how they impact processing in subsequent stations.

Author Contributions

Concept and design: J.Y.S., C.A.A., and C.E.S.; data collection: J.Y.S., K.Y., C.A.A., and C.E.S.; analysis: J.Y.S., C.A.A., and C.E.S.; and writing: J.Y.S., K.Y., C.A.A., and C.E.S.

Funding

National Institutes of Health (NIH) (grants DC002260 to C.E.S. and DC011874 to C.A.A.); Coleman Memorial Fund, and Hearing Research Inc. (San Francisco).

Notes

We thank Dr Brian Malone for helpful comments on the manuscript and Dr Mark Kvale for the use of his SpikeSort 1.3 Bayesian spike-sorting software. Conflict of Interest: The authors declare no competing financial interests.