Inference for Constrained Estimation of Tumor Size Distributions

Summary.

In order to develop better treatment and screening programs for cancer prevention programs, it is important to be able to understand the natural history of the disease and what factors affect its progression. We focus on a particular framework first outlined by Kimmel and Flehinger (1991, Biometrics, 47, 987–1004) and in particular one of their limiting scenarios for analysis. Using an equivalence with a binary regression model, we characterize the nonparametric maximum likelihood estimation procedure for estimation of the tumor size distribution function and give associated asymptotic results. Extensions to semiparametric models and missing data are also described. Application to data from two cancer studies is used to illustrate the finite-sample behavior of the procedure.

1. Introduction

In screening studies involving cancer, the goal is to detect the cancer early so that treatment can lead to a consequent reduction in mortality of the disease. Evaluating the impact of a screening program is difficult. The gold standard for evaluation is a randomized clinical trial in which participants are randomized to either a screening or control protocol. However, such trials are expensive and of long duration. As a result, this necessitates consideration of data from observational studies and cancer databases.

One such example comes from data from the Surveillance, Epidemiology and End Results (SEER) database analyzed by Verschraegen et al. (2005) for breast cancer. Their focus was on modeling the effect of tumor size on breast cancer survival. They consider data on women diagnosed with primary breast cancer between 1988 and 1997 with a lesion graded T1-T2. We focus on an alternative question than that posed by Verschraegen et al. (2005), that of associating tumor size with cancer progression.

An important example of a progression endpoint in cancer is metastasis. There have been proposals for correlating size of tumor with the probability of detecting a metastasis (Kimmel and Flehinger, 1991; Xu and Prorok, 1997, 1998). These authors focused on estimation of the distribution of tumor size at metastatic transition. Kimmel and Flehinger (1991) gave two limiting cases in which the distribution is identifiable. They then provided estimators of this quantity. Xu and Prorok (1997, 1998) developed estimators based on slight modifications of the assumptions utilized by Kimmel and Flehinger (1991).

We focus on the second limiting scenario of Kimmel and Flehinger (1991). It turns out that for this problem, estimating the distribution function of tumor size at metastatic transition corresponds to using a binary regression model with monotonicity constraints. Based on this regression model, we characterize nonparametric maximum likelihood estimation (NPMLE) procedures. Although the estimation procedure dates back to Ayer et al. (1955), no method of variance assessment has been given in the work of Kimmel and Flehinger and of Xu and Prorok. The structure of this article is as follows. In Section 2, we describe the observed data structures and probability model of Kimmel and Flehinger (1991). In Section 3, we describe the NPMLE procedure, along with the associated asymptotic results. In Section 3.3., three methods of confidence interval construction are also provided. Extensions for parametric effects and missing data are discussed in Section 4. We next describe a monotone smoothing spline approach given by Ramsay (1998) that is used for comparison. The finite-sample properties of the estimators are assessed using simulation studies, reported in the Web Appendix. In addition, the proposed methodologies are applied to datasets from two cancer studies in Section 6. We conclude with some discussion in Section 7.

2. Kimmel and Flehinger Framework and Previous Work

We begin by providing a review of the proposal of Kimmel and Flehinger (1991). Let S denote the size of the tumor of detection and δ be an indicator of tumor metastasis (i.e., δ = 1 if metastases are present, δ = 0 otherwise). We observe the data (S_i, δ_i), i = 1,...,n, a random sample from (S, δ). We now state the model assumptions utilized by Kimmel and Flehinger (1991). First, primary cancers grow monotonically, and metastases are irreversible. Let λ₁(x) denote the hazard function for detecting a cancer with metastasis when the tumor size is x. Let λ₀(x) denote the hazard function for detecting a cancer with no metastases when the tumor size is x. Assume that λ₁(x) ≥ λ₀(x). Finally, the cancer samples are characterized by the primary tumor sizes at which metastatic transitions take place. We will denote Y as the random variable for this quantity. Let the cumulative distribution function (cdf) of Y be denoted by F^Y.

The goal is to estimate F^Y. Based on the observed data (S, δ), Kimmel and Flehinger (1991) proposed two scenarios in which F^Y is estimable. Xu and Prorok (1997) showed the general nonidentifiability of the Kimmel-Flehinger model through some simple numerical examples. In this and later work (Xu and Prorok, 1998), they provided some further assumptions needed to guarantee the general identifiability of the distribution functions.

Kimmel and Flehinger (1991) make two simplifying assumptions under which F^Y becomes identifiable. The first situation is when detection of the cancer is not affected by the presence of metastases. The second is when cancers are detected immediately when the metastasis occurs. They refer to these situations as case 1 and case 2, respectively. As shown by Ghosh (2006), these correspond to the situations in which tumor size is treated as an interval-censored and a right-censored random variable, respectively. Here we focus on the case 1 scenario. We focus on case 1 rather than case 2 because Ghosh (2008) has recently shown that restrictive assumptions are needed for validity of the case 2 situation, such as tumor growth being a deterministic function of time.

3. Nonparametric Isotonic Regression Procedures

3.1. Data and Model

We study the effects of the tumor size on the risk of metastasis through the following nonparametric regression model:

$$\mathrm{Pr}(\delta =1|S)=G(S),$$ (1)

where G is assumed to be monotonically increasing and continuously differentiable on [0, ∞) with G(0) = 0 and ${\lim }_{z\to \infty }G(z)=1$. We are interested in making inferences on G.

In comparing our framework to that of Kimmel and Flehinger (1991), it turns out that the model we have written down corresponds exactly to the case 2 scenario. Note that the quantity on the left-hand side in model (1) can be equivalently expressed as Pr(Y < S | S) = F^Y (S). Because we are restricting the right-hand side of (1) to be monotone increasing in S, the quantity we are modeling here is precisely the distribution function of tumor size at metastatic transition, that is, G = F^Y. The main advantage of expressing it in the form of (1) is that regression extensions are immediate; we consider them further in Sections 4.1 and 4.2. Note that we are modeling the effect of S on δ using a binary regression model with identity link. We will comment on the choice of the link in the discussion in Section 7.

A referee raised a comment about the feasibility of estimating F^Y directly based on the observed data. Using the likelihood construction given in Kimmel and Flehinger (1991), we can write

$$G(s)=\frac{g(s,0)}{g(s,0)+g(s,1)},$$

where g(s, 0) = λ₀(s) exp{− $\underset{0}{\overset{s}{\int }}{\lambda }_0(u)du$} {1 − F^Y (s)} and g(s, 1) = λ₁(s) $\underset{0}{\overset{s}{\int }}$ exp [− $\underset{0}{\overset{y}{\int }}$ λ₀ (u) du − $\underset{y}{\overset{s}{\int }}$ λ₁(t) dt] f^Y (y) dy.

Note that estimation of F^Y based on G, while making no parametric assumption on {λ₀(s), λ₁(s)}, is not possible because of the inherent nonidentifiability of the problem. Although it seems that adding the constraint of monotonicity of G should help in improving the estimation of F^Y it appears that the model is still not identifiable. Differentiation of G and imposing the monotonicity constraint is equivalent to requiring that g′(s, 0)g(s, 1) > g′(s, 1)g(s, 0), with g′ being the derivative of g. By the product rule, this leads to ordering conditions on products of the densities corresponding to (λ₀, λ₁) and F^Y. As described in Xu and Prorok (1997), sufficient conditions for identifiability require even stronger conditions on λ₀, λ₁, and F^Y. We thus consider the case 2 limiting scenario of Kimmel and Flehinger (1991) and treat F^Y and G interchangeably here and in the sequel.

Let (δ₁, S₁), (δ₂, S₂),...,(δ_n, S_n) be n independent and identically distributed (i.i.d.) observations from the model in (1). The joint density of (δ, S) is given by

$$p(\delta ,s)={\{G(s)\}}^{\delta }{\{1-G(s)\}}^{1-\delta }h(s),$$ (2)

where h(·) is the density function of S. The likelihood function for the data, up to a multiplicative constant not involving h, is given by

$$L_n({\{{\delta }_i,s_i\}}_{i=1}^n)={\mathrm{\Pi }}_{i=1}^n{\{G(s_i)\}}^{{\delta }_i}{\{1-G(s_i)\}}^{1-{\delta }_i},$$ (3)

Observe that we must constrain G to be monotone increasing, which will complicate the NPMLE procedure.

Before giving the characterization of the NPMLE, we note that an alternative approach to estimation in model (1) is nonparametric smoothing techniques, such as those proposed in Ramsay (1998). However, there are limitations to such procedures. First, these procedures involve a smoothing parameter, whereas the procedure described in Section 3.2 does not. Because of the presence of the smoothing parameter, it is difficult to provide asymptotic results associated with the smoothing-based estimators. In Section 5, we describe the smoothing-spline-based method of Ramsay (1998). We compare it to the NPMLE procedure in a small simulation study in Web Appendix B.

In Section 3, we provide several theoretical results concerning the NPMLE. Although Kimmel and Flehinger (1991) also gave the NPMLE, we provide it here for completeness and also to motivate the proposed confidence set construction methods.

3.2. Nonparametric Maximum Likelihood Estimation and Asymptotic Results

We now consider estimation in (1) by nonparametric maximization of (3). Results from the literature on isotonic regression (Ayer et al., 1955; Robertson, Wright, and Dykstra, 1988) allow us to characterize the NPMLE of G. Let S_(i) denote the ith smallest value of the tumor size and let δ_(i) denote the corresponding indicator (i = 1,...,n). For arbitrary points $P_0\equiv (0,0),P_1\equiv \left(p_{1,1},p_{1,2}\right),\dots ,P_k\equiv (p_{k,1},p_{k,2})$ in R², we will denote by slogcm ${\{P_i\}}_{i=0}^k$ the vector of slopes (left derivatives) of the greatest convex minorant (GCM) of the piecewise linear curve that connects P₀, P₁,...,P_k in that order, computed at the points ${\{p_{i,1}\}}_{i=1}^k$. One characteristic of the NPMLE of $G,{\widehat{G}}_n$, is the right-continuous piecewise constant increasing function that satisfies $G(S_{(i)})={\widehat{u}}_i$ where

$$\left({\widehat{u}}_1,{\widehat{u}}_2,\dots ,{\widehat{u}}_n\right)=\mathrm{slogcm}{\left\{i,\sum _{j=0}^i{\delta }_{(j)}\right\}}_{i=0}^n,$$

and $S_{(0)}={\delta }_{(0)}=0$. Note that NPMLE is uniquely determined only up to its values at the S_i, i = 1,...,n; this is analogous to the ordinary empirical cdf. We now state the asymptotic distribution of the MLE of G(s₀) in model (1). This following result can be proven using arguments paralleling those in the proof of Theorem 5.1 of Groeneboom and Wellner (1992, p. 89).

Lemma 1.

The MLE ${\widehat{G}}_n(s_0)$ has the following limiting distribution:

$$n^{1/3}\{{\widehat{G}}_n(s_0)-G(s_0)\}{\to }_d{\left[\frac{4g(s_0)G(s_0)\{1-G(s_0)\}}{h(s_0)}\right]}^{1/3}Z\equiv CZ,$$

where g(s₀) is the derivative of G evaluated at s₀, and Z is the location of the minimum of W(t) + t²; here W is a standard two-sided Brownian motion starting from 0.

Lemma 1 yields a complicated form for the limiting distribution of the MLE. By contrast, for most statistical estimation problems in which classical regularity conditions are satisfied, the MLE converges at an n^1/2 rate. In addition, the limiting distribution of the NPMLE, properly normalized, is much more complicated than the normal distribution found for regular estimation problems. We will later consider construction of Wald-type confidence intervals based on this result.

To construct likelihood ratio-based confidence intervals, which we discuss in Section 3.3, requires characterization of the constrained MLE of G subject to $G(s_0)={\theta }_0$, which we denote as ${\widehat{G}}_n^0$. Define a ∧ b and a ∨ b to be the minimum and maximum of two real numbers a and b. We construct the vector of slopes of the GCM: $({\tilde{u}}_1^0,\dots ,{\tilde{u}}_m^0)=\mathrm{slogcm}{\{i,\sum _{j=0}^i{\delta }_{(j)}\}}_{i=0}^m$, and

$$({\tilde{u}}_{m+1}^0,\dots ,{\tilde{u}}_n^0)=\mathrm{slogcm}{\left\{i,\sum _{j=0}^i{\delta }_{(m+i)}\right\}}_{i=0}^{n-m},$$

where m is the number of values no greater than z₀. The constrained estimate ${\widehat{G}}_n^0$ is the right-continuous piecewise constant function that satisfies $G(S_{(i)})={\tilde{u}}_i^0\wedge {\theta }_0$ for $1\le i\le m$ and $G(S_{(i)})={\tilde{u}}_i^0\vee {\theta }_0$ for $m+1\le i\le n$. In order to state results about the asymptotic distribution of the likelihood ratio statistic for testing H₀: G(s₀) = θ₀, we will need some more notation. For positive constants a and b, define the process $X_{a,b}(s)\equiv aW(s)+b{s}^2$, where W(s) is the standard two-sided Brownian motion starting from zero. Let g_a,b(s) denote the GCM of X_a,b(s). Let G_a,b(s) be the right derivative of G_a,b(s); this can be shown to be a piecewise constant (increasing) function with finitely many jumps in any compact interval. We construct $G_{a,b}^0(s)$ in the following manner. When s < 0, we restrict ourselves to the set {s < 0} and compute $X_{a,b}(s).G_{a,b}^0(s)$ is the GCM of X_a,b(s), constrained so that its slope (right derivative) is nonpositive. When s > 0, we restrict ourselves to the set {s > 0} and compute $X_{a,b}(s).G_{a,b}^0(s)$ is the GCM of X_a,b(s), constrained so that its slope (right derivative) is nonnegative.

We have that $G_{a,b}^0(s)$ will almost surely have a jump discontinuity at zero. Let $g_{a,b}^0(s)$ be the slope (right derivative) of $G_{a,b}^0(s)$; this, like g_a,b(s), is a piecewise constant (increasing) function, with finitely many jumps in any compact interval and differing almost surely from g_a,b(s) on a finite interval containing zero. Thus, $g_{1,1}$ and $g_{1,1}^0$ are the unconstrained and constrained versions of the slope processes associated with the canonical process $X_{\text{1,1}}\text{(}s\text{)}$. The following result describes the joint limit behavior of the unconstrained and constrained MLEs of G, the constraint being imposed by the null hypothesis ${\text{H}}_0:G(s_0)={\theta }_0$. This can be proven using arguments similar to those in the proof of Theorem 2.6.1 of Banerjee and Wellner (2001):

Lemma 2.

Consider testing the null hypothesis ${\text{H}}_0:G(s_0)={\theta }_0$ with $0<z_0<\infty$ and $0<{\theta }_0<1$ and assume H₀ holds. Let

$$\begin{gathered} X_n(t)=n^{1/3}\{{\widehat{G}}_n(s_0+t{n}^{-1/3})-{\theta }_0\}and \\ {Y}_n(t)=n^{1/3}\{{\widehat{G}}_n^0(s_0+t{n}^{-1/3})-{\theta }_0\}. \end{gathered}$$

Suppose that G is continuously differentiable in a neighborhood of s₀ with g(s₀) > 0 and that h is continuous in a neighborhood of s₀ with h(s₀) > 0. Let

$$a={\left[\frac{G(s_0)\{1-G(s_0)\}}{h(s_0)}\right]}^{1/2}$$

and $b=g(s_0)/2$. Then

$$\begin{gathered} \{X_n(t),Y_n(t)\}\to \{g_{a,b}(t),g_{a,b}^0(t)\} \\ {\equiv }_d\left[a{(b/a)}^{1/3}{g}_{1,1}\{{(b/a)}^{2/3}t\},a{(b/a)}^{1/3}{g}_{1,1}^0\{{(b/a)}^{2/3}t\}\right] \end{gathered}$$

finite dimensionally and also in the space ${\mathcal{L}}_p[-K,K]\times {\mathcal{L}}_p[-K,K]$ for every K > 0 (p ≥ 1), where ${\mathcal{L}}_p[-K,K]$ is the set of functions that are L^p integrable on $[-K,K]$.

Based on this result, we can develop the asymptotic theory for the likelihood ratio test statistic ${\text{H}}_0:G(s_0)={\theta }_0$, whose inversion leads to confidence intervals for G(s₀).

Theorem 1.

If λ_n denotes the likelihood ratio, that is,

$${\lambda }_n=\frac{\prod _{i=1}^n{\{{\widehat{G}}_n(s_i)\}}^{{\delta }_i}{\{1-{\widehat{G}}_n(s_i)\}}^{1-{\delta }_i}}{\prod _{i=1}^n{\{{\widehat{G}}_n^0(s_i)\}}^{{\delta }_i}{\{1-{\widehat{G}}_n^0(s_i)\}}^{1-{\delta }_i}},$$

then the limiting distribution of the likelihood ratio statistic for testing ${\text{H}}_0:G(s_0)={\theta }_0$ is

$$2\log {\lambda }_n{\to }_d\mathcal{D}\equiv \int \left[{\{g_{1,1}(z)\}}^2-{\{g_{1,1}^0(z)\}}^2\right]dz.$$

A heuristic proof of this theorem is given in the Web Appendix. Note that the limiting distribution of Theorem 1 is much different from that in regular statistical problems, where 2 log λ_n converges to a ${\chi }^2$ distribution. The random variable $\mathcal{D}$ can be thought of as an analog of the ${\chi }^2$ distribution to nonregular problems. Although the pdf of $\mathcal{D}$ is of a complicated form, it can be tabulated or simulated relatively easily. For further details, see Banerjee and Wellner (2001).

3.3. Confidence Interval Construction

Three methods for confidence set construction are now described: (i) the Wald-based method; (ii) the subsampling-based method; and (iii) the likelihood-ratio-based method. Recall the limiting distribution of ${\widehat{G}}_n(s_0)$ from Section 3.2:

$$n^{1/3}\{{\widehat{G}}_n(s_0)-G(s_0)\}{\to }_d{\left[\frac{4g(s_0)G(s_0)\{1-G(s_0)\}}{h(s_0)}\right]}^{1/3}Z\equiv CZ.$$

Then it is fairly straightforward to construct a 95% confidence interval for G(s₀):

$$\{G_n(s_0)-n^{-1/3}{\widehat{Q}}_{.975},G_n(s_0)+n^{-1/3}{\widehat{Q}}_{.975}\},$$

where ${\widehat{Q}}_{.975}$ is a consistent estimator of $Q_{\text{.975}}$, the 97.5th percentile of the limiting symmetric random variable CZ. Using the results from Groeneboom and Wellner (2001), the 97.5th percentile of Z is 0.99818. We can then estimate C by

$${\widehat{C}}_n={\left[\frac{4{\widehat{g}}_n(s_0){\widehat{G}}_n(s_0)\{1-{\widehat{G}}_n(s_0)\}}{{\widehat{h}}_n(s_0)}\right]}^{1/3},$$

where ${\widehat{g}}_n$ and ${\widehat{h}}_n$ are estimates of g and h. An asymptotic 95% confidence interval is then given by

$$\{{\widehat{G}}_n(s_0)-n^{-1/3}{\widehat{C}}_n\times .99818,{\widehat{G}}_n(s_0)+n^{-1/3}{\widehat{C}}_n\times .99818\}.$$

The major drawback of the Wald-based intervals is the need to estimate g(s₀) and h(s₀). Because S is observed for all individuals, nonparametric density estimation methods can be used to estimate h(s₀). In this article, we use kernel density estimation for h, where the bandwidth is chosen by maximizing an asymptotic mean squared error criterion (Lehmann, 1999, Section 6.4). On the other hand, g(s₀) is much more difficult to estimate consistently. Due to the monotonicity constraints, we can only estimate G at O_p(n^1/3) support points, which means that we will never have sufficiently large sample sizes for estimating the derivative of G consistently. Here, we chose to use kernel density estimation of the NPMLE where the bandwidth is chosen as before. In simulations not given here, this approach gave better coverage probabilities for the 95% confidence intervals for the Wald approach relative to other proposals from the literature, such as a Weibull model (Keiding et al., 1996) and smoothing splines (Heckman and Ramsay, 2000).

The subsampling technique followed here is due to Politis, Romano, and Wolf (1999) and is part of a general theory for obtaining confidence regions. The basic idea is to approximate the sampling distribution of a statistic, based on the values of the statistic computed over smaller subsets of the data. We start by calculating the unconstrained MLE ${\widehat{G}}_n(s_0)$ for the observed dataset. This leads to the following algorithm:

1. Create a dataset $({\delta }_1^{*},S_1^{*}),\dots ,({\delta }_b^{*},S_b^{*})$, where $({\delta }_j^{*},S_j^{*})$ are a subset of the original data obtained by sampling without replacement, and b is the size of the subsampled dataset.

2. Calculate the unconstrained MLE ${\widehat{G}}_n^{*}(s_0)$ the subsampled dataset.

3. Repeat steps (1) and (2) several times.

By Theorem 2.2.1 of Politis et al. (1999), it follows that if b, $b,n\to \infty$, and $b/n\to 0$, then the conditional distribution of $n^{1/3}\{{\widehat{G}}_n^{*}(s_0)-{\widehat{G}}_n(s_0)\}$ converges to the unconditional distribution of $n^{1/3}\{{\widehat{G}}_n(s_0)-G(s_0)\}$ with probability one. This allows us to use the empirical distribution of $n^{1/3}\{{\widehat{G}}_n^{*}(s_0)-{\widehat{G}}_n(s_0)\}$ to construct confidence intervals. Although this appears to be a promising algorithm, a major issue is the choice of b. For the data example, we use a calibration algorithm, proposed in Delgado, Rodriguez-Poo, and Wolf (2001):

• (a)Fix a selection of reasonable block sizes between limits b_low and b_Up.
• (b)Generate K “pseudo-sequences” ${({\delta }_{ik}^{\star },S_{ik}^{\star })}_{k=1}^K,i=1^n$, which are i.i.d. ${\widehat{P}}_n$, with ${\widehat{P}}_n$ representing the empirical distribution function. This amounts to drawing K bootstrap samples from the actual dataset.
• (c)For each pseudodataset, construct a subsampling-based confidence interval for ${\widehat{\theta }}_n\equiv G_n(s_0)$ for each block size b. Let I_k,b be equal to 1, if ${\widehat{\theta }}_n$ lies in the kth interval based on block size b and zero otherwise.
• (d)Compute $\widehat{h}(b)=K^{-1}{\sum }_{i=1}^K{I}_{k,b}$.
• (e)Find $\tilde{b}$ that minimizes $|\widehat{h}(b)-(1-\alpha )|$ and use this as the block size to compute subsampling-based confidence intervals based on the original data.

The final method we consider is simple inversion of the likelihood ratio test statistic, whose limiting distribution under H₀ was derived in Theorem 1. Confidence sets of level 1 − α with 0 < α < 1 are obtained by inverting the acceptance region of the likelihood ratio test of size α; more precisely if 21og λ_n is the likelihood ratio statistic evaluated under the null hypothesis ${\text{H}}_0:G(s_0)=\theta$, then the set of all values of $\theta$ for which $2\log {\lambda }_n$ is not greater than $d_{\alpha }$, where $d_{\alpha }$ is the (1 − α)th percentile of $\mathcal{D}$, gives us an approximate (1 − α) confidence set for ${\theta }_0$. Denote the confidence set of (approximate) level 1 − α based on a sample of size n from the binary regression problem by $C_{n,\alpha }$. Thus $C_{n,\alpha }=\{\theta :2\log {\lambda }_n\le d_{\alpha }\}.$. Because we are inverting the likelihood ratio statistic, it achieves the correct coverage asymptotically.

4. Extensions

4.1. Adjustment for Covariates

In many situations, it might be the case that we need to adjust for other covariates in (1). Let us denote these by the p-dimensional vector Z. We now consider extending the methodology of Section 4. This would lead to a semiparametric version of (1):

$$\mathrm{Pr}(\delta =1|S,\mathbf{Z})=G_0(S)+{\beta }^T\mathbf{Z},$$ (4)

where β is a p-dimensional vector of unknown regression co-efficients. In (4), G₀ is the distribution function of tumor size at metastatic transition when Z = 0; β_j is the difference in distribution functions associated with a one-unit change in the jth component of Z, adjusting for the other covariates in the model.

Suppose we wish to perform semiparametric MLE in (4). For the purposes of estimation, we could use the method of profile likelihood (Murphy and van der Vaart, 2000). When Z is relatively low dimensional, we can use the arguments of Staniswalis and Thall (2001) to show that the following approach yields profile likelihood estimates:

1. For a given β, compute the residuals from a linear regression of δ on Z;

2. Compute the estimator of G₀ in (4) based on the residuals using the NPMLE method described in Section 3.2.

Performing these two steps over a grid of β values will yield the maximizers for the semiparametric likelihood corresponding to (4). For this model, we can use profile likelihood (Murphy and van der Vaart, 1997) to construct confidence intervals for β.

One limitation of the model is that the fitted probabilities from (4) might fall outside the interval [0,1]. This can be avoided by incorporating a link function for the probability in (4). However, the nonlinearity introduced into the model will make finding MLEs in the model more difficult and is beyond the scope of the article.

4.2. Two-Phase Sampling

We now consider the case where data have only been collected on a subset of tumors; this was also done in the work of Kimmel and Flehinger (1991) and Xu and Prorok (1997, 1998). The problem is reformulated similar to the case-control design with supplemented totals described in Scott and Wild (1997). We assume that there are N₀ tumors without metastases and N₁ tumors with metastases. At the first stage of the study, we collect information on N₀ and N₁. The second stage involves sampling a fraction of both classes of tumors (n₀ and n₁ sampled from the N₀ and N₁ tumors) and collecting $(S_i,{\mathbf{Z}}_i),i=1,\dots ,n$, at the second stage. Note that $n=n_0+n_1$.

What Scott and Wild (1997) were able to show was the equivalence of the retrospective likelihood for case-control sampling with a prospective “likelihood” in which the case-control sampling entered as offset terms. Assume model (1). Our application of the Scott-Wild algorithm is the following:

1. Let ${\widehat{\mu }}_0=n_0/N_0$ and ${\widehat{\mu }}_1=n_1/N_1$.

2. Calculate

   $$\tilde{G}(s)=\frac{{\widehat{\mu }}_0\widehat{G}(s)}{{\widehat{\mu }}_0(1-\widehat{G}(s))+{\widehat{\mu }}_1\widehat{G}(s)}.$$

Step 2 involves utilizing the estimation procedure described in Section 3.1, where the sampling design is taken into account by treating the sampling fractions $(n_0/N_0\text{and}{n}_1/N_1)$ as weights. A related estimator is given by Jewell and van der Laan (2004) for interval-censored data. We can use the subsampling scheme described in Section 3.3 to construct a confidence interval for G. Although the Wald-based or likelihood ratio test is implementable in theory, it is beyond the scope of this article.

Now suppose we wish to perform estimation in model (4). Then we could approximately adapt the approach of Section 4.1 by estimating residuals, followed by calculation of G. Subsampling could be used to construct intervals for the nonparametric component, whereas profile likelihood could be used to construct confidence intervals for β.

5. Nonparametric Monotonic Smoothing Procedures

An alternative approach to NPMLE estimation in (1) is to use smoothing splines, as suggested by Ramsay (1998). Because we compare this approach to NPMLE estimation in Section 6, we describe it briefly here. For ease of discussion, we work with (1). Let D{f(t)} = f′(t) denote the derivative operator and $D^{-1}\{f(t)\}={\int }_{-\infty }^{t}f(s)ds$ the integration operator. By Theorem 1 of Ramsay (1998), one can represent G in (1) as

$$G(s)=C_0+C_1{D}^{-1}[\exp (D^{-1}\{w(s)\})],$$

where C₀ and C₁ are constants and w(s) is the solution to the differential equation D(Df(s)) = w(s)Df(s). This reparametrization allows one to use an unconstrained parametrization for w using the penalized likelihood:

$$\sum _{i=1}^n{({\delta }_i-{\alpha }_0-{\alpha }_{1}m(S_i))}^2+\lambda {\int }_0^T\{w^2(t)\}dt,$$ (5)

where m(t) = D⁻¹exp{D⁻¹w(t)} and λ > 0 is a smoothing parameter. Note that m is uniquely determined by w and vice versa. Ramsay (1998) proposes using B-splines as a basis function space for estimation of w. Given λ, (α₀, α₁) are estimated by penalized least squares. The parameter α can be estimated by cross-validation.

In terms of inference regarding G, two types of intervals are output from the estimation algorithm. The first is a frequentist standard error that assumes G to be a fixed unknown function. The second is a Bayesian standard error that is constructed by assuming that G is a random quantity with a Gaussian process prior. In the simulation studies, we take the latter approach, as Wahba (1983) has shown this to give better coverage probabilities than those based on the former method.

6. Numerical Examples

6.1. Lung Cancer Data Revisited

In Web Appendix B, we describe the results of several simulation studies to assess the finite-sample properties of the various confidence set construction methods described in the article. We now apply the proposed methodologies to the lung cancer data examined by Kimmel and Flehinger (1991). The lung cancer data were collected on a population of male smokers over 45 years old enrolled in a clinical trial involving sputum cytology. There are two types of lung cancer diagnosed, adenocarcinomas (cancers that originate in epithelial cells) and epidermoid cancer (cancers that originate in the epidermis). For the adenocarcinomas, they were detected by radiologic screening and by symptoms; the epidermoids were detected by sputum cytology or by chest X-ray. Presence or absence of metastasis was determined using available staging, clinical, surgical, and pathological readings. There are 141 adenocarcinomas, of which 19 have metastases; of the 87 epidermoid cancers, 6 have metastases. As addressed in Section 4.2, a fraction of the tumors were not measured. We have included this information in Table 1.

Table 1.

Summary of missing values for lung cancer data

	Epidermoids		Adenocarcinomas
Status	Metastatic	Nonmetastatic	Metastatic	Nonmetastatic
Measured	6	81	19	122
Not measured	12	12	15	8

Note: Status refers to whether the tumor size is measured; “not measured” tumors are the analysis. Cell entries are the number of samples under each classification. Using the notation each classification. Using the notation from Section 4.2, N₀ = 223, N₁ = 52, n₀ = 203, n₁ = 25.

We start by estimating model (1) separately for the adenocarcinomas and epidermoids. This is given in Figure 1. We notice that the smoothing-spline-based estimator tends to be negatively biased relative to the NPMLE estimators. Given this finding and the results in the simulation study, we chose to focus on the NPMLE-based procedures here.

Figure 1.

Estimated fits from model (1) for (A) adenocarcinomas and (B) epidermoids. Solid line on each plot represents NPMLE fit, whereas dashed line represents monotone smoothing spline fit using the method of Ramsay (1998).

Next, we treat site of origin (adenocarcinoma/epidermoid) as a single covariate in a semiparametric regression model. It is coded 1 for epidermoids and zero for adenocarcinomas. We first ignore the missing data aspect and fit the model (4). Based on the estimation procedure in Section 4.1, we obtain an estimated regression coefficient of 0.22 with a 95% Cl of (0.01,0.36). This suggests that there is a marginally significant effect of site of origin on risk of metastasis; epidermoid tumors are associated with increased risk of metastasis relative to adenocarcinomas. We also have summarized the estimate of G in (4) at three points and have provided 95% confidence limits based on the subsampling and likelihood ratio inversion methods. We find that the likelihood ratio method gives slightly smaller intervals than the subsampling.

Then we consider the two-phase strategy outlined in Section 4.2. Using profile likelihood to estimate β, we get an estimated regression coefficient of 0.19 with a 95% Cl of (0.02,0.27). The estimate of G in (4) under the case-control sampling scheme, along with associated 95% confidence intervals, is given in Table 2. We qualitatively get the same conclusions here as in the previous paragraph.

Table 2.

Estimator of G from (4) for lung cancer data

s0	$\widehat{G}(s_0)$	95% CI (S)	95% CI (LRT)	$\tilde{G}(s_0)$	95% CI (S)
0.2	0.00	(−0.09,0.08)	(−0.07,0.06)	0	(−0.12,0.13)
3	0.02	(−0.05,0.07)	(−0.03,0.04)	0.01	(−0.06,0.09)
9	0.15	(0.01,0.32)	(0.03,0.28)	0.09	(0.01,0.18)

In terms of the analysis of these data relative to those by previous authors (Kimmel and Flehinger, 1991; Xu and Prorok, 1997), our novel contributions are to provide confidence intervals for the distribution functions as well as regression co-efficients and standard errors summarizing the effect of site of origin on the tumor size distribution at metastatic transition.

6.2. Breast Cancer Dataset

Although we have discussed modeling the distribution function for tumor size at metastasis so far, the approach described in Sections 3 and 4 can be incorporated with other histopathological variables. As an example, we consider breast cancer, in which lymph node status is considered to be one of the most important prognostic factors for overall survival (Amersi and Hansen, 2006). Lymph node startus is typically treated as a binary variable; positive lymph node status is associated with poorer patient survival in breast cancer and breast cancer metastasis. Here, we will take δ to be an indicator of nodal involvement (δ = 1 indicates nodal involvement or node-positive breast cancer; δ = 0 represents no nodal involvement or node-negative breast cancer). In this example, what we will be modeling is the distribution function for tumor size for transition to nodal involvement.

We now return to the breast cancer study referred to in the Introduction. The data we consider are on n = 83,686 cases. They represent women diagnosed with primary breast cancer between 1988 and 1997 with a lesion graded T1-T2 but who did not have a metastasis based on the axillary node dissection results. Of the 83,686 cases, 58,070 were node negative, whereas 25,616 were node positive. Because both states (nonnodal and nodal-involved breast cancer) are typically asymptomatic, the previously proposed framework would be a reasonable assumption here. Note that we are now modeling the distribution of tumor size at transition from nonnodal involvement to nodal involvement. One issue in the analysis is that there are many ties in the data; we jittered the data by adding an independent N(0, 1) random variable.

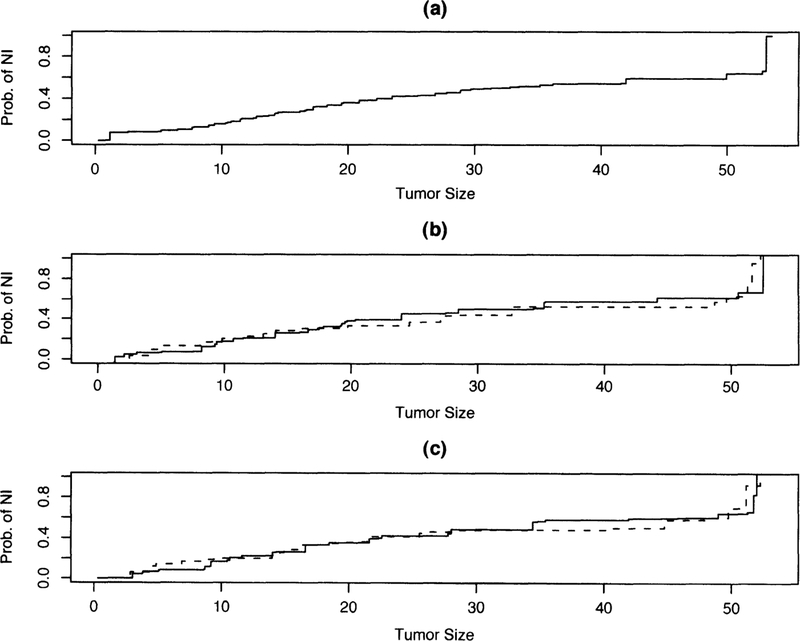
In this analysis, we focus on the following covariates: estrogen receptor (ER) status (positive/negative), and progesterone receptor (PR) status (positive/negative). Plots of the tumor size distribution for the overall population, along with those stratified by ER and PR status, are given in Figure 2. Note that there are no missing data here, so we will be fitting the semiparametric regression models of the form (4) with no case-control sampling. There will typically be no case control/two-phase sampling with data, such as those from the SEER database.

Figure 2.

Distribution function for tumor size at nodal transition for breast cancer SEER data. Figure 2a displays the estimated distribution function for the entire population. Figure 2b shows estimated distribution function stratified by ER status (solid line represents ER-positive cancers, dashed line represents ER-negative cancer). Figure 2c shows estimated distribution function stratified by PR status (solid line represents PR-positive cancers, dashed line represents PR-negative cancers).

We fit a series of three regression models of the form (4). The first was fitting PR status as one covariate; the second was fitting ER status as a covariate; the final model was including both as covariates. The estimates are summarized in Table 3. Based on the results, we find that ER-negative tumors are associated with increased risk of metastasis relative to ER-positive tumors. Alternatively, the probability of metastatic transition is on average 0.3 higher for ER-negative tumors than for ER-positive tumors. Similarly, the probability of metastatic transition is on average 0.02 higher for PR-negative tumors than for PR-positive tumors. Finally, although the results of the univariate regression results are statistically significant, the predictors are not significant in the multiple regression results. This is because of the high correlation between ER and PR status; the odds ratio between these two status variables is 38.8 and is highly significant. Given that the other variable is in the model, either ER or PR status does not significantly add information on prediction of metastasis.

Table 3.

Single covariate and multiple covariate regression results for breast cancer data

	Univariate		Multivariate
Biomarker	$\widehat{\beta }$	95% CI	$\widehat{\beta }$	95% CI
ER status	−0.033	(−0.049, − 0.021)	−0.01	(−0.024, 0.030)
PR status	−0.019	(−0.029, −0.009)	−0.01	(−0.035, 0.020)

Note: ER status coded 1 for ER positive and 0 for ER negative. A similar approach was taken for PR status. Univariate refers to fitting each covariate separately, whereas multivariate refers to fitting one model with both ER std PR status.

7. Discussion

In this article, we have developed general inference procedures for monotonic regression models for the analysis of tumor size-progression data in cancer databases. We have utilized NPMLE estimation in this model and have provided theoretical results based on both Wald and likelihood ratio test statistics in this model. Although the NPMLE method was originally proposed by Ayer et al. (1955) and adapted to the current setting by Kimmel and Flehinger (1991), the inferential procedures proposed in this article are new. In addition, we have described novel extensions to case-control sampling and semiparametric regression. Because we are using profile likelihood methods throughout, we expect the methods to be fully efficient. The simulation study seems to indicate that the likelihood ratio test statistic tends to have better behavior in small samples than does the Wald statistic. This observation has also been made by Murphy and van der Vaart (1997) for semiparametric models as well.

Here, we have assumed the identity link throughout the manuscript. If we were to use a different link, then this would lead to a different characterization for the NPMLE. Potentially, a more interpretable link than the identity link in (1) would be to use the logistic link. This would lead to a more complicated form for characterizing the NPMLE in both the nonparametric and semiparametric situations. Estimation and inference in this setting are currently under investigation.

It should also be noted that we have incorporated the monotonicity assumption in (1) and (4) in a very strong manner. Thus, the data should be collected for subjects who have not received any treatment. For example, in prostate cancer studies, some men might receive hormone treatment; this has the effect of reducing the size of the tumor in the prostate. Thus, a model such as (1) would not be appropriate for this scenario.