Strengthened Temporal Coordination within Pre-existing Sequential Cell Assemblies Supports Trajectory Replay

SUMMARY

A central goal in learning and memory research is to reveal the neural substrates underlying episodic memory formation. The hallmark of sequential spatial trajectory learning, a model of episodic memory, has remained equivocal, with proposals ranging from de novo creation of compressed sequential replay from blank slate networks to selection of pre-existing compressed preplay sequences. Here, we show that increased millisecond-timescale activation of cell assemblies expressed during de novo sequential experience and increased neuronal firing rate correlations can explain the difference between post-experience trajectory replay and robust preplay. This increased activation results from an improved neuronal tuning to specific cell assemblies, higher recruitment of experience-tuned neurons into pre-existing cell assemblies, and increased recruitment of cell assemblies in replay. In contrast, changes in overall neuronal and cell assembly temporal order within extended sequences do not account for sequential trajectory learning. We propose the coordinated strengthening of cell assemblies played sequentially on robust pre-existing temporal frameworks could support rapid formation of episodic-like memory.

In Brief

Farooq et al. demonstrate that time-compressed, internally generated sequential dynamics in the CA1 ensembles are modified by navigational experience primarily via persistent changes in experience-relevant short-timescale neuronal coordination on the framework of largely conserved long-timescale sequential dynamics to form a memory.

INTRODUCTION

Episodic memories are an essential component of our cognitive life (Tulving, 2002). The proposed mechanisms behind the precise remodeling of neuronal circuits supporting formation of episodic memories have, however, remained debated. The demonstration that the hippocampus is crucial for rapid learning and memory formation in humans (Scoville and Milner, 1957), non-human primates (Zola-Morgan et al., 1992), and other species, most notably rodents (Eichenbaum et al., 1999; Morris et al., 1986), sparked a major, concerted effort toward identification of electrophysiological signatures underlying these cognitive functions. Earlier reports revealed post-experience increases in spontaneous firing rate of hippocampal place cells encoding a spatial experience (Pavlides and Winson, 1989), which suggested that increases in firing rates are markers of memory (Martin et al., 2000). With the realization that experience is stored in neuronal ensemble patterns rather than single-cell activity (Wilson and McNaughton, 1993), subsequent studies began to address the nature of experience-induced functional interactions between hippocampal neurons, primarily using rodent CA1 place cells. Those studies proposed that spontaneous cofiring of CA1 cell pairs with overlapping place fields selectively increases in post-experience sleep (Dupret et al., 2010; Wilson and McNaughton, 1994).

The experience-driven changes in single-cell firing rate dynamics and in cofiring of neuronal pairs might not be sufficient to explain the phenomenological nature of episodic memory, which involves binding together multiple sequential events (Tulving, 2002). Hence, a new goal was set in the identification and analysis of place cell sequences. In particular, the replay of place cell sequence order (Lee and Wilson, 2002; Skaggs and McNaughton, 1996) and of animal trajectory (Davidson et al., 2009; Karlsson and Frank, 2009) on linear tracks in post-experience sleep was proposed to represent the ensemble signature for learning and memory in the CA1. In its classic formulation, this proposal posits that experience of novel or familiar place sequences leads to the de novo creation of compressed temporal sequences of firing, i.e., theta sequences (Dragoi and Buzsáki, 2006; Skaggs et al., 1996), from a blank slate network (Lee and Wilson, 2002; Silva et al., 2015), which are recurrently replayed at high rates during the post-experience sleep.

In contrast with this view, however, extended preconfigured neuronal temporal sequences have been observed to occur spontaneously in naive animals prior to and correlated with a de novo spatial experience, a phenomenon termed preplay (Dragoi and Tonegawa, 2011, 2013b), subsequently confirmed by several studies (Grosmark and Buzsáki, 2016;Ólafsdóttir et al., 2015). This preconfiguration was proposed to represent the hippocampal network identity largely facilitating rapid encoding of novel sequential information by a selection and editing of existing neuronal sequence motifs, which would eliminate the need for their de novo creation during the experience (Dragoi and Tonegawa, 2013c; Liu et al., 2018). The discovery of preplay redefined the long-lasting hippocampal signature of a memory for a recent novel experience, which would have to rely on the difference between post- and pre-experience spontaneous sequential activity (Dragoi and Tonegawa, 2013a; Farooq and Dragoi, 2019; Grosmark and Buzsáki, 2016), rather than on the observation of post-experience activity in isolation.

Owing to the variable nature of preplay sequences and their putative role in facilitation of rapid encoding, complex approaches have been employed to determine their statistical significance and through that their biological relevance. Recently, it has been proposed that preplay sequences might emerge merely due to the statistical variability in the stochastic single-cell firing rate dynamics of hippocampal pyramidal neurons during sleep rather than as a biological property of the network (Silva et al., 2015). An important implication of this statistical inference is that the hippocampus inherits temporal structure from the external world and that temporal dynamics in the neuronal networks supporting episodic-like memories are exclusively created during a novel experience and replayed for a limited time post-experience (Lee and Wilson, 2002; Silva et al., 2015). The two competing hypotheses regarding the nature of temporal sequences (i.e., internally generated versus externally driven) provide fundamentally different views on the role of the hippocampus in memory encoding and more generally in internally generated representations (Dragoi and Tonegawa, 2013c; Liu et al., 2018, 2019). Therefore, here, we first revisit this point of debate and provide multiple lines of evidence for robust preplay of future place cell and trajectory sequences in two independent datasets. At the same time, we propose that statistical oversights could lead to a masking of the preplay phenomenon, as reported recently (Silva et al., 2015).

More importantly, the existence of preplay trajectory sequences raises the fundamental question of how the novel experience modifies these time-compressed trajectory sequences and their expression during post-experience trajectory replay. Currently, decoding of animal trajectory based on ensemble neural activity, i.e., Bayesian decoding (Davidson et al., 2009; Karlsson and Frank, 2009; Zhang et al., 1998), is the most comprehensive statistical method to assess the ability of spontaneous network patterns (i.e., trajectory preplay and replay) to represent a sequential spatial experience. Bayesian decoding makes use of all the spiking activity of all neurons and, therefore, integrates firing rate (Pavlides and Winson, 1989), temporal coordination at millisecond timescales (van de Ven et al., 2016; adapted after Peyrache et al., 2009) and neuronal order dynamics (Lee and Wilson, 2002) altogether. However, which of these three neuronal coding schemes support the experience-induced plastic changes in neuronal ensemble activity remains to be established. Here, we perform simultaneous recordings from a large population of hippocampal neurons and use a repertoire of analytical methods and simulations to identify the hippocampal signature of a memory for a recent novel spatial experience. Our results demonstrate that de novo spatial experiences induce an experience-dependent reorganization of firing rates of hippocampal neurons and a strengthening of millisecond-timescale temporal coordination of neurons within pre-existing cell assembly sequences (Hebb, 1949). At the same time, temporal order of neuronal and cell assembly activation into sequences and the average neuronal firing rates are expressed similarly in the pre- and post-experience sleep. Altogether, we propose that replay is a result of plasticity (i.e., persistent changes in the network due to experience) at the short timescale (~20 ms) within hippocampal cell assemblies via reorganization of firing rates and increased coordination of neuronal spiking integrated into largely stable, sequential network dynamics.

RESULTS

Compressed Trajectory Sequence Preplay Precedes De Novo Spatial Experience

We recorded from neuronal ensembles in the dorsal hippocampal CA1 area using independently moveable tetrodes and silicon probes in experimentally naive Long-Evans adult male rats (n = 5) during their first reward-driven exploration of a novel linear track (de novo Run session). The Run session was preceded (i.e., Pre-Run) and followed (i.e., Post-Run) by extended (~2–4 h) sleep sessions (Figure 1A; Table S1; STAR Methods). We commenced our investigation by reconstructing the location of the animal on the track based on the spike trains from the population of recorded neurons at velocities exceeding 5 cm/s, using a Bayesian probabilistic framework (Davidson et al., 2009; Dragoi and Tonegawa, 2013b; Karlsson and Frank, 2009; Zhang et al., 1998). The neuronal population accurately represented the location of the animal during active Run behaviors (median error in decoded location: 7.6 cm versus 54.3 cm in shuffled datasets with permuted time bins, on a 1.5-m linear track during de novo run, using 250-ms time bins; Wilcoxon’s rank sum test: p < 10⁻¹⁰; Figures 1B, 1C, and S1; see Figures S2A–S2C for our results from an independent dataset; Grosmark and Buzsáki, 2016).

Figure 1. Robust Preplay of Future De Novo Run Trajectory during Pre-Run Sleep.

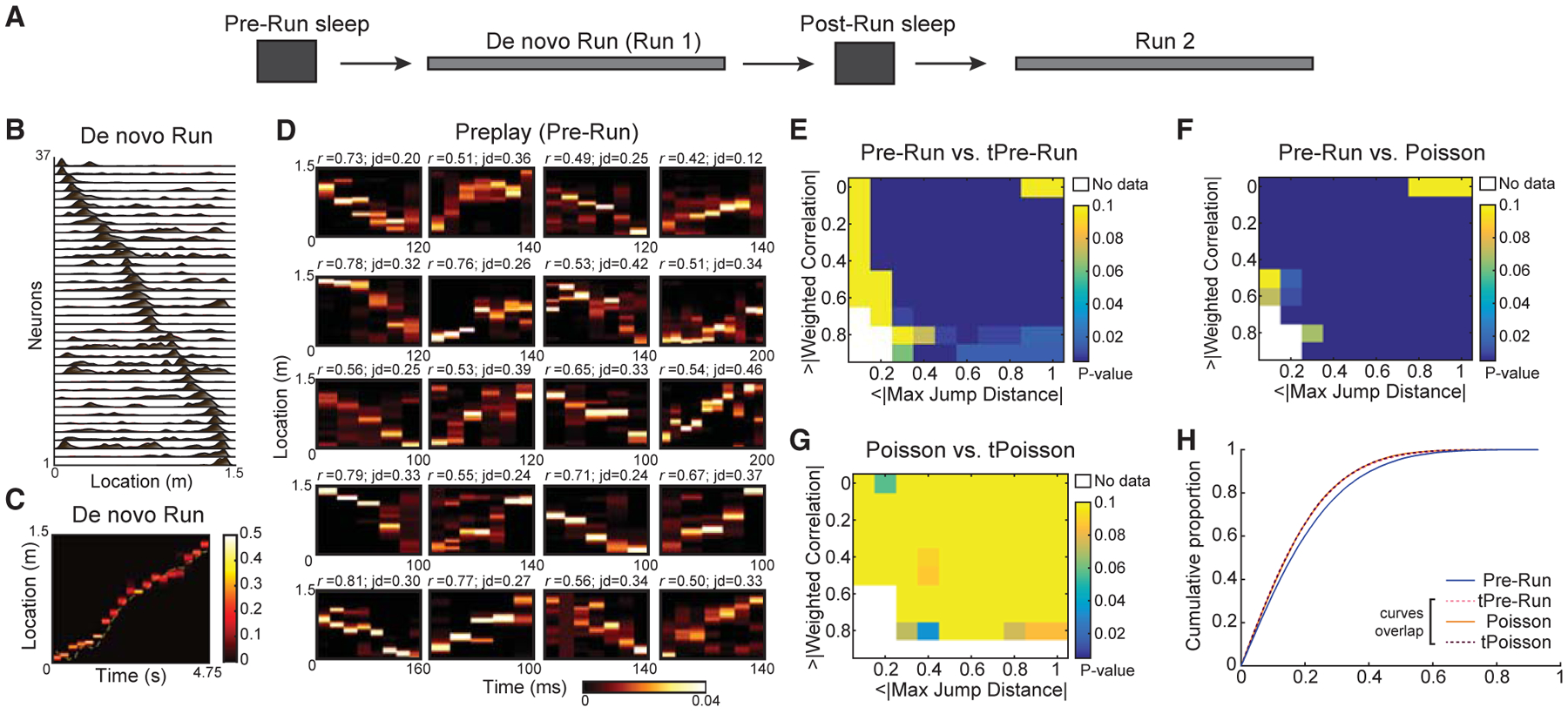
(A) Schematic of the experiment. An extended Pre-Run sleep was followed by a de novo Run session on a linear track (experimentally naive animals) followed by another sleep session (Post-Run sleep) and by a second run (Run 2) on the same track.

(B) Representative place cell sequences during de novo Run in one animal.

(C) Decoded animal location on the linear track in a representative lap during de novo Run based on ensemble neuronal activity using a memoryless Bayesian decoding algorithm.

(D) Representative preplay frames during Pre-Run sleep.

(E–G) Two-feature p value matrices testing significance of Pre-Run (n = 38,820 frames) versus time-bin shuffle, tPre-Run (E), Pre-Run versus five hundred rate-matched Poisson surrogate datasets (F), and Poisson dataset (n = 38,820 frames) versus its shuffle, tPoisson (G).

(H) Comparison of weighted correlations (n = 38,820 frames) of all Pre-Run sleep, tPre-Run, Poisson, and tPoisson data. Note that tPre-Run, Poisson, and tPoisson data have similar (overlapping) cumulative distributions of weighted correlations.

We addressed the hypothesis that trajectory sequences within Pre-Run sleep depict the future Run trajectory by first identifying epochs of heightened hippocampal population activity (termed frames; see STAR Methods) of naive animals during this sleep (Davidson et al., 2009; Dragoi and Tonegawa, 2011; Ji and Wilson, 2007). We defined “frames” as transient increases in the overall population activity of all recorded pyramidal neurons, such that the total activity in the population increased to at least two SDs above its mean. Only the frames spanning 100–800 ms and including activation of a minimum of 5 distinct place cells were used for further analysis (Table S2; STAR Methods). Importantly, in the Pre-Run sleep session, the animals were placed inside high-walled boxes devoid of any experience or exposure to the linear tracks, which were introduced into the room only at the end of the sleep (Dragoi and Tonegawa, 2013b). Using our decoding approach, for each frame in the Pre-Run sleep, we derived a set of time-compressed posterior probability distributions of spatial locations of the following Run trajectory at 20-ms time bin resolution. The strength of sequential representation in each frame was studied by computing the linear Pearson’s product-moment correlation of space-time weighted by the derived posteriors for the frame, called weighted correlation (STAR Methods). To quantify the continuity of spatial representation within trajectory sequences (i.e., the lack of “jumpiness” in space between adjacent decoded positions within trajectory sequences), we computed the maximum of jumps in decoded space between consecutive time bins (Silva et al., 2015) within a frame, called jump distance (Figure 1D; STAR Methods).

Simultaneous quantification of these two features (i.e., weighted correlation and the maximum of jump distances) against shuffled datasets lacking sequential structure has been proposed to accurately characterize trajectory sequences (Silva et al., 2015). Therefore, we simultaneously compared these two features of activity within frames in the Pre-Run sleep to shuffles generated using a commonly employed permutation method termed the time-bin shuffle (n = 500 shuffles). For all frames during sleep, the decoded posteriors in each time bin within a frame were randomly permutated within the frame. A comparison of Pre-Run and time-bin shuffle (i.e., tPre-Run) frames revealed that the Pre-Run sleep has significantly higher incidence of true preplay sequences (i.e., high correlations and low maximum jump distances) compared to shuffled tPre-Run sleep (Figure 1E). This indicates a robust pre-existing sequential structure in the Pre-Run sleep (Figure 1D for examples of preplay sequences; the p values are one-sided statistical comparisons of the proportions of frames in preplay and the shuffled datasets passing the corresponding thresholds for the two features; see STAR Methods).

It is conceivable that alternative sources of nonuniformity, i.e., differences in average firing rates of individual neurons during Pre-Run sleep frames, might lead to spurious masking of preplay in Pre-Run sleep (Silva et al., 2015). To control for this, we generated surrogate frames comprised of spike trains with Poisson distributions that have identical average firing rates of individual neurons across all frames compared to Pre-Run sleep frames (here called Poisson datasets). We directly compared Pre-Run sleep preplay sequences with 500 firing-rate-matched Poisson datasets. Our results revealed that Pre-Run sleep had significantly higher sequential structure than the Poisson data (Figure 1F), thus refuting the possibility that preplay is simply due to inhomogeneities in firing rates across neurons. Consistently, the Poisson data had similar sequential structure (or lack thereof) as its own time-bin shuffle (here called Poisson time-bin shuffle or tPoisson; Figure 1G) and as the time-bin shuffle of the Pre-Run data (i.e., tPre-Run; Figure 1H; average weighted correlations: preplay 0.1916 ± 7.6 × 10⁻⁴ versus tPre-Run 0.1709 ± 6.9 × 10⁻⁴, p < 10⁻¹⁰; Poisson 0.1701 ± 6.7 × 10⁻⁴ versus tPoisson 0.1698 ± 6.7 × 10⁻⁴, p = 0.53; preplay versus Poisson: p < 10⁻¹⁰; preplay versus tPoisson: p < 10⁻¹⁰; Poisson versus tPre-Run: p = 0.41; tPre-Run versus tPoisson: p = 0.84; Wilcoxon’s rank sum tests).

Next, we employed another commonly used method of shuffling data and shuffled the decoded probabilities in the sleep frames in the spatial domain (i.e., circular space-bin shuffle) rather in the temporal domain for both Pre-Run (here called sPre-Run) and Poisson (called sPoisson) data. This method also detected stronger sequential structure in Pre-Run sleep compared with sPre-Run shuffle (Figures S3A and S3B). However, upon closer examination, we found two methodological issues that cautioned us against using it further, as detailed in Figures S3 and S4. Briefly, the use of this shuffle can mislead to an interpretation that Pre-Run and Poisson data are similar only because they are both stronger than their own shuffles (Silva et al., 2015). Accounting for the issues with this shuffle revealed significant preplay (Figures S3 and S4; for details, see STAR Methods).

Overall, these findings show that Pre-Run preplay sequences have significantly greater sequential structure compared with firing-rate-matched Poisson datasets and statistically rigorous shuffles. The robustness of the preplay phenomenon is further demonstrated by its presence at the individual animal level (Figure S1) and by its maintenance when only the middle segment of the track in between reward locations or when the same day second experience on the now familiar track (i.e., Run2) were considered (Figure S5). Finally, we cross-validated our findings on the robustness of preplay and the statistical pitfalls of using the space-bin shuffle, using an independent dataset (Grosmark and Buzsáki, 2016) where preplay occurred during Pre-Run slow-wave sleep confirmed by simultaneous electromyography (Figure S2).

Improved Ensemble Representation of a Recent Experience by Trajectory Replay Sequences

Given that compressed trajectory sequences during slow-wave sleep (SWS) preplay future novel spatial experiences (Dragoi and Tonegawa, 2013b; Figure 1), we next studied whether and how a de novo spatial experience on a linear track affects the dynamics of hippocampal trajectory sequences. To avoid the confounding effects of a different behavioral and brain state and of online access to experiential external sensory cues (e.g., as during awake resting epochs on the track), we compared the properties of Pre-Run preplay with those of trajectory sequence replay expressed exclusively during the Post-Run sleep in the same sleep box (see Figure 2A for representative examples).

Figure 2. Temporally Compressed Replay Represents Run Trajectory Stronger than Preplay during Sleep.

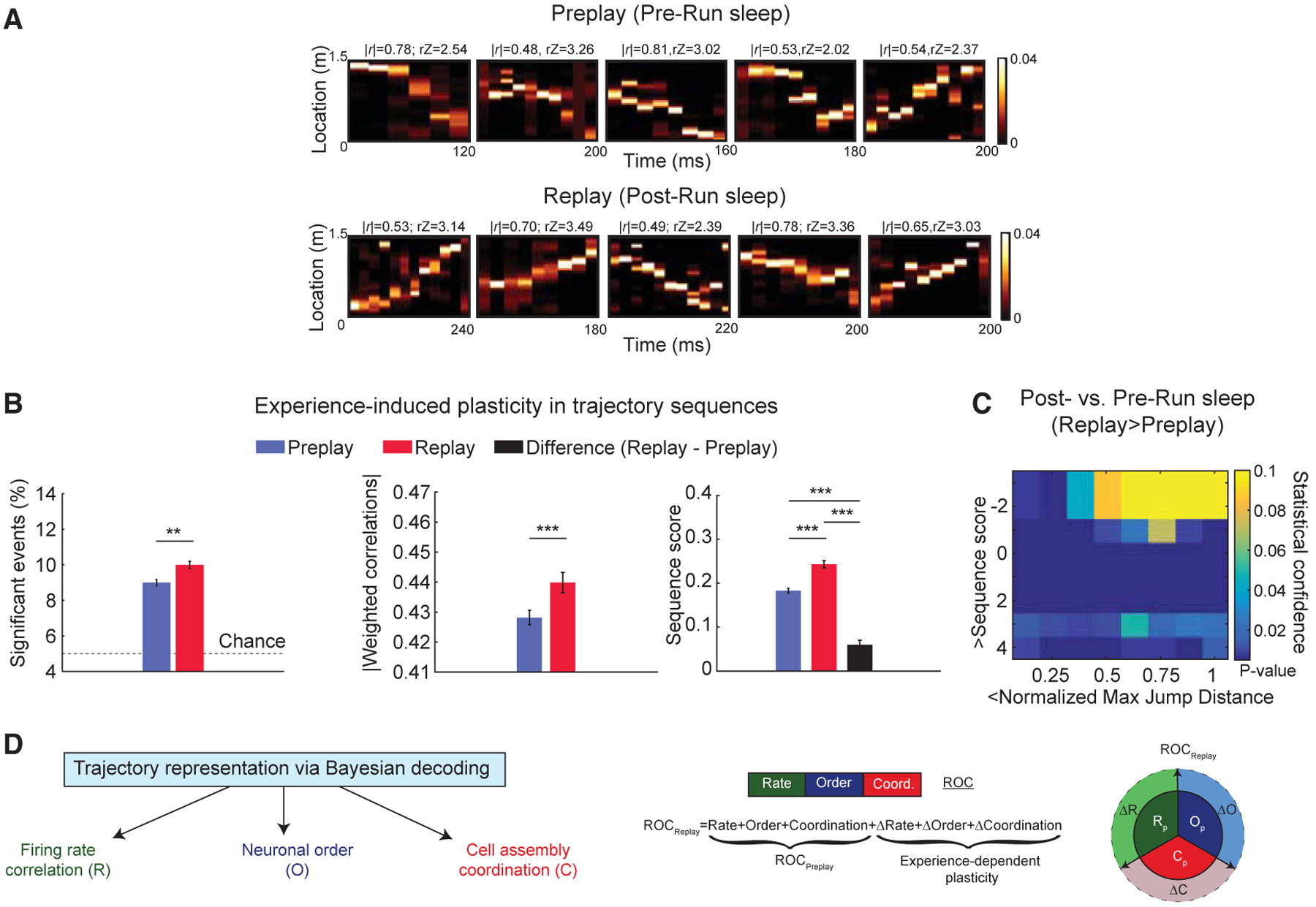
(A) Representative trajectory preplay (in Pre-Run sleep) and replay (in Post-Run sleep) at comparable frame durations using Bayesian decoding.

(B) Comparison of multiple features of trajectory preplay (n = 38,820 frames) and replay (n = 17,637 frames). (Left to right) Proportion of significant events, significant absolute weighted correlations, and sequence scores are shown (black bar: difference between Post- and Pre-Run sleep frames). **p < 0.01, ***p < 0.001. Data are represented as mean ± SEM.

(C) p value matrix of comparisons of sequence scores and normalized maximum jump distances between Pre- and Post-Run sleep frames depiction of de novo Run trajectories.

(D) Trajectory representation using Bayesian decoding is contributed by multiple types of neural codes: firing rate “R,” order of neurons into extended sequences “O,” and coordination of neurons into cell assemblies at millisecond timescales “C,” left. (Middle) Replay is inferred as an experience-related plastic transformation of preplay reflected at the level of the 3 neural codes (R, O, and C). (Right) Graphical representation of experience-induced changes in firing rates (ΔR), coordination of neurons (ΔC), and neuronal order (DO) is shown.

To assess the experience-dependent changes in trajectory sequences during sleep, we compared the strength of trajectory preplay and replay. We found that replay sequences had higher incidence and represented the Run experience stronger compared to preplay, as assessed by weighted correlations and sequence scores (i.e., weighted correlations Z scored by their respective time-bin shuffles) as shown in Figure 2B (Pre-versus Post-Run sleep, mean % significant frames: 9.00% ± 0.18% versus 10.00% ± 0.20%, p < 0.001, Wilcoxon’s signed rank test; mean weighted correlations 0.43 ± 0.0024 versus 0.44 ± 0.0034, p < 0.005; mean sequence score 0.1831 ± 0.0056 versus 0.2430 ± 0.0084, p < 10⁻⁷; Wilcoxon’s rank sum tests). Comparison using individual animal direction as unit of analysis was consistent with this finding (Pre- versus Post-Run sequence scores: p < 0.005; Wilcoxon’s signed rank test; n = 10; data not shown). Similar results were obtained when we employed stricter criteria for slow-wave sleep classification (Figure S6A). Interestingly, the sequential content in preplay exceeded the navigational-experience-induced increase in sequential content from preplay to replay (Figure 1B, right), indicative of a robust pre-existing sequential backbone that is also the primary contributor to the overall sequential activity observed in replay following a de novo experience (Liu et al., 2019). Additionally, we asked whether representation of trajectory sequences was a function of the duration to and from exposure to the track. We subdivided the data into two equal epochs (0 to 1 h and 1 to 2 h to and from experience) and studied each epoch separately. We found that both preplay and replay and their difference were similar across these two epochs with different durations to and from exposure to the track (Figure S6B). The improvement in replay over preplay was also observed when two features, strength and continuity in trajectory representation, were tested simultaneously across Pre- and Post-Run sleep (Figure 2C; see STAR Methods for details), as in Farooq and Dragoi (2019) and Silva et al. (2015). Together, these findings reveal a significant, persistent improvement in representation of Run trajectory after the experience, which includes a coordinated improvement in the strength and continuity of trajectory sequences during Post-Run sleep.

Various mechanisms have been proposed to explain the experience-induced changes in post-experience spontaneous activity of the hippocampal network. These include increases in the net firing rates of previously active place cells (Battaglia et al., 2005; Pavlides and Winson, 1989), changes in the temporal order of neuronal sequences (Lee and Wilson, 2002; Skaggs and McNaughton, 1996), and preferential increases in multi-neuronal coordination at short, millisecond timescales for neurons coactive during the experience (van de Ven et al., 2016; adapted after Peyrache et al., 2009). Because these three changes in hippocampal network activity (i.e., rate, order, and coordination; Figure 2D) have been observed in isolation, it remains unknown whether and to what extent they contribute to the post-experience increase in temporally compressed replay of a recent animal trajectory over its preplay during sleep (Figure 2B). We therefore sought to determine which of these three changes in ensemble activity accounts for the observed improvement in trajectory representation during the sleep following a de novo spatial experience. Our main approach was to isolate and when possible remove the contribution of each of the three factors to the increase in trajectory representation from Pre- to Post-Run sleep.

Contribution of Experience-Related Changes in Firing Rates to Improved Trajectory Representation during Sleep Replay

We observed that place cells had significantly higher firing rates in the Post-Run sleep frames compared with Pre-Run sleep (Figure 3A; mean firing rates in Pre- versus Post-Run sleep: 1.986 ± 0.0742 versus 2.102 ± 0.0868 Hz, p < 10⁻⁵, Wilcoxon’s signed rank test; comparison using individual animal direction as unit of analysis, n = 10: Pre- versus Post-Run sleep firing rate, p < 0.005, Wilcoxon’s signed rank test). We tested the hypothesis that net increases in firing rates of place cells may be the primary contributor to the increased sequential content observed during Post-Run sleep trajectory replay (Figure 2B), as suggested previously (Peyrache et al., 2009).

Figure 3. Contribution of Changes in Firing Rates to the Improvement of Trajectory Representation from Pre-Run to Post-Run Sleep.

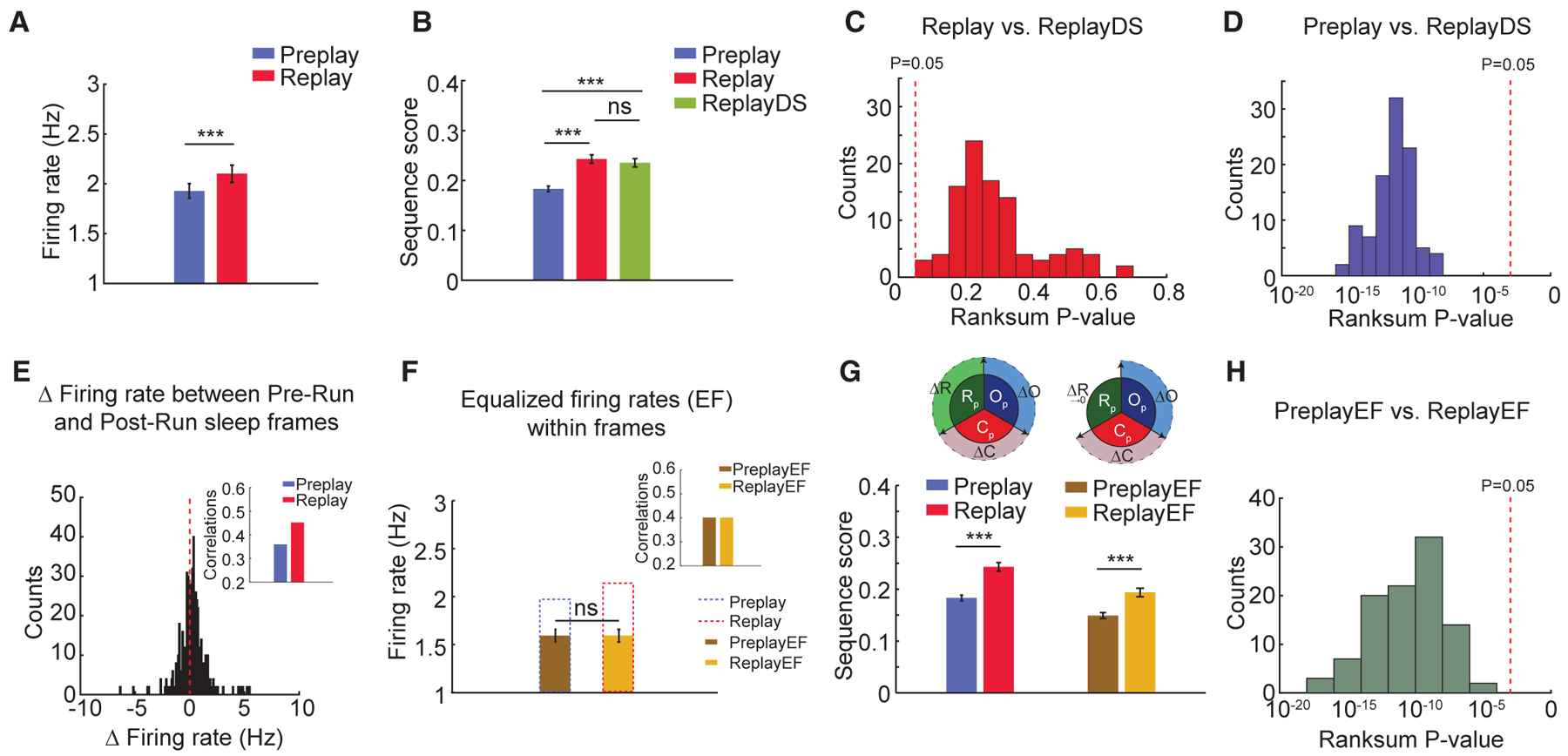
(A) Firing rates of neurons increase from Pre-Run sleep (Preplay) to Post-Run sleep (Replay).

(B) Sequence scores of random down sampling of neuronal firing rates from Post-Run sleep into Pre-Run sleep levels (ReplayDS) demonstrate that experience-related changes in overall firing rates are not sufficient to account for the observed differences between trajectory replay and preplay.

(C and D) ReplayDS sequence scores are similar to the original replay scores (C) and are higher than the preplay scores (D). p values are from 100 independent rank sum tests.

(E) Firing rates within frames change from Pre- to Post-Run sleep variably across neurons. (Inset) Overall correlation of firing rates between sleep frames and Run increases from Pre- to Post-Run sleep.

(F) Equalization of firing rates (EF) and sleep-Run correlations (100 iterations, inset) between Pre-Run (PreplayEF) and Post-Run (ReplayEF) sleep frames after down-sampling spikes from neurons with increased firing rates in specific Pre- and Post-Run sleep sessions.

(G) Preplay and replay sequence scores before and after equalization of firing rates. (Inset) Graphical representation of equalization in firing rates between Preand Post-Run sleep is shown.

(H) p values of comparisons between sequence scores in PreplayEF and ReplayEF (100 iterations).

For (A), (B), (F), and (G): ***p < 0.001, ns = not significant. Data are represented as mean ± SEM.

We studied the effect that increased firing rates during Post-Run sleep has on the strengthening of trajectory representation in replay over preplay. We thus randomly and repeatedly (n = 100) down-sampled spike counts in Post-Run sleep frames until the grand average firing rate for the population matched that of Pre-Run sleep frames (Figure 3B). Subsequently, we compared the sequence score of these down-sampled datasets (i.e., replayDS) to that of the original replay and preplay. We observed no significant difference in sequential trajectory content between replay and replayDS in any of the 100 rate-matched datasets; at the same time, replayDS was stronger than preplay in all tested cases (Figures 3C and 3D; replay versus replayDS: p values ranged from 0.09 to 0.7077; preplay versus replayDS: all p < 10⁻⁵, Wilcoxon’s rank sum test, n = 100). A more drastic reduction in firing rates of all neurons to single spikes per frame during Pre- and Post-Run sleep resulted in significant decreases in sequence scores for Bayesian decoding of trajectories, indicating that trajectory decoding depends on neuronal firing rate (data not shown). Hence, we conclude that net increases in firing rates of place cells cannot alone account for the increases in trajectory representation from preplay to replay during sleep.

Experience-driven reorganization of firing rates of hippocampal neurons might improve trajectory representation during frames in Post-Run sleep (Hirase et al., 2001). We observed a redistribution of firing rates, with some neurons increasing their activity and others reducing their activity in the Post-Run sleep (Figure 3E). Overall, this reorganization resulted in a higher correlation of firing rates between Run experience and Post-Run sleep compared with Pre-Run sleep (Figure 3E, inset: Pre- versus Post-Run sleep frames’ correlations with Run: 0.35 versus 0.45).

We developed a targeted down-sampling approach to test the significance of this rate reorganization on trajectory replay. Spikes from cells exhibiting increased firing rates from Pre- to Post-Run sleep frames were randomly dropped from Post-Run sleep until their individual firing rates matched those in Pre-Run sleep frames (i.e., ReplayEF group). Concomitantly, spikes from cells with a post-experience reduction in firing rates were randomly dropped from Pre-Run sleep, as above (i.e., PreplayEF group; Figure 3F). The average firing rate in both equalization of firing rates (EF) surrogate datasets (n = 100) was 1.6 Hz (Figure 3F; a 25% reduction from Pre-Run; mean firing rates PreplayEF versus ReplayEF; all p = 1; Wilcoxon’s signed rank tests; n = 100). The average correlations of neuronal firing rates in PreplayEF and ReplayEF with Run were also equal (r = 0.39). Importantly, ReplayEF exhibited significantly higher trajectory sequential structure compared to PreplayEF (Figures 3G and 3H; PreplayEF versus ReplayEF sequence strength; 100 out of 100 Wilcoxon’s rank sum tests p < 0.05). We observed only a mild yet significant reduction in Replay/Preplay ratio (mean = 1.33) after equalizing firing rate correlations (mean ReplayEF/PreplayEF = 1.29; p < 10⁻¹⁰; Wilcoxon’s sign rank test). Together, our results demonstrate that reorganization of firing rates alone cannot account in a major way for improved trajectory representation in Post-Run sleep.

Contribution of Experience-Related Changes in Temporal Order of Neuronal Sequences to Improved Trajectory Representation during Sleep Replay

Given the limited contribution of place cell firing rates toward improved trajectory replay, we next investigated whether the temporal order of extended neuronal sequences improved in replay over preplay. To isolate the contribution of temporal order of firing during sleep to the rapid encoding of future place cell sequences, we employed a template-matching method (Diba and Buzsáki, 2007; Dragoi and Tonegawa, 2013b; Foster and Wilson, 2006; Silva et al., 2015). Briefly, we rank ordered place cells according to their peak firing location along the animal’s trajectory and computed two spatial templates per animal, one for each direction of movement. Each spatial template was correlated with the temporal order of firing of the corresponding cells during sleep frames (two correlation coefficients/frame; one for each template; Spearman’s correlation) separately for Pre- and Post-Run sleep (see STAR Methods). As a control, we shuffled the order of place cells within the templates (500 shuffles) and computed correlation coefficients with the original frames during the corresponding sleeps (two correlation coefficients/frame/shuffle; one for each template). We found that Pre-Run frames had stronger correlations and hence more temporal structure than control shuffled datasets (Figure 4A; mean Pre-Run sleep versus shuffle correlations: 0.202 ± 0.002 versus 0.195 ± 0.0001, p < 10⁻¹⁰, Wilcoxon’s rank sum tests, data pooled across 5 animals; 3 of the 5 individual animals were also significant; data not shown). Notably, using simulations based on real datasets recorded during sleep, we found that the outcome of the template-matching method is particularly sensitive to the number of place cells per spatial bin on the linear track (for details, see Figures S3 and S4 and STAR Methods). Accordingly, an increased average density of cells/spatial bin >1.19 randomizes the rank ordering of place cells with firing peaks within a spatial bin, which approaches a random place-cell order similar to shuffled datasets (Figure S3H). This randomization of cell order within spatial bins might lead to false negative results when attempting to detect sleep preplay and replay, as found in our simulations (and might have contributed to the masking of significant neuronal order preplay, i.e., p = 0.08, Wilcoxon’s rank sum test on data versus shuffle, in a recent study; Silva et al., 2015).

Figure 4. Temporal Order of Neuronal Firing within Trajectory Sequences Is Preserved from Pre- to Post-Run Sleep (Template Matching Method).

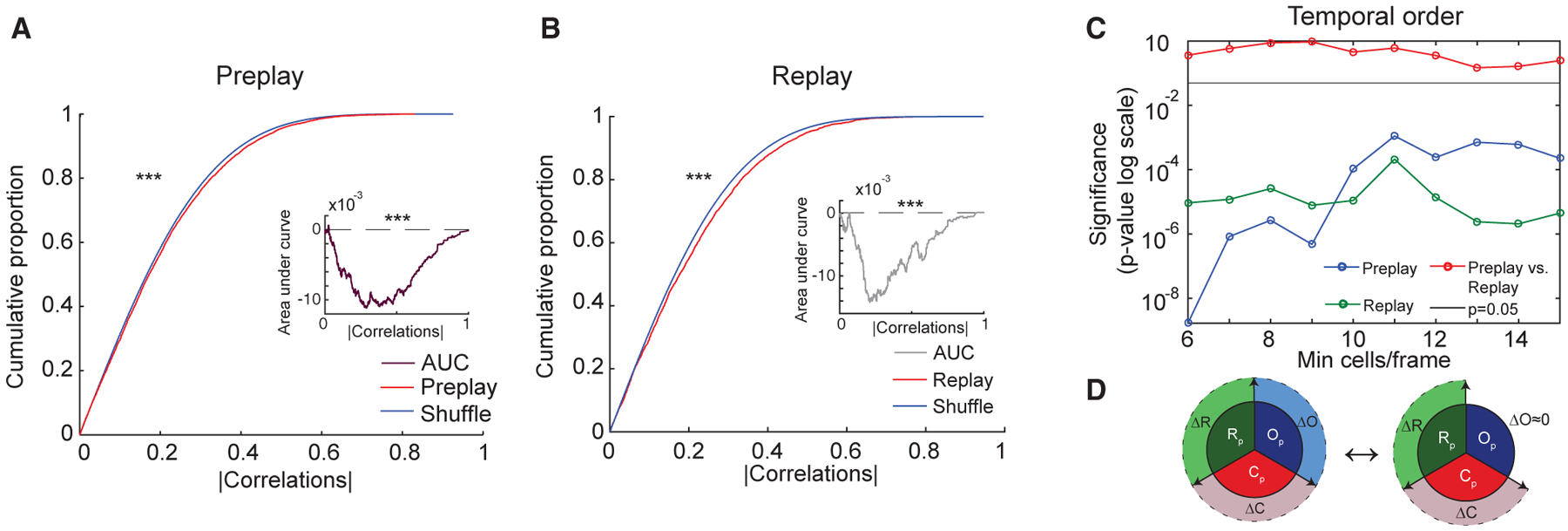
(A and B) Significant temporal order preplay during Pre-Run sleep (A) and replay during Post-Run sleep (B) of place cell sequences in Run for frames with at least 15 cells (template matching method). (Insets) Area under curve (AUC) (preplay, A, or replay, B, minus shuffle) for frames with 6 or more cells. Similar proportions and AUCs are obtained for frames with a minimum of 6–15 neurons (data not shown).

(C) Significance of preplay and replay and their similarity in strength are maintained across a wide range of within-frame number of participating place cells. p values reflect comparisons of preplay with its shuffle (blue), replay with its shuffle (green), and preplay with replay (red).

(D) Graphical representation of the lack of change in temporal order of neuronal firing from Pre- to Post-Run sleep frames with regard to Run.

For (A) and (B): ***p < 0.001.

Similar to Pre-Run sleep frames (Figure 4A), we found that Post-Run sleep frames had stronger correlations and more temporal structure than control shuffled datasets (Figure 4B; Post-Run sleep versus shuffle correlations: 0.207 ± 0.003 versus 0.193 ± 0.0001, p < 10⁻⁸, Wilcoxon’s rank sum tests, data pooled across 5 animals; 4 of the 5 individual animals were also significant; data not shown). Furthermore, the significance of preplay and replay was maintained when the frames with higher number of participating cells were studied exclusively (Figures 4A and 4B; >15 place cells/spiking event: p < 10⁻⁶, p < 10⁻³; Wilcoxon’s rank sum tests; data pooled across 5 animals). Importantly, rank-order correlations with Run were similar in Pre-Run and Post-Run sleep (Figure 4C) in 4 of the 5 animals and were stronger in the Pre-Run sleep in one animal, consistent with an earlier report (Dragoi and Tonegawa, 2013a). Overall, this indicates that preplay and replay trajectory sequences have a similar temporal order representation of a de novo experience, which cannot explain the post-experience plasticity in trajectory replay (Figure 4D).

Contribution of Experience-Related Changes in Millisecond-Timescale Cell Assembly Organization to Improved Trajectory Representation during Sleep Replay

Hippocampal neurons organize into cell assemblies (Hebb, 1949) transiently activated at the millisecond timescale to represent individual locations along the animal’s trajectory (van de Ven et al., 2016). These hippocampal cell assemblies have been shown to be activated stronger in the post- compared with pre-experience sleep (van de Ven et al., 2016), providing a potential mechanism for memory consolidation. Cell assembly formation is expressed by the strict temporal coordination (synchronous activation) of a subset of neurons within millisecond-timescale windows. The exact contribution of cell assembly activation to the formation and plasticity of compressed trajectory sequences remains unknown. Our current results indicate a limited contribution of changes in neuronal firing rate and temporal order to the improved trajectory representation during sleep replay. This raises the possibility that strengthened trajectory replay could primarily be supported by plasticity within individual cell assemblies, presumed to represent individual locations along an animal’s trajectory, played along a rather stable preconfigured trajectory-representing temporal framework.

To reveal and study hippocampal cell assemblies, we detected significant, repeating coactivating multi-neuronal patterns (i.e., cell assemblies) at 20-ms bin-size timescale, based on a principal-component analysis of the observed correlation matrix of all neurons during Run (Peyrache et al., 2009; van de Ven et al., 2016; cell assembly method; see STAR Methods and Figure S4 for schematic representation of the method). This method allows the study of significant millisecond-time-scale interactions within the neuronal ensemble, with two advantages over the traditional methods, such as cell-pair cofiring (Wilson and McNaughton, 1994). First, it enables us to capture the instantaneous dynamics of significant multi-neuronal patterns compared with averaging the cofiring of all neuronal pairs across an entire session. Because compressed sequences are highly variable (Fenton and Muller, 1998) and cell assembly dynamics unfold at the millisecond timescale (Harris et al., 2003), the traditional pairwise cofiring methods cannot provide the temporal resolution to study the dynamic relationship between cell assemblies and neuronal sequences (Lee and Wilson, 2002). Second, this method incorporates higher order interactions, in addition to the pairwise interactions captured by the previous methods.

Discrete locations along the novel track were each encoded by an average of 8.2 cell assemblies uniquely coactive during each direction during Run (Figure 5A for all cell assemblies; Figure 5B for an example of a cell assembly; Table S1). Each cell assembly had an average of 2.5 high-contributing (HC) neurons defined as neurons with principal component weights >2 SD above the mean for a particular cell assembly (Figures 5B, 5C, and S7A). Pairs of these HC neurons exhibited a higher degree of coactivation and place field similarity compared to the other neuronal pairs, which we collectively called non-HC neuronal pairs (Figure 5D; left, mean cofiring correlation for HC versus non-HC: 0.065 ± 0.002 versus 0.005 ± 0.0003, p < 10⁻¹⁰, Wilcoxon’s rank sum test; right, mean place field similarity for HC versus non-HC: 0.33 ± 0.02 versus 0.082 ± 0.002, p < 10⁻¹⁰, Wilcoxon’s rank sum test).

Figure 5. Experience-Dependent Changes in Neuronal Properties of Cell Assemblies from Pre- to Post-Run Sleep.

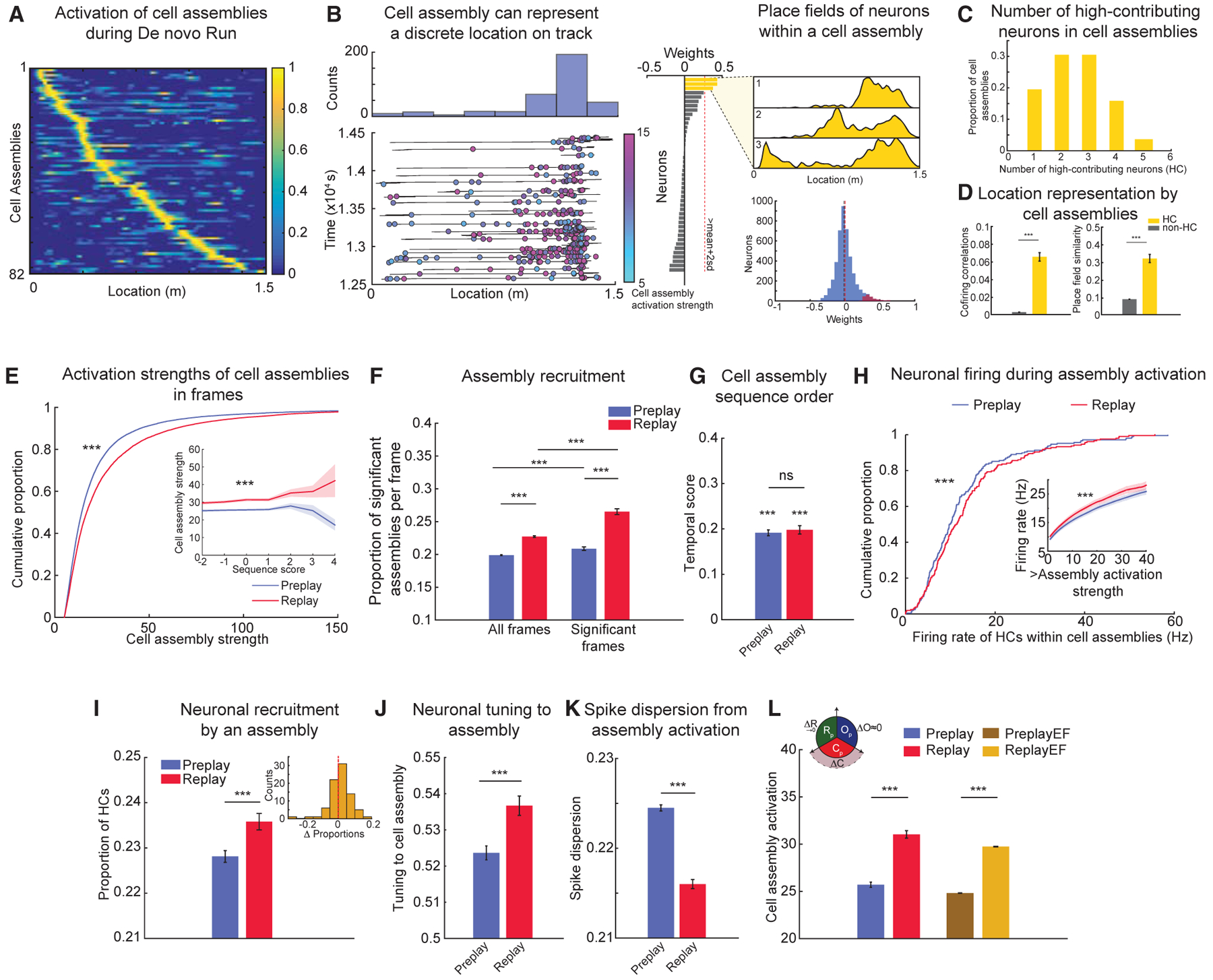
(A) Cell assemblies detected during Run sessions represent discrete locations along an animal’s trajectory through the linear environment.

(B) Representative example of a cell assembly activated on the track (left, bottom); colors and color bar depict activation strengths during Run. Histogram (left, top) depicts counts of activation across multiple laps on the track. (Middle) Weights of neurons contributing to this cell assembly are shown. Note that three neurons (yellow) are high contributors (HCs) to this cell assembly. (Right, top) Place fields of the HC neurons to this cell assembly are shown. (Right, bottom) Weights of all neurons (blue) and HC neurons (red) to cell assemblies are shown. Lines depict median (black) and mean (red) weights.

(C) Number of HC neurons within each cell assembly during Run (n = 82 assemblies).

(D) Cofiring (left) and place field similarity (right) of HC neuronal pairs belonging to a cell assembly are significantly higher than those of pairs of non-HC and HC-non-HC neurons.

(E) Millisecond-timescale activation of cell assemblies within frames increases from Pre- (n = 38,220 frames) to Post-Run sleep (n = 17,367 frames). (Inset) Average activation of cell assemblies at different sequence scores of trajectory sequences is shown.

(F) Proportion of significant cell assemblies activated within a frame increases from Pre- (n = 38,220) to Post-Run sleep frames (n = 17,367).

(G) Temporal order of cell assembly sequences is similar during Pre- and Post-Run sleep.

(H) Within-cell assembly firing rate of HC neurons (n = 208 neurons) increases from Pre-Run to Post-Run sleep. (Inset) Firing of HC neurons at increasing thresholds of activation strengths is shown.

(I) Proportion of HC neurons activated within a significant cell assembly activity increases from Pre- (n = 62,055 events) to Post-Run sleep (n = 31,376 events). (Inset) Distribution of differences in cell assembly activation from Pre- to Post-Run sleep is shown.

(J) Tuning of HC neurons to their respective cell assemblies increases from Pre- (n = 50,284 events) to Post-Run sleep (n = 26,632 events).

(K) Dispersion of spikes of HC neurons outside their respective cell assemblies decreases from Pre- (n = 91,058 events) to Post-Run sleep (n = 41,840 events). Note that only spikes outside the cell assembly activation epoch were considered.

(L) Cell assembly activation after equalizing firing rates and rate correlations is higher in Post- (ReplayEF) compared to Pre-Run sleep (PreplayEF). (Inset) Graphical representation of the dominant contribution of changes in cell assembly strength to improved replay is shown.

For (D)–(L): ***p < 0.001, ns = not significant. Data are represented as mean ± SEM.

We studied the changes occurring within cell assemblies from Pre- to Post-Run sleep. We found that the overall activation of cell assemblies during replay frames exceeded that during preplay (Figures 5E, S7B, and S7C; mean Pre-Run versus Post-Run sleep: maximum assembly strength 25.70 ± 0.27 versus 31.03 ± 0.40; p < 10⁻¹⁰; Wilcoxon’s rank sum test). This overall strengthening in activation of cell assemblies representing Run trajectories from Pre- to Post-Run sleep was due to increases in (1) the proportion of significant cell assemblies activated within a frame (Figure 5F; mean Pre- versus Post-Run sleep in all and in significant frames, respectively: 0.1989 ± 0.0001 versus 0.2273 ± 0.0012 and 0.2087 ± 0.0027 versus 0.2652 ± 0.0044; p < 10⁻¹⁰ and p < 10⁻¹⁰ for proportion of assemblies; Wilcoxon’s rank sum tests) and (2) the proportion of frames in which individual assemblies were activated (Figure S7E; mean Pre- versus Post-Run sleep in all and significant frames, respectively: 0.2000 ± 0.0071 versus 0.2228 ± 0.0077 and 0.2122 ± 0.0085 versus 0.2620 ± 0.0098; p < 10⁻⁷ and p < 10⁻⁸; Wilcoxon’s signed rank tests). Despite all these changes in the strength of activation, the temporal sequence of cell assembly activation within frames (i.e., temporal score; see STAR Methods) did not change from Pre- to Post-Run sleep (Figure 5G; mean Pre- versus Post-Run sleep temporal score: 0.1915 ± 0.0064 versus 0.1981 ± 0.0092; p = 0.56; Wilcoxon’s rank sum test). Together, these results suggest that trajectory replay represents additional individual track locations with higher overall track continuity than trajectory preplay, but the temporal order of locations represented within a sequence remains conserved.

Experience-Dependent Reorganization of Neuronal Firing Characteristics within Cell Assemblies Supports Plasticity in Trajectory Sequences

Our observation that trajectory replay has higher activation of individual cell assemblies led us to study the properties of individual neurons within the cell assemblies. We investigated whether the changes occurring in individual neurons within a cell assembly were correlated with the observed increase in cell assembly activation from Pre- to Post-Run sleep. The duration of cell assembly activation in frames increased by <1 ms from Pre- to Post-Run sleep frames (mean Pre- versus Post-Run sleep assembly duration; 22.26 ± 0.028 versus 22.95 ± 0.047 ms; p < 10⁻¹⁰; Wilcoxon’s rank sum test). Therefore, we isolated the 20-ms epoch within the frames with the maximum activation of cell assemblies (i.e., cell assembly activation epoch; STAR Methods) and studied the firing characteristics of neurons within this epoch. We investigated two broad sets of neuronal changes within cell assemblies from Pre- to Post-Run sleep frames: changes in firing rates within cell assemblies and changes in precision of spikes of constituent neurons of cell assemblies. We found that, within the assembly activation epochs, the firing rates of the HC neurons to the preferred assembly (i.e., <10% of all neurons for each assembly) were increased (median Pre- versus Post-Run sleep: 12.75 ± 0.72 versus 13.93 ± 0.74 Hz for HCs, Figure 5H, p = 0.002 for Wilcoxon’s rank sum tests; comparison with individual animal direction as unit of analysis, n = 10: Pre-versus Post-Run sleep, p < 0.05, Wilcoxon’s signed rank test). Furthermore, we observed that the number of HC neurons coactive in the cell assembly activation epochs (i.e., increased neuronal recruitment to assemblies) also increased from Pre- to Post-Run sleep from 0.228 ± 0.0013 to 0.236 ± 0.003 (Figure 5I; p < 10⁻⁴; Wilcoxon’s rank sum test). In addition, the tuning of HC neurons to their respective cell assembly activation epochs, defined as the proportion of spikes within the cell assembly out of all within-frame spikes, increased from Pre- to Post-Run sleep (Figure 5J; mean tuning Pre- to Post-Run: 0.524 ± 0.002 versus 0.537 ± 0.003, p < 10⁻³, Wilcoxon’s rank sum test). Consistent with these findings, we observed that the dispersion of spikes relative to their epoch of activation (STAR Methods) decreased for HC neurons in Post- compared to Pre-Run sleep (Figure 5K; mean spike dispersion Pre- versus Post-Run sleep frames: 0.2245 ± 0.003 versus 0.2160 ± 0.004, p < 10⁻⁶, Wilcoxon’s rank sum test; comparison with animal direction as unit of analysis, n = 10: Pre- versus Post-Run sleep spike dispersion, p < 0.005, Wilcoxon’s signed rank test).

Given that experience-related reorganization of neuronal firing rates has a limited effect on the plasticity of trajectory sequences during sleep (Figure 2), we next studied its effect on the properties of neurons constituting cell assemblies. We found that, despite equalization of firing rates and correlations between the PreplayEF and ReplayEF conditions (Figure 3F), the activation strength of cell assemblies was significantly higher in the ReplayEF compared to PreplayEF sleep frames (Figure 5L; mean cell assembly activation strength in PreplayEF versus ReplayEF: 24.82 ± 0.028 versus 29.73 ± 0.038; p < 10⁻¹⁰; Wilcoxon’s rank sum test). The residual plasticity in cell assemblies observed across the firing rate correlation-matched PreplayEF and ReplayEF frames (Figure 5L) paralleled a similar residual plasticity in trajectory sequences (i.e., sequence scores) between PreplayEF and ReplayEF frames (Figure 3G).

Overall, we identified two types of changes in cell assembly dynamics from Pre- to Post-Run sleep: (1) increases in firing rates and coactivation of HC neurons within the preferred cell assembly and (2) increased precision of firing of these neurons within preferred cell assemblies during Post-Run sleep replay (i.e., decreased spike dispersion and increased tuning to preferred cell assembly). We propose that these changes in cell assembly dynamics between Pre-Run and Post-Run sleep frames could primarily lead to increased trajectory representation during replay. Intriguingly, the plasticity within cell assemblies occurs at a timescale of ~20 ms, consistent with the period of hippocampal gamma oscillation (Carr et al., 2012), the time window for synaptic plasticity (Bi and Poo, 1999), and previous reports of cell assembly dynamics (Harris et al., 2003).

Diversity in Plasticity across Frames Suggests that Experience-Related Strengthening in Cell Assemblies Is a Prime Contributor to Plasticity in Trajectory Sequences

Previous studies pooled the results from all frames of an entire sleep session (Grosmark and Buzsáki, 2016; Silva et al., 2015). However, we observed a large diversity across frames within a sleep session based on the proportion of place cells activated in the frame. The distributions of frames based on cell participation were non-Gaussian (Lilliefors test for frames in Pre-Run sleep, p < 10⁻³, and for frames in Post-Run sleep, p < 10⁻³), right skewed, and did not change between Pre-Run and Post-Run sleep (Kolmogorov-Smirnov test; p > 0.05; Figure 6A). The frames with higher proportion of place cells had longer frame durations, similarly for Pre- and Post-Run sleep (Wilcoxon’s rank sum test; p > 0.05; Figure 6A, inset). When we analyzed the increase in trajectory sequential content of frames from Pre- to Post-Run sleep, we observed a stronger increase in sequential content in the frames where more than 50% of place cells were active compared with frames with lower cell participation (Pearson’s correlation of proportion of participating cells and difference in replay and preplay; R = 0.78; p < 0.05; Figure 6B and inset). We asked which of the three factors (firing rate, neuronal order, and short-timescale cell assembly coordination) contributes to this selective improvement in replay over preplay. We observed that the improvement in sleep-Run firing rate correlations from Pre- to Post-Run sleep was higher in frames with higher proportion of active place cells (Figure 6C). However, the small changes in neuronal order of firing with increased participation of neurons into frames remained similar between Pre- and Post-Run sleep (Figure 6D; see also Figures 4A–4C). Consistent with the proposed contribution of cell assemblies to improved trajectory replay (Figure 5), we found that in-frame increase in cell assembly strength at higher proportions of in-frame active place cells was stronger during Post- compared with Pre-Run sleep (Figure 6E). This increase paralleled a similar increase in the improvement in trajectory sequence score with a higher participation of neurons into frames (Figure 6B, inset). Indeed, the experience-related increase in plasticity of trajectory sequence score with higher in-frame place cell participation (Figure 6B, inset) was highly correlated with the increase in plasticity at the cell assembly level (Pearson’s correlation R = 0.92; p < 0.005), but not with changes in firing rate correlations of neurons in preplay and replay with Run (R = 0.29; p = 0.53) and temporal order of neurons (R = 0.15; p = 0.75; Figure 6F). This result provides further support to our proposal that an improved trajectory sequence replay over preplay occurs primarily due to an increase in the strength of participating cell assemblies, on the framework of a robust preconfigured network. The coordinated increase in cell assembly and sequential content was persistent in time and did not decay over the duration of our experiments (Figures S6 and S7F).

Figure 6. Preferred Improvement in Trajectory Representation in Post-Run Sleep Frames with More Participating Place Cells Is Related to Increases in Cell Assembly Content, but Not Firing Rate or Neuronal Order.

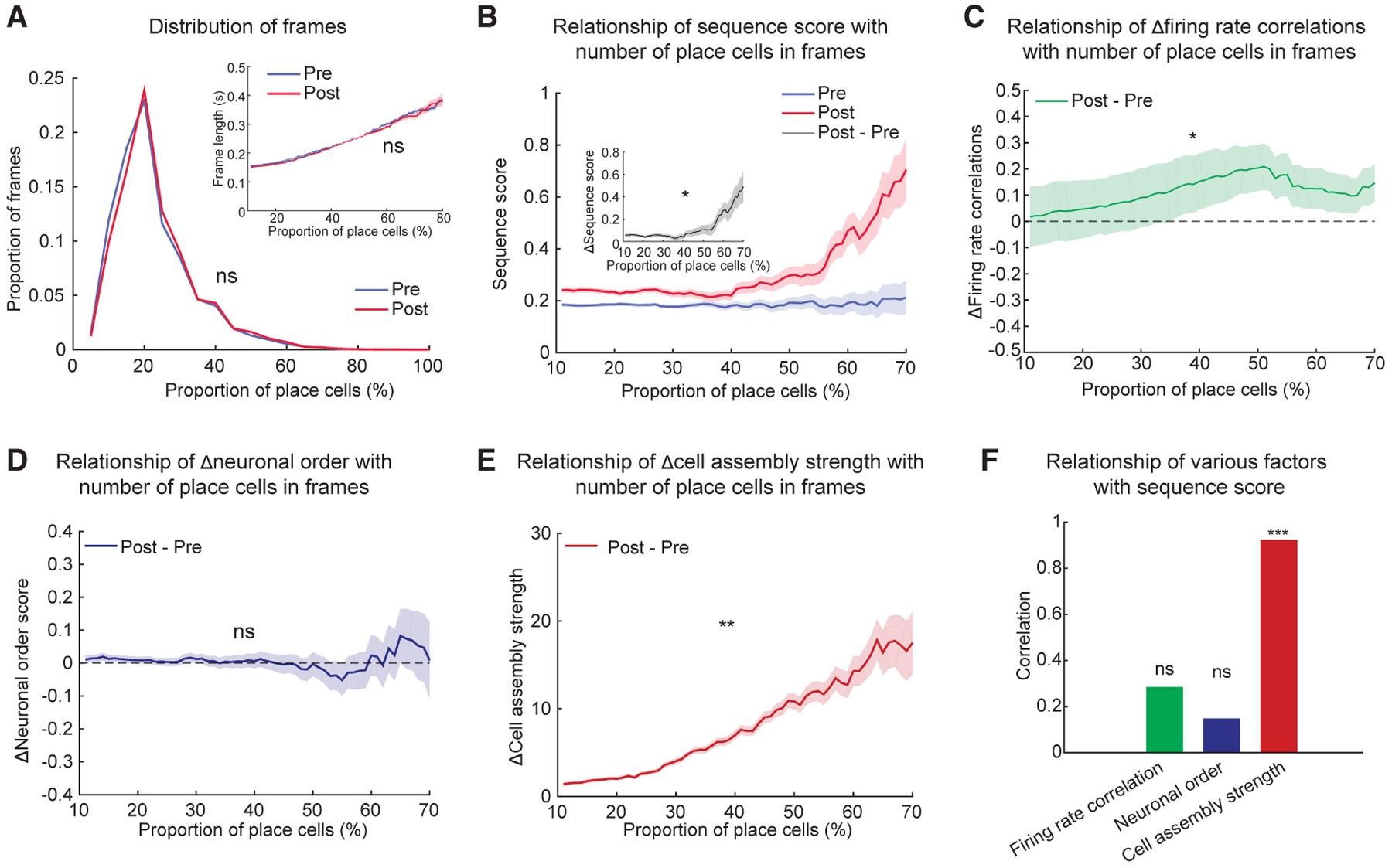
(A) Distribution of frames in Pre- and Post-Run sleep as a function of proportion of place cells active within frames. (Inset) Frames where more place cells are active have longer duration.

(B) Sequence scores in Pre- and Post-Run sleep as a function of proportion on place cells in frames. (Inset) Difference in sequence scores between Post- and Pre-Run sleep as a function of proportion of place cells in frames is shown.

(C–E) Difference in firing rate correlations (C), neuronal order (D), and cell assembly strength (E) between Post- and Pre-Run sleep as a function of proportion of place cells in frames.

(F) Correlations of the difference between firing rate correlations (green, from C), neuronal order (blue, from D), and cell assembly strength (red, from E) with the difference in sequence score from (B) inset between Post- and Pre-Run sleep as a function of proportion of place cells in sleep frames. Data in (B) inset and (C)–(E) are presented as difference in means ± SE of the difference in means.

*p < 0.05, **p < 0.01, ***p < 0.001, ns = not significant.

DISCUSSION

We reveal hippocampal neuronal ensemble mechanisms implicated in rapid encoding, stabilization, and consolidation of novel sequential spatial information. First, we demonstrate that internally generated time-compressed neuronal sequences during sleep robustly preplay future place cell and trajectory sequences that rapidly encode a de novo run experience. We present several lines of evidence to demonstrate that preplay is a true neurobiological phenomenon (Figures 1, S1, S2, and S3). Second, we show that the navigational experience-dependent plasticity occurring in CA1 place cell sequences is primarily due to increased activation and temporal coordination at the millisecond timescale of location-depicting cellular assemblies within a framework of largely homeostatic temporal sequences (Figures 2, 3, 4, 5, and 6). This overall post-experience strengthening in the coordinated activation of neurons within cell assemblies during sleep results from an increased tuning of the neurons that form a cell assembly during the run behavior and from the recruitment of new, experience-tuned neurons into preconfigured cell assemblies. The overall ensemble representation of a recent experience is also strengthened by an increase in the number of participating cell assemblies. This strengthening in representation occurs on a pre-existing framework of neuronal and cell assembly sequential activation, analogous to a Hebbian phase sequence (Hebb, 1949), which is largely maintained from pre- to post-experience sleep (Liu et al., 2019). The offline strengthening of multiple individual location-depicting assemblies is the primary driver for the increase in the overall trajectory sequence representation in post-experience sleep. This is achieved by mainly two mechanisms, increased spike precision and reorganization of firing rates, which lead to an increased within-assembly firing of the constituent neurons. More modest post-experience changes in neuronal average firing rates appear to contribute mostly technically and methodologically to trajectory decoding but are not fully accountable for the change in trajectory representation during post-experience sleep (Figures 3A–3D). We thus propose that strengthened temporal coordination within pre-existing cell assemblies is the primary factor supporting rapid trajectory replay during sleep and possibly spatial memory formation (Figure 7).

Figure 7. Model of Neuronal Ensemble Dynamics Supporting Improved Trajectory Replay.

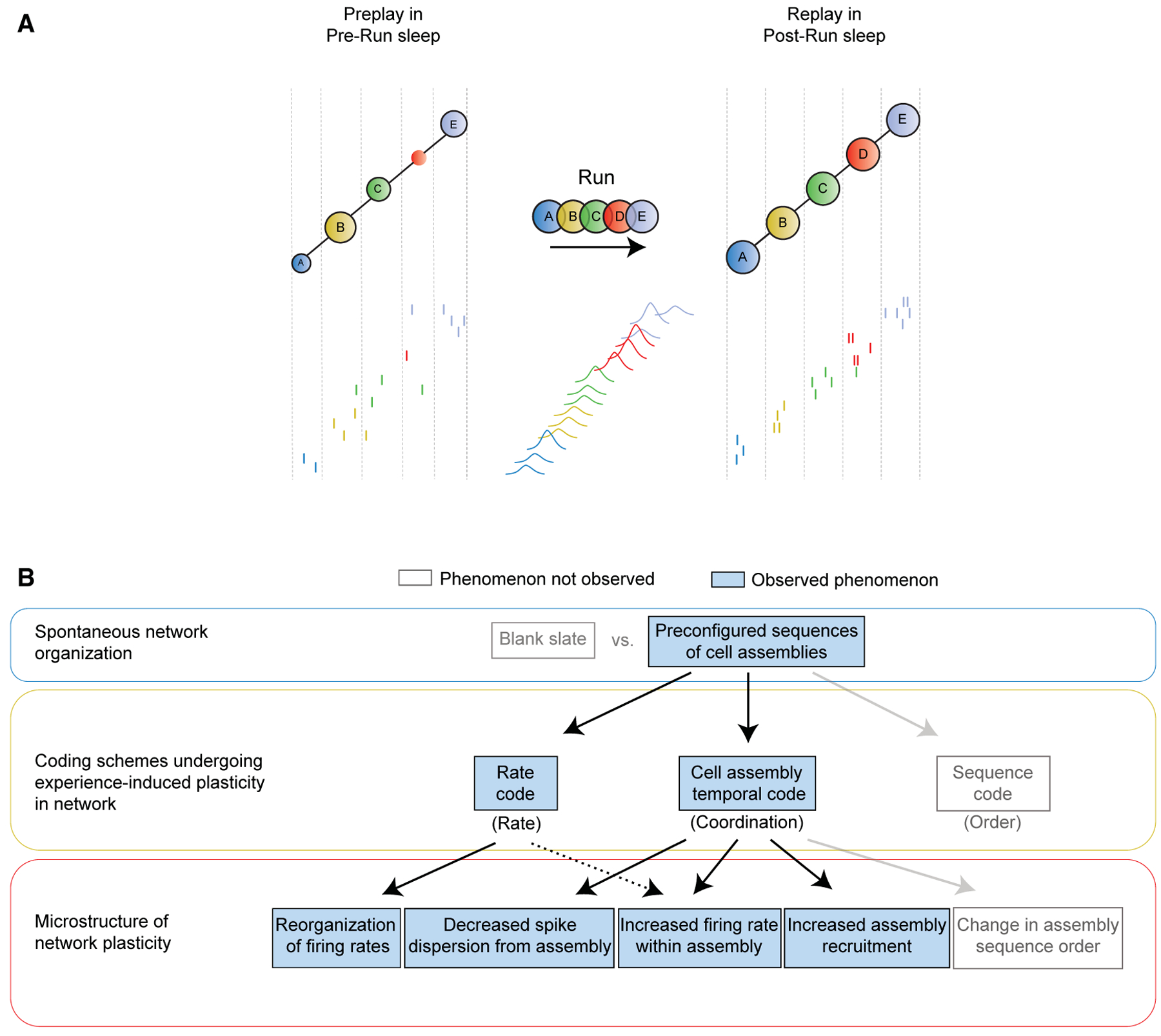
(A) (Top) Cartoon model of hippocampal ensemble activity before (Pre-Run sleep, one frame) and after (Post-Run sleep, one frame) a de novo spatial experience (Run, cell assembly sequence) proposed to underlie episodic-like spatial memory formation. Colored circles depict different significant cell assemblies (multi-neuronal millisecond-timescale coactivation patterns) across sleep and run as detected based on their activity during Run. Letters depict significantly active cell assemblies; variable size of circles during sleep depicts activation strength. Vertical dash lines within sleep frame mark periods of significant activation of each assembly identified based on their activity during Post-Run sleep. (Bottom) Spikes of individual neurons are depicted by short vertical lines color coded according to the cell assembly they belong to during Run.

(B) Schematic depicting confirmed (observed) and unconfirmed (not observed) phenomena proposed to underlie representation of de novo spatial experience by compressed neuronal ensemble dynamics during sleep.

When not fully accounted for, the complexities of the statistical assumptions underlying the characterization of preplay and replay phenomena can occasionally lead to conflicting results and interpretations (Dragoi and Tonegawa, 2013b; Grosmark and Buzsáki, 2016; Silva et al., 2015). Here, we present several lines of evidence using a two-feature analysis (Silva et al., 2015) to establish that hippocampal neuronal sequence and trajectory preplay precede spatial experience. We also perform an extensive analysis of some of these key statistical assumptions and find several statistical pitfalls in the interpretation of the space-bin shuffle and of template matching with large cell counts per spatial bin densities data in a previous study, which might have contributed to the masking of preplay detection (see Figures S3 and S4 for details). Additional related concerns include the comparison of properties of time-compressed sequences across different brain states and animal locations (i.e., sleep preplay off running track versus awake replay on the running track at velocities up to 5 cm/s). We propose that the variability in observing the preplay phenomenon across different research groups using similar experimental protocols is largely reflective of a difference in the methodological approaches to data analysis rather than in the neurobiology of preplay.

Earlier observations of hippocampal replay sequences in post-experience sleep suggested their potential role in consolidation of episodic-like memories (Lee and Wilson, 2002). However, as robust neuronal sequences exist before novel experiences (Dragoi and Tonegawa, 2011), questions regarding the experience-induced plastic changes in these sequences and the primary neuronal ensemble mark of novel trajectory replay and potentially rapid episodic-like memory formation have remained unanswered. To determine the effect of experience on hippocampal trajectory-depicting sequences, we directly compare preplay and replay during sleep using a probabilistic Bayesian framework and reveal a stronger replay. We next characterize which changes in hippocampal neuronal ensemble firing characteristics could account for this plasticity. Historically, three neuronal coding schemes have been implicated in experience-driven plasticity in the hippocampus and have been suggested to mediate temporally compressed storage of a memory: (1) long-term potentiation-like changes in firing rates of neurons; rate coding (Battaglia et al., 2005; Pavlides and Winson, 1989); (2) de novo creation of neuronal sequences (Lee and Wilson, 2002; Silva et al., 2015), representing the sequential nature of the spatial experience (sequence coding); and (3) increased synchrony and coordination at millisecond-timescale of neurons (van de Ven et al., 2016) coherently activated during the experience (cell-assembly temporal coding). Theoretically, each (and a combination) of these changes could support the increased trajectory sequential content in the replay sequences. Our study demonstrates that extended neuronal sequences of firing and sequential activation of cell assemblies exist before the experience and that their neuronal order remains largely conserved from preplay to replay. This indicates that de novo experience has very limited to no significant effect in the overall creation of temporal sequences in the hippocampal network.

Remarkably, we observe a significant increase in the activation of cell assemblies during frames in post-experience sleep that best explains the increase in trajectory replay over preplay. We propose that a strengthening in attractor-based (Hopfield, 2010; Samsonovich and McNaughton, 1997; Wills et al., 2005) activation of cell assemblies, building on a robust pre-existing sequential temporal order of activation (Dragoi and Tonegawa, 2011; Malvache et al., 2016), represents the primary factor supporting trajectory learning in the hippocampus. Diversity in firing and plasticity of individual neurons (Dragoi et al., 2003) was proposed to be instrumental in orchestrating experience-related plasticity in trajectory replay (Grosmark and Buzsáki, 2016). Our results on the diversity in neuronal participation to sleep frames suggest that incorporation of additional neurons into cell assemblies active during sleep and their activity preferentially within frames with increased neuronal participation support experience-dependent plasticity in trajectory replay.

The brain regions involved in generation of hippocampal trajectory sequences in CA1 have not been entirely mapped. Earlier models posited that trajectory representation involves two different processes: (1) attractor-based auto-association within upstream CA3 networks to represent multimodal location-specific stimuli from noisy inputs during recall and (2) hetero-association, i.e., a jump from one attractor pattern to the next (Hebb, 1949; Pfeiffer and Foster, 2015), likely utilizing broader entorhinal-hippocampal loops to represent multiple locations and/or stimuli along a sequence. Recent work, however, demonstrated that hippocampal and entorhinal circuits are not well coordinated during slow-wave sleep and that direct entorhinal input from layer 3 is dispensable for sleep replay in CA1 (O’Neill et al., 2017; Yamamoto and Tonegawa, 2017). We propose an alternative model in which preconfigured hetero-associative networks are employed to encode and later represent a de novo experience (Cai et al., 2016; Deguchi et al., 2011; Dragoi and Tonegawa, 2011; Epsztein et al., 2011; Malvache et al., 2016) on the framework of which post-experience strengthening of intra-hippocampal auto-associative dynamics support consolidation and later recall of a memory. As part of the temporal lobe associative cortex, the hippocampus receives and integrates multimodal information during exploratory states (Aronov et al., 2017; Ji and Wilson, 2007; Terada et al., 2017; Wallenstein et al., 1998; Wood et al., 1999) and broadcasts to a large number of cortical and subcortical areas during rest and sleep (Dragoi et al., 1999; Khodagholy et al., 2017; Logothetis et al., 2012; Siapas and Wilson, 1998). The robust pre-configured sequential dynamics could form the framework on which the experience-driven within-assembly increase in millisecond-timescale neuronal coordination associates and binds features from distinct upstream sensory channels to create and consolidate unique events within a memory episode. The role of experience-dependent plasticity in hippocampal circuits is the Hebbian association of the preconfigured elements of the network with those driven by the external world. What remains to be addressed is how downstream circuits read and interpret preconfigured and memory-related sequences and how neuronal representations underlying more complex incremental learning employ and modify pre-existing dynamics for mnemonic purposes.

STAR★METHODS

LEAD CONTACT AND MATERIALS AVAILABILITY

Further information and requests for resources should be addressed to the Lead Contact, George Dragoi (george.dragoi@yale.edu).

EXPERIMENTAL MODEL AND SUBJECT DETAILS

Five Long-Evans adult male rats (300–400 g) kept experimentally naive on a 12/12-hour light-dark schedule were used for these experiments. Animals were mildly food-deprived (to no less than 90% of their body weight) starting one week before the de novo run to increase their motivation for seeking reward placed at track ends. All animals were provided with ad libitum access to water. All experimental procedures were approved by the Yale University IACUC committee and were performed in accordance with NIH guidelines for ethical treatment of animals.

METHOD DETAILS

Surgical procedures

Under isoflurane anesthesia, 3 rats were implanted with 32-tetrode independently moveable microdrives (tetrodes split between the left and right dorsal hippocampus) and 2 rats were implanted with two Neuronexus 64 channel silicon probe octatrodes, one over each side of the dorsal hippocampus area CA1, attached to miniature moveable microdrives as described earlier (Dragoi and Tonegawa, 2013b). The animals were handled before and after electrode implantation. After recovery from surgery, the electrodes were gradually lowered until the CA1 pyramidal layer of the hippocampus was reached on each side. After obtaining stable recordings from a population of neurons, the behavioral experiment was initiated.

Behavioral experiment

The behavioral experiment consisted of a Pre-Run sleep session, followed by a de novo Run session (Run 1) on a linear track, a Post-Run sleep session, and a second Run session on the same track (Run 2), all in the same room and the same day. Sleep sessions were recorded as animals slept in a small rectangular ‘sleep box’ with high opaque walls for 2–4 h. Pre-Run sleep occurred before the linear tracks were introduced into the room and after which the animals were exposed to a 1.5 m-long novel linear track placed into the room while animals were ending their Pre-Run sleep session in the box. Up until the beginning of the de novo Run session, the animals were kept naive to seeing and running on linear tracks. Chocolate sprinkles were provided as food reward at the ends of the track only. The Run session lasted for 30–45 min and the animals ran 30–50 laps on the track. This was followed by another sleep session (Post-Run sleep) in the same sleep box. Following familiarization with the linear track during Run 1, after the Post-Run sleep session ended the animals ran a second session on the same linear track, Run 2. To increase the likelihood of sleep, the behavioral experiments were performed in the light phase of the day (when rats are more likely to sleep).

Electrophysiological recordings

Recordings were performed via a multiplexed lightweight cable that connected a head-mountable amplifier with a 128-channel Neuralynx digital recording system (DigiLynx). The position of the animal was monitored continuously using an overhead camera that tracked two LEDs separated by 1.5 cm built into the headstage amplifier. Wideband LFP (1–6000 Hz), > 50 microvolts threshold-crossing putative spike waveforms (600–6000 Hz), LEDs position and a video of the experiment were recorded using the Neuralynx recording system. The multiplex cable was attached to sliding pulleys to allow the free movement of the animal during the experiment. After the behavioral experiments, the animals were transcardially perfused with 0.9% saline followed by 4% paraformaldehyde and the brains were harvested. The brains were sectioned and Nissl-stained with Cresyl violet to confirm the recording sites were in the pyramidal layer of the dorsal CA1 area of the hippocampus.

Preprocessing and unit isolation

Manual clustering of the putative units was performed using Xclust3 software as reported before (Dragoi and Tonegawa, 2013b), where the amplitude of detected spike waveforms on different adjacent recording sites, along with inter-spike interval, and cross-correlations were used to separate putative units. Putative pyramidal units were distinguished from interneurons using autocorrelations, average rate and spike width (Dragoi and Tonegawa, 2013b). Only well-isolated putative pyramidal units were used for further analysis. The position of the animal during the behavioral experiment was extracted using the 2 LEDs, any brief missing position samples were linearly interpolated.

Place cell characterization

The number of spikes during animal movement (velocity exceeding 5cm/s) in non-overlapping 1 cm bins were counted and smoothed by a 5 cm Gaussian kernel. This vector was divided by the occupancy (time spent at a speed above 5 cm/s, smoothed by a 5 cm Gaussian kernel) to determine the firing rate map on the track. Pyramidal neurons with a peak firing rate exceeding 1 Hz were considered as place cells as described earlier (Dragoi and Tonegawa, 2013b).

Detection of frames during slow-wave sleep

Candidate epochs for sequence analysis, called frames, were detected during slow-wave sleep periods in the sleep box determined based on continuous animal immobility (velocity below 1 cm/s for at least 5 minutes) and low theta/delta ratio (below 2, after Hilbert transform for respective frequencies, 6–12 Hz for theta and 1–4 Hz for delta, and smoothed with a 5 s Gaussian) to exclude epochs of rapid-eye movement sleep. In addition, sharp-wave ripples were detected using a Hilbert transform and frames containing a ripple event (175–225 Hz) were separated and used to test the robustness of our results. For these slow-wave sleep periods, the combined population activity of all putative pyramidal neurons in 1 ms bins was calculated and convolved by a Gaussian kernel of 15 ms. Periods when the population activity exceeded 2 standard deviations above the mean of the population activity, lasted between 100 ms and 800 ms and contained activation of at least 5 distinct neurons were considered as frames and used for sequence analysis.

Bayesian decoding of location and trajectories

To decode location and trajectories based on ensemble neural activity, we employed a memoryless Bayesian decoding algorithm (Davidson et al., 2009; Zhang et al., 1998) as described below.

According to Bayes’ theorem:

$$\text{Pr}(loc|spk)=\frac{\text{Pr}(loc)\mathit{\text{Pr}}(spk|loc)}{\mathit{\text{Pr}}(spk)}=\frac{\text{Pr}(loc)\mathit{\text{Pr}}(spk|loc)}{{\sum }_{j=1}^L\text{Pr}\left(lo{c}_j\right)\mathit{\text{Pr}}\left(spk|lo{c}_j\right)}$$ (1)

where Pr(loc | spk) is the posterior conditional probability of location given spikes, Pr(loc) is the prior probability of location, Pr(spk | loc) is the probability of spikes given a location, Pr(spk) is the probability of spikes, loc_j is the j^th location on the track out of a total of L locations.

Assuming that spikes follow Poisson distributions and that place cells are statistically independent (Zhang et al., 1998):

$$\text{Pr}(spk|loc)=\prod _{i=1}^{n}Pr\left(s{p}_i|loc\right)=\prod _{i=1}^n\frac{{\left(\tau f_i(\text{loc})\right)}^{s{p}_i}}{s{p}_i!}{e}^{-\tau f_i\left(loc\right)}$$ (2)

Therefore, inserting equation (2) into (1) gives:

$$\text{Pr}(loc|spk)=\mathit{\text{Constant}}(\tau ,spk)\text{Pr}(loc)\left(\prod _{i=1}^n{f}_i{(loc)}^{s{p}_i}\right)e^{-\tau \sum _{i=1}^n{f}_i\left(loc\right)}$$

where Constant(τ, spk) is a normalization factor, such that ${\sum }_{i=1}^{Pn}Pr\left(lo{c}_i|spk\right)=1,f_i\left(loc\right)$, f_i(loc) is the value of the smoothed averaged firing of the i^th neuron at location l, sp_i is the number of spikes fired by the i^th neuron in the time bin being decoded, τ is the duration of the time bin (0.25 s for active behavior on the track and 0.02 s for sleep frames) and n is the total number of neurons. Pr(loc), the prior for location, was set as uniform across the track.

First, to validate the memoryless Bayesian decoder, the activity of all neurons active on the track was binned in 0.25 s non-overlapping time bins during active behavior (velocity > 5 cm/s).

For each time bin, during the run session, the difference between the location with the maximum decoded probability and the actual location of the animal was considered as the error in decoded location.

During sleep, frames were divided into 20 ms bins. The virtual location of the animal based on this binned neural activity was determined via the above Bayesian decoding approach.

Each direction of movement on the linear track was independently analyzed.

Weighted correlations

To determine the sequential content in a frame, a linear correlation between time and location was computed, weighted by the associated posterior probabilities, r(loc,t; Pr).

Initially, the weighted mean was computed for location (m_loc):

$$m_{loc}(loc;Pr)=\sum _{i=1}^T\sum _{j=1}^{L}P{r}_{ij}lo{c}_j/\sum _{i=1}^T\sum _{j=1}^{L}P{r}_{ij}$$

followed by computation of weighted mean for time (m_t) in similar fashion. This was followed by computing the weighted covariance (covar):

$$\mathit{\text{covar}}\left(loc,t;Pr\right)=\frac{{\sum }_{i=1}^T{\sum }_{j=1}^{L}P{r}_{ij}\left(lo{c}_j-m_{loc}\left(loc;Pr\right)\right)\left(t_i-m_t\left(t;Pr\right)\right)}{{\sum }_{i=1}^T{\sum }_{j=1}^{L}P{r}_{ij}}$$

And finally, the weighted correlation (r):

$$r\left(loc,t;Pr\right)=\frac{\mathit{\text{covar}}\left(loc,t;Pr\right)}{\sqrt{\mathit{\text{covar}}\left(loc,loc;Pr\right)\left(\mathit{\text{covar}}\left(t,t;Pr\right)\right)}}$$

where loc_j is the j^th spatial bin, t_i is the i^th temporal (20ms) bin in the frame, Pr_ij is the Bayesian posterior probability for the j^th spatial bin at the i^th temporal bin, T is the total number of temporal bins and L is the total number of spatial bins. Note that ${\sum }_{j=1}^{L}P{r}_{ij}=1$ and ${\sum }_{i=1}^T{\sum }_{j=1}^{L}P{r}_{ij}=T$.

Maximum jump distance

In order to study if trajectory sequences exhibited large jumps (discontinuities in trajectory sequences) during the frames, the peak decoded virtual location was computed for each bin. The maximum of the differences between peak decoded locations in consecutive bins was considered as the maximum jump distance for a particular frame as described earlier (Silva et al., 2015).

Shuffled datasets

To reveal if each frame exhibited a significant trajectory sequence, the properties of sequences (absolute weighted correlation and maximum jump distance) were compared to two shuffled (null) datasets for each frame. The decoded probability vector for each time bin of the frame was circularly shifted by a random amount between 1 and track length minus 1. This circular shift shuffle was performed for each bin independently (space bin shuffle) as described and used earlier (Grosmark and Buzsáki, 2016; Silva et al., 2015). This shuffle randomizes any sequential structure across time bins but maintains the structure of decoded probabilities within a bin (for the most part; see manuscript for statistical issues with this shuffle). Second, a more conservative shuffle was performed, involving a permutation of the time bins within a frame (time bin shuffle) as described and used earlier (Foster, 2017; Grosmark and Buzsáki, 2016).

Two-feature P value matrix for simultaneous study of weighted correlations and maximum jump distance

In order to more rigorously quantify the properties of trajectory sequences, we simultaneously studied weighted correlations and maximum jump distances of frames, as in (Silva et al., 2015). Briefly, increasing or decreasing thresholds for absolute weighted correlations and absolute maximum jump distance, respectively, were applied to frames within a particular sleep session, and the proportion of frames passing both thresholds were calculated. The same method was employed to compute the proportion of shuffles passing these criteria as described earlier (Silva et al., 2015). To determine if the proportion of frames in the data significantly exceeded the proportions observed in shuffled datasets, the number of shuffled datasets (n = 500) with lower proportions than the real sleep was divided by the total number of shuffles. This value was subtracted from 1 to get a P value. The P value matrix was plotted to determine the profile of thresholds at which the real data exceeded shuffled datasets using these two properties of sequences. The thresholds for these properties were > 0 to > 0.9 and < 0.1 to < 1 (for absolute weighted correlations and absolute maximum jump distance respectively), with a difference of 0.1 between successive thresholds. A frame with a high absolute weighted correlation and low maximum jump distance is considered a robust trajectory experience representing the experience.

Poisson surrogate datasets

Poisson surrogate datasets were generated to determine if the significant sequential structure within Pre-Run sleep frames (or Post-Run sleep frames) was an artifact observed due to differences in hippocampal firing rates. For each sleep, the average firing rate of a cell was computed across all frames. Random spiking activity following a Poisson process was generated with the same average firing rate for that cell. This process was repeated for all cells. The resulting surrogate frames were used for sequence analysis.

Weighted circular shift space bin shuffle

Our results reveal that Pre-Run sleep has significantly higher sequential structure than the Poisson data (Figure 1F) refuting the possibility that preplay is simply due to inhomogeneities in firing rates across neurons. This finding prompted us to hypothesize that the circular space-bin shuffle employed in a previous study might not have conserved essential data characteristics, which would have led to the masking of preplay (Silva et al., 2015). In order to test this hypothesis, we first directly compared the space-bin shuffle of Pre-Run sleep and the space-bin shuffle of firing-rate matched Poisson (i.e., sPre-Run versus sPoisson). This comparison revealed that the sPre-Run dataset has significantly higher sequential structure than sPoisson (Figure S3D). These differences between Pre-Run sleep, Poisson, and their respective shuffles were also observed when weighted correlations alone were quantified and compared directly; this further confirms the significance of preplay and reveals the statistical unreliability of this shuffle type. We next sought to determine any essential properties of the data that might not be conserved in the shuffles, but would be maintained in the Poisson datasets, which could have led to the conclusions of (Silva et al., 2015). On inspection, we observed two such potentially relevant key properties of the data. First, the posteriors within the 20 ms time bin within sleep frames preferentially decode adjacent locations over others in the spatial domain (i.e., decoding field). As the space bin shuffle circularly shifts these posteriors, it can divide the spatially-compact decoding field contained within a time bin into two fields situated at the opposite edges of the finite spatial environment (Figure S3E left, red arrows mark the ‘edge effect’, Figure S4 for illustration), see also (Foster, 2017). This edge effect, a result of using the space bin shuffle procedure, can result in systematic errors and reductions in weighted correlations specifically in the shuffled distributions. Second, we observed that the mean decoded posteriors of spatial locations along the track can be highly non-uniform across the track for the Pre-Run and Poisson frames, while they become uniform in the space-bin shuffled datasets (Figure S3E left; mean decoded probabilities across track, Pre-Run versus sPre-Run: p < 10⁻¹⁰, Kolmogorov-Smirnov test). This non-uniformity in decoded location during sleep reflects and potentially results from the well-known non-uniformity in the distribution of place cells, which tend to cluster around rewards and goals located at track ends (Grosmark and Buzsáki, 2016; Hollup et al., 2001). These observations led us to hypothesize that the lack to preserve the non-uniformity in the decoded locations in the space-bin shuffles together with the edge effect contributed significantly to the reductions in the observed strength of sPoisson data-sets (Figure S3C).

To confirm that the lack of preservation of these two key data properties in the shuffles can lead to spurious results, we developed a ‘corrected space-bin shuffle’ (i.e., csPre-Run and csPoisson) for which the probability distribution of locations within frames approaches that of the highly non-uniform Pre-Run and Poisson datasets (Figure S3F left; see S4 for illustration of the shuffle development). First, the maximum decoded location in each bin within the frames of csPre-Run/csPoisson was shifted, weighted by the mean decoded posteriors across the track, to conserve non-uniformity in these shuffles. Second, the decoding field surrounding the maximum decoded location was prevented from being divided at the ends of the track to mitigate the edge effect (Figure S3F; mean decoded posteriors across the track in Pre-Run versus csPre-Run: p < 10⁻¹⁰, Kolmogorov-Smirnov test). To minimize edge effects (the peak decoded locations split across the opposite ends of the finite track), this peak was not shifted to within 10 cm of the ends of the virtual track (empirically set based on the degree of smoothing applied to the place fields). Note that this shuffle does not destroy the structure of activity within the time bin but shifted circularly by a certain amount (a pseudorandom function of the average peak decoded locations). This procedure conserved the non-uniformity in the real data to a great extent in the shuffles in some animals, while in others was not able to do so; as each time bin might have multiple decoded spatial probability peaks comparable in size, this method would not account for the non-primary peaks. This shuffle is a conservative version of the aforementioned space bin shuffle.

Compared with this corrected space-bin shuffle, Pre-Run preplay, but not Poisson data, exhibit significantly higher sequential structure (Figure S3F middle/right; compare with Figure S3E middle/right). Consistent with this observation, the degree to which csPre-Run approached the non-uniformity observed in the Pre-Run sleep correlated with how strong Pre-Run data were in comparison with their corresponding Poisson datasets (R = 0.52; p = 0.02; Figure S3G). Overall, our results demonstrate that preplay is a robust, significant phenomenon and that the apparent similarity between Pre-Run (i.e., preplay) and Poisson datasets described by (Silva et al., 2015) might be contributed largely by two statistical oversights. First, the indirect comparison of the Pre-Run/preplay and the Poisson datasets merely reveals how similar their differences from their matched space-bin shuffles were, but largely misses the significant difference between them, which is revealed here by the direct Pre-Run and Poisson datasets comparison (Figure 1F). Second, the use of space-bin shuffle, which fails to preserve crucial properties of the frames, masks the detection of sequential structure of Pre-Run sleep/preplay, which appear similar to that of Poisson datasets (Figures S3E–S3G).

Neuronal sequence order using template matching

To determine neuronal sequence order, for each place cell, the location on the track where it had the highest firing rate was determined. A template constituting order of activation in space of the place cells was constructed for each running direction (at a spatial bin size of 2 cm for consistency with previous reports). This was done by sorting the cells according to the location of their peak firing along the animal’s trajectory (Diba and Buzsáki, 2007; Dragoi and Tonegawa, 2013b). During frames, the center of mass for each place cell was used, and a Spearman correlation was computed between the ranked orders of activation in the Run template and their order of activation in time within the sleep frame. The IDs of the cells were shuffled (500 shuffles), and the same method used to compute the rank order correlation for them. When computing significance of overall preplay and replay sequences, correlation of all frames with both spatial templates were compared with the group of all one thousand shuffles (500 for each spatial template and frame) using Wilcoxon’s ranksum test. For each of the two spatial templates (one for each direction of movement), if a frame had a correlation exceeding 97.5th percentile or less than 2.5th percentile (for reverse sequences), it was considered a sequence with significant temporal order.

Simulations to study the effect of cell density/spatial bin on the template matching method

We ran a simulation to test and reveal the sensitivity of the results of template matching method to the binning of the data. We hypothesized that datasets with larger number (e.g., ~120) of simultaneously recorded neurons (Silva et al., 2015) impose constraints on analyses using the existing statistical methods for template matching, which were originally developed and validated for smaller datasets, and would thus need to be amended. The impact of cell density, i.e., average number of place cells with peak firing location in the same spatial bin, on temporal order in sleep was studied by simulating place cell sequences and sleep frames. To simulate the relationship between sleep activity and the run sequence, a virtual sequence of 120 place cells were assigned bins by random sampling without replacement, this sequence was considered the target run sequence. Then a 120×120 transition matrix was generated, in which the elements corresponding to cell transition in target run sequence were set to 1 while other elements were 0. Random noise was added to the matrix. For each simulated sleep, 15,000 sleep frames were generated by weighted sampling from place cells, in which the weight is the corresponding element in transition matrix. There were 10% to 15% of place cells in each frame. Then the correlation of simulated run sequence with simulated sleep frames was calculated (Spearman correlation). The amount of random noise was adjusted to make the correlation value of simulated activity as close as possible to the correlation value of run sequence and sleep frames in actual recording data. To test the impact of cell density, a group of run sequences were generated by using different bin size. For example, 2 cell/bin corresponding to using 60 bins for 120 cells. When multiple cells were in one bin, their order was sorted by their cell ID. The correlation of simulated sleep and run sequences with different bin size were calculated and the deviation of correlation value from chance level was evaluated.

Proportion of significant sequence events

The proportion of significant sequences were calculated by comparing the weighted correlation of each individual frames with its respective shuffles. If the weighted correlation was above the 97.5th percentile or below the 2.5th of percentile (for reverse sequences) of the shuffled distributions, it was considered a significant sequence. The proportion was calculated by dividing the number of such frames by the total frames in that sleep.

Sequence score

Weighted correlations are influenced by various additional properties of the frame including but not limited to number of cells, number of time bins, number of spikes etc., see (Grosmark and Buzsáki, 2016) for further details. Therefore, we computed a sequence score to account for such differences across frames. The sequence score is defined as the Z-score of the absolute weighted correlation of a frame relative to the absolute weighted correlations of the shuffled distributions, and is computed as follows:

$$r_Z=\frac{\left|r\right|-\mathit{\text{mean}}\left(\left|r\left(\mathit{\text{shuffled}}\right)\right|\right)}{std\left(\left|r\left(\mathit{\text{shuffled}}\right)\right|\right)}$$

Simultaneous graded thresholding of sequence score and normalized maximum jump distance

The normalized jump distance was the percentile (expressed between 0 to 1), of the maximum jump distance of a spiking event relative to that in the corresponding shuffles. Eight thresholds were set for sequence score and normalized jump distance to ensure appropriate sampling at all thresholds, ranging from −3 to 4 for sequence score and 0.125 to 1 for normalized maximum jump distance.

Equalizing net firing rate analysis

To study the effect of firing rate on sequences, the average firing rate of each cell across all frames was calculated in the sleep. The firing rates were significantly higher in the Post-Run sleep compared to the Pre-Run sleep. Spikes were randomly dropped from the Post-Run sleep until the average firing rates were equal to that of the Pre-Run sleep. One-hundred such down-sampled datasets were generated (and subsequently 500 time-bin shuffles for each down-sampled dataset). Sequence analysis on these down-sampled datasets were performed and the properties of sequences compared to that of Pre- and Post-Run sleep sequences.

Equalizing firing rates and firing rate correlations

To study the effect of experience on activity of individual neurons, we computed the mean firing rate of the neurons across all sleep frames in a session. This firing rate distribution was correlated with the peak firing rate distribution of the neurons during run to study the similarity in firing rate distributions across the population in sleep and run. Subsequently, we selectively and randomly down-sampled spikes from each cell until their firing rates within Pre-Run and Post-Run sleep frames were equal. Specifically, spikes from cells exhibiting increased firing rates within Post-Run sleep frames were randomly down-sampled from Post-Run sleep frames, while spikes from cells exhibiting reductions after experience were down-sampled from the Pre-Run sleep frames until firing rates matched for each neuron within frames in the two sleep sessions. The procedure also equalized the correlations of the distribution of firing rates to the Run.

Cell assembly detection and activation

The procedure for cell assembly detection was adapted from (Peyrache et al., 2009). Briefly, the activity of place cells during active behavior in the Run session was divided into 20 ms bins and Z-scored:

$$z_{i,t}=\frac{sp{k}_{i,t}-{\mu }_{sp{k}_i}}{{\sigma }_{sp{k}_i}}$$

where spk_i,t was the spike count of neuron i in bin t, and ${\mu }_{sp{k}_i}$ and ${\sigma }_{sp{k}_i}$ were the mean and standard deviation of neuron i’s spike counts across bins, respectively. Each direction was analyzed separately. The above Z-scoring was performed to prevent bias toward high firing neurons.

Next, we let Z be the n (number of neurons) by M (number of time bins) matrix with element (i,t) equal to z_i,t. For this matrix, comprising of the z-scored binned activity of the population of cells, cell assemblies were identified as follows:

First, a principal component analysis (PCA) was performed on matrix Z:

$$\sum _{j=1}^n{\lambda }_j{p}_j{p}_j^T=\frac{1}{n}Z{Z}^T$$

where p_j is the j^th principal component with corresponding eigenvalue λ_j, and $\frac{1}{n}Z{Z}^T$ is the correlation matrix of Z, while Z^⊤ is the transposed version of Z. To estimate the number of significant assemblies in the data, the Marcenko-Pastur law (Peyrache et al., 2009) was used. This law states that for a n by M matrix whose elements are independent and identically distributed random variables with zero mean and unit variance, all eigenvalues are asymptotically bounded to the interval $\left[{\left(1-\sqrt{n/M}\right)}^2,{\left(1+\sqrt{n/M}\right)}^2\right]$, i.e., when n, M approach infinity such that M/n converges to a finite positive value. This suggests that if the firing rate of the neurons is independent from each other, then none of the eigenvalues is expected to exceed ${\lambda }_{max}={\left(1+\sqrt{n/M}\right)}^2$. Therefore, only principal components with eigenvalues exceeding λ_max were considered as significant cell assemblies. In order, to study the activation strength during the sleep, the activity during sleep was similarly binned at 20 ms for each cell, and subsequently Z-scored. The weights of the significant principal components were used to calculate the activation strength as follows. A projection matrix, P_k, was constructed from each weight vector by taking the outer product of that weight vector. The diagonal entries of this projection matrix were set to zero to prevent high expression strength caused by the activity of single neurons. This projection matrix was quadratically multiplied to the instantaneous normalized firing rate of the neurons to get the activation strength of each significant assembly.

$$A_c\left(t\right)=z{\left(t\right)}^T{P}_{c}z\left(t\right)$$

where A_c(t) is the activation strength of cell assembly c at time t and z(t) is a vector containing the normalized firing rate of all the neurons at time t.

In order to study cell assembly activation strengths with in preplay/replay sequences, cell assembly activity in frames-only was used for further analysis. The maximum assembly activation strength for each assembly during each frame was calculated. A threshold of 5 (Peyrache et al., 2009) and a minimum activation of two cells within that time bin were used to detect significant cell assemblies.

Properties of cell assemblies and neurons within cell assemblies

Within each frame, the number of cell assemblies with activation strength above 5 (arbitrary units) and containing a minimum of 2 active neurons (to avoid detecting instances of activation with one active cell only) were considered as significant cell assemblies (Peyrache et al., 2009). These were used for further analysis. For each significant cell assembly, the bin with the maximum activation strength was considered as an ‘epoch of cell assembly activation’. The number of significant cell assemblies per frame and the proportion of frames with significant cell assembly activations were computed. This analysis was conducted separately for all frames and for the significant frames only.

Although the distribution of weights of the contributing neurons to a cell assembly lacked any multimodality, we nonetheless divided it into two categories to compare the properties of neurons belonging to various parts of the distribution. Neurons with weights 2 or more standard deviations above the mean were considered as high contributors for that cell assembly (HC), while the remaining neurons were considered as non-high contributors (non-HC).

Temporal score of cell assembly sequences

To study if temporal ordering of cell assemblies within a frame was changed by an experience, we developed a method to study temporal order of cell assemblies, similar to (Almeida-Filho et al., 2014). The times of peak activation of significant cell assemblies in each frame were found. If two assemblies were activated in the same 20 ms bin, the cell assembly with higher activation was chosen for further analysis (the results did not change if the other one was chosen; data not shown). Following this, the peak activation of each cell assembly on the track was found. The order of assemblies’ activation on the track, in space, was correlated with their order of activation in the frame, in time, for the common cell assemblies (Spearman’s Rank Order correlation; R). The cell assembly IDs were shuffled 500 times, and a similar correlation was computed for those shuffles. This analysis was restricted to frames with 5 or more significant cell assemblies. The temporal score (TS) for each cell assembly sequence was the Z-score of the correlation of that cell assembly sequence relative to its respective shuffles.

$$T{S}_z=\frac{abs\left(R\right)-\mathit{\text{mean}}\left(abs\left(R\left(\mathit{\text{shuffled}}\right)\right)\right)}{std\left(abs\left(R\left(\mathit{\text{shuffled}}\right)\right)\right)}$$

Partitioning sleep based on the proportion of place cells in frames

The proportion of active place cells (peak firing rate > 1Hz) out of all recorded place cells was calculated for each frame. Frames were further partitioned based on this proportion into ‘sleep brackets’ and various properties of the frames were compared between Pre-Run sleep and Post-Run sleep for each sleep bracket. The range for each bracket was a non-overlapping 10%. The difference between Pre-Run sleep and Post-Run sleep for these properties (firing rate correlations with Run, correlation of neuronal order of sequences with Run, cell assembly strength) were correlated with sequence score across the sleep brackets to determine if the observed differences between Post-Run and Pre-Run sleep could be explained by any of these 3 factors. As we observed an increase in difference in firing rate correlations between Post-Run sleep and Pre-Run sleep in frames with lower cell proportion brackets, we also only studied these lower brackets (< 50%). The correlation between differences in firing rate correlations and sequential content remained non-significant (R = −0.12; p = 0.84). For illustration purposes, a moving window was used with 1% increments of 20% brackets.

Neuronal order score

The neuronal order score was computed by Z-scoring the Spearman’s Rank Order correlation of neuronal sequences (using the template matching method), by their respective shuffles.

Cross-validation in an independent dataset

The main results on preplay were successfully cross-validated using the same data analysis tools in a comparable independent data-set collected from 4 adult Long-Evans male rats, collected by (Grosmark and Buzsáki, 2016). This dataset is publicly available on the CRCNS - Collaborative Research in Computational Neuroscience data sharing website at http://crcns.org/NWB. This dataset had a similar experimental protocol, with one notable difference: the electromyography-verified slow-wave sleep sessions were performed in a separate room from the one of Run sessions, and the animals were pre-trained in a different room on a cheeseboard maze task similar to (Dupret et al., 2010).

QUANTIFICATION AND STATISTICAL ANALYSIS

Statistical tests

Part of the statistical analysis was performed using permutation tests and Monte Carlo sampling methods. In addition, non-parametric statistical tests (Wilcoxon’s ranksum test or the Wilcoxon’s signed rank test) were performed unless otherwise stated. When multiple comparisons were performed, the appropriate corrections were performed. Most statistical tests were performed with the frame as the individual unit of analysis (Pre-Run sleep number of frames = 38220 versus Post-Run sleep number of frames = 17637; Table S2). Additionally, tests were performed with individual direction of an animal as the unit of analysis (n = 10). In the remaining cases, when the number of samples varied, the number of samples are presented in the Figure legends. All statistical tests with P values less 10⁻¹⁰ are presented as p < 10⁻¹⁰. Data are presented as mean ± standard error of the mean (SEM) unless otherwise stated.

DATA AND CODE AVAILABILITY

All the data are available in the manuscript or the supplementary material. The reported data are archived on file servers at Yale Medical School.

KEY RESOURCES TABLE

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Chemicals, Peptides, and Recombinant Proteins
Isoflurane	Zoetis	ANADA # 200–070
Grip cement	Teets denture material	N/A
Carprofen	Norbrook	55529-131-11
Experimental Models: Organisms/Strains
Rat: Long-Evans	Charles River	https://www.criver.com/
Software and Algorithms
MATLAB R2015b	MathWorks	https://www.mathworks.com/
Xclust3	Wilsonlab	https://github.com/wilsonlab/mwsoft64
Data acquisition software	Neuralynx	Cheetah
Other
128 Channel Digital Amplifier	Neuralynx	Digilynx
12.7 μm tungsten wires	Kanthal	PX000004
Silicon Probes	Neuronexus	Buz-64

Highlights.

• Preconfigured patterns robustly preplay future place cell sequences and trajectories

• Plasticity in trajectory replay is supported by increased cell assembly coordination

• Rate and temporal order coding do not fully account for plasticity in replay

• Plasticity in replay is mainly expressed in epochs with large neuronal participation