Abstract
A set of atomic polarizability parameters for a new polarizable Gaussian model (pGM) has been developed with the goal to accurately reproduce the polarizability anisotropy, taking advantage of its ability to attenuate all short-range electrostatic interactions, by fitting the ab initio molecular polarizability tensors (Apq) calculated at the B3LYP/aug-cc-pVTZ level. For comparison, we also rederived the parameters for three Thole models in which the 1–2 (bonded), 1–3 (separated by two bonds) and 1–4 (separated by three bonds) interactions are fully included.
The average percent errors (APEs) of molecular polarizability tensors for 4842 molecules or dimers are 2.98, 3.76, 3.28, and 3.82% for the pGM, Thole linear, Thole exponential, and Thole Amoeba models, respectively, with atom-type independent, universal screening factors (USF). The APEs are reduced further to 2.30, 2.69, 2.25, and 2.48% for the four corresponding polarizable models with atom-type dependent, variable screening factors (VSF). It is encouraging that the pGM with variable screening factors achieved APEs of 1.83 for 1155 amino acid analogs, dipeptides and tetrapeptides, 1.39 for 28 nucleic acid bases, 0.708 for 1464 water clusters, and 1.99 for 85 dimers of water and biological building blocks. Compared to the new set of models, the APEs of the old Thole models that were fitted to isotropic molecular polarizabilities are 8.7% for the Set A (without the 1–2 and 1–3 interactions) and 6.3% for the Set D (with the 1–2 and 1–3 interactions) models, respectively. MPAD, a metric of molecular polarization anisotropy difference based on the diagonal terms of molecular polarizability tensors was defined and applied to assess the polarizable models in reproducing the ab initio molecular polarization anisotropy. The MPADs are 3.71, 4.70, 4.11, and 4.77% for the pGM, Thole linear, Thole exponential, and Thole Amoeba USF models, respectively. The APEs are reduced further to 2.85, 3.58, 2.90, and 3.15% for the four corresponding VSF models. Thus, the new pGM and Thole models notably improve molecular polarization anisotropy. Since pGM attenuates all short-range electrostatic interactions, its application is expected to improve stability in charge fitting, energy and force calculations and the accuracy of multibody polarization.
Graphical Abstract
1. INTRODUCTION
Force field is an integral and critical component that forms the foundation for molecular modeling. Because of its simplicity and robustness, the effective functional form (Eq. 1) has been extensively used in many biomolecular force fields, which include AMBER FF94,1 FF99,2 FF99SB,3 FF034, FF12SB,5 FF14SB,6 CHARMM,7 OPLS,8–9 and GROMACS,10 and numerous others.
| (1) |
With GPU-accelerated and specialized high-performance computational platforms, it becomes increasingly feasible to conduct simulations at time scales of biological relevance, such as a large scale of conformational transitions in a complex biosystem. While additive models will continue to play important roles, polarizable force fields are expected to extend our ability to more adequately study complex biomolecular systems due to their ability to model changing dielectric environments. Atomic polarization effects play a critical role in ligand-receptor interactions, the interactions of ions with nucleic acids, the environmental changes during protein folding, enzymatic mechanism, and low or heterogeneous dielectric environments.11 Towards the goal of properly including polarization, a great deal of effort has been directed to developing polarizable versions of force fields. A variety of methods have been explored, including induced dipole models,11–17 the fluctuating charge models,18–23 the Drude oscillator models,24–28 and the detailed multipole expansion models.16–17
AMBER Polarizable Force Fields.
We have successfully developed a set of atomic polarizability parameters which reproduce the experimental and ab initio molecular polarizabilities for a 420-molecule dataset.12, 29 Compared to the additive models (FF992 and FF034), the Thole based polarizable models30 can dramatically reduce the RMS errors of the interaction energies for 1400 dimers for which the interaction energies at the MP2/aug-cc-pVTZ level have been calculated. Four papers that document the progress on developing the AMBER polarizable force fields have been published.12–15
In the atomic dipole interaction models (Eqs. 2–4), two variables, fe and ft, which are functions of distance between two atoms, rij, were introduced to avoid “polarization catastrophe” that may occur when two atoms are in close contact.12–13, 15, 31 Both fe and ft take the value of 1 in the Applequist model, while they can be much smaller than 1.0 when rij is small in Thole dipole interaction models.
| (2) |
| (3) |
| (4) |
| (5) |
| (6) |
Where and Ei are the static and total electrostatic fields at i-th atom, respectively, and Ei includes both the static and induced parts; and are two 3N-dimensional vectors (the superscript “T” represents transpose operation); N is the number of atoms; μi is the induced dipole at i-th atom that is determined self-consistently; fe and ft in Eq. 4, which are distance-dependent and take different functional forms for the Thole linear, exponential, and Amoeba models, are defined previously.12 Given atomic dipole interaction models defined above, it is straightforward to compute the molecular polarizability tensor via Eqs. 5–6. Here matrix B−1 is the molecular polarization matrix that accounts for both polarizations due to external field and across atoms. The molecular polarizability tensor is .
As indicated in Eq. 3, the magnitude of the induced dipole moment μi of atom i is proportional to its atomic polarizability αi. Because atomic polarizability plays a pivotal role in polarization calculations, accurate polarizability parameters are essential in the development of polarizable force field. Most of the atomic polarizability parameters were obtained by fitting to either experimental or QM molecular polarizabilities or QM electrostatic potentials.11 The atomic polarizability parameters could also be derived using other fitting schemes. For example, Dehez et al. derived atomic polarizabilities to reproduce the induction energies calculated by a QM perturbation theory32. Kaminski et al. calculated a molecule’s response to a dipolar probe located in a number of positions around the molecule using a density functional theory18. The perturbation of the electrostatic potential was then used to fit isotropic atomic polarizabilities.
Polarizability Anisotropy.
In our previous work,12 we applied a genetic algorithm to optimize atomic polarizabilities to reproduce the experimental molecular polarizabilities of 420 organic solvents for which molecular polarizabilities were derived using refractive indexes through the Lorentz-Lorenz equation.29 The fitting performance of the four sets of polarizable models were encouraging with average percent errors of the isotropic polarizabilities ranged from 1.2% to 1.5%. Extensive evaluation using binding energies for 1400 dimers indicated that these models are significantly more accurate than fixed charge models.13, 15 For example, the root-mean-square errors (RMSEs) of the binding energies are 3.73 and 3.43 kcal/mol for F941 and F034 models, respectively, about 2 kcal/mol larger than 1.41 to 1.46 kcal/mol for the polarizable models.
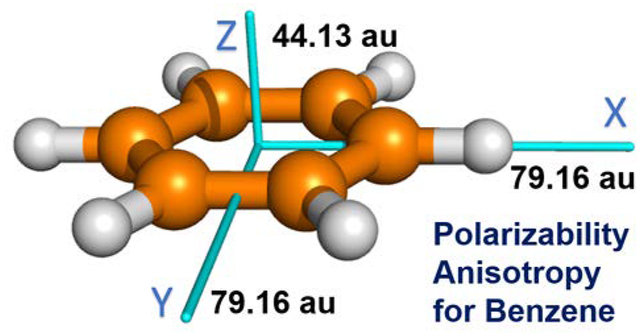
We also identified 44 dimers that have prediction errors larger than 2.5 kcal/mol. We found that most of these outliers involved π-π, cation-π, n-σ* and hydrogen-bonding interactions for which directionality is important, an indication that the previous models are still inadequate in modeling polarization anisotropy. In this work, we further examined the polarization anisotropies that are described by the three diagonal elements of molecular polarizability tensors. We found that the polarizability anisotropies predicted by the previous models were not well aligned with those obtained by the high-level ab initio calculations. For example, the three diagonal components of molecular polarizability tensor of benzene, AXX, AYY, AZZ are 81.6, 81.6 and 44.8 (a.u.) at the B3LYP/aug-cc-pVTZ theory level, and they are in agreement with experimental values (79.16, 79.16 and 44.13 a.u. for the three components, respectively),33 but were 74.10, 74.10 and 63.00 (a.u.) in AL model and 73.83, 73.83 and 64.00 (a.u.) in AE, 74.04, 74.04 and 63.17 (a.u.) in AT models. Thus, the Set A models, in which the 1–2 and 1–3 interactions were excluded, are notably less anisotropic than ab initio and experimental data. More planar molecules that have obvious polarizability anisotropy are shown in Fig. 1. Their molecular polarizabilities and the AXX, AYY, AZZ components calculated by B3LYP/aug-cc-pVTZ//B3LYP/aug-cc-pVTZ and the linear models of Set A (Model AL) and Set D (Model DL) are listed in Table 1. The diagonal terms of the molecular polarizability matrices predicted by the other models are listed in Table S1. We conclude that fitting the isotropic molecular polarizabilities is inadequate and, thus, choose to fit the quantum mechanical molecular polarizability tensors in this work instead. It is notable that the ab initio polarizability was also applied by others to derive the atomic polarizability parameters to develop polarizable force fields, such as the Drude model developed by the CHARMM developers.34
Figure 1.
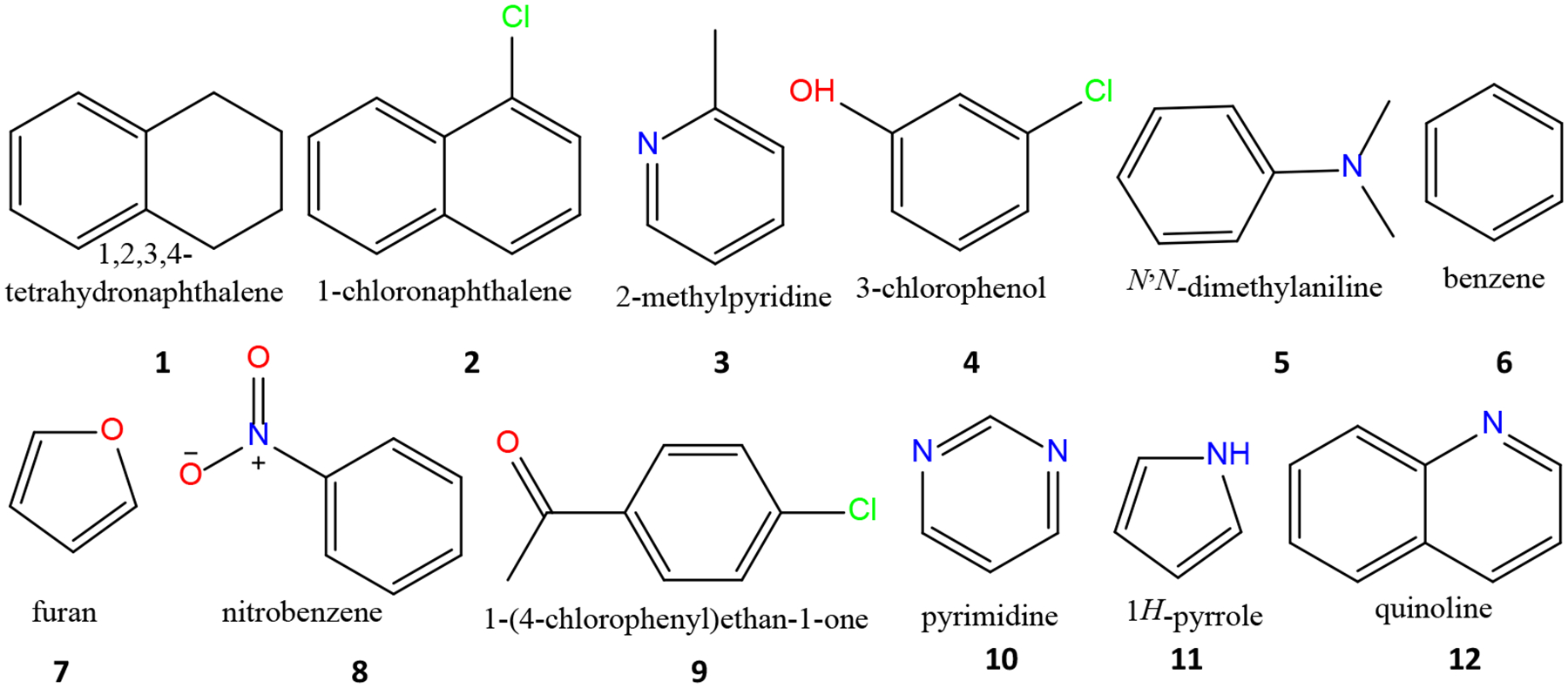
Representative molecules that have substantial polarization anisotropies.
Table 1.
Polarizability anisotropies for 12 representative planar molecules
| Comp. | Expt. | B3LYP/aug-cc-pVTZ//B3LYP/aug-cc-pVTZ | AL | DL | VSF-pGM | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| AXX | AYY | AZZ | Amol | AXX | AYY | AZZ | Amol | AXX | AYY | AZZ | Amol | AXX | AYY | AZZ | Amol | ||
| 1 | 115.1 | 143.7 | 123.0 | 79.0 | 115.2 | 132.1 | 116.4 | 96.6 | 115.0 | 143.4 | 121.6 | 78.7 | 114.6 | 146.1 | 120.7 | 77.1 | 114.7 |
| 2 | 130.7 | 174.6 | 158.0 | 73.1 | 135.2 | 143.1 | 133.8 | 103.6 | 126.8 | 160.2 | 149.1 | 72.7 | 127.3 | 172.0 | 155.6 | 72.2 | 133.3 |
| 3 | 78.1 | 99.7 | 83.5 | 50.5 | 77.9 | 86.2 | 77.9 | 68.5 | 77.5 | 98.7 | 83.4 | 51.7 | 77.9 | 99.7 | 82.6 | 50.5 | 77.6 |
| 4 | 91.8 | 120.8 | 96.5 | 54.5 | 90.6 | 95.9 | 91.7 | 77.1 | 88.2 | 112.2 | 95.0 | 54.7 | 87.3 | 125.3 | 96.8 | 54.6 | 92.2 |
| 5 | 109.9 | 144.6 | 113.5 | 71.1 | 109.7 | 125.4 | 106.2 | 87.6 | 106.4 | 137.2 | 114.1 | 68.7 | 106.6 | 142.3 | 111.7 | 68.0 | 107.3 |
| 6 | 70.5 | 81.6 | 81.6 | 44.8 | 69.3 | 74.1 | 74.1 | 63.0 | 70.4 | 82.2 | 82.2 | 43.5 | 69.3 | 81.7 | 81.7 | 43.5 | 69.0 |
| 7 | 49.6 | 58.5 | 53.4 | 35.0 | 49.0 | 52.5 | 51.0 | 48.8 | 50.8 | 57.6 | 53.3 | 33.6 | 48.1 | 61.7 | 56.2 | 34.0 | 50.6 |
| 8 | 87.7 | 117.0 | 97.1 | 49.7 | 87.9 | 97.1 | 87.6 | 74.6 | 86.4 | 108.9 | 94.1 | 52.4 | 85.1 | 122.1 | 95.8 | 49.4 | 89.1 |
| 9 | 111.4 | 169.5 | 111.9 | 67.5 | 116.3 | 129.4 | 108.5 | 93.3 | 110.4 | 150.0 | 111.8 | 69.9 | 110.6 | 178.0 | 110.6 | 68.8 | 119.2 |
| 10 | 58.0 | 70.4 | 67.2 | 37.0 | 58.2 | 63.0 | 61.9 | 54.6 | 59.8 | 70.8 | 66.1 | 38.6 | 58.5 | 70.5 | 67.1 | 37.5 | 58.4 |
| 11 | 55.5 | 61.4 | 64.2 | 39.2 | 54.9 | 57.3 | 57.6 | 53.2 | 56.0 | 62.8 | 62.3 | 36.1 | 53.7 | 63.5 | 65.2 | 36.3 | 55.0 |
| 12 | 112.4 | 165.2 | 117.2 | 62.3 | 114.9 | 123.5 | 108.8 | 90.1 | 107.5 | 145.1 | 116.6 | 62.0 | 107.9 | 156.3 | 115.0 | 61.3 | 110.9 |
To assess polarizability anisotropy, we define a metric, molecular polarizability anisotropy difference (MPAD), to measure the difference between two molecular polarizability tensors (Eq. 7).
| (7) |
where AXX, AYY, AZZ are the diagonal elements of the molecular polarizability tensor to be compared, and , and are the diagonal elements of the reference molecular polarizability tensor. MPAD measures the relative error of the diagonal elements. Although MPAD is a critical measure of the accuracy, we also measured AUE and RMSE for the entire Aij matrixes that includes both diagonal and off-diagonal terms even though the off-diagonal terms are usually small. As shown in Table 2, the MPADs are 19.01, 19.98, and 19.17% for AL, AE and AT in Set A model series, respectively. The notable deviation of the polarization anisotropy was due to the fact that Set A models do not consider the short-range 1–2 and 1–3 polarization. Indeed, when 1–2 and 1–3 polarization was included in Set D models, the polarization anisotropy was significantly improved and the MPADs were reduced to 4.49, 5.96, and 5.27% for the DL, DE and DT models, correspondingly. Thus, inclusion of 1–2 and 1–3 polarization is crucial for reproducing polarizability anisotropy. Furthermore, this implies that short-range 1–2 and 1–3 interactions, including interactions between charges and induced dipoles, should also be included for an accurate model of molecular anisotropy and the polarization anisotropy. Unfortunately, Set D models were difficult to parameterize because of the over-polarization by nearby charges that are not screened well in the standard Thole models. Thus, to represent anisotropy accurately, a model needs to have all 1–2 and 1–3 terms appropriately screened.
Table 2.
Summary of the Performance of Polarizability Models for 12 Planar Molecules
| Model | Molecular Polarizability | Molecular Polarizability Tensor | MPAD | ||||
|---|---|---|---|---|---|---|---|
| APE | AUE | RMSE | APE | AUE | RMSE | APE | |
| USF-Linear | 1.65 | 1.37 | 1.51 | 4.29 | 3.08 | 3.54 | 4.19 |
| VSF-Linear | 2.08 | 1.69 | 1.93 | 4.06 | 2.46 | 2.46 | 3.41 |
| USF-Exp | 1.83 | 1.56 | 1.92 | 5.27 | 3.95 | 4.50 | 5.40 |
| VSF-Exp | 2.04 | 1.31 | 1.36 | 3.03 | 1.84 | 2.05 | 2.61 |
| USF-Amoeba | 1.92 | 1.63 | 1.77 | 4.57 | 3.11 | 3.43 | 4.25 |
| VSF-Amoeba | 2.01 | 1.47 | 1.64 | 3.24 | 2.18 | 2.25 | 3.05 |
| USF-pGM | 1.70 | 1.40 | 1.60 | 4.27 | 3.12 | 3.61 | 4.27 |
| VSF-pGM | 2.63 | 1.72 | 1.79 | 2.84 | 1.96 | 2.13 | 2.69 |
| AA | 2.53 | 1.91 | 2.02 | 19.77 | 17.56 | 22.50 | 18.85 |
| AE | 2.66 | 2.07 | 2.30 | 20.98 | 18.56 | 23.81 | 19.98 |
| AL | 2.45 | 1.85 | 2.00 | 19.89 | 17.69 | 22.72 | 19.01 |
| AT | 2.57 | 1.98 | 2.15 | 20.11 | 17.85 | 22.88 | 19.17 |
| DA | 10.90 | 9.73 | 10.90 | 27.45 | 21.81 | 29.77 | 26.75 |
| DE | 2.75 | 2.16 | 2.29 | 7.20 | 4.74 | 4.87 | 5.96 |
| DL | 2.53 | 2.05 | 2.29 | 6.44 | 3.74 | 3.47 | 4.49 |
| DT | 2.99 | 2.25 | 2.21 | 7.24 | 4.07 | 3.65 | 5.27 |
Note: (USF, VSF)-Linear, Exp, Amoeba refer to USF and VSF Thole linear, Thole exponential, and Thole Amoeba models. They all have 100% 1–2, 1–3 and 1–4 interactions. Their functional forms are identical to those in DL, DE, DT models, respectively, with updated parameters.
Polarizable Gaussian Model and Molecular Anisotropy.
Recently, Elking et al. proposed to replace atomic point charges and multipoles with Gaussian charge densities,35–36 and derived the atomic polarizabilities in a way similar to Kaminski’s approach.18 The calculated atomic polarizabilities have errors ranging from 1 to 5% depending on molecular species and methods.37 A key advantage of the polarizable Gaussian Model is its proper screening of all short-range electrostatic interactions in a consistent manner, including, but not limited to, charge-charge, charge-dipole, charge-induced dipole, induced-dipole interactions. This is critical for stable charge-fitting in polarizable force fields when polarization of 1–2 and 1–3 charges are included and are needed to reproduce molecular anisotropy, as we reasoned before. The existence of analytical solutions for the electrostatic interactions of any order of multipoles is also a technical advantage.
A key feature of pGM is that each atomic partial charge is represented by a single Gaussian function and each dipole is represented by the derivatives of the same Gaussian function with different amplitudes. Therefore, pGM is a minimalist Gaussian polarizable model. In comparison, the GEM* method developed by Duke et al.38–39 treats nuclear charges explicitly and uses Hermite Gaussian auxiliary basis sets to reproduce atomic electron density. Intuitively, because nuclear charge and electron density have considerably different short-range electrostatic potentials, GEM* model has the potential to represent the short-range interactions more faithfully than pGM model. However, because the computational cost of the nonbonded electrostatic force calculation in simulations is nominally scaled as the square of number of functions of each atom, the multiple functions used to represent each atom in GEM* model can notably increase the computational cost in simulations. The increased number of parameters associated with the functions may also pose additional challenges in parameterization. Another major difference is that GEM*38–40, like several other efforts (e.g., Ref.41, X-pol 42, and Amoeba 16–17), uses electronic structure derived densities in order to treat molecular polarization and other effects. In comparison, pGM will follow Amber tradition and use the ab initio electrostatic potential (ESP) to fit the parameters of atomic partial charges and dipoles. While both density-based and ESP-based approaches are clearly valid, and each has achieved remarkable successes, since the ultimate goal of an electrostatic model is to reproduce the ESP in the vicinity of a molecule, the ESP-based approach, like those used in Amber and CHARMM force field development, has the benefit of convenience. In addition, the ESP-based approach has the freedom of choosing targeted region, typically 3–5 Å from molecular surface, roughly the first two layers of nonbonded neighboring atoms. Given the limited number of multipole terms that inevitably truncates the electrostatic models, such a freedom allows us to focus on the most critical regions. Since we fit the polarizability parameters to the ab initio analytic molecular polarizability tensors, our present work is consistent with the ESP-based approach.
Although pGM can be readily extended to include higher-order moments, in this work, we will focus on the polarizable dipole model. Our present goal is to develop a model comprising only charges and dipoles to reproduce molecular polarizability anisotropy and to avoid expensive calculations of higher-order moments. Specifically, we attempt to develop a model that can accurately reproduce ab initio molecular polarizability tensors.
In the pGM, fe and ft are defined by Eqs. 8–14:37
| (8) |
| (9) |
| (10) |
| (11) |
| (12) |
| (13) |
| (14) |
where and are the Gaussian densities for charge qi and dipole at nuclear center ; β is the Gaussian exponent; si and sj are the screening factors of Atoms i and j, respectively; erf(Sij) is the error function of Sij. It is noted that all the interactions including 1–2, 1–3 and 1–4, are kept in pGM. All charges and multipoles in our pGM are treated as Gaussian functions or their derivatives, which makes pGM significantly different from the existing polarizable force fields including the Amoeba force field16–17. In pGM, both the atomic polarizability, α, and the screening factors, s, are obtained from fitting ab initio data and are kept constant in force and energy calculations. When one single screening factor is used for all the atom types, the polarizable model is called a universal screening factor (USF) model, whereas a model with atom type dependent screening factor is called a variable screening factor (VSF) model. For comparison, we also refined the Set D models with both USF and VSF. The details of atomic polarizability parameterization are presented in Section 3. In the following sections we first describe the parameterization strategy, and then presented the performance of the atomic polarizability sets in reproducing the ab initio polarizability tensors. Finally, we discuss how different states (liquid vs gas) affect the molecular polarizability calculations. However, the critical assessment of the developed models in dimer interaction energy calculations will be presented in a later publication.
2. DATA SETS
Training sets.
Four training sets (Sets 1–4) in Table 3 were compiled to derive the atomic polarizabilities and screening factors using a generic algorithm.12 Set 1 consists of 580 compounds for which experimental molecular polarizabilities are available and 16 biological building blocks that are not well represented by those having experimental values. To guarantee the high quality, an entry that has percent errors of molecular polarizabilities between the experiment and B3LYP/aug-cc-pVTZ larger than 5.0% was removed from a training set of molecules. Seventeen entries from the Bosque and Sales data set29 were filtered out after applying this rule and 177 new entries which have experimentally measured molecular polarizabilities were added to Set 1. Most of the experimental data for the newly introduced entries come from CRC Handbook of Chemistry and Physics.43 Set 1 is used by us to derive most atomic polarizabilities and screen factors. Sets 2–4 comprise specific model compounds (water and charged molecules) that were used for deriving parameters for special atom types.
Table 3.
List of data sets in polarizability calculations
| Data Set | Description | # Entries |
|---|---|---|
| Set1 | Training set of organic molecules | 595 |
| Set2 | Training set of water dimers and clusters | 665 |
| Set3 | Training set of charged molecules [Part 1] | 107 |
| Set4 | Training set of charged molecules [Part 2] | 38 |
| Set5 | Dimers of amino acid analogs | 444 |
| Set6 | Dimers of nucleic acid bases | 28 |
| Set7 | Dimers of water and biologic building blocks | 85 |
| Set8 | Dipeptides | 606 |
| Set9 | Tetrapeptides | 105 |
| Set10 | Organic molecules | 1242 |
| Set11 | Water clusters | 799 |
| Set12 | Charged molecules | 57 |
| Set13 | Dimers of water-charged molecules | 61 |
| Total | 4842 |
Test Sets.
Nine test sets (Sets 5–13) in Table 3 were compiled to evaluate the performance of the polarizable models. Sets 5 and 6 consist of dimers of biological building block analogs; Set 7 includes dimers formed between water and biological building block analogs; Sets 8–9 comprise dipeptides and tetrapeptides; Set 10 contains 1260 structurally diverse molecules that well represent the chemical space of organic and pharmaceutical molecules; Set 11 collects water clusters (up to 10 water molecules); Sets 12 and 13 are charged molecules and dimers formed between water and charged molecules, respectively. In total, there are 4842 molecules/dimers in our training and test data sets.
The Smiles strings of molecules that have measured molecular polarizabilities are presented in the Table S2A. The Smiles strings of charged molecules or dimers (Sets 3–4, 12–13) are presented in Table S2B. The measured and calculated molecular polarizabilities of the 730 molecules in TableS2A are listed in Table S3.
3. METHODS
Ab Initio Calculations.
Although experimental data set for isotropic polarizability is readily available, accurate measurements of the polarizability tensors, Aij, are rather limited. Hickey and Rowley33 recently evaluated a set of ab initio methods for calculating molecular dipole moments and polarizabilities using nine molecules (Table S4) for which the experimental Aii (diagonal elements only) are available. In present work, we rely on ab initio methods to generate reference data Aij tensors. A benefit of this approach is the ability to extend the training sets to many interesting molecules not covered by the previous study, such as water clusters and charged molecules.
We further evaluated different combinations of ab initio methods and optimization methods for a set of nine molecules (Table 4). Moreover, four ab initio protocols, B3LYP/atz//B3LYP/adz, B3LYP/atz//B3LYP/atz, MP2/adz//MP2/6–311++G(d,p) and MP2/atz//MP2/6–311++G(d,p), were extensively evaluated using 366 molecules selected from Set 1 for which the experimental molecular polarizabilities were reported by Bosque and Sales.29 In this paper, atz and adz are the abbreviations of aug-cc-pVTZ and aug-cc-pVDZ, respectively. Molecular polarizabilities calculated at the B3LYP/atz//B3LYP/atz level were used as references to derive both the atomic polarizability and screening factor parameters, as this model can better reproduce experimental molecular polarizabilities and molecular polarizability tensors within reasonable computer time than all other models we examined. For molecules containing iodine, a user-specified basis set was applied: CEP-121 for I and atz for H, C, N, O, S, P, F, Cl and Br. It is worth pointing out the importance of choosing proper basis set to model polarizability for iodine-containing compounds, as discussed elsewhere.44–45 Here we examined several potential basis sets and settled down on the one with the least error, though it is still not satisfactory. Therefore, the iodine parameters are our best guesses and will be refined upon the availability of improved basis set. All ab initio calculations were performed using the Gaussian 09 software package46 and all MP2 calculations in this work were performed with the frozen-cores approximation.
Table 4.
Performance of ab initio methods in anisotropic polarizability calculation for a set of nine compounds that have experimental molecular polarizability tensors.
| Ab Initio Model | Diagonal Terms Aii | Gamma | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Optimization | Polarizability | AUE | RMSE | APE | RMS APE | AUE | RMSE | APE | RMS APE |
| B3LYP/6–311++G(d,p) | B3LYP/adz | 3.13 | 4.14 | 7.06 | 8.39 | 1.67 | 2.29 | 17.47 | 27.15 |
| B3LYP/6–311++G(d,p) | B3LYP/atz | 2.78 | 3.81 | 5.52 | 6.87 | 1.58 | 2.26 | 7.2 | 8.59 |
| MP2/6–311++G(d,p) | MP2/adz | 3.4 | 4.46 | 7.78 | 9.14 | 2.22 | 2.97 | 15.9 | 20.01 |
| MP2/6–311++G(d,p) | MP2/atz | 3.12 | 4.2 | 6.43 | 7.81 | 1.98 | 2.72 | 8.07 | 9.47 |
| B3LYP/adz | B3LYP/adz | 2.99 | 3.9 | 6.68 | 7.96 | 1.54 | 2.12 | 18.63 | 30.05 |
| B3LYP/atz | B3LYP/atz | 2.85 | 3.95 | 5.67 | 7.08 | 1.66 | 2.36 | 7.71 | 8.89 |
| MP2/adz | MP2/adz | 3.19 | 4.08 | 7.22 | 8.45 | 2.07 | 2.66 | 19.75 | 27.55 |
| MP2/atz | MP2/atz | 3.19 | 4.37 | 6.61 | 8.17 | 2.08 | 2.88 | 8.86 | 10.33 |
| B3LYP/atz | B3LYP/adz | 3.21 | 4.28 | 7.21 | 8.59 | 1.71 | 2.38 | 16.79 | 25.95 |
| B3LYP/atz | B3LYP/atz | 2.85 | 3.95 | 5.67 | 7.08 | 1.65 | 2.36 | 7.71 | 8.89 |
| B3LYP/atz | MP2/adz | 3.5 | 4.69 | 7.92 | 9.33 | 2.32 | 3.17 | 19.41 | 26.01 |
| B3LYP/atz | MP2/atz | 3.21 | 4.43 | 6.56 | 8.01 | 2.09 | 2.92 | 10.96 | 13.05 |
Parameterization.
The genetic algorithm (GA) program for developing the Sets A-D polarization models12 was modified to derive atomic polarizabilities and screening factors to reproduce the diagonal elements of ab initio Aij calculated at the B3LYP/atz//B3LYP/atz level. Two scenarios were considered: using a universal screening factor for all atom types and variable screening factors for different atom types. The latter allowed us to better reproduce the ab initio polarization anisotropies.
A step-by-step, bottom-up strategy was applied to derive polarizability and screening factor parameters for the training set of molecules. First of all, parameterizations were performed only for the neutral molecules for which the same atom type definitions described in our previous work were applied.12 The atom type definition file, which is a part of the supporting material (Table S5), can be applied to assign atom types using the atomtype program in Antechamber.47 For the universal screening factor scheme, the screening factor of a polarizable model was determined in this step and was being used in the successive parameterization steps. Next, the polarizability parameters and screening factors were derived only for the water molecule. In the last two steps, new atom types were introduced for the positively and negatively charged functional groups as their chemical environments are distinct from those found in neutral molecules. The parameters of other atom types optimized in Steps 1 and 2 were applied directly to charged molecules without further optimization. For each model and each optimization step, six parallel GA runs were performed and the one with the best APEs of the three diagonal elements of Aij was selected as the final models.
Molecular Polarizability Calculations in Liquid State
Since the ab initio molecular polarizabilities are calculated in gas-phase whereas many experimental measurements are conducted in liquid phase in which nearby molecules have the potential to introduce cross polarization, it is necessary to investigate how the liquid state influences molecular polarizability calculations. We performed molecular dynamics (MD) simulations for a set of 109 solvents for which the experimental molecular polarizabilities and densities are available. These MD simulations were performed using the additive GAFF48 in rectangular boxes of dimensions 35 Å or larger and PME49. For each solvent, a constant pressure MD simulation was first performed for two nanoseconds; after the box dimensions were adjusted to match the experimental density, a constant volume simulation was then performed for additional ten nanoseconds. Twenty-five snapshots from the constant volume MD simulation were collected for post-analysis to calculate the molecular polarizabilities in the liquid state for each polarizability model by comparing molecular polarizabilities with and without the intermolecular polarization.
It should be noted that we did not intend to calculate the liquid polarizability which includes molecular reorientation in electric field and is out of the scope of this work. Instead we intend to investigate how the condensed phase environment affects the molecular polarizabilities when inter-molecular polarization is considered. In comparison, the ab initio molecular polarizability tensors are calculated in gas phase without the inter-molecular polarization. In detail, we first calculated the mean molecular polarizability, Am, without the inter-molecular polarization for each snapshot and averaged over all molecules in the simulation box. We then calculated the ensemble molecular polarizability, Aensemble, with the inter-molecular polarization by constructing the inter-atomic polarization matrix (B in Eqns. 5 and 6) that includes all atoms in the system with the minimum image convention. The average molecular polarizability tensor was calculated from B−1. By comparing Am and As = Aensemble/nmol we were able to determine the influence of liquid state on the polarizability calculations, where nmol is the number of molecules in the simulation box.
GA Optimization.
GA is an effective method in optimizing a complex landscape that have multiple minima or maxima. We introduced both the “elite chromosomes” and “random chromosomes” to make GA escape from being trapped in local minima and keep the best “chromosomes” simultaneously.50 For the first step of our stepwise parameterization procedure, there are 16 atomic polarizability parameters and one screening factor parameter to be optimized for USF models; whereas the parameters to be optimized are almost doubled for VSF models. The GA fitness is defined as the reciprocal of the APE of Aii plus 1.0 and takes values from 0 to 1. Given the fact that most test set APEs are even smaller than those for the training sets (discussed in detail in following section), our polarizability models should be free from the overfitting problem. This conclusion is further supported by the similar GA fitness scores of six independent runs using different random number seeds for each polarizable model. For example, the GA fitness scores are 0.3161, 0.3161, 0.3156, 0.312, 0.314 and 0.316, for six GA runs. The corresponding APEs are 2.163, 2.164, 2.168, 2.200, 2.187 and 2.166%.
4. RESULTS AND DISCUSSION
An Initio Calculations.
Since experimental polarization anisotropy data are only available for a few compounds, a reliable ab initio method must be identified to produce reference data. We evaluated twelve ab initio methods and found that molecular polarizabilities based on B3LYP/aug-cc-pVTZ outperform other methods including MP2/aug-cc-pVTZ in reproducing the experimental results of the Bosque & Sales’ data set. The significantly reduced computational cost of B3LYP method in comparison to the MP2 method is also beneficial since it allows calculation for much larger data set.
The performance of 12 ab initio methods in molecular polarizability calculations for nine compounds for which experimental Aii are available, is summarized in Table 4. For the same basis set, B3LYP always has smaller average percentage errors (APE) than MP2. For the same basis set, both B3LYP and MP2, have smaller APE when the larger the basis set is used. The theory level used for geometry optimization has small impact on the polarizability calculations. For example, the APEs for the MP2/atz method are 6.43, 6.61 and 6.56% for the following three optimization methods: MP2/6–311++G(d,p), MP2/atz and B3LYP/atz, respectively. The Aij matrixes calculated by the above ab initio methods were listed in Table S4. An interesting observation is that all ab initio methods underestimated the molecular polarizabilities in this small set. This is due to both the accuracy of the methods as well as the fact that the ab initio calculations were performed in gas-phase. We will explore the second issue further later. For a much larger data set, which collects 366 compounds having experimental molecular polarizabilities, four ab initio methods were evaluated. Again, B3LYP/atz//B3LYP/atz outperforms all other methods with the smallest APE of 1.76% and highest correlation coefficient square, 0.9917 (Table 5). The Aij matrixes calculated by the four ab initio methods were listed in Table S3. Interestingly, the APE for the MP2/atz//MP2/6–311++G(d,p) method (2.39%) performs worse than that for B3LYP/adz//B3LYP/adz (2.12%). Based on these results, B3LYP/atz//B3LYP/atz was selected to calculate Aij for all the training and test molecules.
Table 5.
Performance of molecular polarizability calculations using four ab Initio methods for 366 compounds
| Ab Initio Methods | AUE | RMSE | APE | RMS APE | R2 | |
|---|---|---|---|---|---|---|
| Polarizability | Optimization | |||||
| B3LYP/atz | B3LYP/adz | 1.74 | 2.58 | 2.12 | 3.01 | 0.9913 |
| B3LYP/atz | B3LYP/atz | 1.41 | 2.19 | 1.76 | 2.68 | 0.9917 |
| MP2/adz | MP2/6–311++G(d,p) | 2.04 | 2.98 | 2.82 | 4.05 | 0.9877 |
| MP2/atz | MP2/6–311++G(d,p) | 1.79 | 2.45 | 2.39 | 3.22 | 0.9911 |
For the 730 molecules that have experimental molecular polarizability (Table S2A), the B3LYP/atz//B3LYP/atz polarizabilities have been successfully calculated for 728 molecules (Table S3). The 584 molecules that have the percent errors smaller than 5.0% were selected as training set molecules in Set 1. The remaining 144 molecules, most were from the molecules outside the Bosque and Sales dataset, were identified as outliers. Among the 11 outliers in the Bosque and Sales dataset, seven molecules are halides and five of them contain iodine. The large prediction errors for iodides are understandable as iodine is out of coverage of the aug-cc-pVTZ basis set and a smaller basis set CEP-121G was used for iodine in the calculation. The experimental vs ab initio molecular polarizability scatter plots are shown in Fig 2. The APE of the training set is 1.73% and that of all 723 molecules is 3.68%.
Fig 2.
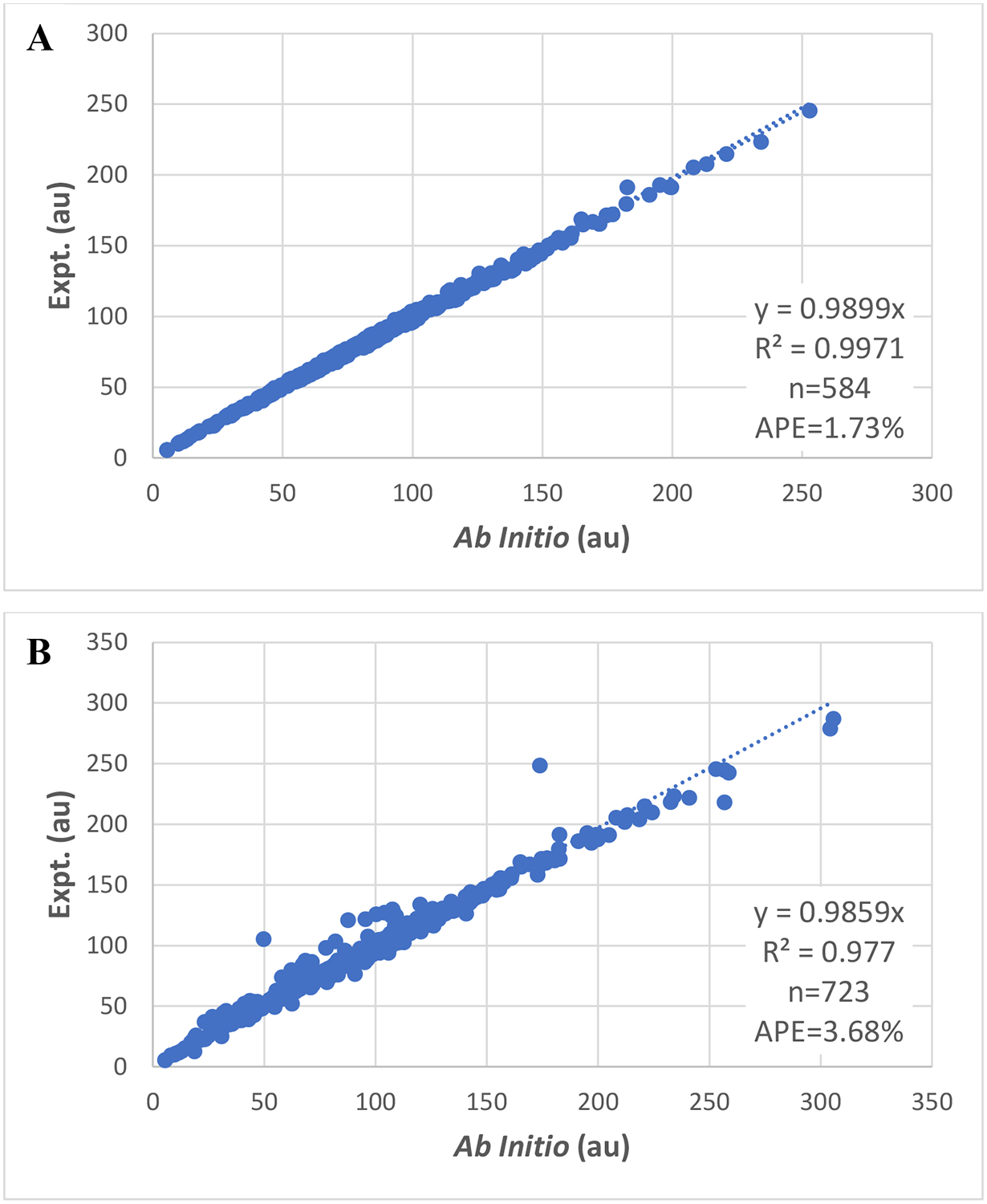
Scatter plots of experimental versus ab initio molecular polarizability for molecules for which experimental data are available. (A): molecules having percent errors smaller than 5.0%; (B): molecules having percent errors smaller than 50.0%. In this work, unless otherwise noted, polarizabilities are reported in atomic units.
Evaluation of Previous Set A and Set D Models.
We first evaluated the performance of four Set A and four Set D polarizability models that were developed previously. The difference between these two model sets is at the treatment of 1–2 and 1–3 interactions; all 1–2 and 1–3 interactions are turned off in Set A models and included in Set D models. Because these models were previously developed by fitting isotropic molecular polarizability that lacks consideration of anisotropy, we anticipate poor performance when we test against the polarizability anisotropy. Indeed, as shown in Table S6, the APEs of 8.76, 8.88, 8.57, 8.65% for the Applequist, Thole Linear, Thole Exponential and Thole Amoeba models, respectively, are quite similar and all are more than 8.5%. The MPAD for the four Set A models are around 10%. For the Set D models in which the 1–2 and 1–3 interactions are turned on, the APEs of the three Thole polarizable models are 6.33, 6.13, 6.77% for Thole Linear, Exponential and Amoeba, respectively (Table S7). Similarly, the MPADs are also reduced for the three Thole models. Thus, Thole models with 1–2 and 1–3 interactions included perform better than those without the 1–2 and 1–3 interactions. A notable exception is the Applequist model with 1–2 and 1–3 interactions that has a significantly larger average error of 21.08%, even much worse than the Applequist model without 1–2 and 1–3 interactions. Clearly, the Applequist model with 1–2 and 1–3 interactions is the most inferior model of all. This is not surprising because, unlike Thole models, Applequist model is a point dipole model that does not attenuate short-range polarization. Thus, the fact that the Applequist with 1–2 and 1–3 interaction is significantly worse than all other models is indicative to the need of appropriate attenuation of the short-range interactions.
Given the 6–9% error of the previous Thole models, regardless of inclusion of 1–2 and 1–3 interactions, it is obvious that neither set is adequate to model polarizability anisotropy. Furthermore, the fact that the Set D models are not satisfactory suggests that only using experimental isotropic molecular polarizabilities to train models is insufficient. The following USF and VSF models were developed using the molecular dipole polarizability tensors calculated at the B3LYP/atz//B3LYP/atz level.
Universal Screening Factor Models.
USF models were developed for the following four polarizability frameworks based on induced dipoles: pGM, Thole Linear, Thole Exponential, and Thole Amoeba. In all these models, the 1–2, 1–3 and 1–4 interactions are fully included without scaling. The performance of these models in anisotropic polarizability calculations is summarized in Table 6. Since the off-diagonal terms are usually small, often leading to enormous percentage errors, we only report AUE and RMSE for the entire Aij matrixes. The APEs of Aii for all the data are 2.98, 3.76, 3.28, and 3.82% for the pGM, Thole Linear, Thole Exponential, and Thole Amoeba, respectively and the RMSEs are 2.73, 3.01, 2.74, and, 3.07au, respectively. The MPADs are 3.71, 4.70, 4.11, and 4.77% for the aforementioned four models, correspondingly. We note that the pGM outperforms the three Thole polarizable models in calculation of molecular polarizabilities.
Table 6.
Summary of four universal screen length dipole-interaction polarizable models in anisotropic polarizability calculations.
| Universal Screening Length | Set1 | Set2 | Set3 | Set4 | Set5 | Set6 | Set7 | Set8 | Set9 | Set10 | Set11 | Set12 | Set13 | All | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| #Data | 595 | 665 | 107 | 38 | 444 | 28 | 85 | 606 | 105 | 1252 | 799 | 57 | 61 | 4842 | |
| Thole Linear | |||||||||||||||
| Diagonal Elements | AUE | 2.65 | 0.87 | 3.78 | 5.71 | 2.47 | 6.26 | 2.22 | 3.82 | 6.69 | 5.82 | 0.80 | 4.02 | 7.83 | 3.28 |
| RMSE | 3.25 | 1.00 | 4.27 | 6.62 | 2.79 | 7.38 | 2.55 | 4.54 | 8.29 | 7.21 | 0.92 | 4.57 | 8.88 | 3.96 | |
| APE | 3.35 | 3.13 | 4.70 | 5.67 | 1.94 | 2.68 | 3.05 | 2.71 | 2.79 | 5.41 | 3.13 | 6.76 | 10.20 | 3.76 | |
| All elements | AUE | 1.59 | 0.53 | 2.59 | 3.72 | 1.92 | 4.47 | 1.48 | 2.77 | 4.23 | 3.50 | 0.49 | 2.50 | 4.38 | 2.09 |
| RMSE | 2.44 | 0.75 | 3.45 | 5.13 | 2.38 | 6.07 | 1.98 | 3.60 | 6.11 | 5.36 | 0.69 | 3.50 | 6.44 | 3.01 | |
| Molecular Polarizability | AUE | 1.39 | 0.60 | 2.39 | 3.70 | 1.07 | 1.73 | 1.36 | 3.14 | 5.37 | 4.41 | 0.54 | 2.31 | 4.77 | 2.29 |
| APE | 1.67 | 1.80 | 2.94 | 3.81 | 0.89 | 0.80 | 1.85 | 2.36 | 2.39 | 4.17 | 1.83 | 3.77 | 5.91 | 2.51 | |
| MPAD | APE | 4.12 | 3.75 | 5.36 | 6.71 | 2.18 | 3.48 | 3.60 | 3.38 | 3.67 | 7.18 | 3.76 | 7.63 | 11.50 | 4.70 |
| Thole Exponential | |||||||||||||||
| Diagonal | AUE | 2.62 | 0.36 | 3.31 | 5.83 | 2.41 | 8.12 | 1.51 | 2.14 | 3.29 | 6.27 | 0.33 | 3.96 | 7.40 | 2.94 |
| RMSE | 3.22 | 0.43 | 3.86 | 6.76 | 2.80 | 9.97 | 1.77 | 2.58 | 3.86 | 7.83 | 0.39 | 4.66 | 8.60 | 3.60 | |
| APE | 3.32 | 2.09 | 4.33 | 5.44 | 1.79 | 3.33 | 2.17 | 1.52 | 1.41 | 5.69 | 1.98 | 7.00 | 9.99 | 3.28 | |
| All Elements | AUE | 1.55 | 0.28 | 2.29 | 3.63 | 1.83 | 5.35 | 1.07 | 1.74 | 2.31 | 3.68 | 0.26 | 2.43 | 4.14 | 1.87 |
| RMSE | 2.40 | 0.37 | 3.09 | 5.05 | 2.31 | 7.66 | 1.42 | 2.21 | 3.10 | 5.75 | 0.35 | 3.53 | 6.22 | 2.74 | |
| Molecular Polarizability | AUE | 1.35 | 0.16 | 1.95 | 4.03 | 1.22 | 6.65 | 0.60 | 1.36 | 2.25 | 4.72 | 0.13 | 2.06 | 4.38 | 1.97 |
| APE | 1.63 | 0.87 | 2.45 | 3.79 | 0.89 | 2.99 | 0.83 | 1.03 | 1.02 | 4.36 | 0.80 | 3.46 | 5.50 | 2.04 | |
| MPAD | APE | 4.05 | 2.41 | 4.94 | 6.38 | 2.05 | 4.55 | 2.56 | 1.87 | 1.71 | 7.62 | 2.30 | 7.86 | 11.55 | 4.11 |
| Thole Amoeba | |||||||||||||||
| Diagonal Elements | AUE | 2.60 | 0.78 | 3.83 | 5.34 | 2.71 | 5.90 | 2.16 | 4.23 | 7.34 | 5.81 | 0.74 | 4.10 | 7.62 | 3.33 |
| RMSE | 3.20 | 0.90 | 4.35 | 6.39 | 3.12 | 7.08 | 2.50 | 5.05 | 9.24 | 7.19 | 0.84 | 4.62 | 8.75 | 4.03 | |
| APE | 3.25 | 3.22 | 4.96 | 5.40 | 2.08 | 2.54 | 3.01 | 3.00 | 3.04 | 5.36 | 3.23 | 7.07 | 10.22 | 3.82 | |
| All Elements | AUE | 1.57 | 0.50 | 2.59 | 3.58 | 2.06 | 4.30 | 1.47 | 3.06 | 4.63 | 3.49 | 0.48 | 2.50 | 4.27 | 2.13 |
| RMSE | 2.42 | 0.69 | 3.45 | 5.04 | 2.59 | 5.87 | 1.95 | 4.00 | 6.79 | 5.35 | 0.65 | 3.50 | 6.34 | 3.07 | |
| Molecular Polarizability | AUE | 1.41 | 0.48 | 2.57 | 3.64 | 1.32 | 2.40 | 1.24 | 3.43 | 5.85 | 4.40 | 0.44 | 2.26 | 4.64 | 2.33 |
| APE | 1.66 | 1.57 | 3.35 | 3.91 | 1.07 | 1.07 | 1.67 | 2.58 | 2.60 | 4.11 | 1.58 | 3.84 | 5.91 | 2.48 | |
| MPAD | APE | 4.02 | 3.82 | 5.65 | 6.71 | 2.43 | 3.31 | 3.55 | 3.76 | 4.09 | 7.10 | 3.81 | 7.75 | 11.61 | 4.77 |
| Polarizable Gaussian Model (pGM) | |||||||||||||||
| Diagonal Elements | AUE | 2.49 | 0.26 | 3.28 | 4.88 | 2.50 | 6.00 | 1.89 | 3.55 | 6.57 | 5.53 | 0.25 | 3.84 | 7.23 | 2.94 |
| RMSE | 3.04 | 0.29 | 3.81 | 5.71 | 2.88 | 7.07 | 2.18 | 4.32 | 8.23 | 6.83 | 0.27 | 4.40 | 8.39 | 3.57 | |
| APE | 3.14 | 1.04 | 4.28 | 4.70 | 1.95 | 2.56 | 2.73 | 2.53 | 2.74 | 5.12 | 1.04 | 6.81 | 9.72 | 2.98 | |
| All Elements | AUE | 1.49 | 0.22 | 2.28 | 3.23 | 1.87 | 4.28 | 1.30 | 2.57 | 4.10 | 3.31 | 0.22 | 2.38 | 4.05 | 1.89 |
| RMSE | 2.29 | 0.27 | 3.10 | 4.43 | 2.35 | 5.77 | 1.71 | 3.41 | 6.05 | 5.07 | 0.26 | 3.37 | 6.09 | 2.73 | |
| Molecular Polarizability | AUE | 1.32 | 0.10 | 1.99 | 3.13 | 1.17 | 2.85 | 0.89 | 2.85 | 5.31 | 4.09 | 0.09 | 2.08 | 4.37 | 2.01 |
| APE | 1.57 | 0.40 | 2.55 | 3.16 | 0.95 | 1.27 | 1.27 | 2.17 | 2.37 | 3.79 | 0.36 | 3.54 | 5.53 | 1.92 | |
| MPAD | APE | 3.84 | 1.19 | 4.93 | 5.61 | 2.23 | 3.29 | 3.19 | 3.23 | 3.65 | 6.72 | 1.17 | 7.55 | 11.20 | 3.71 |
The atomic polarizabilities and screening factors are listed in Table S8 for the four USF models. The performance of the USF models varies for different datasets and the neutral molecules have smaller APEs than the charged molecules (Sets 3–4 and 12–13). For the neutral molecules, the APEs for the training sets (Sets 1 and Set 2) are comparable to those for the test sets (Sets 5–11). It is encouraging that the building blocks of biomolecules and water have smaller APEs. Taking pGM as an example, the APEs are 1.95, 2.56, 2.73, 2.53, 2.74, 1.04% for amino acid analogs, nucleic acid analogs, water-amino acid and water-nucleic acid analog dimers, dipeptides, tetrapeptides, water clusters, respectively.
Variable Screening Factor Models.
Four VSF models were developed for the four aforementioned polarizability frameworks. The performance of those VSF models were summarized in Table 7. Compared to USF, the VSF models have better performance in reproducing Aii (diagonal terms), Aij (whole matrixes) and molecular polarizabilities. The APEs of Aii are 2.30, 2.69, 2.25, and 2.48% for the pGM, Thole Linear, Thole Exponential, Thole Amoeba, respectively. The RMSEs of Aij are 2.05, 2.69, 2.12, and 2.35 au for the above four models, respectively. Similar trend was observed for the MPADs, which are 2.85, 3.58, 2.90, and 3.15% for the four aforementioned models, correspondingly. The APEs of the molecular polarizabilities are also greatly reduced for the four VSF polarizability models, which are 1.57, 1.95, 1.66, and 1.76%, respectively. Compared to USF models, the difference of the performance among the models is smaller. Based on those results, we concluded that pGM and Thole Exponential performs better than the other two polarizability models.
Table 7.
Summary of four variable screen length dipole-interaction polarizable models in anisotropic polarizability calculations.
| Variable Screening Factors | Set1 | Set2 | Set3 | Set4 | Set5 | Set6 | Set7 | Set8 | Set9 | Set10 | Set11 | Set12 | Set13 | All | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| #Data | 595 | 665 | 107 | 38 | 444 | 28 | 85 | 606 | 105 | 1252 | 799 | 57 | 61 | 4842 | |
| Thole Linear | |||||||||||||||
| Diagonal Elements | AUE | 1.93 | 0.25 | 3.61 | 5.18 | 2.57 | 10.10 | 1.68 | 2.89 | 5.04 | 5.60 | 0.22 | 3.96 | 7.03 | 2.81 |
| RMSE | 2.49 | 0.28 | 4.29 | 6.17 | 3.10 | 12.04 | 1.99 | 3.55 | 5.78 | 7.25 | 0.25 | 4.63 | 7.94 | 3.52 | |
| APE | 2.30 | 0.95 | 4.60 | 5.10 | 1.92 | 4.09 | 2.33 | 2.06 | 2.20 | 4.79 | 0.93 | 6.74 | 9.71 | 2.69 | |
| All Elements | AUE | 1.19 | 0.18 | 2.47 | 3.35 | 1.95 | 6.38 | 1.17 | 2.30 | 3.50 | 3.33 | 0.17 | 2.43 | 3.91 | 1.82 |
| RMSE | 1.91 | 0.23 | 3.38 | 4.75 | 2.54 | 9.04 | 1.56 | 2.95 | 4.52 | 5.33 | 0.21 | 3.48 | 5.74 | 2.69 | |
| Molecular Polarizability | AUE | 1.16 | 0.12 | 2.27 | 3.38 | 1.64 | 8.23 | 0.94 | 2.26 | 3.70 | 4.52 | 0.09 | 2.20 | 4.16 | 2.07 |
| APE | 1.29 | 0.42 | 2.78 | 3.40 | 1.28 | 3.67 | 1.25 | 1.70 | 1.68 | 4.11 | 0.37 | 3.71 | 5.60 | 1.95 | |
| MPAD | APE | 3.08 | 1.04 | 5.48 | 6.10 | 2.33 | 5.44 | 2.78 | 2.62 | 2.60 | 6.98 | 1.02 | 7.70 | 10.90 | 3.58 |
| Thole Exponential | |||||||||||||||
| Diagonal Elements | AUE | 1.57 | 0.20 | 3.03 | 4.13 | 2.07 | 5.95 | 1.37 | 2.30 | 4.08 | 4.44 | 0.16 | 3.72 | 6.71 | 2.25 |
| RMSE | 1.97 | 0.23 | 3.47 | 4.70 | 2.38 | 7.35 | 1.57 | 2.79 | 5.02 | 5.59 | 0.19 | 4.28 | 7.65 | 2.76 | |
| APE | 1.86 | 0.80 | 4.09 | 4.25 | 1.63 | 2.36 | 2.01 | 1.64 | 1.71 | 3.97 | 0.73 | 6.63 | 9.39 | 2.25 | |
| All Elements | AUE | 0.94 | 0.18 | 2.03 | 2.77 | 1.53 | 3.64 | 0.96 | 1.77 | 2.72 | 2.64 | 0.16 | 2.26 | 3.75 | 1.45 |
| RMSE | 1.49 | 0.23 | 2.76 | 3.72 | 1.94 | 5.44 | 1.26 | 2.29 | 3.80 | 4.13 | 0.22 | 3.27 | 5.56 | 2.12 | |
| Molecular Polarizability | AUE | 1.06 | 0.14 | 1.86 | 2.18 | 1.25 | 5.35 | 0.51 | 1.63 | 2.93 | 3.49 | 0.11 | 2.21 | 3.90 | 1.63 |
| APE | 1.21 | 0.60 | 2.42 | 2.37 | 0.96 | 2.41 | 0.77 | 1.24 | 1.31 | 3.32 | 0.55 | 3.93 | 5.20 | 1.66 | |
| MPAD | APE | 2.40 | 0.96 | 4.57 | 4.80 | 1.87 | 3.32 | 2.29 | 2.07 | 2.23 | 5.53 | 0.89 | 7.35 | 10.63 | 2.90 |
| Thole Amoeba | |||||||||||||||
| Diagonal elements | AUE | 1.77 | 0.23 | 3.73 | 4.10 | 2.02 | 4.40 | 1.35 | 2.84 | 4.72 | 4.87 | 0.19 | 3.95 | 6.40 | 2.47 |
| RMSE | 2.28 | 0.25 | 4.31 | 4.72 | 2.37 | 5.43 | 1.62 | 3.52 | 5.44 | 6.04 | 0.21 | 4.54 | 7.26 | 3.02 | |
| APE | 2.11 | 0.81 | 4.90 | 4.36 | 1.50 | 1.84 | 1.91 | 2.01 | 2.05 | 4.51 | 0.77 | 6.91 | 9.03 | 2.48 | |
| All elements | AUE | 1.10 | 0.14 | 2.45 | 2.80 | 1.62 | 3.41 | 1.00 | 2.35 | 3.40 | 2.92 | 0.12 | 2.39 | 3.63 | 1.63 |
| RMSE | 1.76 | 0.19 | 3.33 | 3.72 | 2.06 | 4.73 | 1.35 | 2.99 | 4.35 | 4.49 | 0.16 | 3.40 | 5.30 | 2.35 | |
| Molecular polarizability | AUE | 1.14 | 0.14 | 2.18 | 2.21 | 1.06 | 2.14 | 0.69 | 2.15 | 3.74 | 3.76 | 0.10 | 2.21 | 3.68 | 1.76 |
| APE | 1.30 | 0.50 | 2.77 | 2.44 | 0.81 | 0.95 | 0.90 | 1.60 | 1.68 | 3.61 | 0.45 | 3.76 | 5.02 | 1.76 | |
| MPAD | APE | 2.79 | 0.92 | 5.61 | 4.91 | 1.76 | 2.50 | 2.29 | 2.59 | 2.44 | 6.02 | 0.89 | 7.60 | 9.99 | 3.15 |
| Polarizable Gaussian Model (pGM) | |||||||||||||||
| Diagonal Elements | AUE | 1.74 | 0.19 | 3.34 | 4.23 | 1.88 | 3.23 | 1.29 | 2.62 | 5.44 | 4.15 | 0.16 | 3.97 | 6.73 | 2.24 |
| RMSE | 2.16 | 0.21 | 3.81 | 4.89 | 2.10 | 3.99 | 1.47 | 3.05 | 6.55 | 5.10 | 0.18 | 4.44 | 7.47 | 2.68 | |
| APE | 2.16 | 0.73 | 4.46 | 4.38 | 1.66 | 1.39 | 1.99 | 1.89 | 2.31 | 3.88 | 0.69 | 7.05 | 9.39 | 2.30 | |
| All Elements | AUE | 1.04 | 0.16 | 2.21 | 2.84 | 1.36 | 2.51 | 0.90 | 1.89 | 3.56 | 2.51 | 0.15 | 2.37 | 3.74 | 1.44 |
| RMSE | 1.62 | 0.21 | 3.01 | 3.79 | 1.71 | 3.45 | 1.19 | 2.41 | 4.92 | 3.81 | 0.19 | 3.36 | 5.43 | 2.05 | |
| Molecular Polarizability | AUE | 1.07 | 0.11 | 2.05 | 2.34 | 0.97 | 2.06 | 0.45 | 1.84 | 4.14 | 3.06 | 0.08 | 2.42 | 3.79 | 1.52 |
| APE | 1.26 | 0.45 | 2.71 | 2.51 | 0.89 | 0.93 | 0.74 | 1.41 | 1.85 | 2.99 | 0.41 | 4.23 | 5.06 | 1.57 | |
| MPAD | APE | 2.70 | 0.83 | 5.07 | 4.92 | 1.80 | 1.84 | 2.20 | 2.27 | 2.91 | 5.18 | 0.78 | 7.63 | 10.32 | 2.85 |
Similar to USF models, the performance varies for different molecular sets. Again, the APEs for the biological building blocks and water molecules are much smaller than others. For pGM, the APEs are 2.16, 1.66, 1.39, 1.99, 1.89, 2.31% for the main training set (Set 1), amino acid analogs, nucleic acid analogs, water-amino acid and water-nucleic acid analog dimers, dipeptides and tetrapeptides, respectively. The APEs of water and clusters are 0.73 and 0.69% for the training set (Set 2) and test set (Set 11), respectively. The APEs for the 1242 diverse organic molecules in the test set is 3.88%, which is about 25% lower than that of the USF model (5.12%).
For the charged molecules, the APEs of the test sets are notably larger than those of the training sets for both the USF and VSF models. It is not clear if the Aij calculated at the B3LYP/atz//B3LYP/atz are reliable enough for those molecules, or more atom types are needed to better discriminate the subtle difference of chemical environments represented by those charged molecules. However, the observation that the APEs of charged molecules are quite similar for the USF and VSF models suggests that at least some ab initio Aij are questionable. This is in contrast to the fact that the APEs of VSF models are much smaller than the corresponding APEs of USF models for the neutral molecules. Nevertheless, the excellent performance in biomolecule building blocks is encouraging.
The atomic polarizability and screening factor parameters were listed in Table S8 for the four VSF models. The Aij matrixes of molecules in Set 1 calculated by B3LYP/atz//B3LYP/atz and the four VSF models were listed in Table S9A. The ab initio Aij matrixes for charged molecules in Set 3 and Set 4 were listed in Table S9B and Table S9C, respectively.
Polarizable Gaussian Model.
Our results show that lack of proper representation of polarizability anisotropy can be largely remedied by the inclusion of 1–2 and 1–3 interactions and by the development of new atomic polarizability parameters to reproduce the dipole field tensors calculated using high-level ab initio methods. The significant improvement of the USF and VSF models is encouraging. Indeed, the VSF-pGM has achieved excellent performance in both molecular polarizability and molecular polarizability tensor calculations. Table 2 summarizes the performances of the tested models for 12 planar molecules in which anisotropy plays critical roles. In comparison to experiment, the APE, AUE, and RMSE of molecular polarizabilities are 1.79%, 1.72, and 2.63, respectively. When compared to the ab initio molecular polarizability tensors, the APE, AUE, and RMSE are 2.13%, 1.96, and 2.84, respectively. The MPAD for VSF-pGM, 2.69% is only marginally larger than that for VSF-Exp model, 2.61%. The fact that the VSF-Thole Exp model slightly outperforms VSF-pGM is consistent with the notion that electron distribution around an atom is closer to an exponential function than to a Gaussian function. Nevertheless, overall, VSF-pGM achieves one of the best performances in reproducing the ab initio molecular polarizability anisotropy for the 12 planar molecules.
In our previous work, we developed polarizabilities for both Set A and Set D models and selected Set A Thole linear (AL) models to derive atomic charges and other parameters.13–15 One critical reason for such choice was that charge-fitting using Set D models was challenging and divergence was experienced. Such difficulty is due to induction by short-range (1–2 and 1–3) charges because, in all Thole type models, only the interactions between the induced dipoles are attenuated for the short-range interactions and the interactions between charges and induced dipoles are not. Therefore, nearby charges have the potential to over-polarize the induced dipoles, causing instability in fitting as well as in energy and force calculations. Because the USF and VSF Thole models use the same framework as the Set D models, we anticipate a similar level of challenges in subsequent development for atomic charges. Fortunately, the pGM naturally screens all short-range electrostatic interactions, including charge-dipole interactions. In addition, as our preliminary studies indicate, the pGM model is rather robust in fitting the atomic charges and dipoles to electrostatic potential. Thus, we choose pGM for further development.
Neat Solvent Effect.
A critical issue in atomic polarizability parameterization using an ab initio method to generate reference values is to test if the developed parameters can be directly applied in condensed phase. To this end, we have performed MD simulations for 109 solvents for which the measured molecular polarizability in condensed phases are available. For each solvent, we computed Am, the mean molecular polarizability without neat solvent effect (i.e., without the inter-molecular polarization), and As =Aensemble/nmol, the mean molecular polarizability with neat solvent effect (i.e., with the inter-molecular polarization) taken into account. The Am and As of 109 solvents are listed in Table S10 and are compared in Table 8. It is clear that for both USF and VSF models, there are small but non-negligible differences between the average liquid-phase molecular polarizabilities (As) calculated with the inter-molecular polarization and those without (Am). Their log(p)-values (Table S10), calculated based on normal distribution, are all lower than −4.4 and the log(p)-values of USF-pGM and VSF-pGM are −7.5 and −11.0, respectively. Thus, inter-molecular polarization plays small but non-negligible role and has tendency to systematically reduce the average molecular polarization in liquid compared to gas-phase. Clearly, this effect needs to be accounted in the model.
Table 8.
Summary of solvent effect on molecular polarizability calculations for 11 models. Comparisons are made for the molecular polarizabilities between the measured (AE), the means of residue polarizabilities without solvent effect (Am) and the residue polarizabilities with solvent effect taken into account (As).
| Models | Average Difference (%) | Average Absolute Error (%) | ||||
|---|---|---|---|---|---|---|
| (AE - As)/AE | (AE - Am)/AE | (Am -As)/Am | |AE - As|/AE | |AE - Am|/AE | |Am - As|/Am | |
| AL | 0.42 | 0.85 | −0.44 | 1.66 | 1.55 | 0.56 |
| AE | 1.04 | 0.32 | 0.73 | 1.66 | 1.19 | 0.78 |
| Exp_USF | 4.13 | 0.43 | 3.70 | 4.19 | 2.02 | 3.70 |
| Exp_VSF | 4.67 | −0.34 | 4.97 | 4.88 | 2.26 | 4.97 |
| USF-pGM | 2.73 | 0.39 | 2.33 | 3.05 | 2.20 | 2.48 |
| VSF-pGM | 3.32 | 0.09 | 3.20 | 3.54 | 2.35 | 3.20 |
| VSF-pGM2 | 1.15 | −2.26 | 3.31 | 2.28 | 2.84 | 3.31 |
| USF-Linear | 2.31 | 0.32 | 1.97 | 2.90 | 2.27 | 2.36 |
| VSF-Linear | 3.25 | 1.32 | 1.92 | 3.51 | 2.52 | 2.16 |
| USF-Amoeba | 2.46 | 0.33 | 2.11 | 2.99 | 2.33 | 2.39 |
| VSF-Amoeba | 2.18 | −0.02 | 2.17 | 2.57 | 2.18 | 2.29 |
AE: experimental polarizability
Am: calculated average polarizability without inter-molecule polarization.
As: calculated average polarizability in liquid-phase with inter-molecule polarization.
In contrast, the differences between As and Am are much less obvious in Set A linear and exponential models and the inter-molecular polarization effect has minor impact. Since Set A models neglect the short-range 1–2 and 1–3 polarization whereas both USF and VSF models fully account for them, the results indicate that 1–2 and 1–3 interactions plays important roles even in inter-molecular polarization. Indeed, polarization is a multibody effect. When atoms are polarized by other molecules, they polarize nearby atoms through intramolecular polarization and the role that 1–2 and 1–3 interactions play is part of the multibody effect. Thus, without 1–2 and 1–3 interactions, as in the case of Set A models, the multibody polarization effects cannot be modeled properly, further illustrating the need to include them.
Compared to experimental polarizabilities, without intermolecular polarization, Am are close to experimental values and most of the differences are within the error margins. On the other hand, with intermolecular polarization included, As are consistently and notably less than the experimental values. The log(p)-values (Table S10), ranged from −10.8 (USF-Thole Linear) to −18.9 (VSF-Thole Exponential). Therefore, we conclude that Thole models with 1–2 and 1–3 interactions underestimate the average molecular polarization in liquid by about 2–3%, as shown in Table 8 and the reason for such underestimation was due to intermolecular polarization and its secondary effect through short-range 1–2 and 1–3 interactions.
To test whether the systemic errors can be reduced by rescaling the atomic polarizability parameters, we generated a new set of pGM parameters by increasing the atomic polarizability parameters by 3%. This model, called VSL-pGM2, has much smaller systematic errors compared to its parent model, VSL-pGM (Table 8). This suggests that the neat solvent effect can be easily taken into account by scaling the atomic polarizability parameters.
5. CONCLUSION
In this work, a set of new polarization models with explicit consideration of polarizability anisotropy that include atomic dipole interaction have been constructed using the high-quality ab initio polarizability tensor data calculated at B3LYP/atz/B3LYP/atz level. Two sets of polarizable models, USF and VSF, have been developed for the polarizable Gaussian dipole interaction and three Thole based polarizability frameworks, namely, the Thole Linear, Thole Exponential, and Thole Amoeba. These models were developed in a stepwise fashion using four training sets (Sets 1–4) and extensively evaluated by much larger test sets (Sets 5–13). The pGM USF and VSF models outperform the corresponding Thole based models as measured by average percentage errors of Aii and MPAD. The excellent performance suggests that pGM, which applies Gaussian functions to seamlessly treat the multipoles and electron penetration effects, is a promising polarization framework. The study and the polarizability parameters developed in this work paves the way for the development of pGM that extends the Thole framework toward screening all short-range multipole interactions. Our study also indicates that the polarizabilities developed using gas-phase data may have the tendency to slightly underestimate the polarization in condensed phases that can be remedied by scaling up the polarizability parameters by about 2–3 percent.
Supplementary Material
ACKNOWLEDGMENT.
We are grateful to acknowledge the research support from the NIH (R01GM79383, Y. D., P.I., R01GM093040, R. L., P.I.). This work was supported by the Extreme Science and Engineering Discovery Environment (TG-CHE090098 J.W., P.I.) and the Center for Research Computing of University of Pittsburgh.
List of Abbreviations Used in the text:
- A
Molecular polarizability tensor
- AA
Set A Applequist model
- AE
Set A Thole exponential model
- AL
Set A Thole linear model
- APE
Average percent error
- AT
Set A Thole Amoeba model
- AUE
Average unsigned error
- DA
Set D Applequist mode
- DE
Set D Thole exponential model
- DL
Set D Thole linear model
- DT
Set D Thole Amoeba model
- ESP
Electrostatic potential
- FF
Force field
- MPAD
Molecular polarization anisotropy difference
- pGM
Polarizable Gaussian Model
- RMSE
Root-mean-square error
- Set A
Thole polarizable models with 0% 1–2 and 1–3 and 100% 1–4 interactions
- Set D
Thole polarizable models with 100% 1–2, 1–3 and 1–4 interactions
- USF
universal screening factor
- VSF
variable screening factor
Footnotes
SUPPORTING INFORMATION. Compound names and the SMILES notation of the training sets, Ab initio Aij calculated at the B3LYP/atz//B3LYP/atz level, Aij by four variable screening factor models for the training set molecules, the atomic polarizability and screening factors, the atom type definition files, as well as the molecular polarizabilities of 109 solvent molecules can be found in Tables S1–10. The supporting material is available free of charge via the Internet at pubs.acs.org
REFERENCES
- 1.Cornell WD; Cieplak P; Bayly CI; Gould IR; Merz KM Jr; Ferguson DM; Spellmeyer DC; Fox T; Caldwell JW; Kollman PA, A second generation force field for the simulation of proteins, nucleic acids, and organic molecules. J. Am. Chem. Soc 1995, 117, 5179–5197. [Google Scholar]
- 2.Wang J, Cieplak P, Kollman PA, How well does a restrained electrostatic potential (RESP) model perform in calculating conformational energies of organic and biological molecules? J.Comput.Chem 2000, 21, 1049–1074. [Google Scholar]
- 3.Wickstrom L; Okur A; Simmerling C, Evaluating the performance of the ff99SB force field based on NMR scalar coupling data. Biophys. J 2009, 97, 853–856. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Duan Y; Wu C; Chowdhury S; Lee MC; Xiong G; Zhang W; Yang R; Cieplak P; Luo R; Lee T; Caldwell J; Wang J; Kollman P, A point-charge force field for molecular mechanics simulations of proteins based on condensed-phase quantum mechanical calculations. J. Comput. Chem 2003, 24, 1999–2012. [DOI] [PubMed] [Google Scholar]
- 5.Perez A; MacCallum JL; Brini E; Simmerling C; Dill KA, Grid-based backbone correction to the ff12SB protein force field for implicit-solvent simulations. J. Chem. Theory Comput 2015, 11, 4770–4779. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Maier JA; Martinez C; Kasavajhala K; Wickstrom L; Hauser KE; Simmerling C, ff14SB: Improving the Accuracy of Protein Side Chain and Backbone Parameters from ff99SB. J. Chem. Theory Comput 2015, 11, 3696–3713. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Brooks BR; Brooks CL 3rd; Mackerell AD Jr.; Nilsson L; Petrella RJ; Roux B; Won Y; Archontis G; Bartels C; Boresch S; Caflisch A; Caves L; Cui Q; Dinner AR; Feig M; Fischer S; Gao J; Hodoscek M; Im W; Kuczera K; Lazaridis T; Ma J; Ovchinnikov V; Paci E; Pastor RW; Post CB; Pu JZ; Schaefer M; Tidor B; Venable RM; Woodcock HL; Wu X; Yang W; York DM; Karplus M, CHARMM: the biomolecular simulation program. J. Comput. Chem 2009, 30, 1545–1614. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Jorgensen WL; Maxwell DS; Tirado-Rives J, Development and testing of the OPLS all-atom force field on conformational energetics and properties of organic liquids. J. Am. Chem. Soc 1996, 118, 11225–11236. [Google Scholar]
- 9.Kaminski G, Friesner RA, Tirado-Rives J, Jorgensen WL, Evaluation and Reparametrization of the OPLS-AA Force Field for Proteins via Comparison with Accurate Quantum Chemical Calculations on Peptides. J. Phys. Chem. B 2001, 105, 6474–6487. [Google Scholar]
- 10.Schmid N; Eichenberger AP; Choutko A; Riniker S; Winger M; Mark AE; van Gunsteren WF, Definition and testing of the GROMOS force-field versions 54A7 and 54B7. Eur. Biophys. J 2011, 40, 843–856. [DOI] [PubMed] [Google Scholar]
- 11.Cieplak P; Dupradeau FY; Duan Y; Wang J, Polarization effects in molecular mechanical force fields. J. Phys. Condens. Mat 2009, 21, 333102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Wang J; Cieplak P; Li J; Hou T; Luo R; Duan Y, Development of polarizable models for molecular mechanical calculations I: parameterization of atomic polarizability. J. Phys. Chem. B 2011, 115, 3091–3099. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Wang J; Cieplak P; Li J; Wang J; Cai Q; Hsieh M; Lei H; Luo R; Duan Y, Development of polarizable models for molecular mechanical calculations II: induced dipole models significantly improve accuracy of intermolecular interaction energies. J. Phys. Chem. B 2011, 115, 3100–3111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Wang J; Cieplak P; Cai Q; Hsieh MJ; Wang J; Duan Y; Luo R, Development of polarizable models for molecular mechanical calculations. 3. Polarizable water models conforming to Thole polarization screening schemes. J. Phys. Chem. B 2012, 116, 7999–8008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Wang J; Cieplak P; Li J; Cai Q; Hsieh MJ; Luo R; Duan Y, Development of polarizable models for molecular mechanical calculations. 4. van der Waals parametrization. J. Phys. Chem. B 2012, 116, 7088–7101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Ponder JW; Wu C; Ren P; Pande VS; Chodera JD; Schnieders MJ; Haque I; Mobley DL; Lambrecht DS; DiStasio RA Jr.; Head-Gordon M; Clark GN; Johnson ME; Head-Gordon T, Current status of the AMOEBA polarizable force field. J. Phys. Chem. B 2010, 114, 2549–2564. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Shi Y; Xia Z; Zhang J; Best R; Wu C; Ponder JW; Ren P, The Polarizable Atomic Multipole-based AMOEBA Force Field for Proteins. J. Chem. Theory Comput 2013, 9, 4046–4063. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Kaminski GA; Stern HA; Berne BJ; Friesner RA; Cao YX; Murphy RB; Zhou R; Halgren TA, Development of a polarizable force field for proteins via ab initio quantum chemistry: first generation model and gas phase tests. J. Comput. Chem 2002, 23, 1515–1531. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Friesner RA, Modeling Polarization in Proteins and Protein-ligand Complexes: Methods and Preliminary Results. Adv. Protein Chem 2005, 72, 79–104. [DOI] [PubMed] [Google Scholar]
- 20.Patel S; Brooks CL 3rd, CHARMM fluctuating charge force field for proteins: I parameterization and application to bulk organic liquid simulations. J. Comput. Chem 2004, 25, 1–15. [DOI] [PubMed] [Google Scholar]
- 21.Patel S; Mackerell AD Jr; Brooks Iii CL, CHARMM fluctuating charge force field for proteins: II protein/solvent properties from molecular dynamics simulations using a nonadditive electrostatic model. J. Comput. Chem 2004, 25, 1504–1514. [DOI] [PubMed] [Google Scholar]
- 22.Xiao X; Zhu T; Ji CG; Zhang JZH, Development of an Effective Polarizable Bond Method for Biomolecular Simulation. J. Phys. Chem. B 2013, 117, 14885–14893. [DOI] [PubMed] [Google Scholar]
- 23.Lemkul JA; Huang J; Roux B; M. AD Jr., An Empirical Polarizable Force Field Based on the Classical Drude Oscillator Model: Development History and Recent Applications. Chem. Rev 2016, 116, 4983–5013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Jiang W; Hardy DJ; Phillips JC; MacKerell AD; Schulten K; Roux B, High-Performance Scalable Molecular Dynamics Simulations of a Polarizable Force Field Based on Classical Drude Oscillators in NAMD. J. Phys. Chem. Lett 2011, 2, 87–92. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Lamoureux G; Harder E; Vorobyov IV; Roux B; MacKerell AD, A polarizable model of water for molecular dynamics simulations of biomolecules. Chem. Phys. Lett 2006, 418, 245–249. [Google Scholar]
- 26.Lopes PEM; Lamoureux G; Roux B; MacKerell AD, Polarizable empirical force field for aromatic compounds based on the classical drude oscillator. J. Phys. Chem. B 2007, 111, 2873–2885. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Lemkul JA; Huang J; Roux B; MacKerell AD, An Empirical Polarizable Force Field Based on the Classical Drude Oscillator Model: Development History and Recent Applications. Chem. Rev 2016, 116, 4983–5013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Lamoureux G; Roux B, Modeling induced polarization with classical Drude oscillators: Theory and molecular dynamics simulation algorithm. J Chem Phys 2003, 119, 3025–3039. [Google Scholar]
- 29.Bosque R; Sales J, Polarizabilities of solvents from the chemical composition. J. Chem. Inf. Comput. Sci 2002, 42, 1154–1163. [DOI] [PubMed] [Google Scholar]
- 30.Thole BT, Molecular polarizabilities calculated with a modified dipole interaction. Chem. Phys 1981, 59, 341–350. [Google Scholar]
- 31.Wang JM, Cieplak P, Li J, Wang J, Cai Q, Hsieh MJ, Lei H, Luo R, Duan Y, Development of Polarizable Models for Molecular Mechanical Calculations II: Induced Dipole Models Significantly Improve Accuracy of Intermolecular Interaction Energies. J. Phys.Chem 2011, 115, 3100–3111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Dehez F; Angyan JG; Gutierrez IS; Luque FJ; Schulten K; Chipot C, Modeling Induction Phenomena in Intermolecular Interactions with an Ab Initio Force Field. J. Chem. Theory Comput 2007, 3, 1914–1926. [DOI] [PubMed] [Google Scholar]
- 33.Hickey AL; Rowley CN, Benchmarking Quantum Chemical Methods for the Calculation of Molecular Dipole Moments and Polarizabilities. J. Phys. Chem. A 2014, 118, 3678–3687. [DOI] [PubMed] [Google Scholar]
- 34.Anisimov VM; Lamoureux G; Vorobyov IV; Huang N; Roux B; MacKerell AD, Determination of Electrostatic Parameters for a Polarizable Force Field Based on the Classical Drude Oscillator. J. Chem. Theory Comput 2005, 1, 153–168. [DOI] [PubMed] [Google Scholar]
- 35.Elking DM; Cisneros GA; Piquemal JP; Darden TA; Pedersen LG, Gaussian Multipole Model (GMM). J. Chem. Theory Comput 2010, 6, 190–202. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Elking DM; Perera L; Duke R; Darden T; Pedersen LG, Atomic Forces for Geometry-Dependent Point Multipole and Gaussian Multipole Models. J. Comput. Chem 2010, 31, 2702–2713. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Elking D; Darden T; Woods RJ, Gaussian induced dipole polarization model. J. Comput. Chem 2007, 28, 1261–1274. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Duke RE; Starovoytov ON; Piquemal JP; Cisneros GA, GEM*: A Molecular Electronic Density-Based Force Field for Molecular Dynamics Simulations. J. Chem. Theory Comput 2014, 10, 1361–1365. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Piquemal JP; Cisneros GA; Reinhardt P; Gresh N; Darden TA, Towards a force field based on density fitting. J. Chem. Phys 2006, 124, 104101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Cisneros GA, Application of Gaussian Electrostatic Model (GEM) Distributed Multipoles in the AMOEBA Force Field. J Chem Theory Comput 2012, 8 (12), 5072–5080. [DOI] [PubMed] [Google Scholar]
- 41.Gresh N; Cisneros GA; Darden TA; Piquemal J-P, Anisotropic, Polarizable Molecular Mechanics Studies of Inter- and Intramolecular Interactions and Ligand–Macromolecule Complexes. A Bottom-Up Strategy. J. Chem. Theory Comput 2007, 3, 1960–1986. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Gao J; Truhlar DG; Wang Y; Mazack MJM; Löffler P; Provorse MR; Rehak P, Explicit Polarization: A Quantum Mechanical Framework for Developing Next Generation Force Fields. Acc. Chem. Res 2014, 47, 2837–2845. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Lide DRE, CRC Handbook of Chemistry and Physics CRC Press: Boca Raton, FL: 2005, 86th Ed (Section 3), pp 4–523. [Google Scholar]
- 44.Maroulis G, Ab initio determination of the electric multipole moments and static (hyper)polarizability of HCCX, X = F, Cl, Br, and I. J. Comput. Chem 2003, 24, 443–52. [DOI] [PubMed] [Google Scholar]
- 45.Maroulis G, How large is the static electric (hyper)polarizability anisotropy in HXeI? J. Chem. Phys 2008, 129, 044314. [DOI] [PubMed] [Google Scholar]
- 46.Frisch MJT, G. W; Schlegel HB; Scuseria GE; Robb MA; Cheeseman JR; Scalmani G; Barone V; Mennucci B; Petersson GA; Nakatsuji H; Caricato M; Li X; Hratchian HP; Izmaylov AF; Bloino J; Zheng G; Sonnenberg JL; Hada M; Ehara M; Toyota K; Fukuda R; Hasegawa J; Ishida M; Nakajima T; Honda Y; Kitao O; Nakai H; Vreven T; Montgomery JA Jr.; Peralta JE; Ogliaro F; Bearpark M; Heyd JJ; Brothers E; Kudin KN; Staroverov VN; Kobayashi R; Normand J; Raghavachari K; Rendell A; Burant JC; Iyengar SS; Tomasi J; Cossi M; Rega N; Millam NJ; Klene M; Knox JE; Cross JB; Bakken V; Adamo C; Jaramillo J; Gomperts R; Stratmann RE; Yazyev O; Austin AJ; Cammi R; Pomelli C; Ochterski JW; Martin RL; Morokuma K; Zakrzewski VG; Voth GA; Salvador P; Dannenberg JJ; Dapprich S; Daniels AD; Farkas Ö; Foresman JB; Ortiz JV; Cioslowski J; Fox DJ, Gaussian 09, Revision D.01 Gaussian, Inc; Wallingford CT, 2009. [Google Scholar]
- 47.Wang J; Wang W; Kollman PA; Case DA, Automatic atom type and bond type perception in molecular mechanical calculations. J. Mol. Graph. Model 2006, 25, 247–260. [DOI] [PubMed] [Google Scholar]
- 48.Wang JM; Wolf RM; Caldwell JW; Kollman PA; Case DA, Development and testing of a general amber force field. J. Comput. Chem 2004, 25, 1157–1174. [DOI] [PubMed] [Google Scholar]
- 49.Essmann U; Perera L; Berkowitz ML; Darden T; Lee H; Pedersen LG, A smooth particle mesh Ewald method. J. Chem. Phys 1995, 103, 8577–8593. [Google Scholar]
- 50.Wang J; Krudy G; Xie XQ; Wu C; Holland G, Genetic algorithm-optimized QSPR models for bioavailability, protein binding, and urinary excretion. J. Chem. Inf. Model 2006, 46, 2674–2683. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


