Abstract
Motivation: RNA H-type pseudoknots are ubiquitous pseudoknots that are found in almost all classes of RNA and thought to play very important roles in a variety of biological processes. Detection of these RNA H-type pseudoknots can improve our understanding of RNA structures and their associated functions. However, the currently existing programs for detecting such RNA H-type pseudoknots are still time consuming and sometimes even ineffective. Therefore, efficient and effective tools for detecting the RNA H-type pseudoknots are needed.
Results: In this paper, we have adopted a heuristic approach to develop a novel tool, called HPknotter, for efficiently and accurately detecting H-type pseudoknots in an RNA sequence. In addition, we have demonstrated the applicability and effectiveness of HPknotter by testing on some sequences with known H-type pseudoknots. Our approach can be easily extended and applied to other classes of more general pseudoknots.
Availability: The web server of our HPknotter is available for online analysis at http://bioalgorithm.life.nctu.edu.tw/HPKNOTTER/
Contact: cllu@mail.nctu.edu.tw, chiu@cc.nctu.edu.tw
1 INTRODUCTION
RNA pseudoknots are found in almost all classes of naturally occurring RNAs and play very important roles in a variety of biological processes, such as RNA replication, transcription and translation (Kolk et al., 1998). The majority of pseudoknots that have been described to date are of the so-called H-type (or classical) pseudoknot in which nucleotides from a hairpin-loop pair with a single-stranded region outside of the hairpin to form a helical stem that is adjacent or almost adjacent to the the hairpin stem (Pleij and Bosch, 1989; Pleij, 1990; ten Dam et al., 1992; Pleij, 1994). For instance, there are 246 different pseudoknots in PseudoBase1 with 224 of them being H-type. Hence, the detection of H-type pseudoknots should improve our understanding of RNA structures and their associated functions. In principle, an H-type pseudoknot (called H-pseudoknot) may contain two stems (regions A and C in Fig. 1) and three loops (regions B, D and E in Fig. 1), where such stems and loops are usually represented in the 5′ → 3′ direction as S1 (Stem 1), S2 (Stem 2), and L1 (Loop 1), L2 (Loop 2) and L3 (Loop 3), respectively. However, L2 is absent in the most studied type of pseudoknots owing to the coaxial stacking of stems. Classical pseudoknots have simple loops in which all nucleotides are unpaired and complicated loops that contain substructures without pseudoknots, such as several stems with their own internal, hairpin and multibranch loops. Both simple and complicated loops are referred to as pseudoknot loops. For simplicity, all the nucleotides in a pseudoknot loop are counted and their number equals to the size of this loop, whether they are unpaired or not. The pseudoknot stems adopted here are those that are ‘pseudoknotted’ with other stems. They may be interrupted by some bulge loops (or interior loops). By convention, the unpaired nucleotides in these loops are, however, not counted for determining the size of a pseudoknot stem.
Fig. 1.
Schematic representation of the H-type pseudoknot.
In the standard thermodynamic model, a pseudoknot-free RNA secondary structure of minimum free energy (MFE) can be computed using dynamic programming in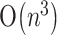 
time (Zuker and Stiegler, 1981; Zuker and Sankoff, 1984; Zuker, 2003; Hofacker, 2003). However, when (general) pseudoknots are allowed in the RNA secondary structure, the computation becomes intractable since it has been shown to be an NP-hard problem (Lyngsø and Pedersen, 2000; Akutsu, 2000). Currently, several polynomial-time algorithms have been proposed to find an MFE secondary structure with a restricted class of pseudoknots (Rivas and Eddy, 1999; Akutsu, 2000; Lyngsø and Pedersen, 2000; Dirks and Pierce, 2003; Reeder and Giegerich, 2004). Rivas and Eddy (1999) first proposed the dynamic programming algorithm that could handle a large class of special pseudoknotted structures. However, the major limitation of this algorithm is its high running time of 
and space of 
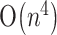, where n is the length of RNA sequence. With other more restricted classes of pseudoknots, Lyngsø and Pedersen (2000) proposed an algorithm of 
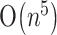time and 
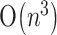space, Akutsu (2000) designed an algorithm of 
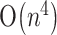time and 
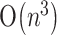space, Dirks and Pierce (2003) described an algorithm of 
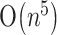time and 
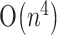space, and Reeder and Giegerich (2004) gave an algorithm of 
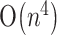time and 
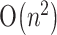space. All these algorithms above can be used to predict an MFE secondary structure of an RNA sequence with H-pseudoknots. However, they are not yet practical for large-scale sequences owing to their high running time and/or space. In addition, our experimental results showed that these algorithms may not be effective to detect an H-pseudoknot that is actually present in the native structure of a long RNA sequence. However, our finding showed that when they were applied to the sequence fragment exactly harboring the H-pseudoknot in a long RNA sequence, they gave a very high probability of successfully folding this fragment into the H-pseudoknot structure. Based on these observations, in this paper we propose a heuristic approach to design a novel tool, called HPknotter, for efficiently and accurately detecting RNA H-pseudoknots in an RNA sequence by incorporating several existing algorithms RNAMotif (Macke et al., 2001), PKNOTS (Rivas and Eddy, 1999), NUPACK (Dirks and Pierce, 2003) and pknotsRG (Reeder and Giegerich, 2004), where RNAMotif is an RNA structural motif search tool, and PKNOTS, NUPACK and pknotsRG are the implemented programs of the algorithms of Rivas and Eddy, Dirks and Pierce, and Reeder and Giegerich, respectively. The key idea of our approach is as follows. For a given RNA sequence, RNAMotif is first used to search for all the subsequences (called hits) that meet the criteria dictating the structural motifs (such as stems and loops) of an H-pseudoknot. PKNOTS/NUPACK/pknotsRG is then used to determine if these hits indeed fold into a stable H-pseudoknot. The purpose of using RNAMotif is to screen out those subsequences that do not possess the required structural motifs in an H-pseudoknot in sequence level, such that the worst case of applying PKNOTS/NUPACK/pknotsRG to all subsequences of the initial RNA sequence can be avoided and as a result, the testing time of PKNOTS/NUPACK/pknotsRG can be greatly shortened. To further speed up the overall performance, a hit filter is designed between RNAMotif and PKNOTS/NUPACK/pknotsRG and its function is to discard those hits that are not possible to fold into a stable pseudoknotted structure. Thus, only a small number of the remaining hits are processed by PKNOTS/NUPACK/pknotsRG. Finally, based on the concept of maximum weight independent set in graph theory, the mutually disjoint H-pseudoknots with minimum total free energy are computed from the remaining hits capable of folding into stable H-pseudoknots to serve as the final output of HPknotter. We have demonstrated the practicability and effectiveness of HPknotter by testing it on several RNA sequences, most of which have been proven to contain the H-type pseudoknotted structures in laboratory approaches.
In addition to the above thermodynamic approaches, several other approaches for predicting RNA secondary structures with (H-type) pseudoknots have been proposed, such as maximum weighted matching (Cary and Stormo, 1995; Tabaska et al., 1998; Ieong et al., 2003), quasi-Monte Carlo searches (Abrahams et al., 1990; Gultyaev, 1991), genetic algorithms (van Batenburg et al., 1995; Gultyaev et al., 1995; Shapiro and Wu, 1997), stochastic context free grammar (Brown and Wilson, 1996; Cai et al., 2003), and others (Ieong et al., 2003; Tahi et al., 2003; Ruan et al., 2004). Particularly, Shapiro and Wu (1997) developed a parallel genetic algorithm for detecting H-pseudoknots on a massively parallel supercomputer MasPar MP-2 with 16 384 processors. Recently, this parallel genetic algorithm has been adapted to MIMD parallel machines (Shapiro et al., 2001), such as SGI ORIGIN 2000 with 64 processors and CRAY T3E with 512 processors, which seem to be hardly accessible to the ordinary users.
2 ALGORITHMS
To simplify algorithmic computation, the H-pseudoknots are classified into four classes as shown in Table 1 based on the sizes of their stems and loops, where the case of size(S1) = size(S2) and size(L1) = size(L3) is allowed to belong to any of four classes. Basically, our designed HPknotter works with five phases as follows (see Fig. 2 for its flow diagram). In the first phase, it runs RNAMotif on the input RNA sequence with a user-specified descriptor for a class of H-pseudoknots, which produces a list of sequence fragments, called hits, that match the user-specified descriptor. RNAMotif (Macke et al., 2001) is an RNA structural motif search tool to find the fragments of a given RNA sequence that conform to a predefined descriptor of defining a particular structural motif. In Figure 3, the RNAMotif descriptor used in our HPknotter to describe the H-type pseudoknotted structures of class 2 is shown. To define the descriptor of each class of H-pseudoknots that fits as closely as possible to the naturally occurring pseudoknots, we further count the frequencies of the occurring stem sizes and loop sizes in PseudoBase (van Batenburg et al., 2000; van Batenburg et al., 2001). The stem- and loop-size distributions of S1, S2, L1, L2 and L3 are shown in Figure 4, where 4 (respectively, 1 and 3) pseudoknots with big loop-size (≥100 bp) are omitted in the case of L1 (respectively, L2 and L3). Then the size ranges that cover the most parts of the distributions are chosen to serve as the default size ranges of the stems and loops in HPknotter, where these default size ranges can be modified by the users to meet their requirements according to their biological knowledge about the tested data.
Table 1.
The conditions of four classes of H-pseudoknots
| Class | Condition 1 | Condition 2 |
|---|---|---|
| 1 | size(S1) ≤ size(S2) | size(L1) ≤ size(L3) |
| 2 | size(S1) ≤ size(S2) | size(L1) ≥ size(L3) |
| 3 | size(S1) ≥ size(S2) | size(L1) ≤ size(L3) |
| 4 | size(S1) ≥ size(S2) | size(L1) ≥ size(L3) |
Fig. 2.
The flow diagram of HPknotter.
Fig. 3.
The RNAMotif descriptor used to describe the H-type pseudoknotted structures of class 2.
Fig. 4.
Frequencies of stem- and loop-sizes of pseudoknots in PseudoBase.
The hit sequences contained in the output of the first stage then serve as input to the next phase. Note that at this moment, each hit has the possibility of folding into the pseudoknotted structure of the H-type as defined in the descriptor of RNAMotif (herein, the H-pseudoknot of this kind is referred to as an RNAMotif H-pseudoknot for convenience). However, whether or not this RNAMotif-pseudoknotted structure is the native structure of the hit, i.e. the stable structure with minimum energy, is still unknown. The simplest verification way is to apply the currently existing prediction program (like PKNOTS/NUPACK/pknotsRG) to each hit sequence and examine whether it indeed folds into a stable H-pseudoknot conforming to the descriptor. However, such a verification for all hit sequences is impractical. The reason is that even for a short RNA sequence, a great number of hit sequences are usually produced by RNAMotif and hence the verification of each hit sequence using PKNOTS, NUPACK or pknotsRG costs much time, which leads the overall process of verification above to being extremely time consuming. Therefore, a more efficient verification is needed to improve the overall performance, especially in speed.
From the thermodynamic viewpoint, a pseudoknotted structure of a hit sequence with very low energy (or the lowest energy) is more likely to form in the native structure of the hit sequence. For a hit sequence, however, if the energy of the pseudoknotted structure with possible stems in their loops (defined by the descriptor) is much greater than that of its pseudoknot-free secondary structure with minimum energy, this hit sequence is unlikely to fold into a native pseudoknot that conforms to the descriptor. And as a result, this hit sequence can be discarded directly without any verification. Based on this observation, a hit filter is designed herein to filter out those hit sequences whose energies calculated based on their RNAMotif-pseudoknotted structures with possible stems in their loops are greater than the minimum energies of their pseudoknot-free secondary structures predicted by the pseudoknot-free secondary structure prediction programs. To make this comparison, the energies of the above pseudoknotted and pseudoknot-free structures are recalculated using the energy computation program provided by NUPACK such that the computed energies are based on the same energy rules and thermodynamic parameters. Note that when computing the energy of the pseudoknotted structure of each hit sequence, we also count the possible energy contributed by the interaction between the hit sequence and the flankingsequences.
Currently, the cost of calculating a secondary structure without pseudoknots is much less than that of predicting a secondary structure with pseudoknots. For example, PKNOTS and NUPACK both cost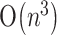 
time for predicting the pseudoknot-free secondary structures of an RNA sequence fragment of length n, whereas these programs as well as pknotsRG cost 
, 
and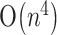 
time respectively, for the case with pseudoknots. With the aid of the hit filter, most hits are determined within 
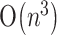time, instead of 
, 
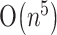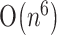or 
. In the second phase, the HPknotter extracts the hit sequences from the output of the first stage and passes them to the hit filter to check if they have the possibility of folding into stable H-pseudoknots. We call the hit sequences passing through the hit filter as filtered hits. According to our experiments (described in next sections), the hit filter significantly speeds up the overall performance of verification because a large number of hit sequences have been filtered out.
In the third phase, the filtered hits are further double checked by the pseudoknotted prediction program PKNOTS/NUPACK/pknotsRG to check whether or not they indeed fold into the stable pseudoknots. A filtered hit is then called as an H-pseudoknot candidate if PKNOTS/NUPACK/pknotsRG is able to fold it into a stable pseudoknot.
It is worth mentioning that each H-pseudoknot candidate generated in the third phase may not be an H-pseudoknot, or may be an H-pseudoknot not capable of conforming to the user-specified descriptor. The reason for the former case is that PKNOTS and NUPACK can predict a more general class of pseudoknots. One reason for the latter case is that one of its H-pseudoknot stems may contain a long loop that violates the known biological knowledge. According to the H-pseudoknots maintained in PseudoBase, most of them contain no loop in their pseudoknot stems. Only a few H-pseudoknots contain one loop in their pseudoknot stems and most of them contain either an interior loop of size 2 or a bulge of size 1. Another possible reason is that the candidate is indeed a stable H-pseudoknot, but it belongs to a different class of H-pseudoknots. Based on these observations, in the fourth phase we further design an H-pseudoknot filter to filter out those H-pseudoknot candidates that are not the desired H-pseudoknots or contain a long loop in their stems. We call the remaining H-pseudoknot candidates passing through the H-pseudoknot filter as the filteredH-pseudoknots.
In fact, several filtered H-pseudoknots may overlap among their ranges in the sequence, which means that they cannot exist in the stable structure of a given RNA sequence simultaneously. Among the filtered H-pseudoknots, therefore, we further find the mutually disjoint H-pseudoknots whose total free energy is minimum in the fifth phase. Actually, this problem becomes a well-known combinatorial problem, called the maximum weight independent set problem on interval graphs, if the range of each filtered H-pseudoknot is considered as an interval in the sequence associated with the magnitude of its free energy as the weight. The maximum weight independent set problem on interval graphs can be solved in linear time (Hsiao et al., 1992). In HPknotter, we have implemented this algorithm to compute the mutually disjoint H-pseudoknots with minimum total free energy among the filtered H-pseudoknots and use them as the final output of HPknotter.
3 IMPLEMENTATION
Based on the phases described in the previous section, we have implemented a novel tool, the HPknotter, by incorporating several existing programs, RNAMotif (Macke et al., 2001), PKNOTS (Rivas and Eddy, 1999), NUPACK (Dirks and Pierce, 2003) and pknotsRG (Reeder and Giegerich, 2004), for detecting the H-pseudoknots of a given RNA sequence. The HPknotter was written in Perl. Its web server, implemented in PHP, is available for online analysis at http://bioalgorithm.life.nctu.edu.tw/HPKNOTTER/. We incorporated the well-developed programs PKNOTS, NUPACK and pknotsRG into our HPknotter pipeline, and compared this combination with these three programs used as stand-alone tools. The experiments were carried out on a number of RNA sequences with known H-pseudoknots. Unless otherwise specified, all programs were run with default parameters on IBM PC with 3.06 GHz processor and 2 GB RAM under Linux system.
4 SELECTION OF THE TEST DATA
The tested sequences were taken from the 5S rRNA of Escherichia coli (5S-rRNA) (Cannone et al., 2002), the RNA sequence inhibiting human immunodeficiency virus type 1 (HIV-1-RT) reverse transcriptase (Tuerk et al., 1992), the 3′-UTR of tobacco mosaic virus (TMV-3′) (van Belkum et al., 1985), the turnip yellow mosaic virus (TYMV-3′) sequence (Rietveld et al., 1982), the 5′-UTR of human parechovirus (HPeV1-5′) (Nateri et al., 2002), the bacteriophage T2 and T4 gene 32 mRNA sequences (T2 and T4) (McPheeters et al., 1988), and the 3′-UTRs of several coronaviruses (BCV-3′, MHV-3′ and SARS-TW1-3′) including severe acute respiratory syndrome virus (SARS) (Williams et al., 1999; Tsai et al., 2004) (see Table 2 for the information of the tested sequences and their H-pseudoknot numbers). All sequences above, except 5S-rRNA, are known to contain at least one H-pseudoknot as reported in the literature.
Table 2.
The sequence and H-pseudoknot information of the tested sequences, where the accession number of HIV-1-RT is not available and TMV-3′-down contains two H-pseudoknots with one in class 2 and the other in class 3
| RNA Sequence | Accession No. | Length (bp) | H-Pseudoknots No. | Class |
|---|---|---|---|---|
| 5S-rRNA | V00336 | 120 | 0 | — |
| HIV-1-RT | N/A | 35 | 1 | 1 |
| TMV-3′-up | AJ011933 | 84 | 3 | 1 |
| T2 | X12460 | 946 | 1 | 1 |
| T4 | J02513 | 1340 | 1 | 1 |
| TYMV-3′ | X16378 | 86 | 1 | 2 |
| BCV-3′ | AF220295 | 345 | 1 | 2 |
| MHV-3′ | AF201929 | 315 | 1 | 2 |
| SARS-TW1-3′ | AY291451 | 341 | 1 | 2 |
| TMV-3′-down | AJ011933 | 105 | 2 | 2,3 |
| HPeV1-5′ | L02971 | 45 | 1 | 3 |
5 EVALUATION AND OBSERVATIONS
A summary of the overall sensitivity and specificity for all experiments, which were run using the general class of the descriptor without an interior or bulge loop in the pseudoknot stems, is shown in Tables 3, in which we let Sbp = (100 × TP)/(TP + FN), Pbp = (100 × TP)/(TP + FP) and Π = (number of correctly predicted H-pseudoknots)/(number of predictedH-pseudoknots) (i.e. the fraction of the correctly predicted H-pseudoknots), where TP = true positive (i.e., the number of the correctly predicted base-pairs in the predicted H-pseudoknots), FN = false negative (i.e. the number of the base-pairs in the published H-pseudoknots that were not predicted), FP = false positive (i.e. the number of the incorrectly predicted base-pairs in the predicted H-pseudoknots). The correctly predicted H-pseudoknots denote those predicted H-pseudoknots reported in the literature.
Table 3.
Summary of prediction results on several RNA sequences, where all experiments are run using the general class of the descriptor and the version of PKNOTS is 1.01
| Experiment | HPknotter | ||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| PKNOTS | NUPACK | pknotsRG | PKNOTS-kernel | NUPACK-kernel | pknotsRG-kernel | ||||||||||||||
| S bp | P bp | Π | S bp | P bp | Π | S bp | P bp | Π | S bp | P bp | Π | S bp | P bp | Π | S bp | P bp | Π | ||
| 5S-rRNA | — | — | 0/0 | — | — | 0/1 | — | — | 0/0 | — | — | 0/1 | — | — | 0/1 | — | — | 0/2 | |
| HIV-1-RT | 100 | 100 | 1/1 | 100 | 100 | 1/1 | 100 | 100 | 1/1 | 100 | 100 | 1/1 | 100 | 100 | 1/1 | 100 | 100 | 1/1 | |
| TMV-3′-up | 0 | 0 | 0/0 | 0 | 0 | 0/0 | 71.4 | 62.5 | 3/3 | 100 | 77.8 | 2/2 | 100 | 77.8 | 3/3 | 71.4 | 62.5 | 3/3 | |
| 77.8 | 87.5 | 0 | 0 | 88.9 | 100 | 77.8 | 87.5 | ||||||||||||
| 88.9 | 100 | 66.7 | 66.7 | 88.9 | 100 | 88.9 | 100 | ||||||||||||
| T2 | — | — | —/— | — | — | —/— | 100 | 100 | 1/1 | 100 | 100 | 1/4 | 100 | 100 | 1/10 | 100 | 100 | 1/16 | |
| T4 | — | — | —/— | — | — | —/— | 0 | 0 | 0/1 | 100 | 100 | 1/3 | 100 | 100 | 1/17 | 100 | 100 | 1/17 | |
| TYMV-3′ | 0 | 0 | 0/0 | 0 | 0 | 0/1 | 100 | 80 | 1/2 | 100 | 80 | 1/1 | 62.5 | 55.6 | 1/2 | 100 | 80 | 1/2 | |
| BCV-3′ | — | — | —/— | — | — | —/— | 100 | 100 | 1/1 | 100 | 100 | 1/1 | 94.4 | 100 | 1/3 | 100 | 100 | 1/3 | |
| MHV-3′ | — | — | —/— | — | — | —/— | 100 | 100 | 1/3 | 100 | 100 | 1/3 | 100 | 100 | 1/5 | 100 | 100 | 1/6 | |
| SARS-TW1-3′ | — | — | —/— | — | — | —/— | 0 | 0 | 0/0 | 93.8 | 100 | 1/2 | 93.8 | 100 | 1/3 | 100 | 100 | 1/5 | |
| TMV-3′-down | 0 | 0 | 0/0 | 60.9 | 42.4 | 1/1 | 0 | 0 | 0/0 | 100 | 100 | 2/2 | 100 | 100 | 2/2 | 100 | 100 | 2/2 | |
| 91.3 | 91.3 | 95.7 | 100 | 100 | 95.7 | ||||||||||||||
| HPeV1-5′ | 0 | 0 | 1/1 | 0 | 0 | 1/1 | 54.5 | 54.5 | 1/1 | 100 | 100 | 1/1 | 100 | 100 | 1/1 | 100 | 100 | 1/1 | |
It should be noted that PKNOTS of version 1.04 can successfully predict two H-pseudoknots of TMV −3′-down. The reason that HPknotter with PKNOTS−kernel missed the second H-pseudoknot of TMV-3′-up is that PKNOTS is not able to fold its corresponding sequence into a pseudoknot.
In this set of experiments, PKNOTS and NUPACK were not able to deal with the cases of T2, T4, BCV-3′, MHV-3′ and SARS-TW1-3′, owing to the running out of memory. For the other sequences, PKNOTS and NUPACK exhibited almost the same prediction results in which the H-pseudoknot of HIV-1-RT was identified, but the H-pseudoknots of TMV-3′-up, TYMV-3′ and HPeV1-5′ were missed2. (Note that PKNOTS could predict two real H-pseudoknots of TMV-3′-down, if the version of PKNOTS was 1.04, instead of 1.01.) Notably, most of the above results were improved when we conducted all the experiments using pknotsRG. However, the H-pseudoknots of T4, SARS-TW1-3′ and TMV-3′-down were still missed by pknotsRG. The inability of detecting the real H-pseudoknots described above evidences the fact that for the long RNA sequence, the MFE model might miss the H-pseudoknots that are actually present in the native structure. In our experiments (Table 3), however, this situation was significantly improved by our HPknotter, because most of the real H-pseudoknots of TMV-3′-up, T4, TYMV-3′, SARS-TW1-3′ and TMV-3′-down were detected with high sensitivity and specificity.
6 DISCUSSION
The key point lies in the fact that our HPknotter first uses RNAMotif to search for all fragments of the given RNA sequence that have the possibility of folding into an H-pseudoknot and then applies PKNOTS/NUPACK/pknotsRG to these fragments for determining if their MFE structures are indeed H-pseudoknots. In this situation, without effect on the nucleotides outside the fragments, PKNOTS/NUPACK/pknotsRG seems to give a higher probability of successfully recognizing the pseudoknotted structures of fragments. This approach, of course, inevitably increases the number of incorrectly predicted H-pseudoknots, because it ignores the global effect of all input nucleotides by considering just the local fragments of the input RNA sequence. In fact, our experiments showed that the number of the incorrectly predicted H-pseudoknots was reasonable because among all these predicted H-pseudoknots, HPknotter applies the concept of maximum weight independent set at the last stage to compute the mutually disjoint H-pseudoknots with minimum total free energy.
Generally speaking, as shown in Table 3, our HPknotter greatly improves sensitivity, specificity and the fraction Π of correctly predicted H-pseudoknots when compared with original PKNOTS, NUPACK and pknotsRG. It should be noted that the number of incorrectly predicted H-pseudoknots in the cases with PKNOTS-kernel are not greater than those in the cases with NUPACK-kernel and pknotsRG-kernel, which seems to imply that PKNOTS itself is more accurate than NUPACK and pknotsRG, even though PKNOTS is more time consuming than NUPACK and pknotsRG from the computational point of view.
It is worth mentioning that as shown in Table 4, the overall prediction accuracy will be further improved if we rerun all tested RNA sequences above, except 5S-rRNA containing no H-pseudoknot, by choosing the specific class to which the predicted H-pseudoknots belong, instead of using the general class of descriptor. Particularly, the Π values (Table 4) and the performance of running time (Table 5) were greatly improved. These experiments indicate that our HPknotter can be served as an effective tool for validating if the tested RNA sequences have the same kind of H-pseudoknots as other closely related RNA sequences whose H-pseudoknots are already known in advance. For instance, SARS, BCV and MHV are all coronaviruses, and the H-pseudoknots of BCV-3′ and MHV-3′, both of which belong to class 2 of H-pseudoknots, are already known and have been proven by previous experiments (Williams et al., 1999). It is reasonable to expect that SARS-TW1-3′ may contain an H-pseudoknot of class 2. Therefore, we can apply our HPknotter to SARS-TW1-3′ by specifying the descriptor to be class 2 so that we are able to quickly obtain the same result as the general descriptor.
Table 4.
Summary of prediction results on several RNA sequences, where experiments 1–4, 5–9 and 10–11 are run using the descriptors of classes 1, 2 and 3, respectively
| Experiment | HPknotter | ||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| PKNOTS | NUPACK | pknotsRG | PKNOTS-kernel | NUPACK-kernel | pknotsRG-kernel | ||||||||||||||
| S bp | P bp | Π | S bp | P bp | Π | S bp | P bp | Π | S bp | P bp | Π | S bp | P bp | Π | S bp | P bp | Π | ||
| HIV-1-RT | 100 | 100 | 1/1 | 100 | 100 | 1/1 | 100 | 100 | 1/1 | 100 | 100 | 1/1 | 100 | 100 | 1/1 | 100 | 100 | 1/1 | |
| TMV-3′-up | 0 | 0 | 0/0 | 0 | 0 | 0/0 | 71.4 | 62.5 | 3/3 | 100 | 87.5 | 2/2 | 0 | 0 | 2/2 | 0 | 0 | 2/2 | |
| 77.8 | 87.5 | 0 | 0 | 88.9 | 100 | 77.8 | 87.5 | ||||||||||||
| 88.9 | 100 | 66.7 | 66.7 | 88.9 | 100 | 88.9 | 100 | ||||||||||||
| T2 | — | — | —/— | — | — | —/— | 100 | 100 | 1/1 | 100 | 100 | 1/3 | 100 | 100 | 1/6 | 100 | 100 | 1/14 | |
| T4 | — | — | —/— | — | — | —/— | 0 | 0 | 0/1 | 100 | 100 | 1/3 | 100 | 100 | 1/11 | 100 | 100 | 1/11 | |
| TYMV-3′ | 0 | 0 | 0/0 | 0 | 0 | 0/1 | 100 | 80 | 1/2 | 100 | 80 | 1/1 | 62.5 | 62.5 | 1/1 | 100 | 80 | 1/1 | |
| BCV-3′ | — | — | —/— | — | — | —/— | 100 | 100 | 1/1 | 100 | 100 | 1/1 | 94.4 | 100 | 1/2 | 100 | 100 | 1/1 | |
| MHV-3′ | — | — | —/— | — | — | —/— | 100 | 100 | 1/3 | 100 | 100 | 1/1 | 100 | 100 | 1/3 | 100 | 100 | 1/4 | |
| SARS-TW1-3′ | — | — | —/— | — | — | —/— | 0 | 0 | 0/0 | 93.8 | 100 | 1/1 | 93.8 | 100 | 1/3 | 100 | 100 | 1/3 | |
| TMV-3′-down | 0 | 0 | 0/0 | 0 | 0 | 0/0 | 0 | 0 | 0/0 | 100 | 100 | 1/1 | 100 | 100 | 1/3 | 100 | 100 | 1/1 | |
| TMV-3′-down | 0 | 0 | 0/0 | 60.9 | 42.4 | 1/1 | 0 | 0 | 0/0 | 91.3 | 91.3 | 1/1 | 95.7 | 100 | 1/1 | 100 | 95.7 | 1/1 | |
| HPeV1-5′ | 0 | 0 | 1/1 | 0 | 0 | 1/1 | 54.5 | 54.5 | 1/1 | 100 | 100 | 1/1 | 100 | 100 | 1/1 | 100 | 100 | 1/1 | |
The first H-pseudoknot of TMV-3′-up was missed by HPknotter with NUPACK-kernel and pknotsRG-kernel because it was filtered out owing to the incorrect class. Notice that TMV-3′-down contains two H-pseudoknots with one in class 2 (that was tested in experiment 9) and the other in class 3 (that was tested in experiment 10).
Table 5.
CPU usage time for PKNOTS, NUPACK, pknotsRG and HPknotter, where in our testing computer environment, PKNOTS and NUPACK cannot deal with the sequences of length >220 and 180 bp, respectively, owing to the running out of memory
| Length (bp) | PKNOTS | NUPACK | pknotsRG | HPknotter (General class) | HPknotter (Specific class) | ||||
|---|---|---|---|---|---|---|---|---|---|
| PKNOTS-kernel | NUPACK-kernel | pknotsRG-kernel | PKNOTS-kernel | NUPACK-kernel | pknotsRG-kernel | ||||
| 84 | 7.3 min | 13.1 s | 0.05 s | 31 s | 27 s | 26 s | 9 s | 7 s | 6 s |
| 105 | 35 min | 44.7 s | 0.1 s | 2.2 min | 35 s | 29 s | 38 s | 10 s | 8 s |
| 200 | 72 h | — | 0.8 s | 5.2 min | 1.8 min | 1.5 min | 1.6 min | 33 s | 30 s |
| 341 | — | — | 7.4 s | 7.1 min | 2.4 min | 2.3 min | 2.2 min | 46 s | 45 s |
| 946 | — | — | 10.1 min | 13.8 min | 7.5 min | 6.9 min | 4.1 min | 2.2 min | 2.1 min |
| 1340 | — | — | 43.5 min | 35.3 min | 11.6 min | 10.9 min | 11.6 min | 3.1 min | 2.5 min |
In fact, our HPknotter is not CPU intensive at all because based on our experiments, a great number of the hit sequences produced by RNAMotif were filtered out by the hit filter. Take the experiments with SARS-TW1-3′ in Table 3 for an example. In the first phase, RNAMotif in total found 2132 hits that conform to the descriptor of general class. If we directly apply PKNOTS to all these unfiltered hits to check if they fold into a stable H-pseudoknot, then the program will require about 51 h to finish the job. However, after running the hit filter, only 43 different hit sequences remained, which then cost the following PKNOTS only about 5.2 min to determine if they are stable pseudoknots. As a result, the third phase of running pseudoknot prediction with PKNOTS left us with only 11 pseudoknot candidates that could fold into stable pseudoknots. Next, only seven candidates remained after running the H-pseudoknot filter in the fourth phase. In fact, some of these filtered H-pseudoknots may have an overlap among their ranges in the sequence, which suggests that they cannot exist simultaneously in a stable pseudoknotted structure in SARS-TW1-3′. Finally, only two H-pseudoknots with minimum free energy were selected in the phase of computing the maximum weight independent set. Table 1 lists the CPU usage time for PKNOTS, NUPACK, pknotsRG and our HPknotter, where all tests were run on IBM PC with 3.06 GHz processor and 2 GB RAM under Linux system.
7 CONCLUSIONS
In this paper, we designed a heuristic approach for efficiently and accurately detecting RNA H-pseudoknots, the ubiquitous pseudoknots in the naturally occurring RNAs. The currently existing thermodynamic-based programs, like PKNOTS, NUPACK and pknotsRG, are useful for finding stable H-pseudoknots. However, most of them are highly time consuming and memory consuming, which limits them to predict short sequences of a couple of hundred bases length. Another main weakness of these programs is that they may not be effective to detect the actually existing H-pseudoknots that are contained in a long RNA sequence, as evidenced by our experiments. Based on our heuristic approach mentioned in this paper, we have implemented a novel program, the HPknotter, capable of efficiently and accurately detecting the H-pseudoknots of a given RNA sequence by incorporating four existing programs RNAMotif, PKNOTS, NUPACK and pknotsRG. In summary, we have demonstrated the practicability and effectiveness of our developed HPknotter by testing it on several RNA sequences, most of which have been proven to contain the H-pseudoknotted structures. Through several experiments, our HPknotter has been shown to be practical for the detection of H-pseudoknots in RNA sequences because it is not computationally expensive and has much better sensitivity and specificity than PKNOTS, NUPACK and pknotsRG. In addition, it is feasible to extend and apply our heuristic approach to detecting the other classes of more generalpseudoknots.
Conflict of Interest: none declared.
Footnotes
1PseudoBase (http://wwwbio.leidenuniv.nl/~Batenburg/PKB.html) is a pseudoknot database maintained by the Leiden Institute of Chemistry and the Institute of Theoretical Biology at the Leiden University.
2Actually, PKNOTS and NUPACK both predicted an H-pseudoknot for HPeV1-5′, but with zero sensitivity and specificity as a result of incorrect base pairings.
REFERENCES
- Abrahams, J.P., et al. 1990. Prediction of RNA secondary structure, including pseudoknotting, by computer simulation. Nucleic Acids Res. 183035–3044 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Akutsu, T. 2000. Dynamic programming algorithms for RNA secondary structure prediction with pseudoknots. Discrete Applied Mathematics 10445–62 [Google Scholar]
- Brown, M. and Wilson, C. 1996. RNA pseudoknot modeling using intersections of stochastic context free grammars with applications to database search. Proceedings of the 1996 Pacific Symposium on Biocomputing , pp. 109–125 [PubMed]
- Cai, L., et al. 2003. Stochastic modeling of RNA pseudoknotted structures: a grammatical approach. Bioinformatics 1966–73 [DOI] [PubMed] [Google Scholar]
- Cannone, J.J., et al. 2002. The comparative RNA web (CRW) site: an online database of comparative sequence and structure information for ribosomal, intron, and other RNAs. BMC Bioinformatics 32. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cary, R.B. and Stormo, G.D. 1995. Graph-theoretic approach to RNA modeling using comparative data. Proceedings of the Third International Conference on Intelligent Systems for Molecular Biology (ISMB'95) , Menlo Park, Calif AAAI Press, pp. 75–80 [PubMed]
- Dirks, R.M. and Pierce, N.A. 2003. A partition function algorithm for nucleic acid secondary structure including pseudoknots. J. Comput. Chem. 241664–1677 [DOI] [PubMed] [Google Scholar]
- Gultyaev, A.P. 1991. The computer simulation of RNA folding involving pseudoknot formation. Nucleic Acids Res. 192489–2494 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gultyaev, A.P., et al. 1995. The computer simulation of RNA folding pathways using a genetic algorithm. J. Mol. Biol. 25037–51 [DOI] [PubMed] [Google Scholar]
- Hofacker, I.L. 2003. Vienna RNA secondary structure server. Nucleic Acids Res. 313429–3431 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hsiao, J.Y., et al. 1992. An efficient algorithm for finding a maximum weight 2-independent set on interval graphs. Information Processing Letters 43229–235 [Google Scholar]
- Ieong, S., et al. 2003. Predicting RNA secondary structures with arbitrary pseudoknots by maximizing the number of stacking pairs. J. Comput. Biol. 10981–995 [DOI] [PubMed] [Google Scholar]
- Kolk, M.H., et al. 1998. NMR structure of a classical pseudoknot: interplay of single- and double-stranded RNA. Science 280434–438 [DOI] [PubMed] [Google Scholar]
- Lyngsø, R.B. and Pedersen, C.N. 2000. RNA pseudoknot prediction in energy-based models. J. Comput. Biol. 7409–427 [DOI] [PubMed] [Google Scholar]
- Macke, T.J., et al. 2001. RNAMotif, an RNA secondary structure definition and search algorithm. Nucleic Acids Res. 294724–4735 [DOI] [PMC free article] [PubMed] [Google Scholar]
- McPheeters, D.S., et al. 1988. Autogenous regulatory site on the bacteriophage T4 gene 32 messenger RNA. J. Mol. Biol. 201517–535 [DOI] [PubMed] [Google Scholar]
- Nateri, A.S., et al. 2002. Terminal RNA replication elements in human parechovirus 1. J. Virol. 7613116–13122 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pleij, C.W. 1990. Pseudoknots: a new motif in the RNA game. TIBS 15143–147 [DOI] [PubMed] [Google Scholar]
- Pleij, C.W. and Bosch, L. 1989. RNA pseudoknots: structure, detection, and prediction. Methods Enzymol. 180289–303 [DOI] [PubMed] [Google Scholar]
- Pleij, C.W.A. 1994. RNA pseudoknots. Curr. Opin. Struct. Biol. 4337–344 [Google Scholar]
- Reeder, J. and Giegerich, R. 2004. Design, implementation and evaluation of a practical pseudoknot folding algorithm based on thermodynamics. BMC Bioinformatics 5104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rietveld, K., et al. 1982. The tRNA-like structure at the 3′ terminus of turnip yellow mosaic virus RNA: differences and similarities with canonical tRNA. Nucleic Acids Res. 101929–1946 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rivas, E. and Eddy, S. 1999. A dynamic programming algorithm for RNA structure prediction including pseudoknots. J. Mol. Biol. 2852053–2068 [DOI] [PubMed] [Google Scholar]
- Ruan, J., et al. 2004. An iterated loop matching approach to the prediction of RNA secondary structures with pseudoknots. Bioinformatics 2058–66 [DOI] [PubMed] [Google Scholar]
- Shapiro, B.A., et al. 2001. The massively parallel genetic algorithm for RNA folding: MIMD implementation and population variation. Bioinformatics 17137–148 [DOI] [PubMed] [Google Scholar]
- Shapiro, B.S. and Wu, J.C. 1997. Predicting RNA H-type pseudoknots with the massively parallel genetic algorithm. CABIOS 13459–471 [DOI] [PubMed] [Google Scholar]
- Tabaska, J.E., et al. 1998. An RNA folding method capable of identifying pseudoknots and base triples. Bioinformatics 14691–699 [DOI] [PubMed] [Google Scholar]
- Tahi, F., et al. 2003. A fast algorithm for RNA secondary structure prediction including pseudoknots. Proceedings of the Third IEEE Symposium on Bioinformatics and Bioengineering (BIBE 2003) , Los Alamitos, CA IEEE, pp. 11–17
- ten Dam, E.B., et al. 1992. Structural and functional aspects of RNA pseudoknots. Biochemistry 3111665–11676 [DOI] [PubMed] [Google Scholar]
- Tsai, Y.T., et al. 2004. MuSiC: a tool for multiple sequence alignment with constraints. Bioinformatics 202309–2311 [DOI] [PubMed] [Google Scholar]
- Tuerk, C., et al. 1992. RNA pseudoknots that inhibit human immunodeficiency virus type 1 reverse transcriptase. Proc. Natl Acad. Sci. USA 896988–6992 [DOI] [PMC free article] [PubMed] [Google Scholar]
- van Batenburg, F.H., et al. 1995. An APL-programmed genetic algorithm for the prediction of RNA secondary structure. J. Theor. Biol. 174269–280 [DOI] [PubMed] [Google Scholar]
- van Batenburg, F.H., et al. 2001. PseudoBase: structural information on RNA pseudoknots. Nucleic Acids Res. 29194–195 [DOI] [PMC free article] [PubMed] [Google Scholar]
- van Batenburg, F.H., et al. 2000. PseudoBase: a database with RNA pseudoknots. Nucleic Acids Res. 28201–204 [DOI] [PMC free article] [PubMed] [Google Scholar]
- van Belkum, A., et al. 1985. Five pseudoknots are present at the 204 nucleotides long 3′ noncoding region of tobacco mosaic virus RNA. Nucleic Acids Res. 137673–7686 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Williams, G.D., et al. 1999. A phylogenetically conserved hairpin-type 39 untranslated region pseudoknot functions in coronavirus RNA replication. J. Virol. 738349–8355 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zuker, M. 2003. Mfold web server for nucleic acid folding and hybridization prediction. Nucleic Acids Res. 313406–3415 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zuker, M. and Sankoff, D. 1984. RNA secondary structure and their prediction. Bull. Math. Biol. 46591–621 [Google Scholar]
- Zuker, M. and Stiegler, P. 1981. Optimal computer folding of large RNA sequences using thermodynamics and auxiliary information. Nucleic Acids Res. 9133–148 [DOI] [PMC free article] [PubMed] [Google Scholar]